Portable NIR Spectroscopy Combined with Machine Learning for Kiwi Ripeness Classification: An Approach to Precision Farming
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Data Collection
2.3. Soluble Solids Content and Firmness Analysis on Kiwifruit
2.4. Data Analysis
2.4.1. Development of a Predictive Model for Soluble Solids Content and Firmness
Data Preprocessing
Performance Analysis of the Prediction Model
2.4.2. Development of a Classification Model for Fruit Ripeness Assessment
Linear Discriminant Analysis (LDA)
Decision Trees (DTs)
Artificial Neural Network (ANN)
Support Vector Machine (SVM)
Performance Analysis of the Classification Model
3. Results and Discussion
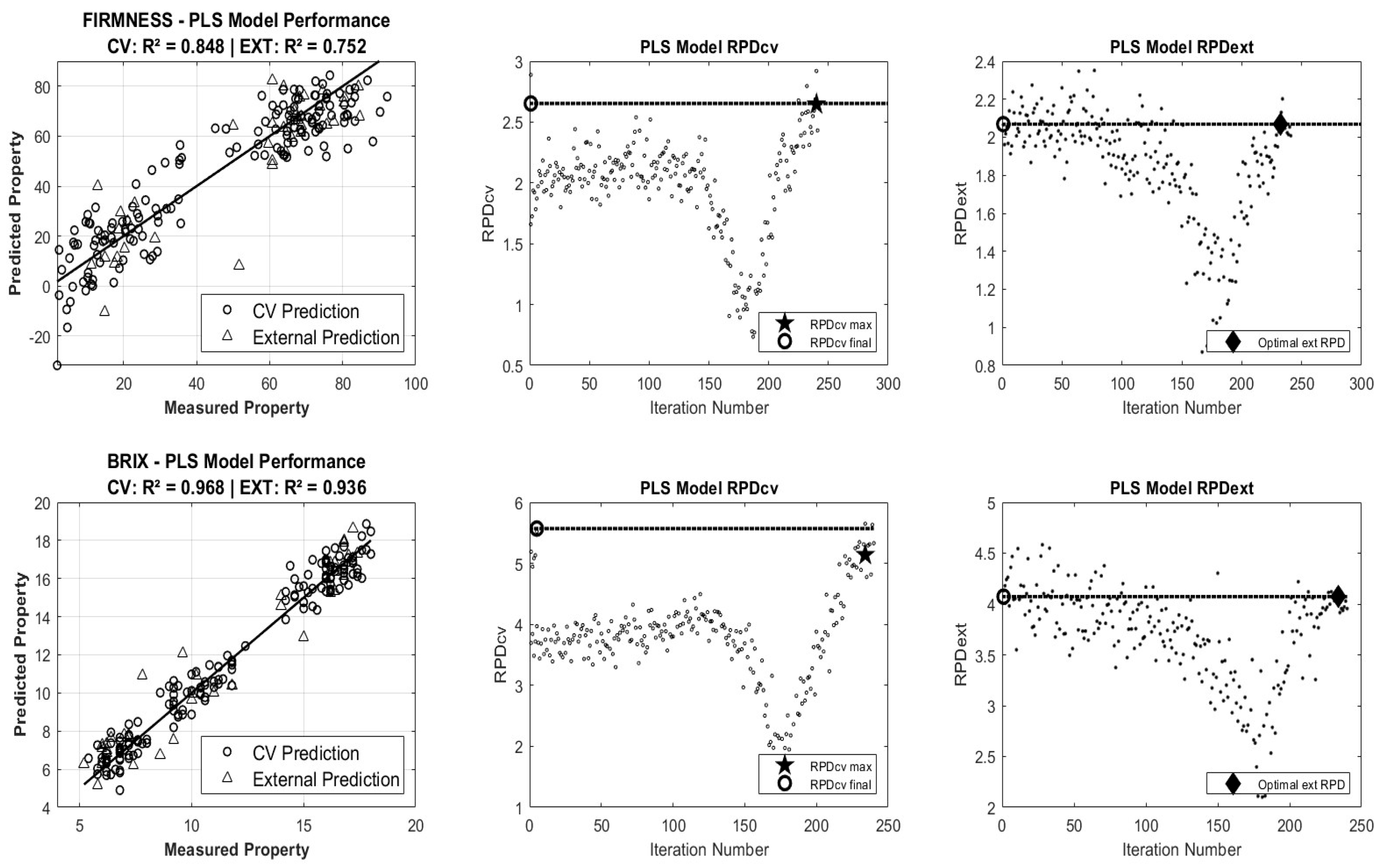
3.1. Firmness and SSC Prediction Results
3.1.1. Partial Least Squares Regression (PLSR) Model Accuracy
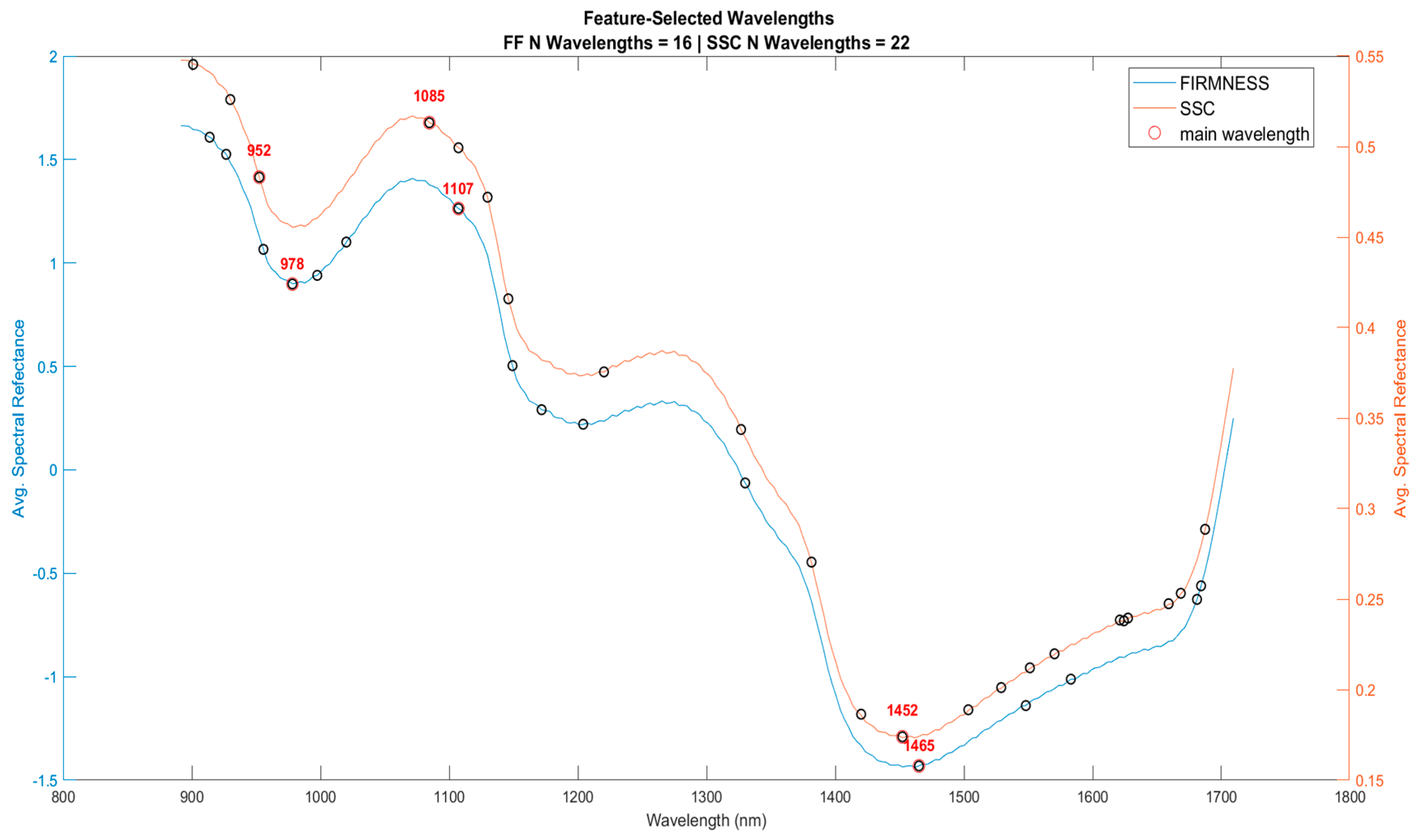
3.1.2. Feature Extraction
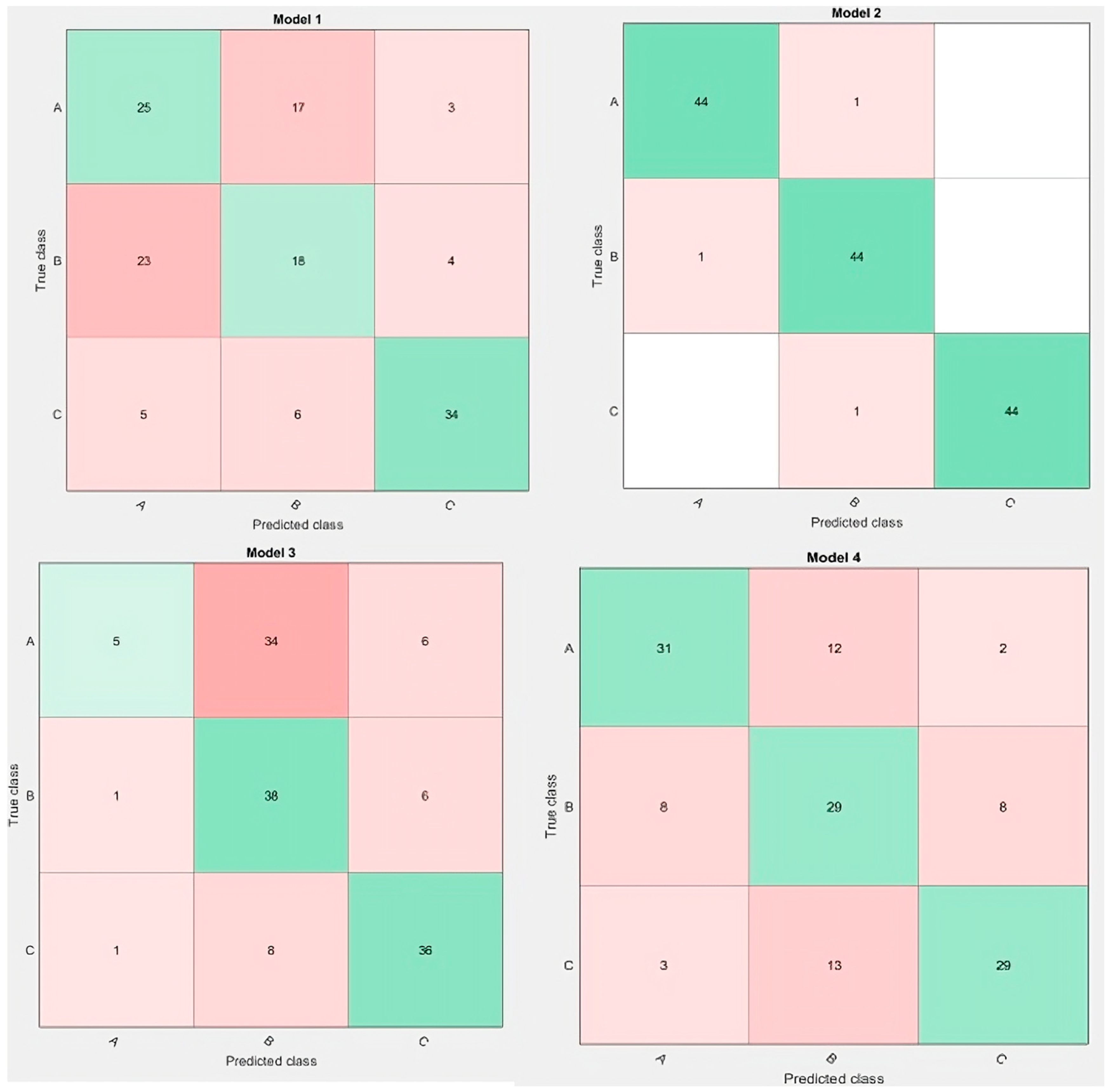
3.2. Ripeness Classification Results
3.2.1. ML Models’ Accuracy
3.2.2. Best ML Models’ Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, J.-E.; Kim, M.-J.; Lee, B.-Y.; Hwan, L.J.; Yang, H.-E.; Kim, M.S.; Hwang, I.G.; Jeong, C.S.; Mo, C. Evaluating Ripeness in Post-Harvest Stored Kiwifruit Using VIS-NIR Hyperspectral Imaging. Postharvest Biol. Technol. 2025, 225, 113496. [Google Scholar] [CrossRef]
- Prasad, K.; Jacob, S.; Siddiqui, M.W. Fruit Maturity, Harvesting, and Quality Standards. In Preharvest Modulation of Postharvest Fruit and Vegetable Quality; Academic Press: Cambridge, MA, USA, 2018; pp. 41–69. [Google Scholar] [CrossRef]
- Gupta, A.K.; Koch, P.; Yumnam, M.; Medhi, M.; Madufor, N.J.; Opara, U.L.; Mishra, P. Biosensors Involved in Fruit and Vegetable Processing Industries. In Biosensors in Food Safety and Quality; CRC Press: Boca Raton, FL, USA, 2022; pp. 111–134. [Google Scholar]
- Li, M.; Pullanagari, R.; Yule, I.; East, A. Segregation of ‘Hayward’ Kiwifruit for Storage Potential Using Vis-NIR Spectroscopy. Postharvest Biol. Technol. 2022, 189, 111893. [Google Scholar] [CrossRef]
- Pandiselvam, R.; Prithviraj, V.; Manikantan, M.R.; Kothakota, A.; Rusu, A.V.; Trif, M.; Mousavi Khaneghah, A. Recent Advancements in NIR Spectroscopy for Assessing the Quality and Safety of Horticultural Products: A Comprehensive Review. Front. Nutr. 2022, 9, 973457. [Google Scholar] [CrossRef]
- Birth, G.; Norris, K. Instrument Using Light Transmittance for Nondestructive Measurement of Fruit Maturity. Food Technol. 1958, 12, 592–595. [Google Scholar]
- Li, B.; Lecourt, J.; Bishop, G. Advances in Non-Destructive Early Assessment of Fruit Ripeness towards Defining Optimal Time of Harvest and Yield Prediction—A Review. Plants 2018, 7, 3. [Google Scholar] [CrossRef]
- Hu, R.; Zhang, L.; Yu, Z.; Zhai, Z.; Technology, R. Optimization of Soluble Solids Content Prediction Models in ‘Hami’melons by Means of Vis-NIR Spectroscopy and Chemometric Tools. Infrared Phys. Technol. 2019, 102, 102999. [Google Scholar] [CrossRef]
- Amoriello, T.; Ciorba, R.; Ruggiero, G.; Masciola, F.; Scutaru, D.; Ciccoritti, R. Vis/NIR Spectroscopy and Vis/NIR Hyperspectral Imaging for Non-Destructive Monitoring of Apricot Fruit Internal Quality with Machine Learning. Foods 2025, 14, 196. [Google Scholar] [CrossRef]
- Xia, Y.; Huang, W.; Fan, S.; Li, J.; Technology, L. Effect of Spectral Measurement Orientation on Online Prediction of Soluble Solids Content of Apple Using Vis/NIR Diffuse Reflectance. Infrared Phys. Technol. 2019, 97, 467–477. [Google Scholar] [CrossRef]
- Xiao, Y.; Li, C.; Jin, C.; Luo, J.; Qi, H.; Zhang, C. Detection of Soluble Solid Content in Citrus Fruit Using Near-Infrared Spectroscopy with Machine Learning Regression: An Exploration of the Influence of Sampling Positions. J. Food Compos. Anal. 2025, 142, 107554. [Google Scholar] [CrossRef]
- Qiao, Y.; Wang, C.; Zhu, W.; Sun, L.; Bai, J.; Zhou, R.; Zhu, Z.; Cai, J. Online Assessment of Soluble Solids Content in Strawberries Using a Developed Vis/NIR Spectroscopy System with a Hanging Grasper. Food Chem. 2025, 478, 143671. [Google Scholar] [CrossRef]
- Ciccoritti, R.; Paliotta, M.; Amoriello, T.; Carbone, K. FT-NIR Spectroscopy and Multivariate Classification Strategies for the Postharvest Quality of Green-Fleshed Kiwifruit Varieties. Sci. Hortic. 2019, 257, 108622. [Google Scholar] [CrossRef]
- Walsh, K.B.; McGlone, V.A.; Han, D.H. The Uses of near Infra-Red Spectroscopy in Postharvest Decision Support: A Review. Postharvest Biol. Technol. 2020, 163, 111139. [Google Scholar] [CrossRef]
- Benelli, A.; Cevoli, C.; Fabbri, A.; Ragni, L. Ripeness Evaluation of Kiwifruit by Hyperspectral Imaging. Biosyst. Eng. 2022, 223, 42–52. [Google Scholar] [CrossRef]
- Fatchurrahman, D.; Nosrati, M.; Amodio, M.L.; Chaudhry, M.M.A.; de Chiara, M.L.V.; Mastrandrea, L.; Colelli, G. Comparison Performance of Visible-NIR and Near-Infrared Hyperspectral Imaging for Prediction of Nutritional Quality of Goji Berry (Lycium barbarum L.). Foods 2021, 10, 1676. [Google Scholar] [CrossRef]
- Walsh, K.B.; Blasco, J.; Zude-Sasse, M.; Sun, X. Visible-NIR ‘point’spectroscopy in Postharvest Fruit and Vegetable Assessment: The Science behind Three Decades of Commercial Use. Postharvest Biol. Technol. 2020, 168, 111246. [Google Scholar] [CrossRef]
- Afonso, A.M.; Antunes, M.D.; Cruz, S.; Cavaco, A.M.; Guerra, R. Non-Destructive Follow-up of ‘Jintao’ Kiwifruit Ripening through VIS-NIR Spectroscopy—Individual vs. Average Calibration Model’s Predictions. Postharvest Biol. Technol. 2022, 188, 111895. [Google Scholar] [CrossRef]
- Cevoli, C.; Iaccheri, E.; Fabbri, A.; Ragni, L. Data Fusion of FT-NIR Spectroscopy and Vis/NIR Hyperspectral Imaging to Predict Quality Parameters of Yellow Flesh “Jintao” Kiwifruit. Biosyst. Eng. 2024, 237, 157–169. [Google Scholar] [CrossRef]
- Xia, Y.; Zhang, W.; Che, T.; Hu, J.; Cao, S.; Liu, W.; Kang, J.; Tang, W.; Li, H. Comparison of Diffuse Reflectance and Diffuse Transmittance Vis/NIR Spectroscopy for Assessing Soluble Solids Content in Kiwifruit Coupled with Chemometrics. Appl. Sci. 2024, 14, 10001. [Google Scholar] [CrossRef]
- Wan, C.; Yue, R.; Li, Z.; Fan, K.; Chen, X.; Li, F. Prediction of Kiwifruit Sweetness with Vis/NIR Spectroscopy Based on Scatter Correction and Feature Selection Techniques. Appl. Sci. 2024, 14, 4145. [Google Scholar] [CrossRef]
- Li, M.; Pullanagari, R.R.; Pranamornkith, T.; Yule, I.J.; East, A.R. Quantitative Prediction of Post Storage ‘Hayward’ Kiwifruit Attributes Using at Harvest Vis-NIR Spectroscopy. J. Food Eng. 2017, 202, 46–55. [Google Scholar] [CrossRef]
- Torkashvand, A.M.; Ahmadi, A.; Nikravesh, N.L. Prediction of Kiwifruit Firmness Using Fruit Mineral Nutrient Concentration by Artificial Neural Network (ANN) and Multiple Linear Regressions (MLR). J. Integr. Agric. 2017, 16, 1634–1644. [Google Scholar] [CrossRef]
- Xiao, Y.; Yuan, D.; Zou, Z.; Li, M.; Wang, Q.; Zhen, J.; Wang, H.; Ku, Q.; Jiang, J.; Xu, L. The Prediction of Kiwi Quality Attributes Based on Multi-Source Data Fusion Comprehensive Analysis Model Using HSI and FHSI. J. Food Compos. Anal. 2025, 144, 107645. [Google Scholar] [CrossRef]
- Shang, J.; Tan, T.; Feng, S.; Li, Q.; Huang, R.; Meng, Q. Quality Attributes Prediction and Maturity Discrimination of Kiwifruits by Hyperspectral Imaging and Chemometric Algorithms. J. Food Process Eng. 2023, 46, e14348. [Google Scholar] [CrossRef]
- Qin, L.; Zhang, J.; Stevan, S.; Xing, S.; Zhang, X. Intelligent Flexible Manipulator System Based on Flexible Tactile Sensing (IFMSFTS) for Kiwifruit Ripeness Classification. J. Sci. Food Agric. 2024, 104, 273–285. [Google Scholar] [CrossRef]
- Hu, W.; Sun, D.-W.; Blasco, J. Rapid Monitoring 1-MCP-Induced Modulation of Sugars Accumulation in Ripening ‘Hayward’ Kiwifruit by Vis/NIR Hyperspectral Imaging. Postharvest Biol. Technol. 2017, 125, 168–180. [Google Scholar] [CrossRef]
- Sarkar, S.; Basak, J.K.; Moon, B.E.; Kim, H.T. A Comparative Study of PLSR and SVM-R with Various Preprocessing Techniques for the Quantitative Determination of Soluble Solids Content of Hardy Kiwi Fruit by a Portable Vis/NIR Spectrometer. Foods 2020, 9, 1078. [Google Scholar] [CrossRef] [PubMed]
- Geladi, P.; MacDougall, D.; Martens, H. Linearization and Scatter-Correction for near-Infrared Reflectance Spectra of Meat. Appl. Spectrosc. 1985, 39, 491–500. [Google Scholar] [CrossRef]
- Candolfi, A.; De Maesschalck, R.; Jouan-Rimbaud, D.; Hailey, P.A.; Massart, D.L. The Influence of Data Pre-Processing in the Pattern Recognition of Excipients near-Infrared Spectra. J. Pharm. Biomed. Anal. 1999, 21, 115–132. [Google Scholar] [CrossRef]
- Steinier, J.; Termonia, Y.; Deltour, J. Smoothing and Differentiation of Data by Simplified Least Square Procedure. Anal. Chem. 1972, 44, 1906–1909. [Google Scholar] [CrossRef]
- Altieri, G.; Genovese, F.; Tauriello, A.; Di Renzo, G.C. Models to Improve the Non-Destructive Analysis of Persimmon Fruit Properties by VIS/NIR Spectrometry. J. Sci. Food Agric. 2017, 97, 5302–5310. [Google Scholar] [CrossRef]
- Ghazal, S.; Qureshi, W.S.; Khan, U.S.; Iqbal, J.; Rashid, N.; Tiwana, M.I. Analysis of Visual Features and Classifiers for Fruit Classification Problem. Comput. Electron. Agric. 2021, 187, 106267. [Google Scholar] [CrossRef]
- Houetohossou, S.C.A.; Houndji, V.R.; Hounmenou, C.G.; Sikirou, R.; Kakaï, R.L.G. Deep Learning Methods for Biotic and Abiotic Stresses Detection and Classification in Fruits and Vegetables: State of the Art and Perspectives. Artif. Intell. Agric. 2023, 9, 46–60. [Google Scholar] [CrossRef]
- Gill, H.S.; Murugesan, G.; Mehbodniya, A.; Sekhar Sajja, G.; Gupta, G.; Bhatt, A. Fruit Type Classification Using Deep Learning and Feature Fusion. Comput. Electron. Agric. 2023, 211, 107990. [Google Scholar] [CrossRef]
- Cheepsomsong, T.; Phuangsombut, A.; Phuangsombut, K.; Sangwanangkul, P.; Siriphanich, J.; Terdwongworakul, A. Evaluation of Durian Maturity Using Short-Range, Coded-Light, Three-Dimensional Scanner with Machine Learning. Postharvest Biol. Technol. 2025, 222, 113342. [Google Scholar] [CrossRef]
- McGlone, V.; Technology, S. Firmness, Dry-Matter and Soluble-Solids Assessment of Postharvest Kiwifruit by NIR Spectroscopy. Postharvest Biol. Technol. 1998, 13, 131–141. [Google Scholar] [CrossRef]
- Li, H.; Pidakala, P.; Billing, D.; Technology, J. Kiwifruit Firmness: Measurement by Penetrometer and Non-Destructive Devices. Postharvest Biol. Technol. 2016, 120, 127–137. [Google Scholar] [CrossRef]
- Khatun, M.S.; Al Masum, A.; Islam, M.H.; Ashik-E-Rabbani, M.; Rahman, A. Short Wave-near Infrared Spectroscopy for Predicting Soluble Solid Content in Intact Mango with Variable Selection Algorithms and Chemometric Model. J. Food Compos. Anal. 2024, 136, 106745. [Google Scholar] [CrossRef]
- Yu, Y.; Yao, M. A Portable NIR System for Nondestructive Assessment of SSC and Firmness of Nanguo Pears. LWT 2022, 167, 113809. [Google Scholar] [CrossRef]
- Nicolaï, B.M.; Beullens, K.; Bobelyn, E.; Peirs, A.; Saeys, W.; Theron, K.I.; Lammertyn, J. Nondestructive Measurement of Fruit and Vegetable Quality by Means of NIR Spectroscopy: A Review. Postharvest Biol. Technol. 2007, 46, 99–118. [Google Scholar] [CrossRef]
- Zhu, H.; Chu, B.; Fan, Y.; Tao, X.; Yin, W.; He, Y. Hyperspectral Imaging for Predicting the Internal Quality of Kiwifruits Based on Variable Selection Algorithms and Chemometric Models. Sci. Rep. 2017, 7, 7845. [Google Scholar] [CrossRef]
- Fu, X.; Ying, Y.; Lu, H.; Xu, H.; Yu, H. FT-NIR Diffuse Reflectance Spectroscopy for Kiwifruit Firmness Detection. Sens. Instrum. Food Qual. Saf. 2007, 1, 29–35. [Google Scholar] [CrossRef]
- Worasawate, D.; Sakunasinha, P.; Chiangga, S. Automatic Classification of the Ripeness Stage of Mango Fruit Using a Machine Learning Approach. AgriEngineering 2022, 4, 32–47. [Google Scholar] [CrossRef]
- Sarakum, T.; Sukpancharoen, S. Non-Destructive Sweetness Classification of Khao Tang Kwa Pomelos Using Machine Learning with Acoustic and Image Processing. J. Food Compos. Anal. 2025, 142, 107385. [Google Scholar] [CrossRef]
| Models | Abbreviation/Details | |
|---|---|---|
| Prediction task | Partial Least Squares Regression (PLSR) | Raw-PLS |
| Standard Normal Variate + PLSR | SNV-PLS | |
| Multiplicative Scatter Correction + PLSR | MSC-PLS | |
| Savitzky–Golay 1st derivative + PLSR | SG1-PLS | |
| Savitzky–Golay 2nd derivative + PLSR | SG2-PLS | |
| Classification task | Linear Discriminant Analysis (LDA) | |
| Decision Trees (DT) |
| |
| Artificial Neural Network (ANN) | 2 hidden layers, 20 neurons per layer; odd-odd or even-even configuration; Levenberg–Marquardt training. | |
| Support Vector Machine (SVM) | Kernels = Radial Basis Function (RBF), Polynomial, Gaussian, Pearson Universal; Regularization parameters: C = {0.01, 0.1, 1, 10, 100}, γ = {0.01, 0.1, 1} |
| Parameter | Model | R2CV | RMSECV | RPDCV | Outliers | N° Samples | Selected Wavelength | R2P | RMSEP | RPDP |
|---|---|---|---|---|---|---|---|---|---|---|
| Firmness | Raw-PLS | 0.856 (0.021) | 10.451 (0.752) | 2.66 (0.18) | 8 | 152 | 30 | 0.728 (0.023) | 12.854 (0.533) | 1.95 (0.08) |
| SNV-PLS | 0.856 (0.014) | 10.501 (0.524) | 2.65 (0.13) | 8 | 152 | 16 | 0.749 (0.011) | 12.342 (0.274) | 2.02 (0.05) | |
| MSC-PLS | 0.872 (0.016) | 9.795 (0.596) | 2.82 (0.17) | 8 | 152 | 22 | 0.662 (0.013) | 14.336 (0.276) | 1.74 (0.03) | |
| SG1-PLS | 0.853 (0.020) | 10.463 (0.697) | 2.64 (0.17) | 8 | 152 | 23 | 0.562 (0.022) | 16.312 (0.415) | 1.53 (0.04) | |
| SG2-PLS | 0.880 (0.015) | 9.462 (0.579) | 2.92 (0.17) | 8 | 152 | 25 | 0.625 (0.014) | 15.088 (0.278) | 1.66 (0.03) | |
| SSC | Raw-PLS | 0.967 (0.004) | 0.753 (0.042) | 5.57 (0.31) | 4 | 156 | 22 | 0.935 (0.003) | 1.142 (0.022) | 3.98 (0.08) |
| SNV-PLS | 0.964 (0.004) | 0.781 (0.046) | 5.33 (0.31) | 0 | 160 | 28 | 0.918 (0.005) | 1.289 (0.039) | 3.53 (0.11) | |
| MSC-PLS | 0.965 (0.004) | 0.770 (0.048) | 5.37 (0.34) | 4 | 156 | 23 | 0.929 (0.003) | 1.194 (0.027) | 3.81 (0.09) | |
| SG1-PLS | 0.968 (0.004) | 0.744 (0.042) | 5.60 (0.32) | 0 | 160 | 22 | 0.934 (0.003) | 1.151 (0.022) | 3.95 (0.08) | |
| SG2-PLS | 0.962 (0.004) | 0.803 (0.042) | 5.18 (0.26) | 3 | 157 | 17 | 0.931 (0.002) | 1.177 (0.017) | 3.86 (0.06) |
| Model | Parameters | Selected Wavelengths |
|---|---|---|
| Raw-PLS | SSC | 901.00, 929.90, 952.41, 1084.58, 1107.19, 1129.81, 1145.96, 1220.28, 1326.78, 1381.52, 1420.09, 1452.17, 1503.38, 1528.92, 1551.23, 1570.33, 1621.09, 1624.25, 1627.42, 1659.01, 1668.46, 1687.35 |
| SNV-PLS | FF | 913.84, 926.69, 955.63, 978.16, 997.48, 1020.04, 1107.19, 1149.19, 1171.81, 1204.12, 1330.00, 1464.99, 1548.05, 1583.04, 1681.06, 1684.20 |
| Model | LDA | ANN | DTs | SVM | |||||
|---|---|---|---|---|---|---|---|---|---|
| Method | J48 | CART | LMT | RBF | Polynomial | Gaussian | Pearson | ||
| Performance | |||||||||
| R2 | 0.48 | 0.95 | 0.48 | 0.50 | 0.48 | 0.65 | 0.59 | 0.61 | 0.57 |
| RMSE | 0.46 | 0.08 | 0.46 | 0.45 | 0.47 | 0.35 | 0.39 | 0.38 | 0.42 |
| MAE | 0.40 | 0.03 | 0.41 | 0.38 | 0.42 | 0.28 | 0.31 | 0.29 | 0.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altieri, G.; Laveglia, S.; Rashvand, M.; Genovese, F.; Matera, A.; Mininni, A.N.; Calabritto, M.; Di Renzo, G.C. Portable NIR Spectroscopy Combined with Machine Learning for Kiwi Ripeness Classification: An Approach to Precision Farming. Appl. Sci. 2025, 15, 6233. https://doi.org/10.3390/app15116233
Altieri G, Laveglia S, Rashvand M, Genovese F, Matera A, Mininni AN, Calabritto M, Di Renzo GC. Portable NIR Spectroscopy Combined with Machine Learning for Kiwi Ripeness Classification: An Approach to Precision Farming. Applied Sciences. 2025; 15(11):6233. https://doi.org/10.3390/app15116233
Chicago/Turabian StyleAltieri, Giuseppe, Sabina Laveglia, Mahdi Rashvand, Francesco Genovese, Attilio Matera, Alba Nicoletta Mininni, Maria Calabritto, and Giovanni Carlo Di Renzo. 2025. "Portable NIR Spectroscopy Combined with Machine Learning for Kiwi Ripeness Classification: An Approach to Precision Farming" Applied Sciences 15, no. 11: 6233. https://doi.org/10.3390/app15116233
APA StyleAltieri, G., Laveglia, S., Rashvand, M., Genovese, F., Matera, A., Mininni, A. N., Calabritto, M., & Di Renzo, G. C. (2025). Portable NIR Spectroscopy Combined with Machine Learning for Kiwi Ripeness Classification: An Approach to Precision Farming. Applied Sciences, 15(11), 6233. https://doi.org/10.3390/app15116233








