A Cascading Delphi Method-Based FMEA Risk Assessment Framework for Surgical Instrument Design: A Case Study of a Fetoscope

Featured Application

Risk assessment for medical device design.

Abstract

Failure Mode and Effect Analysis (FMEA) is crucial for identifying risk reduction opportunities in design. This study aims to aid in the design of sophisticated medical devices by setting guidelines and addressing weaknesses in data collection and risk priority numbers (RPNs). This is achieved by developing an FMEA framework with potential efficiency and efficacy benefits for design engineers, surgeons and patients. The FMEA framework covered risk analysis and risk evaluation by integrating a cascading Delphi method to address data collection and Multi-Criteria Decision-Making (MCDM) technique to address RPN calculations. This study involved the design of a flexible fetoscope for minimally invasive fetal intervention, analyzing and evaluating risks. The cascading FMEA framework had two stages for data collection, namely risk identification by individual interview and risk evaluation by individual email. The cascading Delphi FMEA framework with MCDM identified the potential risks for the mother at the tip (risk score = 0.927) and subsequent risks such as debris loss (risk score = 0.896), material degradation (risk score = 0.896), and glue dislodging (risk score = 0.896) as critical issues. By identifying failure modes early, medical device designers can better mitigate risks during the initial design stages.

1. Introduction

Patient safety is the most important priority in the intricate and resource-intensive process of designing medical devices [1,2,3]. Finding safety flaws later in the development process can cause a significant impact on the structural integrity of the device, worker safety, and patient welfare [4,5]. Risk assessment is critical in the design and development process of advanced medical devices to improve patient safety and reduce adverse medical events [1,2,3]. Implementing risk analysis during the initial design stage can reduce the cost and operational complexities associated with subsequent device redesign [4]. Risk assessment should be applied during the initial conceptual and design stages [6].

Failure Mode and Effect Analysis (FMEA) has been used for the medical device industry to analyze risk [7], but its use within the medical device design paradigm is still intrinsically complicated and challenging. ISO 14971 recommends FMEA as a risk assessment tool [4]. FMEA is in origin an engineering industry technique now also used to identify and analyze risks in healthcare products or equipment [8]. It has been adopted as a prospective method to reduce adverse medical events involving sophisticated equipment [9,10]. This method has been widely used both in initial design [6] and then later in the application, of medical devices and procedures [7]. This technique helps designers and engineers to understand risks by identifying and understanding the potential failure modes of the instrument or procedure [7].

The FMEA procedure is a highly effective technique relying on feedback provided by experts in a subjective approach. A multidisciplinary expert team is required to identify potential failure modes (FMs) [6]. FMEA expert team members’ dedication and agreement are crucial to an effective conclusion [11]. Attempts can be made to minimize undue subjective influences by changing from the experts’ subjective approach to a more objective one. FMEA has become increasingly popular and it is generally considered to be an appropriate and effective method for risk assessment in healthcare systems [9]. However, it has been noted to have several potential issues [12,13], two of which we consider critical: data collection and the calculation of the risk priority number (RPN).

The hazards in data collection are primarily potential group bias and time constraints. To collect data, several approaches were considered, including focus-group discussion [14], brainstorming sessions [15], interviews [16], observations, surveys [17], and related approaches [18]. Alternatively, the Delphi method has been used increasingly for collecting data [17]. The Delphi method is a sophisticated information-collecting technique that allows individuals to resolve complicated issues without having to meet in person [13,17]. The Delphi approach can handle vast amounts of data without group bias [13]. It is a group communication process designed to establish a consensus [7,13]. However, this technique has two drawbacks: it can take a long time and produce a poor response rate [17].

The RPN is calculated by multiplication of severity (S), probability of occurrence (O) and detectability (D) scores [6], with higher risk failures prioritized for corrective actions. However, several studies have raised concerns about the validity of this traditional approach, noting that multiplying three ordinal scales may distort risk rankings [19]. Furthermore, severity, occurrence, and detectability may not contribute equally—severity is typically regarded as most critical [20], while detectability is important for mitigation but generally considered less influential [20].

RPN scoring is subjective [7] and varies based on experts’ opinions [21], and this subjectivity introduces flaws such as equal weighting of S, O, and D, identical RPN values arising from different score combinations, and a failure to reflect the true relationships among factors and inherent uncertainty. In the healthcare context, FMEA struggles further with standardization and expert subjectivity. To resolve these limitations, Multi-Criteria Decision-Making (MCDM) methods, for example grey relational analysis (GRA), Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), Analytic Hierarchy Process (AHP), and fuzzy logic, have been proposed [22].

A promising avenue for future research in this domain also involves an exploration of MCDM techniques aimed at enhancing the reliability of the RPN calculation [23]. To obtain the highest scores (quantitative data) of possible failure causes based on risk scores and severity score, MCDM was applied for calculating and prioritizing the risk scores to overcome traditional RPN calculation. In addition, Pareto theory and severity score were considered in selecting risk scores for corrective actions.

Fetoscopes are used to treat, among other conditions, twin-to-twin transfusion syndrome (TTTS). An unbalanced placental vascularization in the amniotic sacs of monochorionic (shared placenta) twins is one of the leading causes of mortality in the womb of monochorionic twins, especially through TTTS [24,25]. In severe cases of TTTS, fetoscopic laser ablation (FLA) has provided successful outcomes. This procedure, under ultrasound guidance, has become the gold-standard treatment over the last decade [24,25,26,27]. However, there are several issues that have arisen due to poor visibility, a limited field of view, the varying position of the placenta, the identification of blood vessels, occasional bleeding, and poor image quality [28,29,30]. Consequently, a new design of a fetoscope becomes a challenge, and risk assessment is necessary.

Currently, no standard method exists for assessing the risk of surgical instruments. The study aimed to propose a cascading Delphi framework designed to overcome FMEA limitations, specifically regarding data collection and RPN calculation using a case study of flexible fetoscope. The proposed framework systematically collects reliable expert insights.

2. Materials and Methods

The study proposed a framework to identify and evaluate the potential failure modes of the surgical instrument, the flexible fetoscope designed by an engineering team at KU Leuven, Belgium. We improved data-gathering for FMEA, using a cascading Delphi method, RPN calculation, and applying MCDM and uncertainty theory. The cascading Delphi framework provides qualitative and quantitative data. Content analysis techniques were examined for qualitative data including potential failure modes, potential failure effects, potential failure causes, and detectability.

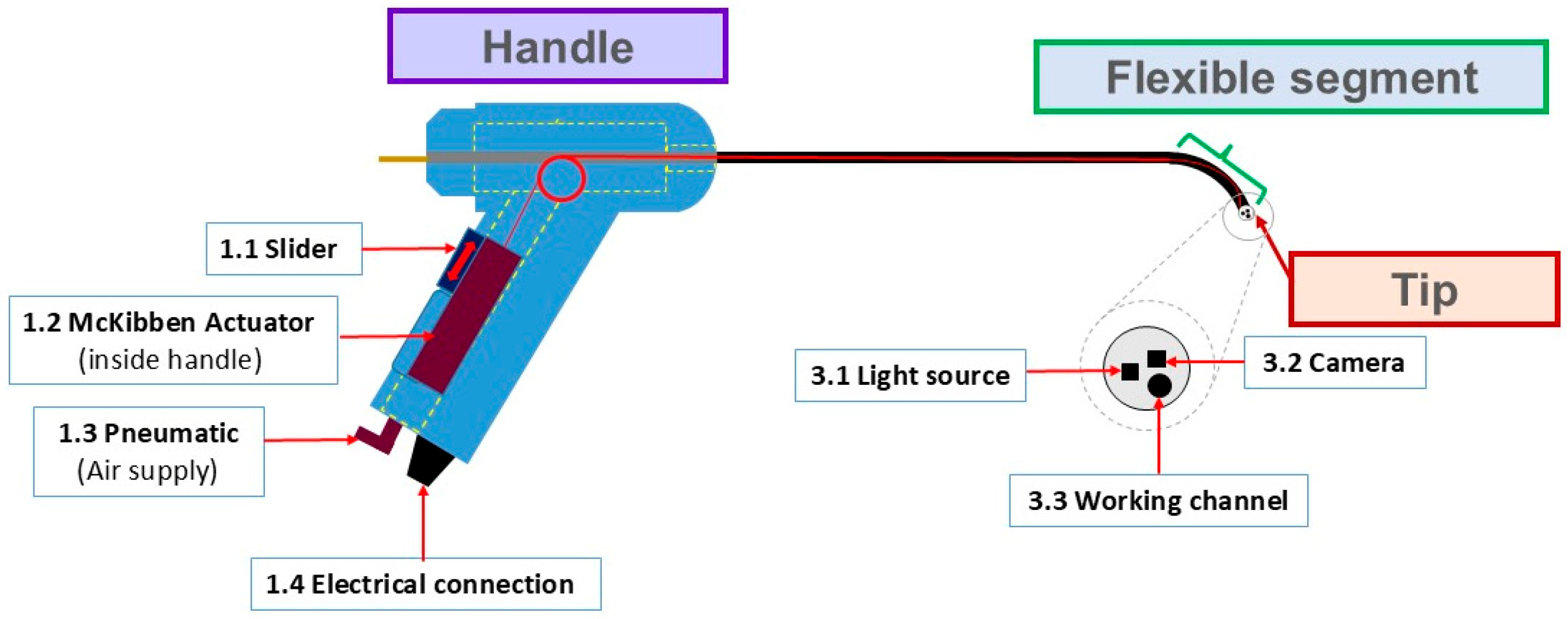
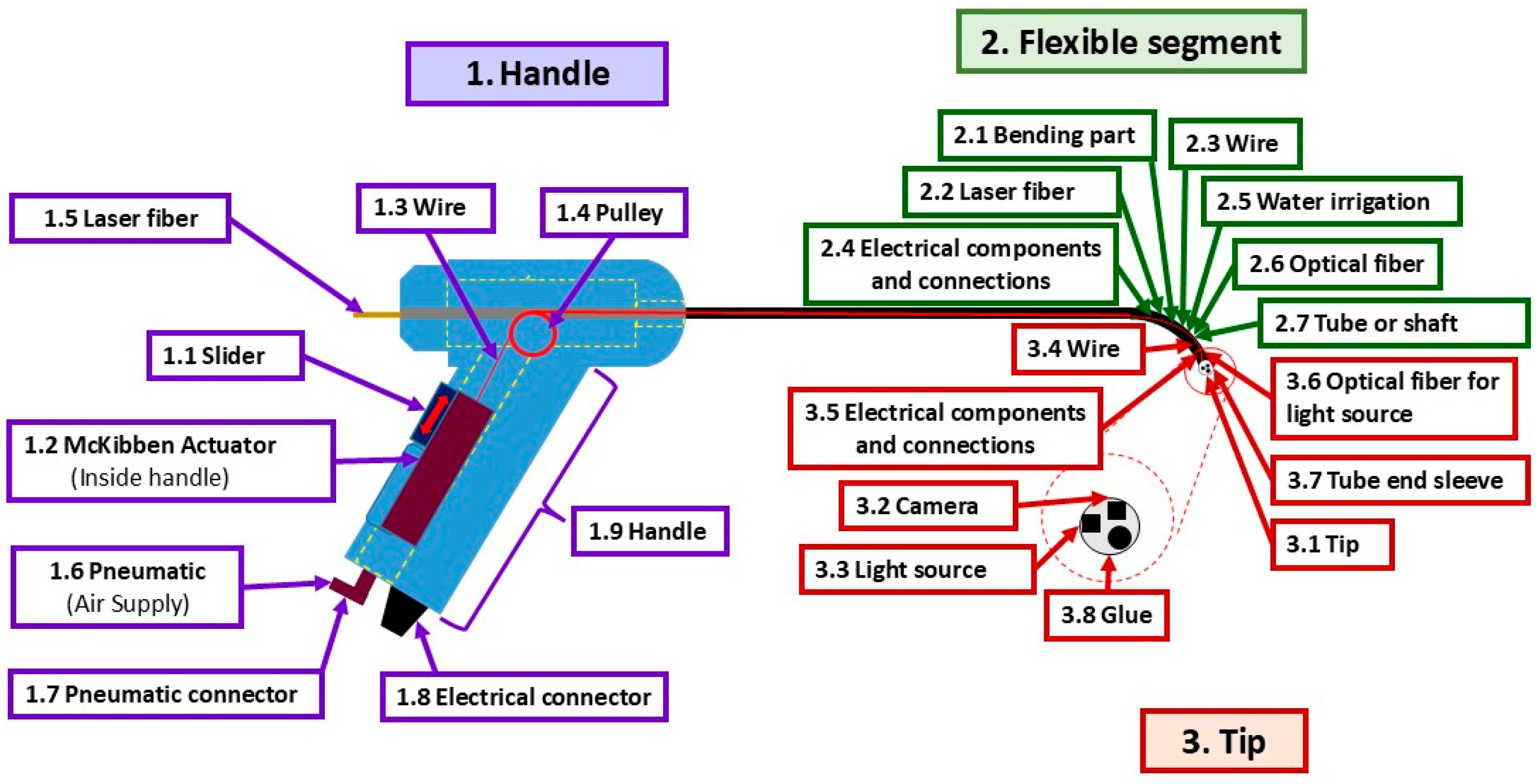
2.1. Flexible Fetoscope

The proposed flexible fetoscope consists of 3 main parts: a handle, a flexible segment, and the tip, as shown in Figure 1. The handle is an ergonomically designed non-conductive pistol grip with a slider to operate the flexible segment. The slider is moved by the surgeon’s thumb to bend the flexible segment. A McKibben actuator inside the handle is operated by pneumatic pressure from an external air supply. A wire transmits the force from the McKibben actuator to bend the flexible segment.

An electrical connection for the actuator and camera is set on the end of the handle. The laser fiber and water irrigation systems are as in the current version. The flexible segment is 3 cm long, has a 3 mm diameter, and can bend up to 90°. The tip contains three channels for a light source, a camera, and the working channel. The light-emitting diode (LED) light source is external to the fetoscope, and the light is transmitted by optical fiber to the tip. The camera is of better quality than the current versions, with higher resolution and better image quality. The working channel carries water irrigation and the laser fiber to coagulate the placental vessels. A medical-grade epoxy adhesive is used to fix and seal all components in the tip. The new parts and components of the flexible fetoscope was adapted from Ahmad et al. [28] as shown in Figure 1.

2.2. FMEA Expert Team

We initially employed purposive sampling by directly reaching out to known individuals in each target group. For obstetric surgeons, recruitment started with the head of the Fetal Therapy Center in Thailand, who then recommended other qualified surgeons from university hospitals in Thailand. This process was further supported by referrals among participants, effectively creating a limited snowball sampling framework. For engineering aspect, the head of research group working on medical device design at KU Leuven, Belgium, invited engineers who have experience in fetoscopes.

Data were collected from 11 experts, consisting of 6 engineers from KU Leuven, Belgium, and 5 obstetric surgeons from three university hospitals in Thailand. This cohort covered the essential disciplines and stakeholders such as designers, engineers, and users. Due to the need for specific knowledge and experience, snowball sampling was used in this study. Snowball sampling creates a network of participants by finding one or two participants and then asking them to identify additional experts when direct recruitment is challenging. This method is suitable for participants with specific knowledge and experience, when it is difficult to locate or contact experts on the topic.

All selected experts have knowledge of and experience with fetoscopes. The experts were asked to register by Google Forms to provide relevant personal information and work experience details. Before data collection, online initial meetings were held in two rounds for six engineers from KU Leuven and five Thai obstetric surgeons to explain the process, their roles, and the objectives of the study. Online individual interview by Zoom was used for an initial meeting and risk identification, and email conversations for subsequent rounds.

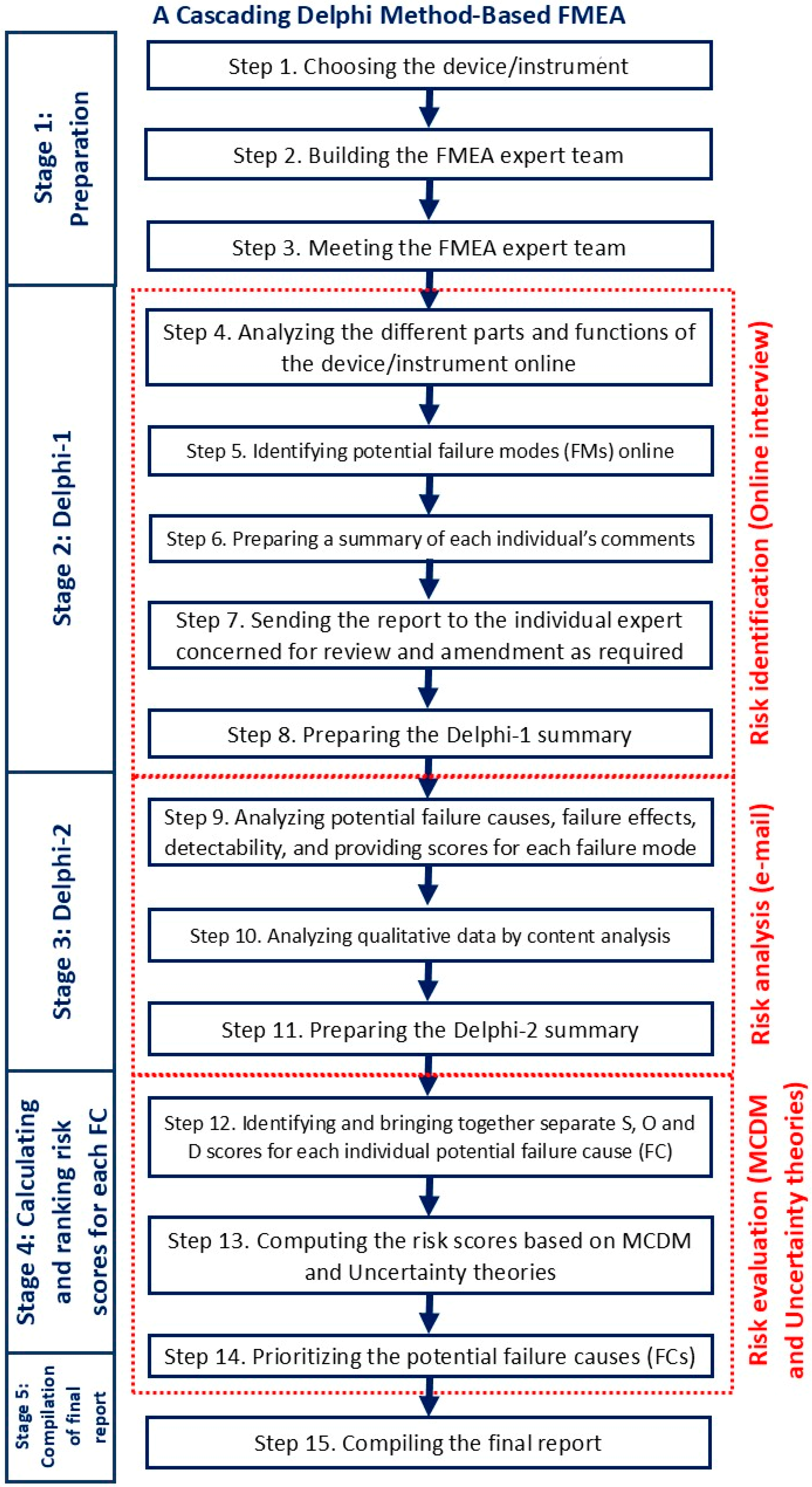
2.3. The Conceptual Framework of a Cascading Delphi Method

The framework proposed in this study was divided into five stages: preparation, Delphi-1 (risk identification), Delphi-2 (risk analysis), the calculation of S, O, and D (risk evaluation), and the compilation of a final report as presented in Figure 2. Each stage had several steps to complete the task. The conceptual framework of a cascading Delphi method approach to data collection for advanced surgical instrument, adapted from Sobaih et al. [31], as shown in Figure 2.

• Stage 1: Preparation: to set the scene for the experts

Step 1. Choosing the device/instrument: a virtual prototype of flexible fetoscope and a clear description of the instrument were explained to the expert team.

Step 2. Building the FMEA expert team: the facilitator chose participants with prior experience and knowledge of the type of instrument being studied, and willingness to provide feedback.

Step 3. Meeting the FMEA expert team: the facilitator explained the objectives, FMEA, the process and their responsibilities to participating experts.

• Stage 2: Delphi-1: to identify the relevant failure modes (FMs)

Step 4. Analyzing the different parts and functions of the device/instrument online: the participants were presented with the figure of flexible fetoscope and an open-ended question (“What are the new parts of the fetoscope, analyzed by function?”) during an individual online interview.

Step 5. Identifying potential failure modes (FMs) online: the experts were asked an open-ended question (“What could possibly go wrong with which parts of the fetoscope in terms of the patients and fetuses?”) about the potential failure modes. Potential failure modes were listed.

Step 6. Preparing a summary of individual’s comments: the facilitator summarized separately each interview with the experts.

Step 7. Sending the report to the individual expert concerned for review and amendment as required: the facilitator reduced the possibility of error or facilitator bias by sending each expert the summary of his/her own interview, for review and amendment as necessary.

Step 8. Preparing the Delphi-1 summary: the facilitator prepared a summary report on the views of all experts together. The outcomes of all experts are combined by the facilitator. Because of different wording of the same failure, some identified failure modes were merged to a single one, effectively avoiding overlap. Content analysis and generative AI (Claude) were applied to analyze qualitative data in this step. The generative AI (Claude) was used to generate new content of potential failure modes from all experts.

• Stage 3: Delphi-2: to analyze causes, effects, and detectability and provide scores for S, O, and D

Step 9. Analyzing potential failure causes, failure effects, detectability, and providing scores for each failure mode: the experts were asked open-ended questions to list the potential failure effects (“What would the consequences be of a particular failure?”), failure causes (“Why would this failure occur?”), and detectability (“What is the potential to detect failures and intervene in time?”).

Two patient safety risk areas—namely, those concerning mother and fetus(es)—were considered when identifying failure effects. The experts provided input via email, and they were asked to score each potential failure mode for severity (S), probability of occurrence (O), and detectability (D). Each potential failure mode (FM) could be associated with more than one potential failure effect. Therefore, one failure mode could generate more than one potential failure cause (FC). To search for the root causes, each FC was taken into account to calculate a risk score.

As in

Table 1. Ratings for severity with respect to the mother [33].

Score	Scale	Description
1	Grade I	Without the need for pharmacological treatment
2	Grade II	Requiring pharmacological treatment
3	Grade IIIa	Intervention not under general anesthesia
4	Grade IIIb	Intervention under general anesthesia
5	Grade IVa	Single organ dysfunction (including dialysis)
6	Grade IVb	Multiorgan dysfunction
7	Grade V	Death of the patient

, the severity rating for the mother and surgeon is on a scale of 1–7, with 1 indicating no injuries and 7 indicating death. The grading system is based on the Clavien–Dindo classification for surgical complications [32,33].

As shown in

Table 2. Ratings for severity with respect to the fetus [33].

Score	Scale	Description
1	Low danger	Does not endanger the fetuses in any way.
2	Moderate danger	Harm to a fetal organ
3	Dangerous	Harm to a fetal organ which requires future intervention
4	Very dangerous	Harm to a fetal organ which is life-threatening
5	Extremely dangerous	Fetal death

, we assigned severity scores for the fetus(es) based on criteria established by the EVERREST International Adverse Event Consensus group, which gives a rating scale from 1 (low danger) to 5 (extremely dangerous) [32,33,34]. This judgment demonstrates how the lives of fetuses are given less weight.

Table 3. Ratings for probability of occurrence [33].

Score	Scale	Description
1	Very low	Failure happens very infrequently (1/10,000–fewer)
2	Low	Failure happens rarely (1/1000–1/10,000)
3	Moderate	Failure happens occasionally (1/100–1/1000)
4	High	Failure happens often (1/10–1/100)
5	Very high	Failure is unavoidable or very possible (1–1/10)

shows an incidence rating scale from 1 (very infrequent) to 5 (very frequent). This is in line with typical medical FMEA practice [33]. Unlike the severity scale, a single incidence scale may be utilized throughout. To make the scale more clear, quantitative probability estimates were added [33,35]. A rate of 1/10,000, for example, suggests that the danger is anticipated to occur in one out of every 10,000 surgical procedures, making the scale very low or extremely infrequent.

Detectability was assessed on a scale of 1 to 5, with 1 representing extremely high and 5 representing extremely low detectability as shown in

Table 4. Ratings for detectability [33].

Score	Scale	Description
1	Very high	Failure is easily detected
2	High	Failure is detected frequently
3	Moderate	Failure is detected occasionally by double checking
4	Low	Failure is rarely detected
5	Very low	Failure is almost never detected

[32,33]. Remember that a high detectability score is given when the likelihood of finding a failure is low.

Step 10. Analyzing qualitative data by content analysis: the outcomes in this stage of all experts were combined and analyzed qualitatively by the facilitator. The facilitator applied content analysis and generative AI (Claude) to analyze qualitative data. The generative AI (Claude) was applied to group the contents of potential failure causes, failure effects, and detectability from all experts.

Step 11. Preparing the Delphi-2 summary: the facilitator summarized the Delphi-2 report which included potential failure causes, failure effects, and detectability for each FM.

• Stage 4: Calculating RPN and prioritizing FCs: this stage was to process the numerical results as quantitative data for S, O, and D and to compute the risk scores. There are several methods of MCDM to improve the RPN calculation. This study applied hybrid MCDM methodology and uncertainty theories to overcome RPN calculation weaknesses. grey relational analysis (GRA) and Evaluation based on Distance from Average Solution (EDAS) are effective methods in MCDM for assessing and prioritizing risk factors in FMEA, particularly during the medical device design stage [12].

Step 12. Identifying and bringing together separate S, O, and D scores for each potential failure cause (FC): each possible cause of failure, after qualitative data analysis, was given S, O, and D scores provided by the experts in Step 9. MCDM was applied for RPN calculations, based on the product of the three risk factors—S, O, and D.

Step 13. Computing the risk scores based on MCDM and uncertainty theories: we calculated the risk scores for each FC using the hybrid approach proposed by Pintelon et al. [12], applying the Entropy method based on uncertainty theory to determine weights of the three factors: severity (S), probability of occurrence (O), and detection (D). The grey relational analysis method was used to assess the relationships between criteria and alternatives, making it suitable for situations involving uncertainty or limited data. It evaluated alternatives based on their grey relational degree, enabling the identification of significant failure modes through the analysis of S, O, and D. We revisited the calculation steps outlined by Pintelon et al. [12], along with the notations presented in the table of abbreviations, which was used throughout this work.

In the failure cause ranking methodology proposed by Pintelon et al. [12], four steps are outlined as follows:

(i)

To form a multidisciplinary team of experts, identify potential failure modes, and assess the relevant evaluation criteria.

(ii)

To determine the distinct weights of the three FMEA factors—severity (S), probability of occurrence (O), and detection (D)—we applied the Entropy method. This technique addresses a key limitation of conventional FMEA, which assumes equal importance for all factors and thus overlooks their context-dependent influence on overall risk.

The Entropy method begins by normalizing the decision matrix to calculate the proportional value $z_{ij}$, as shown below:

$$z_{ij}={\displaystyle \frac{x_{ij}}{{\sum }_{i=1}^n{x}_{ij}}}$$

(1)

$$E_j=\left(-{\displaystyle \frac{1}{\ln \left(n\right)}}\right).{\sum }_{i=1}^n\left(z_{ij}.\ln z_{ij}\right)$$

(2)

$$d_j=1-E_j$$

(3)

$${\omega }_j={\displaystyle \frac{d_j}{{\sum }_{j=1}^m{d}_j}}$$

(4)

(iii)

To normalize the decision matrix using the vector normalization technique from the TOPSIS method to ensure comparability across criteria. After normalization, the Positive Ideal Solution (PIS) and Negative Ideal Solution (NIS) are derived by identifying the best and worst values for each criterion across all alternatives.

$$y_{ij}={\displaystyle \frac{x_{ij}}{\sqrt{{\sum }_{j=1}^m{x}_{ij}^2}}}$$

(5)

$${PIS}_j={max}_i{y}_{ij}$$

(6)

$${NIS}_j={min}_i{y}_{ij}$$

(7)

• (iv) To further assess the relationship between each alternative and the ideal/worst solutions, Grey Relational Coefficients (GRCs) are calculated. These coefficients reflect how closely each alternative aligns with PIS and NIS. The distance between each normalized value and the PIS/NIS is first computed. Then, using these distances, the GRCs for both the best (positive) and worst (negative) references are determined. This step allows for the partial incorporation of inter-criteria relationships and is especially useful under uncertainty.

$${∆}_{ij}^{+}=\left|y_{ij}-{PIS}_j\right|$$

(8)

$${∆}_{ij}^{-}=\left|y_{ij}-{NIS}_j\right|$$

(9)

$$g_{ij}={\displaystyle \frac{m^{\mp }+\xi {\mathrm{M}}^{+}}{{∆}_{ij}^{+}+{\xi \mathrm{M}}^{+}}}$$

(10)

$${\mathrm{v}}_{ij}={\displaystyle \frac{m^{-}+\xi {\mathrm{M}}^{-}}{{∆}_{ij}^{-}+{\xi \mathrm{M}}^{-}}}$$

(11)

$$G=\left(\begin{array}{ccc}{g}_{11}& \dots & g_{1m}\\ & \dots & \\ g_{n1}& \dots & g_{nm}\end{array}\right)$$

(12)

$$V=\left(\begin{array}{ccc}{V}_{11}& \dots & V_{1m}\\ & \dots & \\ V_{n1}& \dots & V_{nm}\end{array}\right)$$

(13)

Step 14. Prioritizing the possible failure causes (FCs): this step follows the methodology proposed by Pintelon et al. [12] to prioritize the risk scores of each failure cause (FC). The Evaluation based on Distance from Average Solution (EDAS) method is applied to calculate appraisal scores. These scores reflect how far each alternative is from the average solution, considering both positive and negative deviations. The resulting scores are then used to rank the FCs according to their relative risk.

$${AV}_{j,best}={\displaystyle \frac{{\sum }_{i=1}^n{g}_{ij}}{n}}$$

(14)

$${AV}_{j,worst}={\displaystyle \frac{{\sum }_{i=1}^n{v}_{ij}}{n}}$$

(15)

$${PDA}_{ij,best}={\displaystyle \frac{\max \left(0,g_{ij}-{AV}_{j,best}\right)}{{AV}_{j,best}}};{NDA}_{ij,best}={\displaystyle \frac{\max \left(0,{AV}_{j,best}-g_{ij}\right)}{{AV}_{j,best}}}$$

(16)

$${PDA}_{ij,worst}={\displaystyle \frac{\max \left(0,v_{ij}-{AV}_{j,worst}\right)}{{AV}_{j,worst}}};{NDA}_{ij,worst}={\displaystyle \frac{\max \left(0,{AV}_{j,worst}-v_{ij}\right)}{{AV}_{j,worst}}}$$

(17)

$${SP}_{i,best}=\sum _{j=1}^m{w}_j\ast {PDA}_{ij,best};{SN}_{i,best}=\sum _{j=1}^m{w}_j\ast {NDA}_{ij,best}$$

(18)

$${SP}_{i,worst}=\sum _{j=1}^m{w}_j\ast {PDA}_{ij,worst};{SN}_{i,worst}=\sum _{j=1}^m{w}_j\ast {NDA}_{ij,worst}$$

(19)

$${NSP}_{i,best}={\displaystyle \frac{{SP}_{i,best}}{\max {SP}_{i,best}}};{NSN}_{i,best}=1-{\displaystyle \frac{{SN}_{i,best}}{\max {SN}_{i,best}}}$$

(20)

$${NSP}_{i,worst}={\displaystyle \frac{{SP}_{i,worst}}{\max {SP}_{i,worst}}};{NSN}_{i,worst}=1-{\displaystyle \frac{{SN}_{i,worst}}{\max {SN}_{i,worst}}}$$

(21)

$${AS}_{i,best}={\displaystyle \frac{{NSP}_{i,best}+{NSN}_{i,best}}{2}}$$

(22)

$${AS}_{i,worst}={\displaystyle \frac{{NSP}_{i,worst}+{NSN}_{i,worst}}{2}}$$

(23)

$${AS}_i={\displaystyle \frac{{AS}_{i,best}+\left(1-{AS}_{i,worst}\right)}{2}}$$

(24)

The goal of FMEA is to find measures by implementing corrective actions to reduce risks. The potential FCs or risks which need to be mitigated must be identified. In healthcare FCs are prioritized according to risk and severity scores. The FCs with the highest risk scores would normally be given priority in FMEA, but in view of the paramount importance of patient safety, high severity scores are also prioritized. Then, Pareto theory (focusing on 20% risk scores) and severity scores were applied in selecting FCs. These combined rankings determine where risk mitigation efforts should focus.

• Stage 5: Compilation of final report: summarizing the report.

Step 15. Compiling the final report: the results were summarized using the facilitator, who combined the Delphi-1 to Delphi-2 outcomes. This stage involved summarizing all results and providing critical reflection. The critical elements were identified for providing corrective actions to eliminate or mitigate possible FCs of the medical device.

3. Results

3.1. Framework Results

This study applied a cascading Delphi method for data collection in FMEA during the design phase of a flexible fetoscope. Stage 2 was conducted by means of individual online interviews, with a response rate of 100%. Experts spent 25–65 min (average 38 min) on this. Data collection in Stage 3 was more difficult. The experts spent 75–150 min (average 108 min) on this, with a response rate of 82%.

3.2. Expert Data

All obstetric surgeons have knowledge of and experience with fetoscopes for twin-to-twin transfusion syndrome (TTTS), more than 5 years. The largest group of experts were five medical teachers (45%), followed by four PhD students (37%), a postdoctoral researcher (9%) and a research engineer (9%). Furthermore, the experts’ specialization and experience are presented in

Table 5. Information of 11 experts.

Topic	Number
1. Occupation	11 (100%)
Engineer from KU Leuven, Belgium (producer)	6 (55%)
Obstetric surgeon from University in Thailand (User)	5 (45%)
2. Position	11 (100%)
Medical teacher	5 (45%)
PhD student	4 (37%)
Research engineer	1 (9%)
Postdoctoral researcher	1 (9%)
3. Specialization	11 (100%)
Maternal–fetal medicine	5 (46%)
Minimally invasive surgery	2 (18%)
Electromechanical engineering	1 (9%)
Medical robotic and control	2 (18%)
Mechanical engineering	1 (9%)
4. Experience	11 (100%)
>5 years	5 (44%)
2–5 years	3 (28%)
≤2 years	3 (28%)

.

3.3. Stage 2: Delphi-1 Result

Engineers (average 45 min) spent more time than surgeons (average 29 min) in this stage. In subsequent email follow-up, most experts (8 out of 11 or 73%) responded, and of those, 3 (27%) made corrections.

New parts of the flexible fetoscope, adapted from Ahmad et al. [28], were classified by the experts in three groups: handle, flexible segment, and tip. Additional components of the handle were identified by experts, including the slider, McKibben actuator, the wire transmitting force between the actuator and the tip, and the air supply, as shown in Figure 3. Furthermore, several new components of the flexible segment were additionally addressed, such as the bending part, laser fiber, the wire, electrical components and connections, and water irrigation. Similarly, new components were identified at the tip of fetoscope, including a camera, light source, wire, electrical components and connections, tube end sleeve, and glue.

Focusing on the patients’ safety (mother and fetus(es)), 26 potential failure modes were identified, with 13 (50%) related to the tip, 7 (27%) to the flexible segment, and 6 (23%) to the handle. There was a degree of consensus among the experts. Four potential failure modes were identified by more than 50% of them, namely excessive force on the wire (73%), an air leak within the handle (55%), damage to the camera at the tip (55%), and a glue overheating or melting (55%), as shown in

Table 6. Potential failure modes of the new part of the flexible fetoscope.

ID	Potential Failure Modes (26)	Number (%) *
1	Handle—6 (23%)
1.1.1	Slider breaks	4 (36%)
1.2.1	Applying excessive force on wire	8 (73%)
1.3.1	Wire suddenly snaps	4 (36%)
1.4.1	Excessive air pressure	3 (27%)
1.4.2	Air leaks within the handle	6 (55%)
1.4.3	Unfiltered or unclean air supply	1 (9%)
2	Flexible segment—7 (27%)
2.1.1	Bending or tip positioning issues	4 (36%)
2.1.2	Permanent plastic deformation due to excessive forces	1 (9%)
2.2.1	Laser fiber snaps—during ablation	3 (27%)
2.2.2	Preventing ablation of laser fiber	2 (18%)
2.3.1	Wire suddenly snaps	1 (9%)
2.4.1	Electrical wire snaps/ disconnects (due to repetitive large bending)	1 (9%)
2.5.1	Leakage of irrigation fluid and contact with bare electrical wire	1 (9%)
3	Tip—13 (50%)
3.1.1	The tip breaks during use	1 (9%)
3.2.1	Damage of the camera	6 (55%)
3.2.2	Camera detachment	2 (18%)
3.3.1	Light-source failure	3 (27%)
3.3.2	Heating or thermal injury	1 (9%)
3.4.1	Wire suddenly snaps	1 (9%)
3.5.1	Fluid contact with bare electrical wires	2 (18%)
3.6.1	Loosening of the tube end sleeve	1 (9%)
3.7.1	Cracking of the glue	1 (9%)
3.7.2	Loss of particles (debris) during use inside the patient	1 (9%)
3.7.3	Dislodging of the glue	2 (18%)
3.7.4	Heating, glue melting	6 (55%)
3.8.1	Contamination of the fetoscope	1 (9%)

* Total 11 FMEA experts.

.

3.4. Stage 3: Delphi-2 Result

In Stage 3: Delphi-2, there were two medical doctors who withdrew from the study, resulting in a participation rate of 82%. At this stage, only three experts responded to the form within one month. The remaining responses were delayed by four to seven months. The engineering experts were particularly dilatory, but responses were eventually forthcoming after face-to-face prompting became possible.

We found 26 potential failure modes (FMs) in total, based on 419 possible failure causes (FCs): 56% (234 FCs) were related to the tip, 30% (128 FCs) to the flexible segment, and 14% (58 FCs) to the handle. Some examples of data collected using the cascading Delphi FMEA method are shown in

Table 7. Illustrative examples of data collected using the cascading Delphi FMEA method.

ID	Potential Failure Modes	Main Effects	Potential Failure Effects (S)	S Score	Potential Failure Causes (O)	O Score	Detectability (D)	D Score
1. Handle
1.1 Slider
1.1.1	Slider breaks
1.1.1A1		Mother	Device configuration issues	1	Slider or handle mechanism issues	1	Visual observation	1
1.1.1B1		Fetuses	Device configuration issues	2	Slider or handle mechanism issues	2	Visual observation	1
1.1.1A2		Mother	Device configuration issues	1	User errors or misuse	2	Visual observation	1
1.1.1B2		Fetuses	Device configuration issues	2	User errors or misuse	2	Visual observation	1

.

Multi-Criteria Decision Making (MCDM) was applied to address the weaknesses of RPN calculation. Based on the calculations in above equations, the weights for each factor—S, O, and D—are determined as shown in

Table 8. Weights of criteria.

Criteria	Weights
Severity	0.265981
Occurrence	0.233806
Detectability	0.500213
Total	1

.

Risk scores were computed FCs based on MCDM and ranked (Step 13 and 14). On the (Pareto-like) assumption that the failure causes with the highest risk scores posed the greatest risks, the top 20% were examined further. Then, severity scores were applied in selecting FCs.

The highest risk scores found was for contamination resulting from manufacturing defects for the mother (ID = 3.8.1A3, risk scores = 0.927) followed by loss of particles (debris) from the tip during use inside the patient caused by assembly defects (ID = 3.7.2A1, risk scores = 0.896), material fatigue and degradation (ID = 3.7.2B6, risk scores = 0.896), dislodging of the glue from the tip caused by assembly defects (ID = 3.7.3A1, risk scores = 0.896) and material fatigue and degradation at the tip (ID = 3.7.3B5, risk scores = 0.896). The potential failure causes (FCs) with the 10 highest risk scores were associated with the tip of the flexible fetoscope, particularly glue-related issues such as cracking, dislodgement and particles loss (debris) and contamination of the entire fetoscope, as shown in

Table 9. Top 20% risk and severity scores ranked by Pareto principle.

Rank	ID	S	O	D	Risk Score	Rank	ID	S	O	D	Risk Score
1	3.8.1A3	7	1	5	0.927	53	2.5.1B9	3	1	5	0.737
2	3.7.2A1	4	2	5	0.896	54	3.5.1B10	3	1	5	0.737
3	3.7.2B6	4	2	5	0.896	55	3.5.1B12	3	1	5	0.737
4	3.7.3A1	4	2	5	0.896	56	3.5.1B13	3	1	5	0.737
5	3.7.3B5	4	2	5	0.896	57	3.5.1B14	3	1	5	0.737
6	3.8.1A1	4.333	2.333	4.333	0.849	58	3.5.1B15	3	1	5	0.737
7	3.7.1B3	3	2	5	0.848	59	3.5.1B16	3	1	5	0.737
8	3.7.1B6	3	2	5	0.848	60	3.5.1B17	3	1	5	0.737
9	3.7.2A5	3	2	5	0.848	61	3.5.1B3	5	2	3	0.722
10	3.7.3A4	3	2	5	0.848	62	3.7.1A1	5	2	3	0.722
11	3.7.2A4	4.143	1.714	4.714	0.844	63	3.8.1A2	4.25	1.5	3.75	0.720
12	1.4.3A2	4	3	4	0.838	64	3.7.3B4	2.444	1.889	4.333	0.717
13	3.8.1B5	4	3	4	0.838	65	3.7.2A3	5	1	4	0.708
14	3.8.1B4	5	1	5	0.826	66	2.5.1B6	3	1.667	4	0.707
15	3.5.1A2	7	2	3	0.823	67	1.2.1B2	3	5	2	0.696
16	1.4.3B2	3.5	3	4	0.818	68	3.5.1A8	4	1.5	3.5	0.686
17	3.8.1B1	3.5	2.333	4.333	0.815	69	2.2.2A3	4	2	3	0.681
18	3.7.3A3	3.889	1.889	4.222	0.79	70	3.3.2A2	4	2	3	0.681
19	3.7.1B5	2.2	2	5	0.787	71	3.3.2A5	4	2	3	0.681
20	2.5.1A10	4	1	5	0.785	72	3.3.2A6	4	2	3	0.681
21	2.5.1A5	4	1	5	0.785	73	3.7.1B1	4	2	3	0.681
22	2.5.1A7	4	1	5	0.785	74	3.7.3B3	4	2	3	0.681
23	2.5.1A8	4	1	5	0.785	75	2.5.1A3	5.5	2	2.5	0.679
24	2.5.1A9	4	1	5	0.785	76	2.5.1B7	4	1	4	0.668
25	3.5.1A11	4	1	5	0.785	77	3.5.1B11	4	1	4	0.668
26	3.5.1A12	4	1	5	0.785	78	3.5.1B5	4	1	4	0.668
27	3.5.1A13	4	1	5	0.785	79	3.7.2B3	4	1	4	0.668
28	3.5.1A14	4	1	5	0.785	80	3.5.1A3	2	2	4	0.654
29	3.5.1A15	4	1	5	0.785	81	3.5.1B2	2	2	4	0.654
30	3.5.1A16	4	1	5	0.785	82	3.5.1B7	2	2	4	0.654
31	3.5.1A9	4	1	5	0.785	83	3.6.1B6	2	2	4	0.654
32	3.8.1B2	4	1	5	0.785	84	3.2.2A4	5	1	3	0.610
33	3.7.1B2	2.667	2	4.667	0.78	85	1.2.1A3	4.5	1.75	2.25	0.575
34	3.7.2B4	2.857	1.714	4.714	0.78	86	2.2.1A12	5	1.5	2	0.526
35	3.7.2A7	4	2	4	0.779	87	1.2.1A1	5	1	2	0.458
36	3.7.2A8	4	2	4	0.779	88	3.1.1A11	5	1	2	0.458
37	3.7.2A9	4	2	4	0.779	89	2.2.1A10	5.333	1.333	1.667	0.457
38	1.4.3A1	2	2	5	0.771	90	3.3.2A7	5.5	1.5	1.5	0.453
39	3.7.1A2	2	2	5	0.771	91	3.3.2B8	4.5	1.5	1.5	0.411
40	3.7.1A5	2	2	5	0.771	92	3.4.1A6	4.4	1.2	1.2	0.307
41	3.7.1A6	2	2	5	0.771	93	1.4.2A1	6	1	1	0.303
42	3.7.2B1	2	2	5	0.771	94	1.4.2A2	6	1	1	0.303
43	3.7.3B1	2	2	5	0.771	95	2.2.1A11	6	1	1	0.303
44	2.5.1A6	6	1	4	0.753	96	2.2.1A7	6	1	1	0.303
45	3.5.1A10	6	1	4	0.753	97	2.2.1A8	6	1	1	0.303
46	3.5.1A5	6	1	4	0.753	98	2.2.1A9	6	1	1	0.303
47	2.5.1A4	3.667	1.667	4	0.741	99	1.3.1A4	5	1	1	0.258
48	3.7.1A3	2.286	2	4.571	0.74	100	2.2.1B6	5	1	1	0.258
49	2.5.1B10	3	1	5	0.737	101	2.3.1A4	5	1	1	0.258
50	2.5.1B11	3	1	5	0.737	102	2.3.1A5	5	1	1	0.258
51	2.5.1B5	3	1	5	0.737	103	2.3.1A6	5	1	1	0.258
52	2.5.1B8	3	1	5	0.737	104	3.4.1A8	5	1	1	0.258

.

The tip was the most frequently identified failure point (66%, with 69 FCs), primarily due to material fatigue and degradation (16 cases) and material defects (14 cases) which led to fluid contact with bare electrical components and connections at the tip. For the flexible segment, the failures were concerned (25%, with 26 FCs) with material defects (6 cases), assembly defect (6 cases) and material fatigue and degradation (5 cases) causing a leakage of irrigation fluid and contact with bare electrical wire at the flexible segment (15 cases). For the handle, the failures were concerned (9%, with 9 FCs) with excessive force or pressure issues (6 cases) on the wire at the McKibben actuator in the handle.

3.5. Sensitivity Analysis of Scenario Weights and Rank Stability

To evaluate the robustness of the ranking obtained by the hybrid approach proposed by Pintelon et al. [12], sensitivity analysis was conducted by testing four distinct weight configurations corresponding to different decision-maker emphasis on severity (S), occurrence (O), and detection (D). These weight vectors are:

• – Scenario 1: (0.2, 0.2, 0.6)—emphasis on detection;
• – Scenario 2: (0.2, 0.6, 0.2)—emphasis on occurrence;
• – Scenario 3: (0.33, 0.33, 0.33)—equal weighting;
• – Scenario 4: (0.6, 0.2, 0.2)—emphasis on severity.

The ranking results for each CF under these scenarios were compared using Kendall’s Tau correlation to access to assess the consistency of rankings across different weighting schemes. Kendall’s Tau is particularly suitable for this analysis, as it measures the ordinal association between ranked variables, making it ideal for evaluating the similarity of prioritizations derived from varying weighting strategies, without assuming any linear relationship between them [36].

Table 10. Kendall’s Tau correlation matrix among scenario weightings.

No.	Scenario 1	Scenario 2	Scenario 3	Scenario 4
Scenario 1	1.000	0.555	0.838	0.552
Scenario 2	0.555	1.000	0.679	0.439
Scenario 3	0.838	0.679	1.000	0.685
Scenario 4	0.552	0.439	0.685	1.000

presents the Kendall’s Tau correlation coefficients, which quantify the consistency of rankings across different weighting scenarios. Among the scenarios, Scenario 3—which applies equal weighting to severity, occurrence, and detection—exhibits consistently high correlations with all other scenarios (τ ≥ 0.679), suggesting that a balanced approach results in stable and representative rankings of the CFs. The strongest agreement is observed between Scenario 1 and Scenario 3 (τ = 0.838), indicating that even when detection is emphasized, the resulting rankings remain closely aligned with those from a balanced weighting. Conversely, the lowest correlation occurs between Scenario 2 and Scenario 4 (τ = 0.439), a finding that aligns with the distinct emphasis each scenario places on different criteria—occurrence in Scenario 2 and severity in Scenario 4—which are likely to prioritize different CFs. Overall, the application of the hybrid approach proposed by Pintelon et al. [12] demonstrates moderate to strong rank stability across various decision-making preferences, confirming its robustness and adaptability for practical applications.

4. Discussion

The big challenge for FMEA during the early design phase is data collection, since the device does not physically exist. The experts have to make predictions based on their experience and knowledge [37]. Accordingly, it may be quite difficult to reach consensus. The proposed cascading Delphi method can generate valuable ideas from the experts. It is important that these ideas should be recognized, rather than being subjected to attempts to “erode” them away through consensus. The proposed cascading Delphi method is less time consuming than traditional FMEA and the traditional Delphi method as the experts can participate on their own schedules without a series of meetings.

Some aspects of the traditional Delphi method were modified to make it more efficient. One-on-one interactions, rather than group discussion, were used to avoid group bias. Additionally, the emphasis on reaching a consensus was reduced. The cascading Delphi method aims to reduce time consumption by using technology such as email and by relaxing the requirement for total consensus, instead aiming to maximize the number of potential failure modes identified. This study found that an individual interview was indeed productive in terms of collecting ideas and analysis because of the opportunity to ask detailed questions. After completing an individual interview, the experts reviewed their feedback as summarized by the facilitator, and each expert had the opportunity to review and edit their answers. Most experts took the opportunity to edit on most occasions, and some revised a given response more than once, which helped to reduce facilitator’s bias.

All potential failure modes (FMs) are examined in Stage 3: Delphi-2 to analyze and give scores for potential failure effects, causes, and detectability. This stage is demanding and time consuming. The experts are expected to give careful consideration to their comments and scores. Accordingly, some of the experts dropped out of the study altogether at this stage, while others were slow in responding. To minimize both effects, the facilitator in the cascading Delphi framework should, for example, provide clear instruction, easy-to-use forms, and full information from the start of the process. Qualitative data from Stage 3: Delphi-2 are more diverse than those from Stage 2: Delphi-1. This makes it more difficult to reach a consensus, especially regarding scores for severity (S), probability of occurrence (O), and detectability (D).

During the FMEA process, patience is essential when preparing data. Meetings play an important role by providing an opportunity to explain the research to all participants. If some experts cannot attend these meetings, individual sessions should be arranged for them. The facilitator can support the experts by developing user-friendly data collection forms and offering clear, straightforward guidelines on data preparation. Providing examples could also be especially helpful, particularly for the data preparation in Step 2, which is conducted via email.

Group members’ dedication and agreement are crucial to the effective completion of FMEA [11]. In an initial meeting between the facilitator and the experts, it is an opportunity for the facilitator to clearly explain the study’s objectives and methodology. The facilitator can get to know the other participants and make the experts more receptive to the questions put to them and thus make for better overall results. Individual interviews can be more time consuming for experts than answering questionnaires, because the individual interviews often involve detailed discussion. However, individual interviews are useful in improving the final outcome by eliciting detailed responses through in-depth questioning. In addition, in the proposed cascading Delphi method, all experts took part in all stages of the process, including reviewing and editing their opinions and comments at each stage. The traditional version of data collection for FMEA had three main drawbacks: group bias, time consumption, and sample size issues [38,39].

Snowball sampling is a suitable method for collecting data for research when experts are difficult to find. Snowball sampling creates a network of participants by finding one or two participants and then asking them to refer others. This method is suitable for participants with specific knowledge and experience when it is difficult to locate or contact experts on the topic. There does not appear to be a standard for the normal or minimum number of experts, but we believe that this cohort represents the essential disciplines and stakeholders, including designers, engineers, and users.

Establishing a team of FMEA experts is an important step, as FMEA is a subjective method that requires input from experts. Experts should be selected to include stakeholders who are involved as both producers and users with direct experience with the equipment or device to be studied, and from a variety of professions to provide a comprehensive perspective. The opinions of the experts should then be diverse, like a puzzle that fits together into a single picture.

Risk priority number (RPN) score is inherently often leading to variations due to differing opinions among teams. The exploration of Multi-Criteria Decision-Making (MCDM) techniques offers a significant advancement in improving reliability and overcoming the limitations of traditional RPN calculations. Conventionally, RPN scores in FMEA have relied on subjective assessments [7], which can lead to inconsistencies due to differing opinions among evaluators [21]. In contrast, MCDM techniques transform this process into a more objective methodology. By systematically integrating multiple criteria and considering the relationships and priorities among them, MCDM enhances the precision and consistency of the RPN assessment. This approach not only addresses the issue of equal weighting for severity, occurrence, and detection but also mitigates the variability arising from individual judgments. The adoption of MCDM techniques thus represents a promising step toward a more robust and reliable risk prioritization framework in FMEA.

Hybrid MCDM approaches, such as the combination of TOPSIS and GRA, are widely employed to address the limitations of the traditional RPN by generating additional priority indices and weighting criteria [12]. These methodologies enhance the analysis by considering a broader range of elements, effectively tackling key weaknesses of conventional approaches. However, it is important to note that MCDM-based FMEA approaches often remain context dependent and may lack robustness in situations characterized by incomplete information, particularly during the design phase of FMEA [12].

Using generative AI in the content analysis can facilitate the process and lead to highlighted risk areas requiring mitigation for a flexible fetoscope. In addition, utilizing generative AI as a copilot has the potential to reduce the time required by more than half and reduce the risk of occupational back pain.

There are several concerns in this study. First, the drop from 100% to 82% participation rate could reduce the diversity of expert opinions, introduce bias, weaken consensus, and affect the validity and consistency of final risk prioritization. These impacts are particularly significant given the small expert sample size. In this study, the limited sample size is due to the confidential nature of early fetoscope design and the need for reliable input from experts with direct, specialized knowledge and experiences. Second, delays of up to seven months in the Stage 3 response could skew the context of earlier discussions.

One way to address the weaknesses identified in this study is by ensuring that the facilitator must have in-depth knowledge and understanding of the equipment’s operation to be studied to be able to analyze the data more accurately. The editing process, which often involves multiple iterations between experts and facilitator, is a process which carries an intrinsic risk of facilitator bias, of which the facilitator must be conscious. Being aware of this risk is essential. The facilitator must be patient and have task-tracking skills. The facilitator must use both art and science in tracking data to maximize cooperation. Multiple communication channels will help in tracking data, especially face-to-face tracking. Good relationships between the research team and experts are very important in obtaining quality data and lowering the dropout rate.

Since the device to be studied is still in the design phase, it is vital that as much information as possible, including detailed drawings, mock-ups, and samples of components which may already exist, should be provided to the experts, either physically, or in the form of images or video clips. We found that experts often confused possible failure modes with possible causes of failure, so it is important to clarify this. Cost and environmental factors should be considered to cover the production of medical devices.

The cascading Delphi method-based FMEA framework, developed in alignment with ISO 14971, addresses risk management challenges for medical devices in the early design phase and applies to a variety of medical devices. The proposed framework could be applied to devices such as new endoscopes or minimal invasive surgical tools. For example, in patient’s safety aspect, similar failure causes and effects related to device’s components could be assessed using the same process. Our proposed framework was previously piloted using an electromagnetic self-tracking fetoscope before being refined and validated with a flexible fetoscope, allowing us to address how key steps can be generalized or adapted for other applications.

While the hybrid MCDM method applied in this study offers a structured and quantitative approach to prioritizing risk, alternative methods such as decision tree models integrated with fuzzy logic may provide additional flexibility and interpretability. These models are particularly useful when expert assessments are qualitative or expressed in linguistic terms. Future work may explore such methods to handle uncertainty in early-stage design even more effectively, allowing rule-based logic and fuzzy inference to complement the numerical analysis of risk.

Future research could add steps to reach consensus by sending expert reports for review both individually and as a group in each stage, but fatigue and impatience of experts must be taken into account. The analysis of qualitative data in Stage 3 was time consuming. Using machine learning or artificial intelligence tools can reduce the workload and save time; however, the facilitator must still collect data to obtain consistent, systematic, and verifiable qualitative data and scores.

This study involved only risk identification, risk analysis, and evaluating which risk scores are calculated and prioritized for potential FCs. High-risk FCs need to be analyzed by experts to provide corrective actions to mitigate or eliminate risks. Finally, the risk is re-evaluated after redesigning to verify that the interventions have effectively lowered it to an acceptable level.

5. Conclusions

In this study, the cascading Delphi framework with MCDM was applied to overcome FMEA weaknesses covering data collection (group bias and time constraints) and RPN calculation, using a flexible fetoscope as a case study. The cascading Delphi method could improve the effectiveness of data collection for risk management to reduce or prevent potential failures. The proposed cascading Delphi method could be utilized to gather data from different stakeholders, such as engineers and surgeons. A multidisciplinary expert team identified, analyzed and evaluated the risk in the design of a flexible fetoscope. The expert team could provide feedback freely without group bias, and at flexible times. Data collection was reliable because the experts could review and correct summaries of their feedback in each round. The results after applying FMEA with cascading Delphi method and MCDM showed that the highest RPN was contamination resulting from manufacturing defects for mothers. It is challenging to reduce the time consuming and increase the reliability of data collection. Furthermore, using high technology such as artificial intelligence can assist the laborious of content analysis.