Beam Dynamics Design of a Multi-Ion RFQ for Medical Application
Abstract
1. Introduction
- Achieving Multi-Ion Compatibility via Dynamic Focus–Defocus Control: By adjusting the focusing strength to achieve a dynamic balance with the defocusing strength, the efficient transmission of multiple ion species within the same RFQ is improved.
- Quantification and Optimization of Stable Longitudinal Phase Space Area: A parameter is introduced to characterize the stable longitudinal phase space area and optimized to maximize beam capture efficiency.
- Error Tolerance Analysis: Using comprehensive error studies, acceptable tolerances for input-beam errors and mechanical fabrication errors are determined, and practical guidelines for RFQ construction and operation are provided.
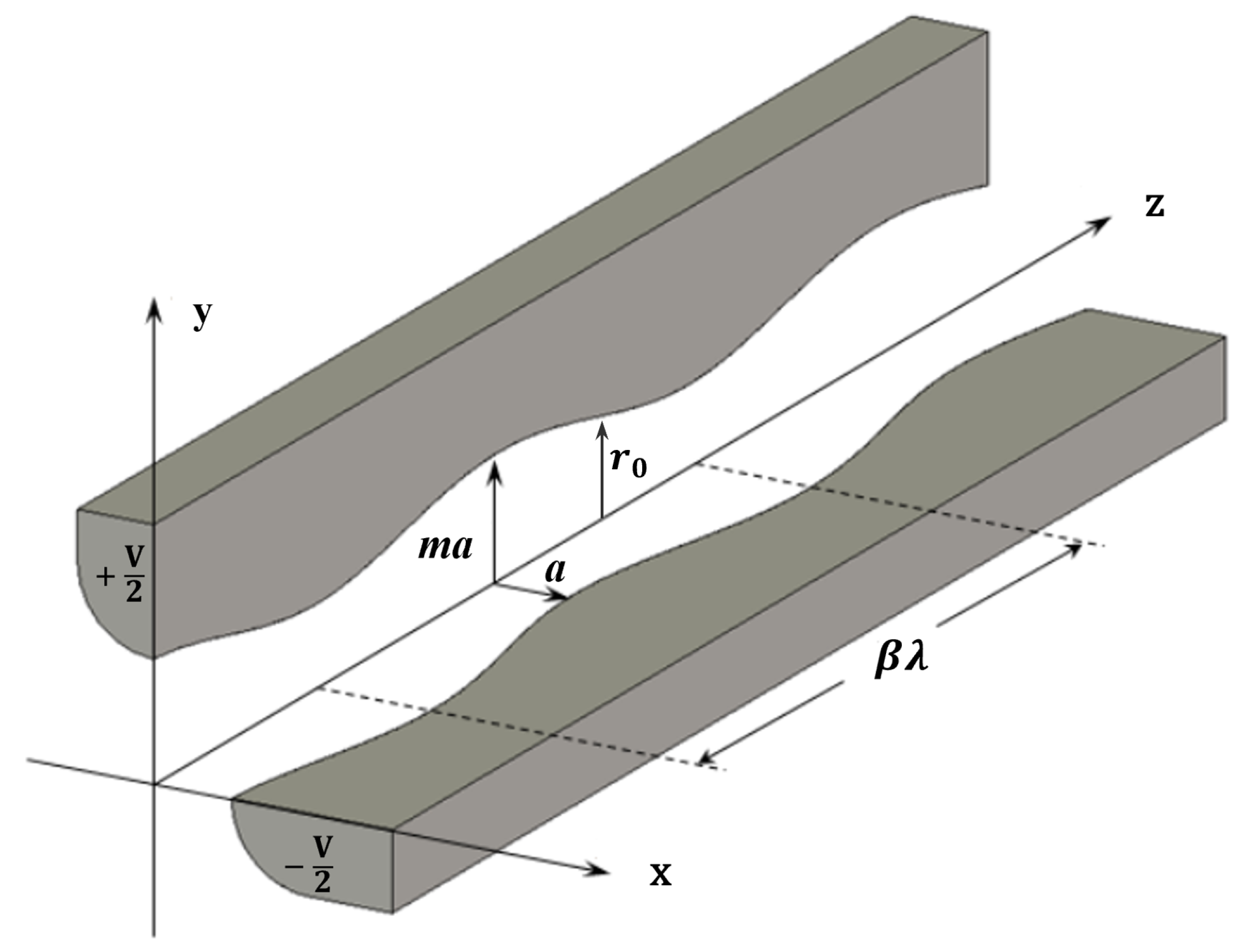
2. Basic Principles of the RFQ
3. Beam Dynamics Design
3.1. Design Considerations
- Beam current: The selection of RFQ beam current is closely related to the dose rate required for clinical particle therapy. Considering the clinical dose rate requirements [29,30] and referencing the beam current settings of the existing medical RFQ accelerator [31,32], the beam current is set to 0.3 mA for C and 1 mA for He.
- Operating frequency: In order to maintain sufficient focusing strength when increasing the RFQ operating frequency, the average aperture must be reduced accordingly. If the average aperture is too small, it is not conducive to beam transmission. On the other hand, if the aperture is not reduced, the voltage needs to be increased, which increases the risk of RF breakdown. Considering the size of the cavity and the frequency of commonly available power sources, the operating frequency of the RFQ is set to 200 MHz.
- Injection energy: The input energy should be consistent with the extraction voltage of the ion source. In addition, it affects the design of the LEBT. If the input energy is too low, space charge effects will be intensified, placing stricter requirements on the vacuum level and magnetic focusing system of the LEBT. Conversely, an excessively high injection energy may lead to an increase in the length of the LEBT. Considering prior experience with stable RFQ operation and established design practices [11,33], the injection energy is ultimately set to 8 keV/u.
- Output energy: The output energy of the RFQ not only affects its own length but is also directly related to the design of the subsequent DTL. If the output energy is too high, the length of the RFQ will increase significantly, leading to higher manufacturing costs and a larger equipment footprint. In contrast, if the injection energy into the DTL is too low, it may result in an uneven radial electric field distribution within the drift tube, leading to degraded beam quality. Considering both the length of the RFQ and the complexity of the subsequent DTL design, the RFQ output energy is ultimately set to 750 keV/u.
- Input emittance: An excessively large input emittance increases beam loss, while an overly small emittance leads to higher beam density and enhanced space charge effects. Therefore, an appropriate input emittance is essential not only for reducing the probability of beam loss but also for ensuring stable beam transport. Ultimately, the input emittance is set to 0.2 mm·mrad.
- Voltage and Kilpatrick factor: To maintain sufficient focusing strength and accelerating gradient, the inter-vane voltage is selected within the range of 60–80 kV. Simultaneously, the Kilpatrick factor is limited to below 1.8 in order to minimize the risk of RF breakdown within the cavity. This choice aligns with the design practices of many RFQs currently in operation at frequencies close to 200 MHz [31,33,34], where similar voltage ranges and Kilpatrick factors are commonly adopted to ensure reliable and stable operation.
- Multi-ion compatibility: Ions with different charge-to-mass ratios exhibit varying sensitivities to space charge effects. Therefore, when designing an RFQ capable of accelerating multi-ion, one of the primary considerations is the influence of space charge effects. In RFQ beam dynamics design, the ability to suppress space charge effects is typically evaluated by examining the reduction in transmission efficiency as the beam current increases. If the degree of efficiency degradation decreases with increasing beam current, it indicates a stronger capability to mitigate space charge effects. Therefore, it demonstrates better compatibility when the RFQ accelerates ions that are more sensitive to space charge effects. Considering the ion species that the RFQ is designed to accommodate and their sensitivity to space charge effects, the transmission efficiency for 1 mA He should be no less than 95%.
- Compact structure: During the design of medical accelerators, compactness is one of the key priorities. A compact structure not only reduces manufacturing and installation costs but also reduces space requirements, making it convenient to use in medical environments. In this study, to balance cost and space constraints, the RFQ length is limited to less than 2.8 m.
- Operational stability: Due to the limitations of actual experimental conditions, the operating state of each accelerator is often not completely ideal. Therefore, it is crucial for the RFQ to have sufficient error tolerance. Considering input beam errors, the RFQ should exhibit adequate tolerance to ensure that the beam transmission efficiency remains above 95%. Under the influence of mechanical manufacturing errors, the emittance growth of the RFQ is required to be kept below 5%, and the extra beam loss should be less than 10%.
3.2. Design Strategy
3.2.1. General Design
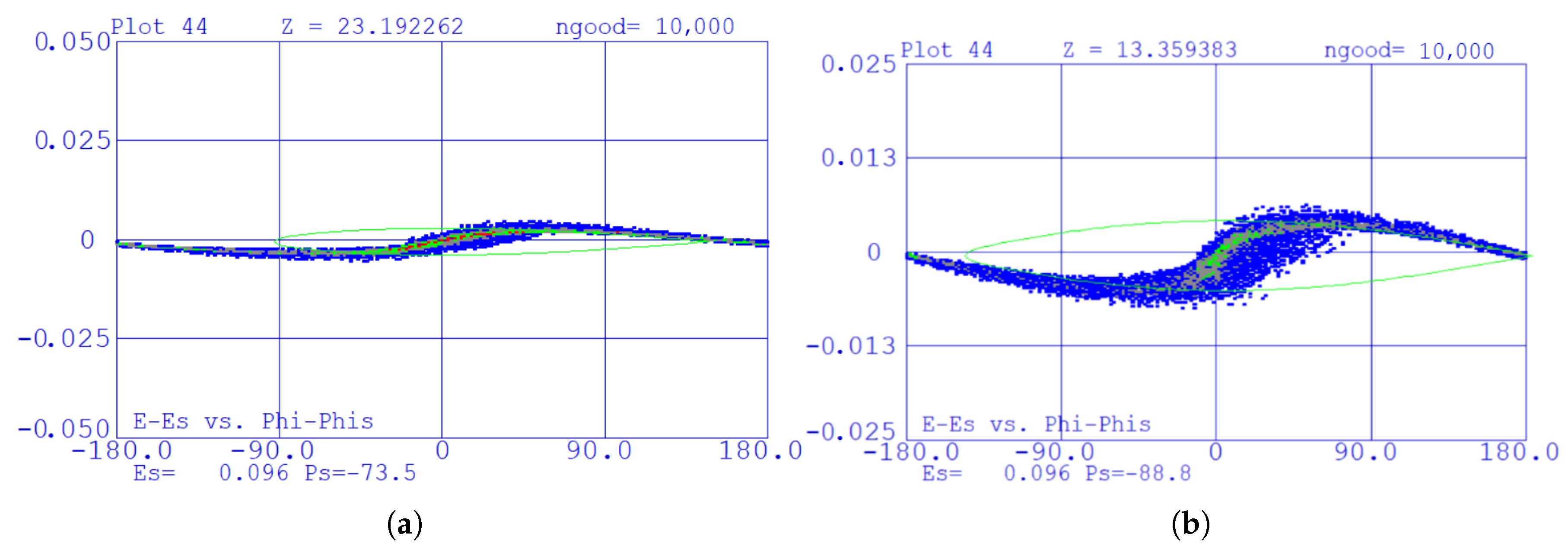
- For 1 mA , the transmission efficiency falls below the required minimum of 95%.
- The beam was not well captured in the shaper section, as observed in Figure 4, resulting in increased longitudinal losses and longitudinal emittance.
- Figure 5 shows the transmission efficiency of the RFQ versus beam current. As the beam current increases to 8 mA, the transmission efficiency decreases from 95.2% to 32%, representing a total reduction of 63.2%. This indicates that the RFQ exhibits high sensitivity to beam current fluctuations and has limited capability in suppressing space charge effects. This limitation becomes especially critical when accelerating different ion species, particularly those that are highly sensitive to space charge effects.
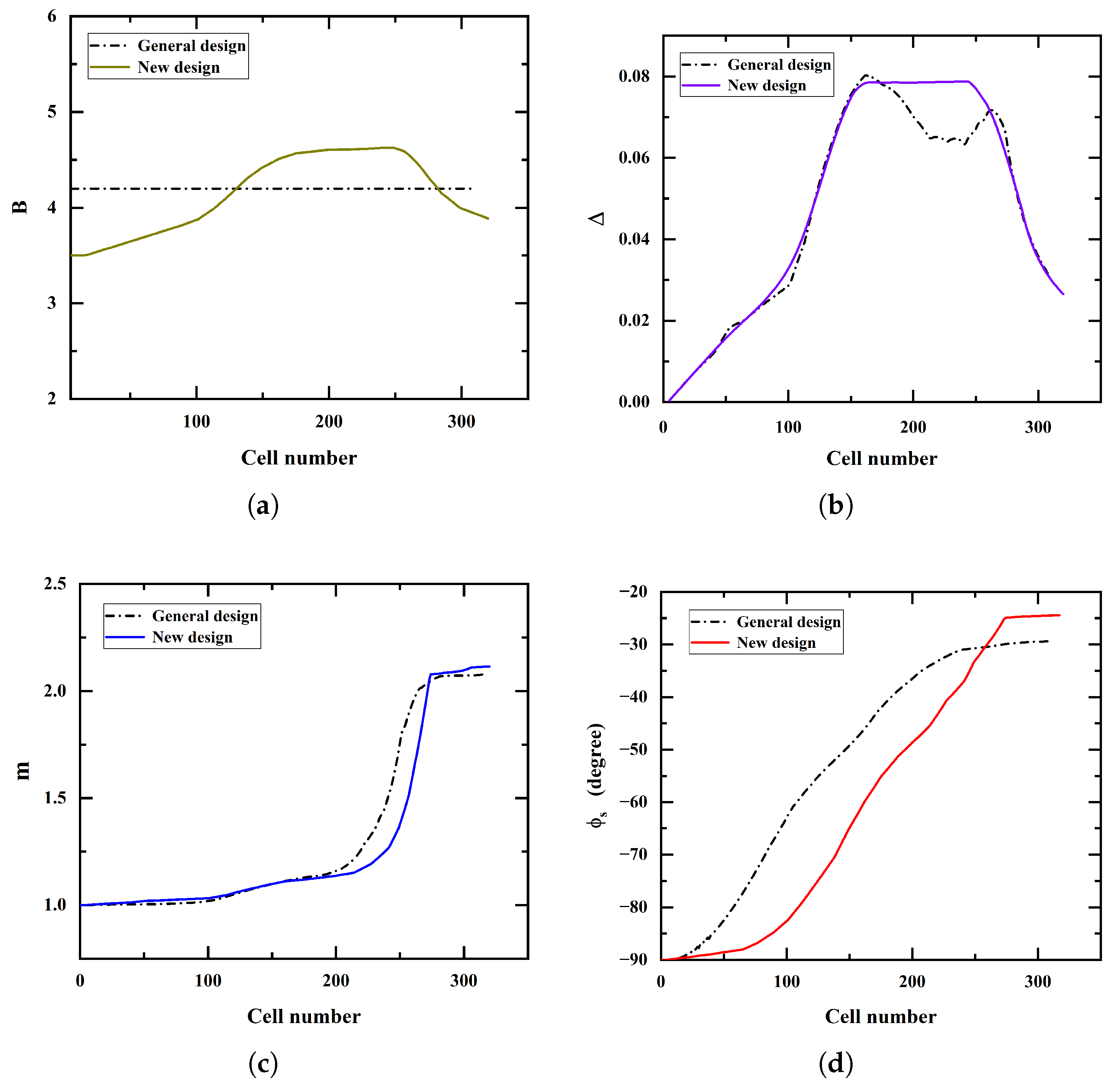
3.2.2. New Design
3.3. Multi-Particle Simulation Results
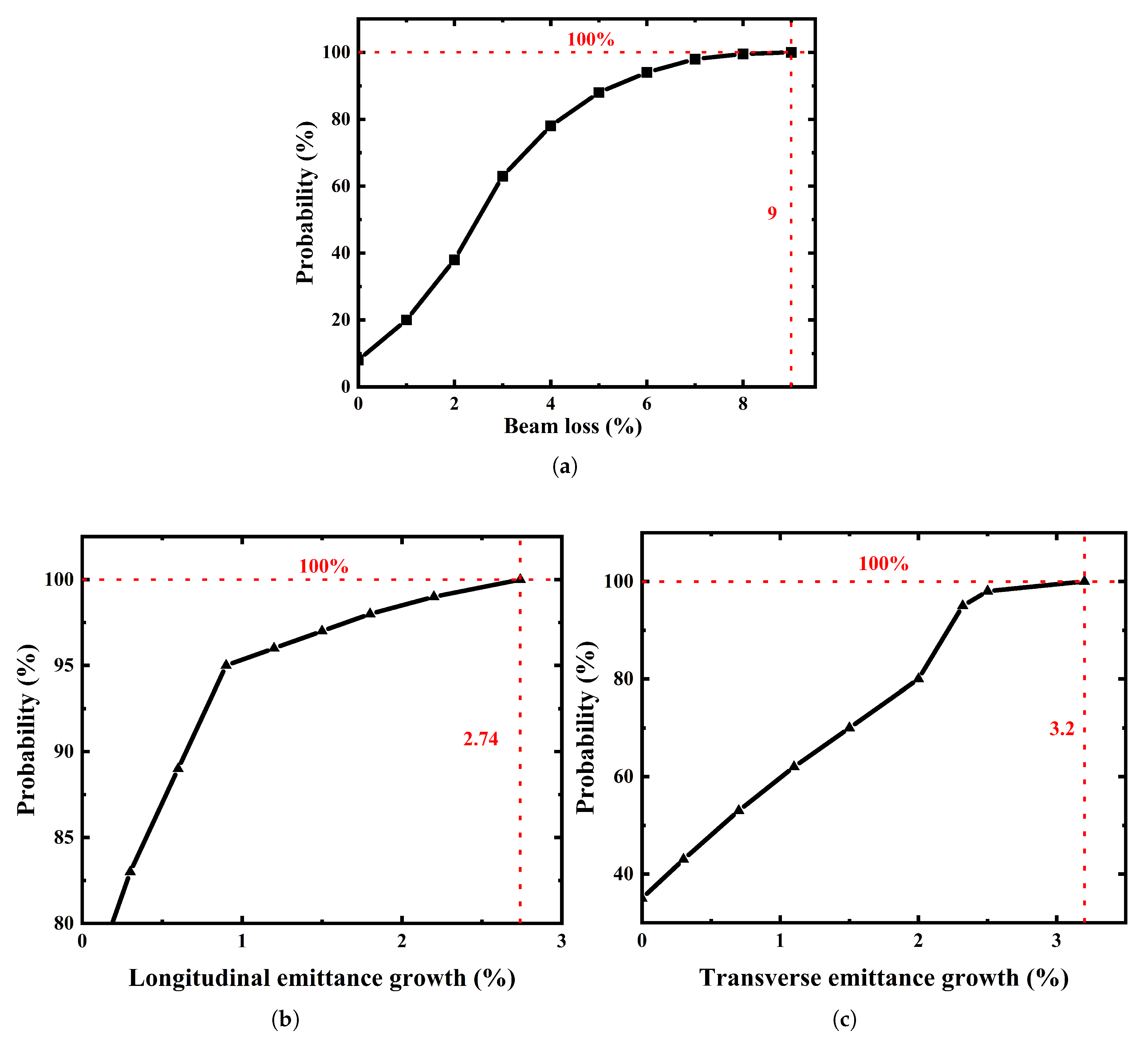
4. Error Analysis
4.1. Input Errors Analysis

4.2. Mechanical Errors Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Park, S.H.; Kang, J.O. Basics of particle therapy i: Physics. Radiat. Oncol. J. 2011, 29, 135. [Google Scholar] [CrossRef] [PubMed]
- Durante, M.; Paganetti, H. Nuclear physics in particle therapy: A review. Rep. Prog. Phys. 2016, 79, 096702. [Google Scholar] [CrossRef] [PubMed]
- Combs, S.E.; Jäkel, O.; Haberer, T.; Debus, J. Particle therapy at the heidelberg ion therapy center (hit)—Integrated research-driven university-hospital-based radiation oncology service in heidelberg, germany. Radiother. Oncol. 2010, 95, 41. [Google Scholar] [CrossRef] [PubMed]
- Noda, K.; Furukawa, T.; Fujimoto, T.; Hara, Y.; Inaniwa, T.; Iwata, Y.; Katagiri, K.; Kanematsu, N.; Mizushima, K.; Mori, S.; et al. Recent progress and future plans of heavy-ion cancer radiotherapy with himac. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2017, 406, 374. [Google Scholar] [CrossRef]
- Ohno, T.; Kanai, T.; Yamada, S.; Yusa, K.; Tashiro, M.; Shimada, H.; Torikai, K.; Yoshida, Y.; Kitada, Y.; Katoh, H.; et al. Carbon ion radiotherapy at the gunma university heavy ion medical center: New facility set-up. Cancers 2011, 3, 4046–4060. [Google Scholar] [CrossRef]
- Yang, J.; Shi, J.; Chai, W.; Xia, J.; Yuan, Y.; Li, Y. Design of a compact structure cancer therapy synchrotron. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2014, 756, 19. [Google Scholar] [CrossRef]
- Inaniwa, T.; Kanematsu, N.; Noda, K.; Kamada, T. Treatment planning of intensity modulated composite particle therapy with dose and linear energy transfer optimization. Phys. Med. Biol. 2017, 62, 5180. [Google Scholar] [CrossRef]
- Kopp, B.; Mein, S.; Dokic, I.; Harrabi, S.; Böhlen, T.T.; Haberer, T.; Debus, J.; Abdollahi, A.; Mairani, A. Development and validation of single field multi-ion particle therapy treatments. Int. J. Radiat. Oncol. Biol. Phys. 2020, 106, 194. [Google Scholar] [CrossRef]
- Ebner, D.K.; Frank, S.J.; Inaniwa, T.; Yamada, S.; Shirai, T. The emerging potential of multi-ion radiotherapy. Front. Oncol. 2021, 11, 624786. [Google Scholar] [CrossRef]
- Wangler, T.P. RF Linear Accelerators; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Ratzinger, U.; Peters, A.; Zhang, C.; Hähnel, H.; Hoeltermann, H.; Podlech, H.; Schuett, M.; Cee, R.; Altürk, S.; Haberer, T. A new rfq for the carbon therapy injector at hit heidelberg. In Proceedings of the 32nd Linear Accelerator Conference (LINAC2024), Chicago, IL, USA, 25–30 August 2024. [Google Scholar]
- Katayama, R.; Kako, E.; Yamaguchi, S.; Michizono, S.; Umemori, K.; Kondo, Y. Design study of compact medical accelerator using superconducting rf quadrupole for boron neutron capture therapy. Phys. Rev. Accel. Beams 2022, 25, 021601. [Google Scholar] [CrossRef]
- Bencini, V.; Pommerenke, H.W.; Grudiev, A.; Lombardi, A.M. 750 mhz radio frequency quadrupole with trapezoidal vanes for carbon ion therapy. Phys. Rev. Accel. Beams 2020, 23, 122003. [Google Scholar] [CrossRef]
- Budanov, Y.A.; Kalinin, V.; Frolov, B. Carbon ion injection system for a complex of radiation therapy. Phys. Part. Nucl. Lett. 2024, 21, 341. [Google Scholar] [CrossRef]
- Yap, J.; Franco, A.D.; Sheehy, S. Future developments in charged particle therapy: Improving beam delivery for efficiency and efficacy. Front. Oncol. 2021, 11, 780025. [Google Scholar] [CrossRef] [PubMed]
- Graeff, C.; Volz, L.; Durante, M. Emerging technologies for cancer therapy using accelerated particles. Prog. Part. Nucl. Phys. 2023, 131, 104046. [Google Scholar] [CrossRef]
- Kraan, A.C.; Guerra, A.D. Technological developments and future perspectives in particle therapy: A topical review. IEEE Trans. Radiat. Plasma Med. Sci. 2024, 8, 453–481. [Google Scholar] [CrossRef]
- Wang, K.-D.; Yuan, Y.-J.; Yin, X.-J.; Yang, J.-C.; Du, H.; Li, Z.-S.; Li, X.-N.; Zhao, H.; Dong, Z.-Q.; Liu, J.; et al. Fast-bunching design of compact heavy ion rfq linac. Nucl. Sci. Tech. 2018, 29, 1. [Google Scholar] [CrossRef]
- Jameson, R.A.; Yee-Rendon, B. Improved bunching and longitudinal emittance control in an rfq. J. Instrum. 2022, 17, P12011. [Google Scholar] [CrossRef]
- Vretenar, M.; Dallocchio, A.; Dimov, V.; Garlaschè, M.; Grudiev, A.; Lombardi, A.; Mathot, S.; Montesinos, E.; Timmins, M. A compact high-frequency rfq for medical applications. In Proceedings of the 27th Linear Accelerator Conference, LINAC2014, Geneva, Switzerland, 31 August–5 September 2014. [Google Scholar]
- Liu, G.; Gu, L.; Yuan, C.; Zhou, W. Beam dynamics design and error analysis of a high frequency rfq for medical application. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2024, 1069, 169930. [Google Scholar] [CrossRef]
- Mehrotra, N.; Nayak, B. Radial matching section of rfq revisited. J. Instrum. 2020, 15, T10001. [Google Scholar] [CrossRef]
- Vretenar, M.; Angoletta, M.E.; Borburgh, J.; Bottura, L.; Taylor, R.; Tranquille, G.; Benedetto, E.; Torims, T.; Paļskis, K.; Sapinski, M.; et al. Jacow: Conceptual design of a compact synchrotron-based facility for cancer therapy and biomedical research with helium and proton beams. JACoW IPAC 2023, 2023, THPM058. [Google Scholar]
- Vretenar, M.; Benedetto, E. New accelerator designs: Nimms. Health Technol. 2024, 14, 945. [Google Scholar] [CrossRef]
- Zink, K.; Baumann, K.S.; Theiss, U.; Subtil, F.; Lahrmann, S.; Eberle, F.; Adeberg, S. Organization and operation of multi particle therapy facilities: The marburg ion-beam therapy center, germany (mit). Health Technol. 2024, 14, 929. [Google Scholar] [CrossRef] [PubMed]
- Kilpatrick, W. Criterion for vacuum sparking designed to include both rf and dc. Rev. Sci. Instrum. 1957, 28, 824. [Google Scholar] [CrossRef]
- Benedetto, E.; Vretenar, M. Innovations in the next generation medical accelerators for therapy with ion beams. J. Phys. Conf. Ser. 2024, 2687, 092003. [Google Scholar] [CrossRef]
- Mairani, A.; Mein, S.; Blakely, E.; Debus, J.; Durante, M.; Ferrari, A.; Fuchs, H.; Georg, D.; Grosshans, D.R.; Guan, F.; et al. Roadmap: Helium ion therapy. Phys. Med. Biol. 2022, 67, 15TR02. [Google Scholar] [CrossRef]
- Suzuki, M.; Kase, Y.; Yamaguchi, H.; Kanai, T.; Ando, K. Relative biological effectiveness for cell-killing effect on various human cell lines irradiated with heavy-ion medical accelerator in chiba (himac) carbon-ion beams. Int. J. Radiat. Oncol. Biol. Phys. 2000, 48, 241. [Google Scholar] [CrossRef]
- Krämer, M.; Scifoni, E.; Schuy, C.; Rovituso, M.; Tinganelli, W.; Maier, A.; Kaderka, R.; Kraft-Weyrather, W.; Brons, S.; Tessonnier, T.; et al. Helium ions for radiotherapy? physical and biological verifications of a novel treatment modality. Med. Phys. 2016, 43, 1995. [Google Scholar] [CrossRef]
- Iwata, Y.; Yamada, S.; Murakami, T.; Fujimoto, T.; Fujisawa, T.; Ogawa, H.; Miyahara, N.; Yamamoto, K.; Hojo, S.; Sakamoto, Y.; et al. Performance of a compact injector for heavy-ion medical accelerators. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2007, 572, 1007. [Google Scholar] [CrossRef]
- Vormann, H.; Schlitt, B.; Clemente, G.; Kleffner, C.; Reiter, A.; Ratzinger, U. Status of the linac components for the italian hadrontherapy centre cnao. In Proceedings of the 11th European Conference, EPAC 2008, Genoa, Italy, 23–27 June 2008; p. 1833. [Google Scholar]
- Wang, K.D.; Yuan, Y.J.; Yin, X.J.; Yang, J.C.; Li, Z.S.; Du, H.; Li, X.N.; Kong, Q.Y.; Wang, K.; Dong, Z.Q.; et al. Rf design of radio-frequency quadrupole accelerator for heavy ion medical machine. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2019, 927, 375. [Google Scholar] [CrossRef]
- Kim, H.-S.; Kwon, H.-J.; Lee, S.-H.; Kim, D.-H.; Yun, S.-P.; Dang, J.-J. Development of an rfq-based compact accelerator system for ion beam applications. J. Korean Phys. Soc. 2023, 83, 140. [Google Scholar] [CrossRef]
- Crandall, K.R. RFQ Design Codes, LANL Report; Tech. Rep. LA-UR-96 (1836); Los Alamos National Laboratory: Los Alamos, NM, USA, 1836; Available online: https://scholar.google.com/scholar?hl=zh-CN&as_sdt=0%2C5&q=Crandall%2C+K.%3B+et+al.+Rfq+Design+Codes%2C+Lanl+Report%3B+Tech.+Rep.+LA-UR-96+%281836%29&btnG=#d=gs_cit&t=1748577274374&u=%2Fscholar%3Fq%3Dinfo%3A_wYCjdUns2QJ%3Ascholar.google.com%2F%26output%3Dcite%26scirp%3D0%26hl%3Dzh-CN (accessed on 25 May 2025).
- Crandall, K.; Stokes, R.; Wangler, T. Rf quadrupole beam dynamics design studies. In Proceedings of the Linear Accelerator Conference, Montauk, NY, USA, 10–14 September 1979. [Google Scholar]
- Zhang, C.; Schempp, A. Beam dynamics studies on a 200 ma proton radio frequency quadrupole accelerator. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2008, 586, 153. [Google Scholar] [CrossRef]
- Bahng, J.; Choi, B.H.; Choi, B.-H.; Kim, D.; Kim, E.-S. Development of rfq for bnct accelerator. In Proceedings of the 8th International Particle Accelerator Conference (IPAC’17), Copenhagen, Denmark, 14–19 May 2017; JACOW: Geneva, Switzerland, 2017; pp. 4260–4262. [Google Scholar]
- Kondo, Y.; Tamura, J.; Yee-Rendon, B. Reference design of the rfq for jaea ads linac. In Proceedings of the 3rd J-PARC Symposium (J-PARC2019), Tsukuba, Japan, 23–27 September 2019; p. 011015. [Google Scholar]
- Gaur, R.; Shrivastava, P. Beam dynamics and electromagnetic design studies of 3 mev rfq for sns programme. J. Electromagn. Anal. Appl. 2010, 2, 519. [Google Scholar] [CrossRef]
- Rao, S.; Singh, P. Design studies of a high-current radiofrequency quadrupole for accelerator-driven systems programme. Pramana 2010, 74, 247. [Google Scholar] [CrossRef]
- Ovsyannikov, A.D.; Ovsyannikov, D.A.; Chung, S.-L. Optimization of a radial matching section. Int. J. Mod. Phys. A 2009, 24, 952. [Google Scholar] [CrossRef]
- Zhang, C.; Schempp, A. Design of an upgradeable 45–100 ma rfq accelerator for fair. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2009, 609, 95. [Google Scholar] [CrossRef]
- Yaramyshev, S.; Barth, W.; Maier, M.; Orzhekhovskaya, A.; Schlitt, B.; Vormann, H.; Cee, R.; Peters, A. Upgrade of the hit injector linac-frontend . In Proceedings of the 11th International Conference on Heavy Ion Accelerator Technology (HIAT’09), Venice, Italy, 8–12 June 2009; pp. 6–9. [Google Scholar]
- Davidson, R.C.; Hong, Q. Physics of Intense Charged Particle Beams in High Energy Accelerators; World Scientific: Singapore, 2001. [Google Scholar]
- Reiser, M. Theory and Design of Charged Particle Beams; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Comunian, M.; Bellan, L.; Pisent, A. Comparison of longitudinal emittance of various rfqs. J. Instrum. 2024, 19, P01024. [Google Scholar] [CrossRef]
- Kumar, S.; Mandal, A. Start to end simulation of high current injector using tracewin code. In Proceedings of the 6th International Particle Accelerator Conference (IPAC2015), Richmond, VA, USA, 3–8 May 2015; MOPWA047. pp. 3–8. [Google Scholar]
- Duperrier, R. Toutatis: A radio frequency quadrupole code. Phys. Rev. Spec. Top.-Accel. Beams 2000, 3, 124201. [Google Scholar] [CrossRef]
- Gambino, N.; Adler, L.; Franco, A.D.; Ecker, F.; Farinon, F.; Guidoboni, G.; Kurfürst, C.; Myalski, S.; Penescu, L.; Pivi, M.; et al. Impact of ion source stability for a medical accelerator. J. Instrum. 2019, 14, C05017. [Google Scholar] [CrossRef]
- Sen, T.; Syphers, M. Effect of power supply ripple on emittance growth in the collider. In Proceedings of the International Conference on Particle Accelerators, Washington, DC, USA, 17–20 May 1993; pp. 146–148. [Google Scholar]
- Cao, Y.; Li, J.Q.; Sun, L.T.; Zhang, X.Z.; Feng, Y.C.; Wang, H.; Ma, B.H.; Li, X.X. An all permanent magnet electron cyclotron resonance ion source for heavy ion therapy. Rev. Sci. Instruments 2014, 85, 02A960. [Google Scholar] [CrossRef]
- Junior, P. Space-charge limits in heavy-ion rfq linacs. Part. Accel. 1983, 13, 231. [Google Scholar]
- Crandall, K.R.; Wangler, T.P.; Young, L.M.; Billen, J.H.; Neuschaefer, G.H.; Schrage, D.L. RFQ Design Codes; LA-UR-96-1836; Los Alamos National Laboratory: Los Alamos, NM, USA, 2005. [Google Scholar]
- Eshraqi, M.; Prisco, R.D.; Miyamoto, R.; Edgar, S.; Dølrath, T.H. Statistical error studies in the ess linac. In Proceedings of the 5th International Particle Accelerator Conference, IPAC 2014, Dresden, Germany, 15–20 June 2014; pp. 3323–3325. [Google Scholar]






| Parameter | Value |
|---|---|
| Particle | C/He |
| Frequency [MHz] | 200 |
| Beam current [mA] | 0.3 (C)/1 (He) |
| Injection energy [keV/u] | 8 |
| Output energy [keV/u] | 750 |
| Input emittance [ mm·mrad] | 0.2 |
| Kilpatrick factor | ≤1.8 |
| Voltage [kV] | 60~80 |
| Length [m] | ≤2.8 |
| Transmission efficiency [%] | ≥95 |
| Emittance growth [%] | ≤5 |
| Extra beam loss [%] | ≤10 |
| Parameter | General Design | New Design |
|---|---|---|
| Particle | C/He | |
| Beam current [mA] | 0.3 (C)/1 (He) | |
| Frequency [MHz] | 200 | |
| Input emittance [ mm·mrad] | ||
| Input energy [keV/u] | 8 | |
| Output energy [keV/u] | 750 | |
| Voltage [kV] | 70 | 65 |
| Modulation parameter | 1~ | 1~ |
| Focusing strength factor | ~ | |
| Synchronous phase [degree] | ~ | ~ |
| Length [m] | ||
| Cell numbers | 310 | 320 |
| Kilpatrick factor | ||
| Transmission efficiency [%] | / | |
| Program | Transmission Efficiency | / | |
|---|---|---|---|
| [%] | [ mm·mrad] | [ mm·mrad] | |
| PARMTEQM | 98.10 | 0.1984/0.1982 | 0.08533 |
| TRACEWIN | 97.30 | 0.1985/0.1984 | 0.08528 |
| TOUTATIS | 97.70 | 0.1983/0.1981 | 0.08531 |
| Program | Transmission Efficiency | / | |
|---|---|---|---|
| [%] | [ mm·mrad] | [ mm·mrad] | |
| PARMTEQM | 97.00 | 0.1972/0.1980 | 0.08158 |
| TRACEWIN | 96.50 | 0.1968/0.1973 | 0.08162 |
| TOUTATIS | 96.90 | 0.1973/0.1975 | 0.08177 |
| Item | Scan Range | Unit |
|---|---|---|
| Beam current | 0~8 | mA |
| vane-voltage multiplier | ~ | - |
| Input emittance | ~ | mm·mrad |
| Energy spread | 0~10 | % |
| Spatial displacement for centroid | ~ | cm |
| Divergence-coordinate displacement for centroid | ~80 | mrad |
| Item | Value | Note |
|---|---|---|
| [mm] | Longitudinal profile | |
| d [mm] | Transverse curvature for the electrode | |
| [mm] | Perpendicular tilt for electrode | |
| [mm] | Parallel tilt for electrode | |
| [mm] | Perpendicular displacement for electrode | |
| [mm] | Parallel displacement error for electrode | |
| [mm] | Longitudinal displacement for electrode | |
| [mm] | Vertical tilt | |
| [mm] | Horizontal tilt | |
| [mm] | Vertical displacement | |
| [mm] | Horizontal displacement | |
| [mm] | Longitudinal displacement |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Cao, G.; Zhang, W. Beam Dynamics Design of a Multi-Ion RFQ for Medical Application. Appl. Sci. 2025, 15, 6182. https://doi.org/10.3390/app15116182
Wang X, Cao G, Zhang W. Beam Dynamics Design of a Multi-Ion RFQ for Medical Application. Applied Sciences. 2025; 15(11):6182. https://doi.org/10.3390/app15116182
Chicago/Turabian StyleWang, Xinran, Guiling Cao, and Wenzhi Zhang. 2025. "Beam Dynamics Design of a Multi-Ion RFQ for Medical Application" Applied Sciences 15, no. 11: 6182. https://doi.org/10.3390/app15116182
APA StyleWang, X., Cao, G., & Zhang, W. (2025). Beam Dynamics Design of a Multi-Ion RFQ for Medical Application. Applied Sciences, 15(11), 6182. https://doi.org/10.3390/app15116182






