Bessel Picosecond Laser Cutting Glass-Ceramics: Optimization of Processing Point Spacing, Incident Power, and Burst Mode
Abstract
1. Introduction
2. Test Materials
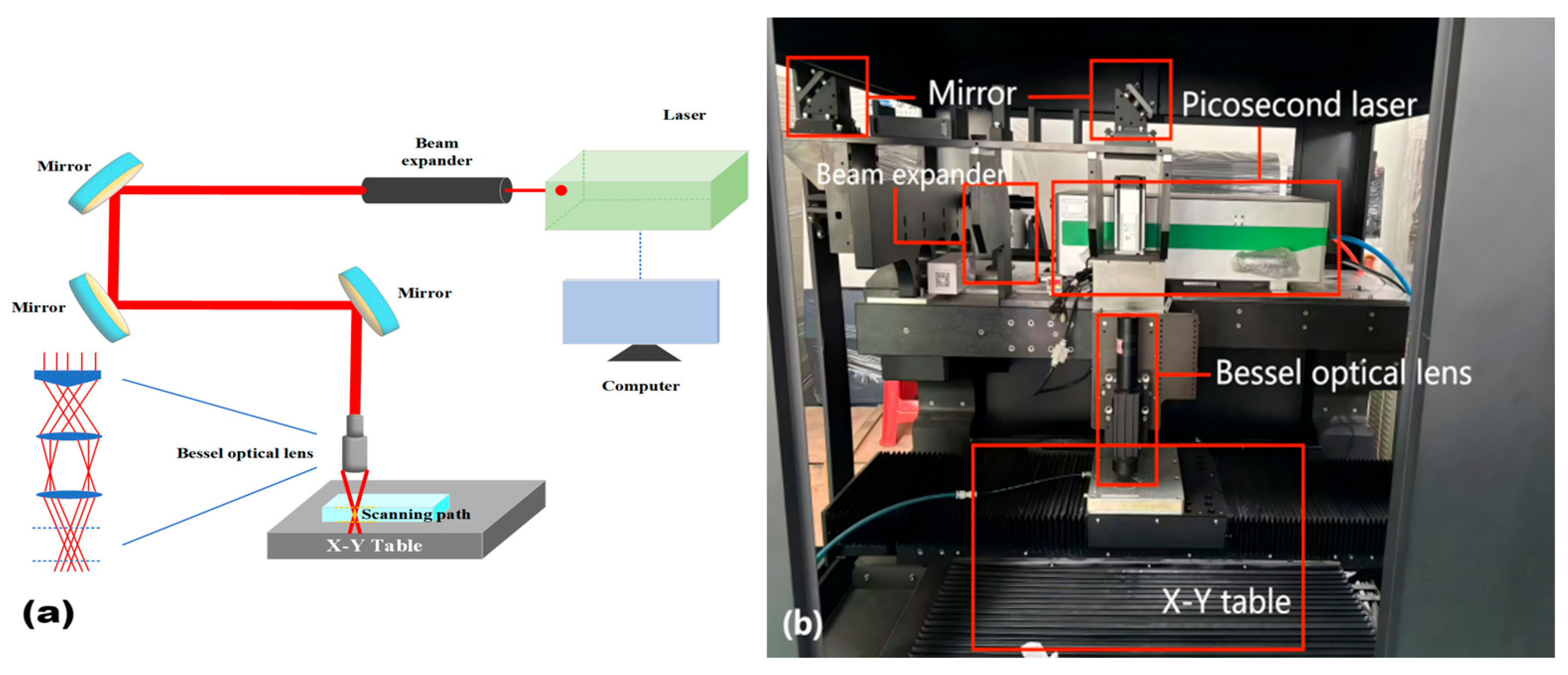
2.1. Test Instruments
2.2. Test and Analysis Methods
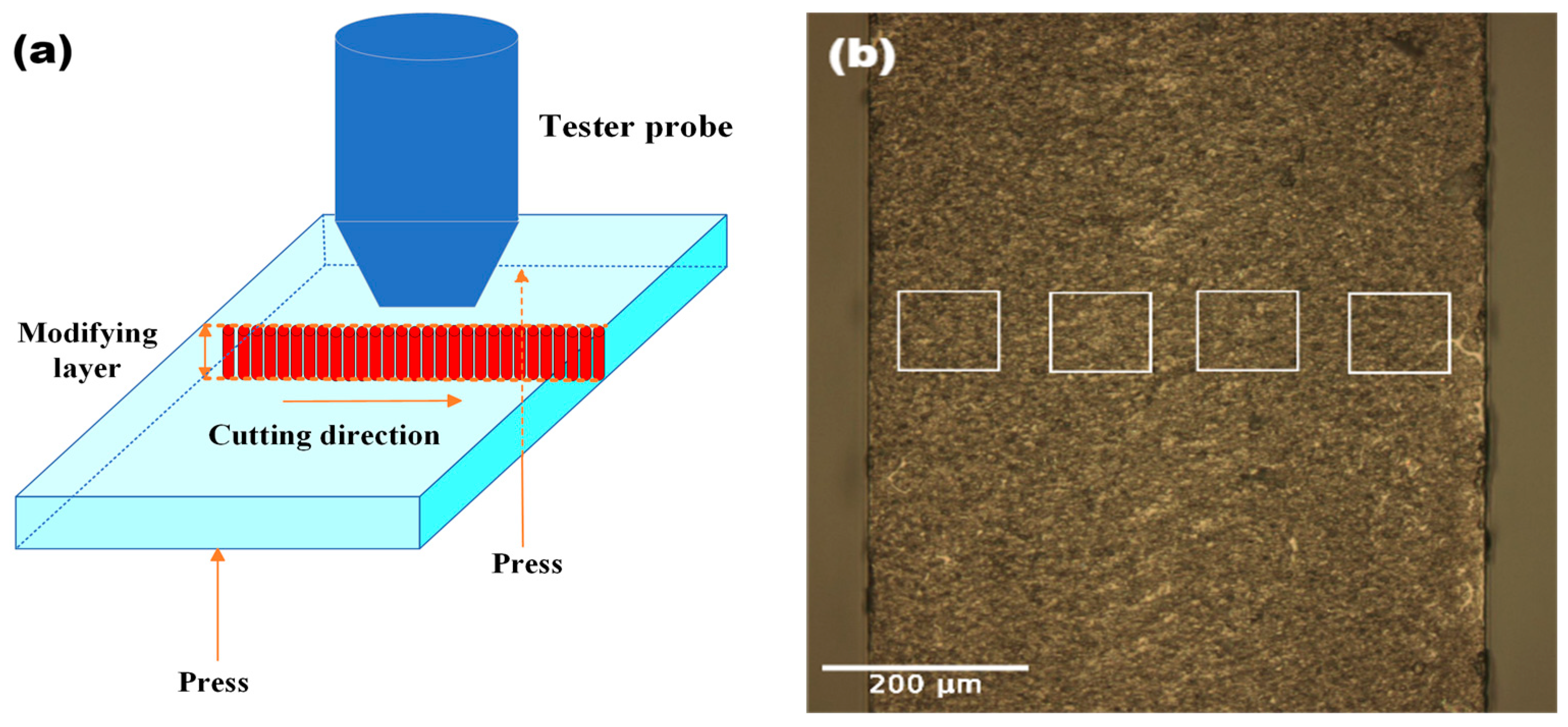
2.2.1. Test Methods
2.2.2. Analysis Method
3. Results and Discussion
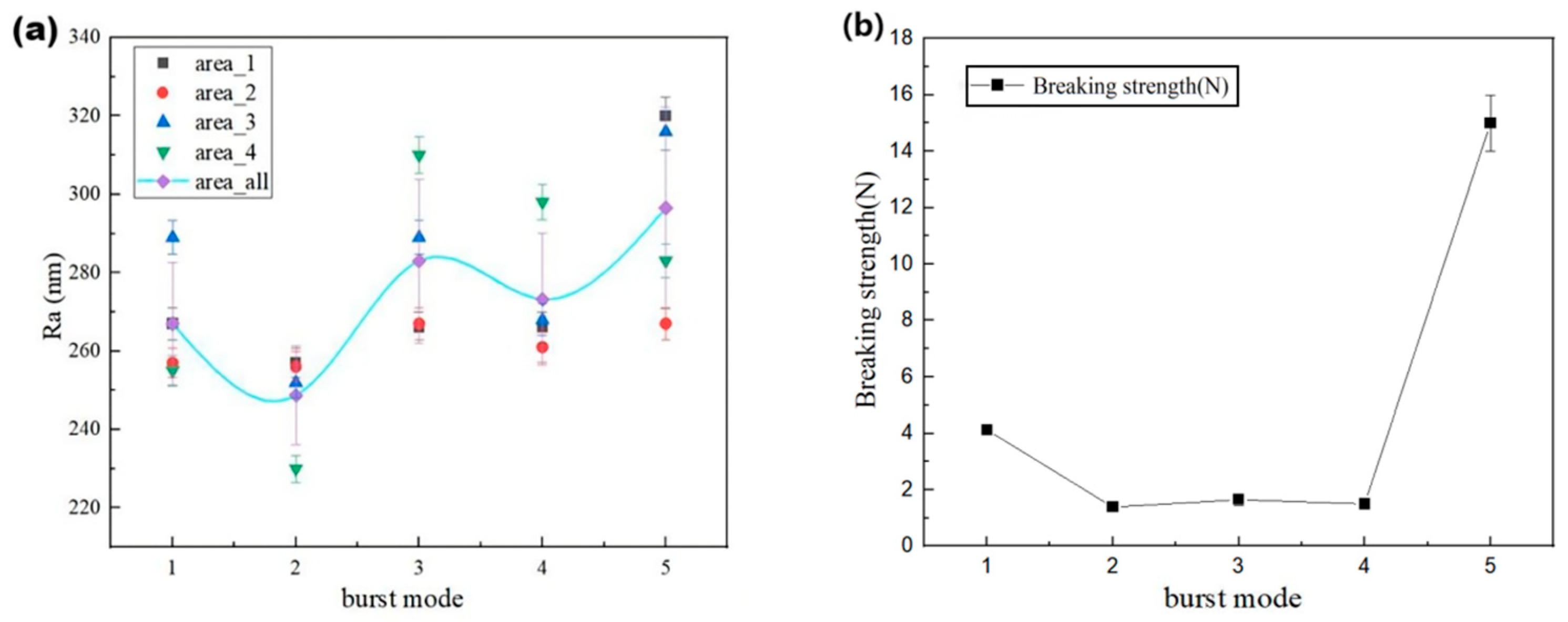
3.1. The Influence of the Number of Processing Pulses on the Cutting Effect
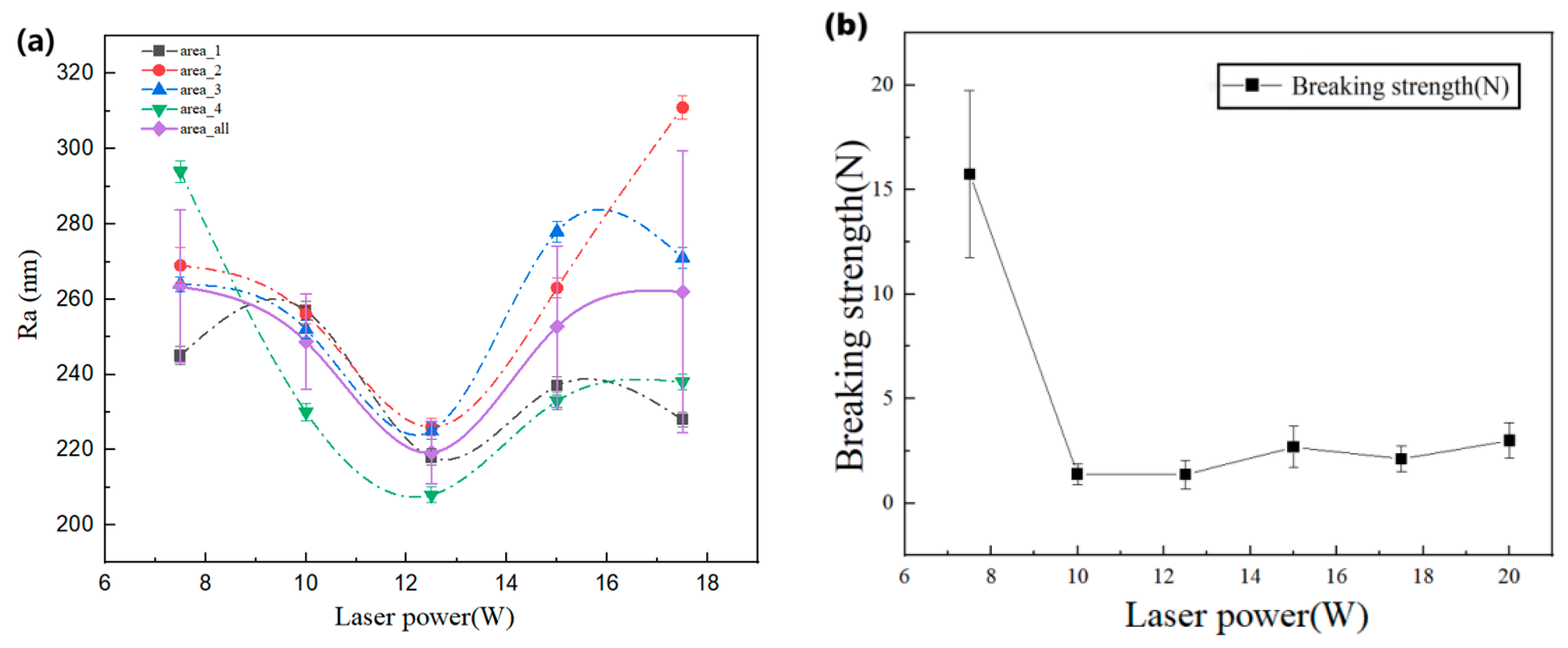
3.2. Influence of Incident Laser Power on the Cutting Effect
3.3. Influence of Machining Point Spacing on Cutting Quality
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deubener, J.; Allix, M.; Davis, M.J.; Duran, A.; Höche, T.; Honma, T.; Komatsu, T.; Krüger, S.; Mitra, I.; Müller, R.; et al. Updated definition of glass-ceramics. J. Non Cryst. Solids 2018, 501, 3–10. [Google Scholar] [CrossRef]
- Kartopu, G.; Oklobia, O.; Tansel, T.; Jones, S.; Irvine, S.J.C. A facile photolithography process enabling pinhole-free thin film photovoltaic modules on soda-lime glass. Sol. Energy Mater. Sol. Cells 2023, 251, 112112. [Google Scholar] [CrossRef]
- Kwon, O.; Takahashi, Y.; Miyazaki, T.; Terakado, N.; Fujiwara, T. Nanostructure and photocatalytic behavior of glass-ceramics in system. J. Ceram. Soc. Jpn. 2020, 128, 839–842. [Google Scholar] [CrossRef]
- Ma, Y.; Guo, C.; Meng, X.; Yang, S.; Kou, S.; Deng, J.; Fan, S.; Liu, X. Corrosion resistance and microstructural evolution of y-al-si-o glass-ceramics environmental barrier coating candidate in the presence of cmas. Mater. Charact. 2025, 220, 114685. [Google Scholar] [CrossRef]
- Ibrahim, S.; El-Kheshen, A.A.; Abdel-baki, M.; Fayad, A.M.; Hamdy, Y.M.; Ibrahim, M.M.; Marzouk, M.A. Synthesis and characterization of erbium silica glass and glass-ceramics for potential low-emissivity coating applications. Ceram. Int. 2025, 51, 458–472. [Google Scholar] [CrossRef]
- Kažukauskas, E.; Butkus, S.; Jukna, V.; Paipulas, D. Surface roughness control in deep engraving of fused silica using femtosecond laser ablation. Surf. Interfaces 2024, 50, 104471. [Google Scholar] [CrossRef]
- Sugioka, K.; Cheng, Y. Ultrafast lasers—Reliable tools for advanced materials processing. Light Sci. Appl. 2014, 3, e149. [Google Scholar] [CrossRef]
- Xiong, S.; Wang, R.; Tao, H. Ultrafast laser micromachining the ultra-low expansion glass-ceramic: Optimization of processing parameters and physical mechanism. J. Eur. Ceram. Soc. 2021, 41, 5990–5999. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, X.; Li, W.; Hang, W. Material removal modes and processing mechanism in microultrasonic machining of ball ceramic tool. Ceram. Int. 2024, 50, 28844–28856. [Google Scholar] [CrossRef]
- Feng, J.; Wang, J.; Liu, H.; Sun, Y.; Fu, X.; Ji, S.; Liao, Y.; Tian, Y. A review of an investigation of the ultrafast laser processing of brittle and hard materials. Materials 2024, 17, 3657. [Google Scholar] [CrossRef]
- Jedrkiewicz, O.; Kumar, S.; Sotillo, B.; Bollani, M.; Chiappini, A.; Ferrari, M.; Ramponi, R.; Di Trapani, P.; Eaton, S.M. Pulsed bessel beam-induced microchannels on a diamond surface for versatile microfluidic and sensing applications. Opt. Mater. Express 2017, 7, 1962–1970. [Google Scholar] [CrossRef]
- Jia, X.; Vrijburg, F.; Zhang, W.; Groenendijk, M.; Pei, Y. Ultrasmooth micromilling of stainless steel by ultrashort pulsed laser ablation using mhz bursts. ACS Appl. Mater. Interfaces 2025, 17, 7989–8002. [Google Scholar] [CrossRef]
- Yildirim, K.; Nagarajan, B.; Tjahjowidodo, T.; Castagne, S. Review of in-situ process monitoring for ultra-short pulse laser micromanufacturing. J. Manuf. Process. 2025, 133, 1126–1159. [Google Scholar] [CrossRef]
- Courvoisier, F.; Zhang, J.; Bhuyan, M.K.; Jacquot, M.; Dudley, J.M. Applications of femtosecond bessel beams to laser ablation. Appl. Phys. A 2012, 112, 29–34. [Google Scholar] [CrossRef]
- Guilberteau, T.; Balage, P.; Lafargue, M.; Lopez, J.; Gemini, L.; Manek-Hönninger, I. Bessel beam femtosecond laser interaction with fused silica before and after chemical etching: Comparison of single pulse, mhz-burst, and ghz-burst. Micromachines 2024, 15, 1313. [Google Scholar] [CrossRef]
- Liang, G.; Sun, S.; Wang, J.; Qu, Z.; Wei, T.; Liu, X.; Sun, H.; Monka, P.P.; Hamza, A. Application of array bessel beam generated by superposition method in electronic glass cutting. Opt. Lasers Eng. 2024, 181, 108384. [Google Scholar] [CrossRef]
- Marx, J.; Seefeldt, M.; Haske, D.; Lutz, C.; Hellmann, R.; Esen, C.; Ostendorf, A. Holographic freeform micro hole processing using bessel beams. Opt. Laser Technol. 2025, 183, 112287. [Google Scholar] [CrossRef]
- Praharaj, P.; Stoian, R.; Bhuyan, M.K. Aberration and self-reconstruction of zero-order bessel beams in isolated and array format generated using positive and negative axicon lenses. Opt. Lasers Eng. 2025, 186, 108823. [Google Scholar] [CrossRef]
- Jaeggi, B.; Neuenschwander, B.; Meier, T.; Zimmermann, M.; Hennig, G. High precision surface structuring with ultra-short laser pulses and synchronized mechanical axes. Phys. Procedia 2013, 41, 319–326. [Google Scholar] [CrossRef]
- Neuenschwander, B.; Jaeggi, B.; Schmid, M.; Hennig, G. Surface structuring with ultra-short laser pulses: Basics, limitations and needs for high throughput. Phys. Procedia 2014, 56, 1047–1058. [Google Scholar] [CrossRef]
- Wang, Y.; Dai, Y.; Mumtaz, F.; Luo, K. Advanced techniques in quartz wafer precision processing: Stealth dicing based on filament-induced laser machining. Opt. Laser Technol. 2024, 171, 110474. [Google Scholar] [CrossRef]
- Yang, S.; Wang, B.; Zeng, R.; Liu, Z.; Xie, Y.; Lu, L. Effect of laser-assisted heat treatment on material removal behavior of sapphire in indentation and scratching. Mater. Sci. Semicond. Process. 2024, 181, 108630. [Google Scholar] [CrossRef]
- You, K.; Yan, G.; Luo, X.; Gilchrist, M.D.; Fang, F. Advances in laser assisted machining of hard and brittle materials. J. Manuf. Process. 2020, 58, 677–692. [Google Scholar] [CrossRef]
- Pham, T.-H.; Luyen, T.-T.; Nguyen, D.-T. Investigating the correlation between surface roughness and degree of chip segmentation in a7075 aluminum alloy milling across varied cutting speeds. Sādhanā 2024, 49, 193. [Google Scholar] [CrossRef]
- Yuqin, W.; Wei, Z.; Jinyuan, T. Research on the correlation between roughness parameters and contact stress on tooth surfaces and its dominant characteristics. Measurement 2024, 238, 115399. [Google Scholar] [CrossRef]
- del Hoyo, J.; Meyer, R.; Furfaro, L.; Courvoisier, F. Nanoscale confinement of energy deposition in glass by double ultrafast bessel pulses. Nanophotonics 2021, 10, 1089–1097. [Google Scholar] [CrossRef]
- Liao, K.; Wang, W.; Mei, X.; Liu, B. High quality full ablation cutting and stealth dicing of silica glass using picosecond laser bessel beam with burst mode. Ceram. Int. 2022, 48, 9805–9816. [Google Scholar] [CrossRef]
- Chen, S.; Luo, Y.; Fan, X.; Wu, C.; Zhang, G.; Huang, Y.; Rong, Y.; Chen, L. Thick glass high-quality cutting by ultrafast laser bessel beam perforation-assisted separation. Micromachines 2024, 15, 854. [Google Scholar] [CrossRef]
- Wang, W.; Mei, X.; Jiang, G. Control of microstructure shape and morphology in femtosecond laser ablation of imprint rollers. Int. J. Adv. Manuf. Technol. 2008, 41, 504–512. [Google Scholar] [CrossRef]
- Jiang, J.; Oliveira, J.P.; Yang, J.; Zheng, M.; Li, H.; Xu, W.; Wu, L.; Dou, T.; Wang, R.; Tan, C.; et al. Effect of defocusing distance on interfacial reaction and mechanical properties of dissimilar laser al/steel joints with a porous high entropy alloy coating. Mater. Charact. 2024, 210, 113751. [Google Scholar] [CrossRef]
- ISO 9385:1990; Glass and Glass-Ceramics—Knoop Hardness Test. ISO: Geneva, Switzerland, 1990.






| Mechanical Property | Standard Value |
|---|---|
| density | 2.53 g/cm3 |
| Poisson’s ratio | 0.24 |
| Thermal conductivity (20 °C) | 1.46 W/(m·K) |
| Knoop hardness HK 0.1/20 (ISO9385) [31] | 620 |
| Refractive index | 1.54 |
| Thermal diffusion coefficient (20 °C) | 0.72 10−6 m2/s |
| Young’s modulus (20 °C) | 84.7 GPa |
| Specific heat capacity (20 °C) | 0.80 J/(g·K) |
| Machining System Related Parameters | Standard Value |
|---|---|
| Laser operating frequency | 50 kHz~1000 kHz |
| Pulse width | ≤8 ps |
| Maximum output power | 30 W |
| Wave length | 1064 nm |
| Positioning accuracy of the platform | ±5 μm |
| repeatability | ±2 μm |
| The scaling factor of the mirror system | 8 |
| Refractive index of the axial cone | 1.45 |
| Incident Laser Power (W) | Mean Roughness of Section (nm) | Regional Maximum Difference (nm) |
|---|---|---|
| 7.5 | 234.35 | 439.6 |
| 10 | 239.75 | 63 |
| 12.5 | 219.25 | 18 |
| 15 | 225.75 | 115 |
| 17.5 | 248.5 | 168 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, X.; Duan, Y.; Song, Y.; Peng, C.; Li, J.; Li, Z.; Deng, C.; Yang, J.; Gao, Q.; Zhang, Z.; et al. Bessel Picosecond Laser Cutting Glass-Ceramics: Optimization of Processing Point Spacing, Incident Power, and Burst Mode. Appl. Sci. 2025, 15, 6172. https://doi.org/10.3390/app15116172
Pan X, Duan Y, Song Y, Peng C, Li J, Li Z, Deng C, Yang J, Gao Q, Zhang Z, et al. Bessel Picosecond Laser Cutting Glass-Ceramics: Optimization of Processing Point Spacing, Incident Power, and Burst Mode. Applied Sciences. 2025; 15(11):6172. https://doi.org/10.3390/app15116172
Chicago/Turabian StylePan, Xinjian, Yunfei Duan, Yi Song, Cheng Peng, Jinxuan Li, Zhili Li, Chunjian Deng, Jianjun Yang, Qingguo Gao, Zhi Zhang, and et al. 2025. "Bessel Picosecond Laser Cutting Glass-Ceramics: Optimization of Processing Point Spacing, Incident Power, and Burst Mode" Applied Sciences 15, no. 11: 6172. https://doi.org/10.3390/app15116172
APA StylePan, X., Duan, Y., Song, Y., Peng, C., Li, J., Li, Z., Deng, C., Yang, J., Gao, Q., Zhang, Z., & Cai, Y. (2025). Bessel Picosecond Laser Cutting Glass-Ceramics: Optimization of Processing Point Spacing, Incident Power, and Burst Mode. Applied Sciences, 15(11), 6172. https://doi.org/10.3390/app15116172






