Analysis of Selected Methods of Computer-Aided Design for Stage Structures

Abstract

This article presents the design process for a modern stage trapdoor, which was designed to optimize the work of cultural facilities personnel and increase the attractiveness of future performances and events. Strength calculations for the supporting structure were carried out in the Soldis DESIGNER program, and based on these, a 3D model of the stage trapdoor was designed and placed in the space of the stage chimney. In order to verify and analyze the strength of the structure, the 3D model was prepared for detailed analysis in the Autodesk Inventor program. Tests were carried out for four load cases of the structure for 15 different load values. Information about the maximum value of the deflection arrow and the maximum stress was obtained. Collected data were organized in tables and displayed in line and column charts, based on which conclusions were drawn. These analyses showed a high degree of compliance between calculations from both programs. It was found that in this type of structure, a detailed analysis in 3D CAD programs is not necessary for the proper design of the supporting structure, which allows for simplification of the design process. The designed trapdoor meets all design requirements and can be implemented as a solution to improve the functionality and aesthetics of the stage’s technical equipment.

1. Problem Description

Stage technology plays a key role in the function of cultural facilities such as theatres, opera houses or congress centers, providing technical support for staging and enabling smooth changes in scenery. It includes a wide range of equipment such as lifts, lighting systems, rotating platforms or curtain control mechanisms. A source that allows us to assess the development of stage technology is D’Uterman’s “History of the city and industry of Valenciennes” [1]. Modern stage systems must combine engineering precision with artistic vision to ensure efficiency as well as safety. We can read about many aspects of stage mechanisms and the possibilities of their potential modernization in the article [2]. Thanks to technological progress, modern theatres and stages are equipped with advanced automation and control systems that not only improve the assembly of scenery, but also enable dynamic effects during a performance. Stage structures are predominantly made of steel. This material plays a key role in the construction industry, which leads to a significant increase in its consumption and production per capita [3]. This increase is driven by a growing population and the increasing demand for industrialization, particularly in developing countries, which is one of many factors influencing this trend [4]. Compared to other construction materials, steel is characterized by several significant advantages, such as its light weight, excellent construction properties, and high level of prefabrication, and the possibility of speeding up the pace of construction [5,6]. Safety is the top priority when designing stage equipment, and the reliability of stage structures is crucial to ensure the continuity of performances and the protection of the lives and health of artists and technicians.

Article [7] presents an assessment of fire protection systems in proscenium theatres, but no studies have been conducted on the strength of stage structures, which is one of the elements that lead to the analysis of cultural facilities in this respect. Information about stresses that occur in steel structures and areas of greatest deformation can be obtained from article [8], but the frame analyzed by the author was small and the analysis was not carried out in sufficient detail. When it comes to stage trapdoors, it is crucial to ensure the stability of the structure, minimize the risk of failure and meet safety standards.

A stage trapdoor is a complex mechanism that must meet stringent technical requirements. Trapdoor construction should ensure a smooth transition between levels, minimizing the risk of failure during operation. The platform of a stage trapdoor is usually at the same level as the stage floor, being an integral part of it. A trapdoor is the basis for shaping the stage space, changing its function and transporting scenery elements from the warehouse. A two-level structure was proposed for this project because such a solution affects the theatre’s staging possibilities [9]. Its main element contains two longitudinal beams (stringers); their deflection at maximum load should not exceed L/600 (i.e., 10,000 mm/600 = 16.6 mm). The upper platform of the trapdoor required attachment points for a personnel trapdoor. The attachment points have flaps measuring approx. 1.20 × 1.20 m made of wood. The front and side edges of the trapdoor required anti-guillotine bars.

In order for the stage trapdoor to function properly, design assumptions also included stops and working positions of the trapdoor in relation to the stage chimney. Below are figures showing (from the left) the upper position of the trapdoor, the resting position of the trapdoor and the lower position of the trapdoor (Figure 1). The stage chimney is a key element that must be precisely designed to enable the smooth operation of the trapdoor. In this paper, design assumptions for integrating the trapdoor with the stage chimney are discussed, taking into account spatial and technical requirements.

The choice of materials is of key importance for the durability and functionality of stage equipment. Wood, steel and aluminum are the most commonly used materials in stage constructions due to their strength and ease of processing. One of the key aspects of stage design is the analysis of loads, which affects the durability and safety of the construction. Modern methods of stage designing rely on advanced computer tools that enable simulation and testing of structures before they are physically implemented. Computer software has become a technical solution in modern engineering. Many applications that are used to assess the load-bearing capacity of structural elements were developed using the FEN (finite element method) [10,11]. CAD programs allow for visualization and analysis of loads, which significantly reduces the risk of design errors. Before modeling an object in FEN programs, it is worth initially creating the object in three dimensions in CAD programs to detect possible collisions [12]. Thanks to a database concerning the properties of materials, computer programs can effectively support designers by providing key and up-to-date information [13]. In this paper, a focus is placed on developing a suitable technical design and conducting load tests using computer programs such as Autodesk Inventor (3D) and Soldis PROJEKTANT (2D).

The future of stage design is linked to the use of modern technologies such as artificial intelligence and the IoT. The automation and integration of stage systems with digital technologies open up new possibilities for designers and engineers. Intelligent systems based on machine learning effectively solve simple design problems, while people are better at tasks that require abstract thinking and intuition [1]. Some problems are difficult to solve with classic optimization algorithms; however, people, often using an heuristic approach (that is based on experience and intuition), can effectively solve some of them [14].

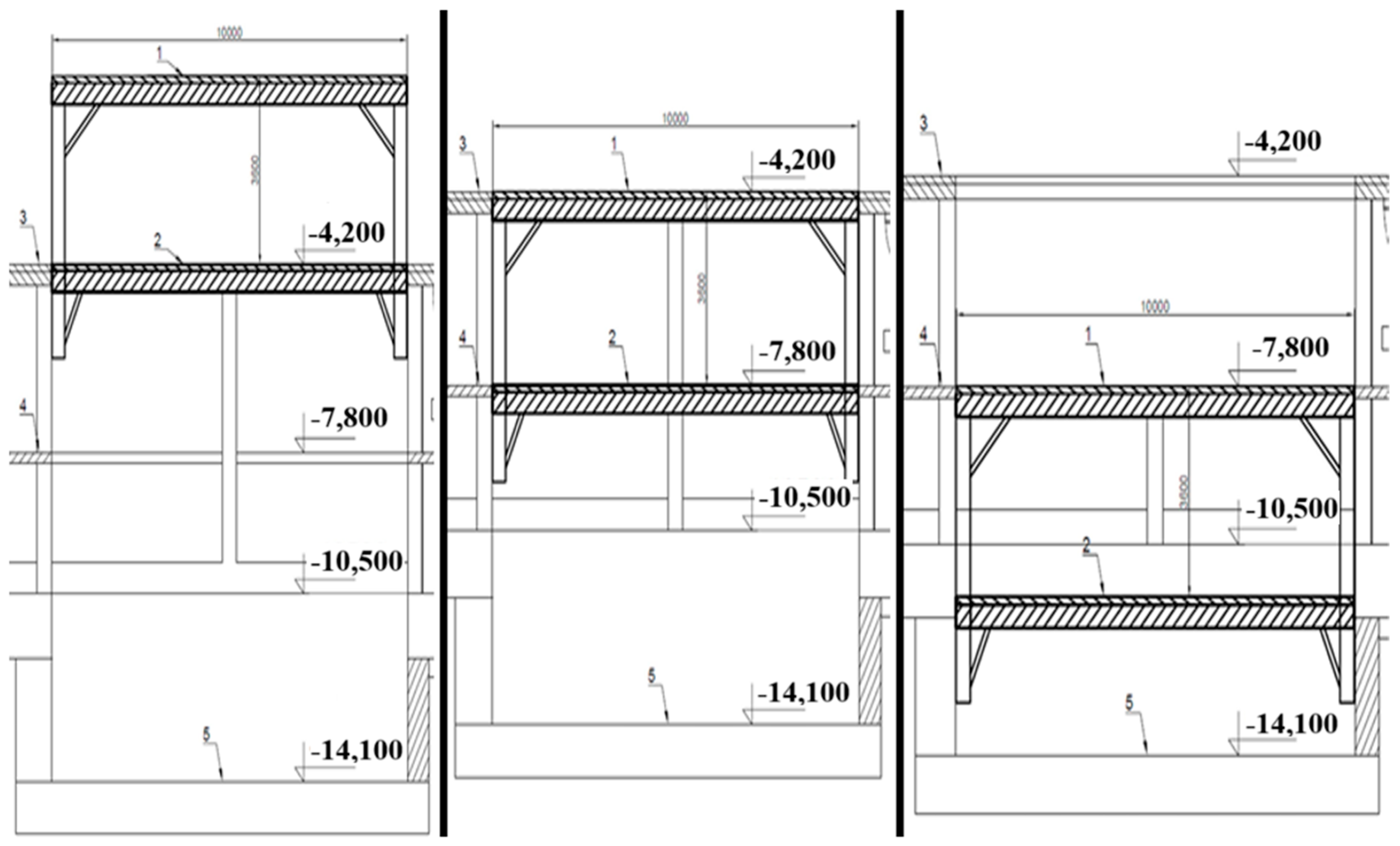
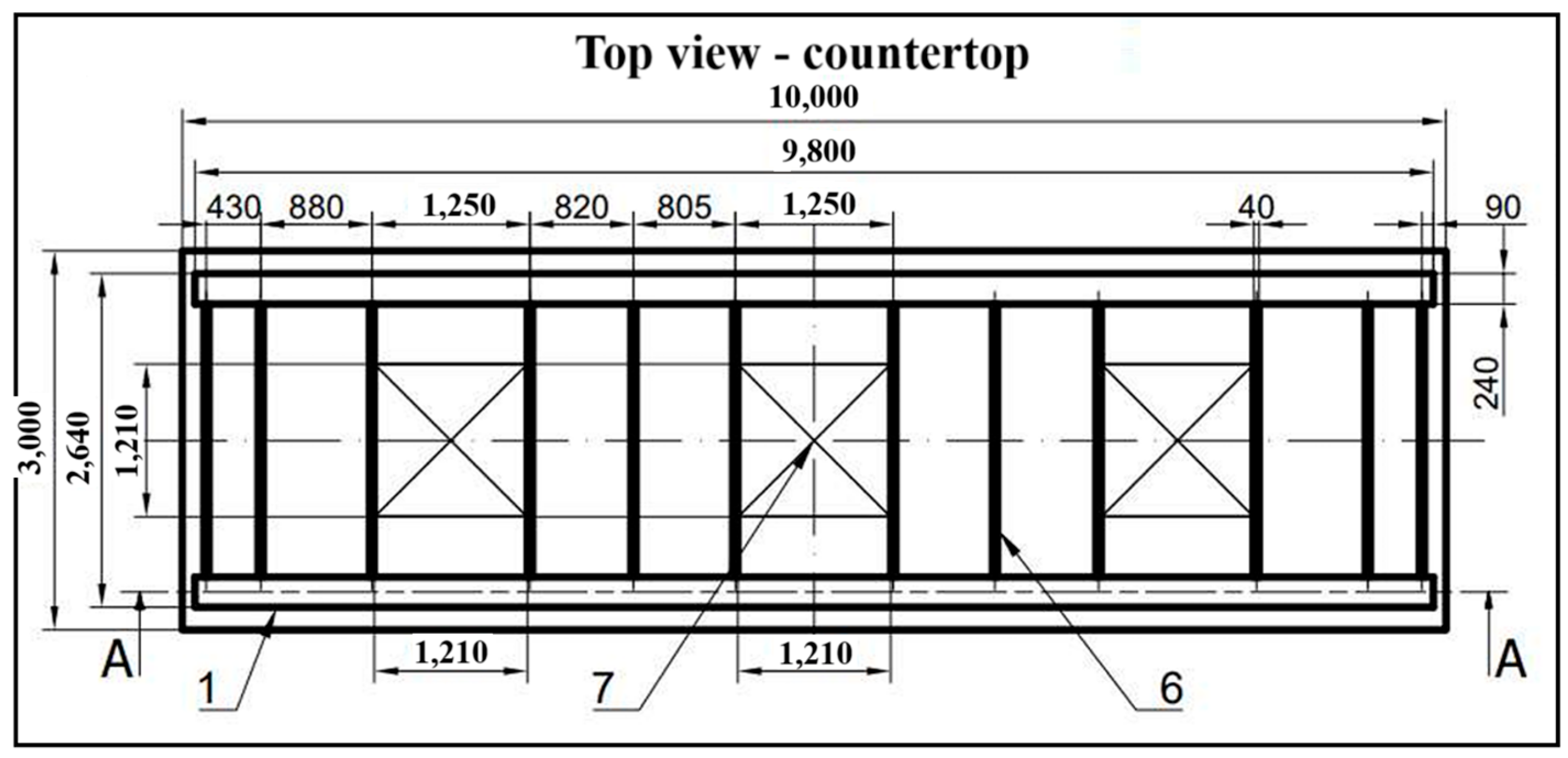
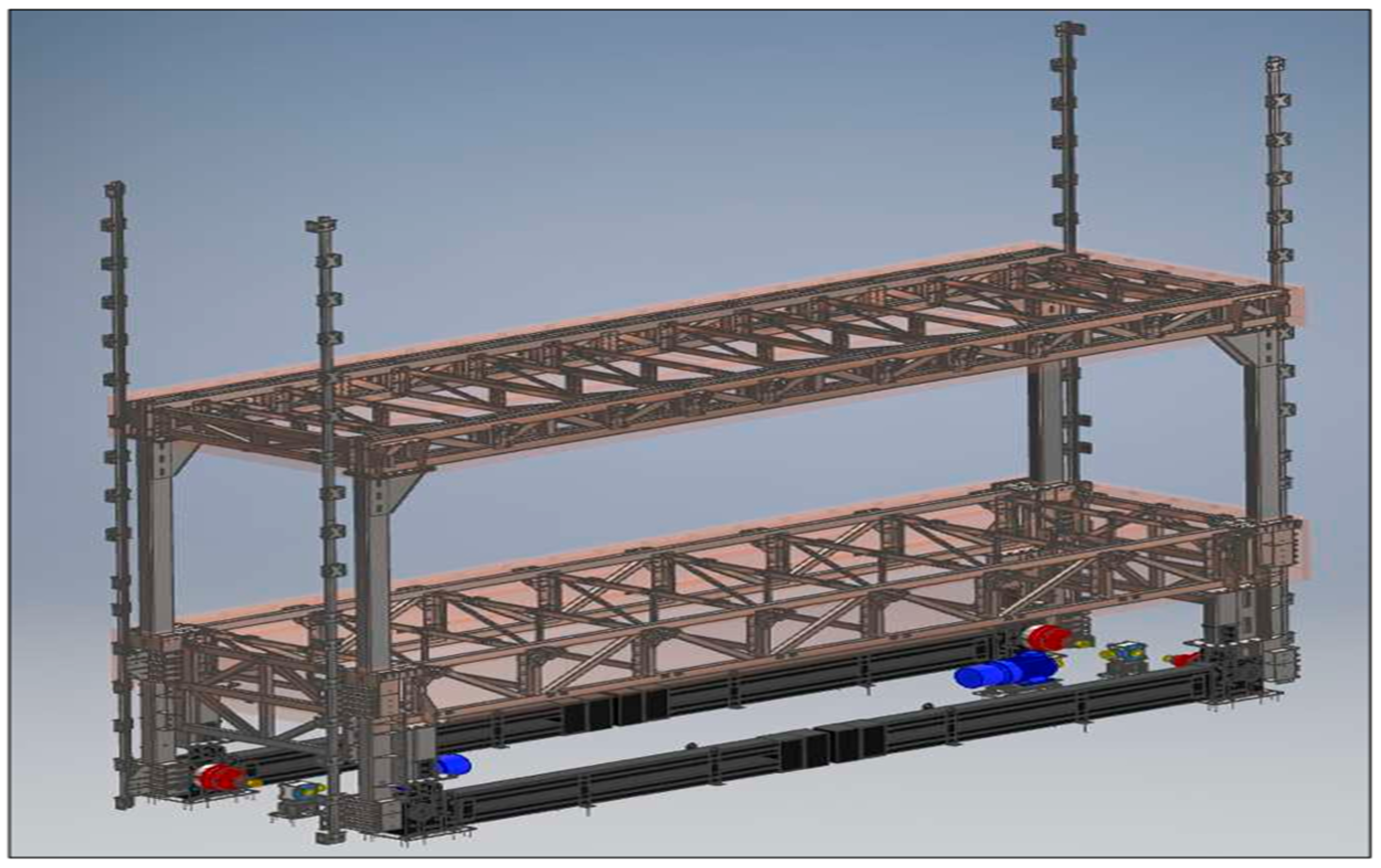
2. Construction Project

The first step in designing the supporting structure was to determine the technical requirements of the stage trapdoor. The following technical data were required to perform the necessary calculations:

(a)

platform dimensions: 3.0 × 10.0 m (two-level construction adjusted to the opening in the scene),

(b)

distance between platforms: 3.6 m,

(c)

load capacity of the platform: 500 kg/m²,

(d)

load-bearing capacity: 250 kg/m²,

(e)

support: crane rails,

(f)

lifting height: 7.2 m.

(g)

number and size of personnel trapdoors: 3 pcs., 1210 × 1210 mm,

(h)

construction material: construction steel S235, S355 (PN-EN 10027-1:2007 [15]), (ASTM A36 [16]).

The second stage in the design of the supporting structure of the stage trapdoor was to design a structural diagram (Figure 2 and Figure 3) that took into account the essential overall dimensions. Below is a diagram of a welded truss with elements made of steel.

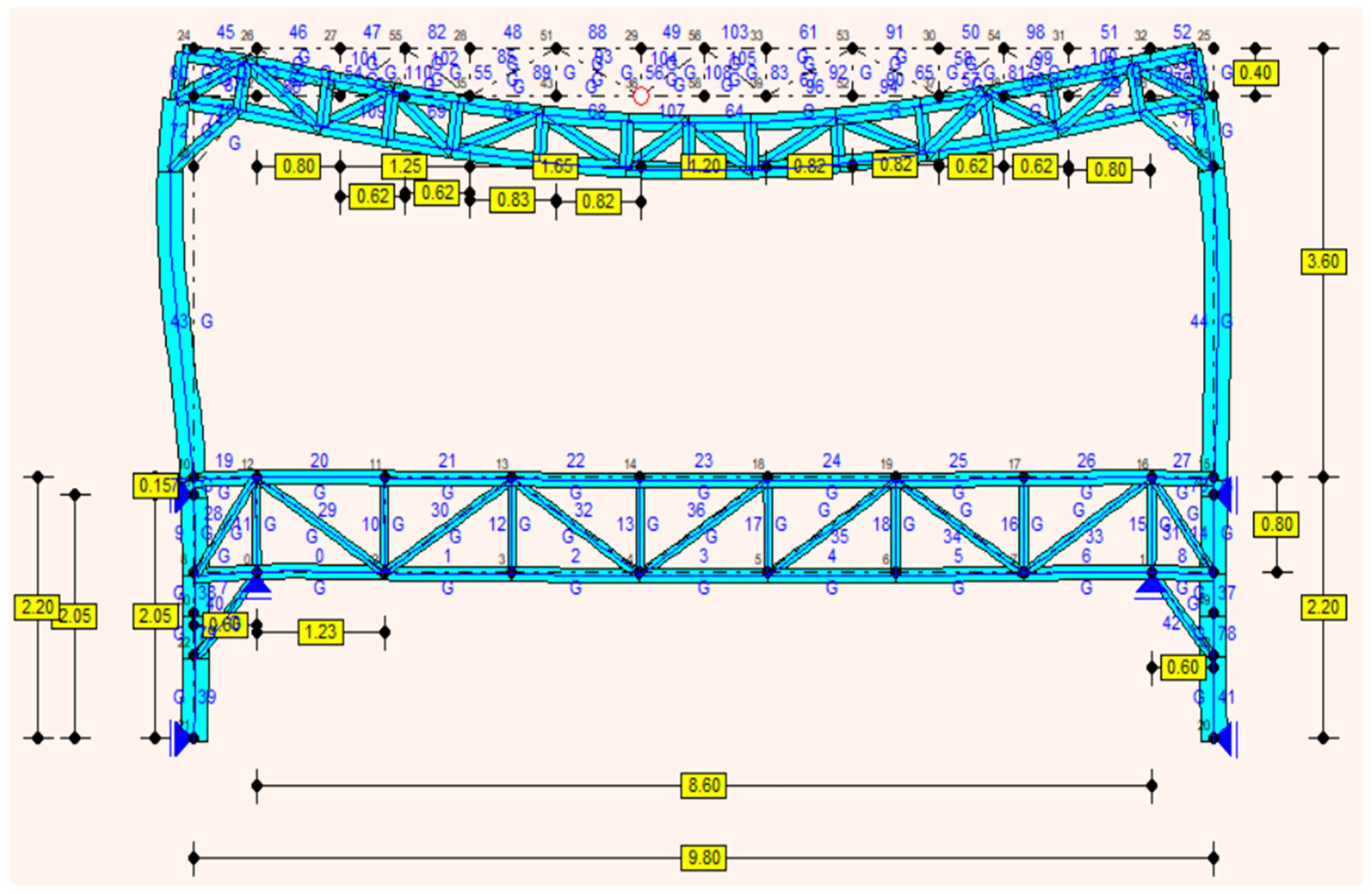
3. Testing and Analysis of the Load-Bearing Structure of a Scenic Trapdoor

The third stage during the design of the supporting structure was the calculation of the main elements of the designed structure [17,18,19,20,21] and analysis using the Soldis PROJEKTANT program for the calculation of supporting structures. Loads results from the operating characteristics of the stage trapdoor were applied. The loads that occurred were calculated according to “DIN 56950:2005-04-Technique for stage performances—Technical machinery and equipment—Safety requirements and tests” [22]. In Autodesk Inventor, a 10 mm square mesh with second-order parabolic elements was used, providing higher accuracy in stress concentration areas, with default convergence settings. In geometric locations that were more difficult, triangular elements were used, with the possibility of adaptive mesh refinement. In the analysis of the structure in the Soldis Designer environment, assumptions of the classical Euler–Bernoulli beam theory were adopted, neglecting torsion effects.

Autodesk Inventor 2022 is equipped with a module for the analysis and testing of frame structures (Figure 4 and Figure 5), which was used to verify calculations carried out in the Soldis PROJEKTANT program. This module also enabled the analysis of the behavior of the structure under increased load. Thanks to its functionality, which takes into account the spatial 3D model (Figure 6), Autodesk Inventor 2022 allowed a more detailed examination of the modeled structure. In contrast, Soldis PROJEKTANT analyzed the structure in a flat 2D model. The examination took into account the actual support model of the supporting structure [23,24,25].

The conducted study precisely indicated the locations of the greatest displacements in the supporting structure (Figure 7). Differences in the calculated displacements may have resulted from the use of a complex 3D model of the entire structure. The favorable deflection values of the upper longitudinal members were influenced by the presence of intermediate frames, which increased the stiffness of the analyzed structure. The occurring stresses did not exceed the yield strength for S235 steel. Therefore, under the analyzed structural operating conditions, the use of S355 steel was not necessary.

In order to thoroughly analyze the steel structure, tests were carried out for four load cases with different values ranging from 9.81 kN (1000 kg) to 147.1 kN (15,000 kg). These cases corresponded to the most commonly occurring loads on stage structures and the most realistic operating conditions to which they may be subjected. The first type of load was a constant load with a constant value q acting evenly over the entire length of the structure. In the second case, the frame was also loaded along its entire length, but the value of q increased every 2500 mm according to the formula described later in this article. The third type of load was characterized by three q values, arranged in such a way that the highest value occurred at the central point of the structure. In the fourth case, the highest loads were located at the outer edges of the structure, and the lowest in its central part. Load distributions for all cases are shown in the illustration below (Figure 8).

In case 2, ∑qi values of the individual load groups, provided that the condition q1 < q2 < q3 < q4 is met, are calculated as follows:

$$\mathrm{q}1={\displaystyle \frac{\sum qi}{10}}⦁1,\mathrm{q}2={\displaystyle \frac{\sum qi}{10}}⦁2,\mathrm{q}3={\displaystyle \frac{\sum qi}{10}}⦁3,\mathrm{q}4={\displaystyle \frac{\sum qi}{10}}⦁4,$$

In cases 3 and 4, the values of the load groups meet the following condition:

q1 < q2 < q3

Table 1. Deflection and Smax values for case 1.

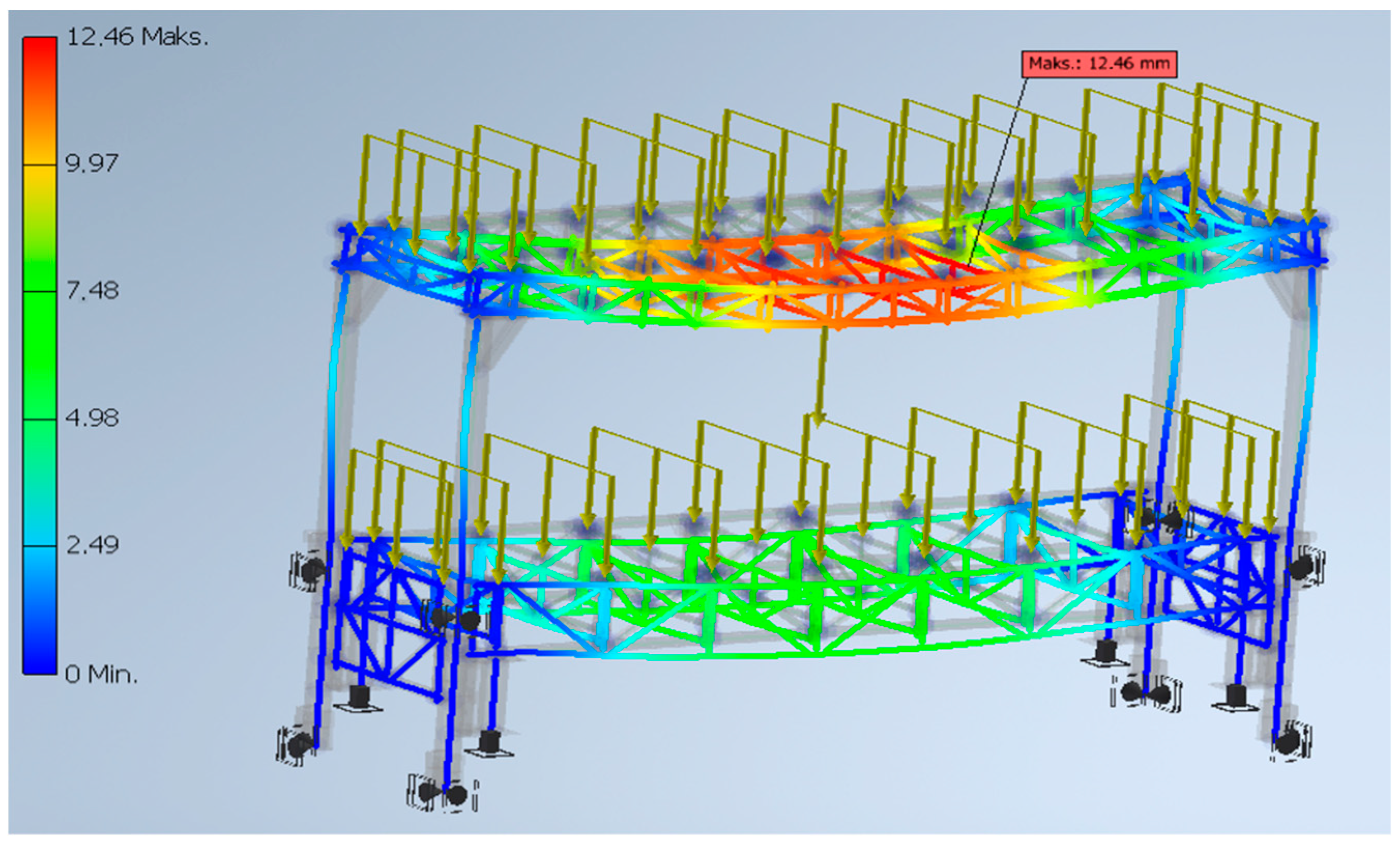
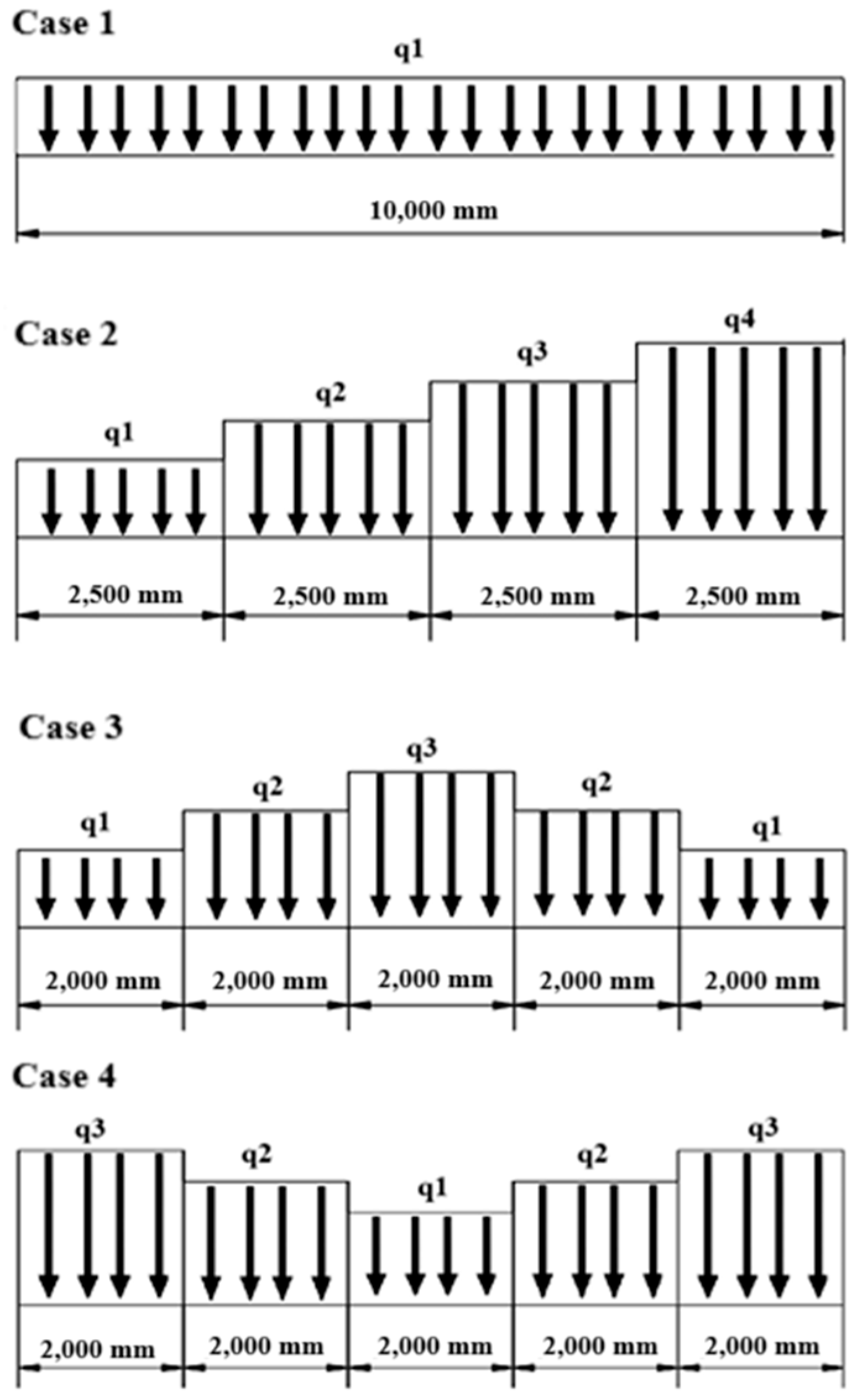
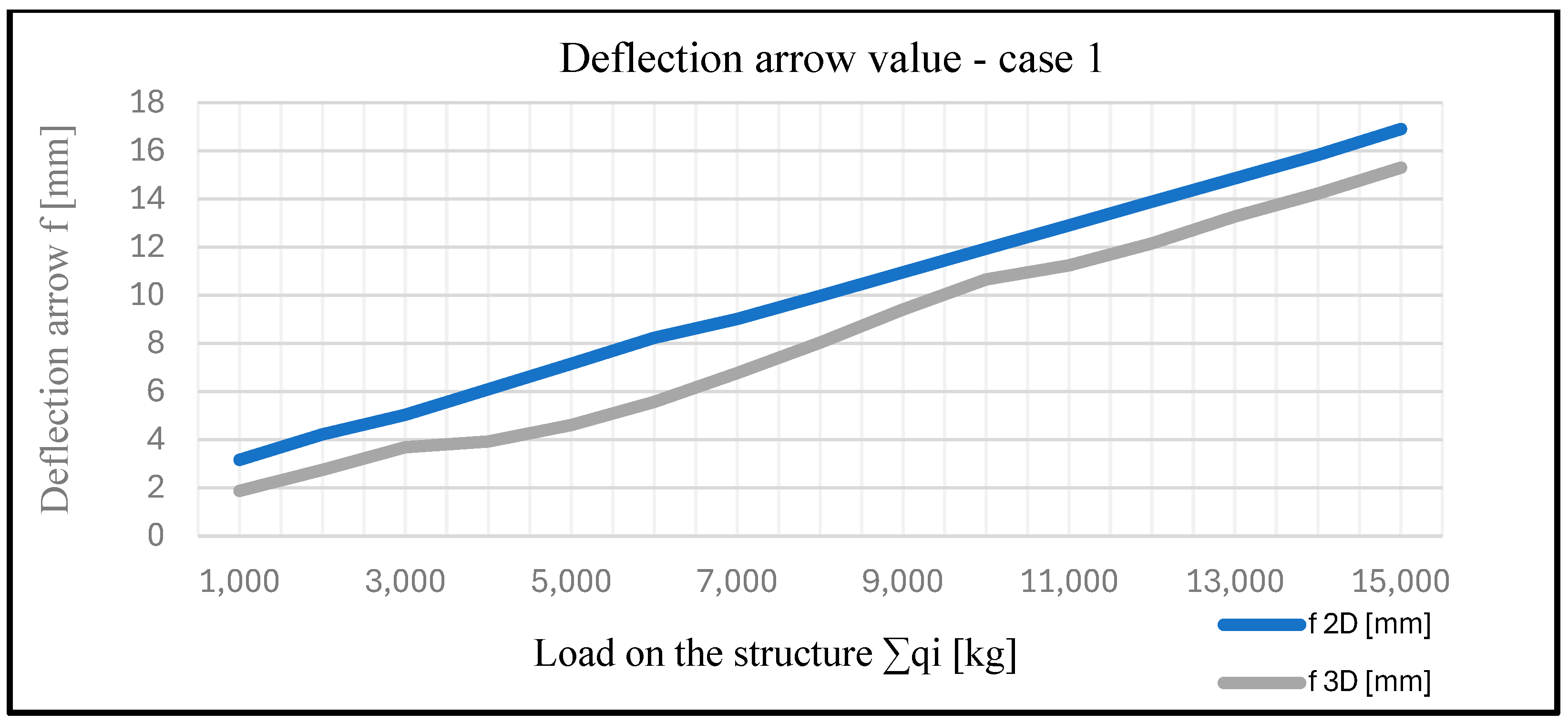
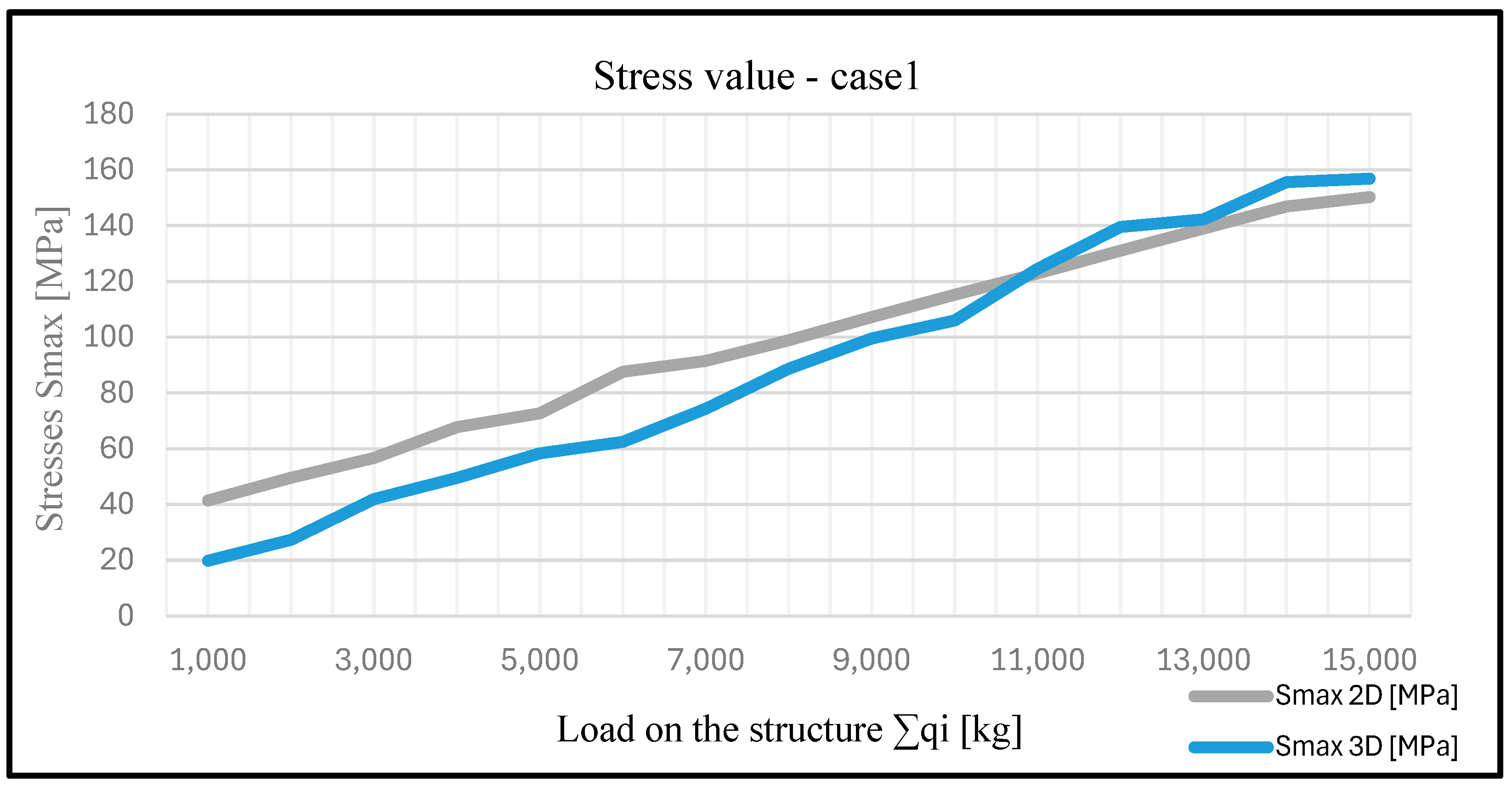
Load Results
Case 1
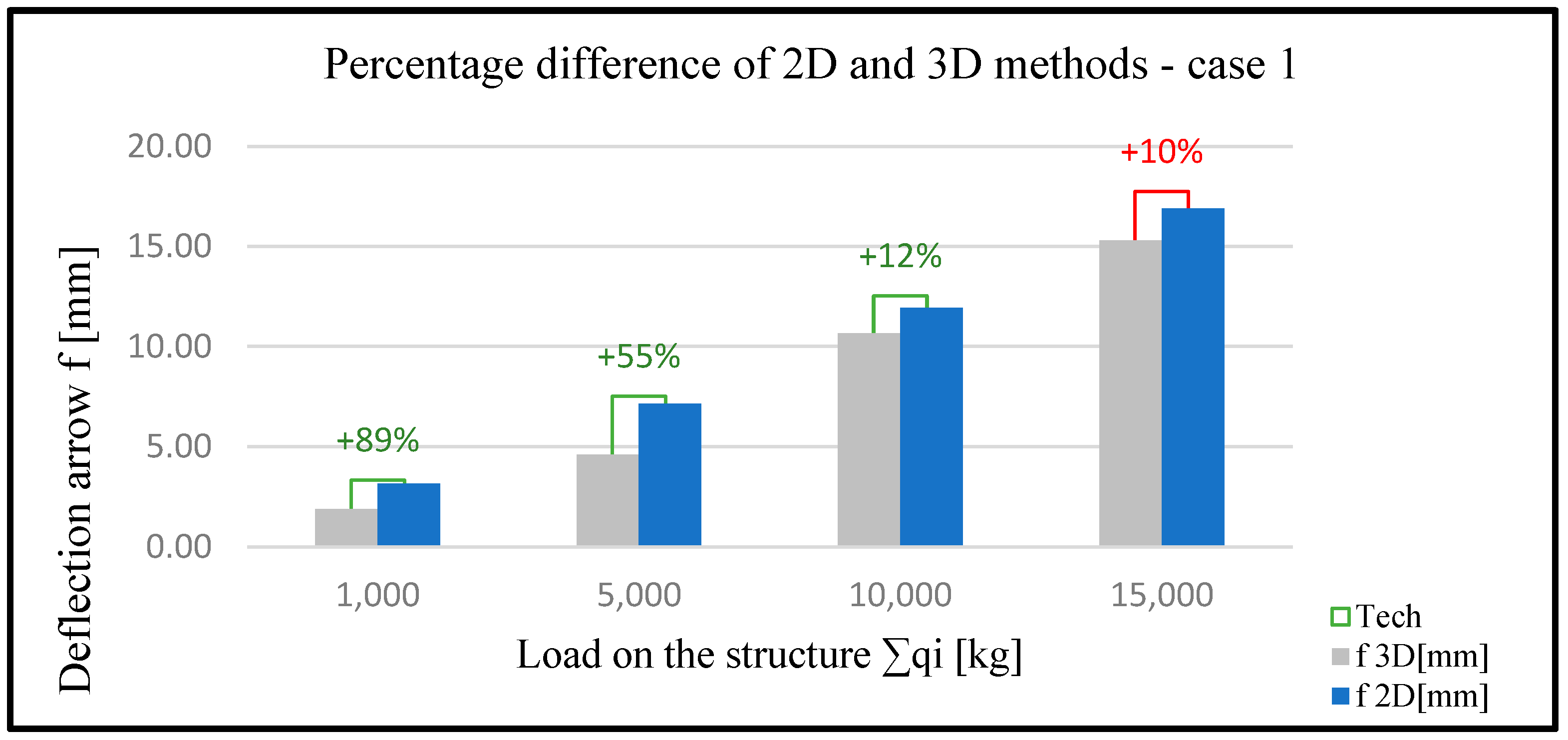
q1 [kg]	∑qi [kg]	f 2D [mm]	f 3D [mm]	Smax 2D [MPa]	Smax 3D [MPa]
1000	1000	3.16	1.88	41.49	19.88
2000	2000	4.22	2.74	49.61	27.34
3000	3000	5.03	3.68	56.7	41.98
4000	4000	6.09	3.92	67.7	49.5
5000	5000	7.15	4.6	72.65	58.36
6000	6000	8.23	5.56	87.63	62.45
7000	7000	9.01	6.764	91.46	74.37
8000	8000	9.97	8.03	98.9	88.71
9000	9000	10.95	9.4	107.23	99.6
10,000	10,000	11.93	10.65	115.21	106
11,000	11,000	12.9	11.24	122.88	124.5
12,000	12,000	13.88	12.15	131.04	139.51
13,000	13,000	14.85	13.26	138.96	142.3
14,000	14,000	15.82	14.21	146.88	155.6
15,000	15,000	16.9	15.3	150.27	156.9

presents results for the first type of structural load. It contains the maximum deflection arrow for 15 different load levels and the maximum stress (Smax) values occurring in the structure. The 2D symbol refers to results obtained in the Soldis PROJEKTANT program, while the 3D symbol refers to results obtained in Autodesk Inventor.

The diagram in Figure 9 illustrates changes in the deflection arrow value depending on the load acting on the structure. A relatively steady increase in this value was visible using both calculation programs.

The diagram in Figure 10 presents changes in the maximum stress in the structure. In the load range from 10 to 68 kN, maximum stress (Smax) values differed significantly depending on the method used (2D or 3D). Together with increasing load, results obtained in the Inventor and Soldis programs became increasingly similar. At a load of approximately 108 kN, stresses in the 3D model exceeded values obtained in the 2D model, and this trend continued up to the maximum tested value of 147 kN.

The diagram below, in Figure 11, presents the change in the deflection arrow value under the influence of the change in the load value acting on the structure. The values of deflection arrow obtained in the 2D program placed in

Table 2. Deflection arrow and Smax values for case 2.

Load Results
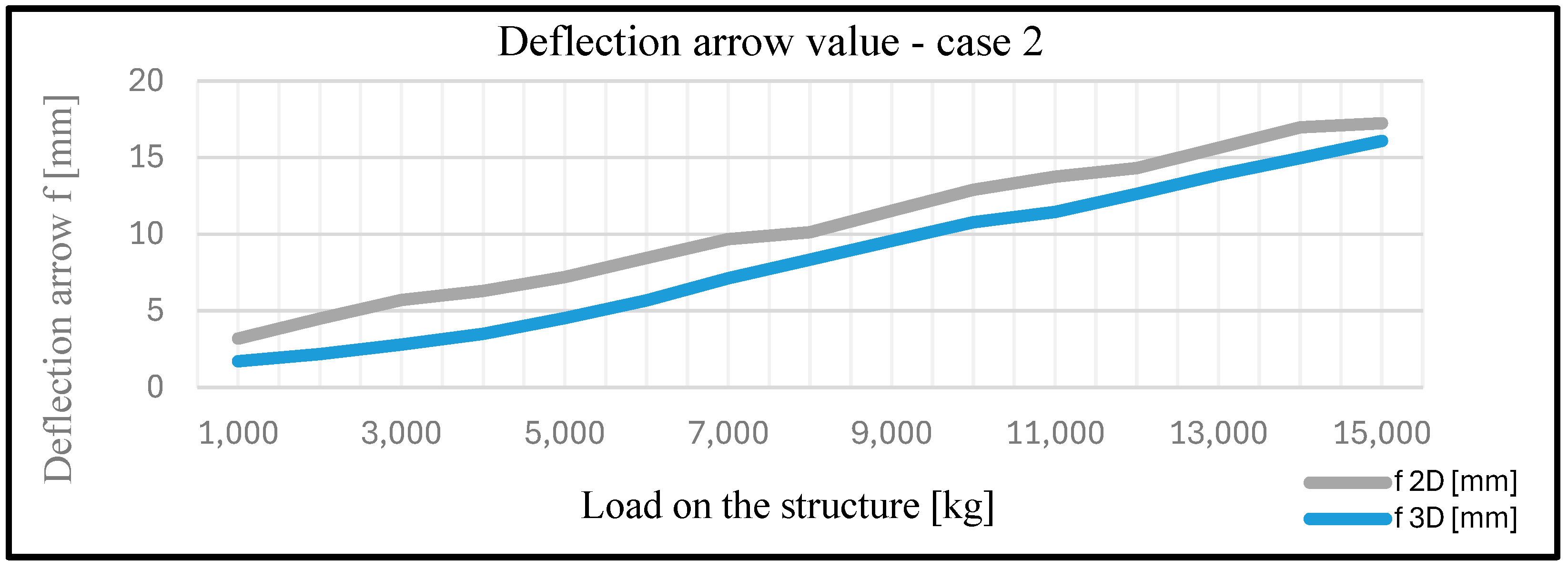
Case 2
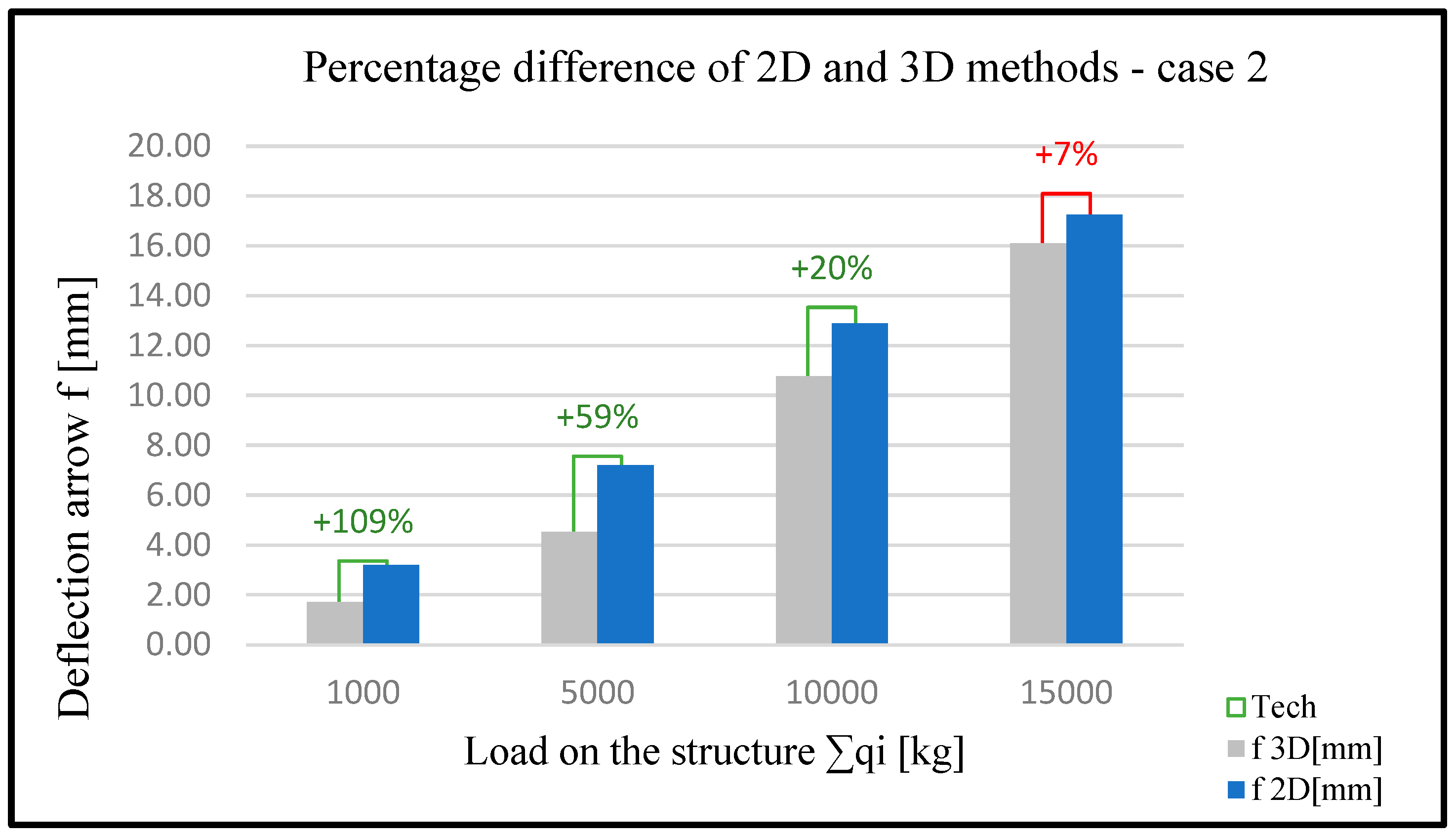
q1 [kg]	q2 [kg]	q3 [kg]	q4 [kg]	∑qi [kg]	f 2D [mm]	f 3D [mm]	Smax 2D [MPa]	Smax 3D [MPa]
100	200	300	400	1000	3.2	1.71	40.47	18.31
200	400	600	800	2000	4.5	2.18	50.16	29.6
300	600	900	1200	3000	5.7	2.8	61	36.2
400	800	1200	1600	4000	6.3	3.49	67.51	40.02
500	1000	1500	2000	5000	7.2	4.52	74.81	47.71
600	1200	1800	2400	6000	8.45	5.67	83.15	60.45
700	1400	2100	2800	7000	9.67	7.12	88.64	75.12
800	1600	2400	3200	8000	10.12	8.34	95.2	90.36
900	1800	2700	3600	9000	11.53	9.56	100.38	105.67
1000	2000	3000	4000	10,000	12.89	10.78	106.7	120.89
1100	2200	3300	4400	11,000	13.76	11.45	110.68	134.9
1200	2400	3600	4800	12,000	14.31	12.63	120.94	145.37
1300	2600	3900	5200	13,000	15.64	13.87	135.57	155
1400	2800	4200	5600	14,000	16.98	14.96	145.83	160.11
1500	3000	4500	6000	15,000	17.24	16.1	152.33	166.8

are larger than 3D. A relatively uniform increase in deflection arrow values in both calculation programs was also noticeable, but for higher loads, values obtained from both programs were closer to each other.

The diagram in Figure 12 illustrates the change in the maximum stress in the structure. For load ranges between 10 and 60 kN, values of the maximum stress (Smax) differed significantly depending on the method used (2D or 3D). Together with the increasing load, results obtained in the Inventor and Soldis programs became increasingly similar. At a load of approximately 88 kN, stresses in the 3D model exceeded values obtained in the 2D model, and this trend continued up to the maximum tested value of 147 kN.

The graph in Figure 13 illustrates the change in the deflection arrow(

Table 3. Deflection arrow and Smax values for case 3.

Load Results
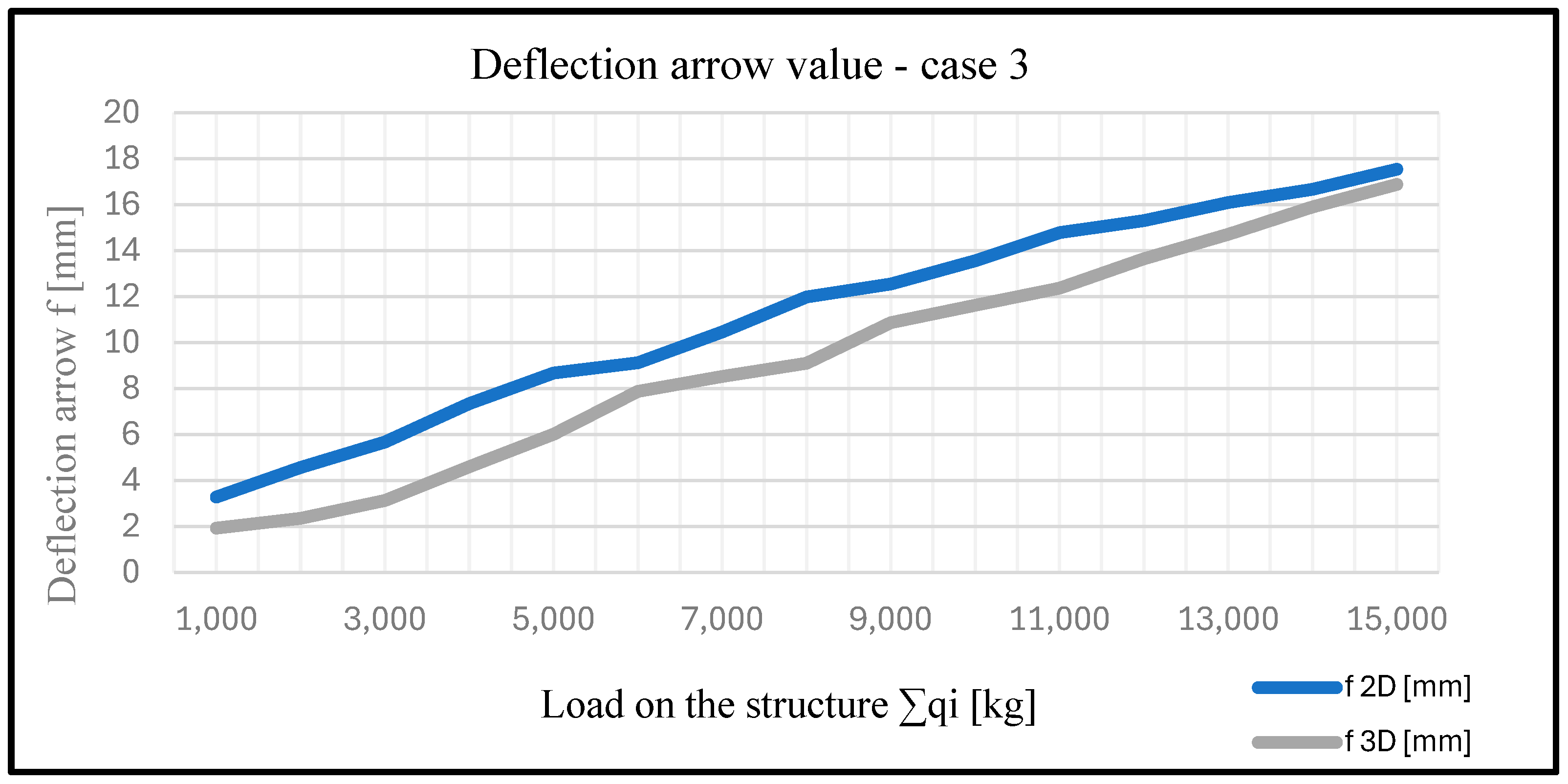
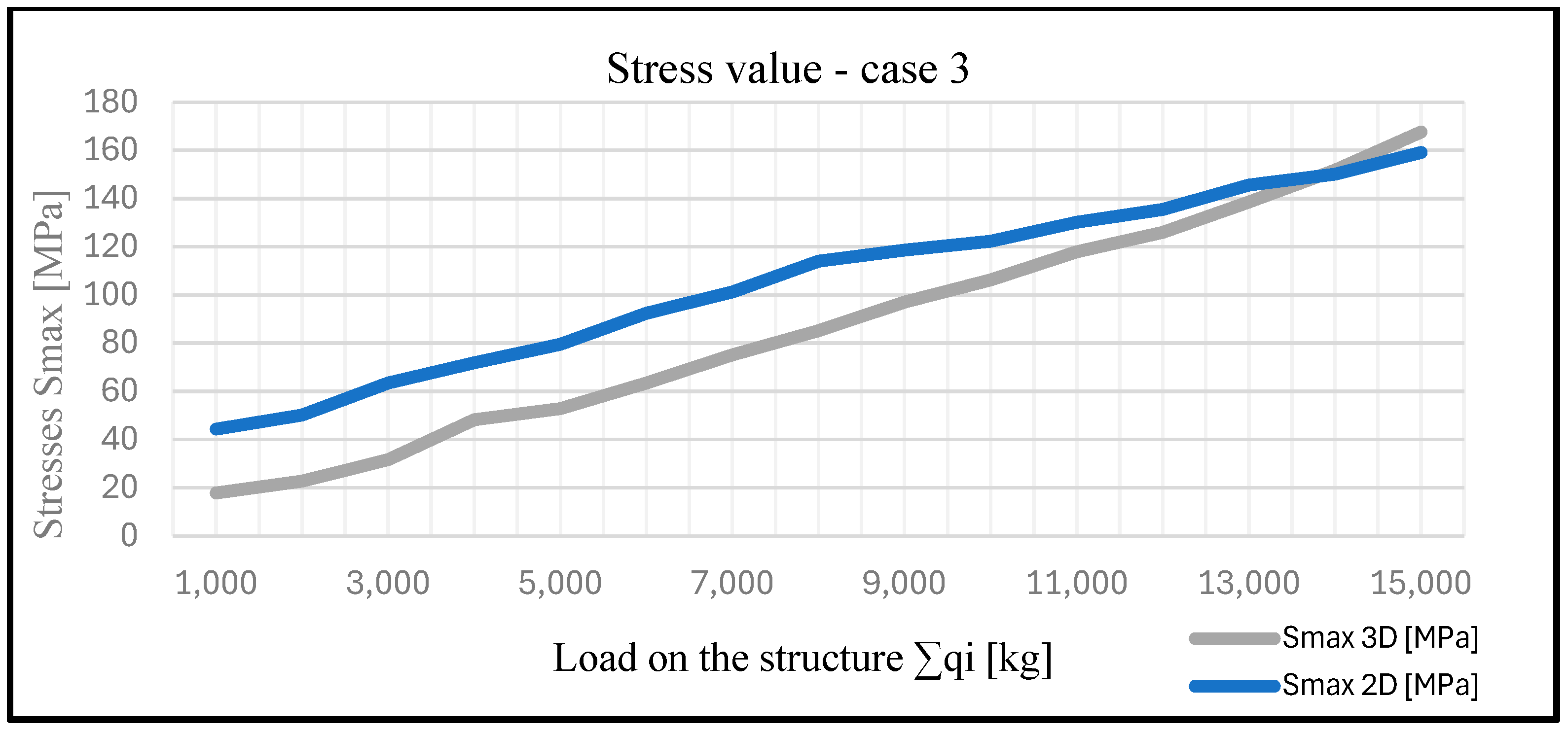
Case 3
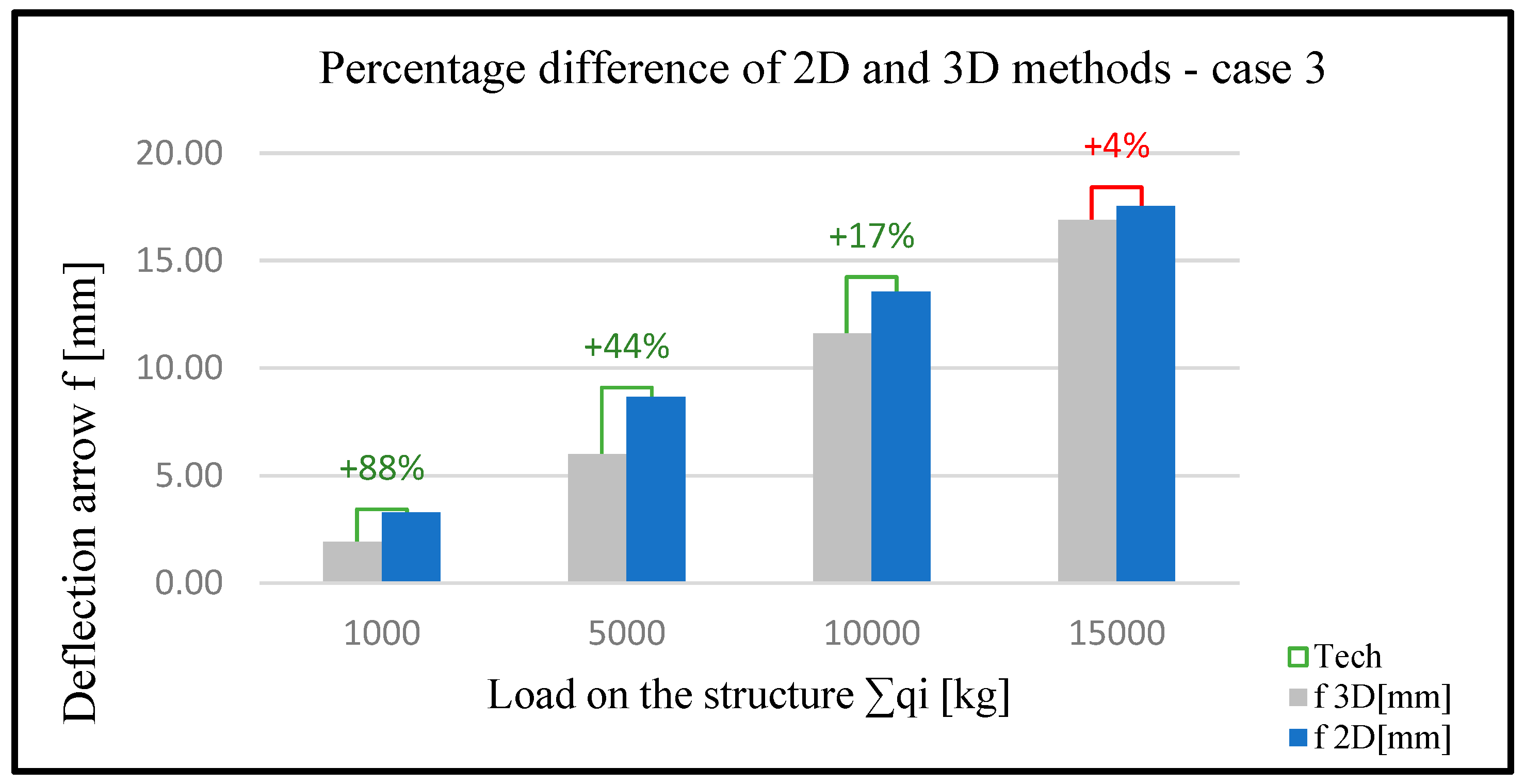
q1 [kg]	q2 [kg]	q3 [kg]	∑qi [kg]	f 2D [mm]	f 3D [mm]	Smax 2D [MPa]	Smax 3D [MPa]
100	200	400	1000	3.28	1.93	44.39	17.85
200	400	800	2000	4.56	2.35	50.12	22.68
300	600	1200	3000	5.67	3.13	63.45	31.6
400	800	1600	4000	7.34	4.6	71.8	48.19
500	1000	2000	5000	8.67	6.01	79.48	52.83
600	1200	2400	6000	9.12	7.87	92.39	63.46
800	1200	3000	7000	10.46	8.52	101.23	75.08
1000	1500	3000	8000	11.98	9.1	114	85.14
1000	2000	3000	9000	12.55	10.86	118.64	97.03
1000	2000	4000	10,000	13.56	11.62	122.25	106.2
1100	2200	4400	11,000	14.78	12.37	130.11	117.84
1200	2400	4800	12,000	15.3	13.64	135.45	125.96
1300	2600	5200	13,000	16.09	14.71	145.62	138.5
1400	2800	5600	14,000	16.67	15.9	150.12	151.71
2000	3000	5000	15,000	17.54	16.88	159.2	167.67

) value depending on the load acting on the structure. In both calculation programs, a relatively uniform increase in this value was observed. In contrast to the previous two cases, there was a greater discrepancy in the results at lower load values. With increasing load, the difference between deflection arrow values gradually decreased.

The diagram in Figure 14 illustrates the change in the maximum stress in the structure. For load ranges between 10 and 88 kN, values of the maximum stress (Smax) differed significantly depending on the method used (2D or 3D). Together with the increasing load, results obtained in the Inventor and Soldis programs became increasingly similar. At a load of approximately 138 kN, stresses in the 3D model exceeded values obtained in the 2D model, and this trend continued up to the maximum tested value of 147 kN.

The graph below, in Figure 15, presents the change in the deflection arrow (

Table 4. Deflection arrow and Smax values for case 4.

Load Results
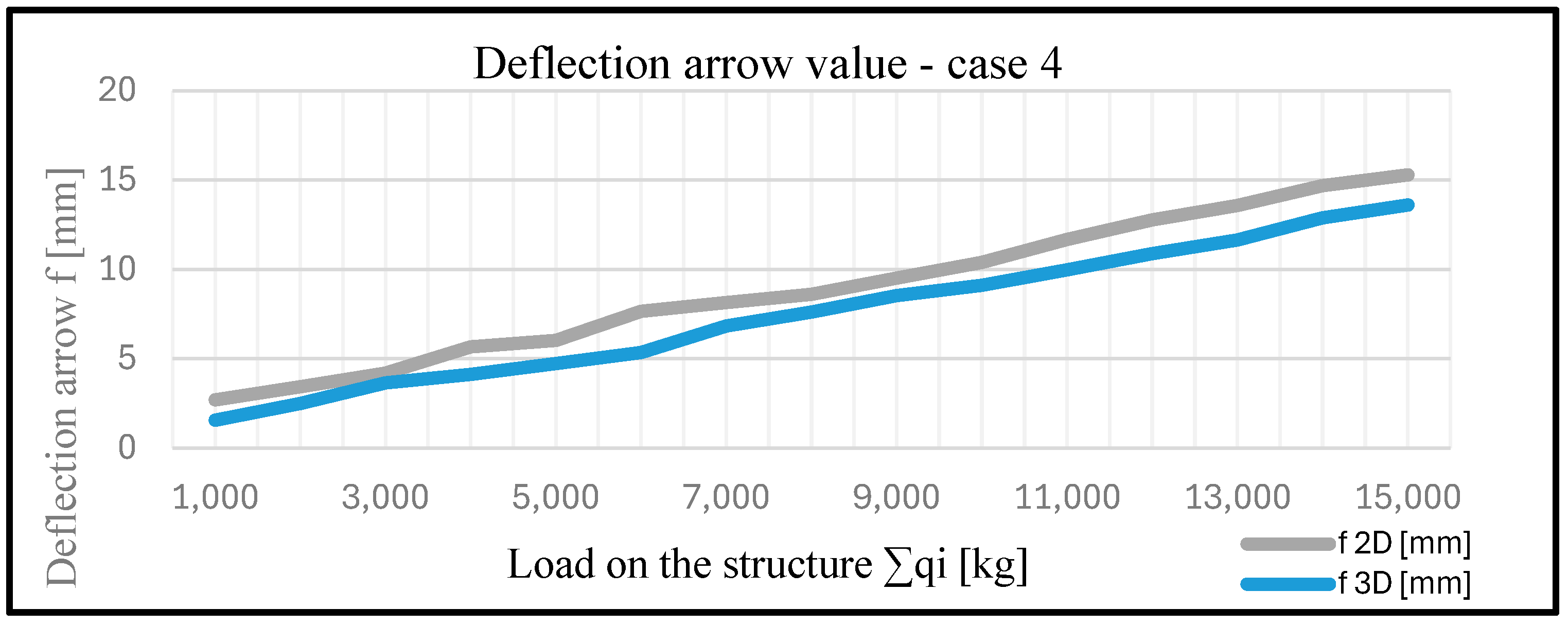
Case 4
q1 [kg]	q2 [kg]	q3 [kg]	∑qi [kg]	f 2D [mm]	f 3D [mm]	Smax 2D [MPa]	Smax 3D [MPa]
100	200	250	1000	2.7	1.56	35.64	15.24
200	400	500	2000	3.43	2.5	43.05	19.7
300	600	750	3000	4.19	3.65	50.86	24.65
400	800	1000	4000	5.66	4.12	58.04	30.15
500	1000	1250	5000	6.02	4.72	65.38	48.64
600	1200	1500	6000	7.65	5.34	70.2	55.12
800	1400	1700	7000	8.14	6.82	76.9	64.63
1000	1600	1900	8000	8.6	7.61	82.5	77.5
1100	1800	2150	9000	9.5	8.53	90.65	88.67
1200	1900	2500	10,000	10.38	9.1	98.6	103.5
1300	2250	2600	11,000	11.67	9.97	108.6	112.58
1400	2400	2900	12,000	12.76	10.87	111.48	120.65
1500	2500	3250	13,000	13.57	11.64	119.34	131.49
1600	2600	3600	14,000	14.68	12.88	127.98	137.27
2000	2750	3750	15,000	15.28	13.6	138.65	144.5

) value under the influence of the change in the load value acting on the structures. Deflection arrow values obtained in the 2D program were higher than those in 3D. A relatively uniform increase in the deflection arrow value in both calculation programs was also noticeable.

The graph in Figure 16 shows the change in values of the maximum stress in the structure. Within the range of loads from 10 to 55 kN, maximum stress (Smax) values differed significantly depending on the method used (2D or 3D). As the load increased, results obtained in the Inventor and Soldis programs became increasingly similar. At a load of approximately 92 kN, stresses in the 3D model exceeded values obtained in the 2D model, and this trend continued up to the maximum tested value, which was 147 kN.

The illustration below (Figure 17) presents differences in results depending on the type of program used in the form of a column chart. It can be observed that the deflection arrow value of the structure simulated in the 2D program (Soldis) is higher for each load value as compared to results obtained in the 3D program (Inventor). Another conclusion is that the decrease in the percentage difference between these results increased as the load increased. For a low load value (1000 kN), the difference was as much as 89%, while for a load of 15 kN, the difference decreased to 10%.

The illustration below (Figure 18) shows differences in resmults depending on the type of program used in the form of a column chart. It can be seen that the deflection arrow value of the structure simulated in the 2D program (Soldis) is higher for each load value when compared to results obtained in the 3D program (Inventor). Another conclusion is that the percentage difference between these results decreased when the load increased. For a low load value (1000 kN), the difference was as much as 109%, while for a load of 15 kN, it decreased to 7%.

In the illustration below (Figure 19), differences in results depending on the type of program used are shown in the form of a column chart. It can be observed that the deflection arrow value of the structure simulated in the 2D program (Soldis) is higher for each load value when compared to results obtained in the 3D program (Inventor). Another conclusion is that the decreasing difference in percentage between results increased when the load was higher. For a low load value (1000 kN), the difference was as much as 88%, while for a load of 15 kN, it decreased to 4%.

The illustration below (Figure 20) presents differences in results depending on the type of program used in the form of a bar chart. It can be observed that the deflection arrow value of the structure simulated in the 2D program (Soldis) is greater for each load value compared to the results obtained in the 3D program (Inventor). Another conclusion is that the percentage difference between these results decreased as the load increased. For a low load value (1000 kN), the difference was as much as 111%, while at a load of 15 kN, it decreased to 12%.

4. Conclusions

The conducted research and structural analysis, based on maximum stress values and deflection arrows, confirmed that calculations carried out in the 2D program (Soldis PROJEKTANT) showed acceptable compliance with results obtained by means of an advanced 3D program (Autodesk Inventor). The results obtained demonstrate the high precision and reliability of the calculation methods used in Soldis PROJEKTANT, which emphasizes its usefulness in the design of this type of construction. It has been observed that although a detailed analysis of the supporting structure in 3D CAD programs ensures higher accuracy of spatial modelling, for this type of equipment it is not necessary to obtain satisfactory results. The advantage of the less precise 2D method is that its results are more conservative than those of the 3D method, which has a positive effect on the selection of structural elements, ensuring adequate frame stiffness. This means that designers can successfully use simpler and less complex calculation tools, such as Soldis PROJEKTANT, saving time and reducing costs associated with engineering analysis. These findings are of great importance for the design of stage mechanisms such as trapdoors. The use of 2D tools such as Soldis PROJEKTANT allows for the quick and efficient preparation of the supporting structure design, including strength and safety analysis, which makes this program particularly useful in conditions with limited design resources. On the other hand, 3D CAD tools can be used in more advanced projects where detailed spatial simulation or optimization of the structure for specific dynamic loads is required. In summary, this study showed that for the designed stage trapdoor, simpler calculation tools were fully sufficient to meet the design requirements. Therefore, the possibility of optimizing the design process was confirmed, which is crucial in cultural organizations where lead-time and design costs play key roles.