ViT-Based Classification and Self-Supervised 3D Human Mesh Generation from NIR Single-Pixel Imaging

Abstract

Accurately estimating 3D human pose and body shape from a single monocular image remains challenging, especially under poor lighting or occlusions. Traditional RGB-based methods struggle in such conditions, whereas single-pixel imaging (SPI) in the Near-Infrared (NIR) spectrum offers a robust alternative. NIR penetrates clothing and adapts to illumination changes, enhancing body shape and pose estimation. This work explores an SPI camera (850–1550 nm) with Time-of-Flight (TOF) technology for human detection in low-light conditions. SPI-derived point clouds are processed using a Vision Transformer (ViT) to align poses with a predefined SMPL-X model. A self-supervised PointNet++ network estimates global rotation, translation, body shape, and pose, enabling precise 3D human mesh reconstruction. Laboratory experiments simulating night-time conditions validate NIR-SPI’s potential for real-world applications, including human detection in rescue missions.

1. Introduction

The field of 3D body reconstruction is crucial in various industries, such as virtual reality [1], augmented reality [2], and biomedical applications [3]. This process involves reconstructing a detailed 3D model of the human body from a single 2D image [4], a task fraught with challenges due to the ill-posed nature of obtaining three-dimensional data from two-dimensional representations [5]. This complexity arises because multiple 3D points can project identically onto a 2D plane, introducing significant ambiguity in the reconstruction process. Despite these hurdles, advances in computational techniques continue to improve the precision and reliability of 3D body reconstruction [6], broadening its applicability in fields such as medical imaging [7], gaming [8], and robotics [9].

In particular, reconstructing an accurate 3D human form from imperfect and incomplete data requires advanced handling of non-rigid body dynamics and articulated joint movements [10]. Recent breakthroughs in deep learning have enabled more sophisticated end-to-end reconstructions of human shapes [11], including detailed meshes that capture complex articulations. Historically, deep neural networks have faced challenges, such as producing rugged, blurred, or distorted meshes [12]. However, models such as Skinned MultiPerson Linear (SMPL) [13] and its extension, SMPL eXpressive (SMPL-X) [14], have revolutionized this domain. These models offer streamlined representations of 3D human figures. When integrated with deep learning techniques, they facilitate the extraction of robust image features and the regression of accurate body shape and pose parameters from standard RGB images. This enhanced methodology pushes the limits of what is possible in 3D human body cloud point reconstruction, promising increasingly accurate and versatile applications [15].

Various technologies are used to estimate human pose [16], including RGB cameras [17], thermal cameras [18], Hyperspetral [19] and IR-Ultra-wideband (UWB) RADAR [20]. Although infrared cameras excel in object detection under low-light conditions, particularly for objects with higher temperatures, they perform poorly with cooler objects. Alternatively, RGB cameras are challenged by low-light environments, although using them in the NIR spectrum can be costly. Single-pixel imaging (SPI) systems present a viable alternative [21], which overcomes many limitations of conventional and thermal cameras in dim settings. SPI systems capture images by measuring the light reflected from an object using a single-pixel detector, even in the infrared spectral bands [22]. Using deep learning, single-pixel imaging (SPI) can reconstruct high-quality images from sparse measurements. It is particularly effective for capturing 3D human body point clouds in challenging scenarios such as night-time surveillance or rescue operations. This capability establishes SPI as a leading method for detailed and accurate pose detection under low-light conditions. Deep learning techniques are highly recommended in such scenarios, and the Vision Transformer (ViT) [23] is emerging as a robust approach to handling low-resolution data.

A key advantage of SPI over conventional cameras is its ability to capture data in the NIR spectrum, significantly enhancing 3D point cloud imaging [24]. NIR imaging performs exceptionally well under low light conditions, providing superior clarity for object detection and tracking, an essential feature for advanced rescue applications [25]. When combined with time-of-flight (TOF) sensors, SPI technology produces highly accurate 2D and 3D environmental images [26]. This integration enhances the depth of the data, offering detailed insight into the spatial arrangement and motion of objects within a scene. Furthermore, SPI is not limited to low-light scenarios; it remains highly effective in challenging environments, such as those with dust or fog, where traditional cameras struggle, ensuring consistent and reliable 3D data acquisition under various conditions.

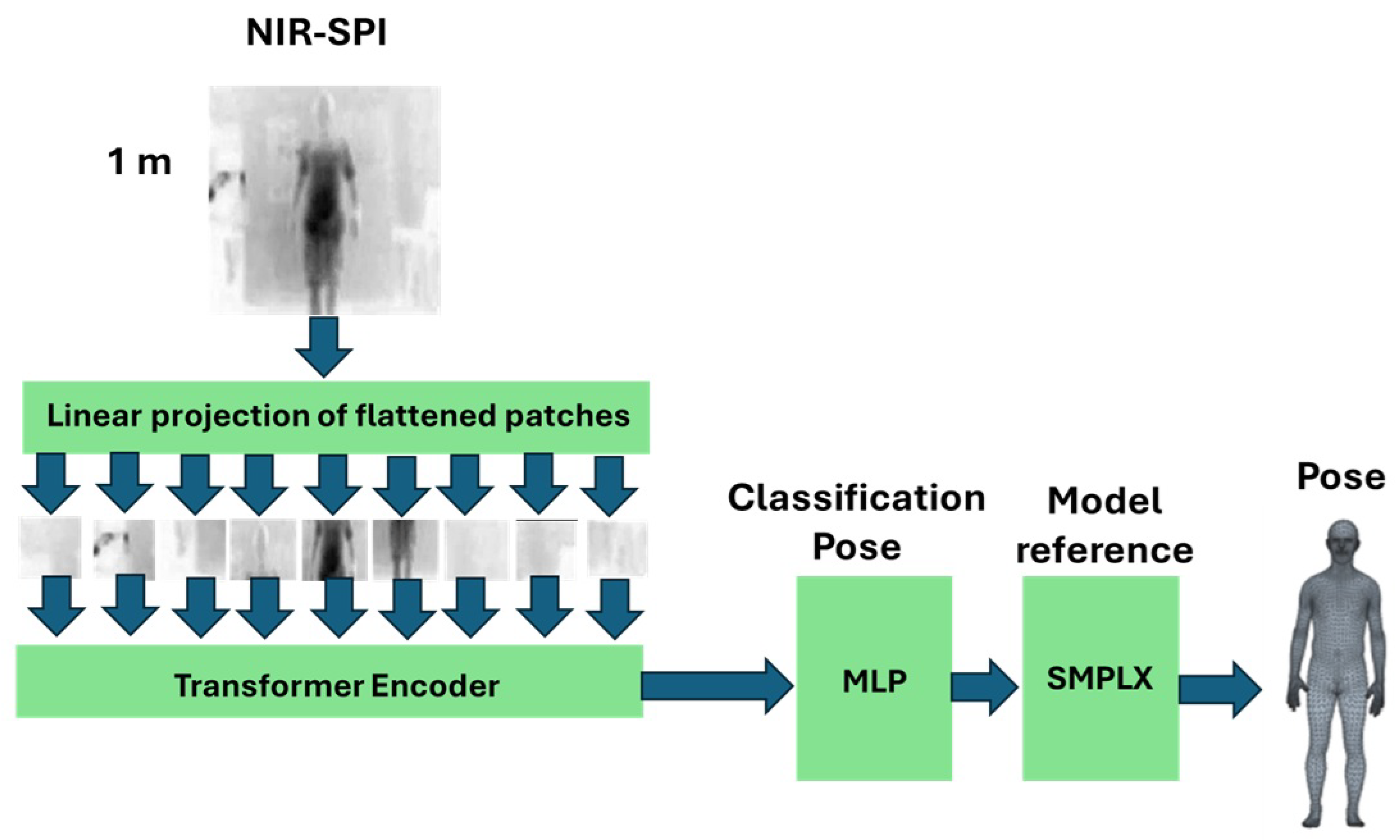
This study presents an SPI system with active illumination in the near-infrared (NIR) wavelength range of 850–1500 nm. The system utilizes single InGaAs photodetectors to capture NIR-SPI images, which are the foundation for generating 3D human meshes based on point clouds for depth perception. In addition, it incorporates a ViT-based classification model to determine the initial pose to implement an SMPL-X-based reconstruction framework. Our approach processes point clouds to generate high-fidelity 3D human meshes, using a self-supervised learning framework [27] to enhance accuracy. We introduce a novel 3D human pose reconstruction method that surpasses previous state-of-the-art techniques by integrating a probabilistic human model with depth information. This innovation achieves a new benchmark in accuracy, outperforming ViT-based models and setting a new standard for handling missing data and low-resolution scenarios. The final output is a detailed and precise 3D representation of the human pose in the SMPL-X model, providing an accurate reconstruction of human figures in three dimensions. Therefore, in this work, we propose the following:

• Exploring the capability of Single-Pixel Imaging for generating 3D human pose point clouds from low-resolution 2D images.
• Implementation of the ViT (Vision Transformer) model applied to SPI images to define a pre-trained SMPL-X human pose model.
• Testing a self-supervised Deep Learning model for 3D reconstruction from the point cloud.
• This work addresses the challenging task of predicting 3D hand poses from low-resolution 2D images. This can be applied to sensors used in rescue operations where lighting conditions are difficult.

2. Related Work

2.1. Depth-Based 3D Pose Estimation

Depth-based 3D pose estimation techniques are classified into generative and discriminative models [28]. Generative models, which resemble template matching, utilize human-body templates to establish correspondences between the input and the templates. The Iterative Closest Point (ICP) algorithm is commonly employed to track the 3D human body within these models [29]. In contrast, discriminative models bypass template matching and directly predict body poses. These models typically use random forests (RF) to classify body parts from a single-depth image, subsequently estimating the 3D joint locations [30]. Implemented a random tree walk algorithm (RTW) [31] to regress joint positions and improve processing speed. Researchers have developed a viewpoint-invariant model in deep learning that combines convolutional and recurrent neural networks for human pose estimation. Another innovative approach includes a tree-structured region ensemble network specifically designed for 3D position regression, leveraging image features. Furthermore, the Voxel-to-Voxel network (V2V-PoseNet) [32] represents a significant advance, as it processes point clouds to estimate the likelihood of the location of each body joint within each voxel. V2V-PoseNet then extracts precise 3D joint positions from the resulting heatmaps [33].

2.2. 3D Human Body

3D human body modeling from depth images involves two primary approaches: template-based and template-less methods [34]. Template-based methods leverage predefined priors such as skeletal structures [35], template models, or parametric designs to reconstruct the 3D body model [36]. These priors provide substantial prior knowledge, enhancing the robustness of 3D body reconstruction. For example, these methods adapt a prescanned template to match each input depth image using an innovative L0-based motion regularizer that effectively minimizes errors in large movements [37]. On the other hand, templateless methods generate 3D body models without any preexisting knowledge of body shape. These methods integrate all captured depth maps to build 3D models in real time. However, they are limited to capturing slow movements. Recent advancements have merged template priors with templateless methods to accommodate more significant human movements. Both approaches require establishing point correspondences for each frame using a method that searches for the closest 3D points [38]. These correspondences often need to be more accurate when based on a single depth input because of significant variations in human poses and shapes compared to the template. Point correspondences might also be directly predicted from depth images of human bodies using techniques like random forests or through matching learned feature descriptors. Following the establishment of these correspondences, 3D body models are reconstructed by aligning the template with the depth data. The LBS Autoencoder [39] is designed to fit articulated mesh models to point clouds by calculating joint angles and deformations of an LBS template, although it is intended primarily for complete 3D shapes rather than depth image-based point clouds.

2.3. Semi-Supervised Approaches in 3D Human Mesh Estimation

While supervised learning remains the predominant approach in traditional human pose estimation methods, obtaining accurate 3D mesh ground truth data presents a significant obstacle. To address the scarcity of high-quality annotations, researchers have developed weakly or semi-supervised techniques [40]. These methods make use of more readily available annotations. Specifically, semi-supervised learning employs 3D skeletons—less detailed than full meshes—as a base, whereas weakly supervised learning utilizes 2D or approximated 3D annotations [41]. Techniques such as exploiting 2D keypoint annotations enable the estimation of SMPL body model parameters through CNNs [42]. This process helps reconstruct 3D human meshes based on segmented body parts. The approach includes two anatomically informed losses within a weakly supervised framework to facilitate learning from extensive real-world 2D data and controlled 3D indoor/synthetic environments. The researchers advocate for weakly supervised methods that employ multi-view consistency losses in 2.5D pose estimation, utilizing multiview geometry and independent 2D annotations to resolve ambiguities in 3D depth [43].

2.4. Advanced 3D Imaging Methods in the Infrared Spectrum

Recent advancements have demonstrated that the 3D position and pose of a human can be accurately reconstructed from single- or multiview infrared (IR) images by leveraging reflections from common objects that capture the infrared radiation emitted by the human body [44]. This approach integrates priors learned from pre-trained 3D generative models with differentiable rendering techniques to infer reflections [45]. By framing the reconstruction process as an optimization problem, a synthesis-by-analysis methodology is employed to interpret the observed thermal reflections. These findings underscore the potential of IR cameras as valuable tools for studying human activities in real-world environments. However, existing data sets are often limited in object diversity and imaging conditions, which poses challenges to generalization [46]. Although 3D object reconstruction techniques—such as Structure from Motion (SfM) [46], Simultaneous Localization and Mapping (SLAM) [47], Semi-Global Matching (SGM) [48], silhouette-based 3D reconstruction [49], Shape from Interaction [50], and deep learning-based methods—are fast and robust for generating 3D models from visible-light imagery, they lack accuracy when applied to infrared data [51]. This limitation stems from the low contrast and lack of distinct features in infrared (IR) images, necessitating a feature extraction method capable of robustly handling subtle IR variations to enable accurate 3D object reconstruction within the IR domain. 3D modeling presents a robust and scalable methodology for the large-scale generation of infrared (IR) image datasets, enabling substantial advancements in the analytical methodologies and practical implementation of infrared imaging technologies.

3. Single-Pixel Image Reconstruction

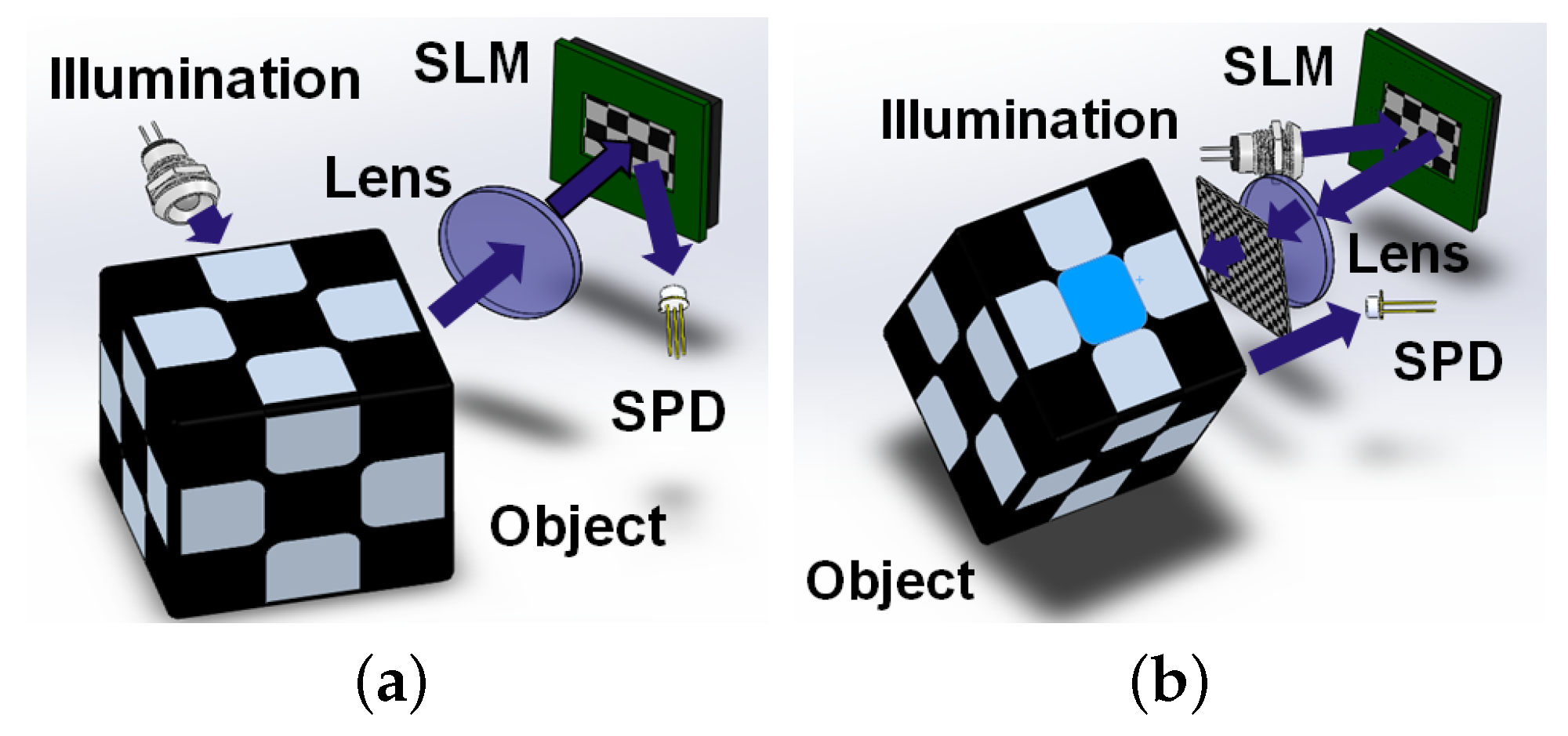
The Single-Pixel Imaging (SPI) technique [21,22], reconstructs images by measuring correlated intensity on a detector that lacks spatial resolution. SPI cameras employ spatial light modulators (SLMs), such as Digital Micro-Mirror Devices (DMD), to generate spatially structured light patterns (resembling Hadamard patterns) that interrogate a scene. These cameras function according to two main architectures: structured detection and structured illumination, as illustrated in Figure 1.

In structured detection, an object is illuminated by a light source, and the reflected light is subsequently modulated by a Spatial Light Modulator (SLM) before being measured by a single-pixel (bucket) detector. In contrast, in structured illumination, represented by the modulation pattern $\mathrm{\Phi }$, the SLM is used to spatially modulate incident light before it illuminates the object O. The light reflected from the object is captured by the bucket detector and subsequently converted into an electrical signal $y_k$, as defined in Equation (1).

$$y_k=\alpha \sum _{i=1}^M\sum _{j=1}^{N}O\left(i,j\right)\mathrm{\Phi }\left(i,j\right)$$

(1)

Here, $\alpha$ represents a constant factor influenced by the optoelectronic characteristics of the photodetector. The electrical signal generated by the photodetector is derived from the correlation between the spatial pattern of the light and the light reflected from the object. The corresponding sequence of electrical signals is produced by projecting a series of these spatial patterns. These signals are then computationally processed to reconstruct the image. Specifically, the image $x_k$ is reconstructed from the captured signal $y_k$ and the corresponding pattern $\mathrm{\Phi }$, as described in Equation (2) [22]

$$x_k=\alpha \sum _{i=1}^M\sum _{j=1}^N{y}_k\mathrm{\Phi }\left(i,j\right)$$

(2)

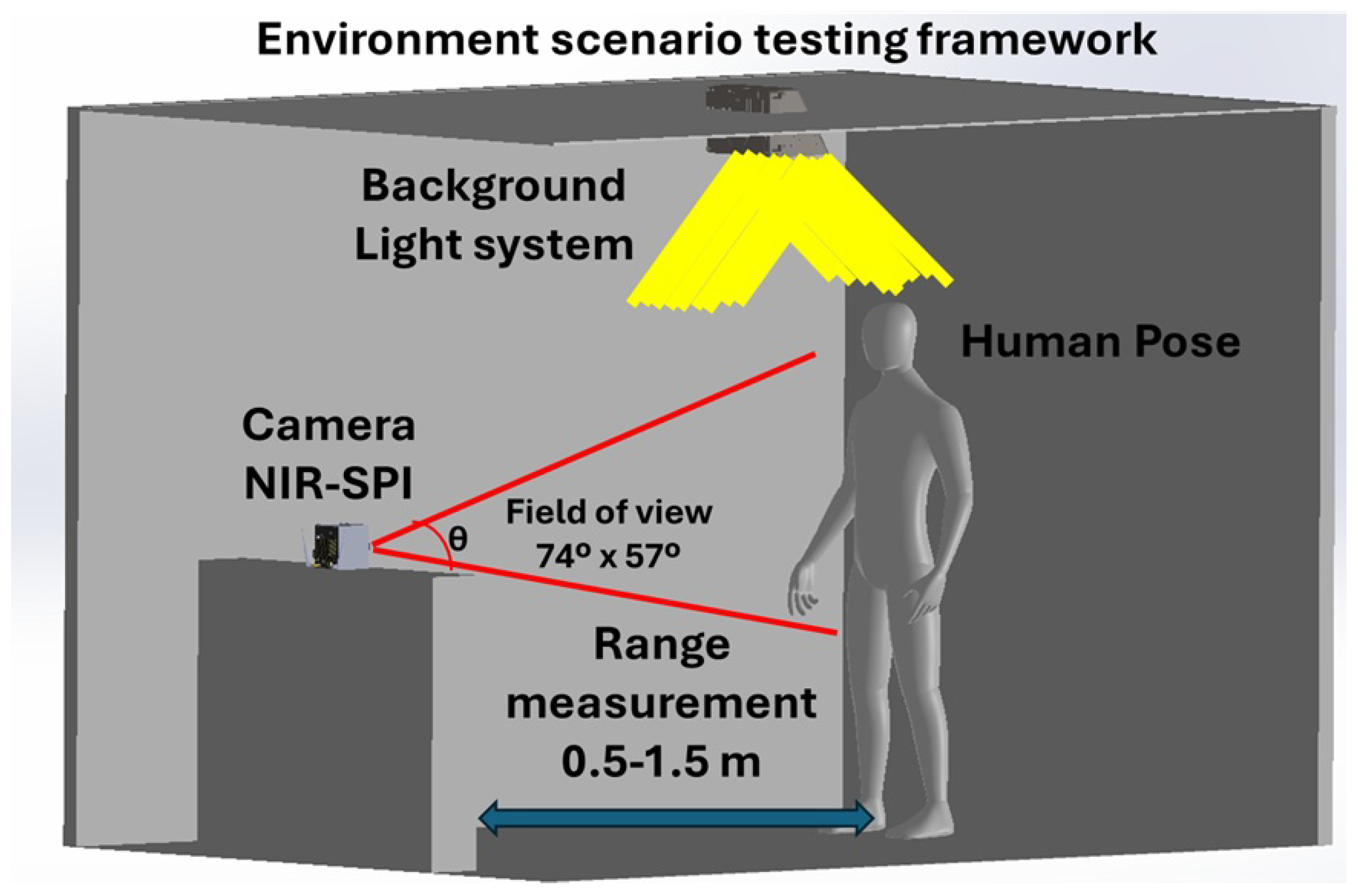
In this study, we used an array of 32 × 32 near-infrared LEDs (NIR-LEDs) that emit at a peak wavelength of 1550 nm for generating Hadamard-like patterns $\mathrm{\Phi }$ through active illumination. This wavelength was chosen to minimize the effect of water scattering and absorption coefficients. The LED array is positioned perpendicular to the lens’s focal plane, allowing the light patterns to be projected toward infinity. However, due to the dimensions of the matrix, the effective projection range is limited to 0.3–2 m.

3.1. Fusion Strategy for Enhancing TOF and Single-Pixel Imaging Resolution

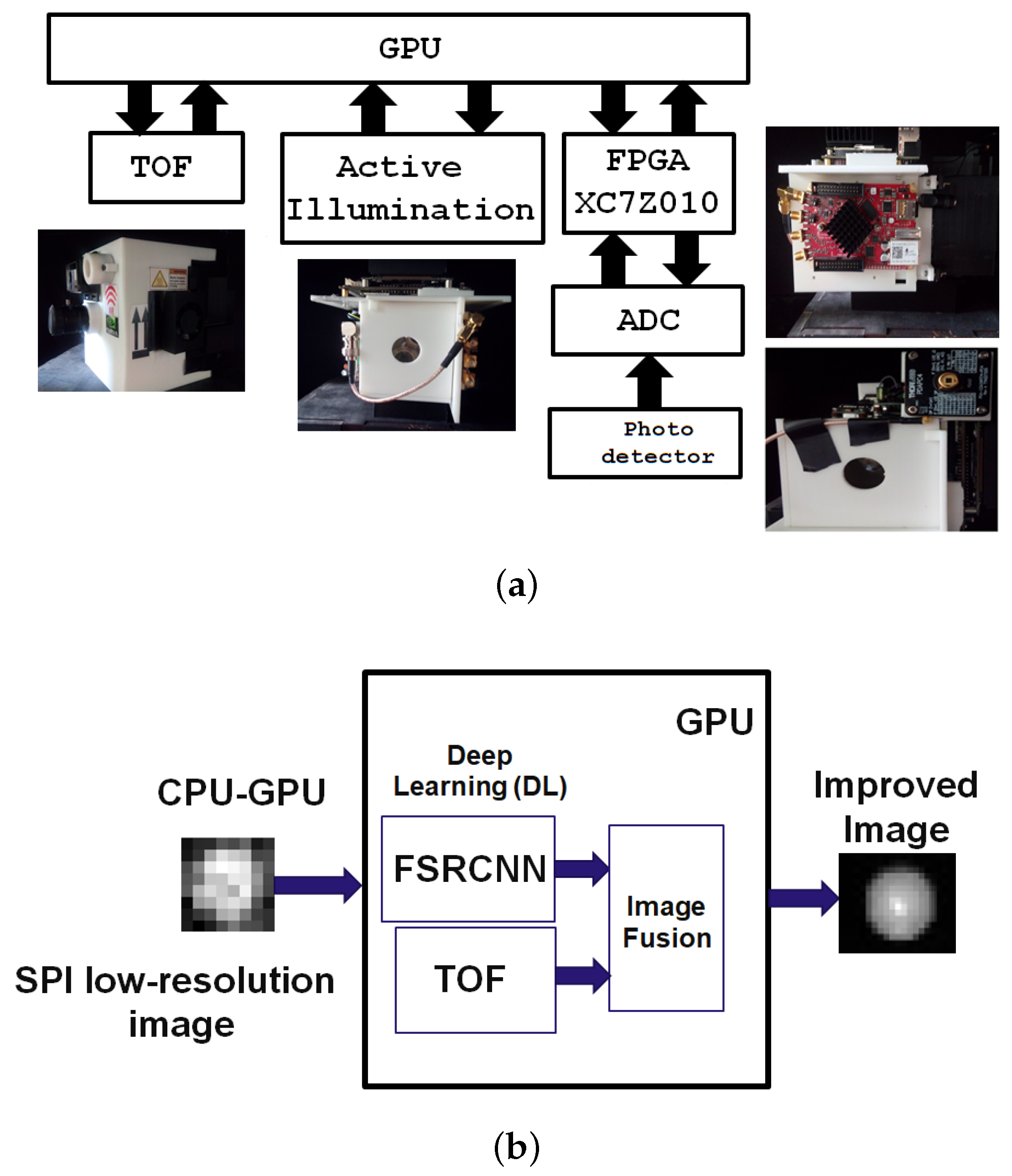
For fusing TOF imaging and low-resolution SPI to generate a high-resolution image to employ a Deep Learning-based Super-Resolution (SR) model (see Figure 2b), which takes advantage of the complementary advantages of both modalities. The ToF depth map and the SPI intensity image are initially pre-processed and spatially registered. The ToF modality delivers precise structural depth information, while the SPI system contributes high-contrast intensity details. A dual-branch CNN extracts spatial features separately from TOF and SPI, with the TOF branch focusing on structural information (low-frequency components) and the SPI branch enhancing fine details and textures (high-frequency components). The extracted features are subsequently concatenated and passed through a Fusion Network, which learns to compute optimal blending weights to preserve essential structural information. To further enhance resolution, a Fast Super-Resolution Convolutional Neural Network (FSRCNN) [26] is applied to upscale the fused low-resolution image, reconstructing high-quality textures and spatial details. Finally, a refinement layer removes artifacts and enhances sharpness, producing a high-resolution fused image with improved texture, depth consistency, and spatial clarity.

3.2. SPI Camera

Our study introduces structured illumination to improve image quality in difficult lighting conditions, such as solid backlighting and stray light interference. We utilized a time-of-flight (TOF) system with a wavelength of 850 nm and an InGaAs photodiode as the bucket detector, which operates at 1550 nm. Our proposed architecture, named NIR-SPI, comprises two primary components. The first component involves fundamental elements based on the single-pixel imaging principle, including an InGaAs photodetector (specifically the Thorlabs FGA015 diode operating at 1550 nm), a series of NIR-LEDs for light emission, a TOF system, and an analog-to-digital converter (ADC). For a visual depiction of this setup, see Figure 2a. The second component includes a subsystem designed to process the electrical output of the bucket detector. The ADC digitizes the electrical signal, and the data is processed by an embedded system in a module (SoM) [52], notably GPU-Jetson Xavier NX, also illustrated in Figure 2a. This SOM is tasked with generating Hadamard-like patterns and processing the digitized data from the ADC. The OMP-GPU Algorithm is applied within the SoM to facilitate the generation of 2D images. The processing duration for each phase of the 2D image reconstruction is detailed. For more information on the SPI camera, further reading is recommended.

3.3. 2D Reconstruction Algorithm

We initiated the process by acquiring and digitizing the electrical signal $y_k$ through an analog-to-digital conversion mechanism (ADC). This step involved projecting the signal with a Hadamard matrix, resulting in a vector of signals $y_k$ (refer to Equation (1)). We then applied the Orthogonal Matching Pursuit (OMP) algorithm (see Algorithm 1) to derive the image $x_k$ (refer to Equation (2)). Our goal was to satisfy condition $\left|y_k-\mathrm{\Phi }(i,j)x_k\right|<\epsilon$ [22]. To enhance the computational efficiency of the 2D SPI image reconstruction algorithm, matrix inversion was carried out using the Cholesky decomposition technique, as described in the literature [53,54]. This approach required us to compute the symmetric and positive Gram matrix, denoted $G_k={\mathrm{\Phi }}^T\mathrm{\Phi }$ [55]. Furthermore, an initial projection $p^0={\mathrm{\Phi }}^T{y}_k$ was performed (see Algorithm 1, line 3) to support the implementation of the Cholesky method.

$$L_{new}=\left[\begin{array}{cc}L& 0\\ w^T& \sqrt{1-w^{T}w}\end{array}\right]$$

(3)

Algorithm 1: OMP-GPU algorithm [55], Input: OMP-GPU algorithm input data: Patterns $\mathrm{\Phi }$, input signal $y_k$, Output: OMP-GPU algorithm output data: sparse representation $x_k$ that fulfills the relation $y_k\approx \mathrm{\Phi }{x}_k$.
1:  procedure OMP-GPU($\mathrm{\Phi }$,$y_k$):
2:      set: $L_1$=[1], k=1,$p^0={\mathrm{\Phi }}^T{y}_k$
3:      set: $\epsilon =y_k{y}_k^T$, $G_k={\mathrm{\Phi }}^T\mathrm{\Phi }$, $p=p^0$
4:      while ${\epsilon }_{k-1}>ϵ$ do
5:          $M={arg\; max}_K\left|p\right|$	▹ Finding the new atom
6:          if $M>1$ then
7:             $w_k=\left\{L_{k-1}{w}_k=G_{k-1,K}\right\}$ $w_k$	▹ Solver
8:             $L_k=\left[\begin{array}{cc}{L}_{k-1}& 0\\ w_k^T& \sqrt{1-w_k^T{w}_k}\end{array}\right]$	▹ Update of Cholesky
9:
10:         end if
11:         $x_k=\left\{L_k{L}_k^T{x}_k=p^o\right\}$	▹ Solver $x_k$
12:         $\beta =G_k{x}_k$	▹ Matrix-sparse-vector product for each path
13:         $p=p^o-\beta$
14:         ${\delta }^k=x_k^T\beta$	▹ Calculate error
15:         ${\epsilon }^k={\epsilon }^{k-1}-{\delta }^k+{\delta }^{k-1}$	▹ Calculate norm $\epsilon$
16:
17:         $k=k+1$	▹ increasing iteration
18:     end while
19:     return $x_k$
20: end procedure

The matrix G can be decomposed into two triangular matrices through Cholesky decomposition, expressed as $L_k{L}_k^T$ (see Equation (3)). In this expression, $L_k$ denotes the triangular Cholesky factor [56] (refer to Algorithm 1, line 8). To address this matrix, we establish a system $L_k{L}_k^T{x}_k={\mathrm{\Phi }}^T{y}_k$. This system is addressed by considering it as a triangular system, formulated as $L_{k}u=b$ with $b=\mathrm{\Phi }{y}_k$ and $L_k^T{x}_k=u$ (see Algorithm 1, line 11). The matrix $L_k$ is determined using the approach described in Equation (3) [55], where $w_k=L_k^{-1}{G}_k$ (see Algorithm 1, line 7). For reconstructing the signal $x_k$, which involves transforming a vector image into an NxN matrix through a reshape operation, a stopping criterion is established by comparing the norm of the residual with a threshold $\epsilon$ (see Algorithm 1, line 15), thus bypassing the need to compute the residual $\delta$ (see Algorithm 1, lines 12–14). To improve algorithm efficiency, we suggest that it be deployed in the Compute Unified Device Architecture (CUDA) to facilitate parallel processing in the reconstruction task [57] (see Algorithm 1).

To generate the final 2D image, we first obtain the SPI image using the method described in Algorithm 1 and then integrate it with post-processed depth data from a TOF system. This depth data is improved through a normalization technique. The FSRCNN network method, as detailed in [26], fuses the initial input image with data from the TOF system. This fusion process enhances the image to two times its initial resolution, producing a final output image with dimensions of 64 × 64 pixels. The complete system illustrated in Figure 2b details the processing algorithm of the proposed NIR-SPI vision system. This system starts with a low-resolution SPI image, processes it through the FSRCNN network [26], and combines it with data from the TOF system.

3.4. SPI Acquisition Protocol

In developing the SPI camera, we focused on two crucial parameters essential to capture SPI images: the detector exposure time ($T_{ext}$ and the frequency of pattern projection $F_{patterns}$). We used a theoretical model of the NIR-SPI system [58] to determine the appropriate exposure time. This model accounts for factors such as maximum measurement distance, scattering effects, and the correlation between photon incidence on the sensor and the noise threshold. We established the exposure time, $T_{ext}$, to range between 80 and 120 $\mathsf{\mu }$s, optimal for measurement distances of 0.3 to 1 m. From this exposure time, we derived that the minimum frequency for the ADC must be at least 60 KHz. The frequency patterns are based on Equation (4) [59], using the parameter $F_{min}$ to evaluate the efficiency at the individual pixel level. The ideal configuration occurs at $F=F_{min}$ (where F denotes the actual sensor pixel count), which facilitates the highest ADC measurement rate at the lowest sensor resolution ($F_{ADC}$ = 125 MHz). This setup significantly improves the signal-to-noise ratio in outdoor conditions. When the design condition is below $F<F_{min}$, the frequency patterns limit the resolution of the measurement. In contrast, exceeding this value ($F>F_{min}$), the pattern generation frequency, defined within the range of $F_{patterns}$ = 40 KHz, can achieve a measurement rate three times faster.

$$F_{min}={\displaystyle \frac{F_{ADC}}{F_{patterns}}}$$

(4)

4. Deep Learning Classification for Human Pose Estimation

ViT Transformer-Based Classification for the Estimation of SMPL-X Pose from Low-Resolution SPI

The proposed framework utilizes Vision Transformer (ViT) [23] to classify infrared (IR) images from the LWIRPOSE dataset [60], which includes pose information for 12 activities: Direction, Discussion, Eating, greeting, Phone conversation, Posing, Purchases, Sitting, Smoking, Taking Photos, Waiting and Walking. To define the classification model, we evaluated the performance of various architectures, including CNN [61], VGG10 [62], ResNet [63], and ViT. As shown in

Table 1. Classification performance of various models on the LWIRPOSE dataset using infrared (IR) images. The dataset includes pose information for 12 activities: Direction (P1), Discussion (P2), Eating (P3), Greeting (P4), Phone Talk (P5), Posing (P6), Purchases (P7), Sitting (P8), Smoking (P9), Taking Photos (P10), Waiting (P11), and Walking (P12). The results highlight the performance of different models, demonstrating the superior effectiveness of ViT in accurately classifying human poses.

Model	P1	P2	P3	P4	P5	P6	P7	P8	P9	P10	P11	P12
CNN	0.48	0.52	0.54	0.31	0.42	0.56	0.66	0.98	0.73	0.52	0.44	0.94
VGG10	0.69	0.69	0.79	0.70	0.59	0.64	0.69	0.97	0.77	0.55	0.71	0.99
ResNet	0.81	0.61	0.82	0.68	0.74	0.75	0.89	0.74	0.78	0.93	0.75	0.93
ViT	0.83	0.70	0.73	0.88	0.82	0.88	0.98	0.93	0.99	0.79	0.77	0.98

and

Table 2. Evaluation of the classification models based on Precision, Recall, and F1-Score metrics [64]. The table compares the performance of different architectures, including CNN, VGG10, ResNet, and ViT. ViT achieves the highest scores across all metrics, demonstrating its effectiveness in classifying infrared images from the LWIRPOSE dataset.

Model	Precision	Recall	F1-Score
CNN	0.43	0.40	0.40
VGG10	0.63	0.57	0.54
ResNet	0.71	0.61	0.62
ViT	0.75	0.73	0.70

, ViT demonstrates superior accuracy, making it the preferred choice for this task. This classification constitutes a critical preprocessing stage for pose estimation within the SMPL-X model, thereby improving the accuracy of 3D human pose reconstruction from low-resolution SPI infrared images. By integrating deep learning-based feature extraction and classification, the proposed approach effectively addresses challenges in thermal imaging, such as low-resolution and noisy data, thereby improving human pose estimation in complex environments (see Figure 3).

1.

Input IR image acquisition

• The system receives an SPI-based low-resolution infrared image that captures a human figure.
• The LWIRPOSE dataset, consisting of thermal images depicting various human activities, serves as the main input data source.
• These images, acquired in the Long-Wave Infrared (LWIR) spectrum, exhibit low spatial resolution, making direct 3D human pose reconstruction challenging.

2.

Image tokenization & feature embedding

• The input image is divided into smaller non-overlapping patches, following the standard ViT patch embedding mechanism.
• Each patch is flattened and linearly projected into a high-dimensional feature space, ensuring that local spatial features are retained.
• These projected embeddings serve as input tokens to the ViT Transformer encoder.

3.

Transformer-based feature extraction

• The Transformer Encoder processes the embedded patches using multihead self-attention (MHSA) and feedforward layers [65].
• This enables the model to capture both local and global dependencies in the IR image, preserving structural details essential for pose recognition.
• The Transformer aggregates spatial relationships between different body regions, enhancing the understanding of human posture even in low-resolution IR data.

4.

Classification via Multi-Layer Perceptron (MLP)

• The extracted feature representation from the Transformer Encoder is fed into a Multi-Layer Perceptron (MLP) [23] for human activity classification.
• The confusion matrix in the figure demonstrates the system’s ability to classify different activities, such as walking, sitting, taking photos, eating, smoking, and talking on the phone, achieving high precision in most categories.
• Accurate classification is crucial for defining a pre-pose configuration that aligns with real-world human movements.

5.

Pre-pose estimation with SMPL-X model

• The classified activity is mapped onto the SMPL-X human pose model, a 3D parametric representation of the human body that captures detailed articulations and anatomical structure.
• The prepose definition based on classification output serves as an initial pose estimation, allowing for more refined 3D reconstructions of human movement.

5. Proposed Method

Our proposed method outlines an innovative approach to generate a detailed 3D human model using the SMPL-X framework from images captured by an imaging NIR-SPI system (see Figure 4). This system is particularly advantageous when traditional imaging fails due to low light or obstructions. Using advanced machine learning techniques, including deep convolutional neural networks and self-supervised learning from 3D generation, human figures of data were obtained from SPI with noise and missing information. The process involves several key stages, including depth map generation, depth perception enhancement, depth thresholding, and sophisticated 3D mesh reconstruction. The ultimate goal is to optimize the 3D mesh to fit the SMPL-X model by adjusting global rotation, translation, body shape, and pose parameters extracted from the depth data, producing a highly accurate and realistic human model.

5.1. Selection of Key Hyperparameters

The design decisions and hyperparameter configurations throughout the present work were carefully formulated to develop an accurate, efficient, and robust pipeline for reconstructing 3D human poses (see Figure 4). Each component was optimized to achieve an optimal trade-off between computational efficiency and reconstruction fidelity, ensuring seamless integration across the entire pipeline, from data acquisition to model generation. The proposed method achieves enhanced performance by optimizing the hyperparameters, exhibiting strong robustness to noise and high adaptability to low-resolution inputs, while effectively maintaining realistic representations of human poses. The following step-by-step breakdown outlines the entire workflow, encompassing SPI-based image acquisition, depth perception enhancement, and 3D human mesh reconstruction using the SMPL-X model.

Figure 4. The image illustrates a comprehensive method for constructing a 3D human model using a NIR-SPI system. The process begins with acquiring an NIR-SPI image and generating a depth map using deep learning techniques. Enhanced depth perception is achieved through additional image processing, which then undergoes thresholding to isolate the human figure. A self-supervised neural network utilizes the processed data to generate a 3D human mesh, extracting crucial parameters such as global rotation, translation, shape, and pose. The final output is a probabilistic human model in the SMPL-X format, offering a precise and articulated 3D representation of the subject captured under challenging imaging conditions.

Figure 4. The image illustrates a comprehensive method for constructing a 3D human model using a NIR-SPI system. The process begins with acquiring an NIR-SPI image and generating a depth map using deep learning techniques. Enhanced depth perception is achieved through additional image processing, which then undergoes thresholding to isolate the human figure. A self-supervised neural network utilizes the processed data to generate a 3D human mesh, extracting crucial parameters such as global rotation, translation, shape, and pose. The final output is a probabilistic human model in the SMPL-X format, offering a precise and articulated 3D representation of the subject captured under challenging imaging conditions.

1.

Single-Pixel Imaging acquisition (NIR-SPI)

• Process overview: Utilize NIR-SPI system to capture an image. SPI systems collect data by measuring the total amount of light reflected from a scene through a series of programmable masks without forming a traditional image (see Algorithm 1).

2.

Depth map

• Deep Learning model: Implement Vision Transformer (ViT) to infer a depth map from the SPI image. The ViT would be trained on a dataset [66] and the LWIRPOSE dataset [60] comprising SPI images and their corresponding depth maps, enabling it to predict depth from unseen SPI data.
• Output Specifications: The resulting depth map assigns a depth value to each pixel, encoded as color intensities, illustrating the distance of objects from the imaging setup (see Figure 5).

3.

Depth thresholding

• Segmentation process: Apply a thresholding algorithm to the enhanced depth map to isolate the human figure from the background. This binary segmentation helps simplify the input for the subsequent 3D modeling steps [67].

  $$S(x,y)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}D(x,y)\le T\hfill \\ 0,\hfill & \mathrm{if}D(x,y)>T\hfill \end{array}\right.$$

  (5)

  where $D(x,y)$ is the depth value at pixel location $(x,y)$, T is the threshold value, and $S(x,y)$ is the resulting binary mask.

  Figure 5. Generation of depth maps using NIR-SPI Images and the LWIRPOSE dataset (a) Images from the LWIRPOSE dataset depicting various human poses, depth maps generated from the dataset images and 3D depth perception, (b) NIR-SPI images of human subjects, depth maps generated from NIR-SPI images and 3D depth perception at distance 0.5 m, (c) NIR-SPI images, depth maps and 3D depth perception at distance 1 m.

  Figure 5. Generation of depth maps using NIR-SPI Images and the LWIRPOSE dataset (a) Images from the LWIRPOSE dataset depicting various human poses, depth maps generated from the dataset images and 3D depth perception, (b) NIR-SPI images of human subjects, depth maps generated from NIR-SPI images and 3D depth perception at distance 0.5 m, (c) NIR-SPI images, depth maps and 3D depth perception at distance 1 m.
• Segmentation output: The output is a point cloud $P=\left\{(x_i,y_i,z_i)\right\}$ where the human figure is distinctly separated. This can be derived from the segmentation mask as:

  $$P=\{(x_i,y_i,z_i)\mid S(x_i,y_i)=1\}$$

  (6)

  where $z_i=D(x_i,y_i)$ represents the depth at the coordinates $(x_i,y_i)$.
  The output point cloud P focuses on the points corresponding to the human figure, facilitating more targeted processing in the subsequent 3D modeling steps.

4.

Self-supervised 3D human mesh generation

• Model architecture: Use a self-supervised learning framework based on PointNet++ [68] capable of reconstructing 3D human meshes from processed images. This might involve a sophisticated deep learning architecture that predicts 3D geometry from 2D data. For training, the CAPE dataset [69] was employed alongside the Adam optimization algorithm, with a learning rate set to ${10}^{-4}$.
• Parameter extraction: Extract key parameters such as global rotation R, translation t, body shape $\beta$, and pose $\theta$ from the thresholded depth image, using these to construct and refine the 3D mesh.
• Loss function: The overall loss function $L=L_{recon}+L_{pose}+L_{shape}+L_{reg}$ combines multiple components to ensure the accurate reconstruction of the 3D human mesh:

  (a)

  Reconstruction loss (${\mathit{L}}_{\mathit{recon}}$): Measures the error between the predicted mesh and the ground truth mesh. This loss encourages the network to produce an accurate 3D reconstruction of the human body.

  $$L_{recon}={∥M_{pred}(R,t,\beta ,\theta )-M_{gt}∥}^2$$

  (7)

  where $M_{pred}(R,t,\beta ,\theta )$ is the predicted 3D mesh generated using the SMPLX parameters and $M_{gt}$ is the ground truth 3D mesh.

  (b)

  Pose loss (${\mathit{L}}_{\mathit{pose}}$): Ensures that the predicted pose $\theta$ closely matches the ground truth pose. This is crucial because the pose directly influences the human body’s appearance in 3D space.

  $$L_{pose}={∥{\theta }_{pred}-{\theta }_{gt}∥}^2$$

  (8)

  where ${\theta }_{pred}$ is the predicted pose parameters and ${\theta }_{gt}$ is the ground truth pose.

  (c)

  Shape loss (${\mathit{L}}_{\mathit{shape}}$): Encourages the predicted body shape $\beta$ to match the actual body shape from the dataset. This loss helps refine the human mesh to match the body proportions of the subject.

  $$L_{shape}={∥{\beta }_{pred}-{\beta }_{gt}∥}^2$$

  (9)

  where ${\beta }_{pred}$ is the predicted shape parameters and ${\beta }_{gt}$ is the ground truth shape.

  (d)

  Regularization loss (${\mathit{L}}_{\mathit{reg}}$): To avoid unrealistic poses and shapes, regularization is added to the predicted parameters. This typically includes terms that penalize large deviations from expected values.

  $$L_{reg}={\lambda }_{pose}·{∥{\theta }_{pred}∥}^2+{\lambda }_{shape}·{∥{\beta }_{pred}∥}^2$$

  (10)

  where ${\lambda }_{pose}$ = 0.1 and ${\lambda }_{shape}$ = 0.01 are hyperparameters that control the regularization strength.

5.

Probabilistic human model fitting

• SMPL-X model: Use the SMPL-X model, which provides a parametric mesh of the human body that can articulate and deform to match the observed data [70], it can be described as a function $V=M\left(\theta ,\beta ,\psi \right)$, $\theta$ pose parameters (rotation angles of joints), $\beta$ shape parameters (capturing the individual’s body shape), and $\psi$ expression parameters (expressions of the face and hand).
• Optimization technique: The goal is to adjust the SMPL-X parameters $\theta ,\beta ,\psi$ so that the model fits the observed depth data from cloud point estimation We can formulate this as a probabilistic optimization problem, minimizing an error function $E(\theta ,\beta ,\psi )=E_{data}\left(M\left(\theta ,\beta ,\psi \right)\right)+{\lambda }_{reg}·E_{reg}\left(\theta ,\beta ,\psi \right)$, where $E_{data}=E_{data}={\sum }_{i=1}^N{∥v_i-d_i∥}^2$ This term measures the error between the predicted model points $v_i$ and the estimated depth points observed $d_i$ from the NIR-SPI image. The term $E_{reg}={∥\beta ∥}^2+{∥\psi ∥}^2+{∥\theta ∥}^2$ is used to avoid overfitting the control of deviations from the shape and expression parameters.
• Gaussian correction error pose model estimate: Pose parameters $\theta$ can be adjusted iteratively by applying a Gaussian correction based on the error between the observed and predicted joint angles [71]. The updated pose parameters are refined by: ${\theta }^{(k+1)}={\theta }^{\left(k\right)}-\alpha ·{▽}_{\theta }·E\left({\theta }^k,{\beta }^k,{\psi }^k\right)$, where $\alpha$ is the step size, and the error gradient E is calculated to $\theta$, allowing for a gradual correction of the model pose.
• Fit refinement: The refinement process seeks to reduce the overall error by iteratively adjusting the parameters $\theta$, $\beta$, and $\psi$ until convergence is achieved. Each iteration k updates the parameters ${\theta }_{k+1}={\theta }_k-\alpha ·{▽}_{\theta }·L$, ${\beta }_{k+1}={\beta }_k-\alpha ·{▽}_{\beta }·L$, ${\psi }_{k+1}={\psi }_k-\alpha ·{▽}_{\psi }·L$.

6.

Output

• Final model: The final output is a detailed new 3D model of the human body SMPL-X format.

5.2. Robustness and Sensitivity Analysis

Variations significantly influence the robustness of the 3D SMPL-X human pose model in key parameters, including pose ($\theta$), body shape ($\beta$), translation (t), and rotation (R). A sensitivity analysis was performed by perturbing these parameters within a range of ±20% to assess their impact on the reconstruction error (see Figure 6a). The pose parameter is highly sensitive to perturbations, leading to substantial variations in the reconstruction error. A strong correlation between pose ($\theta$) perturbations and reconstruction error is observed, underscoring its dominant influence. Deviations in pose angles significantly degrade model accuracy. Body shape ($\beta$) variations introduce moderate fluctuations in the reconstruction error, suggesting that morphological changes impact reconstruction but are less critical than pose perturbations. Similarly, rotational perturbations introduce measurable errors, particularly at extreme perturbation levels. However, they remain more stable compared to pose variations, with both parameters exhibiting weaker correlations with error, indicating relatively lower sensitivity (see Figure 6b). Among all the factors evaluated, the translation parameter t demonstrates the lowest sensitivity, suggesting that minor global shifts exert minimal influence on the precision of the reconstructed output. The weak correlation between translation perturbations (t) and the reconstruction error further reinforces the robustness of the model to slight positional variations (see Figure 6b).

6. Experimental Results

The experimental results demonstrate the process of obtaining a 3D human model from NIR-SPI imaging at distances of 0.5 m and 1 m from the NIR-SPI camera under night-time illumination conditions using the methods proposed in Section 5 (see Figure 4). This process involves several key components that ensure accurate pose estimation and 3D reconstruction (see Figure 7):

• NIR-SPI Imaging System:
  • The NIR-SPI camera captures depth-encoded images using near-infrared illumination, allowing for reliable imaging under low-light conditions.
  • The camera is positioned at a fixed location to maintain consistent capture angles across different experiments. The subject was placed at predefined distances (0.5 m and 1.0 m) using floor markers to maintain accuracy between trials.
  • The field of view (${74}^{\circ }$× ${57}^{\circ }$) is selected to cover human movements within the experimental range.
• Illumination control and environmental isolation:
  • A background lighting system is integrated to simulate controlled night-time conditions, reducing the effects of ambient light interference.
  • This system ensures that the near-infrared (NIR) signals remain dominant, improving the accuracy of the depth estimation.
  • The experiments were conducted in a light-controlled chamber to prevent external light leakage that could affect image capture. The walls and floor materials were selected to minimize reflections and absorb stray light.
  • The clothing and background materials of the human subject were standardized to reduce variations in light absorption and scattering.
• Deep Learning Models and Data Processing:
  • The approach leverages deep learning models proposed for the LWIRPOSE dataset [60], ensuring high accuracy in pose estimation.
  • The calibration of the vision system is performed using established methods [72] the alignment between the depth maps and the NIR-SPI images.
  • The experimental data are collected in a controlled laboratory setting, where the performance of the vision system is evaluated (Figure 7).
• Evaluation metrics for reconstruction quality [70]:
  • Mean Vertex-to-Vertex Distance (V2V): Measures the accuracy of surface reconstruction (lower values indicate better performance).
  • Mean Per-Joint Position Error (MPJPE): Evaluates pose accuracy by comparing predicted joint positions with ground truth (lower values indicate better performance).
  • These metrics provide a comprehensive evaluation of the effectiveness of the self-supervised learning model and the robustness of the proposed methodology (

    Table 3. The results are Mean Vertex-to-Vertex (V2V) (in mm) and Mean Per-Joint Position Error (MPJPE) (in mm) body for the different human positions.

    Human Pose	V2V Error ↓	MPJPE Error ↓
    IPNET [73]	28.2	43.8
    PTF [74]	23.1	41.1
    VIBE [75]	57.29	53
    Our method	36.1	39

    ).

Discussion of the Proposed Method

For evaluation of the proposed network architecture (see Figure 4), we tested different NIR-SPI-based image reconstruction approaches using the SMPL-X model to reconstruct human positions at night-time from distances 0.5 m and 1 m while taking into consideration the limited field of view of the single-pixel camera, which is ${74}^{\circ }$× ${57}^{\circ }$. We captured NIR-SPI images of human poses. We observed some limitations concerning the reference image in the hand and body positions, particularly in the bending position, due to loss of information in the input NIR-SPI image and points cloud generated resulting from reflection effects and low resolution in the reconstructed NIR-SPI image. The 3D human reconstruction demonstrated improved accuracy regarding the positions of the vertex and joint, as detailed in Table 3. Our model registers a V2V error of 36.1 mm, ranking it second behind PTF and ahead of IPNET and VIBE. This indicates a commendable performance, although there remains a potential to enhance the accuracy of finer geometric details relative to the top-performing model. Regarding MPJPE, our model demonstrates the best performance with the lowest error at 39 mm, showcasing its superior accuracy in joint localization compared to the other models. This achievement is particularly significant, as precise joint prediction is critical for many practical applications involving human body pose estimation.

7. Conclusions

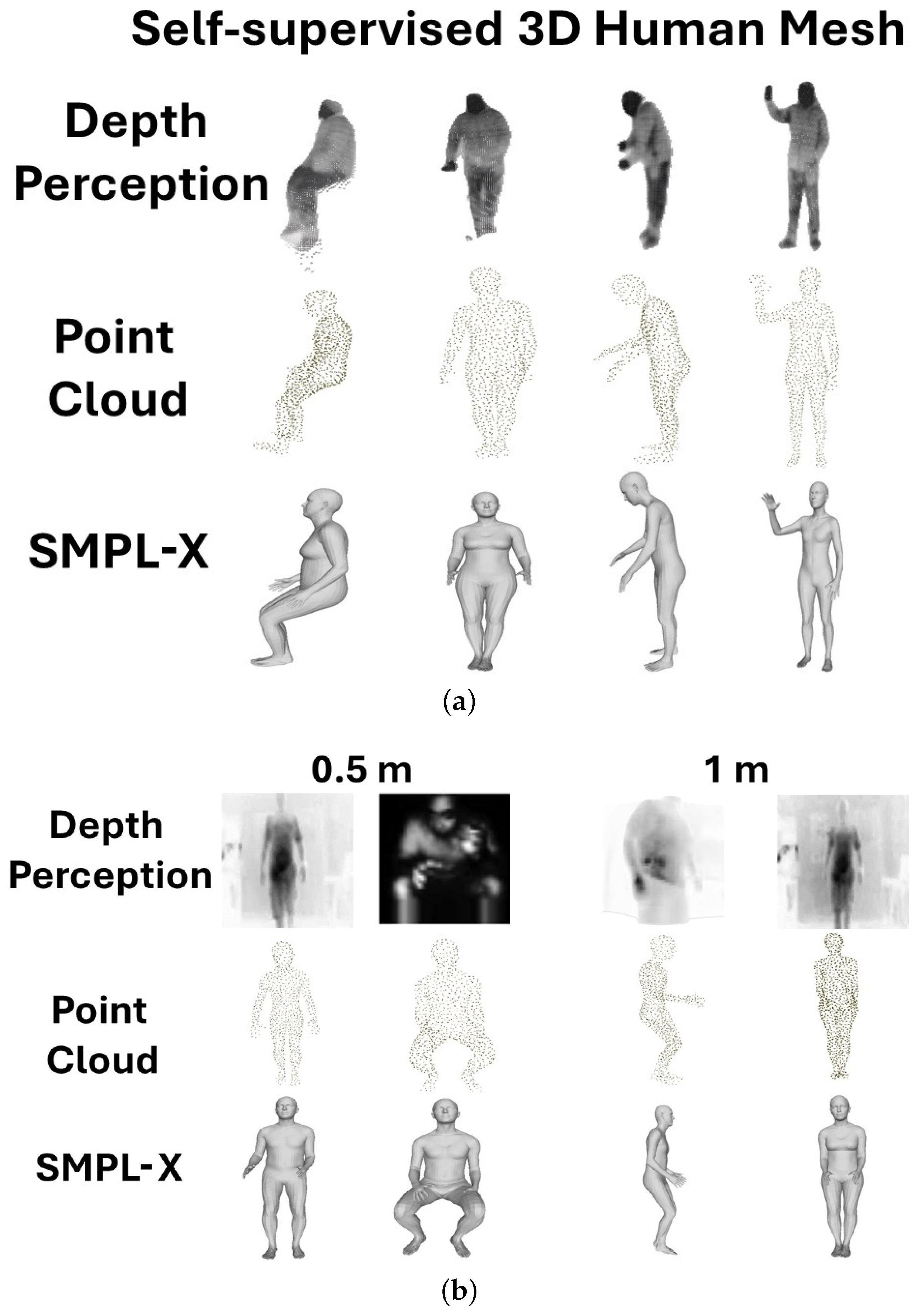
This work introduces a novel methodology that leverages NIR-SPI imaging to generate 3D human models through point cloud generation and integration of ViT classification in a self-supervised learning framework. The approach has demonstrated strong performance in creating accurate 3D reconstructions; however, accurately localizing the hands remains challenging because of the inherently low contrast of the NIR-SPI images. Despite this limitation, both qualitative and quantitative assessments (see Table 3) indicate that the detection of core people retains high accuracy in the estimation of 3D poses, highlighting the potential of the method for single-image modeling of the human body—even at low resolutions (Figure 8).

The experimental results show that our model achieves a V2V error of 36.1 mm, placing it between IPNET (28.2 mm) and VIBE (57.29 mm). Although our method does not produce the lowest V2V error, it significantly outperforms competing approaches in the mean per-joint position error (MPJPE), achieving a minimum deviation of approximately 39 mm. This suggests that, although our model may exhibit lower precision in vertex placement relative to IPNET, it demonstrates greater accuracy in estimating joint positions. PTF, which reports the second-lowest MPJPE (41.1 mm), also performs well, but our model maintains a slight advantage. These findings are highly pertinent to application domains such as motion capture and rescue operations, where precise joint localization is essential to achieve high-fidelity performance and realism. The relatively higher V2V error indicates potential areas for refinement, such as enhanced vertex placement strategies or the integration of more detailed surface geometry features. However, the method achieves a well-calibrated trade-off between vertex-level and joint-level accuracy, offering a robust and versatile solution for a wide range of human body estimation and tracking applications. Furthermore, it represents a significant advancement in the expressive reconstruction of body, hand, and facial features using NIR-SPI imaging, particularly under low-resolution conditions (see

Table 4. Comparison of 3D human pose estimation methods based on MPJPE (Mean Per Joint Position Error), complexity, and performance. The evaluated methods include VIBE (Video Inference for Body Pose and Shape Estimation), IPNET (Implicit Part Network), PTF (Piecewise Trans-Formation Fields), GCMR (Graph Convolutional Mesh Regression), HMR (Human Mesh Recovery), UP (Unite the People), and SMPLify, VIBE with Vit and our proposed method strategies to enhance 3D reconstructions from low-resolution images.

Method	MPJPE (mm)	Complexity
VIBE [75]	65.6	Combines deep learning and optimization techniques.
IPNET [73]	43.8	Computationally complex due to high-density reconstruction.
PTF [74]	60.2	Designed for high-fidelity 3D human pose estimation with dense geometry.
GCMR [76]	71.9	Utilizes graph convolutional networks for mesh regression; computationally intensive but effective for detailed reconstructions.
HMR [77]	87.9	Balances complexity and efficiency; suitable for real-time applications.
UP [78]	80.7	Complexity varies depending on implementation; flexible but computationally expensive.
SMPLify [14]	82.3	Optimization-based approach to fitting the SMPL body model, requiring iterative refinement.
VIBE with Vit [70]	42.0	Integrates ViT and VIBE methodologies for improved accuracy and robustness in low-resolution scenarios.
Our method	39.0	Enhancing ViT and VIBE by integrating a probabilistic human model and depth information for improved 3D pose estimation.

and

Table 5. Performance comparison of 3D human pose reconstruction methods, highlighting accuracy, computational demands, and suitability for dynamic and low-resolution scenarios.

Method	Performance
VIBE	Delivers improved accuracy in dynamic scenarios.
IPNET	Computational complexity and precision in shape reconstruction.
PTF	High-fidelity 3D human pose estimation, particularly excelling in scenarios with dense geometry.
GCMR	Performance can be computationally demanding.
HMR	Achieves a good balance between accuracy and speed.
UP	Ensures reliable performance.
SMPLify	Deliver reasonable accuracy in controlled environments.
VIBE with Vit	Capable of generating 3D reconstructions from low-resolution images.
Our method	Enhancing 3D human pose reconstruction through NIR-SPI in scenarios with missing information and low-resolution inputs.

). Future research will aim to improve the accuracy at the vertex level while preserving or further improving the precision of the joint position.

Although laboratory results for the NIR-SPI system are promising, real-world outdoor deployment introduces additional complexities, such as variable weather conditions, background clutter, and dynamic lighting. To overcome these challenges, future work will focus on adaptive calibration strategies, real-time environmental compensation algorithms, and advanced noise filtering techniques. Further efforts will involve integrating machine learning–driven correction mechanisms and implementing hardware-level optimizations to ensure robust and reliable system performance in diverse outdoor environments.

8. Patents

Carlos Alexander Osorio Quero, Daniel Durini Romero, José de Jesus Rangel Magdaleno, José Martnez Carranza, Ruben Ramos-Garcia, “Sistema y método de creación de imágenes 3D-NIR ampliado”, File No.: MX/a/2022/016091, priority date: 14 December 2022.