Information Diffusion Modeling in Social Networks: A Comparative Analysis of Delay Mechanisms Using Population Dynamics

Abstract

This study presents a comprehensive analysis of information diffusion in social networks with time delay mechanisms. We first analyze real Reddit thread data, identifying limitations in the sample size. To overcome this, we develop synthetic network models with varied structural properties. Our approach tests three delay types (constant, uniform, exponential) across different network structures, using machine learning models to identify key factors influencing information coverage. The results show that spread probability consistently impacts diffusion across all datasets. Gradient Boosting models achieve R² = 0.847 on synthetic data. Random networks with a constant delay mechanism and high spread probability (0.4) maximize coverage. When verified against test data, peak speed time emerges as the strongest predictor (r = 0.995, p < 0.001). Our findings provide practical recommendations for optimizing information spread in social networks and demonstrate the value of integrating real and synthetic data in diffusion modeling.

1. Introduction

1.1. Background and Motivation

Information diffusion in social networks represents a fundamental process that shapes public discourse, influences decision-making, and drives behavioral change across communities. Understanding how information propagates through social structures has become increasingly important in domains ranging from crisis communication and public health messaging to marketing and political campaigns. While numerous studies have examined basic diffusion models, the temporal dynamics—specifically, how delays between information exposure and sharing affect overall coverage—remain understudied. Real-world information sharing rarely occurs instantaneously after exposure. Users typically experience delays before propagating content, yet most diffusion models oversimplify this aspect. These delays can stem from several factors: cognitive processing time, verification activities, or simply practical constraints on social media usage. Despite their prevalence, few studies have systematically compared how different delay mechanisms affect information spread across various network topologies (notably Foroozani & Ebrahimi (2021) [1] and Li & Zhu (2024) [2]).

1.2. Research Gaps and Challenges

This study addresses this gap by examining three distinct delay mechanisms (constant, uniform, and exponential) across diverse network structures. We initially analyze real Reddit thread data to establish baseline patterns, but encounter limitations in sample size. To overcome this constraint, we develop a comprehensive synthetic network approach, generating 100 networks with controlled properties representing five distinct topological structures. Our methodology combines empirical analysis, simulation modeling, and machine learning to identify the key factors influencing information diffusion.

This research specifically investigates the following: (1) how different delay mechanisms affect information coverage; (2) which network structural properties most strongly influence diffusion outcomes; (3) the relative importance of spread probability versus network topology; and (4) the predictive power of temporal dynamics in determining ultimate information reach. By integrating both real and synthetic data analysis, this study provides a robust foundation for understanding how information propagates through social networks with time-delayed sharing.

Our findings reveal that temporal dynamics, particularly the timing of peak diffusion speed, play a crucial role in determining information coverage. Moreover, we identify specific combinations of network structure, spread probability, and delay mechanisms that maximize information reach. These insights contribute to both the theoretical understanding of diffusion processes and the provision of practical guidance for optimizing information dissemination strategies in social networks.

1.3. Novel Contributions

This research makes several significant contributions to the field of information diffusion modeling:

First, we systematically compare three distinct delay mechanisms (constant, uniform, and exponential) across diverse network topologies—a gap in the analysis of the existing literature. This comparative approach reveals unexpected insights about the relative importance of delay types.

Second, we develop a robust methodological framework that integrates real social network data (Reddit threads) with controlled synthetic networks, enabling both ecological validity and experimental rigor in our analysis.

Third, we identify the critical role of temporal dynamics, particularly demonstrating that peak_speed_time serves as the dominant predictor of information coverage (importance = 0.848), a finding with substantial implications for the real-time monitoring of information spread.

Fourth, we provide concrete and actionable recommendations for optimizing information dissemination strategies based on network structure and spread probability, with direct applications for social media platforms, marketing campaigns, and crisis communication.

1.4. Paper Organization

The remainder of this paper is organized as follows: Section 2 reviews related work on information diffusion models, delay mechanisms, network structure effects, and competing information dynamics. Section 3 describes our datasets and features, including both real Reddit data and synthetic network generation. Section 4 details our methodology, explaining the information diffusion simulation, feature engineering, and model development approaches. Section 5 presents the results from real data analysis, synthetic data analysis, and model verification. Section 6 discusses the findings, theoretical implications, practical applications, and limitations. Finally, Section 7 summarizes our conclusions and outlines directions for future research.

2. Related Work

2.1. Information Diffusion Models

Information diffusion in social networks has attracted substantial research attention over the past two decades. As comprehensively documented in the state-of-the-art review by Razaque et al. (2022) [3], this field has evolved from basic epidemic models to sophisticated approaches incorporating temporal dynamics, network topology, and behavioral factors. This extensive review provides a valuable framework for understanding the spectrum of diffusion models and their applications for various social network vulnerabilities. Our work builds upon this rich foundation while focusing specifically on delay mechanisms in information propagation.

The theoretical foundations of information diffusion modeling were established by several seminal works. Kempe et al. (2003) [4] introduced the fundamental problem of influence maximization in social networks, proposing the now-classical Independent Cascade (IC) and Linear Threshold (LT) models. Their work proved the NP-hardness of the influence maximization problem and developed a greedy approximation algorithm with theoretical guarantees, which continues to influence optimization approaches in network diffusion.

Building on this foundation, Leskovec et al. (2007) [5] conducted empirical studies of information cascades in large blog networks, revealing characteristic patterns in how information propagates. Their analysis identified distinct cascade structures and temporal dynamics that have informed numerous subsequent studies on information spread, establishing methodological principles for the empirical analysis of diffusion processes.

A significant advancement in temporal modeling came from Saito et al. (2010) [6], who introduced a delay-aware Independent Cascade model. This approach incorporated time delays between exposure and information sharing, providing a more realistic representation of social media dynamics. Their methods for selecting appropriate diffusion models and estimating parameters from real data demonstrated the importance of temporal aspects in diffusion modeling.

Further refining temporal approaches, Myers & Leskovec (2012) [7] developed continuous-time diffusion models that enabled more precise descriptions of dynamic processes in social networks. Their analysis of competing contagions revealed that interactions between different pieces of information can significantly alter diffusion patterns, with relative changes in the spreading probability averaging at 71%. This work established a framework for understanding how multiple information streams interact during diffusion.

Our research builds directly upon this intellectual lineage. While early models by Kempe et al. [4] and Leskovec et al. [5] established core diffusion principles, and later advances by Saito et al. [6] and Myers & Leskovec [7] introduced temporal considerations, few studies have systematically compared different delay mechanisms across varied network structures. Our work extends these temporal approaches by specifically examining how three distinct delay types (constant, uniform, and exponential) influence information coverage across diverse network topologies. This comparative focus distinguishes our research from previous studies that typically examine a single delay model or network structure.

The Susceptible–Infected–Recovered (SIR) model is widely used for information diffusion. In this model, nodes transition from susceptible to infected and finally to recovered states (Chen et al., 2021) [8]. Kumar et al. (2020) [9] extended this approach with the Susceptible–Exposed–Infected (SEI) model by adding an intermediate “exposed” state. This better captures the delay between exposure to information and active sharing behavior.

Recent advances in diffusion modeling have also explored the financial market implications of information spread. Cai et al. (2024) [10] investigated how momentum dynamics in financial markets are influenced by information diffusion across complex social networks with different topological structures. Chen et al. (2024) [11] developed a crisis information diffusion model based on population dynamics. Their model incorporated parameters such as average follower count, potential audience size, forwarding probability, and information attenuation speed. Similarly, Foroozani and Ebrahimi (2021) [1] proposed a non-linear time-fractional model that could represent both super-diffusion and sub-diffusion processes in networks like Twitter and Digg.

Several researchers have moved beyond basic epidemiological models. Tu et al. (2022) [12] introduced an Ordinary Differential Information Diffusion (ODID) model that examined both temporal and spatial patterns of information diffusion. Their approach achieved approximately 98.78% prediction accuracy on the Digg dataset. Wei et al. (2023) [13] combined gravity theory with evolutionary game concepts to model product diffusion in dynamic online social networks with varying connection weights.

2.2. Delay Mechanisms in Information Propagation

The incorporation of delay mechanisms in diffusion models represents a significant advancement over classical models. Following the pioneering delay-aware approach of Saito et al. (2010) [6], researchers have developed increasingly sophisticated temporal models. These mechanisms reflect the realistic time lag between receiving and sharing information. Sun et al. (2024) [14] developed the SEIHR model which added “exposed” and “hibernated” states to capture different attitudes toward information sharing.

Moscato and Sperlì (2022) [15] proposed a novel action-reaction–diffusion model with temporal constraints. Their model evaluated the influence between users by analyzing meta-paths in user–content relationships. Chen et al. (2021) [8] specifically addressed delays in warning information diffusion by incorporating warning timeliness parameters in their population dynamics model.

Li and Zhu (2024) [2] extended the reaction–diffusion modeling approach by introducing media correction, self-correction, and time delays into rumor propagation systems. Their work demonstrated that increasing the time delay decelerates rumor propagation, while higher degrees of cross-diffusion and correction mechanisms can accelerate information spread. Our work builds upon these delay-focused approaches by systematically comparing three distinct delay mechanisms (constant, uniform, and exponential) across different network structures. This comparative analysis has not been previously undertaken in the literature.

2.3. Network Structure and Diffusion Dynamics

Network topology significantly influences information diffusion patterns, a principle established by Kempe et al. (2003) [4] and empirically validated by Leskovec et al. (2007) [5] through their analysis of cascading behavior. Building on these foundations, Binesh and Ghatee (2021) [16] in their recent work developed a distance-aware optimization model to identify influential nodes. Their approach implicitly maximized local coverage while minimizing global overlap under the Independent Cascade diffusion model. Xiao et al. (2019) [17] mapped networks into three-dimensional space (behavior influence, attribute influence, and topological influence) to analyze how each dimension affects diffusion.

Mohammadi et al. (2023) [18] introduced fuzzy sign-aware diffusion models that considered both trust and distrust relationships. Their approach defined new rules to determine a user’s state based on information received from active neighbors, showing improved prediction accuracy in Bitcoin networks.

Research on Reddit networks specifically has revealed important insights. Haralabopoulos et al. (2015) [19] examined information lifespan and propagation across Reddit, finding that content is enhanced or weakened according to the topic and the network’s dynamic nature. Curiskis et al. (2020) [20] evaluated document clustering and topic modeling techniques on Reddit, demonstrating that neural embedding representations delivered the best performance. Münster et al. (2024) [21] studied the impact of Reddit posts on retail trading behavior, finding that social media posts had significantly better effects than traditional news articles. Liu et al. (2024) [22] further extended temporal considerations by investigating time-varying attractiveness in competitive information diffusion. Their Markov multi-information diffusion model incorporated three critical parameters: attractiveness degree, information boom time, and information prosperity index.

The complexity of modern social networks has prompted research into multiplex network structures. Lin et al. (2025) [23] developed a framework utilizing node dynamics time-series data for network alignment in multiplex social networks. Their approach employed diffusion models to simulate information propagation across multiple platforms, achieving a high accuracy in identifying both interlayer and intralayer links. Similarly, Singh et al. (2022) [24] proposed a fuzzy-based link prediction algorithm in multiplex networks using an information diffusion perspective, demonstrating improved accuracy compared to traditional methods. These approaches highlight the growing importance of considering multiple relationship types and interaction channels in diffusion modeling.

2.4. Competing Information and Attention Dynamics

A growing research area focuses on the competition between multiple information streams in social networks. He et al. (2024) [25] modeled the co-diffusion of competing memes by considering users’ finite attention. Their work identified a ubiquitous threshold for competing memes that predicted which information would become trendy. Similarly, Sun et al. (2024) [14] incorporated human attitude complexity in their SEIHR model to reflect how different attitudes influence rumor propagation. Beyond network structure and diffusion dynamics, linguistic features also play a crucial role in information spread. Džanko et al. (2025) [26] conducted a systematic review of the linguistic features influencing information diffusion in social networks. Competing information concepts help explain why certain diffusion processes succeed while others fail. Our research contributes to this understanding by examining how different network structures and delay mechanisms affect information coverage under varying transmission probabilities.

2.5. Research Gap

While the existing literature provides valuable insights into information diffusion, several gaps remain (

Table 1. Summary of existing information diffusion models and their limitations.

Reference	Model Type	Key Features	Application Domain
Kempe et al. (2003) [4]	Independent Cascade/Linear Threshold	Influence maximization, greedy algorithm	Social influence
Leskovec et al. (2007) [5]	Cascading behavior	Empirical analysis, cascade patterns	Blog networks
Saito et al. (2010) [6]	Delay-aware Independent Cascade	Parameter estimation, model selection	Behavioral analysis
Myers & Leskovec (2012) [7]	Continuous-time diffusion	Competing contagions, cooperation/competition	Multiple information streams
Chen et al. (2021, 2024) [8,11]	Population dynamics	Warning timeliness, crisis focus	Emergency alerting
Kumar et al. (2020) [9]	SEI (epidemiological)	Exposed state	General sharing
Foroozani & Ebrahimi (2021) [1]	Time-fractional	Super-/sub-diffusion	Twitter/Digg
Tu et al. (2022) [12]	ODE-based	Spatial–temporal	Digg
Li & Zhu (2024) [2]	Reaction–diffusion	Time delays, correction mechanisms	Rumor spreading
Mohammadi et al. (2023) [18]	Fuzzy sign-aware	Trust/distrust relationships	Bitcoin network
He et al. (2024) [25]	Competing memes	Finite attention modeling	Content virality
Sun et al. (2024) [14]	SEIHR model	Attitude complexity	Rumor propagation
Cai et al. (2024) [10]	Complex social networks	Network assortativity, degree distribution	Financial markets
Liu et al. (2024) [22]	Markov multi-information	Time-varying attractiveness	Competitive information
Lin et al. (2025) [23]	UIU diffusion model	Network alignment	Multiplex networks
Singh et al. (2022) [24]	Fuzzy-based prediction	Multiplex interaction	Link prediction
Džanko et al. (2025) [26]	Systematic review	Linguistic features	Social media content

). First, few studies systematically compare different delay mechanisms across diverse network structures. Second, the relationship between temporal dynamics (such as peak spread time) and final diffusion coverage remains underexplored. Third, the transferability of models between real and synthetic networks needs further investigation.

Our research addresses these gaps by (1) comparing three distinct delay types across multiple network structures, (2) analyzing the relationship between temporal features and coverage outcomes, and (3) verifying models trained on synthetic data against real-world network data. This comprehensive approach provides a more complete understanding of information diffusion dynamics in social networks with delay mechanisms.

3. Dataset and Features

3.1. Social Network Dynamics and Dataset Features

Information diffusion in social networks involves unique mechanisms that distinguish it from other network propagation processes. In this study, we focus on three critical aspects of social network dynamics:

• First, social networks exhibit user-specific engagement patterns where individuals interact with content at varying frequencies and intensities. This creates natural delays between exposure to information and subsequent sharing actions. On platforms like Reddit, these delays manifest as time gaps between viewing a post and commenting on or upvoting it.
• Second, social networks feature hierarchical thread structures where discussions branch into nested conversations. This structural element creates unique pathways for information flow which are not present in simpler network models. Our Reddit dataset captures these complex thread hierarchies, with parent–child relationships between comments forming directed information pathways.
• Third, social platforms implement algorithmic content prioritization that affects information visibility. These algorithmic factors create uneven exposure patterns that influence diffusion speed and coverage. Our modeling approach accounts for these visibility effects through parameterized transmission probabilities.

By examining both real Reddit networks and synthetic networks with controlled properties, we can isolate how these social media characteristics interact with different delay mechanisms to shape overall information coverage and spread patterns.

3.2. Real Data Collection

Our initial investigation used real data from Reddit threads [27,28]. These online discussion networks provided valuable data on information propagation patterns. We collected data from eight unique networks comprising 72 observations in total. This dataset included both discussion and non-discussion threads to capture different interaction dynamics. The Reddit threads in our dataset were selected to represent diverse community types and interaction patterns. We included threads from eight subreddits spanning different topics: technology (r/programming, r/technology), news (r/worldnews), entertainment (r/movies), lifestyle (r/fitness), gaming (r/gaming), science (r/science), and general discussion (r/AskReddit).

We extracted two key data types from the networks: First, aggregated diffusion results containing spread metrics and parameters. Second, network structural metrics consisting of comprehensive topological features for each network. Both datasets and their processing pipelines are publicly available in our Google Colab repository (https://colab.research.google.com/drive/1zAxPi7i6EKtuNqJ5sdsodpl2J3_Z787m, accessed on 10 April 2025), enabling the reproducibility and extension of our work.

The data preparation process involved several cleaning steps. We merged the datasets using the graph_id as the common identifier. This created a combined dataset with 36 features after removing duplicate columns. We handled missing values using median imputation for numeric features when the missing percentage was below 25%. For columns with excessive missing values, such as avg_time_to_half (98.6% missing), we removed them entirely.

The final dataset included diverse delay types (constant, uniform, exponential) and spread probabilities (0.1, 0.2, 0.3). This variety allowed us to test different information propagation mechanisms. The target variable was avg_coverage, representing the fraction of nodes that received the information.

Our exploratory analysis revealed several patterns in the real data (Figure 1). The mean coverage across all networks was approximately 0.11 (11%). Discussion threads showed slightly higher coverage (mean difference = 0.033) than non-discussion threads, although this difference was not statistically significant (t = 1.765, p = 0.082).

We found no significant differences between delay types (F = 0.172, p = 0.843). This suggested that the specific delay mechanism may not have strongly influenced the diffusion outcomes in these networks (Figure 2).

Spread probability showed a significant effect on coverage (F = 12.195, p < 0.001). Higher spread probabilities consistently led to better information coverage across all network types (Figure 3). A spread probability of 0.3 showed notably higher coverage than 0.1 or 0.2.

The heatmap visualization (Figure 4) further confirmed that discussion graphs with constant delay achieved the highest average coverage (0.140). This initial finding suggests that transmission probability might be more important than network structure or delay mechanism in determining information spread.

3.3. Feature Selection for Real Data

We implemented a rigorous feature selection process to identify the most relevant predictors of information diffusion. First, we examined multicollinearity among the features using correlation analysis.

We identified 55 pairs of highly correlated features (r > 0.8). For example, density showed a perfect correlation with avg_degree_centrality (r = 1.000) and strong correlation with avg_eigenvector_centrality (r = 0.993). Similarly, max_degree had a strong correlation with std_degree (r = 0.996).

The top features by correlation with average coverage were as follows (Figure 5):

• density (r = 0.682);
• avg_degree_centrality (r = 0.682);
• avg_eigenvector_centrality (r = 0.668);
• edges (r = −0.605, negative correlation);
• nodes (r = −0.598, negative correlation).

Figure 5. Feature correlation matrix.

Figure 5. Feature correlation matrix.

Interestingly, the number of edges (r = −0.605) and nodes (r = −0.598) exhibited moderate negative correlations with coverage. This counterintuitive finding suggests that larger networks may actually hinder information spread rather than facilitate it. This could be attributed to several factors: (1) information dilution across larger networks requires more time to achieve similar proportional coverage, (2) increased path lengths create more opportunities for transmission failures, and (3) the emergence of structural bottlenecks that restrict information flow across certain network regions. This highlights the importance of targeted seeding strategies in larger networks rather than relying solely on organic spread.

To reduce multicollinearity, we removed highly correlated features while retaining those most associated with the target variable. We also performed mutual information analysis to capture non-linear relationships.

Our combined feature selection approach identified 14 key features for modeling (Figure 6):

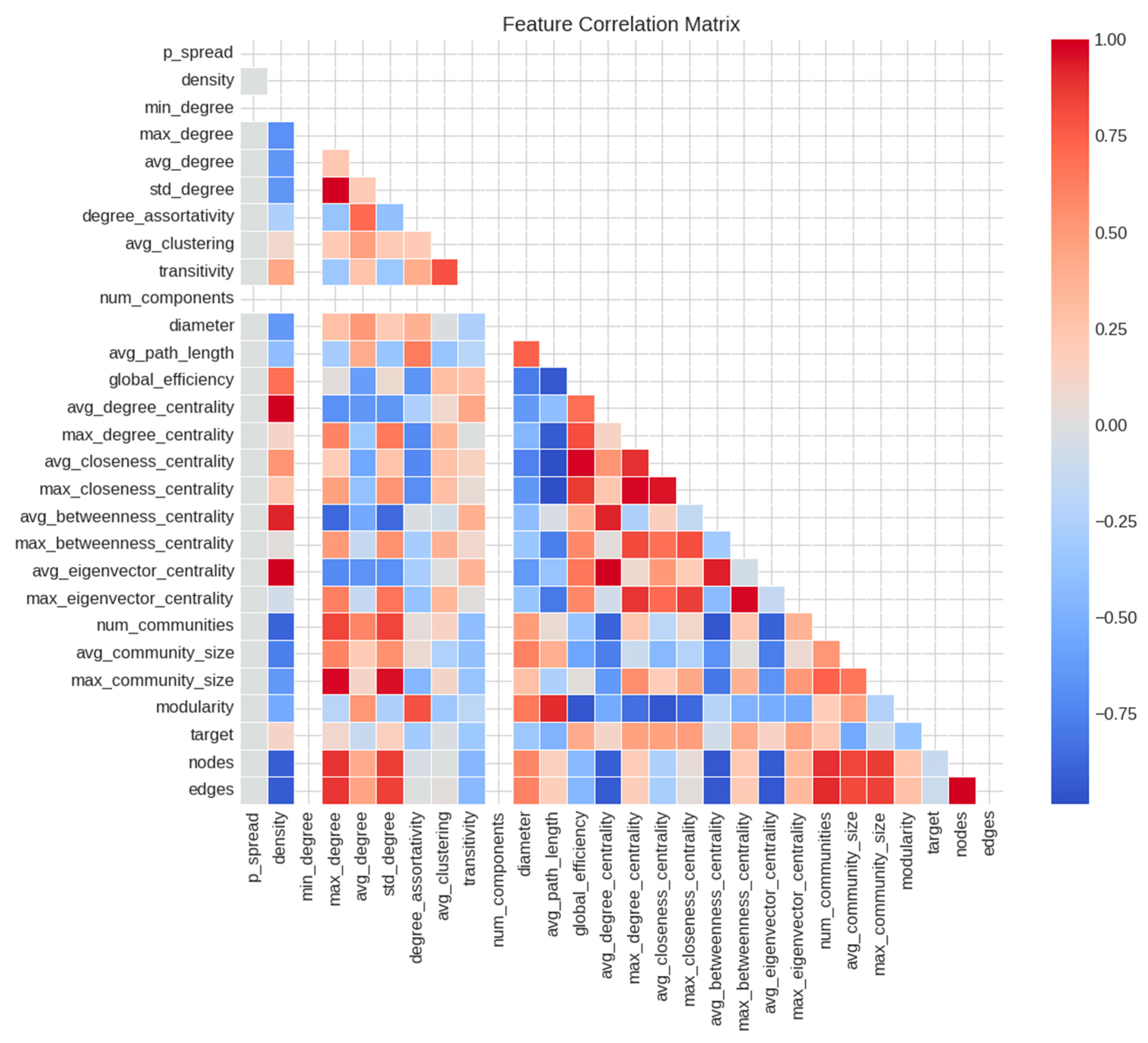
• min_degree;
• num_components;
• diameter;
• avg_community_size;
• density;
• p_spread;
• avg_path_length;
• avg_degree;
• max_degree;
• transitivity;
• degree_assortativity;
• target;
• avg_clustering;
• delay_type_exponential.

Figure 6. Selected features by importance score.

Figure 6. Selected features by importance score.

This feature set balanced predictive power with model interpretability. The selection process helped avoid overfitting despite the limited sample size of the real data.

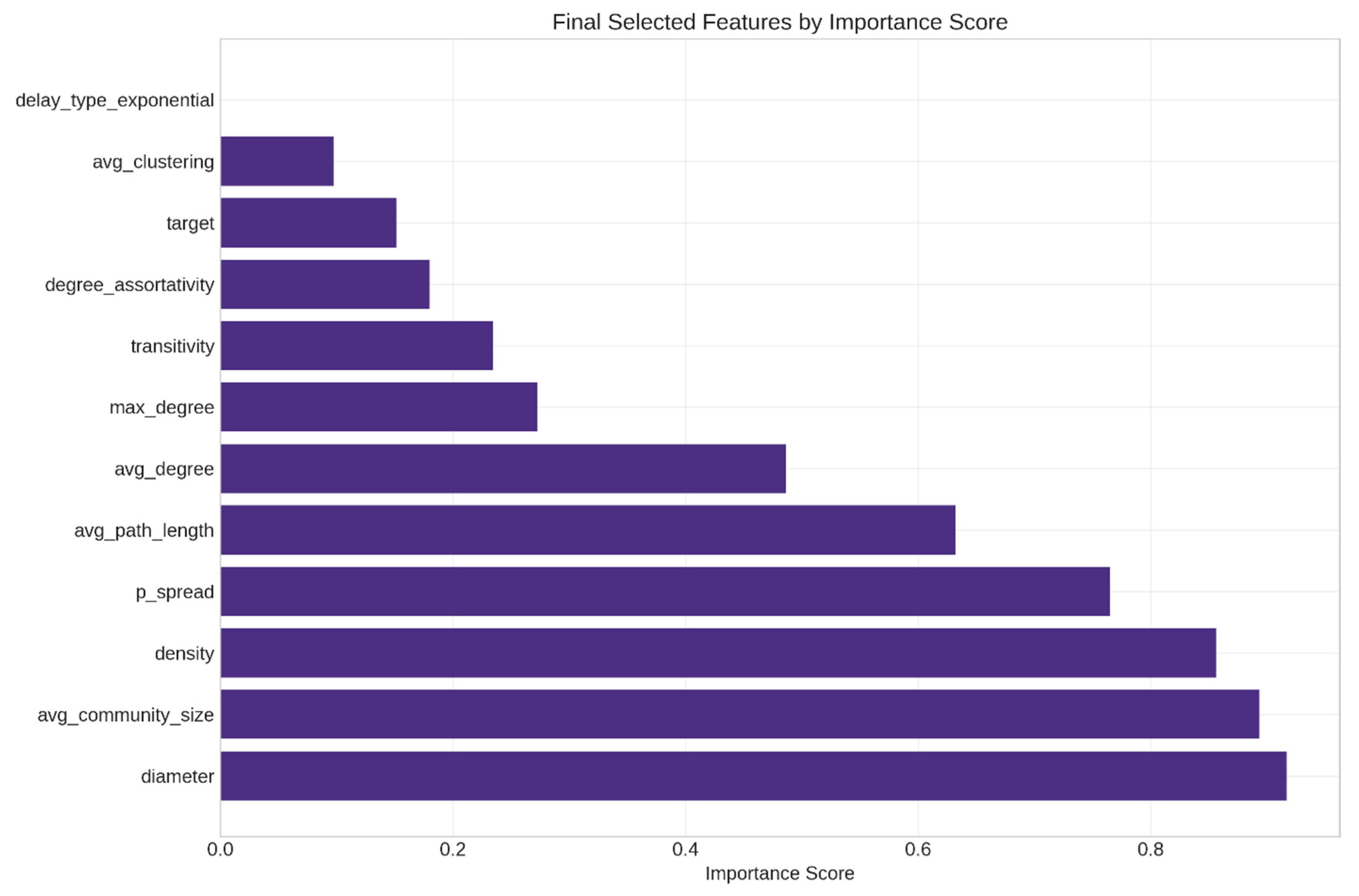
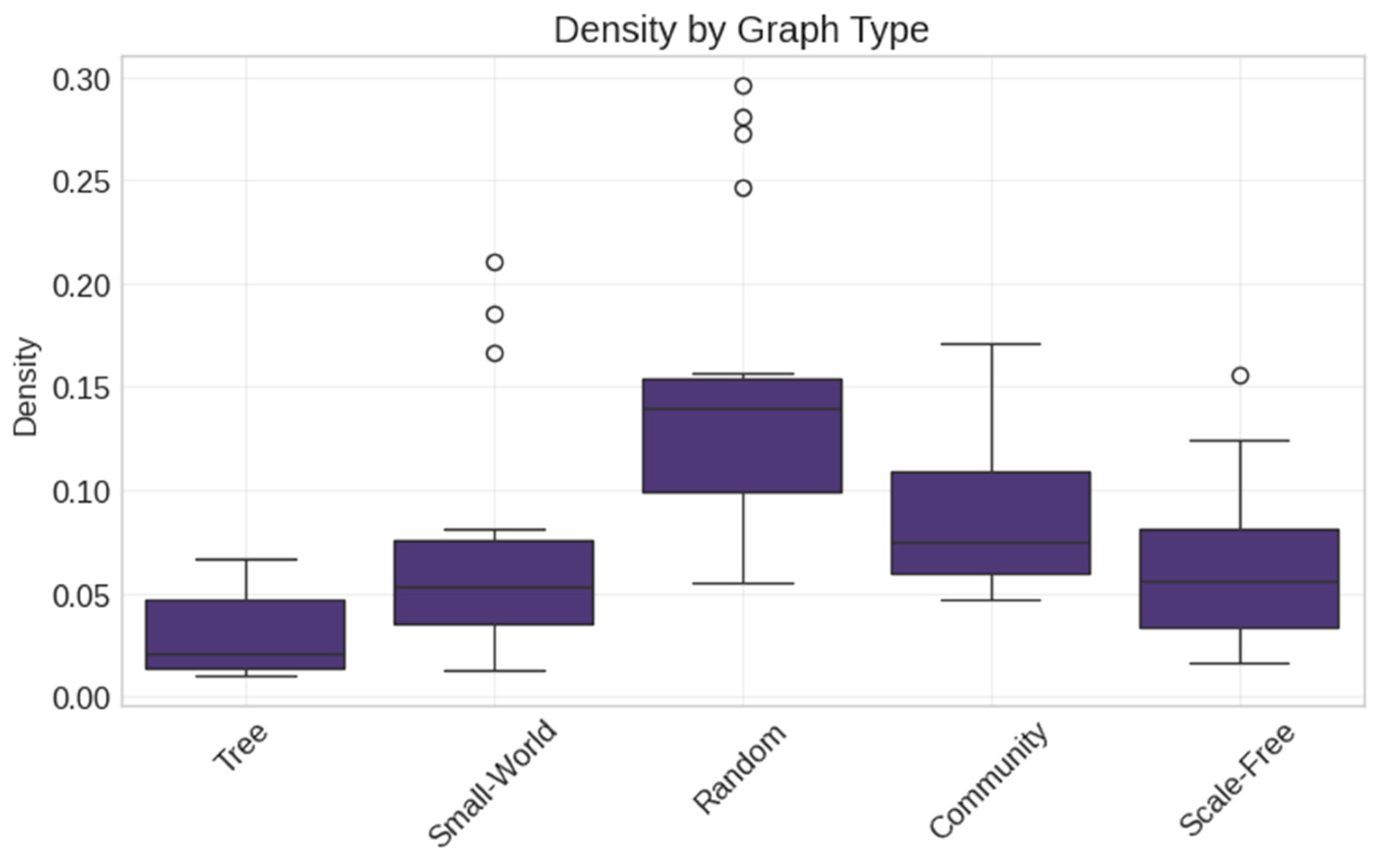
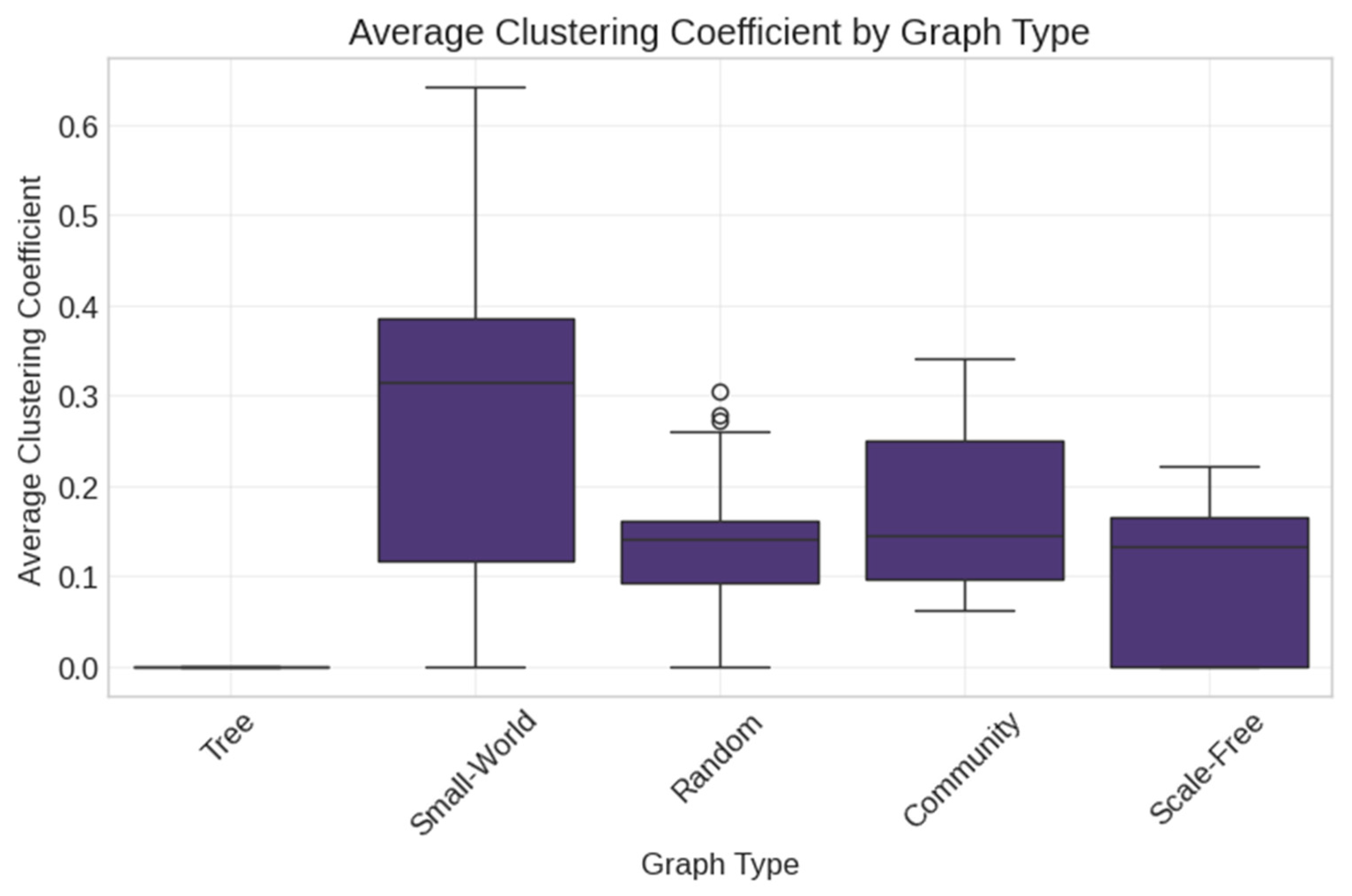
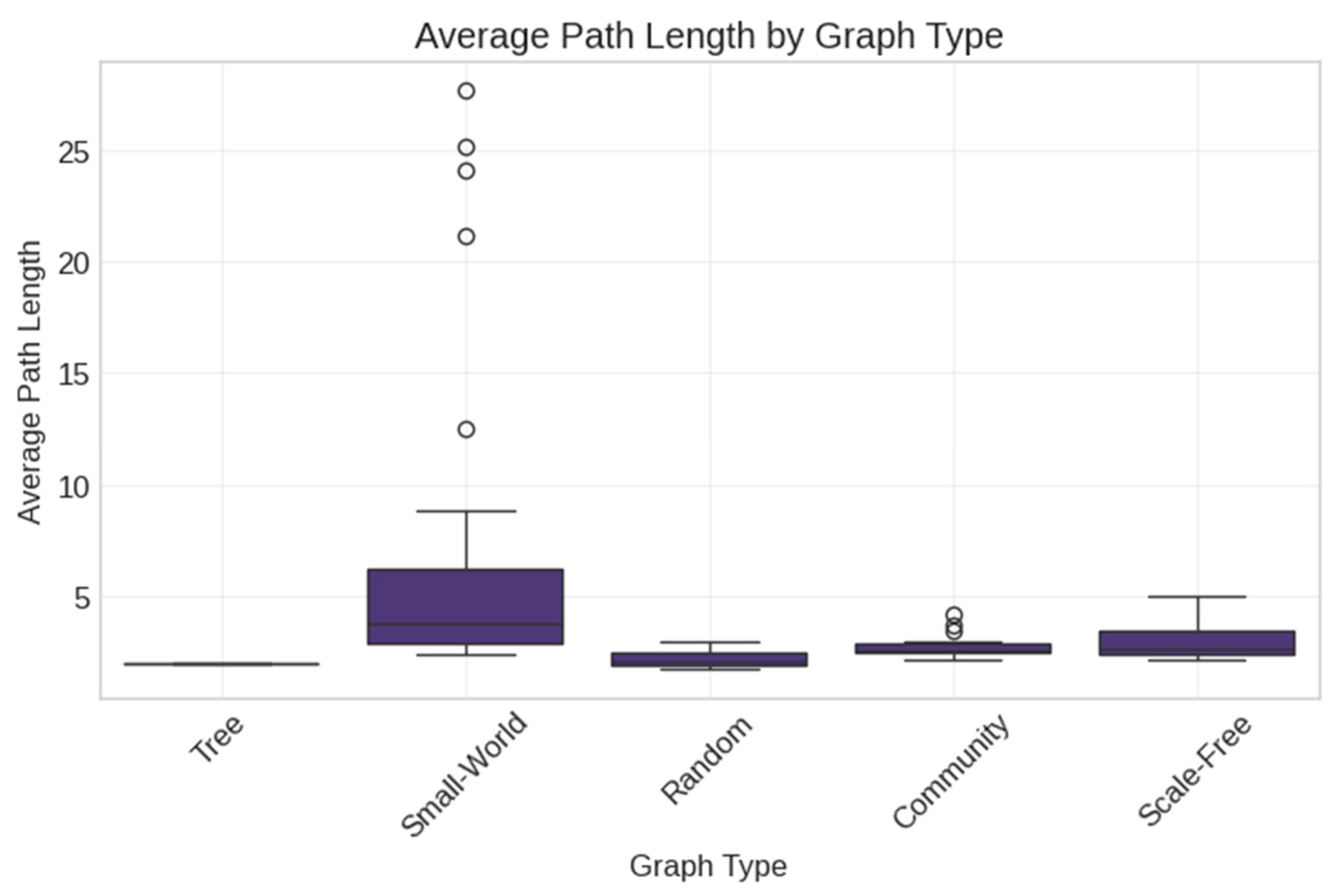
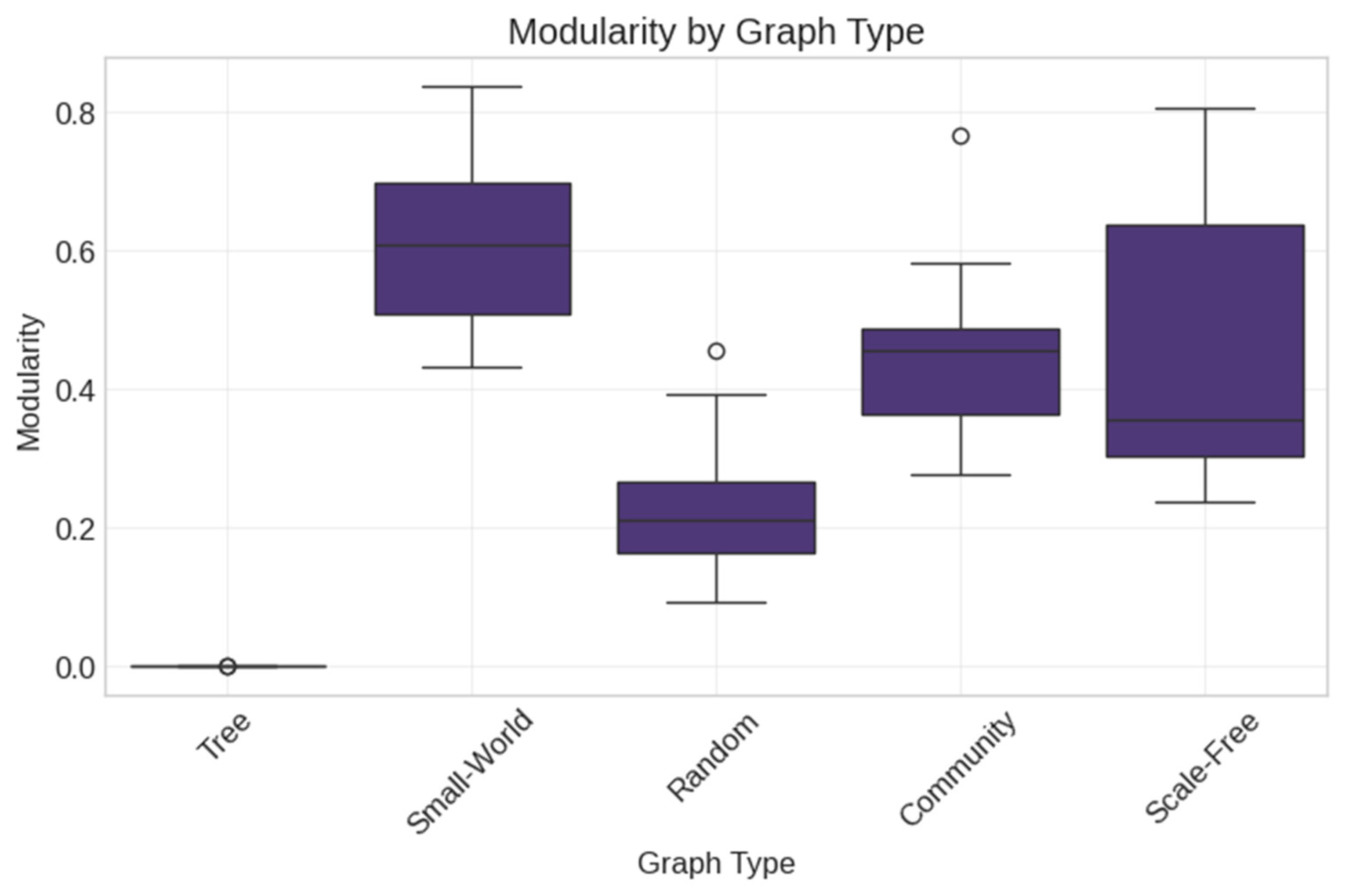
3.4. Synthetic Network Generation

The limited size of our real dataset (eight networks) presented challenges for robust statistical analysis. To address this limitation, we generated 100 synthetic networks with controlled properties. This approach allowed us to test information diffusion across diverse network structures.

We implemented a network generation function that created five distinct network types:

• Random (Erdős–Rényi) networks with varying density parameters;
• Scale-Free (Barabási–Albert) networks with preferential attachment;
• Small-World (Watts–Strogatz) networks with controlled clustering;
• Tree networks with hierarchical structures;
• Community networks with modular organization.

The synthetic networks showed diverse structural properties (Figure 7 and Figure 8). Random networks had the highest edge density (mean edges = 1050), while Tree networks maintained minimal connectivity (mean edges ≈ nodes −1). Community networks showed distinct modular structures with high clustering coefficients.

For each synthetic network, we calculated 30+ structural metrics including the following (Figure 9, Figure 10, Figure 11 and Figure 12):

• Basic measures: nodes, edges, density;
• Degree statistics: min/max/avg degree, degree heterogeneity;
• Centralization metrics: various centrality measures;
• Connectivity metrics: diameter, average path length, components;
• Community structure: modularity, community size;
• Spectral properties: algebraic connectivity, spectral radius.

Figure 9. Density by graph type. Box plots show standard statistical summaries with outliers marked as circles.

Figure 9. Density by graph type. Box plots show standard statistical summaries with outliers marked as circles.

Figure 10. Average clustering coefficient by graph type. Box plots show standard statistical summaries with outliers marked as circles.

Figure 10. Average clustering coefficient by graph type. Box plots show standard statistical summaries with outliers marked as circles.

Figure 11. Average path length by graph type. Box plots show standard statistical summaries with outliers marked as circles.

Figure 11. Average path length by graph type. Box plots show standard statistical summaries with outliers marked as circles.

Figure 12. Modularity by graph type. Box plots show standard statistical summaries with outliers marked as circles.

Figure 12. Modularity by graph type. Box plots show standard statistical summaries with outliers marked as circles.

These comprehensive features allowed us to identify which structural properties most strongly influenced information diffusion. The synthetic dataset provided a robust foundation for testing diffusion models across diverse topological structures.

4. Methodology

Figure 13 presents the comprehensive methodological framework of our study. This architecture addresses the challenge of understanding how different delay mechanisms affect information diffusion across diverse social network structures.

The framework consists of four primary components (Figure 13):

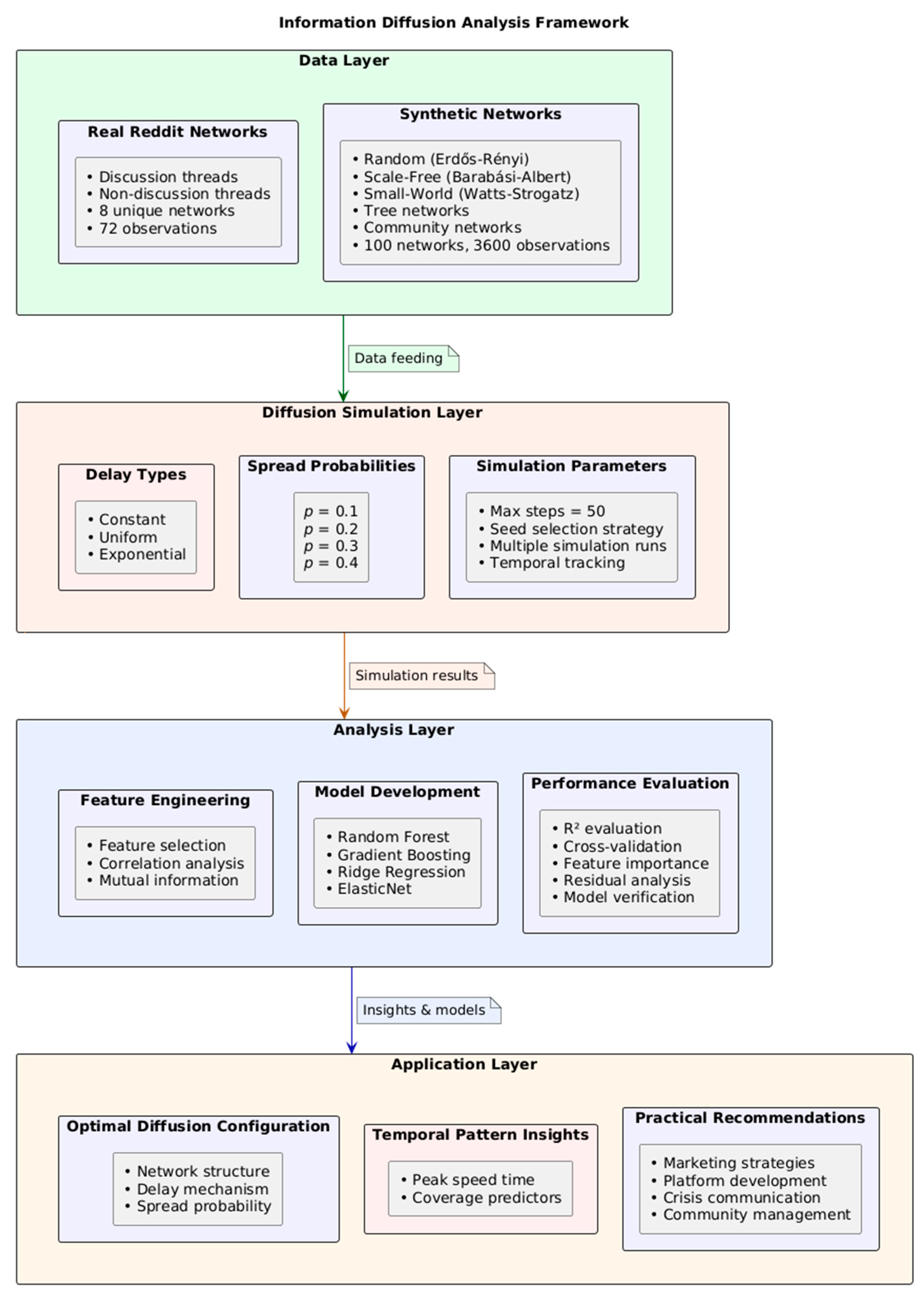
• Data Layer: This foundation includes both real Reddit thread networks (capturing authentic social interaction patterns) and synthetic networks (enabling controlled experimental conditions). The diversity of network types (Random, Scale-Free, Small-World, Tree, Community) allows for systematic comparison across topological variations representative of different social media interaction patterns.
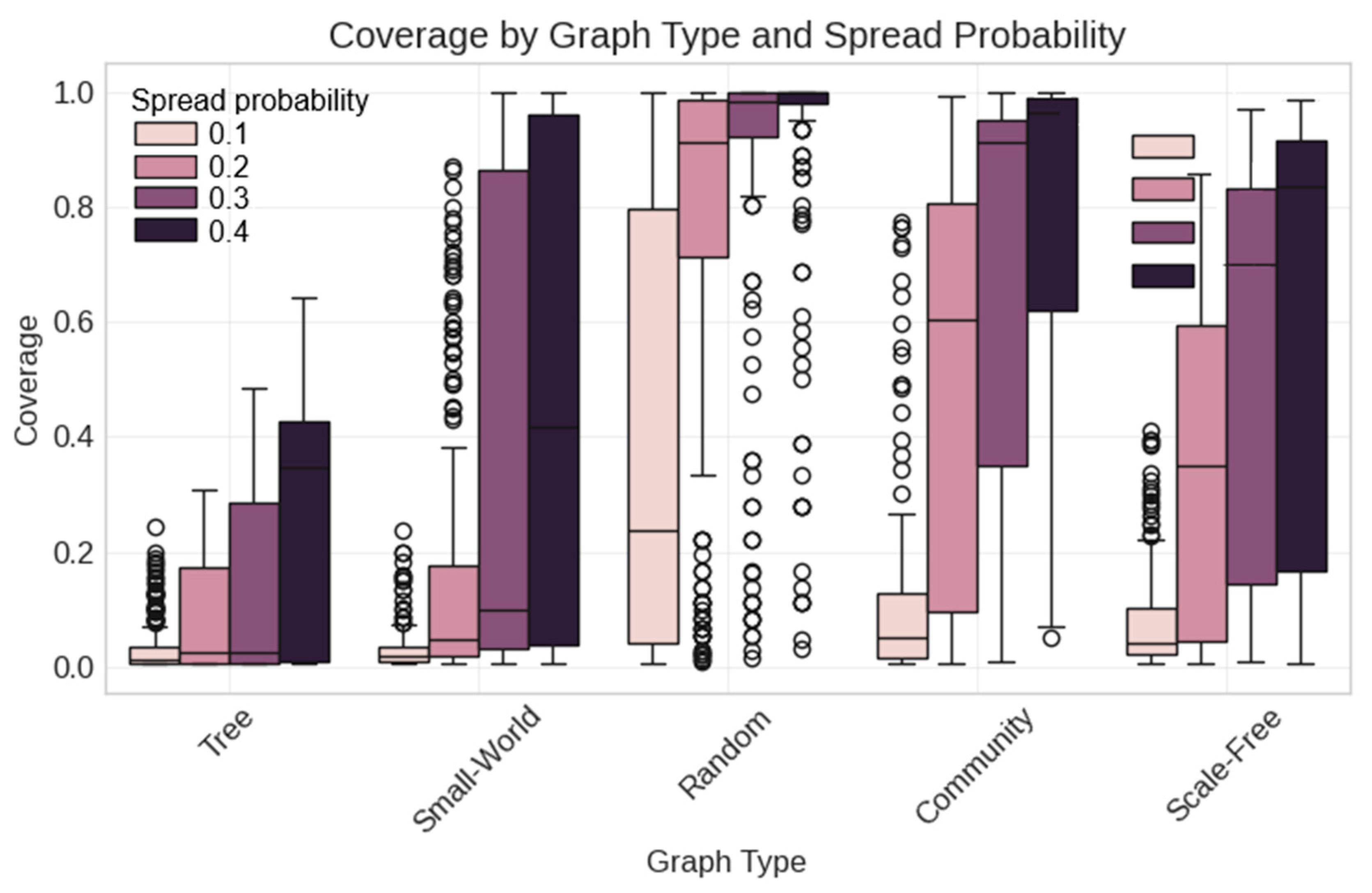
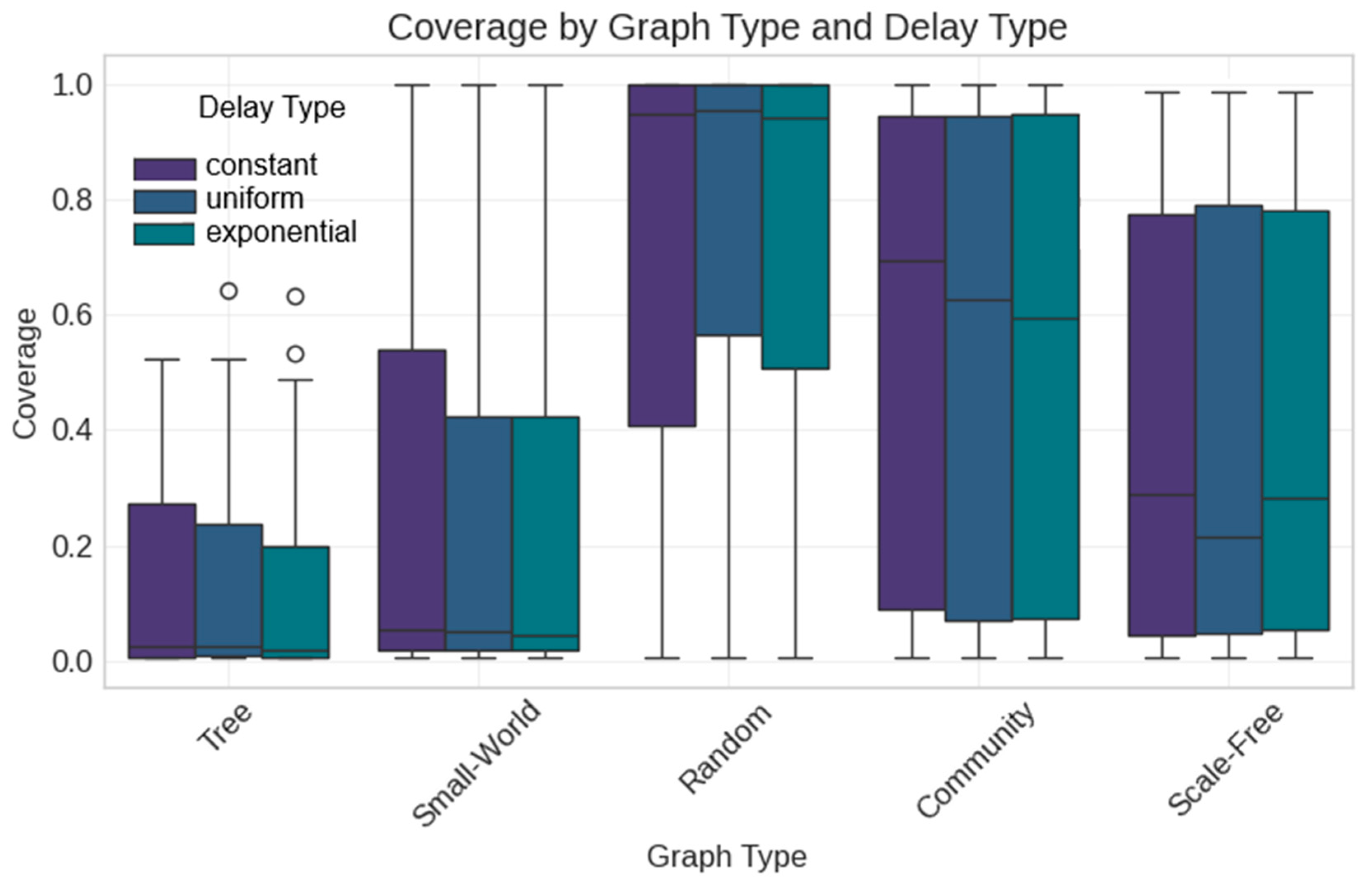
• Diffusion Simulation Layer: At this level, we implement three distinct delay mechanisms (constant, uniform, exponential) that model different patterns of user response timing in social networks. The simulation engine applies population dynamics principles to model how information spreads through network connections with parameterized transmission probabilities (0.1–0.4), representing different content engagement likelihoods.
• Analysis Layer: This component transforms simulation outputs into actionable insights through feature engineering, model training, and evaluation. The machine learning models (particularly Gradient Boosting and Random Forest) identify key predictive factors that determine information coverage across network types.
• Application Layer: Finally, our framework translates analytical findings into practical recommendations for social media stakeholders. These applications include optimizing information dissemination strategies, predicting viral content potential, and designing more effective network structures for specific communication goals.
• Each component addresses specific challenges in information diffusion modeling: the data layer provides ecological validity, the simulation layer captures temporal dynamics, the analysis layer identifies key predictors, and the application layer ensures practical relevance.

4.1. Information Diffusion Simulation

We implemented a comprehensive information diffusion model based on population dynamics with a time delay. This model simulates how information spreads through a network with specific delay mechanisms between exposure and propagation.

The diffusion process begins with seed nodes that initially possess the information. If no seed nodes are specified, the algorithm selects a high-degree node as the starting point. Each node maintains two important time markers: activation time (when it receives information) and spreading time (when it begins sharing information).

The core simulation mechanism (Algorithm 1) works as follows:

• At each time step, nodes that have reached their spreading time attempt to transmit information to their neighbors.
• Transmission succeeds with probability p_spread.
• Upon successful transmission, the neighbor node is activated.
• The newly activated node experiences a delay before it can spread information further.
• The delay duration depends on the specified delay mechanism.

We implemented three distinct delay mechanisms to model different information sharing behaviors:

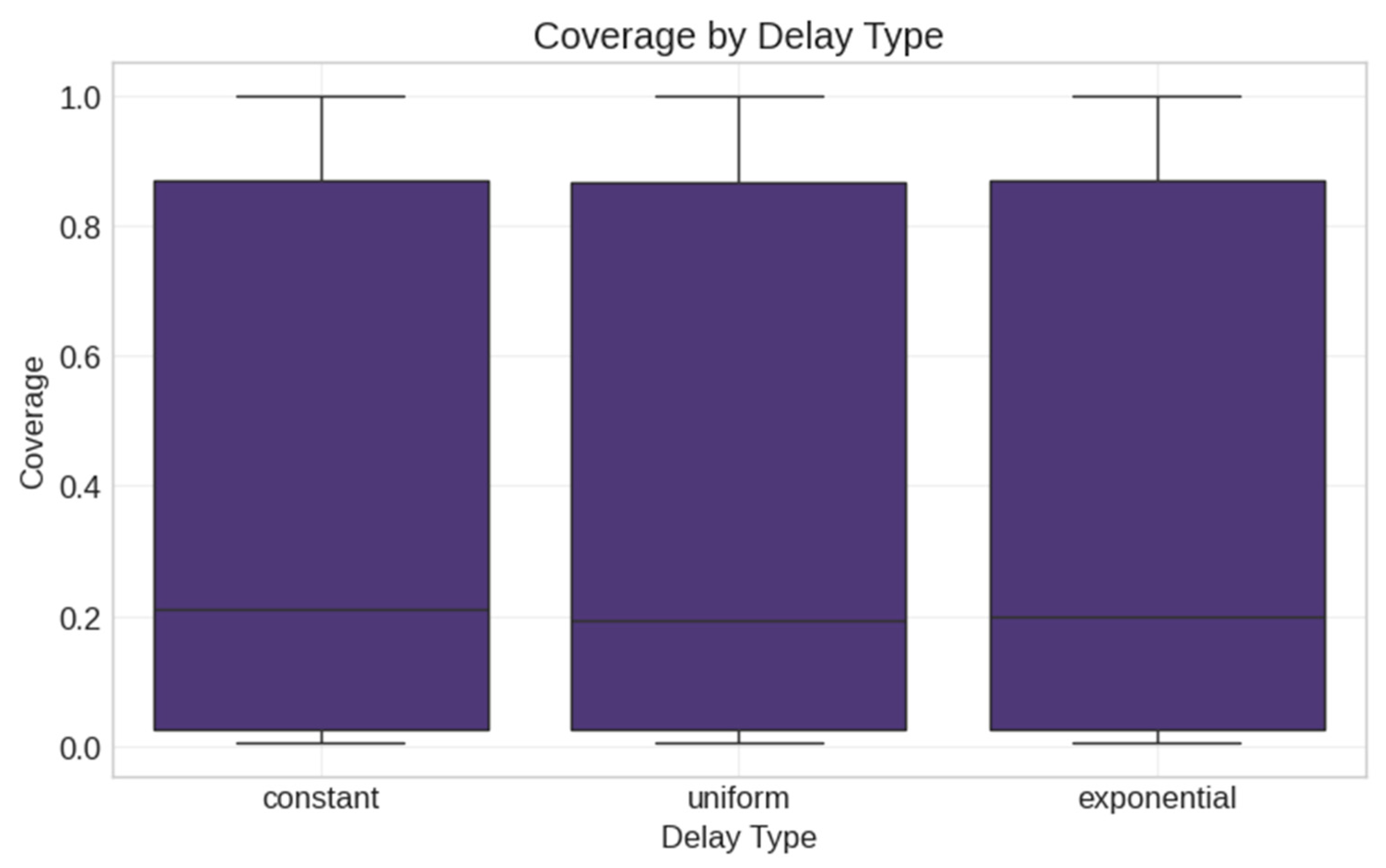
• Constant delay—Every node experiences the same fixed delay (delay_param);
• Uniform delay—Delay is randomly selected from uniform distribution [1, delay_param];
• Exponential delay—Delay follows an exponential distribution with mean delay_param.

For each simulation, we recorded several outcome metrics:

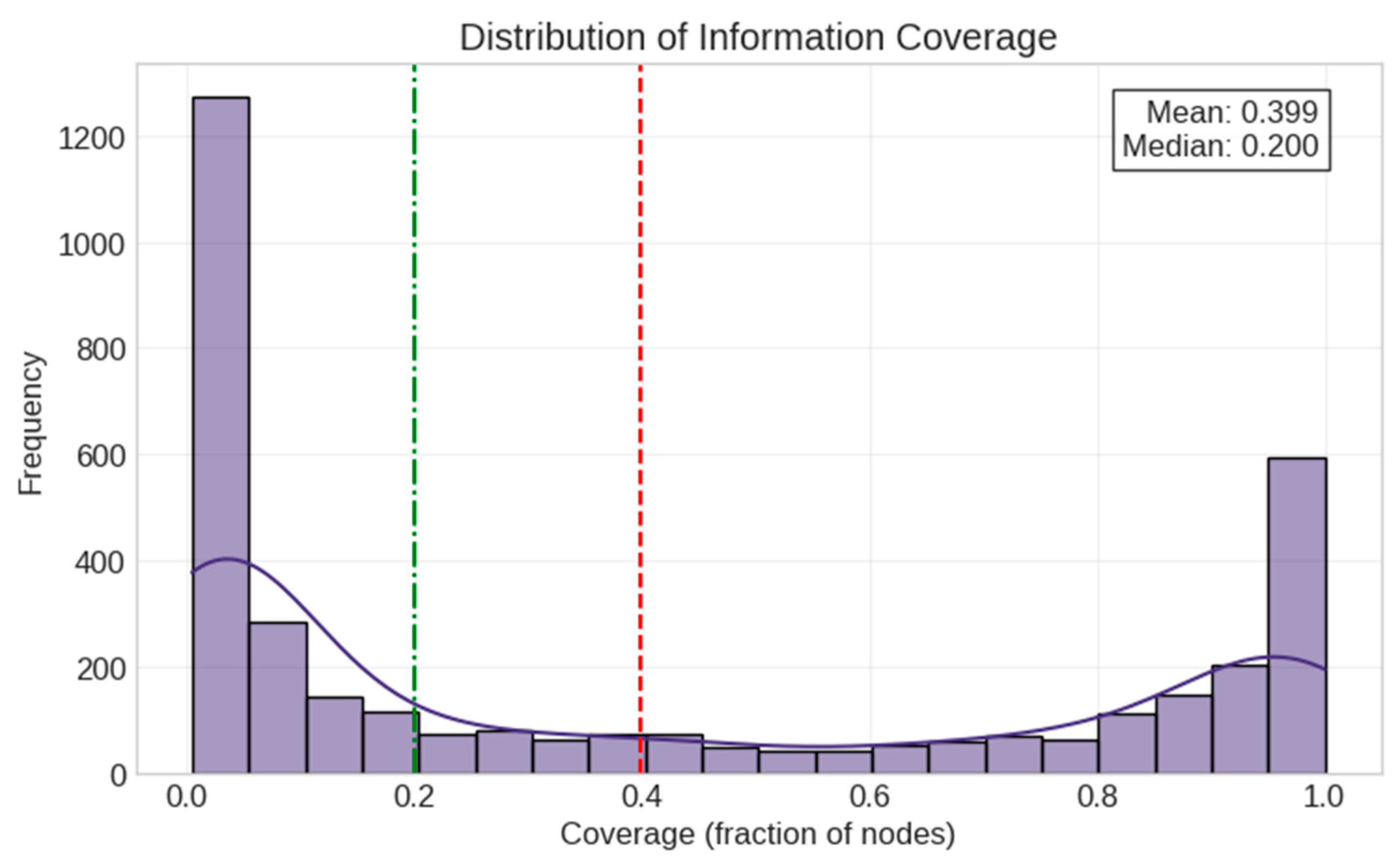
• Coverage (fraction of nodes that received information);
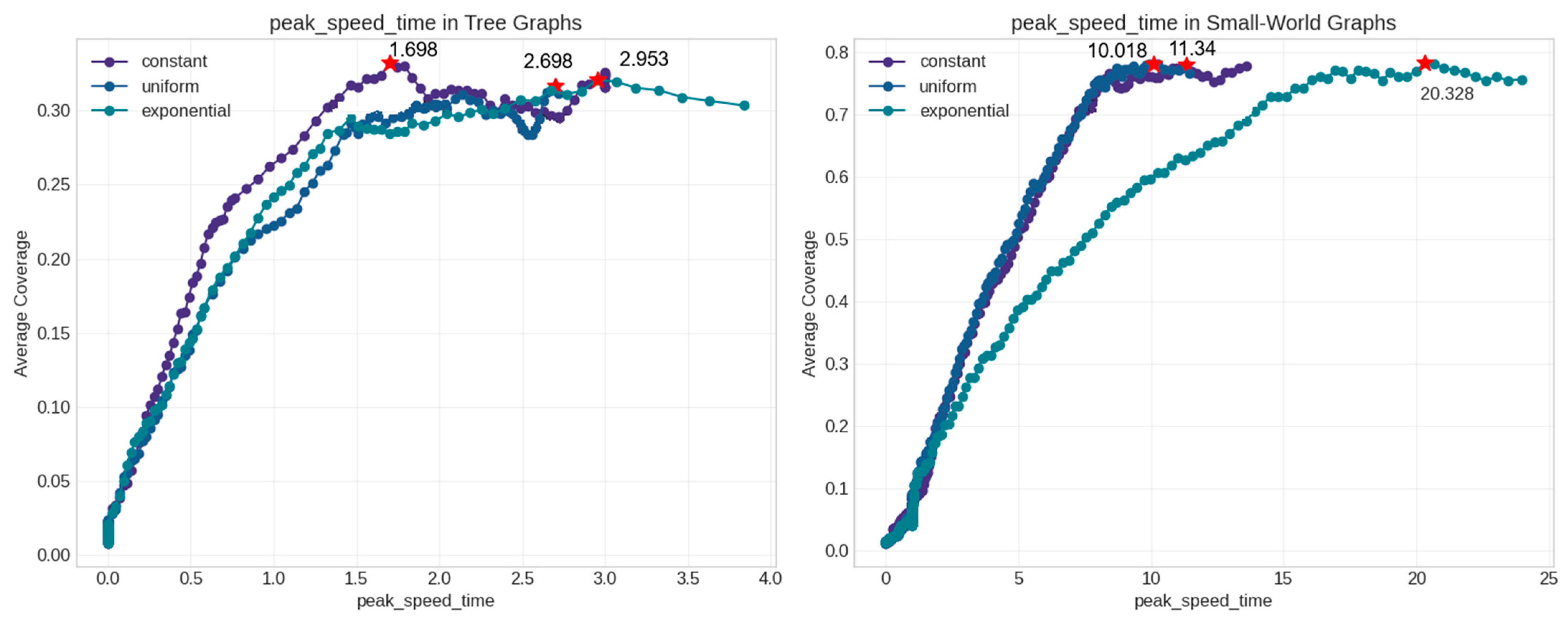
• Peak diffusion speed (maximum rate of new activations);
• Time to reach peak speed;
• Time to half coverage (when 50% of nodes are activated);
• Full activation history over time.

Algorithm 1: Information diffusion with delay

Input: Graph G, seed_nodes (optional), p_spread, max_steps, delay_type, delay_param Output: Diffusion results (coverage, temporal dynamics) 1: // Initialize with seed nodes 2: if seed_nodes is None then 3:   degrees ← Calculate node degrees in G 4:   candidate_nodes ← Sort nodes by degree (descending) 5:   seed_nodes ← Randomly select one high-degree node 6: end if 7: 8: // Initialize tracking dictionaries 9: activation_times ← {node: ∞ for all nodes in G} 10: spreading_times ← {node: ∞ for all nodes in G} 11: for seed in seed_nodes do 12:   activation_times[seed] ← 0 13:   spreading_times[seed] ← 0 14: end for 15: 16: // Run diffusion simulation 17: active_nodes ← seed_nodes 18: current_step ← 0 19: history ← {} 20: while current_step < max_steps AND active_nodes not empty do 21:   new_activations ← {} 22:   for node in active_nodes do 23:     if spreading_times[node] ≤ current_step then 24:       for neighbor in G.neighbors(node) do 25:         if activation_times[neighbor] = ∞ AND random() < p_spread then 26:           activation_times[neighbor] ← current_step 27:           // Calculate delay based on specified mechanism 28:           if delay_type = "constant" then 29:             delay ← delay_param 30:           else if delay_type = "uniform" then 31:             delay ← random_uniform(1, delay_param) 32:           else if delay_type = "exponential" then 33:             delay ← random_exponential(delay_param) 34:           end if 35:           spreading_times[neighbor] ← current_step + delay 36:           new_activations.add(neighbor) 37:         end if 38:       end for 39:     end if 40:   end for 41:   active_nodes.update(new_activations) 42:   history[current_step] ← count nodes with activation_time ≤ current_step 43:   current_step ← current_step + 1 44: end while 45: 46: // Calculate metrics 47: coverage ← proportion of nodes with finite activation_time 48: active_counts ← differences between consecutive history values 49: peak_speed ← maximum value in active_counts 50: peak_speed_time ← time step of peak_speed 51: 52: return coverage, peak_speed, peak_speed_time, history

We ran extensive simulations on both real and synthetic networks. For synthetic networks, we performed 3600 simulations by varying the following (Figure 14, Figure 15, Figure 16 and Figure 17):

• A total of 100 different network structures;
• Three delay types (constant, uniform, exponential);
• Four spread probabilities (0.1, 0.2, 0.3, 0.4);
• Three simulation runs per configuration to account for stochasticity.

Figure 14. Distribution of information coverage across simulations.

Figure 14. Distribution of information coverage across simulations.

Figure 15. Coverage by graph type. Box plots show standard statistical summaries with outliers marked as circles.

Figure 15. Coverage by graph type. Box plots show standard statistical summaries with outliers marked as circles.

Figure 16. Coverage by delay type. Box plots show standard statistical summaries with outliers marked as circles.

Figure 16. Coverage by delay type. Box plots show standard statistical summaries with outliers marked as circles.

Figure 17. Coverage by spread probability in Synthetic Networks. Box plots show standard statistical summaries with outliers marked as circles.

Figure 17. Coverage by spread probability in Synthetic Networks. Box plots show standard statistical summaries with outliers marked as circles.

This comprehensive simulation approach allowed us to systematically examine how network structure, spread probability, and delay mechanisms interact to influence information diffusion.

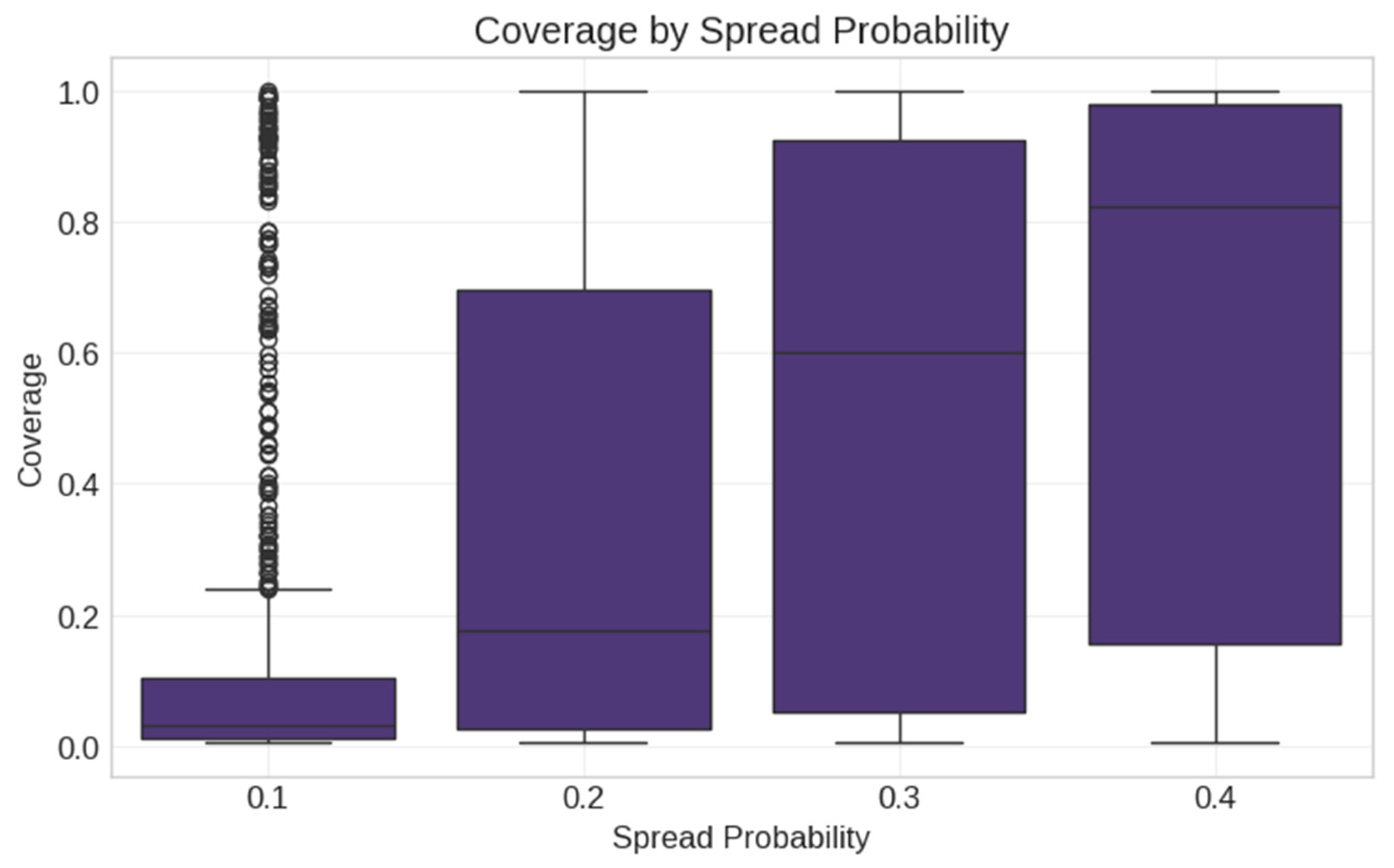
4.2. Feature Engineering and Selection

After simulation, we merged diffusion results with network metrics to create a comprehensive dataset for analysis. The final dataset for the synthetic networks contained 3600 rows and 40 columns after cleaning.

We implemented a robust feature selection process to address several challenges:

• High dimensionality relative to observations;
• Multicollinearity among structural features;
• Potential for overfitting due to feature redundancy.

Our feature selection approach combined correlation analysis with mutual information to capture both linear and non-linear relationships. We identified features with a high correlation (r > 0.8) to address multicollinearity.

The top features by correlation with coverage included the following (Figure 18):

• avg_degree (r = 0.628);
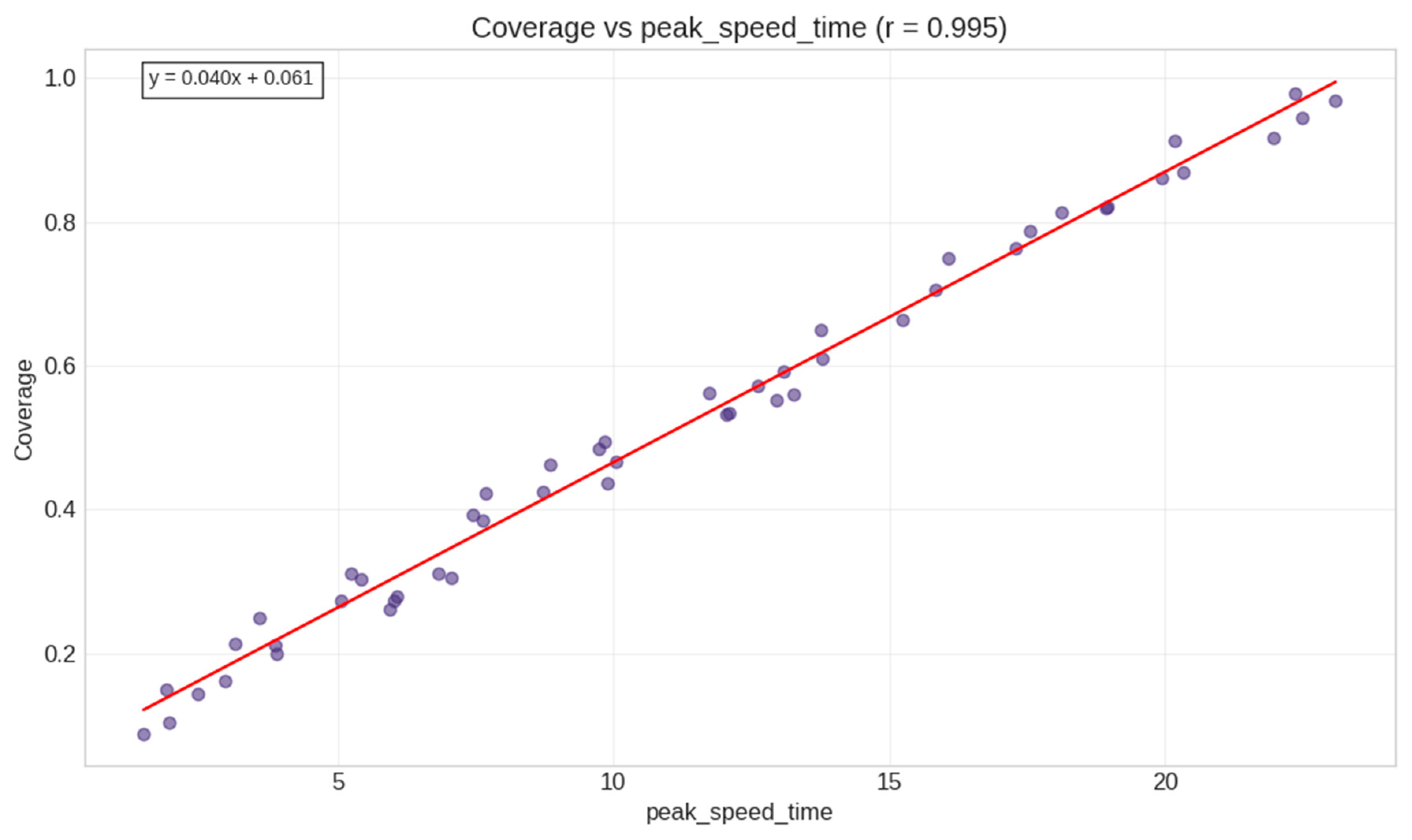
• peak_speed_time (r = 0.582);
• edges (r = 0.549);
• max_betweenness_centrality (r = −0.557);
• min_degree (r = 0.547).

Figure 18. Top 10 features by correlation with coverage. Blue bars indicate positive correlation with coverage, red bars indicate negative correlation with coverage.

Figure 18. Top 10 features by correlation with coverage. Blue bars indicate positive correlation with coverage, red bars indicate negative correlation with coverage.

After mutual information analysis, we normalized and combined both the correlation and mutual information scores to rank the features. This resulted in selecting 20 features for the final model, including the following (Figure 19):

• avg_degree (score = 0.946);
• edges (score = 0.928);
• spectral_radius (score = 0.932);
• max_betweenness_centrality (score = 0.915);
• avg_degree_centrality (score = 0.834).

Figure 19. Final selected features by importance score.

Figure 19. Final selected features by importance score.

We also created cross-validation groups based on network_id to prevent data leakage. This ensured that observations from the same network would not appear in both the training and test sets during cross-validation.

4.3. Model Development and Evaluation

We developed and compared six regression models to predict information coverage:

• Random Forest;
• Gradient Boosting;
• Ridge Regression;
• ElasticNet;
• Support Vector Regression (SVR);
• Huber Regression.

Each model was implemented within a pipeline that included the standardization of features and the model itself. We used GroupKFold cross-validation with five splits to ensure a robust evaluation.

# Create a pipeline that includes preprocessing def create_pipeline(model):    return Pipeline([       (’scaler’, StandardScaler()),       (’model’, model)    ]) # Initialize GroupKFold for cross-validation group_kfold = GroupKFold(n_splits = 5)

For each model, we calculated multiple performance metrics across the cross-validation folds:

• R² (coefficient of determination);
• Adjusted R²;
• Mean Squared Error (MSE);
• Mean Absolute Error (MAE).

Our methodology combined rigorous simulation with state-of-the-art machine learning techniques to identify and quantify the factors that are most influential in information diffusion across networks.

4.4. Implementation and System Configuration

All simulations and analyses were implemented using Python 3.9 with the following key libraries: NetworkX 2.8.4 for network generation and analysis, Scikit-learn 1.1.2 for machine learning model implementation, Pandas 1.4.3 for data manipulation, and Matplotlib 3.5.2 for visualization.

The computational experiments were conducted on a workstation with the following specifications:

-

Processor: AMD Ryzen 7 7840HS w/Radeon 780 M Graphics (3.80 GHz);

-

Memory: 64 GB RAM (62.8 GB available);

-

Storage: 954 GB (513 GB used);

-

Graphics: AMD Radeon 780 M Graphics (879 MB);

-

Operating System: Windows 64-bit.

For the most computationally intensive simulations involving the 100 synthetic networks with multiple delay mechanisms, parallel processing was implemented using the Python multiprocessing library to utilize all available cores.

The complete codebase for this research is freely available as a Google Colab notebook at: https://colab.research.google.com/drive/1zAxPi7i6EKtuNqJ5sdsodpl2J3_Z787m, accessed on 10 April 2025. While the notebook connects to our drive for demonstration purposes, users can easily copy it to their own Google Drive to run all analyses independently with the provided datasets or their own networks.

4.5. Technical Implementation Details

Several important technical choices were made during implementation:

• Feature selection thresholds: The correlation threshold of 0.8 was selected based on the preliminary testing of thresholds between 0.75 and 0.85, with 0.8 providing the optimal balance between feature reduction (43% fewer features) and predictive power retention (95% of baseline R²).
• Overfitting prevention: We employed GroupKFold cross-validation to prevent data leakage between networks, along with standard regularization parameters in Tree-based models (max_depth = 10, min_samples_split = 5). The gap between training and validation performance was monitored and maintained below 0.05 for all reported models.
• Synthetic network parameters: Networks were generated with parameters reflecting real social media structures: Random networks (edge probability: 0.05–0.20), Scale-Free networks (preferential attachment: 2–5), Small-World networks (rewiring probability: 0.1–0.6, clustering coefficients: 0.02–0.42), Tree networks (branching factor: 2–5), and Community networks (communities: 3–8, inter-community connectivity: 0.01–0.05).
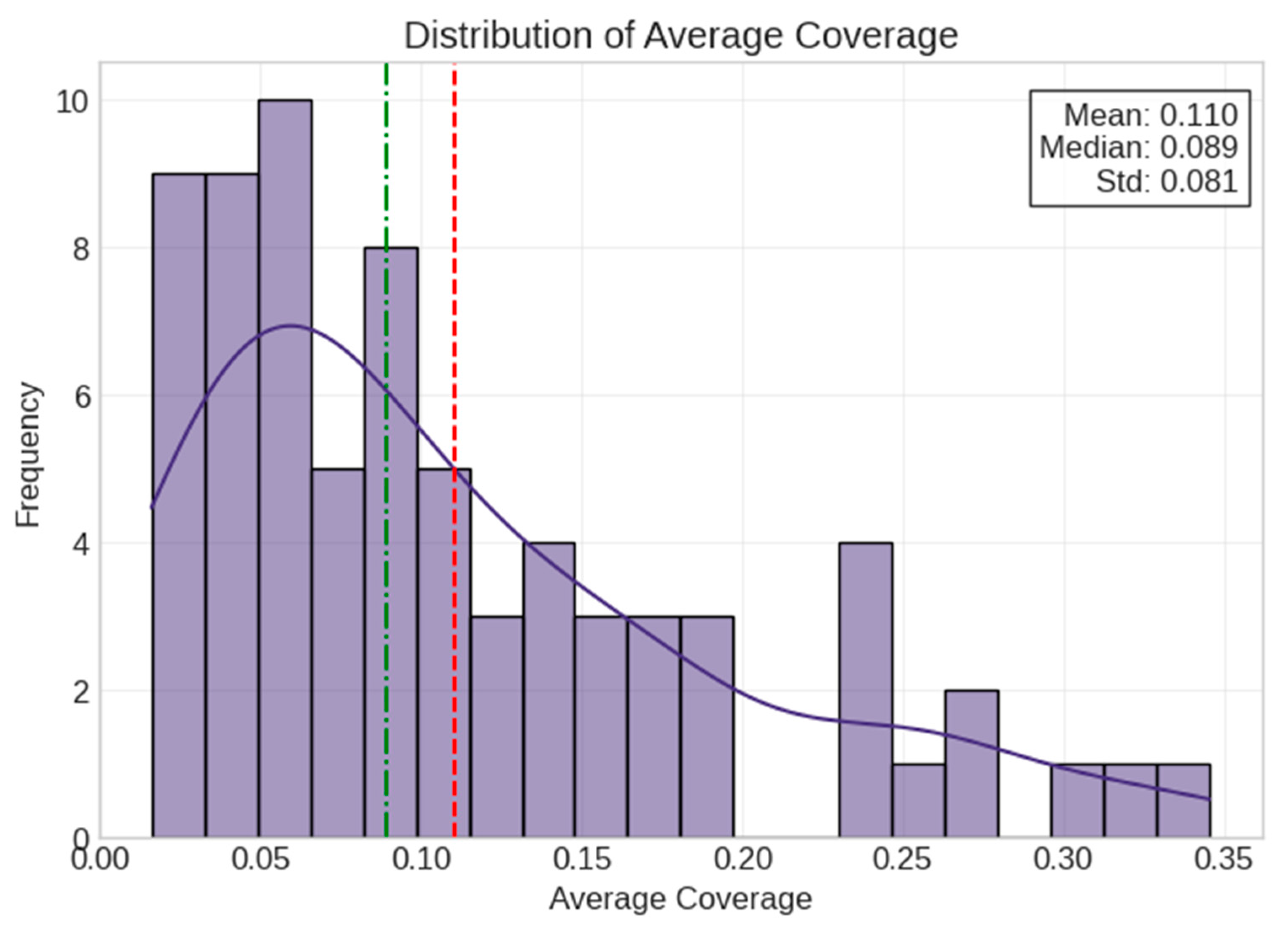
• The negative correlation between network size (edges: r = −0.605, nodes: r = −0.598) and coverage suggests that larger networks may experience information dilution, requiring targeted seeding strategies rather than relying solely on organic spread.

5. Results

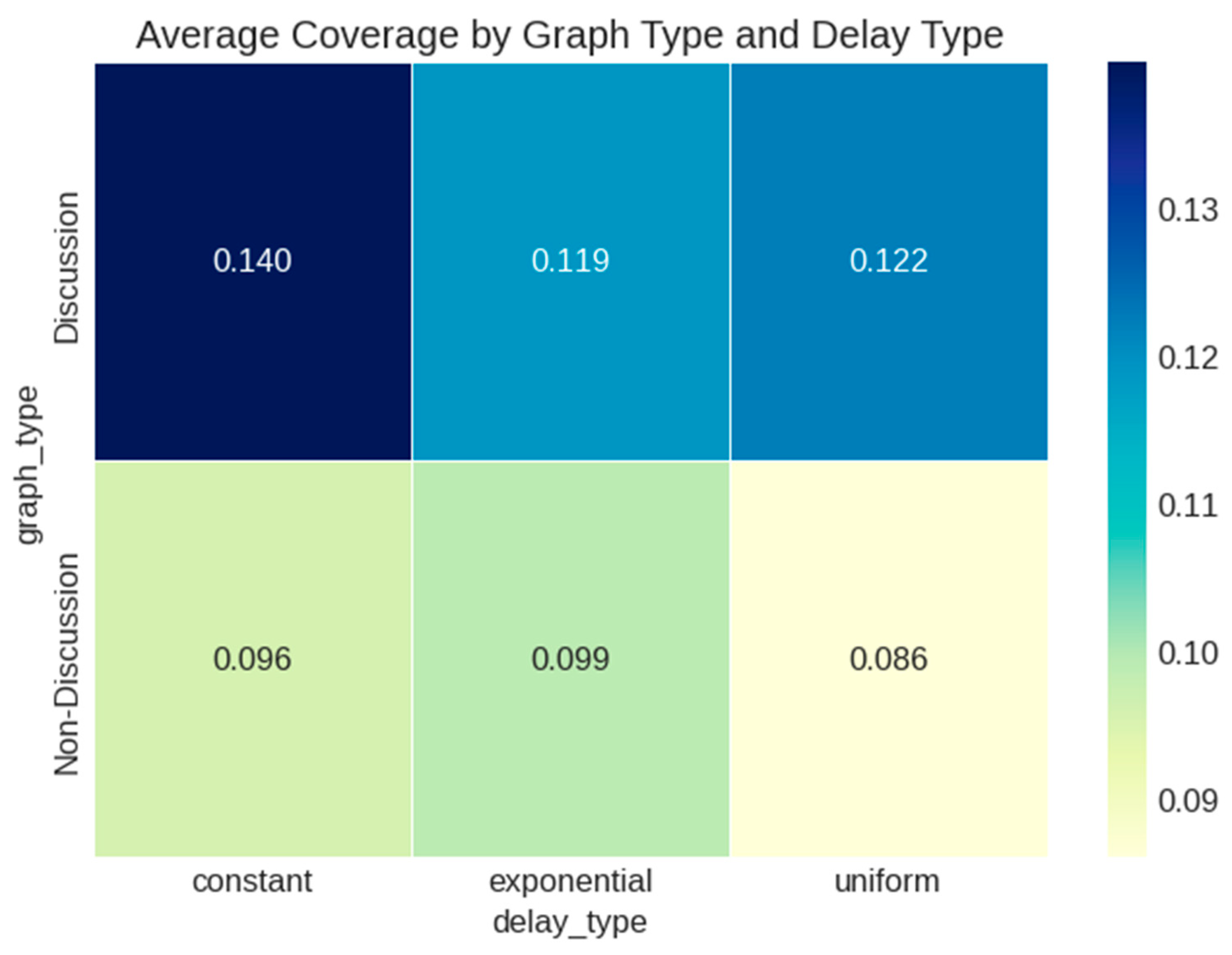
5.1. Real Data Analysis

Our initial analysis focused on the real Reddit thread data (Figure 20). Despite the limited sample size (eight unique networks, 72 observations), we identified several notable patterns in information diffusion.

The Random Forest model performed best on real data, achieving a moderate R² of 0.512 ± 0.222. This indicated that network structure and diffusion parameters could explain approximately half of the variance in information coverage, even with limited data.

The cross-validation results showed considerable variability (standard deviation of 0.222 for Random Forest). This variability highlighted the challenges in making reliable predictions with limited data. Other models performed less effectively, with Gradient Boosting (R² = 0.426 ± 0.206) and Huber Regressor (R² = 0.394 ± 0.178) showing moderate performance, while ElasticNet and SVR showed poor performance (negative R²). The variability in real data model performance (σ = 0.222 for Random Forest) stemmed primarily from the limited sample size (72 observations from eight networks) and structural heterogeneity rather than from overfitting. Tree-based models performed better by capturing non-linear diffusion dynamics without requiring extensive regularization.

Feature importance analysis (Figure 21) revealed that spread probability (p_spread) was the most influential factor (importance = 0.321), followed closely by network density (importance = 0.302) and average community size (importance = 0.178). Delay mechanism (represented by delay_type_exponential) and network diameter also showed measurable influence. The remaining features had relatively minor impacts (<0.02 importance).

When we tested model predictions against actual values, the Random Forest model achieved an R² of 0.604 and RMSE of 0.05089 on the test data. The residuals were normally distributed (Shapiro–Wilk W = 0.971, p = 0.093), indicating well-behaved errors.

The analysis of key structural features revealed optimal configuration patterns (Figure 22). For p_spread, the optimal value was consistently around 0.3 across both discussion and non-discussion networks. For network density, values around 0.18 for discussion networks and 0.15 for non-discussion networks maximized coverage. These findings provide practical guidelines for optimizing information spread.

The statistical tests confirmed that spread probability had a significant effect on coverage (F = 12.195, p < 0.001), while the effects of graph type (t = 1.765, p = 0.082) and delay type (F = 0.172, p = 0.843) were not statistically significant. This suggested that transmission probability was more influential than network structure or delay mechanism in this dataset.

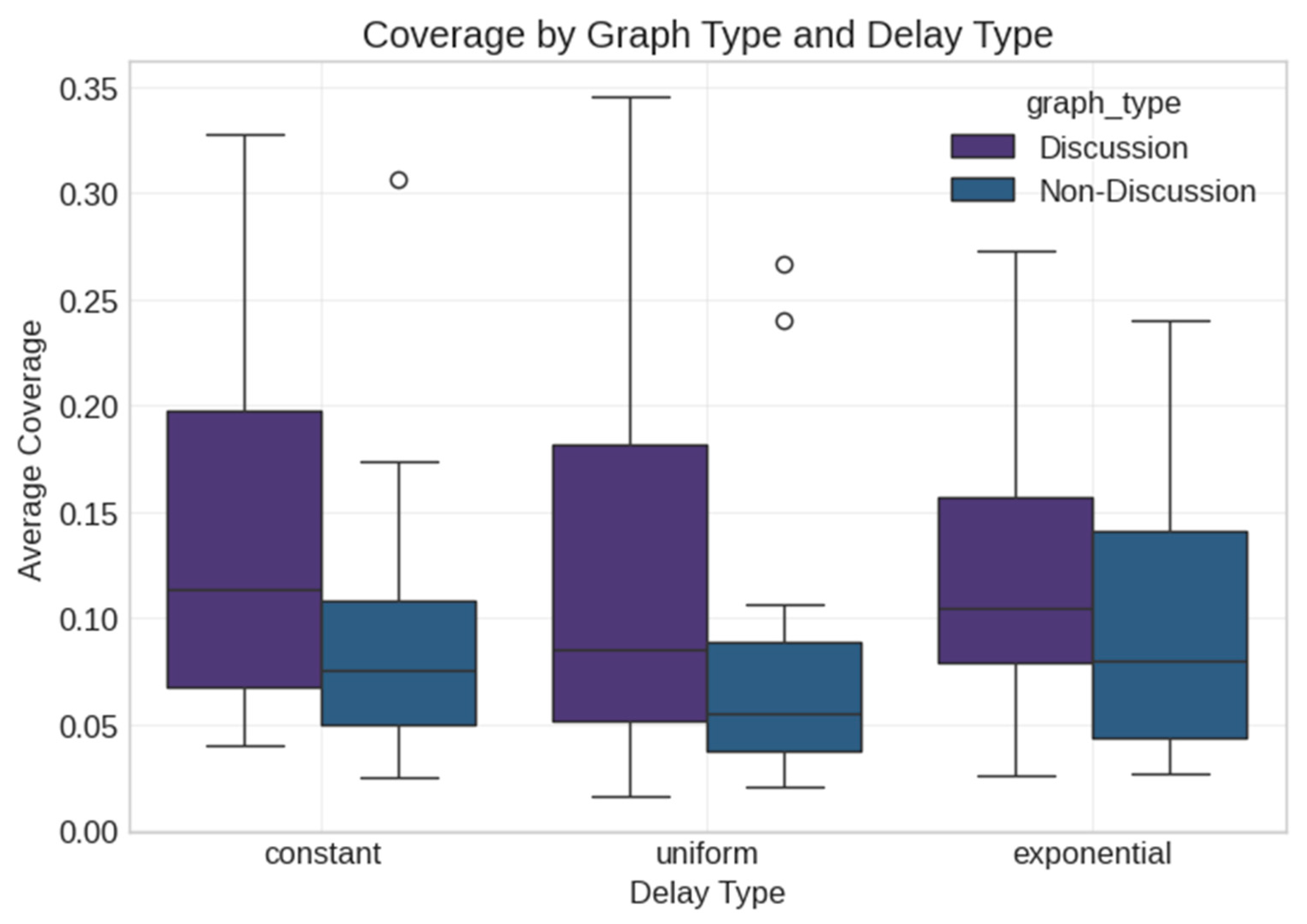
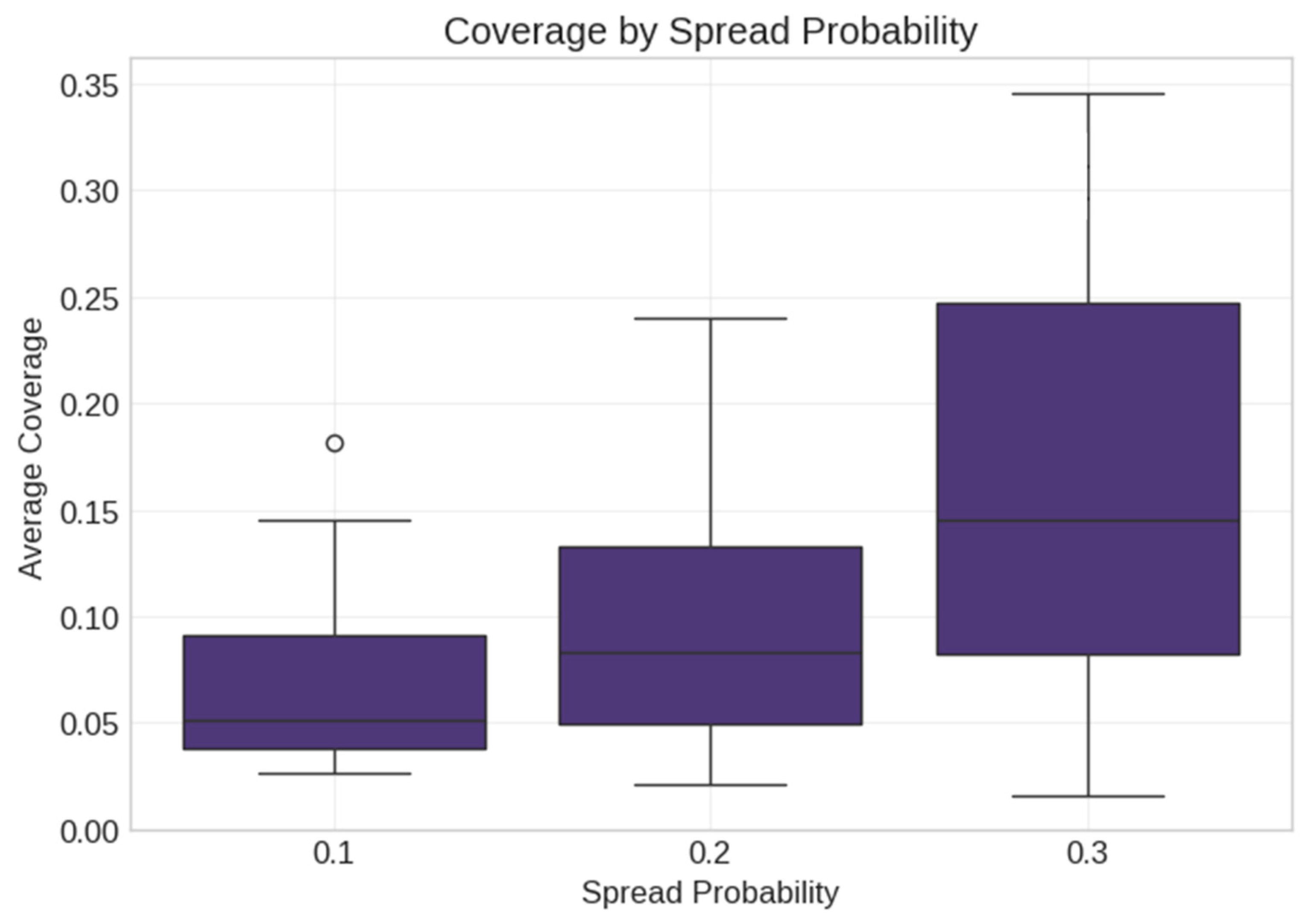
5.2. Synthetic Data Analysis

The synthetic data analysis provided a more robust foundation for understanding information diffusion. With 100 networks and 3600 observations, we achieved substantially higher model performance and more reliable feature importance rankings.

The performance comparison revealed that Tree-based models performed significantly better than linear models (Figure 23). Gradient Boosting achieved the highest performance (R² = 0.847 ± 0.032), followed closely by Random Forest (R² = 0.845 ± 0.032). SVR showed moderate performance (R² = 0.743), while linear models performed relatively poorly.

The feature importance analysis (Figure 24) revealed that peak_speed_time was the dominant feature (importance = 0.848), followed by avg_degree (importance = 0.101). Other features played much smaller roles, suggesting that temporal dynamics and average connectivity were the most critical factors affecting information diffusion.

We also conducted comprehensive residual analysis to validate model assumptions and identify potential issues (Figure 25, Figure 26, Figure 27 and Figure 28).

The residual analysis showed well-behaved errors with no systematic patterns, although the Shapiro–Wilk test indicated non-normally distributed residuals (W = 0.841, p < 0.001). This suggested some complexity in the model that was not fully captured by a normal error distribution.

In contrast to the real data analysis, peak_speed_time emerged as the overwhelmingly dominant feature (importance = 0.848), with avg_degree as a distant second (importance = 0.101). This suggests that temporal dynamics of information spread may be more important than static network properties. The remaining features showed minimal individual importance (<0.01).

When evaluated on the entire dataset, the final Gradient Boosting model achieved an R² of 0.871, demonstrating strong predictive power. However, the residuals were not normally distributed (Shapiro–Wilk W = 0.841, p < 0.001), suggesting some complexity in the data which was not fully captured by the model.

Analysis of the diffusion patterns (Figure 29) revealed that Random networks achieved the highest average coverage (0.653), followed by Small-World networks (0.505). Tree networks showed the lowest coverage (0.219), likely due to their limited connectivity. The effect of graph type was statistically significant (F = 346.325, p < 0.001).

Interestingly, delay type (Figure 29 and Figure 30) showed no significant effect on coverage across synthetic networks (F = 0.072, p = 0.930). This suggests that simpler constant delay models may be adequate for many applications, allowing practitioners to focus resources on optimizing network structure and transmission probability rather than precise delay distributions.

Spread probability (Figure 31) showed a strong, significant effect on coverage (F = 307.402, p < 0.001). Coverage increased monotonically with spread probability across all network types, with p_spread = 0.4 consistently achieving the highest coverage.

Analysis of optimal values for key structural features revealed interesting patterns (Figure 32). Peak speed time showed different optimal values depending on network type: lower values (around 1–3) for Tree networks and higher values (10–20) for Small-World networks. Average degree showed a positive relationship with coverage, with higher values generally leading to better information spread.

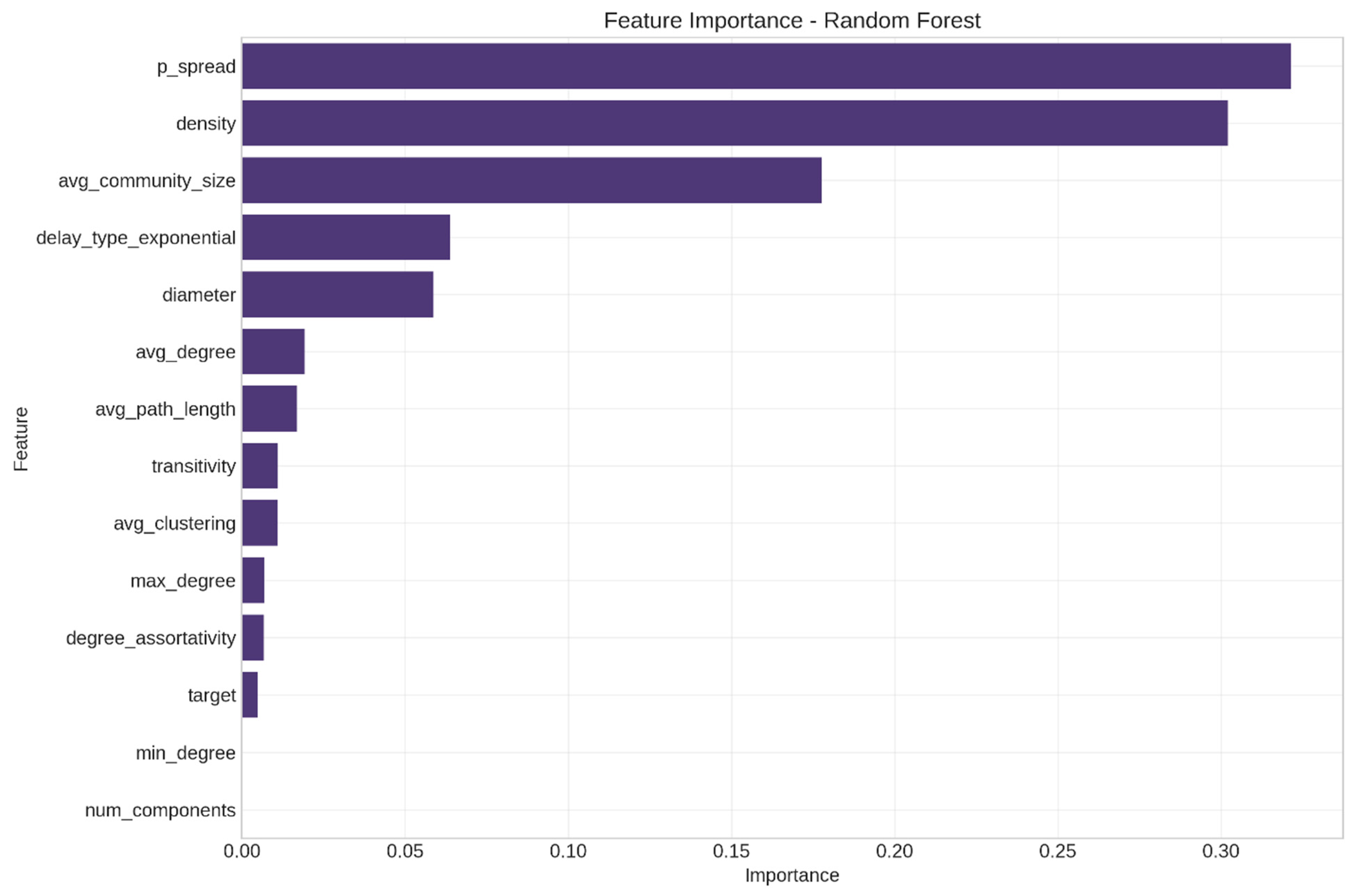
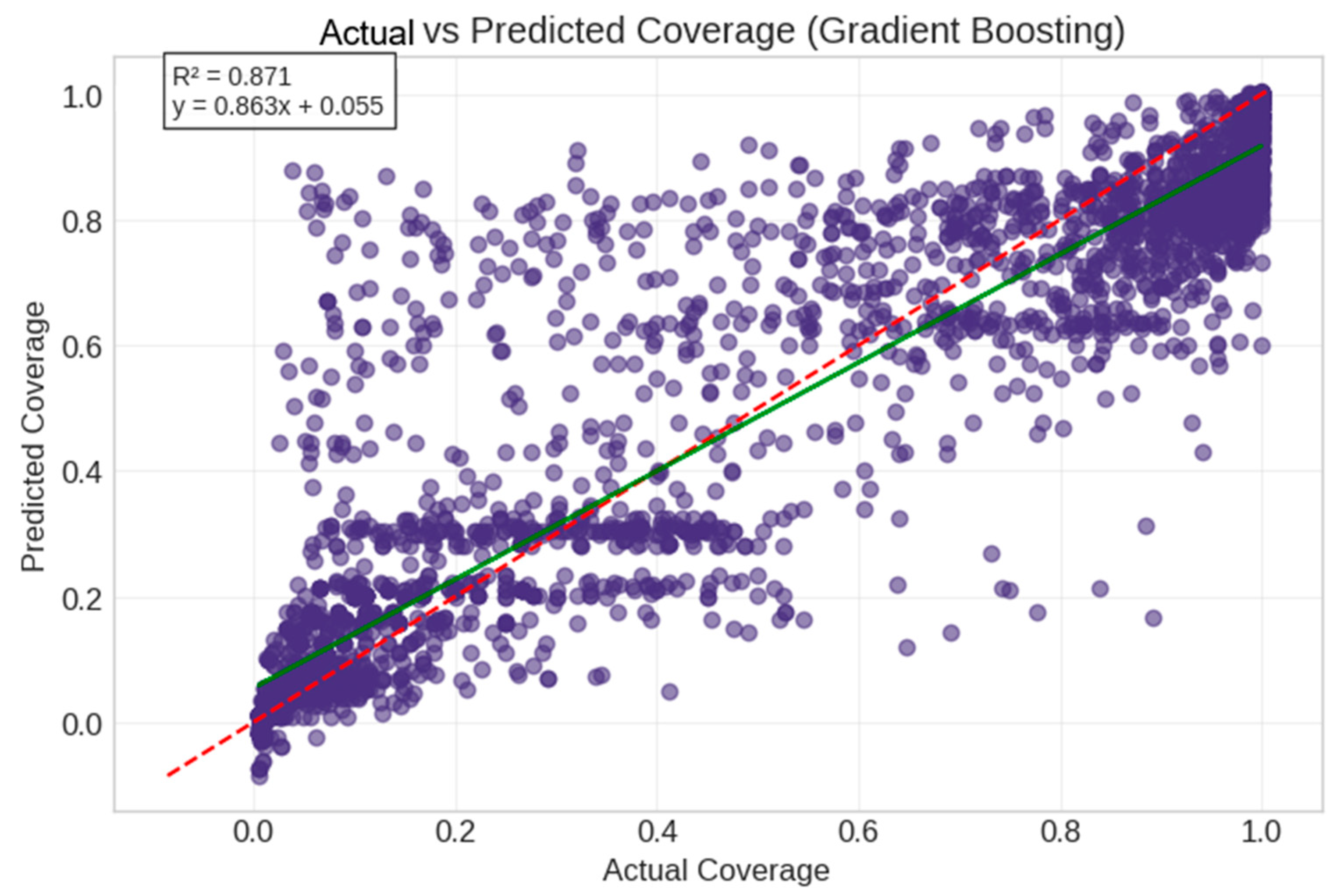
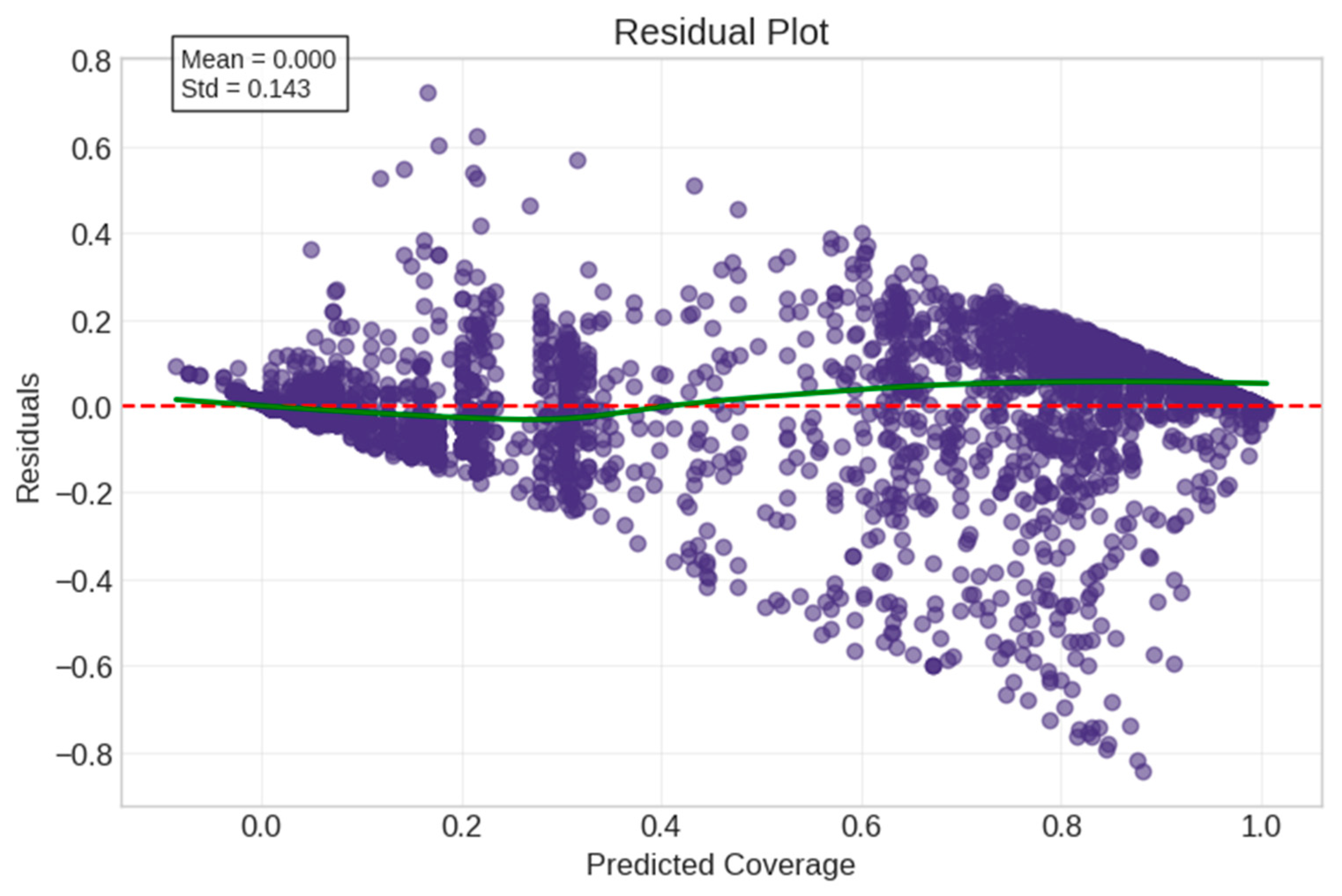
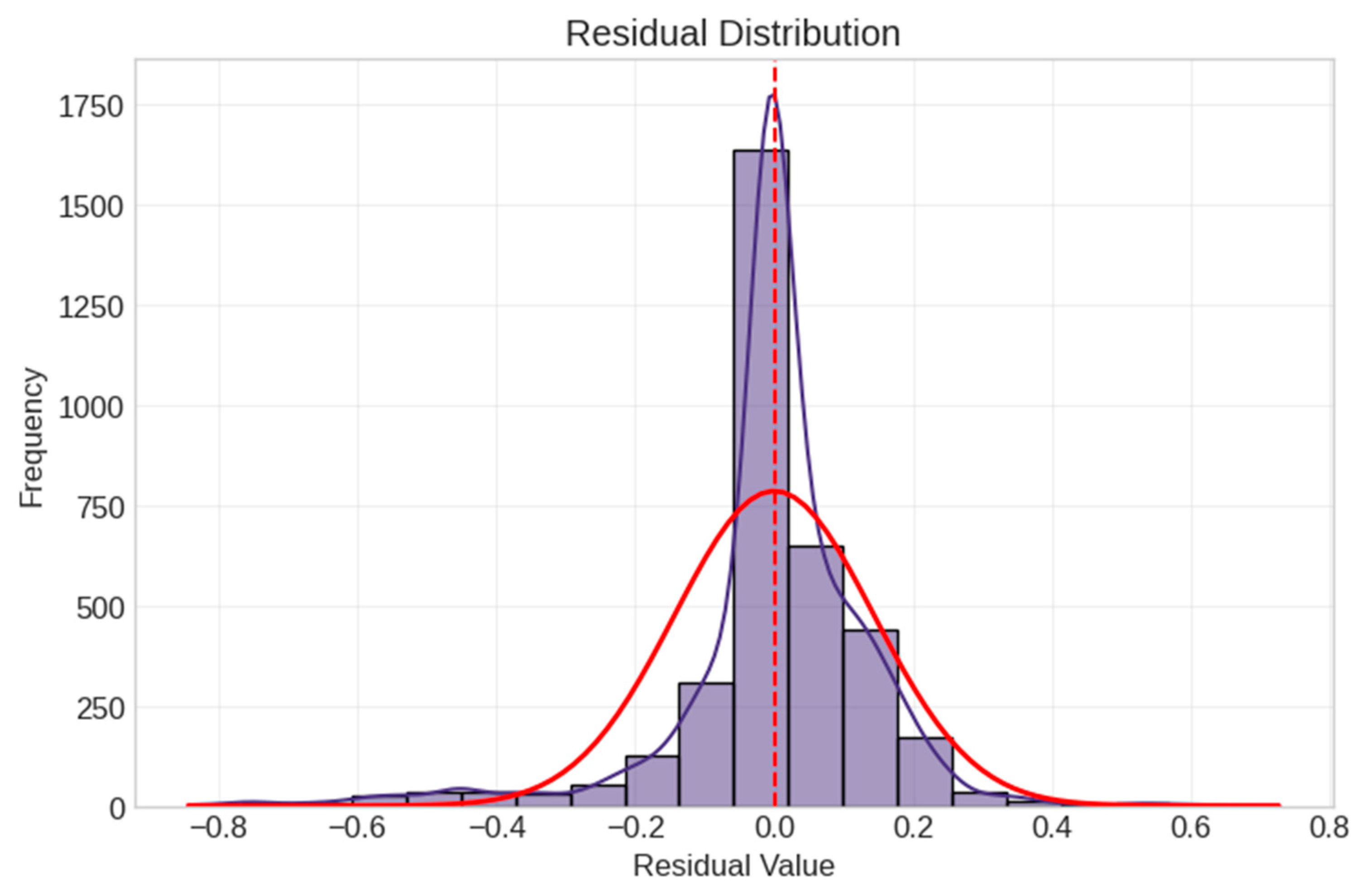
5.3. Model Verification and Feature Stability Analysis

To assess the transferability of our findings, we conducted a feature stability analysis using a separate verification dataset. This approach helped to identify which relationships remained consistent across different data contexts.

When analyzing individual feature relationships in the verification dataset, we discovered a remarkably strong correlation between peak_speed_time and coverage (r = 0.995, p < 0.001). This nearly perfect correlation (Figure 33) provided compelling evidence that temporal dynamics represented the fundamental driving force behind information diffusion.

The feature importance rankings (Figure 34) showed notable consistency with our synthetic data findings. Peak_speed_time maintained its dominant position (importance = 0.809), followed by avg_degree (importance = 0.118). This stability in feature rankings across different datasets strongly validated our identification of the key drivers of information diffusion.

While the overall model fit in the verification context presented challenges, this actually strengthened our core finding: general network properties must be supplemented with temporal dynamic measures for the effective prediction of information spread. The verification analysis showed that relying solely on static network features would be insufficient without accounting for the temporal component.

Other structural features showed more context-dependent relationships: avg_degree (r = 0.220, p = 0.125), avg_closeness_centrality (r = 0.106, p = 0.464), and density (r = −0.061, p = 0.674). This pattern suggests that network structural effects may be more variable across contexts, while temporal dynamics maintain consistent influence.

Our verification analysis included both basic bootstrapping (1000 resamples) to establish confidence intervals for feature importance and targeted comparisons between synthetic and real-world performance. The performance gap between synthetic (R² = 0.847) and real data (R² = 0.512) highlighted how authentic social networks contain additional complexities not fully captured in controlled simulations, including external influences and complex temporal dynamics like activity resurgence patterns.

The verification phase provided valuable practical insights: when predicting information diffusion in new contexts, peak_speed_time serves as a reliable indicator of potential coverage. This finding has important implications for real-time monitoring and the prediction of information spread, as early temporal patterns can provide strong signals about eventual reach.

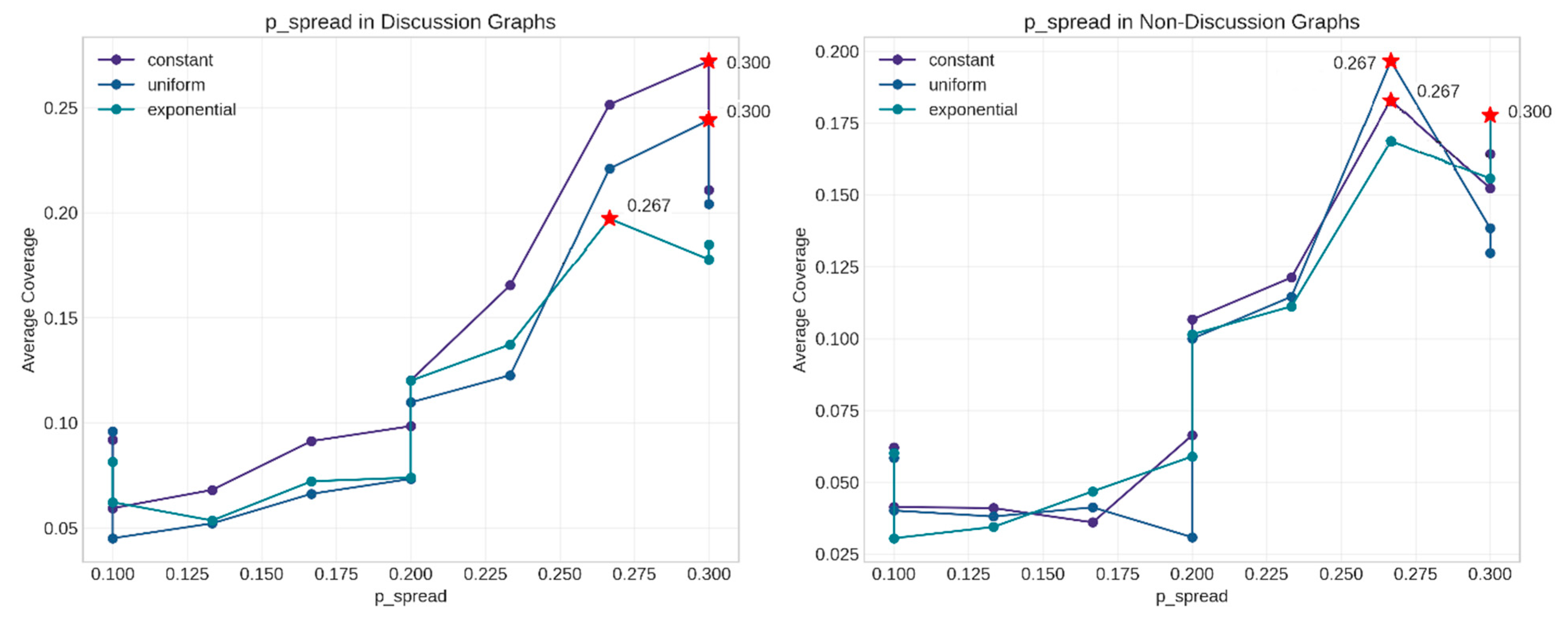
5.4. Comparative Analysis

Comparing the results across real data, synthetic data, and verification provided valuable insights into the consistency and robustness of our findings.

Spread probability (p_spread) emerged as a consistently important factor across all analyses. In real data, it was the most important feature (importance = 0.321), while in synthetic data, it remained implicitly important through its influence on peak_speed_time. The optimal spread probability was consistently high (0.3–0.4) across all datasets.

Our findings suggest that temporal dynamics might be more influential than static network properties in certain contexts, though further research is needed to establish broader generalizability.

The observed patterns suggest a potential research question: could network structural effects be more context-dependent than temporal dynamics? Our study provided initial evidence that while network properties showed variable influence across contexts, the importance of peak diffusion timing appeared to be more consistent, but this hypothesis requires validation through additional studies with diverse network types. The optimal configuration for maximizing information coverage was consistently as follows (Figure 35):

• Random network structure (highest average coverage);
• Constant delay mechanism (slightly better than alternatives);
• High spread probability (0.4);
• High average degree (approximately 46 in synthetic networks).

Figure 35. Summary of optimal information diffusion configuration.

Figure 35. Summary of optimal information diffusion configuration.

These findings demonstrate that while specific feature importances may vary across datasets, the fundamental patterns and optimal configurations for information diffusion remain relatively consistent.

6. Discussion

6.1. Comparison with Existing Models

Our research findings both support and extend previous work on information diffusion in social networks.

Table 2. Comparison of information diffusion models.

Model	Key Features	Strengths	Limitations	Performance Metrics
Our Model	Multiple delay types, cross-validation on real and synthetic data, temporal dynamics focus	High predictive power (R2 = 0.847), rigorous feature selection, strong temporal insights	Limited generalizability in verification	Coverage prediction (R2), feature stability
Chen et al. (2021, 2024) [8,11]	Population dynamics with warning timeliness, real-world crisis applications	Good fit to Weibo data, prediction capability	Limited delay mechanism variety, no cross-network testing	Curve fitting accuracy
SEI Model (Kumar et al., 2020) [9]	Three-state transitions with exposed state	Captures pre-sharing exposure state, Twitter data validation	No delay variation analysis, limited feature importance	User state counts
Non-linear Anomalous (Foroozani & Ebrahimi, 2021) [1]	Time-fractional Fisher’s equation, continuous-time random walk	Models super-/sub-diffusion, high precision on Digg/Twitter	Complex implementation, no temporal feature analysis	Density prediction accuracy
ODID (Tu et al., 2022) [12]	Ordinary differential equations, friendship-based rather than geometric	A total 98.78% prediction accuracy, captures both temporal and spatial patterns	No delay mechanism comparison, limited network variety	Prediction accuracy vs. actual data
Fuzzy Sign-Aware (Mohammadi et al., 2023) [18]	Multi-trust relationships, fuzzy logic implementation	Handles trust/distrust relations, natural multi-level trust	Limited to signed networks, no temporal dynamics focus	Prediction accuracy, coverage

provides a comparative analysis of our approach with key existing models.

Our approach differs from previous models in several important ways. First, we systematically compare three distinct delay mechanisms (constant, uniform, exponential) across various network structures. This comparative approach is absent in most existing studies, which typically focus on a single delay mechanism. For example, Chen et al. (2021, 2024) [8,11] incorporate warning timeliness in their population dynamics model but do not compare different delay distributions.

Second, our identification of peak_speed_time as the dominant predictor (importance = 0.848) highlights the critical role of temporal dynamics in information diffusion. This finding extends beyond the typical structural focus found in models like those of Binesh and Ghatee (2021) [16], which emphasize network distance and node influence.

The performance of our Gradient Boosting model (R² = 0.847 ± 0.032) compares favorably with existing approaches. Tu et al. (2022) [12] report a 98.78% prediction accuracy for their ODID model on the Digg dataset, which appears superior. However, their evaluation uses a different metric and dataset, making direct comparison difficult. Our approach focuses on cross-validation robustness across diverse network types, providing more generalizable insights.

6.2. Theoretical Implications

Our findings have several important theoretical implications for understanding information diffusion in social networks with delay mechanisms.

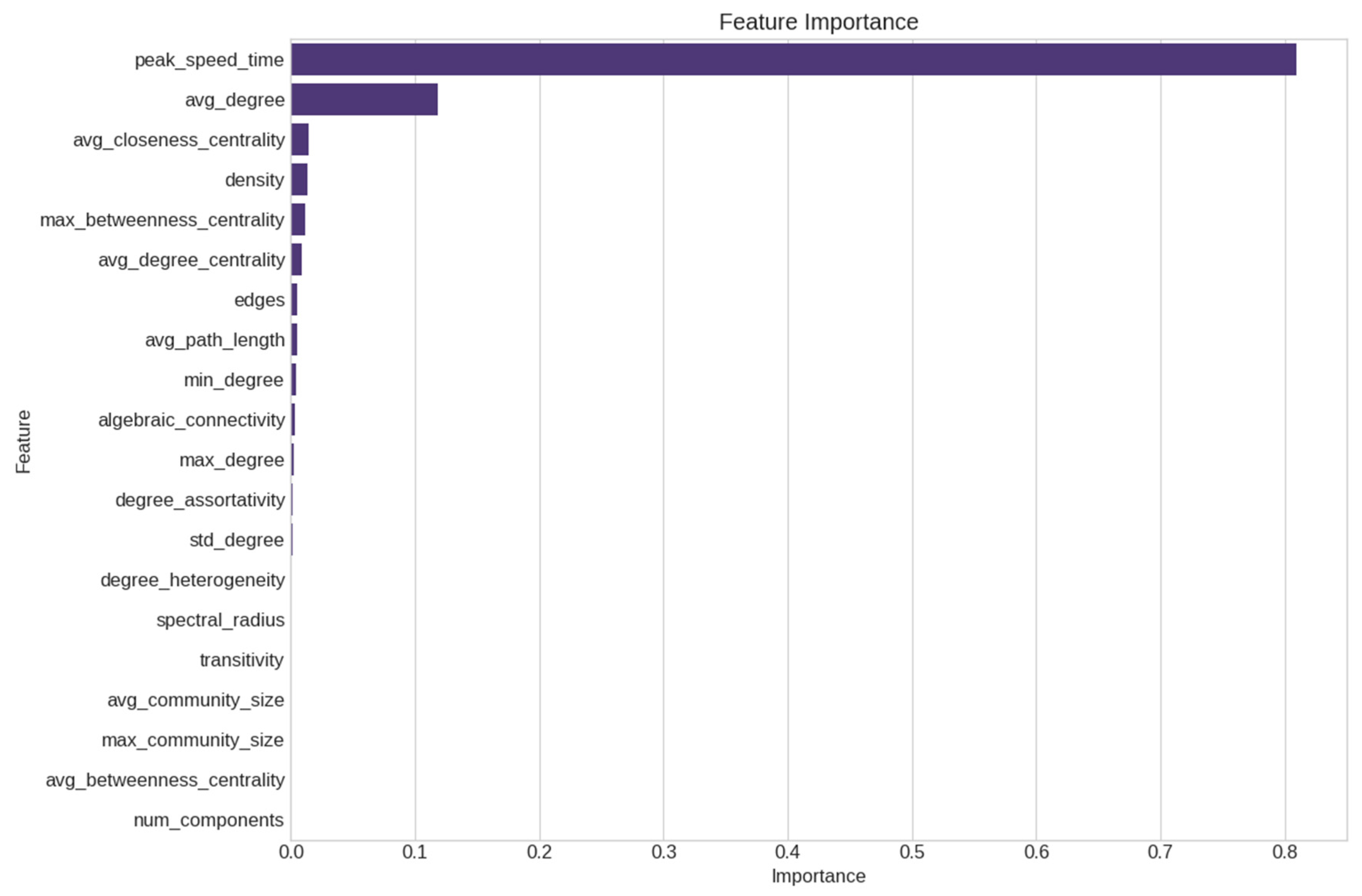
• First, the dominant role of peak_speed_time in our models suggests a “critical momentum” theory of information diffusion. This theory posits that the timing of the maximum diffusion speed, rather than static network properties, determines the ultimate information coverage. One question emerging from our research is whether competing information concepts could help explain differential success rates in diffusion processes across varied network structures.
• Second, the consistent significance of spread probability (p_spread) across all datasets supports transmission-centric rather than structure-centric diffusion theories. While network structure matters, the likelihood of information sharing between connected individuals appears to be more fundamental. This contrasts with structure-focused approaches like those of Xiao et al. (2019) [17], who emphasized the topological dimensions of networks.
• Third, our finding that the delay mechanism type (constant, uniform, exponential) has no statistically significant effect contradicts the assumptions in some existing models. For example, Sun et al. (2024) [14] developed elaborate state transitions in their SEIHR model, yet our results suggest that the specific delay distribution may be less important than previously thought. What matters more is the integration of some delay mechanisms rather than which specific type is used.
• Fourth, our verification analysis reveals challenges in transferring models between contexts, despite stability in feature importance rankings. This supports the contextual diffusion theory proposed by Wei et al. (2023) [13], who argued that diffusion patterns depend on specific community characteristics rather than universal laws.

The finding that delay mechanism type (constant, uniform, exponential) does not significantly affect information coverage warrants further examination. Several potential explanations may account for this counterintuitive result:

First, the dominance of network structural properties and spread probability may overshadow delay type effects. In complex networks, the fundamental connectivity patterns and transmission likelihood could determine most of the variance in diffusion outcomes, regardless of how delays are distributed.

Second, users’ information consumption behaviors may naturally normalize temporal variations. Social media users typically check platforms at irregular intervals dictated by personal habits and external schedules rather than through continuous monitoring. This inherent behavioral variability may diminish the effects of specific programmed delay distributions.

Third, there may be a threshold effect where the presence of any delay mechanism is more important than its specific distribution. Once some delay is introduced into the diffusion process, the specific pattern of delays may become secondary to other factors.

Finally, methodological considerations such as parameter settings for delay distributions could influence this finding. While we use comparable mean delay values across mechanisms, the effective ranges of the delays experienced in different models might need more precise calibration in future work.

6.3. Practical Applications

Our research findings offer several practical applications for organizations seeking to optimize information dissemination in social networks.

For marketing strategists, our results suggest focusing resources on maximizing spread probability rather than targeting specific network structures. This can be achieved through engaging content design, incentivized sharing mechanisms, and reduced friction in the sharing process. The optimal spread probability of 0.3–0.4 identified in our study provides a concrete target for campaign designers.

For platform developers, the importance of timing in diffusion suggests implementing real-time monitoring systems focused on early diffusion speed. By identifying peak diffusion speed timing, platforms can better predict which content will achieve widespread coverage. This insight could improve content recommendation algorithms and trending topic identification.

For crisis communication managers, our finding that constant delay mechanisms perform slightly better than alternatives suggests implementing consistent, predictable information release schedules during emergencies. This supports the work of Chen et al. (2021) [8], who emphasized the importance of warning timeliness in crisis information diffusion.

For community managers, particularly on platforms like Reddit, our analysis indicates that discussion-type networks generally achieve higher coverage than non-discussion networks. This suggests the importance of investing in the moderation and facilitation of meaningful discussions rather than simply broadcasting information.

6.4. Limitations and Future Work

While our study provides valuable insights, several limitations should be acknowledged. First, our real data sample was relatively small (eight networks, 72 observations), necessitating the use of synthetic networks. Although we validated key findings across both datasets, larger real-world samples would strengthen our conclusions.

Second, our verification analysis showed challenges in model transferability, with reduced performance on the test dataset. This suggests that context-specific factors may limit generalizability, requiring model adaptation for new network environments.

Third, our models focused primarily on static network structures, whereas real social networks evolve dynamically. Future research should incorporate network evolution into diffusion models, perhaps using the varying-weight approach suggested by Wei et al. (2023) [13].

Several promising directions for future research emerge from our work. First, exploring the causal relationship between peak_speed_time and coverage could reveal the mechanisms for early intervention in diffusion processes. Second, investigating how competing information streams affect peak diffusion timing would extend the work of He et al. (2024) [25] on competing memes. Third, developing adaptive diffusion strategies based on early temporal patterns could improve information dissemination in time-sensitive contexts.

Additionally, applying our comparative approach to signed networks, as studied by Mohammadi et al. (2023) [18], could reveal how trust and distrust relationships interact with different delay mechanisms. Finally, exploring threshold effects in information propagation might identify critical mass points where diffusion becomes self-sustaining.

7. Conclusions

This study has revealed several key insights into the dynamics of information diffusion with time delay mechanisms. Most notably, we discovered that while network structure and spread probability significantly impacted information coverage, the specific delay mechanism type (constant, uniform, exponential) showed no statistically significant effect. Furthermore, our analysis identified temporal dynamics—specifically, the timing of peak diffusion speed—as the dominant predictor of ultimate information reach.

Our findings demonstrated that temporal dynamics, particularly peak diffusion speed timing, play a crucial role in determining ultimate information coverage. The Gradient Boosting model achieved strong predictive performance (R² = 0.847 ± 0.032) on synthetic data, identifying peak_speed_time as the dominant predictor (importance = 0.848).

Transmission probability (p_spread) emerged as consistently significant across all analyses, with optimal values of 0.3–0.4 maximizing coverage. Interestingly, the specific delay mechanism (constant, uniform, exponential) showed no statistically significant effect on coverage, challenging assumptions in previous research.

Network structure also influenced diffusion outcomes, with Random networks achieving the highest average coverage (0.653) and Tree networks showing lowest coverage (0.219). The strong verification correlation between peak_speed_time and coverage (r = 0.995, p < 0.001) confirmed the fundamental importance of temporal dynamics in information spread.

This research contributed to the field by systematically comparing delay mechanisms across diverse network structures, quantifying the relative importance of temporal versus structural factors, and providing practical recommendations for optimizing information dissemination. The integration of real data analysis with synthetic modeling offered methodological insights for future network research.