A Fast Method for the Acceleration Response Analysis of Two-Dimensional Sites Under Seismic Excitations
Abstract
1. Introduction
2. Seismic Response Calculation Method for Soil Layers Based on the Modal Superposition Method
2.1. Theoretical Background
2.2. Required Modes for Acceleration Response Analysis
2.3. Approximate Calculation Method for Acceleration Time History
3. Homogeneous Site
3.1. Numerical Model and Input Ground Motion
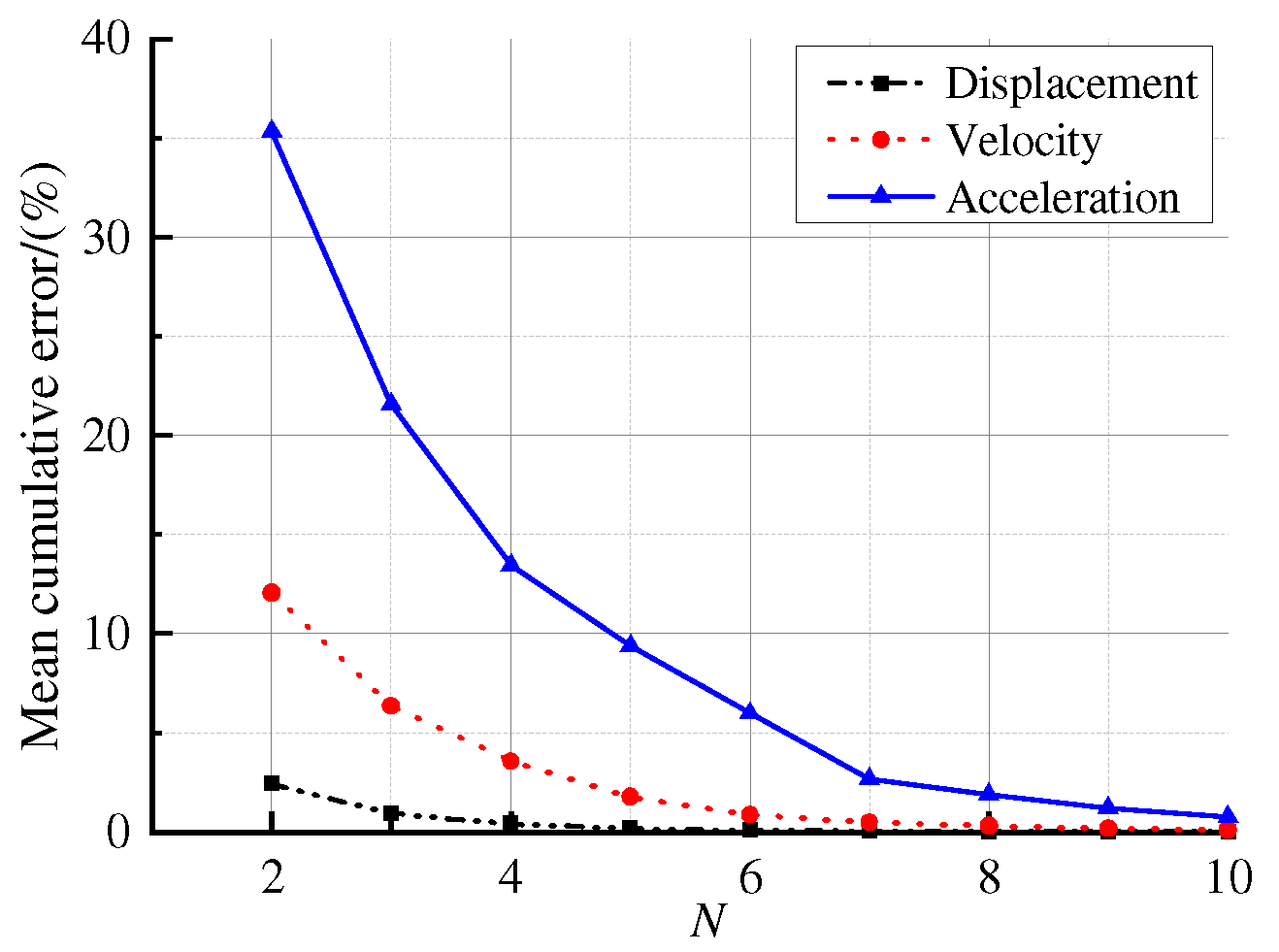
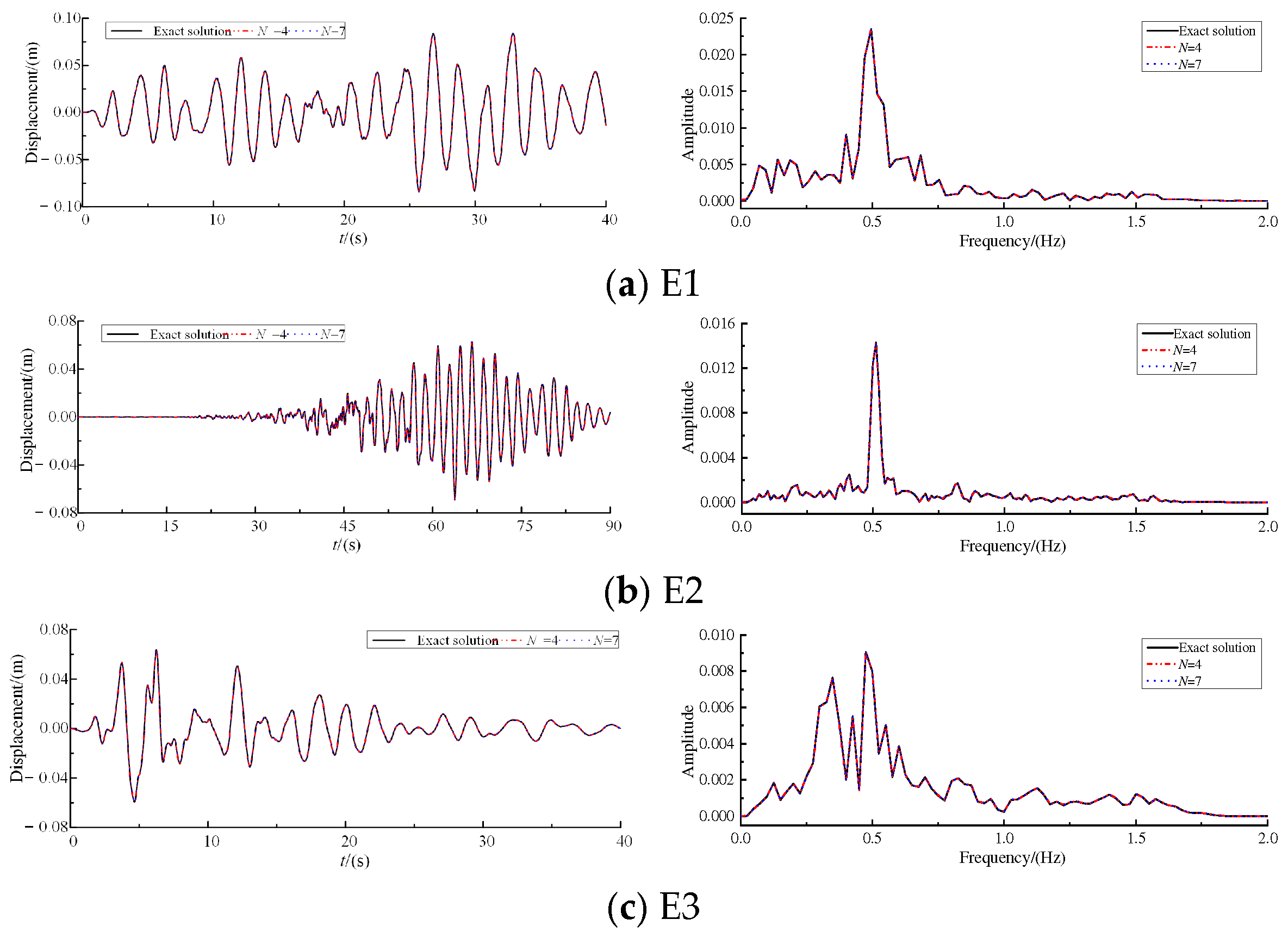
3.2. Modal Truncation Error for Time-History Analysis
- (1)
- When N = 4, the calculation error of uA is only 0.42%, indicating that the number of modes selected based on modal participation mass is enough to calculate displacement response.
- (2)
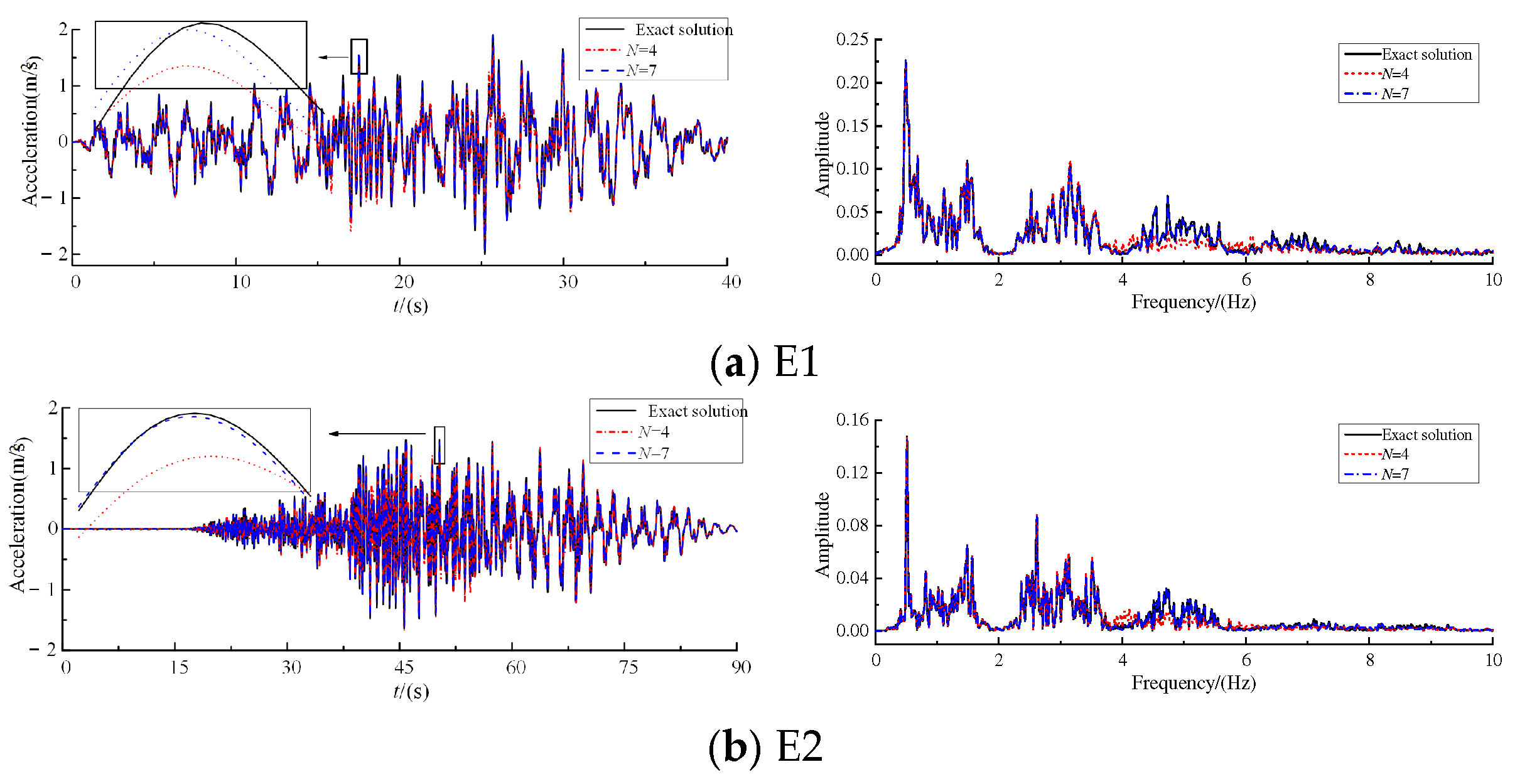
- The error of displacement response is the smallest compared with velocity and acceleration, while the error of acceleration response is the largest. The reason is that the higher modes have a greater impact on acceleration than on the displacement. Comparing Figure 5 and Figure 6, it can be observed that the differences in the Fourier spectra of the accelerations are greater than those of the displacement Fourier spectra, which confirms this finding.
- (3)
- The error of acceleration, , is 13.44% when N = 4, while the error is less than 5% when N = 7. Therefore, when modal participation mass and modal contribution factor are used as truncation criteria, the resulting number of modes is suitable for displacement response analysis, but may introduce significant errors in acceleration response. For high-precision acceleration response, the modal contribution factor of acceleration should be adopted as the truncation criterion.
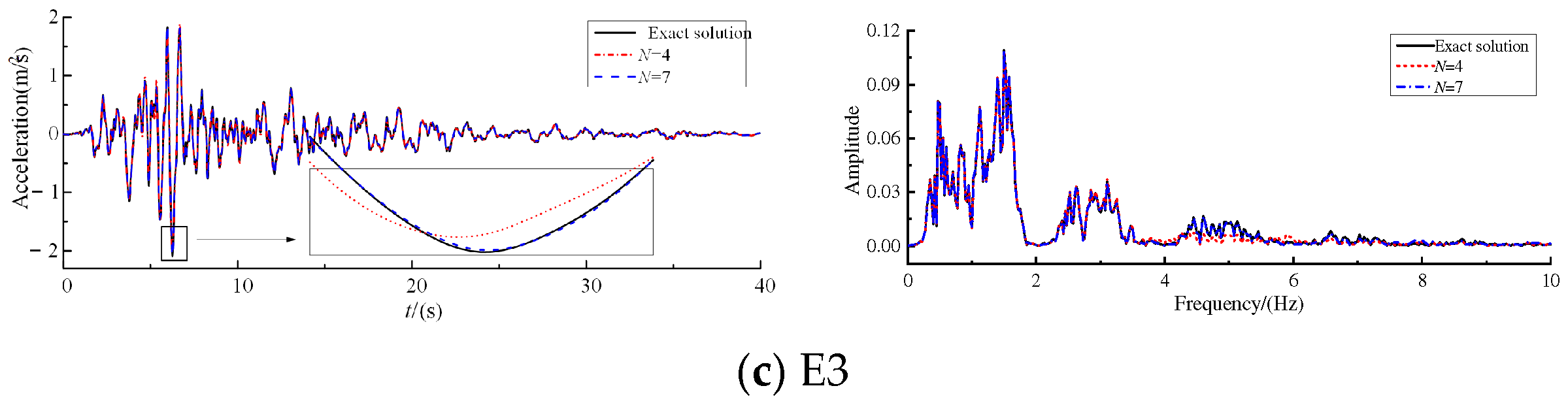
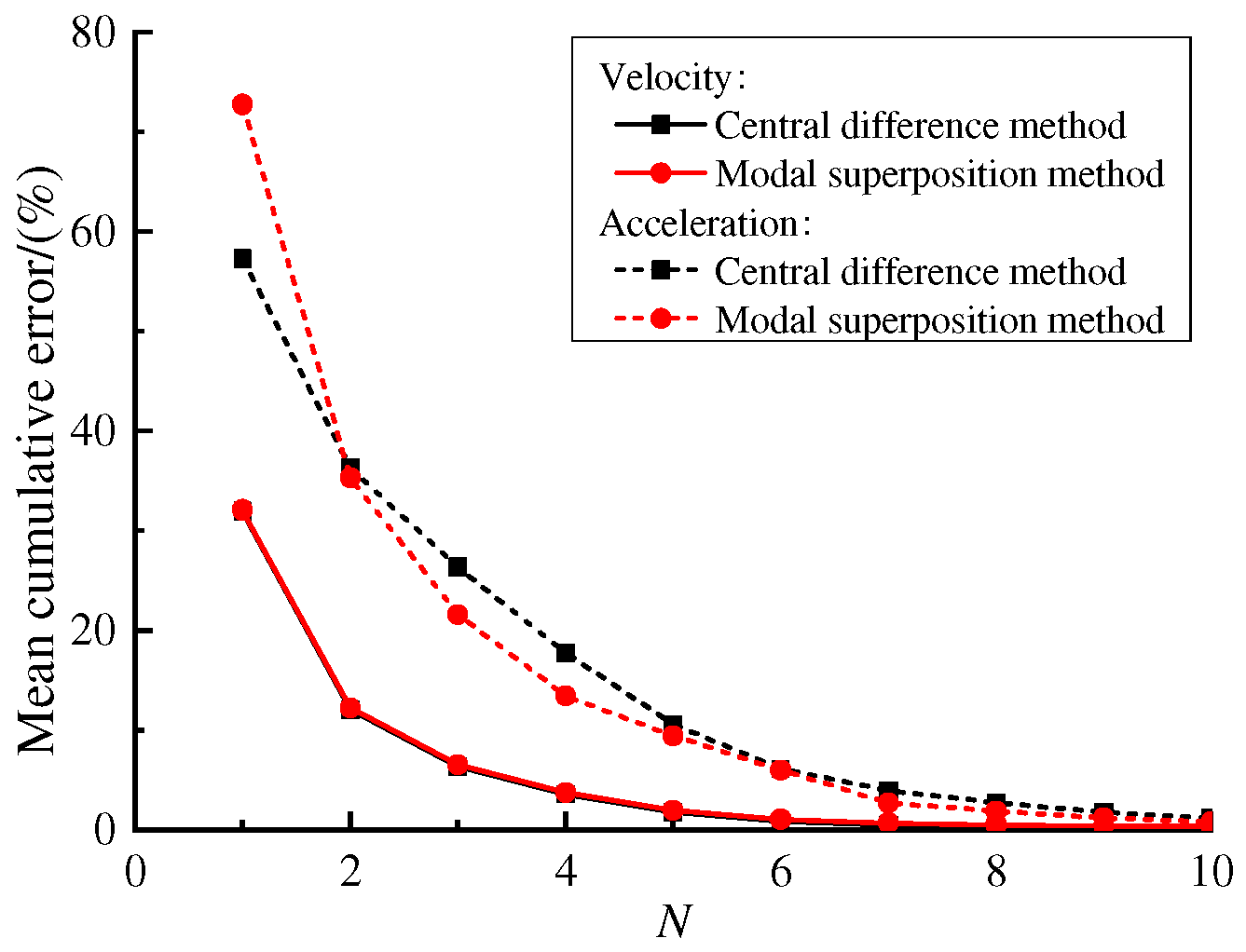
3.3. The Relative Errors of Acceleration Time History for Approximation Method
- (1)
- For velocity response, the calculation errors of the central difference method are almost the same as those by the direct modal superposition method, indicating that both the central difference method and the direct modal superposition method can be used for the calculation of velocity responses.
- (2)
- When N > 5, the acceleration response errors obtained by the central difference method and the modal superposition method are essentially the same. Considering the number of modes determined by different truncation criteria, if the cumulative modal contribution factor of acceleration is used as the truncation index, the central difference method can be employed to compute the acceleration response.
4. Scarp Topography Site
4.1. Finite Element Model
4.2. Modal Truncation Error for Time-History Analysis
- (1)
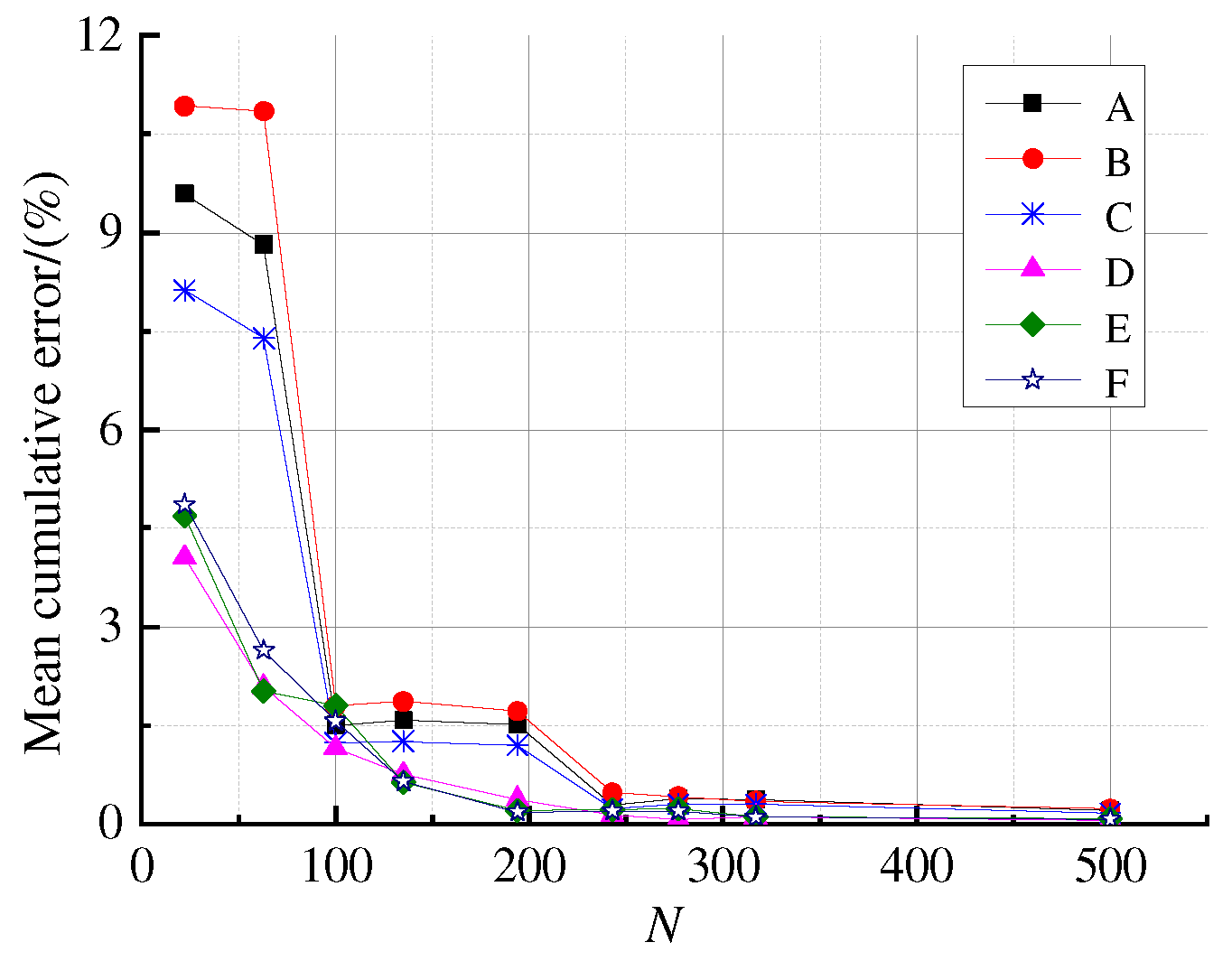
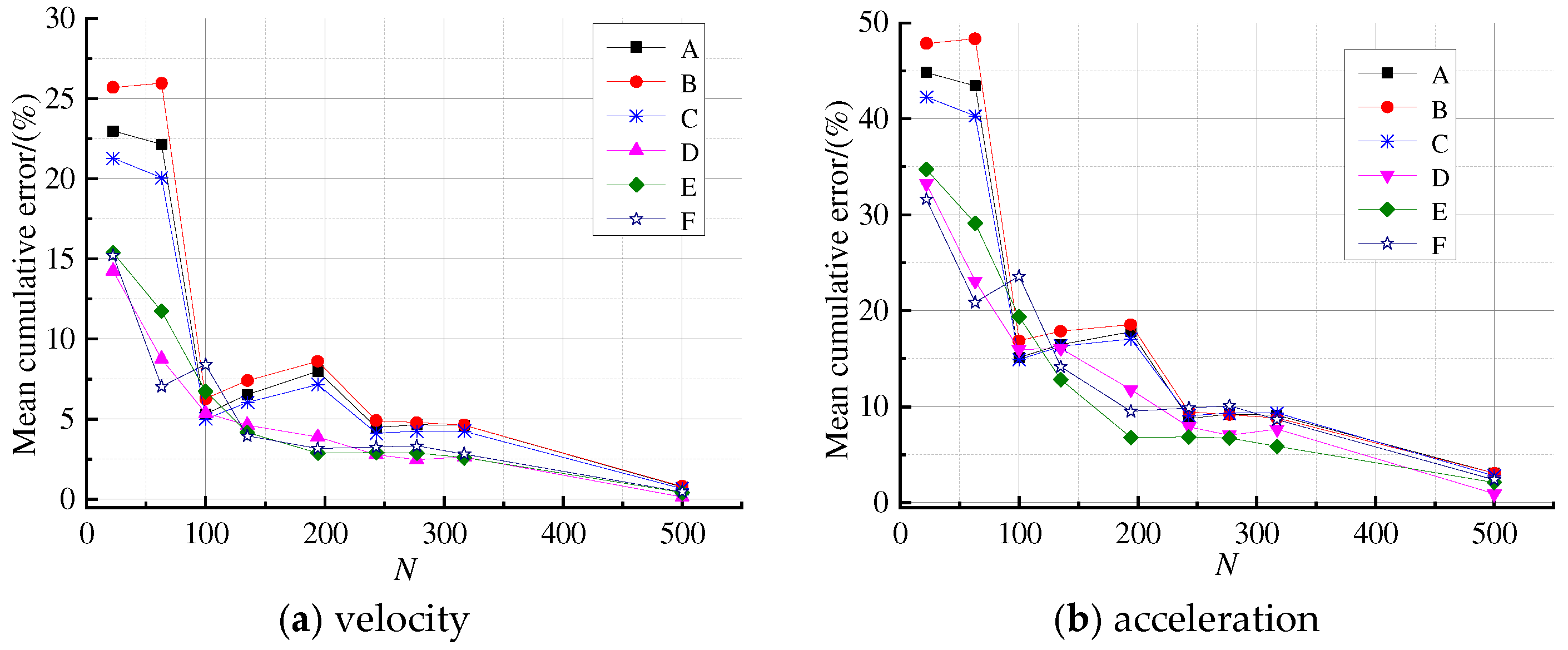
- If the threshold is set to 10% for modal truncation, the mode number selected based on em is 63, the mode number selected based on euA, euB, euC, euD, euE, euF are 22, 63, 63, 22, 22, 22, respectively, and the mode number selected based on eaA, eaB, eaC, eaD, eaE, eaF are 317, 277, 194, 135, 100, and 135, respectively.
- (2)
- For displacement response, when N ≥ 63, except for uB whose calculation error is slightly greater than 10%, the cumulative error of displacement at all other points is less than 10%, indicating that the mode number selected based on modal participation mass for displacement response analysis is reasonable. The required mode numbers for (i = A, B, …, F) are 243, 243, 243, 243, 194, and 277 respectively. The truncation numbers based on the eai are much larger than the em and eui. This demonstrates once again that the cumulative modal contribution factor of acceleration should be used as the modal truncation criterion for acceleration response.
- (3)
- The cumulative error of acceleration is the largest, followed by velocity, and the smallest is displacement.
- (4)
- The cumulative errors of displacement, velocity, and acceleration at the lower step are all greater than those at the upper step. The reason is that the contributions of higher modes to the lower step are larger than to the upper step. For the points A, B, and C on the lower step, 277 modes obtained by eaB would make the cumulative error at all points less than 10%. Therefore, the modal contribution factor of acceleration at the position with a distance of one step height from the toe of the slope at the lower step can be used as the basis for modal truncation.
- (5)
- When N ≥ 277, the velocity and acceleration response errors obtained by the central difference method are less than 10%, which indicates that taking the cumulative modal contribution factor of acceleration as the basis for modal truncation, and calculating acceleration by the central difference method, shows high accuracy.
5. Conclusions
- (1)
- The contributions of the higher modes to acceleration are larger than to the displacement. Therefore, more modes need to be included in the calculation of acceleration response for the modal superposition method. The cumulative modal contribution factor of acceleration can be used as a modal truncation index for acceleration response. The modal participation mass and displacement-based modal contribution factor can only be used as a modal truncation index for displacement response.
- (2)
- The mode number of modal truncations is related to the selected degrees of freedom. For a homogeneous site, the acceleration at the site surface can be regarded as the key response quantity. For scarp topography, the position with a distance of one step height from the toe of the slope at the lower step can be used as the basis for modal truncation.
- (3)
- When the cumulative modal contribution factor of acceleration is used as the truncation criterion, the accuracy of velocity and acceleration obtained by the central difference method is essentially consistent with the results from the modal superposition method. Therefore, displacement responses can be computed using the modal superposition method, and then the velocity and acceleration responses at locations of interest can be obtained using the central difference method.
- (4)
- The theoretical foundation of this method is the modal superposition approach, which is suitable for linear elastic analysis. However, for nonlinear seismic response analysis of soil layers, the equivalent linearization method is commonly used. Therefore, during each iteration step, the computational method proposed in this paper can be employed to improve the efficiency of equivalent linearization calculations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Castro, R.R.; Pérez-Campos, X.; Zúñiga, R.; Ramírez-Guzmán, L.; Aguirre, J.; Husker, A.; Cuéllar, A.; Sánchez, T. A review on advances in seismology in Mexico after 30 years from the 1985 earthquake. J. South Am. Earth Sci. 2016, 70, 49–54. [Google Scholar] [CrossRef]
- Mahmood, K.; Zamin, B.; Iqbal, S.; Rehman, Z.U.; Afzal, S.; Safdar, M.; Iqbal, Q.; Ali, A. Local site effect on seismic hazard of the relocated new Balakot town. Soil Dyn. Earthq. Eng. 2022, 11, 107451. [Google Scholar] [CrossRef]
- Shreyasvi, C.; Venkataramana, K.; Chopra, S. Local site effect incorporation in probabilistic seismic hazard analysis—A case study from southern peninsular India, an intraplate region. Soil Dyn. Earthq. Eng. 2019, 123, 381–398. [Google Scholar] [CrossRef]
- Idriss, I.M.; Seed, H.B. Seismic response of horizontal soil layer. J. Soil Mech. Found. Div. 1968, 94, 1003–1031. [Google Scholar] [CrossRef]
- Nishanth Kiran, D.; Muzzaffar Khan, M.; Madhu Sudhan Reddy, M.; Kalyan Kumar, G. Earthquake response analysis of sites using DEEPSOIL. In Proceedings of the 7th Indian Young Geotechnical Engineers Conference, Silchar, India, 15–16 March 2019; 2020; pp. 309–315. [Google Scholar]
- Hashash, Y. DEEPSOIL5.0 User Manual and Tutorial; University of Illinois: Urbana, IL, USA, 2011. [Google Scholar]
- Idriss, I.M.; Sun, J.I. User’s Manual for SHAKE91: A Computer Program for Conducting Equivalent Linear Seismic Response Analyses of Horizontally Layered Soil Deposits; Center for Geotechnical Modeling Department of Civil & Environmental Engineering, University of California: Berkeley, CA, USA, 1992. [Google Scholar]
- Puri, N.; Jain, A.; Mohanty, P.; Bhattacharya, S. Earthquake response analysis of sites in state of Haryana using DEEPSOIL software. Procedia Comput. Sci. 2018, 125, 357–366. [Google Scholar] [CrossRef]
- Davis, L.L.; West, L.R. Observed effects of topography on ground motion. Bull. Seismol. Soc. Am. 1973, 63, 283–298. [Google Scholar] [CrossRef]
- Celebi, M. Topographic and geological amplification determined from strong motion and aftershock records of March 1985 Chile earthquake. Bull. Seismol. Soc. Am. 1987, 77, 1147–1167. [Google Scholar] [CrossRef]
- Bustos, J.; Pastén, C.; Pavez, D.; Acevedo, M.; Ruiz, S.; Astroza, R. Two-dimensional simulation of the seismic response of the Santiago Ba-sin, Chile. Soil Dyn. Earthq. Eng. 2023, 164, 107569. [Google Scholar] [CrossRef]
- Jin, D.D.; Chen, G.X.; Dong, F.F. Large-Scale two-dimensional nonlinear analysis on seismic effect of Fuzhou Basin. Appl. Mech. Mater. 2011, 90–93, 1426–1433. [Google Scholar] [CrossRef]
- McGann, C.R.; Bradley, B.; Wotherspoon, L.; Lee, R. Basin effects and limitations of 1Dsite response analysis from 2D numerical models of the Thorndon basin. Bull. New Zealand Soc. Earthq. Eng. 2021, 54, 21–30. [Google Scholar] [CrossRef]
- Ayoubi, P.; Mohammadi, K.; Asimaki, D. A systematic analysis of basin effects on surface ground motion. Soil Dyn. Earthq. Eng. 2021, 141, 106490. [Google Scholar] [CrossRef]
- Yiming, L.; Guoxin, W.; Yang, D. Nonlinear seismic response analysis of slopes considering the coupled effect of slope geometry and soil stratigraphy. Geophys. J. Int. 2024, 238, 616–630. [Google Scholar]
- Martin Philippe, P.; Bolton Seed, H. One dimensional dynamic ground response analysis. J. Geotech. Eng. Div. 1982, 108, 935–954. [Google Scholar] [CrossRef]
- Yoshida, N.; Kobayashi, S.; Suetomi, I.; Miura, K. Equivalent linear method considering frequency dependent characteristics of stiffness and damping. Soil Dyn. Earthq. Eng. 2002, 22, 205–222. [Google Scholar] [CrossRef]
- Mojtahedzadeh, N.; Siddharthan, R. Estimating free field seismic settlement history in a saturated layered soil profile. Soil Dyn. Earthq. Eng. 2021, 150, 106937. [Google Scholar] [CrossRef]
- Pan, D.G.; Fu Xq Qi, W.R. The Direct integration method with virtual initial conditions on the free and forced vibration of a system with hysteretic damping. Appl. Sci. 2019, 9, 3707. [Google Scholar] [CrossRef]
- Liu, Z.; Qiao, Y.; Cheng, X.; El Naggar, M.H. Nonlinear seismic response and amplification effect of 3D sedimentary basin based on bounding surface constitutive model. Soil Dyn. Earthq. Eng. 2022, 158, 107292. [Google Scholar] [CrossRef]
- Chen, W.; Lin, J.; Zheng, Y.; Su, L.; Chen, G.; Huang, L. Nonlinear seismic response of seabed with terrain variation and seawater-seabed coupling. Soil Dyn. Earthq. Eng. 2024, 180, 108579. [Google Scholar] [CrossRef]
- Chandran, D.; Anbazhagan, P. 2D nonlinear site response analysis of typical stiff and soft soil sites at shallow bed-rock region with low to medium seismicity. J. Appl. Geophys. 2020, 179, 104087. [Google Scholar] [CrossRef]
- Li, X.J.; Pan, D.G.; Shi, S.Z. A modal-superposition-based equivalent linearization method for seismic response analysis of two-dimensional sites. Eng. Mech. 2023, 40, 179–189. (In Chinese) [Google Scholar]
- Wilson, E.L. Three-Dimensional Statical and Dynamic Analysis of Structures; Computers and Structures: Berkeley, CA, USA, 2002. [Google Scholar]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Pan, D.; LI, X.; Tan, J. Modal truncation method on cantilever-type structures under seismic excitations. J. Build. Struct. 2020, 41, 55–62. (In Chinese) [Google Scholar]
- D’Aveni, A.; Muscolino, G. Response of non-classically damped structures in the modal subspace. Earthq. Eng. Struct. Dyn. 1995, 24, 1267–1281. [Google Scholar] [CrossRef]
- Bai, J.; Dong, S. Selection of lateral artificial boundary distance and analysis of its influence factors in seismic responses analysis of sites. World Inf. Earthq. Eng. 2018, 34, 179–187. [Google Scholar]
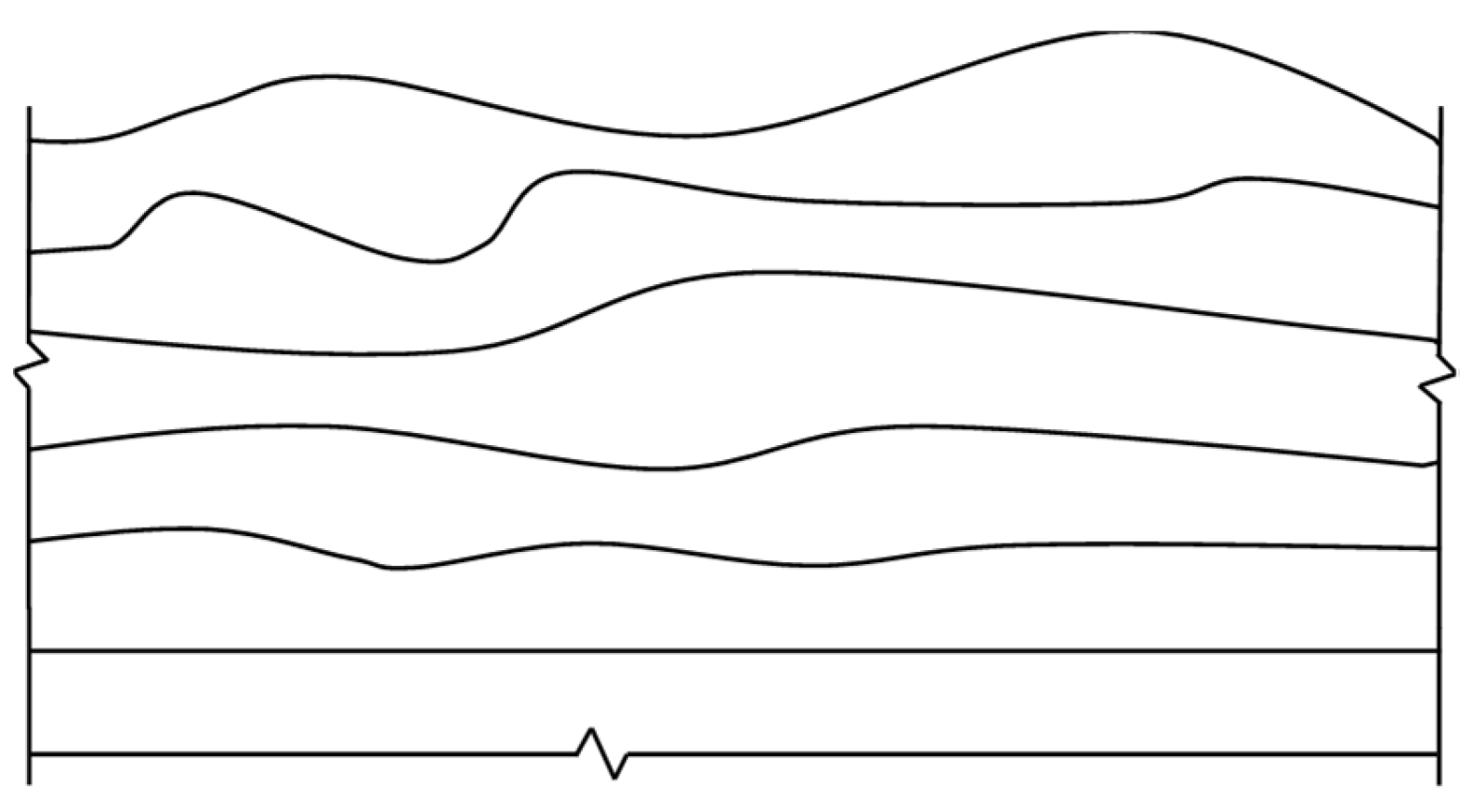
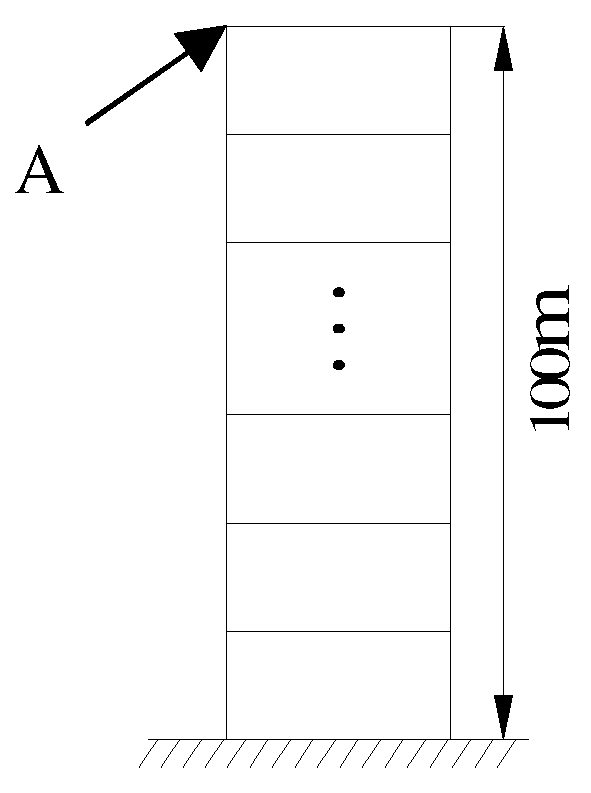
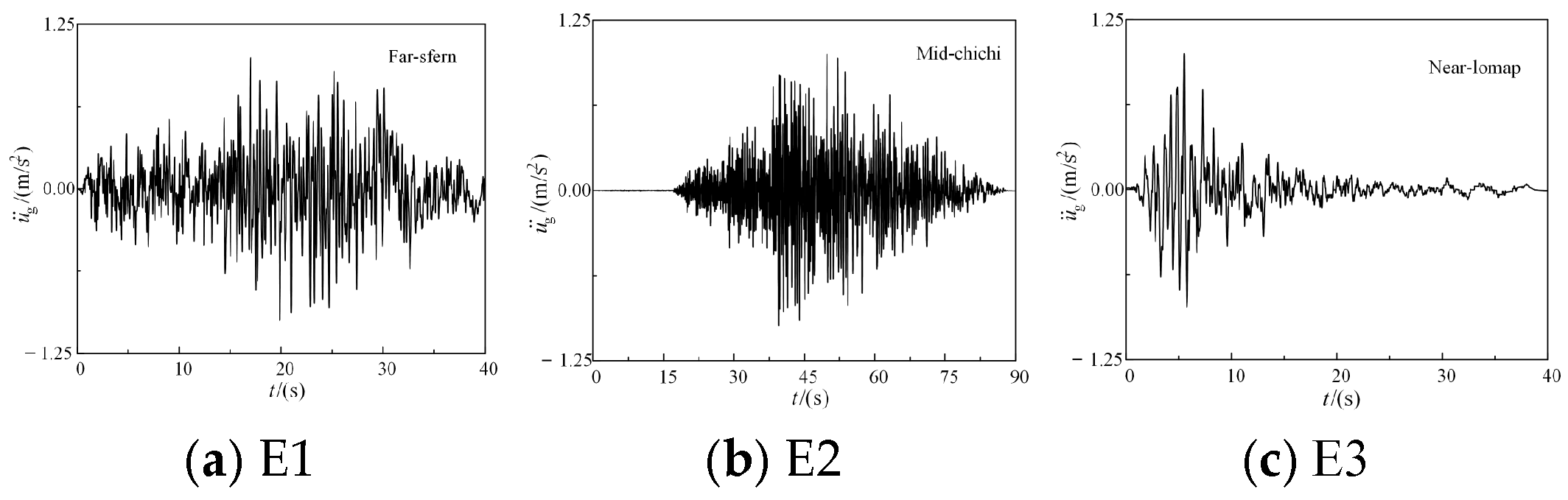

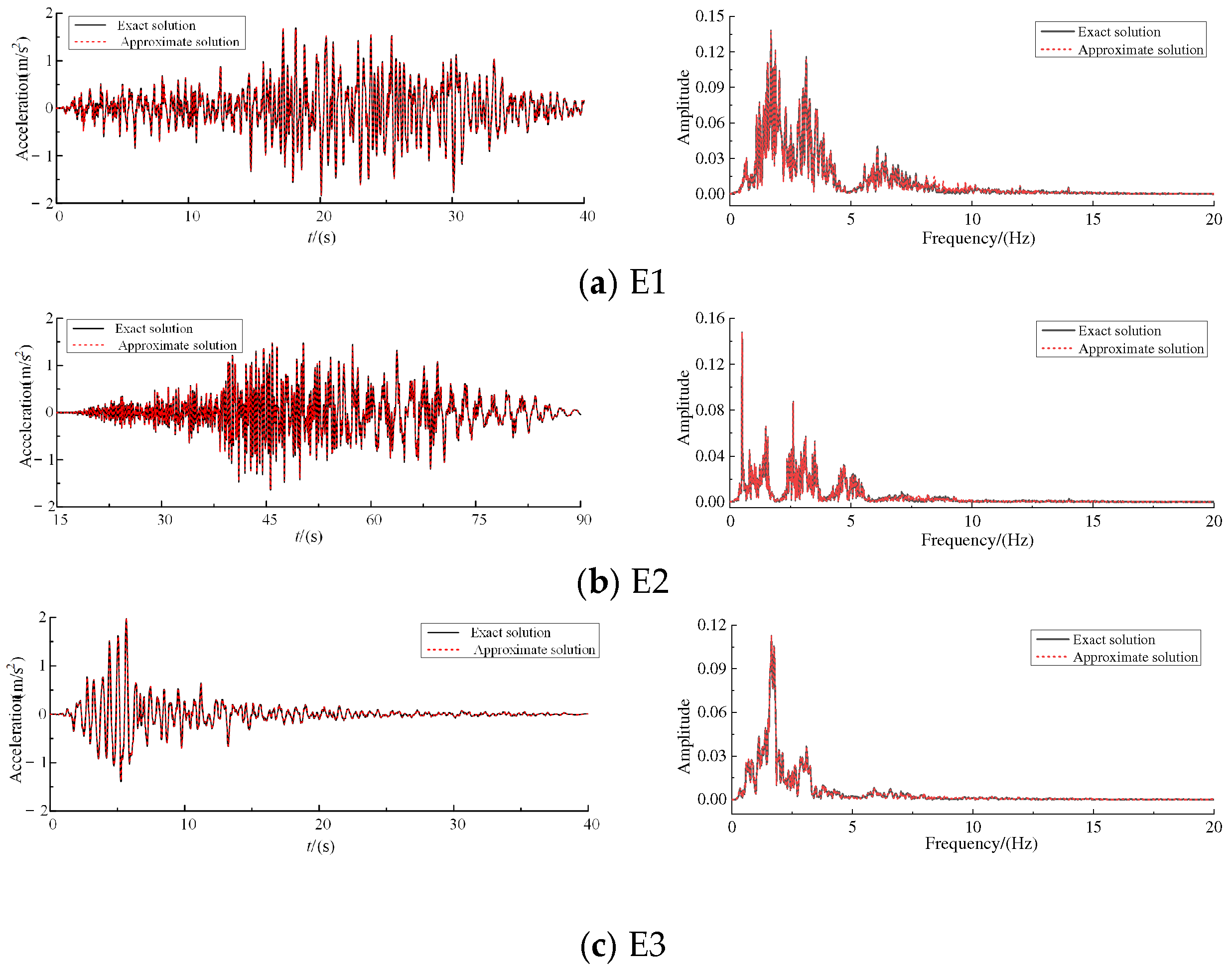
| No. | Seismic Wave | Time | Monitoring Station | Earthquake |
|---|---|---|---|---|
| E1 | Far-sfern | 2 September 1971 | Isabella Dam | San Fernando |
| E2 | Mid-chichi | 20 September 1999 | TTNO25 | Chi-Chi Taiwan |
| E3 | Near-lomp | 18 October 1989 | Belmont-Envirotech | Loma Prieta |
| N | Frequency/Hz | γ | em/% | euA/% | eaA/% |
|---|---|---|---|---|---|
| 1 | 0.499 | 603.9 | 17.93 | 3.20 | 27.31 |
| 2 | 1.499 | −201.1 | 8.83 | 0.62 | 15.08 |
| 3 | 2.496 | −120.4 | 5.57 | 0.24 | 10.29 |
| 4 | 3.489 | 85.73 | 3.91 | 0.10 | 7.78 |
| 5 | 4.477 | 66.41 | 2.92 | 0.02 | 6.22 |
| 6 | 5.457 | −54.05 | 2.26 | 0.01 | 5.17 |
| 7 | 6.429 | 45.44 | 1.79 | 0 | 4.41 |
| 8 | 7.392 | 39.09 | 1.46 | 0 | 3.83 |
| 9 | 8.343 | −34.19 | 1.19 | 0 | 3.38 |
| 10 | 9.281 | −30.29 | 0.99 | 0 | 3.01 |
| Seismic Wave | uA | |||||
|---|---|---|---|---|---|---|
| 4 | 7 | 4 | 7 | 4 | 7 | |
| E1 | 0.39 | 0.05 | 3.69 | 0.6 | 3.69 | 0.61 |
| E2 | 0.61 | 0.06 | 4.81 | 0.60 | 23.65 | 4.65 |
| E3 | 0.26 | 0.03 | 2.23 | 0.31 | 12.98 | 2.83 |
| Mean value | 0.42 | 0.047 | 3.58 | 0.51 | 13.44 | 2.69 |
| N | f/(Hz) | em | euA | euB | euC | euD | euE | euF | eaA | eaB | eaC | eaD | eaE | eaF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 22 | 1.88 | 12.69 | 7.95 | 17.60 | 13.61 | 8.00 | 7.85 | 6.47 | 31.57 | 31.78 | 24.45 | 17.49 | 0.21 | 0.22 |
| 63 | 3.09 | 9.86 | 2.12 | 5.85 | 3.85 | 3.36 | 3.04 | 0.65 | 26.25 | 31.11 | 20.41 | 1.25 | 7.64 | 11.92 |
| 100 | 4.02 | 7.86 | 1.25 | 2.87 | 2.16 | 0.08 | 0.06 | 0.38 | 13.81 | 13.23 | 8.32 | 4.39 | 8.59 | 13.12 |
| 135 | 4.58 | 6.65 | 0.24 | 0.56 | 0.33 | 0.14 | 0.09 | 0.13 | 15.16 | 15.83 | 10.34 | 9.95 | 9.75 | 9.02 |
| 194 | 5.57 | 5.94 | 0.24 | 0.51 | 0.40 | 0.09 | 0.04 | 0.04 | 14.37 | 14.26 | 9.88 | 9.08 | 4.29 | 5.72 |
| 243 | 6.09 | 5.40 | 0.01 | 0.16 | 0.01 | 0.03 | 0.02 | 0.04 | 7.09 | 10.67 | 3.74 | 2.63 | 4.73 | 6.35 |
| 277 | 6.50 | 5.38 | 0.06 | 0.14 | 0.07 | 0.01 | 0.02 | 0.04 | 10.08 | 9.54 | 6.98 | 2.53 | 4.49 | 6.74 |
| 317 | 6.89 | 4.95 | 0.06 | 0.10 | 0.10 | 0.03 | 0.01 | 0.02 | 9.65 | 8.02 | 7.05 | 4.17 | 4.15 | 5.75 |
| 500 | 8.37 | 4.43 | 0.05 | 0.10 | 0.07 | 0.01 | 0.02 | 0.02 | 6.59 | 6.32 | 4.16 | 0.73 | 3.56 | 4.08 |
| 1000 | 10.54 | 3.91 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 4.20 | 4.19 | 3.28 | 1.38 | 0.99 | 1.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Yong, Y.; Li, X.; Pan, D. A Fast Method for the Acceleration Response Analysis of Two-Dimensional Sites Under Seismic Excitations. Appl. Sci. 2025, 15, 6082. https://doi.org/10.3390/app15116082
Chen H, Yong Y, Li X, Pan D. A Fast Method for the Acceleration Response Analysis of Two-Dimensional Sites Under Seismic Excitations. Applied Sciences. 2025; 15(11):6082. https://doi.org/10.3390/app15116082
Chicago/Turabian StyleChen, Hongkai, Yi Yong, Xueju Li, and Danguang Pan. 2025. "A Fast Method for the Acceleration Response Analysis of Two-Dimensional Sites Under Seismic Excitations" Applied Sciences 15, no. 11: 6082. https://doi.org/10.3390/app15116082
APA StyleChen, H., Yong, Y., Li, X., & Pan, D. (2025). A Fast Method for the Acceleration Response Analysis of Two-Dimensional Sites Under Seismic Excitations. Applied Sciences, 15(11), 6082. https://doi.org/10.3390/app15116082






