Fracture Evolution Mechanisms and Roof Failure Assessment in Shallow-Buried Soft Coal Seams Under Fully Mechanized Caving Mining
Abstract
1. Introduction
2. Materials and Methods
2.1. General Situation of the Project
2.2. Mechanical Model and Fracture Analysis of the Roof After Coal Seam Mining
2.2.1. Basic Assumptions
- (1)
- Given that the length of the main roof’s suspended section along the working face direction surpasses 13 times its thickness, it is reasonable to model this structural element as a 1 m wide beam element aligned with the working face direction.
- (2)
- The strata above and below the main roof are regarded as elastic foundation layers conforming to the Winkler elastic foundation theory, while the main roof is modeled as a beam element supported by this dual elastic foundation framework.
- (3)
- It is assumed in the model that deformation compatibility exists without shear displacement at the interface between the main roof and the elastic foundation. This assumption specifically addresses scenarios with significant stiffness contrasts between the primary roof and the overlying/underlying weak strata (immediate roof/coal seam) in the study area. In practical conditions where weak interlayers exist, shear slippage may induce stress concentration at the roof edges, potentially exacerbating fracture risks.
- (4)
- The overburden load is simplified as a uniformly distributed stress field, omitting the mining-induced stress arching effect. This simplification is valid for shallow-buried coal seams (burial depth: 120–150 m, where stress arching remains underdeveloped) but requires modification for deep mining applications. Given this study’s focus on shallow-buried, weakly cemented strata, the uniform loading assumption satisfies engineering accuracy requirements. The stress arching effect will be explicitly addressed in subsequent comparative studies of deep versus shallow coal seam mechanics.
2.2.2. Establishment and Solution of the Mechanical Model
- (1)
- Differential Equation of Main Roof Deflection
- (2)
- Model Boundary Conditions
- (3)
- Model Solution Process
2.2.3. Analysis of the Roof Fracture Location
2.3. Establishment of the Numerical Model
3. Results and Discussion
3.1. The Fracture Law of the Overlying Rock
3.2. The Time Evolution Law of Vertical Displacement of Overlying Rock Strata
3.3. Analysis of Ground Surface Subsidence
3.4. Stage Evolution of Overlying Rock Fracture
4. Conclusions
- (1)
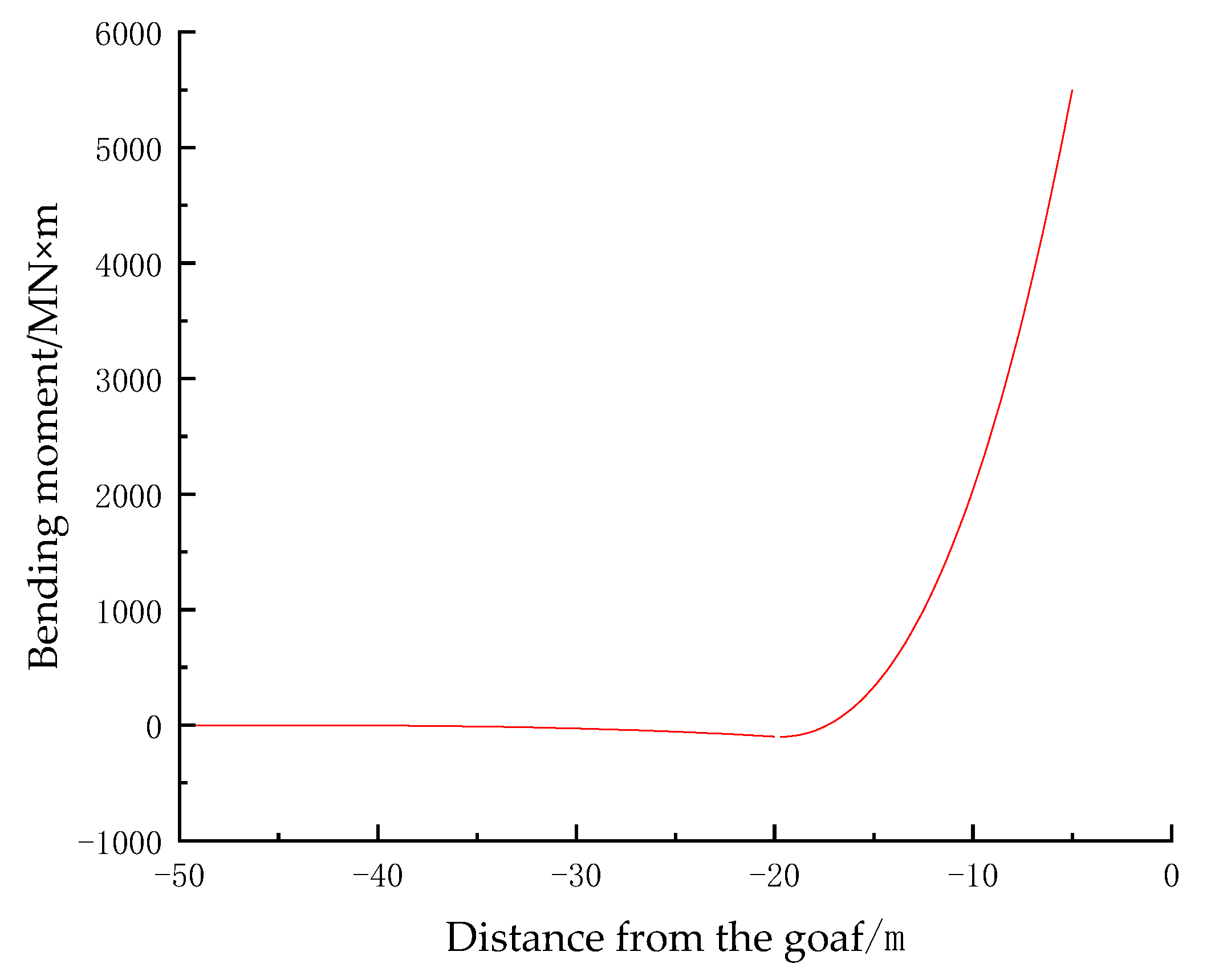
- Based on the actual mining situation, assuming the main roof is fixed by the upper and lower elastic rock layers, an elastic foundation boundary model is established for this mechanical configuration. A section behind the working face is selected as the research object. A mechanical model of the action of the roof on the underlying coal and rock strata after coal seam mining is established. Through analysis, it is concluded that the fracture position of the main roof is at a location 0.5 m away from the edge of the goaf.
- (2)
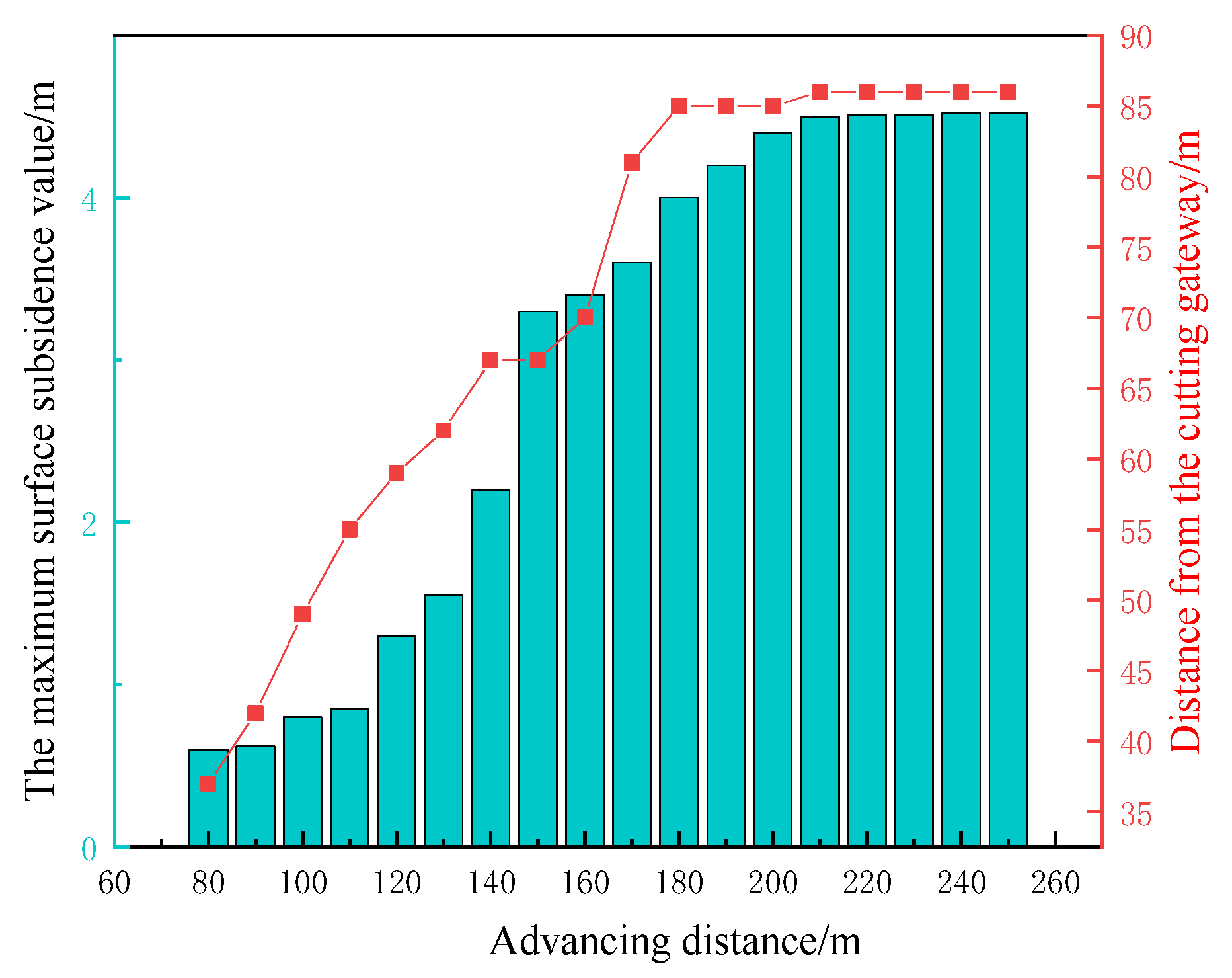
- During the entire process of advancing the working face, the time evolution law of vertical displacement exhibits three distinct configurations: evolving from an early-stage “rectangle–trapezoid” distribution, transitioning to a quasi-hyperbolic pattern, and finally forming a trapezoidal field upon reaching the surface influence threshold, which tends to stabilize when the advancement reaches 250 m.
- (3)
- Surface subsidence characteristics initiate when the working face advances to 80 m, consistent with field observations; the subsidence basin develops smoothly into a trapezoidal shape, with maximum displacement of 4.57 m and an influence radius approximately twice the mining height.
- (4)
- This study demonstrates that in shallowly buried weak rock strata scenarios, surface impacts manifest with accelerated temporal characteristics owing to enhanced strata–ground coupling. The rapid goaf backfilling process effectively reduces peak subsidence magnitudes through timely stress redistribution. Roof fracturing initiates overburden delamination and collapse, establishing direct correlations between surface settlement patterns and the spatial extent of overlying strata failure along the advancement direction. Numerical simulation of progressive roof fracturing mechanisms enables predictive modeling of subsidence trough morphology, providing critical guidance for surface infrastructure protection strategies. Analysis of roof bending moment distributions under varying advancement step distances facilitates optimization of mining parameters, achieving equilibrium between operational safety and extraction efficiency. Notable limitations arise from the PFC model’s simplification of material heterogeneity—actual geological sequences containing interbedded weak layers may significantly alter fracture propagation pathways. Future investigations should incorporate stochastic mechanical parameter distributions and validate numerical predictions through field monitoring data integration, particularly regarding time-dependent deformation characteristics and fracture network evolution patterns.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kang, H.; Xu, G.; Wang, B.; Wu, Y.; Jiang, P.; Pan, J.; Ren, H.; Zhang, Y.; Pang, Y. Forty years of development and prospects of underground coal mining and strata control technologies in China. J. Min. Strat. Control. Eng. 2019, 1, 013501. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Q.; Sun, Y.; Cai, W.; Zhang, J.; Chen, C. Analysis of the stability of the surrounding rock structure in gob-side entry driving in shallow buried and thin bedrock. J. Min. Saf. Eng. 2020, 37, 647–654. [Google Scholar] [CrossRef]
- Yang, J.; Wu, Z.; Li, H.; Zhang, B.; Ji, W. Simulation test of water and sand burst in shallow and thin bedrock face and analysis of influencing factors. Coal Sci. Technol. 2021, 49, 1–8. [Google Scholar] [CrossRef]
- Wang, J.; Xu, J.; Yang, S.; Wang, Z. Development of strata movement and its control in underground mining: In memory of 40 years of Voussoir Beam Theory proposed by Academician Minggao Qian. Coal Sci. Technol. 2023, 51, 80–94. [Google Scholar] [CrossRef]
- Kwasniewski, M.; Lasek, S. Numerical analysis of methane migration from floor strata to a longwall face. Gór. Geoinżynieria 2007, 31, 307–322. [Google Scholar]
- Tomiczek, K. A brief analysis of behaviour possibility of a jointed rock mass near to longwall excavation face simulation using Distinct Elements Method (DEM) in the context of the Beam on Elastic Foundation (BEF) theory. In Proceedings of the 5th International Scientific Conference on Civil Engineering-Infrastructure-Mining, Cracow, Poland, 17–18 January 2019; Volume 106. [Google Scholar] [CrossRef]
- Sun, B.; Yuan, L.; Zhang, P.; Wu, R. Experimental study on photoelectric sensing of overburden movement and separation evolution in the stope under massive thick conglomerate. J. China Univ. Min. Technol. 2024, 53, 977–992. [Google Scholar] [CrossRef]
- Sun, J.; Cao, Z.; Wang, H.; Sun, B.; Li, Z. Full—Cycle overburden movement law of high—Stage fully—Mechanized top—Coal caving face in steeply inclined and extra—Thick coal seam. Min. Res. Dev. 2024, 44, 56–63. [Google Scholar] [CrossRef]
- Chang, Y.; Xue, J.; Zheng, L.; Ma, J.; Gao, X.; Zhu, Y. Research on the movement and failure laws of overlying strata in a fully—Mechanized top—Coal caving face with shallow—Buried, thick and hard bedrock. Coal Eng. 2024, 56, 144–151. [Google Scholar]
- Li, J.; Wang, W.; Wang, C.; Wu, X. Research on the mechanism and control of slope instability and sliding induced by overburden movement during side—Coal mining. Coal Sci. Technol. 2025, 53, 127–143. Available online: http://kns.cnki.net/kcms/detail/11.2402.td.20240407.1606.001.html (accessed on 13 February 2025).
- Li, B.; Chen, J.; He, B.; Pi, G. Research on the overburden movement and surface damag e characteristics of pillarless mining in shallow—Buried ultra—Thin coal seams. Coal Eng. 2024, 56, 104–111. [Google Scholar]
- Wang, D.; Zhang, Y.; Xie, P.; Huang, B.; Qu, L.; Wu, S.; Lin, W.; Yang, H. Research on the overburden movement law in the pseudo—Inclined stope of steeply inclined medium—Thick coal seams. Coal Eng. 2023, 55, 76–80. [Google Scholar]
- Nan, H.; Wang, Z. Research on the overburden movement and mine pressure behavior law of the fully—Mechanized top—Coal caving face under the disturbance of the upper coal seam. Saf. Coal Mines 2023, 54, 133–141. [Google Scholar] [CrossRef]
- Wu, Z.; Sun, Q.; Wang, Y. Evolution Laws of Water-Flowing Fracture Zone and Mine Pressure in Mining Shallow-Buried, Hard, and Extra-Thick Coal Seams. Appl. Sci. 2024, 14, 2915. [Google Scholar] [CrossRef]
- Wang, S.R.; Wu, X.G.; Zhao, Y.H.; Hagan, P. Mechanical Performances of Pressure Arch in Thick Bedrock during Shallow Coal Mining. Geofluids 2018, 2018, 2419659. [Google Scholar] [CrossRef]
- Xu, Z.H.; Li, Q.S.; Li, X.B. Overburden Migration and Failure Characteristics in Mining Shallow Buried Coal Seam with Thick Loose Layer. Adv. Mater. Sci. Eng. 2020, 2020, 9024751. [Google Scholar] [CrossRef]
- Huang, Q.; Du, J.; Hou, E.; Yang, F. Research on overburden and ground surface cracks distribution and formation mechanism in shallow coal seams group mining. Caikuang Yu Anquan Gongcheng Xuebao/J. Min. Saf. Eng. 2019, 36, 7–15. [Google Scholar]
- Zheng, J.; Tian, L.; Li, Y.; Xu, L.; Li, X.; Yu, F.; Wu, Z.; Sun, S. Research on the stability of composite roof in shallow -buried fully—Mechanized mining face and key monitoring technologies. Coal Eng. 2024, 56, 46–54. [Google Scholar]
- Lv, K.; He, F.; Xu, X.; Zhai, W.; Qin, B. Fracture characteristics and stability analysis of the main roof structure with special—Shaped load—Elastic foundation. Chin. J. Rock Mech. Eng. 2023, 42, 930–947. [Google Scholar] [CrossRef]
- Liu, H.; Luo, Z.; Han, Z.; Han, Z.; Chen, X.; Peng, J. Study on evolution law of overburden fracture in fully-mechanized top-coal caving face with large mining height in thick coal seam. Coal Sci. Technol. 2024, 52, 1–12. [Google Scholar] [CrossRef]
- Jiao, F.; Zhang, X.; Fan, Y. Research on the law of surface movement and deformation in layered paste backfill mining of thick coal seams. Coal Technol. 2024, 43, 24–28. [Google Scholar] [CrossRef]
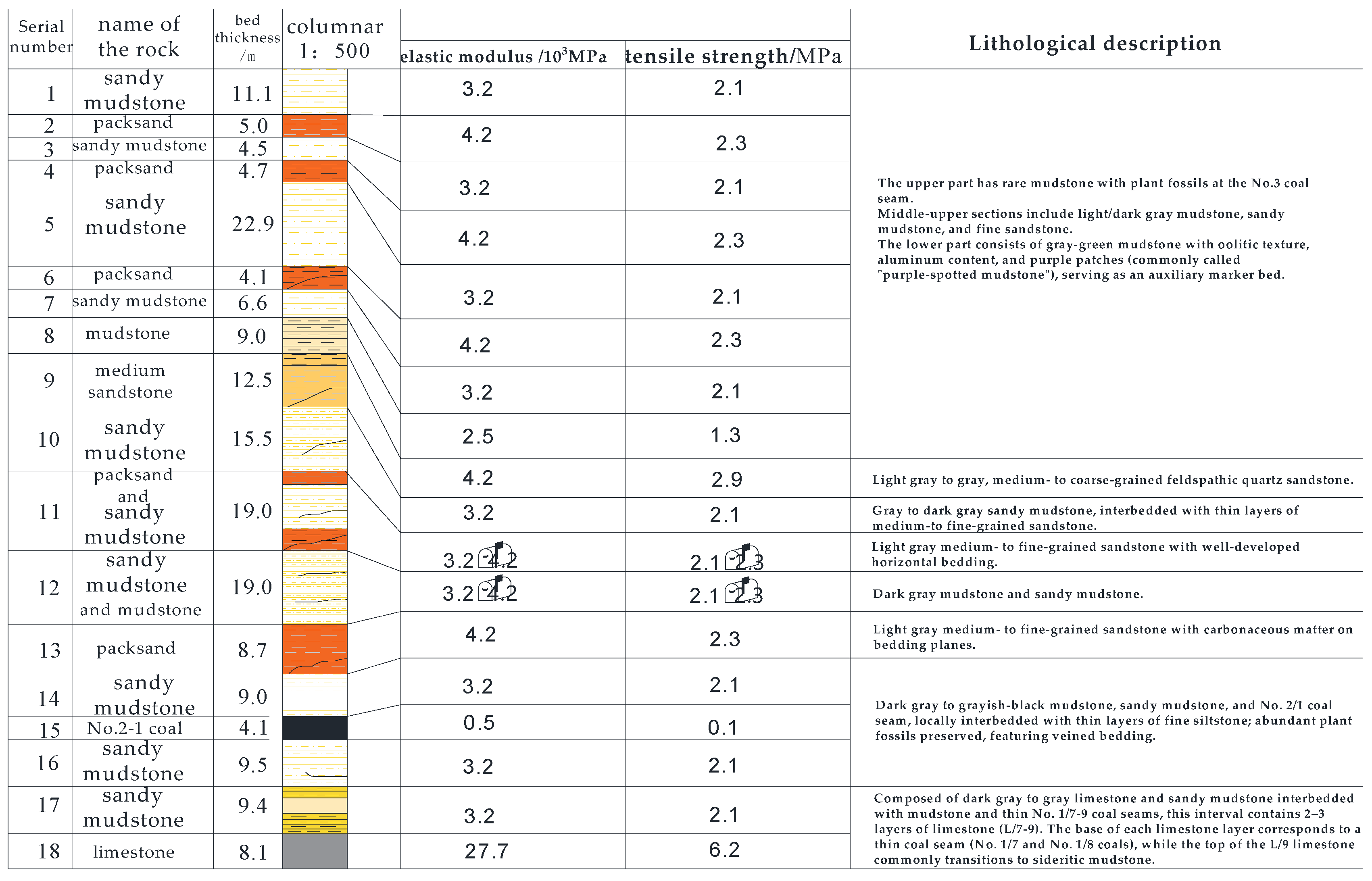






| Lithology | Elastic Modulus /GPa | Tensile Strength /MPa | Cohesion /MPa | Internal Friction Angle /° | Poisson Ratio |
|---|---|---|---|---|---|
| Sandy mudstone | 3.2 | 2.1 | 3.5 | 25 | 0.31 |
| Packsand | 4.2 | 2.3 | 4.4 | 22 | 0.24 |
| Mudstone | 2.5 | 1.3 | 2.2 | 24 | 0.17 |
| Medium sandstone | 4.2 | 2.9 | 5.9 | 26 | 0.27 |
| No. 2-1 coal | 0.5 | 0.1 | 1.5 | 22 | 0.24 |
| Limestone | 27.7 | 6.2 | 45.8 | 12.6 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Fan, X.; Hu, G.; Li, S.; Zhu, K. Fracture Evolution Mechanisms and Roof Failure Assessment in Shallow-Buried Soft Coal Seams Under Fully Mechanized Caving Mining. Appl. Sci. 2025, 15, 6036. https://doi.org/10.3390/app15116036
Yang Y, Fan X, Hu G, Li S, Zhu K. Fracture Evolution Mechanisms and Roof Failure Assessment in Shallow-Buried Soft Coal Seams Under Fully Mechanized Caving Mining. Applied Sciences. 2025; 15(11):6036. https://doi.org/10.3390/app15116036
Chicago/Turabian StyleYang, Yongkang, Xiaolin Fan, Guoyou Hu, Shuai Li, and Konghao Zhu. 2025. "Fracture Evolution Mechanisms and Roof Failure Assessment in Shallow-Buried Soft Coal Seams Under Fully Mechanized Caving Mining" Applied Sciences 15, no. 11: 6036. https://doi.org/10.3390/app15116036
APA StyleYang, Y., Fan, X., Hu, G., Li, S., & Zhu, K. (2025). Fracture Evolution Mechanisms and Roof Failure Assessment in Shallow-Buried Soft Coal Seams Under Fully Mechanized Caving Mining. Applied Sciences, 15(11), 6036. https://doi.org/10.3390/app15116036






