Analyzing and Predicting the Agronomic Effectiveness of Fertilizers Derived from Food Waste Using Data-Driven Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Experiments About Kitchen Waste Recycling as Fertilizer for Plant Growth
2.1.1. In-House Experimental Procedures
- In the first scenario, effective microorganisms (EM) were added directly to the model waste.
- In the second scenario, the waste was left to decay for 12 days before introducing a double dose of EM.
- In the third and fourth scenarios, the waste was sterilized after 12 days; however, only the third scenario included EM addition.
- In the final scenario, the waste was allowed to decay and was sterilized but not inoculated with EM.
2.1.2. External Investigations
2.2. Dataset Preparation and Processing
- PY: Represented in kilograms of total solids per hectare (kg/ha), PY reflects the agricultural output per unit area.
- IENU: Measured in kilograms of nitrogen per hectare (kg N/ha), IENU evaluates the effectiveness of nitrogen use in supporting crop growth.
- Three explanatory features were analyzed:
- NC: The nitrogen percentage in fertilizer affects crop growth and nitrogen efficiency.
- T: The crop growth duration (in days) influences nutrient uptake and development.
- D: The fertilizer amount applied per hectare impacts yield outcomes.
2.3. Machine Learning Modeling Approach
- GB:
- CB:
- XGB:
- RF:
2.4. Evaluation Metrics
3. Results and Discussion
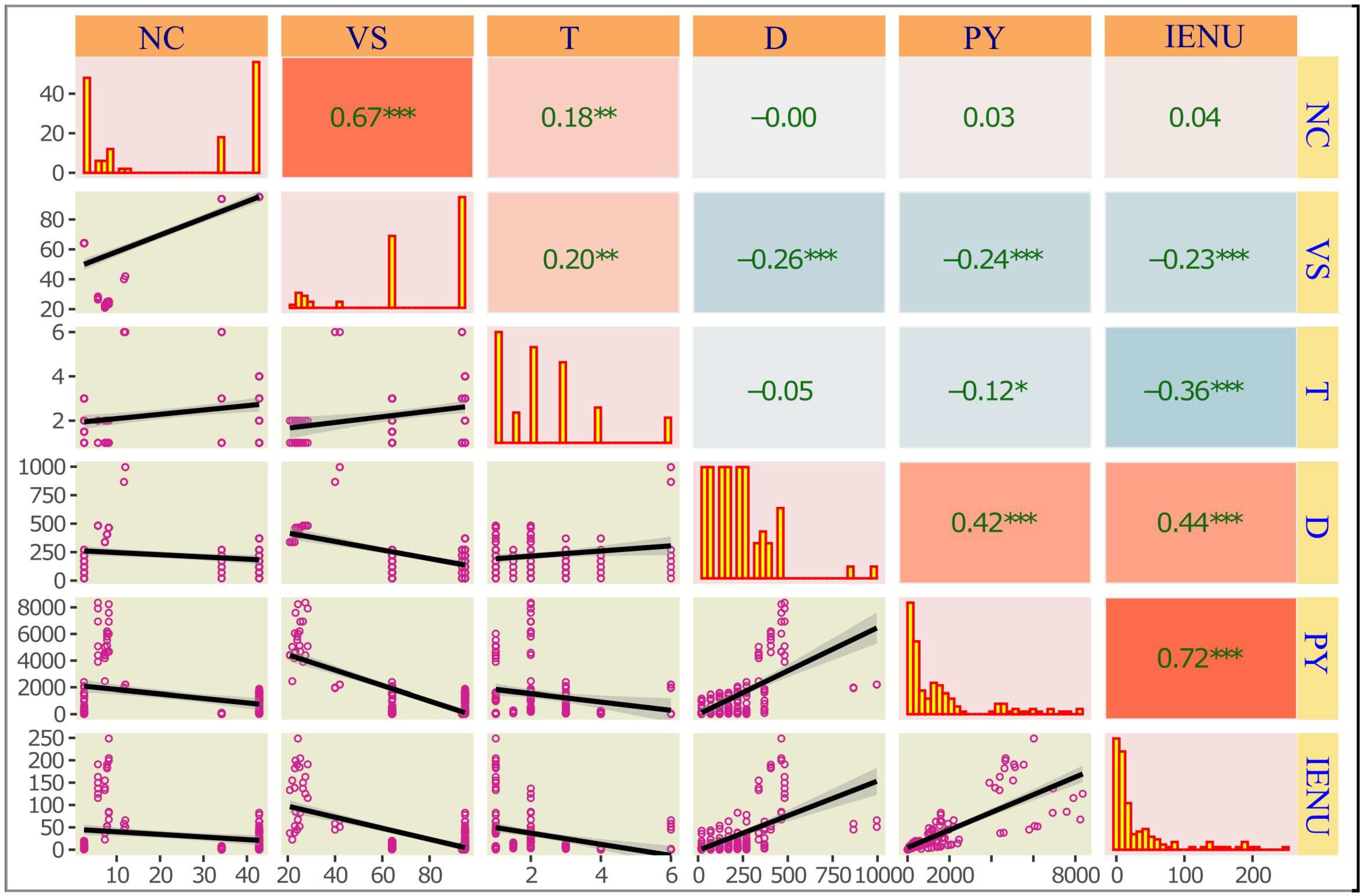
3.1. Exploratory Data Analysis
3.2. Prediction of Plant Yield
3.2.1. Linear Regression
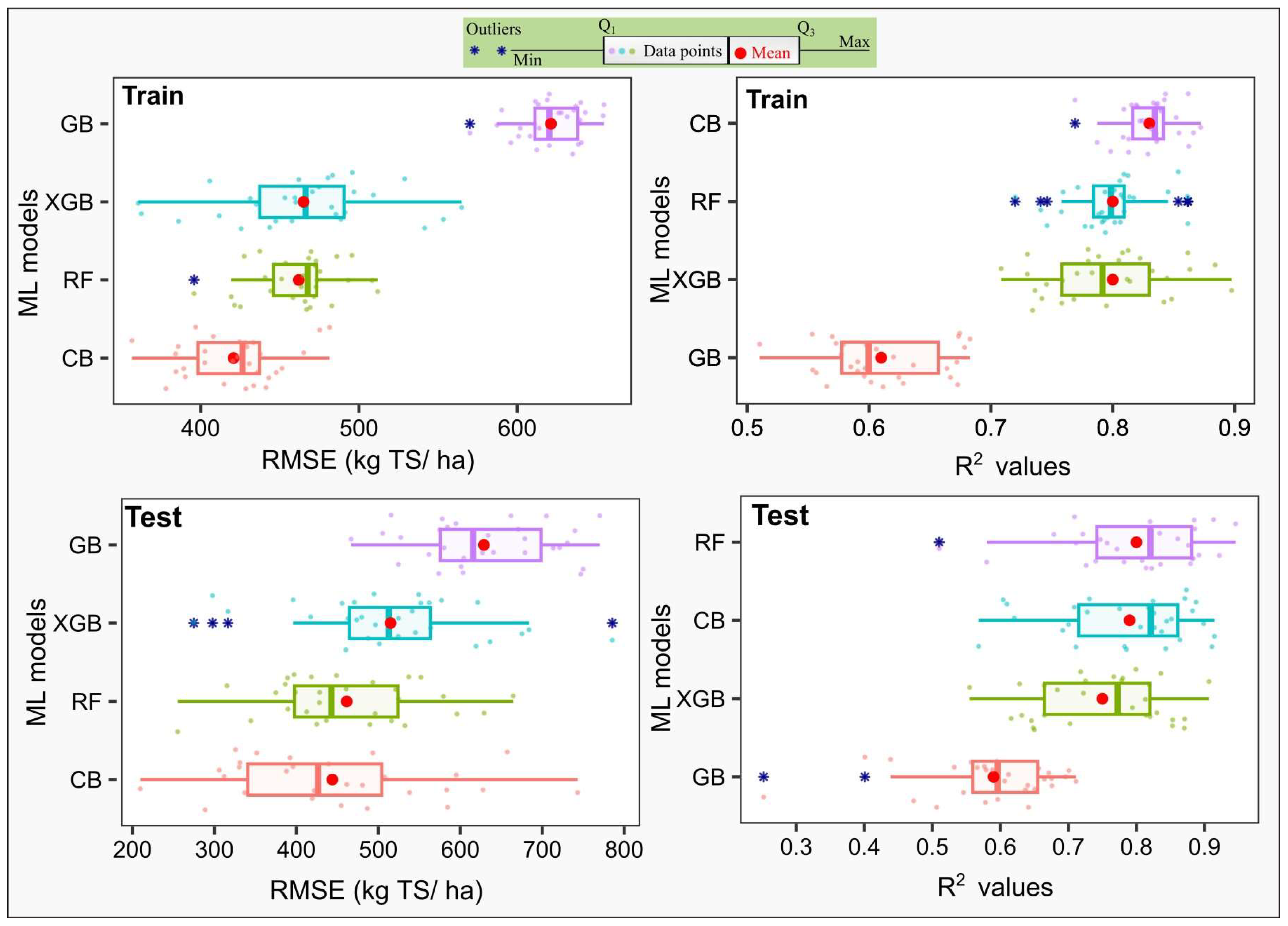
3.2.2. Machine Learning
3.3. Prediction of IENU
3.3.1. Linear Regression
3.3.2. Machine Learning
4. Limitations and Practical Applications
4.1. Limitations
4.2. Practical Applications
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Álvarez Salas, M.; Sica, P.; Rydgård, M.; Sitzmann, T.J.; Nyang’au, J.O.; El Mahdi, J.; Moshkin, E.; de Castro e Silva, H.L.; Chrysanthopoulos, S.; Kopp, C.; et al. Current challenges on the widespread adoption of new bio-based fertilizers: Insights to move forward toward more circular food systems. Front. Sustain. Food Syst. 2024, 8, 1386680. [Google Scholar] [CrossRef]
- Steffens, M.; Bünemann, E.K. Quality of bio-based fertilizers is decisive for improving soil quality in Europe—A meta-analysis. Soil Use Manag. 2025, 41, e70012. [Google Scholar] [CrossRef]
- O’Connor, J.; Hoang, S.A.; Bradney, L.; Rinklebe, J.; Kirkham, M.B.; Bolan, N.S. Value of dehydrated food waste fertiliser products in increasing soil health and crop productivity. Environ. Res. 2022, 204, 111927. [Google Scholar] [CrossRef] [PubMed]
- Cheong, J.C.; Lee, J.T.E.; Lim, J.W.; Song, S.; Tan, J.K.N.; Chiam, Z.Y.; Yap, K.Y.; Lim, E.Y.; Zhang, J.; Tan, H.T.W.; et al. Closing the food waste loop: Food waste anaerobic digestate as fertilizer for the cultivation of the leafy vegetable, xiao bai cai (Brassica rapa). Sci. Total Environ. 2020, 715, 136789. [Google Scholar] [CrossRef]
- Gao, S.; Lu, D.; Qian, T.; Zhou, Y. Thermal hydrolyzed food waste liquor as liquid organic fertilizer. Sci. Total Environ. 2021, 775, 145786. [Google Scholar] [CrossRef]
- The World Counts. Global Challenges. 2022. Available online: https://www.theworldcounts.com/challenges/people-and-poverty/hunger-and-obesity/food-waste-statistics (accessed on 15 December 2024).
- FAO. “Energy-Smart” Food for People and Climate: Issue Paper; Food and Agriculture Organization of the United Nations: Rome, Italy, 2011. [Google Scholar]
- Elgarahy, A.M.; Eloffy, M.G.; Alengebawy, A.; El-Sherif, D.M.; Gaballah, M.S.; Elwakeel, K.Z.; El-Qelish, M. Sustainable management of food waste; pre-treatment strategies, techno-economic assessment, bibliometric analysis, and potential utilizations: A systematic review. Environ. Res. 2023, 225, 115558. [Google Scholar] [CrossRef]
- Razouk, A.; Tiganescu, E.; von Glahn, A.J.; Abdin, A.Y.; Nasim, M.J.; Jacob, C. The future in the litter bin—Bioconversion of food waste as driver of a circular bioeconomy. Front. Nutr. 2024, 11, 1325190. [Google Scholar] [CrossRef]
- Meng, X.; Zeng, B.; Wang, P.; Li, J.; Cui, R.; Ren, L. Food waste anaerobic biogas slurry as fertilizer: Potential salinization on different soil layer and effect on rhizobacteria community. Waste Manag. 2022, 144, 490–501. [Google Scholar] [CrossRef]
- Song, S.; Lim, J.W.; Lee, J.T.E.; Cheong, J.C.; Hoy, S.H.; Hu, Q.; Tan, J.K.N.; Chiam, Z.; Arora, S.; Lum, T.Q.H.; et al. Food-waste anaerobic digestate as a fertilizer: The agronomic properties of untreated digestate and biochar-filtered digestate residue. Waste Manag. 2021, 136, 143–152. [Google Scholar] [CrossRef]
- Siddiqui, Z.; Hagare, D.; Jayasena, V.; Swick, R.; Rahman, M.M.; Boyle, N.; Ghodrat, M. Recycling of food waste to produce chicken feed and liquid fertiliser. Waste Manag. 2021, 131, 386–393. [Google Scholar] [CrossRef]
- Kuligowski, K.; Konkol, I.; Świerczek, L.; Chojnacka, K.; Cenian, A.; Szufa, S. Evaluation of Kitchen Waste Recycling as Organic N-Fertiliser for Sustainable Agriculture under Cool and Warm Seasons. Sustainability 2023, 15, 7997. [Google Scholar] [CrossRef]
- Yang, X.; Nguyen, X.C.; Tran, Q.B.; Huyen Nguyen, T.T.; Ge, S.; Nguyen, D.D.; Nguyen, V.T.; Le, P.C.; Rene, E.R.; Singh, P.; et al. Machine learning-assisted evaluation of potential biochars for pharmaceutical removal from water. Environ. Res. 2022, 214, 113953. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, X.C.; Bui, V.K.H.; Cho, K.H.; Hur, J. Practical application of machine learning for organic matter and harmful algal blooms in freshwater systems: A review. Crit. Rev. Environ. Sci. Technol. 2023, 54, 953–975. [Google Scholar] [CrossRef]
- Balasubramanian, P.; Prabhakar, M.R.; Liu, C.; Li, F.; Nguyen, X.C.; Nageshwari, K.; Zhang, Z.; Zhang, P. Predictive Capability of Phosphate Recovery from Wastewater Using a Rough Set Machine Learning Model. ACS EST Eng. 2024, 4, 2449–2459. [Google Scholar] [CrossRef]
- Nguyen, X.C.; Ly, Q.V.; Peng, W.; Nguyen, V.H.; Nguyen, D.D.; Tran, Q.B.; Huyen Nguyen, T.T.; Sonne, C.; Lam, S.S.; Ngo, H.H.; et al. Vertical flow constructed wetlands using expanded clay and biochar for wastewater remediation: A comparative study and prediction of effluents using machine learning. J. Hazard. Mater. 2021, 413, 125426. [Google Scholar] [CrossRef]
- Li, X.; Dai, W.; Gao, H.; Xu, W.; Wei, X. Correlation between Grain Yield and Fertilizer Use Based on Back Propagation Neural Network. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2017, 48, 186–192. [Google Scholar] [CrossRef]
- Wang, F.; Dong, Z.; Wu, Z.; Fang, K. Optimization of maize planting density and fertilizer application rate based on BP neural network. Trans. Chin. Soc. Agric. Eng. 2017, 33, 92–99. [Google Scholar] [CrossRef]
- Meng, L.; Liu, H.; Ustin, S.L.; Zhang, X. Predicting maize yield at the plot scale of different fertilizer systems by multi-source data and machine learning methods. Remote Sens. 2021, 13, 3760. [Google Scholar] [CrossRef]
- Thai, T.H.; Omari, R.A.; Barkusky, D.; Bellingrath-Kimura, S.D. Statistical analysis versus the m5p machine learning algorithm to analyze the yield of winter wheat in a long-term fertilizer experiment. Agronomy 2020, 10, 1779. [Google Scholar] [CrossRef]
- Santa-María, G.E.; Moriconi, J.I.; Oliferuk, S. Internal efficiency of nutrient utilization: What is it and how to measure it during vegetative plant growth? J. Exp. Bot. 2015, 66, 3011–3018. [Google Scholar] [CrossRef]
- Rochester, I.J. Assessing internal crop nitrogen use efficiency in high-yielding irrigated cotton. Nutr. Cycl. Agroecosystems 2011, 90, 147–156. [Google Scholar] [CrossRef]
- Kuligowski, K.; Konkol, I.; Świerczek, L.; Woźniak, A.; Cenian, A. Conversion of Kitchen Waste into Sustainable Fertilizers: Comparative Effectiveness of Biological, Microbial, and Thermal Treatments in a Ryegrass Growth Trial. Appl. Sci. 2025, 15, 5281. [Google Scholar] [CrossRef]
- Lee, J.-J.; Park, R.-D.; Kim, Y.-W.; Shim, J.-H.; Chae, D.-H.; Rim, Y.-S.; Sohn, B.-K.; Kim, T.-H.; Kim, K.-Y. Effect of food waste compost on microbial population, soil enzyme activity and lettuce growth. Bioresour. Technol. 2004, 93, 21–28. [Google Scholar] [CrossRef]
- Tampio, E.; Salo, T.; Rintala, J. Agronomic characteristics of five different urban waste digestates. J. Environ. Manag. 2016, 169, 293–302. [Google Scholar] [CrossRef] [PubMed]
- Gondek, K.; Filipek-Mazur, B. Accumulation of microelements in oat biomass and their availability in soil fertilised with compost of plant wastes. Acta Agrophysica 2006, 8, 579–590. (In Polish) [Google Scholar]
- Keeling, A.A.; Griffiths, B.S.; Ritz, K.; Myers, M. Effects of compost stability on plant growth, microbiological parameters and nitrogen availability in media containing mixed garden-waste compost. Bioresour. Technol. 1995, 54, 279–284. [Google Scholar] [CrossRef]
- Cordovil, C.M.; Cabral, F.; Coutinho, J. Potential mineralization of nitrogen from organic wastes to ryegrass and wheat crops. Bioresour. Technol. 2007, 98, 3265–3268. [Google Scholar] [CrossRef]
- Gondek, K.; Filipek-Mazur, B. Fertilization Value of Green Waste Compost from Krakow. Probl. Books Prog. Agric. Sci. 2003, 494, 113–121. [Google Scholar]
- Jasiewicz, C.; Antonkiewicz, J.; Baran, A. The Effect of Fertilization on Yielding and Nitrogen Content in Tall Oat Grass. Probl. Books Prog. Agric. Sci. 2006, 513, 149. (In Polish) [Google Scholar]
- Wiater, J. The Sequent Impact of Organic Wastes on Yielding and Chemical Composition of Winter Whea. Probl. Books Prog. Agric. Sci. 2003, 494, 525–532. [Google Scholar]
- Martyniak, D.; Prokopiuk, K.; Żurek, G.; Rybka, K. Measuring Fluorescence as a Means to Evaluate the Physiological Reaction to Growth Retardant Applied to Manage Turf. Agronomy 2022, 12, 1776. [Google Scholar] [CrossRef]
- Jasiewicz, C.; Antonkiewicz, J. The Effect of a Dose and Kind of Fertilizer on Maize Nitrogen Concentration. In Proceedings of the Environmental Pollution by Nitrogen, Olecko, Poland; 2005. Date not available publication in Polish. [Google Scholar]
- Jamison, J.; Khanal, S.K.; Nguyen, N.H.; Deenik, J.L. Assessing the Effects of Digestates and Combinations of Digestates and Fertilizer on Yield and Nutrient Use of Brassica juncea (Kai Choy). Agronomy 2021, 11, 509. [Google Scholar] [CrossRef]
- Sullivan, D.M.; Bary, A.I.; Thomas, D.R.; Fransen, S.C.; Cogger, C.G. Food Waste Compost Effects on Fertilizer Nitrogen Efficiency, Available Nitrogen, and Tall Fescue Yield. Soil Sci. Soc. Am. J. 2002, 66, 154–161. [Google Scholar] [CrossRef]
- Simon, F.; Junior, A.; Loss, A.; Malinowski, C.; Matias, M. Effects of food waste digested materials on Lactuva sativa growth and soil composition. Int. J. Environ. Sci. Technol. 2022, 20, 9013–9028. [Google Scholar] [CrossRef]
- Messiga, A.J.; Sharifi, M.; Munroe, S. Combinations of cover crop mixtures and bio-waste composts enhance biomass production and nutrients accumulation: A greenhouse study. Renew. Agric. Food Syst. 2016, 31, 507–515. [Google Scholar] [CrossRef]
- Sung, J.; Kim, W.; Oh, T.-K.; So, Y.-S. Nitrogen (N) use efficiency and yield in rice under varying types and rates of N source: Chemical fertilizer, livestock manure compost and food waste-livestock manure compost. Appl. Biol. Chem. 2023, 66, 4. [Google Scholar] [CrossRef]
- Dragicevic, I.; Sogn, T.A.; Eich-Greatorex, S. Recycling of Biogas Digestates in Crop Production—Soil and Plant Trace Metal Content and Variability. Front. Sustain. Food Syst. 2018, 2, 45. [Google Scholar] [CrossRef]
- Asagi, N.; Minamide, K.; Uno, T.; Saito, M.; Ito, T. Acidulocompost, a food waste compost with thermophilic lactic acid fermentation: Its effects on potato production and weed growth. Plant Prod. Sci. 2016, 19, 132–144. [Google Scholar] [CrossRef]
- Gondek, K.; Filipek-Mazur, B. Agro-chemical assessment of fertilizer value of composts of various origin. Acta Agrophysica 2005, 5, 271–282. (In Polish) [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Du, Z.; Yang, L.; Zhang, D.; Cui, T.; He, X.; Xiao, T.; Xie, C.; Li, H. Corn variable-rate seeding decision based on gradient boosting decision tree model. Comput. Electron. Agric. 2022, 198, 107025. [Google Scholar] [CrossRef]
- Quinlan, J.R. Combining instance-based and model-based learning. In Proceedings of the Tenth International Conference on International Conference on Machine Learning, Amherst, MA, USA, 13–19 July 1993; pp. 236–243. [Google Scholar]
- Quinlan, J.R. Learning with continuous classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, Tasmania, 16–18 November 1992; pp. 343–348. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013; pp. 101–139. [Google Scholar]
- Nguyen, X.C.; Nguyen, T.T.H.; La, D.D.; Kumar, G.; Rene, E.R.; Nguyen, D.D.; Chang, S.W.; Chung, W.J.; Nguyen, X.H.; Nguyen, V.K. Development of machine learning—Based models to forecast solid waste generation in residential areas: A case study from Vietnam. Resour. Conserv. Recycl. 2021, 167, 105381. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Naghdyzadegan Jahromi, M.; Zand-Parsa, S.; Razzaghi, F.; Jamshidi, S.; Didari, S.; Doosthosseini, A.; Pourghasemi, H. Developing machine learning models for wheat yield prediction using ground-based data, satellite-based actual evapotranspiration and vegetation indices. Eur. J. Agron. 2023, 146, 126820. [Google Scholar] [CrossRef]
- Huber, F.; Yushchenko, A.; Stratmann, B.; Steinhage, V. Extreme Gradient Boosting for yield estimation compared with Deep Learning approaches. Comput. Electron. Agric. 2022, 202, 107346. [Google Scholar] [CrossRef]
- Islam, A.; Khair, I.; Ifty, R.A.; Hossain, S.; Arefin, M.N.; Abid, F.B.A. Bangladeshi Agricultural Product Forecasting Approach Using Permutation Driven Machine Learning Algorithm. In Proceedings of the 2022 International Conference on Recent Progresses in Science, Engineering and Technology (ICRPSET), Rajshahi, Bangladesh, 26–27 December 2022; pp. 1–6. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. In Selected Papers of Hirotugu Akaike; Parzen, E., Tanabe, K., Kitagawa, G., Eds.; Springer: New York, NY, USA, 1998; pp. 215–222. [Google Scholar]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Nguyen, X.C.; Nguyen, T.P.; Lam, V.S.; Le, P.C.; Vo, T.D.H.; Hoang, T.H.T.; Chung, W.J.; Chang, S.W.; Nguyen, D.D. Estimating ammonium changes in pilot and full-scale constructed wetlands using kinetic model, linear regression, and machine learning. Sci. Total Environ. 2024, 907, 168142. [Google Scholar] [CrossRef]
- Bernal, M.P.; Alburquerque, J.A.; Moral, R. Composting of animal manures and chemical criteria for compost maturity assessment. A review. Bioresour. Technol. 2009, 100, 5444–5453. [Google Scholar] [CrossRef] [PubMed]
- Gianico, A.; Gallipoli, A.; Montecchio, D.; Mininni, G. Land Application of Biosolids in Europe: Possibilities, Con-Straints and Future Perspectives. Water 2021, 13, 103. [Google Scholar] [CrossRef]
- Li, R.; Wang, J.J.; Zhang, Z.; Shen, F.; Zhang, G.; Qin, R.; Li, X.; Xiao, R. Nutrient transformations during composting of pig manure with bentonite. Bioresour. Technol. 2012, 121, 362–368. [Google Scholar] [CrossRef]
- Pantazi, X.E.; Moshou, D.; Alexandridis, T.; Whetton, R.L.; Mouazen, A.M. Wheat yield prediction using machine learning and advanced sensing techniques. Comput. Electron. Agric. 2016, 121, 57–65. [Google Scholar] [CrossRef]
- Rashid, M.; Bari, B.S.; Yusup, Y.; Kamaruddin, M.A.; Khan, N. A Comprehensive Review of Crop Yield Prediction Using Machine Learning Approaches with Special Emphasis on Palm Oil Yield Prediction. IEEE Access 2021, 9, 63406–63439. [Google Scholar] [CrossRef]
- Emamgholizadeh, S.; Parsaeian, M.; Baradaran, M. Seed yield prediction of sesame using artificial neural network. Eur. J. Agron. 2015, 68, 89–96. [Google Scholar] [CrossRef]
- Whetton, R.; Zhao, Y.; Shaddad, S.; Mouazen, A.M. Nonlinear parametric modelling to study how soil properties affect crop yields and NDVI. Comput. Electron. Agric. 2017, 138, 127–136. [Google Scholar] [CrossRef]
- Santos, L.B.; Gentry, D.; Tryforos, A.; Fultz, L.; Beasley, J.; Gentimis, T. Soybean yield prediction using machine learning algorithms under a cover crop management system. Smart Agric. Technol. 2024, 8, 100442. [Google Scholar] [CrossRef]
- van Klompenburg, T.; Kassahun, A.; Catal, C. Crop yield prediction using machine learning: A systematic literature review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- Lischeid, G.; Webber, H.; Sommer, M.; Nendel, C.; Ewert, F. Machine learning in crop yield modelling: A powerful tool, but no surrogate for science. Agric. For. Meteorol. 2022, 312, 108698. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, Z.; Luo, Y.; Zhang, L.; Zhang, J.; Li, Z.; Tao, F. Wheat yield predictions at a county and field scale with deep learning, machine learning, and google earth engine. Eur. J. Agron. 2021, 123, 126204. [Google Scholar] [CrossRef]
- Sharma, V.; Honkavaara, E.; Hayden, M.; Kant, S. UAV Remote Sensing Phenotyping of Wheat Collection for Response to Water Stress and Yield Prediction Using Machine Learning. Plant Stress 2024, 12, 100464. [Google Scholar] [CrossRef]
- Liu, Y.; Heuvelink, G.B.M.; Bai, Z.; He, P.; Xu, X.; Ma, J.; Masiliūnas, D. Space-time statistical analysis and modelling of nitrogen use efficiency indicators at provincial scale in China. Eur. J. Agron. 2020, 115, 126032. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, Y.; Tao, X.; Chen, X.; Li, X. Rapid prediction of winter wheat yield and nitrogen use efficiency using consumer-grade unmanned aerial vehicles multispectral imagery. Front. Plant Sci. 2022, 13, 1032170. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Cui, S.; Zhang, Z.; Zhuang, K.; Wang, Z.; Zhang, Q. Determining effects of water and nitrogen input on maize (Zea mays) yield, water- and nitrogen-use efficiency: A global synthesis. Sci. Rep. 2020, 10, 9699. [Google Scholar] [CrossRef] [PubMed]
- Correndo, A.A.; Rotundo, J.L.; Tremblay, N.; Archontoulis, S.; Coulter, J.A.; Ruiz-Diaz, D.; Franzen, D.; Franzluebbers, A.J.; Nafziger, E.; Schwalbert, R.; et al. Assessing the uncertainty of maize yield without nitrogen fertilization. Field Crops Res. 2021, 260, 107985. [Google Scholar] [CrossRef]
- Chen, L.; He, P.; Zhang, H.; Peng, W.; Qiu, J.; Lü, F. Applications of machine learning tools for biological treatment of organic wastes: Perspectives and challenges. Circ. Econ. 2024, 3, 100088. [Google Scholar] [CrossRef]
- Durai, S.K.S.; Shamili, M.D. Smart farming using Machine Learning and Deep Learning techniques. Decis. Anal. J. 2022, 3, 100041. [Google Scholar] [CrossRef]
- Gupta, R.; Ouderji, Z.H.; Uzma, Y.Z.; Sloan, W.T.; You, S. Machine learning for sustainable organic waste treatment: A critical review. npj Mater. Sustain. 2024, 2, 5. [Google Scholar] [CrossRef]

| Nr | Treatment | Season | Growth Time (Months) | Plant | References |
|---|---|---|---|---|---|
| 1 | (1) Effective Microbes 1 M Incubation, pelleted; (2) Anaerobically Digested, centrifuged; (3) Anaerobically Digested, centrifuged, dried; | Cold, Warm | 1, 2, 3, 4, & 6 | Ryegrass | [13] |
| 2 | (1) Dried, pelletized; (2) Effective Microbes 1 M Incubation, ground; (3) Effective Microbes ×2 1 M Incubation, ground; (4) Sterilized at 70 °C, dried; (5) Stillage added, Anaerobically Digested, centrifuged; (6) Fish waste, Stillage added, Anaerobically Digested, centrifuged | Warm | 1, 1.5, & 2, 3 | Ryegrass | [24] |
| 3 | FW Compost 340, 680, 1020 | Warm | 0.5, 1, & 1.5 | Lettuce | [25] |
| 4 | FW 1.1, 1.2, 1.3; Organic Fraction of MSW 1.1, 1.2, 1.3; FW 1, 2, 3 digested; Organic Fraction of MSW digested | Warm | 1, 2, & 5.3 | Ryegrass | [26] |
| 5 | Green Waste compost in different ratios | NA | 2.73, 3.0, 3.63, & 9.37 | Oat | [27] |
| 6 | Garden Waste compost in different ratios | NA | 0.75, 1.5, 3.0, 9, & 13 | Ryegrass | [28] |
| 7 | Composted municipal solid waste 1.1, 2.1, 2.2 | NA | 4 | Ryegrass and wheat | [29] |
| 8 | Green Waste Compost 1, 2 | NA | 12 | Oat | [30] |
| 9 | Compost 1.1, 1.2, 2.1, 2.2 | NA | NA | Oat grass | [31] |
| 10 | Straw + slops compost 1.1, 1.2; Slops compost 1.1, 1.2 | NA | NA | Winter wheat | [32] |
| 11 | Fertilizer granulate obtained from biogas digestate in different ratios | NA | 12, 24, 36, & 48 | Grass | [33] |
| 12 | Compost 1, 2 | NA | 1 | Corn | [34] |
| 13 | 100% FW digestate; 10% FWD, 90% fertilizer; 50% FWD, 50% fertilizer | Cold | 40 | Shoots Kai choy | [35] |
| 14 | FW + yard trimmings + paper; FW + wood waste + sawdust | Warm | 180 | Grass | [36] |
| 15 | Mixed DD, LD, and MIN | Warm and Cold | 62 & 64 | Lactuva sativa | [37] |
| 16 | Municipal solid FW compost | Cold | 120 | Oat | [38] |
| 17 | Chemical fertilizer + 100%, 150%, and 300% FW-livestock manure compost | Warm | 180 | Rice | [39] |
| 18 | FW digestate, I, II; FW co-digested with sewage sludge, I and II | Warm | NA | Barley and Oats | [40] |
| 19 | Acidulous composting FW | Spring | 85, 99 & 100 | Potato | [41] |
| 20 | Green waste compost | NA | 2.73, 3.00, 3.63, & 9.37 | Oat | [42] |
| Variable | Unit | Mean ± SD | Range (Min–Max) | CV (%) |
|---|---|---|---|---|
| N content (NC) | g/kg TS | 24.05 ± 15.54 | 1.78–57.10 | 64.62 |
| Volatile solids (VS) | % | 55.38 ± 31.65 | 1.23–95.00 | 57.15 |
| Growth time (T) | Month | 8.17 ± 16.00 | 0.50–100.00 | 195.84 |
| Dosage (D) | kg N/ ha | 189.27 ± 181.05 | 0.10–1020 | 95.7 |
| Plant yield (PY) | kg/ ha | 2268.42 ± 3099.00 | 0.00–18,008.11 | 136.61 |
| Internal efficiency of nitrogen utilization (IENU) | kg N/ ha | 32.26 ± 92.51 | 0.00–1285.71 | 286.76 |
| Crop | Frequency (%) |
|---|---|
| Barley (Hordeum vulgare L.) | 0.45 |
| Corn | 0.45 |
| Grass | 10.76 |
| Grass—Festuca arundinacea | 0.90 |
| Lactuva sativa | 1.79 |
| Lettuce | 2.02 |
| Oats combined | 4.87 |
| Potato (Solanum tuberosum L. ‘Dansyakuimo’) | 1.35 |
| Rice Oryza sativa L. cv. Saechucheong | 0.67 |
| Ryegrass | 73.77 |
| Shoots Kai choy (Brassica juncea, var. Hirayama) | 0.67 |
| Triple mix (a mixture of 70% timothy (Phleum pretense) + 15% red clover + 15% alsike) TM | 0.22 |
| Wheat combined | 1.34 |
| Oat combined with hairy vetch OHV | 0.22 |
| Oat combined with red clover Trifolium pretense ORC | 0.22 |
| Data | Phase | Model | Equation | R2 | RSE | AIC | RMSE |
|---|---|---|---|---|---|---|---|
| Data 1 | Training | PY~D + T + N | PY = 2.05 D + 96.84 T − 63.16 NC + 3008.99 | 0.24 | 2832 | 5739.00 | |
| Testing | Trained model | 2430.10 | |||||
| Data 2 * | Training | PY~D + T + N | PY = 2.94 D + 62.42 T − 8.05 NC + 745.50 | 0.41 | 739.7 | 3793.86 | |
| Testing | 759.30 | ||||||
| Data 3 | Training | PY~D + T + N | PY = 1.74 D + 76.76 T − 46.28 NC + 569.14 | 0.18 | 2877 | 4343.30 | |
| Testing | 2422.05 | ||||||
| Data 4 | Training | PY~D + T + N | PY = 2.89 D + 58.25 T − 11.41 NC + 1347.47 | 0.32 | 573.4 | 3735.80 | |
| Testing | 1263.57 |
| Data | Metric | XGB | RF | CB | GB |
|---|---|---|---|---|---|
| Data 1 | RMSE | 1229.65 a | 1297.74 a | 1142.77 a | 1509.56 a |
| R2 | 0.86 | 0.84 | 0.88 | 0.79 | |
| Data 2 | RMSE | 505.16 a | 493.22 a | 494.71 a | 651.19 b |
| R2 | 0.75 | 0.77 | 0.76 | 0.57 | |
| Data 3 | RMSE | 1460.60 a | 1577.07 a | 1422.36 a | 1929.11 b |
| R2 | 0.79 | 0.76 | 0.80 | 0.65 | |
| Data 4 | RMSE | 793.13 a | 809.99 a | 709.77 a | 1111.26 b |
| R2 | 0.78 | 0.76 | 0.82 | 0.58 |
| Data | Phase | Model | Equation | R2 | RSE | AIC | RMSE |
|---|---|---|---|---|---|---|---|
| Data 1 | Training | IENU~D + T + N | IENU = −0.03D + 36.56T − 1.97NC – 0.39 | 0.28 | 95.4 | 2325.03 | - |
| Testing | Trained model | 71.57 | |||||
| Data 2 | Training | IENU~D + T + N | IENU = 9.62 + 0.03D − 2.96T + 0.12NC | 0.29 | 6.87 | 1398.00 | - |
| Testing | Trained model | 8.29 | |||||
| Data 3 | Training | IENU~D + T + N | IENU = 45.06 + 0.05D + 0.51T − 0.87NC | 0.02 | 92.76 | 3254.10 | - |
| Testing | Trained model | 45.96 | |||||
| Data 4 | Training | IENU~D + T + N | IENU = 7.06 − 0.01D − 0.21T + 0.10NC | 0.1 | 7.61 | 1592.23 | - |
| Testing | Trained model | 8.38 |
| Data | Metric | XGB | RF | CB | GB |
|---|---|---|---|---|---|
| Data 1 | RMSE | 53.38 a | 63.40 a | 55.06 a | 61.07 a |
| R2 | 0.67 | 0.47 | 0.70 | 0.54 | |
| Data 2 | RMSE | 3.91 a | 3.97 a | 3.98 a | 5.58 b |
| R2 | 0.81 | 0.80 | 0.79 | 0.60 | |
| Data 3 | RMSE | 51.33 a | 63.02 a | 56.38 a | 60.99 a |
| R2 | 0.74 | 0.52 | 0.68 | 0.59 | |
| Data 4 | RMSE | 4.47 a | 4.48 a | 4.19 a | 5.68 a |
| R2 | 0.72 | 0.71 | 0.74 | 0.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuligowski, K.; Tran, Q.B.; Nguyen, C.C.; Kaczyński, P.; Konkol, I.; Świerczek, L.; Cenian, A.; Nguyen, X.C. Analyzing and Predicting the Agronomic Effectiveness of Fertilizers Derived from Food Waste Using Data-Driven Models. Appl. Sci. 2025, 15, 5999. https://doi.org/10.3390/app15115999
Kuligowski K, Tran QB, Nguyen CC, Kaczyński P, Konkol I, Świerczek L, Cenian A, Nguyen XC. Analyzing and Predicting the Agronomic Effectiveness of Fertilizers Derived from Food Waste Using Data-Driven Models. Applied Sciences. 2025; 15(11):5999. https://doi.org/10.3390/app15115999
Chicago/Turabian StyleKuligowski, Ksawery, Quoc Ba Tran, Chinh Chien Nguyen, Piotr Kaczyński, Izabela Konkol, Lesław Świerczek, Adam Cenian, and Xuan Cuong Nguyen. 2025. "Analyzing and Predicting the Agronomic Effectiveness of Fertilizers Derived from Food Waste Using Data-Driven Models" Applied Sciences 15, no. 11: 5999. https://doi.org/10.3390/app15115999
APA StyleKuligowski, K., Tran, Q. B., Nguyen, C. C., Kaczyński, P., Konkol, I., Świerczek, L., Cenian, A., & Nguyen, X. C. (2025). Analyzing and Predicting the Agronomic Effectiveness of Fertilizers Derived from Food Waste Using Data-Driven Models. Applied Sciences, 15(11), 5999. https://doi.org/10.3390/app15115999







