Development and Validation of a Coupled Hygro-Chemical and Thermal Transport Model in Concrete Using Parallel FEM
Abstract
1. Introduction
2. Basic Transport Formulation of Unsaturated Concrete
2.1. Governing Equation
2.2. Material Models
2.2.1. Capacity and Diffusivity Coefficients of Multi-Species in Non-Saturated Concrete
2.2.2. Coupling Parameters
and
and
3. Implementation of Parallel Finite Element Method
3.1. Numerical Modeling with Finite Element Method
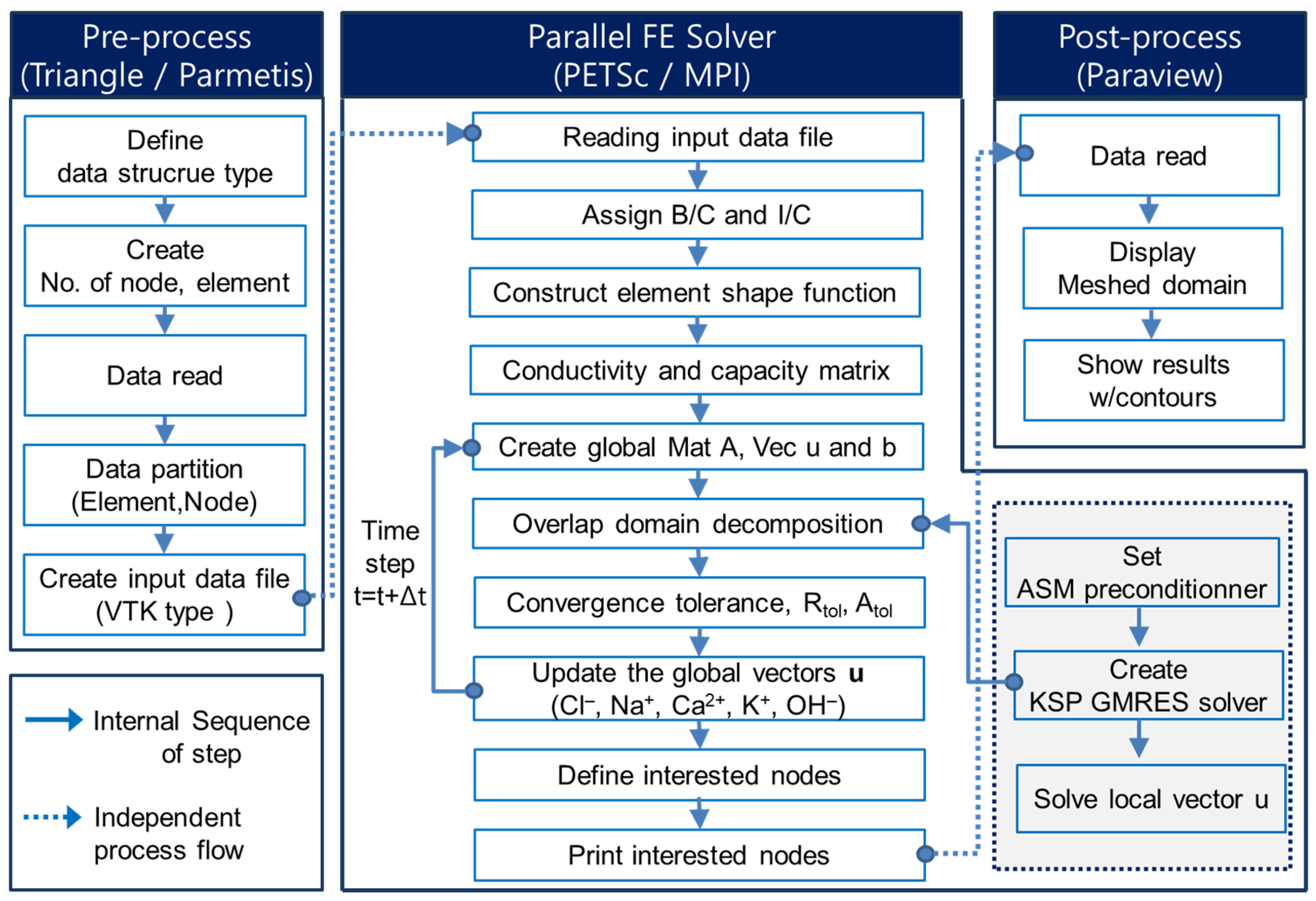
3.2. Framework of Parallel Finite Element Method
3.3. Overlapping Domain Decomposition Method
4. Results
4.1. Validation of Hygro-Chemo-Thermo Transport Model
4.1.1. Experimental Validation of Chloride Ingress Under Temperature Gradient
4.1.2. Comparison of Experimental and Numerical Results
4.2. Numerical Prediction with Hygro-Chemo-Thermo Transport Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Mehta, P.K. Durability of Concrete in Marine Environment—A Review. In Performance of Concrete in Marine Environment; Malhotra, V.M., Ed.; ACI Publication: Farmington Hills, MI, USA, 1980; pp. 1–20. [Google Scholar]
- Thomas, M.D.A.; Moffatt, E.G. The Performance of Concrete in a Marine Environment. In Proceedings of the ICDCS 2018, Vienna, Austria, 2–5 July 2018. [Google Scholar]
- Pratiwi, W.D.; Putra, F.D.D.; Triwulan; Tajunnisa, Y.; Husin, N.A.; Wulandari, K.D. A Review of Concrete Durability in Marine Environment; (IOP Conference Series: Materials Science and Engineering); IOP Publishing Ltd.: Bristol, UK, 2021. [Google Scholar]
- Coppola, L.; Beretta, S.; Bignozzi, M.C.; Bolzoni, F.; Brenna, A.; Cabrini, M.; Candamano, S.; Caputo, D.; Carsana, M.; Cioffi, R.; et al. The Improvement of Durability of Reinforced Concretes for Sustainable Structures: A Review on Different Approaches. Materials 2022, 15, 2728. [Google Scholar] [CrossRef]
- Ababneh, A.; Xi, Y. An Experimental Study on the Effect of Chloride Penetration on Moisture Diffusion in Concrete. Mater. Struct. 2002, 35, 659–664. [Google Scholar] [CrossRef]
- Ababneh, A.; Benboudjema, F.; Xi, Y. Chloride penetration in Nonsaturated concrete. J. Mater. Civ. Eng. 2003, 15, 183–191. [Google Scholar] [CrossRef]
- Suwito, A.; Cai, X.C.; Xi, Y. Parallel finite element method for coupled chloride moisture diffusion in concrete. Int. J. Numer. Anal. Model. 2006, 3, 481–503. [Google Scholar]
- Li, L.Y.; Page, C.L. Modelling of electrochemical chloride extraction from concrete: Influence of ionic activity coefficients. Comput. Mater. Sci. 1998, 9, 303–308. [Google Scholar] [CrossRef]
- Li, L.Y.; Page, C.L. Finite element modeling of chloride removal from concrete by an electrochemical method. Corros. Sci. 2000, 42, 2145–2165. [Google Scholar] [CrossRef]
- Truc, O.; Olliver, J.P.; Nillson, L.O. Numerical simulation of multi-species diffusion. Mater. Struct. 2000, 33, 566–573. [Google Scholar] [CrossRef]
- Lorente, S.; Carcassè, M.; Ollivier, J. Penetration of ionic species into saturated porous media: The case of concrete. Int. J. Energy Res. 2003, 27, 907–917. [Google Scholar]
- Nguyen, T.Q.; Baroghel-Bouny, V.; Dangla, P. Prediction of chloride ingress into saturated concrete on the basis of multi-species model by numerical calculations. Comput. Concr. 2006, 3, 401–422. [Google Scholar] [CrossRef]
- Wang, Y.; Li, L.-Y.; Page, C. A two-dimensional model of electrochemical chloride removal from concrete. Comput. Mater. Sci. 2001, 20, 196–212. [Google Scholar]
- Wang, Y.; Li, L.-Y.; Page, C. Modelling of chloride ingress into concrete from a saline environment. Build. Environ. 2005, 40, 1573–1582. [Google Scholar] [CrossRef]
- Yogarajah, E.; Hatanaka, A.; Kurumisawa, K.; Nawa, T. Modelling of Chloride Ion Transport in Slag Blended Cementitious Materials: Influence of Tortuosity and Surface Electrical Properties. In Proceedings of the 3rd International Congress on Durability of Concrete, Adelaide, Australia, 22–25 October 2017. [Google Scholar]
- Samson, E.; Lemaire, G.; Marchand, J.; Beaudoin, J. Modeling chemical activity effects in strong ionic solutions. Comput. Mater. Sci. 1999, 15, 285–294. [Google Scholar] [CrossRef]
- Samson, E.; Marchand, J. Numerical Solution of the Extended Nernst–Planck Model. J. Colloid Interface Sci. 1999, 215, 1–8. [Google Scholar] [CrossRef]
- Samson, E.; Marchand, J. Modeling the transport of ions in unsaturated cement-based materials. Comput. Struct. 2007, 85, 1740–1756. [Google Scholar] [CrossRef]
- Nielsen, E.P.; Geiker, M.R. Chloride diffusion in partially saturated cementitious material. Cem. Concr. Res. 2003, 33, 133–138. [Google Scholar] [CrossRef]
- Mao, L.; Li, L.; Kim, B. Modelling of Multi-species Transport in Concrete Under the Action of External Electric Field: Influence of the Overpotential at Electrode-electrolyte. J. Electroanal. Chem. 2022, 159, 116079. [Google Scholar] [CrossRef]
- Sharmilan, S.; Stang, H.; Michel, A. A Multi-species Reactive Transport Model Based on Ion-solid Phase Interaction for Saturated Cement-based Materials. Cem. Concr. Res. 2022, 159, 106861. [Google Scholar] [CrossRef]
- Sharmilan, S.; Stang, H.; Michel, A. Enhancement of a Multi-species Reactive Transport Model for Cement-based Materials under Cyclic Wetting and Drying Conditions. J. Build. Eng. 2023, 77, 107532. [Google Scholar] [CrossRef]
- Sharmilan, S.; Stang, H.; Michel, A. A Multi-species Reactive Transport Model Based on Gas-ion-solid Phase Interaction for the Carbonation of Cement-based Materials. Cem. Concr. Res. 2024, 175, 107349. [Google Scholar] [CrossRef]
- Xi, Y.; Bazant, Z.P.; Molina, L.; Jennings, H.M. Moisture diffusion in cementitious materials: Adsorption isotherm. Adv. Cem.Based Mater. 1994, 1, 248–257. [Google Scholar] [CrossRef]
- Xi, Y.; Bazant, Z.P.; Molina, L.; Jennings, H.M. Moisture diffusion in cementitious materials: Moisture capacity and diffusivity. Adv. Cem. Based Mater. 1994, 1, 258–266. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Thonguthai, W. Pore Pressure and Drying of concrete at high temperature. J. Eng. Mech. Div. 1978, 5, 1059–1079. [Google Scholar] [CrossRef]
- Bazant, Z.P.; Chern, J.; Thonguthai, W. Finite element program for moisture and heat transfer in heated concrete. Nucl. Eng. Des. 1981, 68, 61–70. [Google Scholar] [CrossRef]
- Saetta, A.V.; Schrefler, B.A.; Vitaliani, R. The carbonation of concrete and the mechanism of moisture, heat and carbonation dioxide flow through porous materials. Cem. Concr. Res. 1993, 23, 761–772. [Google Scholar] [CrossRef]
- Sih, G.C.; Shih, M.T. Transient hygrothermal stresses in composites: Coupling of moisture and heat with temperature varying diffusivity. Int. J. Eng. Sci. 1980, 18, 19–42. [Google Scholar] [CrossRef]
- Lien, H.P.; Wittmann, F.H. Mass transfer in inhomogeneous porous media under thermal gradients. Nucl. Eng. Des. 1998, 179, 179–189. [Google Scholar] [CrossRef]
- Cervera, M.; Oliver, J.; Prato, T. Thermo-Chemo-Mechanical Model for Concrete. I: Hydration and Aging. J. Eng. Mech. 1999, 125, 1018–1027. [Google Scholar] [CrossRef]
- Gasch, T.; Malm, R.; Ansell, A. A Coupled Hygro-thermo-mechanical Model for Concrete Subjected to Variable Environmental Conditions. Int. J. Solids Struct. 2016, 91, 143–156. [Google Scholar] [CrossRef]
- Maric, M.K.; Ozbolt, J.; Balabanic, G. Application of the 3D Chemo-hygro-thermo Mechanical Model on Existing Bridges Exposed to Chlorides and Mechanical Damages. In Proceedings of the 7th International Conference on Euro Asia Civil Engineering Forum, Stuttgart, Germany, 30 September–2 October 2019. [Google Scholar]
- Isgor, O.B.; Razaqpur, A.G. Finite element modelling of coupled heat transfer, moisture transport and carbonation processes in concrete structures. Cem. Concr. Compos. 2004, 26, 57–73. [Google Scholar] [CrossRef]
- Isteita, M.; Xi, Y. The Effect of Temperature Variation on Chloride Penetration in Concrete. Constr. Build. Mater. 2017, 156, 73–82. [Google Scholar] [CrossRef]
- Tabrizinejadas, S.; Carrayrou, J.; Saaltink, M.W.; Baalousha, H.M.; Fahs, M. On the Validity of the Null Current Assumption for Modeling Sorptive Reactive Transport and Electro-Diffusion in Porous Media. Water 2021, 13, 2221. [Google Scholar] [CrossRef]
- Xi, Y.; Willam, K.; Frangopol, D.M. Multiscale modeling of interactive diffusion processes in concrete. J. Eng. Mech. 2003, 126, 258–265. [Google Scholar] [CrossRef]
- Xi, Y.; Bažant, Z.P. Modeling Chloride Penetration in Saturated Concrete. J. Mater. Civ. Eng. 1999, 11, 58–65. [Google Scholar] [CrossRef]
- Christensen, R.M. Mechanics of Composite Materials; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Homan, L.; Ababneh, A.N.; Xi, Y. The effect of moisture transport on chloride penetration in concrete. Constr. Build. Mater. 2016, 125, 1189–1195. [Google Scholar] [CrossRef]
- Triangle. Available online: https://www.cs.cmu.edu/~quake/triangle.html (accessed on 19 March 2025).
- Balay, S.; Buschelman, K.; Eijkhout, V.; Gropp, W.D.; Kaushik, D.; Knepley, M.G.; McInnes, L.C.; Smith, B.F.; Zhang, H. PETSc-Users Manual. In Technical Report ANL-95/11—Revision 2.1.5; Argonne National Laboratory: Lemont, IL, USA, 2008. [Google Scholar]
- MPICH Team. MPICH: A Portable Implementation of MPI. 1996–2005. Available online: https://www.anl.gov/mcs/mpich-a-highperformance-portable-implementation-of-mpi (accessed on 19 March 2025).
- Karypis, G. ParMETIS: Parallel Graph Partitioning and Sparse Matrix Ordering. 1996–2005. Available online: https://github.com/KarypisLab/ParMETIS (accessed on 19 March 2025).
- Paraview. Available online: https://www.paraview.org/ (accessed on 19 March 2025).
- Cai, X.-C. Overlapping domain decomposition methods. In Advanced Topics in Computational Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 2003; Chapter 2; pp. 57–95. [Google Scholar]
- Cai, X.-C.; Saad, Y. Overlapping domain decomposition algorithms for general sparse matrices. Numer. Linear Algebra Appl. 1996, 3, 221–237. [Google Scholar] [CrossRef]
- Damrongwiriyanupap, N.; Li, L.; Limkatanyu, S.; Xi, Y. Temperature effect on multi-ionic species diffusion in saturated concrete. Int. J. Comput. Concr. 2014, 13, 149–171. [Google Scholar] [CrossRef]









| Designed Strength at 28 Days | Water-Cement Ratio | Water (kg/m3) | Cement (kg/m3) | Fine Aggregate (kg/m3) | Coarse Aggregate (kg/m3) |
|---|---|---|---|---|---|
| 21 MPa | 0.55 | 213 | 380 | 702 | 911 |
| 15 MPa | 0.65 | 232 | 356 | 847 | 1031 |
| w/c | Temp. | Time (Day) | Measuring Depth (mm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0–6 | 6–12 | 12–18 | 18–24 | 24–30 | 30–36 | 36–42 | |||
| 0.55 | 35 °C | 3 | 0.416 | 0.169 | 0.091 | 0.060 | 0.037 | 0.036 | 0.031 |
| 6 | 0.785 | 0.329 | 0.094 | 0.066 | 0.054 | 0.049 | 0.045 | ||
| 12 | 0.986 | 0.389 | 0.117 | 0.092 | 0.065 | 0.055 | 0.053 | ||
| 24 | 1.452 | 0.590 | 0.483 | 0.136 | 0.155 | 0.080 | 0.072 | ||
| 50 °C | 3 | 0.650 | 0.225 | 0.136 | 0.088 | 0.048 | 0.045 | 0.038 | |
| 6 | 1.159 | 0.390 | 0.173 | 0.131 | 0.095 | 0.081 | 0.067 | ||
| 12 | 1.357 | 0.622 | 0.241 | 0.168 | 0.110 | 0.099 | 0.092 | ||
| 24 | 2.594 | 1.452 | 0.899 | 0.446 | 0.265 | 0.209 | 0.153 | ||
| 0.65 | 35 °C | 3 | 0.312 | 0.166 | 0.049 | 0.040 | 0.035 | 0.032 | 0.021 |
| 6 | 0.471 | 0.180 | 0.099 | 0.055 | 0.079 | 0.070 | 0.059 | ||
| 12 | 0.541 | 0.238 | 0.115 | 0.113 | 0.090 | 0.079 | 0.070 | ||
| 24 | 0.785 | 0.483 | 0.205 | 0.158 | 0.139 | 0.117 | 0.102 | ||
| 50 °C | 3 | 0.377 | 0.221 | 0.054 | 0.044 | 0.037 | 0.034 | 0.023 | |
| 6 | 0.717 | 0.356 | 0.162 | 0.127 | 0.089 | 0.076 | 0.066 | ||
| 12 | 1.122 | 0.405 | 0.216 | 0.157 | 0.097 | 0.092 | 0.068 | ||
| 24 | 2.000 | 1.076 | 0.529 | 0.433 | 0.228 | 0.134 | 0.125 | ||
| Species | Unit | K+ | Na+ | Cl− | OH− | Ca2+ | |
|---|---|---|---|---|---|---|---|
| Charge number | +1 | +1 | −1 | −1 | +2 | ||
| Diffusion coefficient | m2/s | 4.0 × 10−11 | 2.8 × 10−11 | Refer to Equation (15) | 5.3 × 10−10 | 1.6 × 10−11 | |
| Initial condition | at top surface | mol/L | 0 | 0.513 | 1.053 | 0 | 0.27 |
| in pore solution | mol/L | 0.0995 | 0.0389 | 0 | 0.1384 | 0 | |
| Cement type | I/II | ||||||
| Water-cement ratio | 0.55 | ||||||
| Volume fraction of aggregate | 0.65 | ||||||
| Outside RH/Temperature | %/°C | 100/20 °C, 35 °C, 50 °C | |||||
| Inside RH/Temperature | %/°C | 60/20 °C | |||||
| Total analysis duration | day | 400 | |||||
| Time step | day | 0.5 | |||||
| Relative tolerance (Rtol) | 10−4 | ||||||
| Absolute tolerance (Atol) | 10−10 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Na, O.; Lee, G. Development and Validation of a Coupled Hygro-Chemical and Thermal Transport Model in Concrete Using Parallel FEM. Appl. Sci. 2025, 15, 5989. https://doi.org/10.3390/app15115989
Na O, Lee G. Development and Validation of a Coupled Hygro-Chemical and Thermal Transport Model in Concrete Using Parallel FEM. Applied Sciences. 2025; 15(11):5989. https://doi.org/10.3390/app15115989
Chicago/Turabian StyleNa, Okpin, and Giyeol Lee. 2025. "Development and Validation of a Coupled Hygro-Chemical and Thermal Transport Model in Concrete Using Parallel FEM" Applied Sciences 15, no. 11: 5989. https://doi.org/10.3390/app15115989
APA StyleNa, O., & Lee, G. (2025). Development and Validation of a Coupled Hygro-Chemical and Thermal Transport Model in Concrete Using Parallel FEM. Applied Sciences, 15(11), 5989. https://doi.org/10.3390/app15115989






