Sensor-Generated In Situ Data Management for Smart Grids: Dynamic Optimization Driven by Double Deep Q-Network with Prioritized Experience Replay
Abstract
1. Introduction
- Design of a hierarchical storage structure: A classification mechanism is designed to preprocess data with different attributes based on the diverse characteristics of in situ data, and store it in server clusters at different hierarchical levels to enhance system access efficiency.
- Design of personalized demand queues: When access demands for in situ data from different hierarchical levels arise, they are received and recorded through personalized demand queues, ensuring timely responses to demands from each level.
- Setting up an algorithm-driven demand response mechanism: For access demands in different personalized demand queues, the Double Deep Q-Network with Prioritized Experience Replay algorithm is introduced to assist in decision-making and response.
2. Related Works
2.1. Technological Background of Smart Grid
2.2. Related Research on In Situ Data
2.3. Reinforcement Learning in Data Management
2.4. In Situ Data Storage Management
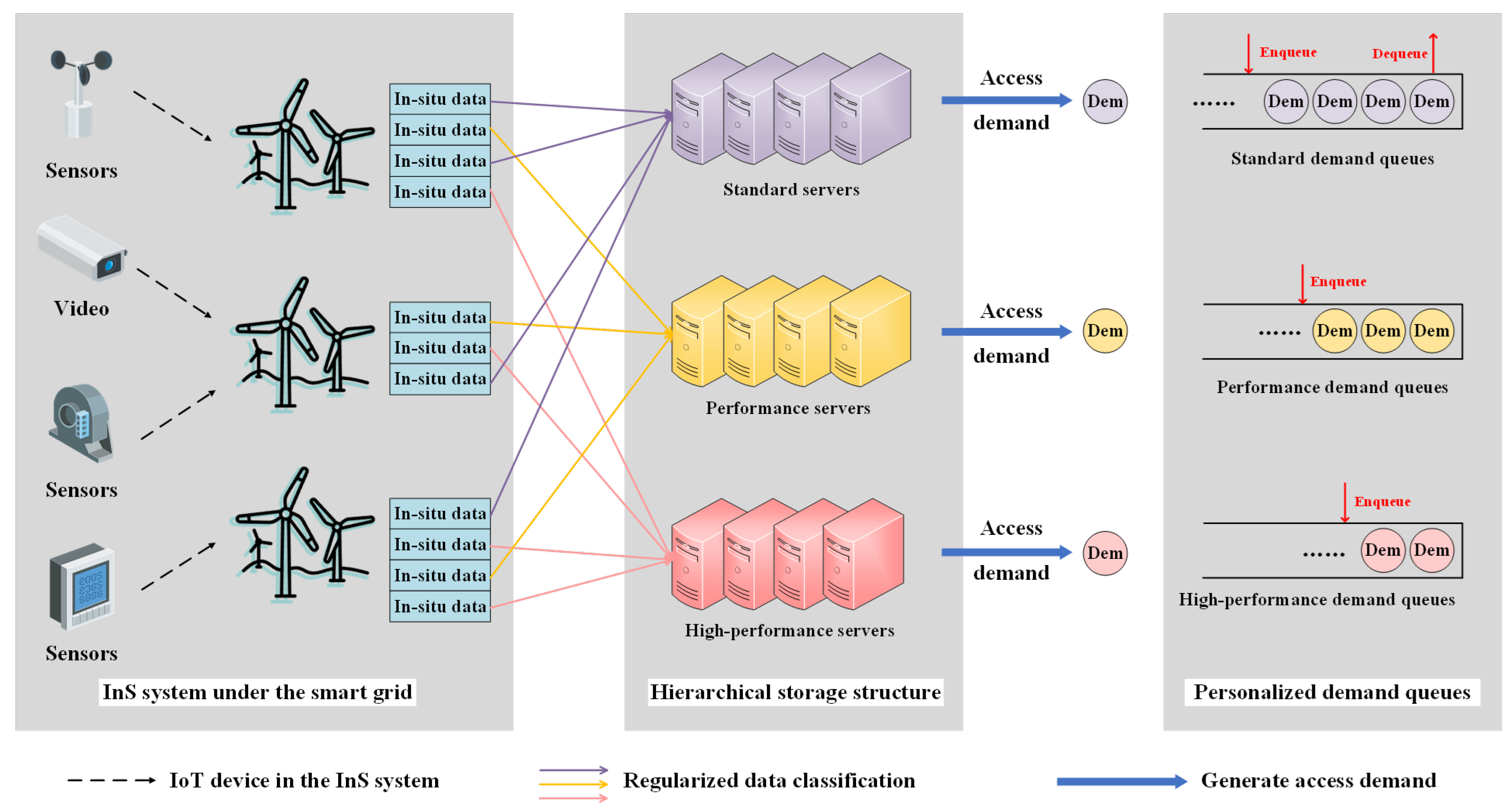
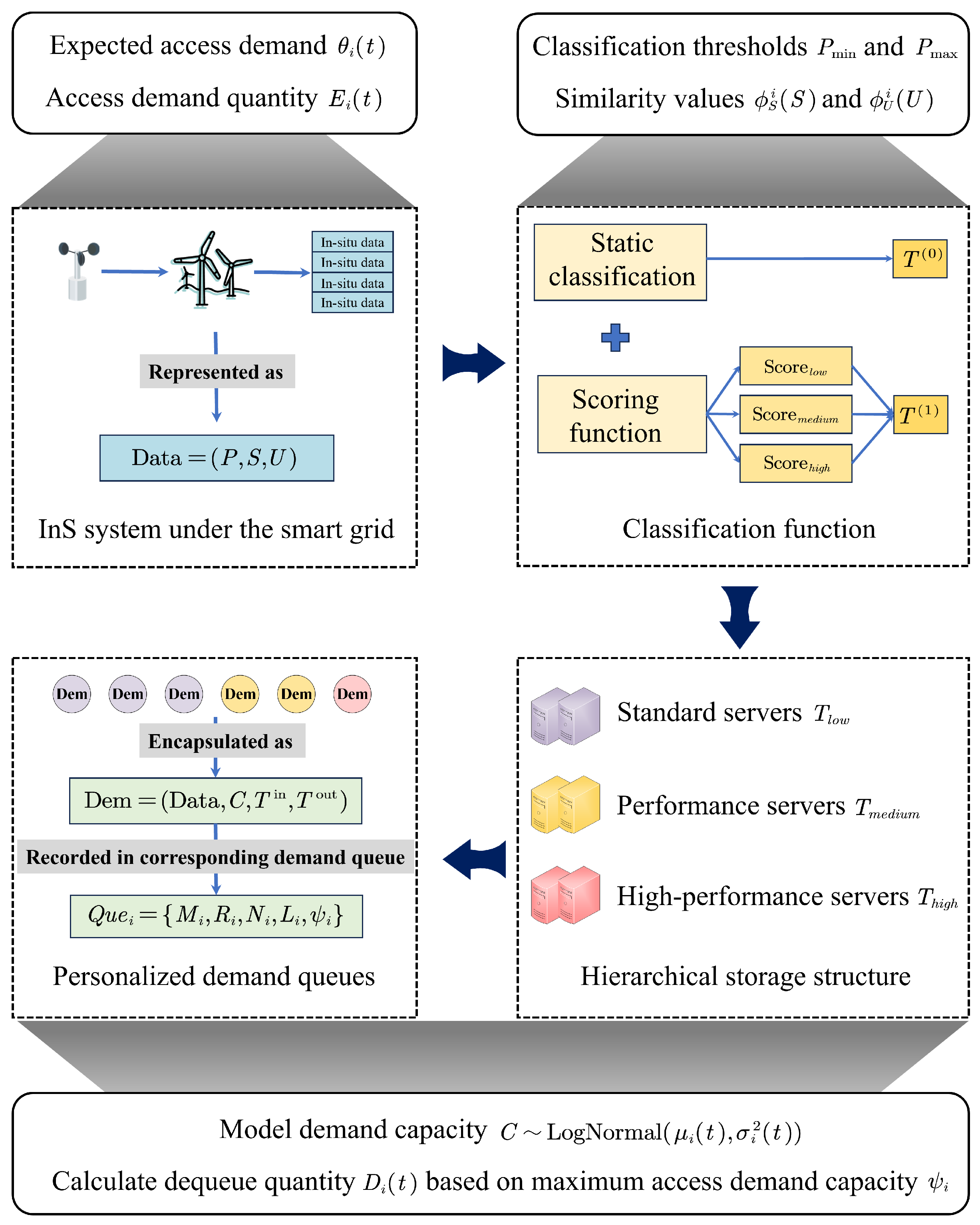
3. System Modeling
3.1. Hierarchical Storage Structure
3.2. Personalized Demand Queues
3.3. Evaluation Metrics
3.3.1. Average Waiting Delay
3.3.2. Average Residual Requirements
3.3.3. Average Response Latency
4. Algorithm
4.1. Demand Enqueue Rules
| Algorithm 1 Demand Enqueue Rules |
|
4.2. Demand Dequeue Rules
| Algorithm 2 Demand Dequeue Rules |
|
4.3. Markov Modeling
4.4. Double Deep Q-Network with Prioritized Experience Replay
| Algorithm 3 DDQN-PER-Based In Situ Data Management Method |
|
5. Experimental Analysis
5.1. Comparison Algorithms
5.2. Experimental Setup
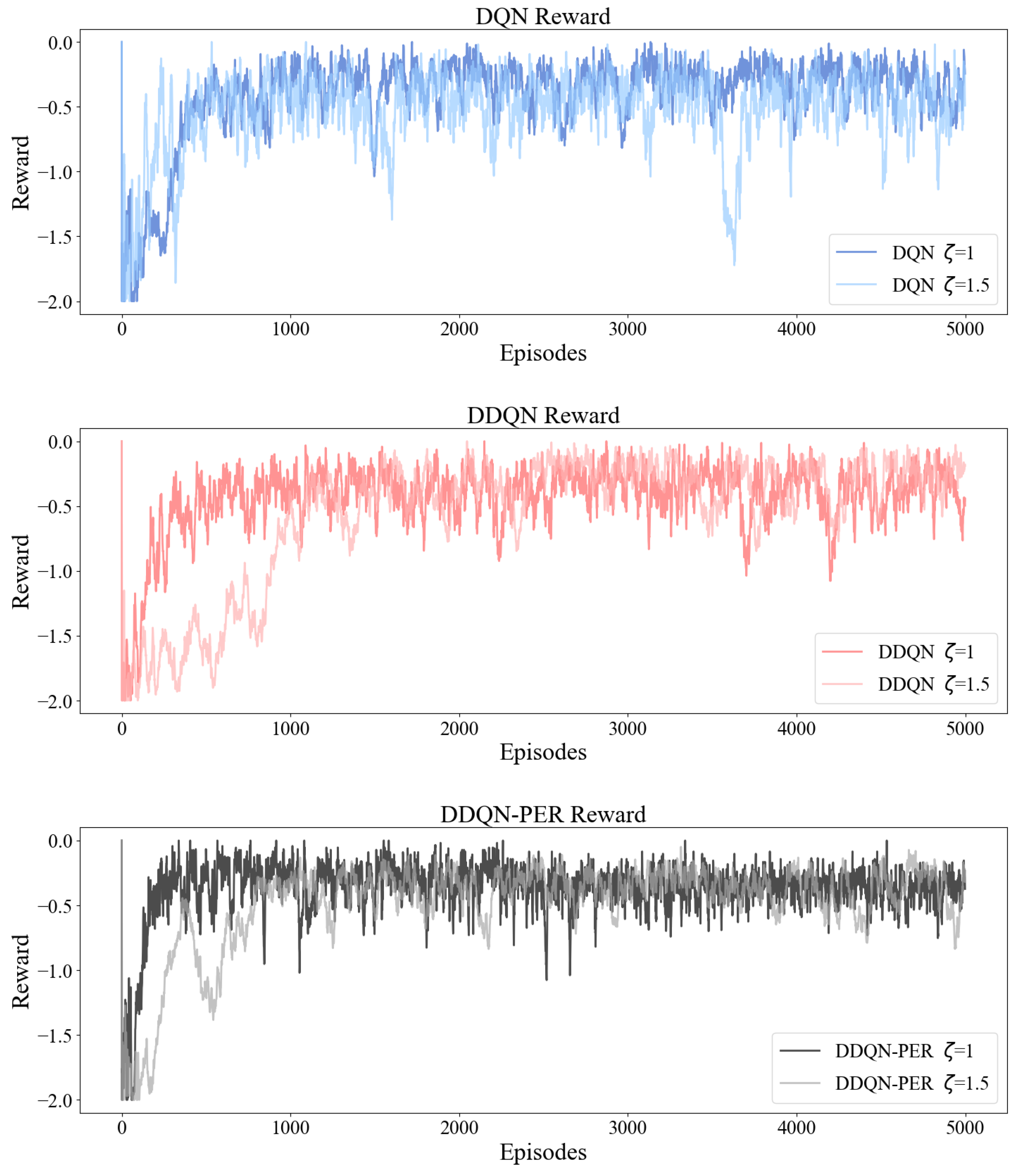
5.3. Convergence Comparison
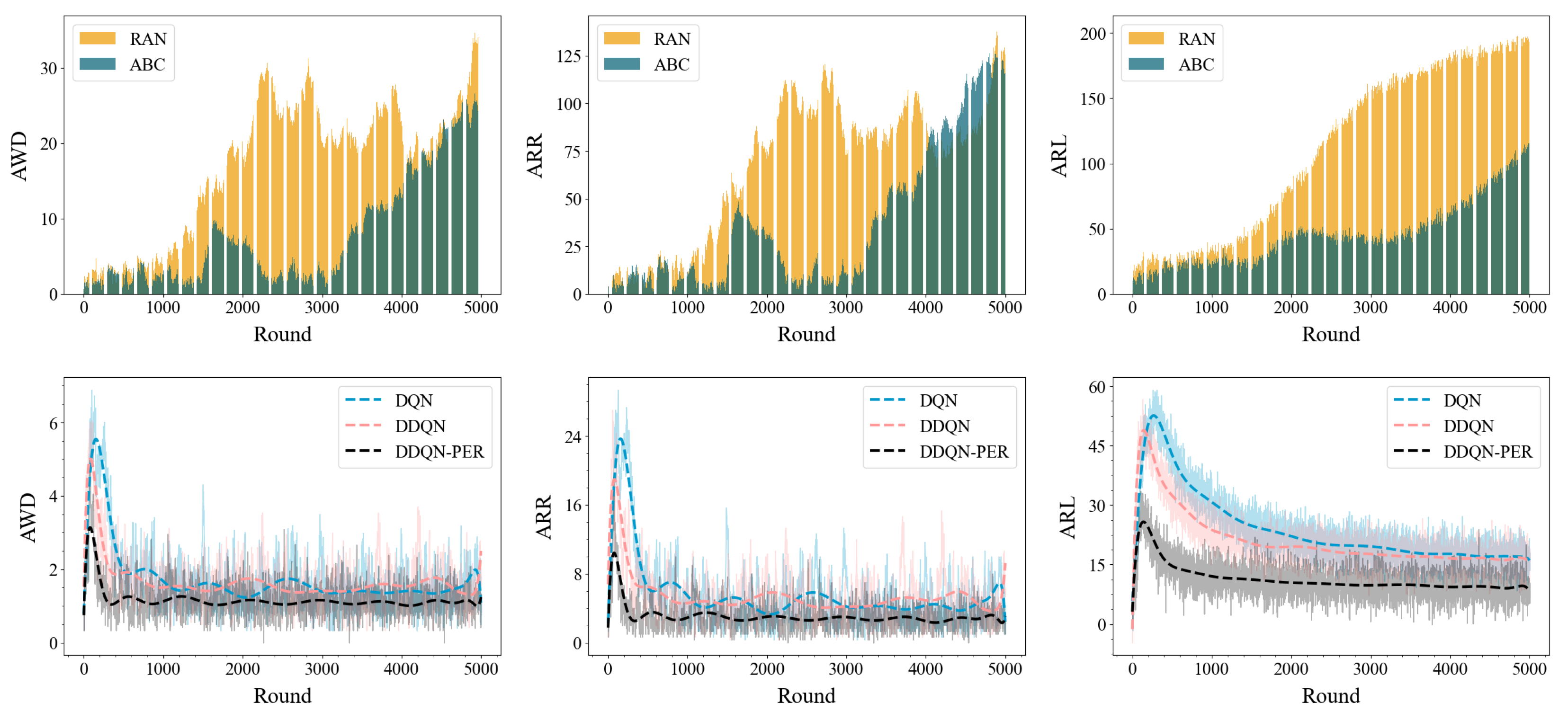
5.4. Comparison of System Metrics
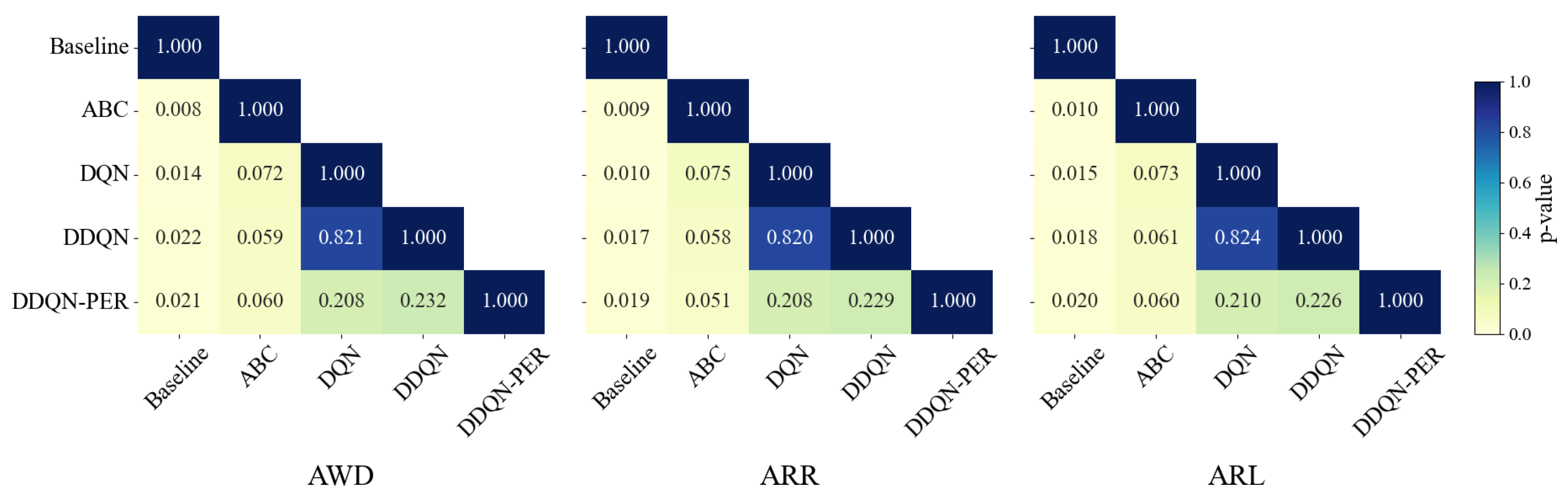
5.5. Statistical Tests
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| InS | In situ Server System |
| DQN | Deep Q-Network |
| DDQN | Double Deep Q-Network |
| PER | Prioritized Experience Replay |
| DDQN-PER | Double Deep Q-Network with Prioritized Experience Replay |
References
- Krishna, M.S.R.; Khasim Vali, D. Meta-RHDC: Meta Reinforcement Learning Driven Hybrid Lyrebird Falcon Optimization for Dynamic Load Balancing in Cloud Computing. IEEE Access 2025, 13, 36550–36574. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhang, L.; Hao, Z.; Qu, S.; Liu, J.; Ding, X.; Liu, C.; Li, N.; Li, R. Assisting Offshore Production Optimization Technology in Intelligent Completion Operation Based on Edge-Cloud Collaborative Technologies. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 4–7 November 2024; SPE: Houston, TX, USA, 2024; p. D021S037R003. [Google Scholar]
- Li, J.; Xia, Y.; Sun, X.; Chen, P.; Li, X.; Feng, J. Delay-Aware Service Caching in Edge Cloud: An Adversarial Semi-Bandits Learning-Based Approach. In Proceedings of the 2024 IEEE 17th International Conference on Cloud Computing (CLOUD), Shenzhen, China, 7–13 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 411–418. [Google Scholar]
- Zhang, L.; Hao, P.; Zhou, W.; Ma, J.; Li, K.; Yang, D.; Wan, J. A thermostatically controlled loads regulation method based on hybrid communication and cloud–edge–end collaboration. Energy Rep. 2025, 13, 680–695. [Google Scholar] [CrossRef]
- Wu, D.; Li, Z.; Shi, H.; Luo, P.; Ma, Y.; Liu, K. Multi-Dimensional Optimization for Collaborative Task Scheduling in Cloud-Edge-End System. Simul. Model. Pract. Theory 2025, 141, 103099. [Google Scholar] [CrossRef]
- Xiao, L.; Jia, G.; Lin, X. Construction of Manufacturing Data Acquisition System Based on Edge Computing. In Proceedings of the 2024 International Conference on Computers, Information Processing and Advanced Education (CIPAE), Ottawa, ON, Canada, 26–28 August 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 571–576. [Google Scholar]
- Wan, Z.; Zhao, S.; Dong, X.; Huang, Z.; Tan, Y. Joint DRL and ASL-Based “Cloud-Edge-End” Collaborative Caching Optimization for Metaverse Scenarios. In Proceedings of the 2024 IEEE 30th International Conference on Parallel and Distributed Systems (ICPADS), Belgrade, Serbia, 10–14 October 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 342–349. [Google Scholar]
- Hasan, N.; Alam, M. Role of machine learning approach for industrial internet of things (IIoT) in cloud environment-a systematic review. Int. J. Adv. Technol. Eng. Explor. 2023, 10, 1391. [Google Scholar]
- Tang, Y. Tiansuan Constellation: Intelligent Software-Defined Microsatellite with Orbital Attention for Sustainable Development Goals. In Proceedings of the International Conference on Big Data Intelligence and Computing, Shanghai, China, 16–18 December 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 3–21. [Google Scholar]
- Zeng, L.; Ye, S.; Chen, X.; Zhang, X.; Ren, J.; Tang, J.; Yang, Y.; Shen, X.S. Edge Graph Intelligence: Reciprocally Empowering Edge Networks with Graph Intelligence. IEEE Commun. Surv. Tutorials 2025, 27, 1–16. [Google Scholar] [CrossRef]
- Leng, J.; Chen, Z.; Sha, W.; Ye, S.; Liu, Q.; Chen, X. Cloud-edge orchestration-based bi-level autonomous process control for mass individualization of rapid printed circuit boards prototyping services. J. Manuf. Syst. 2022, 63, 143–161. [Google Scholar] [CrossRef]
- Xiao, J.; Wang, Y.; Zhang, X.; Luo, G.; Xu, C. Multi source data security protection of smart grid based on edge computing. Meas. Sens. 2024, 35, 101288. [Google Scholar] [CrossRef]
- Hong, H.; Suo, Z.; Wu, H.; Li, D.; Wang, J.; Lu, H.; Zhang, Y.; Lu, H. Large-scale heterogeneous terminal management technology for power Internet of Things platform. In Proceedings of the 2022 2nd International Conference on Consumer Electronics and Computer Engineering (ICCECE), Guangzhou, China, 14–16 January 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 161–164. [Google Scholar]
- He, X.; Dong, H.; Yang, W.; Li, W. Multi-source information fusion technology and its application in smart distribution power system. Sustainability 2023, 15, 6170. [Google Scholar] [CrossRef]
- Zeng, F.; Pang, C.; Tang, H. Sensors on internet of things systems for the sustainable development of smart cities: A systematic literature review. Sensors 2024, 24, 2074. [Google Scholar] [CrossRef]
- Li, C.; Hu, Y.; Liu, L.; Gu, J.; Song, M.; Liang, X.; Yuan, J.; Li, T. Towards sustainable in-situ server systems in the big data era. ACM Sigarch Comput. Archit. News 2015, 43, 14–26. [Google Scholar] [CrossRef]
- Cisco. Cisco Technology Radar Trends, 2014. White Paper. Available online: https://davidhoglund.typepad.com/files/tech-radar-trends-infographics.pdf (accessed on 15 May 2025).
- Zhang, F.; Lasluisa, S.; Jin, T.; Rodero, I.; Bui, H.; Parashar, M. In situ feature-based objects tracking for large-scale scientific simulations. In Proceedings of the 2012 SC Companion: High Performance Computing, Networking Storage and Analysis, Salt Lake City, UT, USA, 10–16 November 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 736–740. [Google Scholar]
- Lakshminarasimhan, S.; Boyuka, D.A.; Pendse, S.V.; Zou, X.; Jenkins, J.; Vishwanath, V.; Papka, M.E.; Samatova, N.F. Scalable in situ scientific data encoding for analytical query processing. In Proceedings of the 22nd International Symposium on High-Performance Parallel and Distributed Computing, New York, NY, USA, 17–21 June 2013; pp. 1–12. [Google Scholar]
- Park, J.; Choi, S.; Kim, J.; Koo, G.; Yoon, M.K.; Oh, Y. TM-Training: An Energy-Efficient Tiered Memory System for Deep Learning Training in NPUs. ACM Trans. Storage, 2025; in press. [Google Scholar] [CrossRef]
- Anjum, M.; Kraiem, N.; Min, H.; Dutta, A.K.; Daradkeh, Y.I.; Shahab, S. Opportunistic access control scheme for enhancing IoT-enabled healthcare security using blockchain and machine learning. Sci. Rep. 2025, 15, 7589. [Google Scholar] [CrossRef] [PubMed]
- Guan, H.; Yu, L.; Zhou, L.; Xiong, L.; Chowdhury, K.; Xie, L.; Xiao, X.; Zou, J. Privacy and Accuracy-Aware AI/ML Model Deduplication. arXiv 2025, arXiv:2503.02862. [Google Scholar]
- Yuan, Q.; Pi, Y.; Kou, L.; Zhang, F.; Li, Y.; Zhang, Z. Multi-source data processing and fusion method for power distribution internet of things based on edge intelligence. Front. Energy Res. 2022, 10, 891867. [Google Scholar] [CrossRef]
- Zielosko, B.; Jabloński, K.; Dmytrenko, A. Exploiting Data Distribution: A Multi-Ranking Approach. Entropy 2025, 27, 278. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Tang, G.; Li, Y.; Cai, Z.; Zhang, X.; Zhou, T. A survey on edge computing systems and tools. Proc. IEEE 2019, 107, 1537–1562. [Google Scholar] [CrossRef]
- Nain, G.; Pattanaik, K.; Sharma, G. Towards edge computing in intelligent manufacturing: Past, present and future. J. Manuf. Syst. 2022, 62, 588–611. [Google Scholar] [CrossRef]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double q-learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized experience replay. arXiv 2015, arXiv:1511.05952. [Google Scholar]
- Xiong, X.; Zheng, K.; Lei, L.; Hou, L. Resource Allocation Based on Deep Reinforcement Learning in IoT Edge Computing. IEEE J. Sel. Areas Commun. 2020, 38, 1133–1146. [Google Scholar] [CrossRef]
- Melo, F.S. Convergence of Q-Learning: A Simple Proof; Technical Report; Institute of Systems and Robotics, University of Coimbra: Coimbra, Portugal, 2001; pp. 1–4. [Google Scholar]
- Landis, J.R.; Koch, G.G. The measurement of observer agreement for categorical data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [PubMed]


| Aspect | Cloud-Edge-End Architecture | InS System |
|---|---|---|
| Applicable Scenarios | General-purpose terminals and large-scale application scenarios | Terminal systems requiring in situ data processing |
| Data Processing | Data is transmitted to remote edge nodes and then uploaded to the cloud | InS performs processing directly near the data source; cloud and edge computing are considered only when necessary |
| Data Generation Location | Terminal data generated near urban areas | Terminal data generated near wind turbines |
| End Node Characteristics | Distributed in urban areas with higher computing demand density | Distributed in remote areas due to constraints such as wind conditions and geographic limitations |
| Edge Nodes Location | Edge nodes are primarily deployed in areas with higher demand density | Edge nodes are primarily deployed in areas with higher demand density |
| Transmission to Edge Nodes | Relatively short transmission distance | Relatively long transmission distance, significantly constrained by latency and bandwidth limitations |
| Method | Description | Algorithm Complexity | Code Complexity |
|---|---|---|---|
| Baseline | Without considering the delay and congestion of the system’s personalized demand queues, a queue is randomly selected for response in each round. | ||
| ABC | The Artificial Bee Colony (ABC) optimization algorithm allocates and optimizes resources through exploration, following, and scouting processes, aiming to find the optimal media selection strategy. | ||
| DQN | Based on the DQN algorithm, system states are considered for continuous decision-making optimization, selecting the best response queue in each round [29]. | ||
| DDQN | A double Q-value update mechanism is introduced on the basis of the DQN algorithm, along with a target network, to address the issue of overestimation of action values in DQN [27]. | ||
| DDQN + PER (ours) | Based on the DDQN algorithm, the introduction of the Prioritized Experience Replay mechanism enables more frequent training on experiences that have a greater impact on the Q-Network, thereby accelerating the learning process. |
| Parameter | Baseline | ABC | DQN | DDQN | DDQN + PER |
|---|---|---|---|---|---|
| max epochs | 5000 | 5000 | 5000 | 5000 | 5000 |
| Adjustment Factor () | 1 / 1.5 | 1 / 1.5 | 1 / 1.5 | 1 / 1.5 | 1 / 1.5 |
| Discount Factor () | - | - | 0.99 | 0.99 | 0.99 |
| Epsilon () | - | - | 1.0 | 1.0 | 1.0 |
| Epsilon Decay () | - | - | 0.995 | 0.995 | 0.995 |
| Learning Rate () | - | - | 0.001 | 0.001 | 0.001 |
| Comparison | Metric | ||
|---|---|---|---|
| DDQN + PER | AWD (↓) | 96.83% | 99.54% |
| vs. | ARR (↓) | 97.99% | 99.76% |
| Baseline | ARL (↓) | 95.28% | 99.18% |
| DDQN + PER | AWD (↓) | 95.76% | 99.38% |
| vs. | ARR (↓) | 97.87% | 99.68% |
| ABC | ARL (↓) | 91.60% | 99.09% |
| DDQN + PER | AWD (↓) | 41.93% | 5.20% |
| vs. | ARR (↓) | 58.47% | 11.73% |
| DQN | ARL (↓) | 45.08% | 56.49% |
| DDQN + PER | AWD (↓) | 36.23% | 52.99% |
| vs. | ARR (↓) | 53.87% | 65.22% |
| DDQN | ARL (↓) | 43.13% | 43.94% |
| Algorithm Group | Metric | Fleiss’ Kappa | Consistency Interpretation |
|---|---|---|---|
| Baseline, ABC | AWD | 0.12 | Slight consistency |
| ARR | 0.08 | Poor consistency | |
| ARL | 0.15 | Slight consistency | |
| DQN, DDQN, DDQN-PER | AWD | 0.45 | Moderate consistency |
| ARR | 0.52 | Moderate consistency | |
| ARL | 0.36 | Fair consistency |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Li, S.; Li, D.; Ding, Q.; Shi, L. Sensor-Generated In Situ Data Management for Smart Grids: Dynamic Optimization Driven by Double Deep Q-Network with Prioritized Experience Replay. Appl. Sci. 2025, 15, 5980. https://doi.org/10.3390/app15115980
Zhang P, Li S, Li D, Ding Q, Shi L. Sensor-Generated In Situ Data Management for Smart Grids: Dynamic Optimization Driven by Double Deep Q-Network with Prioritized Experience Replay. Applied Sciences. 2025; 15(11):5980. https://doi.org/10.3390/app15115980
Chicago/Turabian StyleZhang, Peiying, Siyi Li, Dandan Li, Qingyang Ding, and Lei Shi. 2025. "Sensor-Generated In Situ Data Management for Smart Grids: Dynamic Optimization Driven by Double Deep Q-Network with Prioritized Experience Replay" Applied Sciences 15, no. 11: 5980. https://doi.org/10.3390/app15115980
APA StyleZhang, P., Li, S., Li, D., Ding, Q., & Shi, L. (2025). Sensor-Generated In Situ Data Management for Smart Grids: Dynamic Optimization Driven by Double Deep Q-Network with Prioritized Experience Replay. Applied Sciences, 15(11), 5980. https://doi.org/10.3390/app15115980






