Multi-Objective Optimal Allocation of Regional Water Resources Based on the Improved NSGA-III Algorithm
Abstract
1. Introduction
2. Construction of a Water Resource Optimization Model
2.1. Objective Function
- (1)
- Economic Objective: The objective function is to maximize the water supply benefits.
- (2)
- Social objective. The objective function is to minimize the total water shortage of water users.
- (3)
- Ecological and Environmental Objective: The objective function is to minimize the pollutant emissions.
2.2. Constraints
- (1)
- Water Availability Constraint:
- (2)
- Water Demand Constraint
- (3)
- Pollutant discharge limit constraint:
- (4)
- Non-negativity constraint on variables:
3. Algorithm Improvement and Scheme Evaluation
3.1. Improvement Strategy for the NSGA-III Algorithm
3.1.1. Reference Point Improvement Strategy
3.1.2. Dynamic Solution Retention Mechanism
3.1.3. Optimization of Selection Strategy
3.1.4. Algorithm Implementation Process:
| Algorithm 1: Pseudo-code of I-NSGA-III |
| 1: Input: P0, Tm, N, H (Initial population, maximum number of iterations, Population size, reference point set) 2: Output: Pareto solutions 3: Initialize uniform distribution reference points H; t = 0; 4: Compute Zmin from feasible solutions in P0; 5: 6: while termination conditions are not satisfied (t < Tm) do 7: 8: if t < Tm/4 and rand () < 0.5 then 9: Use Improvement 1 to identify and reserve elite solution q; 10: g = 1; (Indicates that a high-quality solution is selected) 11: else 12: g = 0; 13: end if 14: 15: (Section 3.1.3. Optimization of Selection Strategy) 16: Perform non-dominated sorting on Pt; 17: Use Improvement 2 to dynamically adjust selection Number of candidate individuals K; 18: ζ= adaptive tournament selection (Pt, g); 19: 20: Qt = Recombination & Mutation(ζ); 21: Ct = Pt ∪ Qt; 22: Perform non-dominated sorting on Ct; 23: Pt+1 = SelectSolutions (Ct, g); 24: 25: if g > 0 then 26: Add reserved elite solution q to Pt+1; 27: end if 28: 29: Use Reference Point Improvement Strategy (Section 3.1.1) to generate new reference points based on current front; 30: Update reference point set H; 31: 32: t = t + 1; 33: 34: end while 35: 36: return Non-dominated solutions in Pt as Pareto-optimal front |
3.1.5. Algorithm Testing
3.2. Evaluation of Water Resource Allocation Plans
3.2.1. Establishment of an Indicator System
3.2.2. Multi-System Coupling Coordination Degree Evaluation Model
4. Overview of the Study Area and Model Setup
4.1. Overview of the Study Area
4.2. Data Source
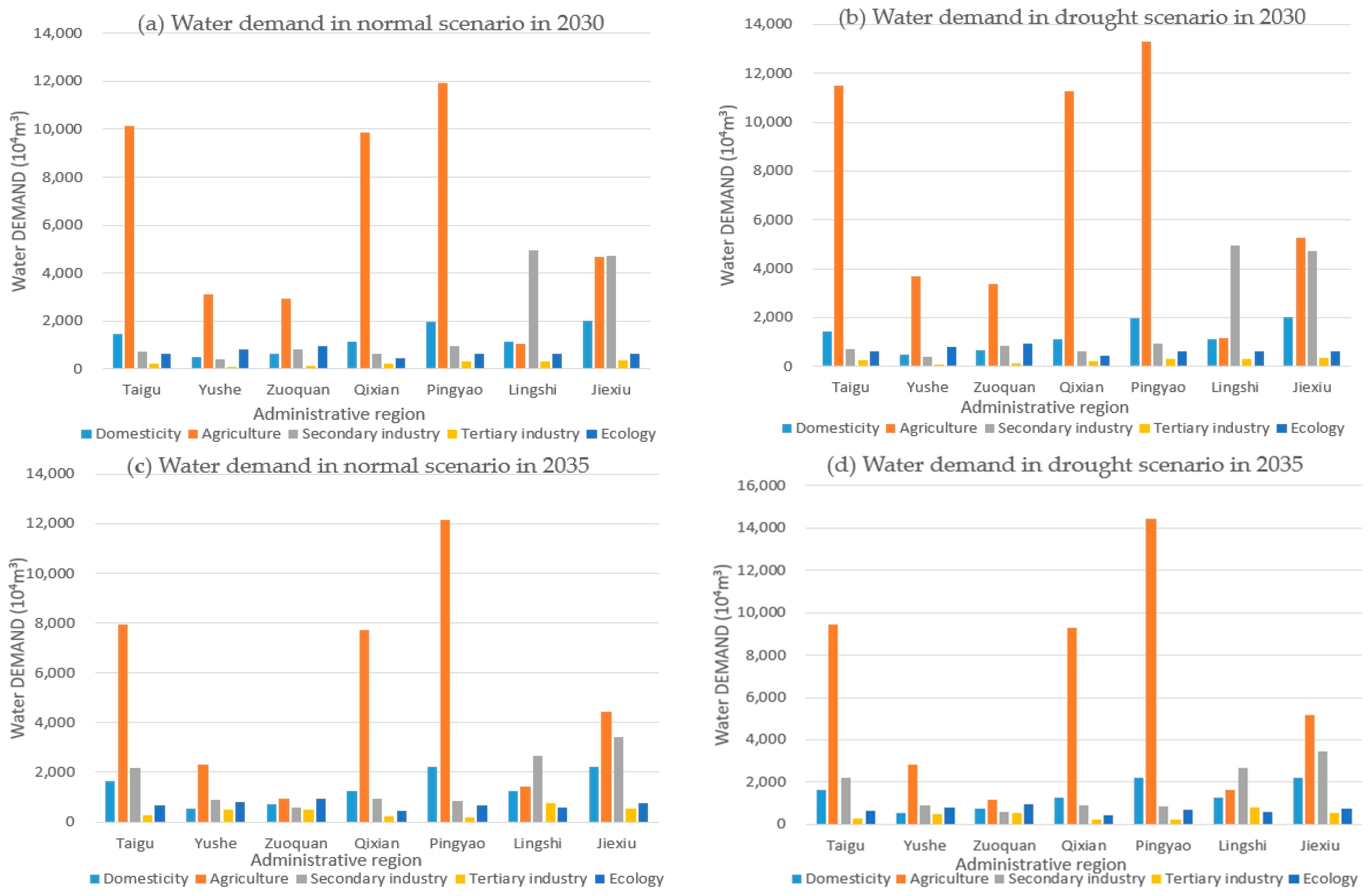
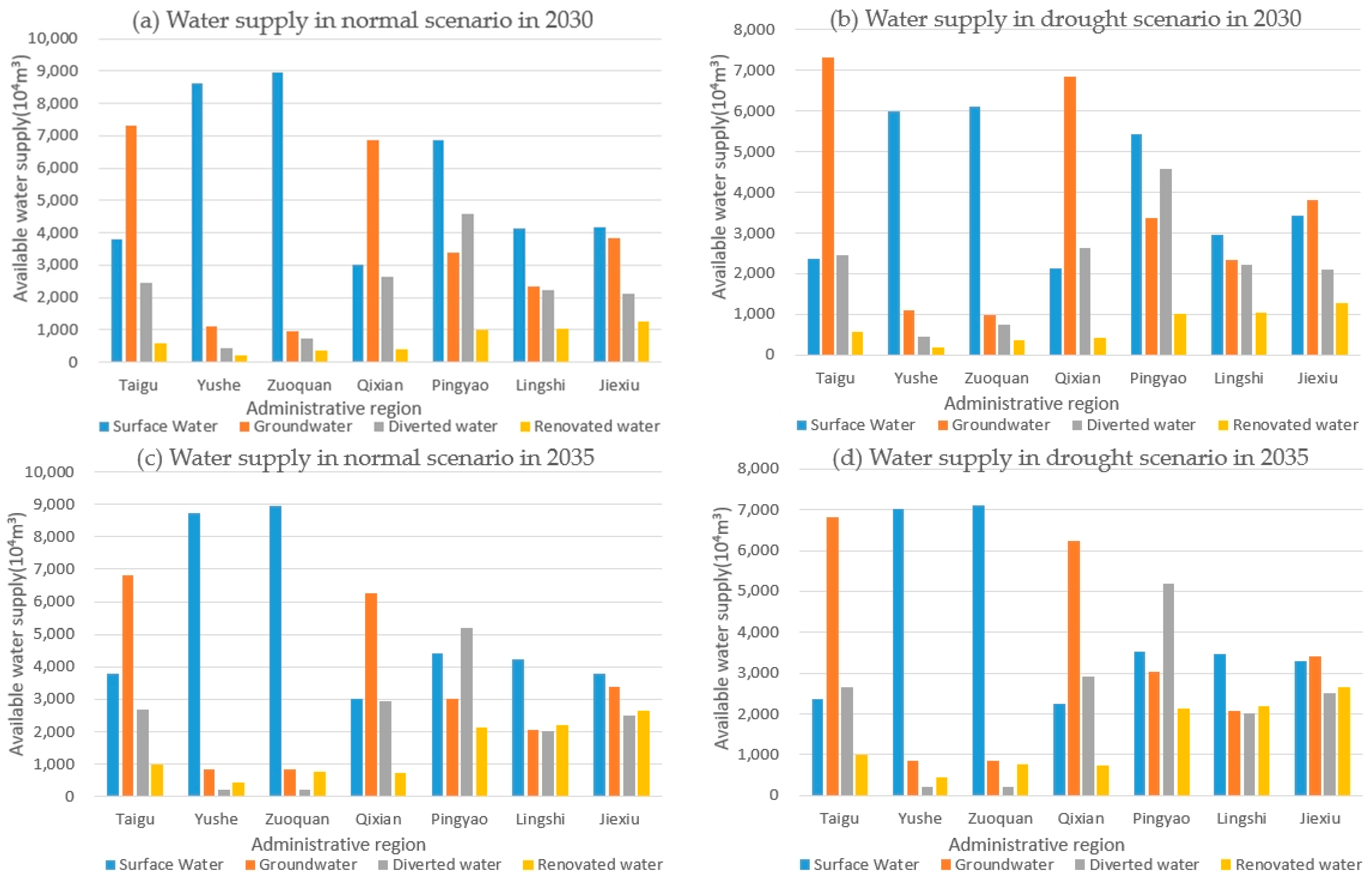
4.3. Water Supply and Demand Forecast
4.4. Model Parameters
5. Results and Analysis
5.1. Evaluation of Scheme Effectiveness
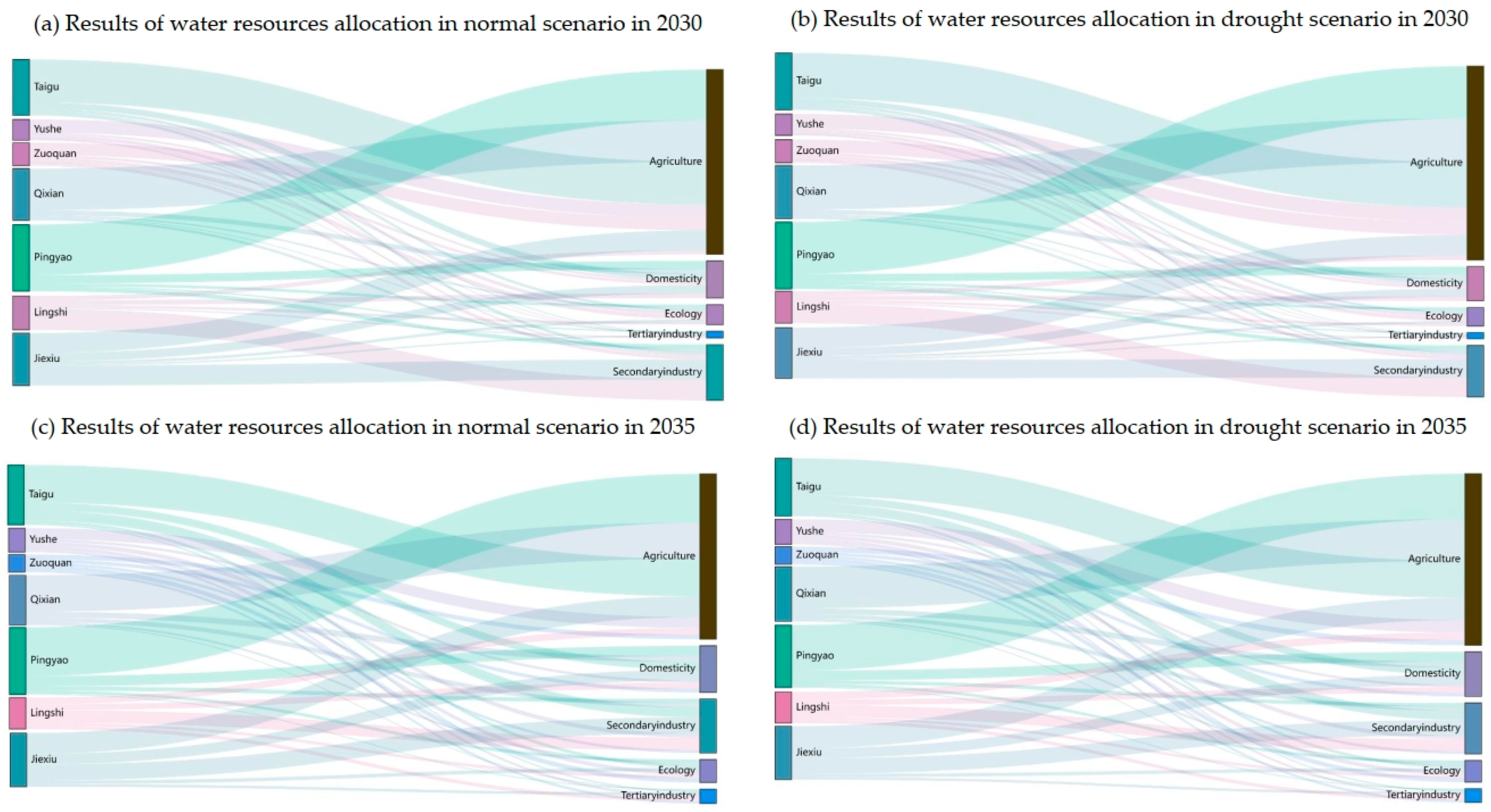
5.2. Water Resource Allocation Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abdulbaki, D.; Al-Hindi, M.; Yassine, A.; Yassine, A.; Abou Najm, M. An optimization model for the allocation water resources. J. Clean. Prod. 2017, 164, 994–1006. [Google Scholar] [CrossRef]
- Zhang, F.; Wu, Z.; Di, D.; Wang, H. Water resources allocation based on water resources supply-demand forecast and comprehensive values of water resources. J. Hydrol. Reg. Stud. 2023, 47, 101421. [Google Scholar] [CrossRef]
- Wei, F.; Zhang, X.; Xu, J.; Bing, J.; Pan, J.G. Simulation of water resource allocation for sustainable urban development: An integrated optimization approach. J. Clean. Prod. 2020, 273, 122537. [Google Scholar] [CrossRef]
- Genova, P.; Wei, Y. A socio-hydrological model for assessing water resource allocation and water environmental regulations in the Maipo River basin. J. Hydrol. 2023, 617, 129159. [Google Scholar] [CrossRef]
- Liu, W. Analysis of urban water resources pollution control and environmental protection. Heilongjiang Environ. J. 2025, 38, 118–120. [Google Scholar]
- Jia, Z.; Liu, P.; Ma, Y.; Zheng, F. An Analysis of the Dynamic Evolution and Utilization of Water Resources in China. Water Resour. Power 2023, 41, 27–30. [Google Scholar] [CrossRef]
- Wu, Y.; Zeng, C.; Yang, K.; Yu, Y.; He, Q.; Zhong, X. Multi-objective optimal allocation of water resources based on improved NSGA-II algorithm. Yellow River 2020, 42, 71–75. [Google Scholar]
- Yuan, Z.; Yang, K.; Chen, J.; Qian, L.; Li, Z.; Wu, J. Multi-objective optimal allocation scheme decision of regional water resources based on NSGA-III. Yellow River 2024, 46, 79–84+153. [Google Scholar]
- Haimes, Y.Y.; Lasdon, L.S.; Wismer, D.A. On a Bicriterion Formulation of the Problems of Integrated System Identification and System Optimization. In IEEE Transactions on Systems, Man, and Cybernetics; IEEE Advancing Technology for Humanity: Piscataway, NJ, USA, 1971; Volume SMC-1, pp. 296–297. [Google Scholar] [CrossRef]
- Haimes, Y.Y.; Hall, W.A. Multiobjectives in water resource systems analysis: The Surrogate Worth Trade Off Method. Water Resour. Res. 1974, 10, 615–624. [Google Scholar] [CrossRef]
- Loucks, D.P.; van Beek, E. (Eds.) Modeling Uncertainty. In Water Resource Systems Planning and Management: An Introduction to Methods, Models, and Applications; Springer International Publishing: Cham, Switzerland, 2017; pp. 301–330. [Google Scholar]
- Roozbahani, R.; Schreider, S.; Abbasi, B. Economic sharing of basin water resources between competing stakeholders. Water Resour. Manag. 2013, 27, 2965–2988. [Google Scholar] [CrossRef]
- Choi, B.; Lee, G.; Lee, M. Modeling and stochastic dynamic optimization for optimal energy resource allocation. Comput. Aided Chem. Eng. 2012, 31, 765–31769. [Google Scholar]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–73. Available online: https://www.jstor.org/stable/24939139 (accessed on 15 November 2024). [CrossRef]
- Arabi, M.; Govindaraju, R.S.; Hantush, M.M. Cost-effective allocation of watershed management practices using a genetic algorithm. Water Resour. Res. 2006, 42, 2405–2411. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar]
- Jahandideh-Tehrani, M.; Bozorg-Haddad, O.; Loáiciga, H.A. Application of particle swarm optimization to water management: An introduction and overview. Environ. Monit. Assess. 2020, 192, 281. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, S.; Gelatt, J.C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Aerts, J.C.J.H.; Heuvelink, G.B.M. Using simulated annealing for resource allocation. Int. J. Geogr. Inf. Sci. 2002, 16, 571–587. [Google Scholar] [CrossRef]
- Zhang, J.; Dong, Z.; Chen, T. Multi-Objective Optimal Allocation of Water Resources Based on the NSGA-2 Algorithm While Considering Intergenerational Equity: A Case Study of the Middle and Upper Reaches of Huaihe River Basin, China. Int. J. Environ. Res. Public Health 2020, 17, 9289. [Google Scholar] [CrossRef]
- Baltar, A.M.; Fontane, D.G. Use of multiobjective particle swarm optimization in water resources management. J. Water Resour. Plan. Manag. 2008, 134, 257–265. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. In IEEE Transactions on Evolutionary Computation; IEEE Computational Intelligence Society: Park Avenue, NY, USA, 2007; Volume 11, pp. 712–731. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, X.; Wu, W.; Yao, L.; Guo, Q. Optimal allocation of water resources in Taiyuan City based on NSGA-II + ARSBX algorithm. Adv. Sci. Technol. Water Resour. 2025, 45, 79–86+103. [Google Scholar]
- Li, Z.; Zhao, X.; Li, J.; Li, Y. Research on the optimal allocation of water resources in Yangquan City based on improved particle swarm optimization algorithm. J. N. China Univ. Water Resour. Electr. Power 2024, 45, 15–21. [Google Scholar]
- Li, C.; Jiang, H.; He, Y.; Mu, Z. Study on water resources allocation and scheme optimization based on WRMM model. J. Water Resour. Water Eng. 2016, 27, 32–38. [Google Scholar]
- Bezdan, A.; Bezdan, J.; Marković, M.; Mirčetić, D.; Baumgertel, A.; Salvai, A.; Blagojević, B. An objective methodology for waterlogging risk assessment based on the entropy weighting method and machine learning. CATENA 2025, 249, 108618. [Google Scholar] [CrossRef]
- Guo, J.; Jiang, Z.; Ying, J.; Feng, X.; Zheng, F. Optimal allocation model of port emergency resources based on the improved multi-objective particle swarm algorithm and TOPSIS method. Mar. Pollut. Bull. 2024, 209, 117214. [Google Scholar] [CrossRef]
- Yuan, L.; Liu, H.; Lu, Y.; Zhou, C.; Zhou, C.; Lu, Y. Multi-objective integrated decision method of cascade hydropower stations based on optimization algorithm and evaluation model. J. Hydrol. 2024, 638, 131533. [Google Scholar] [CrossRef]
- Zhao, Q.; Bai, Q.; Nie, K.; Wang, H.; Zeng, X. Multi-objective optimal allocation of regional water resources based on NSGA-III algorithm and TOPSIS decision. J. Drain. Irrig. Mach. Eng. 2022, 40, 1233–1240. [Google Scholar]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: Handling constraints and extending to an adaptive approach. IEEE Trans. Evol. Comput. 2014, 18, 602–622. [Google Scholar] [CrossRef]
- Das, I.; Dennis, J.E. Normal-boundary intersection: A new method for generating the Pareto surface in nonlinear multicriteria optimization problems. SIAM J. Optim. 1998, 8, 631–657. [Google Scholar] [CrossRef]
- Bi, X.; Wang, C. An improved NSGA-III algorithm based on objective space decomposition for many-objective optimization. Soft Comput. 2017, 21, 4269–4296. [Google Scholar] [CrossRef]
- Yuan, T.; Yin, Y.; Huang, F.; Chen, Y. Adaptive weight adjustment MOEA/D with global replacement. Control. Theory Appl. Control. Theory Appl. 2023, 40, 653–662. [Google Scholar]
- Changming, J.; Haoyu, M.; Yang, P. Research on evolutionary algorithm for multi-objective optimal operation of cascade reservoirs. J. Hydraul. Eng. 2020, 51, 1441–1452. [Google Scholar]
- Jia, Z.; Zhao, X.; Cui, C. Research on decision-making method of water resources allocation based on coordinated equilibrium. Henan Water Resour. South–North Water Divers. 2020, 49, 35–37. [Google Scholar]
- Fu, L.; Yang, K.; Liu, J.; Zhong, J.; Qiu, G.; Gu, G.; Jiang, M.; Wang, X.; Liang, Y. Evaluation model of reclaimed water based on multi-level superiority evaluation method. Water Resour. Power 2018, 36, 34–37. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, S. Research on the spatial-temporal coupling coordination of carbon emission-technological innovation-green development in the Yangtze River Economic Belt. Resour. Environ. Yangtze Basin 2025, 34, 494–506. [Google Scholar]
- GB 50318-2017; Code for Planning of Urban Drainage Engineering. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2017.
- Li, M.; Zhao, X.; Zhang, Z.; Zuo, Q. An optimal allocation model of water resources in water-deficient areas for high-quality development and its application. Yellow River 2024, 46, 73–79. [Google Scholar]
- DB14/1928-2019; Integrated Wastewater Discharge Standards. Shanxi Provincial Department of Ecology and Environment: Taiyuan, China, 2019.
- Zhu, S.; Li, Z. Optimal allocation of water resources in Jinzhong City based on improved NSGA-II algorithm. China Rural. Water Hydropower 2023, 91–97+105. Available online: https://link.cnki.net/urlid/42.1419.TV.20220711.1416.079 (accessed on 23 May 2025).
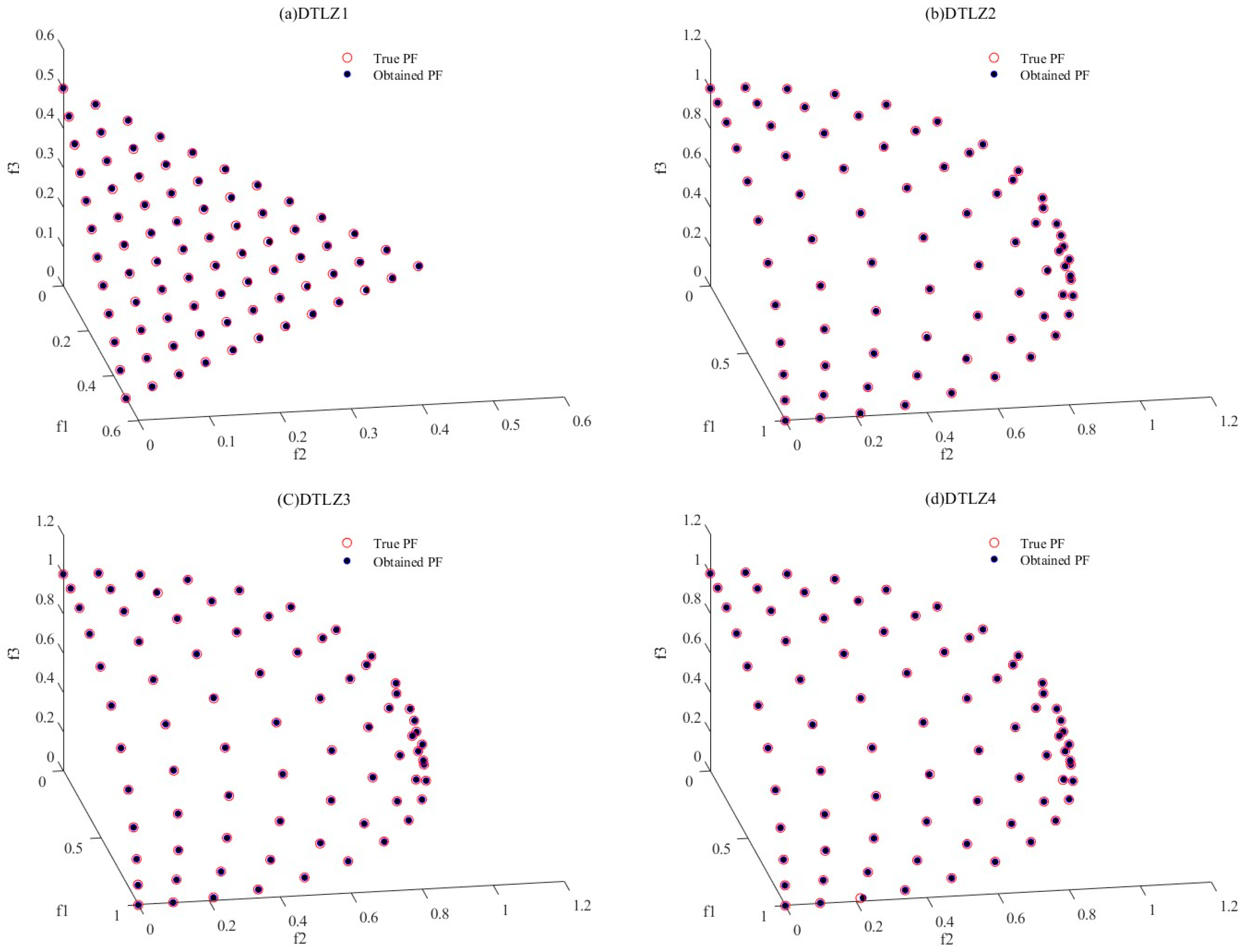



| Function | Characteristics | Maximum Iteration |
|---|---|---|
| DTLZ1 | Linear, multimodal | 200 |
| DTLZ2 | Concave | 500 |
| DTLZ3 | Concave, multimodal | 700 |
| DTLZ4 | Concave, biased | 400 |
| Function | Model | IGD | HV | ||
|---|---|---|---|---|---|
| Median | Std. | Median | Std. | ||
| DTLZ1 | I-NSGA-III | 6.26 × 10−4 | 1.01 × 10−3 | 8.31 × 10−1 | 1.47 × 10−1 |
| NSGA-III | 1.26 × 10−3 | 1.15 × 10−3 | 8.09 × 10−1 | 2.86 × 10−1 | |
| NSGA-II | 3.17 × 10−2 | 1.07 × 10−3 | 7.82 × 10−1 | 3.25 × 10−1 | |
| MOEA/D | 2.20 × 10−2 | 8.56 × 10−2 | 7.93 × 10−1 | 2.73 × 10−1 | |
| RVEA | 2.78 × 10−2 | 1.57 × 10−1 | 8.02 × 10−1 | 1.76 × 10−1 | |
| DTLZ2 | I-NSGA-III | 2.72 × 10−4 | 3.99 × 10−5 | 5.71 × 10−1 | 1.06 × 10−5 |
| NSGA-III | 2.87 × 10−4 | 7.27 × 10−5 | 5.41 × 10−1 | 1.88 × 10−5 | |
| NSGA-II | 8.62 × 10−2 | 4.41 × 10−3 | 5.18 × 10−1 | 3.98 × 10−1 | |
| MOEA/D | 2.75 × 10−4 | 2.76 × 10−4 | 5.51 × 10−1 | 1.21 × 10−5 | |
| RVEA | 2.45 × 10−4 | 4.26 × 10−5 | 5.51 × 10−1 | 7.64 × 10−5 | |
| DTLZ3 | I-NSGA-III | 1.36 × 10−2 | 1.42 × 10−2 | 5.54 × 10−1 | 8.12 × 10−3 |
| NSGA-III | 1.71 × 10−2 | 1.78 × 10−2 | 5.15 × 10−1 | 1.45 × 10−2 | |
| NSGA-II | 9.02 × 10−2 | 4.18 × 10−3 | 4.96 × 10−1 | 1.44 × 10−1 | |
| MOEA/D | 1.91 × 10−2 | 1.52 × 10−2 | 5.22 × 10−1 | 2.41 × 10−2 | |
| RVEA | 2.22 × 10−2 | 3.17 × 10−1 | 5.32 × 10−1 | 1.26 × 10−2 | |
| DTLZ4 | I-NSGA-III | 3.66 × 10−4 | 3.40 × 10−1 | 5.51 × 10−1 | 4.93 × 10−2 |
| NSGA-III | 3.85 × 10−4 | 3.37 × 10−1 | 4.39 × 10−1 | 1.34 × 10−1 | |
| NSGA-II | 8.39 × 10−2 | 2.74 × 10−1 | 5.23 × 10−1 | 1.33 × 10−1 | |
| MOEA/D | 2.64 × 10−1 | 3.47 × 10−1 | 4.44 × 10−1 | 1.12 × 10−1 | |
| RVEA | 3.82 × 10−4 | 2.67 × 10−1 | 5.29 × 10−1 | 6.65 × 10−2 | |
| Function | Model | IGD (Median) | IGD (Std.) | IGD p-Value | HV(Median) | HV (Std.) | HV p-Value |
|---|---|---|---|---|---|---|---|
| DTLZ1 | I-NSGA-III | 6.08 × 10−4 | 4.12 × 10−3 | — | 8.31 × 10−1 | 8.04 × 10−3 | — |
| NSGA-III | 1.19 × 10−3 | 7.45 × 10−3 | 0.0001 | 8.13 × 10−1 | 2.89 × 10−1 | 0.0004 | |
| DTLZ2 | I-NSGA-III | 2.76 × 10−4 | 2.47 × 10−5 | — | 5.71 × 10−1 | 1.06 × 10−5 | — |
| NSGA-III | 2.83 × 10−4 | 1.85 × 10−5 | 0.0021 | 5.51 × 10−1 | 1.88 × 10−5 | 0.0001 | |
| DTLZ3 | I-NSGA-III | 1.15 × 10−2 | 1.24 × 10−2 | — | 5.41 × 10−1 | 8.12 × 10−3 | — |
| NSGA-III | 1.78 × 10−2 | 1.13 × 10−2 | 0.0348 | 5.36 × 10−1 | 1.54 × 10−2 | 0.0266 | |
| DTLZ4 | I-NSGA-III | 3.09 × 10−4 | 3.02 × 10−1 | — | 5.50 × 10−1 | 4.93 × 10−2 | — |
| NSGA-III | 3.79 × 10−4 | 3.39 × 10−1 | 0.1559 | 3.39 × 10−1 | 1.33 × 10−1 | 0.0348 |
| First-Level Indicator | Second-Level Indicator | Unit | Attributes |
|---|---|---|---|
| Economic | per capita GDP | CNY | Positive |
| Proportion of secondary industry | % | Positive | |
| Proportion of tertiary industry | % | Positive | |
| Social | per capita water supply | m3/person | Positive |
| Water shortage rate | % | Negative | |
| Ecological | per capita pollutants Emissions | % | Negative |
| Ecological water shortage rate | % | Negative |
| Coordination Degree | Coordination Stage | Coordination Degree | Coordination Stage |
|---|---|---|---|
| [0.0, 0.1) | Extreme Imbalance | [0.5, 0.6) | Barely Coordinated |
| [0.1, 0.2) | Severe Imbalance | [0.6, 0.7) | Primary Coordination |
| [0.2, 0.3) | Moderate Imbalance | [0.7, 0.8) | Intermediate Coordination |
| [0.3, 0.4) | Mild Imbalance | [0.8, 0.9) | Good Coordination |
| [0.4, 0.5) | Borderline Imbalance | [0.9, 1.0) | High-Quality Coordination |
| First-Level Indicator | First-Level Indicator Weight | Second-Level Indicator | Second-Level Indicator Weight | ||
|---|---|---|---|---|---|
| AHP | Entropy Weight Method | Comprehensive Weight | |||
| Economic | 1/3 | per capita GDP | 0.47 | 0.29 | 0.38 |
| Proportion of secondary industry | 0.3 | 0.28 | 0.29 | ||
| Proportion of tertiary industry | 0.23 | 0.43 | 0.33 | ||
| Social | 1/3 | per capita water supply | 0.56 | 0.64 | 0.60 |
| Water shortage rate | 0.44 | 0.36 | 0.40 | ||
| Ecological | 1/3 | per capita pollutants Emissions | 0.5 | 0.29 | 0.39 |
| Ecological water shortage rate | 0.5 | 0.71 | 0.61 | ||
| Pm = 0.05 | Pm = 1/D | |||
|---|---|---|---|---|
| HV (Median) | HV (Std.) | HV (Median) | HV (Std.) | |
| Pc = 0.7 | 0.42 | 2.56 × 10−5 | 0.48 | 3.15 × 10−5 |
| Pc = 0.8 | 0.46 | 4.32 × 10−5 | 0.54 | 1.76 × 10−5 |
| Pc = 0.9 | 0.37 | 6.32 × 10−5 | 0.45 | 1.58 × 10−5 |
| Scheme | Economic Score | Social Score | Environmental Score | Comprehensive Score | Coupling Degree | Coordination Degree | |
|---|---|---|---|---|---|---|---|
| 2030 | P = 50% | 0.8512 | 0.4017 | 0.9967 | 0.7499 | 0.9315 | 0.8358 |
| P = 75% | 0.6855 | 0.4416 | 0.7710 | 0.6327 | 0.9731 | 0.7847 | |
| 2035 | P = 50% | 0.7097 | 0.6295 | 0.8783 | 0.7392 | 0.9904 | 0.8556 |
| P = 75% | 0.7317 | 0.6207 | 0.9556 | 0.7693 | 0.9841 | 0.8701 |
| Scheme | Administrative Region | Domesticity | Agriculture | Secondary Industry | Tertiary Industry | Ecology | Total |
|---|---|---|---|---|---|---|---|
| Normal Scenario | Taigu | 1454 | 10,139 | 731 | 237 | 633 | 13,194 |
| Yushe | 490 | 3108 | 407 | 79 | 823 | 4907 | |
| Zuoquan | 644 | 2920 | 834 | 107 | 950 | 5455 | |
| Qixian | 1115 | 9857 | 610 | 207 | 435 | 12,224 | |
| Pingyao | 1965 | 11,939 | 934 | 289 | 624 | 15,751 | |
| Lingshi | 1115 | 1023 | 4939 | 325 | 614 | 8016 | |
| Jiexiu | 1998 | 4134 | 4329 | 329 | 576 | 10,966 | |
| Total | 8781 | 43,120 | 12,784 | 1573 | 4655 | 70,913 | |
| Drought Scenario | Taigu | 1375 | 9894 | 660 | 208 | 596 | 12,733 |
| Yushe | 490 | 3666 | 407 | 79 | 823 | 5465 | |
| Zuoquan | 644 | 3384 | 834 | 107 | 950 | 5919 | |
| Qixian | 1015 | 9878 | 560 | 175 | 405 | 12,033 | |
| Pingyao | 1837 | 10,883 | 874 | 236 | 573 | 14,403 | |
| Lingshi | 1115 | 1172 | 4939 | 325 | 614 | 8165 | |
| Jiexiu | 1758 | 3903 | 4115 | 294 | 563 | 10,632 | |
| Total | 8232 | 42,780 | 12,388 | 1424 | 4525 | 69,349 |
| Scheme | Administrative Region | Domesticity | Agriculture | Secondary Industry | Tertiary Industry | Ecology | Total |
|---|---|---|---|---|---|---|---|
| Baseline Scenario | Taigu | 1644 | 7927 | 2177 | 287 | 662 | 12,697 |
| Yushe | 551 | 2322 | 890 | 503 | 818 | 5084 | |
| Zuoquan | 720 | 944 | 580 | 514 | 955 | 3713 | |
| Qixian | 1244 | 7716 | 925 | 230 | 452 | 10,567 | |
| Pingyao | 2205 | 10,327 | 804 | 192 | 631 | 14,159 | |
| Lingshi | 1242 | 1404 | 2648 | 773 | 602 | 6669 | |
| Jiexiu | 2223 | 4425 | 3425 | 554 | 751 | 11,377 | |
| Total | 9828 | 35,064 | 11,450 | 3054 | 4871 | 64,268 | |
| Water—Saving Scenario | Taigu | 1644 | 8203 | 2089 | 287 | 630 | 12,853 |
| Yushe | 551 | 2832 | 890 | 503 | 818 | 5594 | |
| Zuoquan | 720 | 1141 | 580 | 514 | 955 | 3911 | |
| Qixian | 1244 | 9278 | 925 | 230 | 452 | 12,129 | |
| Pingyao | 2205 | 10,089 | 780 | 199 | 617 | 13,890 | |
| Lingshi | 1242 | 1652 | 2648 | 773 | 602 | 6917 | |
| Jiexiu | 2223 | 4926 | 3403 | 541 | 739 | 11,832 | |
| Total | 9828 | 38,121 | 11,316 | 3048 | 4813 | 67,127 |
| Scheme | Water Shortage (104 m3) | Economic Benefit (108 CNY) | COD Emission (104 t) | |
|---|---|---|---|---|
| 2030 | P = 50% | 1390 | 175.6215 | 6.3144 |
| P = 75% | 8447 | 161.9397 | 6.0303 | |
| 2035 | P = 50% | 1319 | 218.1919 | 6.7996 |
| P = 75% | 6155 | 212.7355 | 6.9074 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, Y.; He, B. Multi-Objective Optimal Allocation of Regional Water Resources Based on the Improved NSGA-III Algorithm. Appl. Sci. 2025, 15, 5963. https://doi.org/10.3390/app15115963
Wang Y, Wang Y, He B. Multi-Objective Optimal Allocation of Regional Water Resources Based on the Improved NSGA-III Algorithm. Applied Sciences. 2025; 15(11):5963. https://doi.org/10.3390/app15115963
Chicago/Turabian StyleWang, Yuhao, Yi Wang, and Bin He. 2025. "Multi-Objective Optimal Allocation of Regional Water Resources Based on the Improved NSGA-III Algorithm" Applied Sciences 15, no. 11: 5963. https://doi.org/10.3390/app15115963
APA StyleWang, Y., Wang, Y., & He, B. (2025). Multi-Objective Optimal Allocation of Regional Water Resources Based on the Improved NSGA-III Algorithm. Applied Sciences, 15(11), 5963. https://doi.org/10.3390/app15115963





