An Improved Large Neighborhood Search Algorithm for the Comprehensive Container Drayage Problem with Diverse Transport Requests
Abstract
1. Introduction
- (1)
- A comprehensive CDP is mathematically formulated as an innovative MILP model based on the DAOV graph, which is capable of simultaneously accommodating all types of transport requests, two trucking operation modes, two empty container repositioning strategies, and empty container constraints across multiple depots. Given the non-pairing of IE and OE requests, the forbidden arc is introduced into the model. Although there is only one terminal, it is handled in two distinct ways, depending on the request types. The terminal vertices of IE and OE requests are uniquely numbered to ensure that each request is executed, while those of IF/OF-related requests are ignored by using hyperarcs to reduce unnecessary arcs.
- (2)
- From a methodological perspective, the inherent complexity of the comprehensive CDP renders the attainment of an exact solution for industrial-sized instances highly challenging. To efficiently solve the problem, an improved LNS algorithm is developed by incorporating the “Sequential insertion” and the “Solution re-optimization” methods. The “Sequential insertion” method is responsible for converting the solution into multiple truck routes, while the “Solution re-optimization” method is used to refine the quality of solutions and ensure the feasibility of the truck routing plan.
- (3)
- The performance of the proposed LNS is evaluated by comparing it with MILP and GA for varying scale instances. The results not only demonstrate the effectiveness and efficiency of the LNS but also reinforce its potential as a more optimal approach in solving the problem at hand. Moreover, a sensitivity analysis is carried out to investigate the effect of the number and distribution of depots and empty containers, offering useful managerial insights for decision makers.
2. Literature Review
3. Problem Definition and Formulations
3.1. Problem Description
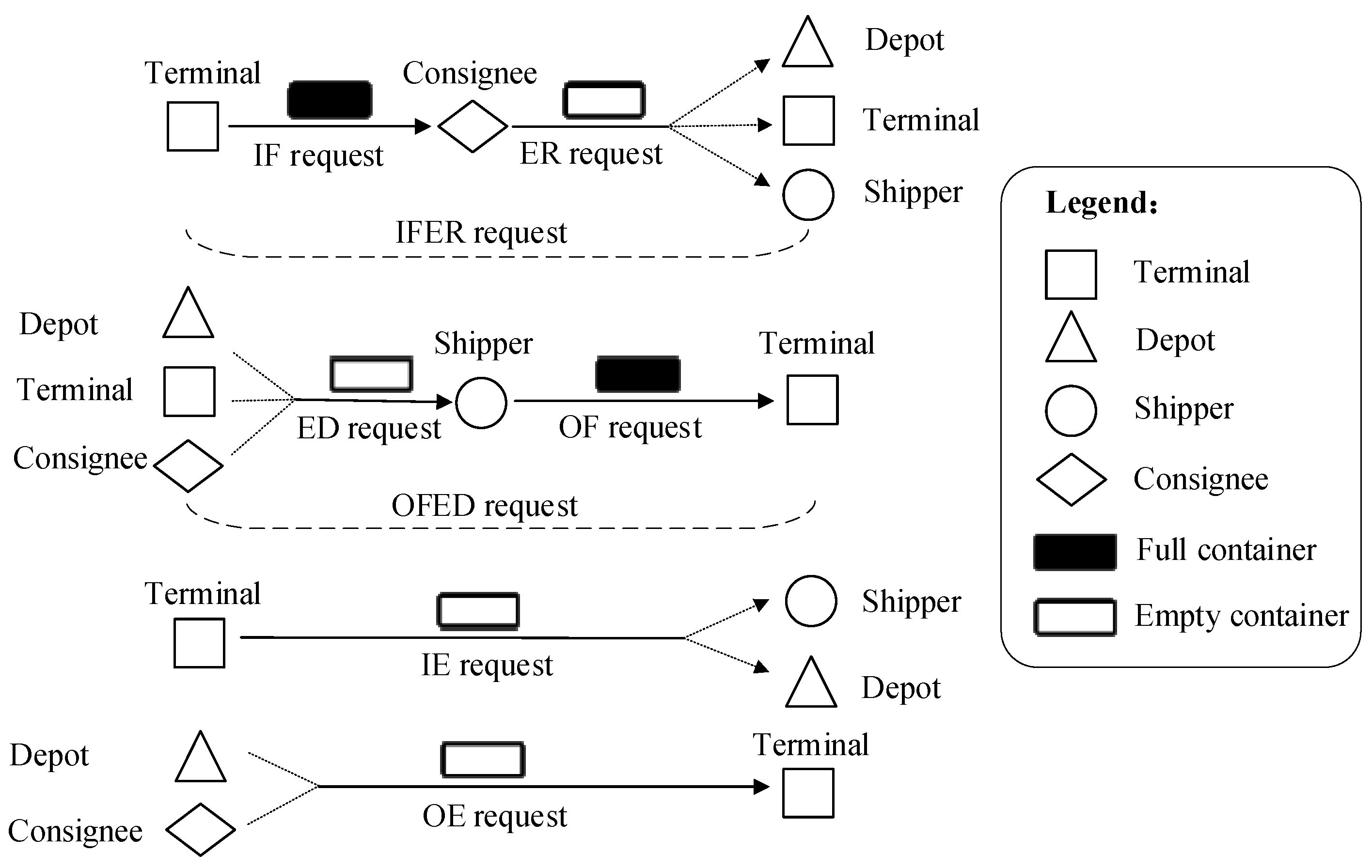
- (1)
- IF request: This requires hauling the inbound full container from the terminal (Origin) to the consignee (Destination). This kind of request is very common, as sometimes a container cannot be unpacked on the same day as it is delivered, and the emptied container will need to be picked up the other day.
- (2)
- ER request: This refers to hauling back the emptied container from the consignee (Origin) to the terminal, a depot, or a shipper demanding an empty container after an IF container has been unpacked. The destination of an ER request is flexible, thus offering potential for optimization at the operational level.
- (3)
- ED request: This involves hauling an empty container from a terminal, a depot, or a consignee to a shipper (Destination) demanding it. The ED request is not always combined with OF request, as the empty container may not be packed immediately after its arrival, and thus the loaded container transport request can only be submitted afterward.
- (4)
- OF request: This specifies hauling the outbound full container from the shipper (Origin) to the terminal (Destination).
- (5)
- IE request: This entails hauling the inbound empty container from the terminal (Origin) to a depot or a shipper who demands it. However, the destination of an IE request cannot be the terminal. If the destination is the terminal in a one-terminal scenario, the transportation will be handled by internal or in-port trucks, which are not managed by the trucking company.
- (6)
- OE request: This implies hauling the outbound empty container from a depot or a consignee to the terminal (Destination). The IE and OE requests are submitted by shipping companies due to the requirement of empty container repositioning between different terminals or regions.
- (7)
- IFER request: This is a composite request, which means that a consignee requires an IF container to be picked up from the terminal and delivered to their location, and the empty container to be picked up immediately after unpacking and repositioned to a suitable place.
- (8)
- OFED request: This is also a composite request, which indicates that a shipper requires an empty container to be delivered from the location where it is available to their location, and the OF container to be picked up immediately after packing and finally delivered to the terminal.
3.2. Graphical Formulation
3.2.1. The DAOV Graph
3.2.2. Network Flow Constraints
3.3. Mathematical Formulation
3.3.1. Notations and Parameters
3.3.2. Decision Variables
3.3.3. Formulation
3.3.4. Linearization
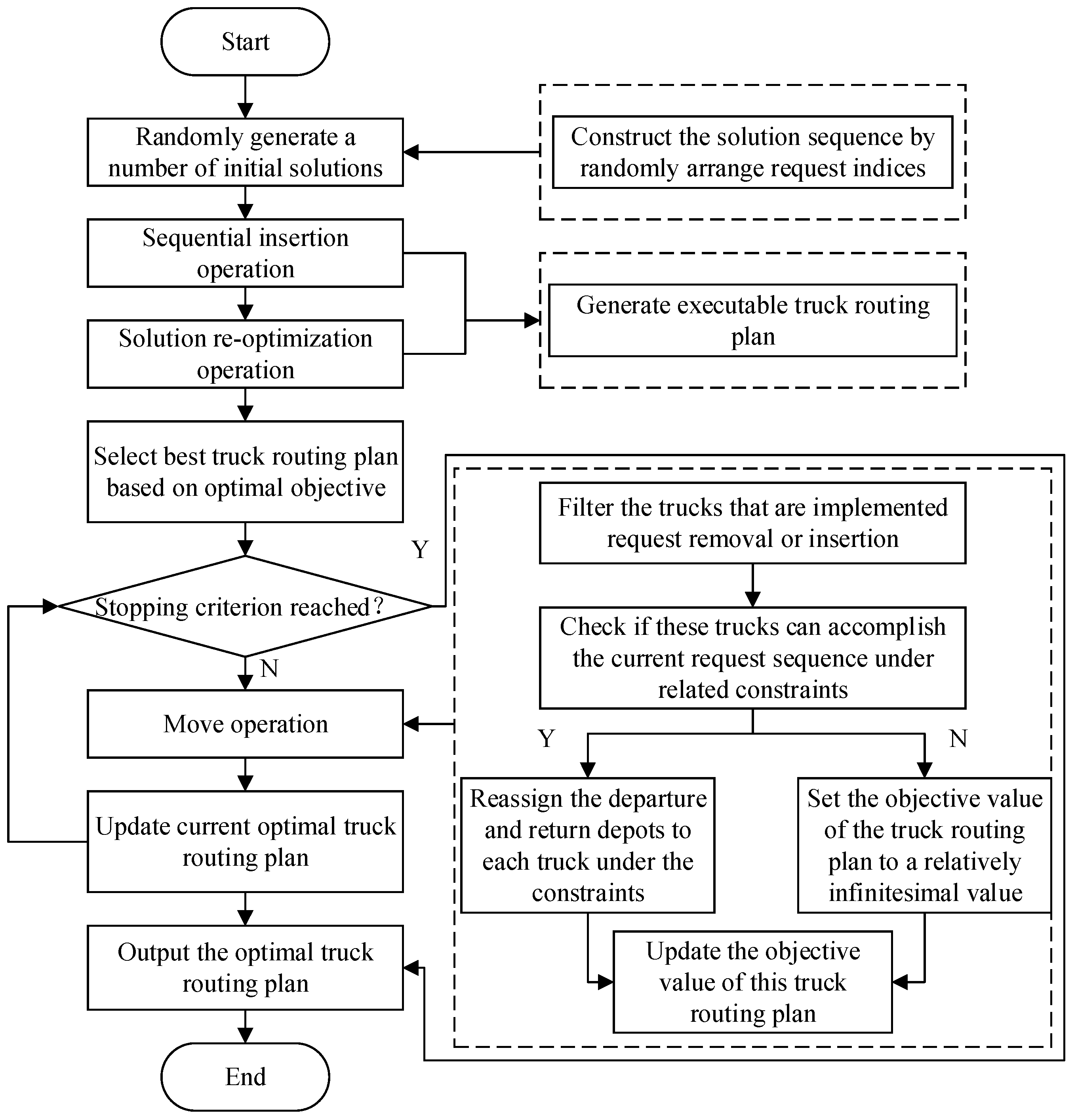
4. Solution Algorithm
4.1. Generation of Initial Solution
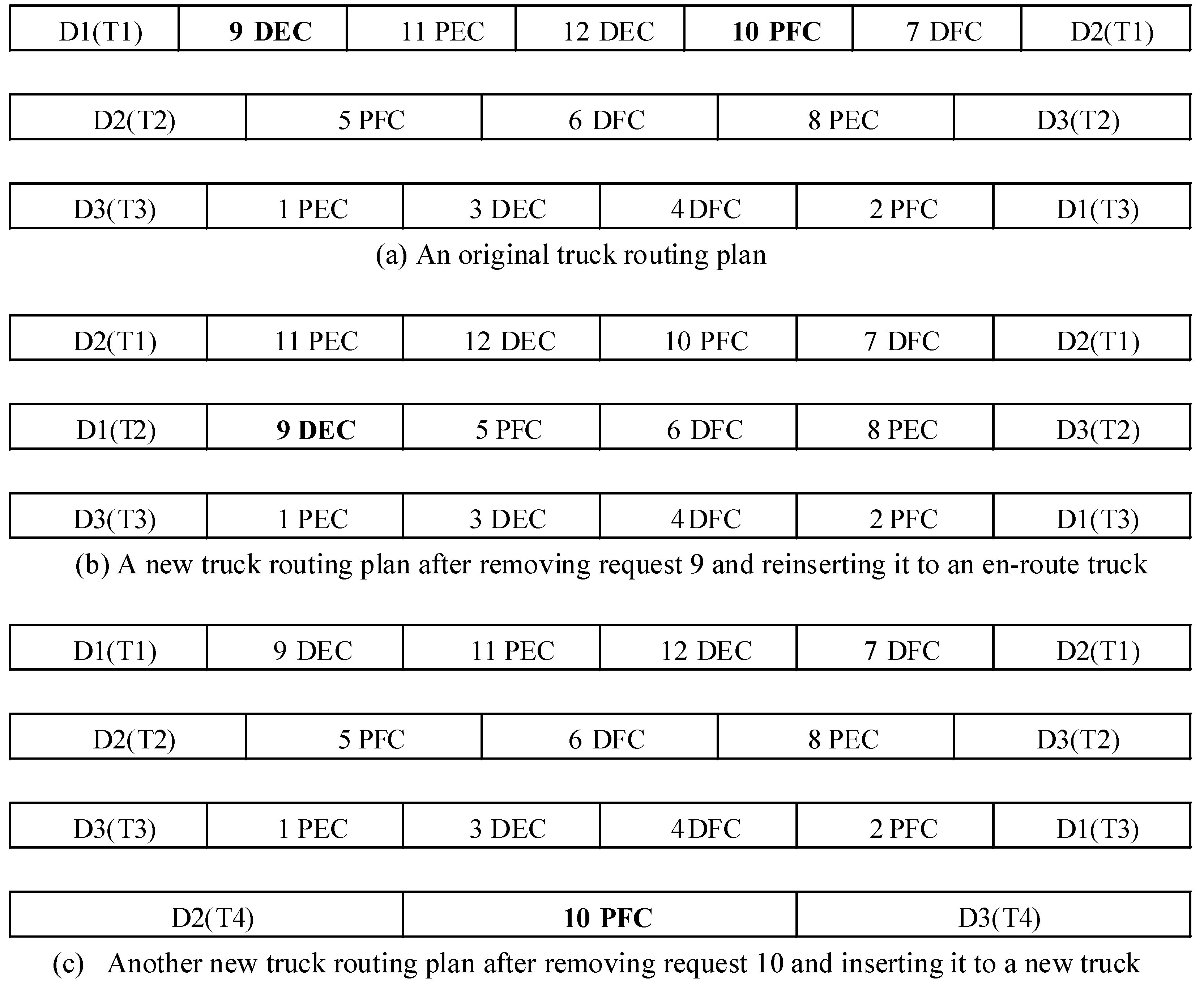
4.2. Sequential Insertion and Solution Re-Optimization Methods
4.3. Move Operation
4.4. Stopping Criterion
5. Numerical Experiments
5.1. Experiments Setting and Instances Generation
5.2. Experiments on Small- and Medium-Scale Instances
5.3. Experiments on Large- and Super-Large-Scale Instances
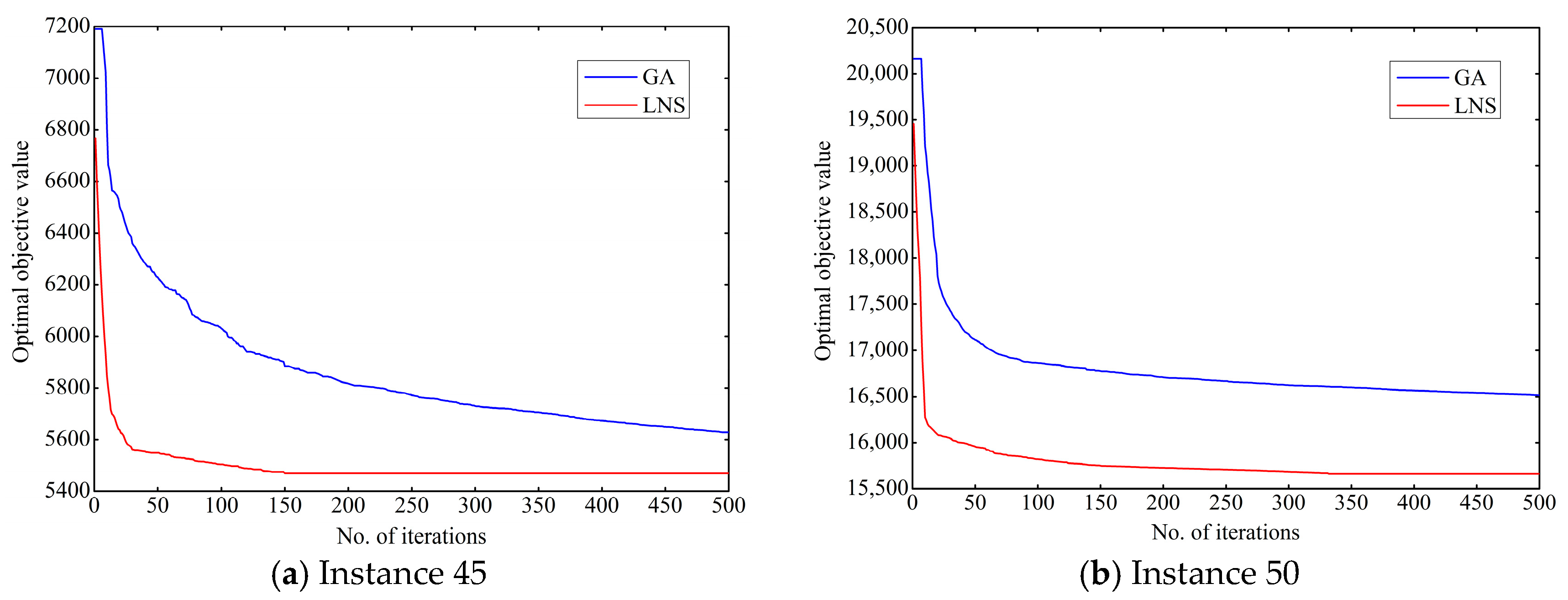
5.4. Stability Analysis of the LNS
5.5. Sensitivity Analysis
5.5.1. Effect of the Number of Depots and Empty Containers
5.5.2. Effect of the Distribution of Depots and Empty Containers
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, S.; Wu, W.; Ma, X.; Zhong, M.; Safdar, M. Modelling Medium- and Long-Term Purchasing Plans for Environment-Orientated Container Trucks: A Case Study of Yangtze River Port. Transp. Saf. Environ. 2023, 5, tdac043. [Google Scholar] [CrossRef]
- Cui, H.; Chen, S.; Chen, R.; Meng, Q. A Two-Stage Hybrid Heuristic Solution for the Container Drayage Problem with Trailer Reposition. Eur. J. Oper. Res. 2022, 299, 468–482. [Google Scholar] [CrossRef]
- Lee, S.; Moon, I. Robust Empty Container Repositioning Considering Foldable Containers. Eur. J. Oper. Res. 2020, 280, 909–925. [Google Scholar] [CrossRef]
- Wang, X.; Regan, A.C. Local Truckload Pickup and Delivery with Hard Time Window Constraints. Transp. Res. B Methodol. 2002, 36, 97–112. [Google Scholar] [CrossRef]
- Moghaddam, M.; Pearce, R.H.; Mokhtar, H.; Prato, C.G. A Generalised Model for Container Drayage Operations with Heterogeneous Fleet, Multi-Container Sizes and Two Modes of Operation. Transp. Res. E Logist. Transp. Rev. 2020, 139, 101973. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, J.; Liang, Z.; Ye, C. An Exact Algorithm for the Container Drayage Problem under a Separation Mode. Transp. Res. E Logist. Transp. Rev. 2017, 106, 231–254. [Google Scholar] [CrossRef]
- Imai, A.; Nishimura, E.; Current, J. A Lagrangian Relaxation-Based Heuristic for the Vehicle Routing with Full Container Load. Eur. J. Oper. Res. 2007, 176, 87–105. [Google Scholar] [CrossRef]
- Chen, R.; Meng, Q.; Jia, P. Container Port Drayage Operations and Management: Past and Future. Transp. Res. E: Logist. Transp. Rev. 2022, 159, 102633. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, Y. A Branch-and-Price-and-Cut Algorithm for the Inland Container Transportation Problem with Limited Depot Capacity. Appl. Sci. 2024, 14, 11958. [Google Scholar] [CrossRef]
- Zhang, R.; Huang, C.; Wang, J. A Novel Mathematical Model and a Large Neighborhood Search Algorithm for Container Drayage Operations with Multi-Resource Constraints. Comput. Ind. Eng. 2020, 139, 106143. [Google Scholar] [CrossRef]
- Yu, X.; Feng, Y.; He, C.; Liu, C. Modeling and Optimization of Container Drayage Problem with Empty Container Constraints across Multiple Inland Depots. Sustainability 2024, 16, 5090. [Google Scholar] [CrossRef]
- Fazi, S.; Choudhary, S.K.; Dong, J.-X. The Multi-Trip Container Drayage Problem with Synchronization for Efficient Empty Containers Re-Usage. Eur. J. Oper. Res. 2023, 310, 343–359. [Google Scholar] [CrossRef]
- Jula, H.; Dessouky, M.; Ioannou, P.; Chassiakos, A. Container Movement by Trucks in Metropolitan Networks: Modeling and Optimization. Transp. Res. E Logist. Transp. Rev. 2005, 41, 235–259. [Google Scholar] [CrossRef]
- Chung, K.H.; Ko, C.S.; Shin, J.Y.; Hwang, H.; Kim, K.H. Development of Mathematical Models for the Container Road Transportation in Korean Trucking Industries. Comput. Ind. Eng. 2007, 53, 252–262. [Google Scholar] [CrossRef]
- Vidović, M.; Popović, D.; Ratković, B.; Radivojević, G. Generalized Mixed Integer and VNS Heuristic Approach to Solving the Multisize Containers Drayage Problem. Int. Trans. Oper. Res. 2017, 24, 583–614. [Google Scholar] [CrossRef]
- Yang, X.; Daham, H.A. A Column Generation-Based Decomposition and Aggregation Approach for Combining Orders in Inland Transportation of Containers. OR Spectr. 2020, 42, 261–296. [Google Scholar] [CrossRef]
- Bruglieri, M.; Mancini, S.; Peruzzini, R.; Pisacane, O. The Multi-Period Multi-Trip Container Drayage Problem with Release and Due Dates. Comput. Oper. Res. 2021, 125, 105102. [Google Scholar] [CrossRef]
- Bjelić, N.; Vidović, M.; Popović, D.; Ratković, B. Rolling-Horizon Approach in Solving Dynamic Multisize Multi-Trailer Container Drayage Problem. Expert. Syst. Appl. 2022, 201, 117170. [Google Scholar] [CrossRef]
- Jia, S.; Cui, H.; Chen, R.; Meng, Q. Dynamic Container Drayage with Uncertain Request Arrival Times and Service Time Windows. Transp. Res. B Methodol. 2022, 166, 237–258. [Google Scholar] [CrossRef]
- Chen, R.; Jia, S.; Meng, Q. Dynamic Container Drayage Booking and Routing Decision Support Approach for E-Commerce Platforms. Transp. Res. E Logist. Transp. Rev. 2023, 177, 103220. [Google Scholar] [CrossRef]
- Ran, C.; Zhang, Y. The Driving Force of Carbon Emissions Reduction in China: Does Green Finance Work. J. Clean. Prod. 2023, 421, 138502. [Google Scholar] [CrossRef]
- Xiao, L.; Chen, L.; Sun, P.; Laporte, G.; Baldacci, R. The Container Drayage Problem for Electric Trucks with Charging Resource Constraints. Transp. Res. C Emerg. Technol. 2025, 174, 105100. [Google Scholar] [CrossRef]
- Caris, A.; Janssens, G.K. A Local Search Heuristic for the Pre- and End-Haulage of Intermodal Container Terminals. Comput. Oper. Res. 2009, 36, 2763–2772. [Google Scholar] [CrossRef]
- Lai, M.; Crainic, T.G.; Di Francesco, M.; Zuddas, P. An Heuristic Search for the Routing of Heterogeneous Trucks with Single and Double Container Loads. Transp. Res. E Logist. Transp. Rev. 2013, 56, 108–118. [Google Scholar] [CrossRef]
- Ghezelsoflu, A.; Di Francesco, M.; Frangioni, A.; Zuddas, P. A Set-Covering Formulation for a Drayage Problem with Single and Double Container Loads. J. Ind. Eng. Int. 2018, 14, 665–676. [Google Scholar] [CrossRef]
- Xue, Z.; Zhang, C.; Lin, W.-H.; Miao, L.; Yang, P. A Tabu Search Heuristic for the Local Container Drayage Problem under a New Operation Mode. Transp. Res. E Logist. Transp. Rev. 2014, 62, 136–150. [Google Scholar] [CrossRef]
- Wang, D.; Moon, I.; Zhang, R. Multi-Trip Multi-Trailer Drop-and-Pull Container Drayage Problem. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19088–19104. [Google Scholar] [CrossRef]
- Wang, N.; Meng, Q.; Zhang, C. A Branch-Price-and-Cut Algorithm for the Local Container Drayage Problem with Controllable Vehicle Interference. Transp. Res. B Methodol. 2023, 178, 102835. [Google Scholar] [CrossRef]
- You, J.; Miao, L.; Zhang, C.; Xue, Z. A Generic Model for the Local Container Drayage Problem Using the Emerging Truck Platooning Operation Mode. Transp. Res. B Methodol. 2020, 133, 181–209. [Google Scholar] [CrossRef]
- Xue, Z.; Lin, H.; You, J. Local Container Drayage Problem with Truck Platooning Mode. Transp. Res. E Logist. Transp. Rev. 2021, 147, 102211. [Google Scholar] [CrossRef]
- Yan, X.; Xu, M.; Xie, C. Local Container Drayage Problem with Improved Truck Platooning Operations. Transp. Res. E Logist. Transp. Rev. 2023, 169, 102992. [Google Scholar] [CrossRef]
- You, J.; Wang, Y.; Xue, Z. An Exact Algorithm for the Multi-Trip Container Drayage Problem with Truck Platooning. Transp. Res. E Logist. Transp. Rev. 2023, 175, 103138. [Google Scholar] [CrossRef]
- Huang, Y.; Jin, Z.; Liu, P.; Wang, W.; Zhang, D. Container Drayage Problem Integrated with Truck Appointment System and Separation Mode. Comput. Ind. Eng. 2024, 193, 110307. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, R.; Dong, M.; Xie, X. Drop-and-Pull Container Drayage with Route Balancing and Its Matheuristic Algorithm. Expert Syst. Appl. 2024, 255, 124625. [Google Scholar] [CrossRef]
- Zhang, R.; Yun, W.Y.; Moon, I. A Reactive Tabu Search Algorithm for the Multi-Depot Container Truck Transportation Problem. Transp. Res. E Logist. Transp. Rev. 2009, 45, 904–914. [Google Scholar] [CrossRef]
- Zhang, R.; Yun, W.Y.; Kopfer, H. Heuristic-Based Truck Scheduling for Inland Container Transportation. OR Spectr. 2010, 32, 787–808. [Google Scholar] [CrossRef]
- Nossack, J.; Pesch, E. A Truck Scheduling Problem Arising in Intermodal Container Transportation. Eur. J. Oper. Res. 2013, 230, 666–680. [Google Scholar] [CrossRef]
- Sterzik, S.; Kopfer, H. A Tabu Search Heuristic for the Inland Container Transportation Problem. Comput. Oper. Res. 2013, 40, 953–962. [Google Scholar] [CrossRef]
- Braekers, K.; Caris, A.; Janssens, G.K. Integrated Planning of Loaded and Empty Container Movements. OR Spectr. 2013, 35, 457–478. [Google Scholar] [CrossRef]
- Zhang, R.; Yun, W.Y.; Kopfer, H. Multi-Size Container Transportation by Truck: Modeling and Optimization. Flex. Serv. Manuf. J. 2015, 27, 403–430. [Google Scholar] [CrossRef]
- Funke, J.; Kopfer, H. A Model for a Multi-Size Inland Container Transportation Problem. Transp. Res. E Logist. Transp. Rev. 2016, 89, 70–85. [Google Scholar] [CrossRef]
- Yang, X.; Daham, H.A.; Salhi, A. Combined Strip and Discharge Delivery of Containers in Heterogeneous Fleets with Time Windows. Comput. Oper. Res. 2021, 127, 105141. [Google Scholar] [CrossRef]
- Zhang, R.; Yun, W.Y.; Moon, I.K. Modeling and Optimization of a Container Drayage Problem with Resource Constraints. Int. J. Prod. Econ. 2011, 133, 351–359. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, Y.; Wang, W.; Xue, M. A Branch and Price Algorithm for the Drop-and-Pickup Container Drayage Problem with Empty Container Constraints. Sustainability 2023, 15, 5638. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, R. Container Drayage Transportation Scheduling With Foldable and Standard Containers. IEEE Trans. Eng. Manage 2023, 70, 3497–3511. [Google Scholar] [CrossRef]
- Shaw, P. Using Constraint Programming and Local Search Methods to Solve Vehicle Routing Problems. In Principles and Practice of Constraint Programming—CP98; Maher, M., Puget, J.-F., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1520, pp. 417–431. ISBN 978-3-540-65224-3. [Google Scholar]
- Hintsch, T.; Irnich, S. Large Multiple Neighborhood Search for the Clustered Vehicle-Routing Problem. Eur. J. Oper. Res. 2018, 270, 118–131. [Google Scholar] [CrossRef]
- Hojabri, H.; Gendreau, M.; Potvin, J.-Y.; Rousseau, L.-M. Large Neighborhood Search with Constraint Programming for a Vehicle Routing Problem with Synchronization Constraints. Comput. Oper. Res. 2018, 92, 87–97. [Google Scholar] [CrossRef]
- Bustos-Coral, D.; Costa, A.M. Adaptive Large Neighborhood Search for Drayage Routing Problems Involving Longer Combination Vehicles. Comput. Oper. Res. 2025, 173, 106826. [Google Scholar] [CrossRef]
- He, W.; Jin, Z.; Huang, Y.; Xu, S. The Inland Container Transportation Problem with Separation Mode Considering Carbon Dioxide Emissions. Sustainability 2021, 13, 1573. [Google Scholar] [CrossRef]


| Article | Request Type | Operation Modes | Empty Strategies | Feature | Methodology | ||||
|---|---|---|---|---|---|---|---|---|---|
| S.W. | D.P. | D.S. | S.S. | m-depot | Empty | Exact | Heuristic | ||
| Imai et al. [7] | 7, 8 | √ | × | × | √ | × | × | × | √ |
| Caris and Janssens [23] | 7, 8 | √ | × | × | √ | × | × | × | √ |
| Lai et al. [24] | 7, 8 | √ | × | × | √ | × | × | × | √ |
| Ghezelsoflu et al. [25] | 7, 8 | √ | × | × | √ | × | × | × | √ |
| Xue et al. [26] | 7, 8 | × | √ | × | √ | × | × | × | √ |
| Cui et al. [2] | 7, 8 | × | √ | × | × | √ | × | × | √ |
| Wang et al. [27] | 7, 8 | × | √ | × | × | × | × | × | √ |
| Wang et al. [28] | 7, 8 | × | √ | √ | √ | × | × | √ | × |
| You et al. [29] | 7, 8 | √ | × | √ | √ | × | × | √ | √ |
| Xue et al. [30] | 7, 8 | √ | × | √ | √ | × | × | √ | √ |
| Yan et al. [31] | 7, 8 | √ | × | √ | √ | × | × | √ | √ |
| You et al. [32] | 7, 8 | √ | × | √ | √ | × | × | √ | × |
| Huang et al. [33] | 7, 8 | × | √ | √ | √ | × | × | √ | √ |
| Wang et al. [34] | 7, 8 | × | √ | √ | × | × | × | √ | √ |
| Zhang et al. [35] | 5, 6, 7, 8 | √ | × | √ | √ | √ | × | × | √ |
| Zhang et al. [36] | 5, 6, 7, 8 | √ | × | √ | √ | √ | × | × | √ |
| Nossack and Pesch [37] | 5, 6, 7, 8 | √ | × | √ | √ | √ | × | × | √ |
| Sterzik and Kopfer [38] | 5, 6, 7, 8 | √ | × | √ | × | √ | √ | √ | √ |
| Braekers et al. [39] | 5, 6, 7, 8 | √ | √ | √ | √ | × | × | × | √ |
| Zhang et al. [40] | 5, 6, 7, 8 | √ | × | √ | √ | × | × | × | √ |
| Zhang et al. [10] | 5, 6, 7, 8 | √ | × | √ | √ | × | √ | × | √ |
| Funke and Kopfer [41] | 5, 6, 7, 8 | √ | √ | √ | √ | × | × | √ | × |
| Yang et al. [42] | 5, 6, 7, 8 | √ | √ | √ | √ | √ | × | √ | √ |
| Zhang et al. [43] | 5, 7, 8 | √ | × | √ | √ | × | √ | √ | √ |
| Song et al. [6] | 6, 7, 8 | × | √ | √ | √ | × | × | √ | × |
| Song et al. [44] | 6, 7, 8 | × | √ | √ | √ | × | √ | √ | × |
| Huang and Zhang [45] | 6, 7, 8 | √ | √ | √ | √ | × | √ | × | √ |
| Fazi et al. [12] | 1, 3, 4, 7, 8 | √ | × | √ | √ | × | √ | √ | √ |
| Moghaddam et al. [5] | 1, 2, 3, 4, 7, 8 | √ | √ | √ | √ | × | × | √ | √ |
| Yu et al. [11] | 1, 2, 3, 4, 7, 8 | √ | √ | √ | √ | √ | √ | √ | √ |
| Request Vertices | Request Types | Activities at Request Vertices |
|---|---|---|
| ED, OE | Delivering an empty container to either a customer or the terminal | |
| IF | Delivering a full container to a customer | |
| ER, IE | Picking up an empty container from either a customer or the terminal | |
| OF | Picking up a full container from a customer |
| / | Picking up an empty container from the depot i and proceeding to vertex j | Proceeding to the terminal, picking up an import full container, and proceeding to the consignee j | Proceeding to vertex j | Proceeding to the shipper j | |
| Returning to the depot j | / | Proceeding to the terminal, picking up an import full container, and proceeding to the consignee j | Proceeding to vertex j | Proceeding to the shipper j | |
| Returning to the depot j | / | Proceeding to the terminal, picking up an import full container, and proceeding to the consignee j | Proceeding to vertex j | Proceeding to the shipper j | |
| Returning to the depot j and dropping off an empty container | Proceeding to vertex j | / | / | / | |
| Proceeding to the terminal, dropping off an export full container, and returning to the depot j | / | Proceeding to the terminal to drop off an export full container, then picking up an import full container, and proceeding to the consignee j | Proceeding to the terminal, dropping off an export full container, and proceeding to vertex j | Proceeding to the terminal, dropping off an export full container, and proceeding to the shipper j | |
| Instance | No. of Requests | No. of Empty Containers | Cost | Time (s) | Gap (%) | ||
|---|---|---|---|---|---|---|---|
| Gurobi | LNS | Gurobi | LNS | ||||
| 1 | 5 (1, 0, 0, 1, 1, 1, 0, 1) | (1, 0, 1, 0, 0, 0) | 89.8 | 89.8 | 26 | 1.21 | 0.00 |
| 2 | 6 (1, 1, 0, 1, 0, 1, 1, 1) | (1, 0, 1, 0, 0, 0) | 113.6 | 113.6 | 33 | 1.30 | 0.00 |
| 3 | 7 (0, 1, 1, 2, 1, 0, 0, 2) | (1, 0, 1, 0, 0, 0) | 145.3 | 145.3 | 45 | 1.27 | 0.00 |
| 4 | 8 (1, 1, 0, 1, 1, 0, 0, 4) | (1, 0, 1, 0, 0, 0) | 198.9 | 198.9 | 66 | 2.25 | 0.00 |
| 5 | 10 (2, 0, 0, 1, 0, 2, 3, 2) | (1, 0, 1, 0, 0, 0) | 211.5 | 211.5 | 78 | 7.66 | 0.00 |
| 6 | 12 (1, 1, 2, 0, 1, 2, 2, 3) | (1, 0, 0, 2, 1, 0) | 244.5 | 246.3 | 195 | 12.39 | 0.74 |
| 7 | 14 (1, 1, 3, 3, 1, 1, 2, 2) | (0, 1, 1, 0, 0, 0) | 245.1 | 248.8 | 213 | 19.54 | 1.51 |
| 8 | 16 (3, 0, 1, 3, 1, 1, 2, 5) | (0, 0, 1, 2, 1, 0) | 352.7 | 356.1 | 581 | 25.01 | 0.96 |
| 9 | 18 (2, 3, 3, 2, 0, 2, 3, 3) | (1, 0, 0, 0, 2, 1) | 343.6 | 348.0 | 634 | 16.23 | 1.28 |
| 10 | 20 (5, 3, 2, 3, 1, 1, 3, 2) | (4, 1, 0, 0, 3, 0) | 361.4 | 373.5 | 729 | 22.09 | 3.35 |
| Instance | No. of Requests | No. of Empty Containers | Cost | Time (s) | Gap (%) | ||
|---|---|---|---|---|---|---|---|
| Gurobi | LNS | Gurobi | LNS | ||||
| 11 | 20 (0, 4, 0, 0, 0, 1, 4, 11) | (5, 0, 0, 3, 0, 0) | 569.7 | 591.4 | 3600 | 30.25 | 3.81 |
| 12 | 23 (5, 2, 3, 2, 2, 1, 5, 3) | (0, 3, 5, 0, 0, 0) | 461.4 | 476.2 | 3600 | 34.66 | 3.21 |
| 13 | 26 (5, 2, 1, 5, 2, 3, 4, 4) | (3, 0, 0, 1, 0, 2) | 514.5 | 544.1 | 3600 | 15.11 | 5.75 |
| 14 | 26 (2, 0, 1, 2, 0, 1, 10, 10) | (0, 5, 2, 0, 0, 1) | 759.0 | 752.1 | 3600 | 22.54 | −0.91 |
| 15 | 29 (3, 1, 3, 6, 2, 3, 5, 6) | (0, 1, 0, 0, 3, 1) | 573.9 | 543.5 | 3600 | 45.32 | −5.30 |
| 16 | 29 (2, 0, 1, 2, 0, 2, 8, 14) | (4, 0, 4, 4, 0, 1) | 795.2 | 814.8 | 3600 | 52.27 | 2.46 |
| 17 | 29 (2, 0, 1, 1, 1, 1, 10, 13) | (0, 0, 3, 0, 1, 0) | 771.4 | 722.6 | 3600 | 26.95 | −6.33 |
| 18 | 31 (3, 5, 4, 6, 1, 2, 4, 6) | (1, 0, 4, 3, 0, 0) | 592.8 | 579.0 | 3600 | 53.26 | −2.33 |
| 19 | 33 (6, 0, 1, 8, 2, 4, 5, 7) | (0, 3, 2, 0, 0, 0) | 724.6 | 765.9 | 3600 | 64.55 | 5.70 |
| 20 | 35 (2, 1, 0, 2, 0, 3, 11, 16) | (0, 5, 0, 1, 1, 0) | 926.5 | 845.7 | 3600 | 72.28 | −8.72 |
| Instance | No. of Requests | No. of Empty Containers | Cost | Time (s) | Gap (%) | ||
|---|---|---|---|---|---|---|---|
| GA | LNS | GA | LNS | ||||
| 21 | 38 (9, 3, 2, 4, 6, 2, 4, 8) | (4, 4, 0, 0, 0, 5) | 789.1 | 772.1 | 60.37 | 50.07 | −2.15 |
| 22 | 43 (10, 5, 5, 5, 5, 0, 5, 8) | (5, 3, 4, 1, 0, 2) | 863.9 | 821.5 | 51.38 | 42.81 | −4.91 |
| 23 | 46 (6, 3, 4, 10, 2, 7, 8, 6) | (0, 1, 2, 0, 1, 2) | 882.7 | 874.4 | 62.93 | 57.99 | −0.94 |
| 24 | 46 (3, 3, 3, 3, 0, 0, 14, 20) | (0, 2, 0, 0, 6, 0) | 1248.9 | 1200.8 | 89.76 | 81.42 | −3.85 |
| 25 | 48 (3, 0, 1, 0, 1, 1, 18, 24) | (8, 0, 6, 4, 4, 0) | 1387.2 | 1345.3 | 70.21 | 68.59 | −3.02 |
| 26 | 49 (6, 6, 4, 8, 4, 5, 6, 10) | (2, 4, 0, 2, 0, 1) | 1152.6 | 1099.5 | 43.78 | 42.62 | −4.61 |
| 27 | 54 (6, 3, 6, 12, 3, 6, 10, 8) | (0, 0, 4, 1, 0, 0) | 1031.8 | 1025.2 | 74.23 | 64.41 | −0.64 |
| 28 | 54 (4, 0, 2, 2, 0, 2, 20, 24) | (0, 0, 4, 0, 6, 0) | 1572.0 | 1522.1 | 98.83 | 94.65 | −3.17 |
| 29 | 58 (10, 4, 4, 10, 6, 6, 9, 9) | (0, 4, 5, 0, 2, 0) | 1183.4 | 1120.6 | 71.27 | 70.12 | −5.31 |
| 30 | 58 (4, 0, 0, 3, 3, 4, 22, 22) | (6, 5, 4, 0, 5, 0) | 1588.7 | 1523.2 | 105.44 | 88.87 | −4.12 |
| 31 | 59 (14, 8, 3, 6, 6, 3, 4, 15) | (5, 5, 5, 0, 0, 5) | 1224.6 | 1215.1 | 83.55 | 82.54 | −0.78 |
| 32 | 63 (11, 6, 4, 10, 5, 7, 8, 12) | (4, 5, 2, 0, 3, 0) | 1209.3 | 1186.0 | 89.87 | 88.90 | −1.93 |
| 33 | 68 (7, 7, 7, 16, 1, 9, 11, 10) | (0, 2, 0, 2, 4, 0) | 1378.1 | 1315.5 | 95.13 | 94.64 | −4.54 |
| 34 | 68 (4, 2, 2, 6, 2, 2, 22, 28) | (4, 4, 0, 0, 0, 0) | 1945.1 | 1912.8 | 109.32 | 104.26 | −1.66 |
| 35 | 70 (1, 3, 3, 2, 4, 1, 40, 16) | (7, 7, 7, 3, 7, 1) | 2012.7 | 1900.3 | 125.79 | 124.20 | −5.58 |
| 36 | 75 (12, 7, 5, 12, 7, 8, 12, 12) | (2, 5, 5, 0, 1, 0) | 1465.5 | 1413.6 | 101.95 | 97.84 | −3.54 |
| 37 | 75 (9, 9, 9, 17, 0, 7, 9, 15) | (2, 5, 5, 0, 1, 0) | 1502.4 | 1391.6 | 82.60 | 82.37 | −7.37 |
| 38 | 75 (16, 16, 6, 9, 1, 3, 15, 9) | (2, 5, 5, 0, 1, 0) | 1458.3 | 1366.2 | 105.59 | 105.98 | −6.32 |
| 39 | 75 (6, 3, 4, 2, 0, 0, 30, 30) | (2, 5, 5, 0, 1, 0) | 2185.8 | 2091.1 | 96.33 | 95.52 | −4.33 |
| 40 | 75 (6, 3, 4, 2, 0, 0, 25, 35) | (2, 5, 5, 0, 1, 0) | 2206.2 | 2167.4 | 115.71 | 106.85 | −1.76 |
| Instance | No. of Requests | No. of Empty Containers | Cost | Time (s) | Gap (%) | ||
|---|---|---|---|---|---|---|---|
| GA | LNS | GA | LNS | ||||
| 41 | 100 (10, 5, 5, 10, 5, 5, 20(0), 40(0)) | (0, 7, 6, 8, 4, 8) | 2498.5 | 2404.3 | 324.52 | 302.13 | −3.77 |
| 42 | 120 (5, 5, 5, 5, 0, 0, 40(10), 60(10)) | (8, 8, 8, 8, 9, 9) | 3502.1 | 3441.7 | 445.26 | 423.85 | −1.72 |
| 43 | 140 (10, 5, 10, 10, 0, 5, 50(0), 50(0)) | (0, 10, 10, 10, 10, 10) | 3510.4 | 3423.0 | 864.15 | 821.54 | −2.49 |
| 44 | 190 (10, 0, 10, 10, 0, 10, 75(15), 75(15)) | (15, 15, 15, 10, 10, 10) | 5652.1 | 5538.9 | 1528.91 | 1523.07 | −2.00 |
| 45 | 220 (20, 5, 15, 20, 5, 15, 60(0), 80(0)) | (20, 15, 10, 10, 10, 10) | 5627.9 | 5468.9 | 1169.42 | 1148.12 | −2.83 |
| 46 | 260 (10, 5, 5, 10, 5, 5, 120(20), 100(20)) | (20, 20, 20, 20, 10, 10) | 8122.8 | 7900.5 | 1670.33 | 1652.46 | −2.74 |
| 47 | 300 (20, 15, 0, 20, 5, 0, 100(0), 140(0)) | (20, 20, 20, 20, 10, 10) | 8320.6 | 8018.6 | 3428.25 | 3371.27 | −3.63 |
| 48 | 360 (15, 5, 5, 15, 10, 10, 110(30), 190(30)) | (30, 30, 20, 20, 20, 20) | 11,797.0 | 11,008.2 | 3641.74 | 3197.35 | −6.69 |
| 49 | 420 (25, 5, 10, 25, 15, 20, 140(20), 180(20)) | (30, 20, 30, 30, 30, 30) | 13,635.0 | 12,608.4 | 3659.30 | 3350.16 | −7.53 |
| 50 | 480 (30, 10, 25, 30, 10, 15, 160(40), 200(40)) | (40, 40, 30, 30, 30, 30) | 16,517.2 | 15,661.1 | 3685.66 | 3549.81 | −5.18 |
| Instance | Minimum | Maximum | Average | Difference (%) |
|---|---|---|---|---|
| 25 | 1343.1 | 1348.6 | 1346.2 | 0.41 |
| 30 | 1520.7 | 1526.4 | 1522.9 | 0.37 |
| 35 | 1898.2 | 1905.8 | 1902.4 | 0.40 |
| 40 | 2166.5 | 2171.3 | 2169.8 | 0.22 |
| 45 | 5463.9 | 5470.2 | 5466.1 | 0.12 |
| 50 | 15,652.0 | 15,667.2 | 15,659.3 | 0.10 |
| Instance | Cost of Depot and Empty Container Distribution | Cost Savings from R/R (%) | |||
|---|---|---|---|---|---|
| R/R | U/U | F/F | U/U | F/F | |
| 30 | 1523.2 | 1482.5 | 1425.9 | 2.67 | 6.39 |
| 34 | 1912.8 | 1853.7 | 1782.0 | 3.09 | 6.84 |
| 38 | 1366.2 | 1345.4 | 1289.5 | 1.52 | 5.61 |
| 42 | 3441.7 | 3325.2 | 3156.1 | 3.38 | 8.30 |
| 46 | 7900.5 | 7692.3 | 7005.8 | 3.65 | 11.32 |
| 50 | 15,661.1 | 15,125.8 | 13,739.6 | 3.80 | 12.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; He, C. An Improved Large Neighborhood Search Algorithm for the Comprehensive Container Drayage Problem with Diverse Transport Requests. Appl. Sci. 2025, 15, 5937. https://doi.org/10.3390/app15115937
Yu X, He C. An Improved Large Neighborhood Search Algorithm for the Comprehensive Container Drayage Problem with Diverse Transport Requests. Applied Sciences. 2025; 15(11):5937. https://doi.org/10.3390/app15115937
Chicago/Turabian StyleYu, Xuhui, and Cong He. 2025. "An Improved Large Neighborhood Search Algorithm for the Comprehensive Container Drayage Problem with Diverse Transport Requests" Applied Sciences 15, no. 11: 5937. https://doi.org/10.3390/app15115937
APA StyleYu, X., & He, C. (2025). An Improved Large Neighborhood Search Algorithm for the Comprehensive Container Drayage Problem with Diverse Transport Requests. Applied Sciences, 15(11), 5937. https://doi.org/10.3390/app15115937





