Primary Stability Assessment of Patient-Specific Transfemoral Osseointegrated Implants During Static Load-Bearing Exercise: A Comparative Analysis
Abstract
1. Introduction
2. Materials and Methods
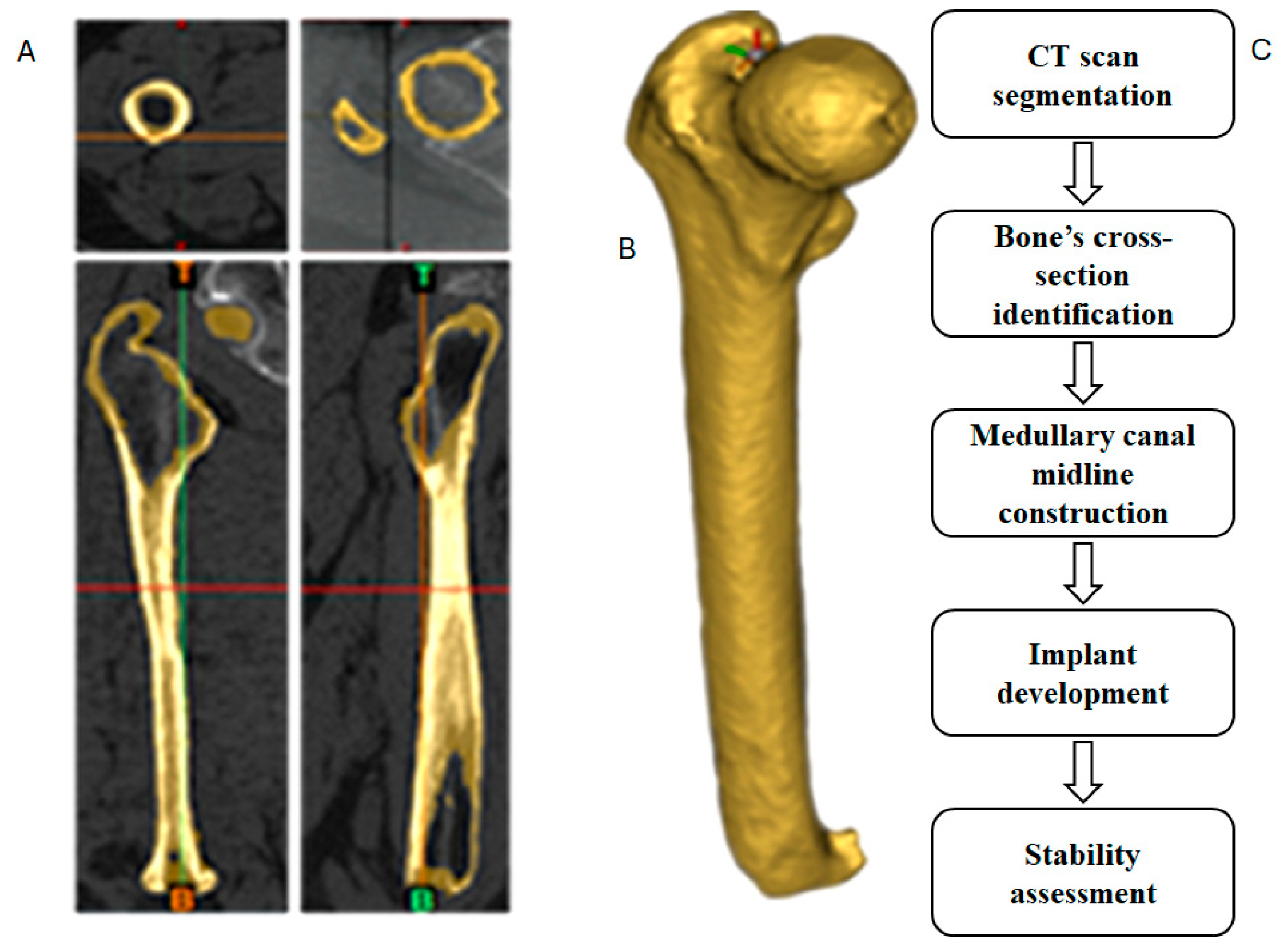
2.1. CT Scan Segmentation
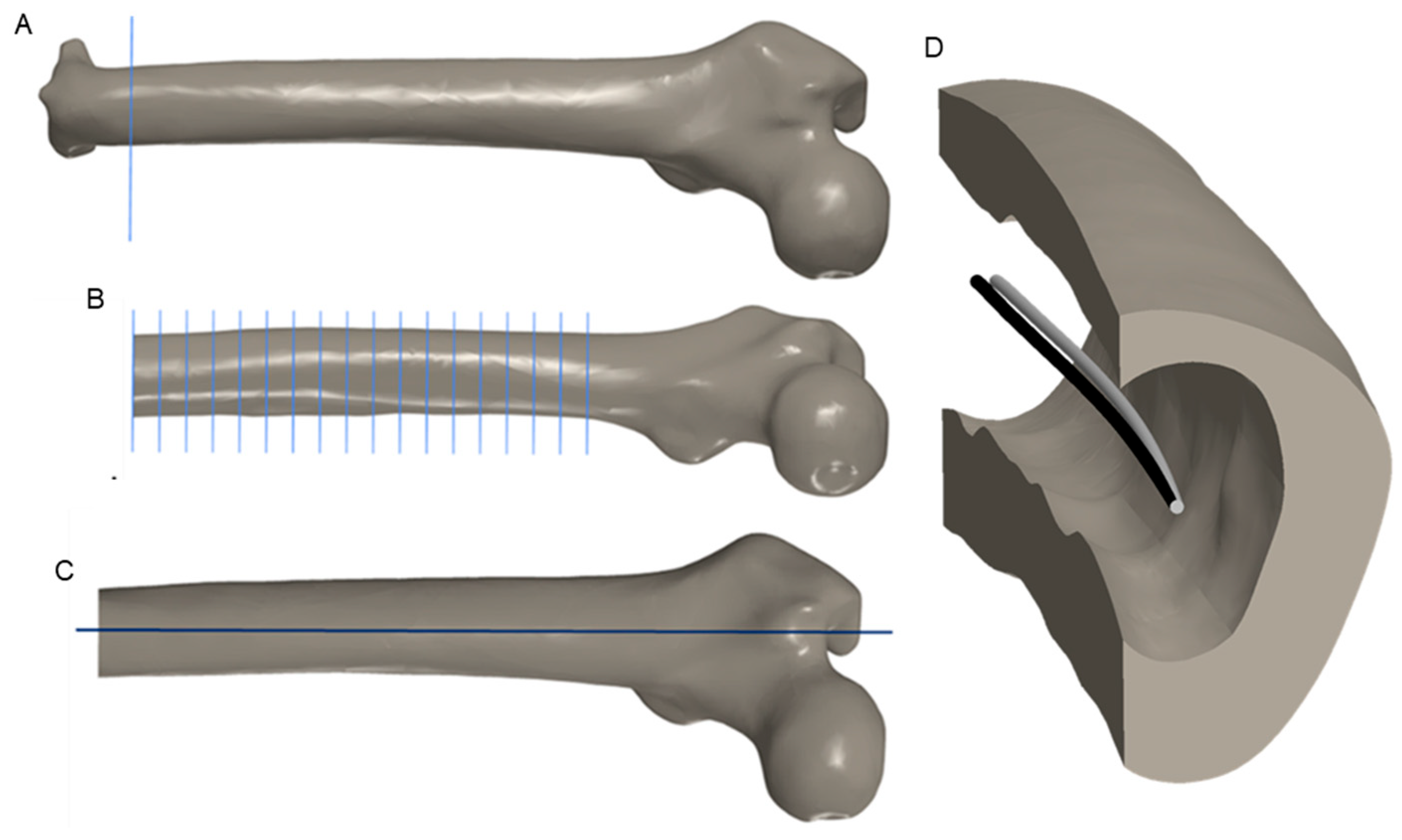
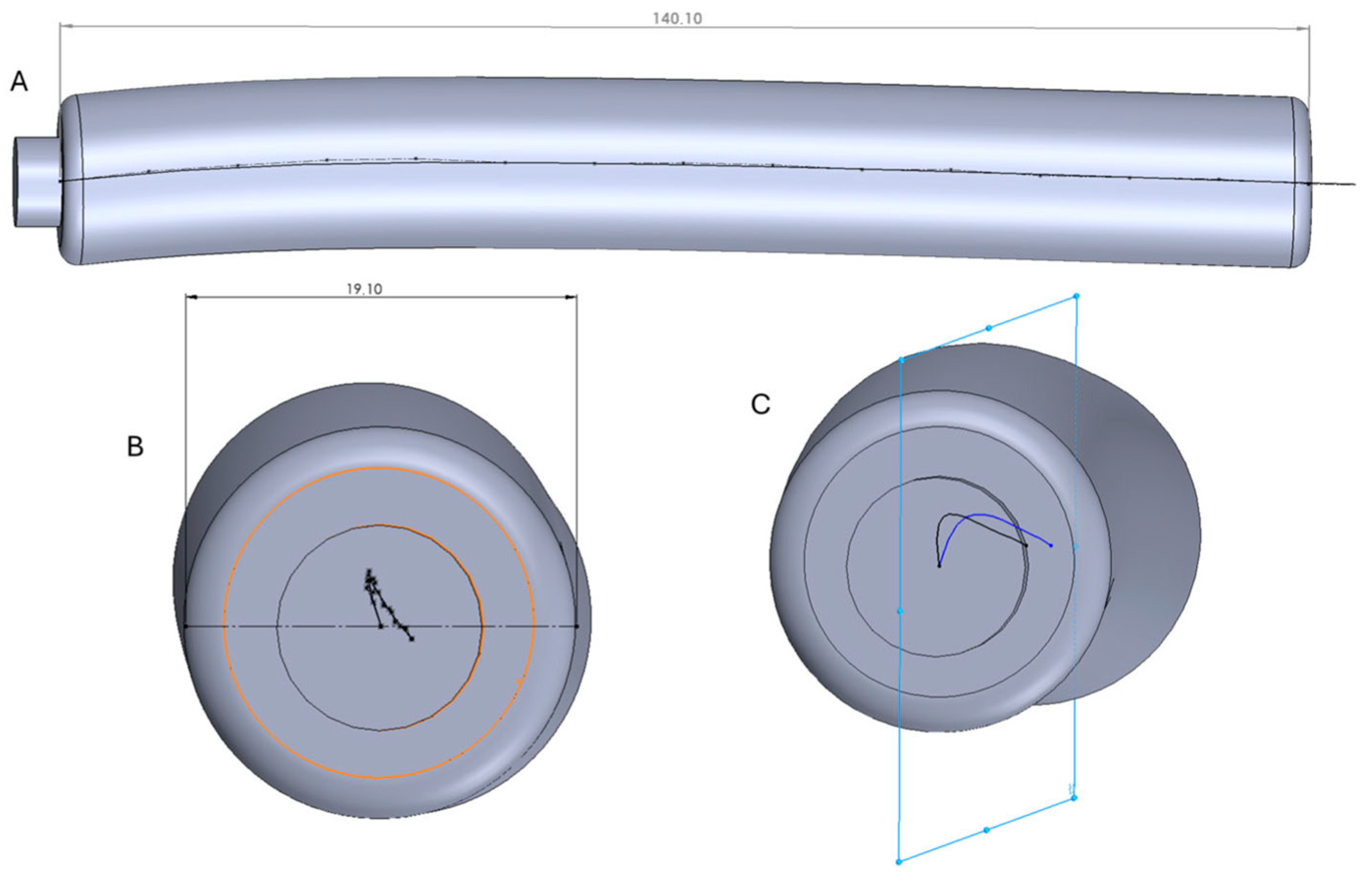
2.2. CAD Modeling
2.3. FE Analysis
2.3.1. Material Properties
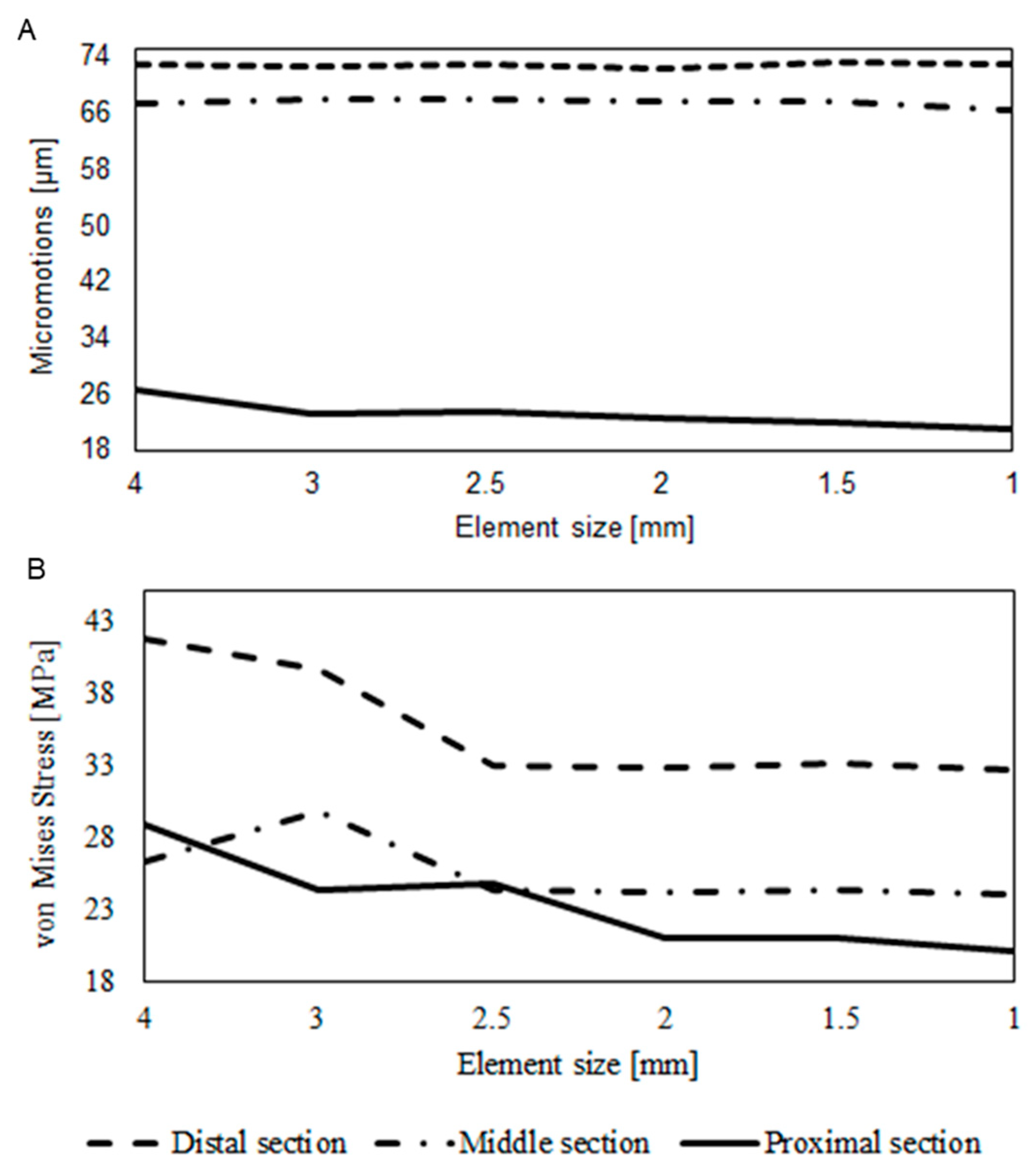
2.3.2. Mesh
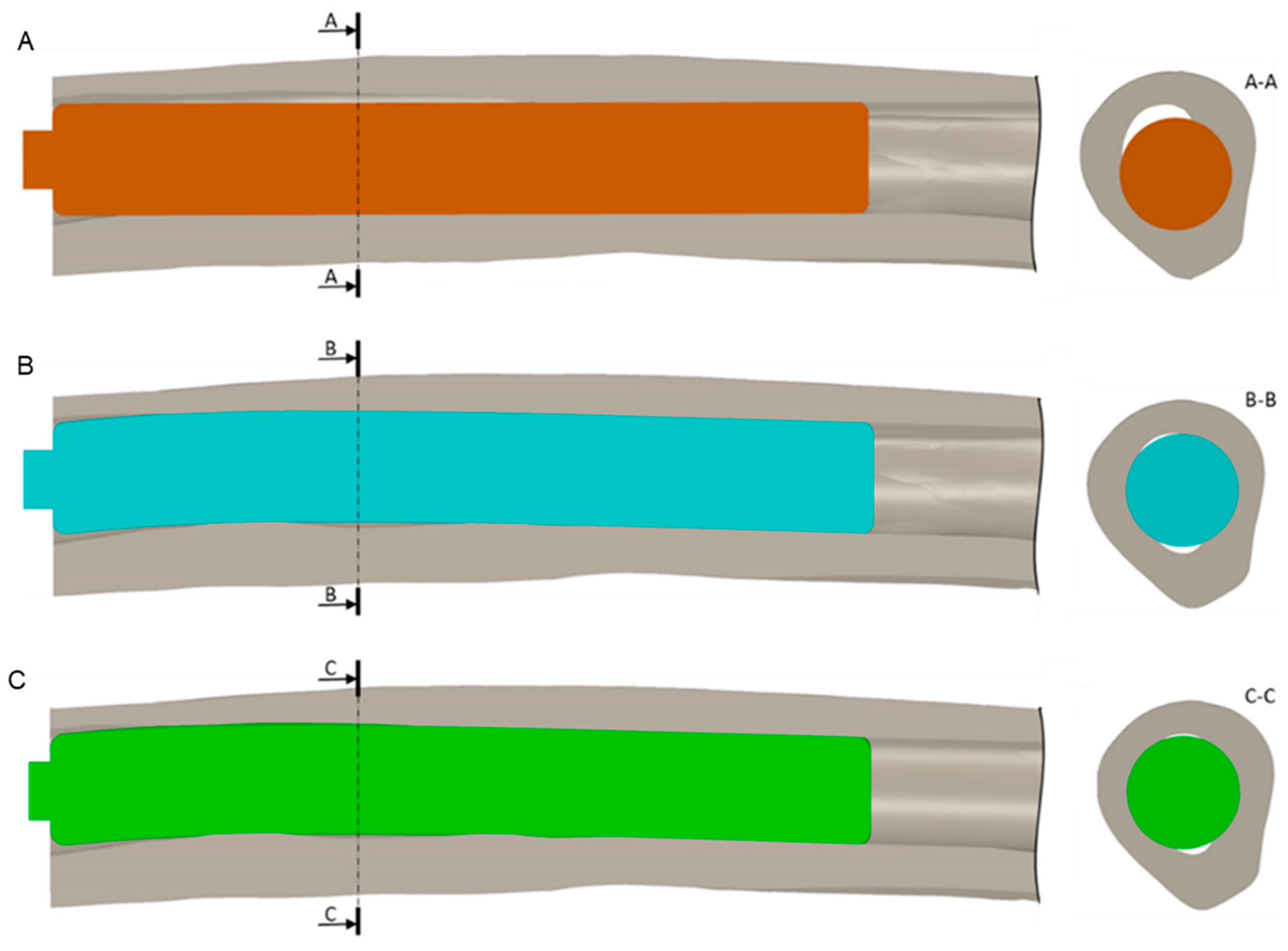
2.3.3. Boundary Conditions
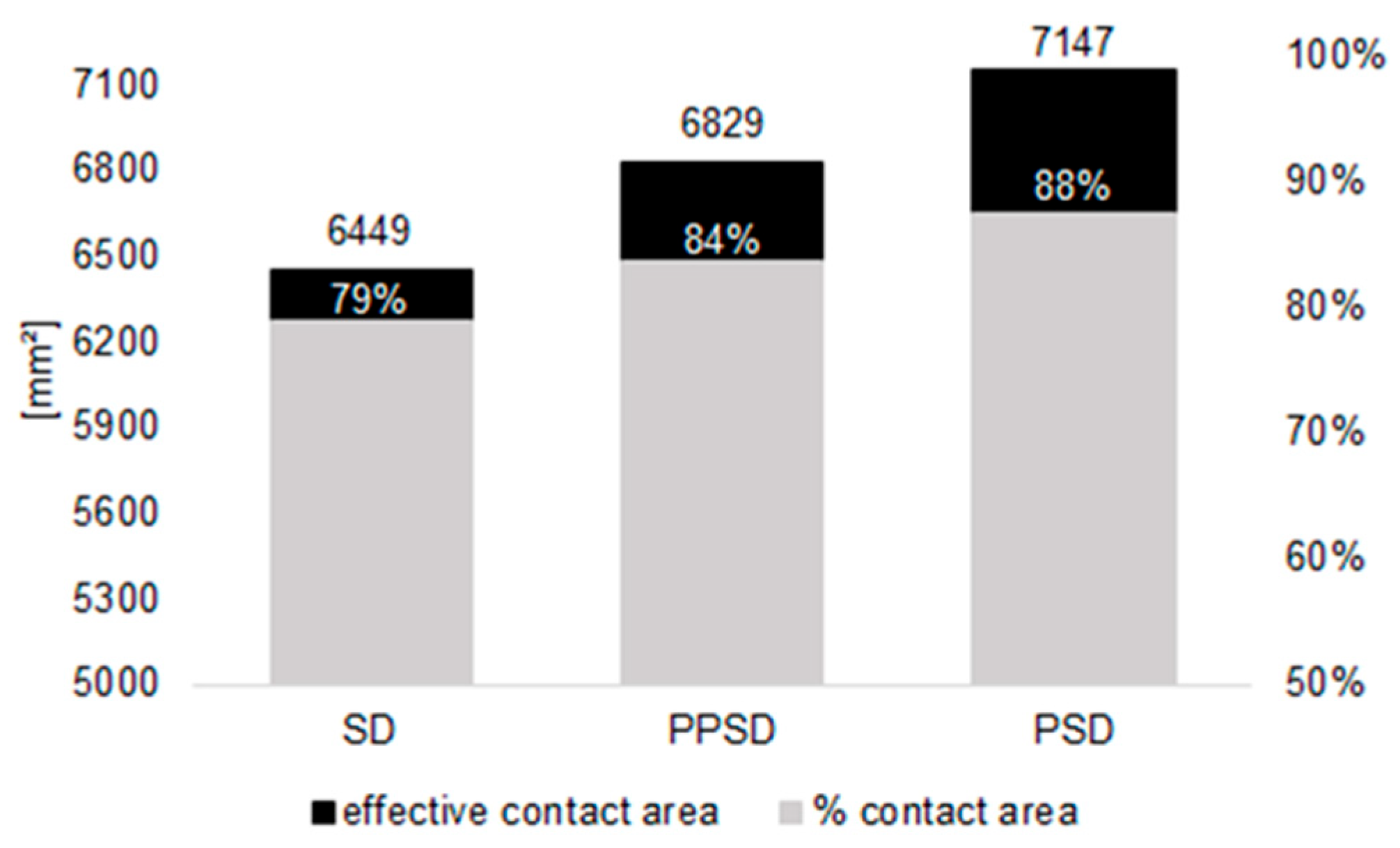
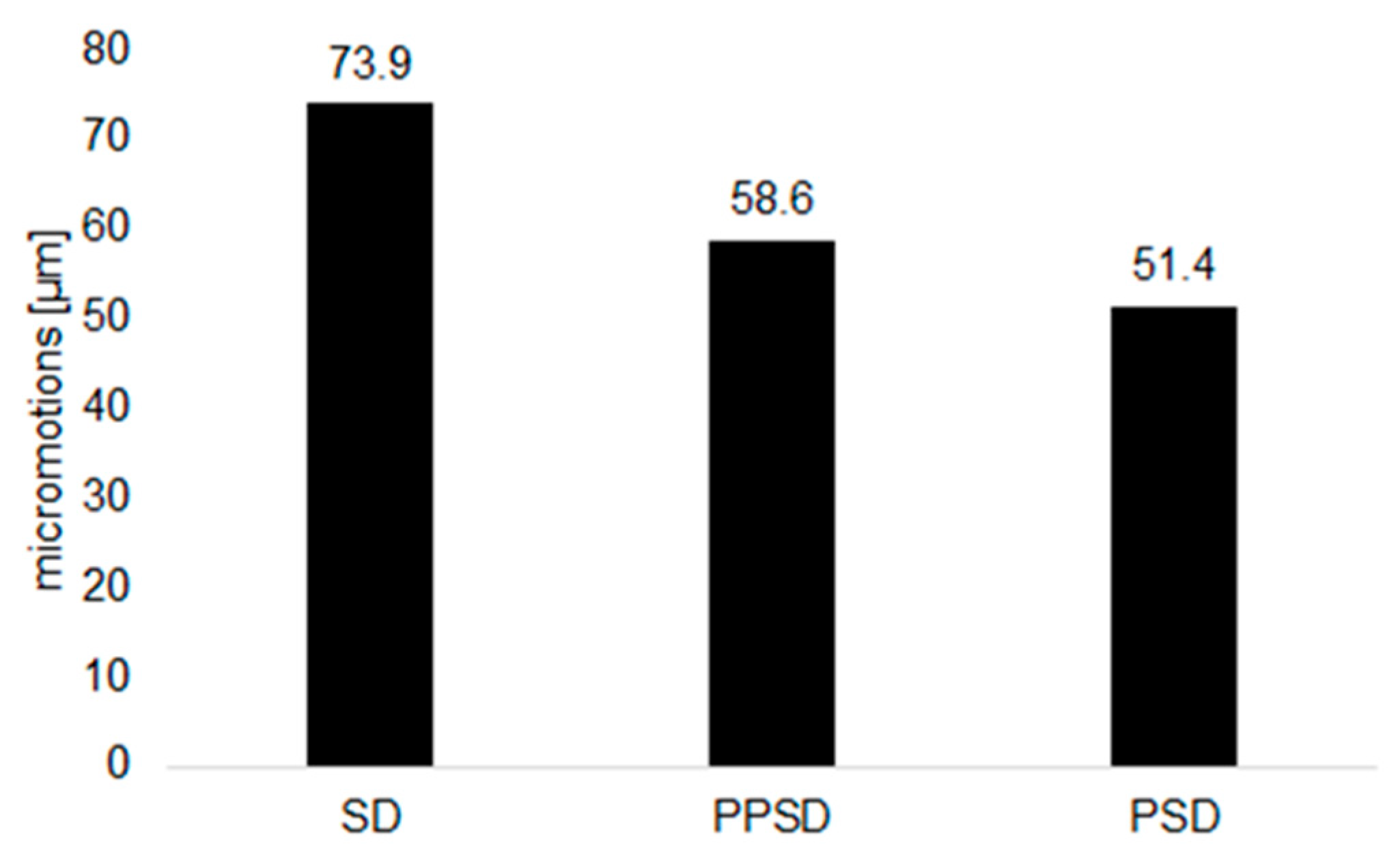
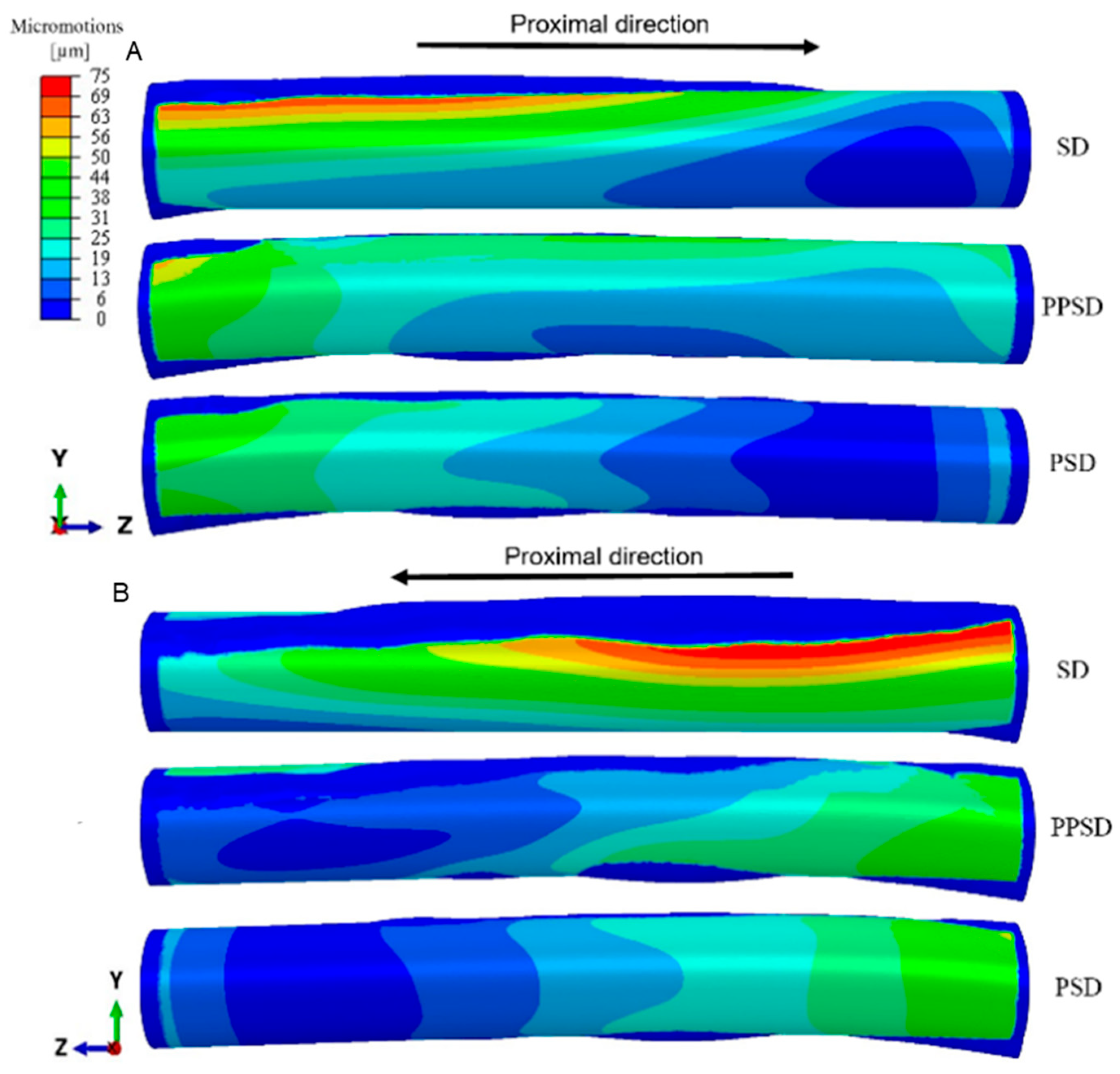
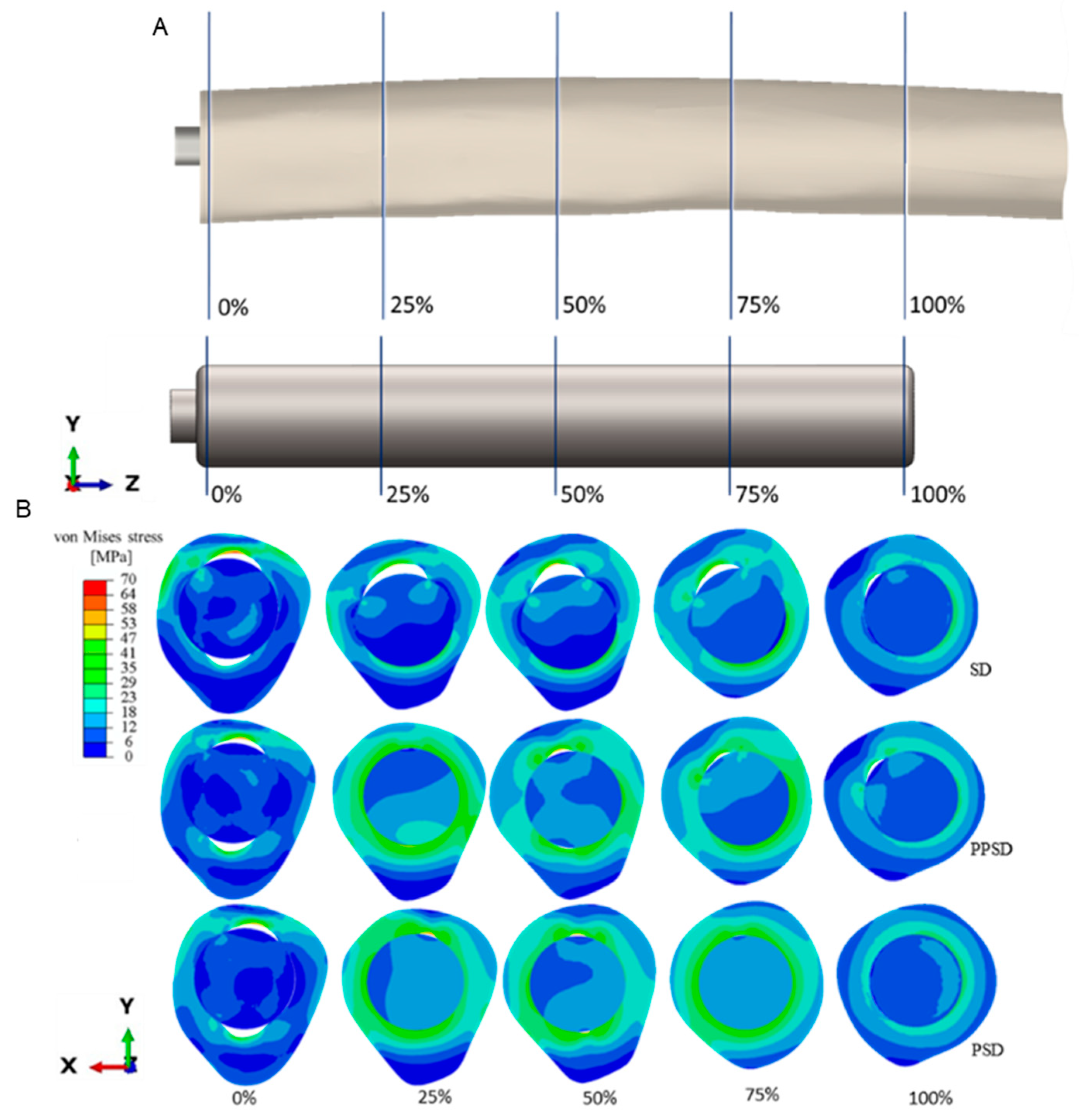
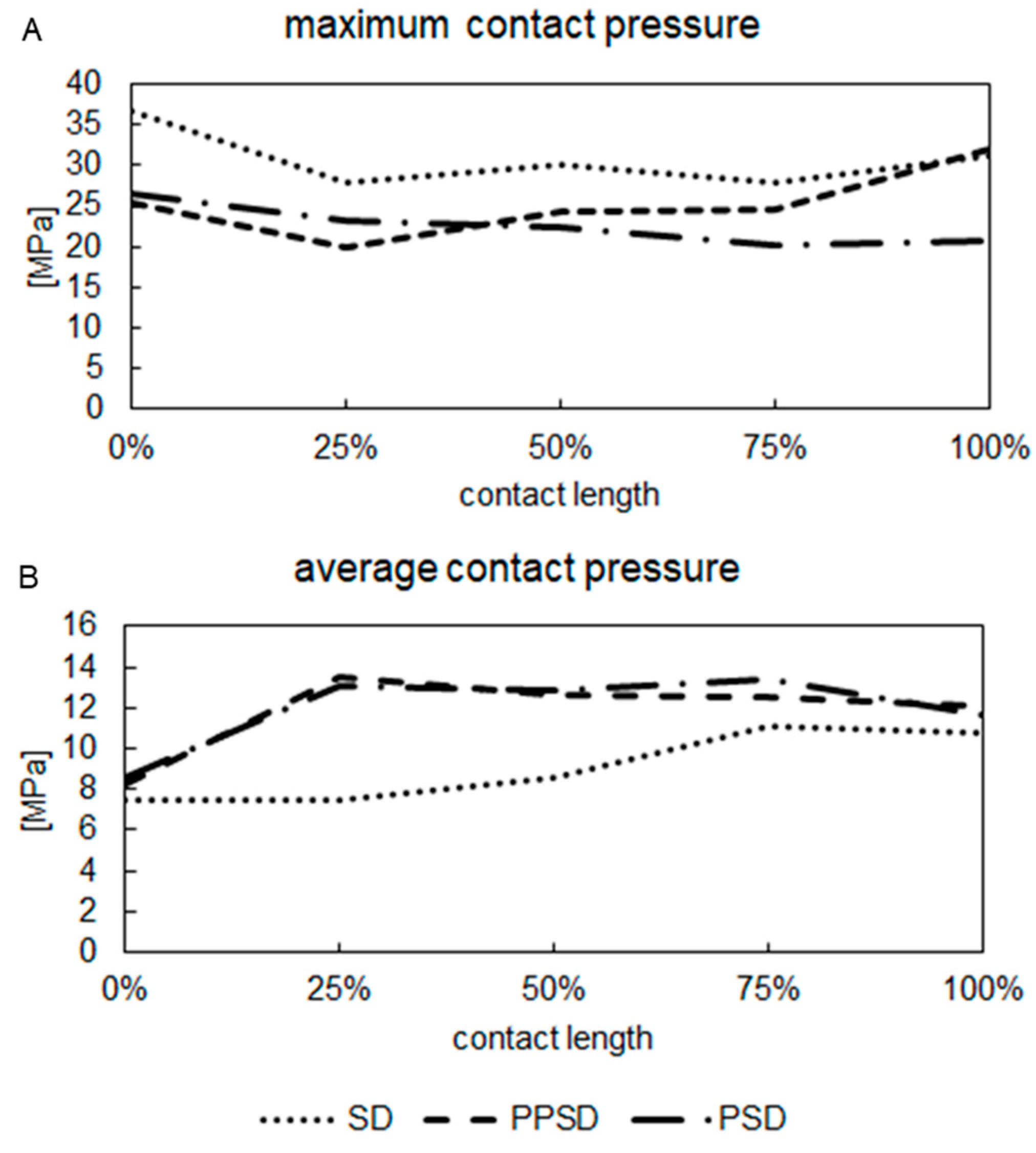
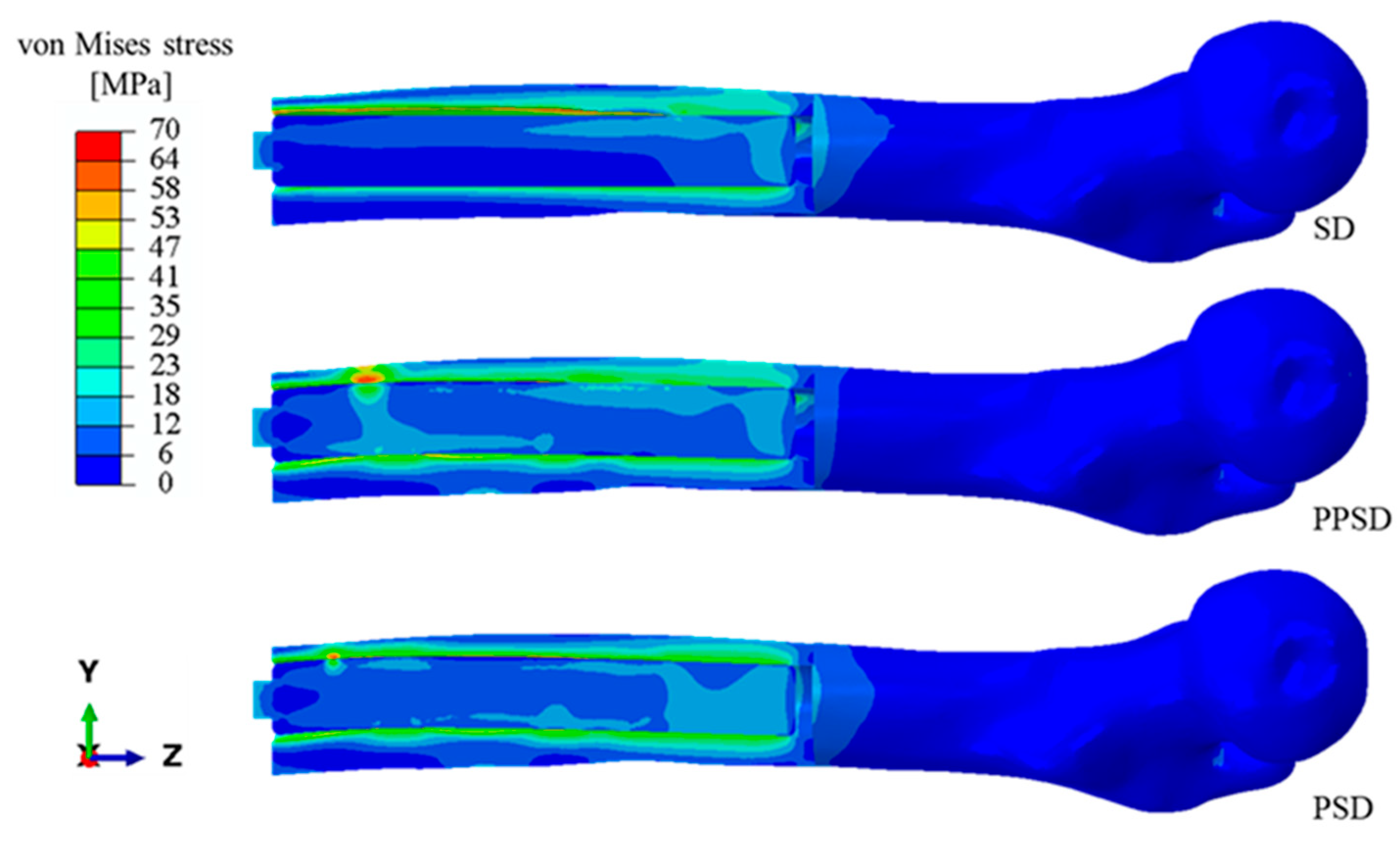
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| OI | Osseointegrated |
| PPSD | Planar patient-specific design |
| PSD | Patient-specific design |
| SD | Straight design |
References
- Brånemark, R.; Brånemark, P.-I.; Rydevik, B.; Myers, R.R. Osseointegration in Skeletal Reconstruction and Rehabilitation: A Review. J. Rehabil. Res. Dev. 2001, 38, 175–181. [Google Scholar] [PubMed]
- Hoellwarth, J.S.; Tetsworth, K.; Rozbruch, S.R.; Handal, M.B.; Coughlan, A.; Al Muderis, M. Osseointegration for Amputees: Current Implants, Techniques, and Future Directions. JBJS Rev. 2020, 8, e0043. [Google Scholar] [CrossRef] [PubMed]
- Al Muderis, M.; Khemka, A.; Lord, S.J.; Van De Meent, H.; Frolke, J.P.M. Safety of Osseointegrated Implants for Transfemoral Amputees: A Two-Center Prospective Cohort Study. J. Bone Jt. Surg. Am. Vol. 2016, 98, 900–909. [Google Scholar] [CrossRef]
- Pitkin, M. Design Features of Implants for Direct Skeletal Attachment of Limb Prostheses. J. Biomed. Mater. Res. A 2013, 101, 3339–3348. [Google Scholar] [CrossRef]
- Thesleff, A.; Brånemark, R.; Håkansson, B.; Ortiz-Catalan, M. Biomechanical Characterisation of Bone-Anchored Implant Systems for Amputation Limb Prostheses: A Systematic Review. Ann. Biomed. Eng. 2018, 46, 377–391. [Google Scholar] [CrossRef] [PubMed]
- Prochor, P.; Sajewicz, E. The Influence of Geometry of Implants for Direct Skeletal Attachment of Limb Prosthesis on Rehabilitation Program and Stress-Shielding Intensity. Biomed. Res. Int. 2019, 2019, 6067952. [Google Scholar] [CrossRef]
- Damm, N.B.; Morlock, M.M.; Bishop, N.E. Influence of Trabecular Bone Quality and Implantation Direction on Press-Fit Mechanics. J. Orthop. Res. 2017, 35, 224–233. [Google Scholar] [CrossRef]
- Safari, R. Lower Limb Prosthetic Interfaces: Clinical and Technological Advancement and Potential Future Direction. Prosthet. Orthot. Int. 2020, 44, 384–401. [Google Scholar] [CrossRef]
- Di Paolo, S.; Barone, G.; Alesi, D.; Mirulla, A.I.; Gruppioni, E.; Zaffagnini, S.; Bragonzoni, L. Longitudinal Gait Analysis of a Transfemoral Amputee Patient: Single-Case Report from Socket-Type to Osseointegrated Prosthesis. Sensors 2023, 23, 4037. [Google Scholar] [CrossRef]
- Ovesy, M.; Voumard, B.; Zysset, P. A Nonlinear Homogenized Finite Element Analysis of the Primary Stability of the Bone–Implant Interface. Biomech. Model. Mechanobiol. 2018, 17, 1471–1480. [Google Scholar] [CrossRef]
- Hebert, J.S.; Rehani, M.; Stiegelmar, R. Osseointegration for Lower-Limb Amputation: A Systematic Review of Clinical Outcomes. JBJS Rev. 2017, 5, e10. [Google Scholar] [CrossRef] [PubMed]
- Atallah, R.; van de Meent, H.; Verhamme, L.; Frölke, J.P.; Leijendekkers, R.A. Safety, Prosthesis Wearing Time and Health-Related Quality of Life of Lower Extremity Bone-Anchored Prostheses Using a Press-Fit Titanium Osseointegration Implant: A Prospective One-Year Follow-up Cohort Study. PLoS ONE 2020, 15, e0230027. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Fraulob, M.; Haïat, G. Biomechanical Behaviour of Bone-Implant Interface: A Review Biomechanical Behaviours of the Bone-Implant Interface: A Review. J. R. Soc. Interface 2019, 16, 20190259. [Google Scholar] [CrossRef]
- Le Béguec, P.; Sieber, H.-P. The Concept of “Press-Fit”. In Revision of Loose Femoral Prostheses: With a Stem System Based on the “Press-Fit” Principle: A Concept and a System of Implants: A Method and Its Results; Le Béguec, P., Sieber, H.-P., Eds.; Springer: Paris, France, 2007; pp. 19–27. ISBN 978-2-287-39629-8. [Google Scholar]
- Viceconti, M.; Muccini, R.; Bernakiewicz, M.; Baleani, M.; Cristofolini, L. Large-Sliding Contact Elements Accurately Predict Levels of Bone-Implant Micromotion Relevant to Osseointegration. J. Biomech. 2000, 33, 1611–1618. [Google Scholar] [CrossRef] [PubMed]
- Viceconti, M.; Pancanti, A.; Dotti, M.; Traina, F.; Cristofolini, L. Effect of the Initial Implant Fitting on the Predicted Secondary Stability of a Cementless Stem. Med. Biol. Eng. Comput. 2004, 42, 222–229. [Google Scholar] [CrossRef]
- Reggiani, B.; Cristofolini, L.; Varini, E.; Viceconti, M. Predicting the Subject-Specific Primary Stability of Cementless Implants during Pre-Operative Planning: Preliminary Validation of Subject-Specific Finite-Element Models. J. Biomech. 2007, 40, 2552–2558. [Google Scholar] [CrossRef]
- Tomaszewski, P.K.; van Diest, M.; Bulstra, S.K.; Verdonschot, N.; Verkerke, G.J. Numerical Analysis of an Osseointegrated Prosthesis Fixation with Reduced Bone Failure Risk and Periprosthetic Bone Loss. J. Biomech. 2012, 45, 1875–1880. [Google Scholar] [CrossRef]
- Lee, W.C.C.; Doocey, J.M.; Brånemark, R.; Adam, C.J.; Evans, J.H.; Pearcy, M.J.; Frossard, L.A. FE Stress Analysis of the Interface between the Bone and an Osseointegrated Implant for Amputees—Implications to Refine the Rehabilitation Program. Clin. Biomech. 2008, 23, 1243–1250. [Google Scholar] [CrossRef]
- Ramamurti, B.S.; Orr, T.E.; Bragdon, C.R.; Lowenstein, J.D.; Jasty, M.; Harris, W.H. Factors Influencing Stability at the Interface between a Porous Surface and Cancellous Bone: A Finite Element Analysis of a Canine in Vivo Micromotion Experiment. J. Biomed. Mater. Res. 1997, 36, 274–280. [Google Scholar] [CrossRef]
- Saravana Kumar, G.; George, S.P. Optimization of Custom Cementless Stem Using Finite Element Analysis and Elastic Modulus Distribution for Reducing Stress-Shielding Effect. Proc. Inst. Mech. Eng. Part H 2017, 231, 149–159. [Google Scholar] [CrossRef]
- Pettersen, S.H.; Wik, T.S.; Skallerud, B. Subject Specific Finite Element Analysis of Implant Stability for a Cementless Femoral Stem. Clin. Biomech. 2009, 24, 480–487. [Google Scholar] [CrossRef] [PubMed]
- Hériveaux, Y.; Le Cann, S.; Fraulob, M.; Vennat, E.; Nguyen, V.H.; Haïat, G. Mechanical Micromodeling of Stress-Shielding at the Bone-Implant Interphase under Shear Loading. Med. Biol. Eng. Comput. 2022, 60, 3281–3293. [Google Scholar] [CrossRef] [PubMed]
- Conlisk, N.; Howie, C.R.; Pankaj, P. Quantification of Interfacial Motions Following Primary and Revision Total Knee Arthroplasty: A Verification Study versus Experimental Data. J. Orthop. Res. 2018, 36, 387–396. [Google Scholar] [CrossRef] [PubMed]
- Solitro, G.F.; Whitlock, K.; Amirouche, F.; Santis, C. Measures of Micromotion in Cementless Femoral Stems-Review of Current Methodologies. Biomater. Biomech. Bioeng. 2016, 3, 85–104. [Google Scholar] [CrossRef]
- Ingrassia, T.; Nigrelli, V.; Ricotta, V.; Nalbone, L.; D’Arienzo, A.; D’Arienzo, M.; Porcellini, G. A New Method to Evaluate the Influence of the Glenosphere Positioning on Stability and Range of Motion of a Reverse Shoulder Prosthesis. Injury 2019, 50, S12–S17. [Google Scholar] [CrossRef]
- Ingrassia, T.; Nigrelli, V.; Pecorella, D.; Bragonzoni, L.; Ricotta, V. Influence of the Screw Positioning on the Stability of Locking Plate for Proximal Tibial Fractures: A Numerical Approach. Appl. Sci. 2020, 10, 4941. [Google Scholar] [CrossRef]
- Park, J.; Park, S.; Kang, I.; Noh, G. Biomechanical Effects of Bone Quality and Design Features in Dental Implants in Long-Term Bone Stability. J. Comput. Des. Eng. 2022, 9, 1538–1548. [Google Scholar] [CrossRef]
- Tomaszewski, P.K.; Verdonschot, N.; Bulstra, S.K.; Rietman, J.S.; Verkerke, G.J. Simulated Bone Remodeling around Two Types of Osseointegrated Implants for Direct Fixation of Upper-Leg Prostheses. J. Mech. Behav. Biomed. Mater. 2012, 15, 167–175. [Google Scholar] [CrossRef]
- Newcombe, L.; Dewar, M.; Blunn, G.W.; Fromme, P. Effect of Amputation Level on the Stress Transferred to the Femur by an Artificial Limb Directly Attached to the Bone. Med. Eng. Phys. 2013, 35, 1744–1753. [Google Scholar] [CrossRef]
- Helgason, B.; Pálsson, H.; Rúnarsson, T.P.; Frossard, L.; Viceconti, M. Risk of Failure during Gait for Direct Skeletal Attachment of a Femoral Prosthesis: A Finite Element Study. Med. Eng. Phys. 2009, 31, 595–600. [Google Scholar] [CrossRef]
- Ghaziani, A.O.; Soheilifard, R.; Kowsar, S. The Effect of Functionally Graded Materials on Bone Remodeling around Osseointegrated Trans-Femoral Prostheses. J. Mech. Behav. Biomed. Mater. 2021, 118, 104426. [Google Scholar] [CrossRef] [PubMed]
- Taylor, C.E.; Henninger, H.B.; Bachus, K.N. Finite Element Analysis of Transhumeral and Transtibial Percutaneous Osseointegrated Endoprosthesis Implantation. Front. Rehabil. Sci. 2021, 2, 744674. [Google Scholar] [CrossRef] [PubMed]
- Prochor, P. Finite Element Analysis of Stresses Generated in Cortical Bone during Implantation of a Novel Limb Prosthesis Osseointegrated Fixation System. Biocybern. Biomed. Eng. 2017, 37, 255–262. [Google Scholar] [CrossRef]
- Tomaszewski, P.K.; Verdonschot, N.; Bulstra, S.K.; Verkerke, G.J. A Comparative Finite-Element Analysis of Bone Failure and Load Transfer of Osseointegrated Prostheses Fixations. Ann. Biomed. Eng. 2010, 38, 2418–2427. [Google Scholar] [CrossRef]
- Lu, S.; Vien, B.S.; Russ, M.; Fitzgerald, M.; Chiu, W.K. Novel Osseointegration Implant Optimization—Australasian Congress on Applied Mechanics. In Proceedings of the ACAM10: 10th Australasian Congress on Applied Mechanics, Online, 1–3 December 2021; pp. 66–78. [Google Scholar]
- Cirello, A.; Ingrassia, T.; Marannano, G.; Mirulla, A.I.; Nigrelli, V.; Petrucci, G.; Ricotta, V. A New Automatic Process Based on Generative Design for CAD Modeling and Manufacturing of Customized Orthosis. Appl. Sci. 2024, 14, 6231. [Google Scholar] [CrossRef]
- Li, Y.; Felländer-Tsai, L. The Bone Anchored Prostheses for Amputees—Historical Development, Current Status, and Future Aspects. Biomaterials 2021, 273, 120836. [Google Scholar] [CrossRef]
- Al Muderis, M.; Aschoff, H.H.; Bosley, B.; Raz, G.; Gerdesmeyer, L.; Burkett, B. Direct Skeletal Attachment Prosthesis for the Amputee Athlete: The Unknown Potential. Sports Eng. 2016, 19, 141–145. [Google Scholar] [CrossRef]
- Frölke, J.P.M.; Leijendekkers, R.A.; van de Meent, H. Osseointegrierte Prothese Für Patienten Nach Amputation: Multidisziplinärer Behandlungsansatz in Den Niederlanden. Unfallchirurg 2017, 120, 293–299. [Google Scholar] [CrossRef]
- Bernakiewicz, M.; Viceconti, M. The Role of Parameter Identification in Finite Element Contact Analyses with Reference to Orthopaedic Biomechanics Applications. J. Biomech. 2002, 35, 61–67. [Google Scholar] [CrossRef]
- Stenlund, P.; Trobos, M.; Lausmaa, J.; Brånemark, R.; Thomsen, P.; Palmquist, A. Effect of Load on the Bone around Bone-Anchored Amputation Prostheses. J. Orthop. Res. 2017, 35, 1113–1122. [Google Scholar] [CrossRef]
- Russell, R.D.; Huo, M.H.; Rodrigues, D.C.; Kosmopoulos, V. Stem Geometry Changes Initial Femoral Fixation Stability of a Revised Press-Fit Hip Prosthesis: A Finite Element Study. Technol. Health Care 2016, 24, 865–872. [Google Scholar] [CrossRef] [PubMed]
- Ashman, R.B.; Cowin, S.C.; Van Buskirk, W.C.; Rice, J.C. A Continuous Wave Technique for the Measurement of the Elastic Properties of Cortical Bone. J. Biomech. 1984, 17, 349–361. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.Y.; Cai, Z.B.; Zhou, Z.R.; Zhu, M.H. Fretting Behavior of Cortical Bone against Titanium and Its Alloy. Wear 2005, 259, 910–918. [Google Scholar] [CrossRef]
- Vertriest, S.; Coorevits, P.; Hagberg, K.; Brånemark, R.; Häggström, E.; Vanderstraeten, G.; Frossard, L. Static Load Bearing Exercises of Individuals with Transfemoral Amputation Fitted with an Osseointegrated Implant: Reliability of Kinetic Data. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 423–430. [Google Scholar] [CrossRef]
- Dassault Systèmes Simulia Corp. ABAQUS/Standard User’s Manual, Version 2021; Simulia: Johnston, RI, USA, 2021. [Google Scholar]
- Mirulla, A.I.; Pinelli, S.; Zaffagnini, S.; Nigrelli, V.; Ingrassia, T.; Di Paolo, S.; Bragonzoni, L. Numerical Simulations on Periprosthetic Bone Remodeling: A Systematic Review. Comput. Methods Programs Biomed. 2021, 204, 106072. [Google Scholar] [CrossRef]
- Thomson, S.; Thomson, A.; Tetsworth, K.; Lu, W.; Zreiqat, H.; Al Muderis, M. Radiographic Evaluation of Bone Remodeling Around Osseointegration Implants among Transfemoral Amputees. J. Orthop. Trauma. 2019, 33, 303–308. [Google Scholar] [CrossRef]
- Benfratello, S.; Cirello, A.; Palizzolo, L.; Sanfilippo, C.; Valenza, A. Experimental Analysis and Numerical Modelling of the Mechanical Behavior of a Sisal-Fiber-Reinforced Geopolymer. Appl. Sci. 2024, 14, 5216. [Google Scholar] [CrossRef]
- Abdelaal, O.; Darwish, S.; El-Hofy, H.; Saito, Y. Patient-Specific Design Process and Evaluation of a Hip Prosthesis Femoral Stem. Int. J. Artif. Organs 2019, 42, 271–290. [Google Scholar] [CrossRef]


| Ex | Ey | Ez | Gxy | Gyz | Gxz | νxy | νyz | νxz | |
|---|---|---|---|---|---|---|---|---|---|
| Cortical bone | 12 GPa | 13.4 GPa | 20 GPa | 4.53 GPa | 6.23 GPa | 5.61 GPa | 0.376 | 0.235 | 0.222 |
| Ti6Al4V | 110 GPa | // | // | // | // | // | 0.3 | // | // |
| Contact element surface to surface | Contact formulation finite sliding | Normal behaviour “Hard” penalty | Normal stiffness 600 N/mm | Tangential behaviour penalty |
| Friction coefficient 0.29 | Elastic slip 0.005 mm | Interference Ø 0.1 mm | Contact control 0.20% | Line search control iterations 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valenti, A.; Cirello, A.; Ingrassia, T.; Marannano, G.; Nigrelli, V.; Ricotta, V.; Mirulla, A.I. Primary Stability Assessment of Patient-Specific Transfemoral Osseointegrated Implants During Static Load-Bearing Exercise: A Comparative Analysis. Appl. Sci. 2025, 15, 5913. https://doi.org/10.3390/app15115913
Valenti A, Cirello A, Ingrassia T, Marannano G, Nigrelli V, Ricotta V, Mirulla AI. Primary Stability Assessment of Patient-Specific Transfemoral Osseointegrated Implants During Static Load-Bearing Exercise: A Comparative Analysis. Applied Sciences. 2025; 15(11):5913. https://doi.org/10.3390/app15115913
Chicago/Turabian StyleValenti, Andrea, Antonino Cirello, Tommaso Ingrassia, Giuseppe Marannano, Vincenzo Nigrelli, Vito Ricotta, and Agostino Igor Mirulla. 2025. "Primary Stability Assessment of Patient-Specific Transfemoral Osseointegrated Implants During Static Load-Bearing Exercise: A Comparative Analysis" Applied Sciences 15, no. 11: 5913. https://doi.org/10.3390/app15115913
APA StyleValenti, A., Cirello, A., Ingrassia, T., Marannano, G., Nigrelli, V., Ricotta, V., & Mirulla, A. I. (2025). Primary Stability Assessment of Patient-Specific Transfemoral Osseointegrated Implants During Static Load-Bearing Exercise: A Comparative Analysis. Applied Sciences, 15(11), 5913. https://doi.org/10.3390/app15115913








