A Fast, Simple, and Approximate Method for a Minimal Unit Cell Design of Glide-Symmetric Double-Corrugated Parallel-Plate Waveguides
Abstract
:1. Introduction
2. Materials and Methods
Theory and Design Strategy
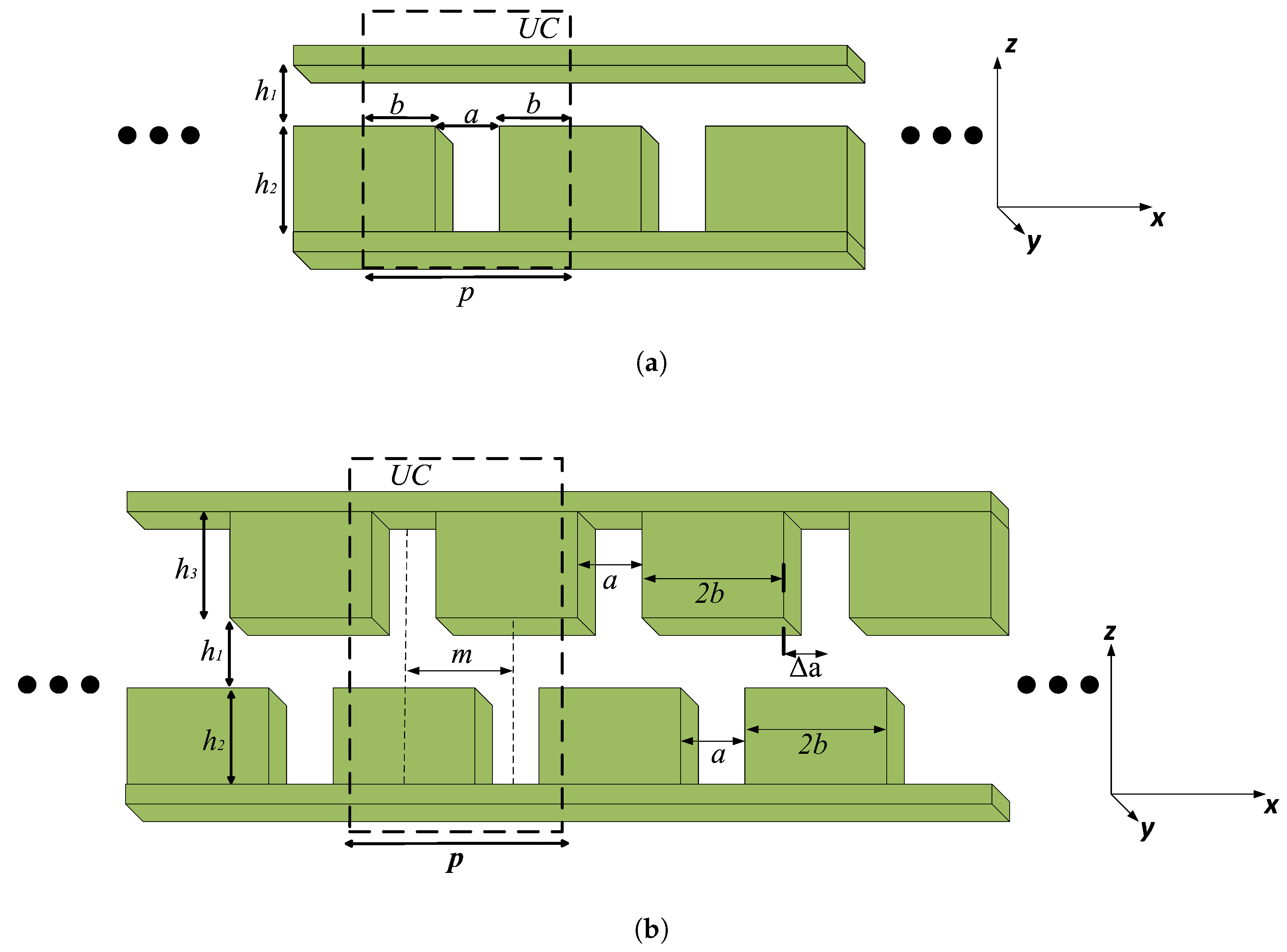
- Step 1: Select single/glide-symmetric double CPPW model and start appropriate unit cell configuration.
- Step 2: Constrain the design space so that the dimensional parameters of the unit cell based on the circuit model given in Figure 2 are in the appropriate range.
- Step 3: Modify the dimensions in the limited design space obtained in Step 2, and determine the appropriate unit cell parameters satisfying the given design requirements employing Equation (5).
- Step 4: Connect the designed unit cells back-to-back a finite number of times to meet the design requirements and obtain the filter responses with full-wave simulators.
3. Results and Discussion
3.1. Numerical Examples
- (a) Ku-band filter design with a suppression level of more than −50 dB in the 15.20–17.78 GHz range for a single CPPW.
- (b) X-band filter design with a suppression level of more than −60 dB in the 8.27–10.91 GHz range for glide-symmetric double CPPWs.
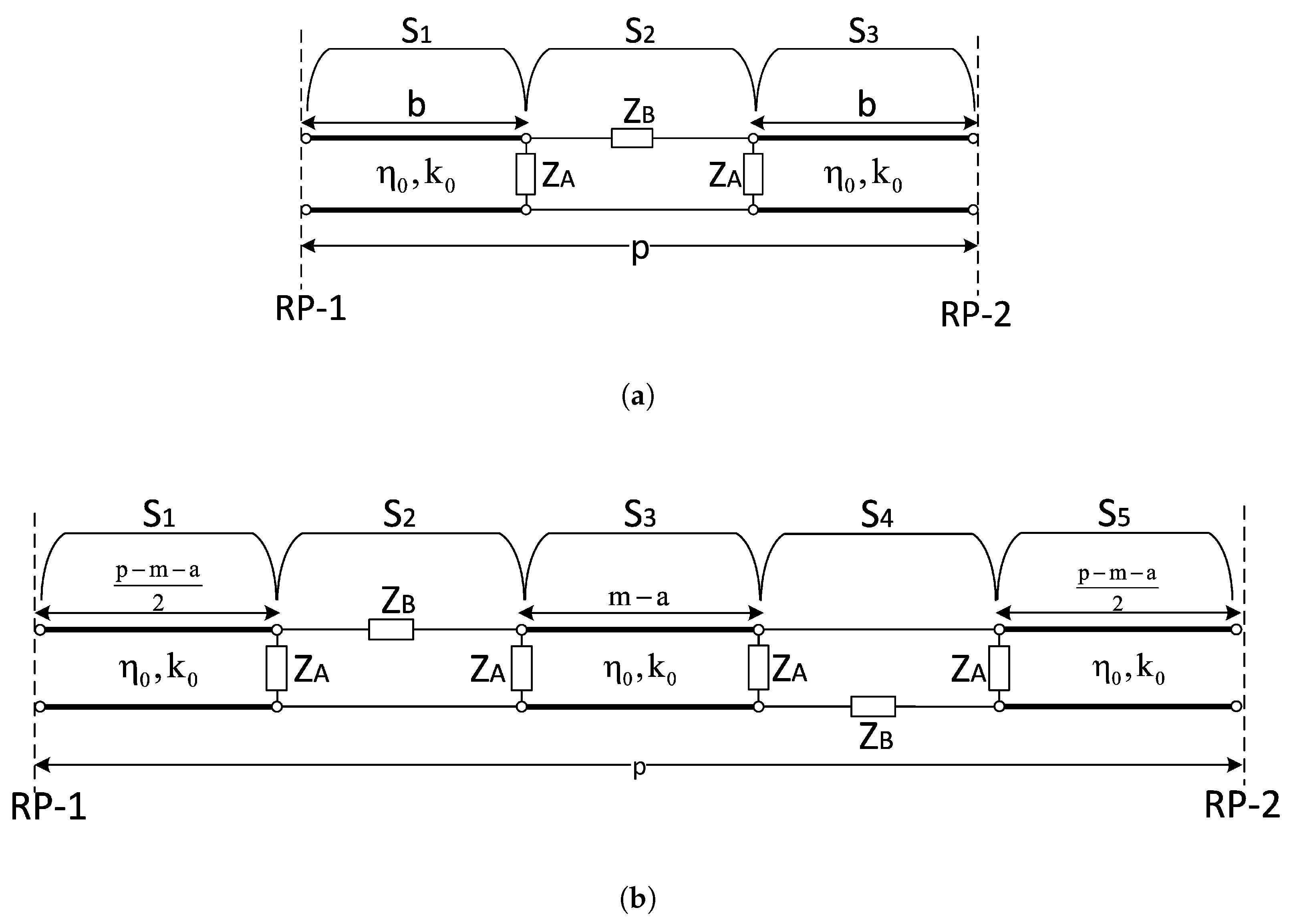
3.2. Design of Unit Cell and Cascade Connection Analysis of Corrugated PPW Structures
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MM-GSM | Mode Matching–Generalized Scattering Matrix |
| BSF | Band Stop Filter |
| HFSS | High-Frequency Structure Simulator |
| CST | Computer Simulation Technology |
| FHMSIW | Folded Half-Mode Substrate Integrated Waveguide |
| SSPP | Spoof Surface Plasmon Polaritons |
| UC | Unit Cell |
Appendix A. Network Representation Explanation of Expanded Version of Equivalent Circuit of Corrugations and Obtaining S-Parameters of Unit Cell with All Definitions
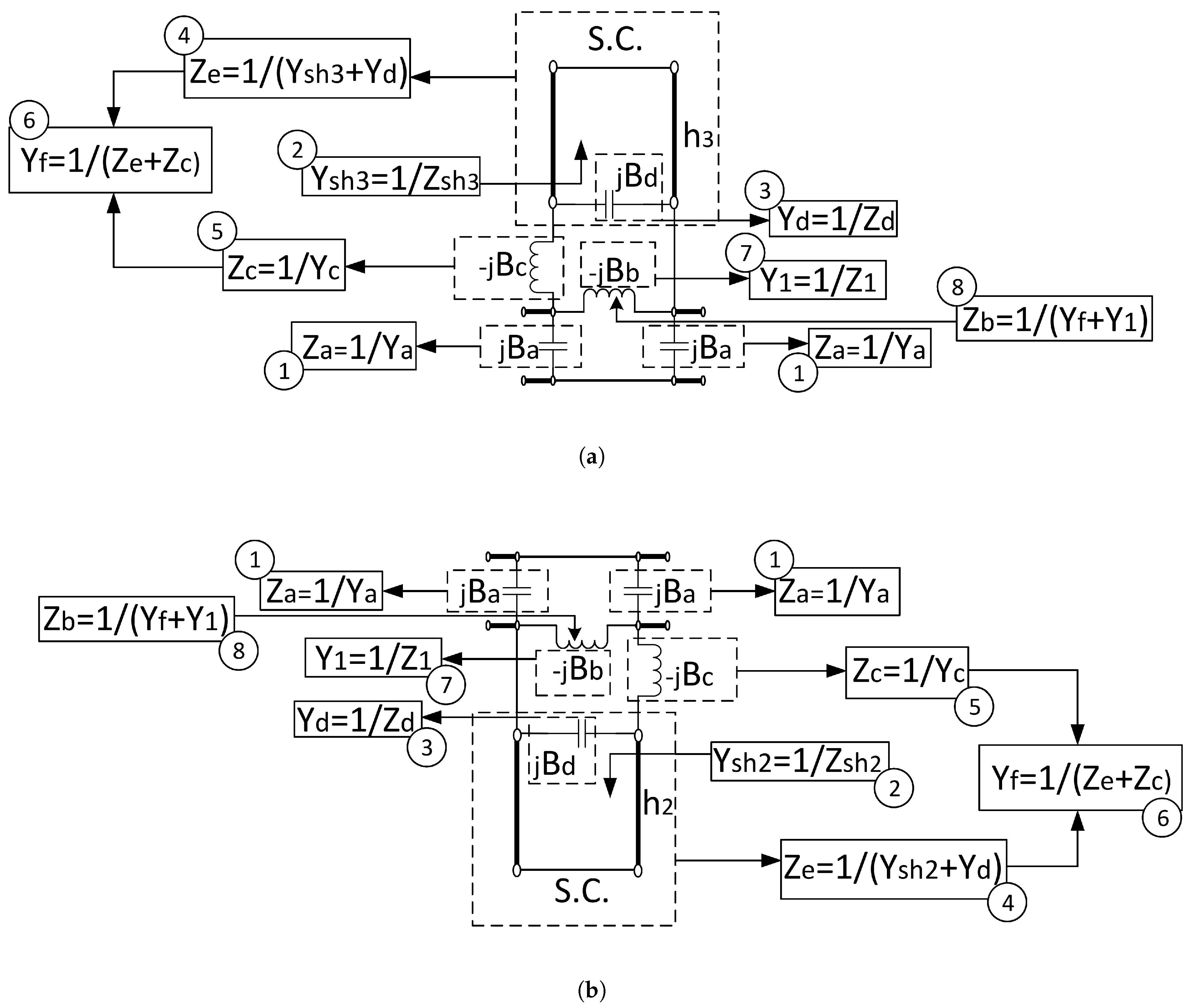
Appendix B. Notation List
| The A and D elements of ABCD parameters | |
| a | The corrugate width of single and glide-symmetric double CPPW |
| , | The normalized power waves used in scattering parameters |
| b | The length of half of each ridge in the CPPW |
| The Floquet phase factor propagating in the x direction | |
| The frequency deviation | |
| The width of the stopband | |
| The dielectric constant of the material loaded in the CPPW | |
| The tangential component of the electric field | |
| f | The frequency |
| The last frequency of the stopband | |
| The first frequency of the stopband | |
| The height between corrugated parallel plates | |
| The height of the bottom section of corrugated parallel plates | |
| The height of the top section of corrugated parallel plates | |
| The tangential component of the magnetic field | |
| The block identity matrix | |
| l | The length of any transmission line |
| The eigenvalue | |
| m | The gliding operator |
| N | The number of unit cells |
| p | The period of the periodic structure |
| The elements of a classical scattering matrix of a two-port network | |
| The block submatrices of the generalized scattering matrix | |
| The complete form of auxiliary functions | |
| The reduced form of auxiliary functions |
References
- Hessel, A.; Chen, M.H.; Li, R.C.; Oliner, A.A. Propagation in periodically loaded waveguides with higher symmetries. Proc. IEEE 1973, 61, 183–195. [Google Scholar] [CrossRef]
- Navarro, M.S.; Rozzi, T.E.; Lo, Y.T. Propagation in a rectangular waveguide periodically loaded with resonant irises. IEEE Trans. Microw. Theory Tech. 1980, 8, 857–865. [Google Scholar] [CrossRef]
- Amari, S.; Vahldieck, R.; Bornemann, J.; Leuchtmann, P. Spectrum of corrugated and periodically loaded waveguides from classical matrix eigenvalues. IEEE Trans. Microw. Theory Tech. 2000, 3, 453–460. [Google Scholar] [CrossRef]
- Lech, R.; Mazur, J. Propagation in rectangular waveguides periodically loaded with cylindrical posts. IEEE Microw. Wirel. Compon. Lett. 2004, 14, 177–179. [Google Scholar] [CrossRef]
- Simsek, S.; Topuz, E. Some properties of generalized scattering matrix representations for metallic waveguides with periodic dielectric loading. IEEE Trans. Microw. Theory Tech. 2007, 11, 2336–2344. [Google Scholar] [CrossRef]
- Othman, M.A.K.; Pan, X.; Atmatzakis, G.; Christodoulou, C.G.; Capolino, F. Experimental demonstration of degenerate band edge in metallic periodically loaded circular waveguide. IEEE Trans. Microw. Theory Tech. 2017, 11, 4037–4045. [Google Scholar] [CrossRef]
- Ertay, A.O.; Simsek, S. Detection of band edge frequencies in symmetric/asymmetric dielectric loaded helix slow-wave structures. Int. J. Circuit Theory Appl. 2022, 50, 507–524. [Google Scholar] [CrossRef]
- Petek, M.; Rico-Fernández, J.; Vásquez, J.A.T.; Valerio, G.; Mesa, F.; Quevedo-Teruel, O.; Vipiana, F. Numerical Modelling of Higher-Symmetric Periodic Structures with Hexagonal Lattice. IEEE Trans. Antennas Propag. 2025, 73, 1650–1661. [Google Scholar] [CrossRef]
- Tahir, G.; Hassan, A.; Ali, S.; Bermak, A. Unit Cell Optimization of Groove Gap Waveguide for High Bandwidth Microwave Applications. Appl. Sci. 2024, 14, 10891. [Google Scholar] [CrossRef]
- Jimenez-Suarez, J.M.; Mesa, F.; Quevedo-Teruel, O. A Symmetry-Based Multimodal Transfer-Matrix Method for the Analysis of 2D-Periodic Structures. IEEE Trans. Microw. Theory Tech. 2025, 1–11. [Google Scholar] [CrossRef]
- Şimşek, S.; Topuz, E.; Niver, E. A novel design method for electromagnetic bandgap based waveguide filters with periodic dielectric loading. AEU-Int. J. Electron. Commun. 2012, 66, 228–234. [Google Scholar] [CrossRef]
- Coves, A.; San-Blas, A.A.; Bronchalo, E. Analysis of the dispersion characteristics in periodic Substrate Integrated Waveguides. AEU-Int. J. Electron. Commun. 2021, 139, 153914. [Google Scholar] [CrossRef]
- Mesa, F.; Rodríguez-Berral, R.; Medina, F. On the computation of the dispersion diagram of symmetric one-dimensionally periodic structures. Symmetry 2018, 10, 307. [Google Scholar] [CrossRef]
- Ertay, A.O.; Şimşek, S. A comprehensive auxiliary functions of generalized scattering matrix (AFGSM) method to determine bandgap characteristics of periodic structures. AEU-Int. J. Electron. Commun. 2018, 94, 139–144. [Google Scholar] [CrossRef]
- Karamirad, M.; Pouyanfar, N.; Alibakhshikenari, M.; Ghobadi, C.; Nourinia, J.; See, C.H.; Falcone, F. Low-loss and dual-band filter inspired by glide symmetry principle over millimeter-wave spectrum for 5G cellular networks. Iscience 2023, 26, 1–14. [Google Scholar] [CrossRef]
- Xu, S.; Wu, J.; Chen, X. Design of Broadband Highly Efficient Power Amplifier Based on Low-Pass Filtering Network with Periodic Structure. Int. J. Circuit Theory Appl. 2024. [Google Scholar] [CrossRef]
- Liu, Z.; Lu, H.; Liu, J.; Yang, S.; Liu, Y.; Lv, X. Compact fully metallic millimeter-wave waveguide-fed periodic leaky-wave antenna based on corrugated parallel-plate waveguides. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 806–810. [Google Scholar] [CrossRef]
- Maci, S.; Minatti, G.; Casaletti, M.; Bosiljevac, M. Metasurfing: Addressing waves on impenetrable metasurfaces. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 1499–1502. [Google Scholar] [CrossRef]
- Alex-Amor, A.; Mesa, F.; Palomares-Caballero, Á.; Molero, C.; Padilla, P. Exploring the potential of the multi-modal equivalent circuit approach for stacks of 2-D aperture arrays. IEEE Trans. Antennas Propag. 2021, 69, 6453–6467. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Valerio, G.; Sipus, Z.; Rajo-Iglesias, E. Periodic structures with higher symmetries: Their applications in electromagnetic devices. IEEE Microw. Mag. 2020, 21, 36–49. [Google Scholar] [CrossRef]
- Palomares-Caballero, Á.; Alex-Amor, A.; Padilla, P.; Valenzuela-Valdés, J.F. Dispersion and filtering properties of rectangular waveguides loaded with holey structures. IEEE Trans. Microw. Theory Tech. 2020, 68, 5132–5144. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Chen, Q.; Mesa, F.; Fonseca, N.J.; Valerio, G. On the benefits of glide symmetries for microwave devices. IEEE J. Microwaves 2021, 1, 457–469. [Google Scholar] [CrossRef]
- Ghasemifard, F.; Norgren, M.; Quevedo-Teruel, O. Twist and polar glide symmetries: An additional degree of freedom to control the propagation characteristics of periodic structures. Sci. Rep. 2018, 8, 11266. [Google Scholar] [CrossRef] [PubMed]
- Dahlberg, O.; Mitchell-Thomas, R.; Quevedo-Teruel, O. Reducing the dispersion of periodic structures with twist and polar glide symmetries. Sci. Rep. 2017, 7, 10136. [Google Scholar] [CrossRef]
- Arnberg, P.; Barreira Petersson, O.; Zetterstrom, O.; Ghasemifard, F.; Quevedo-Teruel, O. High refractive index electromagnetic devices in printed technology based on glide-symmetric periodic structures. Appl. Sci. 2020, 10, 3216. [Google Scholar] [CrossRef]
- Ebrahimpouri, M.; Quevedo-Teruel, O.; Rajo-Iglesias, E. Design guidelines for gap waveguide technology based on glide-symmetric holey structures. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 542–544. [Google Scholar] [CrossRef]
- Tamayo-Dominguez, A.; Fernandez-Gonzalez, J.M.; Quevedo-Teruel, O. One-plane glide-symmetric holey structures for stop-band and refraction index reconfiguration. Symmetry 2019, 11, 495. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Ebrahimpouri, M.; Kehn, M.N.M. Ultrawideband metasurface lenses based on off-shifted opposite layers. IEEE Antennas Wirel. Propag. Lett. 2015, 15, 484–487. [Google Scholar] [CrossRef]
- Ghasemifard, F.; Norgren, M.; Quevedo-Teruel, O.; Valerio, G. Analyzing glide-symmetric holey metasurfaces using a generalized Floquet theorem. IEEE Access 2018, 6, 71743–71750. [Google Scholar] [CrossRef]
- Herran, L.F.; Chen, Q.; Mesa, F.; Quevedo-Teruel, O. Electromagnetic Bandgap Based on a Compact Three-Hole Double-Layer Periodic Structure. IEEE Trans. Antennas Propag. 2023, 72, 1045–1050. [Google Scholar] [CrossRef]
- Ghasemifard, F.; Norgren, M.; Quevedo-Teruel, O. Dispersion analysis of 2-D glide-symmetric corrugated metasurfaces using mode-matching technique. IEEE Microw. Wirel. Components Lett. 2017, 28, 1–3. [Google Scholar] [CrossRef]
- Valerio, G.; Ghasemifard, F.; Sipus, Z.; Quevedo-Teruel, O. Glide-symmetric all-metal holey metasurfaces for low-dispersive artificial materials: Modeling and properties. IEEE Trans. Microw. Theory Tech. 2018, 66, 3210–3223. [Google Scholar] [CrossRef]
- Fischer, B.; Valerio, G. Dispersion properties of glide-symmetric corrugated metasurface waveguides. Int. J. Microw. Wirel. Technol. 2024, 16, 13–20. [Google Scholar] [CrossRef]
- Memeletzoglou, N.; Sanchez-Cabello, C.; Pizarro-Torres, F.; Rajo-Iglesias, E. Analysis of periodic structures made of pins inside a parallel plate waveguide. Symmetry 2019, 11, 582. [Google Scholar] [CrossRef]
- Chen, Q.; Mesa, F.; Yin, X.; Quevedo-Teruel, O. Accurate characterization and design guidelines of glide-symmetric holey EBG. IEEE Trans. Microw. Theory Tech. 2020, 68, 4984–4994. [Google Scholar] [CrossRef]
- Valerio, G.; Sipus, Z.; Grbic, A.; Quevedo-Teruel, O. Accurate equivalent-circuit descriptions of thin glide-symmetric corrugated metasurfaces. IEEE Trans. Antennas Propag. 2017, 65, 2695–2700. [Google Scholar] [CrossRef]
- Ertay, A.O. Modeling, Analysis, and Comparison of Rectangular Waveguide Structures Having Glide Symmetrical Step Discontinuity with Periodic Dielectric Loading. Erzincan Univ. J. Sci. Technol. 2024, 17, 826–839. [Google Scholar] [CrossRef]
- Fischer, B.; Valerio, G. Quasi-static homogenization of glide-symmetric holey parallel-plate waveguides with ultra-wideband validity. IEEE Trans. Antennas Propag. 2022, 70, 10569–10582. [Google Scholar] [CrossRef]
- Lai, W.Y.; Kehn, M.N.M. Analysis of Rotated Corrugated Parallel Plate Waveguide Using Asymptotic Corrugation Boundary Conditions. In Proceedings of the 2019 IEEE International Symposium on Antennas and Propagation and USNC-URSI Radio Science Meeting, Atlanta, GA, USA, 7–12 July 2019; pp. 837–838. [Google Scholar]
- Mesa, F.; Valerio, G.; Rodriguez-Berral, R.; Quevedo-Teruel, O. Simulation-assisted efficient computation of the dispersion diagram of periodic structures: A comprehensive overview with applications to filters, leaky-wave antennas and metasurfaces. IEEE Antennas Propag. Mag. 2020, 63, 33–45. [Google Scholar] [CrossRef]
- Petek, M.; Rivero, J.; Vásquez, J.A.T.; Valerio, G.; Quevedo-Teruel, O.; Vipiana, F. Method of Moments for the Dispersion Modeling of Glide-Symmetric Periodic Structures. IEEE Trans. Antennas Propag. 2024, 72, 756–766. [Google Scholar] [CrossRef]
- Castillo-Tapia, P.; Mesa, F.; Yakovlev, A.; Valerio, G.; Quevedo-Teruel, O. Study of forward and backward modes in double-sided dielectric-filled corrugated waveguides. Sensors 2021, 21, 6293. [Google Scholar] [CrossRef] [PubMed]
- Castillo-Tapia, P.; Mesa, F.; Quevedo-Teruel, O. Multimodal Transfer Matrix Approach for the Analysis and Fundamental Understanding of Periodic Structures with Higher Symmetries. In Proceedings of the 2022 16th European Conference on Antennas and Propagation (EuCAP), Madrid, Spain, 27 March–1 April 2022; pp. 1–5. [Google Scholar]
- Bagheriasl, M.; Quevedo-Teruel, O.; Valerio, G. Bloch analysis of artificial lines and surfaces exhibiting glide symmetry. IEEE Trans. Microw. Theory Tech. 2019, 67, 2618–2628. [Google Scholar] [CrossRef]
- Castillo-Tapia, P. The Multimodal Transfer Matrix Method: And Its Application to Higher-Symmetric Periodic Structures. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2022. [Google Scholar]
- Mesa, F.; Rodriguez-Berral, R.; Medina, F. Unlocking complexity using the ECA: The equivalent circuit model as an efficient and physically insightful tool for microwave engineering. IEEE Microw. Mag. 2018, 19, 44–65. [Google Scholar] [CrossRef]
- Şimşek, S. A fast and accurate design method for broad omnidirectional bandgaps of one dimensional photonic crystals. AEU-Int. J. Electron. Commun. 2014, 68, 865–868. [Google Scholar] [CrossRef]
- Ertay, A.O.; Şimşek, S. Determination of stopband characteristics of asymmetrically loaded helix slow wave structures with Auxiliary Functions of Generalized Scattering Matrix (AFGSM) method. AEU-Int. J. Electron. Commun. 2018, 95, 271–278. [Google Scholar] [CrossRef]
- Marcuvitz, N. Waveguide Handbook; P. Peregrinus on Behalf of the Institution of Electrical Engineers: London, UK, 1986. [Google Scholar]
- Şimşek, S.; Rezaeieh, S.A. A design method for substrate integrated waveguide electromagnetic bandgap (SIW-EBG) filters. AEU-Int. J. Electron. Commun. 2013, 67, 981–983. [Google Scholar] [CrossRef]
- Padilla, P.; Herran, L.; Tamayo-Dominguez, A.; Valenzuela-Valdes, J.; Quevedo-Teruel, O. Glide symmetry to prevent the lowest stopband of printed corrugated transmission lines. IEEE Microw. Wirel. Components Lett. 2018, 28, 750–752. [Google Scholar] [CrossRef]
- Padilla, P.; Palomares-Caballero, A.; Alex-Amor, A.; Valenzuela-Valdes, J.; Fernández-Gonzalez, J.; Quevedo-Teruel, O. Broken glide-symmetric holey structures for bandgap selection in gap-waveguide technology. IEEE Microw. Wirel. Compon. Lett. 2019, 29, 327–329. [Google Scholar] [CrossRef]
- Monje-Real, A.; Fonseca, N.; Zetterstrom, O.; Pucci, E.; Quevedo-Teruel, O. Holey glide-symmetric filters for 5G at millimeter-wave frequencies. IEEE Microw. Wirel. Components Lett. 2019, 30, 31–34. [Google Scholar]
- Zhu, H.; Mao, J. Miniaturized tapered EBG structure with wide stopband and flat passband. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 314–317. [Google Scholar]
- Ertay, A.O.; Şimşek, S. A compact bandstop filter design for X-band applications. In Proceedings of the 2016 International Symposium on Fundamentals of Electrical Engineering (ISFEE), Bucharest, Romania, 30 June–2 July 2016; pp. 1–6. [Google Scholar]
- Reines, I.; Park, S.J.; Rebeiz, G.M. Compact low-loss tunable X-band bandstop filter with miniature RF-MEMS switches. IEEE Trans. Microw. Theory Tech. 2010, 58, 1887–1895. [Google Scholar] [CrossRef]
- Zheng, G.; Papapolymerou, J. Monolithic reconfigurable bandstop filter using RF MEMS switches. Int. J. RF Microw. Comput.-Aided Eng. 2004, 14, 373–382. [Google Scholar] [CrossRef]
- Hou, F.; Li, L.; Shen, Y.; Sun, C.; Luan, H.; Hu, S. Wideband switchable sharp-rejection filter in compact 3-D heterogeneous integration. IEEE Trans. Compon. Packag. Manuf. Technol. 2022, 12, 1583–1590. [Google Scholar] [CrossRef]
- Cabello-Sánchez, J.; Drakinskiy, V.; Stake, J.; Rodilla, H. Analysis of the electromagnetic interaction between periodically corrugated transmission lines through the mutual capacitance and mutual inductance. IEEE Access. 2022, 10, 15818–15834. [Google Scholar]
- Wu, C.H.; Zhou, G.; Ma, P.; Wu, Y.; Li, K.; Shen, L.; Shen, Q.; Zhang, H.; Yan, J.; You, Y.; et al. A corrugated planar-Goubau-line termination for terahertz waves. IEEE Microw. Wirel. Technol. Lett. 2023, 33, 643–646. [Google Scholar]
- Wang, S.; Chung, K.L.; Du, L.; Kong, F.; Li, K. Design and analysis of a compact frequency beam-scanning antenna based on composite FHMSIW/SSPP waveguide. IEEE Antennas Wirel. Propag. Lett. 2021, 21, 546–550. [Google Scholar] [CrossRef]
- Yan, X.T.; Tang, W.; Liu, J.F.; Wang, M.; Gao, X.X.; Cui, T.J. Glide symmetry for mode control and significant suppression of coupling in dual-strip SSPP transmission lines. Soc. Photo-Opt. Instrum. Eng. 2021, 3, 026001. [Google Scholar] [CrossRef]
- Wang, S.; Chung, K.L.; Kong, F.; Du, L.; Li, K. A simple circularly polarized beam-scanning antenna using modulated slotline-spoof surface plasmon polariton slow-wave transmission line. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 1109–1113. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering: Theory and Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]

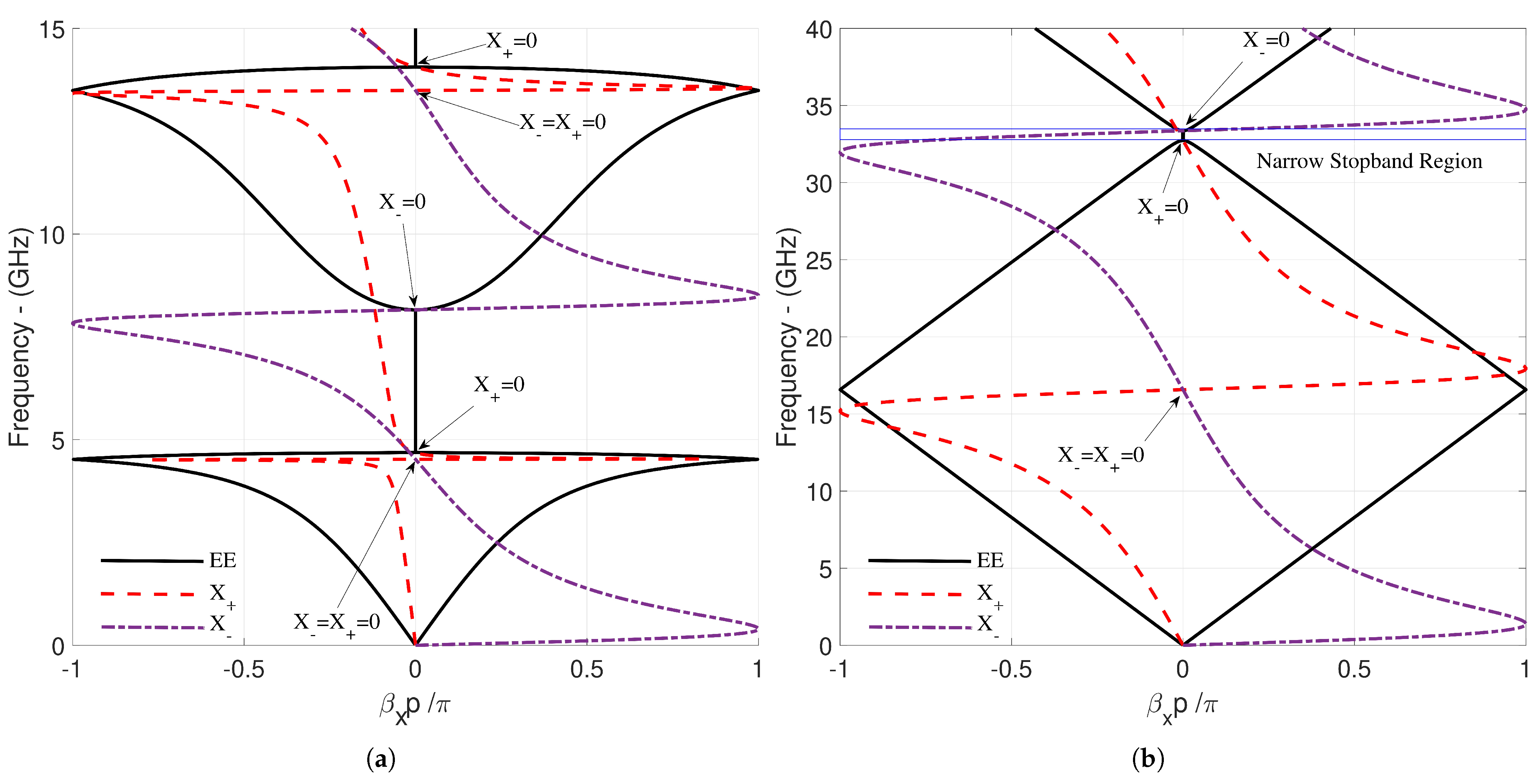
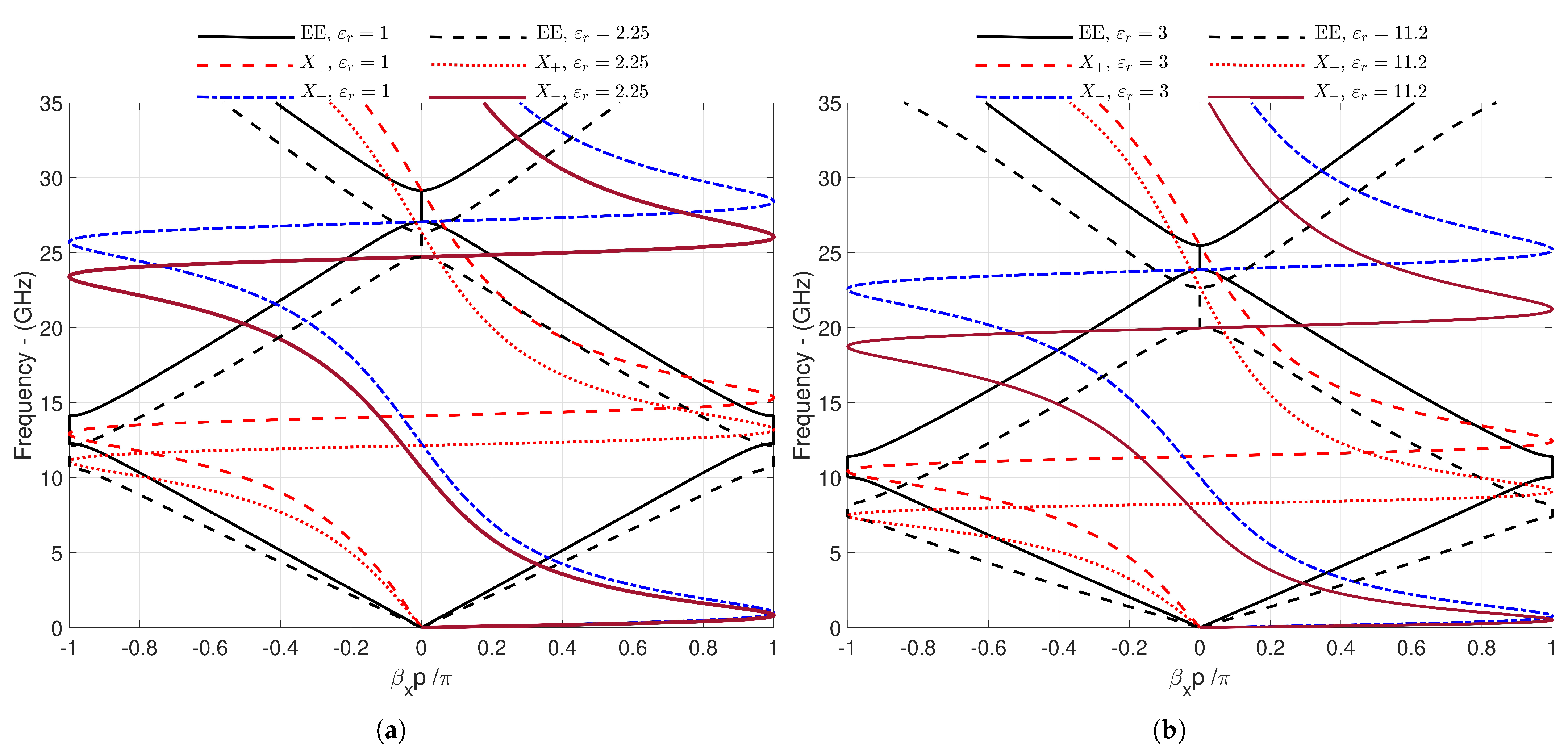
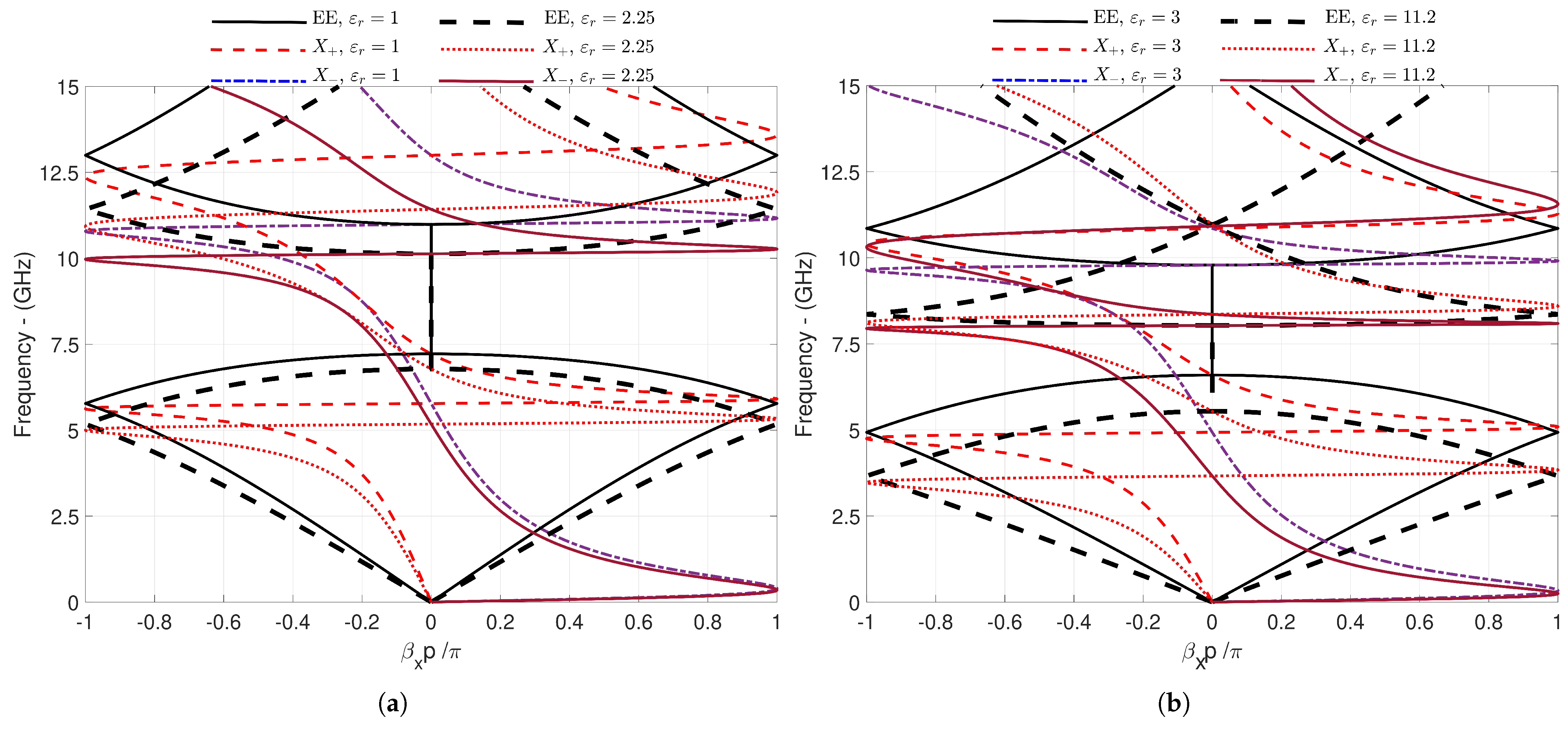


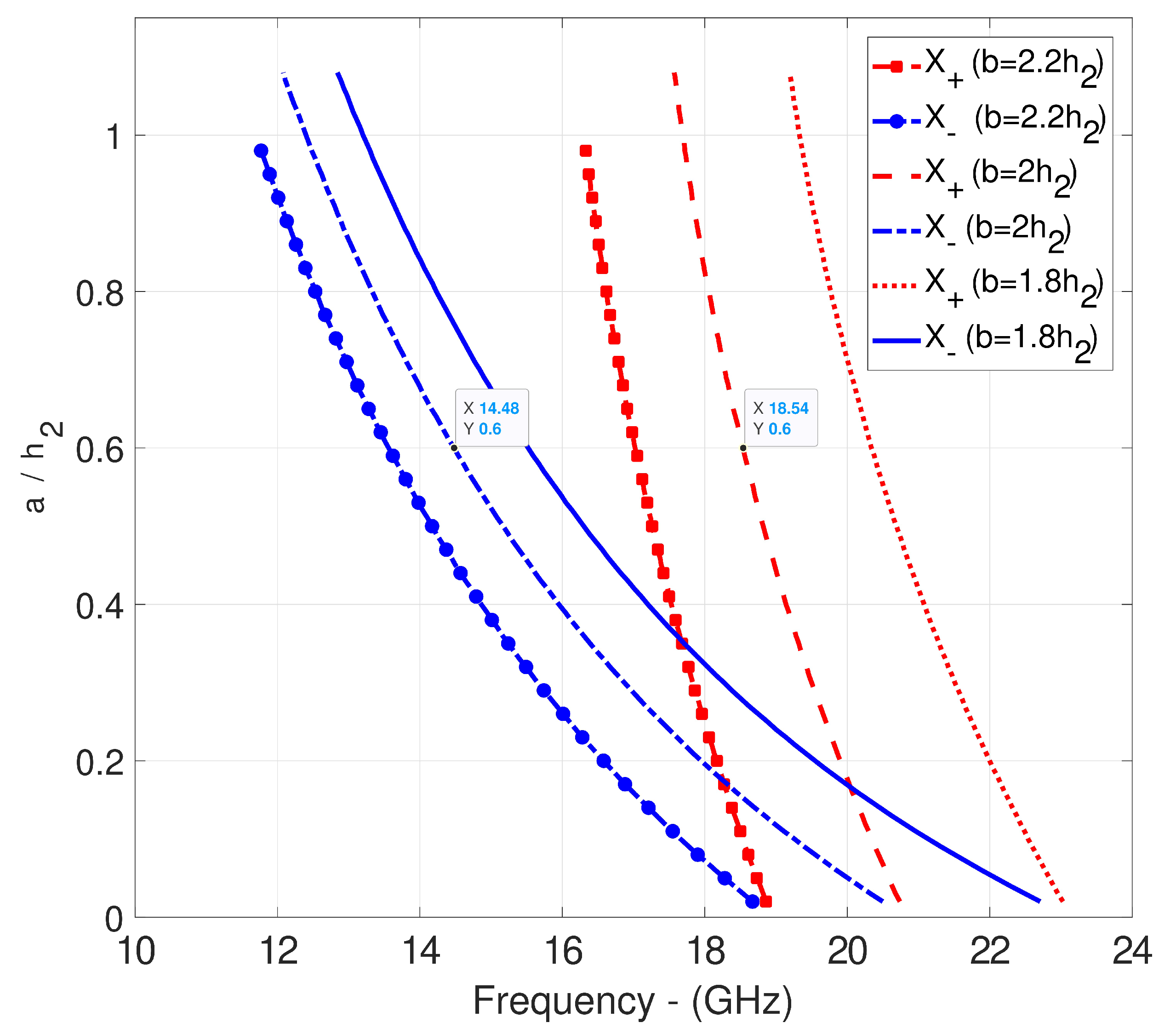
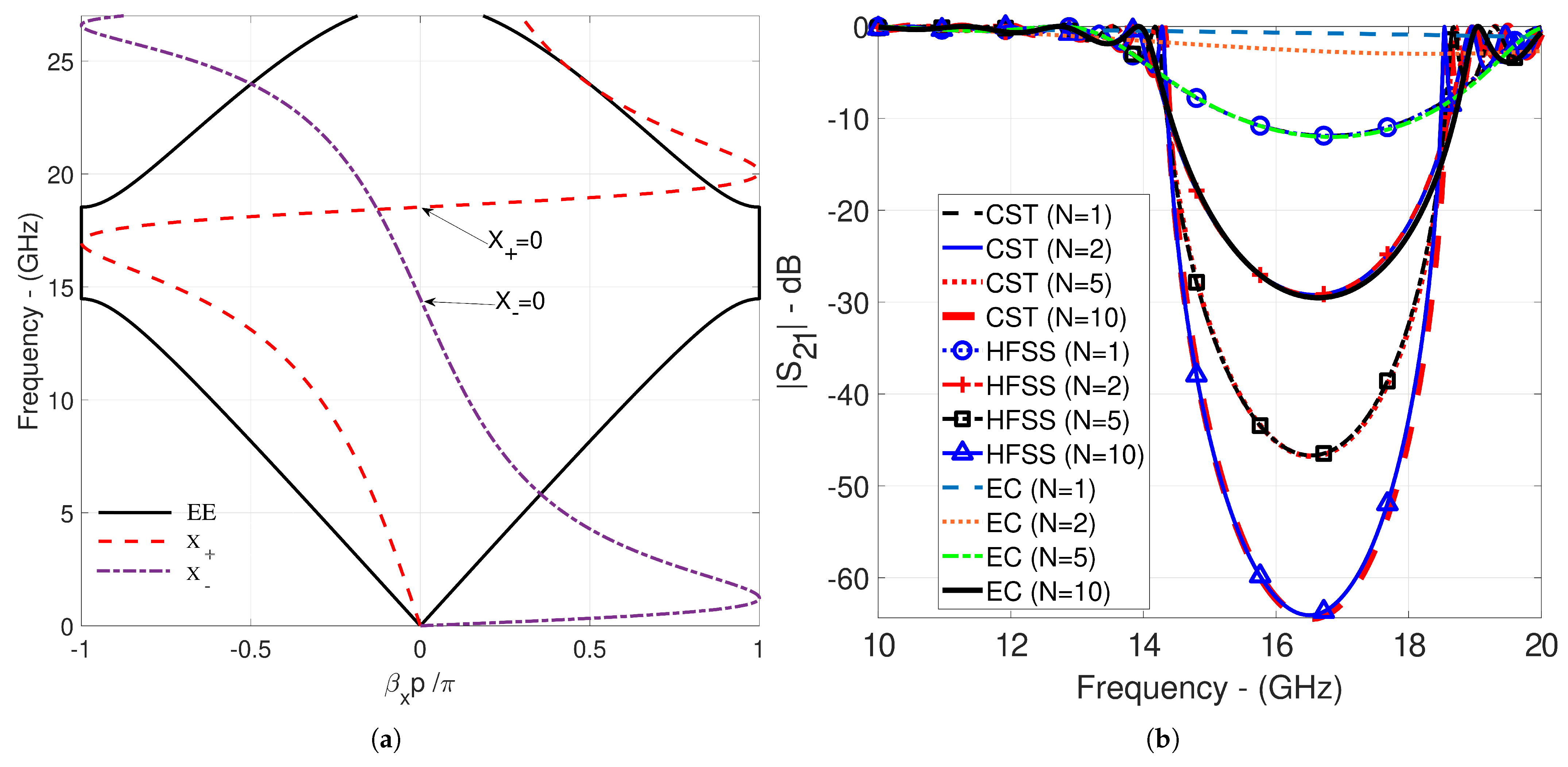


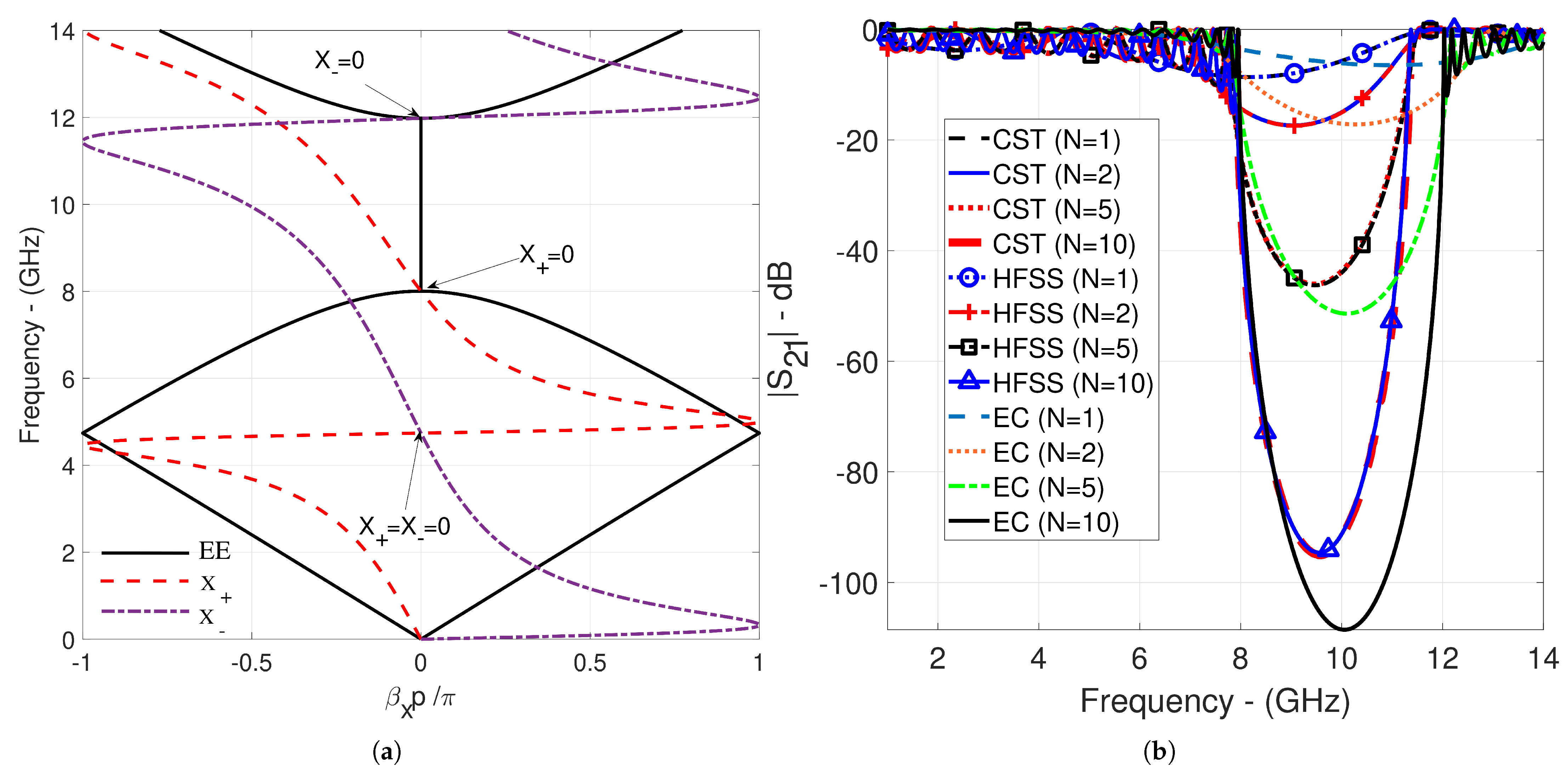
| Figures | [GHz] | [GHz] | EE [GHz] | [GHz] |
|---|---|---|---|---|
| Figure 4a | 4.681 | 8.157 | 4.69–8.15 | 4.52, 13.49 |
| Figure 4b | 32.729 | 33.364 | 32.73–33.363 | 16.57 |
| a | b | |||
|---|---|---|---|---|
| [GHz] | [MHz] | [mm] | [mm] | [mm] |
| 1.8 | 30 | 1.1 | 1.1 | 13.6 |
| 2 | 10 | 1.2 | 1.1 | 13.5 |
| 2.7 | 10 | 1.5 | 1.2 | 13.2 |
| 1.7 | 1 | 13.3 | ||
| 3 | 10 | 1.2 | 1.8 | 12.9 |
| 3.2 | 10 | 1.5 | 1.5 | 12.9 |
| 3.6 | 10 | 1.7 | 1.5 | 12.8 |
| 2.1 | 1.1 | 13.1 | ||
| 3.8 | 10 | 1.3 | 2.2 | 12.5 |
| 1.7 | 1.6 | 12.7 | ||
| 2.2 | 1.1 | 13.1 | ||
| 4 | 20 | 1.5 | 2 | 12.5 |
| 1.9 | 1.5 | 12.7 | ||
| 2 | 1.4 | 12.8 | ||
| 2.1 | 1.3 | 12.9 | ||
| 2.2 | 1.2 | 13 | ||
| 2.3 | 1.1 | 13.1 | ||
| 4.4 | 10 | 2 | 1.6 | 12.6 |
| 10 | 2.4 | 1.2 | 13 | |
| 4.8 | 2.4 | 1.4 | 12.8 |
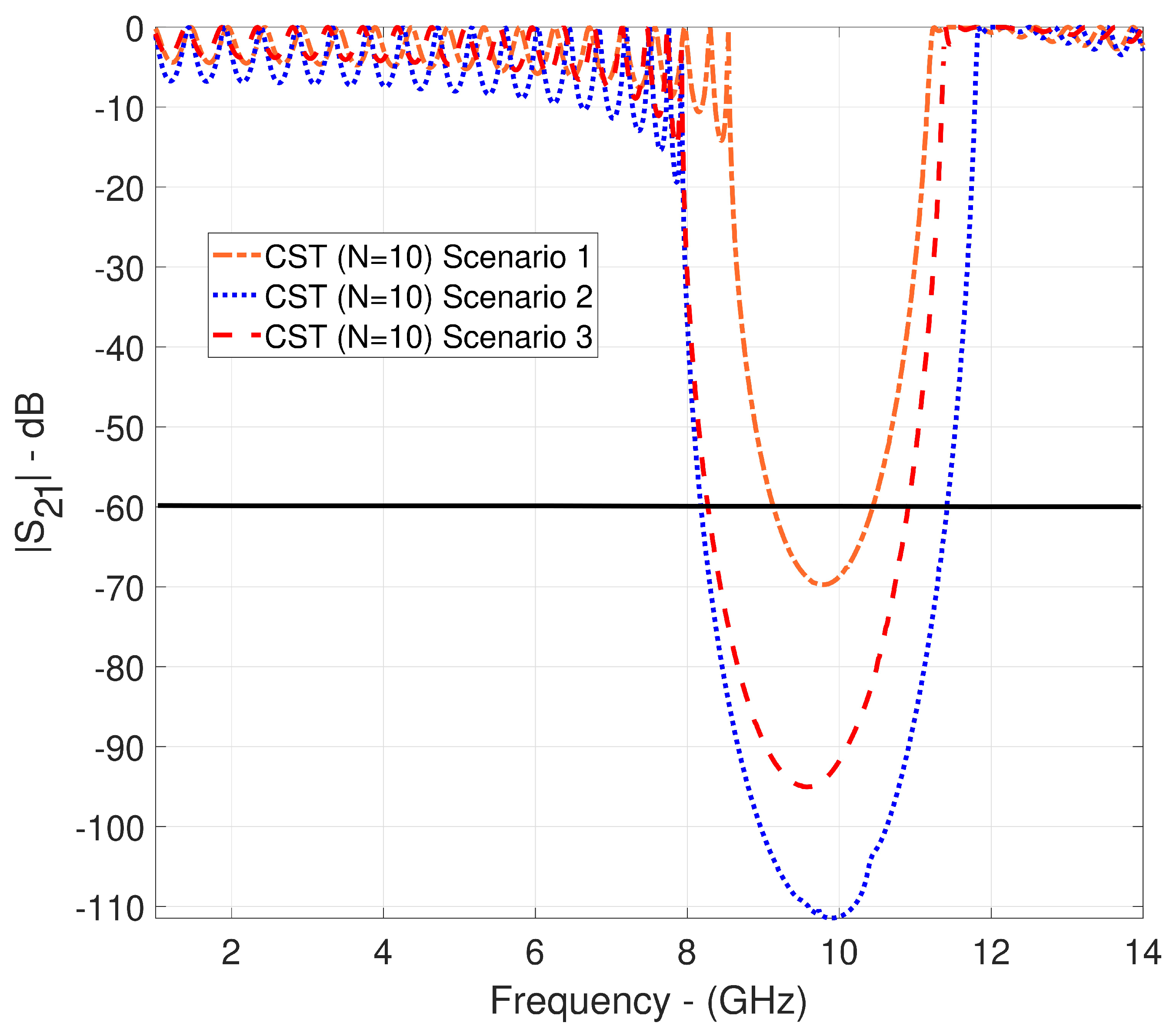
| Studies | a [mm] | b [mm] | [mm] | [mm] | p [mm] | [mm] | TFD [mm] |
|---|---|---|---|---|---|---|---|
| Scenario 1 | 1.5 | 13.2 | 0.5 | 1.2 | 27.9 | 2.9 | 279 |
| Scenario 2 | 1.5 | 12.5 | 0.5 | 2 | 26.5 | 4.5 | 265 |
| Scenario 3 | 2.3 | 13.1 | 0.5 | 1.1 | 28.5 | 2.7 | 285 |
| Works | [GHz] | * [dB] | * [dB] | [GHz] | * [dB/GHz] | * [dB/GHz] | Physical Dimensions [mm × mm × mm] | NCS * × × |
|---|---|---|---|---|---|---|---|---|
| [5], Figure 10, MM-GSM | 9, Waveguide | ∼1 | ∼1 | @-60 dB, 0.1 | ∼370 | ∼370 | 1120.14 × 22.86 × 10.16 | Not given |
| [55], Figure 6, SONNET | 9.7, Microstrip | ∼0.1 | ∼0.1 | @-60 dB, 1 | ∼33.04 | ∼20.56 | 12.87 × 7.04 × 0.25 | 0.65 × 0.36 × 0.01 |
| [58], Figure 9, Conv. BSF | 9.3, Waveguide | ∼0.6 | ∼0.6 | @-60 dB, 1.23 | ∼10.57 | ∼37 | 86 × 74 × 18 | Not given |
| [58], Figure 9, Prop. BSF | 9.35, Hybrid | ∼0.6 | ∼0.6 | @-55.5 dB, 2.67 | ∼61.67 | ∼370 | 15 × 8 × 1 | 0.5 × 0.25 × 0.04 |
| [56], Figure 10a, State (01) | 10.3, Microstrip | ∼0.15 | ∼0.56 | @-20 dB, 0.215 | ∼92.5 | ∼46.25 | 7.3 × 7.5 × 0.508 | 0.4 × 0.42 × 0.03 |
| [56], Figure 10a, State (10) | 10.2, Microstrip | ∼0.15 | ∼0.51 | @-20 dB, 0.22 | NA * | NA * | 7.3 × 7.5 × 0.508 | 0.4 × 0.42 × 0.03 |
| [56], Figure 14a, = 25 V | 9.56, Microstrip | ∼0.10 | ∼0.16 | @-20 dB, 0.192 | ∼119.35 | ∼84.09 | 7.3 × 7.5 × 0.508 | 0.38 × 0.39 × 0.03 |
| [57], Table 5, Open-short | 9, Microstrip | ∼0.5 | ∼0.5 | @-10 dB, 0.7 | NA * | NA * | 6.1 × 6.2 × 0.4 | 0.51 × 0.52 × 0.03 |
| This work, Scenario 2, Figure 14, CST | 9.59, Waveguide | ∼6.6 | ∼2.5 | @-60 dB, 2.64 | ∼148 | ∼185 | 265 × 26.5 × 4.5 | 8.47 × 0.85 × 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Çolak, F.; Ertay, A.O. A Fast, Simple, and Approximate Method for a Minimal Unit Cell Design of Glide-Symmetric Double-Corrugated Parallel-Plate Waveguides. Appl. Sci. 2025, 15, 5876. https://doi.org/10.3390/app15115876
Çolak F, Ertay AO. A Fast, Simple, and Approximate Method for a Minimal Unit Cell Design of Glide-Symmetric Double-Corrugated Parallel-Plate Waveguides. Applied Sciences. 2025; 15(11):5876. https://doi.org/10.3390/app15115876
Chicago/Turabian StyleÇolak, Fatih, and Agah Oktay Ertay. 2025. "A Fast, Simple, and Approximate Method for a Minimal Unit Cell Design of Glide-Symmetric Double-Corrugated Parallel-Plate Waveguides" Applied Sciences 15, no. 11: 5876. https://doi.org/10.3390/app15115876
APA StyleÇolak, F., & Ertay, A. O. (2025). A Fast, Simple, and Approximate Method for a Minimal Unit Cell Design of Glide-Symmetric Double-Corrugated Parallel-Plate Waveguides. Applied Sciences, 15(11), 5876. https://doi.org/10.3390/app15115876








