Multi-Channel Speech Enhancement Using Labelled Random Finite Sets and a Neural Beamformer in Cocktail Party Scenario
Abstract
1. Introduction
- i.
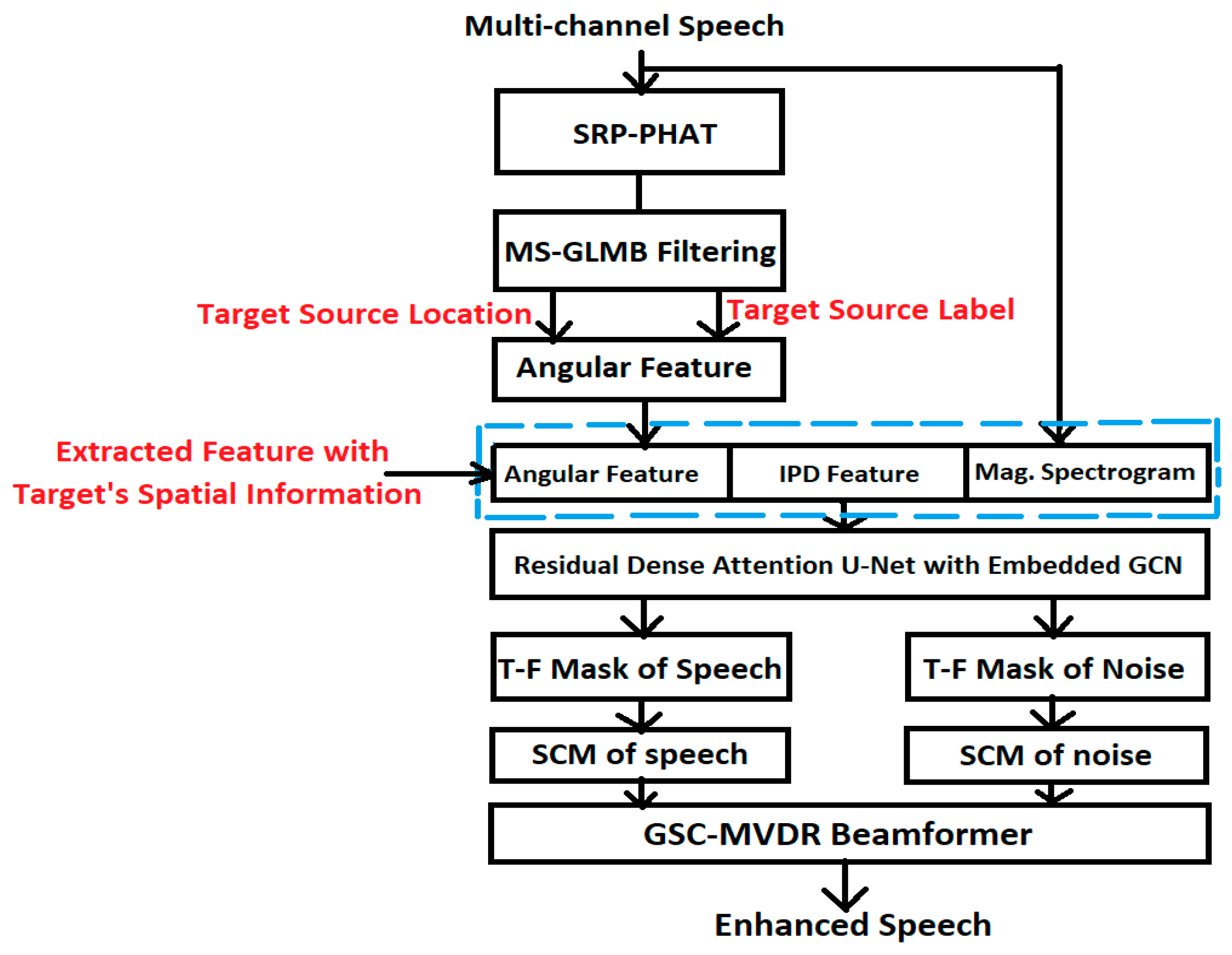
- Construction of label-set data for training a neural architecture for target speech enhancement with the help of MS-GLMB filtering-based multi-source tracking and a time-varying MVDR beamformer, one which takes into account the effect of reverberation, noise and motion of the sources at each time frame. While the GLMB-assisted tracking relies on initial location information provided by steered response power phase transform (SRP-PHAT) [46], the inclusion of the tracking framework within the neural training procedure helps to develop the knowledge of spectro-spatial information of the moving sources within the neural architecture, so that it is able to generalize to “unseen” acoustic conditions as well and directly predict the desired T-F mask.
- ii.
- Construction of a residual dense convolutional U-Net architecture with an embedded GCRNN module, referred to as RD-graph-U-Net, which is applied in a GAN setting to predict the target source-specific mask.
2. System Model
2.1. Steered Response Power Phase Transform (SRP-PHAT)
2.2. MS-GLMB Filtering
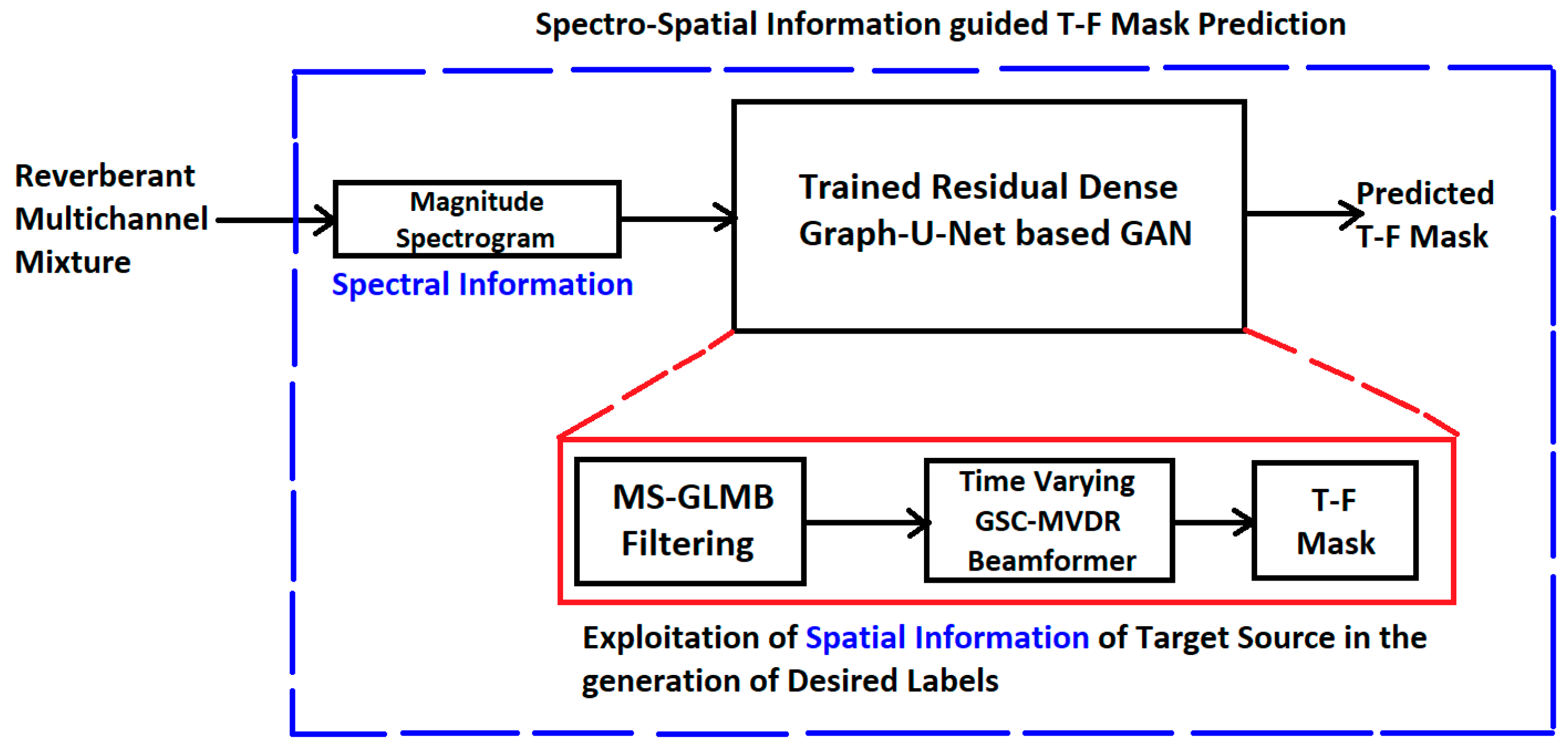
2.3. Spectro-Spatial Information-Guided T-F Domain Masking for GSC-MVDR Beamformer
2.4. TV-GSC-MVDR Beamformer
- A.
- T-F Mask Generation for constructing label set for training neural architecture.
- B.
- Dataset Construction
- (i)
- Selection of clean speech signals corresponding to three speakers from publicly available speech databases such as LibriSpeech and WSJ0mix. This is also mentioned in Section 4 on experimental results.
- (ii)
- Generation of acoustic room impulse responses (RIRs) using the image source method (ISM).
- (iii)
- Selection of reverberation times—RT60 of 550 ms, 250 ms and 50 ms—in three rooms of different dimensions.
- (iv)
- Generation of noise samples at different acoustic SNRs.
- (v)
- Creation of reverberant, noisy mixture of speech signals by convolution of clean speech signals with generated RIRs, with the addition of reverberation and noise samples.
- (vi)
- Estimation of position coordinates and label of each source using MS-GLMB filtering algorithm.
- (vii)
- Enhanced speech signal corresponding to target source across different time frames using GSC-MVDR beamforming.
- (viii)
- Construction of T-F mask from the output of beamformer as explained in Section 2.4 A.
- (ix)
- Creation of training dataset (to train the neural architecture) comprising the reverberant speech mixtures as input data and T-F masks as corresponding labels. In addition, the dataset is split into training, validation and testing datasets. This is further elaborated in quantitative terms in Section 4, where the experimental setup is described.
3. Residual Dense Convolutional Graph-U-Net-Based GAN for Target Speech Enhancement
3.1. Graph Signal Processing: Basic Concepts
3.2. Generative Adversarial Network: Basic Concepts
3.3. Architecture of Residual Dense-U-Net with Embedded GCRNN
3.3.1. Generator Network: Residual Dense Graph-U-Net
- A.
- Graph Construction
- B. Operation of the GCRNN module
3.3.2. Discriminator Network
3.3.3. Loss Function Used in Residual Dense Graph-U-Net GAN
3.4. Loss Function
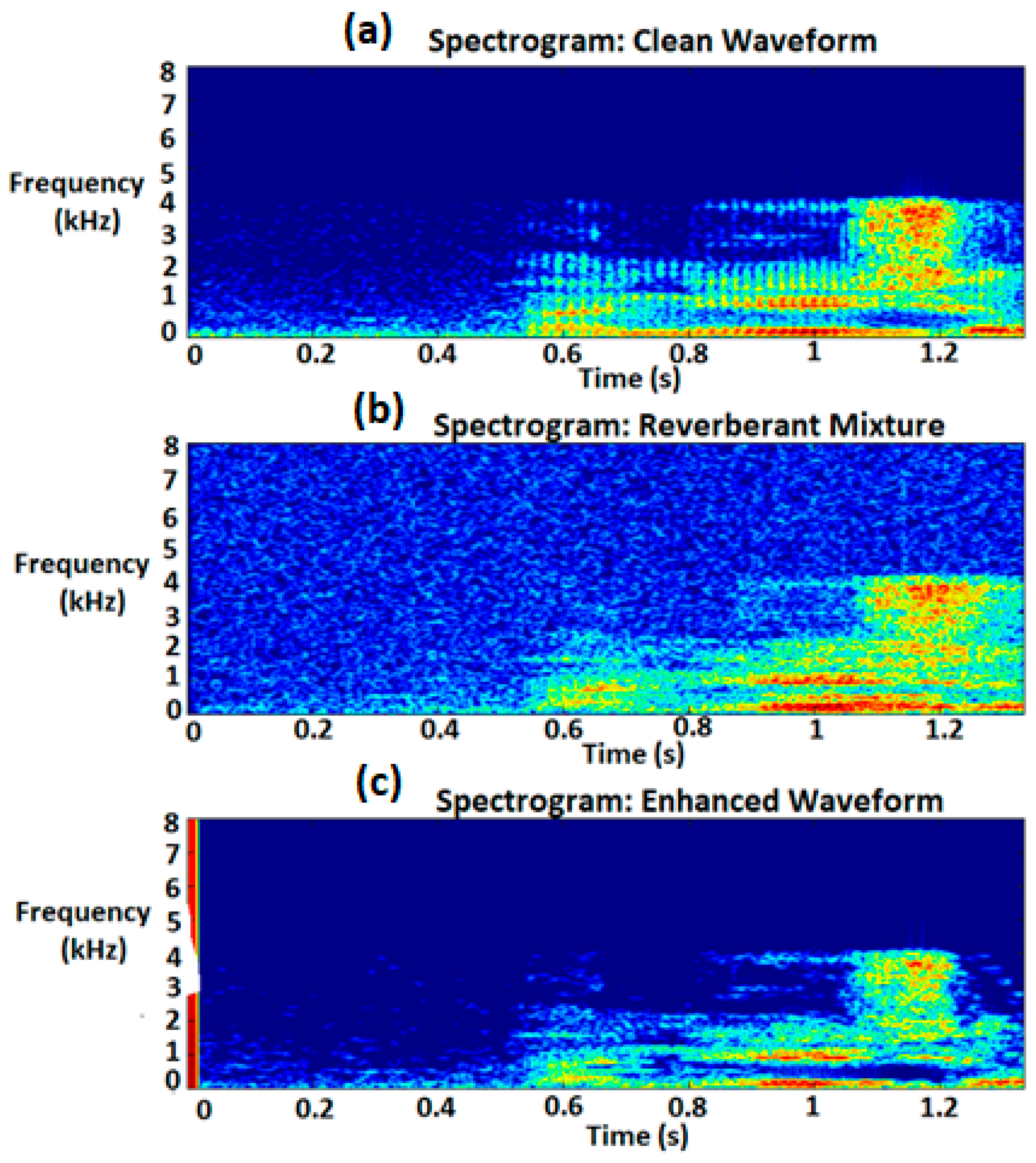
4. Computer Simulation Results
4.1. Experimental Dataset
4.1.1. Speech Source Parameters
4.1.2. MS-GLMB Filtering Parameters
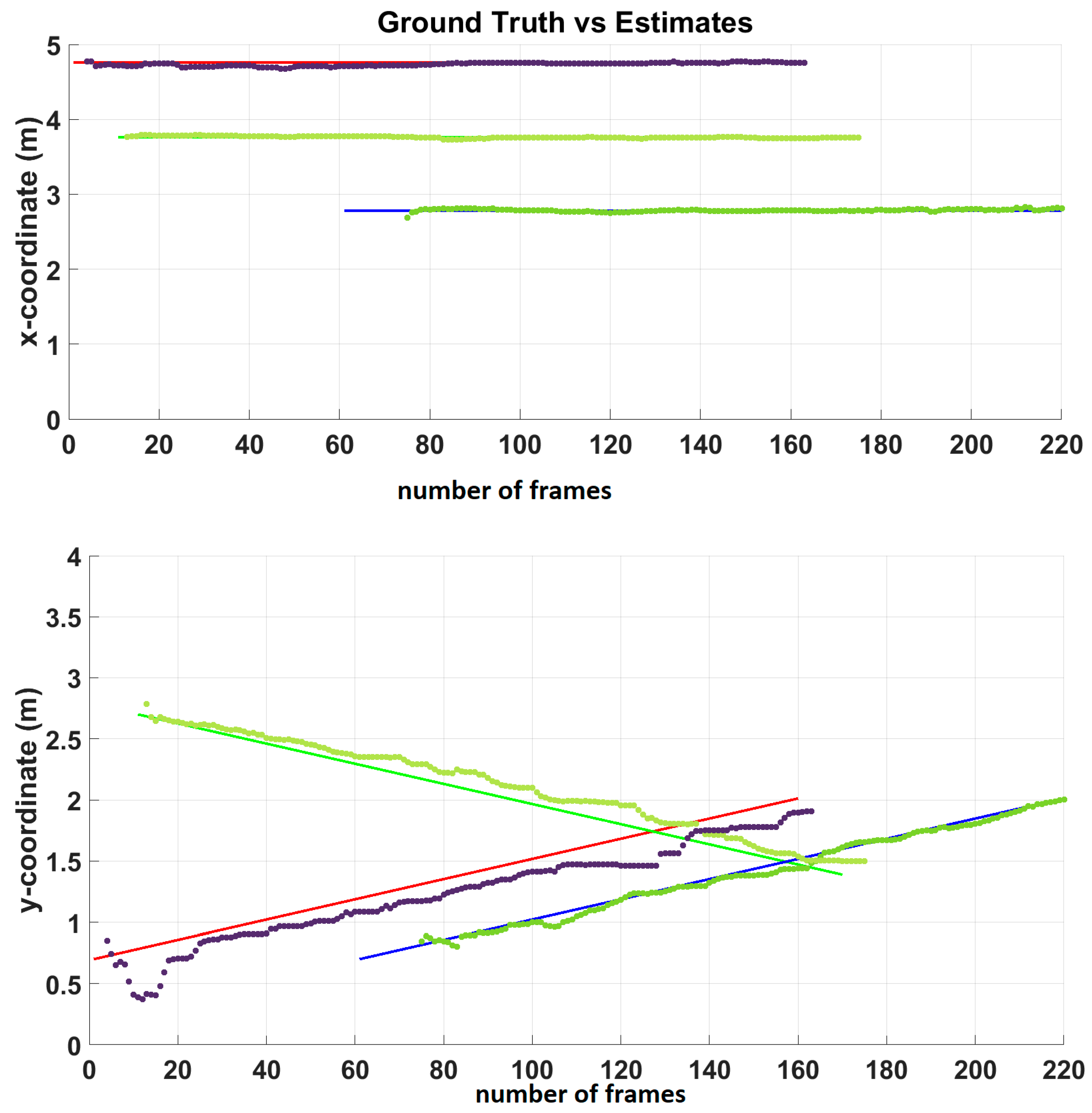
4.2. MS-GLMB Filtering Based Multi-Source Tracking Filter
4.3. Experimental Setup for the Residual Dense Graph-U-Net
4.4. Evaluation Metrics
4.4.1. Beamformer Baselines for Performance Comparison
TI-MVDR Beamformer Baseline
Online MVDR Beamformer Baseline
Block MVDR Beamformer Baseline
DOA-Based MVDR Beamformer Baseline
Mask-Based MVDR Beamformer Baseline Based on Attention Mechanism
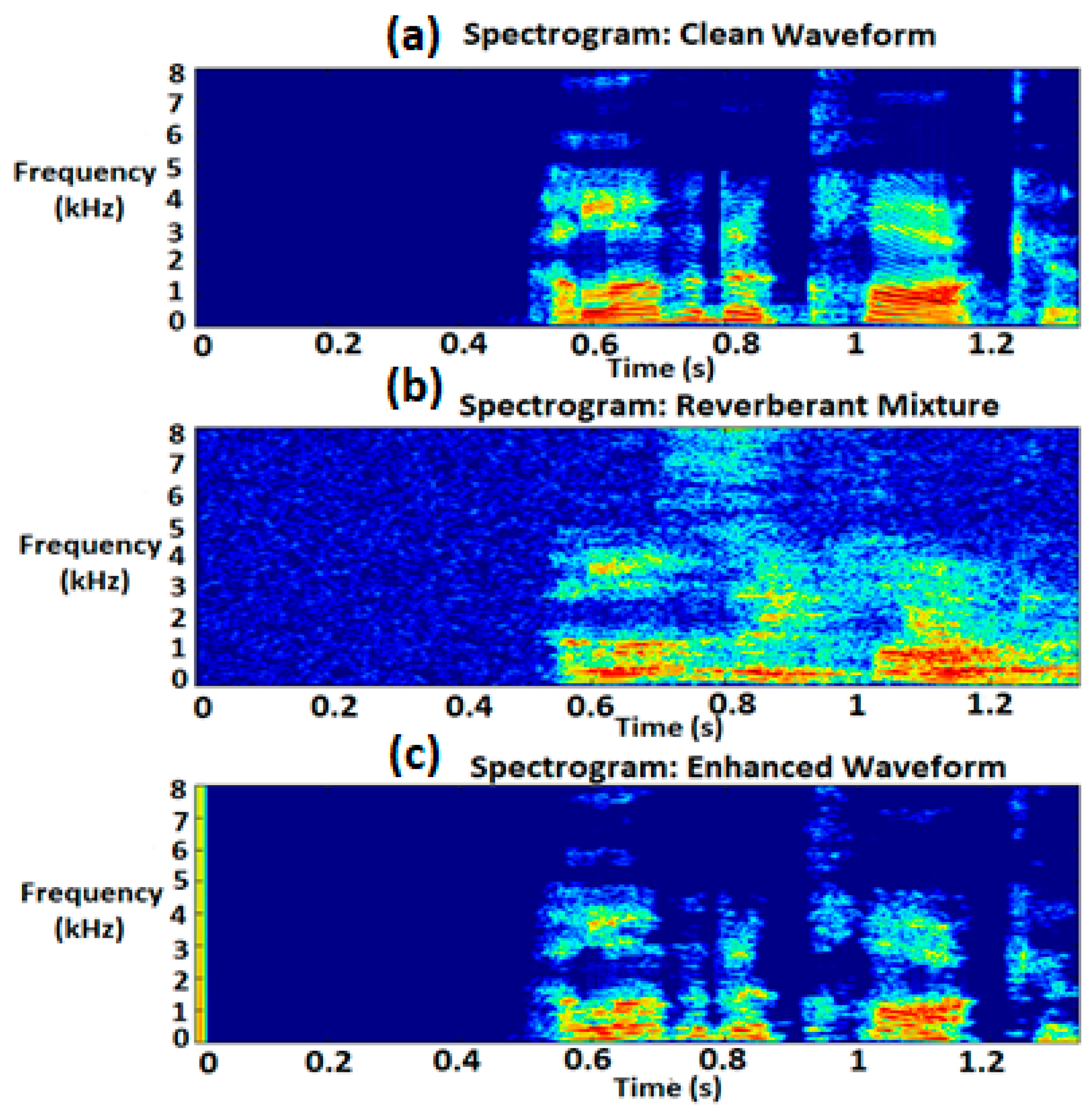
4.4.2. Performance Comparison of Proposed Approach on Simulated and Recorded RIRs
4.4.3. ANOVA Analysis
4.4.4. Ablation Study
5. Discussion
6. Application Scenarios of the Proposed Approach
6.1. Applications in Conferencing Scenarios
6.2. Applications in Assistive Listening Devices
6.3. Applications in Automatic Speech Recognition for Speakers in Motion
7. Conclusions
8. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DL | Deep learning |
| MVDR | Minimum variance unbiased response |
| GAN | Generative adversarial network |
| MS-GLMB | Multi-sensor generalized labeled multi-Bernoulli |
| RFS | Random finite set |
| T-F | Time–frequency |
| SNR | Signal-to-noise ratio |
| CSM | Complex spectral mapping |
| FoV | Field of view |
| GCRNN | Graph convolutional recurrent neural network |
| RDN | Residual dense network |
| SRP-PHAT | Steered response power phase transform |
| IPD | Inter-microphone phase difference |
| TV | Time-varying |
| GSC | Generalized side-lobe canceller |
| GSP | Graph signal processing |
| GCN | Graph convolutional network |
| CM | Contiguous memory |
| LFF | Local feature fusion |
| ReLU | Rectified linear unit |
| IN | Instance normalization |
| k-NN | k-nearest neighbors |
| LSTM | Long short-term memory |
| SI-SNR | Scale invariant signal-to-noise ratio |
| MSE | Mean square error |
| ISM | Image source method |
| RIR | Room impulse response |
| ESTOI | Enhanced short time objective intelligibility |
| PESQ | Perceptual evaluation of speech quality |
| SDR | Signal-to-distortion ratio |
| TI-MVDR | Time invariant minimum variance unbiased response |
| SCM | Signal covariance matrix |
| ISCM | Instantaneous signal covariance matrix |
| AIR | Aachen impulse response |
| ANOVA | Analysis-of-variance |
References
- Brendel, A.; Haubner, T.; Kellermann, W. A Unifying View on Blind Source Separation of Convolutive Mixtures Based on Independent Component Analysis. IEEE Trans. Sig. Proc. 2023, 71, 816–830. [Google Scholar] [CrossRef]
- Wang, T.; Yang, F.; Yang, J. Convolutive Transfer Function-Based Multichannel Nonnegative Matrix Factorization for Overdetermined Blind Source Separation. IEEE/ACM Trans. Audio Speech Lang. Proc. 2022, 30, 802–815. [Google Scholar] [CrossRef]
- Nionm, D.; Mokios, K.N.; Sidiropoulos, N.D.; Potamianos, A. Batch and Adaptive PARAFAC-based Blind Separation of Convolutive Speech Mixtures. IEEE Trans. Audio Speech Lang. Proc. 2010, 18, 1193–1207. [Google Scholar] [CrossRef]
- Gannot, S.; Vincent, E.; Markovich-Golan, S.; Ozerov, A. A consolidated perspective on multimicrophone speech enhancement and source separation. IEEE/ACM Trans. Audio Speech Lang. Proc. 2017, 25, 692–730. [Google Scholar] [CrossRef]
- Markovich-Golan, S.; Gannot, S.; Kellermann, W. Combined LCMV-TRINICON Beamforming for Separating Multiple Speech Sources in Noisy and Reverberant Environments. IEEE/ACM Trans. Audio Speech Lang. Proc. 2016, 25, 320–332. [Google Scholar] [CrossRef]
- Ong, J.; Vo, B.T.; Nordholm, S. Blind Separation for Multiple Moving Sources with Labeled Random Finite Sets. IEEE/ACM Trans. Audio Speech Lang. Proc. 2021, 29, 2137–2151. [Google Scholar] [CrossRef]
- Morgan, J.P. Time-Frequency Masking Performance for Improved Intelligibility with Microphone Arrays. Master’s Thesis, University of Kentucky, Lexington, KY, USA, 2017. [Google Scholar]
- Ochiai, T.; Delcroix, M.; Nakatani, T.; Araki, S. Mask-Based Neural Beamforming for Moving Speakers with Self-Attention-Based Tracking. IEEE/ACM Trans. Audio Speech Lang. Proc. 2023, 31, 835–848. [Google Scholar] [CrossRef]
- Tammen, M.; Ochiai, T.; Delcroix, M.; Nakatani, T.; Araki, S.; Doclo, S. Array Geometry-Robust Attention-Based Neural Beamformer for Moving Speakers. arXiv 2024, arXiv:2402.03058. [Google Scholar]
- Wang, Y.; Politis, A.; Virtanen, T. Attention-Driven Multichannel Speech Enhancement in Moving Sound Source Scenarios. In Proceedings of the 2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024. [Google Scholar]
- Xu, Y.; Yu, M.; Zhang, S.; Chen, L.; Weng, C.; Liu, J.; Yu, D. Neural Spatio-Temporal Beamformer for Target Speech Separation. In Proceedings of the INTERSPEECH 2020, Shanghai, China, 25–29 October 2020. [Google Scholar]
- Xu, Y.; Zhang, Z.; Yu, M.; Zhang, S.-X.; Yu, D. Generalized Spatio-Temporal RNN Beamformer for Target Speech Separation. In Proceedings of the INTERSPEECH 2021, Brno, Czech Republic, 30 August–3 September 2021. [Google Scholar]
- Guo, A.; Wu, J.; Gao, P.; Zhu, W.; Guo, Q.; Gao, D.; Wang, Y. Enhanced Neural Beamformer with Spatial Information for Target Speech Extraction. In Proceedings of the 2023 Asia Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC) 2023, Taipei, Taiwan, 31 October–3 November 2023. [Google Scholar]
- Tan, K.; Wang, Z.-Q.; Wang, D. Neural spectrospatial filtering. IEEE/ACM Trans. Audio Speech Lang. Proc. 2022, 30, 605–621. [Google Scholar] [CrossRef]
- Wang, Z.-Q.; Wang, D. Combining spectral and spatial features for deep learning based blind speaker separation. IEEE/ACM Trans. Audio Speech Lang. Proc. 2019, 27, 457–468. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Y.; Yu, M.; Zhang, S.-X.; Chen, L.; Yu, D. ADLMVDR: All deep learning MVDR beamformer for target speech separation. In Proceedings of the 2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021. [Google Scholar]
- Gu, R.; Chen, L.; Zhang, S.-X.; Zheng, J.; Xu, Y.; Yu, M.; Su, D.; Zou, Y.; Yu, D. Neural spatial filter: Target speaker speech separation assisted with directional information. In Proceedings of the INTERSPEECH 2019, Graz, Austria, 15–19 September 2019. [Google Scholar]
- Luo, Y.; Mesgarani, N. Conv-TasNet: Surpassing ideal time-frequency magnitude masking for speech separation. IEEE/ACM Trans. Audio Lang. Proc. 2019, 27, 1256–1266. [Google Scholar] [CrossRef]
- Tolooshams, B.; Giri, R.; Song, A.H.; Isik, U.; Krishnaswamy, A. Channel-Attention Dense U-Net for Multichannel Speech Enhancement. In Proceedings of the 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020. [Google Scholar]
- Nair, A.A.; Reiter, A.; Zheng, C.; Nayar, S. Audiovisual Zooming: What You See Is What You Hear. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019. [Google Scholar]
- Soni, M.H.; Shah, N.; Patil, H.A. Time-Frequency Masking-Based Speech Enhancement Using Generative Adversarial Network. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018. [Google Scholar]
- Baby, D. iSEGAN: Improved Speech Enhancement Generative Adversarial Networks. arXiv 2020, arXiv:2002.08796v1. [Google Scholar] [CrossRef]
- Michelsanti, D.; Tan, Z.-H. Conditional Generative Adversarial Networks for Speech Enhancement and Noise-Robust Speaker Verification. In Proceedings of the INTERSPEECH 2017, Stockholm, Sweden, 20–24 August 2017. [Google Scholar]
- Pascual, S.; Bonafonte, A.; Serrà, J. SEGAN: Speech Enhancement Generative Adversarial Network. arXiv 2017, arXiv:1703.09452v3. [Google Scholar] [CrossRef]
- Zhou, L.; Zhong, Q.; Wang, T.; Lu, S.; Hu, H. Speech Enhancement via Residual Dense Generative Adversarial Network. Comp. Sys. Sci. Eng. 2021, 38, 279–289. [Google Scholar] [CrossRef]
- Datta, J.; Firoozabadi, A.D.; Zabala-Blanco, D.; Soria, F.R.C.; Adams, M.; Perez, C. Multi-channel Target Speech Enhancement using Labeled Random Finite Sets and Deep Learning under Reverberant Environments. In Proceedings of the 2023 IEEE 5th Eurasia Conference on IOT, Communication and Engineering (ECICE), Yunlin, Taiwan, 27–29 October 2023. [Google Scholar]
- Binh, N.H.; Hai, D.V.; Dat, B.T.; Chau, H.N.; Cuong, N.Q. Multi-channel speech enhancement using a minimum variance distortionless response beamformer based on graph convolutional network. Int. J. Adv. Comput. Sci. Appl. 2022, 13, 739–747. [Google Scholar] [CrossRef]
- Chau, H.N.; Bui, T.D.; Nguyen, H.B.; Duong, T.T.H.; Nguyen, Q.C. A Novel Approach to Multi-Channel Speech Enhancement Based on Graph Neural Networks. IEEE/ACM Trans. Audio Speech Lang. Proc. 2024, 32, 1133–1144. [Google Scholar] [CrossRef]
- Tzirakis, P.; Kumar, A.; Donley, J. Multi-channel speech enhancement using graph neural networks. Proceedings of 2021 the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021. [Google Scholar]
- Zhang, C.; Xiang, P. Single-channel speech enhancement using Graph Fourier Transform. In Proceedings of the INTERSPEECH 2022, Incheon, Republic of Korea, 18–22 September 2022. [Google Scholar]
- Ong, J.; Vo, B.T.; Nordholm, S.; Vo, B.-N.; Moratuwage, D.; Shim, C. Audio-Visual Based Online Multi-Source Separation. IEEE/ACM Trans. Audio. Speech. Lang. Proc. 2022, 30, 1219–1234. [Google Scholar] [CrossRef]
- Vo, B.-N.; Vo, B.-T.; Beard, M. Multi-sensor multi-object tracking with the generalized labeled multi-bernoulli filter. IEEE Trans. Signal Process. 2019, 67, 5952–5967. [Google Scholar] [CrossRef]
- Thomas, R.W.; Larson, J.D. Inverse Reinforcement Learning for Generalized Labeled Multi-Bernoulli Multi-Target Tracking. In Proceedings of the 2021 IEEE Aerospace Conference (50100), Big Sky, MT, USA, 6–13 March 2021. [Google Scholar]
- Jiang, D.; Qu, H.; Zhao, J. Multi-level graph convolutional recurrent neural network for semantic image segmentation. Telecom. Sys. 2021, 77, 563–576. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Abadie, J.P.; Mirza, M.; Xu, B.; Farley, D.W.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. arXiv 2014, arXiv:1406.2661v1. [Google Scholar] [CrossRef]
- Pan, Z.; Yu, W.; Yi, X.; Khan, A.; Yuan, F.; Zheng, Y. Recent Progress on Generative Adversarial Networks (GANs): A Survey. IEEE Access. 2019, 7, 36322–36333. [Google Scholar] [CrossRef]
- Marques, A.G.; Kiyavash, N.; Moura, J.M.F.; Van De Ville, D.; Willett, R. Graph Signal Processing: Foundations and Emerging Directions [From the Guest Editors]. IEEE Sig. Proc. Mag. 2020, 37, 11–13. [Google Scholar] [CrossRef]
- Li, G.; Muller, M.; Thabet, A.; Ghanem, B. DeepGCNs: Can GCNs go as deep as CNNs? In Proceedings of IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019.
- Seo, Y.; Defferrard, M.; Vandergheynst, P.; Bresson, X. Structured Sequence Modeling with Graph Convolutional Recurrent Networks. arXiv 2016, arXiv:1612.07659. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015, Proceedings of the MICCAI 2015, Munich, Germany, 5–9 October 2014; Navab, N., Hornegger, J., Wells, W., Frangi, A., Eds.; Lecture Notes in Computer Science 9351; Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385v1. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Q.; Wang, Y. Road Extraction by Deep Residual U-Net. IEEE Geosci. Remote Sens. Lett. 2018, 15, 749–753. [Google Scholar] [CrossRef]
- Yang, X.; Li, X.; Ye, Y.; Zhang, X.; Zhang, H.; Huang, X. Road Detection via Deep Residual Dense U-Net. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019. [Google Scholar]
- Huang, G.; Liu, Z.; van der Laurens, M.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Piscataway, NJ, USA, 21–26 July 2017. [Google Scholar]
- Datta, J.; Adams, M.; Perez, C. Dense-U-Net assisted Localization of Speech Sources in Motion under Reverberant conditions. In Proceedings of the 2023 12th International Conference on Control, Automation and Information Sciences (ICCAIS), Hanoi, Vietnam, 27–29 November 2023. [Google Scholar] [CrossRef]
- Do, H.; Silverman, H.F.; Yu, Y. A real-time SRP-PHAT source location implementation using stochastic region contraction (SRC) on a large-aperture microphone array. In Proceedings of the 2007 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Honolulu, HI, USA, 16–20 April 2007. [Google Scholar]
- Paul, D.B.; Baker, J. The design for the wall street journal-based CSR corpus. In Proceedings of the 1992 Workshop on Speech and Natural Language, Harriman, NY, USA, 23–26 February 1992. [Google Scholar]
- Panayotov, V.; Chen, G.; Povey, D.; Khudanpur, S. Librispeech: An ASR corpus based on public domain audio books. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbance, QLD, Australia, 19–24 April 2015. [Google Scholar]
- Barker, J.; Marxer, R.; Vincent, E.; Watanabe, S. The third ‘CHiME’ speech separation and recognition challenge: Dataset, task and baselines. In Proceedings of the 2015 IEEE Workshop on Automatic Speech Recognition and Understanding (ASRU), Scottsdale, AZ, USA, 13–17 December 2015. [Google Scholar]
- Thiemann, J.; Ito, N.; Vincent, E. The diverse environments multichannel acoustic noise database: A database of multichannel environmental noise recordings. J. Acoust. Soc. Am. 2013, 133, 3591. [Google Scholar] [CrossRef]
- Piczak, K.J. ESC: Dataset for Environmental Sound Classification. In Proceedings of the 23rd Annual ACM Conference on Multimedia, Brisbane, Australia, 26–30 October 2015. [Google Scholar]
- Jensen, J.; Taal, C.H. An algorithm for predicting the intelligibility of speech masked by modulated noise maskers. IEEE/ACM Trans. Audio Speech Lang. Proc. 2016, 24, 2009–2022. [Google Scholar] [CrossRef]
- Rix, A.W.; Beerends, J.G.; Hollier, M.P.; Hekstra, A.P. Perceptual evaluation of speech quality (PESQ)-a new method for speech quality assessment of telephone networks and codecs. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech, Signal Processing, Salt Lake City, UT, USA, 7–11 May 2001. [Google Scholar]
- Le Roux, J.; Wisdom, S.; Erdogan, H.; Hershey, J.R. SDR–half-baked or well done? In Proceedings of 2019 IEEE International Conference on Acoustics, Speech, Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019.
- Lehmann, E.A.; Johansson, A.M.; Nordholm, S. Reverberation-time prediction method for room impulse responses simulated with the image source model. In Proceedings of the 2007 IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, USA, 21–24 October 2007. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Jeub, M.; Sch¨afer, M.; Kr¨uger, H.; Nelke, C.; Beaugeant, C.; Vary, P. Do we need dereverberation for hand-held telephony? In Proceedings of 2010 International Congress on Acoustics (ICA), Sydney, Australia, 23–27 August 2010.
- Rao, W.; Fu, Y.; Hu, Y.; Xu, X.; Jv, Y.; Han, J.; Jiang, Z.; Xie, L.; Wang, Y.; Watanabe, S.; et al. Conferencingspeech Challenge: Towards Far-Field Multi-Channel Speech Enhancement for Video Conferencing. In Proceedings of the 2021 IEEE Automatic Speech Recognition and Understanding Workshop (ASRU), Cartagena, Colombia, 13–17 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 679–686. [Google Scholar] [CrossRef]
- Pasha, S.; Lundgren, J.; Ritz, C.; Zou, Y. Distributed Microphone Arrays, Emerging Speech and Audio Signal Processing Platforms: A Review. Adv. Sci. Technol. Eng. Syst. J. 2020, 5, 331–343. [Google Scholar] [CrossRef]
- Audhkhasi, K.; Georgiou, P.G.; Narayanan, S.S. Analyzing quality of crowd-sourced speech transcriptions of noisy audio for acoustic model adaptation. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 4137–4140. [Google Scholar] [CrossRef]



| Room Dimensions in x,y Coordinates (in m) | X (14 m) | Y (22 m) |
|---|---|---|
| SNR (in dB) | 0–60 (training) | 15, 35, 80 (testing) |
| Reverberation time, T60 (in ms) | 50, 250, 550 | 550 |
| Microphone array | Linear | 6 sensors per array |
| Number of speakers | 3 (training) | 3 (testing) |
| Parameters | Values |
|---|---|
| (in s−1) | 10 |
| (in ms−1) | 1 |
| (in ms) | 32 |
| (in ms−1) |
| 0.005 | |
| 0.005 | |
| 0.005 | |
| diag( | |
| diag( | |
| diag( |
| Configuration of Mask Estimation Network (Generator) | |
|---|---|
| ENCODER | |
| Number of down-sampling layers | 5 |
| Number of RDBs in each encoder layer | 1 |
| Kernels of CNN layers in each encoder block | {64, 128, 128, 128, 32} |
| Kernel sizes of CNN layers | 3 × 3 |
| Stride | 2 × 2 |
| Padding | 0 |
| DECODER | |
| Number of up-sampling layers | 5 |
| Number of RDBs in each decoder layer | 5 |
| Kernels of CNN layers in each decoder block | {32, 128, 128, 128, 64} |
| Kernel sizes of CNN layers | 3 × 3 |
| Stride | 2 × 2 |
| Padding | 0 |
| Loss Function | MSE |
| Optimization criterion | ADAM |
| Learning rate | 10−4 |
| Batch size | 32 |
| Test Room I | 5.80 m by 3.30 m by 2.00 m |
| Test Room II | 7.50 m by 3.50 m by 2.80 m |
| Test Room III | 10.50 m by 6.50 m by 3.40 m |
| Position 1 | [(2.40, 0.3), (2.60, 0.3), (2.80, 0.3), (3.0, 0.3), (3.20, 0.3), (3.40, 0.3)] |
| Position 2 | [(4.00, 0.3), (4.20, 0.3), (4.40, 0.3), (4.60, 0.3), (4.80, 0.3), (5.00, 0.3)] |
| Position 3 | [(3.6, 3.11), (3.4, 3.11), (3.2, 3.11), (3.0, 3.11), (2.8, 3.11), (2.6, 3.11)] |
| Method | RT60 = 550 ms | RT60 = 250 ms | RT60 = 50 ms | |||
|---|---|---|---|---|---|---|
| PESQ | SI-SNR (dB) | PESQ | SI-SNR (dB) | PESQ | SI-SNR (dB) | |
| MS-GLMB filter-assisted DS | 2.41 | 4.42 | 2.79 | 10.73 | 2.91 | 13.94 |
| TI-MVDR | 2.43 | 2.35 | 2.73 | 4.42 | 2.76 | 5.13 |
| Online-MVDR | 3.22 | 4.85 | 3.38 | 5.62 | 3.45 | 6.52 |
| MS-GLMB filter-assisted MVDR | 3.28 | 5.65 | 3.44 | 6.55 | 3.51 | 7.66 |
| DOA-MVDR | 3.43 | 8.85 | 3.49 | 9.75 | 3.55 | 10.36 |
| Mask-MVDR with self-attention | 3.57 | 10.37 | 3.60 | 10.55 | 3.65 | 12.66 |
| U-Net with embedded GCN | 3.56 | 10.54 | 3.65 | 11.66 | 3.67 | 12.78 |
| RD-GAN | 3.58 | 10.58 | 3.67 | 11.72 | 3.69 | 12.82 |
| RD-Graph-U-Net-GAN (proposed approach) | 3.60 | 10.77 | 3.70 | 11.88 | 3.85 | 12.86 |
| Method | RT60 = 550 ms | RT60 = 250 ms | RT60 = 50 ms | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ESTOI (%) | PESQ | SI-SNR (dB) | SDR (dB) | ESTOI (%) | PESQ | SI-SNR (dB) | SDR (dB) | ESTOI (%) | PESQ | SI-SNR (dB) | SDR (dB) | |
| MS-GLMB filter-assisted DS | 47.63 | 1.81 | −2.60 | 1.40 | 63.88 | 2.23 | 3.71 | 6.27 | 68.80 | 2.32 | 5.96 | 8.06 |
| TI-MVDR | 40.53 | 1.74 | −5.42 | 0.24 | 40.77 | 1.89 | −2.87 | 2.71 | 41.95 | 1.89 | −3.49 | 2.28 |
| Online-MVDR | 45.20 | 1.79 | −4.06 | 1.00 | 55.57 | 2.05 | −0.89 | 4.14 | 52.78 | 1.99 | −1.85 | 3.47 |
| MS-GLMB filter-assisted MVDR | 56.80 | 2.02 | 0.46 | 3.76 | 79.23 | 2.75 | 8.31 | 10.86 | 79.71 | 2.75 | 7.95 | 10.72 |
| DOA-MVDR | 40.70 | 1.76 | −4.68 | 0.94 | 54.91 | 2.26 | −1.44 | 4.28 | 50.00 | 2.16 | −2.14 | 3.55 |
| Mask-MVDR with self-attention | 46.74 | 1.84 | −3.48 | 1.61 | 59.59 | 2.25 | −0.22 | 5.02 | 54.00 | 2.10 | −1.82 | 3.54 |
| U-Net with embedded GCN | 72.32 | 2.56 | 2.03 | 5.97 | 75.10 | 2.67 | 3.36 | 7.58 | 78.71 | 2.78 | 5.87 | 9.44 |
| RD-GAN | 46.99 | 1.87 | −3.14 | 1.40 | 58.22 | 2.16 | −1.19 | 3.06 | 60.65 | 2.24 | 0.25 | 3.96 |
| RD-Graph-U-Net (proposed approach) | 75.00 | 2.70 | 2.16 | 6.12 | 79.60 | 2.88 | 3.77 | 7.80 | 80.50 | 2.90 | 5.96 | 9.66 |
| Method | Office Room (RT60 = 0.52 s) | Corridor (RT60 = 1.25 s) | ||
|---|---|---|---|---|
| PESQ | ESTOI (%) | PESQ | ESTOI (%) | |
| RD-Graph-U-Net (proposed approach) | 3.06 | 77.40 | 2.56 | 75.58 |
| MS-GLMB filter-assisted MVDR | 2.77 | 74.46 | 2.25 | 72.23 |
| Mask-MVDR with self-attention | 2.85 | 75.56 | 2.36 | 73.39 |
| U-Net with embedded GCN | 2.84 | 75.32 | 2.29 | 72.78 |
| Speech Enhancement Approach | PESQ | ESTOI | ||
|---|---|---|---|---|
| p-Value | F-Value | p-Value | F-Value | |
| Proposed approach -> noisy speech | 0.001 | 50.25 | 0.001 | 54.24 |
| Proposed approach -> MS-GLMB filtering-assisted MVDR beamformer | 0.023 | 12.17 | 0.042 | 09.45 |
| Proposed approach -> mask MVDR with self-attention | 0.021 | 20.07 | 0.031 | 15.15 |
| Proposed approach -> U-Net with embedded GCN | 0.012 | 14.76 | 0.039 | 12.15 |
| Method | RT60 = 550 ms | RT60 = 250 ms | RT60 = 50 ms | |||
|---|---|---|---|---|---|---|
| PESQ | ESTOI | PESQ | ESTOI | PESQ | ESTOI | |
| Proposed approach | 2.70 | 75.00% | 2.88 | 79.60% | 2.90 | 80.50% |
| w/o GCRNN block in skip connections | 2.65 | 72.60% | 2.84 | 76.70% | 2.87 | 78.40% |
| w/o Residual block in encoder and decoder | 2.57 | 69.50% | 2.75 | 72.22% | 2.78 | 76.32% |
| w/o Discriminator | 2.67 | 74.43% | 2.85 | 77.45% | 2.89 | 79.20% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Datta, J.; Dehghan Firoozabadi, A.; Zabala-Blanco, D.; Castillo-Soria, F.R. Multi-Channel Speech Enhancement Using Labelled Random Finite Sets and a Neural Beamformer in Cocktail Party Scenario. Appl. Sci. 2025, 15, 2944. https://doi.org/10.3390/app15062944
Datta J, Dehghan Firoozabadi A, Zabala-Blanco D, Castillo-Soria FR. Multi-Channel Speech Enhancement Using Labelled Random Finite Sets and a Neural Beamformer in Cocktail Party Scenario. Applied Sciences. 2025; 15(6):2944. https://doi.org/10.3390/app15062944
Chicago/Turabian StyleDatta, Jayanta, Ali Dehghan Firoozabadi, David Zabala-Blanco, and Francisco R. Castillo-Soria. 2025. "Multi-Channel Speech Enhancement Using Labelled Random Finite Sets and a Neural Beamformer in Cocktail Party Scenario" Applied Sciences 15, no. 6: 2944. https://doi.org/10.3390/app15062944
APA StyleDatta, J., Dehghan Firoozabadi, A., Zabala-Blanco, D., & Castillo-Soria, F. R. (2025). Multi-Channel Speech Enhancement Using Labelled Random Finite Sets and a Neural Beamformer in Cocktail Party Scenario. Applied Sciences, 15(6), 2944. https://doi.org/10.3390/app15062944








