You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Applied Sciences
Download PDF
  • Article
  • Open Access

23 May 2025

Optimal Lower Step Height of Tunnel Excavation Designs by Using the Non-Dominated Sorting Genetic Algorithm-II

,
,
and
1
College of Mining Engineering, Taiyuan University of Technology, Taiyuan 030024, China
2
School of Aerospace Engineering, North University of China, Taiyuan 030051, China
*
Author to whom correspondence should be addressed.
Appl. Sci.2025, 15(11), 5854;https://doi.org/10.3390/app15115854
Version Notes
Order Reprints

Abstract

In order to control the stability of tunnel surrounding rock, reduce the construction cost, and improve the construction schedule, the deformation behavior and instability mechanisms of tunnel surrounding rock are studied by numerical simulation and field monitoring methods according to the engineering characteristics of the fractured slate zone under construction of Longshu Tunnel in the central Yunnan water diversion project. The results show that step excavation technology can effectively control the deformation of the tunnel surrounding rock. The deformation range of the top and bottom of the tunnel is 32 mm~35 mm, the deformation range of the left shoulder is 25 mm~28 mm, and the deformation range of the right shoulder is 26 mm~29 mm. The stability range of the tunnel surrounding rock is about 25 m away from the palm surface, and the concentrated stress on both sides of the tunnel is at a low level.

1. Introduction

When tunneling in weak or fractured rock masses, maintaining the stability of the tunnel surrounding rock presents significant challenges [1,2]. Numerous scholars, based on field engineering practices, have conducted research through theoretical analysis, numerical simulation, and other approaches [3].
Lunardi, P [4] introduced the New Austrian Tunneling Method (NATM), emphasizing the importance of controlling tunnel deformation by enhancing the stiffness of the pre-excavated rock mass, thereby ensuring tunnel safety. Shen, Y. and others [5], based on a large-scale fault zone tunnel project, designed a variable-stiffness lining structure for fault-crossing tunnels using the seismic design concepts of “attract” and “let go”. This design aims to induce structural deformation and reduce the range of earthquake damage. They also conducted shaking table tests on the variable-stiffness lining of fault-crossing tunnels for validation. Huang, J. and others [6] analyzed the risk assessment reports of railway tunnel projects to identify the safety risk factors in fault fracture zone tunnel construction. They extracted the causal logic between these safety risk factors and constructed a safety risk transmission network. Woodcock, N.H. and Mort, K. [7] conducted a classification study on fault breccias, analyzed their impact on tunnel construction, and provided valuable insights for tunnel design. Jie, Y. and others [8], based on silo theory and the stress distribution characteristics of strata, considered the geometric features of fault fracture zones and surrounding rock properties. They established a simplified calculation model for vertical loads in tunnels within fault fracture zones and solved it using stress transfer principles. Zhang, Y. and others [9], to explore tunnel construction through fault fracture zones, considered the example of different fault morphologies at the Wulipo Tunnel on the Mianjiu Expressway. They performed a three-factor, four-level orthogonal numerical simulation experiment to conduct a sensitivity analysis of the surrounding rock. Wang, L. and others [10], based on the limit equilibrium theory, derived the expression for the ultimate support pressure on the excavation face of a shield tunnel. They studied the variation in ultimate support force and the tilt angle of the failure body during the process of shield tunneling approaching the interface between intact rock and fault fracture zones.
Yang, J. and others [11] used theoretical analysis and discrete element numerical simulation methods, combined with field monitoring results, to conduct a comprehensive analysis of the case of tunnel construction through fault zones in high-speed railway projects. The study found that when a tunnel crosses a water-rich fault fracture zone, the rock mass is characterized by well-developed structural planes, with many planes filled with debris or clay fillings. Zhao, X. [12], based on an engineering project, established a seepage numerical model to analyze the groundwater seepage patterns around the tunnel under different grout ring thicknesses and permeability coefficients. Fu, H. and others [13] studied the stability of a surrounding rock and structure when tunneling through a high-pressure water-rich fault fracture zone. By establishing a 3D fluid–solid coupling numerical model, they analyzed the distribution of the seepage field, protrusion deformation, plastic zone volume, water inflow, and shear deformation of the grouting reinforcement ring during face advance under different working conditions. Huang, F. and others [14], based on the Nanwan Tunnel of the Hong Kong–Zhuhai–Macao Bridge connecting line, established a two-dimensional analysis model using discrete element software PFC2D 3.1. The results showed that under the influence of fault fracture zones, the stress of the tunnel surrounding rock is asymmetric. The field monitoring results indicated that when the fault intersects with the tunnel side wall, the displacement at this section is the largest and significantly greater than that of other sections.
Liang, B. and others [15] used three-dimensional finite difference computational software to analyze the seismic reduction technology of large-section tunnels in fault fracture zones. They conducted numerical simulations to analyze the effects of different stiffness lining materials and grouting reinforcement of the surrounding rock on the seismic performance of the lining in fault fracture zones. Yu, H. and others [16], based on a continuous–discrete coupled analysis method, established a multi-scale mechanical model for fault engineering sites. They used an artificial synthetic rock mass model based on the discrete element method to simulate the fault fracture zone and applied the finite difference method to describe the macroscopic dynamic characteristics under the influence of tunnel excavation in the hanging and footwalls of the fault.
Thomas, A. [17] highlighted the application of shotcrete linings in tunnel construction, demonstrating their effectiveness in controlling surrounding rock deformation. Lunardi, P. [18] explored the application of the ADECO-RS method in tunnel construction, emphasizing the importance of real-time monitoring and adjustment of surrounding rock deformation for tunnel safety. Guo, Y. and others [19] analyzed the causes of large deformation phenomena in carbonaceous shale diversion tunnels and proposed control measures for the large deformation stage. Yan, J. [20] focused on the small-section diversion tunnel of the Liangshan Hydropower Station as a case study and explored the construction technology for ultra-small-section diversion tunnels under limited financial conditions. On the other hand, recent advancements in geotechnical modeling and data-driven approaches have also shown a successful degree of contribution to the subsurface characterization of heterogeneous geological conditions [21,22,23,24,25]. The integration of 3D geo-modeling and ensemble deep learning approaches further enhances prediction reliability and uncertainty analysis in geological modeling [26]. Moreover, researchers, such as Rangarajan et al. [24] and Demin et al. [27], have emphasized the role of groundwater flow and high-stress zones in excavation stability, suggesting that hydromechanical interactions must be thoroughly considered. Stability assessments of stratified rock masses and reinforcement strategies, such as those presented by Imashev et al. [28], provide further insights into securing longwall operations and excavation fronts. Based on the analysis above, it can be found that the most optimal tunnel excavation methods were mainly determined based on engineers’ experience; in other words, the determination process is subjective and not scientific, and the optimal result would not be the optimal one. Soomro, M.A. [29] proposed a novel multi-objective optimization approach for tunnel support design considering construction cost and safety. While their study provided important insights, it did not incorporate dynamic feedback from staged numerical simulations, nor did it implement a fully automated optimization workflow. However, because of the complex and variable geological conditions during tunnel construction, the construction methods for sections with poor geological conditions still require further research and improvement.
In order to address the issues of low construction efficiency and tight project timelines in tunnel engineering, this study, based on the Longshu Tunnel of the Central Yunnan Water Diversion Project, which crosses a slate fracture zone, combines numerical simulation with engineering practice to comparatively study the deformation pattern, stress distribution, and instability mechanism of tunnel surrounding rock when using full-face and step-by-step construction methods in a slate fracture zone. The results provide a basis for controlling the stability of the tunnel surrounding rock. Additionally, the NSGA-II optimization algorithm is applied, based on the FLAC3D numerical simulation platform, with secondary development using the Python programming language, to determine the optimal step parameters, which are then applied to engineering practice.

2. Project Overview

The exit section of the Longshu Tunnel is located at the southern foot of Yunlong Mountain, characterized by tectonic erosion. The tunnel alignment exposes many layers of slate strata with a layered fractured structure and poor integrity. The surrounding rock consists of a fractured slate mass with overall low strength, and the surrounding rock mass is classified as unstable. During tunnel construction through the slate fracture zone, significant deformation of the surrounding rock occurs, causing a severe reduction in the cross-section (Figure 1). This greatly increases the risk of collapse, leading to engineering accidents, personnel injuries, and property damage. The construction method is the main factor causing the collapse of the surrounding rock. The selection of scientific excavation techniques plays a key role in controlling the stability of the tunnel surrounding rock [30,31,32,33]. The tunnel is located at a depth of 130 m, with a width of 4.12 m and a height of 4.86 m. The tunnel cross-section is shown in Figure 2.
Figure 1. Tunnel surrounding rock deformation diagram.
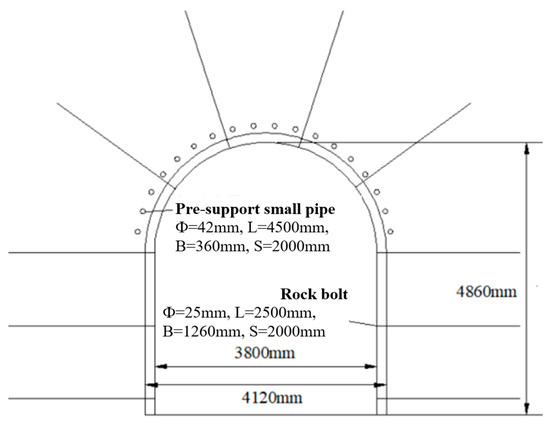
Figure 2. Tunnel support cross-section diagram.

3. Tunnel Deformation Theory

According to the shear slip theory of the loosening zone [34,35,36], based on the tunnel’s symmetry and stress field equations, the circumferential stress is the maximum principal stress, and the radial stress is the minimum principal stress.
τ α = σ θ − σ r 2 sin ⁡ 2 α ,
σ α = σ θ + σ r 2 + σ θ − σ r 2 cos ⁡ 2 α ,
It is also assumed that the shear strength ( τ m a x ) is:
τ max = f σ α + c 0 ,
where f is the friction coefficient, f = tan ⁡ φ , where φ is the friction angle, (°), and c0 is the cohesion (MPa) [37,38,39].

4. Numerical Simulation Analysis

To compare and analyze the stability of the tunnel surrounding rock under two excavation methods, the displacement and stress evolution characteristics of the tunnel surrounding rock were analyzed separately. Based on the site geological conditions, the model dimensions were set as length × width × height = 50 m × 60 m × 50 m, with the tunnel dimensions of width × height = 4.12 m × 4.86 m. The 3D numerical model is shown in Figure 3, where the bottom and sides are fixed with boundary constraints, and the top serves as the stress boundary.
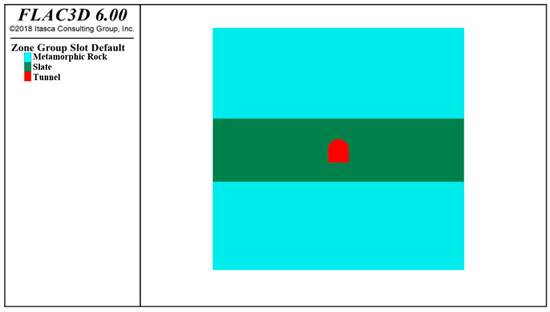
Figure 3. Numerical model diagram.
The physical and mechanical parameters of the rock layers obtained from the laboratory tests are shown in Table 1. The model uses the Mohr–Coulomb failure criterion to describe the strength characteristics of the rock mass. The expression of the Mohr–Coulomb failure criterion is:
σ 1 = 1 + sin ⁡ φ 1 − sin ⁡ φ σ 3 + 2 C   cos ⁡ φ 1 − sin ⁡ φ ,
where σ1 is the maximum principal stress, σ3 is the minimum principal stress, C is the cohesion, and φ is the internal friction angle.
Table 1. Physical and mechanical properties of rock layers.

4.1. Analysis of Full-Face Excavation Results

Based on the numerical simulation results, as shown in Figure 4, Figure 5 and Figure 6, after a full-face excavation of 20 m, the maximum displacement of the tunnel surrounding rock occurs at the bottom and top, with a maximum displacement of approximately 0.031 m. The deformation displacement of the left and right shoulders of the tunnel surrounding rock is about 0.016 m.
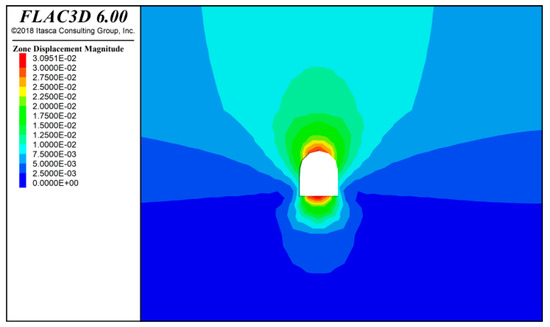
Figure 4. Full-face excavation tunnel surrounding rock displacement diagram at a 20 m excavation.
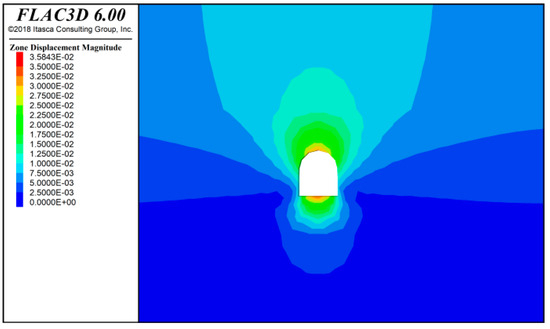
Figure 5. Full-face excavation tunnel surrounding rock displacement diagram at a 40 m excavation.
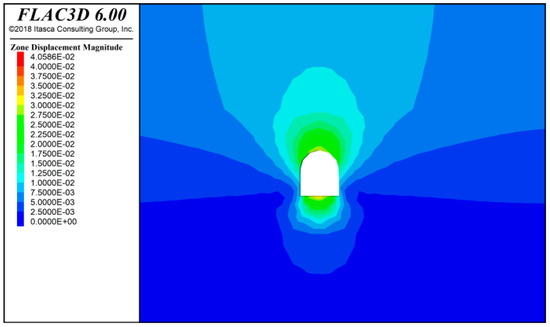
Figure 6. Full-face excavation tunnel surrounding rock displacement diagram at a 60 m excavation.
As shown in Figure 7, Figure 8 and Figure 9, after a tunnel excavation of 20 m, stress concentration occurs on both sides of the tunnel surrounding rock. The maximum compressive stress is approximately 6.44 × 106 Pa, with lower compressive stress values distributed at the top and bottom of the tunnel surrounding rock. The minimum compressive stress is located at the bottom of the tunnel, with a value of about 5.23 × 105 Pa. After a tunnel excavation of 40 m, stress concentration appears on both sides of the tunnel surrounding rock. The maximum compressive stress is approximately 6.56 × 106 Pa, with lower compressive stress values at the top and bottom of the tunnel surrounding rock. The minimum compressive stress is located at the bottom of the tunnel, with a value of about 5.55 × 105 Pa. After a tunnel excavation of 60 m, stress concentration occurs on both sides of the tunnel surrounding rock. The maximum compressive stress is approximately 6.83 × 106 Pa, with lower compressive stress values at the top and bottom of the tunnel surrounding rock. The minimum compressive stress is located at the bottom of the tunnel, with a value of about 5.86 × 105 Pa.
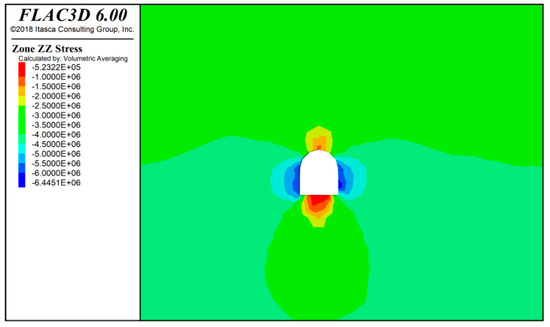
Figure 7. Full-face tunnel surrounding rock stress diagram at a 20 m excavation.
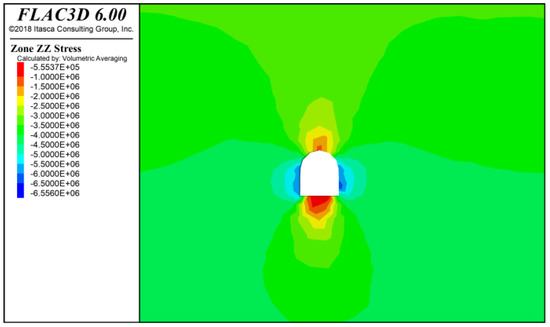
Figure 8. Full-face excavation tunnel surrounding rock stress diagram at a 40 m excavation.
Figure 9. Full-face excavation tunnel surrounding rock stress diagram at a 60 m excavation.

4.2. Determining the Step Height Parameters Based on the NSGA-II Multi-Objective Optimization Algorithm

4.2.1. Step Height Parameter Optimization Problem

Considering the large deformation and significant stress concentration during full-face excavation, we used the step-by-step excavation method. In this study, the term “step-by-step excavation” refers to a staged excavation method in which the tunnel cross-section is divided into two parts: the upper step and the lower step (as in Figure 10). The excavation is first carried out in the upper part (pilot step) to a certain length, followed by the excavation of the lower part (completion step). This method is commonly used in fractured and weak surrounding rock zones, as it helps reduce deformation concentration, control face stability, and improve construction safety.
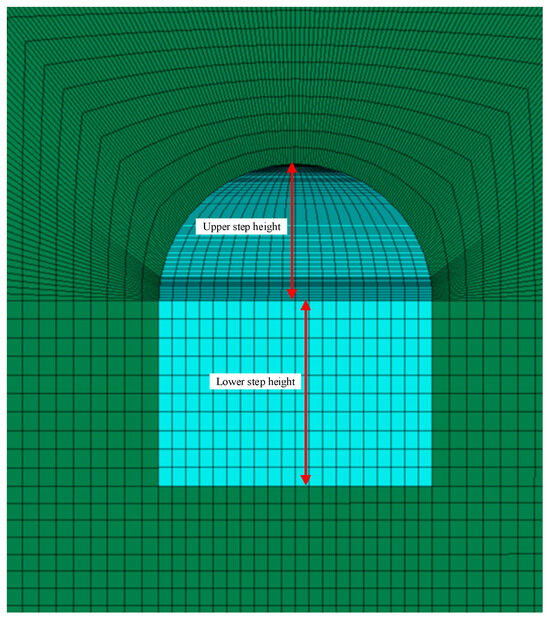
Figure 10. Step height parameters.
Let the lower step height be denoted as x; then, the upper step excavation height is 4.86 − x. The lower step height x is the variable to be solved in this optimization problem. During the excavation process, the upper step must be excavated first, followed by the lower step. Considering the influence of deformation, the tunnel deformation after 20 m, 40 m, and 60 m of lower step excavation is set as an objective function. It can be observed that there are three objective functions; therefore, the NSGA-II multi-objective optimization algorithm was selected in this paper to solve for the optimal step height design parameters.

4.2.2. NSGA-II Optimization Algorithm

NSGA-II (Non-dominated Sorting Genetic Algorithm-II) is a fast, non-dominated multi-objective optimization algorithm that uses an elitist preservation strategy. It is based on Pareto optimal solutions [40,41,42,43].
The core idea of Pareto optimal solutions is that when the system’s state evolves to another state, at least one objective function is improved, provided that the other objective functions do not worsen. This process is called Pareto improvement, and the process of obtaining the optimal solution through iterative application of this improvement strategy is defined as Pareto optimization.
Additionally, in NSGA-II, the method of crowding distance and crowding comparison is used to replace the traditional sharing function method. The crowding distance refers to the number of solutions surrounding a particular solution xᵢ, and in the iterative computation process, the crowding distance is used to maintain the diversity of the population. The main calculation process of the crowding distance is as follows:
First, initialize the crowding distance of each point: id = 0.
Next, perform non-dominated sorting on the population, and set the crowding distance of the two individuals at the boundary to infinity.
Finally, calculate the crowding distance for the remaining (i − 2) individuals:
i d = ∑ j = 1 m | f j i + 1 − f j i − 1 | ,
where id represents the crowding distance of point i, fji+1 represents the value of the j-th objective function at point i + 1, and fji−1 represents the value of the j-th objective function at point i − 1.
Then, compare the two attributes, i.e., non-dominated sorting (irank) and crowding distance (id). If any of the following conditions is met, individual i wins.
(1) i r a n k < j r a n k . At this point, the non-dominated layer of individual i is superior to that of individual j.
(2) i r a n k = j r a n k ∩ i d > j d . When individual i and individual j belong to the same level, individual i has a larger crowding distance.
For ease of the subsequent programming calculations, Figure 11 shows a flowchart of the NSGA-II optimization algorithm.
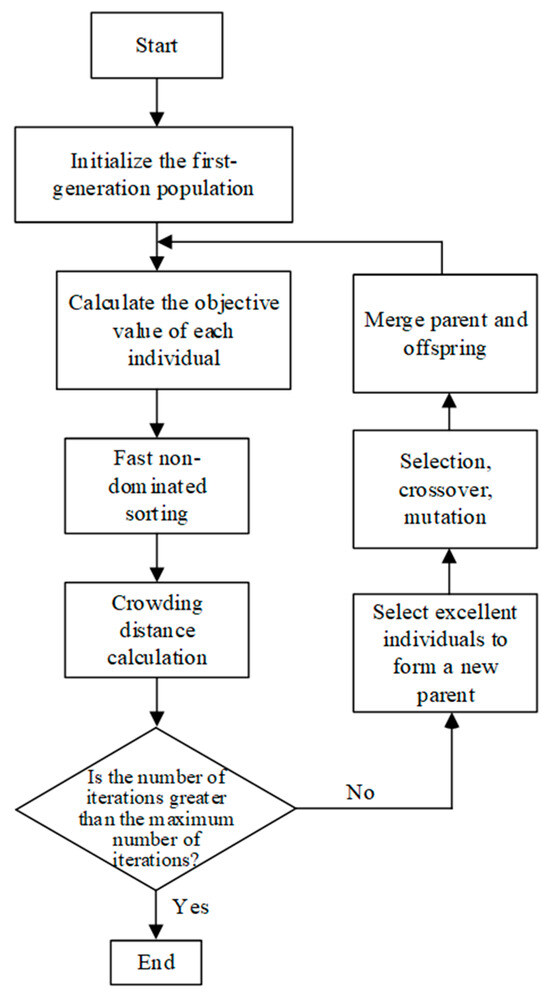
Figure 11. Flowchart of the NSGA-II optimization algorithm.
Among various multi-objective optimization algorithms, NSGA-II was selected for this study because of its reliable performance and compatibility with numerical simulation workflows. Compared with other popular methods, such as SPEA2 and MOPSO, NSGA-II has the following advantages:
(1) NSGA-II offers efficient non-dominated sorting, elitist selection, and a crowding distance mechanism, which together ensure good solution diversity and convergence speed with relatively simple parameter settings.
(2) SPEA2 provides enhanced elitism and external archive management but typically involves more complex memory and computational overhead.
(3) MOPSO (Multi-Objective Particle Swarm Optimization) is known for fast convergence and global search capability; however, it is prone to premature convergence and is sensitive to inertia weight and velocity update strategies.
Considering the trade-off between robustness, ease of implementation in Python, and computational efficiency during integration with FLAC3D, NSGA-II was deemed the most suitable choice for this study.

4.2.3. Determining the Optimal Step Parameters Based on the NSGA-II Optimization Algorithm

The variable to be determined in the numerical simulation was the lower step height x. The objective function values primarily involved three factors: the maximum deformation y1 after 20 m of lower step excavation, the maximum deformation y2 after 40 m of lower step excavation, and the maximum deformation y3 after 60 m of lower step excavation.
To integrate the NSGA-II optimization algorithm with FLAC3D numerical simulation, secondary development was carried out using the built-in Python programming language in FLAC3D. Using Python, the entire process was implemented, including step height parameter setting, command file generation, retrieval of numerical simulation results, integration of numerical simulation results, and updating of the new step parameters based on the current step parameters. The numerical simulation process was automated without manual intervention, and when the termination condition was met, the simulation ended, yielding the optimal step height parameters [44,45,46,47].
Step 1: Initialize the hyperparameters of the NSGA-II multi-objective optimization algorithm, with a population size of N = 20 and a maximum iteration count of Max_iter = 10,000, and initialize the current iteration count Now_iter to 0.
Step 2: Initialize the population. Since the population size N is 20, generate 20 lower step height parameters x, with the parameter values ranging from 0.1 to 4.85.
Step 3: Based on the 20 sets of step parameters, generate 20 FLAC3D command flow files using a Python script. Perform numerical simulations for each file to obtain the maximum deformation values y1, y2, and y3 of the tunnel after 20 m, 40 m, and 60 m of lower step excavation, respectively. To accelerate the computation speed, conduct 20 FLAC3D numerical simulations simultaneously using parallel processing.
Step 4: Based on the 20 lower step height parameters and the corresponding maximum deformation values y1, y2, and y3 of the tunnel after 20 m, 40 m, and 60 m of lower step excavation, update the 20 new lower step height parameter values using the NSGA-II optimization algorithm.
Step 5: Increment the current iteration count Now_iter by 1. If Now_iter exceeds the maximum iteration count Max_iter, end the calculation (Step 6); otherwise, proceed to Step 2.
Step 6: End the calculation.
The optimization variable in this study was the lower step height (x), with a search range of 0.1 m to 4.85 m, corresponding to the tunnel height minus a minimal construction clearance. The population size was set to 20, and the maximum generation number was 10,000, resulting in up to 200,000 solution candidates evaluated through NSGA-II. These parameter settings were chosen to balance optimization accuracy and computational efficiency.
While the NSGA-II algorithm yields a Pareto front of optimal solutions in terms of objective functions (deformations at 20 m, 40 m, and 60 m), engineering validation is also required. Therefore, the final chosen value (3 m) was not only optimal in the simulation but was also verified through field monitoring results, confirming that the predicted deformations align with actual measured values. This two-stage validation ensured that the selected parameter was both algorithmically optimal and practically effective.
Through iterative calculation, the optimal lower step parameter x was obtained as 3 m, with the upper step height being 1.86 m.

4.2.4. Analysis of Calculation Results

To verify the validity of the numerical simulation results, Figure 12, Figure 13 and Figure 14 show the deformation of the tunnel after 20 m, 40 m, and 60 m of lower step excavation (numerical simulation results with a lower step height of 3 m).
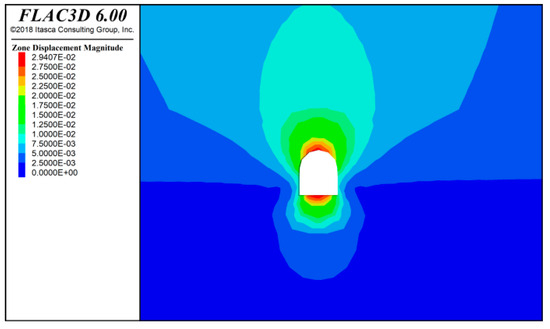
Figure 12. Tunnel surrounding rock displacement diagram after the lower step excavation at 20 m.
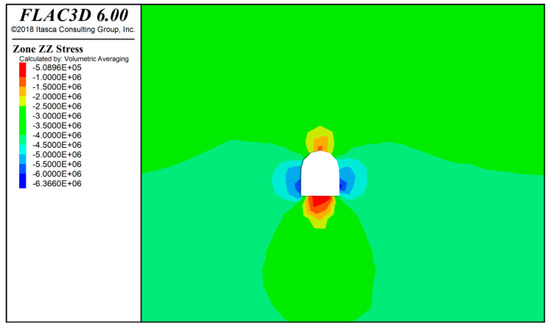
Figure 13. Tunnel surrounding rock stress diagram after the lower step excavation at 20 m.
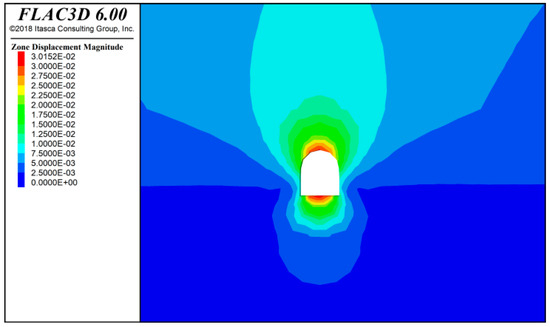
Figure 14. Tunnel surrounding rock displacement diagram after the lower step excavation at 40 m.
As shown in Figure 15, Figure 16 and Figure 17, after 20 m of tunnel excavation, the maximum compressive stress on both sides is approximately 6.36 × 106 Pa, the minimum compressive stress at the bottom is about 5.09 × 106 Pa, and the compressive stress at the top is about 9.98 × 105 Pa. After 40 m of tunnel excavation, the maximum compressive stress on both sides is approximately 6.46 × 106 Pa, the minimum compressive stress at the bottom is about 5.25 × 106 Pa, and the compressive stress at the top is about 1.01 × 106 Pa. After 60 m of tunnel excavation, the maximum compressive stress on both sides is approximately 6.56 × 106 Pa, the minimum compressive stress at the bottom is about 5.46 × 106 Pa, and the compressive stress at the top is about 1.56 × 106 Pa.
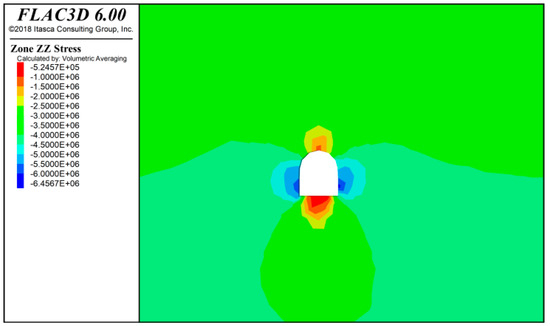
Figure 15. Tunnel surrounding rock stress diagram after the lower step excavation at 40 m.
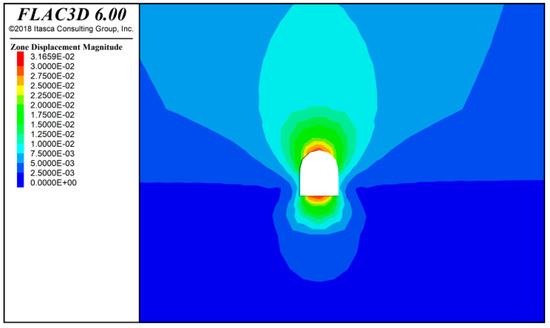
Figure 16. Tunnel surrounding rock displacement diagram after the lower step excavation at 60 m.
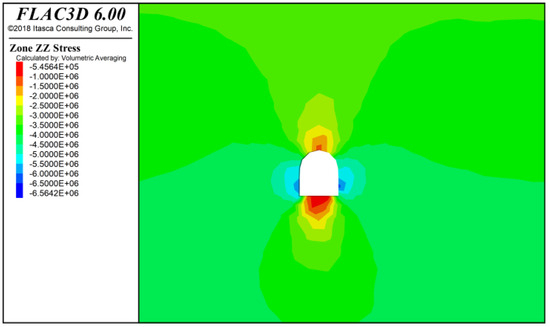
Figure 17. Tunnel surrounding rock stress diagram after the lower step excavation at 60 m.
From the simulation results of both the full-face excavation and step excavation techniques, it can be seen that compared to the step excavation technique (with a lower step height of 3 m), after tunnel excavation using the full-face method, the larger excavation cross-section leads to a larger loosening range of the tunnel free face and surrounding rock. The surrounding rock stress is released more rapidly, and the redistribution of the surrounding rock stress leads to significant deformation of the tunnel structure, resulting in high levels of concentrated stress on both sides of the tunnel, which is unfavorable for the stability control of the tunnel surrounding rock [47,48,49,50].

5. Field Engineering Practice

Although full-face excavation technology has a high degree of mechanization and fast construction speed on site, this excavation method has limitations when dealing with fractured and unstable rock masses. The large excavation cross-section tends to form a large-scale hanging arch, which can lead to roof collapse accidents [51,52,53]. Based on the analysis of the numerical simulation results, it can be seen that using the step excavation method for the Longshu Tunnel when passing through the slate fracture zone can effectively control the deformation of the surrounding rock. Therefore, the construction technique uses the step excavation method, with the lower step height set to 3 m (as in Figure 18). In the field engineering tests, surface observation points are installed to measure the deformation of the tunnel’s top, bottom, left shoulder, and right shoulder during the excavation process and to analyze the deformation patterns of the surrounding rock during excavation.
Figure 18. Step-by-step tunnel construction.
As shown in Figure 19, the maximum deformation at the tunnel top and bottom is 34 mm, the left shoulder deformation is 29 mm, and the right shoulder deformation is 27 mm. As shown in Figure 20, the maximum deformation at the tunnel top and bottom is 35 mm, the left shoulder deformation is 29 mm, and the right shoulder deformation is 28 mm. As shown in Figure 21, the maximum deformation at the tunnel top and bottom is 31 mm, the left shoulder deformation is 26 mm, and the right shoulder deformation is 25 mm. As shown in Figure 22, the maximum deformation at the tunnel top and bottom is 32 mm, the left shoulder deformation is 27 mm, and the right shoulder deformation is 26 mm. From the deformation patterns of the measurement points, it can be observed that after the measurement point is approximately 25 m from the tunnel face, the surrounding rock tends to stabilize. The engineering practice results show that setting the lower step height to 3 m is reasonable. The measured displacements at the crown, invert, and shoulders show good agreement with the simulation predictions in both trend and magnitude, supporting the effectiveness of the model. The step excavation technique is beneficial for controlling the tunnel surrounding rock stability, improving construction efficiency, and enhancing construction safety.
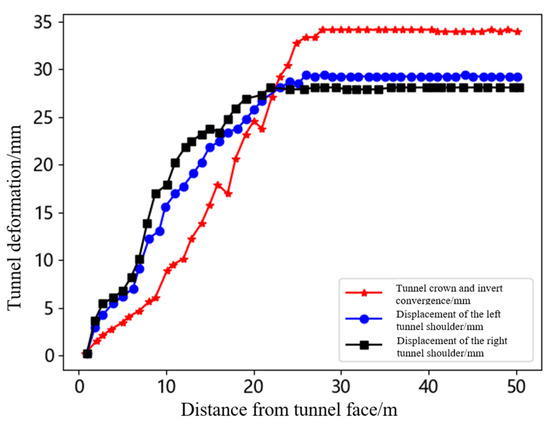
Figure 19. Displacement diagram of tunnel deformation monitoring station 1.
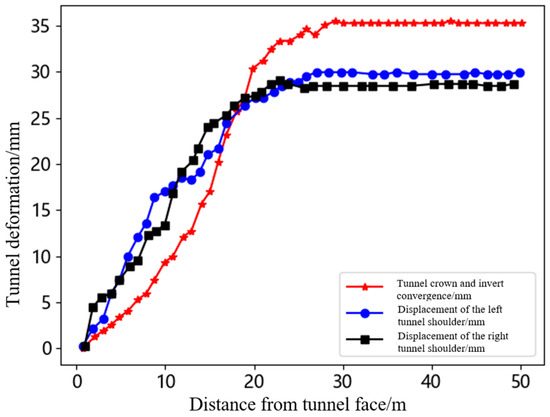
Figure 20. Displacement diagram of tunnel deformation monitoring station 2.
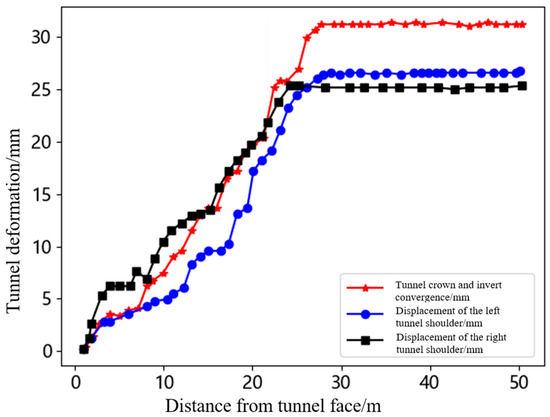
Figure 21. Displacement diagram of tunnel deformation monitoring station 3.
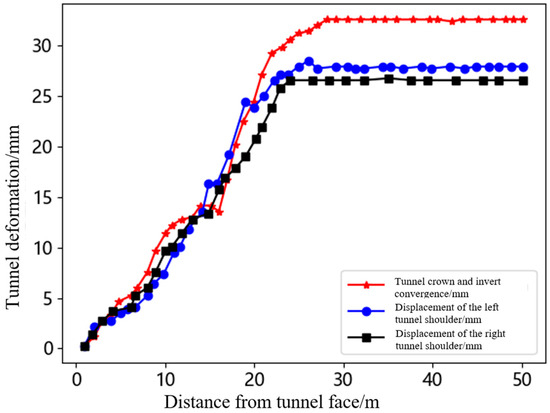
Figure 22. Displacement diagram of tunnel deformation monitoring station 4.

6. Discussion

Although the current study demonstrates the feasibility and effectiveness of integrating NSGA-II optimization with FLAC3D numerical modeling for tunnel excavation in fractured slate zones, several limitations and areas for further improvement remain.
First, the modeling framework is deterministic and based on average input parameters derived from laboratory tests. In practice, spatial variability in geological conditions, such as heterogeneous distribution of rock and soil types, clay sensitivity, or the presence of weak interlayers, can significantly affect tunnel behavior and stability. These effects are not explicitly considered in the current simulation.
Second, the uncertainty associated with geological modeling and parameter selection—such as cohesion, friction angle, and stiffness of the surrounding rock—could influence the optimization outcomes. As a technical limitation, the presented model does not incorporate probabilistic or stochastic components that would help quantify confidence intervals or risk in excavation design. Referring to the attractiveness of 3D modeling [22,23], the potential of the methodologies with a promising perspective in future geo-modeling under uncertain conditions can be highlighted [21,25,26].
Third, while the Python-FLAC3D integration greatly improves computational efficiency through automation and parallel processing, the computational cost can still be significant when evaluating many generations of individuals in large-scale 3D simulations. This highlights the need for balancing model fidelity with optimization performance in practical applications.
Finally, this study focuses on a case-specific validation using field data from the Longshu Tunnel. Although the observed deformation trends are consistent with the simulation results, a comparative evaluation with other numerical models or optimization frameworks (e.g., SPEA2, MOPSO) was not conducted. This will be considered in future studies to further validate the methodology’s generalizability.

7. Conclusions

This study investigates the stability of tunnel surrounding rock during excavation through a fractured slate zone using the Longshu Tunnel of the Central Yunnan Water Diversion Project as a case study. A combination of full-face and step-by-step excavation simulations, NSGA-II-based optimization, and field validation is employed to derive excavation strategies suitable for weak and complex geological environments. The key findings are summarized as follows:
(1) The numerical simulations revealed that step-by-step excavation leads to significantly reduced deformation at critical locations of the tunnel cross-section—including the crown, invert, and shoulders—compared to full-face excavation. Furthermore, the stress concentrations on both sides of the tunnel were consistently lower, improving the mechanical stability of the surrounding rock.
(2) An automated optimization framework was developed by integrating the NSGA-II algorithm with the FLAC3D platform using Python scripting. This framework enabled efficient parameter tuning based on multi-stage deformation objectives. The optimal lower step height was identified as 3.0 m, offering a balance between deformation control and construction efficiency.
(3) Field monitoring data confirmed the accuracy of the simulation results, with measured displacements at the tunnel crown and invert ranging from 32 mm to 35 mm and shoulder displacements ranging from 25 mm to 29 mm. Stabilization of the surrounding rock was observed approximately 25 m behind the tunnel face, validating the model’s predictive capability.
(4) The optimized step excavation method significantly improved construction performance, enabling better control of ground deformation, reducing the need for excessive support and remedial work, and contributing to overall cost efficiency and construction safety.
(5) It was also acknowledged that the current model is deterministic in nature. Considering the geological heterogeneity in fractured slate zones, future work could incorporate probabilistic analysis to evaluate the impact of geological uncertainty on excavation stability and optimization outcomes.

Author Contributions

S.N.: investigation, writing—review and editing, and data curation. J.W.: Supervision, Methodology, Funding acquisition. J.Z.: writing—review and editing and investigation. J.P.: writing—review and editing, supervision, and investigation. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Basic Research Program of Shanxi Province (No. 202303021221042) and the Research Program of Shanxi Province (No. 202403021221119).

Institutional Review Board Statement

Not applicable.

Data Availability Statement

The original contributions presented in this study are included in this article. Further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. She, G.; Duan, J.; Ma, G.; Zhang, J. Selection Analysis of Shield Tunneling in Shenzhen with Uneven Soft and Hard Strata. Hans J. Civ. Eng. 2020, 09, 1357–1363. [Google Scholar] [CrossRef]
  2. Su, Y.; Su, Y.; Zhao, M.; Vlachopoulos, N. Tunnel Stability Analysis in Weak Rocks Using the Convergence Confinement Method. Rock Mech. Rock Eng. 2021, 54, 559–582. [Google Scholar] [CrossRef]
  3. Huang, J.; Huang, M.; Tan, Z. Phased Control Standards of Primary Support Deformation of East Tianshan Tunnel Crossing Fault Fracture Zone. Tunn. Constr. 2022, 42, 155–165. (In Chinese) [Google Scholar]
  4. Lunardi, P. Design and Construction of Tunnels—Analysis of Controlled Deformation in Rock and Soils (ADECO-RS); Springer: Milano, Italy, 2008. [Google Scholar]
  5. Shen, Y.; Zhang, X.; Chang, M.; Pan, X.; Li, W.; Tao, W.; Zhao, H.; Shen, Y.; Zhang, X.; Chang, M.; et al. Shaking table test on segmental tunnel lining with variable stiffness passing through fault rupture zone. Chin. J. Civ. Eng. 2024, 7, 1–15. (In Chinese) [Google Scholar]
  6. Huang, J.; Yang, Y.; Cai, Q.; Cai, C. Research on multiple risk network of railway tunnel construction crossing fault fracture zone. J. Railw. Sci. Eng. 2021, 18, 2780–2787. (In Chinese) [Google Scholar]
  7. Woodcock, N.H.; Mort, K. Classification of fault breccias and related fault rocks. Geol. Mag. 2008, 145, 435–440. [Google Scholar] [CrossRef]
  8. Jie, Y.; Dong, J. Analysis of Longitudinal Deformation and Stress Characteristics of Tunnel Crossing fault Fracture Zone. China J. Highw. Transp. 2021, 34, 211–224. (In Chinese) [Google Scholar]
  9. Zhang, Y.; Xu, Z.; Xie, Y.; Qiu, J.; Yang, T.; Xie, Y. Analysis of Surrounding Rock Sensitivity and Settlement Control of Tunnel in Fault Fracture Zone. Sci. Technol. Eng. 2023, 23, 3493–3501. (In Chinese) [Google Scholar]
  10. Wang, L.; Han, K.; Guo, C.; Xie, T.; Luo, J. The face stability of shield tunnel traversing the fault fracture zone. China Civ. Eng. J. 2020, 53, 93–98. (In Chinese) [Google Scholar]
  11. Yang, J.; Shen, K.; Zhou, J.; Xue, Y. Mechanism and prevention of tunnel collapse through water-rich fault fracture zone. J. Eng. Geol. 2023, 31, 248–257. (In Chinese) [Google Scholar]
  12. Zhao, X. Construction Parameters Optimization for Double⁃sidewalls Guiding⁃hole Method of Shallow Buried Urban Subway Tunnel in Loess Formation. Railw. Eng. 2022, 62, 119–121+131. (In Chinese) [Google Scholar]
  13. Fu, H.; An, P.; Li, K.; Li, J.; Cheng, G.; Zhang, J. Analysis on the Process of Tunnel Passing through High-pressure Fault Fractured Zone With Abundant Water Rich. Mod. Tunn. Technol. 2020, 57, 458–465. (In Chinese) [Google Scholar]
  14. Huang, F.; Dong, G.; Li, T.; Gao, X.; Peng, Y. Study on discrete element simulation of tunnel surrounding rock stability with fault fracture. Sci. Technol. Eng. 2020, 20, 7429–7440. (In Chinese) [Google Scholar]
  15. Liang, B.; Yang, S.; Ren, Z.; Zhao, F. Research on Anti-seismic Technology of Super Large Section Highway Tunnel in Fault Fracture Zone. Mod. Tunn. Technol. 2020, 57, 136–142. (In Chinese) [Google Scholar]
  16. Yu, H.; Li, T.; Chen, Z.; Yan, X. Stochastic analysis of fault dislocation induced by tunnel excavation considering distribution characteristics of joints in fracture zones. Chin. J. Geotech. Eng. 2018, 46, 746–754. (In Chinese) [Google Scholar]
  17. Thomas, A. Sprayed Concrete Lined Tunnels, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2019; p. 288. [Google Scholar]
  18. Lunardi, P. The underground as a resource and reserve for new spaces; ADECO-RS as an effective tool to be able to realize them (part 1). In Proceedings of the World Tunnel Congress, Cassani G World Tunnel Congress, Iguassu Falls, Brazil, 9–15 May 2014. [Google Scholar]
  19. Guo, Y.; Chen, Y.; Jiang, Y.; Yin, Z.; Hu, T. Study on Stability Control Measures for Large Deformation of Carbonaceous Slate at Diversion Tunnel of Guzeng Hydropower Station. Pearl River 2020, 41, 58–64. (In Chinese) [Google Scholar]
  20. Yan, J. The Construction Technology of Section Tunnel of Building Little Hydroelectric Station in LiangShan. West-China Explor. Eng. 2009, 21, 132–134. (In Chinese) [Google Scholar]
  21. Ghaderi, A.; Abbaszadeh Shahri, A.; Larsson, S. An artificial neural network based model to predict spatial soil type distribution using piezocone penetration test data (CPTu). Bull. Eng. Geol. Environ. 2019, 78, 4579–4588. [Google Scholar] [CrossRef]
  22. Rangarajan, S.; Rahardjo, H.; Satyanaga, A.; Li, Y. Influence of 3D subsurface flow on slope stability for unsaturated soils. Eng. Geol. 2024, 339, 107665. [Google Scholar] [CrossRef]
  23. Abbaszadeh Shahri, A.; Kheiri, A.; Hamzeh, A. Subsurface Topographic Modeling Using Geospatial and Data Driven Algorithm. ISPRS Int. J. Geo-Inf. 2021, 10, 341. [Google Scholar] [CrossRef]
  24. Abbaszadeh Shahri, A.; Malehmir, A.; Juhlin, C. Soil classification analysis based on piezocone penetration test data. Eng. Geol. 2015, 189, 32–47. [Google Scholar] [CrossRef]
  25. Ghaderi, A.; Abbaszadeh Shahri, A.; Larsson, S. A visualized hybrid intelligent model to delineate Swedish fine-grained soil layers using clay sensitivity. CATENA 2022, 214, 106289. [Google Scholar] [CrossRef]
  26. Abbaszadeh Shahri, A.; Chunling, S.; Larsson, S. A hybrid ensemble-based automated deep learning approach to generate 3D geo-models and uncertainty analysis. Eng. Comput. 2024, 40, 1501–1516. [Google Scholar] [CrossRef]
  27. Demin, V.; Khalikova, E.; Rabatuly, M.; Amanzholov, Z.; Zhumabekova, A.; Syzdykbaeva, D.; Bakhmagambetova, G.; Yelzhanov, Y. Research into mine working fastening technology in the zones of increased rock pressure. Min. Miner. Depos. 2024, 18, 27–36. [Google Scholar] [CrossRef]
  28. Imashev, A.; Suimbayeva, A.; Zhunusbekova, G.; Adoko, A.C.; Issakov, B. Assessing stability of mine workings driven in stratified rock mass. Min. Miner. Depos. 2024, 18, 82–88. [Google Scholar] [CrossRef]
  29. Soomro, M.A.; Mangnejo, D.A.; Bhanbhro, R.; Memon, N.A.; Memon, M.A. 3D finite element analysis of pile responses to adjacent excavation in soft clay: Effects of different excavation depths systems relative to a floating pile. Tunn. Undergr. Space Technol. 2019, 86, 138–155. [Google Scholar] [CrossRef]
  30. Aygar, E.B. Evaluation of new Austrian tunnelling method applied to Bolu tunnel’s weak rocks. J. Rock Mech. Geotech. Eng. 2020, 12, 541–556. [Google Scholar] [CrossRef]
  31. Barla, G. Full-face excavation of large tunnels in difficult conditions. J. Rock Mech. Geotech. Eng. 2016, 8, 294–303. [Google Scholar] [CrossRef]
  32. Zhou, P.; Jiang, Y.; Zhou, F.; Gong, L.; Qiu, W.; Yu, J. Stability Evaluation Method and Support Structure Optimization of Weak and Fractured Slate Tunnel. Rock Mech. Rock Eng. 2022, 55, 6425–6444. [Google Scholar] [CrossRef]
  33. Wang, B.; Wang, J.; Wu, D.; Zhao, Y.; Zhang, B.; Li, Z. Study on application of yielding supporting system for large-deformation in soft rock highway tunnel. J. Railw. Sci. Eng. 2016, 13, 1985–1993. (In Chinese) [Google Scholar]
  34. Wang, Z.; Ma, W. Classification of the loosening zones and estimation of the loosening pressures of tunnels in layered jointed rock strata. Sci. Prog. 2022, 105, 368504221098886. [Google Scholar] [CrossRef] [PubMed]
  35. Sun, H.; Song, S.; Lu, W.; Ren, Q.; Li, X.; Miao, X. Safety design of tunnel lining structure considering bond-slip failure mechanism. Arab. J. Geosci. 2022, 15, 489. [Google Scholar] [CrossRef]
  36. Wang, M.; Zhang, X.; Li, Y.; Yang, H. A semi-analytical method for stress-strain analysis of tunnels under dip-slip faulting based on an elastic-plastic foundation beam model. Soil Dyn. Earthq. Eng. 2024, 179, 108506. [Google Scholar] [CrossRef]
  37. Bernard, E.; Thomas, A. Fibre reinforced sprayed concrete for ground support. Tunn. Undergr. Space Technol. 2020, 99, 103302. [Google Scholar] [CrossRef]
  38. Carranza-Torres, C.; Diederichs, M. Mechanical analysis of circular liners with particular reference to composite supports. Tunn. Undergr. Space Technol. 2009, 24, 506–532. [Google Scholar] [CrossRef]
  39. Zhang, Y.; Zhang, Q.-Y.; Duan, K.; Yu, G.-Y.; Jiao, Y.Y. Reliability analysis of deep underground research laboratory in Beishan for geological disposal of high-level radioactive waste. Comput. Geotech. 2020, 118, 103328. [Google Scholar] [CrossRef]
  40. Verma, S.; Pant, M.; Snasel, V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
  41. Lotfinejad, P.; Tarkashvand, A.; Sanaieian, H. A computational approach for integration of greenhouse and “Shanashir” to enhance thermal comfort of occupants, utilizing NSGA-II algorithm. Build. Environ. 2025, 273, 112717. [Google Scholar] [CrossRef]
  42. Deng, W.; Zhang, X.; Zhou, Y.; Liu, Y.; Zhou, X.; Chen, H.; Zhao, H. An enhanced fast non-dominated solution sorting genetic algorithm for multi-objective problems. Inf. Sci. 2022, 585, 441–453. [Google Scholar] [CrossRef]
  43. Doerr, B.; Ivan, T.; Krejca, M.S. Speeding Up the NSGA-II With a Simple Tie-Breaking Rule. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Institut Polytechnique de Paris: Paris, France, 2024. [Google Scholar] [CrossRef]
  44. El Hafdaoui, H.; Khallaayoun, A.; AIMajeed, S. Controlled Non-Dominated Sorting Genetic Algorithms for Multi-Objective Op-timal Design of Standalone and Grid-Connected Renewable Energy Systems in Integrated Energy Sectors. IEEE Access 2025, 13, 14658–14685. [Google Scholar] [CrossRef]
  45. Bakhshi Ani, A.; Ale Ebrahim, H. Modeling and Multi-objective Optimization of a Packed Bed Reactor for Sulfur Dioxide Removal by Magnesium Oxide Using Non-dominated Sorting Genetic Algorithm II. Chem. Biochem. Eng. Q. 2021, 35, 251–266. [Google Scholar] [CrossRef]
  46. Pazooki, F.; Zibafar, A.; Rahmati Lish, M. Optimization and design of general aviation aircrafts wing using non-dominated sorting genetic algorithms II. J. Aeronaut. Eng. 2021, 23, 100–115. [Google Scholar] [CrossRef]
  47. Liu, B.; Lin, H.; Chen, Y.; Liu, J.; Guo, C. Deformation stability response of adjacent subway tunnels considering excavation and support of foundation pit. Lithosphere 2022, 2022, 7227330. [Google Scholar] [CrossRef]
  48. Song, F.; Rodriguez-Dono, A.; Olivella, S. Hydro-mechanical modelling and analysis of multi-stage tunnel excavations using a smoothed excavation method. Comput. Geotech. 2021, 135, 104150. [Google Scholar] [CrossRef]
  49. Huang, M.; Li, H.; Yu, J.; Zhang, C.; Ni, Y. On the simplified method for evaluating tunnel response due to overlying foundation pit excavation. Transp. Geotech. 2023, 42, 101048. [Google Scholar] [CrossRef]
  50. Li, S.; Zhang, Y.; Cao, M.; Wang, Z. Study on excavation sequence of pilot tunnels for a rectangular tunnel using numerical sim-ulation and field monitoring. Rock Mech. Rock Eng. 2022, 55, 3507–3523. [Google Scholar] [CrossRef]
  51. Bian, W.H.; Yang, J.; Zhu, C.; Wang, K.X.; Xu, D.M. Application of excavation compensation method for enhancing stability and efficiency in shallow large-span rock tunnels. J. Cent. S. Univ. 2024, 31, 3242–3263. [Google Scholar] [CrossRef]
  52. Martiane, W.; Indrawan, I.G.B.; Anggara, F. Determination of Excavation Method and Support System for Sultan Alimuddin—Kakap Tunnel Based on Surface Geology Mapping and Excavation Face. IOP Conf. Ser. Earth Environ. Sci. 2024, 1416, 012009. [Google Scholar] [CrossRef]
  53. Sun, Y.; Xu, S.; Xu, C.; Huang, W.; He, J.; Rong, Y.; Zheng, F.; Ding, L. Study on the Stress and Deformation of Surrounding Rock and Support Structure of Super Large Section Tunnels Based on Different Excavation Methods. Appl. Sci. 2024, 14, 7025. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Structural Fingerprinting of Crystalline Materials from XRD Patterns Using Atomic Cluster Expansion Neural Network and Atomic Cluster Expansion
Previous
Biodynamic Characteristics and Blood Pressure Effects of Stanford Type B Aortic Dissection Based on an Accurate Constitutive Model
Next