Investigation of the Stress Intensity Factor in Heterogeneous Materials Based on the Postprocessing Routine of Commercial Finite Element Software
Abstract
1. Introduction
2. Fracture Parameter Solution Method Based on the Postprocessing Routine of ABAQUS
2.1. Selection of Integration Domain and Extraction of ABAQUS Result
2.2. Construction of Auxiliary Fields
2.3. Computation of Interaction Integral
2.4. Computation of Stress Intensity Factors
2.5. The Advantages of the Present Method
3. Numerical Examples
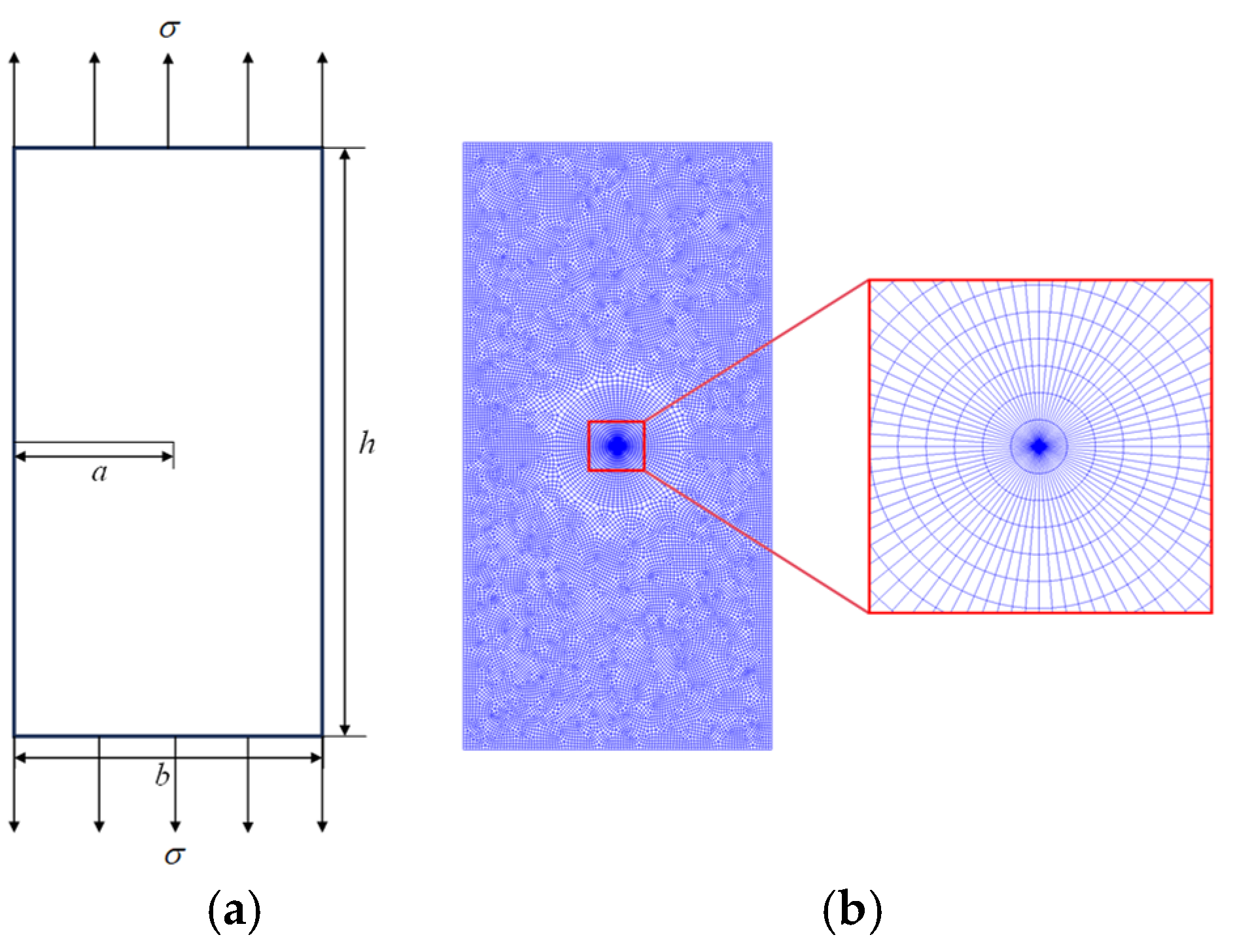
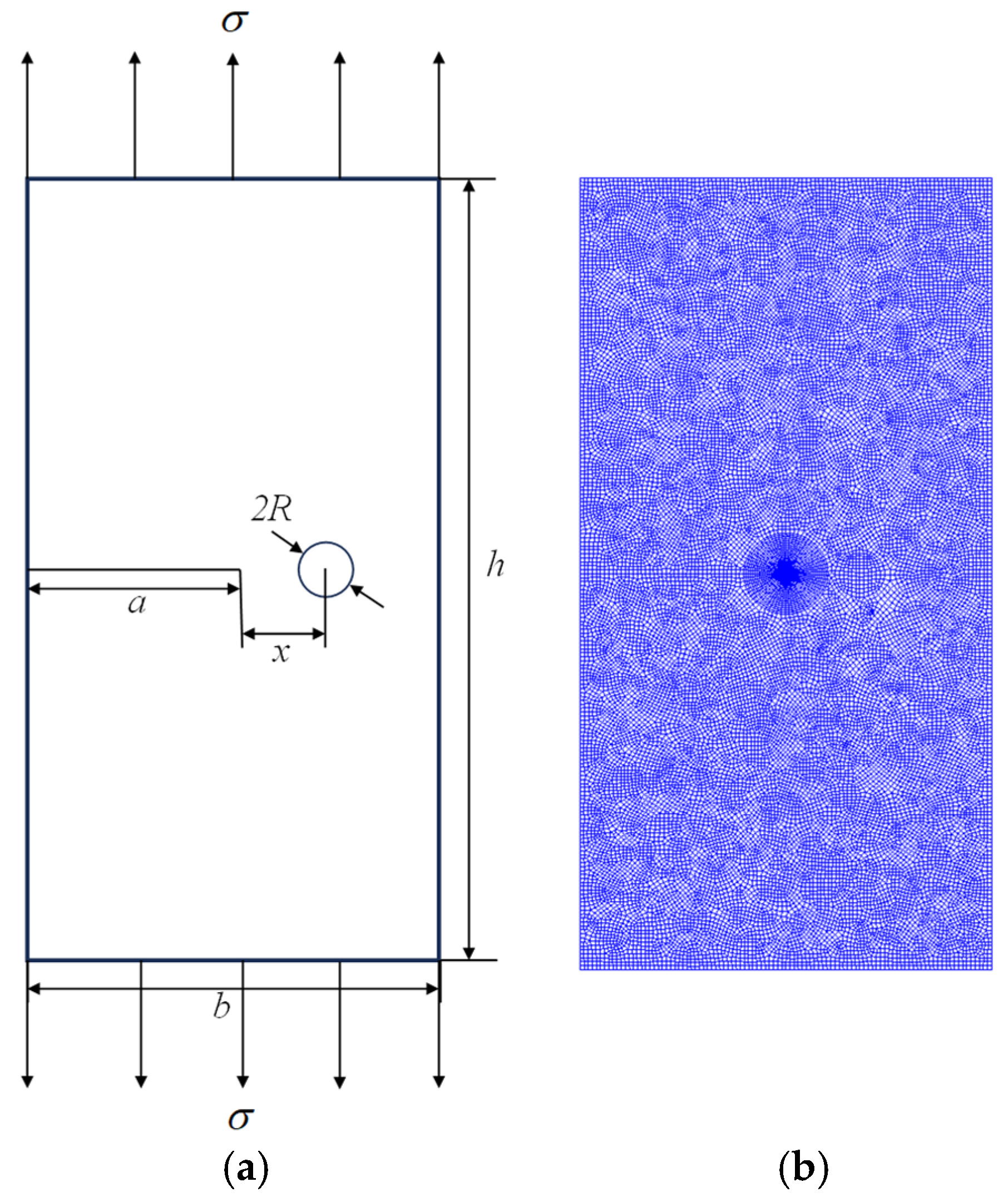
3.1. Numerical Examples of Homogeneous Material
- (a)
- Homogeneous Rectangular Plate with Edge Crack under Unidirectional Tensile Load
- (b)
- Homogeneous Rectangular Plate with a Center-Inclined Crack Under Unidirectional Tensile Load
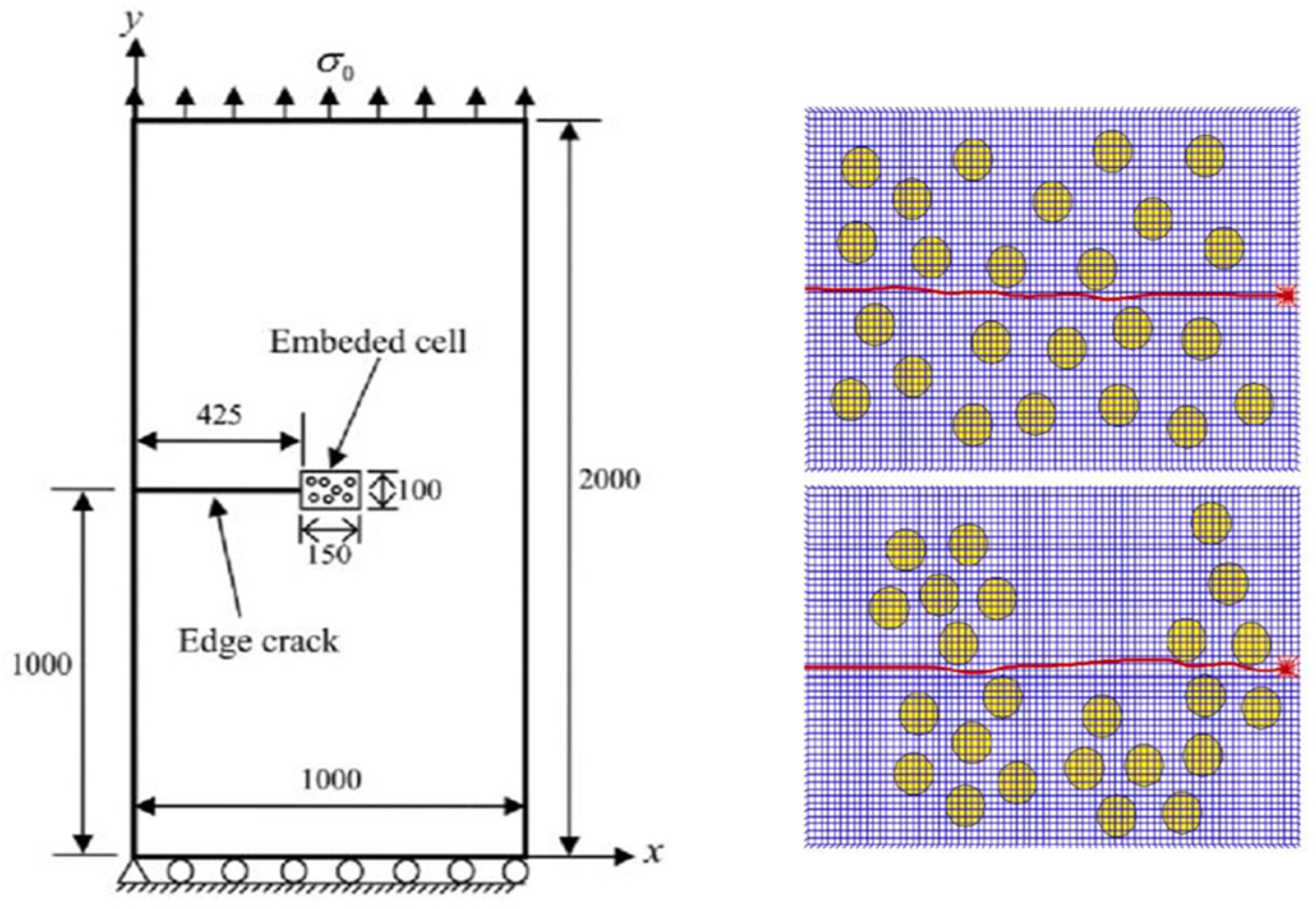
3.2. Numerical Examples of Heterogeneous Material Containing Inclusions
4. Summary and Conclusions
- (1)
- The present method can be directly implemented within ABAQUS, and the computational results exhibit good accuracy, mesh convergence, and domain-independence.
- (2)
- For two-dimensional and three-dimensional models with inclusions, the results show that when the integration domain intersects the inclusions, the stress intensity factors calculated by ABAQUS fail to accurately reflect the crack-tip state, while the present method demonstrates good domain-independence, thereby expanding the practical application scope of ABAQUS.
- (3)
- The influence of the inclusion’s properties on the stress intensity factor was analyzed. The results show that high-modulus inclusions near the crack tip reduce the stress intensity factor. Conversely, low-modulus inclusions in the same area increase it.
- (4)
- The proposed method in this paper can be applied to heterogeneous materials with complex interfaces, such as particulate-reinforced composites and solid rocket motor grains. It can guide the crack conditions and crack propagation of practical components. In the future, it can also be combined with other software to provide guidance for engineering applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chairi, M.; El Bahaoui, J.; Hanafi, I.; Cabrera, F.M.; Di Bella, G. Composite materials: A review of polymer and metal matrix composites, their mechanical characterization, and mechanical properties. In Next Generation Fiber-Reinforced Composites-New Insights; Intechopen: London, UK, 2023. [Google Scholar]
- Janssen, M.; Zuidema, J.; Wanhill, R. Fracture Mechanics: Fundamentals and Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; p. 35. [Google Scholar]
- Stern, M.; Becker, E.B.; Dunham, R.S. A contour integral computation of mixed-mode stress intensity. Int. J. Fract. 1976, 12, 359–368. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Yu, H.J.; Wang, Z.H. A local mesh replacement method for modeling near-interfacial crack growth in 2D composite structures. Theor. Appl. Fract. Mech. 2015, 75, 70–77. [Google Scholar] [CrossRef]
- Li, Y.K.; Yu, H.J.; Guo, L.C.; Huang, K.; Bai, X.M. A new domain-independent interaction integral for three-dimensional non-homogeneous thermoelastic materials. Eng. Fract. Mech. 2020, 233, 107084. [Google Scholar] [CrossRef]
- Wang, S.S.; Yau, J.F.; Corten, H.T. Three-dimensional stress fields of elastic interface cracks. J. Appl. Mech. 1980, 16, 247–259. [Google Scholar]
- Nakamura, T. A mixed-mode crack analysis of rectilinear anisotropic solids using conservation laws of elasticity. Int. J. Fract. 1991, 58, 939–946. [Google Scholar]
- Tabaza, O.; Okada, H.; Yusa, Y. A new approach of the interaction integral method with correction terms for cracks in three-dimensional functionally graded materials using the tetrahedral finite element. Theor. Appl. Fract. Mech. 2021, 115, 103065. [Google Scholar] [CrossRef]
- Nahta, R.; Moran, B. Domain integrals for axisymmetric interface crack problems. Int. J. Solids Struct. 1993, 30, 2027–2040. [Google Scholar] [CrossRef]
- Gosz, M.; Dolbow, J.; Moran, B. Domain integral formulation for stress intensity factor computation along curved three-dimensional interface cracks. Int. J. Solids Struct. 1998, 35, 1763–1783. [Google Scholar] [CrossRef]
- Gosz, M.; Moran, B. An interaction energy integral method for computation of mixed-mode stress intensity factors along non-planar crack fronts in three dimensions. Eng. Fract. Mech. 2002, 69, 299–319. [Google Scholar] [CrossRef]
- Nagashima, T.; Omoto, Y.; Tani, S. Stress intensity factor analysis of interface cracks using X-FEM. Int. J. Numer. Methods Eng. 2003, 56, 1151–1173. [Google Scholar] [CrossRef]
- Sukumar, N.; Huang, Z.Y.; Prévost, J.H.; Suo, Z. Partition of unity enrichment for bimaterial interface cracks. Int. J. Numer. Methods Eng. 2004, 59, 1075–1102. [Google Scholar] [CrossRef]
- Cisilino, A.P.; Ortiz, J.E. Three-dimensional boundary element assessment of a fibre/matrix interface crack under transverse loading. Comput. Struct. 2005, 83, 856–869. [Google Scholar] [CrossRef]
- Ortiz, J.E.; Cisilino, A.P. Boundary element method for J-integral and stress intensity factor computations in three-dimensional interface cracks. Int. J. Fract. 2005, 133, 197–222. [Google Scholar] [CrossRef]
- Merzbacher, M.J.; Horst, P. A model for interface cracks in layered orthotropic solids: Convergence of modal decomposition using the interaction integral method. Int. J. Numer. Methods Eng. 2009, 77, 1052–1071. [Google Scholar] [CrossRef]
- Kim, J.H.; Paulino, G.H. T-stress, mixed-mode stress intensity factors, and crack initiation angles in functionally graded materials: A unified approach using the interaction integral method. Comput. Methods Appl. Mech. Eng. 2003, 192, 1463–1494. [Google Scholar] [CrossRef]
- Yildirim, B. An equivalent domain integral method for fracture analysis of functionally graded materials under thermal stresses. J. Therm. Stress 2006, 29, 371–397. [Google Scholar] [CrossRef]
- Duflot, M. The extended finite element method in thermoelastic fracture mechanics. Int. J. Numer. Methods Eng. 2008, 74, 827–847. [Google Scholar] [CrossRef]
- Pathak, H. Crack interaction study in functionally graded materials (FGMs) using XFEM under thermal and mechanical loading environment. Mech. Adv. Mater. Struct. 2020, 27, 903–926. [Google Scholar] [CrossRef]
- Zhu, S.; Yu, H.J.; Zhang, Y.B.; Yan, H.R.; Man, S.H.; Guo, L.C. Generalized dynamic domain-independent interaction integral in the transient fracture investigation of magneto-electro-elastic composites. Eng. Fract. Mech. 2023, 292, 109653. [Google Scholar] [CrossRef]
- Guo, F.N.; Yu, H.J.; Zhang, Y.Y.; Guo, L.C. An interaction energy integral method for an interface crack in nonhomogeneous materials containing complex interfaces under thermal loading. Int. J. Solids Struct. 2023, 264, 112089. [Google Scholar] [CrossRef]
- Yu, H.J.; Wu, L.Z.; Guo, L.C.; Du, S.Y.; He, Q.L. Investigation of mixed-mode stress intensity factors for nonhomogeneous materials using an interaction integral method. Int. J. Solids Struct. 2009, 46, 3710–3724. [Google Scholar] [CrossRef]
- Yu, H.J.; Kuna, M. Interaction integral method for computation of crack parameters K–T–A review. Eng. Fract. Mech. 2021, 249, 107722. [Google Scholar] [CrossRef]
- Williams, M.L. On the stress distribution at the base of a stationary crack. J. Appl. Mech. 1957, 24, 109–114. [Google Scholar] [CrossRef]
- Gupta, M.; Alderliesten, R.C.; Benedictus, R. A review of T-stress and its effects in fracture mechanics. Eng. Fract. Mech. 2015, 134, 218–241. [Google Scholar] [CrossRef]
- Moran, B.; Shih, C.F. Crack tip and associated domain integrals from momentum and energy balance. Eng. Fract. Mech. 1987, 27, 615–642. [Google Scholar] [CrossRef]










| Symbol | Meaning | Unit/Definition |
|---|---|---|
| E | Young’s modulus | MPa |
| Poisson’s ratio | / | |
| u | Actual displacement | / |
| σ | Actual stress | / |
| ε | Actual strain | / |
| r | Radial coordinate | mm |
| θ | Angular coordinate | ° |
| uaux | Auxiliary displacement | / |
| σaux | Auxiliary stress | / |
| εaux | Auxiliary strain | / |
| W | Strain energy density | J/mm3 |
| C | Stiffness matrix | / |
| S | Compliance matrix | / |
| Stip | Compliance matrix at crack tip | / |
| J | J-integral | J/mm2 |
| I | Interaction integral | J/mm2 |
| K | Stress intensity factor | MPa·m1/2 |
| q | Weight function | / |
| μ | Shear modulus | MPa |
| KI | Mode I stress intensity factor | MPa·m1/2 |
| KII | Mode II stress intensity factor | MPa·m1/2 |
| KIII | Mode III stress intensity factor | MPa·m1/2 |
| a/b | Present | Theoretical | ABAQUS | Error A 1 [%] | Error B 2 [%] |
|---|---|---|---|---|---|
| 0.1 | 1.176 | 1.184 | 1.171 | 0.7 | 0.4 |
| 0.2 | 1.362 | 1.373 | 1.360 | 0.8 | 0.1 |
| 0.3 | 1.653 | 1.665 | 1.651 | 0.7 | 0.1 |
| 0.4 | 2.098 | 2.113 | 2.101 | 0.7 | 0.1 |
| 0.5 | 2.821 | 2.843 | 2.823 | 0.8 | 0.1 |
| β [°] | Type | Present | Theoretical | ABAQUS | Error A 1 [%] | Error B 2 [%] |
|---|---|---|---|---|---|---|
| 22.5 | KI/K0 | 0.745 | 0.735 | 0.745 | 1.4 | 0 |
| KII/K0 | 0.279 | 0.272 | 0.280 | 2.6 | 0.4 | |
| 45 | KI/K0 | 0.438 | 0.438 | 0.438 | 0 | 0 |
| KII/K0 | 0.406 | 0.396 | 0.405 | 2.5 | 0.2 | |
| 67.5 | KI/K0 | 0.127 | 0.124 | 0.127 | 2.4 | 0 |
| KII/K0 | 0.287 | 0.286 | 0.286 | 0.3 | 0.3 | |
| 75 | KI/K0 | 0.058 | 0.057 | 0.058 | 1.8 | 0 |
| KII/K0 | 0.202 | 0.206 | 0.202 | 1.9 | 0 |
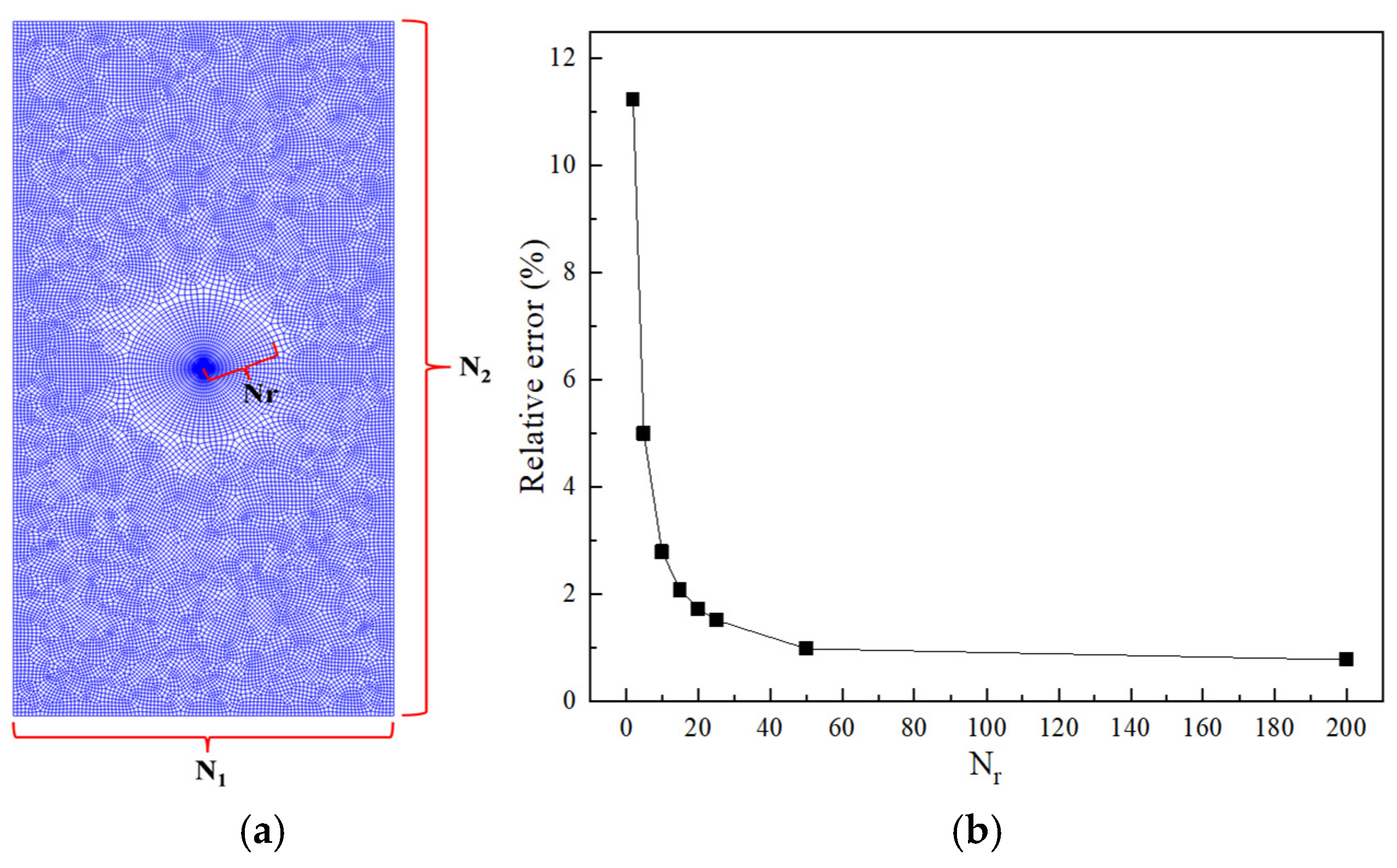
| N1 × N2 | 8 × 16 | 10 × 20 | 34 × 66 | 100 × 200 | 166 × 334 |
|---|---|---|---|---|---|
| KI/K0 | 2.797 | 2.801 | 2.819 | 2.820 | 2.821 |
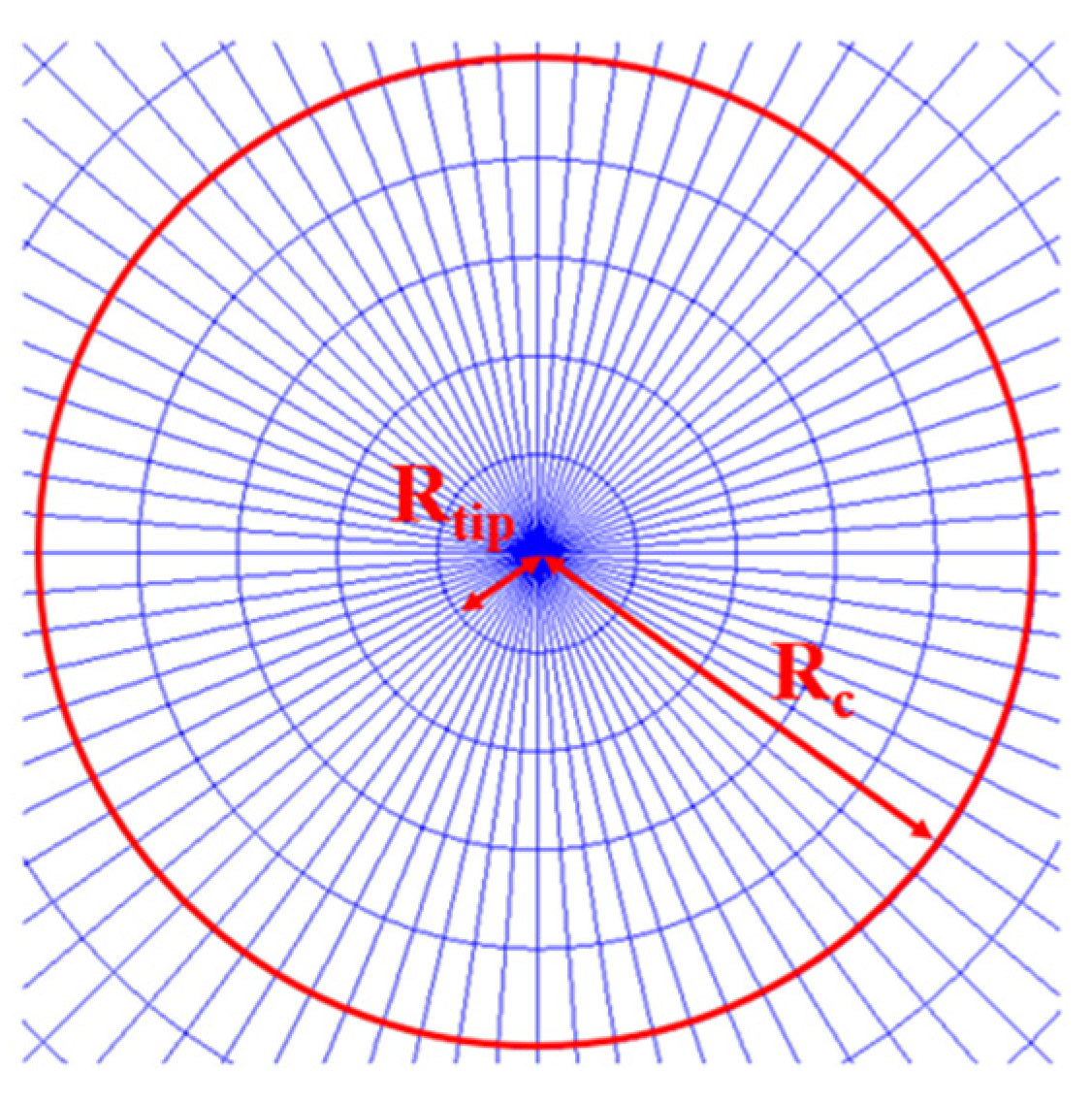
| Rc/Rtip | 5 | 8 | 10 | 15 | 20 |
|---|---|---|---|---|---|
| KI/K0 | 2.818 | 2.820 | 2.820 | 2.821 | 2.820 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, F.; Li, Y.; Chen, Y.; Liu, P.; Wang, X. Investigation of the Stress Intensity Factor in Heterogeneous Materials Based on the Postprocessing Routine of Commercial Finite Element Software. Appl. Sci. 2025, 15, 5827. https://doi.org/10.3390/app15115827
Guo F, Li Y, Chen Y, Liu P, Wang X. Investigation of the Stress Intensity Factor in Heterogeneous Materials Based on the Postprocessing Routine of Commercial Finite Element Software. Applied Sciences. 2025; 15(11):5827. https://doi.org/10.3390/app15115827
Chicago/Turabian StyleGuo, Fengnan, Yiming Li, Yufu Chen, Pengfei Liu, and Xiaodong Wang. 2025. "Investigation of the Stress Intensity Factor in Heterogeneous Materials Based on the Postprocessing Routine of Commercial Finite Element Software" Applied Sciences 15, no. 11: 5827. https://doi.org/10.3390/app15115827
APA StyleGuo, F., Li, Y., Chen, Y., Liu, P., & Wang, X. (2025). Investigation of the Stress Intensity Factor in Heterogeneous Materials Based on the Postprocessing Routine of Commercial Finite Element Software. Applied Sciences, 15(11), 5827. https://doi.org/10.3390/app15115827






