Conditions for Guaranteeing Non-Overshooting Control of Nonlinear Systems with Full-State Constraints
Abstract
1. Introduction
- (1)
- Compared with the BLF [11], this paper uses the mapping constraint function, which is a direct constraint method, thus reducing the calculation burden of constraint parameters.
- (2)
- (3)
- (4)
- The most difficult problem that arises when designing the algorithm in this paper relates to obtaining a CLS that can solve the expression of tracking error. To obtain a CLS that can easily calculate the expression of tracking error, this paper needs to convert the situation in which each subsystem is nonlinear into a system that only contains the n-th subsystem as nonlinear (such as (25)). Otherwise, it is difficult to calculate the expression of tracking error for the obtained CLS. Then, this algorithm provides a method to transform the controlled system into a system that is simpler to deal with. Compared with the existing control results with NOTC, this algorithm is simpler.
2. Problem Formulation
- (1)
- All signals of the CLS are bounded, and the tracking error satisfies ;
- (2)
- The tracking error satisfies the condition of NOTC; that is, always keeps or ;
- (3)
- The constraint property of the BLFs is not violated; that is, the system state () satisfies the following constraintswhere and are constraint parameters.
3. Full-State Constraints Control and Control Design
4. Non-Overshooting Tracking Control
- (1)
- The situation when .
- (2)
- The situation when .
- (1)
- If , then NOTC can satisfy (41) or (42);
- (2)
- If , then NOTC can satisfy (46) or (47).
- (3)
- The situation when .
- (1)
- If , NOTC conditions need to satisfy one of the conditions (51)–(64);
- (2)
- If , NOTC conditions need to satisfy one of the conditions (66)–(73);
- (3)
- If , NOTC conditions need to satisfy one of the conditions (76)–(83);
- (4)
- If , NOTC conditions need to satisfy one of the conditions (85)–(92);
- (5)
- If , NOTC conditions need to satisfy one of the conditions (94)–(97).
- (4)
- The situation when .
- (1)
- If , the NOTC condition needs to satisfy the condition (104);
- (2)
- If , the NOTC condition needs to satisfy the condition (112).
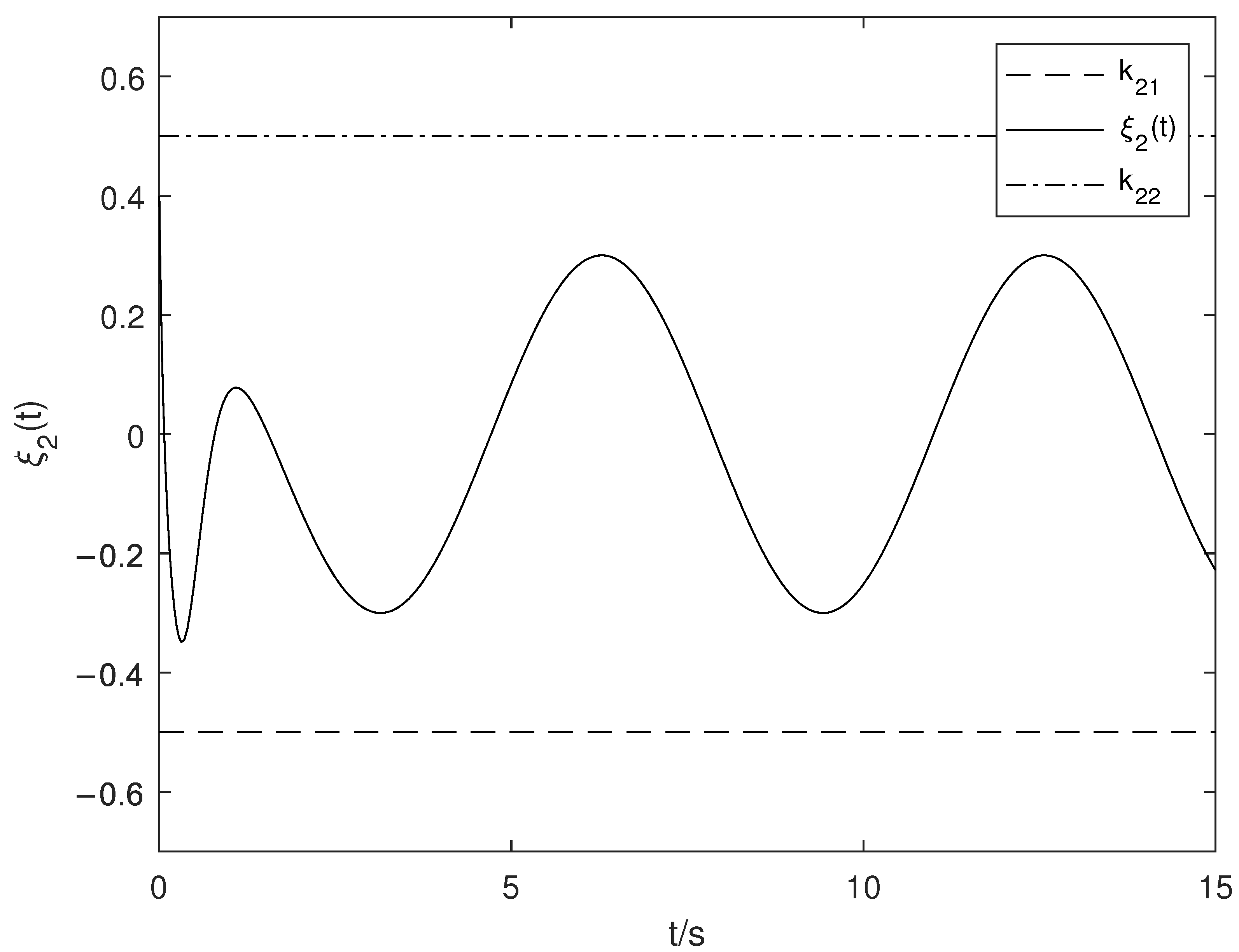
5. Simulation Example
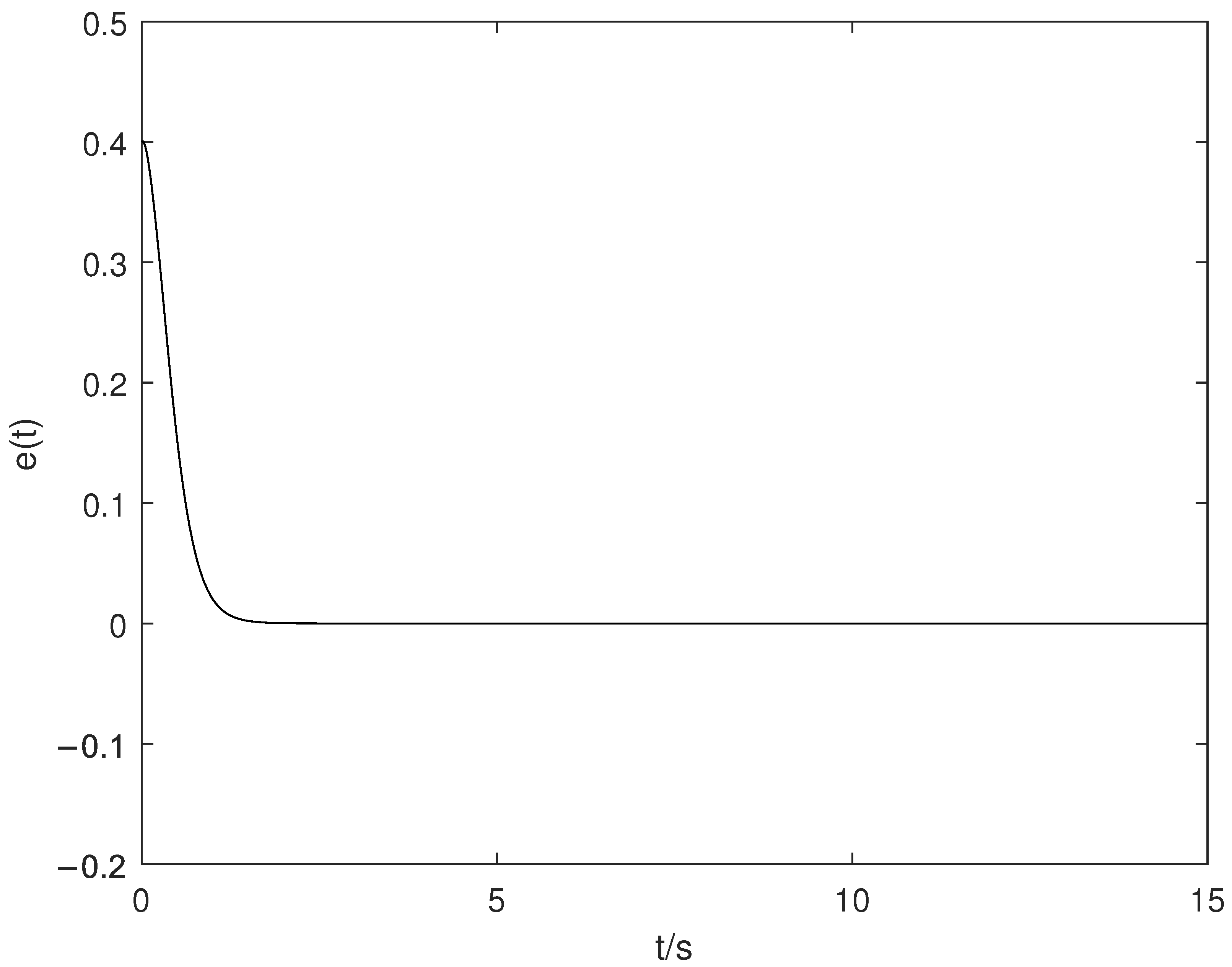
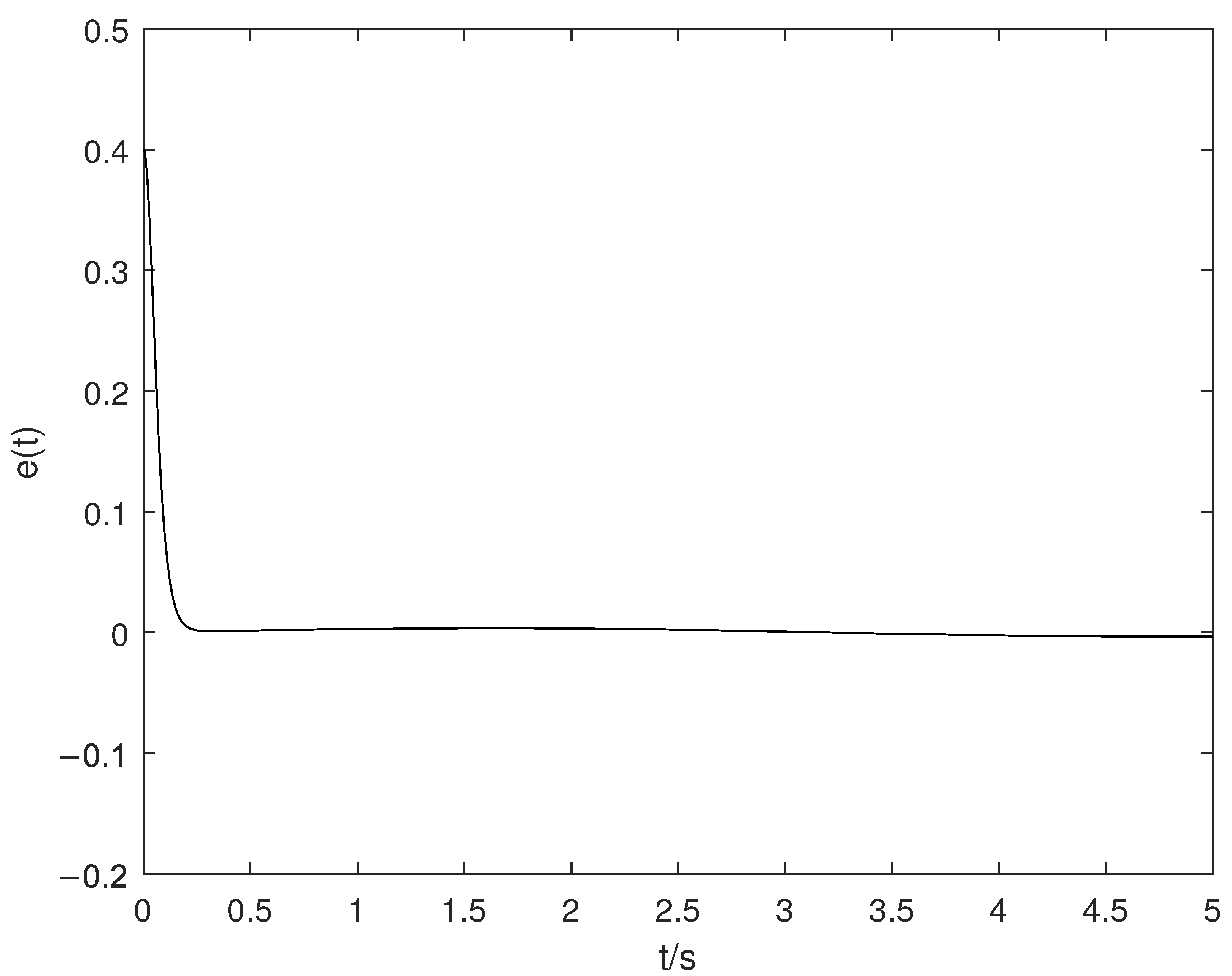
- (1)
- Figure 1 shows that the tracking error is non-overshoot, which shows that the non-overshoot algorithm in this paper is effective.
- (2)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NOTC | Non-Overshooting Tracking Control |
| FSCs | Full-State Constraints |
| CLS | Closed-Loop System |
| BLF | Barrier Lyapunov Function |
References
- Campbell, D.K. Nonlinear Science. In Los Alamos Science; University of Minnesota: Minneapolis, MN, USA, 1987. [Google Scholar]
- Cui, G.Z.; Xu, S.Y.; Ma, Q.; Li, Y.M.; Zhang, Z.Q. Prescribed performance distributed consensus control for nonlinear multi-agent systems with unknown dead-zone input. Int. J. Control 2018, 91, 1053–1065. [Google Scholar] [CrossRef]
- Zhang, T.L.; Su, S.F.; Wei, W.; Yeh, R.H. Practically Predefined-Time Adaptive Fuzzy Tracking Control for Nonlinear Stochastic Systems. IEEE Trans. Cybern. 2023, 53, 8000–8012. [Google Scholar] [CrossRef]
- Zhao, K.; Song, Y.D.; Ma, T.D.; He, L. Prescribed Performance Control of Uncertain Euler-Lagrange Systems Subject to Full-State Constraints. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3478–3489. [Google Scholar] [PubMed]
- Shi, S.; Gu, J.; Xu, S.Y.; Min, H.F. Globally Fixed-Time High-Order Sliding Mode Control for New Sliding Mode Systems Subject to Mismatched Terms and Its Application. IEEE Trans. Ind. Electron. 2020, 67, 10776–10786. [Google Scholar] [CrossRef]
- Wang, L.; Sun, W.; Su, S.F.; Zhao, X.D. Adaptive Asymptotic Tracking Control for Flexible-Joint Robots With Prescribed Performance: Design and Experiments. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 3707–3717. [Google Scholar] [CrossRef]
- Tang, F.H.; Niu, B.; Wang, H.Q.; Zhang, L.; Zhao, X.D. Adaptive Fuzzy Tracking Control of Switched MIMO Nonlinear Systems With Full State Constraints and Unknown Control Directions. IEEE Trans. Circ. Syst. II-Express Briefs 2022, 69, 2912–2916. [Google Scholar] [CrossRef]
- Tran, T.T. Feedback linearization and backstepping: An equivalence in control design of strict-feedback form. IMA J. Math. Control Inf. 2020, 37, 1049–1069. [Google Scholar] [CrossRef]
- Min, H.F.; Xu, S.Y.; Zhang, B.Y.; Ma, Q.; Yuan, D.M. Fixed-Time Lyapunov Criteria and State-Feedback Controller Design for Stochastic Nonlinear Systems. IEEE-CAA J. Autom. Sin. 2022, 9, 1005–1014. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S.K. Sliding Mode Control: Theory and Applications; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Liu, S.L.; Niu, B.; Zong, G.D.; Zhao, X.D.; Xu, N. Adaptive Neural Dynamic-Memory Event-Triggered Control of High-Order Random Nonlinear Systems with Deferred Output Constraints. IEEE Trans. Autom. Sci. Eng. 2018, 21, 923–933. [Google Scholar] [CrossRef]
- Jia, F.J.; Lu, J.W.; Li, Y.M. Neural network adaptive output regulation for non-linear uncertain systems with full-state constraints. IMA J. Math. Control Inf. 2021, 38, 992–1009. [Google Scholar] [CrossRef]
- Liu, Y.J.; Tong, S.C. Barrier Lyapunov Functions-based adaptive control for a class of nonlinear pure-feedback systems with full state constraints. Automatica 2016, 64, 70–75. [Google Scholar] [CrossRef]
- Jia, F.J.; Yan, X.; Wang, X.H.; Lu, J.W.; Li, Y.M. Robust adaptive prescribed performance dynamic surface control for uncertain nonlinear pure-feedback systems. J. Frankl. Inst. 2020, 357, 2752–2772. [Google Scholar] [CrossRef]
- Liang, X.L.; Ge, S.S.; Li, D.Y. Coordinated tracking control of multi agent systems with full-state constraints. J. Frankl. Inst. 2023, 360, 12030–12054. [Google Scholar] [CrossRef]
- Niu, B.; Zhang, Y.; Zhao, X.D.; Wang, H.Q.; Sun, W. Adaptive Predefined-Time Bipartite Consensus Tracking Control of Constrained Nonlinear MASs: An Improved Nonlinear Mapping Function Method. IEEE Trans. Cybern. 2023, 53, 6017–6026. [Google Scholar] [CrossRef]
- Ortiz, D.C.; Chairez, I.; Poznyak, A. Sliding-Mode Control of Full-State Constraint Nonlinear Systems: A Barrier Lyapunov Function Approach. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 6593–6606. [Google Scholar] [CrossRef]
- Zhang, T.P.; Xia, M.Z.; Yi, Y. Adaptive neural dynamic surface control of strict-feedback nonlinear systems with full state constraints and unmodeled dynamics. Automatica 2017, 81, 232–239. [Google Scholar] [CrossRef]
- Krstic, M.; Bement, M. Nonovershooting control of strict-feedback nonlinear systems. IEEE Trans. Autom. Control 2006, 51, 1938–1943. [Google Scholar] [CrossRef]
- Zhan, J.Z.; Liu, Y.L. The design of a sinter furnace hearting control system for quick temperature rise without overshooting. Ind. Instrum. Autom. 2006, 3, 64–65. [Google Scholar]
- Darbha, S.; Bhattacharyya, S.P. On the synthesis of controllers for a non-overshooting step response. IEEE Trans. Autom. Control 2003, 48, 797–799. [Google Scholar] [CrossRef]
- Bement, M.; Jayasuriysa, S. Construction of a set of non-overshooting tracking controllers. J. Dyn. Syst. Meas. Control 2004, 126, 558–567. [Google Scholar] [CrossRef]
- Bement, M.; Jayasuriysa, S. Use of state feedback to achieve a non-overshooting step response for a class of non-minimum phase systems. J. Dyn. Syst. Meas. Control 2004, 126, 657–660. [Google Scholar] [CrossRef]
- Lin, S.K.; Fang, C.J. Nonovershooting and monotone nondecreasing step responses of a third-order SISO linear system. IEEE Trans. Autom. Control 1997, 42, 1299–1303. [Google Scholar]
- Darbha, S. On the synthesis of controllers for continuous time LTI systems that achieve a non-negative impulse response. Automatica 2003, 39, 159–165. [Google Scholar] [CrossRef]
- Chen, X.P.; Xu, H.B. Non-overshooting control for a class of nonlinear systems. Control Decis. 2013, 28, 627–631. [Google Scholar]
- Zhu, C.; Zhao, C.C. Non-overshooting output tracking of feedback linearisable nonlinear systems. Int. J. Control 2013, 86, 821–832. [Google Scholar] [CrossRef]
- Jia, F.J. Non-overshooting control of nonlinear pure-feedback systems. Syst. Control Lett. 2025, 185, 105743. [Google Scholar] [CrossRef]
- Jia, F.J. Non-overshooting tracking control for nonlinear systems with prescribed finite-time. ISA Trans. 2024, 151, 174–182. [Google Scholar] [CrossRef] [PubMed]
- Jia, F.J.; Zhu, Q.X. Non-Overshooting Tracking Control for Nonlinear Pure-Feedback Systems. IEEE Trans. Syst. Man Cybern. Syst. 2025, 55, 1277–1285. [Google Scholar] [CrossRef]
- Hazem, Z.B.; Guler, N.; Altaif, A.H. A study of advanced mathematical modeling and adaptive control strategies for trajectory tracking in the Mitsubishi RV-2AJ 5-DOF Robotic Arm. Discov. Robot. 2025, 1, 2. [Google Scholar] [CrossRef]
- Li, W.Q.; Krstic, M. Mean-nonovershooting control of stochastic nonlinear systems. IEEE Trans. Autom. Control 2021, 66, 5756–5771. [Google Scholar] [CrossRef]
- Song, L.; Tong, S.C. Finite-time mean-nonovershooting control for stochastic nonlinear systems. Int. J. Syst. Sci. 2023, 54, 1047–1055. [Google Scholar] [CrossRef]
- Tee, K.P.; Ge, S.Z. Control of nonlinear systems with partial state constraints using a barrier Lyapunov function. In. J. Control 2011, 84, 2008–2023. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z.Q.; Liu, Z.X.; Zhang, X.H. Distributed robust consensus control for nonlinear multiagent systems by using output regulation approach. IMA J. Math. Control Inf. 2014, 32, 515–535. [Google Scholar] [CrossRef]
- Jia, F.J.; Lu, J.W.; Li, Y.M.; Li, F.Y. Fuzzy adaptive stabilization control for nonlinear systems with FSCs. Fuzzy Sets Syst. 2024, 473, 108738. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, X.-Q.; Zhang, C. Conditions for Guaranteeing Non-Overshooting Control of Nonlinear Systems with Full-State Constraints. Appl. Sci. 2025, 15, 5816. https://doi.org/10.3390/app15115816
Xiang X-Q, Zhang C. Conditions for Guaranteeing Non-Overshooting Control of Nonlinear Systems with Full-State Constraints. Applied Sciences. 2025; 15(11):5816. https://doi.org/10.3390/app15115816
Chicago/Turabian StyleXiang, Xiang-Qin, and Chi Zhang. 2025. "Conditions for Guaranteeing Non-Overshooting Control of Nonlinear Systems with Full-State Constraints" Applied Sciences 15, no. 11: 5816. https://doi.org/10.3390/app15115816
APA StyleXiang, X.-Q., & Zhang, C. (2025). Conditions for Guaranteeing Non-Overshooting Control of Nonlinear Systems with Full-State Constraints. Applied Sciences, 15(11), 5816. https://doi.org/10.3390/app15115816




