Methodology for Feature Selection of Time Domain Vibration Signals for Assessing the Failure Severity Levels in Gearboxes
Abstract
1. Introduction
- 1.
- The design of a structured methodology for selecting relevant time-domain condition indicators from vibration signals.
- 2.
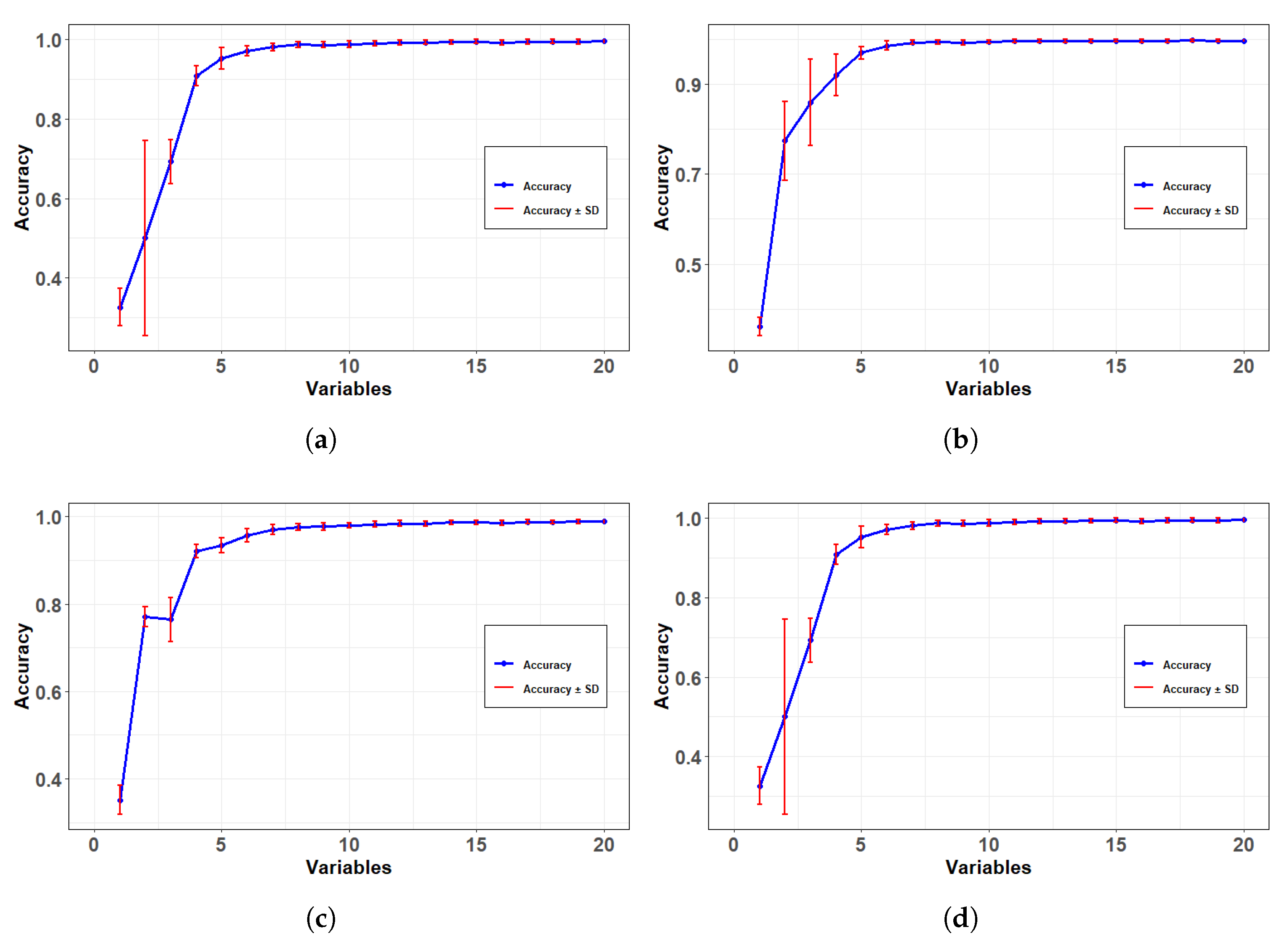
- The validation of this selection using two widely adopted classifiers in the literature (Random Forest and K-nearest neighbours)
- 3.
- The experimental evaluation of the effect of sensor position and inclination on fault classification performance in gear systems.
2. Materials and Methods
2.1. Experimental Bench
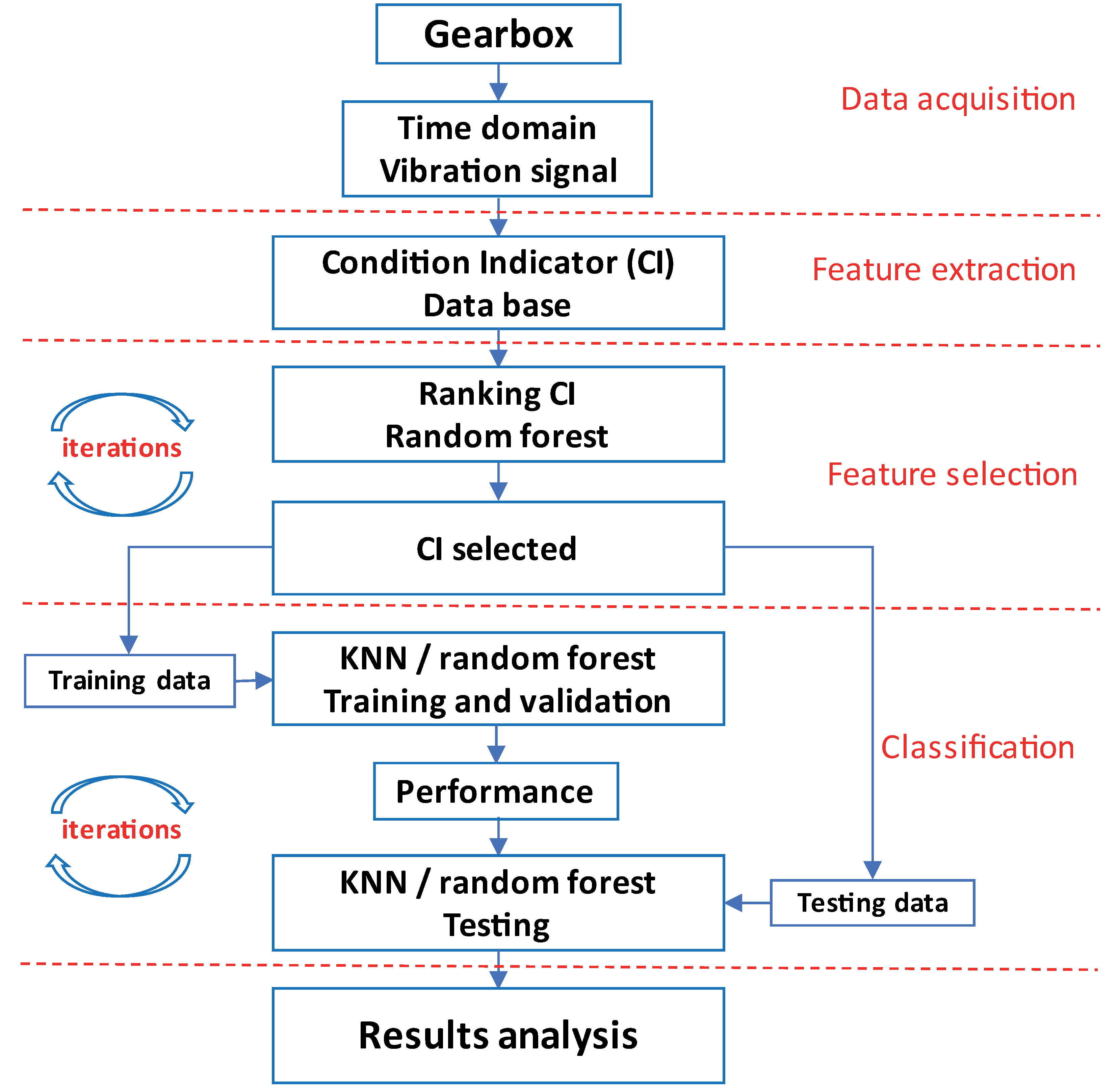
2.2. Methodology
2.2.1. Data Acquisition
2.2.2. Feature Extraction
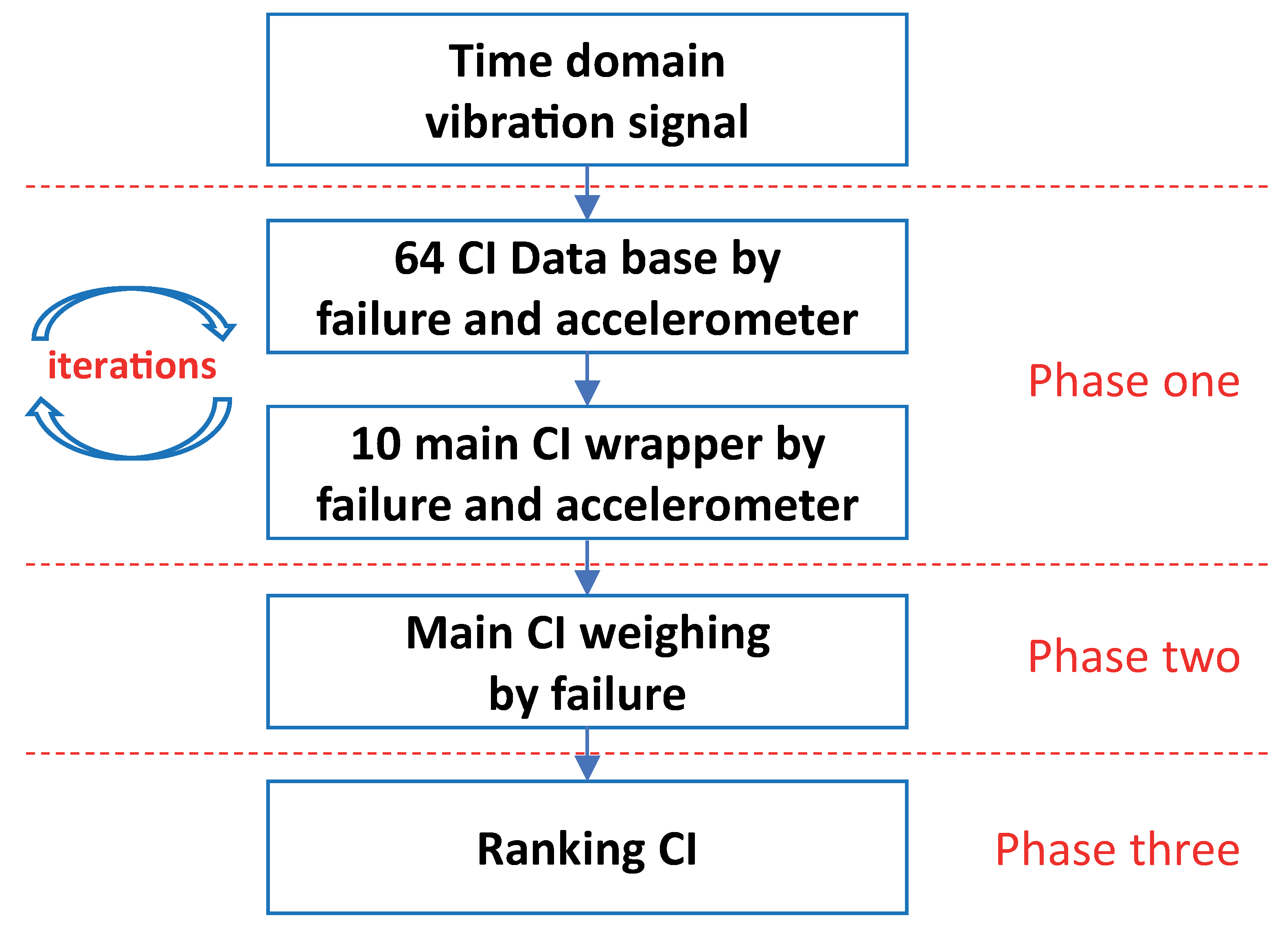
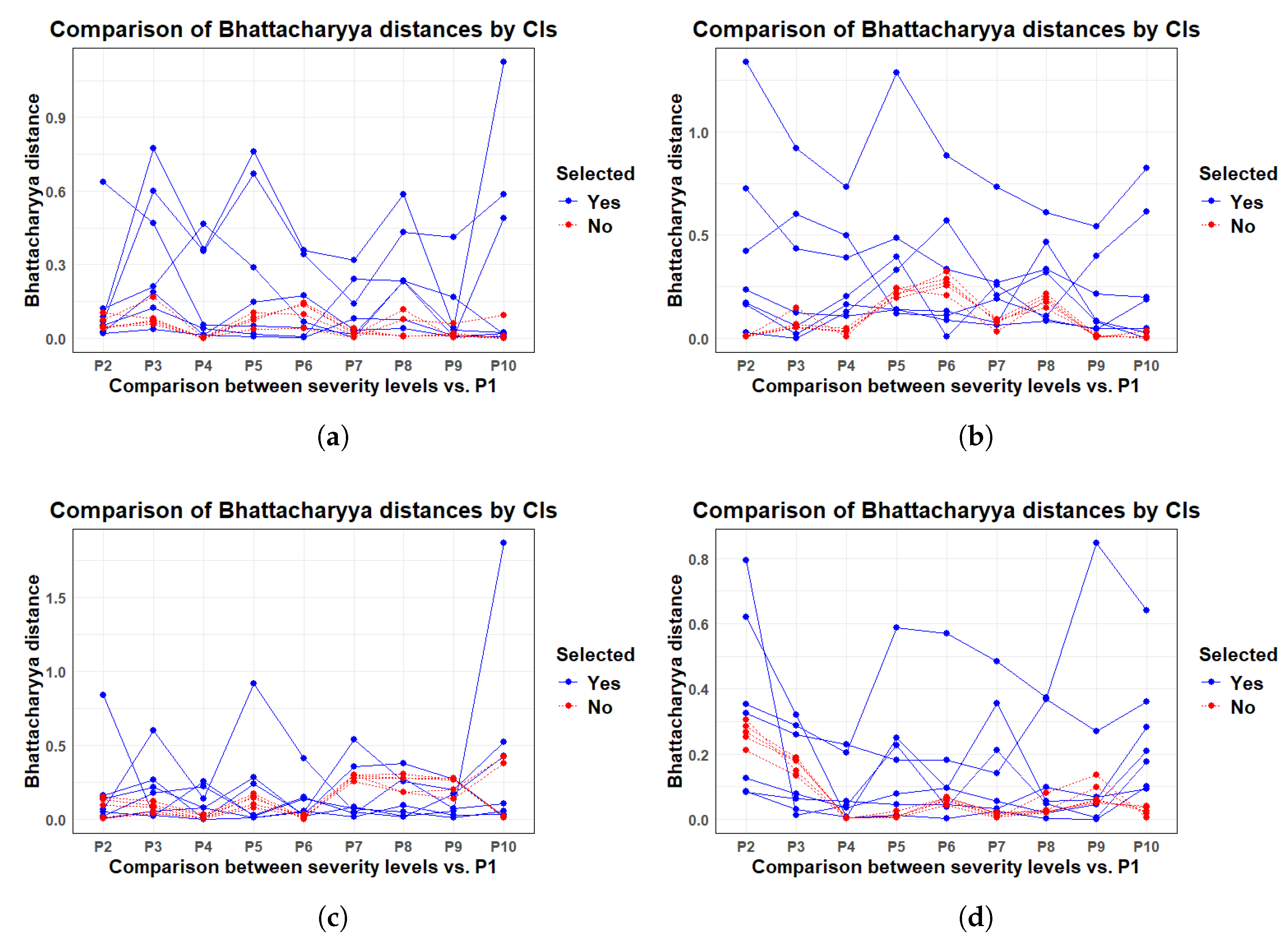
2.2.3. Feature Selection
- Phase 1:
- Phase 2:
- Phase 3:
2.2.4. Classification Models
- Random forest (RF): RF is a classification model represented by Equation (1), composed of multiple tree-based classifiers. For each ith tree, an independent random vector is generated. Each tree is trained on a subset of the data and votes for the most popular category in the input vector . The classification error, described by Equation (2), depends on the margin , which measures the average number of votes received for the correct class, and on the probability distribution in the feature-label space [30].
- k-nearest neighbours (K-NN): K-NN is a non-parametric algorithm used for classification tasks in which new instances are categorised based on their proximity to existing samples within the feature space. The method assigns weights according to distance and infers the class of an unknown observation through a majority voting mechanism [31]. K-NN requires only the selection of the parameter k to define the number of neighbours and the appropriate distance metric [32].The K-NN classification algorithm works as follows:Given a training set , where is a training vector and its class label, and a test instance , the predicted class is determined using Equation (3):Here, is a candidate class label, is the label of the ith nearest neighbour, is the indicator function returning 1 if the labels match and 0 otherwise, and , as defined in Equation (4), represents a weighting coefficient derived from the distance between the query instance and its ith nearest neighbour.The default distance metric is Euclidean, although alternatives such as Mahalanobis, Manhattan, and Minkowski distances can also be used [33].
2.2.5. Analysis of the Effect of Sensor Position and Inclination on the Vibration Signal
2.2.6. Computational Tools
3. Results and Discussion
4. Conclusions
5. Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CIs | Condition indicators |
| RF | Random forest |
| K-NN | K-nearest neighbors |
| AUC | Area under the curve |
| ROC | Receiver operating characteristic |
| ANOVA | Analysis of variance |
| CBM | Condition-based monitoring |
| FFT | Fast Fourier transform |
| DB | Database |
| TMHO | Temporal moment higher order |
| SSC | Slope sign change |
Appendix A
| N. | Condition Indicator | Formula |
|---|---|---|
| 1 | Mean | |
| 2 | Variance | |
| 3 | Standar desviation | |
| 4 | Root mean square (RMS) | |
| 5 | Max value | |
| 6 | Kurtosis | |
| 7 | Skewness | |
| 8 | Energy operator | |
| 9 | Absolute mean | |
| 10 | CPT1 | |
| 11 | CPT2 | |
| 12 | CPT3 | |
| 13 | Fifth statistic moment | |
| 14 | Shape factor | |
| 15 | Impulse factor | |
| 16 | Clearance factor | |
| 17 | Delta RMS | |
| 18 | Root sum of squares | |
| 19 | Energy | |
| 20 | Latitude factor | |
| 21 | Weighted SSR absolute | |
| 22 | Mean square error | |
| 23 | Normalized normal negative likelihoog | |
| 24 | Mean deviation | |
| 25 | Standard deviation impulse factor | |
| 26 | Log-Log ratio | |
| 27 | Kth central moment | Where E(x) is the expected value of x. K is set to 3 |
| 28 | Histogram lower bound | |
| 29 | Histogram upper bound | |
| 30 | Normalized moment | |
| 31 | Shannon entropy | |
| 32 | Log energy entropy | where, log(0)=0 |
| 33 | Threshold entropy | p is set to 0.2 |
| 34 | Sure entropy | such that p is set to 0.2 |
| 35 | Norm entropy | p is set to 0.2 |
| 36 | Peak to peak | |
| 37 | Minimum value | |
| 38 | Peak value | |
| 39 | 6th statistical moment | |
| 40 | Crest factor | |
| 41 | Integrated signal | |
| 42 | Square root amplitude value | |
| 43 | Zero crossing | |
| 44 | Wavelength | |
| 45 | Wilson amplitude | T = threshold set to 0.2 |
| 46 | Slope sign change | |
| 47 | Log detector | |
| 48 | Modified mean absolute value 1 | |
| 49 | Modified mean absolute value 2 | |
| 50 | Mean absolute value slope | |
| 51 | Mean of amplitude | |
| 52 | Log RMS | |
| 53 | Conduction velocity of signal | |
| 54 | Average amplitude change (AAC) | |
| 55 | V-Order 3 | |
| 56 | Maximum fractal length | |
| 57 | Difference absolute standard deviation | |
| 58 | Myopulse percentage rate | the threshold is set to 0.2 |
| 59 | Temporal moments higher order | Where m is set to 3 as default |
| 60 | Difference absolute variance value | |
| 61 | Margin index | |
| 62 | Waveform indicators | |
| 63 | Weibull negative log-likelihood | Where is the scale factor and SF the shape factor |
| 64 | Pulse indicators |
References
- Dong, E.; Zhang, E.; Zhan, X.; Cheng, Z. A novel dynamic predictive maintenance framework for gearboxes utilizing 341 nonlinear Wiener process. Meas. Sci. Technol. 2024, 35, 126210. [Google Scholar] [CrossRef]
- Goswami, P.; Rai, R.N. A systematic review on failure modes and proposed methodology to artificially seed faults for promoting PHM studies in laboratory environment for an industrial gearbox. Eng. Fail. Anal. 2023, 146, 107076. [Google Scholar] [CrossRef]
- Cerrada, M.; Zurita, G.; Cabrera, D.; Sánchez, R.V.; Artés, M.; Li, C. Fault diagnosis in spur gears based on genetic algorithm and random forest. Mech. Syst. Signal Process. 2016, 70, 87–103. [Google Scholar] [CrossRef]
- Pérez-Torres, A.; Sánchez, R.V.; Barceló-Cerdá, S. Selection of the level of vibration signal decomposition and mother wavelets to determine the level of failure severity in spur gearboxes. Qual. Reliab. Eng. Int. 2024, 40, 3439–3451. [Google Scholar] [CrossRef]
- Sendlbeck, S.; Fimpel, A.; Siewerin, B.; Otto, M.; Stahl, K. Condition monitoring of slow-speed gear wear using a transmission error-based approach with automated feature selection. Int. J. Progn. Health Manag. 2021, 12. [Google Scholar] [CrossRef]
- Seo, M.K.; Yun, W.Y. Gearbox Condition Monitoring and Diagnosis of Unlabeled Vibration Signals Using a Supervised Learning Classifier. Machines 2024, 12, 127. [Google Scholar] [CrossRef]
- Sharma, V.; Parey, A. A review of gear fault diagnosis using various condition indicators. Procedia Eng. 2016, 144, 253–263. [Google Scholar] [CrossRef]
- Hızarcı, B.; Ümütlü, R.C.; Kıral, Z.; Öztürk, H. Fault severity detection of a worm gearbox based on several feature extraction methods through a developed condition monitoring system. SN Appl. Sci. 2021, 3, 129. [Google Scholar] [CrossRef]
- Salameh, J.P.; Cauet, S.; Etien, E.; Sakout, A.; Rambault, L. Gearbox condition monitoring in wind turbines: A review. Mech. Syst. Signal Process. 2018, 111, 251–264. [Google Scholar] [CrossRef]
- Sanchez, R.V.; Lucero, P.; Vásquez, R.E.; Cerrada, M.; Macancela, J.C.; Cabrera, D. Feature ranking for multi-fault diagnosis of rotating machinery by using random forest and KNN. J. Intell. Fuzzy Syst. 2018, 34, 3463–3473. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.; Xin, Y.; An, Z. Gear fault intelligent diagnosis based on frequency-domain feature extraction. J. Vib. Eng. Technol. 2019, 7, 159–166. [Google Scholar] [CrossRef]
- Vakharia, V.; Gupta, V.K.; Kankar, P.K. A comparison of feature ranking techniques for fault diagnosis of ball bearing. Soft Comput. 2016, 20, 1601–1619. [Google Scholar] [CrossRef]
- Nayana, B.; Geethanjali, P. Analysis of statistical time-domain features effectiveness in identification of bearing faults from vibration signal. IEEE Sens. J. 2017, 17, 5618–5625. [Google Scholar] [CrossRef]
- Lei, Y.; Zuo, M.J. Gear crack level identification based on weighted K nearest neighbor classification algorithm. Mech. Syst. Signal Process. 2009, 23, 1535–1547. [Google Scholar] [CrossRef]
- Patel, D.; Saxena, A.; Wang, J. A Machine Learning-Based Wrapper Method for Feature Selection. Int. J. Data Warehous. Min. (IJDWM) 2024, 20, 1–33. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, X.; Zuo, M.J.; Xu, H. Feature selection for fault level diagnosis of planetary gearboxes. Adv. Data Anal. Classif. 2014, 8, 377–401. [Google Scholar] [CrossRef]
- Maseno, E.M.; Wang, Z. Hybrid wrapper feature selection method based on genetic algorithm and extreme learning machine for intrusion detection. J. Big Data 2024, 11, 24. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar] [CrossRef]
- Raschka, S. Model evaluation, model selection, and algorithm selection in machine learning. arXiv 2018, arXiv:1811.12808. [Google Scholar] [CrossRef]
- Caesarendra, W.; Widodo, A.; Yang, B.S. Combination of probability approach and support vector machine towards machine health prognostics. Probabilistic Eng. Mech. 2011, 26, 165–173. [Google Scholar] [CrossRef]
- Shandhoosh, V.; Venkatesh S, N.; Chakrapani, G.; Sugumaran, V.; Ramteke, S.M.; Marian, M. Intelligent fault diagnosis for tribo-mechanical systems by machine learning: Multi-feature extraction and ensemble voting methods. Knowl.-Based Syst. 2024, 305, 112694. [Google Scholar] [CrossRef]
- Guo, K.; Wan, X.; Liu, L.; Gao, Z.; Yang, M. Fault diagnosis of intelligent production line based on digital twin and improved random forest. Appl. Sci. 2021, 11, 7733. [Google Scholar] [CrossRef]
- Pichika, S.N.; Yadav, R.; Rajasekharan, S.G.; Praveen, H.M.; Inturi, V. Optimal sensor placement for identifying multi-component failures in a wind turbine gearbox using integrated condition monitoring scheme. Appl. Acoust. 2022, 187, 108505. [Google Scholar] [CrossRef]
- Vanraj; Dhami, S.; Pabla, B. Optimization of sound sensor placement for condition monitoring of fixed-axis gearbox. Cogent Eng. 2017, 4, 1345673. [Google Scholar] [CrossRef]
- Islam, M.S.; Kim, K.; Kim, H.Y. Data-Driven Approach for Fault Diagnosis of Harmonic Drives Using Wireless Acceleration Sensors and Machine Learning. Int. J. Precis. Eng. Manuf.-Green Technol. 2025, 12, 951–968. [Google Scholar] [CrossRef]
- Asutkar, S.; Tallur, S. An explainable unsupervised learning framework for scalable machine fault detection in Industry 4.0. Meas. Sci. Technol. 2023, 34, 105123. [Google Scholar] [CrossRef]
- Rigas, S.; Papachristou, M.; Sotiropoulos, I.; Alexandridis, G. Explainable Fault Classification and Severity Diagnosis in Rotating Machinery Using Kolmogorov–Arnold Networks. Entropy 2025, 27, 403. [Google Scholar] [CrossRef]
- Palaniappan, R. Comparative analysis of support vector machine, random forest and k-nearest neighbor classifiers for predicting remaining usage life of roller bearings. Informatica 2024, 48, 39–52. [Google Scholar] [CrossRef]
- Du, P.; Abdel Jabbar, N.M.; Wilhite, B.A.; Kravaris, C. Fault Diagnosis in Chemical Reactors with Data-Driven Methods. Ind. Eng. Chem. Res. 2025, 64, 6060–6076. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Dudani, S.A. The Distance-Weighted k-Nearest-Neighbor Rule. IEEE Trans. Syst. Man Cybern. 1976, SMC-6, 325–327. [Google Scholar] [CrossRef]
- Yu, Z.; Chen, H.; Liu, J.; You, J.; Leung, H.; Han, G. Hybrid k-Nearest Neighbor Classifier. IEEE Trans. Cybern. 2016, 46, 1263–1275. [Google Scholar] [CrossRef] [PubMed]
- Prasath, V.; Alfeilat, H.A.A.; Hassanat, A.; Lasassmeh, O.; Tarawneh, A.S.; Alhasanat, M.B.; Salman, H.S.E. Distance and Similarity Measures Effect on the Performance of K-Nearest Neighbor Classifier—A Review. arXiv 2017, arXiv:1708.04321. [Google Scholar] [CrossRef]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024. [Google Scholar]
- Choi, E.; Lee, C. Feature extraction based on the Bhattacharyya distance. Pattern Recognit. 2003, 36, 1703–1709. [Google Scholar] [CrossRef]
- Rencher, A.C. Multivariate Statistical Inference and Applications; Wiley: New York, NY, USA, 1998; Volume 635. [Google Scholar]
- Patel, R.K.; Giri, V. Feature selection and classification of mechanical fault of an induction motor using random forest classifier. Perspect. Sci. 2016, 8, 334–337. [Google Scholar] [CrossRef]




| Failure | A1 | A2 | A3 | Weighing | |||
|---|---|---|---|---|---|---|---|
| Variable (CI) | MI | Variable (CI) | MI | Variable (CI) | MI | Value | |
| Breaking | TMHO | 11.88 | Mean | 10.75 | Zero crossing | 11.74 | 10 |
| Mean | 11.83 | TMHO | 10.70 | Energy operator | 11.18 | 9 | |
| Zero crossing | 11.17 | Zero crossing | 10.53 | Mean | 11.06 | 8 | |
| Shape factor | 9.78 | Energy operator | 10.48 | TMHO | 11.01 | 7 | |
| SDIF | 9.67 | Kurtosis | 9.31 | SSC | 10.94 | 6 | |
| SSC | 8.80 | Latitud factor | 9.11 | Crest factor | 9.14 | 5 | |
| Skewness | 8.73 | Waveform | 8.63 | Impulse factor | 8.93 | 4 | |
| Energy operator | 8.51 | SSC | 8.61 | Latitud factor | 8.89 | 3 | |
| Margin index | 8.43 | Log-Log ratio | 8.61 | Kurtosis | 8.32 | 2 | |
| Log-Log ratio | 8.28 | Crest factor | 8.59 | Skewness | 8.17 | 1 | |
| Crack | Skewness | 11.29 | SSC | 10.14 | Skewness | 12.55 | 10 |
| Mean | 10.06 | Clearance factor | 10.10 | SSC | 11.62 | 9 | |
| TMHO | 10.05 | Skewness | 9.88 | Zero crossing | 11.25 | 8 | |
| Energy operator | 9.98 | TMHO | 8.98 | Energy operator | 9.20 | 7 | |
| SSC | 9.38 | Mean | 8.95 | FSM | 9.14 | 6 | |
| SDIF | 9.03 | FSM | 8.93 | Mean | 8.82 | 5 | |
| Kurtosis | 8.95 | Zero crossing | 8.71 | TMHO | 8.81 | 4 | |
| Shape factor | 8.93 | Kurtosis | 8.32 | Latitud factor | 7.76 | 3 | |
| FSM | 8.89 | NNNL | 8.30 | Clearance factor | 7.32 | 2 | |
| Zero crossing | 8.55 | Energy operator | 7.84 | Kurtosis | 7.24 | 1 | |
| Pitting | Skewness | 12.58 | Energy operator | 10.06 | SSC | 12.49 | 10 |
| TMHO | 11.37 | SSC | 9.99 | Mean | 10.73 | 9 | |
| Mean | 11.25 | TMHO | 9.60 | TMHO | 10.70 | 8 | |
| SDIF | 10.09 | Mean | 9.55 | Zero crossing | 10.09 | 7 | |
| Shape factor | 10.06 | Clearance factor | 9.51 | Energy operator | 9.79 | 6 | |
| FSM | 9.03 | Kurtosis | 9.48 | Skewness | 9.39 | 5 | |
| Kurtosis | 8.80 | Waveform | 8.35 | Kurtosis | 8.37 | 4 | |
| Energy operator | 8.23 | Shape factor | 8.25 | Latitud factor | 8.17 | 3 | |
| Latitud factor | 8.23 | Impulse factor | 8.20 | Shape factor | 7.79 | 2 | |
| Log-Log ratio | 8.20 | SDIF | 8.15 | SDIF | 7.76 | 1 | |
| Scuffing | TMHO | 11.82 | TMHO | 11.60 | TMHO | 11.69 | 10 |
| Mean | 11.72 | Mean | 11.55 | Mean | 11.69 | 9 | |
| Zero crossing | 11.30 | FSM | 10.46 | Skewness | 10.92 | 8 | |
| Skewness | 10.47 | Zero crossing | 9.95 | FSM | 10.67 | 7 | |
| SDIF | 10.11 | Skewness | 8.69 | Energy operator | 8.54 | 6 | |
| Shape factor | 9.80 | Waveform | 8.65 | Impulse factor | 8.18 | 5 | |
| SSC | 9.60 | Clearance factor | 8.51 | Zero crossing | 8.02 | 4 | |
| Kurtosis | 9.04 | Pulse | 8.42 | Kurtosis | 8.01 | 3 | |
| FSM | 8.38 | Kurtosis | 8.26 | Clearance factor | 7.99 | 2 | |
| Wavelength | 8.34 | Impulse factor | 8.23 | Crest factor | 7.94 | 1 | |
| CI Breaking | Weighing | CI Cracking | Weighing | CI Pitting | Weighing | CI Scuffing | Weighing |
|---|---|---|---|---|---|---|---|
| Mean | 27 | Skewness | 28 | TMHO | 25 | TMHO | 30 |
| Zero crossing | 26 | SSC | 25 | Mean | 24 | Mean | 27 |
| TMHO | 26 | Mean | 20 | Energy operator | 19 | Skewness | 21 |
| Energy operator | 19 | TMHO | 19 | SSC | 19 | Zero crossing | 19 |
| SSC | 14 | Energy operator | 15 | Skewness | 15 | FSM | 17 |
| Kurtosis | 8 | FSM | 13 | Kurtosis | 13 | Kurtosis | 8 |
| Latitud factor | 8 | Zero crossing | 13 | Shape factor | 11 | Energy operator | 6 |
| Shape factor | 7 | Clearance factor | 11 | SDIF | 9 | Impulse factor | 6 |
| SDIF | 6 | Kurtosis | 8 | Zero crossing | 7 | Clearance factor | 6 |
| Crest factor | 6 | SDIF | 5 | Clearance factor | 6 | SDIF | 6 |
| Skewness | 5 | Shape factor | 3 | FSM | 5 | Shape factor | 5 |
| Waveform | 4 | Latitud factor | 3 | Latitud factor | 5 | Waveform | 5 |
| Impulse factor | 4 | NNNL | 2 | Waveform | 4 | SSC | 4 |
| Log-Log ratio | 3 | Impulse factor | 2 | Pulse index | 3 | ||
| Margin index | 2 | Log-Log ratio | 1 | Wavelength | 1 | ||
| Crest factor | 1 |
| Ranking CI | # Failures | Weighing | Ranking CI | # Failures | Weighing |
|---|---|---|---|---|---|
| TMHO | 4 | 100 | Clearance factor | 3 | 23 |
| Mean | 4 | 98 | Latitud factor | 3 | 16 |
| Skewness | 4 | 70 | Waveform | 3 | 13 |
| Zero crossing | 4 | 65 | Impulse factor | 3 | 12 |
| SSC | 4 | 61 | Crest factor | 2 | 7 |
| Energy operator | 4 | 59 | Log-Log ratio | 2 | 5 |
| Kurtosis | 4 | 37 | Pulse | 1 | 3 |
| FSM | 3 | 35 | Verosneg | 1 | 2 |
| SDIF | 4 | 27 | MarginI | 1 | 1 |
| Shape factor | 4 | 25 | Wavelength | 1 | 1 |
| CI | Formula |
|---|---|
| Temporal moments higher order | m = 3 as default |
| Mean | |
| Skewness | |
| Zero crossing | |
| Slope sign change | |
| Energy operator | |
| Kurtosis |
| CI | P10_P1 | P2_P1 | P3_P1 | P4_P1 | P5_P1 | P6_P1 | P7_P1 | P8_P1 | P9_P1 | Selected |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 0.0064 | 0.0201 | 0.0358 | 0.0120 | 0.0078 | 0.0022 | 0.0814 | 0.0765 | 0.0093 | ✓ |
| Kurtosis | 1.1276 | 0.0884 | 0.7727 | 0.3634 | 0.7616 | 0.3588 | 0.3181 | 0.5865 | 0.0418 | ✓ |
| Skewness | 0.5866 | 0.0673 | 0.5990 | 0.3561 | 0.6712 | 0.3422 | 0.1406 | 0.4332 | 0.4136 | ✓ |
| Energy operator | 0.4896 | 0.6353 | 0.4698 | 0.0545 | 0.0502 | 0.0424 | 0.0176 | 0.2303 | 0.0057 | ✓ |
| Zero crossing | 0.0179 | 0.1221 | 0.2126 | 0.4674 | 0.2867 | 0.0666 | 0.0040 | 0.2359 | 0.1662 | ✓ |
| Slope sign change | 0.0194 | 0.0261 | 0.1891 | 0.0148 | 0.1490 | 0.1738 | 0.0322 | 0.0399 | 0.0064 | ✓ |
| TMHO | 0.0230 | 0.0533 | 0.1255 | 0.0410 | 0.0162 | 0.0074 | 0.2399 | 0.2359 | 0.0340 | ✓ |
| Log detector | 0.0006 | 0.0404 | 0.0724 | 0.0021 | 0.0840 | 0.1366 | 0.0213 | 0.0087 | 0.0112 | X |
| Norm entropy | 0.0007 | 0.0453 | 0.0661 | 0.0012 | 0.0823 | 0.1366 | 0.0281 | 0.0086 | 0.0149 | X |
| Log energy entropy | 0.0008 | 0.0476 | 0.0577 | 0.0019 | 0.0742 | 0.1435 | 0.0386 | 0.0073 | 0.0185 | X |
| Wilson amplitude | 0.0091 | 0.1034 | 0.0797 | 0.0033 | 0.1043 | 0.0973 | 0.0146 | 0.1169 | 0.0027 | X |
| Mean square error | 0.0950 | 0.0739 | 0.1665 | 0.0016 | 0.0375 | 0.0415 | 0.0025 | 0.0768 | 0.0597 | X |
| CI | P10_P1 | P2_P1 | P3_P1 | P4_P1 | P5_P1 | P6_P1 | P7_P1 | P8_P1 | P9_P1 | Selected |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 0.0467 | 0.2361 | 0.1220 | 0.1081 | 0.1406 | 0.0883 | 0.0663 | 0.0858 | 0.0475 | ✓ |
| Kurtosis | 0.6123 | 0.4206 | 0.6007 | 0.4965 | 0.1207 | 0.1125 | 0.1914 | 0.1097 | 0.3974 | ✓ |
| Skewness | 0.1861 | 0.1702 | 0.0594 | 0.2048 | 0.3946 | 0.0068 | 0.2588 | 0.0923 | 0.0442 | ✓ |
| Energy operator | 0.8258 | 1.3385 | 0.9205 | 0.7314 | 1.2859 | 0.8833 | 0.7326 | 0.6106 | 0.5430 | ✓ |
| Zero crossing | 0.0289 | 0.1653 | 0.0218 | 0.1630 | 0.1393 | 0.1320 | 0.0774 | 0.4657 | 0.0853 | ✓ |
| Slope sign change | 0.0016 | 0.0301 | 0.0016 | 0.1294 | 0.3304 | 0.5692 | 0.2089 | 0.3196 | 0.0809 | ✓ |
| TMHO | 0.1989 | 0.7253 | 0.4340 | 0.3886 | 0.4875 | 0.3356 | 0.2727 | 0.3328 | 0.2164 | ✓ |
| Log energy entropy | 0.0069 | 0.0121 | 0.0523 | 0.0367 | 0.1946 | 0.2538 | 0.0917 | 0.1494 | 0.0118 | X |
| Norm entropy | 0.0074 | 0.0137 | 0.0577 | 0.0370 | 0.2174 | 0.2710 | 0.0837 | 0.1746 | 0.0093 | X |
| Wave form | 0.0370 | 0.0103 | 0.1494 | 0.0105 | 0.2426 | 0.2064 | 0.0313 | 0.1865 | 0.0043 | X |
| Log detector | 0.0093 | 0.0144 | 0.0666 | 0.0468 | 0.2375 | 0.2878 | 0.0763 | 0.2004 | 0.0075 | X |
| Wilson amplitude | 0.0018 | 0.0075 | 0.0526 | 0.0345 | 0.2109 | 0.3241 | 0.0926 | 0.2138 | 0.0181 | X |
| CI | P10_P1 | P2_P1 | P3_P1 | P4_P1 | P5_P1 | P6_P1 | P7_P1 | P8_P1 | P9_P1 | Selected |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 0.0344 | 0.0079 | 0.0576 | 0.0756 | 0.0103 | 0.0551 | 0.0165 | 0.0969 | 0.0273 | ✓ |
| Kurtosis | 1.8664 | 0.1378 | 0.2153 | 0.0763 | 0.2812 | 0.0229 | 0.0822 | 0.0239 | 0.0544 | ✓ |
| Skewness | 0.4265 | 0.0650 | 0.6016 | 0.1370 | 0.9159 | 0.4084 | 0.0473 | 0.0161 | 0.1699 | ✓ |
| Energy operator | 0.5188 | 0.8403 | 0.0285 | 0.0011 | 0.0130 | 0.0513 | 0.5376 | 0.2571 | 0.2024 | ✓ |
| Zero crossing | 0.0545 | 0.0504 | 0.0194 | 0.2574 | 0.0243 | 0.1362 | 0.0741 | 0.0494 | 0.0109 | ✓ |
| Slope sign change | 0.0179 | 0.1600 | 0.2648 | 0.0039 | 0.2379 | 0.0339 | 0.3576 | 0.3789 | 0.2742 | ✓ |
| TMHO | 0.1061 | 0.0216 | 0.1777 | 0.2243 | 0.0270 | 0.1476 | 0.0393 | 0.2778 | 0.0729 | ✓ |
| Clearence factor | 0.3758 | 0.0045 | 0.0405 | 0.0121 | 0.1001 | 0.0329 | 0.2984 | 0.1857 | 0.1385 | X |
| Pulse | 0.4189 | 0.0105 | 0.0527 | 0.0051 | 0.0752 | 0.0239 | 0.2541 | 0.1810 | 0.1995 | X |
| Wilson amplitude | 0.0223 | 0.0961 | 0.0833 | 0.0059 | 0.1526 | 0.0015 | 0.3008 | 0.3050 | 0.2722 | X |
| Log detector | 0.0143 | 0.1348 | 0.0958 | 0.0278 | 0.1441 | 0.0088 | 0.2943 | 0.2784 | 0.2781 | X |
| Norm entropy | 0.0102 | 0.1506 | 0.1200 | 0.0335 | 0.1722 | 0.0168 | 0.2747 | 0.2784 | 0.2680 | X |
| CI | P10_P1 | P2_P1 | P3_P1 | P4_P1 | P5_P1 | P6_P1 | P7_P1 | P8_P1 | P9_P1 | Selected |
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 0.0916 | 0.0829 | 0.0618 | 0.0545 | 0.0442 | 0.0441 | 0.0333 | 0.0979 | 0.0664 | ✓ |
| Kurtosis | 0.6395 | 0.3533 | 0.2871 | 0.2039 | 0.5874 | 0.5694 | 0.4844 | 0.3728 | 0.8484 | ✓ |
| Skewness | 0.2082 | 0.0850 | 0.0304 | 0.0070 | 0.2501 | 0.0966 | 0.0539 | 0.0202 | 0.0445 | ✓ |
| Energy operator | 0.1757 | 0.7935 | 0.0116 | 0.0435 | 0.2258 | 0.0384 | 0.2111 | 0.0480 | 0.0040 | ✓ |
| Zero crossing | 0.2809 | 0.1266 | 0.0771 | 0.0356 | 0.0772 | 0.0958 | 0.3544 | 0.0552 | 0.0606 | ✓ |
| Slope sign change | 0.0997 | 0.6204 | 0.3210 | 0.0049 | 0.0124 | 0.0011 | 0.0246 | 0.0010 | 0.0000 | ✓ |
| TMHO | 0.3601 | 0.3251 | 0.2599 | 0.2294 | 0.1819 | 0.1822 | 0.1395 | 0.3670 | 0.2683 | ✓ |
| Wave form | 0.0176 | 0.2126 | 0.1325 | 0.0012 | 0.0259 | 0.0645 | 0.0202 | 0.0260 | 0.0968 | X |
| Log entropy | 0.0391 | 0.2530 | 0.1784 | 0.0045 | 0.0060 | 0.0688 | 0.0162 | 0.0248 | 0.0505 | X |
| Norm entropy | 0.0336 | 0.2667 | 0.1801 | 0.0043 | 0.0066 | 0.0609 | 0.0128 | 0.0221 | 0.0559 | X |
| Log Detector | 0.0245 | 0.2847 | 0.1892 | 0.0042 | 0.0058 | 0.0564 | 0.0075 | 0.0193 | 0.0595 | X |
| Wilson amplitude | 0.0043 | 0.3042 | 0.1484 | 0.0051 | 0.0039 | 0.0429 | 0.0055 | 0.0799 | 0.1350 | X |
| A | Breaking | Cracking | Pitting | Scuffing | ||||
|---|---|---|---|---|---|---|---|---|
| RF | K-NN | RF | K-NN | RF | K-NN | RF | K-NN | |
| A1 | 0.9841 | 0.9807 | 0.9960 | 0.9983 | 0.9849 | 0.9850 | 0.9805 | 0.9850 |
| A2 | 0.9884 | 0.9886 | 0.9948 | 0.9967 | 0.9921 | 0.9904 | 0.9827 | 0.9928 |
| A3 | 0.9872 | 0.9826 | 0.9949 | 0.9909 | 0.9906 | 0.9928 | 0.9908 | 0.9959 |
| A4 | 0.9908 | 0.9960 | 0.9939 | 0.9974 | 0.9923 | 0.9897 | 0.9894 | 0.9920 |
| A5 | 0.9929 | 0.9871 | 0.9948 | 0.9967 | 0.9904 | 0.9858 | 0.9899 | 0.9941 |
| A6 | 0.9974 | 0.9875 | 0.9911 | 0.9947 | 0.9947 | 0.9918 | 0.9943 | 0.9962 |
| A | Breaking | Cracking | Pitting | Scuffing | ||||
|---|---|---|---|---|---|---|---|---|
| RF | K-NN | RF | K-NN | RF | K-NN | RF | K-NN | |
| A1 | 0.9922 | 0.9871 | 0.9965 | 0.9988 | 0.9885 | 0.9894 | 0.9905 | 0.9929 |
| A2 | 0.9920 | 0.9930 | 0.9970 | 0.9982 | 0.9969 | 0.9962 | 0.9943 | 0.9968 |
| A3 | 0.9956 | 0.9913 | 0.9950 | 0.9921 | 0.9935 | 0.9949 | 0.9952 | 0.9982 |
| A4 | 0.9959 | 0.9980 | 0.9950 | 0.9987 | 0.9981 | 0.9967 | 0.9971 | 0.9970 |
| A5 | 0.9964 | 0.9959 | 0.9983 | 0.9969 | 0.9926 | 0.9926 | 0.9961 | 0.9976 |
| A6 | 0.9994 | 0.9960 | 0.9937 | 0.9961 | 0.9973 | 0.9978 | 0.9992 | 0.9990 |
| Factor | Df | Sum Square | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| A | 3 | 0.2150 | 0.07168 | 1295.10 | <0.001 |
| Failure | 3 | 0.1954 | 0.06512 | 1176.70 | <0.001 |
| Classifier | 1 | 0.0000 | 0.00000 | 0.00 | <0.001 |
| A:Failure | 9 | 0.2012 | 0.02236 | 404.00 | <0.001 |
| Failure:Classifier | 3 | 0.0762 | 0.02539 | 458.70 | <0.001 |
| A:Classifier | 3 | 0.0184 | 0.00614 | 111.00 | <0.001 |
| Factor | Df | Sum Square | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| A | 2 | 0.0829 | 0.04145 | 680.78 | <0.001 |
| Failure | 3 | 0.3211 | 0.10704 | 1757.89 | <0.001 |
| Classifier | 1 | 0.0065 | 0.00655 | 107.49 | <0.001 |
| A:Failure | 6 | 0.1427 | 0.02378 | 390.56 | <0.001 |
| Failure:Classifier | 3 | 0.0689 | 0.02296 | 377.06 | <0.001 |
| A:Classifier | 2 | 0.0089 | 0.00446 | 73.31 | <0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Torres, A.; Sánchez, R.-V.; Barceló-Cerdá, S. Methodology for Feature Selection of Time Domain Vibration Signals for Assessing the Failure Severity Levels in Gearboxes. Appl. Sci. 2025, 15, 5813. https://doi.org/10.3390/app15115813
Pérez-Torres A, Sánchez R-V, Barceló-Cerdá S. Methodology for Feature Selection of Time Domain Vibration Signals for Assessing the Failure Severity Levels in Gearboxes. Applied Sciences. 2025; 15(11):5813. https://doi.org/10.3390/app15115813
Chicago/Turabian StylePérez-Torres, Antonio, René-Vinicio Sánchez, and Susana Barceló-Cerdá. 2025. "Methodology for Feature Selection of Time Domain Vibration Signals for Assessing the Failure Severity Levels in Gearboxes" Applied Sciences 15, no. 11: 5813. https://doi.org/10.3390/app15115813
APA StylePérez-Torres, A., Sánchez, R.-V., & Barceló-Cerdá, S. (2025). Methodology for Feature Selection of Time Domain Vibration Signals for Assessing the Failure Severity Levels in Gearboxes. Applied Sciences, 15(11), 5813. https://doi.org/10.3390/app15115813







