Transformation of Coordinates of Boundary Points of Neighboring Mining Areas Using an Authorial Procedure Based on the Method of Independent Models—A Case Study
Abstract
:1. Introduction
2. Materials and Methods
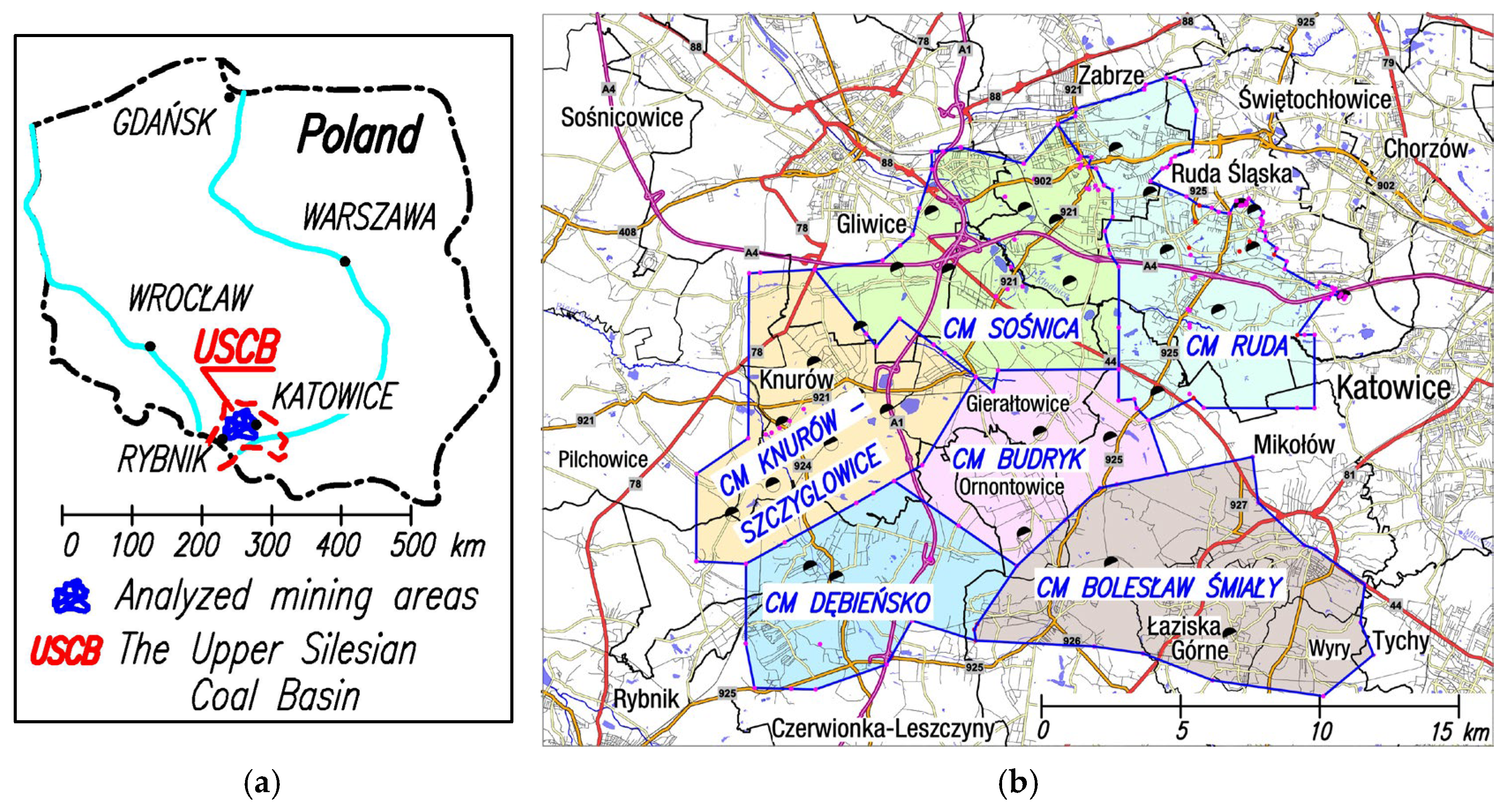
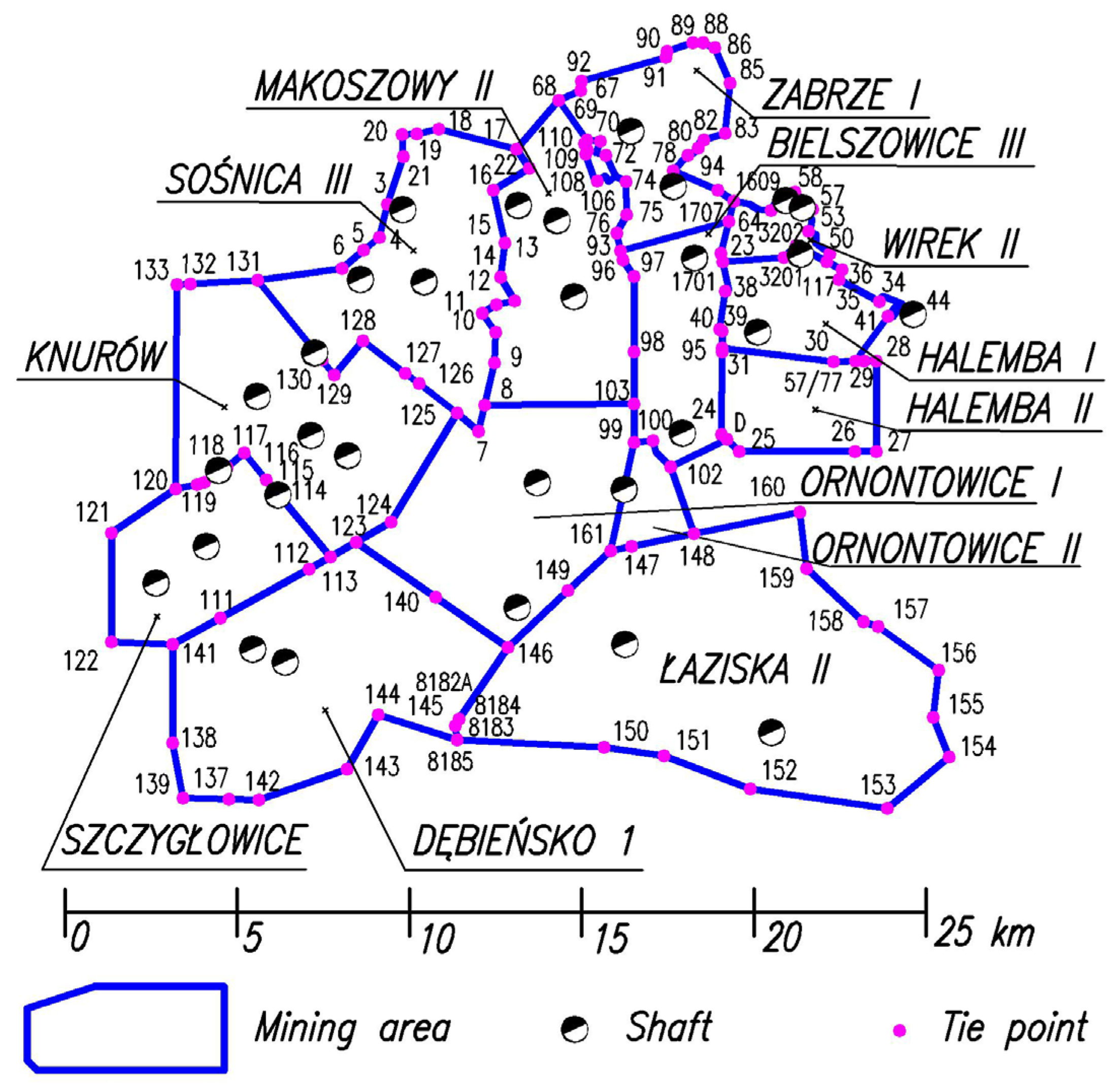
2.1. Location of the Study Area and Source Materials
2.2. Methodology
2.2.1. Single-Step Transformation—Separate
- -
- The selection and analysis of adjustment points obtained from the mine or obtained as a result of direct field measurements.
- -
- The determination of the degree and type of transformation based on the adjustment points obtained from the mines. The first-degree conformal transformation (Helmert) was adopted in this research—due to the possibility to obtain transformation coefficients consistent with those currently used by the mine.
- -
- Comparison of the coordinates of the adjustment points with the coordinates obtained from the transformation. The verification process should include the calculation of the differences in the x and y coordinates and the resultant difference. If the deviation exceeds the assumed maximum error values, then the transformation parameters should be re-determined.
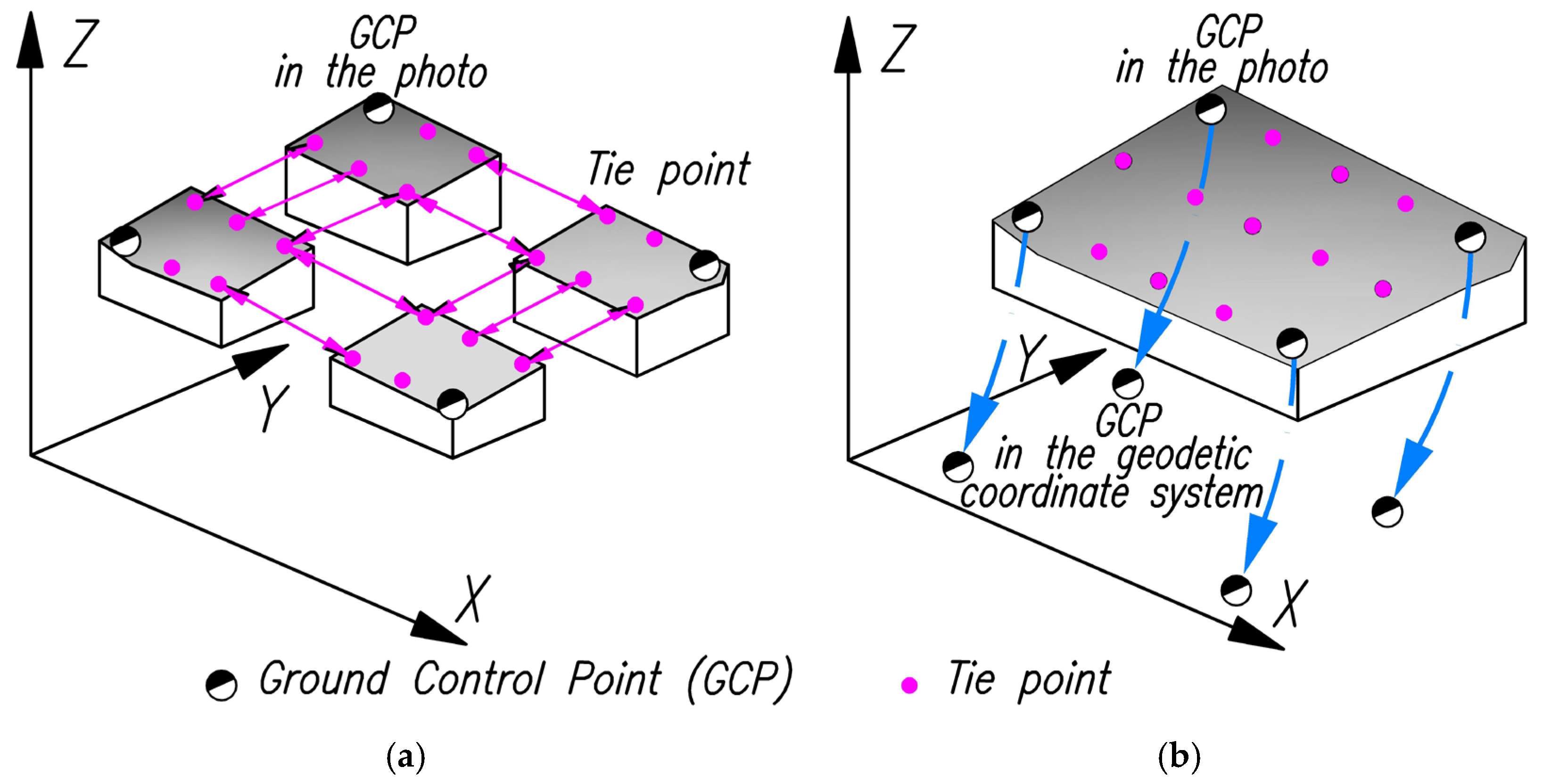
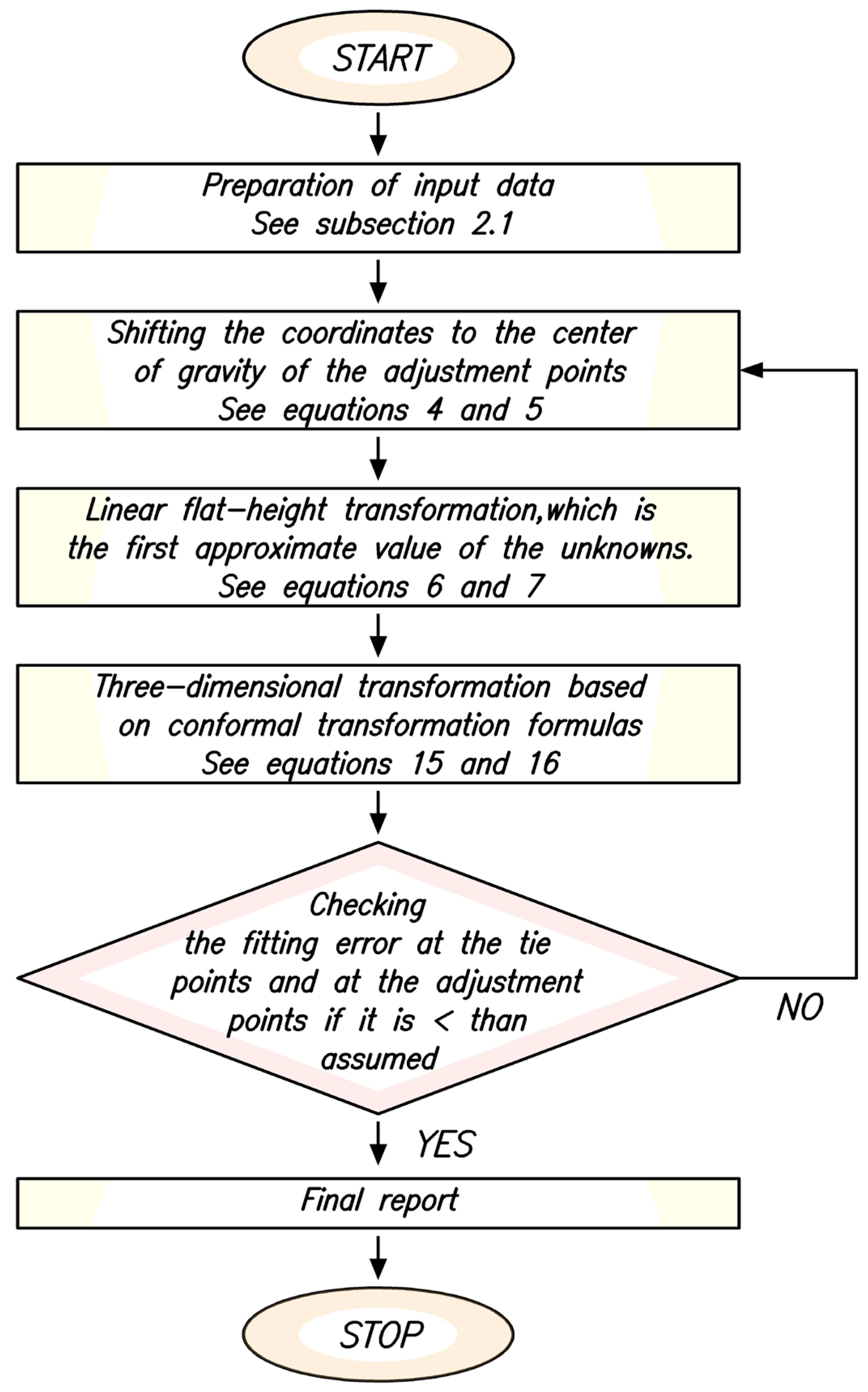
2.2.2. Transformation Using the Authorial Procedure Based on the Method of Independent Models
- -
- Obtaining the coordinates of the boundary points of mining areas and shafts located in these areas;
- -
- Analyzing the obtained data for completeness and quality;
- -
- If necessary, conducting field measurements to determine the coordinates of the shafts;
- -
- Preparing the appropriate input files.
- -
- Calculating the coordinates of the center of gravity in two systems: primary (x0, y0) and secondary (X0, Y0), according to the following formulas:
- -
- Shifting the coordinates to the center of gravity based on the following formulas:
- -
- In the case of points with known (adjustments) coordinates:
- -
- In case of tie points:
- -
- In the case of points with known (adjustments) coordinates:
- -
- In the case of tie points:
- -
- The matrix notation of the transformation equation is expressed as follows:
- -
- Using the so-called small rotation matrix:
- -
- Substituting the following values:
- -
- We obtain the equations of the adjustment points (15):
- -
- For the tie points, Equation (16) was used:
- -
- The precise orthogonal matrix corresponding to the calculated rotations is determined from Formula (17):
3. Results
4. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EU | European Union |
| ROW | Rybnik Coal Area |
| GOP | Upper Silesian Industrial Region |
| S-JTSK | System of the Unified Trigonometrical Cadastral Network |
| KUL | Union of Lublin Mound-Lviv |
| MIM | method of independent models |
| USCB | Upper Silesian Coal Basin |
| CL | coal mine |
| MA | mining area |
| GCP | Ground Control Point |
References
- Sokoła-Szewioła, V.; Kotyrba, A.; Alheib, M. Methods on Assessment and Monitoring of Seismic Hazards in Coal Post-Mining Areas Guidelines; Sokoła-Szewioła, V., Kotyrba, A., Alheib, M., Eds.; Silesian University of Technology Publishing House: Gliwice, Poland, 2023; p. 117. Available online: https://delibra.bg.polsl.pl/Content/77017/Methods-on-assessment-and-monitoring-of-seismic-hazards_2023.pdf (accessed on 5 May 2025).
- Dominique, P.; Aochi, H.; Morel, J. Triggered seismicity in a former flooded coal mining basin (Gardanne area). Mine Water Environ. 2022, 41, 317–334. [Google Scholar] [CrossRef]
- Namjesnik, D.; Kinscher, J.; Contrucci, I.; Klein, E. Impact of past mining on public safety: Seismicity in area of flooded abandoned coal Gardanne mine, France. Int. J. Coal Sci. Technol. 2022, 9, 90. [Google Scholar] [CrossRef]
- Directive 2007/2/EC of the European Parliament and of the Council of 14 March 2007 Establishing an Infrastructure for Spatial Information in the European Community (INSPIRE); European Parliament and of the Council of the European Union: Brussels, Belgium, 2007. L 108. Available online: https://eur-lex.europa.eu/eli/dir/2007/2/oj (accessed on 5 May 2025).
- Act of March 4, 2010 on spatial information infrastructure/Ustawa z dnia 4 marca 2010 r. o infrastrukturze informacji przestrzennej. 2010. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=wdu20100760489 (accessed on 5 May 2025).
- Act of May 17, 1989 Geodetic and cartographic law/Ustawa z dnia 17 maja 1989 r. Prawo geodezyjne i kartograficzne. 1989. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU19890300163 (accessed on 5 May 2025).
- Regulation of the Council of Ministers of October 15, 2012 on the State System of Spatial References/Rozporządzenie Rady Ministrów z Dnia 15 Października 2012 r. w Sprawie Państwowego Systemu Odniesień Przestrzennych. 2012. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20120001247 (accessed on 5 May 2025).
- Act of June 9, Geological and Mining Law/Ustawa z Dnia 9 Czerwca 2011 r. Prawo Geologiczne i Górnicze. 2011. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=wdu20111630981 (accessed on 5 May 2025).
- Regulation of the Minister of the Environment of October 28, 2015 on Surveying and Geological Documentation/Rozporządzenie Ministra Środowiska z dnia 28 Października 2015 r. w Sprawie Dokumentacji Mierniczo-Geologicznej. 2015. Available online: https://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20150001941 (accessed on 5 May 2025).
- Sokoła-Szewioła, V. Statutory Research/Badania Statutowe BK NR 06/050/BK17/0042. Ocena DokłAdnośCi I Opracowanie Parametrów Transformacji Lo-Kalnych UkłAdów WspółRzędnych ProstokąTnych PłAskich Stosowanych W Przedsiębiorstwach Górniczych Do UkłAdu Państ-Wowego Z Oprogramowaniem W Systemie Klasy GIS; Silesian University of Technology: Gliwice, Poland, 2017. [Google Scholar]
- Sokoła-Szewioła, V.; Poniewiera, M.; Mierzejowska, A. Coordinate transformation using the author’s software in GIS class system—Case study. Geoinf. Pol. Pr. Kom. Geoinformatyki Pol. Akad. Umiejętności 2021, 20, 7–19. [Google Scholar] [CrossRef]
- Janssen, V. Understanding coordinate systems, datums and transformations in Australia. Int. J. Geoinf. 2009, 5, 697–715. Available online: https://www.researchgate.net/publication/228649896 (accessed on 5 May 2025).
- James, B. A practical approach to transformation between commonly used reference systems. Aust. Surv. 2012, 35, 248–264. [Google Scholar] [CrossRef]
- Sisman, Y. Coordinate transformation of cadastral maps using different adjustment methods. Surv. Rev. 2014, 37, 869–882. [Google Scholar] [CrossRef]
- Sprinsky, W. Transformation of Survey Coordinates—Another Look at an Old Problem. J. Surv. Eng. 2002, 128, 200–209. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Z.; Ran, J. Robust Solution for Coordinate Transformation Based on Coordinate Component Weighting. J. Surv. Eng. 2023, 149, 3. [Google Scholar] [CrossRef]
- Yang, R.; Deng, C.; Yu, K.; Li, Z.; Pan, L. A New Way for Cartesian Coordinate Transformation and Its Precision Evaluation. Remote Sens. 2022, 14, 864. [Google Scholar] [CrossRef]
- Yilmaz; Tekdal, E. Analysis of Coordinate Transformation Methods for Deformation Monitoring. Surv. Land Inf. Sci. 2023, 82, 87–93. [Google Scholar]
- Chen, Z.; Dong, X.; Li, Y.; Hu, C. Formation Design for Single-Pass GEO InSAR Considering Earth Rotation Based on Coordinate Rotational Transformation. Remote Sens. 2020, 12, 573. [Google Scholar] [CrossRef]
- Al-Rawabdeh, A.; He, F.; Habib, A. Automated Feature-Based Down-Sampling Approaches for Fine Registration of Irregular Point Clouds. Remote Sens. 2020, 12, 1224. [Google Scholar] [CrossRef]
- Staňková, H.; Černota, P.; Pospíšil, J. Use of the Ott’s system of coordinate for the protection of buildings and people in the Ostrava-Karvina Coal District. J. Sustain. Min. 2015, 14, 93–100. [Google Scholar] [CrossRef]
- Staňková, H.; Černota, P.; Novosad, M. An analysis of the possibility of intersystem transformations for purposes of geo-referencing old mine workings. GeoScience Eng. 2012, LVIII, 1–12. [Google Scholar] [CrossRef]
- Żogała, M. Zastosowanie Metody NiezależNych Modeli Do Transformacji Lokalnych UkłAdów WspółRzędnych Stosowanych W Kopalniach Węgla Kamiennego. Ph.D. Thesis, Silesian University of Technology, Gliwice, Poland, 2022. [Google Scholar]
- Fourcade, H.G. A New Method of Aerial Surveying. Trans. R. Soc. S. Afr. 1929, 18, 237–246. [Google Scholar] [CrossRef]
- Thompson, E.H. Review of methods of independent model aerial triangulation. Photogramm. Rec. 1965, 5, 72–79. [Google Scholar] [CrossRef]
- Poivilliers, G. International Archives of Photogrammetry. In Proceedings of the 7th International Congress of Photogrammetry, Washington, DC, USA, 4–16 September 1952; Volume XI. [Google Scholar]
- Thompson, E.H. Thompson-Watts plotting machine. Photogramm. Rec. 1954, 1, 5–28. [Google Scholar] [CrossRef]
- Sitek, Z. Polskie Towarzystwo Fotogrametryczne, Photogrammetria 1958–1959. Photogrammetria 1959, XV, 177. [Google Scholar]
- Saxena, K.C. Independent Model Triangulation—An Improved Method. Photogramm. Eng. Remote Sens. 1976, 42, 1187–1190. Available online: https://www.asprs.org/wp-content/uploads/pers/1976journal/sep/1976_sep_1187-1190.pdf (accessed on 5 May 2025).
- Scaioni, M.; Forlani, G. Independent model triangulation of terrestrial laser scanner data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2003, XXXIV, 308–313. Available online: https://www.isprs.org/proceedings/xxxiv/5-w12/proceedings/75.pdf (accessed on 5 May 2025).
- Adami, A.; Guerra, F.; Vernier, P. Laser scanner and architectural accuracy text. In Proceedings of the XXI International CIPA Symposium, Athens, Greece, 1–6 October 2007. [Google Scholar]
- Gaździcki, J. Numeryczne opracowanie aerotriangulacji przestrzennej metodą AEROBLOK. Pr. Inst. Geodez. Kartogr. 1973, XX, 46. [Google Scholar]
- Musiał, E. Technologia numerycznego opracowania aerotriangulacji AERONET. Pr. Inst. Geodez. Kartogr 1979, XXVI, 51–89. Available online: http://bc.igik.edu.pl/Content/460/PDF/PI_1979_63_5.pdf (accessed on 5 May 2025).
- Mizerski, W. Analiza i kryteria wyboru najwłaściwszej metody opracowania analitycznego fotogrametrycznych zdjęć naziemnych. Pr. Inst. Geodez. Kartogr. 1979, XXVI. Available online: http://212.180.216.235/Content/602/PDF/Prace_IGiK_1(61)_2.pdf (accessed on 5 May 2025).
- Poniewiera, M. Zastosowanie metody niezależnych modeli do transformacji map numerycznych. Kartografia Numeryczna i Informatyka Geodezyjna. In Proceedings of the 1st National Scientific and Technical Conference, Rzeszów, Poland, 28–30 September 2005; pp. 193–202. [Google Scholar]
- Wojewódzki Ośrodek Dokumentacji Geodezyjnej i Kartograficznej. Available online: www.wodgik.katowice.pl (accessed on 12 November 2024).
- Kurczyński, Z. Fotogrametria; Wydawnictwo Naukowe PWN: Warszawa, Poland, 2014; Available online: https://repo.pw.edu.pl/info/book/WUTb5bcabea75ca4b47972709fbdb8f4429/ (accessed on 5 May 2025).
- Bernasik, J. Elementy Fotogrametrii i Teledetekcji, 2nd ed.; AGH Publishing House: Kraków, Poland, 2003; p. 108. Available online: https://katalog.panschelm.edu.pl/index.php?KatID=0&typ=record&001=CHE%20PWSZ13000689 (accessed on 5 May 2025).
- Jagielski, A. Geodezja II, 2nd ed.; Geodpis: Kraków, Poland, 2007; pp. 311–322. [Google Scholar]
- System Kopalnianych Map Numerycznych Geolisp. Available online: www.geolisp.pl (accessed on 12 November 2024).
- Algorytmy i Rozwiązania Informatyczne Dla Geodezji, Kartografii, Systemów GNSS. Available online: www.geonet.net.pl (accessed on 12 November 2024).

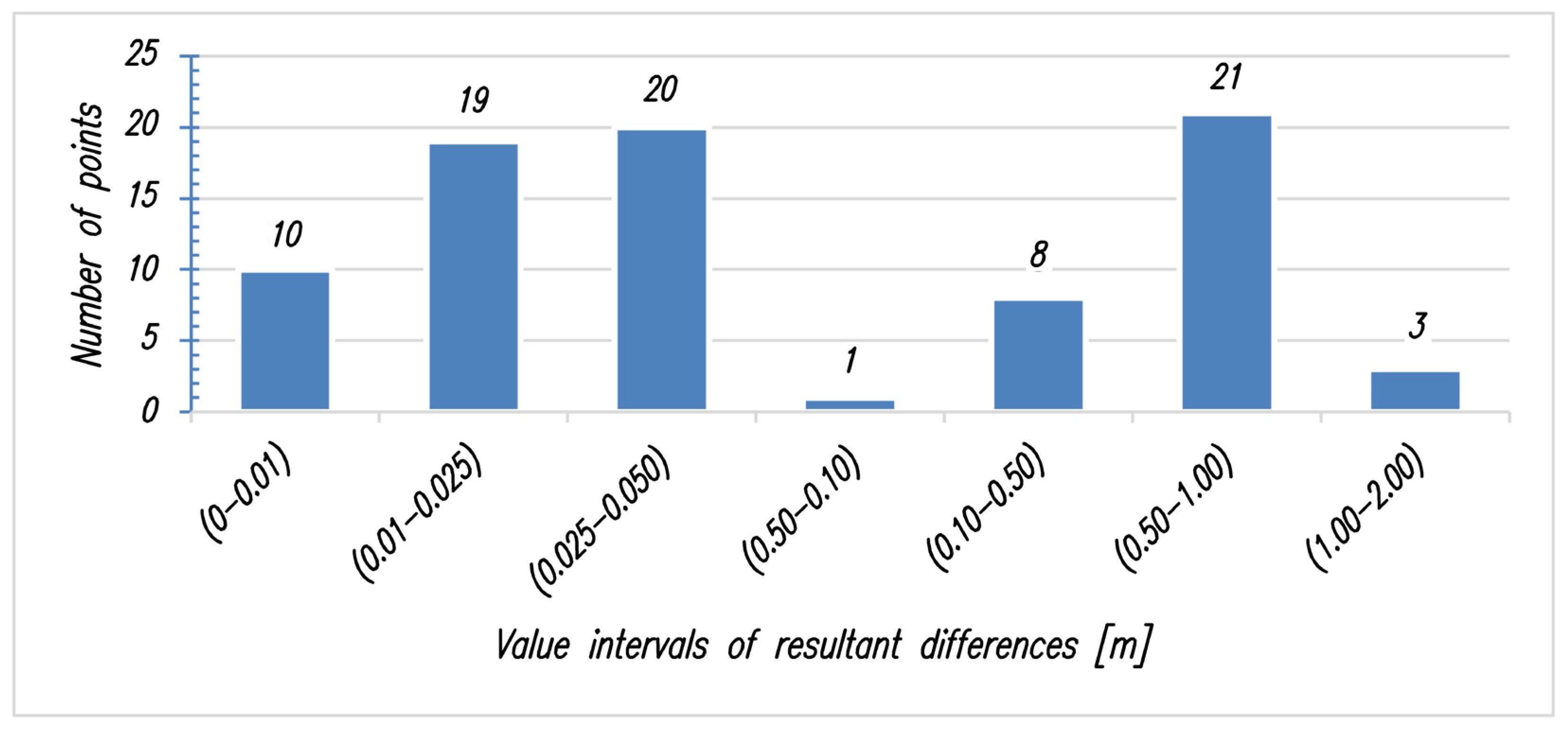
| No. | Name of Coal Mine (CM) | Name of Mining Area | Number of Boundary Points (Tie Points) | Number of Adjustment Points (Shafts) |
|---|---|---|---|---|
| 1 | CM Bolesław Śmiały | Łaziska II | 18 | 3 |
| 2 | CM Budryk | Ornontowice I | 11 | 4 |
| 3 | CM Budryk | Ornontowice II | 7 | 1 |
| 4 | CM Dębieńsko | Dębieńsko 1 | 19 | 2 |
| 5 | CM Knurów-Szczygłowice | Knurów | 19 | 8 |
| 6 | CM Knurów-Szczygłowice | Szczygłowice | 13 | 5 |
| 7 | CM Sośnica | Makoszowy II | 28 | 5 |
| 8 | CM Ruda | Bielszowice III | 18 | 6 |
| 9 | CM Ruda | Zabrze I | 30 | 3 |
| 10 | CM Ruda | Halemba I | 15 | 5 |
| 11 | CM Ruda | Halemba II | 9 | - |
| 12 | CM Ruda | Halemba-East Shaft | 10 | 1 |
| 13 | CM Ruda | Wirek II | 24 | 3 |
| 14 | CM Sośnica | Sośnica III | 27 | 6 |
| Name of Mining Area | Deviation Values [mm] | |||
|---|---|---|---|---|
| Sx | Sy | S | Smax | |
| Łaziska II | 0.0 | 0.0 | 0.0 | 0.0 |
| Ornontowice I | 0.0 | 0.0 | 0.0 | 0.0 |
| Ornontowice II | - | - | - | - |
| Dębieńsko 1 | 0.0 | 0.0 | 0.0 | 0.0 |
| Knurów | 0.0 | 0.0 | 0.0 | 0.0 |
| Szczygłowice | 1.4 | 1.5 | 2.0 | 2.5 |
| Makoszowy II | 0.0 | 0.0 | 0.0 | 0.0 |
| Bielszowice III | 2.7 | 2.6 | 3.7 | 6.9 |
| Zabrze I | 2.7 | 0.5 | 2.8 | 3.4 |
| Halemba I | 1.8 | 2.7 | 3.3 | 5.0 |
| Halemba II | - | - | - | - |
| Halemba-East Shaft | - | - | - | - |
| Wirek II | 1.3 | 3.5 | 3.8 | 4.8 |
| Sośnica III | 0.0 | 0.0 | 0.0 | 0.0 |
| Point No. | Bordering Areas | “Separate” | MIM | ||||
|---|---|---|---|---|---|---|---|
[m] | [m] | [m] | [m] | [m] | [m] | ||
| 8185 | M.A. Łaziska II—M.A Dębieńsko 1 | 0.850 | 0.542 | 1.008 | 0.000 | 0.000 | 0.000 |
| 8184 | M.A. Łaziska II—M.A. Dębieńsko 1 | 1.937 | −0.169 | 1.945 | 0.000 | 0.000 | 0.000 |
| 8183 | M.A. Łaziska II—M.A. Dębieńsko 1 | 1.001 | 0.061 | 1.003 | 0.000 | 0.000 | 0.000 |
| 8182A | M.A. Łaziska II—M.A. Dębieńsko 1 | 0.735 | 0.210 | 0.765 | −0.001 | −0.001 | 0.001 |
| 8181 | M.A. Łaziska II—M.A. Dębieńsko 1 | 0.860 | 0.217 | 0.887 | −0.001 | 0.001 | 0.001 |
| 8181 | M.A. Łaziska II—M.A. Ornontowice I | 0.886 | 0.197 | 0.908 | −0.001 | 0.000 | 0.001 |
| 9461 | M.A. Łaziska II—M.A. Ornontowice I | 0.794 | 0.210 | 0.821 | 0.000 | −0.001 | 0.001 |
| 8182 | M.A. Łaziska II—M.A. Ornontowice I | 0.729 | 0.218 | 0.761 | 0.000 | 0.001 | 0.001 |
| 8181 | M.A. Dębieńsko 1—M.A. Ornontowice I | 0.026 | −0.020 | 0.032 | 0.000 | −0.001 | 0.001 |
| MinΔx [mm] | MaxΔx [mm] | [mm] | MinΔy [mm] | MaxΔy [mm] | [mm] | MinΔxy [mm] | MaxΔxy [mm] | [mm] |
|---|---|---|---|---|---|---|---|---|
| 0.00 | 1937.00 | 417.89 | 0.00 | 542.00 | 81.76 | 2.00 | 1945.00 | 349.23 |
| MinΔx [mm] | MaxΔx [mm] | [mm] | MinΔy [mm] | MaxΔy [mm] | [mm] | MinΔxy [mm] | MaxΔxy [mm] | |
|---|---|---|---|---|---|---|---|---|
| 0.00 | 1.00 | 0.55 | 0.00 | 1.00 | 0.55 | 0.00 | 1.00 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Żogała, M.; Sokoła-Szewioła, V.; Poniewiera, M. Transformation of Coordinates of Boundary Points of Neighboring Mining Areas Using an Authorial Procedure Based on the Method of Independent Models—A Case Study. Appl. Sci. 2025, 15, 5812. https://doi.org/10.3390/app15115812
Żogała M, Sokoła-Szewioła V, Poniewiera M. Transformation of Coordinates of Boundary Points of Neighboring Mining Areas Using an Authorial Procedure Based on the Method of Independent Models—A Case Study. Applied Sciences. 2025; 15(11):5812. https://doi.org/10.3390/app15115812
Chicago/Turabian StyleŻogała, Monika, Violetta Sokoła-Szewioła, and Marian Poniewiera. 2025. "Transformation of Coordinates of Boundary Points of Neighboring Mining Areas Using an Authorial Procedure Based on the Method of Independent Models—A Case Study" Applied Sciences 15, no. 11: 5812. https://doi.org/10.3390/app15115812
APA StyleŻogała, M., Sokoła-Szewioła, V., & Poniewiera, M. (2025). Transformation of Coordinates of Boundary Points of Neighboring Mining Areas Using an Authorial Procedure Based on the Method of Independent Models—A Case Study. Applied Sciences, 15(11), 5812. https://doi.org/10.3390/app15115812







