Supersonic Pulse-Jet System for Filter Regeneration: Molecular Tagging Velocimetry Study and Computational Fluid Dynamics Validation
Abstract
Featured Application
Abstract
1. Introduction
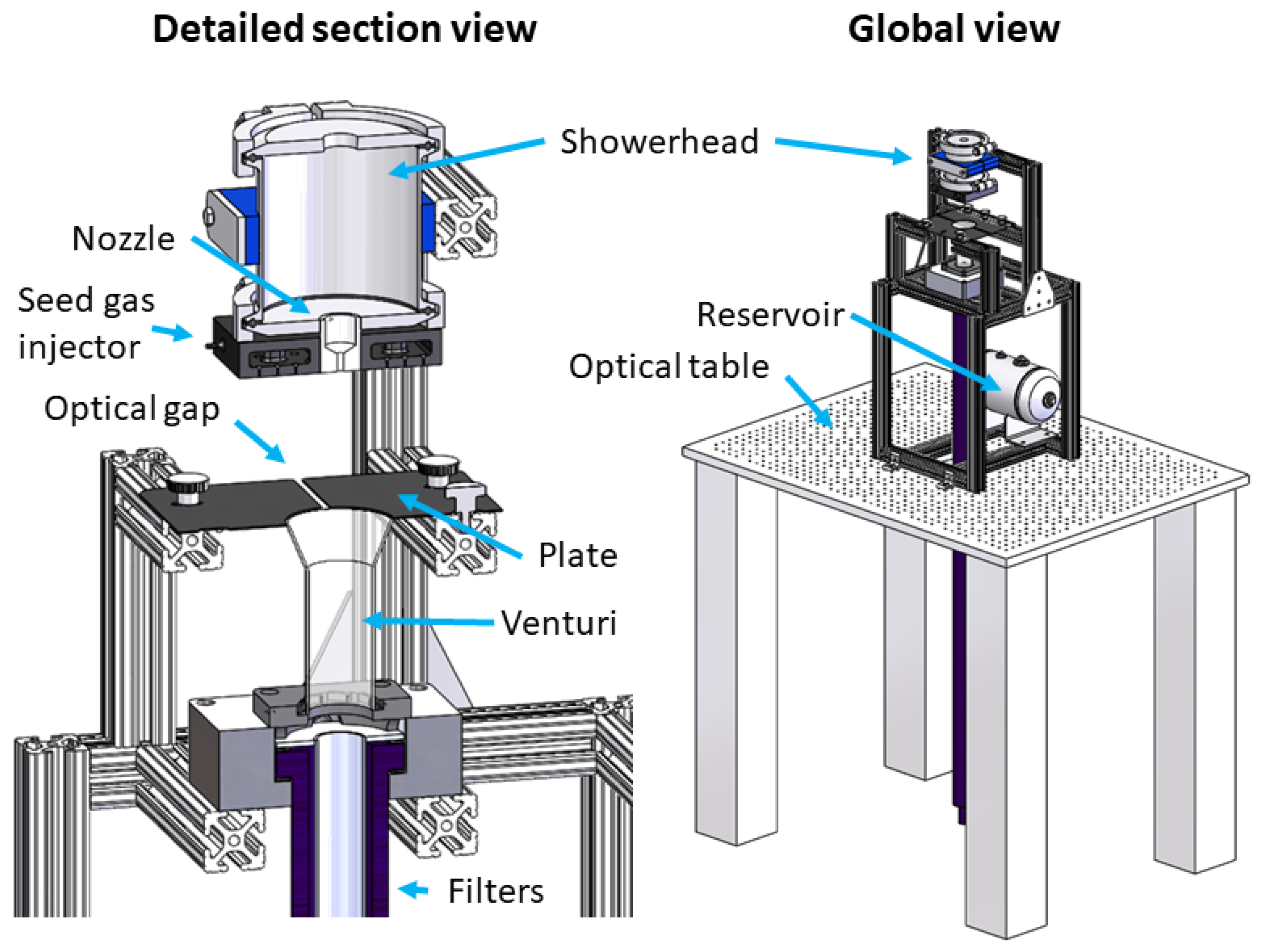
2. Experimental Setup
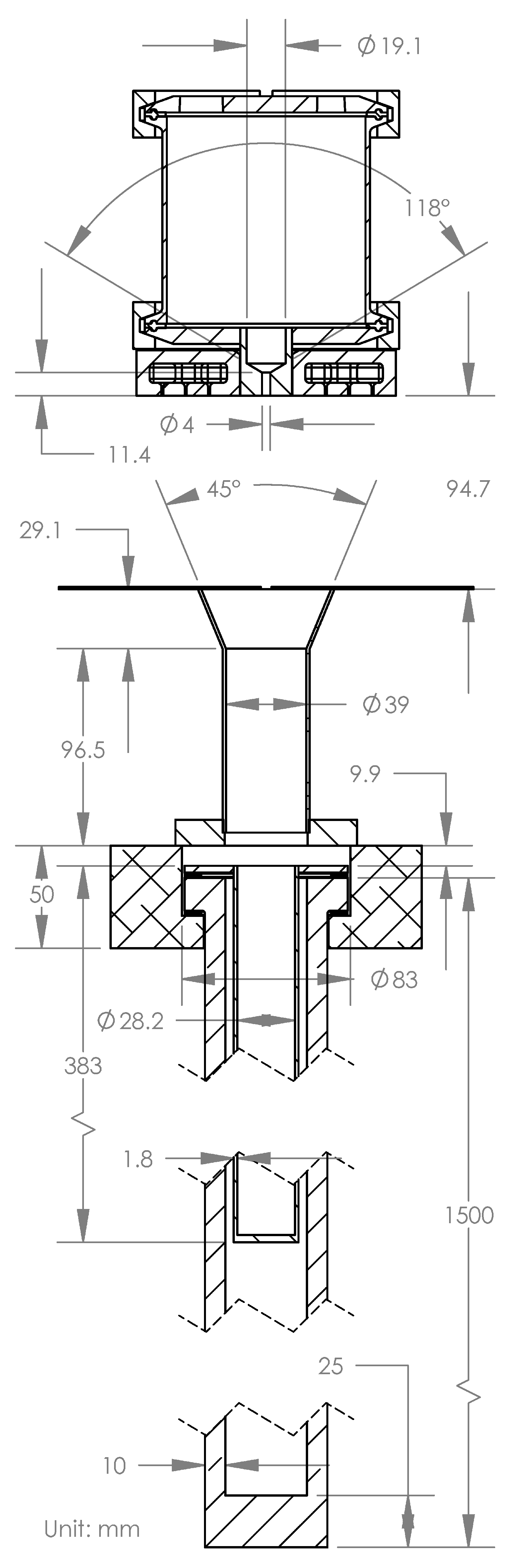
2.1. Test Rig
2.2. Shadowgraphy Configuration
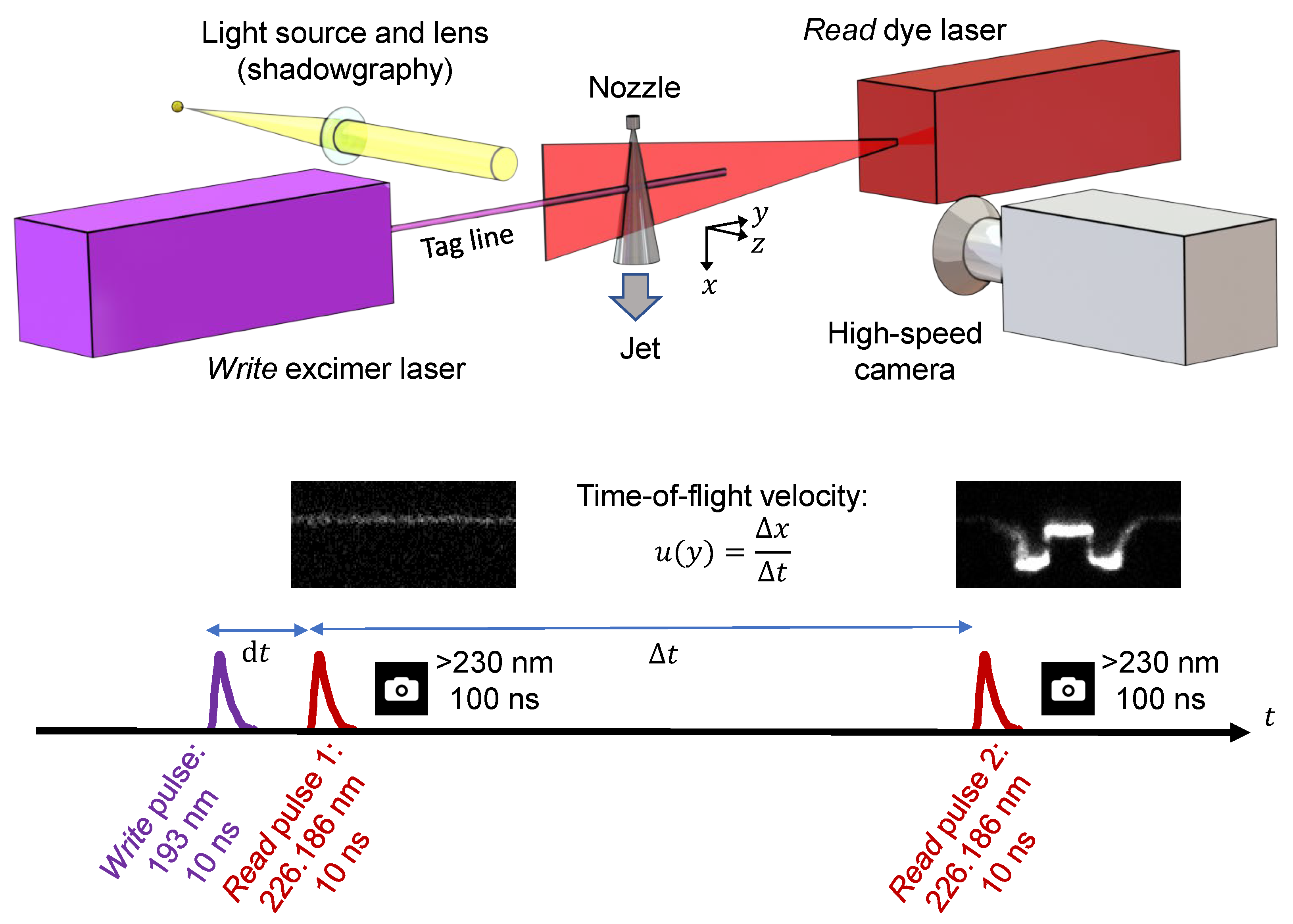
2.3. Molecular Tagging Velocimetry Configuration
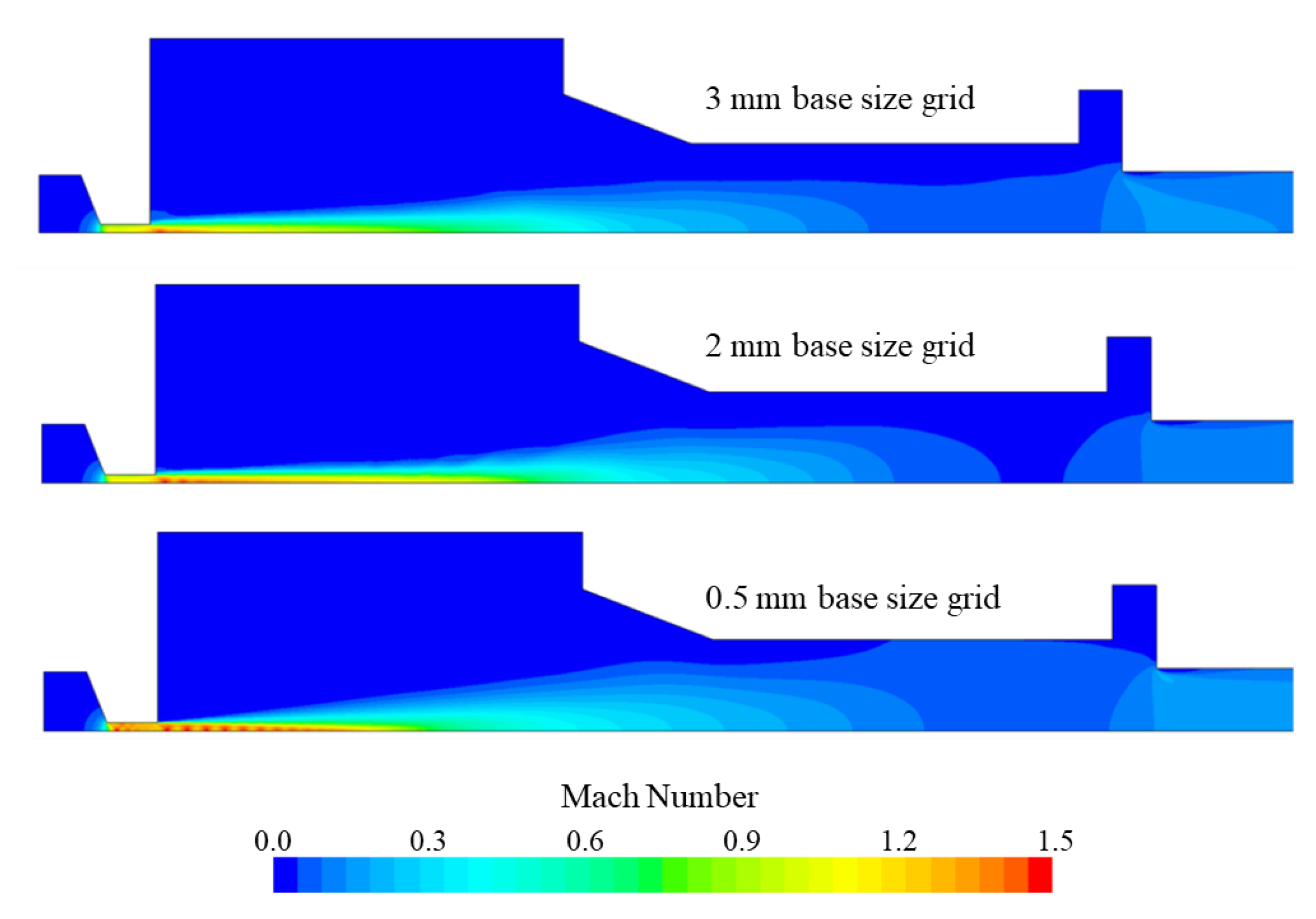
3. Computational Methods
4. Results
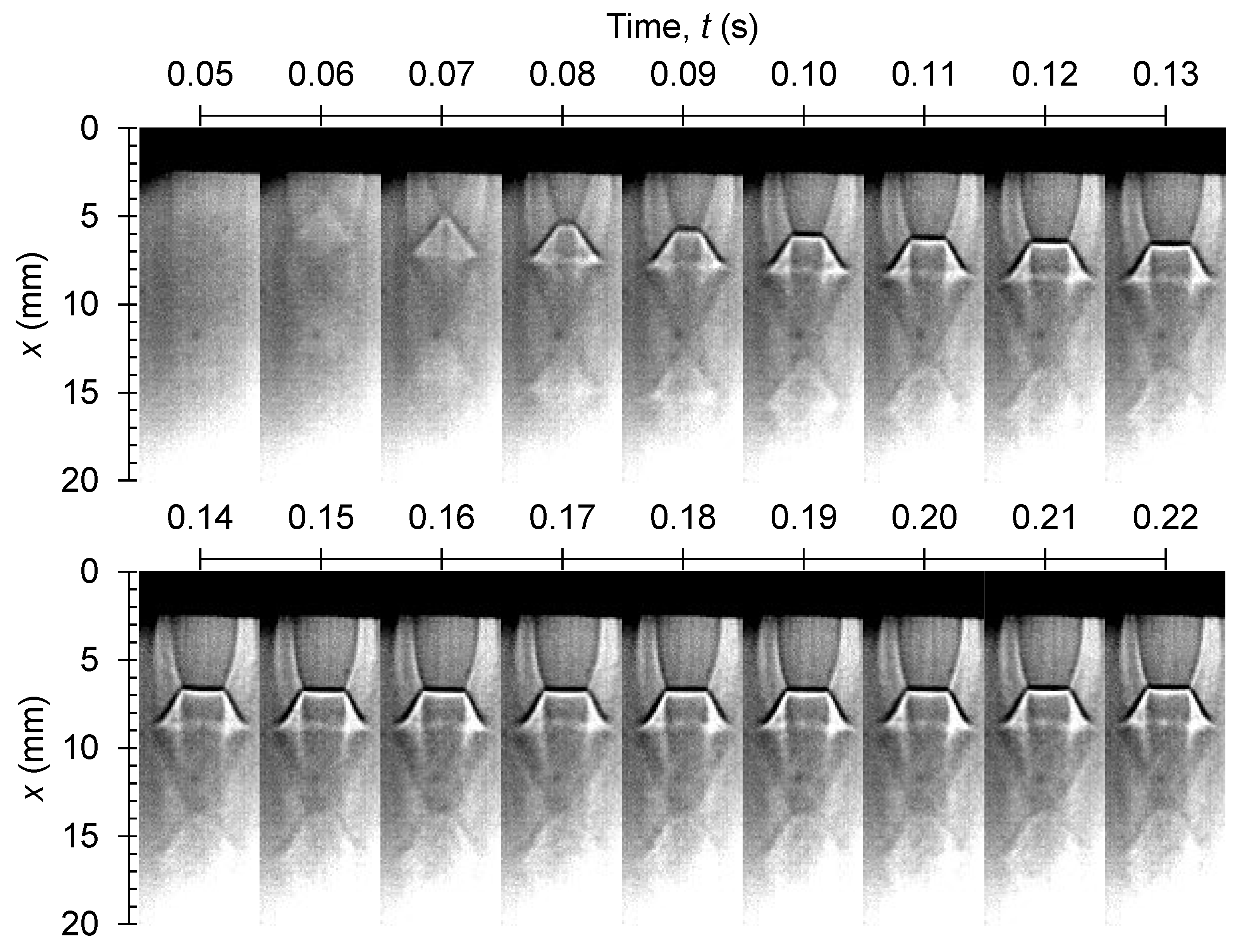
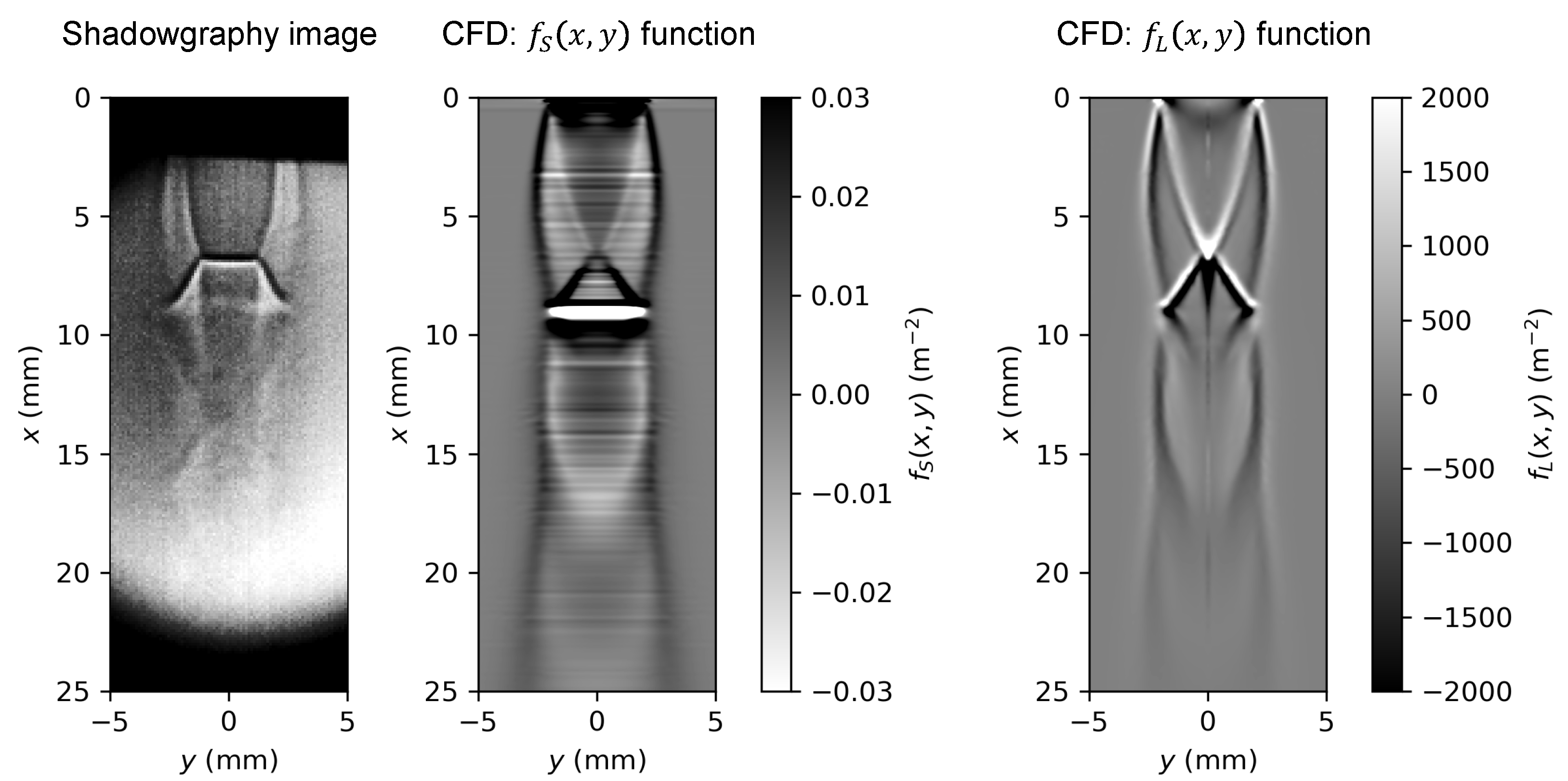
4.1. Shadowgraphy Results
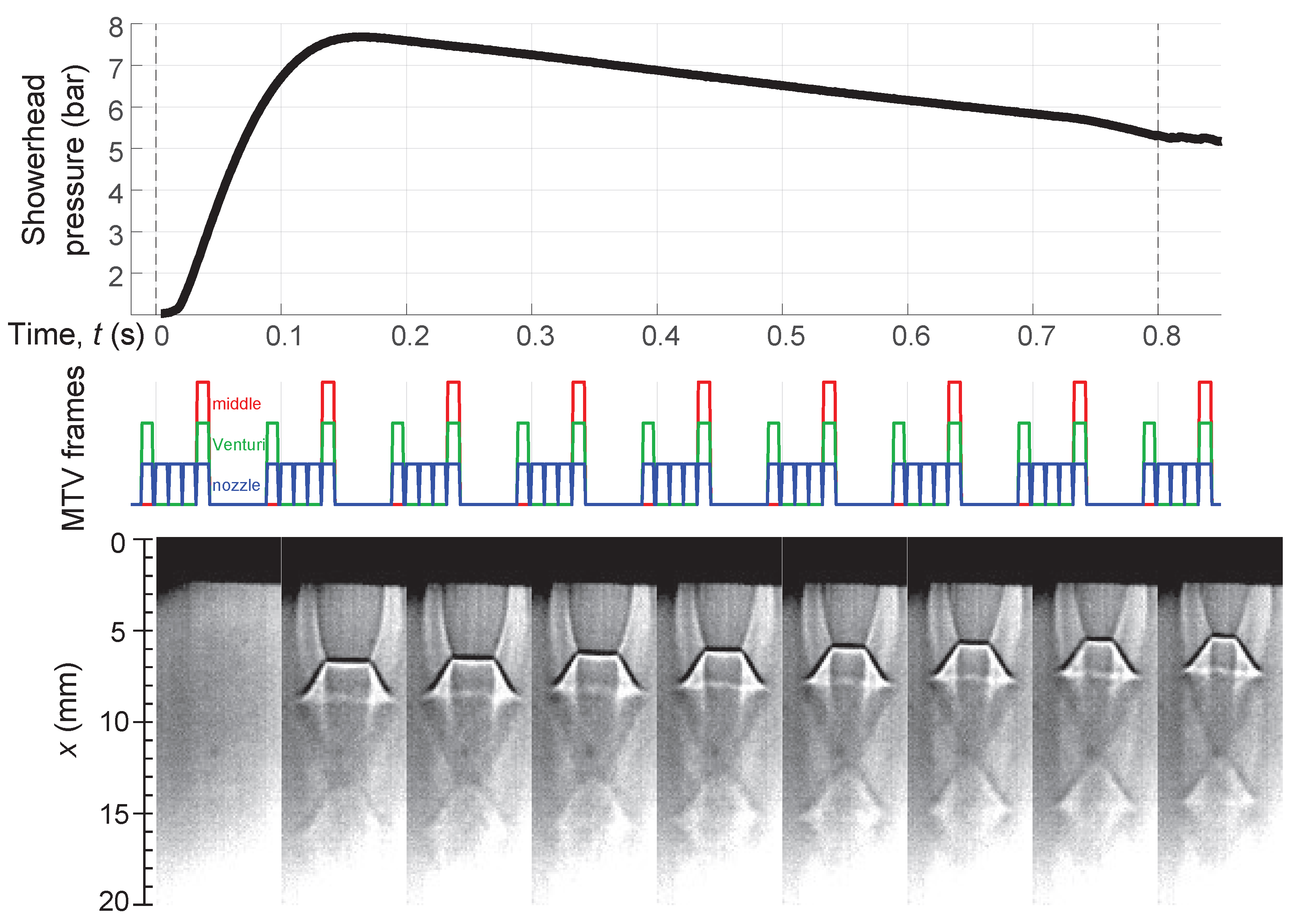
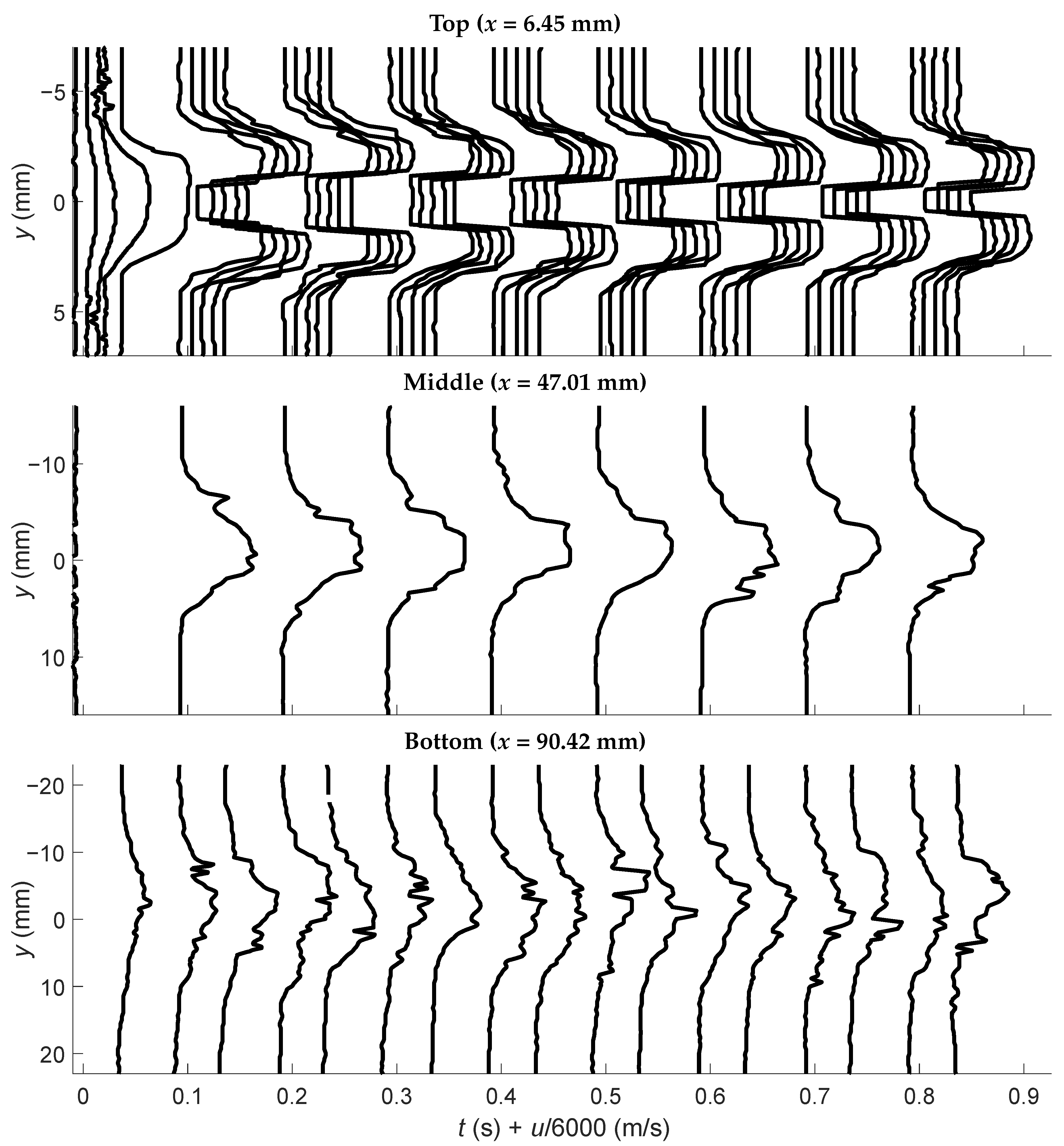
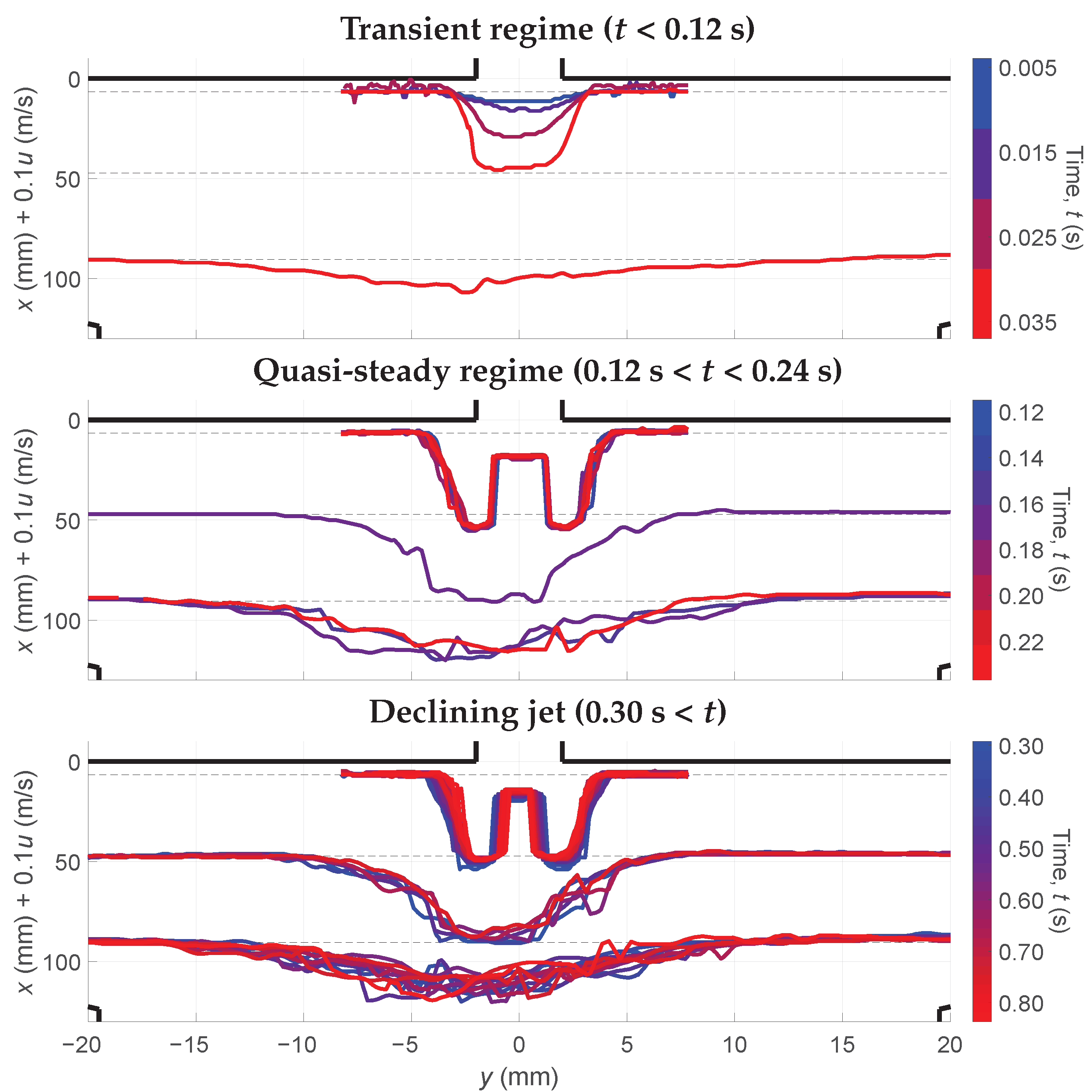
4.2. Molecular Tagging Velocimetry Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Numerical Shadowgraphy Functions
References
- Heidenreich, S. Chapter Eleven—Hot Gas Filters. In Progress in Filtration and Separation; Tarleton, S., Ed.; Academic Press: Oxford, UK, 2015; pp. 499–525. [Google Scholar]
- Ito, S. Pulse jet cleaning and internal flow in a large ceramic tube filter. In Gas Cleaning at High Temperatures; Clift, R., Seville, J.P.K., Eds.; Springer: Dordrecht, The Netherlands, 1993; pp. 266–279. [Google Scholar]
- Lo, L.M.; Hu, S.C.; Chen, D.R.; Pui, D.Y.H. Numerical study of pleated fabric cartridges during pulse-jet cleaning. Powder Technol. 2010, 198, 75–81. [Google Scholar] [CrossRef]
- Andersen, B.O.; Nielsen, N.F.; Walther, J.H. Numerical and experimental study of pulse-jet cleaning in fabric filters. Powder Technol. 2016, 291, 284–298. [Google Scholar] [CrossRef]
- Hsu, A.G.; Srinivasan, R.; Bowersox, R.D.; North, S.W. Two-component molecular tagging velocimetry utilizing NO fluorescence lifetime and NO2 photodissociation techniques in an underexpanded jet flowfield. Appl. Opt. 2009, 48, 4414–4423. [Google Scholar] [CrossRef] [PubMed]
- Inman, J.; Danehy, P.; Bathel, B.; Nowak, R. Laser-induced fluorescence velocity measurements in supersonic underexpanded impinging jets. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar]
- Parziale, N.J.; Smith, M.S.; Marineau, E.C. Krypton tagging velocimetry of an underexpanded jet. Appl. Opt. 2015, 54, 5094–5101. [Google Scholar] [CrossRef]
- Pitz, R.W.; Danehy, P.M. Molecular tagging velocimetry. In Optical Diagnostics for Reacting and Non-Reacting Flows: Theory and Practice; Steinberg, A., Roy, S., Eds.; AIAA: Reston, VA, USA, 2023; pp. 539–588. [Google Scholar]
- Stewart, J.R. CFD modelling of underexpanded hydrogen jets exiting rectangular shaped openings. Process Saf. Environ. Prot. 2020, 139, 283–296. [Google Scholar] [CrossRef]
- Hata, M.; Kanaoka, C.; Furuuchi, M.; Inagaki, T. Analysis of Pulse-Jet Cleaning of Dust Cake from Ceramic Filter Element; Technical Report; Kanazawa University: Kanazawa, Japan, 2002. [Google Scholar]
- Laux, S.B.H.U.; Giernoth, B.; Bulak, H.; Renz, U. Aspects of pulse-jet cleaning of ceramic filter elements. In Gas Cleaning at High Temperatures; Clift, R., Seville, J.P.K., Eds.; Springer: Dordrecht, The Netherlands, 1993; pp. 203–224. [Google Scholar]
- Morris, K.; Cursley, C.J.; Allen, R.W.K. The role of venturis in pulse-jet filters. Filtr. Sep. 1991, 28, 33–36. [Google Scholar] [CrossRef]
- Liu, X.; Shen, H. Effect of venturi structures on the cleaning performance of a pulse jet baghouse. Appl. Sci. 2019, 9, 3687. [Google Scholar] [CrossRef]
- André, M.A.; Burns, R.A.; Danehy, P.M.; Cadell, S.R.; Woods, B.G.; Bardet, P.M. Development and application of molecular tagging velocimetry for gas flows in thermal hydraulics. Nucl. Technol. 2019, 205, 262–271. [Google Scholar] [CrossRef]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ϵ eddy viscosity model for high Reynolds number turbulent flows. Comput. Fluids 2016, 24, 227–238. [Google Scholar] [CrossRef]
- Deng, X. A unified framework for non-linear reconstruction schemes in a compact stencil. Part 1: Beyond second order. J. Comput. Phys. 2023, 481, 112052. [Google Scholar] [CrossRef]
- Deng, X. A new open-source library based on novel high-resolution structure-preserving convection schemes. J. Comput. Sci. 2023, 74, 102150. [Google Scholar] [CrossRef]
- Vuorinen, V.; Yu, J.; Tirunagari, S.; Kaario, O.; Larmi, M.; Duwig, C.; Boersma, B.J. Large-eddy simulation of highly underexpanded transient gas jets. Phys. Fluids 2013, 25, 016101. [Google Scholar] [CrossRef]
- Hamzehloo, A.; Aleiferis, P.G. Numerical modelling of transient under-expanded jets under different ambient thermodynamic conditions with adaptive mesh refinement. Int. J. Heat Fluid Flow 2016, 61, 711–729. [Google Scholar] [CrossRef]
- Settles, G.S. Basic Concepts. In Schlieren and Shadowgraph Techniques: Visualizing Phenomena in Transparent Media; Springer: Berlin/Heidelberg, Germany, 2001; pp. 25–38. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lenci, G.; Fort, C.; André, M.A.; Petrov, V.; Jones, R.E.; Marks, C.R.; Bardet, P.M. Supersonic Pulse-Jet System for Filter Regeneration: Molecular Tagging Velocimetry Study and Computational Fluid Dynamics Validation. Appl. Sci. 2025, 15, 5764. https://doi.org/10.3390/app15105764
Lenci G, Fort C, André MA, Petrov V, Jones RE, Marks CR, Bardet PM. Supersonic Pulse-Jet System for Filter Regeneration: Molecular Tagging Velocimetry Study and Computational Fluid Dynamics Validation. Applied Sciences. 2025; 15(10):5764. https://doi.org/10.3390/app15105764
Chicago/Turabian StyleLenci, Giancarlo, Charles Fort, Matthieu A. André, Victor Petrov, Ryan E. Jones, Chuck R. Marks, and Philippe M. Bardet. 2025. "Supersonic Pulse-Jet System for Filter Regeneration: Molecular Tagging Velocimetry Study and Computational Fluid Dynamics Validation" Applied Sciences 15, no. 10: 5764. https://doi.org/10.3390/app15105764
APA StyleLenci, G., Fort, C., André, M. A., Petrov, V., Jones, R. E., Marks, C. R., & Bardet, P. M. (2025). Supersonic Pulse-Jet System for Filter Regeneration: Molecular Tagging Velocimetry Study and Computational Fluid Dynamics Validation. Applied Sciences, 15(10), 5764. https://doi.org/10.3390/app15105764





