Development of an In-Line Vision-Based Measurement System for Shape and Size Calculation of Cross-Cutting Boards—Straightening Process Case

Abstract

In the production process of cross-cutting boards, real-time measurement of dimensions online has been a long-standing technical problem in the production field. Currently, the detection of board dimensions in the production field relies on manual observation based on workers’ operational experience or stopping the machine for measurement. This paper proposes a machine vision-based real-time online measurement system for dimensional measurements of cross-cutting units. A certain angle measurement model is established by using a face-array industrial camera, and a more accurate edge contour extraction is realized by deep learning. A novel edge intersection extraction algorithm based on line fitting and least squares method was proposed to accurately measure the length, width, diagonal lines of cross-cutting boards using four intersection coordinates. The measurement of 100 cross-cutting boards in the industrial production site shows that the proposed online measurement system for cross-cut board dimensions in this article has high accuracy, with a length perception error of ±50 mm, width of ±2 mm, and diagonal difference of ±5 mm, meeting the production requirements in industrial settings. The on-site shutdown measurement work was reduced, thereby doubling the production efficiency and saving two staff members.

1. Introduction

With the continuous improvement of the shape and quality requirements for sheet and strip materials in the steel industry [1], straightening by tension bending is an important process for strip straightening, aiming to improve board shape [2]. Previous research on strip steel has mainly focused on issues such as warping and waviness, while there has been limited study on accurate measurement of strip dimensions during the straightening process in cross-cutting units. If there are significant deviations in strip dimensions, it can have a major impact on subsequent products and may result in scrap of cross-cut boards.

In the past, the sizing of board strips in the cross-cutting machine unit was mainly measured through manual sampling during shutdowns, which could only obtain accurate dimensions for some boards and could not reflect the sizes of all boards. This not only consumed a large amount of manpower and resources but also severely restricted production efficiency. Recently, with the rapid development of machine vision technology, its advantages such as fast detection speed, high accuracy, and strong robustness [3,4] have been widely popularized and applied in industrial measurement.

On the hot rolling mill, Montague [5] introduced a kind of strip slab arc machine vision measuring system, providing the basis for the slab radian control; the machine vision method it proposed has significant advantages in non-contact accuracy and real-time control, but the algorithm efficiency and multi-sensor fusion capability need to be further optimized. Wang’s [6] system, based on machine vision, for measuring the length of the large hot forging systematically evaluated the plate shape control ability of the hot rolling mill through the finite element method. Its theoretical analysis provided an important reference for the design and parameter optimization of the rolling mill, but there were limitations in the model dimension, dynamic control, and industrial verification. Feng’s [7] method, based on surface defect data augmentation (SDDA) enhancement of cold rolled steel sheet surface defect data, is a data augmentation method that has significant advantages in small sample processing and multimodal feature fusion, but the efficiency and environmental adaptability of the generative model need to be further optimized. Yuansong Wang [8] put forward a kind of DIC based on the convolution neural network (CNN) strain field image semantic segmentation technique; this method has significant advantages in the accuracy of automated detection and adaptability to complex damages, but the computational efficiency and generalization ability need to be further optimized. Shuzong Yan [9] proposed a system based on machine vision technology and image detection and non-contact online measurement for strip deviation; the core advantage of this system lies in non-contact, high-precision, and real-time measurement, but it has limitations in terms of environmental adaptability, computational efficiency. and data dependence. Stavropoulos [10] proposed a computationally efficient PBF-LB/M thermal modeling method; through the innovative combination of enthalpy methods and multi-scale strategies, it provides an efficient simulation tool for thermal management in additive manufacturing. Its core advantage lies in the balance between computational efficiency and accuracy. However, model simplification and dynamic adaptability remain the main limitations. In the future, data-driven methods and multi-physics coupling technologies need to be integrated to address more complex industrial demands.

In this paper, an online real-time measurement system with fast and high accuracy is proposed. The size of the cross-cutting board straightening is based on visual inspection, which achieves online real-time measurement of the length, width, and diagonal of the cross-cutting board. Compared with the above-mentioned work, this measurement system has high computational efficiency, low missed detection rate, and higher robustness.

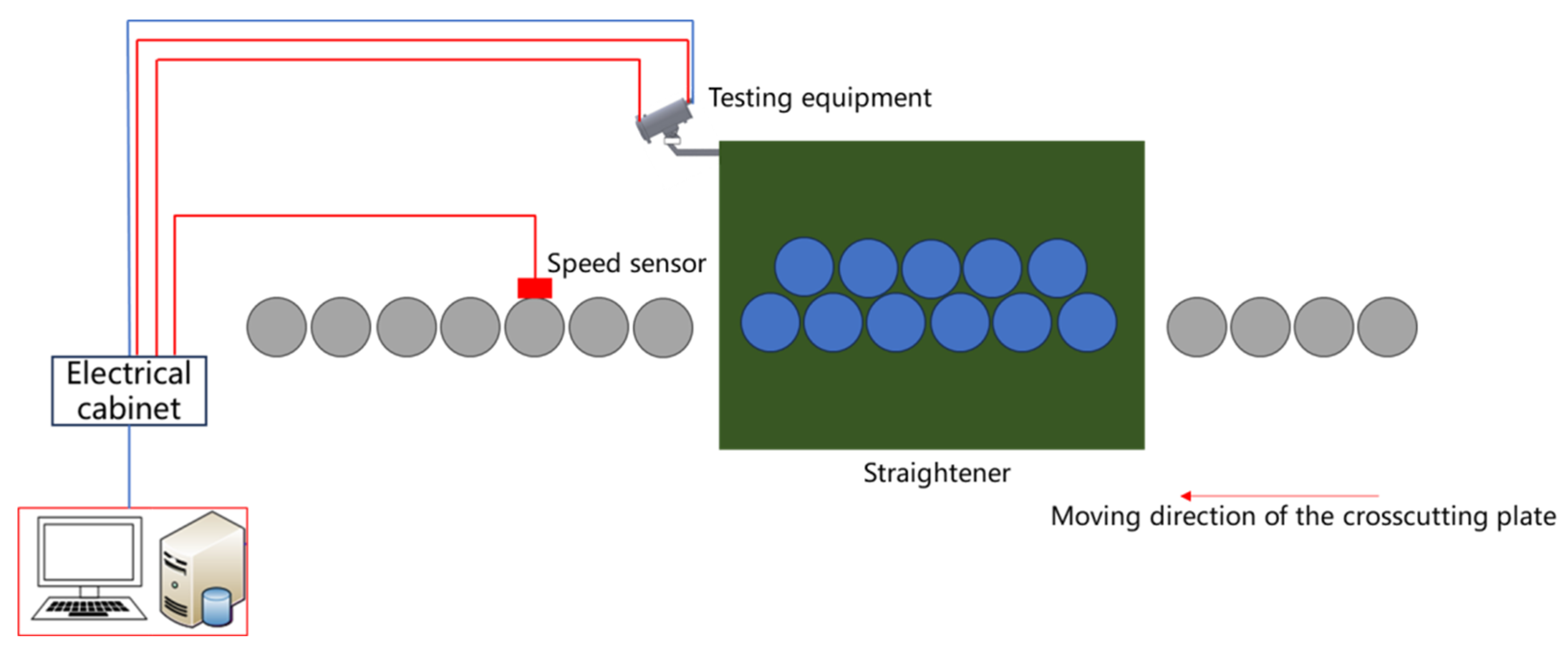
2. Online Measurement System Overall Architecture

When the cross-cutting board bites into the straightening machine, the CMOS area array industrial camera is activated and starts real-time imaging of the cross-cutting board. Then, the images are transmitted to the image processing industrial control computer in the control room through a gigabit Ethernet cable and optical fiber. The industrial control computer processes images in real time, calculates the length, width, and diagonal of the cross-cutting board, and visualizes these values in real time.

The layout of the online measurement system for board size during the straightening process of the cross-cutting unit proposed in this article is shown in Figure 1. According to the requirements of industrial sites, the detection equipment can be flexibly installed at the entrance and exit of the straightening machine frame, and the height and angle of the equipment can be adjusted flexibly according to the industrial site environment, achieving precise measurement of cross-cutting board dimensions.

2.1. Optical Equipment

The optical equipment contains 1 CMOS area array industrial camera, 1 industrial lens, 1 laser sensor, 1 industrial switch and single-mode optical fiber. These equipments were purchased from Hikvision, Hangzhou and China. The pixel count of the area array camera sensor is 4096 × 3000. For the sake of the long-distance identification, a 12-million-pixel lens with 25 mm focal length is selected. To accurately trigger the camera’s operation, an ultra-compact and sensitive red light laser sensor was selected.

2.2. Detecting System Fixed Device

The fixing devices of this measurement system mainly include a camera cooling system, universal joint, fixed bracket, camera fixing board, and shock absorption damping. Since both the inlet and outlet of the straightening machine are equipped with centering devices, the measurement system introduced in this article has a certain inclination angle when measuring the cross-cutting board. Therefore, the installation of the measurement system has some characteristics. Firstly, the industrial camera fixing plate is used to fix the camera inside the camera cooling system device. At the same time, the camera cooling system device is fixed with the universal joint using screws. Secondly, the universal joint is fixed on the fixing bracket with bolts, and the fixing bracket is fixed on the straightener platform from above with bolts. Bolts are reinforced by spot welding. In addition, shock absorption damping is installed at all fastening points to reduce vibrations that may occur on site. Furthermore, the installation of the measurement system on the production site can be achieved, and the measurement system can be adjusted at any angle through universal joints.

3. Measurement System Measures the Core Algorithm

The algorithm flow of the online measurement system for the size of the straightening process board in the cross-cutting machine unit is shown in Figure 2. Firstly, the internal and external parameters of the industrial camera were determined by the calibration method, and the calibration files were generated. The acquisition frequency and exposure level of the industrial camera were determined according to the moving speed of the cross-cutting board, the network bandwidth, and the production environment, and the preparation work for the inspection was completed. When the cross-cutting board passes through the laser sensor, it triggers the CMOS array industrial camera installed above the straightening machine to start working, capturing real-time images of the cross-cutting board and preprocessing them. Then, the Canny algorithm is used to perform edge measurements on the cross-cutting board. The length is calculated by detecting the speed of the cross-cutting board using a velocity sensor, and then obtaining the numerical value of its length through the formula for variable motion distance.

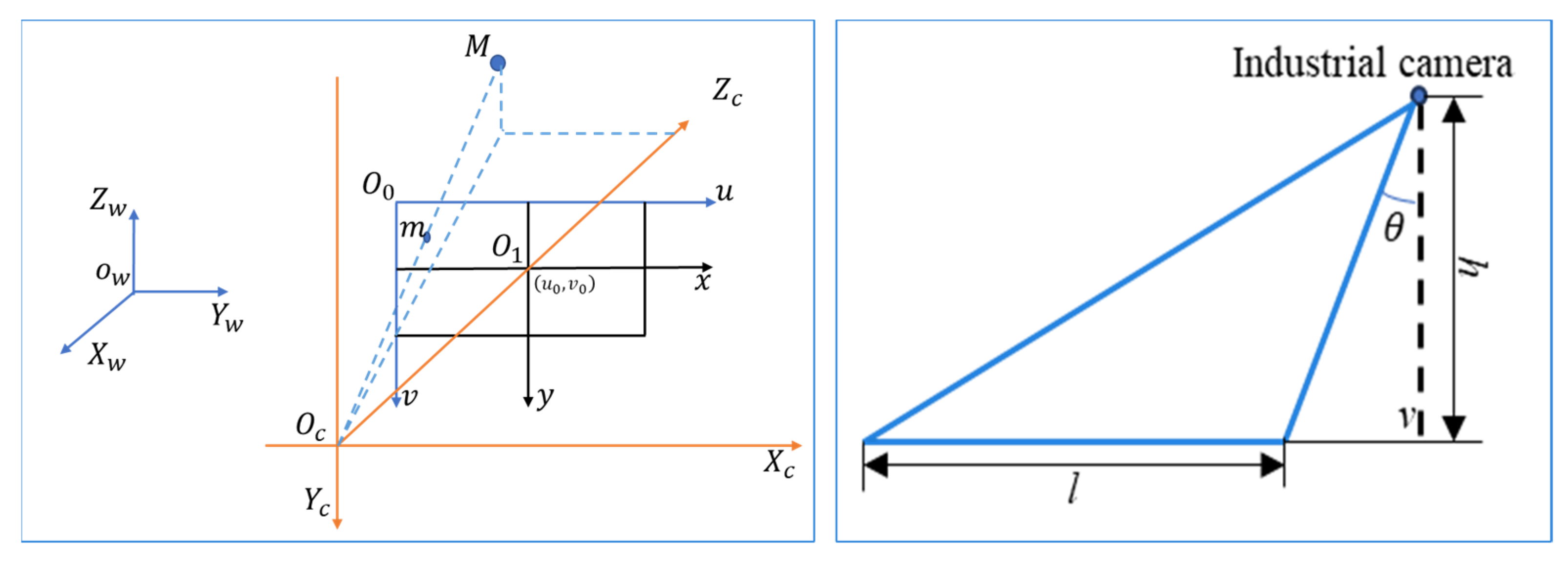
3.1. Measurement Principle

The detection principles and methods of monocular vision have been extensively studied [11] and are relatively mature. The detection principle coordinate system is shown in Figure 3. $u{O}_{0}v$ is the image pixel coordinate system, $x{O}_{1}y$ is the image physical coordinate system, $O_c{X}_c{Y}_c{Z}_c$ is the camera coordinate system, $O_w{X}_w{Y}_w{Z}_w$ is the world coordinate system. The length of $O_1{O}_c$ is the focal length $f$ of the camera.

Mathematical relationship between the world coordinate system and the camera coordinate system:

$$\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]=\left[\begin{array}{cc}R& T\\ 0& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]$$

(1)

Camera coordinate system and image mathematical relationship exists between the physical coordinate system:

$$s\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{ccc}f& 0& \begin{array}{cc}0& 0\end{array}\\ 0& f& \begin{array}{cc}0& 0\end{array}\\ 0& 0& \begin{array}{cc}1& 0\end{array}\end{array}\right]\left[\begin{array}{c}{X}_c\\ Y_c\\ Z_c\\ 1\end{array}\right]$$

(2)

Mathematical relationship between the physical coordinate system of an image and image pixel coordinate system; $dx,dy$ represents the length of a unit pixel on the x and y axes in the coordinate system $x{O}_{1}y$:

$$\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}1/dx& 0& u_0\\ 0& 1/dy& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ 1\end{array}\right]$$

(3)

Mathematical relationship between world coordinate system and image pixel coordinate system:

$$\begin{array}{c}s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}1/dx& 0& u_0\\ 0& 1/dy& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}f& 0& \begin{array}{cc}0& 0\end{array}\\ 0& f& \begin{array}{cc}0& 0\end{array}\\ 0& 0& \begin{array}{cc}1& 0\end{array}\end{array}\right]\left[\begin{array}{cc}R& T\\ 0& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]\\ =\left[\begin{array}{ccc}{f}_x& 0& \begin{array}{cc}{u}_0& 0\end{array}\\ 0& f_y& \begin{array}{cc}{v}_0& 0\end{array}\\ 0& 0& \begin{array}{cc}1& 0\end{array}\end{array}\right]\left[\begin{array}{cc}R& T\\ 0& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]\end{array}$$

(4)

Due to the impact of the site environment, there is a slight tilt angle between the measurement system and the cross-cutting board in order to correct the skew error of the $u{O}_{0}v$ coordinate system’s axes. Introducing parameters $\gamma =f_x•\tan \theta$, $\gamma =f_x•\tan \theta$ is a key term in the camera tilt model that describes geometric deformation or correction. Its essence is the product of the focal length and the tangent of the tilt angle, reflecting the coupled influence of tilt installation on the image coordinates. By embedding it into the homography matrix or coordinate mapping formula, high-precision image correction and measurement can be achieved. In practical applications, parameters need to be optimized in combination with calibration data to ensure the robustness of the model. $\theta$ indicates the degree of inclination of a plane along the $v$-axis; its value was obtained through experiments on different angles; h is the distance from the industrial camera to the roller conveyor; l represents the maximum field of view of the measurement system. The Equation (4) can be written as follows:

$$\begin{array}{c}s\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}1/dx& \gamma & u_0\\ 0& 1/dy& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}f& 0& \begin{array}{cc}0& 0\end{array}\\ 0& f& \begin{array}{cc}0& 0\end{array}\\ 0& 0& \begin{array}{cc}1& 0\end{array}\end{array}\right]\left[\begin{array}{cc}R& T\\ 0& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]\\ =\left[\begin{array}{ccc}{f}_x& \gamma & \begin{array}{cc}{u}_0& 0\end{array}\\ 0& f_y& \begin{array}{cc}{v}_0& 0\end{array}\\ 0& 0& \begin{array}{cc}1& 0\end{array}\end{array}\right]\left[\begin{array}{cc}R& T\\ 0& 1\end{array}\right]\left[\begin{array}{c}{X}_w\\ Y_w\\ Z_w\\ 1\end{array}\right]\end{array}$$

(5)

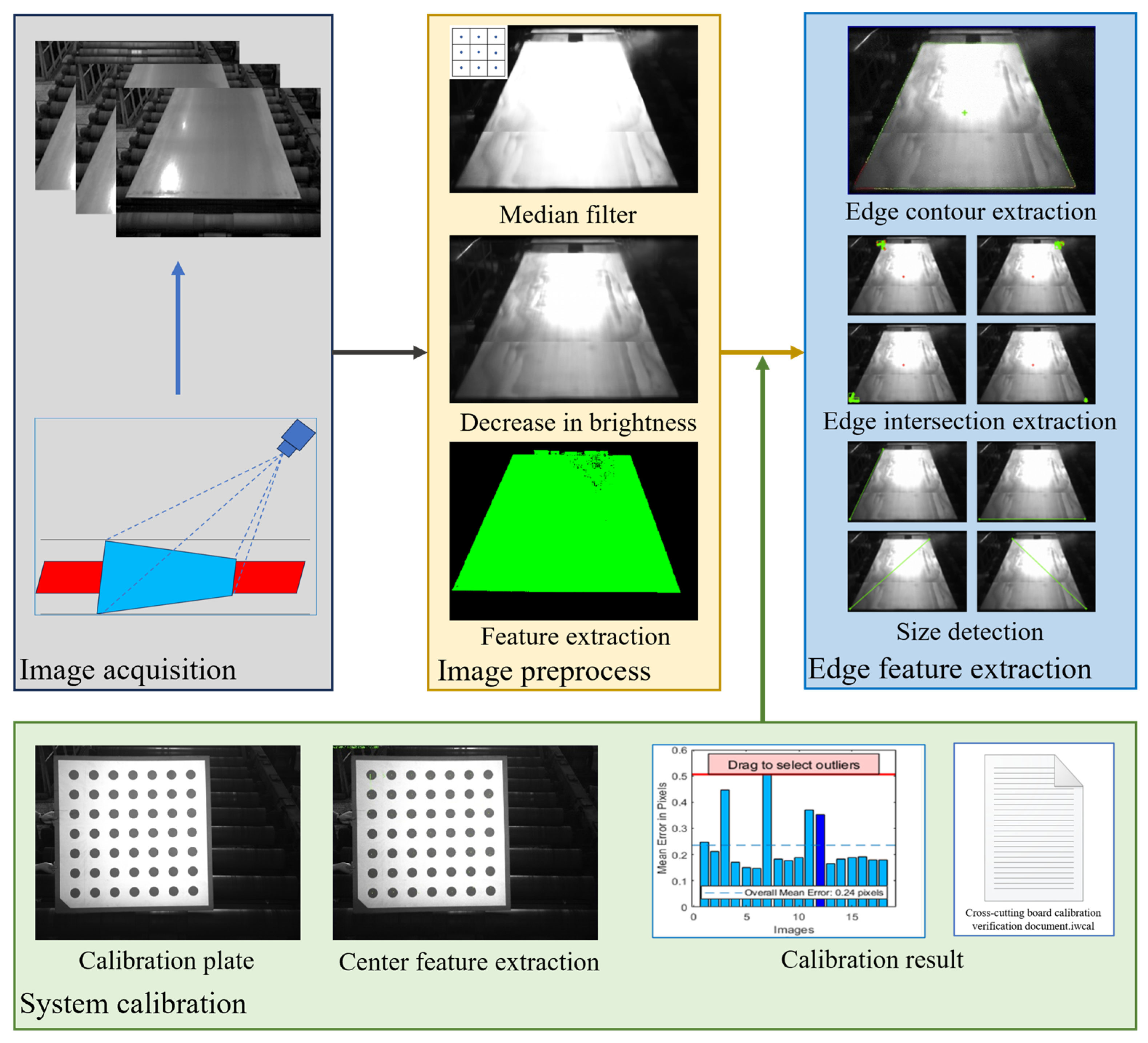
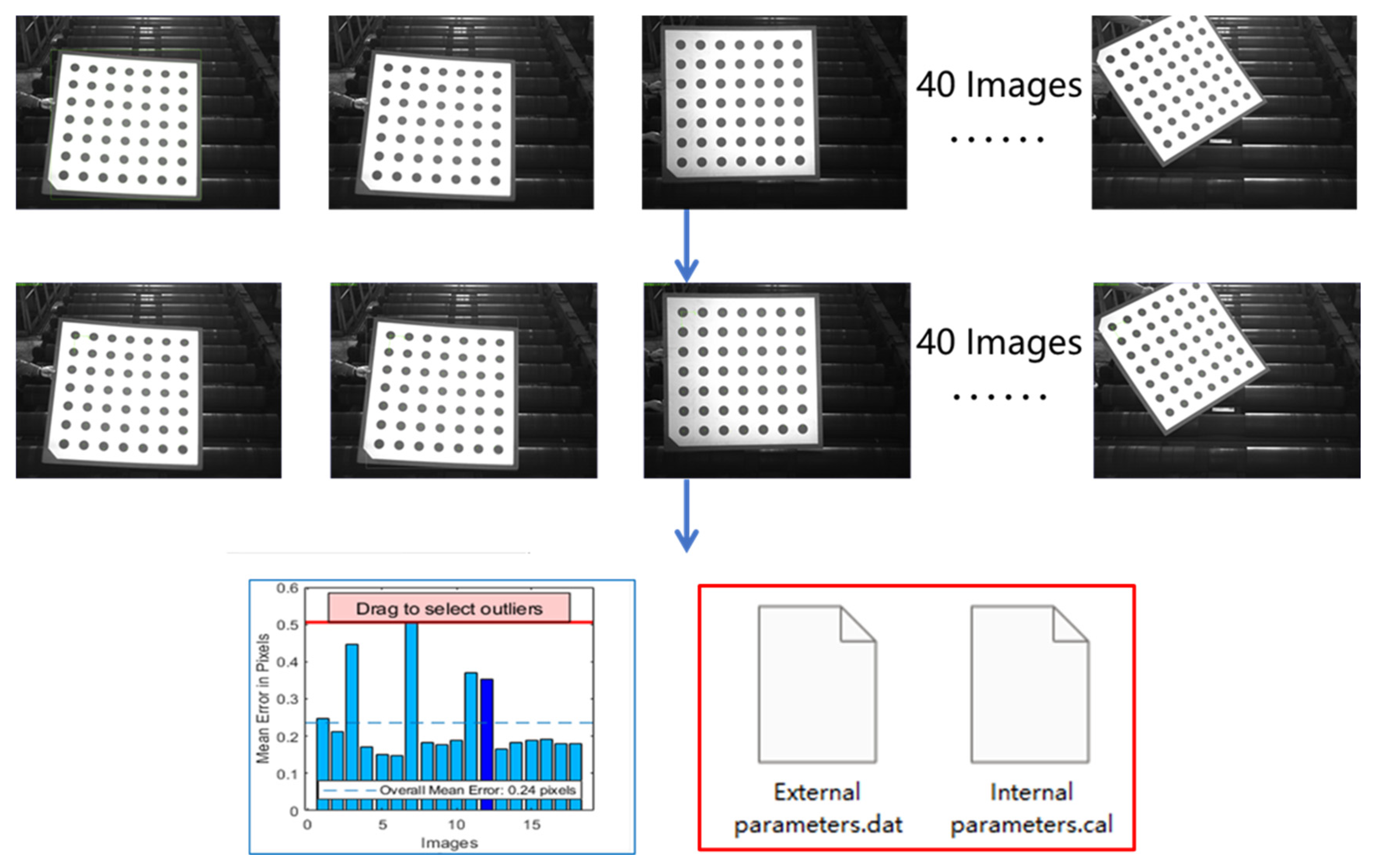
3.2. System Calibration Detection

Based on the detection principle, this paper uses Zhang Zhengyou’s calibration algorithm [12] to calibrate industrial cameras. The calibration plate used was a 7 × 7 circular calibration plate with a size of 1000 × 1000 × 5 mm, as shown in Figure 4.

Field calibration image acquisition, through the acquisition of image calibration plate image of circle center recognition processing, determine the pixel coordinates of the center of the circle and the parameter relationship between the world coordinates, and then calculate the internal and external parameters of the camera and complete the measurement system calibration work, as shown in Figure 5.

3.3. Image Preprocessing

In the process of collecting cross-cutting board images, image quality is influenced by numerous factors. In addition to hardware factors such as cameras, lenses, and lighting used for image acquisition, adverse environmental conditions at the scene can also have a significant impact on cross-cutting board images. For example, factors such as light intensity and vibration can have a certain impact on the detection accuracy. For instance, excessive or insufficient light intensity can result in unclear image acquisition, and in severe cases, no image may be captured at all. Vibration of the on-site detection equipment directly affects the detection accuracy, which has been addressed in Section 2.2 by installing shock-absorbing dampers during device installation. The impact caused by light intensity needs to be resolved through image preprocessing. Therefore, image preprocessing is often an indispensable part in visual measurement, which can greatly eliminate the non-ideal information in the image and enhance the real feature effect of the image. Commonly used image preprocessing mainly includes image filtering and noise reduction, threshold segmentation, morphological processing, and so on [13,14,15].

(1)

Median Filtering

Median filtering is to cover the original image with a certain window shape according to a certain moving order, calculate the median value of all the pixels in the area, and use this value to represent the center pixel of the covered area.

$$G\left(x,y\right)=med\left\{f\left(x-k,y-l,k,l\in W\right)\right\}$$

(6)

The process of the filtering algorithm is simple and easy to implement with less effect on the image boundary, as shown in Figure 6.

(2)

Cross-cutting board feature extraction

Image feature extraction is based on image gray level, shape, and other parameters; the image is divided into different sub-regions to remove unnecessary information and extract target features. The extracted image shows obvious differences between different regions, while the same feature shows a high degree of similarity. The automatic threshold segmentation algorithm is based on an image gray histogram to determine the gray threshold; no obvious difference in the background and the target gray has a good feature extraction effect under the condition [16]. In this paper, an adaptive threshold image feature extraction algorithm based on the maximum measure of inter-class variance is proposed. The adaptive threshold image feature extraction algorithm can effectively solve the impact caused by unstable on-site lighting intensity. It adjusts the system exposure according to changes in lighting intensity, thereby ensuring the clarity of captured images.

If the image can be divided into target feature Y, background and other interference factors Z after automatic segmentation, then the distribution of pixel values of the same category should be uniform, and the distribution of pixel values between classes should be significantly different [17]. Researchers often use the variance to measure the homogeneity of class or differences; an optimal threshold can maximize the variance between target class A and background class B [18,19].

The between-class variance ${\sigma }^2\left(K\right)$ can be represented as follows:

$${\sigma }^2\left(K\right)=P_A{\left({\mu }_A-\mu \right)}^2+P_B\left({\mu }_B-\mu \right)$$

(7)

In the equation, ${\sigma }^2\left(K\right)$ is the between-class variance;

$K$ is the optimal threshold for maximizing variance;

$P_A,{\mu }_A,P_B,{\mu }_B$ are the probabilities and means of the grayscale values appearing in two categories of pixels, A and B.

$\mu$ represents the average grayscale value of the overall image.

$$\left\{\begin{array}{l}{P}_A={\displaystyle \sum _{i=1}^K{P}_i=P\left(K\right)}\\ P_B={\displaystyle \sum _{i=K+1}^K{P}_i=1-P\left(K\right)}\end{array}\right.$$

(8)

$$\left\{\begin{array}{l}{\mu }_A={\displaystyle \frac{{\displaystyle \sum _{i=1}^{K}i{P}_i}}{P_A}}={\displaystyle \frac{\mu \left(K\right)}{P\left(K\right)}}\\ {\mu }_B={\displaystyle \frac{{\displaystyle \sum _{i=K+1}^{M}i{P}_i}}{P_B}}={\displaystyle \frac{\mu -\mu \left(K\right)}{1-P\left(K\right)}}\end{array}\right.$$

(9)

$$\mu ={\displaystyle \sum _{i=1}^{M}i{P}_i}$$

(10)

Image feature extraction algorithm: an adaptive threshold in the process of detection can effectively differentiate between target and background image, as shown in Figure 7.

(3)

Extraction of contour of cross-cutting board edge

Deep learning extracts edge contours.

Due to the cross-cutting board always being in motion during the straightening process, the traditional Canny algorithm [20,21,22,23,24] may have the problem of processing lag. Therefore, the latest deep learning edge contour feature extraction is adopted in this paper.

In addition to using the Canny algorithm for edge contour extraction, this article also compares it with a new method that employs deep learning to extract edge contours.

Deep learning methods:

Using the manual marking method, carefully annotate each image and draw the contour line of the transverse strip. This process not only improves the recognizability of images, but also provides a necessary foundation for subsequent feature extraction based on deep learning. During the annotation process, curvature constraint annotation specifications and a two-person mutual review mechanism are used to ensure contour accuracy, ultimately generating a multidimensional annotation file containing coordinate sequences and semantic masks (see Figure 8 for manual calibration results). After completing the manual labeling, as shown in Figure 8, we divided the dataset into different parts, including the cross-cutting board part and the background part, for the purpose of model training and evaluation. Specifically, 70% of the data will be used for training so that the model can learn sufficient features; 15% is used for validation to monitor the performance of the model and adjust hyperparameters. The remaining 15% will be used for testing to evaluate the model’s generalization ability on unseen data. Considering the complex imaging variations in industrial scenes, this paper uses an enhanced model for training. The model is based on the U-Net++ architecture for industrial scene adaptation and has attention mechanisms for multi-scale feature extraction and contour prior guidance. To enhance the robustness of the model, a multimodal data augmentation strategy is implemented before training, which specifically includes the following.

Luminous domain enhancement: implement ±20% brightness adjustment (simulating ±10% voltage fluctuations of LED lighting in the workshop), ±15% contrast stretching (adapting to the reflection difference of Ra = 0.2–1.6 μm on the surface of the strip), and ±20% saturation perturbation (processing color shift caused by strip surface reflection) in binary images.

The training results of the model show that the loss rate is between 0.03 and 0.06, indicating good performance of the model during training and demonstrating good convergence. A low loss rate signifies that the model can effectively learn the features in the dataset without overfitting, as shown in Figure 9.

In the training results, we observed that the recognition rate of the contour of the strip remained stable at around 99%, indicating that the model performed well in effectively segmenting the transverse board from the background. This high recognition rate indicates that the model can accurately identify the contour of the strip in most cases and successfully capture key information. However, it is worth noting that the model may still encounter some issues in cases of poor image quality or blurring. For example, leakage occurs from time to time, resulting in some strip contours not being correctly identified. Meanwhile, the model may also incorrectly identify multiple points in the background as part of the strip, leading to unnecessary fitting. In addition, in some cases, the model may also incorrectly recognize the background in the middle of the strip, further affecting the accuracy of recognition. These issues are directly related to the completeness of dynamic fuzzy simulation and the learning efficiency of low contrast edge features in data augmentation strategies. Subsequently, optimization can be achieved by introducing edge gradient loss and motion compensation convolution.

4. Measurement of the Length, Width, and Diagonal of a Cross-Cutting Board

The above implementation accurately extracts the contour of the cross-cutting board’s edges. In this chapter, two options are proposed to calculate the length, width, and diagonal of the cross-cutting board. Option 1: a novel edge intersection extraction algorithm is used to process the edges. By fitting straight lines to the extracted edge contours and then solving for their intersections pairwise, the four precise intersection points of the cross-cutting board are obtained, namely Intersection 1 $\left(x_1,y_1\right)$, Intersection 2 $\left(x_2,y_2\right)$, Intersection 3 $\left(x_3,y_3\right)$, and Intersection 4 $\left(x_4,y_4\right)$. The measurements of length, width, and diagonal of the cross-cut board are calculated based on these four world coordinates, as shown in Figure 10.

4.1. Fitting Straight Lines to Edge Contours

The result of extracting the contour of the cutting board edge is a point cloud collection formed by numerous points, rather than a single line, as shown in Figure 11.

Therefore, in order to accurately locate and identify the intersection points of the edge, it is necessary to perform line fitting on the point cloud of the cross-cutting board’s edge contour. The commonly used fitting methods include the algebraic approximation method, orthogonal distance regression method, and least squares method [25,26,27,28]. This article uses the least squares method to achieve linear fitting. The least squares method matches the optimal point coordinates by finding the minimum sum of squared errors.

Linear regression:

Assume that the equation of the fitted line is as follows:

$$y=kx+b$$

(11)

Among them, $k$ represents the slope of the line, $b$ represents the intercept. Assuming that the coordinates of points on the linear contour are $\left(x_i,y_i\right)$ with a total quantity of $M$, $x_i$ is known accurately; the least squares method aims to find suitable values for $k$ and $b$ in order to minimize the weighted sum ($Q_l$) of squared deviations in $y_i$. This can be expressed as follows:

$$Q_l={{\displaystyle \sum _{i=1}^M\left[y_i-\left(kx+b\right)\right]}}^2$$

(12)

Taking the partial derivative of Equation (12) and rearranging, we obtain the following:

$$\left\{\begin{array}{l}bM+k{\displaystyle \sum x_i={\displaystyle \sum y_i}}\\ b{\displaystyle \sum x_i+k{\displaystyle \sum {x_i}^2={\displaystyle \sum x_i{y}_i}}}\end{array}\right.$$

(13)

Assuming that the four edges of the cross-section board can be fitted with a linear equation,

Line one:

$$y_1=k_1{x}_1+b_1$$

(14)

Then:

$$Q_{l1}={{\displaystyle \sum _{i=1}^{M_1}\left[y_{1i}-\left(k_1{x}_1+b_1\right)\right]}}^2$$

(15)

Taking the partial derivative of Equation (15):

$$\left\{\begin{array}{l}{b}_1{M}_1+k_1{\displaystyle \sum x_{1i}={\displaystyle \sum y_{1i}}}\\ b_1{\displaystyle \sum x_{1i}+k_1{\displaystyle \sum {x_{1i}}^2={\displaystyle \sum x_{1i}{y}_{1i}}}}\end{array}\right.$$

(16)

Line two:

$$y_2=k_2{x}_2+b_2$$

(17)

Then:

$$Q_{l2}={{\displaystyle \sum _{i=1}^{M_2}\left[y_{2i}-\left(k_2{x}_2+b_2\right)\right]}}^2$$

(18)

Taking the partial derivative of Equation (18),

$$\left\{\begin{array}{l}{b}_1{M}_1+k_1{\displaystyle \sum x_{2i}={\displaystyle \sum y_{2i}}}\\ b_1{\displaystyle \sum x_{2i}+k_1{\displaystyle \sum {x_{2i}}^2={\displaystyle \sum x_{2i}{y}_{2i}}}}\end{array}\right.$$

(19)

Line three:

$$y_3=k_3{x}_3+b_3$$

(20)

Then:

$$Q_{l3}={{\displaystyle \sum _{i=1}^{M_3}\left[y_{3i}-\left(k_3{x}_3+b_3\right)\right]}}^2$$

(21)

Taking the partial derivative of Equation (21),

$$\left\{\begin{array}{l}{b}_3{M}_3+k_3{\displaystyle \sum x_{3i}={\displaystyle \sum y_{3i}}}\\ b_3{\displaystyle \sum x_{3i}+k_3{\displaystyle \sum {x_{3i}}^2={\displaystyle \sum x_{3i}{y}_{3i}}}}\end{array}\right.$$

(22)

Line four:

$$y_4=k_4{x}_4+b_4$$

(23)

Then:

$$Q_{l4}={{\displaystyle \sum _{i=1}^{M_4}\left[y_{4i}-\left(k_4{x}_4+b_4\right)\right]}}^2$$

(24)

Taking the partial derivative of Equation (24),

$$\left\{\begin{array}{l}{b}_4{M}_4+k_4{\displaystyle \sum x_{4i}={\displaystyle \sum y_{4i}}}\\ b_4{\displaystyle \sum x_{4i}+k_4{\displaystyle \sum {x_{4i}}^2={\displaystyle \sum x_{4i}{y}_{4i}}}}\end{array}\right.$$

(25)

For example, taking the cross-cutting board image shown in this article, the calculated results for fitting line parameters are shown in

Table 1. Calculation results of fitting line parameters.

Line Name	Slope k	Intercept b
Line one	0	5030
Line two	$-{\displaystyle \frac{5020}{101}}$	$-{\displaystyle \frac{3,472,830}{101}}$
Line three	0	5010
Line four	${\displaystyle \frac{5020}{101}}$	$-{\displaystyle \frac{3,472,830}{101}}$

.

From Table 1, it can be concluded that the linear fitting has a good effect, and the equations for the four lines can be obtained.

Line one:

$$y_1=5030$$

(26)

Line two:

$$y_2=-{\displaystyle \frac{5020}{101}}x-{\displaystyle \frac{3,472,830}{101}}$$

(27)

Line three:

$$y_3=5010$$

(28)

Line four:

$$y_4={\displaystyle \frac{5020}{101}}x-{\displaystyle \frac{3,472,830}{101}}$$

(29)

The results of the straight-line fitting for the point cloud on the edge of the cross-cutting board are shown in Figure 12.

4.2. Measurement of Cross-Cutting Board Dimensions

(1)

Measurement of width and diagonal

The equations of lines one, two, three, and four obtained from 4.1 yield the four intersection points of the cross-cutting plate:

The intersection 1 $\left(x_1,y_1\right)$ can be obtained from line 1 and line 2, as shown in Equation (30):

$$\left\{\begin{array}{l}{y}_1=k_1{x}_1+b_1\\ y_2=k_2{x}_2+b_2\end{array}\right.$$

(30)

The intersection 2 $\left(x_2,y_2\right)$ can be obtained from line 1 and line 4, as shown in Equation (31):

$$\left\{\begin{array}{l}{y}_1=k_1{x}_1+b_1\\ y_4=k_4{x}_4+b_4\end{array}\right.$$

(31)

The intersection 3 $\left(x_3,y_3\right)$ can be obtained from line 2 and line 3, as shown in Equation (32):

$$\left\{\begin{array}{l}{y}_2=k_2{x}_2+b_2\\ y_3=k_3{x}_3+b_3\end{array}\right.$$

(32)

The intersection 4 $\left(x_4,y_4\right)$ can be obtained from line 3 and line 4, as shown in Equation (33):

$$\left\{\begin{array}{l}{y}_3=k_3{x}_3+b_3\\ y_4=k_4{x}_4+b_4\end{array}\right.$$

(33)

Then measure the width (W):

$$W=\sqrt{{\left(y_2-y_1\right)}^2+{\left(x_2-x_1\right)}^2}$$

(34)

Measurement of the difference between two diagonals is $\mathrm{\Delta }d$:

$$\mathrm{\Delta }d=\sqrt{{\left(y_3-y_2\right)}^2+{\left(x_3-x_2\right)}^2}-\sqrt{{\left(y_4-y_1\right)}^2+{\left(x_4-x_1\right)}^2}$$

(35)

(2)

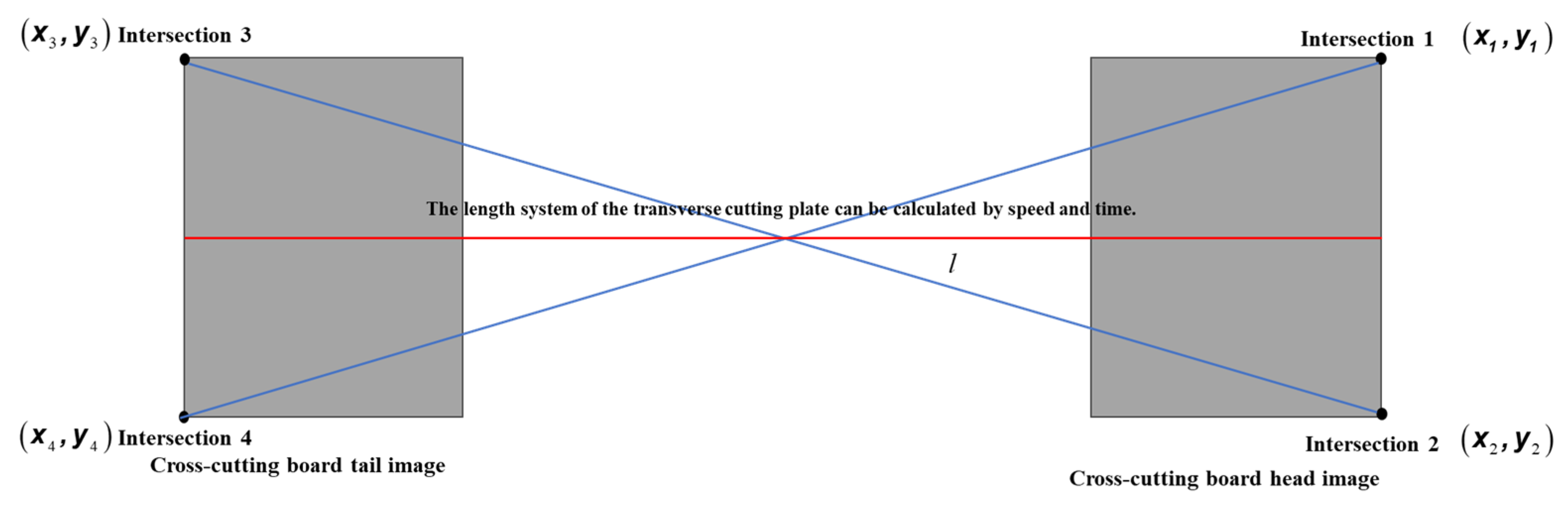
Measurement of length (l)

Due to the problem of the tilt angle of the industrial camera and the length of the cross-cut board, using four intersection points for length calculation results in a large error, which cannot meet the needs of on-site production. Therefore, in terms of length measurement, this system uses a speed sensor to detect the real-time running speed of the cross-cut board, and then obtains its length through Equation (36).

$$l=\underset{\lambda \to 0}{\lim }{\displaystyle \sum _{i=1}^n{v}_i}\mathrm{\Delta }{t}_i$$

(36)

If the i-th time interval in the cross-cutting board motion is $\left[t_{i-1},t_i\right]$, then $\mathrm{\Delta }{t}_i=t_i-t_{i-1}$. In the equation $\lambda =\max \left\{\mathrm{\Delta }{t}_i\right\}$.

(3)

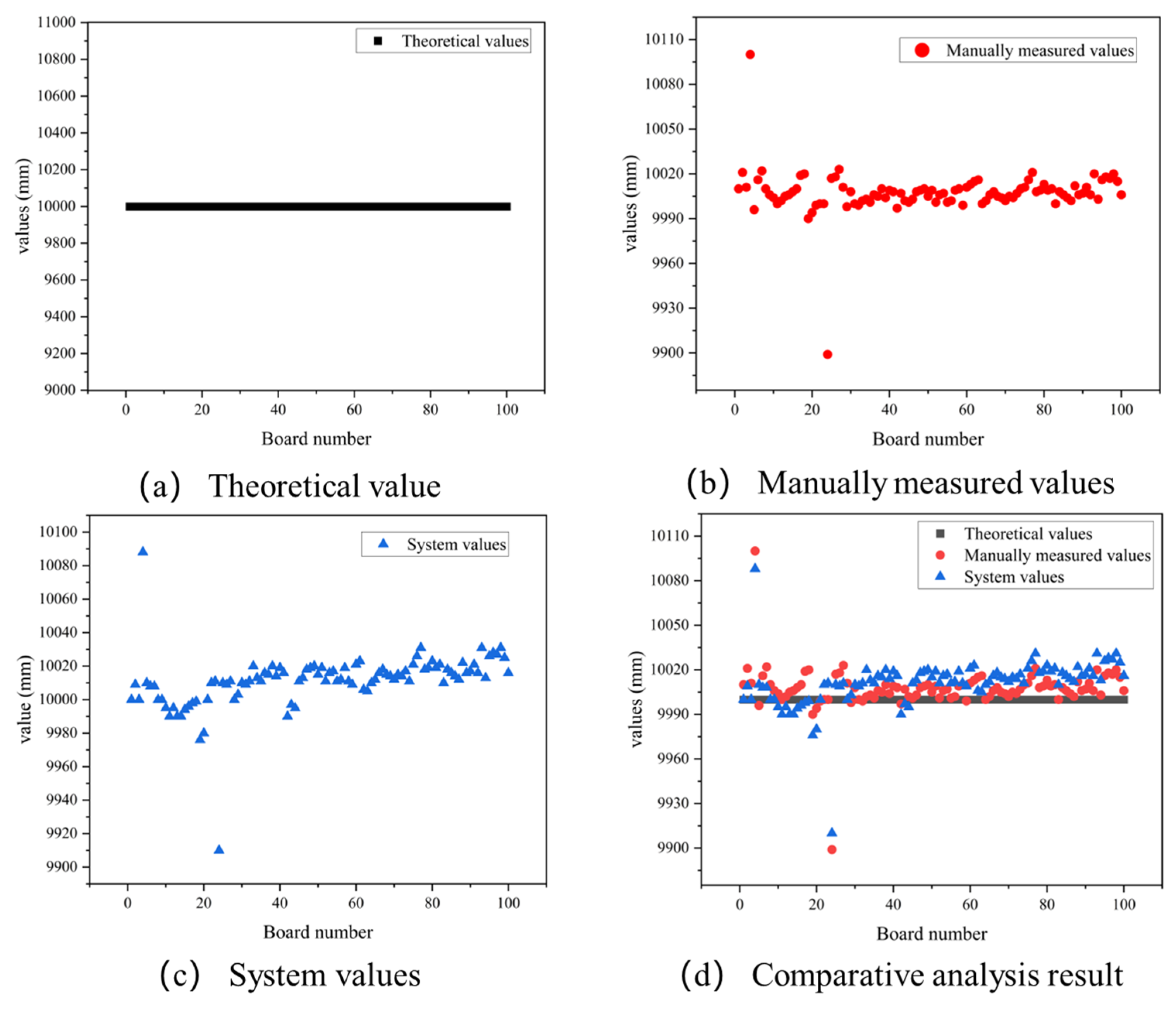
Analysis of the measurement accuracy of the length, width, and diagonal difference of the cross-cutting board

Taking the sample image mentioned in the article as an example, we obtain four equations for fitting straight lines in Section 4.1. The coordinates of the four intersection points can be obtained by Equations (30) from (33): Intersection 1 $\left(-793,5030\right)$, Intersection 2 $\left(793,5030\right)$, Intersection 3 $\left(-591,-5010\right)$, Intersection 4 $\left(591,-5010\right)$, as shown in Figure 13.

By combining the coordinates of the four intersection points obtained from Equations (34)–(36), the length of the crosscut board is determined to be 10,040 mm, with a width of 1586 mm and a diagonal difference of 0. The measurement results are shown in Figure 14.

In the industrial field, the manual measurement values obtained during shutdown are as follows: length 10,008, width 1585, and a difference of 1 mm in diagonal measurements. By comparing the manually measured values with the detected values as shown in

Table 2. Measurement results of the cross-cutting board dimensions.

Parameter	Theoretical Values/mm	Manually Measured Values/mm	System Values/mm	Measurement Error/mm
Length	10,000	10,008	10,040	32
Width	1585	1585	1586	1
Diagonal difference	0	1	0	1

, it can be concluded that the detection accuracy of the proposed system in this paper is high and meets the production needs on site. In this table, the measurement result of the cross-cutting board length is 10,040, which differs from the theoretical value by 40 mm and from the manually measured value by 32 mm. After analysis, the reason for this error is that the cross-cutting board will vibrate for a moment when entering the straightening machine, thus causing this error. According to the literature provided by the reviewers, in the future, the author will continue to attempt further research in aspects such as camera positioning [29,30].

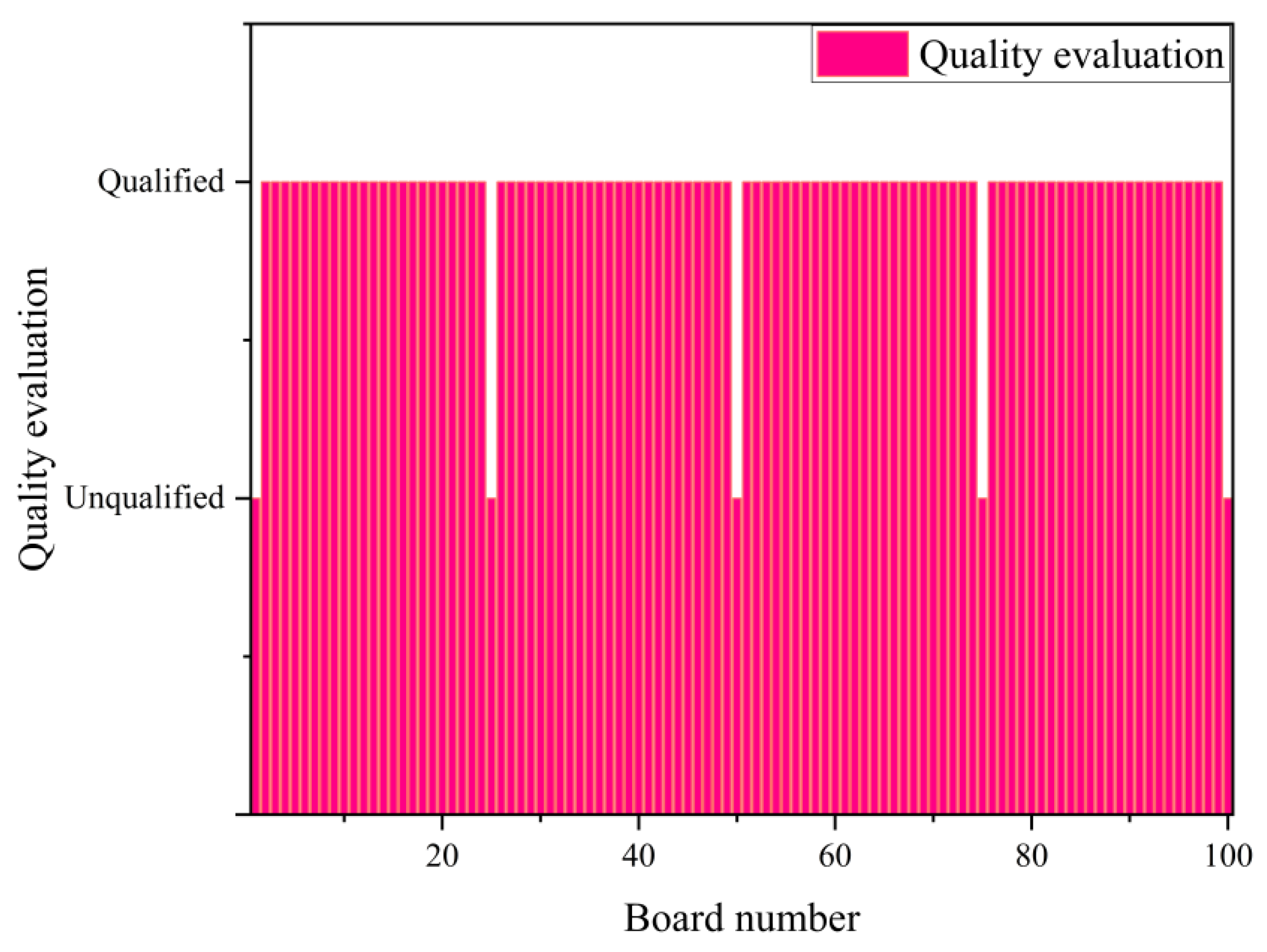
5. Analysis of Industrial Field Application Results

The measurement system described in this article has been applied in the industrial field, mainly including site hardware installation, integrated circuit layout, control system development, and visual interface software, as shown in Figure 15.

To verify the measurement error and evaluate the performance of the measurement system, this paper analyzes and compares three results: theoretical values of 100 cross-section boards, actual measured values by humans, and values obtained from the measurement system. The manual measurements are shown in Figure 15 to further test the measurement accuracy of the measurement system. The comparative results are as follows. The measurement standards in industrial production sites allow for a length measurement error of ≤50 mm, width measurement error of ≤5 mm, and diagonal difference measurement error of ≤5 mm.

(1)

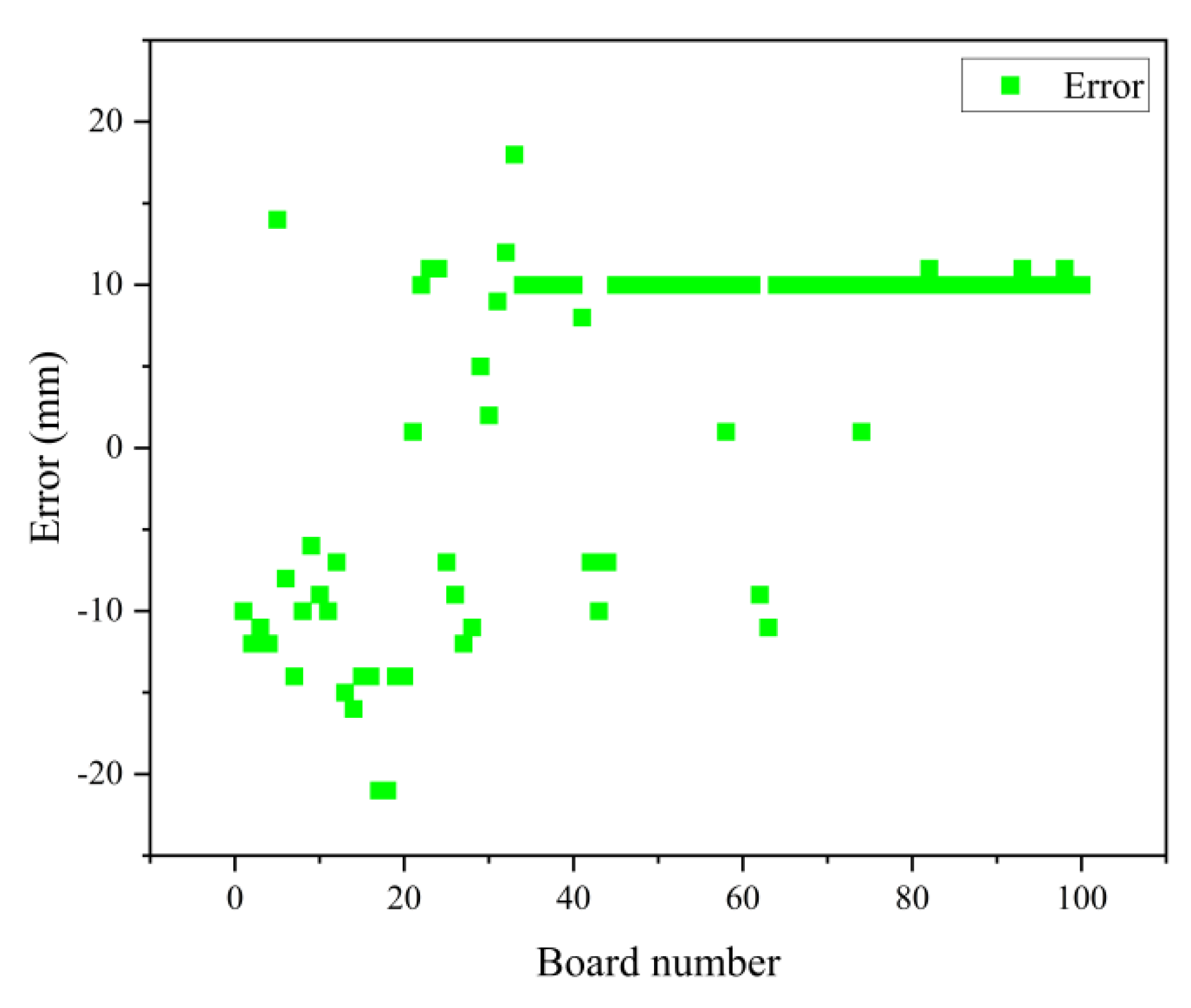
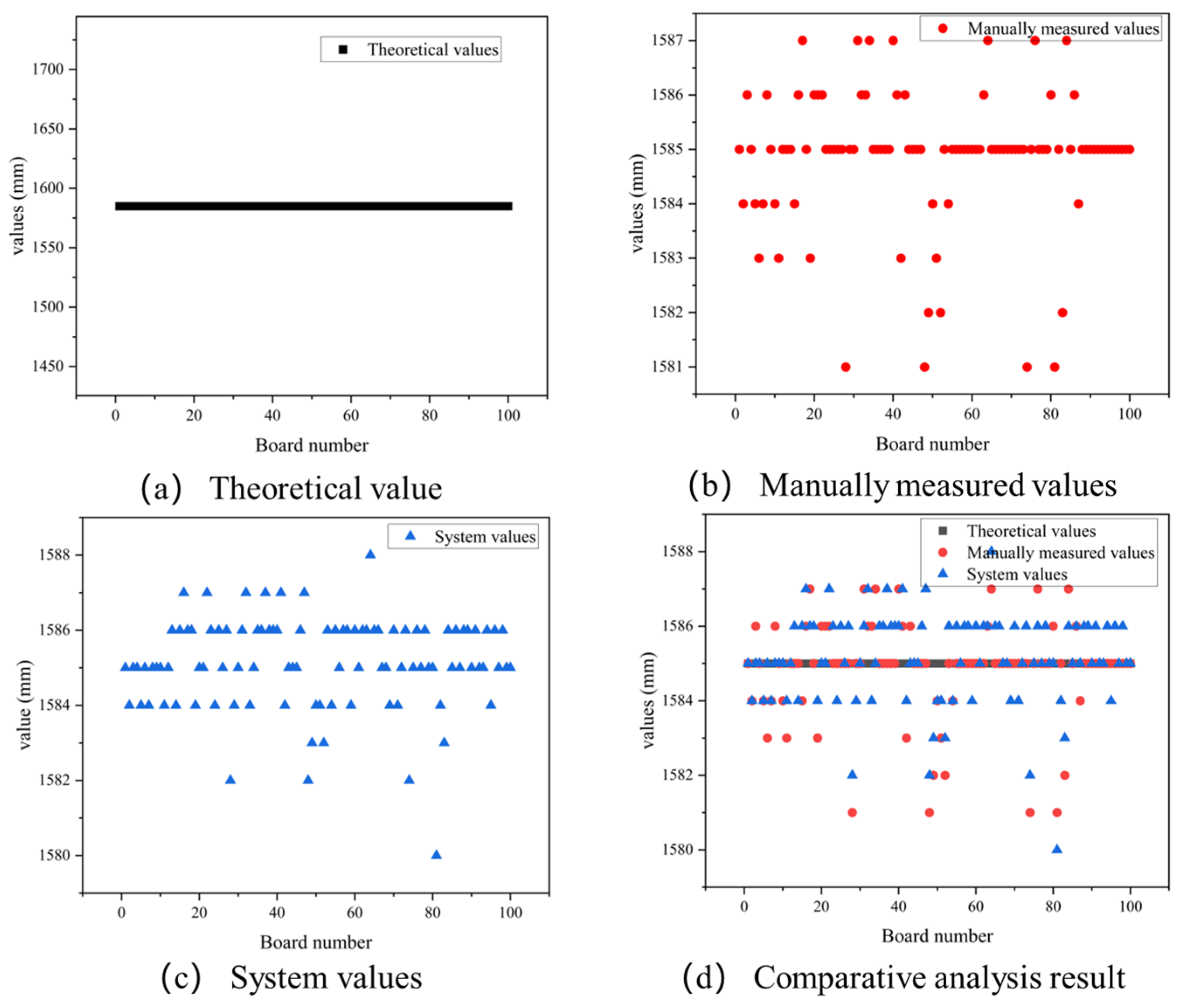
Results of the cross-cutting board length inspection

The theoretical values, actual measurement values, detection values, and detection error results for the length of 100 cross-cutting boards on site are shown in

Table 3. Measurement results of the length of 100 cross-cutting boards.

Board Number	Theoretical Values/mm	Manually Measured Values/mm	System Values/mm	Error
1	10,000	10,010	10,000	−10
2	10,000	10,021	10,009	−12
3	10,000	10,011	10,000	−11
4	10,000	10,100	10,088	−12
5	10,000	9996	10,010	14
6	10,000	10,016	10,008	−8
7	10,000	10,022	10,008	−14
……	……	……	……	……
99	10,000	10,015	10,025	10
100	10,000	10,006	10,016	10

.

The graph in Figure 16 shows the variation curve of theoretical values, actual measured values, and measurement system values for the length of 100 cut boards. The theoretical values are represented by a black line, the manually measured values are represented by a red line, and the detection values are represented by a blue line. Theoretical values are merely ideal production values, but there will be differences in the actual production process. The accuracy of the measurement system is mainly verified by comparing the manually measured values with the system-measured values. According to Figure 17, the length detection error can be obtained as follows: the maximum is 18 mm, the minimum is −21 mm, and the overall error is ≤±25 mm. After board #40, the speed of the roller conveyor was reduced, and the vibration amplitude of the cross-cutting board decreased. Therefore, the measured values tended to be stable. Overall, it meets the requirements for on-site production.

(2)

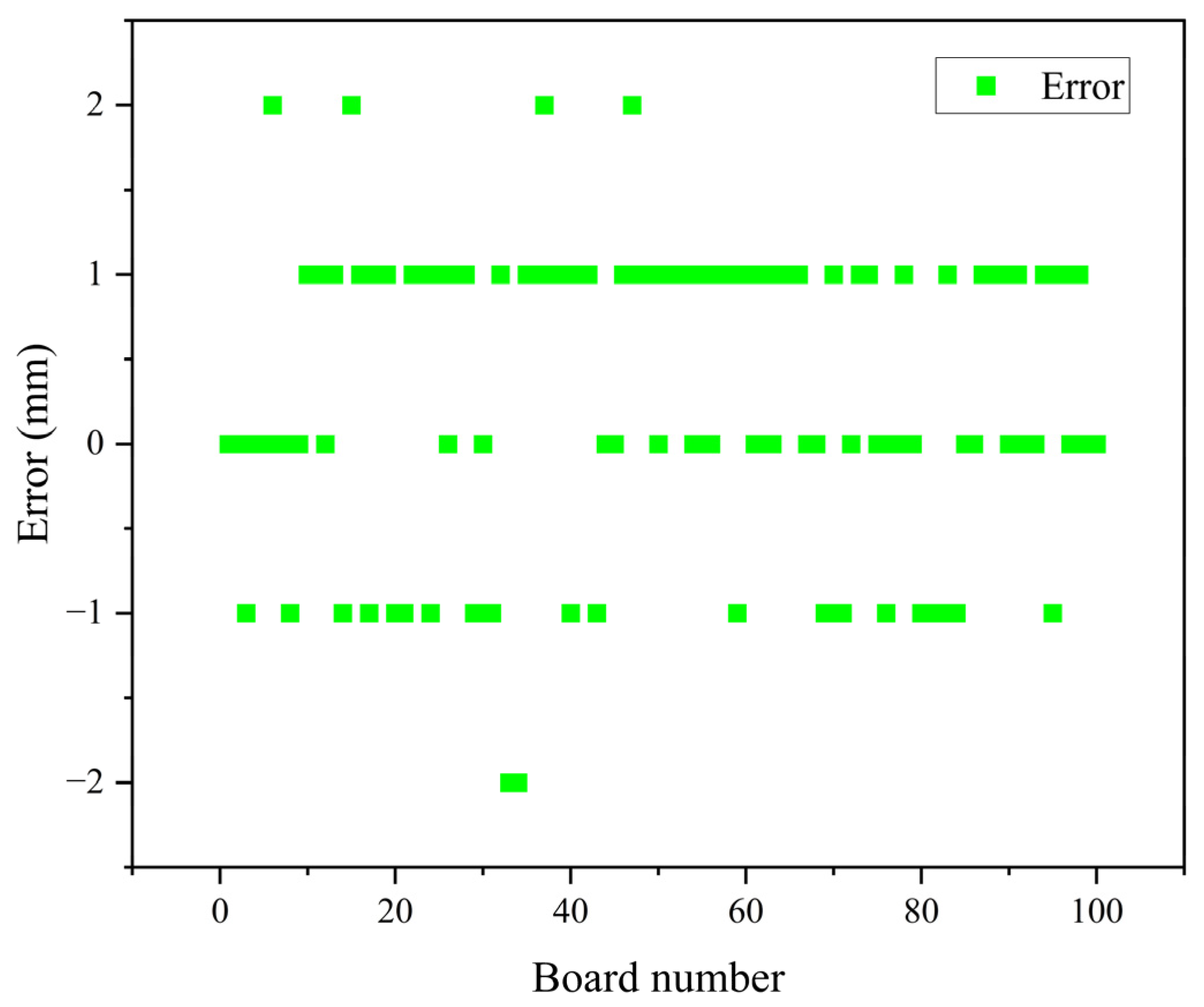
Width detection result of the cross-cutting board

The theoretical values, actual measurement values, detection values, and detection error results for the width of 100 cross-cutting boards on site are shown in

Table 4. Measurement results of the width of 100 cross-cutting boards.

Board Number	Theoretical Values/mm	Manually Measured Values/mm	System Values/mm	Error
1	1585	1585	1585	0
2	1585	1584	1584	0
3	1585	1586	1585	−1
4	1585	1585	1585	0
5	1585	1584	1584	0
6	1585	1583	1585	2
7	1585	1584	1584	0
……	……	……	……	……
99	1585	1585	1585	0
100	1585	1585	1585	0

.

The industrial application of the measurement system is shown in Figure 18. The graph in Figure 19 shows the variation curve of theoretical values, actual measured values, and measurement system values for the width of 100 cut boards. The theoretical values are represented by a black line, the manually measured values are represented by a red line, and the detection values are represented by a blue line. Theoretical values are merely ideal production values, but there will be differences in the actual production process. The accuracy of the measurement system is mainly verified by comparing the manually measured values with the system-measured values. According to the error analysis in Figure 20, it can be concluded that the maximum width detection error is 2 mm, the minimum is −2 m, and most of the detection accuracy is ≤±1, which meets the requirements for on-site production.

(3)

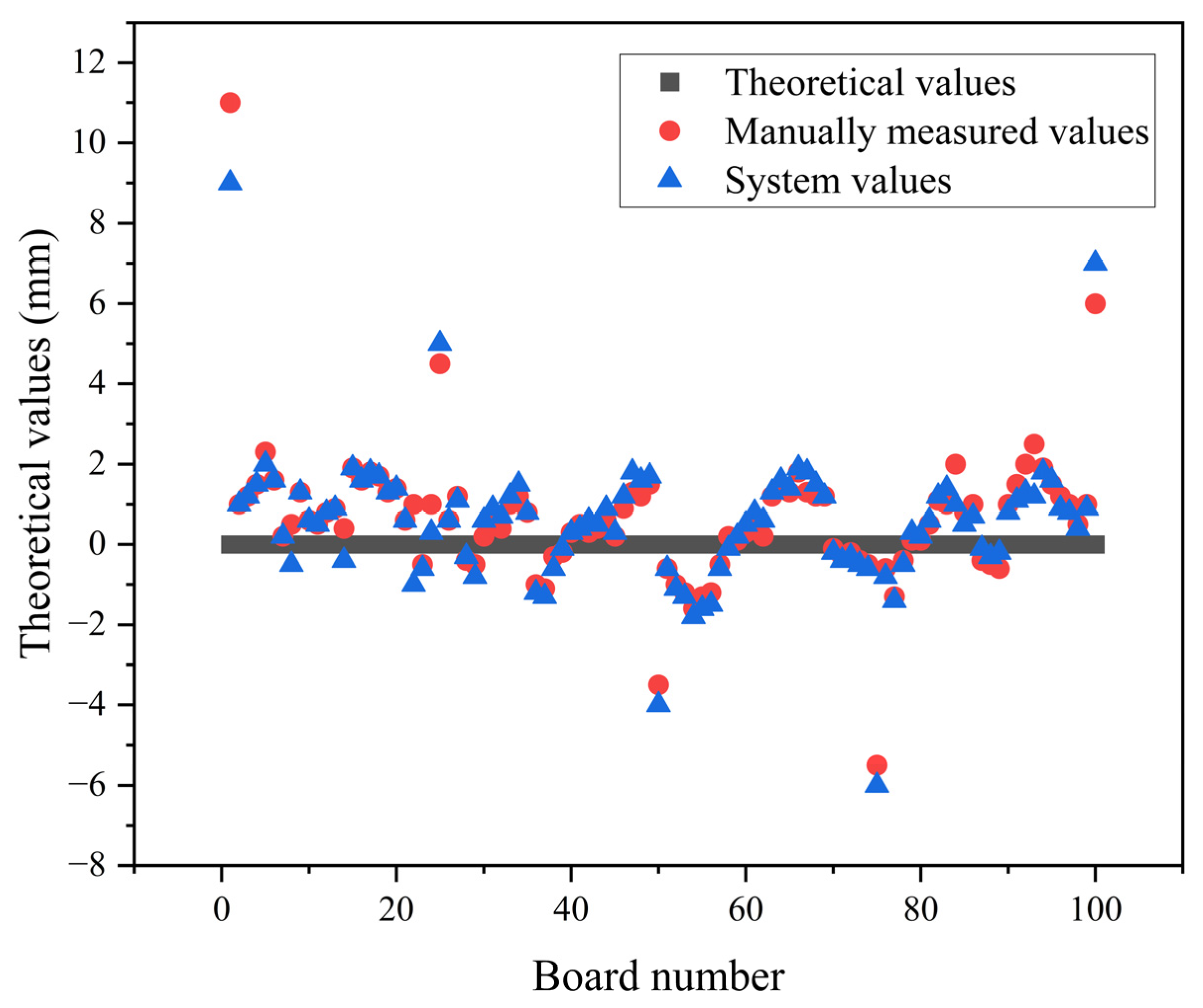
Diagonal detection result of the cross-cutting boards

Based on the above measurements of length and width, it can be concluded that the overall accuracy of the measurement system is good. Therefore, for 100 cross-cutting boards on site, the difference between two diagonals is measured to evaluate their quality. The evaluation criterion is a diagonal difference of <±5 mm for qualified and ≥±5 mm for unqualified, as shown in

Table 5. Measurement results of the diagonal of 100 cross-cutting boards.

Board Number	Manually Measured Values/mm	System Values/mm	Quality Evaluation
1	11	9	Unqualified
2	1	1	Qualified
3	1.2	1.2	Qualified
4	1.5	1.5	Qualified
5	2.3	2	Qualified
6	1.5	1.6	Qualified
7	0	0.2	Qualified
……		……	……
99	1	0.9	Qualified
100	6	7	Unqualified

.

The curve in Figure 21 shows the variation of diagonal difference values for 100 cross-cutting boards. Diagonal detection error: maximum of 2 mm, minimum of −1 mm. Based on the quality evaluation in Figure 22, it can be concluded that out of the one hundred boards, four boards were found to be defective, which is consistent with the on-site production quality inspection results, which meets the requirements for on-site production.

The requirements for industrial production sites are as follows: (1) achieve online real-time detection of the length, width, and diagonal of the cross-cut board; (2) detection accuracy: length ≤ ±50 mm, width ≤ ±2 mm, diagonal difference ≤ ±5 mm. Based on the above industrial application scenarios, it can be concluded that the maximum length detection error is 18 mm and the minimum is −21 mm, with an overall error of ≤±50 mm; the maximum width detection error is 2 mm and the minimum is −2 mm, while most of them have an accuracy of ≤±1 mm; the diagonal detection error ranges from a maximum of 2 mm to a minimum of −1 mm, with an overall error of ≤±2 mm. By comparison, it can be seen that all measured data from the measurement system meet the requirements in industrial production sites.

6. Conclusions

This article proposes a real-time online measurement system for the size of the cross-cutting board during the transverse board straightening process, which has been successfully applied in industrial sites. The main content of this measurement system is as follows:

(1)

In order to address the industrial environment, industrial cameras need to capture images of cross-cutting boards at a certain angle. A visual inspection coordinate transformation model suitable for the industrial field has been established, which can effectively reduce detection errors caused by camera tilt.

(2)

Aiming at the influence of environmental factors such as dust and iron scrap in the industrial site, this paper developed a series filter based on morphological processing to effectively remove the noise in the field environment by comparing the existing filtering techniques such as median filtering, mean filtering, and Gaussian filtering.

(3)

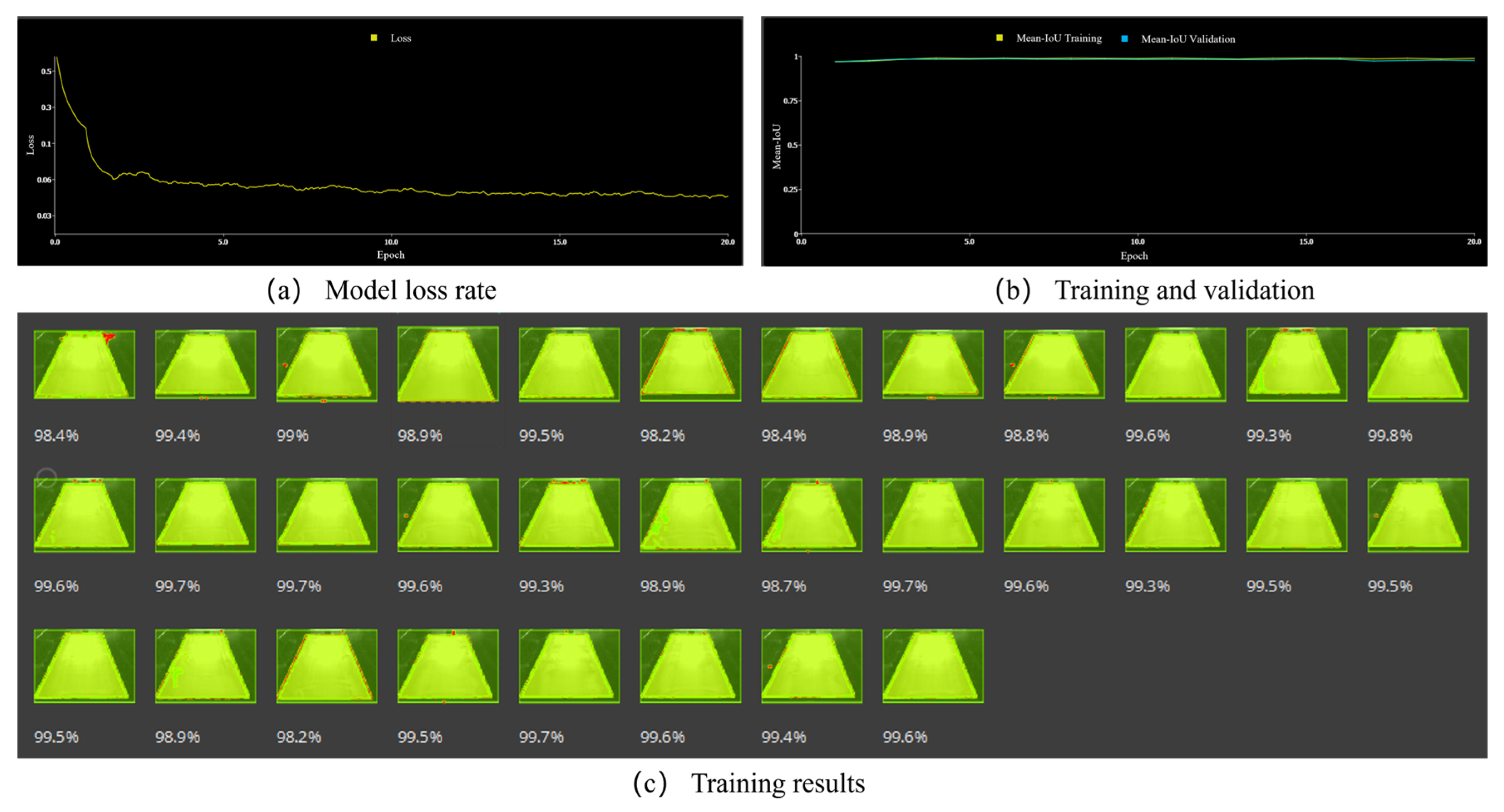
According to the dynamic characteristics of the production process of cross-cutting boards, this article adopts the method of deep learning to achieve the accurate extraction of the edge contour of cross-cutting boards.

(4)

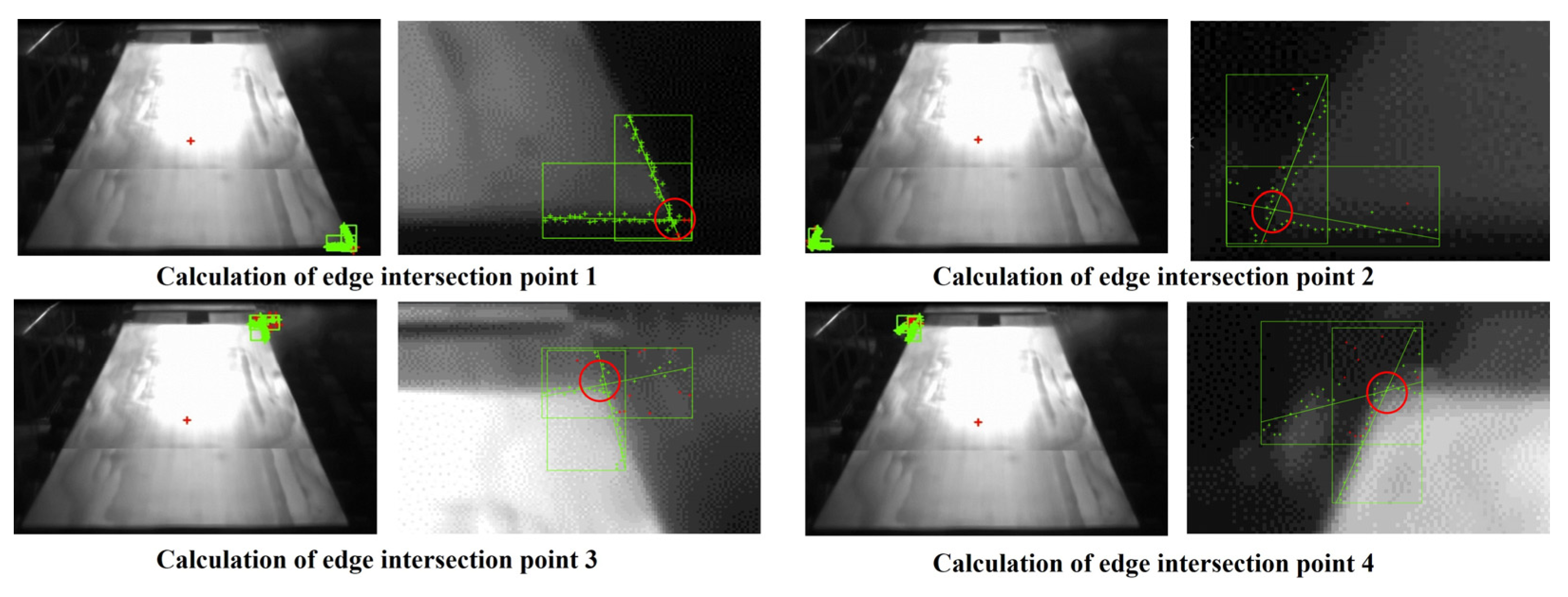
The article proposes a novel edge intersection extraction algorithm based on the line fitting and least squares methods. It fits the extracted edge contours with straight lines, obtains the optimal $k$ and $b$ through the least squares method, and then calculates the edge intersections using a pairwise line intersection model.

(5)

The article proposes to calculate the dimensions of the cross-cutting board based on the coordinates of its four intersection points. The length detection error is ≤±25 mm, and the width detection error is ≤±2 mm. The diagonal detection results are good, which meets the requirements for on-site production.

(6)

The measurement system also has certain limitations. It can only measure cross-cutting boards with a length of less than 10,000 mm. If the length exceeds 10,000 mm, the field of view of the measurement system will not be able to fully cover the cross-cutting boards. In the future, if this problem is to be solved, it is necessary to improve the algorithm of the measurement system and add a fast image stitching algorithm to achieve the measurement of longer cross-cutting boards.