The Effects of Cutting Pick Parameters on Cutting Head Performance in Tunneling–Bolting Combined Machines
Abstract
1. Introduction
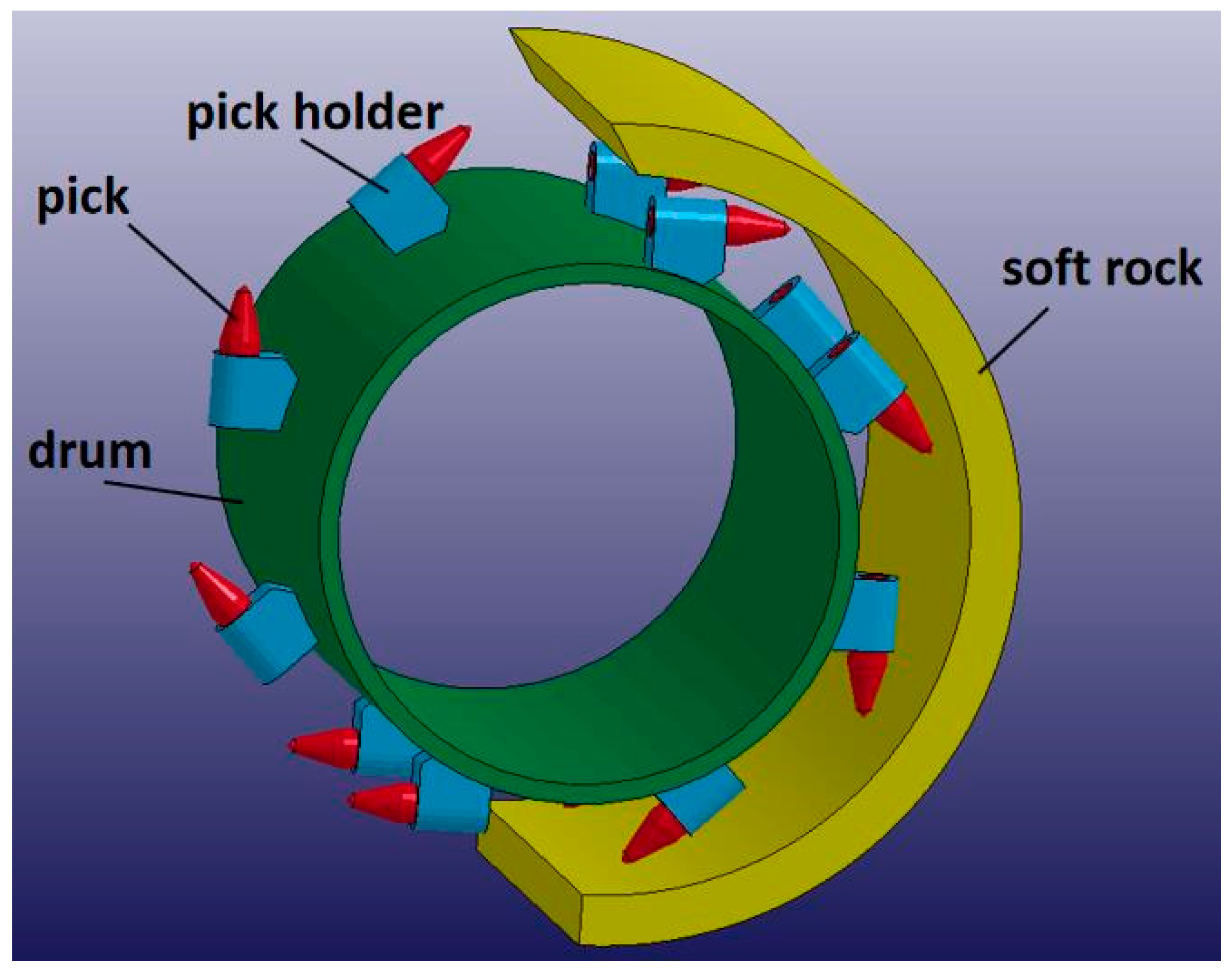
2. Finite Element Modeling of the Cutting Head Cutting Rock
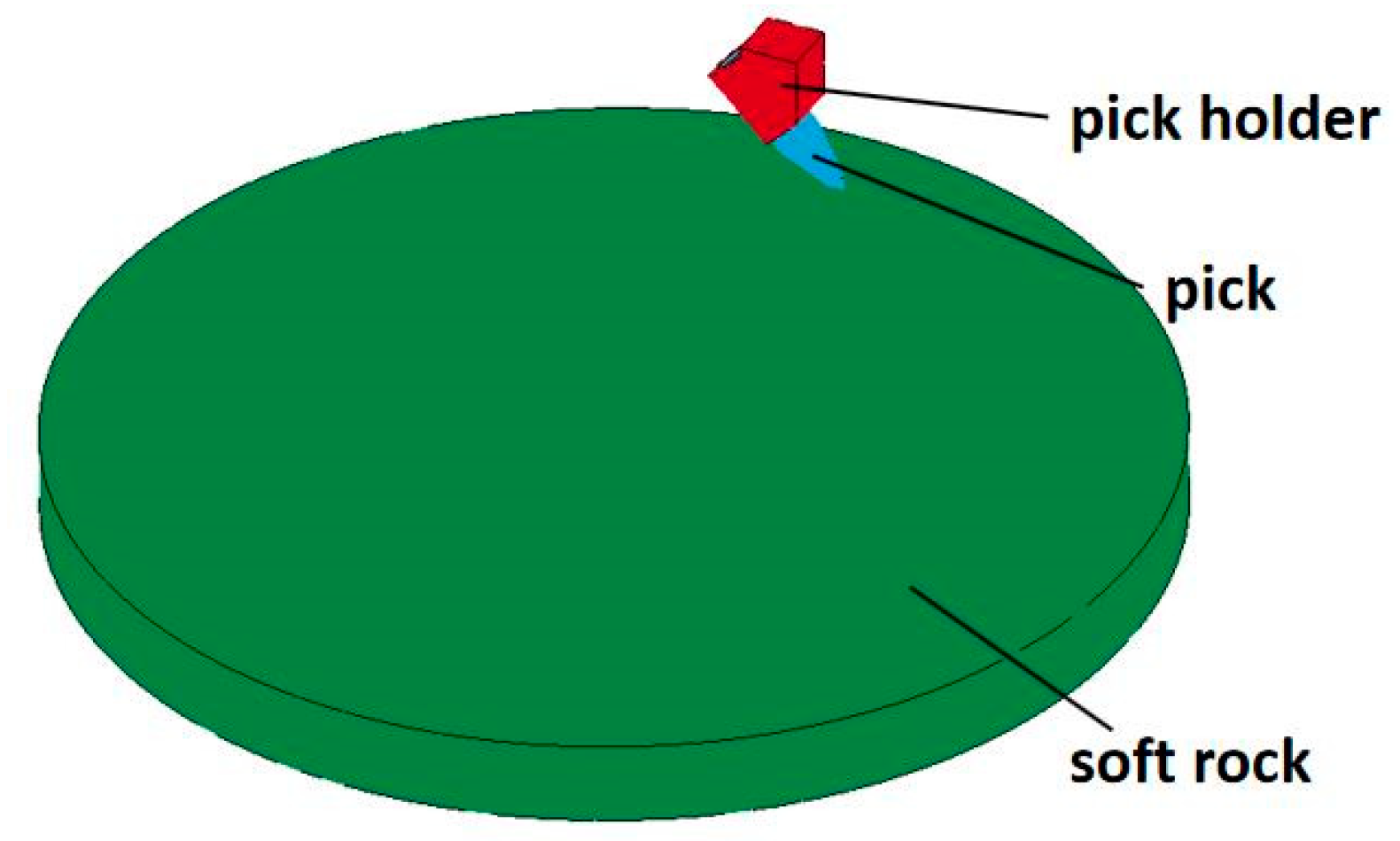
2.1. Establishment of the Model
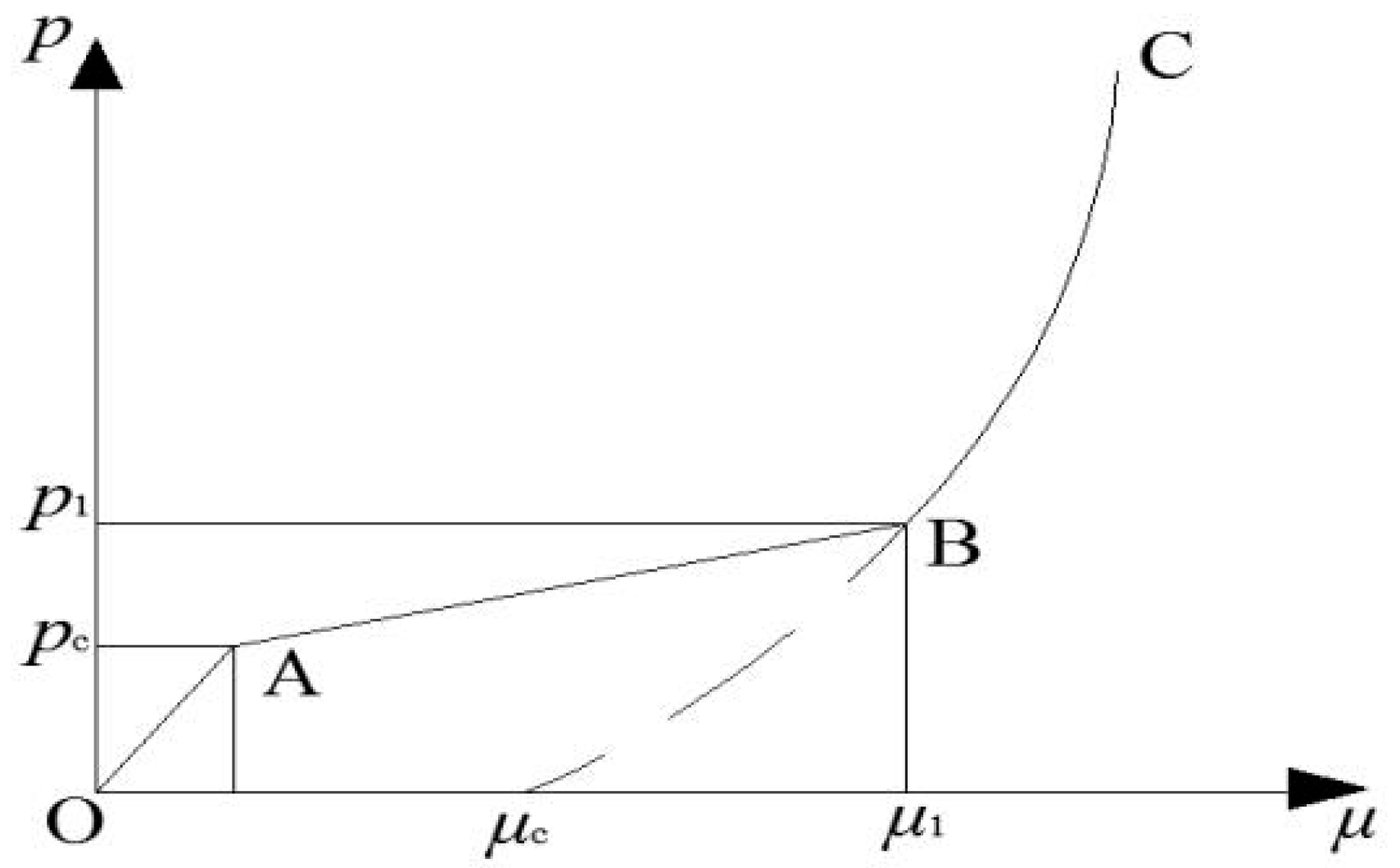
2.2. Determination of the Material Parameters
- Elastic deformation (0 ≤ μ ≤ μc):
- 2.
- Plastic deformation (μc ≤ μ ≤ μ1):
- 3.
- Compaction deformation (μ ≥ μ1):
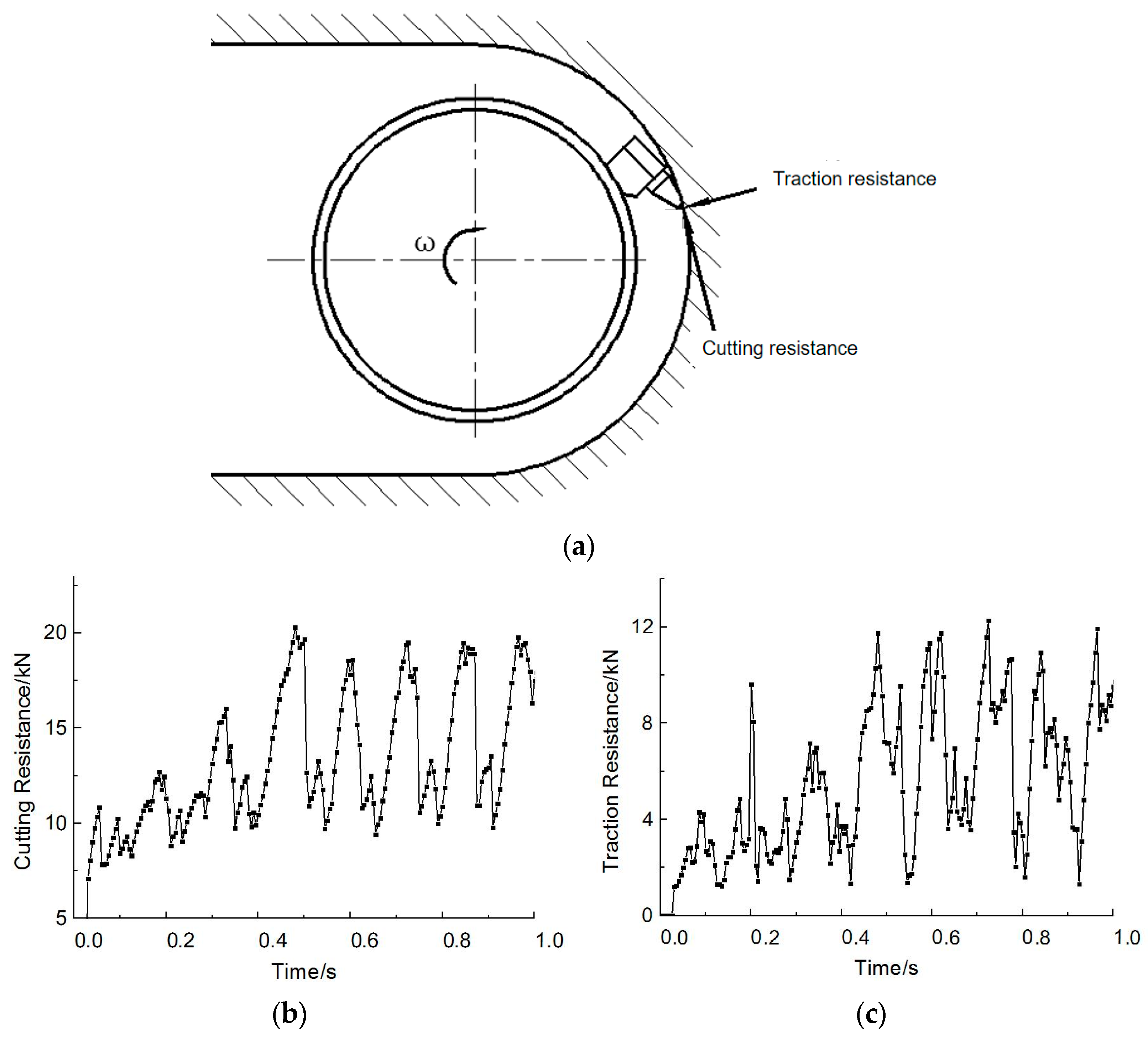
2.3. Simulation Results
3. Experimental Verification of the Modeling Method and Parameter Settings
3.1. Experimental Devices
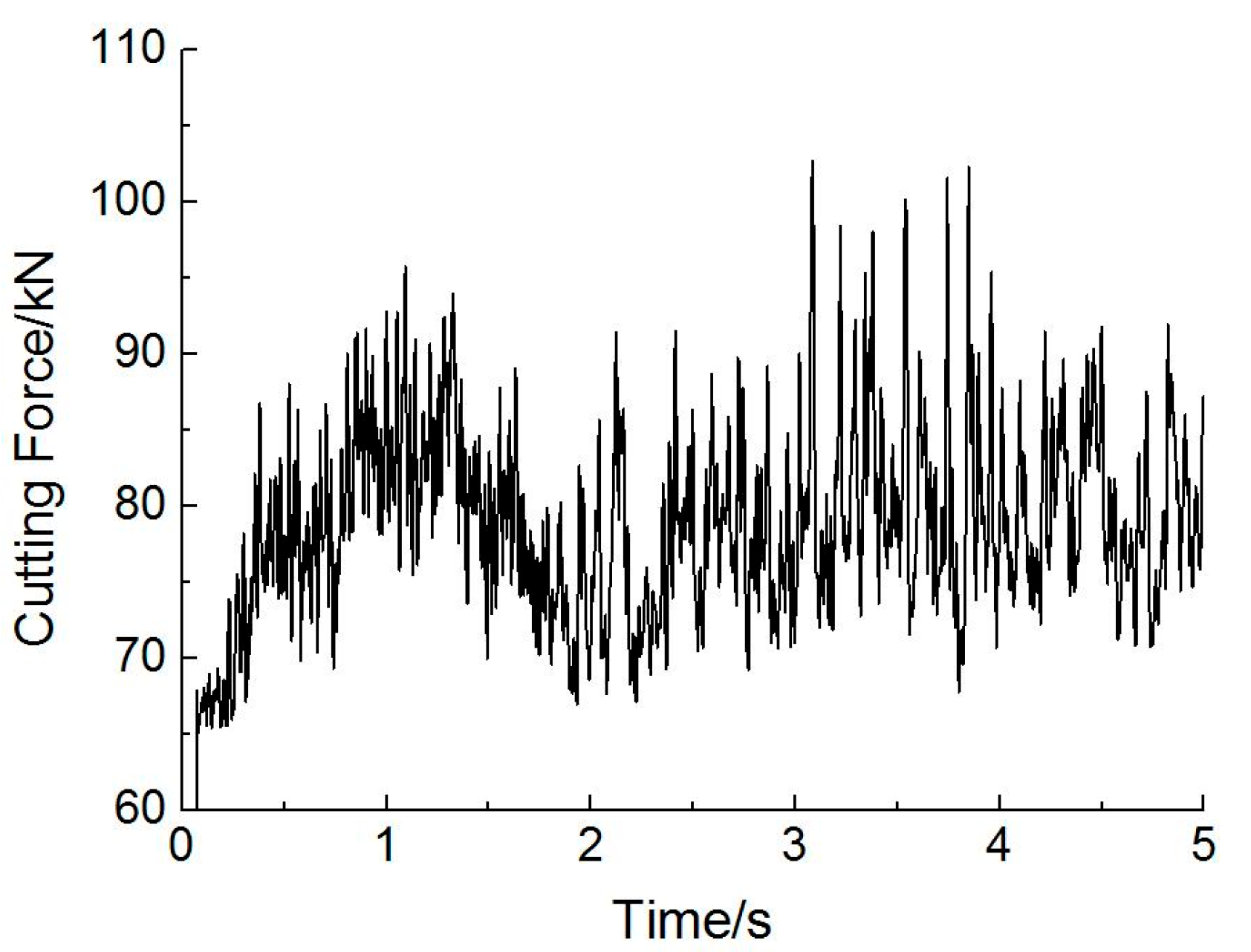
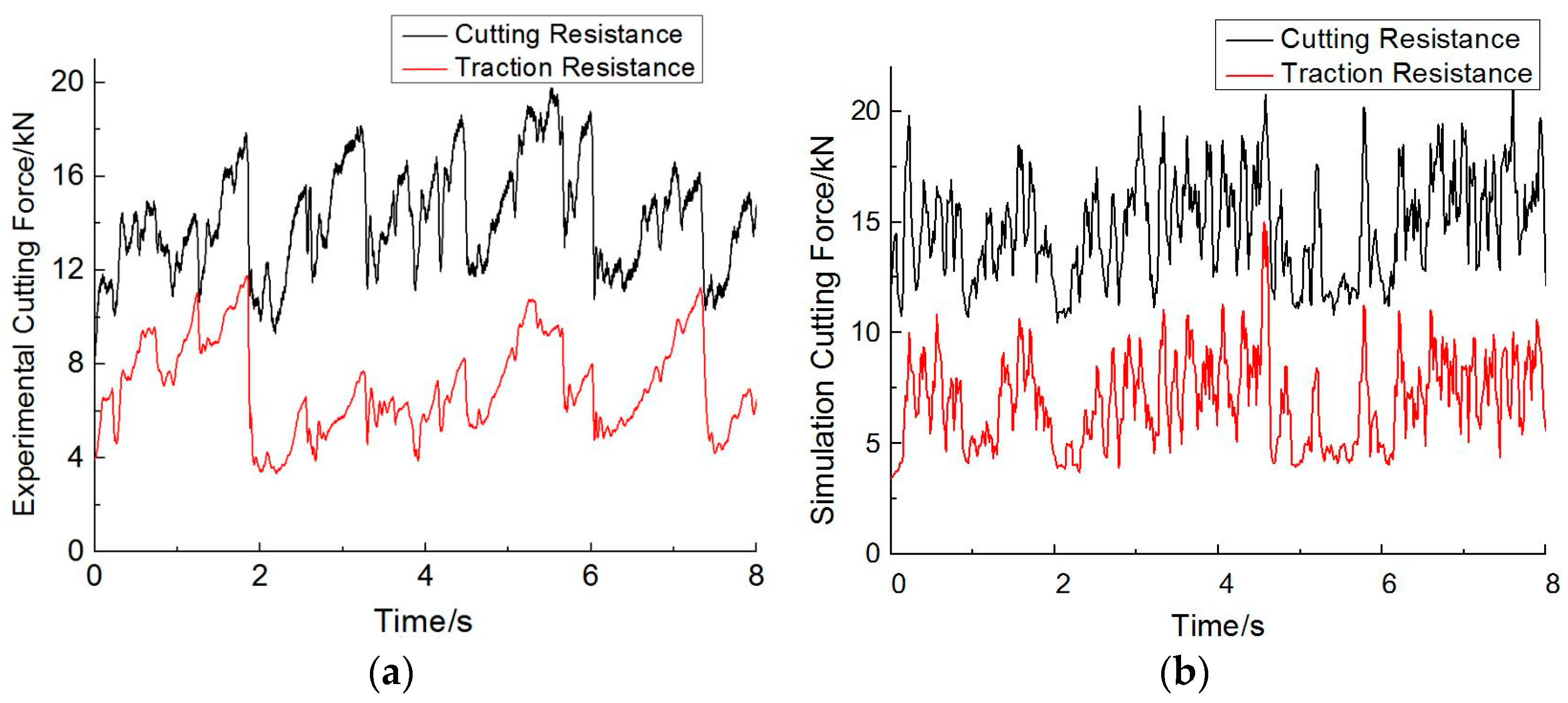
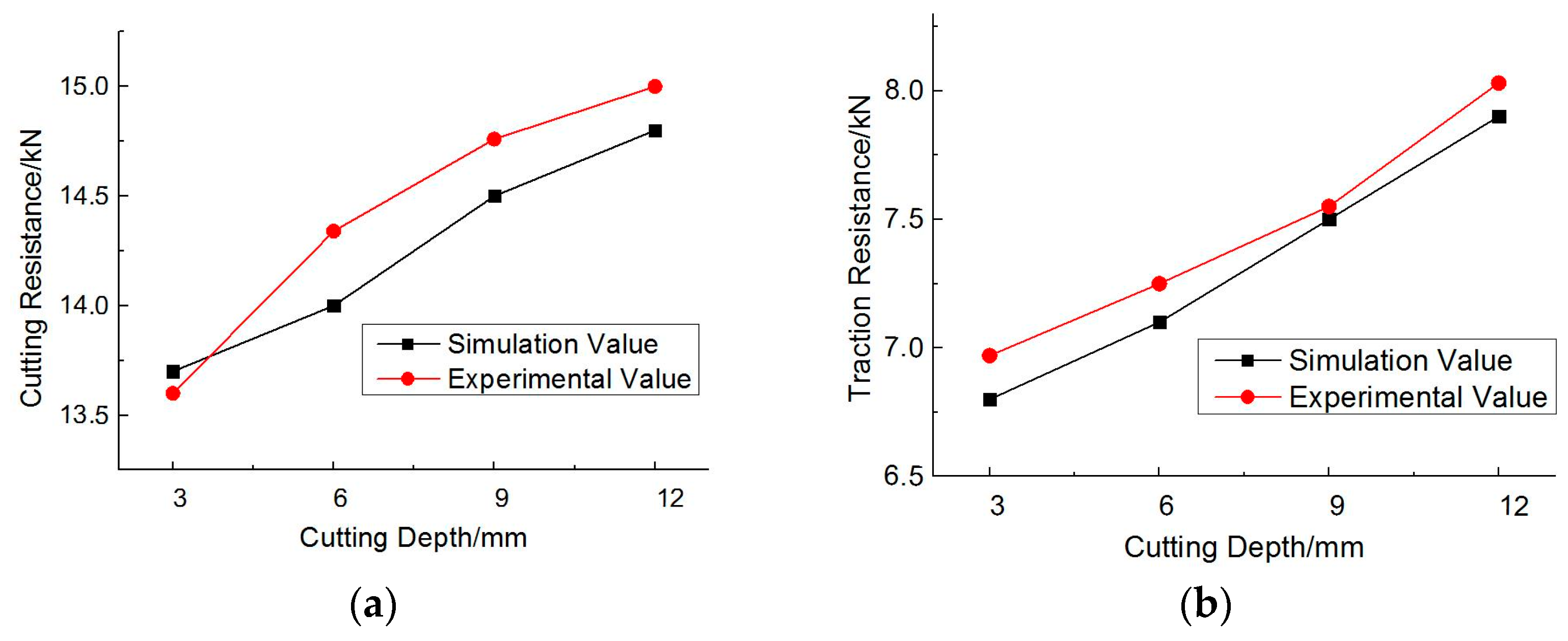
3.2. Comparative Analysis of the Experimental Results
4. Influence of the Pick Parameters on the Cutting Force
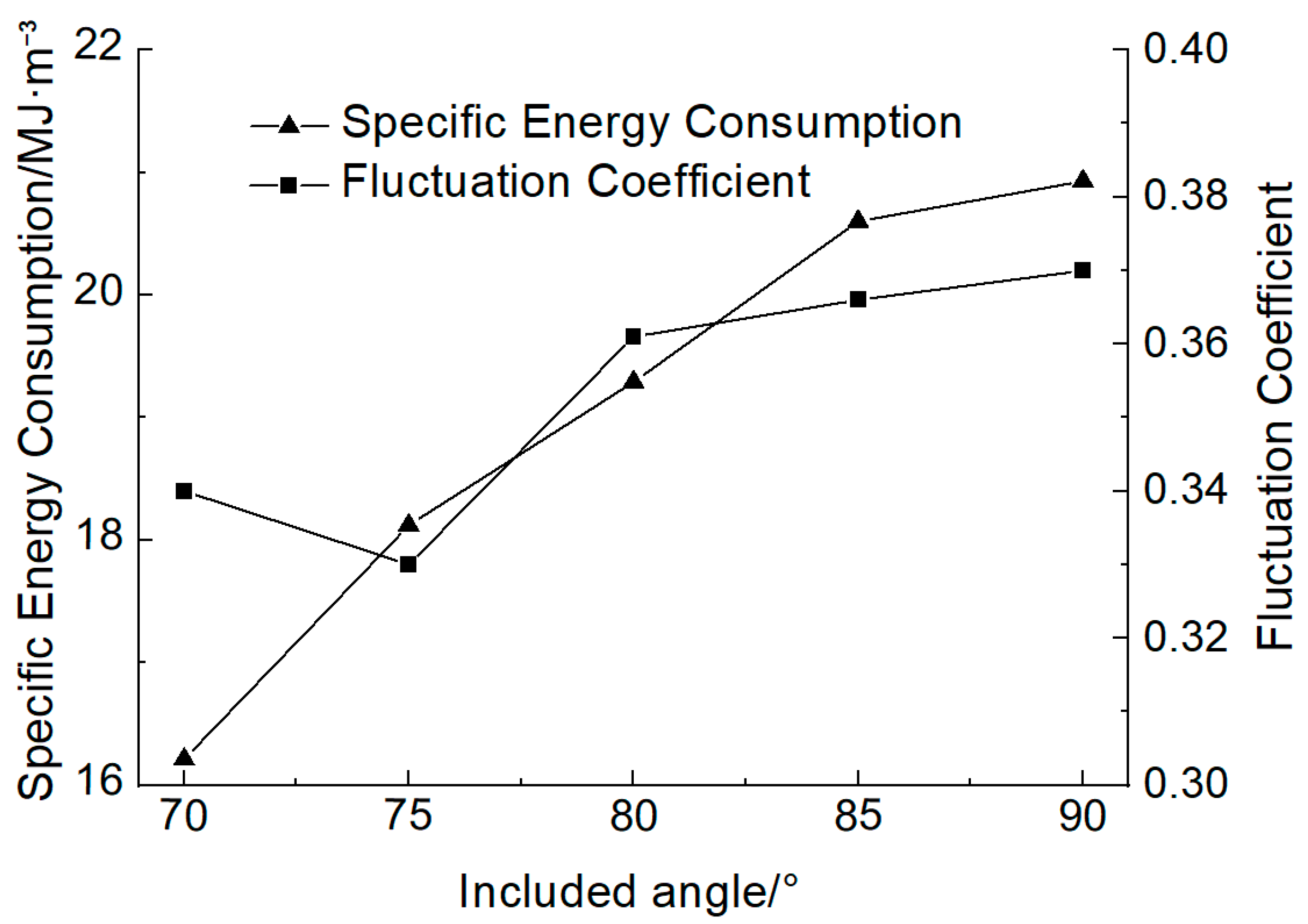
4.1. Influence of the Included Angle on the Cutting Force
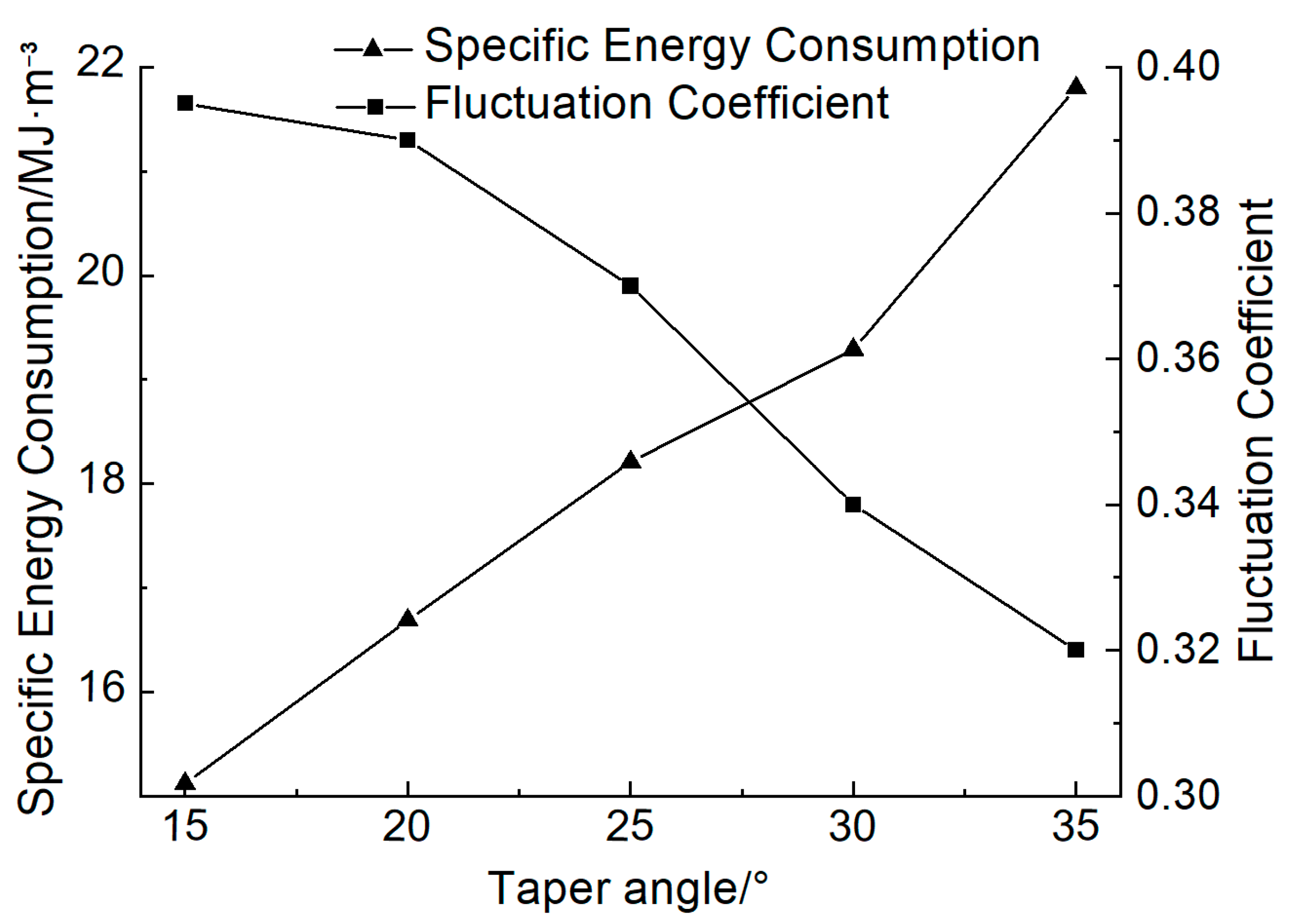
4.2. The Influence of the Taper Angle on the Cutting Force
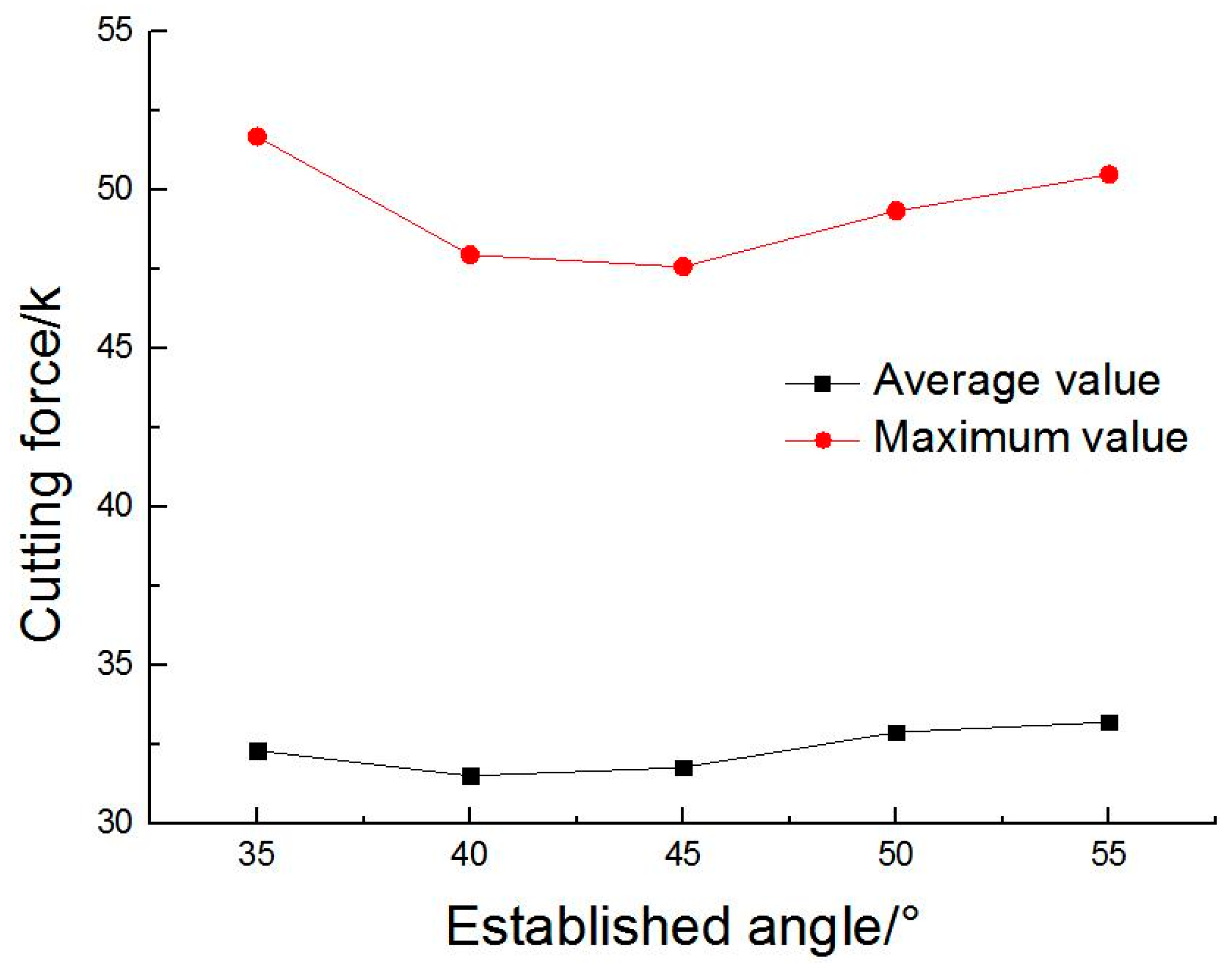
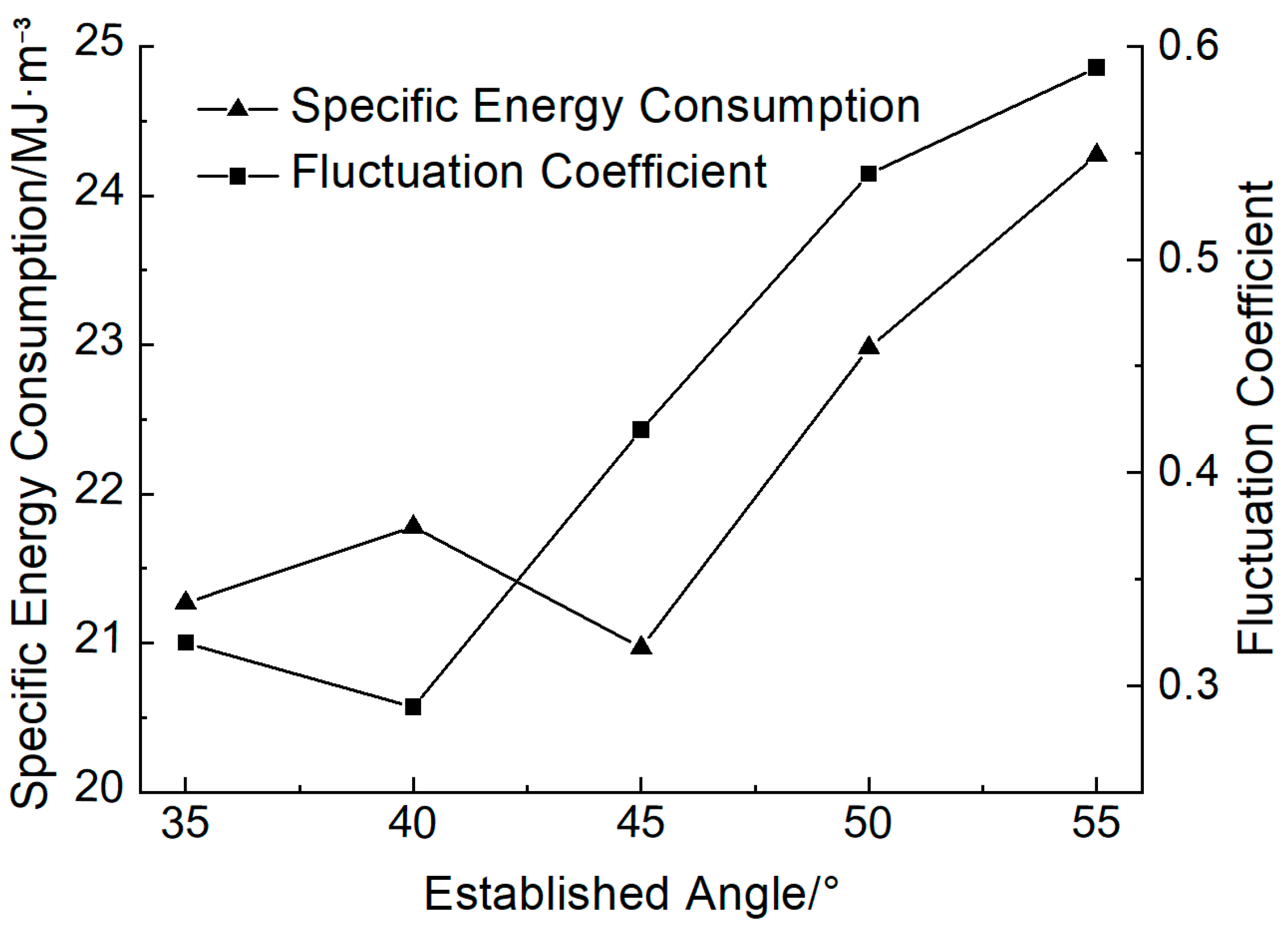
4.3. The Influence of the Established Angle on the Cutting Force
5. Engineering Application
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bertingnoll, H. Alpine bolter miner Austrian technology for rapid roadway development. Min. Technol. 1995, 77, 163–165. [Google Scholar]
- Vierhaus, R.; Terbach, G. Development of a high-performance drivage by “Bolter-Miner” technology. Gluckauf Die Fachzeitschrift fur Rohstoff Bergbau und Energie 2002, 138, 425–429. [Google Scholar]
- Baldwin, J. Innovation in roofbolted development roadways the Voest Alpine ABM 20 continuous miner bolter. CIM Bull. 1996, 89, 40–45. [Google Scholar]
- Leeming, J.J.; Flook, S.D.; Altounyan, P. Bolter miners for longwall development. Gluckauf Die Fachzeitschrift fur Rohstoff Bergbau und Energie 2001, 137, 633–637. [Google Scholar]
- Mogk, E.; Eberhard, M.; Kulassek, M.; Michael, A.C. Bolter miner operation at Walsum colliery. Gluckauf Die Fachzeitschrift fur Rohstoff Bergbau und Energie 2002, 138, 436–440. [Google Scholar]
- Shao, W.; Li, X.; Sun, Y.; Huang, H. Parametric study of rock cutting with SMART*CUT picks. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2017, 61, 134–144. [Google Scholar] [CrossRef]
- Yasar, S.; Yilmaz, A.O. A Novel Mobile Testing Equipment for Rock Cuttability Assessment: Vertical Rock Cutting Rig (VRCR). Rock Mech. Rock Eng. 2017, 50, 857–869. [Google Scholar] [CrossRef]
- Balci, C.; Bilgin, N. Correlative study of linear small and full-scale rock cutting tests to select mechanized excavation machines. Int. J. Rock Mech. Min. Sci. 2007, 44, 468–476. [Google Scholar] [CrossRef]
- Bilgin, N.; Demircin, M.A.; Copur, H.; Balci, C.; Tuncdemir, H.; Akcin, N. Dominant rock properties affecting the performance of conical picks and the comparison of some experimental and theoretical results. Int. J. Rock Mech. Min. Sci. 2006, 43, 139–156. [Google Scholar] [CrossRef]
- Fu, L.; Du, C.L.; Liu, S.Y.; Luo, C.X. Research on load characteristics of picks on auger drill miner’s aiguille. China Mech. Eng. 2013, 24, 2021–2024. [Google Scholar]
- Zhao, L.J.; He, J.J.; Li, F.Q. Numerical simulation of coal breaking process of plow bit. J. China Coal Soc. 2012, 37, 878–883. [Google Scholar]
- Liu, S.Y. Method to determine installing angle of conical point attack pick. J. Cent. South Univ. 2012, 18, 1994–2000. [Google Scholar] [CrossRef]
- Liu, C.S.; Wang, Q.H.; Li, D. Fractal characteristic and specific energy model of conical picks cutting resistance spectrum. J. China Coal Soc. 2015, 40, 2623–2628. [Google Scholar]
- Prokopenko, S.A.; Ludzish, V.S.; Kurzina, I.A. Improvement of picks to enhance performance of heading machines in rocks. J. Min. Sci. 2016, 52, 153–159. [Google Scholar] [CrossRef]
- Liu, S.Y.; Du, C.L.; Cui, X.X. Experimental research on picks arrangement of shearer drum. J. Cent. South Univ. 2009, 40, 1281–1287. [Google Scholar]
- Qiao, S.; Xia, Y.M.; Liu, Z.Z.; Liu, J.S.; Ning, B.; Wang, A.L. Performance evaluation of bolter miner cutting head by using multicriteria decision-making approaches. J. Adv. Mech. Des. Syst. Manuf. 2017, 11, 59. [Google Scholar] [CrossRef]
- Qin, D.T.; Jia, H.J. Hybrid dynamic modeling of shearer’s drum driving system and the influence of housing topological optimization on the dynamic characteristics of gears. J. Adv. Mech. Des. Syst. Manuf. 2018, 12, 20–29. [Google Scholar] [CrossRef]
- Zeng, Q.L.; Jiang, K.; Gao, K.D.; Wan, L.R. Dynamic characteristics analysis on shearer drum in condition of cutting coal with different distributed rocks. J. Vibroeng. 2018, 20, 2796–2809. [Google Scholar] [CrossRef]
- Ordin, A.A.; Nikol’sky, A.M. Optimizing Cutting Width and Capacity of Shearer Loaders in Longwall Mining of Gently Dipping Coal Seams. Sci. Min. Mach. 2018, 54, 69–76. [Google Scholar] [CrossRef]
- Gao, K.D. Model test of helical angle effect on coal loading performance of shear drum. Int. J. Min. Sci. Technol. 2012, 22, 165–168. [Google Scholar]
- Gao, K.D.; Du, C.L.; Liu, S.Y.; Fu, L. Analysis on significance of the factors influencing shearer drum cutting performance. Int. J. Oil Gas Coal Technol. 2014, 7, 386–398. [Google Scholar] [CrossRef]
- Qin, D.T.; Wang, Z.; Hu, M.H.; Liu, C.; Ge, S.S. Dynamic matching of optimal drum movement parameters of shearer based on multi-objective optimization. J. China Coal Soc. 2015, 40, 532–538. [Google Scholar]
- Xia, Y.M.; Xue, J.; Zhou, X.W. 3-D dimensional numerical simulation of soft rock cutting process. J. Chang Univ. 2010, 30, 102–106. [Google Scholar]
- Fang, Q.; Kong, X.-Z.; Wu, H.; Gong, Z. Determination of Holmquist-Johnson-Cook consitiutive model parameters of rock. Eng. Mech. 2014, 31, 179–204. [Google Scholar]
- Li, C.W.; Wang, J.G.; Xie, B.J. Numerical simulation of SHPB tests for coal by using HJC model. J. Min. Saf. Eng. 2016, 33, 158–164. [Google Scholar]
- Hanchak, S.J.; Forrestal, M.J.; Young, E.R.; Ehrgott, J.Q. Perforation of concrete slabs with 48 MPa (7 ksi) and 140 MPa (20 ksi) unconfined compressive strengths. Int. J. Impact Eng. 1992, 12, 1–7. [Google Scholar] [CrossRef]
- Alexis, K.; Gilles, P.; Shehab, A. Experimental investigation of the rock cutting process and derivation of the 3D spatial distribution of the formation strength using in-cutter sensing. J. Pet. Explor. Prod. Technol. 2024, 14, 365–380. [Google Scholar]






| Parameters | Value | Parameters | Value |
|---|---|---|---|
| (kg/m3) | 1594 | 0.01 | |
| G (Pa) | 5.8 × 108 | T (Pa) | 1.86 × 106 |
| Fc (Pa) | 9 × 106 | Pcrush (Pa) | 3 × 106 |
| A | 0.4 | 8 × 10−4 | |
| B | 0.7 | Plock (Pa) | 1 × 109 |
| C | 0.005 | 0.12 | |
| N | 0.5 | k1 (Pa) | 8.5 × 1010 |
| Smax | 7 | k2 (Pa) | −1.7 × 10−11 |
| D1 | 0.0031 | k3 (Pa) | 2.08 × 1011 |
| D2 | 1 | EPSO | 60 |
| Pick Simulation Parameters | Parameter Values |
|---|---|
| Included angle/(°) | 70, 75, 80, 85, 90 |
| Taper angle/(°) | 15, 20, 25, 30, 35 |
| Established angle/(°) | 35, 40, 45, 50, 55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ning, B.; Li, M.; Zhang, J. The Effects of Cutting Pick Parameters on Cutting Head Performance in Tunneling–Bolting Combined Machines. Appl. Sci. 2025, 15, 5746. https://doi.org/10.3390/app15105746
Ning B, Li M, Zhang J. The Effects of Cutting Pick Parameters on Cutting Head Performance in Tunneling–Bolting Combined Machines. Applied Sciences. 2025; 15(10):5746. https://doi.org/10.3390/app15105746
Chicago/Turabian StyleNing, Bo, Mingzhu Li, and Jinhua Zhang. 2025. "The Effects of Cutting Pick Parameters on Cutting Head Performance in Tunneling–Bolting Combined Machines" Applied Sciences 15, no. 10: 5746. https://doi.org/10.3390/app15105746
APA StyleNing, B., Li, M., & Zhang, J. (2025). The Effects of Cutting Pick Parameters on Cutting Head Performance in Tunneling–Bolting Combined Machines. Applied Sciences, 15(10), 5746. https://doi.org/10.3390/app15105746





