Interpretable Optimization: Why and How We Should Explain Optimization Models
Abstract
1. Introduction: Interpretability in Machine Learning and Optimization
1.1. Interpretability in Machine Learning
1.2. Interpretability in Optimization
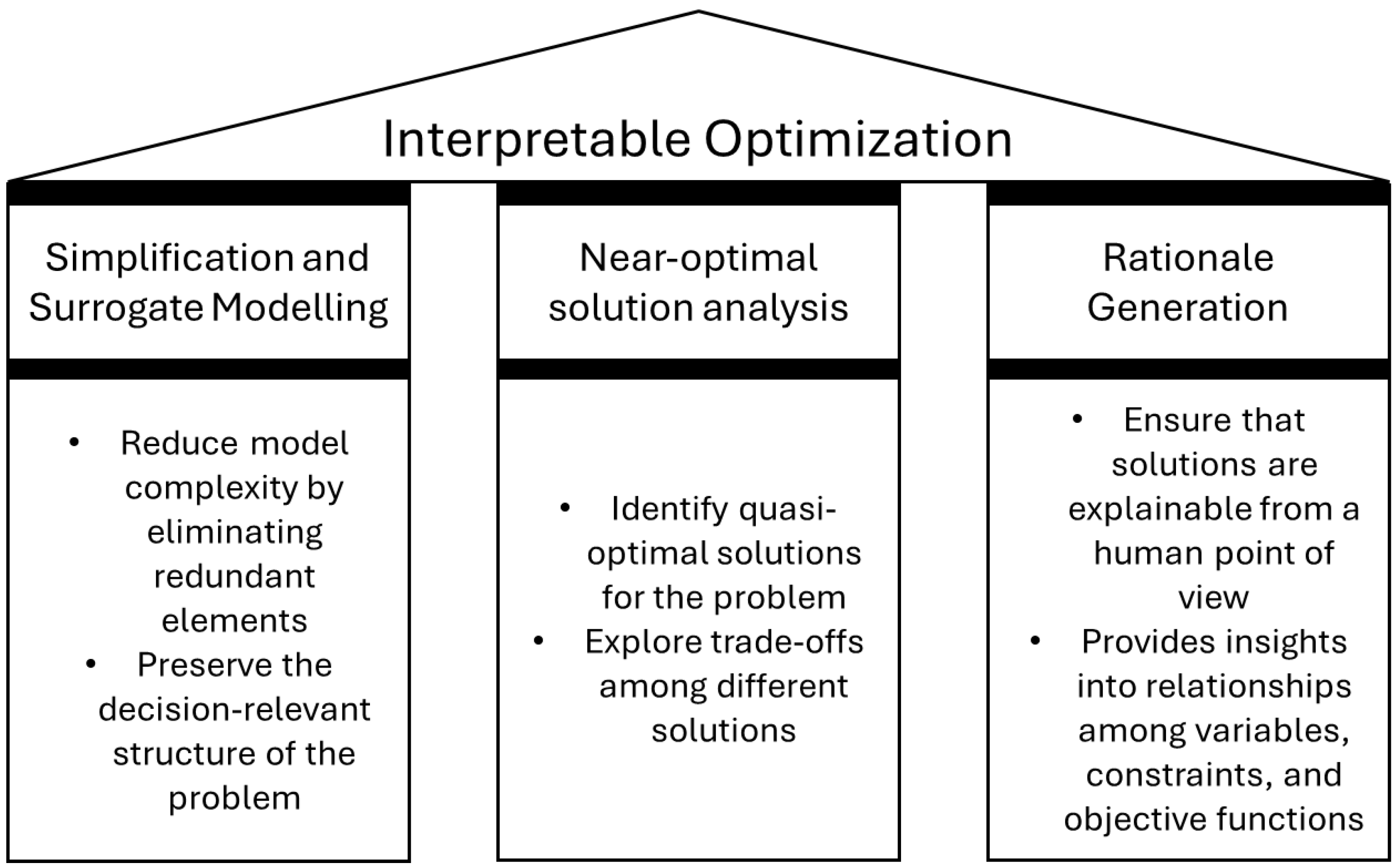
2. What Is Interpretable Optimization?
2.1. The Potential for Transparency in Optimization
2.2. The Many Definitions of Interpretability
2.3. The Pillars of Interpretability in Optimization
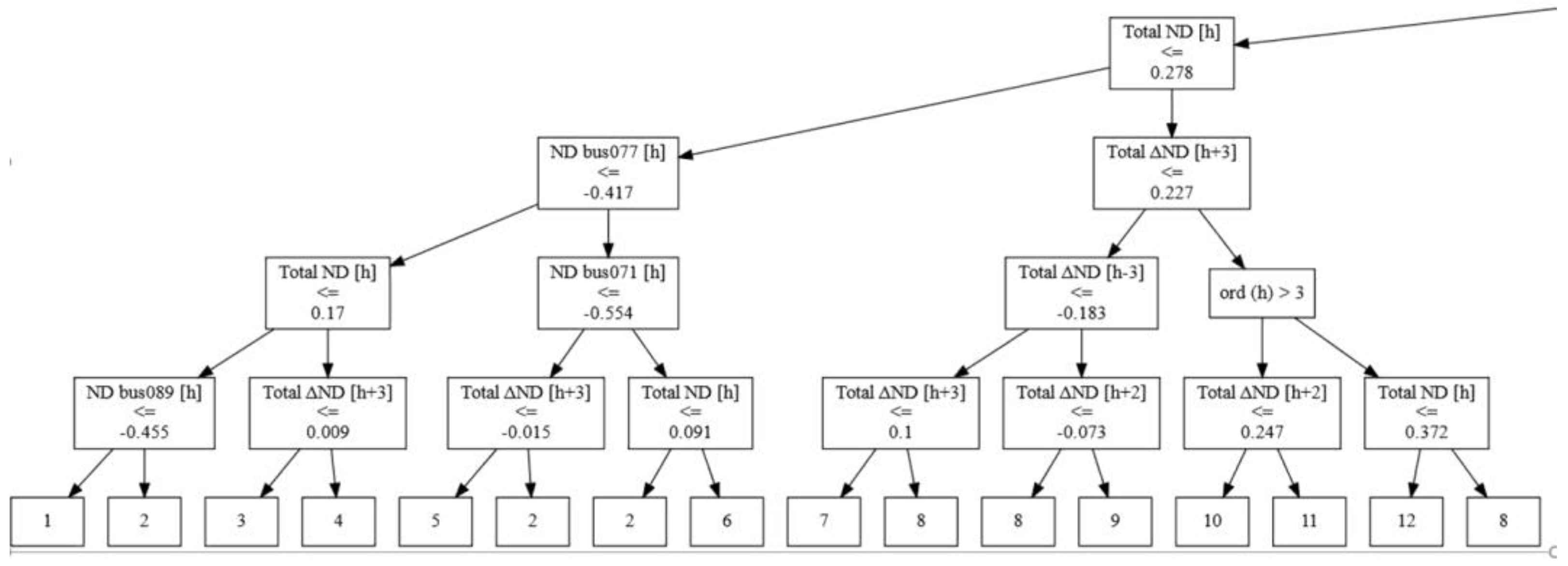
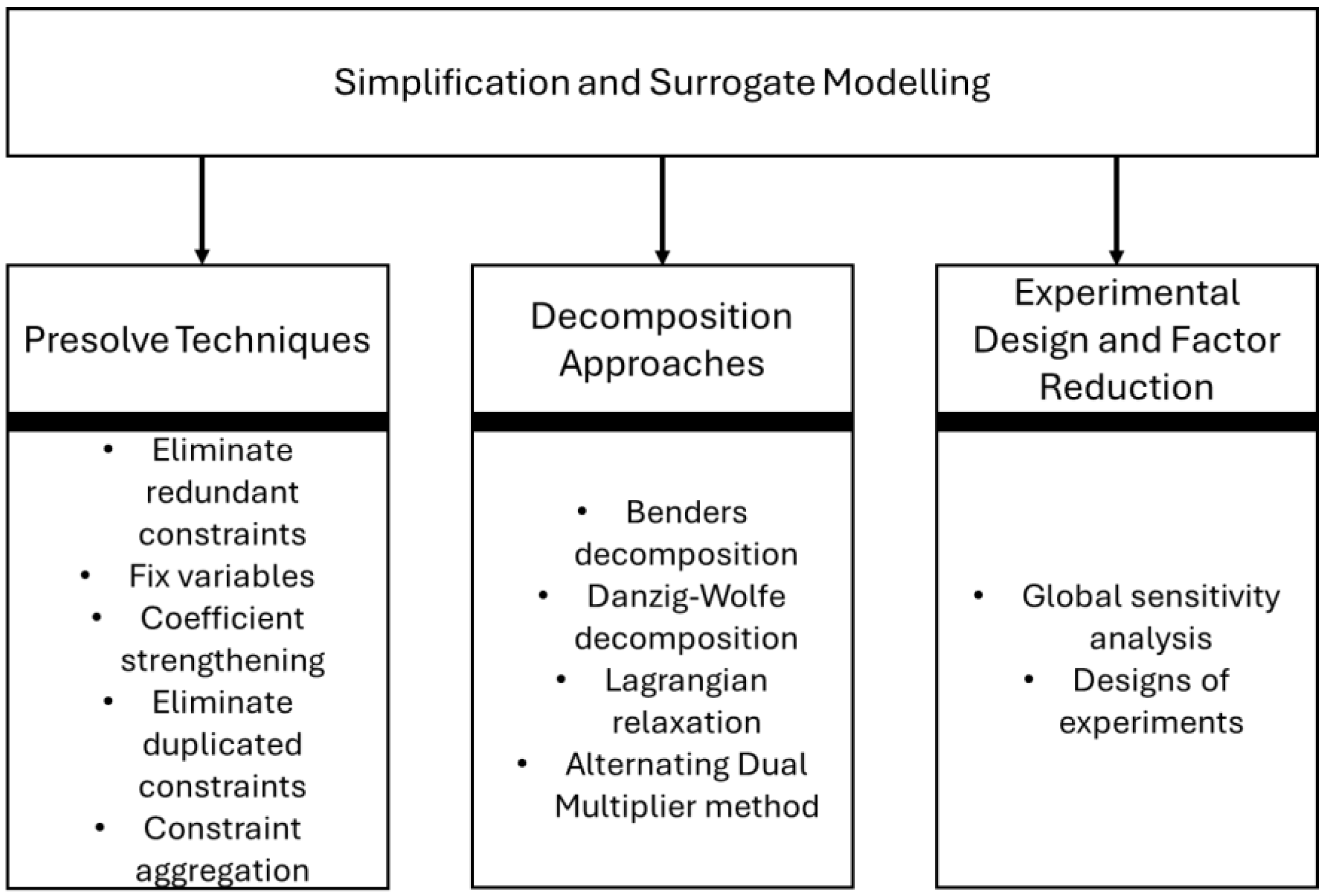
3. Problem Reduction and Surrogate Model Building
3.1. Can Problem Reductions Be Meaningful?
3.2. Presolve Techniques
- Eliminating redundant constraints: Constraints that do not impact the feasible region can be removed without affecting the optimal solution. This is particularly useful in large-scale problems where constraints may have been introduced for generality but are not binding in practice. Many different alternative strategies exist to prioritize constraints. For instance, in [36], several metrics were used to rank constraints by how likely they were to be bound. These metrics included the angle that the constraint formed with respect to the objective function, or how far some bounds of the left-hand side were from the right-hand side of the constraint (i.e., how far a constraint was from being bound).
- Fixing variables: If the bounds of a variable force it to take a single value, that variable can be removed from the model, effectively turning it into a constant. This occurs in highly constrained problems where the interaction of multiple constraints results in a fixed solution for some variables. For example, in energy systems planning, transmission line constraints may fix the operational status of certain infrastructure components, making explicit modeling unnecessary [32].
- Coefficient strengthening: If a constraint coefficient can be tightened without changing the feasible region, it enhances numerical stability and interpretability. This method is particularly useful in logistics and scheduling problems, where resource constraints can be reformulated for clarity [35].
- Detecting and eliminating dominated constraints: Some constraints are made redundant by stronger constraints that enforce the same restrictions more effectively. Identifying and removing these constraints reduces problem size and eliminates unnecessary complexity in decision analysis.
- Constraint aggregation: Certain sets of constraints can be combined into a single constraint, reducing the overall number of constraints while preserving the problem’s structure. This technique is commonly used in supply chain management and network flow problems to consolidate redundant constraints. For instance, identifying such umbrella constraints is key in problems such as a security-constrained power flow, where a planning solution must consider an unmanageably large number of constraints describing potential failures [37].
3.3. Decomposition Approaches
3.4. Experimental Design and Factor Reduction
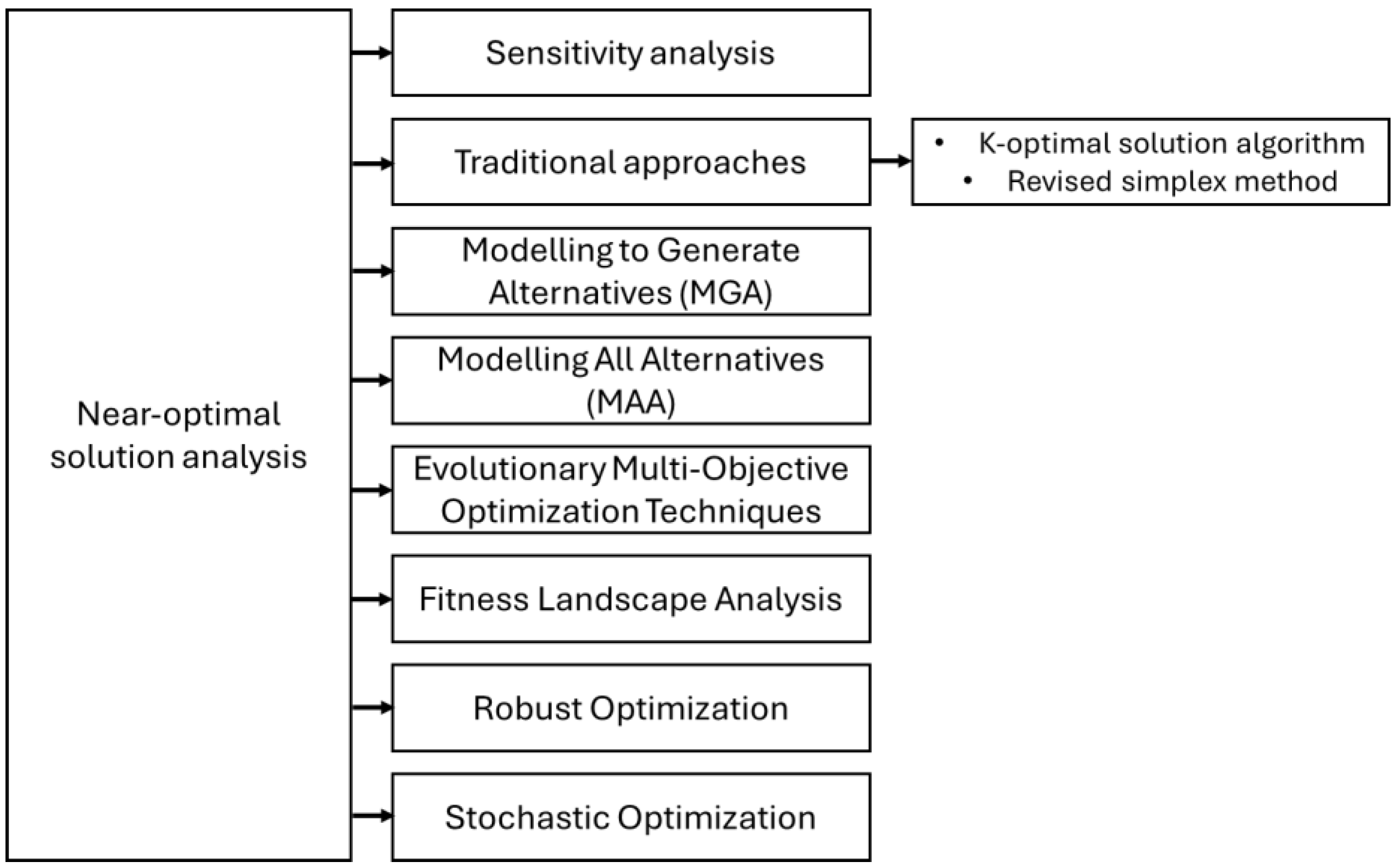
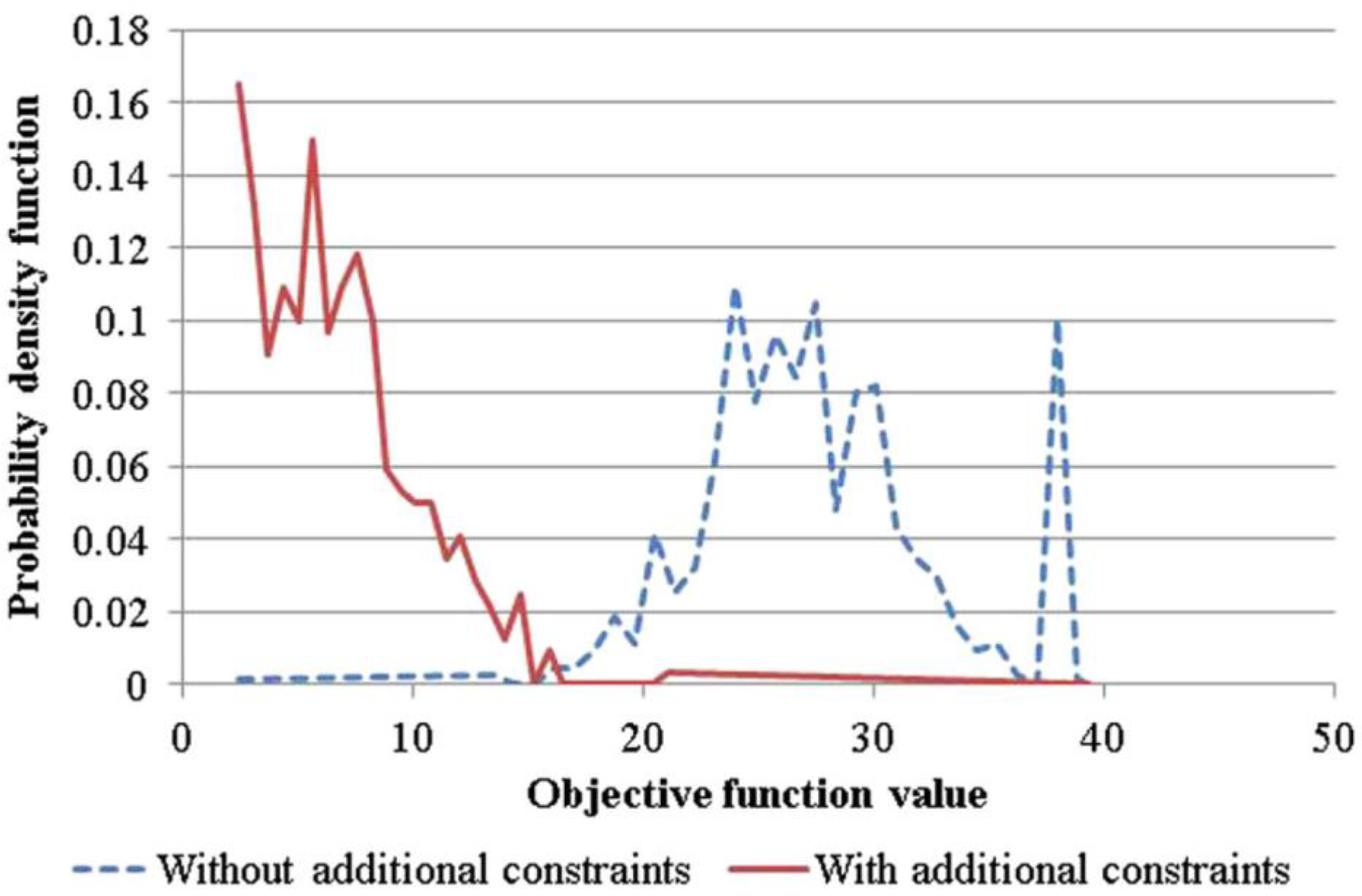
4. Analysis of Near-Optimal Solutions
4.1. A Degenerate Class of Problems
4.2. Sensitivity Analysis
4.3. Traditional Approaches
4.4. Model Generating Alternatives and Mapping All Alternatives
4.5. QOAs in Evolutionary Computation
4.6. Other Approaches That Are Related but Do Not Directly Correspond to This Pillar
4.7. A Need to Integrate Optimization
5. Generating Solution Rationales
6. Example Applications
6.1. Energy Systems and Carbon Emission Reduction
6.2. Ethical Policy Spending and Fair Budget Allocation
6.3. Healthcare
7. Conclusions: The Road Ahead
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Attard-Frost, B.; De los Ríos, A.; Walters, D.R. The ethics of AI business practices: A review of 47 AI ethics guidelines. AI Ethics 2023, 3, 389–406. [Google Scholar] [CrossRef]
- Washington, A.L. How to Argue with an Algorithm: Lessons from the COMPAS-ProPublica Debate. Color. Technol. Law. J. 2018, 17, 131. Available online: https://scholar.law.colorado.edu/ctlj/vol17/iss1/4 (accessed on 25 February 2025).
- Roscher, R.; Bohn, B.; Duarte, M.F.; Garcke, J. Explainable Machine Learning for Scientific Insights and Discoveries. IEEE Access 2020, 8, 42200–42216. [Google Scholar] [CrossRef]
- Mosca, E.; Szigeti, F.; Tragianni, S.; Gallagher, D.; Groh, G. SHAP-Based Explanation Methods: A Review for NLP Interpretability. In Proceedings of the 29th International Conference on Computational Linguistics, Gyeongju, Republic of Korea, 12–17 October 2022; Calzolari, N., Huang, C.-R., Kim, H., Pustejovsky, J., Wanner, L., Choi, K.-S., Ryu, P.-M., Chen, H.-H., Donatelli, L., Ji, H., et al., Eds.; International Committee on Computational Linguistics: Gyeongju, Republic of Korea, 2022; pp. 4593–4603. [Google Scholar]
- Antonini, A.S.; Tanzola, J.; Asiain, L.; Ferracutti, G.R.; Castro, S.M.; Bjerg, E.A.; Ganuza, M.L. Machine Learning model interpretability using SHAP values: Application to Igneous Rock Classification task. Appl. Comput. Geosci. 2024, 23, 100178. [Google Scholar] [CrossRef]
- Zafar, M.R.; Khan, N. Deterministic Local Interpretable Model-Agnostic Explanations for Stable Explainability. Mach. Learn. Knowl. Extr. 2021, 3, 525–541. [Google Scholar] [CrossRef]
- Pizarroso, J.; Portela, J.; Muñoz, A. NeuralSens: Sensitivity Analysis of Neural Networks. J. Stat. Softw. 2022, 102, 1–36. [Google Scholar] [CrossRef]
- Slack, D.; Hilgard, S.; Jia, E.; Singh, S.; Lakkaraju, H. Fooling LIME and SHAP: Adversarial Attacks on Post hoc Explanation Methods. In Proceedings of the AAAI/ACM Conference on AI, Ethics, and Society, Jose, CA, USA, 21–23 October 2024; ACM: New York, NY, USA, 2020; pp. 180–186. [Google Scholar]
- Izquierdo, J.L.; Ancochea, J.; Soriano, J.B. Clinical Characteristics and Prognostic Factors for Intensive Care Unit Admission of Patients With COVID-19: Retrospective Study Using Machine Learning and Natural Language Processing. J. Med. Internet Res. 2020, 22, e21801. [Google Scholar] [CrossRef]
- Bertsimas, D.; Pauphilet, J.; Van Parys, B. Sparse Regression: Scalable Algorithms and Empirical Performance. Stat. Sci. 2020, 35, 555–578. [Google Scholar] [CrossRef]
- Forel, A.; Parmentier, A.; Vidal, T. Explainable data-driven optimization: From context to decision and back again. In Proceedings of the 40th International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; JMLR.org: Honolulu, HI, USA, 2023. [Google Scholar]
- Aigner, K.-M.; Goerigk, M.; Hartisch, M.; Liers, F.; Miehlich, A. A framework for data-driven explainability in mathematical optimization. In Proceedings of the Thirty-Eighth AAAI Conference on Artificial Intelligence and Thirty-Sixth Conference on Innovative Applications of Artificial Intelligence and Fourteenth Symposium on Educational Advances in Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; AAAI Press: Washington, DC, USA, 2024. [Google Scholar]
- Korikov, A.; Beck, J.C. Objective-Based Counterfactual Explanations for Linear Discrete Optimization. In Proceedings of the Integration of Constraint Programming, Artificial Intelligence, and Operations Research: 20th International Conference, CPAIOR 2023, Nice, France, 29 May–1 June 2023; Proceedings. Springer: Berlin/Heidelberg, Germany, 2023; pp. 18–34. [Google Scholar]
- Kurtz, J.; Birbil, Ş.İ.; Hertog, D.d. Counterfactual Explanations for Linear Optimization. arXiv 2024, arXiv:2405.15431. [Google Scholar] [CrossRef]
- Ciocan, D.F.; Mišić, V.V. Interpretable Optimal Stopping. Manag. Sci. 2022, 68, 1616–1638. [Google Scholar] [CrossRef]
- Čyras, K.; Letsios, D.; Misener, R.; Toni, F. Argumentation for Explainable Scheduling. Proc. AAAI Conf. Artif. Intell. 2019, 33, 2752–2759. [Google Scholar] [CrossRef][Green Version]
- Goerigk, M.; Hartisch, M. A framework for inherently interpretable optimization models. Eur. J. Oper. Res. 2023, 310, 1312–1324. [Google Scholar] [CrossRef]
- Lumbreras, S.; Tejada, D.; Elechiguerra, D. Explaining the solutions of the unit commitment with interpretable machine learning. Int. J. Electr. Power Energy Syst. 2024, 160, 110106. [Google Scholar] [CrossRef]
- Amram, M.; Dunn, J.; Zhuo, Y.D. Optimal policy trees. Mach. Learn. 2022, 111, 2741–2768. [Google Scholar] [CrossRef]
- Bertsimas, D.; Dunn, J.; Mundru, N. Optimal prescriptive trees. Inf. J. Optim. 2019, 1, 164–183. [Google Scholar] [CrossRef]
- Wolsey, L.A.; Nemhauser, G.L. Integer and Combinatorial Optimization; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1988; ISBN 978-0-471-82819-8. [Google Scholar]
- Papadimitriou, C.H.; Steiglitz, K. Combinatorial Optimization: Algorithms and Complexity; Dover Books on Computer Science; Dover Publications: Garden City, NY, USA, 1998; ISBN 978-0-486-40258-1. [Google Scholar]
- Doshi-Velez, F.; Kim, B. Towards A Rigorous Science of Interpretable Machine Learning. arXiv Mach. Learn. 2017, arXiv:1702.08608. [Google Scholar] [CrossRef]
- Allen, A.E.A.; Tkatchenko, A. Machine learning of material properties: Predictive and interpretable multilinear models. Sci. Adv. 2022, 8, eabm7185. [Google Scholar] [CrossRef]
- Priego, E.J.C.; Olivares-Nadal, A.V.; Cobo, P.R. Integer constraints for enhancing interpretability in linear regression. Sort-Stat. Oper. Res. Trans. 2020, 44, 69–78. [Google Scholar]
- Schneider, L.; Bischl, B.; Thomas, J. Multi-Objective Optimization of Performance and Interpretability of Tabular Supervised Machine Learning Models. In Proceedings of the Genetic and Evolutionary Computation Conference, Lisbon, Portugal, 15–19 July 2023; Association for Computing Machinery: New York, NY, USA, 2023; pp. 538–547. [Google Scholar]
- Nguyen, A.-P.; Moreno, D.L.; Le-Bel, N.; Rodríguez Martínez, M. MonoNet: Enhancing interpretability in neural networks via monotonic features. Bioinforma. Adv. 2023, 3, vbad016. [Google Scholar] [CrossRef]
- Murdoch, W.J.; Singh, C.; Kumbier, K.; Abbasi-Asl, R.; Yu, B. Definitions, methods, and applications in interpretable machine learning. Proc. Natl. Acad. Sci. USA 2019, 116, 22071–22080. [Google Scholar] [CrossRef] [PubMed]
- Zionts, S.; Wallenius, J. A Method for Identifying Redundant Constraints and Extraneous Variables in Linear Programming. In Redundancy in Mathematical Programming; Springer: Berlin/Heidelberg, Germany, 1983; pp. 28–35. [Google Scholar]
- Newman, M.E.J. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef]
- Lumbreras, S.; Ramos, A. The new challenges to transmission expansion planning. Survey of recent practice and literature review. Electr. Power Syst. Res. 2016, 134, 19–29. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio Selection. J. Finance 1952, 7, 77–91. [Google Scholar]
- Achterberg, T.; Bixby, R.E.; Gu, Z.; Rothberg, E.; Weninger, D. Presolve Reductions in Mixed Integer Programming. Inf. J. Comput. 2020, 32, 473–506. [Google Scholar] [CrossRef]
- Andersen, E.D.; Andersen, K.D. Presolving in linear programming. Math. Program. 1995, 71, 221–245. [Google Scholar] [CrossRef]
- Tsarmpopoulos, D.G.; Nikolakakou, C.D.; Androulakis, G.S. A Class of Algorithms for Solving LP Problems by Prioritizing the Constraints. Am. J. Oper. Res. 2023, 13, 177–205. [Google Scholar] [CrossRef]
- Ardakani, A.J.; Bouffard, F. Identification of Umbrella Constraints in DC-Based Security-Constrained Optimal Power Flow. IEEE Trans. Power Syst. 2013, 28, 3924–3934. [Google Scholar] [CrossRef]
- IBM ILOG CPLEX Optimization Studio Advanced Presolve Routines. Available online: https://www.ibm.com/docs/en/icos/22.1.2?topic=techniques-advanced-presolve-routines (accessed on 17 April 2025).
- Maximal Software GUROBI Presolve Parameter Options. Available online: https://www.maximalsoftware.com/solvopt/optGrbPresolve.html (accessed on 17 April 2025).
- FICO Xpress Optimization Help. Available online: https://www.fico.com/fico-xpress-optimization/docs/latest/solver/optimizer/HTML/PRESOLVE.html (accessed on 17 April 2025).
- Achterberg, T.; Wunderling, R. Mixed Integer Programming: Analyzing 12 Years of Progress. In Facets of Combinatorial Optimization: Festschrift for Martin Grötschel; Jünger, M., Reinelt, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 449–481. ISBN 978-3-642-38189-8. [Google Scholar]
- Meindl, B.; Templ, M. Analysis of Commercial and Free and Open Source Solvers for the Cell Suppression Problem. Trans. Data Priv. 2013, 6, 147–159. [Google Scholar]
- Rahmaniani, R.; Crainic, T.G.; Gendreau, M.; Rei, W. The Benders decomposition algorithm: A literature review. Eur. J. Oper. Res. 2017, 259, 801–817. [Google Scholar] [CrossRef]
- Conejo, A.J.; Castillo, E.; Mínguez, R.; García-Bertrand, R. Decomposition Techniques in Mathematical Programming, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 978-3-540-27685-2. [Google Scholar]
- Beheshti Asl, N.; MirHassani, S.A. Accelerating benders decomposition: Multiple cuts via multiple solutions. J. Comb. Optim. 2019, 37, 806–826. [Google Scholar] [CrossRef]
- Magnanti, T.L.; Wong, R.T. Accelerating Benders Decomposition: Algorithmic Enhancement and Model Selection Criteria. Oper. Res. 1981, 29, 464–484. [Google Scholar] [CrossRef]
- Vanderbeck, F.; Savelsbergh, M.W.P. A generic view of Dantzig–Wolfe decomposition in mixed integer programming. Oper. Res. Lett. 2006, 34, 296–306. [Google Scholar] [CrossRef]
- Huang, Z.; Zheng, Q.P.; Liu, A.L. A Nested Cross Decomposition Algorithm for Power System Capacity Expansion with Multiscale Uncertainties. Inf. J. Comput. 2022, 34, 1919–1939. [Google Scholar] [CrossRef]
- Ceselli, A.; Létocart, L.; Traversi, E. Dantzig–Wolfe reformulations for binary quadratic problems. Math. Program. Comput. 2022, 14, 85–120. [Google Scholar] [CrossRef]
- Geoffrion, A.M. Lagrangean relaxation for integer programming. In Approaches to Integer Programming; Balinski, M.L., Ed.; Springer: Berlin/Heidelberg, Germany, 1974; pp. 82–114. ISBN 978-3-642-00740-8. [Google Scholar]
- Sahin, M.F.; Eftekhari, A.; Alacaoglu, A.; Latorre, F.; Cevher, V. An inexact augmented lagrangian framework for nonconvex optimization with nonlinear constraints. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Curran Associates Inc.: Red Hook, NY, USA, 2019. [Google Scholar]
- Tang, Z.; Jiang, Y.; Yang, F. An Efficient Lagrangian Relaxation Algorithm for the Shared Parking Problem. Comput. Ind. Eng. 2023, 176, 108860. [Google Scholar] [CrossRef]
- Nishihara, R.; Lessard, L.; Recht, B.; Packard, A.; Jordan, M.I. A general analysis of the convergence of ADMM. In Proceedings of the 32nd International Conference on International Conference on Machine Learning, Lille, France, 6−11 July 2015; JMLR.org: Lille, France, 2015; Volume 37, pp. 343–352. [Google Scholar]
- Bartali, L.; Grabovic, E.; Gabiccini, M. A consensus-based alternating direction method of multipliers approach to parallelize large-scale minimum-lap-time problems. Multibody Syst. Dyn. 2024, 61, 481–507. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, M.; Pan, X.; Tan, J. Partial symmetric regularized alternating direction method of multipliers for non-convex split feasibility problems. AIMS Math. 2025, 10, 3041–3061. [Google Scholar] [CrossRef]
- Paleari, L.; Movedi, E.; Zoli, M.; Burato, A.; Cecconi, I.; Errahouly, J.; Pecollo, E.; Sorvillo, C.; Confalonieri, R. Sensitivity analysis using Morris: Just screening or an effective ranking method? Ecol. Model. 2021, 455, 109648. [Google Scholar] [CrossRef]
- Crusenberry, C.R.; Sobey, A.J.; TerMaath, S.C. Evaluation of global sensitivity analysis methods for computational structural mechanics problems. Data-Centric Eng. 2023, 4, e28. [Google Scholar] [CrossRef]
- Menberg, K.; Heo, Y.; Augenbroe, G.; Choudhary, R. New Extension Of Morris Method For Sensitivity Analysis Of Building Energy Models. In Proceedings of the BSO Conference 2016: Third Conference of IBPSA, Newcastle Upon Tyne, UK, 12–14 September 2016; IBPSA-England: Newcastle, UK, 2016; Volume 3, pp. 89–96. [Google Scholar]
- Ge, Q.; Menendez, M. Extending Morris method for qualitative global sensitivity analysis of models with dependent inputs. Reliab. Eng. Syst. Saf. 2017, 162, 28–39. [Google Scholar] [CrossRef]
- Li, Q.; Huang, H.; Xie, S.; Chen, L.; Liu, Z. An enhanced framework for Morris by combining with a sequential sampling strategy. Int. J. Uncertain. Quantif. 2023, 13, 81–96. [Google Scholar] [CrossRef]
- Ţene, M.; Stuparu, D.E.; Kurowicka, D.; Serafy, G.Y.E. A copula-based sensitivity analysis method and its application to a North Sea sediment transport model. Environ. Model. Softw. 2018, 104, 1–12. [Google Scholar] [CrossRef]
- Shi, W.; Chen, X. Controlled Morris method: A new distribution-free sequential testing procedure for factor screening. In Proceedings of the 2017 Winter Simulation Conference (WSC), Las Vegas, NV, USA, 3–6 December 2017; pp. 1820–1831. [Google Scholar]
- Shi, W.; Chen, X. Controlled Morris method: A new factor screening approach empowered by a distribution-free sequential multiple testing procedure. Reliab. Eng. Syst. Saf. 2019, 189, 299–314. [Google Scholar] [CrossRef]
- Usher, W.; Barnes, T.; Moksnes, N.; Niet, T. Global sensitivity analysis to enhance the transparency and rigour of energy system optimisation modelling. Open Res. Eur. 2023, 3, 30. [Google Scholar] [CrossRef] [PubMed]
- Karna, S.K.; Sahai, R. An Overview on Taguchi Method. Int. J. Eng. Math. Sci. 2012, 1, 11–18. [Google Scholar]
- Wald, A. Sequential Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1947. [Google Scholar]
- Pukelsheim, F. Optimal Design of Experiments; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2006; ISBN 978-0-89871-604-7. [Google Scholar]
- Nabi, S.; Ahanger, M.A.; Dar, A.Q. Investigating the potential of Morris algorithm for improving the computational constraints of global sensitivity analysis. Environ. Sci. Pollut. Res. 2021, 28, 60900–60912. [Google Scholar] [CrossRef]
- Confalonieri, R.; Bellocchi, G.; Bregaglio, S.; Donatelli, M.; Acutis, M. Comparison of sensitivity analysis techniques: A case study with the rice model WARM. Ecol. Model. 2010, 221, 1897–1906. [Google Scholar] [CrossRef]
- Hisam, M.W.; Dar, A.A.; Elrasheed, M.O.; Khan, M.S.; Gera, R.; Azad, I. The Versatility of the Taguchi Method: Optimizing Experiments Across Diverse Disciplines. J. Stat. Theory Appl. 2024, 23, 365–389. [Google Scholar] [CrossRef]
- Lakens, D. Performing high-powered studies efficiently with sequential analyses. Eur. J. Soc. Psychol. 2014, 44, 701–710. [Google Scholar] [CrossRef]
- Roy, R.K. Design of Experiments Using The Taguchi Approach: 16 Steps to Product and Process Improvement; Wiley: Hoboken, NJ, USA, 2021; ISBN 978-0-471-36101-5. [Google Scholar]
- Myers, R.H.; Monthgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments, 4th ed.; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2016; ISBN 978-1-118-91601-8. [Google Scholar]
- Proschan, M.A.; Lan, K.K.G.; Wittes, J.T. Statistical Monitoring of Clinical Trials, 1st ed.; Statistics for Biology and Health; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 978-0-387-30059-7. [Google Scholar]
- Tsirpitzi, R.E.; Miller, F.; Burman, C.-F. Robust optimal designs using a model misspecification term. Metrika 2023, 86, 781–804. [Google Scholar] [CrossRef]
- Panciatici, P.; Campi, M.C.; Garatti, S.; Low, S.H.; Molzahn, D.K.; Sun, A.X.; Wehenkel, L. Advanced optimization methods for power systems. In Proceedings of the 2014 Power Systems Computation Conference, Wroclaw, Poland, 18–22 August 2014; pp. 1–18. [Google Scholar]
- Ho, Y.-C.; Zhao, Q.-C.; Jia, Q.-S. Ordinal Optimization: Soft Optimization for Hard Problems, 1st ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; ISBN 978-0-387-68692-9. [Google Scholar]
- Ward, J.E.; Wendell, R.E. Approaches to sensitivity analysis in linear programming. Ann. Oper. Res. 1990, 27, 3–38. [Google Scholar] [CrossRef]
- Saltelly, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelly, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2007; ISBN 978-0-470-72518-4. [Google Scholar]
- Voll, P.; Hennen, M.; Klaffke, C.; Lampe, M.; Bardow, A. Exploring the Near-Optimal Solution Space for the Synthesis of Distributed Energy Supply Systems. Chem. Eng. Trans. 2013, 35, 277–282. [Google Scholar] [CrossRef]
- Pearce, J.P.; Tambe, M. Quality guarantees on k-optimal solutions for distributed constraint optimization problems. In Proceedings of the 20th International Joint Conference on Artifical Intelligence, Hyderabad, India, 6–12 January 2007; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2007; pp. 1446–1451. [Google Scholar]
- Wagner, H.M. A Comparison of the Original and Revised Simplex Methods. Oper. Res. 1957, 5, 361–369. [Google Scholar] [CrossRef]
- Li, F.G.N.; Trutnevyte, E. Investment appraisal of cost-optimal and near-optimal pathways for the UK electricity sector transition to 2050. Appl. Energy 2017, 189, 89–109. [Google Scholar] [CrossRef]
- Brill, E.D., Jr.; Chang, S.-Y.; Hopkins, L.D. Modeling to generate alternatives: The HSJ approach and an illustration using a problem in land use planning. Manag. Sci. 1982, 28, 221–235. [Google Scholar] [CrossRef]
- DeCarolis, J.; Daly, H.; Dodds, P.; Keppo, I.; Li, F.; McDowall, W.; Pye, S.; Strachan, N.; Trutnevyte, E.; Usher, W.; et al. Formalizing best practice for energy system optimization modelling. Appl. Energy 2017, 194, 184–198. [Google Scholar] [CrossRef]
- Pedersen, T.T.; Victoria, M.; Rasmussen, M.G.; Andresen, G.B. Modeling all alternative solutions for highly renewable energy systems. Energy 2021, 234, 121294. [Google Scholar] [CrossRef]
- Neumann, F.; Brown, T. The near-optimal feasible space of a renewable power system model. Electr. Power Syst. Res. 2021, 190, 106690. [Google Scholar] [CrossRef]
- Schricker, H.; Schuler, B.; Reinert, C.; von der Aßen, N. Gotta catch ’em all: Modeling All Discrete Alternatives for Industrial Energy System Transitions. arXiv 2023, arXiv:230710687. [Google Scholar] [CrossRef]
- Grochowicz, A.; Greevenbroek, K.V.; Benth, F.E.; Zeyringer, M. Intersecting near-optimal spaces: European power systems with more resilience to weather variability. Energy Econ. 2023, 118, 106496. [Google Scholar] [CrossRef]
- Dubois, A.; Ernst, D. Computing necessary conditions for near-optimality in capacity expansion planning problems. Electr. Power Syst. Res. 2022, 211, 108343. [Google Scholar] [CrossRef]
- Lumbreras, S.; Ramos, A.; Sánchez-Martín, P. Offshore wind farm electrical design using a hybrid of ordinal optimization and mixed-integer programming. Wind. Energy 2015, 18, 2241–2258. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2001; ISBN 978-0-471-87339-6. [Google Scholar]
- Pitzer, E.; Affenzeller, M. A Comprehensive Survey on Fitness Landscape Analysis. In Recent Advances in Intelligent Engineering Systems; Fodor, J., Klempous, R., Suárez Araujo, C.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 161–191. ISBN 978-3-642-23229-9. [Google Scholar]
- Bertsimas, D.; Brown, D.B.; Caramanis, C. Theory and Applications of Robust Optimization. SIAM Rev. 2011, 53, 464–501. [Google Scholar] [CrossRef]
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming, 2nd ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; ISBN 978-1-4939-3703-5. [Google Scholar]
- GAMS Sensitivity Analysis with GAMS/CPLEX and GAMS/OSL. Available online: https://www.gams.com/docs/pdf/sensi.pdf (accessed on 21 April 2025).
- Gurobi Sensitivity Analysis of Linear Programming Problems. Available online: https://www.gurobi.com/resources/lp-chapter-7-sensitivity-analysis-of-linear-programming-problems/ (accessed on 21 April 2025).
- Fiacco, A.V.; Ishizuka, Y. Sensitivity and stability analysis for nonlinear programming. Ann. Oper. Res. 1990, 27, 215–235. [Google Scholar] [CrossRef]
- Nasseri, S.H.; Attari, H.; Ebrahimnejad, A. Revised simplex method and its application for solving fuzzy linear programming problems. Eur. J. Ind. Eng. 2012, 6, 259. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006; ISBN 978-0-387-30303-1. [Google Scholar]
- Lau, M.; Patankar, N.; Jenkins, J.D. Measuring exploration: Evaluation of modelling to generate alternatives methods in capacity expansion models. Environ. Res. Energy 2024, 1, 045004. [Google Scholar] [CrossRef]
- Lombardi, F.; Pickering, B.; Pfenninger, S. What is redundant and what is not? Computational trade-offs in modelling to generate alternatives for energy infrastructure deployment. Appl. Energy 2023, 339, 121002. [Google Scholar] [CrossRef]
- Funke, C.S.; Brodnicke, L.; Lombardi, F.; Sansavini, G. Funplex: A Modified Simplex Algorithm to Efficiently Explore Near-Optimal Spaces. arXiv 2024, arXiv:2406.19809. [Google Scholar] [CrossRef]
- Guazzelli, C.S.; Cunha, C.B. Exploring K-best solutions to enrich network design decision-making. Omega 2018, 78, 139–164. [Google Scholar] [CrossRef]
- Deb, K. Multi-objective Optimisation Using Evolutionary Algorithms: An Introduction. In Multi-Objective Evolutionary Optimisation for Product Design and Manufacturing; Wang, L., Ng, A.H.C., Deb, K., Eds.; Springer: London, UK, 2011; pp. 3–34. ISBN 978-0-85729-652-8. [Google Scholar]
- Ji, J.-Y.; Wong, M.L. An improved dynamic multi-objective optimization approach for nonlinear equation systems. Inf. Sci. 2021, 576, 204–227. [Google Scholar] [CrossRef]
- Joy, G.; Huyck, C.; Yang, X.-S. Review of Parameter Tuning Methods for Nature-Inspired Algorithms. In Benchmarks and Hybrid Algorithms in Optimization and Applications; Yang, X.-S., Ed.; Springer Nature: Singapore, 2023; pp. 33–47. ISBN 978-981-9939-70-1. [Google Scholar]
- Zou, F.; Chen, D.; Liu, H.; Cao, S.; Ji, X.; Zhang, Y. A survey of fitness landscape analysis for optimization. Neurocomputing 2022, 503, 129–139. [Google Scholar] [CrossRef]
- Do, A.V.; Guo, M.; Neumann, A.; Neumann, F. Evolutionary Multi-objective Diversity Optimization. In Parallel Problem Solving from Nature—PPSN XVIII; Affenzeller, M., Winkler, S.M., Kononova, A.V., Trautmann, H., Tušar, T., Machado, P., Bäck, T., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 117–134. [Google Scholar]
- Jonathan Rosenhead, M.E.; Gupta, S.K. Robustness and Optimality as Criteria for Strategic Decisions. J. Oper. Res. Soc. 1972, 23, 413–431. [Google Scholar] [CrossRef]
- Mao, J.-Y.; Benbasat, I. The Use of Explanations in Knowledge-Based Systems: Cognitive Perspectives and a Process-Tracing Analysis. J. Manage Inf. Syst. 2000, 17, 153–179. [Google Scholar]
- Ye, L.R.; Johnson, P.E. The Impact of Explanation Facilities on User Acceptance of Expert Systems Advice. MIS Q. 1995, 19, 157–172. [Google Scholar] [CrossRef]
- Mueller, C.E.; Keil, S.I. Citizens’ Initiatives in the Context of Germany’s Power Grid Expansion: A Micro-econometric Evaluation of Their Effects on Members’ Protest Behavior. Z. Energiewirtschaft 2019, 43, 101–116. [Google Scholar] [CrossRef]
- Broadbent, I.D.; Nixon, C.L. Refusal of planning consent for the Docking Shoal offshore wind farm: Stakeholder perspectives and lessons learned. Mar. Policy 2019, 110, 103529. [Google Scholar] [CrossRef]
- Guan, J.; Zepp, H. Factors Affecting the Community Acceptance of Onshore Wind Farms: A Case Study of the Zhongying Wind Farm in Eastern China. Sustainability 2020, 12, 6894. [Google Scholar] [CrossRef]
- LeRoux, K. Managing Stakeholder Demands: Balancing Responsiveness to Clients and Funding Agents in Nonprofit Social Service Organizations. Adm. Soc. 2009, 41, 158–184. [Google Scholar] [CrossRef]
- Frooman, J. Stakeholder Influence Strategies. Acad. Manage. Rev. 1999, 24, 191–205. [Google Scholar] [CrossRef]
- Anessi-Pessina, E.; Barbera, C.; Langella, C.; Manes-Rossi, F.; Sancino, A.; Sicilia, M.; Steccolini, I. Reconsidering public budgeting after the COVID-19 outbreak: Key lessons and future challenges. J. Public. Budg. Account. Financ. Manag. 2020, 32, 957–965. [Google Scholar] [CrossRef]
- Jung, H. Online Open Budget: The Effects of Budget Transparency on Budget Efficiency. Public. Finance Rev. 2022, 50, 91–119. [Google Scholar] [CrossRef]
- Farazmand, A.; De Simone, E.; Gaeta, G.L.; Capasso, S. Corruption, lack of Transparency and the Misuse of Public Funds in Times of Crisis: An introduction. Public. Organ. Rev. 2022, 22, 497–503. [Google Scholar] [CrossRef]
- IAmExpat. Dutch Tax Authority Admits to Singling out People with Dual Nationality for Stricter Checks. IAmExpat in the Netherlands. Available online: https://www.iamexpat.nl/expat-info/dutch-expat-news/dutch-tax-authority-admits-singling-out-people-dual-nationality-stricter (accessed on 15 February 2024).
- Crown, W.; Buyukkaramikli, N.; Thokala, P.; Morton, A.; Sir, M.Y.; Marshall, D.A.; Tosh, J.; Padula, W.V.; Ijzerman, M.J.; Wong, P.K.; et al. Constrained Optimization Methods in Health Services Research—An Introduction: Report 1 of the ISPOR Optimization Methods Emerging Good Practices Task Force. Value Health 2017, 20, 310–319. [Google Scholar] [CrossRef] [PubMed]
- Kraus, M.; Feuerriegel, S.; Saar-Tsechansky, M. Data-Driven Allocation of Preventive Care with Application to Diabetes Mellitus Type II. Manuf. Serv. Oper. Manag. 2024, 26, 137–153. [Google Scholar] [CrossRef]
- Rundo, L.; Pirrone, R.; Vitabile, S.; Sala, E.; Gambino, O. Recent advances of HCI in decision-making tasks for optimized clinical workflows and precision medicine. J. Biomed. Inform. 2020, 108, 103479. [Google Scholar] [CrossRef]
- Alves, M.; Seringa, J.; Silvestre, T.; Magalhães, T. Use of Artificial Intelligence tools in supporting decision-making in hospital management. BMC Health Serv. Res. 2024, 24, 1282. [Google Scholar] [CrossRef]
| Benders’ Decomposition | Dantzig-Wolfe | Lagrangian Relaxation | ADMM | |
|---|---|---|---|---|
| Problem Structure | Complicating variables | Complicating constraints | Complex constraints | Separable objective |
| Best Suited for | LP/MIP problems with complicating variables, continuous non-complicating ones | LP problems with complicating constraints | Problems with nonlinear constraints | Large-scale convex problems |
| Potential for Interpretability | Medium | Low | Medium | Medium |
| Morris Method | Taguchi Method | Sequential Analysis | Optimal Design | |
|---|---|---|---|---|
| Strengths | Simple to implement and computationally efficient [68,69] | Robust to noise factors and requires a reduced number of experiments [70] | It is an adaptive method where experiments are based on previous results and it uses resources efficiently [66,71] | It is a flexible and efficient method that can incorporate complicated constraints [67] |
| Weaknesses | Mostly qualitative and results may be unstable if there are strong nonlinearities [56,57] | Less suited for complex iterations [72,73] | It requires ongoing analyses and it is sensitive to initial sampling biases [74] | It requires accurate model hypotheses [75] |
| Main aim | Identification of key variables at an early stage | Problems where robustness is important | Reduce number of experiments when problem features are unclear | Reduce number of experiments when problems are clear |
| Method | Strengths | Weaknesses |
|---|---|---|
| Sensitivity Analysis | It is available in most solvers, and therefore its application is straightforward [96,97]. | It only evaluates the feasible region close to the optimal solution and offers limited performance if the problem is not linear [98]. |
| Revised Simplex Method (with perturbation) | It is computationally efficient [99]. | Its main usefulness relies on LP problems [100]. |
| Modeling to Generate Alternatives (MGA) | It maintains a balance between exploring the feasible region to generate near-optimal solutions and the computational burden [101]. | It may be computationally intense, and it does not guarantee a thorough exploration of each near-optimal zone of the feasible region [102,103]. |
| K-optimal Solution Algorithms | It facilitates the decision-making process by providing solutions in a structured way [104]. | It may be difficult to apply to large-scale problems if the parameter k is very large because it requires executing the model k times [104]. |
| Modeling All Alternatives (MAA) | It performs an exhaustive evaluation of the feasible region and is guaranteed to find all near-optimal solutions closer than a specified threshold [86]. | It is very computationally intense [86]. |
| Evolutionary Multi-Objective Optimization (EMO) | It is particularly well suited for multiobjective problems and can deal with nonlinearities [105,106]. | It may need expert tuning of parameters, and there is no guarantee of optimality [107]. |
| Fitness Landscape Analysis (FLA) | It helps us understand features of complicated problems [108]. | It has seen minimal use in multiobjective problems so far [108]. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lumbreras, S.; Ciller, P. Interpretable Optimization: Why and How We Should Explain Optimization Models. Appl. Sci. 2025, 15, 5732. https://doi.org/10.3390/app15105732
Lumbreras S, Ciller P. Interpretable Optimization: Why and How We Should Explain Optimization Models. Applied Sciences. 2025; 15(10):5732. https://doi.org/10.3390/app15105732
Chicago/Turabian StyleLumbreras, Sara, and Pedro Ciller. 2025. "Interpretable Optimization: Why and How We Should Explain Optimization Models" Applied Sciences 15, no. 10: 5732. https://doi.org/10.3390/app15105732
APA StyleLumbreras, S., & Ciller, P. (2025). Interpretable Optimization: Why and How We Should Explain Optimization Models. Applied Sciences, 15(10), 5732. https://doi.org/10.3390/app15105732










