Abstract
Wind power plays a significant role in sustainable energy production, but the reliability of wind turbines depends heavily on the integrity of their gearboxes. Gearbox failures can lead to significant downtime and operational disruption. In this context, this paper provides an overview of the evolution of gearbox monitoring techniques, culminating in the emergence of digital twin (DT) technology. We explore the application of DT technology to gearbox condition monitoring, focusing on two critical components: bearings and gears. This includes a comprehensive review of methodologies involving model-based approaches and data-driven techniques using signal processing (SP) and artificial intelligence (AI) algorithms. We address the challenges of “learning with minimal knowledge” and propose a framework for the effective application of DT technology. Finally, we discuss future research directions and potential contributions to advancing the field of gearbox condition monitoring through the continued development and implementation of DT-based solutions.
1. Introduction
Demographic and industrial growth in many countries is driving an increasing demand for energy supply. Under this pressure, intense competition for resources has led some nations to adopt solutions that are harmful to the climate and, more critically, to human well-being [1]. In 2023, global statistics showed that 82% of energy production came from fossil fuels, compared to only 13% from renewables and 5% from nuclear power. Among the clean and sustainable alternatives are wind, ocean currents, and solar power [2]. Wind energy, in particular, stands out as a viable solution for many countries, with two main configurations: onshore and offshore wind turbines [3]. In 2023, global installed capacity reached 906 GW, with 68% from onshore installations and 32% from offshore [4]. This growth is driven by high efficiency, substantial power output, and a competitive cost ranging between USD 26 and 54/MWh [5]. That same year, wind turbines reached power outputs of up to 18 MW for offshore models and 10 MW for onshore ones. In the near future, the market is projected to reach USD 102.4 billion, supported by the deployment of 25 MW offshore turbines and 15 MW onshore turbines, equipped with rotor diameters of 350 and 270 m, respectively [4]. However, like any system or machine, wind turbines cannot operate indefinitely without experiencing faults. These machines rely on complex transmission systems and function under harsh environmental and operational conditions. High humidity, for instance, accelerates lubricant degradation, increasing friction and reducing efficiency. Dust carried by wind can contaminate the lubricant, leading to premature wear and diminished lubrication performance [6]. In addition, unsteady wind forces generate impact loads and variable torque throughout the transmission chain, promoting fatigue in components, particularly in the gearbox, which is often the first to fail [7]. Another contributing factor is the mechanical contact between transmission elements, which increases surface wear and fatigue [8]. Altogether, these challenges contribute to a high failure rate, potential power outages, safety hazards, and considerable economic losses [9,10]. Monitoring data history has shown that this system accounts for 65% of all turbine shutdowns [11]. To reduce these interruptions, a portion of the generation cost is allocated to the operations and maintenance (O&M) department. This sector represents between 15% and 20% of total costs for onshore turbines and between 25% and 35% for offshore ones [7].
Various maintenance strategies have been adopted to address these challenges. Corrective maintenance is implemented after a fault occurs, involving the repair or replacement of defective components. While this approach can address issues, it does not prevent unexpected downtime, and for critical components, the resulting damage can be incalculable [12]. Another approach is systematic preventive maintenance, which involves replacing components before they reach the end of their useful life, ideally during non-work hours. Although this helps to avoid unexpected downtime, it results in component replacement regardless of their actual condition [13]. Condition-based maintenance allows for the replacement of defective components at the optimal time, just before the end of their useful life, according to their condition. However, this requires effective monitoring systems to assess the state of the component [14]. Finally, predictive maintenance uses the current condition of the components to estimate their useful life. This approach relies on data collected through various monitoring systems, enabling proactive interventions and improving operational efficiency [7].
The O&M department plays a critical role in ensuring safe and stable system operation by deploying effective monitoring tools [15]. These tools fall into two primary categories: (1) basic inspection devices including vibration testers, thermocouples, viscosity testers, and multimeters designed for routine measurements at predefined locations, where results are compared against established reference values, alarm thresholds, or danger levels, and (2) advanced diagnostic instruments such as spectrum analyzers, thermal cameras, microphone arrays, and real-time monitoring systems that require specialized expertise for proper data interpretation and comprehensive equipment assessment. To systematically address the complexities of industrial maintenance, the field has evolved into three distinct but interconnected disciplines: detection, diagnosis, and prognosis [16]. Fault detection involves binary classification between healthy and faulty states. It can be performed using simple tools, such as a vibration tester, followed by comparison with standards or previous records. Depending on the severity of the issue, the machine is either stopped or moved to the diagnosis phase. Fault diagnosis identifies the type of fault from among the potential issues affecting the machine. This process involves comparing fault patterns with the current behavior of the machine [17]. Once the fault is identified, the next step is either to replace the defective component immediately or proceed with prognosis. Fault prognosis monitors the health condition of the machine and estimates the remaining useful life of the equipment [18]. The purpose of subdividing this monitoring task is to allocate responsibilities among the maintenance personnel according to their expertise and provide each discipline with the necessary tools and resources.
These three disciplines can be implemented using two traditional approaches: data-driven and model-based [19]. The data-driven approach relies on measurements collected through monitoring techniques to evaluate the health status of the machine, such as infrared thermography (detects excessive heat emissions, which can indicate the presence of a fault in the machine) and vibration or acoustic measurements (utilize accelerometers or microphones and are widely employed for monitoring purposes and provide detailed insights into the machine’s conditio). Other techniques may be used in specific cases or for environmental constraints. Imaging is suitable for monitoring underwater structures affected by biofouling. Oil analysis is a diagnostic tool for machines with lubrication systems, such as gearboxes and internal combustion engines. Each technique is tailored to specific applications and contributes uniquely to ensure effective monitoring and maintenance of industrial machines [11]. Sometimes the obtained data are noisy, which requires Signal Processing (SP) or image processing techniques.
This approach offers numerous advantages, which explains its widespread adoption in the industry [20]. It enables real-time monitoring and can be integrated with artificial intelligence (AI) to ensure autonomy. It does not require specialized knowledge of degradation or fatigue phenomena to detect faults [21]. Additionally, it is easy to deploy, as modern machines are often equipped with various built-in sensors. By analyzing the data from these sensors, faults can be detected at their inception. However, this approach also has certain limitations; it requires a labeled dataset for all potential faults that may affect the monitored machine, a requirement that is not always feasible, especially for high-tech or recently installed machines [7]. Direct exploitation of the data is rarely possible due to acquisition noise and fault interference, necessitating efficient SP methods to extract meaningful information. This can hinder the system’s ability to detect faults in real time and often prevents the physical interpretation of the underlying phenomena [21].
The model-based approach relies on the physical reproduction of the kinematic and dynamic phenomena occurring within a machine or a specific component. This requires prior knowledge of geometric properties, material characteristics, and understanding and modeling of motion: this includes analyzing the movement of individual components, their interactions, and the forces involved [15]. It also involves developing mathematical representations of these dynamics to accurately simulate real-world behavior. By solving the multiphase system using mathematical methods, the machine signatures in various states can be obtained. This approach is studied using two main methods: numerical simulation and physical modeling. Numerical simulation is based on a series of steps, starting with computer-aided design (CAD) of the various components of the mechanism being studied. Next, these components are assembled using connections and contact constraints. This step can be performed using dedicated software such as SolidWorks or AutoCAD. The following step involves defining the type of analysis required: dynamic, static, thermal, etc. For machine monitoring in general, dynamic analysis is typically used, except for specific studies. Afterward, meshing and mesh analysis are carried out to ensure the convergence of the simulation. This allows the simulation to be run, ultimately concluding with the visualization and analysis of the results. The simulation steps can be executed using dedicated software such as ANSYS or Abaqus [7]. The physical modeling method is based on fundamental laws or pre-established models. The framework flow involves defining boundary conditions and initial conditions and solving the system using mathematical tools to address differential equations, including partial differential equations and ordinary differential equations. This approach offers a deeper understanding of the physical phenomena by breaking them down into fundamental principles [22].
The model-based approach is essential for diagnosing machine behavior, predicting failures, and optimizing performance, providing valuable insights for industrial applications. It allows for a detailed understanding of the phenomena underlying faults, contributing to greater reliability in the design and manufacturing of components and machinery. Additionally, it facilitates the estimation of component fatigue cycles and the prediction of part replacements, thereby strengthening predictive maintenance strategies [21]. However, its implementation comes with certain challenges. It requires multidisciplinary knowledge, which can pose a skill-related barrier. Moreover, associated simulations require significant computational time, especially when accounting for all operating parameters and potential phenomena. Another major limitation lies in the unavailability of some essential physical parameters required for accurate simulations, which can reduce the effectiveness of the approach [23].
To overcome the limitations of both data-driven and model-based approaches, a new concept was introduced by Professor Grieves in the early 21st century, known as the digital twin (DT) [24]. This approach is designed to meet the requirements of Industry 4.0 while also serving as a key enabler for Industry 5.0, which aims to reintegrate humans into industrial processes [25]. This emerging technology is governed by a set of standards essential for its correct deployment. Da et al. [26] addressed this aspect by identifying seven key categories of standards: (1) Reference architecture standards for constructing the digital model from a physical system, primarily Reference Architectural Model for Industry (RAMI) 4.0 and the Industrial Internet Reference Architecture (IIRA) [27]. (2) Telecommunication and data exchange standards, such as IEEE P2413 [28] and ISO 23247-1 [29], ensure interoperability between components [26]. (3) Visualization and simulation standards, crucial for bridging the physical system and its virtual counterpart and for validating the twin through simulation. Examples include ISO/PAS 17506:2012 [30], used in computer-aided design (CAD) [31]. (4) Cloud computing standards, given that data transfer and processing, especially in large-scale and geographically distributed energy systems, relies heavily on cloud infrastructure, such as ISO/IEC TR 22678:2019 [32], dedicated to cloud resource management [27]. (5) Security and data protection standards, which are indispensable in cloud-based environments. The industry uses network security protocols like IEC 62443 and implements cryptographic algorithms following standards such as RFC 3447 [33]. (6) Communication protocol standards, including TCP, UDP, and MQTT, which facilitate reliable data transmission. (7) Connectivity standards for sensors and actuators, encompassing both wireless technologies (Wi-Fi, Bluetooth, LoRa) and wired options (CAN, SPI), as defined by IEEE 1451 and IEEE 2888 [34]. In its broadest sense, the digital twin (DT) concept involves creating a digital model that accurately replicates a physical object, operation, or system as it functions in the real world [35]. This versatile technology has been successfully applied across various domains, including aerospace, healthcare, smart cities, agriculture, transportation, construction, and energy [36]. These applications showcase the potential of DTs in enabling real-time monitoring, optimization, and decision-making across complex environments. In the specific context of machine monitoring, DT technology is used to develop a digital representation of a machine that faithfully reproduces its behavior under different operating conditions, including both healthy and faulty states. Achieving this requires the integration of both model-based and data-driven approaches [37]. The application of DT technology in wind energy generation has been demonstrated through real-world examples. The first example involves a collaboration between Siemens Gamesa and NVIDIA, where the Omniverse platform is used to optimize wind turbine layout and enhance overall energy production [38]. The second example is General Electric’s Predix Platform, which enables the collection, visualization, and analysis of data based on DT principles, aiming to optimize the operation of wind turbines and boost energy output [39].
Real-world phenomena are manifested through various parameters, such as vibration, acoustics, current, voltage, and temperature. These parameters must align with the outputs of the physical model for each operational state. This alignment allows for the anticipation of machine states and enables timely and real-time responses to potential issues [40]. The development of a DT involves several key stages. First, the systems to be monitored must be clearly defined. Next, appropriate monitoring tools must be installed, using techniques such as vibration analysis, infrared thermography, or oil analysis. Following this, a highly accurate model of the system must be constructed, incorporating kinematic and dynamic properties to replicate the system’s behavior effectively. The model is then used to calculate outputs based on the monitored variables and sensor placements [41]. Finally, the healthy state of the machine is used to calibrate and fine-tune the model to ensure its accuracy. This final step is particularly critical because it addresses unavoidable real-world phenomena. For example, on the mechanical side, even with precise manufacturing, there is always a tolerance margin. Similarly, on the data acquisition side, the noise introduced by the acquisition chain is inevitable. By accounting for these factors, the DT becomes a reliable tool for anticipating machine behavior, optimizing performance, and minimizing downtime [42].
The analysis presented highlights the critical need to deploy effective monitoring systems as a top priority in the wind energy sector. In this regard, the DT framework emerges as a promising solution, particularly through the integration of artificial intelligence and signal processing techniques. This paper reviews previous work on gearbox monitoring using DTs, emphasizing the development of the twin model and the contribution of AI and SP in implementing the proposed solution. The study also outlines future directions and opportunities for enhancing fault detection accuracy. This paper highlights the following contributions:
- -
- An overview of recent frameworks utilizing DT technology for gearbox and component monitoring.
- -
- A discussion of research opportunities in gearbox monitoring enabled by DT technology.
- -
- A critical review of the role of SP techniques in advancing DTs for gearbox monitoring.
- -
- A critical review of the role of AI techniques in advancing DTs for gearbox monitoring.
- -
- A presentation of research addressing the challenge of data scarcity and the contribution of DT technology to overcome this issue.
- -
- An exploration of future directions and opportunities for contributions in the field of gearbox monitoring based on the DT approach.
This paper is organized as follows: The first section provides an introduction to wind turbine-based energy generation, the evolution of fault monitoring to ensure safe operation, and the transformative role of DT technology in this domain. The second section outlines a methodology for deploying DTs for gearbox monitoring, based on a combination of mathematical modeling and data-driven approaches. The third section discusses the contributions of SP and AI in enhancing the accuracy of the DT, as well as the role of the DT in addressing the challenge of data scarcity for training machine monitoring networks. The fourth section explores the prospects of this framework for gearbox monitoring using DT technology, highlighting key perspectives and potential contributions to future research. Finally, the fifth section concludes the paper.
2. Digital Twin-Assisted Gearbox Monitoring
Power generation relies on converting mechanical motion into electricity using generators driven by inexhaustible natural forces such as wind, ocean currents, and waves [34]. These generators, in their simplest form, as shown in Figure 1, consist of aerodynamic blades designed to convert the directional movement of currents into rotational motion. This rotational motion is transmitted to the generator through a gearbox, enabling the conversion of mechanical power into electricity. This critical component serves to multiply the input shaft speed (from the blades) to the output shaft speed (toward the generator) [43]. In the gearbox, motion transmission occurs as follows: the input shaft, supported by a bearing, delivers motion to the pinion. Through the contact between the pinion teeth and the gear teeth, the motion is transferred to the output shaft, which is also supported by a bearing. This entire transformation chain is supported by the yaw system, which orients the turbine in the direction of the incoming wind. Figure 1 also shows the potential sensor locations for monitoring the transmission system, numbered from 1 to 8, from the blade to the generator.
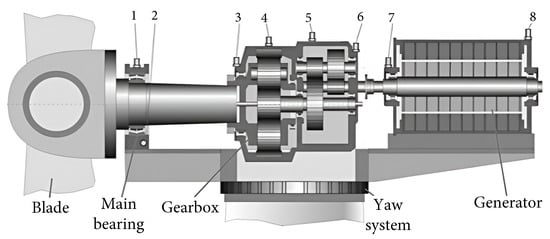
Figure 1.
Wind turbine components [43].
In terms of reliability, the gearbox consists of a series of interconnected components, where the failure of a single element directly affects the overall performance. In addition to its critical role, it has an annual failure rate ranging from 0.1 to 0.15 failures/turbine/year, with an average repair time of 6 to 15 days [14]. This leads to the replacement of the gearbox within a period of 5 to 6 years, despite the wind turbine’s total estimated lifespan of 25 years [7]. The two most critical components in gearboxes, due to their potential for damage and high failure rates, are the bearings and gears. Bearing-related faults are the most common, accounting for 76.2% of all gearbox failures, followed by gear faults at 17.3%. The remaining 6.5% are attributed to other components [44,45]. In the following section, an approach for implementing a digital twin (DT) strategy to monitor these components is discussed. As explained in the Introduction, a DT integrates a modeling aspect and a data-driven aspect, both of which are described in detail.
2.1. Bearing Faults
2.1.1. Model-Based Development
The role of the bearing in this transmission system is to minimize contact and energy loss. Bearings generally operate at high speeds, causing a rise in temperature due to excessive friction. Several fault modes can affect these components, such as electric melting, plastic deformation, corrosion, and wear, as shown in Figure 2. Corrosion occurs due to lubricant degradation from chemical factors such as oxygen-induced oxidation or water infiltration, particularly in marine environments (offshore turbines). An additional electrochemical factor involves stray currents within generators. Bearing corrosion initially appears as gray-to-black surface pitting that progressively expands over time. Wear can be initiated by corrosion (which increases surface susceptibility to abrasion) or caused by physical lubricant contamination from wind-borne particles or internal component wear debris, typically accompanied by abnormal vibration and noise. Electric melting results from high current passing between races through rolling elements, generating localized heating that leads to contact zone melting and surface micro-welding, identifiable by characteristic dark fluting patterns on rollers and raceways. Plastic deformation primarily stems from excessive cyclic loading or improper installation, causing permanent geometric changes in contact zones between rolling elements and bearing races [46,47].

Figure 2.
Bearing fault modes: (a) corrosion, (b) fatigue, (c) plastic deformation, (d) electric melting [48].
These faults can affect the three parts of a bearing: inner race fault, outer race fault, and rolling elements fault, as shown in Figure 3. Each of these faults has a characteristic frequency determined by its geometric parameters and rotation speed [48].
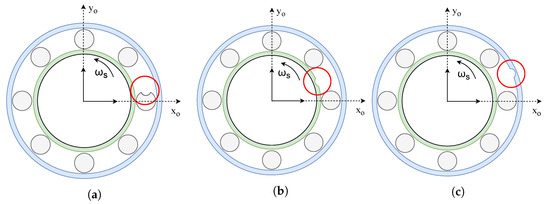
Figure 3.
Bearing fault types: (a) rolling bearing fault, (b) inner race fault, (c) outer race fault [48].
The model adopted for the dynamic modeling of bearing faults is the nonlinear dynamic model of a rolling bearing with five degrees of freedom (DOFs), as shown in Figure 4a, knowing that some reduce to four DOFs while maintaining almost the same axes, as shown in Figure 4b. This model has been extensively studied in previous frameworks, particularly in the context of DT applications, due to its simplicity and fidelity. The model includes two DOFs for the inner race () and the outer race (), and one DOF for the unit resonator (), where x and y represent the horizontal and vertical axes, respectively [49]. The five-DOF model includes one additional degree of freedom for the resonator mass , compared to the four-DOF model. This added degree of freedom enhances the model’s fidelity, allowing for more realistic simulations and capturing the interactions between the rotor and stator. On the other hand, the five-DOF representation has some drawbacks, and it requires more parameters to be identified before the simulation can be run. This additional complexity increases computation time and demands higher storage capacity.
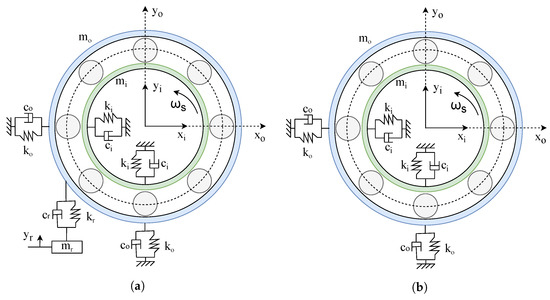
Figure 4.
Bearing dynamic model with: (a) 5 DOFs [50], (b) 4 DOFs [40].
The dynamic behavior of the system is governed by a set of second-order differential equations that model the motion of the inner race, outer race, and the unit resonator. The parameters include the shaft speed (), the stiffness of the inner race (), the outer race (), and the resonator (), along with their respective damping coefficients (, , and ) [51].
Inner race motion in the x-direction:
This equation describes the translational motion of the inner race along the horizontal axis. The terms represent, respectively, the inertial force, damping force, and restoring force due to the stiffness of the inner race. The contact forces and arise from interaction with the other elements such as rolling elements [22].
Inner race motion in the y-direction:
This equation models the vertical displacement of the inner race. The right-hand side includes the gravitational force , while the left-hand side includes inertia, damping, stiffness, and vertical contact forces.
Outer race motion in the x-direction:
This equation captures the horizontal motion of the outer race. The contact forces and act in the opposite direction compared to the inner race due to Newton’s third law.
Unit resonator motion in the y-direction:
This equation defines the vertical motion of the resonator relative to the outer race. The resonator experiences restoring and damping forces relative to the outer race displacement and is also subject to gravity.
Outer race motion in the y-direction:
This equation governs the vertical dynamics of the outer race, accounting for gravitational force, its own damping and stiffness, vertical contact forces, and the coupling interaction with the resonator via both damping and stiffness terms.
At this stage, the fundamental principle of dynamics is applied to the system (inner race, outer race, and rolling elements), resulting in a system of differential equations equal to the number of DOFs. Solving this system of differential equations using numerical solvers allows for the determination of the outputs, which are the vibrations corresponding to the five DOFs. Subsequently, it becomes possible to simulate faults that may affect a bearing and obtain the vibrational signature of each fault.
Regarding the use of Finite Element Modeling (FEM), it has been the subject of several studies on bearing condition monitoring based on the DT approach. Liu et al. [52] used FEM to simulate bearing fault signals in order to compensate for the lack of real fault data. Time-domain features were extracted and used to train an SVM classifier. The method achieved high accuracy across six fault types, demonstrating that FEM-generated signals can enhance fault diagnosis when experimental data are scarce. Zhao et al. [15] developed an FEM-based model to simulate bearing degradation under multiple conditions. A domain adaptation technique was applied to align simulated and real data, improving the prediction of RUL. This hybrid approach enhanced prediction accuracy, showcasing the benefit of combining FEM with transfer learning for robust diagnostics. Wang et al. [53] addressed the high computational cost of FEM in real-time applications by proposing the KKR-DT system, which integrates k-nearest neighbors, Kriging, and Radial Basis Functions. A reduced-order model was constructed from FEM data and extended to various working conditions. The system predicts the RUL of roller bearings and enables rapid, real-time computations. Testing on industrial equipment confirmed its effectiveness for dynamic fault prediction. Huang et al. [49] introduced multi-fidelity information fusion, a method for continuous bearing fault diagnosis using digital twins and class-incremental learning. A low-fidelity DT generates synthetic data, which are fused with a limited number of high-fidelity measurements. This system maintains strong diagnostic performance while significantly reducing training time compared to traditional joint training. It effectively mitigates catastrophic forgetting and supports adaptive fault diagnosis over time.
2.1.2. Experimental Procedure
For the experimental procedure to study bearing faults, it is preferable to minimize the transmission components as much as possible. In fact, bearing failures are often implicit in nature and can easily be overshadowed by other faults or poor mechanical designs [54]. At this stage, it is crucial to measure the rotational speed of the shaft attached to the test bearing and then estimate the fault frequencies that could affect the bearing. Based on these frequencies, the required sampling frequency is calculated by following Shannon–Nyquist’s theorem, which states that a signal must be sampled at a rate at least twice its maximum frequency in order to be accurately captured [55]. This principle forms a bridge between a continuous signal and its discrete representation. Moreover, a higher sampling frequency increases the fidelity of the discrete signal. However, if the frequency is too high, it can lead to slower processing due to redundant data and storage issues. These two factors are particularly critical in real-time monitoring, making the appropriate choice of sampling frequency essential. In practice, signals are typically sampled at 5 to 10 times the maximum defect frequency to capture transient impacts and account for the roll-off of anti-aliasing filters. These frequency considerations also directly influence sensor selection, as the transducer must have adequate bandwidth and sensitivity over the relevant range to effectively detect faults. Bearings are generally sourced from well-known manufacturers. It is therefore recommended to consult catalogs to extract information about the bearing’s geometric characteristics and the material used for its manufacturing. If the material information is unavailable, it can be determined using characterization methods. The geometry and material data can then be used to calculate the weight of each bearing component. As for the stiffness and damping values, a modal analysis is necessary to estimate them [56].
The first example from [22] involves data collected on a laboratory test bench. To validate the response accuracy of a constructed five-DOF dynamic bearing model, the ABLT-1A test bench was used to acquire real vibration signals from a 6205 bearing. The rotational speed was set to 1500 rpm (i.e., 24.88 Hz). The dataset was sampled at a frequency of 12 kHz, with each sample containing 2048 data points. Measurements were taken under four conditions: healthy (HN), ball fault (BF), inner ring fault (IF), and outer ring fault (OF). The corresponding theoretical fault frequencies were 134.73 Hz (IF), 117.51 Hz (BF), and 89.19 Hz (OF). Both the measured and simulated waveforms exhibited periodic impulses with similar trends across the different fault types.
The second example from [21] is based on real-world vibration data collected from three 1.5 MW wind turbines located at a wind farm in Wuzhong, Ningxia (China), each with known pitch bearing conditions. The data acquisition system included W610-500 IEPE accelerometers (500 mV/g, 0.1 Hz–10 kHz bandwidth), a data logger, and a host computer connected via Ethernet. The optimal accelerometer placement was identified as the outer race of the pitch bearing. However, due to physical constraints, the accelerometers were instead installed at point 3 on the internal web of the hub, where signal intensity (RMS) and cross-correlation with points 1 and 2 remained high. Vibrational data were recorded over 80-s intervals at a sampling frequency of 2560 Hz. This setup enabled the collection of high-quality signals for fault diagnosis, even in a constrained environment.
It is worth noting that both studies yielded high-quality results, although they focus on different aspects: the first on fault diagnosis, and the second on fault detection. Laboratory conditions are stable and controllable, whereas real-world environments are subject to fluctuations. Moreover, the acquisition frequency used in laboratory experiments is often significantly higher than that of field applications, and even higher than the minimum required by the Shannon–Nyquist theorem.
2.2. Gear Faults
2.2.1. Model-Based Development
Gears generate vibrations and noise even in a healthy state, particularly in the case of straight-toothed gears. These vibrations occur at the meshing frequency, which corresponds to each contact between gear teeth. This fundamental frequency is * and equal to *, where z represents the number of teeth and f the rotational frequency [57]. Several fault modes can affect gears, caused by the load supported by the gear teeth or, in some cases, manufacturing defects that lead to these faults. Among these fault modes are cracks, pitting, wear, chipped teeth, or missing teeth, as shown in Figure 5.

Figure 5.
Gear fault modes: (a) healthy, (b) root crack, (c) chipped tooth, (d) missing tooth, (e) surface wear [58].
Accurate analysis of these vibratory phenomena relies on precise modeling of gear tooth contact. Our recent work has led to significant advances in this domain. On one hand, we developed a simplified formulation of the fundamental equations of gear contact, reducing the classical system of five nonlinear equations to only two [59]. This approach provides better numerical stability and enables parametric analysis of misalignment effects—both in-plane and out-of-plane—on the contact path, transmission error, and pressure distribution. On the other hand, a three-dimensional generalization of the contact problem, based on a novel parameterization of the contacting surfaces, was introduced [60]. This allows for efficient handling of the relative motion between two toothed surfaces rotating about fixed axes in space and improved accuracy.
In a faulty state, two scenarios may arise. If the fault is distributed across all the teeth, the impact between teeth becomes more pronounced, which amplifies vibrations at the meshing frequency. Conversely, if the fault is localized, it generates vibrations at the rotational frequency of the gear with the defective tooth [61]. In this context, the development of a digital twin dedicated to gear monitoring relies on computing the energies resulting from deformation and contact between one or two pairs of teeth, including Hertzian, bending, shear, and axial compressive energies. The relationship between these energies and tooth stiffness is then used to estimate the gear mesh stiffness [62].
A widely used model for simulating single-stage gear transmissions is the six-DOF model, illustrated in Figure 6. Although more complex models, such as the 21-DOF and 34-DOF models shown in Figure 7 and Figure 8, respectively, are available, the 6-DOF model remains popular due to its simplicity and computational efficiency. It is particularly effective for analyzing systems where torsional effects dominate. Its main strengths lie in its ease of implementation and low computational cost, which make it especially suitable for basic applications and educational purposes. However, this simplicity comes at the expense of accuracy. The model cannot capture complex interactions such as vibrations or nonlinear behaviors, and it assumes perfectly rigid bearings—an assumption that is often unrealistic in industrial settings. Moreover, it is not suitable for analyzing high-frequency phenomena. In contrast, the 21-DOF model offers a good balance between complexity and accuracy. It captures the coupling between torsional and translational dynamics, as well as gear mesh forces, and it includes the modeling of gear transmission errors, making it a valuable tool for studying gear noise and vibration. The computational effort remains reasonable for simulations requiring moderate precision. Nonetheless, it has its limitations: it assumes linear damping, neglects nonlinearities in the bearings, and does not account for contact losses. As a result, it is less effective for fine fault detection or for analyzing vibrations in the gearbox housing. The 34-DOF model represents the most advanced approach, capable of capturing a wide range of complex phenomena. It considers nonlinear bearing characteristics, such as variable stiffness, models localized defects, and enables detailed analysis of housing resonances. This level of detail makes it particularly well suited for predictive maintenance and advanced fault detection. However, such comprehensiveness comes at a significant computational cost, requiring longer simulation times and a detailed understanding of the system’s physical parameters for proper calibration. As a result, this model is best suited for specialized applications where high precision is essential.
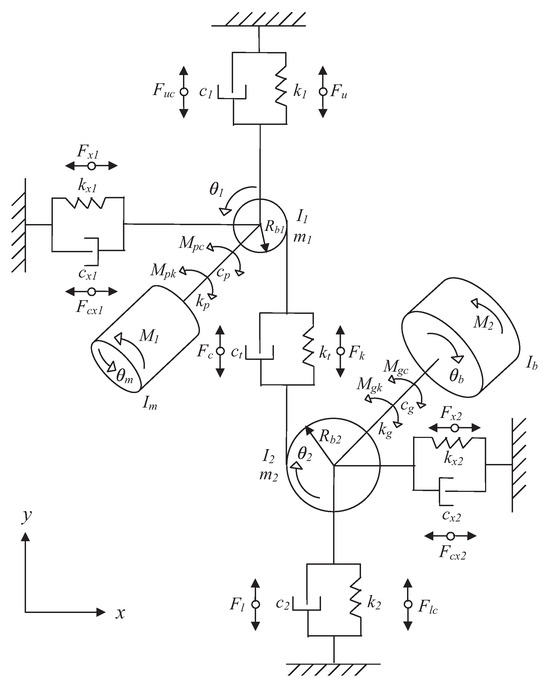
Figure 6.
Gearbox dynamic model with 6 DOFs [63].
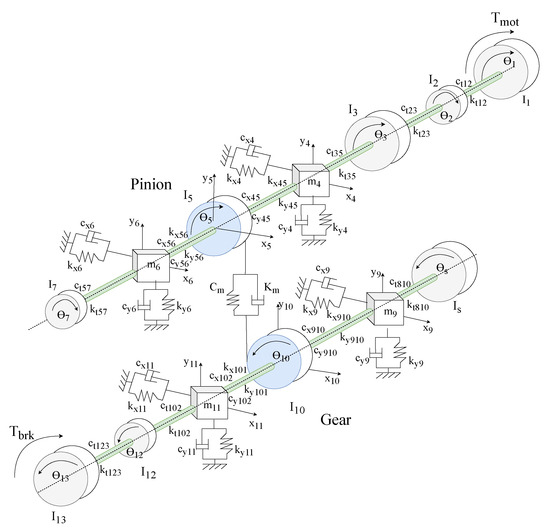
Figure 7.
Gearbox dynamic model with 21 DOFs [64].
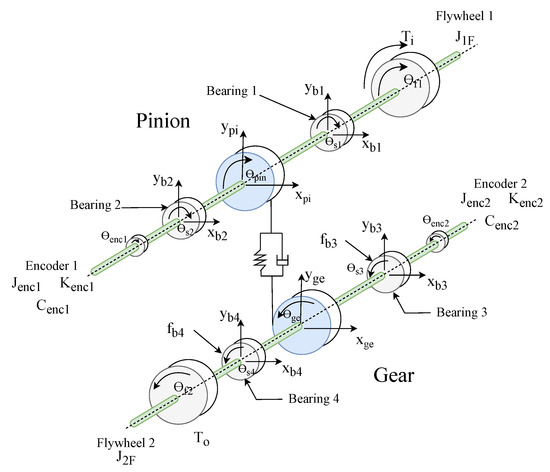
Figure 8.
Gearbox dynamic model with 34 DOFs [65].
Despite its simplicity and the limited number of physical parameters involved, the six-DOF model has proven effective in reproducing the vibratory behavior of gear systems. The modeling process begins with the calculation of various forms of energy involved in power transmission—namely, Hertzian contact, bending, axial compression, and shear energy—based on the physical and geometric parameters depicted in Figure 6. These energy components require a range of physical and geometric inputs to ensure accurate estimation [23].
List of model parameters:
- Im:
- Moment of inertia associated with the motor.
- Ib:
- Moment of inertia of the applied load.
- Im:
- Moment of inertia of the pinion.
- Im:
- Moment of inertia of the gear.
- M1:
- Torque generated by the motor.
- M2:
- Torque exerted by the load.
- m1:
- Mass of the pinion.
- m2:
- Mass of the gear.
- Rb1:
- Radius of the pinion’s base circle.
- Rb2:
- Radius of the gear’s base circle.
Coupling Characteristics:
- kp:
- Torsional rigidity of the input coupling.
- kg:
- Torsional rigidity of the output coupling.
- cp:
- Damping factor of the input coupling.
- cg:
- Damping factor of the output coupling.
Bearing Properties:
- kx1:
- Radial stiffness in the horizontal direction for the input bearing.
- kx2:
- Radial stiffness in the horizontal direction for the output bearing.
- ky1:
- Radial stiffness in the vertical direction for the input bearing.
- ky2:
- Radial stiffness in the vertical direction for the output bearing.
- cx1:
- Horizontal viscous damping coefficient of the input bearing.
- cx2:
- Horizontal damping coefficient of the output bearing.
- cy1:
- Vertical damping coefficient of the input bearing.
- cy2:
- Vertical damping coefficient of the output bearing.
Gear Mesh Dynamics:
- kt:
- Stiffness of the gear meshing.
- ct:
- Damping coefficient at the mesh interface.
Translational Displacements:
- x1:
- Axial displacement of the pinion along the meshing direction (x-axis).
- x2:
- Axial displacement of the gear along the x-axis.
- y1:
- Radial displacement of the pinion in the perpendicular direction (y-axis).
- y2:
- Radial displacement of the gear on the y-axis.
Angular Displacements:
- θm:
- Motor shaft rotation angle.
- θ1:
- Angular rotation of the pinion.
- θ2:
- Angular rotation of the gear.
- θb:
- Angular rotation of the load.
Equations of motion derived from Newton’s second law:
Vertical translation of the pinion:
Vertical translation of the gear:
Rotation of the pinion:
Rotation of the gear:
Rotation of the motor:
Rotation of the load:
Definitions of forces and moments:
Vertical support forces:
Gear mesh contact force:
Moments from bearing stiffness and damping:
An overview of FEM-based approaches for gear monitoring supported by DT technology follows. Llopis et al. [7] integrated CAD and FEM tools to optimize gearbox design by reducing weight and stress while improving reliability. FEM simulations were used to identify high-stress zones, facilitating better structural decisions and enabling predictive maintenance. Zhang et al. [66] utilized FEM (via HyperMesh and ABAQUS) to simulate gear faults under realistic operating conditions. Combined with deep learning models, the method achieved high accuracy in detecting various faults such as wear, pitting, and broken teeth, thereby supporting real-time fault monitoring. Wei et al. [67], though focused on ship structures, demonstrated that inverse FEM can reconstruct real-time deformations from sensor data. This approach is adaptable to real-time structural health monitoring in gearboxes. El Amli et al. [68] combined FEM with dynamic modeling to simulate gearbox vibrations under both healthy and faulty conditions. Time-varying mesh stiffness (TVMS), extracted using FEM, was integrated into the dynamic model to enhance vibration-based fault detection.
2.2.2. Experimental Procedure
For gear faults, the maximum fault frequency occurs when the fault is distributed across all the teeth, resulting in a vibration at the same frequency as the meshing frequency. In contrast, a localized fault on the gear will have the same frequency as the rotational frequency. This allows us to define the maximum acquisition frequency as at least twice the meshing frequency. This information is crucial for selecting the acquisition board and the sensor. Regarding sensor placement, it should be fixed on the bearing, as it is the closest location to the rotor [69].
To evaluate digital twin-based approaches for gear condition monitoring, two experimental studies were conducted under different setups and objectives. In the first study [64], an endurance testing campaign was carried out to assess gear surface degradation monitoring methodology. Two tests were performed: one under lubricated conditions and the other under dry conditions. The lubricated test was conducted at an applied torque of 20 Nm and an operational speed of 20 Hz, whereas the dry test used a reduced torque of 5 Nm and a speed of 10 Hz. High-resolution vibration signals were collected using Brüel&Kjær (B&K) 4396 accelerometers, sampled at 100 kHz over 10-s intervals. This setup ensured detailed data acquisition under controlled laboratory conditions, allowing the researchers to evaluate the severity and progression of gear surface wear.
In the second study [70], a digital twin framework was tested for fault diagnosis in a wind turbine planetary gearbox. The test bench included a motor, a spur gear stage, a planetary gear system, a magnetic powder brake, a data acquisition board (STM32), and several strain gauge sensors. The system was tested under realistic conditions mimicking a wind turbine environment. The motor was operated at 750 rpm (12.5 Hz), resulting in a spindle speed of around 18 rpm and a torque of 33 Nm. Fault scenarios included healthy and broken tooth conditions on the planetary gear. Strain gauge sensors (type 350-3AA, 350 resistance) were strategically installed on critical regions such as the ring gear and tooth root. Vibration and strain data were collected at a sampling frequency of 500 Hz.
While both studies focus on gear health evaluation using digital twin principles, they differ in their experimental contexts and signal acquisition setups. The first experiment benefits from highly controlled lab conditions and high-frequency sampling (100 kHz), ideal for tracking fine surface degradation. In contrast, the second study replicates real wind turbine operating conditions with lower sampling frequency (500 Hz) but includes realistic mechanical configurations and physical constraints, which makes it highly relevant for practical fault diagnosis applications.
2.3. Digital Twin
Figure 9 summarizes the two previous steps: development of the model-based approach for bearings and gears. After setting up the acquisition chain to record the vibratory signal while adhering to the previously mentioned requirements, the sensor must be fixed in the desired direction as defined in the model (Figure 1 (from 1 to 8). The calculated and estimated parameters must be injected to solve the system of equations while maintaining an appropriate time step for the resolution. If the resolution method does not follow a fixed time step, a resampling step should be considered as a post-processing step [71].
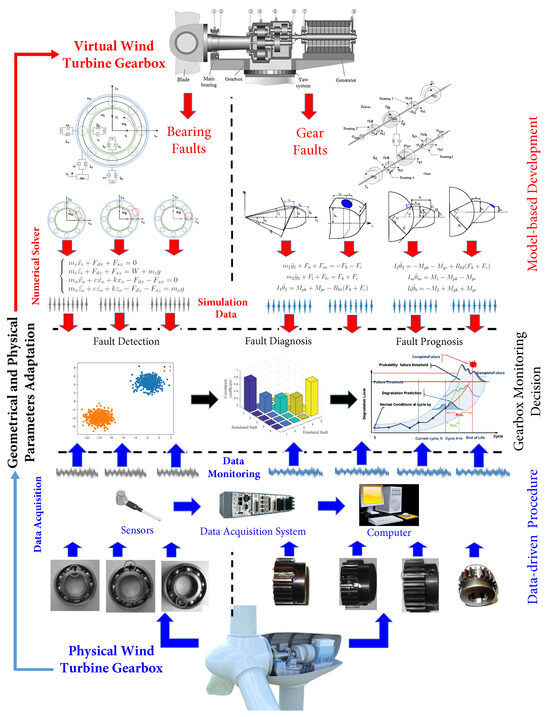
Figure 9.
Flowchart for digital twin monitoring [58,72,73].
At this stage, adapting the signals is essential to ensure the model accurately reflects experimental observations. This alignment can be achieved through SP techniques, which help establish a clear correspondence between the simulated fault classes and their real-world counterparts. Alternatively, AI methods, particularly those involving advanced feature extraction from time-series data or signal images, can enhance this adaptation process due to their proven effectiveness [74].
Now that the adaptation step is complete, real-time deployment can proceed. This can be achieved using SP techniques such as correlation measurement or similarity analysis between real signals and those obtained from the model. These techniques trigger the detection of a faulty state, identify the type of fault for diagnosis, and, if possible, estimate the remaining useful life for prognosis. Similarly, this step can be carried out using AI techniques for the various monitoring stages. It is important to note that SP techniques have the advantage of not requiring significant resources for implementation, unlike AI networks. On the other hand, SP techniques have become less effective compared to the significant advancements in AI for feature extraction. The effectiveness of the proposed methodology is assessed using statistical criteria that compare predicted values to true values. For fault detection and diagnosis, the task is framed as a classification problem, which can be evaluated using accuracy to provide an overall measure of performance. More detailed insights can be obtained using class-specific metrics such as the confusion matrix, as well as evaluation indicators like F1-score, recall, and precision, as formulated in [75]. For prognostics, which is typically a regression task, prediction quality is assessed using continuous error metrics. Among the most commonly used regression criteria are root mean square error (RMSE), mean absolute error (MAE), mean square error (MSE), and mean absolute percentage error (MAPE), as formulated in [76].
If the previous step is successfully executed, human–machine interactivity can be enhanced using software dedicated to designing graphical interfaces. Several software tools, such as 3DS-MAX or Unity, can be utilized for this purpose.
3. Signal Processing and Artificial Intelligence for DT Development
The integration of signal processing (SP) and artificial intelligence (AI) is critical for deploying effective digital twin (DT) systems to enable reliable predictive monitoring of gearboxes. Figure 10 illustrates this through a simplified workflow showcasing their combined roles in a DT-based approach.
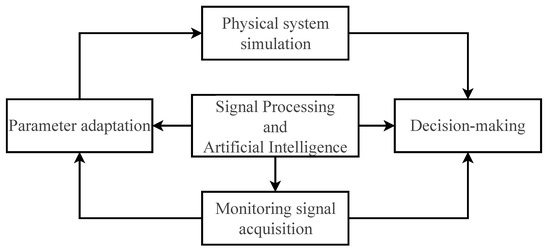
Figure 10.
Signal processing and artificial intelligence for gearbox monitoring.
The process begins with real system-to-DT alignment, where physical parameters are synchronized with their virtual counterparts. Since sensor data often contain noise, gaps, or interference, SP techniques clean the signals and extract meaningful vibrational patterns from healthy gearbox operation. When direct measurements are unavailable, AI fills these gaps, and generative models reconstruct missing data from historical patterns, enabling accurate DT initialization. With clean, synchronized data, the DT can then simulate various fault conditions (cracks, misalignments, wear) to train diagnostic models.
During fault signature analysis, complex interactions between multiple defects can create non-physical signal patterns. For instance, vibrations from a cracked gear tooth may overlap with those from a failing bearing, producing obscured or combined frequency signatures. SP methods like time–frequency analysis and blind source separation isolate these overlapping components, while AI automatically detects subtle fault characteristics even in noisy environments.
The final decision-making phase leverages both technologies: AI models classify fault types and predict remaining useful life, enabling preventive maintenance before failures occur. Simultaneously, SP techniques like spectral correlation validate these findings against known reference patterns. This dual approach ensures robust diagnostics across varying operating conditions and data limitations.
3.1. Signal Processing for DT Development
Signal processing (SP) is a critical step in the design of a DT. This process is categorized into three types of analyses: time, frequency, and time–frequency analysis [77]. Time analysis involves extracting statistical indicators from signals, such as root mean square (RMS), kurtosis, and skewness, which provide essential insights into the signal’s characteristics [78]. Frequency analysis, on the other hand, transforms the signal from the time domain to the frequency domain. Techniques like Fast Fourier Transform (FFT) and Power Spectral Density (PSD) are commonly employed in this context. Both time and frequency analyses are typically suited for stationary signals [79]. Meanwhile, for non-stationary signals, time–frequency analysis is preferred as it provides a combined perspective of temporal and frequency evolution. Techniques such as Wavelet Transform and Short-Time Fourier Transform (STFT) are widely used for this purpose [80].
These techniques are utilized in various ways to construct a DT for gearbox monitoring. Li et al. [22] employed the Discrete Wavelet Transform for feature extraction, followed by a step to select the most relevant features. This approach effectively distinguished between bearing faults in acquired signals and those generated by the DT. Similarly, Xia et al. [81] applied frequency analysis to validate the DT of a helical gear, a crucial step to ensure the fidelity of the twin. A similarity criterion was subsequently used to adapt the model to real-world signals. Yu et al. [82] refined the model to match experimental signals through feature matching, integrating both types of signals using Variational Mode Decomposition (VMD) after phase correlation. Envelope spectrum analysis was also applied to reduce noise and improve accuracy in diagnosing planetary gearboxes. Matania et al. [83] utilized synchronous averaging for noise reduction, followed by a Discrete Fourier Transform. These steps allowed for the adaptation of virtual and real signals and the calculation of two feature indicators, CI1 and CI2, to estimate the severity of gear tooth cracks. Zhu et al. [84] used simple spectral analysis to detect fault frequencies and meshing frequencies. Meanwhile, Wang et al. [70] applied Empirical Mode Decomposition (EMD) to select the most relevant mode based on energy entropy criteria, enabling signal denoising. Additionally, Zhu et al. [85] used Discrete Wavelet Transform for time–frequency feature extraction, ensuring the alignment of model-generated signals with real-world data. Further framework by Jia et al. [86] employed lifting wavelets to extract features and adapt data distributions between the physical system and the DT. Similarly, Ming et al. [87] conducted frequency decomposition for feature extraction to align the physical system’s signals with those of its twin. Habbouche et al. [23] utilized VMD to separate fault signatures from noise by calculating the highest correlation between meshing frequencies and decomposition modes. This noise was subsequently added to fault signatures to produce signals resembling real-world fault signals. Qin et al. [88] aligned model data with experimental data using spectral analysis, as described by Zhu et al. [84]. Furthermore, Shi et al. [89] adapted model signals to experimental data through Markov transfer, transforming signals into images based on SP and the extraction of temporal and frequency-based features. Lastly, Piltan et al. [90] extracted RMS from acoustic emission signals to monitor bearings. The RMS signal was then sampled and modeled using an autoregressive fuzzy Gauss–Laguerre approach, a method referred to as the “smooth sliding DT”, which was used to classify the severity of bearing cracks. Liu et al. [69] used a hash algorithm to represent the time–frequency data obtained from the real system and the DT. Then, they computed the Hamming distance as a similarity criterion between the classes of real and simulated faults across different operating modes.
Refs. [22,85] highlight that the discrete wavelet transform is computationally expensive, particularly for measured and real signals, in addition to requiring a careful selection of the mother wavelet. Refs. [81,83,84,87] point out that the use of frequency analysis for adaptation limits this approach in non-stationary regimes. Such a technique must always be preceded by a detection step before proceeding to diagnosis. Refs. [23,82] note that VMD often requires a careful choice of parameters, which has not been clearly specified, and is frequently combined with an optimization algorithm. Ref. [82] explains that envelope analysis is limited to detecting high-amplitude faults, as low-signature faults are often filtered out by the envelope. Ref. [70] states that EMD, as a decomposition method, has demonstrated its effectiveness in handling mixed modes compared to VMD. However, this drawback reduces its utility for combined faults. Refs. [86,89] propose methods based on Lifting Wavelets and Markov Transform, which are relatively difficult to implement and require a prior study of the wave characteristics before processing. Ref. [90] bases its bearing condition monitoring on a statistical indicator, which, despite its effectiveness, remains sensitive to operational variations such as changes in operating modes.
Table 1 provides an overview of previous frameworks for gearbox monitoring based on DTs and SP, highlighting their respective advantages and limitations.

Table 1.
Overview of DT approaches using SP.
3.2. Artificial Intelligence with DT
The purpose of artificial intelligence (AI) is to emulate human reasoning, particularly in diagnosing faults by identifying fault types and estimating the health state for prognosis [91]. AI, in its basic form, is a set of rules designed to mimic human thought processes. Over time, it evolved into machine learning (ML), which involves training a network on data and testing it on unseen data, allowing the network to learn from the training data. However, machine learning has limitations when dealing with large datasets or performing complex tasks. To address these limitations, researchers developed more complex networks with a substantial number of parameters to optimize configurations and achieve better performance [92]. Learning in AI is broadly divided into two main categories: supervised learning and unsupervised learning. Supervised learning relies on labeled data, whereas unsupervised learning operates with unlabeled data. Within these two categories, two primary tasks are classification and regression. For monitoring purposes, classification is typically employed for detection and diagnosis, whereas regression is generally utilized for prognosis [93].
DT has always been combined with AI to enable autonomous and real-time monitoring. Li et al. [22] used transfer learning as a classifier for scalograms. Xi et al. [94] based their approach on meta-learning, which allows the developed network to learn from small or complex datasets. Xu et al. [95] applied graph neural networks (GNNs) to adapt model data to real-world data, achieving accurate fault detection. Ma et al. [96] combined transfer learning, as in [22], with meta-learning from [94], leveraging the advantages of pre-trained networks for better classification while benefiting from meta-learning’s ability to learn from limited data. Similarly, Cui et al. [97] employed non-Euclidean convolution graph neural networks combined with standard regularization to minimize discrepancies between simulated and real-world data, improving predictive capabilities. He et al. [98] also used GNNs, as in [95,97], for data adaptation but integrated BiLSTM to analyze temporal sequences, utilizing its memory capabilities to estimate the RUL of bearings. Li et al. [99] combined a deep branched network with a CNN for accurate diagnosis of wear faults in bearings. Hu et al. [21] utilized a combination of a one-class support vector machine for fault state detection and a CNN variant called CapsNet, which automatically designs its architecture. This combination outperformed the state of the art for bearing fault diagnosis. Zhang et al. [51] relied on a transformer-based network to learn from bearing model data and adapt it to experimental test data. Wang et al. [70] combined atom search optimization with a support vector machine, training it on simulated data and testing it on experimental data for planetary gearbox diagnosis. Zhang et al. [100] enhanced fault classification through transfer learning, integrating additional modules called the Similarity Attention Module and an Efficient Channel Attention module. This approach improved feature extraction and tracking between simulated and real-world data. Liu et al. [101] utilized a transfer model reinforced with a generative adversarial network (GAN) for deep feature extraction and a long short-term memory (LSTM) network to extract features from time series. This combination enabled the classification of unseen experimental data generated by the DT. Meng et al. [102] employed a GAN to generate data from simulated bearing model data. Regression for fatigue estimation and RUL prediction was performed using an encoder–decoder-based gated recurrent unit (GRU). Sow et al. [103] focused on fault classification using a multi-class support vector machine trained on simulation signals and tested on experimental data. Huang et al. [49] used a one-dimensional convolutional neural network with a first-layer wide convolutional kernel for bearing fault diagnosis. The first layer, with a large 16 × 1 kernel, enables global learning of information between simulated and real signals, considering the inevitable differences between them. This network is enhanced by the Feature Boosting and Compression algorithm, which helps mitigate forgetting and improve classification efficiency. Kumar et al. [104] implemented various domain adaptation methods to bridge the gap between simulated and real data, including Domain Adaptation Network, Maximum Classifier Discrepancy, and Self-Ensembling for Visual Domain Adaptation. These algorithms were applied to detect bearing faults in a centrifugal pump. Xiao et al. [105] studied degradation monitoring using a dynamic bearing model and real data, relying on a graph convolutional memory network to learn degradation simulation and project it onto real monitoring data. The learning network used is designed for time series and was compared with similar networks to demonstrate its effectiveness.
Refs. [95,98] emphasize that this type of network requires a good graphical representation to adapt simulation signals to real signals. Additionally, studies have shown the necessity of providing a large quantity of data, which must also be preprocessed. Ref. [96] is expected to deliver good results compared to the framework presented in [94], which is based on meta-models, and [22,100], which rely on transfer learning networks. However, it also inherits their drawbacks. On one hand, there is the complexity of learning with meta-models, and on the other, the challenge of adapting new data to the data on which the transfer model was initially trained, which has been thoroughly detailed in [106]. It is worth noting that the attention mechanism introduced in [100] enhances its feature extraction efficiency and simplifies the task of the transfer network. Ref. [97] proposes a combination that addresses the complex nature of monitoring signals but, at the same time, limits the possibility of real-time deployment and increases the computational resources required. Ref. [99] presents a robust combination of branched networks and CNNs, which is effective but demands a significant amount of data for training. Ref. [51] highlights that transformer networks require significantly more computational resources and memory due to their reliance on attention mechanisms. They are generally more complex and need more data to achieve optimal performance, which limits their use in scenarios with data scarcity. Refs. [101,102] propose two ideal learning combinations to address the issue of data scarcity by using generative networks to create synthetic data. However, they suffer from convergence issues, and the synthetic data often fail to reflect the physical nature of the phenomenon, limiting their applicability. The authors of [103] point out that SVMs are relatively simple networks and are not capable of capturing complex relationships, especially for multi-class tasks. They can handle relatively simple binary classification tasks, as shown in [21], or be preceded by an optimization step to facilitate classification, as in [70].
Table 2 summarizes all the works presented in this section, which focus on deploying DTs for gearbox monitoring based on AI techniques, as well as the addressed limitations.

Table 2.
Overview of DT approaches using AI.
3.3. Emerging AI Technologies Integrated with DT for Gearbox Monitoring Needs
Emerging technologies in machine learning, such as federated learning (FL) and edge computing, have been developed to address critical needs in data privacy, real-time decision-making, and resilience against cyberattacks.
Federated learning is designed to enhance data privacy by preventing the transmission of raw data to a central server. Instead, model training takes place locally at the site level, and only model updates are sent to a central server for aggregation. This decentralized training approach is particularly valuable in the context of gearbox monitoring in wind turbines, where it improves model accuracy by leveraging multiple datasets while simultaneously preserving data confidentiality [107]. In the context of DT systems, FL enables the sharing of knowledge derived from physical models, obtained through simulation or modeling, without exposing sensitive raw data. This offers a major advantage, as it reduces the risk of revealing proprietary gearbox technology or modeling techniques [108].
One of the key challenges in gearbox monitoring is the need for real-time fault detection, which is essential to minimizing system impact and avoiding costly failures. While modern AI approaches often seek to improve accuracy through increasingly deep neural networks, they typically rely on centralized data processing, transmitting large volumes of monitoring data to distant servers. This reliance can compromise real-time performance [109]. Edge computing addresses this issue by minimizing latency through local data processing. By deploying lightweight neural networks or compressed digital twin models near the monitoring stations, this approach enables faster reaction times, improves real-time anomaly detection, and enhances predictive maintenance capabilities. Overall, the integration of FL and edge computing with DT systems represents a significant step toward intelligent, autonomous, and privacy-aware industrial monitoring [110].
3.4. Data Augmentation in DT Applications
Recent deep learning networks have become increasingly deeper in terms of the number of layers, nodes, and, consequently, the number of learnable parameters. Training these networks involves updating these parameters to perform tasks such as classification or regression. However, one major challenge is the significant number of parameters requiring a large amount of data for effective updating [111]. While signals corresponding to healthy states are often available in abundance, faulty state signals are typically scarce, as the goal is to detect faults at their earliest stages [106]. This challenge has been identified as the “minimum knowledge” problem, characterized by data scarcity or imbalanced datasets. To address this, a new discipline called data augmentation has emerged [112]. Data generation for augmentation can be achieved in various ways:
- -
- Removing elements from signals or images or adding noise [75].
- -
- Traditional operations such as rotation, cropping, and shifting [113].
- -
- Using generative networks to create signals or images resembling each class [114].
- -
- Employing a faithful DT of the monitored component to generate signals for underrepresented classes.
The first three approaches can improve classification accuracy but require a substantial amount of data to train the generative networks or create new images or signals. Conversely, the DT offers the ability to generate unseen data with high fidelity, modeling any potential state the system may encounter, such as gearbox faults. Data generation using the DT has been the focus of numerous recent studies aimed at addressing the problem of monitoring under data scarcity.
The issue of data scarcity has been the focus of several recent studies, and solutions based on Decision Trees have been proposed. Li et al. [22] addressed the data scarcity problem by using a five-DOF dynamic bearing model to augment the dataset and enhance bearing fault diagnosis. Similarly, Cui et al. [97] tackled the lack of data for bearing fault prognosis and remaining useful life (RUL) estimation by developing a dynamic model to simulate bearing degradation and generate signals using the DT. Li et al. [99] also filled data gaps using a similar approach but focused on bearing fault diagnosis. Instead of generating additional data, Zhang et al. [100] introduced two modules for feature extraction and tracking between simulated and real-world data, achieving robust performance even with limited datasets. Ming et al. [87] simulated scenarios of imbalanced bearing fault data and resolved this imbalance by generating data using a DT. Qin et al. [88] addressed imbalanced datasets by generating signals with an inverse physics-informed neural network. This network learned the fault signatures of bearings from a dynamic model. Cui et al. [115] distinguished the vibrational behavior of faulty bearings by measuring the impulsive characteristics of the signal. They then evaluated the uncertainty of fault severity using kernel density estimation. Yan et al. [116] conducted a dynamic simulation of a planetary gearbox with five different classes. A subdomain adaptive mechanism was implemented between the model signals and the experimental signals. This step enhances the model’s fidelity to address the issue of data scarcity in planetary gearbox diagnosis.
4. DT-Based Gearbox Monitoring: A Framework for Future Research
This framework paves the way for innovative research contributions that will further refine and enhance DT-based gearbox monitoring techniques.
- The development of a DT for monitoring combined faults in gears and bearings is a realistic approach, as these faults often interact in real-world systems. The vibrational or acoustic signatures of these faults can overlap, making their detection and diagnosis more complex. A DT allows for modeling these interactions and a better understanding of the phenomena of fault signature dominance. This paves the way for more robust detection algorithms capable of distinguishing faults even in the presence of noise or parasitic signals.
- Beyond classical faults (gears and bearings), it is crucial to integrate less-studied but equally critical faults into DTs, such as shaft misalignment or structural nonlinearities. These faults can have a significant impact on the overall system dynamics, causing abnormal vibrations, accelerated wear, or even catastrophic failures. A DT capable of simulating these faults would allow for better anticipation of their effects and optimization of maintenance strategies.
- Leveraging DTs to optimize sensor placement is a major contribution. By identifying strategic points where fault signatures are most visible, the number of required sensors can be reduced, lowering installation and maintenance costs. Additionally, this limits the volume of data to collect, store, and analyze while improving monitoring efficiency.
- Integrating complex physical phenomena, such as heat propagation due to excessive friction, enhances the capabilities of DTs. By combining thermal models with data from thermal cameras, it becomes possible to remotely monitor component conditions and detect thermal anomalies before they lead to failures. This enables more precise predictive maintenance and reduces the risk of unexpected breakdowns.
- The DT approach can be extended to other rotating machines, such as turbines, compressors, or electric motors. Each type of machine has its own dynamic and operational specificities (rotational speed, applied loads, environment, etc.), requiring model adaptation. For example, turbines may be subject to variable aerodynamic loads, while compressors may experience overpressure phenomena. DTs must incorporate these specificities to be effective.
- Environmental conditions (wind, temperature, humidity) significantly impact wind turbine dynamics. A DT can simulate these effects to study how they accelerate fault propagation, such as cracks in blades or shafts. Frequent acceleration and deceleration due to wind variations can lead to increased material fatigue. By integrating these factors, DTs enable better failure prediction and optimization of maintenance cycles.
- Faults in gears or bearings can lead to energy loss due to reduced transmission efficiency. A DT can estimate this energy loss for each type of fault, even before it becomes critical. This helps define a fault criticality order and prioritize maintenance interventions based on their impact on energy efficiency.
- Integrating cost–benefit analysis into DTs allows for evaluating the economic impact of maintenance strategies. This includes modeling maintenance costs, downtime, and component replacement costs. By comparing predictive and corrective maintenance costs, DTs can help identify the most cost-effective strategies and justify investments in advanced monitoring technologies.
- Unifying monitoring processes (detection, diagnosis, prognosis) into a single methodology is essential for a coherent approach. DTs can serve as an integrated platform for these three steps, using the same data and models to detect anomalies, diagnose faults, and predict their evolution. This simplifies the monitoring process and improves the accuracy of the prediction.
- For high-speed machines, it is crucial to integrate the phenomenon of shaft critical speed into DTs. Flexible shafts with a low diameter-to-length ratio can enter resonance at certain rotational speeds, causing excessive vibrations and failures. DTs can simulate these effects to identify critical speeds and optimize machine design and operation.
- Improving the alignment between the signals simulated by DTs and the real-world signals is a major challenge. This requires accounting for complex phenomena, such as the response of the gearbox to mechanical play or bearing excitations. By refining models to better reflect reality, DTs become more reliable and useful for monitoring and predictive maintenance.
Table 3 presents an evaluation of potential future contributions based on two key criteria: industrial priority and technological priority. This assessment is accompanied by identified technical bottlenecks and required resources.

Table 3.
Prioritization of future research directions for DT-based gearbox monitoring.
5. Conclusions
This paper has explored the development of monitoring strategies for wind turbine gearboxes, culminating in the application of digital twin technology. By combining DT technology with advanced signal processing and artificial intelligence techniques, it is possible to detect and diagnose faults autonomously and in real time. This is critical to ensuring the reliability and availability of wind turbines by enabling proactive maintenance and minimizing unplanned downtime. This paper reviewed existing frameworks, identified challenges such as data scarcity, and proposed solutions using digital twin technology. In addition, it outlined promising paths for future research, including the development of more advanced digital twin models, the integration of advanced artificial intelligence algorithms, and the application of these techniques to other critical wind turbine components. The results of this review-based investigation will further advance strategies for monitoring the condition of wind turbine gearboxes, thereby improving the efficiency and reliability of wind power generation.
Several promising perspectives emerge for advancing DT technology in condition monitoring. These include modeling combined and less-studied faults, optimizing sensor placement, and integrating complex phenomena such as heat propagation or critical shaft speeds. Extending DTs to diverse machines and environmental conditions enhances their applicability, while unifying detection, diagnosis, and prognosis improves monitoring coherence. Finally, incorporating energy efficiency analysis and cost–benefit evaluation reinforces DTs as strategic tools for predictive and economically optimized maintenance.
Author Contributions
Conceptualization, H.H., Y.A. and M.B., Methodology, H.H., Y.A. and M.B.; Validation, H.H., Y.A. and M.B.; Formal analysis, H.H., Y.A. and M.B.; Writing—original draft, H.H.; Writing—review & editing, H.H., Y.A. and M.B.; Visualization, H.H., Y.A. and M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Popa, D.C.; Szabó, L. Overcoming Catch-22 for rare earth metals in green transition: Solutions in electrical machine manufacturing. Renew. Sustain. Energy Rev. 2025, 207, 114917. [Google Scholar] [CrossRef]
- Khurshid, H.; Mohammed, B.S.; Al-Yacoubya, A.M.; Liew, M.; Zawawi, N.A.W.A. Analysis of hybrid offshore renewable energy sources for power generation: A literature review of hybrid solar, wind, and waves energy systems. Dev. Built Environ. 2024, 19, 100497. [Google Scholar] [CrossRef]
- Hu, W.; Fang, J.; Zhang, Y.; Liu, Z.; Verma, A.S.; Liu, H.; Cong, F.; Tan, J. Digital Twin of Wind Turbine Surface Damage Detection Based on Deep Learning-Aided Drone Inspection. Renew. Energy 2025, 241, 122332. [Google Scholar] [CrossRef]
- Backwell, B.; Emerson Clarke, E.; Fang, R.; Fiestas, J.; Gitobu, N.; Khinda, R.; Ladwa, A.; Lathigara, W.; Liang, W.; Global Wind Report 2023. Technical Report, Global Wind Energy Council. 2023. Available online: https://sawea.org.za/sites/default/files/content-files/Market%20Reports/GWEC-2023_interactive.pdf (accessed on 6 November 2023).
- De Kooning, J.D.; Stockman, K.; De Maeyer, J.; Jarquin-Laguna, A.; Vandevelde, L. Digital twins for wind energy conversion systems: A literature review of potential modelling techniques focused on model fidelity and computational load. Processes 2021, 9, 2224. [Google Scholar] [CrossRef]
- Greco, A.; Sheng, S.; Keller, J.; Erdemir, A. Material wear and fatigue in wind turbine systems. Wear 2013, 302, 1583–1591. [Google Scholar] [CrossRef]
- Llopis-Albert, C.; Rubio, F.; Devece, C.; García-Hurtado, D. Digital twin-based approach for a multi-objective optimal design of wind turbine gearboxes. Mathematics 2024, 12, 1383. [Google Scholar] [CrossRef]
- Vrba, J.; Cejnek, M.; Steinbach, J.; Krbcova, Z. A machine learning approach for gearbox system fault diagnosis. Entropy 2021, 23, 1130. [Google Scholar] [CrossRef]
- Berghout, T.; Benbouzid, M. UBO-EREX: Uncertainty Bayesian-Optimized Extreme Recurrent EXpansion for Degradation Assessment of Wind Turbine Bearings. Electronics 2024, 13, 2419. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. Foundational Research Gaps and Future Directions for Digital Twins; National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 2023. [Google Scholar]
- Moghadam, F.K.; Nejad, A.R. Online condition monitoring of floating wind turbines drivetrain by means of digital twin. Mech. Syst. Signal Process. 2022, 162, 108087. [Google Scholar] [CrossRef]
- Pujana, A.; Esteras, M.; Perea, E.; Maqueda, E.; Calvez, P. Hybrid-model-based digital twin of the drivetrain of a wind turbine and its application for failure synthetic data generation. Energies 2023, 16, 861. [Google Scholar] [CrossRef]
- Regis, A.; Arroyave-Tobón, S.; Linares, J.M.; Mermoz, E. Physic-based vs data-based digital twins for bush bearing wear diagnostic. Wear 2023, 526, 204888. [Google Scholar] [CrossRef]
- Mehlan, F.C.; Nejad, A.R.; Gao, Z. Digital twin based virtual sensor for online fatigue damage monitoring in offshore wind turbine drivetrains. J. Offshore Mech. Arct. Eng. 2022, 144, 060901. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, C.; Wang, J.; Wang, S.; Lv, D.; Qin, F. Research on digital twin driven rolling bearing model-data fusion life prediction method. IEEE Access 2023, 11, 48611–48627. [Google Scholar] [CrossRef]
- Khan, P.W.; Byun, Y.C. A Review of machine learning techniques for wind turbine’s fault detection, diagnosis, and prognosis. Int. J. Green Energy 2024, 21, 771–786. [Google Scholar] [CrossRef]
- Gawde, S.; Patil, S.; Kumar, S.; Kamat, P.; Kotecha, K. An explainable predictive maintenance strategy for multi-fault diagnosis of rotating machines using multi-sensor data fusion. Decis. Anal. J. 2024, 10, 100425. [Google Scholar] [CrossRef]
- Habbouche, H.; Benkedjouh, T.; Amirat, Y.; Benbouzid, M. Rotating machine bearing health prognosis using a data driven approach based on KS-density and BiLSTM. IET Sci. Meas. Technol. 2025, 19, e12215. [Google Scholar] [CrossRef]
- Li, J.; Wang, S.; Yang, J.; Zhang, H.; Zhao, H. A digital twin-based state monitoring method of gear test bench. Appl. Sci. 2023, 13, 3291. [Google Scholar] [CrossRef]
- Hu, Y.; Taha, O.W.; Yang, K. Fault Detection in Active Magnetic Bearings Using Digital Twin Technology. Appl. Sci. 2024, 14, 1384. [Google Scholar] [CrossRef]
- Hu, W.; Jiao, Q.; Liu, H.; Wang, K.; Jiang, Z.; Wu, J.; Cong, F.; Hao, G. A transferable diagnosis method with incipient fault detection for a digital twin of wind turbine. Digit. Eng. 2024, 1, 100001. [Google Scholar] [CrossRef]
- Li, S.; Jiang, Q.; Xu, Y.; Feng, K.; Zhao, Z.; Sun, B.; Huang, G.Q. Digital twin-assisted interpretable transfer learning: A novel wavelet-based framework for intelligent fault diagnostics from simulated domain to real industrial domain. Adv. Eng. Inform. 2024, 62, 102681. [Google Scholar] [CrossRef]
- Habbouche, H.; Amirat, Y.; Benkedjouh, T.; Benbouzid, M. Digital twin-based gearbox fault diagnosis using variational mode decomposition and dynamic vibration modeling. Measurement 2025, 246, 116669. [Google Scholar] [CrossRef]
- Yu, X.; Sun, X.; Ou, L. Graphics-based modular digital twin software framework for production lines. Comput. Ind. Eng. 2024, 193, 110308. [Google Scholar] [CrossRef]
- Barata, J.; Kayser, I. How will the digital twin shape the future of industry 5.0? Technovation 2024, 134, 103025. [Google Scholar] [CrossRef]
- Da Rocha, H.; Pereira, J.; Abrishambaf, R.; Espirito Santo, A. An interoperable digital twin with the IEEE 1451 standards. Sensors 2022, 22, 7590. [Google Scholar] [CrossRef] [PubMed]
- Lindner, M.; Bank, L.; Schilp, J.; Weigold, M. Digital twins in manufacturing: A RAMI 4.0 compliant concept. Sci 2023, 5, 40. [Google Scholar] [CrossRef]
- IEEE-P2413; Standard for an Architectural Framework for the Internet of Things (IOT). IEEE: Piscataway, NJ, USA, 2016.
- ISO 23247-1:2021; Automation Systems and Integration–Digital Twin Framework for Manufacturing—Part 1: Overview and General Principles. International Organization for Standardization (ISO): Geneva, Switzerland, 2021.
- ISO/PAS 17506:2012; Industrial Automation Systems and Integration—COLLADA Digital Asset Schema Specification for 3D Visualization of Industrial Data. International Organization for Standardization (ISO): Geneva, Switzerland, 2012.
- Lee, B.N.; Pei, E.; Um, J. An overview of information technology standardization activities related to additive manufacturing. Prog. Addit. Manuf. 2019, 4, 345–354. [Google Scholar] [CrossRef]
- ISO/IEC TR 22678:2019; Information Technology—Cloud Computing—Guidance for Policy Development. International Organization for Standardization and International Electrotechnical Commission: Geneva, Switzerland, 2019. Available online: https://www.iso.org/standard/73642.html (accessed on 19 May 2025).
- Cindrić, I.; Jurčević, M.; Hadjina, T. Mapping of Industrial IoT to IEC 62443 Standards. Sensors 2025, 25, 728. [Google Scholar] [CrossRef]
- Wang, K.; Wang, Y.; Li, Y.; Fan, X.; Xiao, S.; Hu, L. A review of the technology standards for enabling digital twin: [version 2; peer review: 2 approved]. Digit. Twin 2024, 1, 4. [Google Scholar]
- Minghui, H.; Ya, H.; Xinzhi, L.; Ziyuan, L.; Jiang, Z.; Bo, M. Digital twin model of gas turbine and its application in warning of performance fault. Chin. J. Aeronaut. 2023, 36, 449–470. [Google Scholar]
- Kanaga Priya, P.; Reethika, A. A review of digital twin applications in various sectors. In Transforming Industry Using Digital Twin Technology; Springer: Cham, Switzerland, 2024; pp. 239–258. [Google Scholar]
- Bofill, J.; Abisado, M.; Villaverde, J.; Sampedro, G.A. Exploring Digital Twin-Based Fault Monitoring: Challenges and Opportunities. Sensors 2023, 23, 7087. [Google Scholar] [CrossRef]
- Nickpasand, M.; Gaspar, H.M.; Energy, S.G.R. Digital Twin for Agile Manufacturing: Challenges from the Offshore Wind Turbine Industry. In Proceedings of the ECMS, Florence, Italy, 20–23 June 2023; pp. 442–450. [Google Scholar]
- Zorchenko, N.; Tyupina, T.; Parshutin, M. Technologies Used by General Electric to Create Digital Twins for Energy Industry. Power Technol. Eng. 2024, 58, 521–526. [Google Scholar] [CrossRef]
- Feng, K.; Xu, Y.; Wang, Y.; Li, S.; Jiang, Q.; Sun, B.; Zheng, J.; Ni, Q. Digital twin enabled domain adversarial graph networks for bearing fault diagnosis. IEEE Trans. Ind. Cyber-Phys. Syst. 2023, 1, 113–122. [Google Scholar] [CrossRef]
- Fu, C.; Gao, C.; Zhang, W. A Digital-Twin Framework for Predicting the Remaining Useful Life of Piezoelectric Vibration Sensors with Sensitivity Degradation Modeling. Sensors 2023, 23, 8173. [Google Scholar] [CrossRef] [PubMed]
- Yao, H.; Zhang, X.; Guo, Q.; Miao, Y.; Guan, S. Fault diagnosis method for oil-immersed transformers integrated digital twin model. Sci. Rep. 2024, 14, 20355. [Google Scholar] [CrossRef]
- Machado, M.; Dutkiewicz, M. Wind turbine vibration management: An integrated analysis of existing solutions, products, and Open-source developments. Energy Rep. 2024, 11, 3756–3791. [Google Scholar] [CrossRef]
- Owolabi, O.I.; Madushele, N.; Adedeji, P.A.; Olatunji, O.O. FEM and ANN approaches to wind turbine gearbox monitoring and diagnosis: A mini review. J. Reliab. Intell. Environ. 2023, 9, 399–419. [Google Scholar] [CrossRef]
- Zhu, X.; Shi, W.; Huang, Z.; Shi, L. Geometry-Based Synchrosqueezing S-Transform with Shifted Instantaneous Frequency Estimator Applied to Gearbox Fault Diagnosis. Sensors 2025, 25, 540. [Google Scholar] [CrossRef]
- Peng, H.; Zhang, H.; Shangguan, L.; Fan, Y. Review of tribological failure analysis and lubrication technology research of wind power bearings. Polymers 2022, 14, 3041. [Google Scholar] [CrossRef]
- ISO 15243; Rolling Bearings—Damages and Failures—Terms Characteristics and Causes. British Standards Institution (BSI): Buckinghamshire, UK, 2004.
- Velásquez, R.M.A. Bearings faults and limits in wind turbine generators. Results Eng. 2024, 21, 101891. [Google Scholar] [CrossRef]
- Huang, X.; Xie, T.; Luo, S.; Wu, J.; Luo, R.; Zhou, Q. Incremental learning with multi-fidelity information fusion for digital twin-driven bearing fault diagnosis. Eng. Appl. Artif. Intell. 2024, 133, 108212. [Google Scholar] [CrossRef]
- Ruan, D.; Chen, Y.; Gühmann, C.; Yan, J.; Li, Z. Dynamics modeling of bearing with defect in Modelica and application in direct transfer learning from simulation to test bench for bearing fault diagnosis. Electronics 2022, 11, 622. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, J.; Ren, Z.; Ni, Q.; Gu, F.; Feng, K.; Yu, K.; Ge, J.; Lei, Z.; Liu, Z. Digital twin-driven partial domain adaptation network for intelligent fault diagnosis of rolling bearing. Reliab. Eng. Syst. Saf. 2023, 234, 109186. [Google Scholar] [CrossRef]
- Liu, X.; Huang, H.; Xiang, J. A personalized diagnosis method to detect faults in a bearing based on acceleration sensors and an FEM simulation driving support vector machine. Sensors 2020, 20, 420. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, L.; Liu, X. Rapid deployment of digital twin for life prediction of rolling bearings. Appl. Intell. 2025, 55, 666. [Google Scholar] [CrossRef]
- Huo, W.; Jiang, Z.; Sheng, Z.; Zhang, K.; Xu, Y. Cyclostationarity blind deconvolution via eigenvector screening and its applications to the condition monitoring of rotating machinery. Mech. Syst. Signal Process. 2025, 222, 111782. [Google Scholar] [CrossRef]
- Garrett, H.; Long, D.G. Frequency-Constrained QR: Signal and Image Reconstruction. Remote Sens. 2025, 17, 464. [Google Scholar] [CrossRef]
- Husung, S.; Koch, Y.; Welzbacher, P.; Kraus, B.; Roehnert, F.; Faheem, F.; Kirchner, E. Systemic conception of the data acquisition of Digital Twin solutions for use case-oriented development and its application to a gearbox. Systems 2023, 11, 227. [Google Scholar] [CrossRef]
- Xiao, H.; Li, Z.; Zhang, X.; Wang, L.; Khanbareh, H.; Bowen, C. Mathematic modeling of vibration transmission path with discontinuous contact interfaces for gear dynamics in the gear-shaft-bearing-housing system. Measurement 2024, 226, 114054. [Google Scholar] [CrossRef]
- Afia, A.; Rahmoune, C.; Benazzouz, D.; Merainani, B.; Fedala, S. New intelligent gear fault diagnosis method based on Autogram and radial basis function neural network. Adv. Mech. Eng. 2020, 12, 1687814020916593. [Google Scholar] [CrossRef]
- Temirkhan, M.; Tariq, H.B.; Kaloudis, K.; Kalligeros, C.; Spitas, V.; Spitas, C. Parametric quasi-static study of the effect of misalignments on the path of contact, transmission error, and contact pressure of crowned spur and helical gear teeth using a novel rapidly convergent method. Appl. Sci. 2022, 12, 10067. [Google Scholar] [CrossRef]
- Temirkhan, M.; Spitas, C.; Wei, D. A computationally robust solution to the contact problem of two rotating gear surfaces in space. Meccanica 2023, 58, 2455–2466. [Google Scholar] [CrossRef]
- Liu, R.; Ding, X.; Wu, Q.; He, Q.; Shao, Y. An interpretable multiplication-convolution network for equipment intelligent edge diagnosis. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 3284–3295. [Google Scholar] [CrossRef]
- Yikun, E.; Liu, Z.; Chen, H.; Zhang, Y.; Li, Z.; Feng, H.; Feng, Z. Dynamic modeling and vibration analysis for fault diagnosis of rotate vector reducers. Mech. Syst. Signal Process. 2025, 224, 111965. [Google Scholar]
- Dong, H.; Zhang, J.; Wang, L. Study on bifurcation characteristics of multi-clearance bending torsional coupling gear transmission based on EHL. Adv. Mech. Eng. 2020, 12, 1687814020937500. [Google Scholar] [CrossRef]
- Feng, K.; Ji, J.; Zhang, Y.; Ni, Q.; Liu, Z.; Beer, M. Digital twin-driven intelligent assessment of gear surface degradation. Mech. Syst. Signal Process. 2023, 186, 109896. [Google Scholar] [CrossRef]
- Deshpande, L.; Sawalhi, N.; Randall, R. Gearbox bearing fault simulation using a finite element model reduction technique. J. Phys. Conf. Ser. 2012, 364, 012082. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, Z.; An, B.; Sun, R.; Cui, Y. Digital Twin-Based Technical Research on Comprehensive Gear Fault Diagnosis and Structural Performance Evaluation. Sensors 2025, 25, 2775. [Google Scholar] [CrossRef]
- Wei, P.; Li, C.; Jiang, Z.; Wang, D. Real-time digital twin of ship structure deformation field based on the inverse finite element method. J. Mar. Sci. Eng. 2024, 12, 257. [Google Scholar] [CrossRef]
- El Amli, A.; El Yousfi, B.; Soualhi, A.; Guillet, F. A Novel Hybrid FEM–Dynamic Modeling Approach for Enhanced Vibration Diagnostics in a Two-Stage Spur Gearbox. Energies 2025, 18, 2176. [Google Scholar] [CrossRef]
- Liu, W.; Han, B.; Zheng, A.; Zheng, Z. Fault Diagnosis for Reducers Based on a Digital Twin. Sensors 2024, 24, 2575. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, W.; Liu, L.; Wang, B.; Bao, S.; Jiang, R. Fault diagnosis of wind turbine planetary gear based on a digital twin. Appl. Sci. 2023, 13, 4776. [Google Scholar] [CrossRef]
- Zayed, S.M.; Attiya, G.; El-Sayed, A.; Sayed, A.; Hemdan, E.E.D. An efficient fault diagnosis framework for digital twins using optimized machine learning models in smart industrial control systems. Int. J. Comput. Intell. Syst. 2023, 16, 69. [Google Scholar] [CrossRef]
- Allal, Z.; Noura, H.N.; Vernier, F.; Salman, O.; Chahine, K. Wind turbine fault detection and identification using a two-tier machine learning framework. Intell. Syst. Appl. 2024, 22, 200372. [Google Scholar] [CrossRef]
- Alexakos, C.T.; Karnavas, Y.L.; Drakaki, M.; Tziafettas, I.A. A combined short time fourier transform and image classification transformer model for rolling element bearings fault diagnosis in electric motors. Mach. Learn. Knowl. Extr. 2021, 3, 228–242. [Google Scholar] [CrossRef]
- Ma, S.; Flanigan, K.A.; Bergés, M. State-of-the-art review and synthesis: A requirement-based roadmap for standardized predictive maintenance automation using digital twin technologies. Adv. Eng. Inform. 2024, 62, 102800. [Google Scholar] [CrossRef]
- Rashid, H.; Habbouche, H.; Amirat, Y.; Mamoune, A.; Titah-Benbouzid, H.; Benbouzid, M. B-FLOWS: Biofouling Focused Learning and Observation for Wide-Area Surveillance in Tidal Stream Turbines. J. Mar. Sci. Eng. 2024, 12, 1828. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Zhang, S.; Long, T.; Liang, J. Error fusion of hybrid neural networks for mechanical condition dynamic prediction. Sensors 2021, 21, 4043. [Google Scholar] [CrossRef]
- Benbouzid, M. Signal Processing for Fault Detection and Diagnosis in Electric Machines and Systems; Institution of Engineering & Technology: Stevenage, UK, 2021. [Google Scholar]
- Mpoyi, D.K.; Ekuakille, A.L.; Ugwiri, M.A.; Casavola, C.; Pappalettera, G. Wear monitoring based on vibration measurement during machining: An application of FDM and EMD. Meas. Sens. 2024, 32, 101051. [Google Scholar] [CrossRef]
- Nasiri, A.; Rahideh, A.; Agah, G.R.; Kia, S.H. Ball-Bearing Fault Detection of Squirrel-Cage Induction Motors Based on Single-Phase Stator Current Using Wavelet Packet Decomposition and Statistical Features. IEEE Trans. Energy Convers. 2024, early access. [Google Scholar] [CrossRef]
- Habbouche, H.; Benkedjouh, T.; Amirat, Y.; Benbouzid, M. A Wavelet Transform-Based Transfer Learning Approach for Enhanced Shaft Misalignment Diagnosis in Rotating Machinery. Electronics 2025, 14, 341. [Google Scholar] [CrossRef]
- Xia, J.; Huang, R.; Liao, Y.; Li, J.; Chen, Z.; Li, W. Digital twin-assisted gearbox dynamic model updating toward fault diagnosis. Front. Mech. Eng. 2023, 18, 32. [Google Scholar] [CrossRef]
- Yu, J.; Wang, S.; Wang, L.; Sun, Y. Gearbox fault diagnosis based on a fusion model of virtual physical model and data-driven method. Mech. Syst. Signal Process. 2023, 188, 109980. [Google Scholar] [CrossRef]
- Matania, O.; Bechhoefer, E.; Bortman, J. Digital Twin of a Gear Root Crack Prognosis. Sensors 2023, 23, 9883. [Google Scholar] [CrossRef]
- Zhu, D.; Li, Z.; Hu, N. Multi-body dynamics modeling and analysis of planetary gearbox combination failure based on digital twin. Appl. Sci. 2022, 12, 12290. [Google Scholar] [CrossRef]
- Zhu, P.; Deng, L.; Tang, B.; Yang, Q.; Li, Q. Digital twin-enabled entropy regularized wavelet attention domain adaptation network for gearboxes fault diagnosis without fault data. Adv. Eng. Inform. 2025, 64, 103055. [Google Scholar] [CrossRef]
- Jia, S.; Sun, D.; Noman, K.; Wang, X.; Li, Y. Lifting wavelet-informed hierarchical domain adaptation network: An interpretable digital twin-driven gearbox fault diagnosis method. Reliab. Eng. Syst. Saf. 2025, 254, 110660. [Google Scholar] [CrossRef]
- Ming, Z.; Tang, B.; Deng, L.; Yang, Q.; Li, Q. Digital twin-assisted fault diagnosis framework for rolling bearings under imbalanced data. Appl. Soft Comput. 2025, 168, 112528. [Google Scholar] [CrossRef]
- Qin, Y.; Liu, H.; Wang, Y.; Mao, Y. Inverse physics–informed neural networks for digital twin–based bearing fault diagnosis under imbalanced samples. Knowl.-Based Syst. 2024, 292, 111641. [Google Scholar] [CrossRef]
- Shi, H.; Yang, T.; Hu, Y.; Song, Z. A Model-Data Combination Driven Digital Twin Model for Few Samples Fault Diagnosis of Rolling Bearings. Meas. Sci. Technol. 2024, 35, 095103. [Google Scholar] [CrossRef]
- Piltan, F.; Kim, C.H.; Kim, J.M. Bearing crack diagnosis using a smooth sliding digital twin to overcome fluctuations arising in unknown conditions. Appl. Sci. 2022, 12, 6770. [Google Scholar]
- Kurucan, M.; Özbaltan, M.; Yetgin, Z.; Alkaya, A. Applications of artificial neural network based battery management systems: A literature review. Renew. Sustain. Energy Rev. 2024, 192, 114262. [Google Scholar] [CrossRef]
- Mian, Z.; Deng, X.; Dong, X.; Tian, Y.; Cao, T.; Chen, K.; Al Jaber, T. A literature review of fault diagnosis based on ensemble learning. Eng. Appl. Artif. Intell. 2024, 127, 107357. [Google Scholar] [CrossRef]
- Li, G.; Yu, Z.; Yang, K.; Lin, M.; Chen, C.P. Exploring Feature Selection With Limited Labels: A Comprehensive Survey of Semi-Supervised and Unsupervised Approaches. IEEE Trans. Knowl. Data Eng. 2024, 36, 6124–6144. [Google Scholar] [CrossRef]
- Xi, D.; Hou, L.; Luo, J.; Liu, F.; Qin, Y. The meta-defect-detection system for gear pitting based on digital twin. Adv. Eng. Inform. 2023, 56, 102003. [Google Scholar] [CrossRef]
- Xu, Y.; Jiang, Q.; Li, S.; Zhao, Z.; Sun, B.; Huang, G.Q. Digital twin-driven discriminative graph learning networks for cross-domain bearing fault recognition. Comput. Ind. Eng. 2024, 193, 110292. [Google Scholar] [CrossRef]
- Ma, L.; Jiang, B.; Xiao, L.; Lu, N. Digital twin-assisted enhanced meta-transfer learning for rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2023, 200, 110490. [Google Scholar] [CrossRef]
- Cui, L.; Xiao, Y.; Liu, D.; Han, H. Digital twin-driven graph domain adaptation neural network for remaining useful life prediction of rolling bearing. Reliab. Eng. Syst. Saf. 2024, 245, 109991. [Google Scholar] [CrossRef]
- He, D.; Zhao, J.; Jin, Z.; Huang, C.; Zhang, F.; Wu, J. Prediction of bearing remaining useful life based on a two-stage updated digital twin. Adv. Eng. Inform. 2025, 65, 103123. [Google Scholar] [CrossRef]
- Li, Z.; Ding, X.; Song, Z.; Wang, L.; Qin, B.; Huang, W. Digital twin-assisted dual transfer: A novel information-model adaptation method for rolling bearing fault diagnosis. Inf. Fusion 2024, 106, 102271. [Google Scholar] [CrossRef]
- Zhang, C.; Qin, F.; Zhao, W.; Li, J.; Liu, T. Research on rolling bearing fault diagnosis based on digital twin data and improved ConvNext. Sensors 2023, 23, 5334. [Google Scholar] [CrossRef]
- Liu, S.; Qi, Y.; Gao, X.; Liu, L.; Ma, R. Transfer learning-based multiple digital twin-assisted intelligent mechanical fault diagnosis. Meas. Sci. Technol. 2023, 35, 025133. [Google Scholar] [CrossRef]
- Meng, W.; Wang, Y.; Zhang, X.; Li, S.; Bai, X.; Hou, L. Prediction of fault evolution and remaining useful life for rolling bearings with spalling fatigue using digital twin technology. Appl. Intell. 2023, 53, 28611–28626. [Google Scholar] [CrossRef]
- Sow, S.; Farhat, M.H.; Chiementin, X.; Rasolofondraibe, L.; Cousinard, O. Gearbox Digital Twin Data Used in Supervised Learning. J. Vib. Eng. Technol. 2024, 12, 3087–3099. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, R.; Xiang, J.; Qiao, Z.; Zhou, Y.; Shao, H. Digital twin-assisted AI framework based on domain adaptation for bearing defect diagnosis in the centrifugal pump. Measurement 2024, 235, 115013. [Google Scholar] [CrossRef]
- Xiao, Y.; Cui, L.; Liu, D.; Pan, X. Digital Twin-Driven Graph Convolutional Memory Network for Defect Evolution Assessment of Rolling Bearings. IEEE Trans. Instrum. Meas. 2024, 73, 3519210. [Google Scholar] [CrossRef]
- Mo, R.; Zhou, H.; Yin, H.; Si, X. A survey on few-shot learning for remaining useful life prediction. Reliab. Eng. Syst. Saf. 2025, 257, 110850. [Google Scholar] [CrossRef]
- Ait Abdelmoula, I.; Oufettoul, H.; Lamrini, N.; Motahhir, S.; Mehdary, A.; El Aroussi, M. Federated learning for solar energy applications: A case study on real-time fault detection. Sol. Energy 2024, 282, 112942. [Google Scholar] [CrossRef]
- Salim, M.M.; Camacho, D.; Park, J.H. Digital twin and federated learning enabled cyberthreat detection system for IoT networks. Future Gener. Comput. Syst. 2024, 161, 701–713. [Google Scholar] [CrossRef]
- Nain, G.; Pattanaik, K.; Sharma, G. Towards edge computing in intelligent manufacturing: Past, present and future. J. Manuf. Syst. 2022, 62, 588–611. [Google Scholar] [CrossRef]
- Lu, S.; Lu, J.; An, K.; Wang, X.; He, Q. Edge computing on IoT for machine signal processing and fault diagnosis: A review. IEEE Internet Things J. 2023, 10, 11093–11116. [Google Scholar] [CrossRef]
- Gao, R.X.; Krüger, J.; Merklein, M.; Möhring, H.C.; Váncza, J. Artificial Intelligence in manufacturing: State of the art, perspectives, and future directions. CIRP Ann. 2024, 73, 723–749. [Google Scholar] [CrossRef]
- Liu, G.; Wu, L. Incremental bearing fault diagnosis method under imbalanced sample conditions. Comput. Ind. Eng. 2024, 192, 110203. [Google Scholar] [CrossRef]
- Ju, Z.; Chen, Y.; Qiang, Y.; Chen, X.; Ju, C.; Yang, J. A systematic review of data augmentation methods for intelligent fault diagnosis of rotating machinery under limited data conditions. Meas. Sci. Technol. 2024, 35, 122004. [Google Scholar] [CrossRef]
- Habbouche, H.; Rashid, H.; Amirat, Y.; Banerjee, A.; Benbouzid, M. A 2D VMD video image processing-based transfer learning approach for the detection and estimation of biofouling in tidal stream turbines. Ocean Eng. 2024, 312, 119283. [Google Scholar] [CrossRef]
- Cui, L.; Li, W.; Wang, X.; Liu, D. A novel quantitative diagnosis method for rolling bearing faults based on digital twin model. ISA Trans. 2024, 157, 381–391. [Google Scholar] [CrossRef]
- Yan, S.; Zhong, X.; Shao, H.; Ming, Y.; Liu, C.; Liu, B. Digital twin-assisted imbalanced fault diagnosis framework using subdomain adaptive mechanism and margin-aware regularization. Reliab. Eng. Syst. Saf. 2023, 239, 109522. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).