Research on Continuous Obstacle Avoidance Picking Planning Based on Multi-Objective Clustered Crabapples
Abstract
1. Introduction
2. Related Work
2.1. Information About Robotic Arms
2.2. Research Comparison
2.3. Preliminaries
3. Environment Set Up
3.1. Sugarcane Tree 3D Reconstruction
3.2. Robotic Arm Collision Detection Method
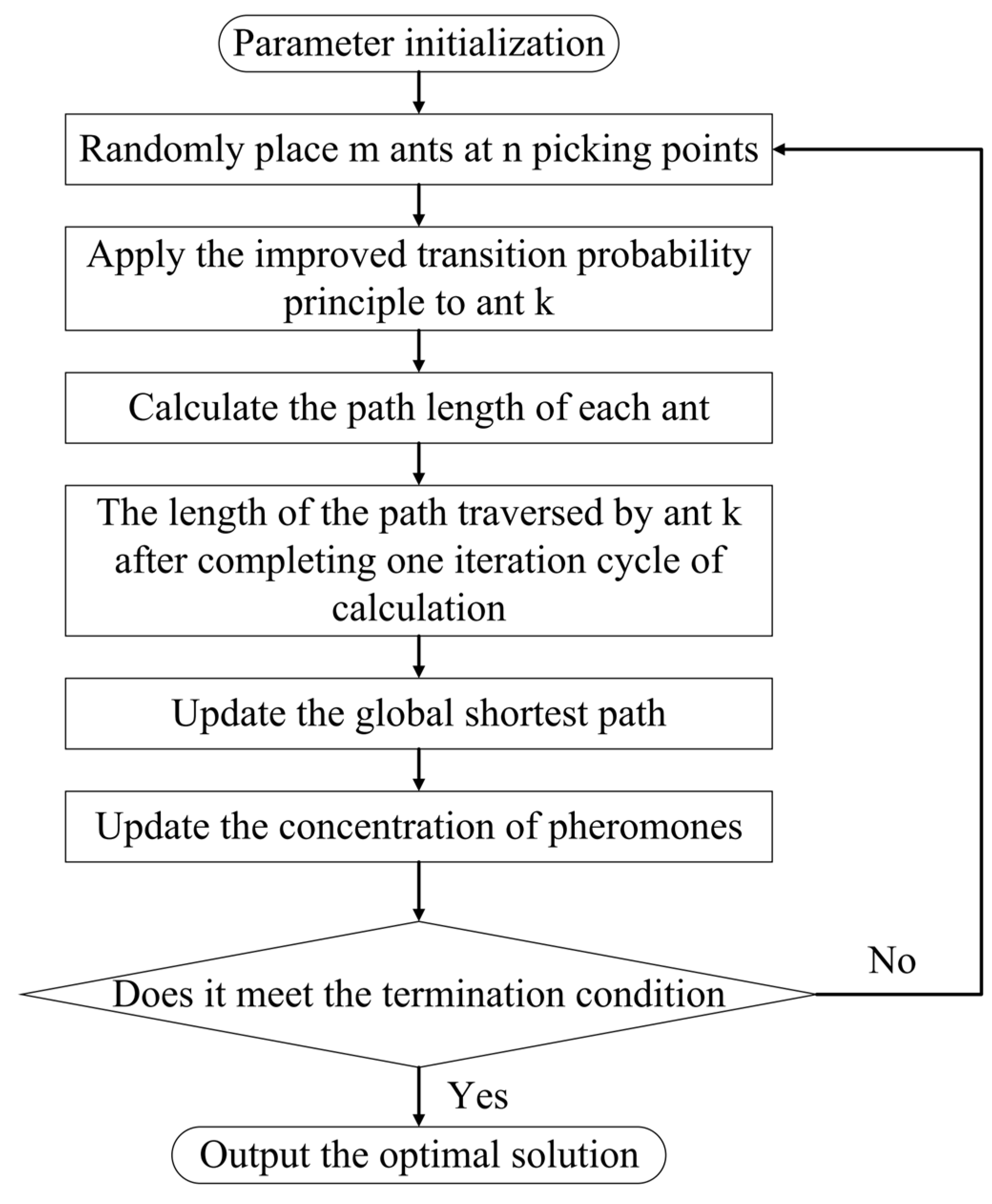
4. ACO Algorithm Path Planning and Improvement
4.1. Improved Transfer Probability
4.2. Optimized Pheromone Concentration Updates
4.3. Comparative Analysis of Parameter Influence
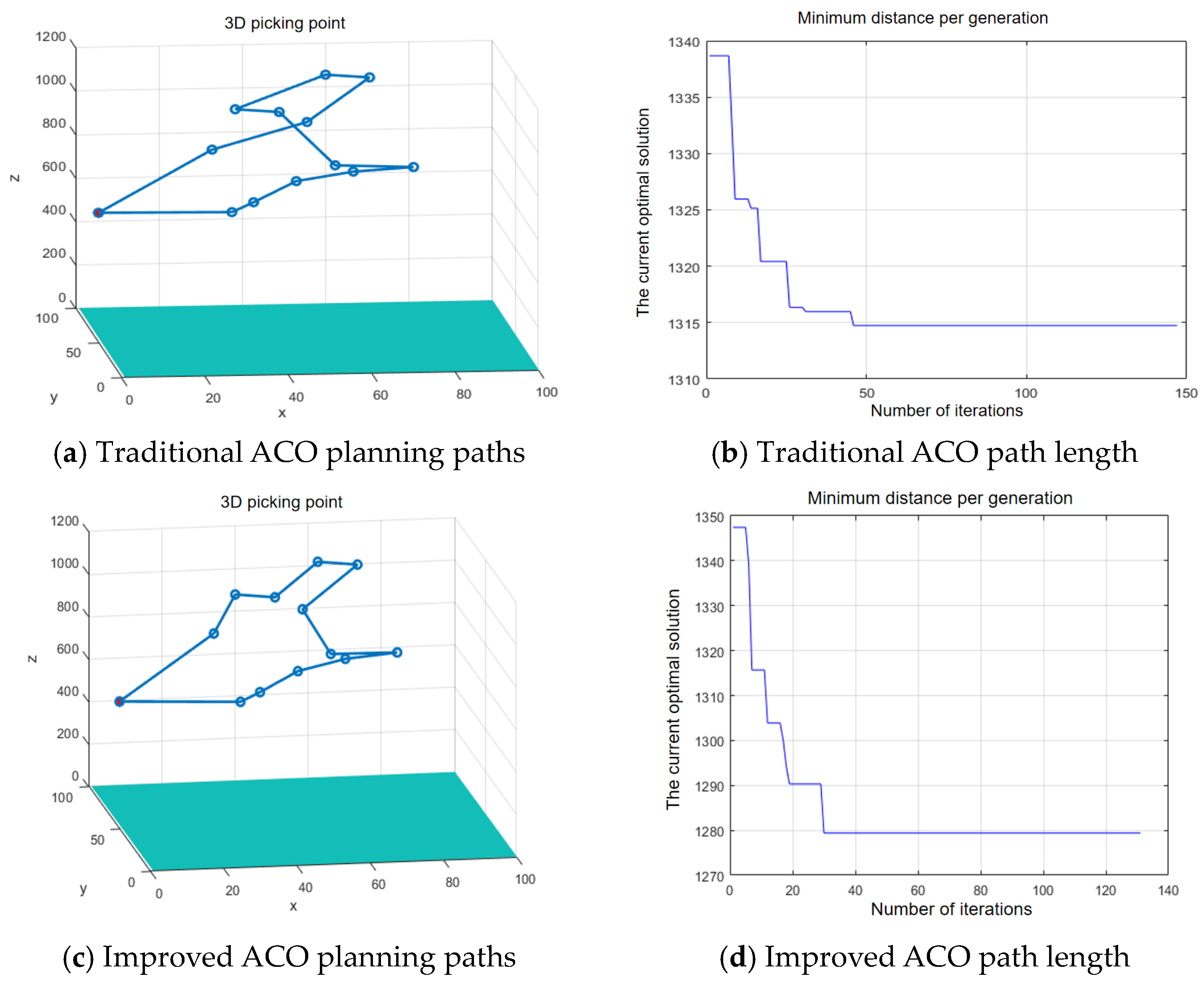
4.4. Comparison of Ant Colony Algorithm Before and After Improvement
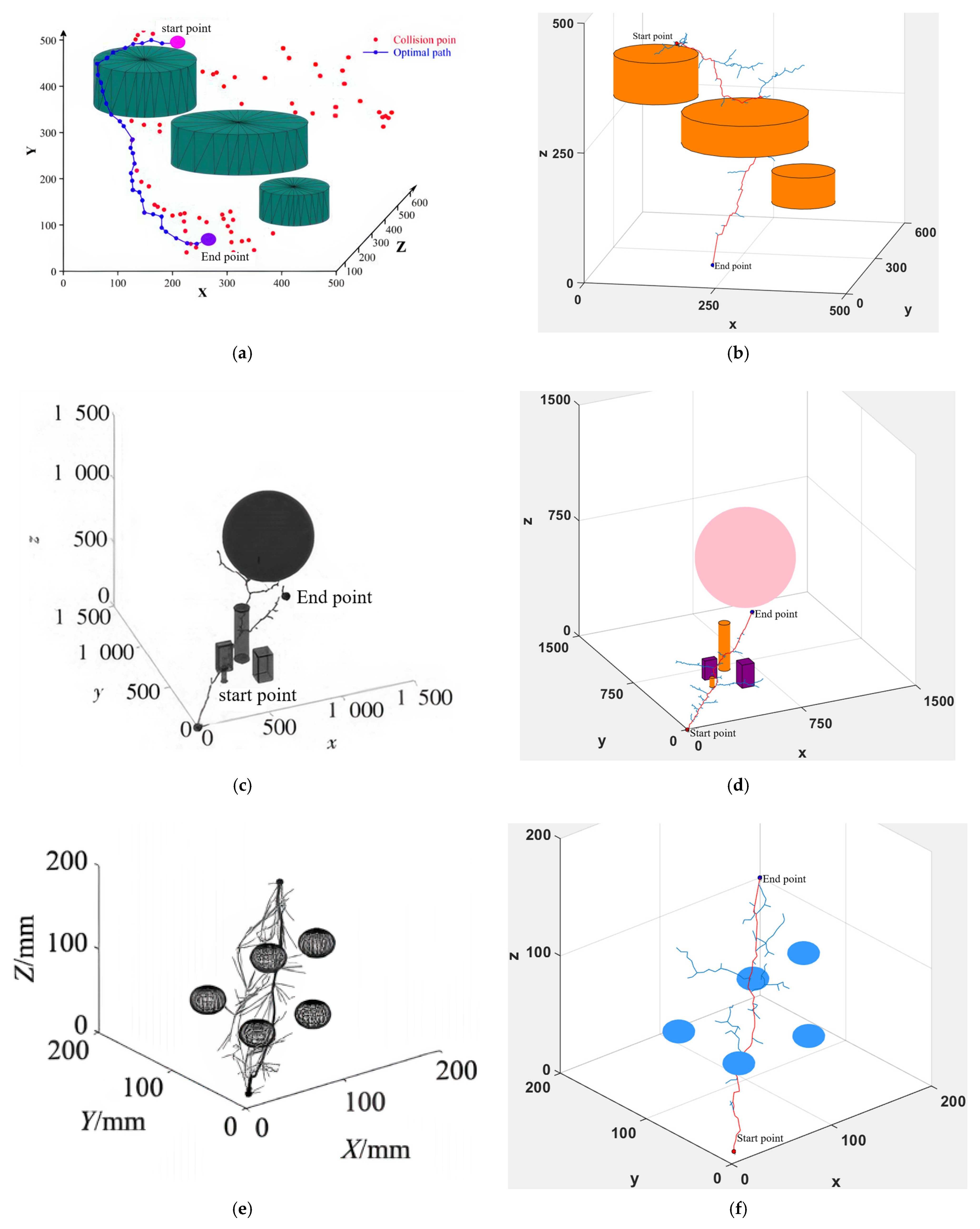
5. Improve Obstacle Avoidance Path Planning for RRT
5.1. Based on RRT and APF Algorithms
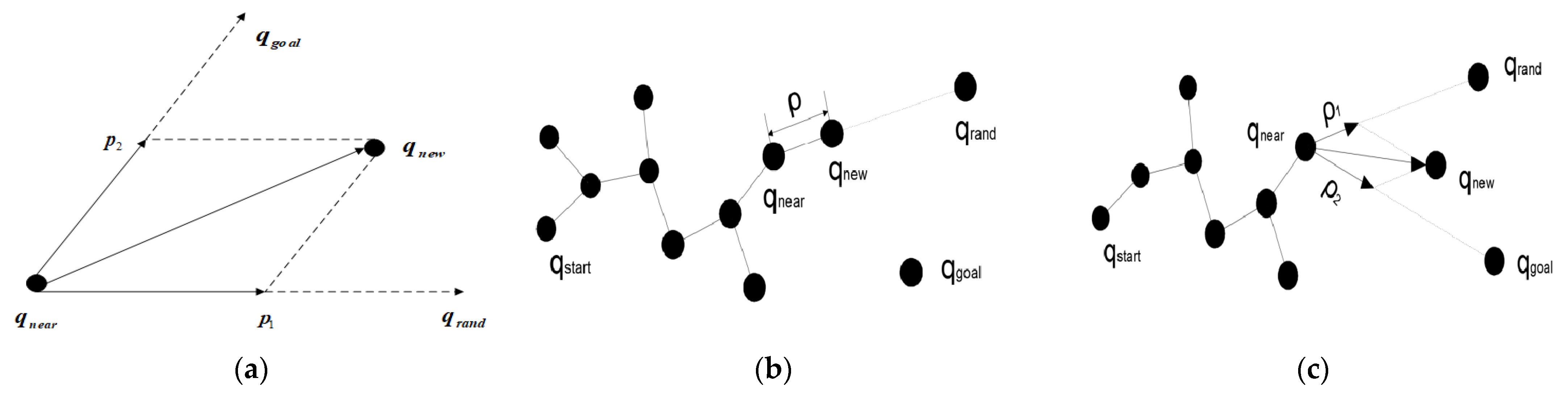
5.2. Improvements to RRT
- (1)
- Set as the starting point of exploration, as the final destination point, where both and are points in the workspace ;
- (2)
- Set as the root node of random tree ;
- (3)
- Sampling points are obtained by random sampling in the working interval for each iteration;
- (4)
- Search for the node closest to in the random tree , denote it as ;
- (5)
- Starting from , generate a new node with a specific step size in the direction from to , and generate a new node under the gravitational field of the target point with a certain step size from , where both new nodes and are in the working space ;
- (6)
- Generate a new node in the direction of the diagonals formed by the parallelogram from to and from to ; then, denote the path from node to the new node as ;
- (7)
- Judge whether meets the obstacle avoidance conditions within the working area . If it does, set as the new node; if not, return to step (3) to re-find a randomly sampled point ;
- (8)
- If the obstacle avoidance conditions are met, repeat steps (3) to step (7) in the next iteration cycle until node is reached, and to paths are output. The improved RRT algorithm flowchart is shown in Figure 10, and the pseudocode can be found in Supplementary S2. The comparison chart of RRT before and after improvement is shown in Figure 11.
- (1)
- In the node sampling stage, although the basic characteristics of random sampling are still maintained, the continuous guidance of the gravitational field makes the sampling points naturally biased towards the direction of the target point, significantly improving the target directionality.
- (2)
- During the tree expansion process, whenever a new node is generated, APF calculates the attraction and repulsion in real-time based on the current environment. Attraction pulls the node towards the target point, while repulsion pushes the node away from obstacles. The balance of these forces allows the new node to automatically avoid obstacles while maintaining the expansion direction.
- (3)
- At the level of overall path optimization, the continuous effect of APF enables the tree structure grown to naturally form smooth detours in areas with dense obstacles, while maintaining the characteristic of approaching the target in a straight line in open areas. This not only avoids the redundant exploration that may occur in traditional RRT but also makes the final path both safe and optimal through dynamic adjustment of the force field.
5.3. Comparison of RRT Before and After Improvement
6. Picking Test and Result Analysis
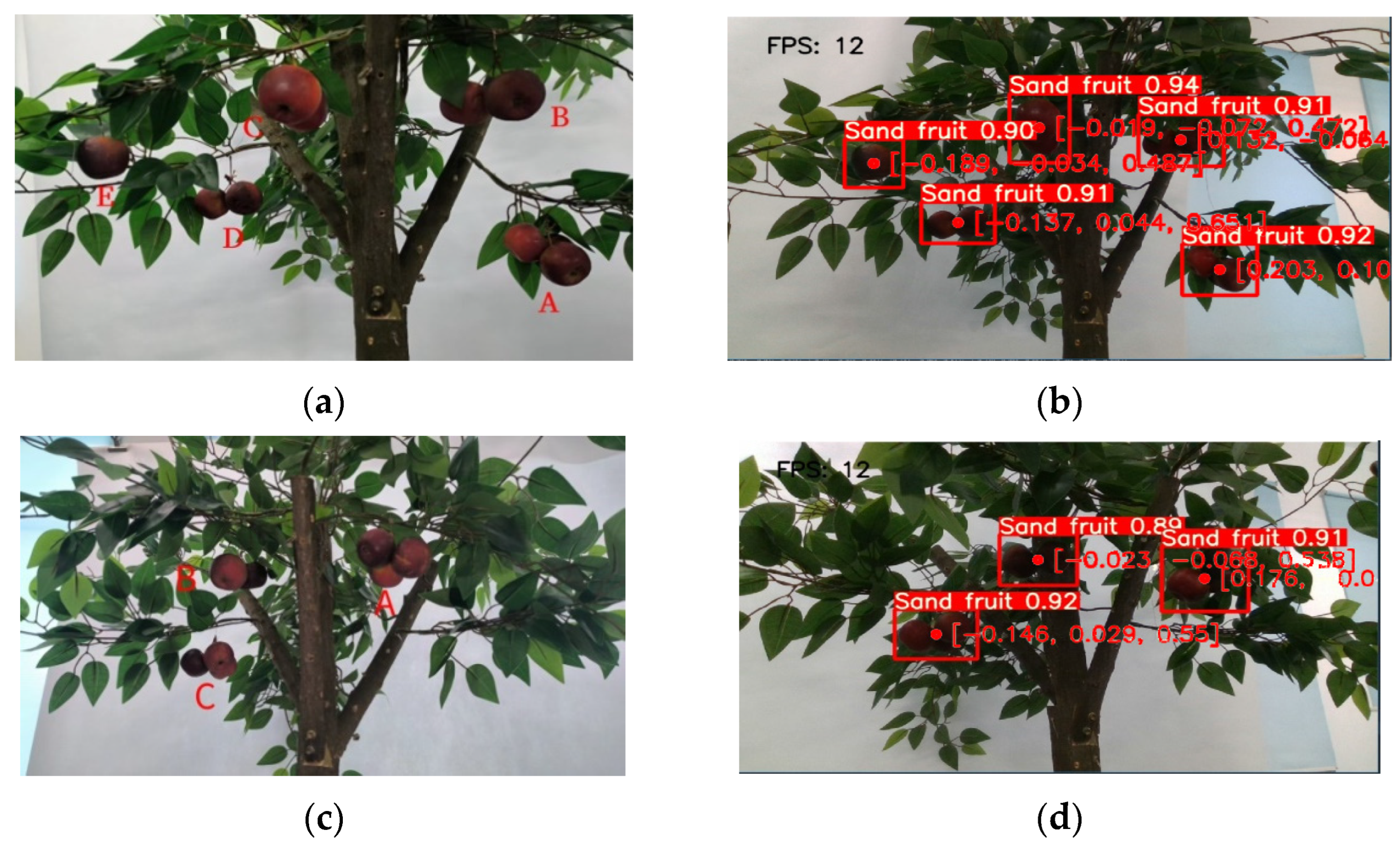
6.1. Identification and Positioning
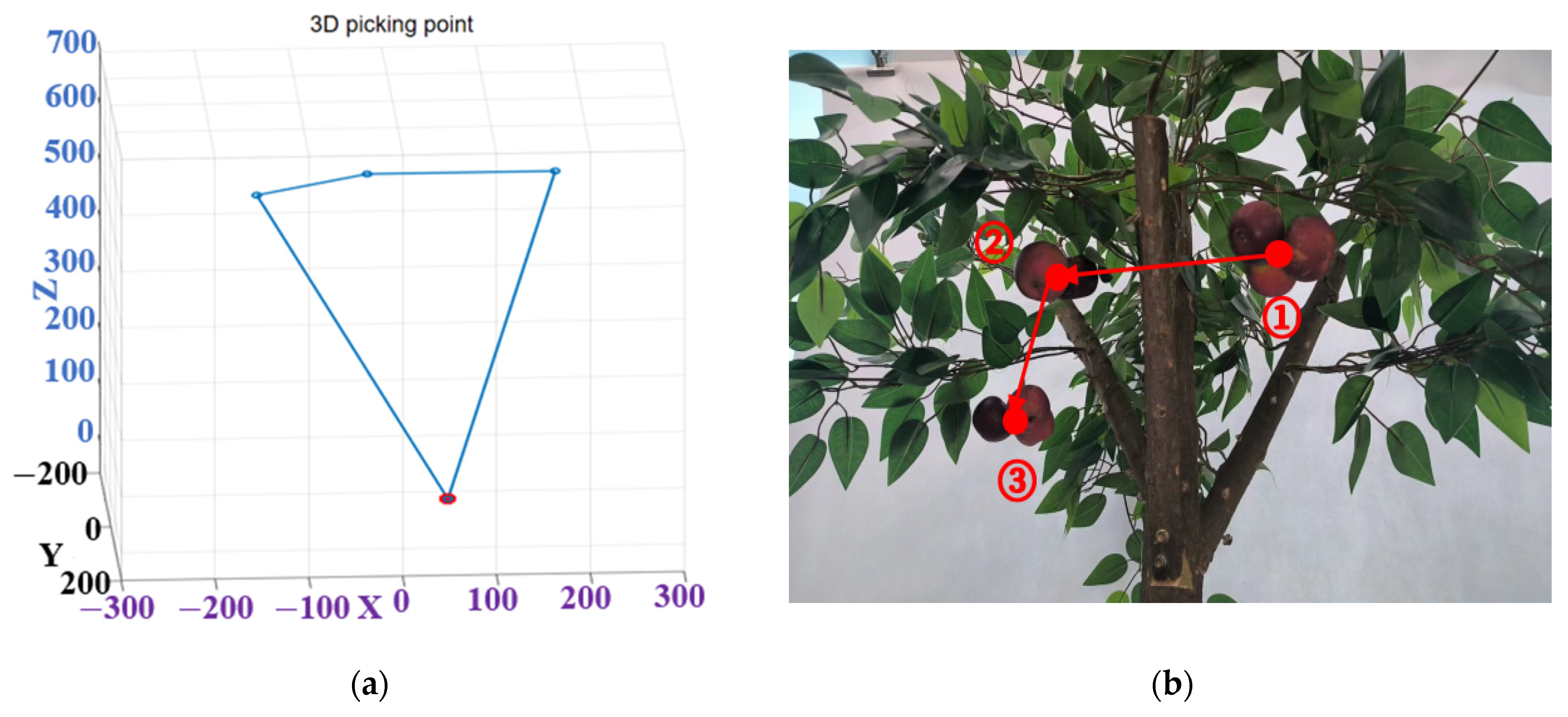
6.2. Multi-Objective Picking Sequence Planning on Crabapple Trees
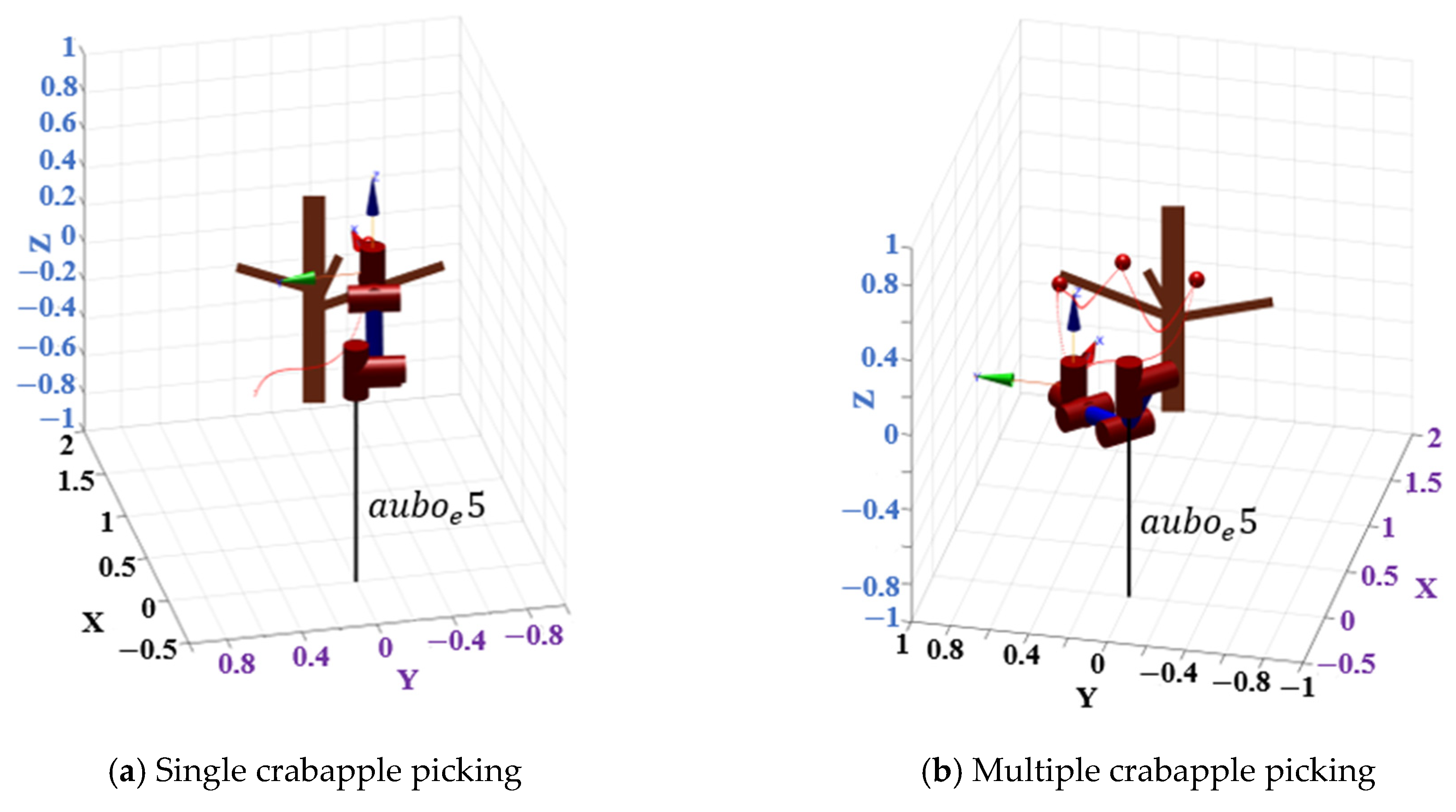
6.3. Simulation Analysis of Crabapple Picking Robotic Arm
6.4. Multi-Target Clustered Crabapples Picking Experiment
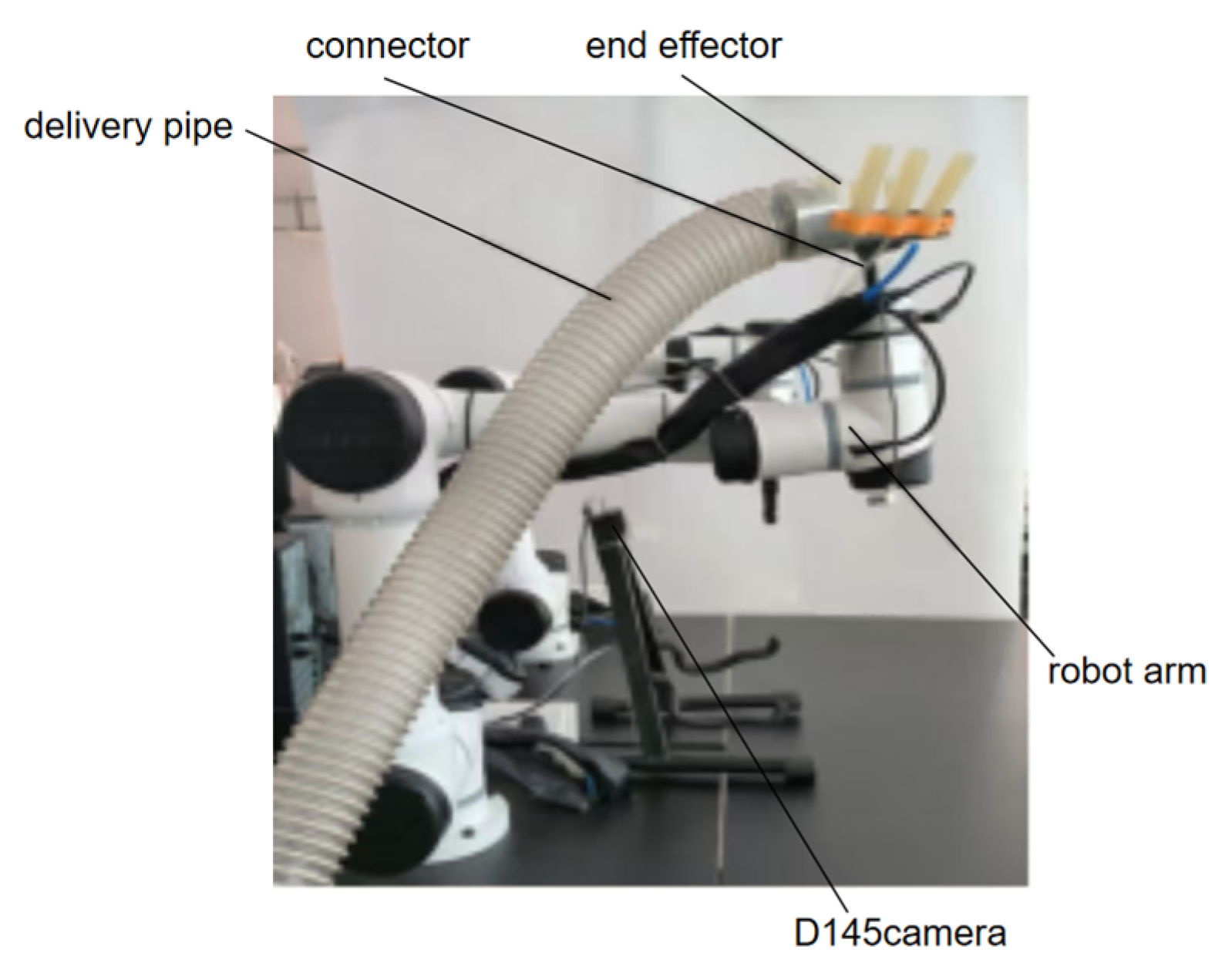
6.4.1. Rigid-Flexible Pneumatic Coupling Picking Manipulator
6.4.2. Construction of the Picking Test Platform
6.4.3. Crabapples Picking Test
7. Discussion of Experimental Results
- (1)
- In terms of the rationality of the experimental design, the experiment simulated the growing environment of sand fruit based on the real picking scene. Five and three sand fruit types were set at different locations on the sand fruit tree, and the number of sand fruit was different for each cluster, covering diverse scenes such as different cluster distributions, fruit density, and branches and leaves occlusion degree. Compared with the traditional AOC algorithm and the traditional RRT algorithm, the path planning and path length are set up in the experiment. Through the comparison of simulation data, the superiority of the algorithm is demonstrated.
- (2)
- As for the scientific evaluation of the results, the experimental results show the success rate of identification, positioning, picking, and collision with the robotic arm of different groups, which are all important evaluation indicators to measure the obstacle avoidance algorithm, and the experimental results are scientific, rigorous, and convincing.
- (3)
- The experimental results also have an impact on the actual picking operation. The experimental results show that the algorithm can improve the picking efficiency of the picking robot arm in the actual scene, which reflects the adaptability to the clustered sand fruit environment and meets the requirements of continuous picking.
- (4)
- In terms of improvement and applicability, the algorithm planning effect can be further improved by combining deep learning, reinforcement learning, and other methods. The algorithm can be applied not only to sand fruit trees, but also to grapes, cherries, and other clustered fruits.
8. Conclusions and Future Work Plan
8.1. Conclusions
- (1)
- The problem of picking the sequence of multiple crabapples on the tree was simplified to the TSP in three-dimensional space. The ACO algorithm was improved by improving the transition probability and optimizing the pheromone concentration update. Compared with the traditional ACO algorithm, it can be concluded that the improved ACO algorithm has shorter picking sequence paths, fewer iterations, faster convergence speed, and can effectively plan the picking sequence of multiple crabapples on the tree.
- (2)
- To avoid collisions between the robotic arm and the tree branches during picking progress, which may cause damage to the robotic arm and the trees, the APF algorithm and the RRT algorithm were combined, and a gravitational field was introduced to enhance the directional guidance of the RRT algorithm’s path search. Compared to the original RRT algorithm, it can be concluded that the improved RRT algorithm has fewer turning points and faster convergence speed and can achieve an obstacle-avoidant picking path planning for the robotic arm.
- (3)
- To verify the effectiveness and feasibility of the algorithm proposed in this article, a picking test platform was constructed to conduct multiple groups of picking tests on clustered crabapples (1 to 6 clusters) on an artificial simulation crabapple tree. The test results show that the average recognition success rate is 95.83%, the average positioning success rate is 93.75%, and the average picking success rate is 89.58%. Moreover, there are no collisions between the robotic arm and the main branches of the tree during the picking process, and the robotic arm can pick the crabapples according to the planned picking sequence with no collision, meeting the actual picking requirements and achieving the goal of picking.
8.2. Future Work Plan
- (1)
- The rigid-flexible pneumatic coupling picking manipulator needs to be further optimized. Although some fruits can be successfully identified and positioned, the picking manipulator cannot fully envelop and pick fruits, thus reducing the success rate of picking.
- (2)
- With the continuous change and development of computer technology, target detection technology is also constantly changing. This study adopts the YOLOv5 algorithm as the basis for research, and other novel detection algorithms can be explored in the following research.
- (3)
- In this study, the AUBO-E5 robotic arm is used, which has high input and maintenance costs. Next, a robotic arm that meets the requirements of picking will be studied, and collection boxes and walking mechanisms will be assembled for field picking.
- (4)
- In the later stage, an integrated deep learning model will be added on the basis of this algorithm to improve the detection accuracy and real-time algorithm optimization. The complex orchard picking situation will be deeply studied, and the algorithms of other studies will be copied and compared with this algorithm to improve the obstacle avoidance and retrieval ability of this algorithm.
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, C.; Gong, L.; Yuan, J.; Li, Y. Current Status and Development Trends of Agricultural Robots. Trans. Chin. Soc. Agric. Mach. 2022, 53, 1–22+55. [Google Scholar]
- Ma, J.; Shen, Z.; Zhang, A.; Zhang, J.; Ren, M.; Wang, C. Analysis of antioxidant components and activities of sand fruit juice during processing. J. Oiqihar Univ. (Nat. Sci. Ed.) 2023, 39, 76–80+94. [Google Scholar]
- Jiang, N.; Ma, J.; Zhang, J.; Zhang, A.; Shen, Z.; Liu, J.; Zhang, Y.; Du, G.; Wang, C. Effects of Slice Thickness and Hot-air Temperature on Drying Characteristics, Physico-chemical Properties and Antioxidants of Mumsasiatica Nakai Slices. Sci. Technol. Food Ind. 2024, 45, 32–39. [Google Scholar]
- Li, S.; Sun, T.; Yuan, L.; Wu, L. Design and experimental research of pneumatic soft picking manipulator. Chin. J. Eng. Des. 2022, 29, 684–694. [Google Scholar]
- Sun, C.; Yan, J.; Zhang, F.; Gou, Y.; Xu, Y. Research progress of vegetable picking robot and its key technologies. J. Chin. Agric. Mech. 2023, 44, 63–72. [Google Scholar]
- Yang, X.; Zhou, W.; Li, Y.; Qi, X.; Zhang, Q. Review of path planning algorithms for picking manipulator. J. Chin. Agric. Mech. 2023, 44, 161–169. [Google Scholar]
- Kurtser, P.; Edan, Y. Planning the sequence of tasks for harvesting robots. Robot. Auton. Syst. 2020, 131, 103591. [Google Scholar] [CrossRef]
- Li, T.; Qiu, Q.; Zhao, C.; Xie, F. Task planning of multi-arm harvesting robots for high-density dwarf orchards. Trans. Chin. Soc. Agric. Eng. 2021, 37, 1–10. [Google Scholar]
- Ye, L.; Duan, J.L.; Yang, Z.; Zou, X.J.; Chen, M.Y.; Zhang, S. Collision-free motion planning for the litchi-picking robot. Comput. Electron. Agric. 2021, 185, 106151. [Google Scholar] [CrossRef]
- Cao, X.M.; Zou, X.J.; Jia, C.Y.; Chen, M.Y.; Zeng, Z.Q. RRT-based path planning for an intelligent litchi-picking manipulator. Comput. Electron. Agric. 2019, 156, 105–118. [Google Scholar] [CrossRef]
- Sun, S.Y.; Mao, S.R.; Xue, X.S.; Wang, C.W.; Ma, H.W.; Guo, Y.F.; Yuan, H.N.; Su, H. Research on Obstacle-Avoidance Trajectory Planning for Drill and Anchor Materials Handling by a Mechanical Arm on a Coal Mine Drilling and Anchoring Robot. Sensors 2024, 24, 6866. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Yang, J.W.; Wang, X.; Fu, L.Y.; Li, S.W. Adaptive Step RRT*-Based Method for Path Planning of Tea-Picking Robotic Arm. Sensors 2024, 24, 7759. [Google Scholar] [CrossRef]
- Wang, W. An intelligent obstacle avoidance method for six degree of freedom robotic arm based on assembly sequence planning. Appl. Math. Nonlinear Sci. 2024, 9, 3018. [Google Scholar] [CrossRef]
- Fu, J.; Mu, L.; Di, X.; Zhang, X.; Zhang, H. Research on Complex Obstacle Avoidance Path Planning for Robotic Arm Based on Improved RRT Algorithm. Mod. Electron. Tech. 2025, 48, 180–186. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Y.; Jin, H.; Deng, J.; Li, T. Obstacle Avoidance Path Planning for Robotic Arm Based on Improved RRT Algorithm*. Modul. Mach. Tool Autom. Manuf. Tech. 2024, 8, 6–12. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, L.; Tian, R.; Wang, X. Research on obstacle avoidance motion planning method of manipulator in complex multi scene. J. Northwestern Polytech. Univ. 2023, 41, 500–509. [Google Scholar] [CrossRef]
- Shi, W.; Ning, N.; Song, C.; Ning, W. Path Planning of Mobile Robots Based on Ant Colony Algorithm and Artificial Potential Field Algorithm. Trans. Chin. Soc. Agric. Mach. 2023, 54, 407–416. [Google Scholar]
- Shen, Z.; Ding, W.; Liu, Y.; Yu, H. Unmanned sailboat path planning based on improved adaptive ant colony algorithm. J. Harbin Eng. Univ. 2023, 44, 969–976. [Google Scholar]
- Wang, Y.; Jiang, W.S.; Luo, Z.; Yang, L.; Wang, Y.Q. Path planning of a 6-DOF measuring robot with a direction guidance RRT method. Expert Syst. Appl. 2024, 238, 122057. [Google Scholar] [CrossRef]
- Zhang, R.; Guo, H.; Andriukaitis, D.; Li, Y.B.; Królczyk, G.; Li, Z.X. Intelligent path planning by an improved RRT algorithm with dual grid map. Alex. Eng. J. 2024, 88, 91–104. [Google Scholar] [CrossRef]
- Wu, Z.T.; Dai, J.Y.; Jiang, B.P.; Karimi, H.R. Robot path planning based on artificial potential field with deterministic annealing. Isa Trans. 2023, 138, 74–87. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Hao, W.; Wu, Y.; Sun, C. Research on Robot Obstacle Avoidance Path Planning Based on Improved Artificial Potential Field Method. Comput. Simul. 2023, 40, 431–436+442. [Google Scholar]
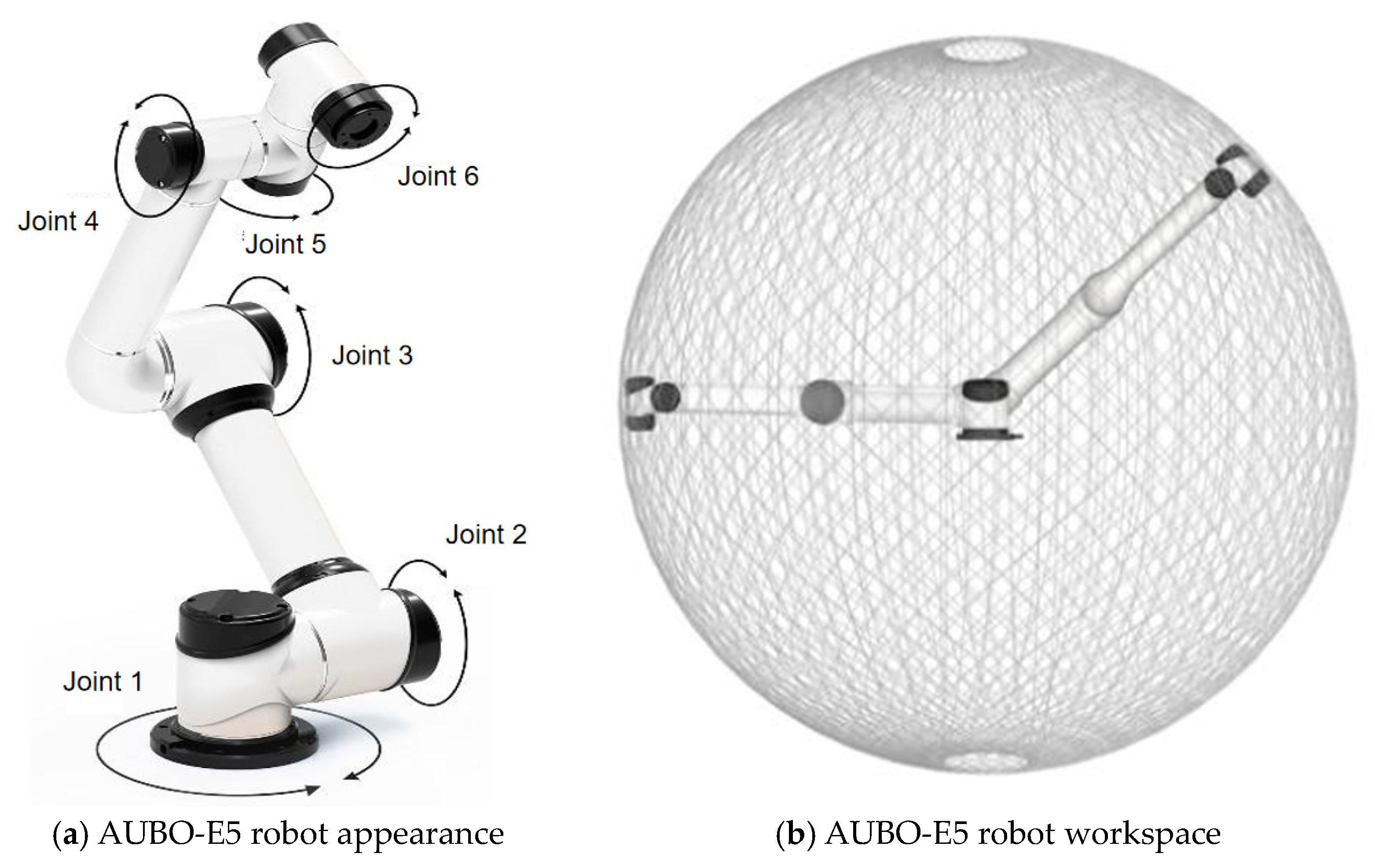
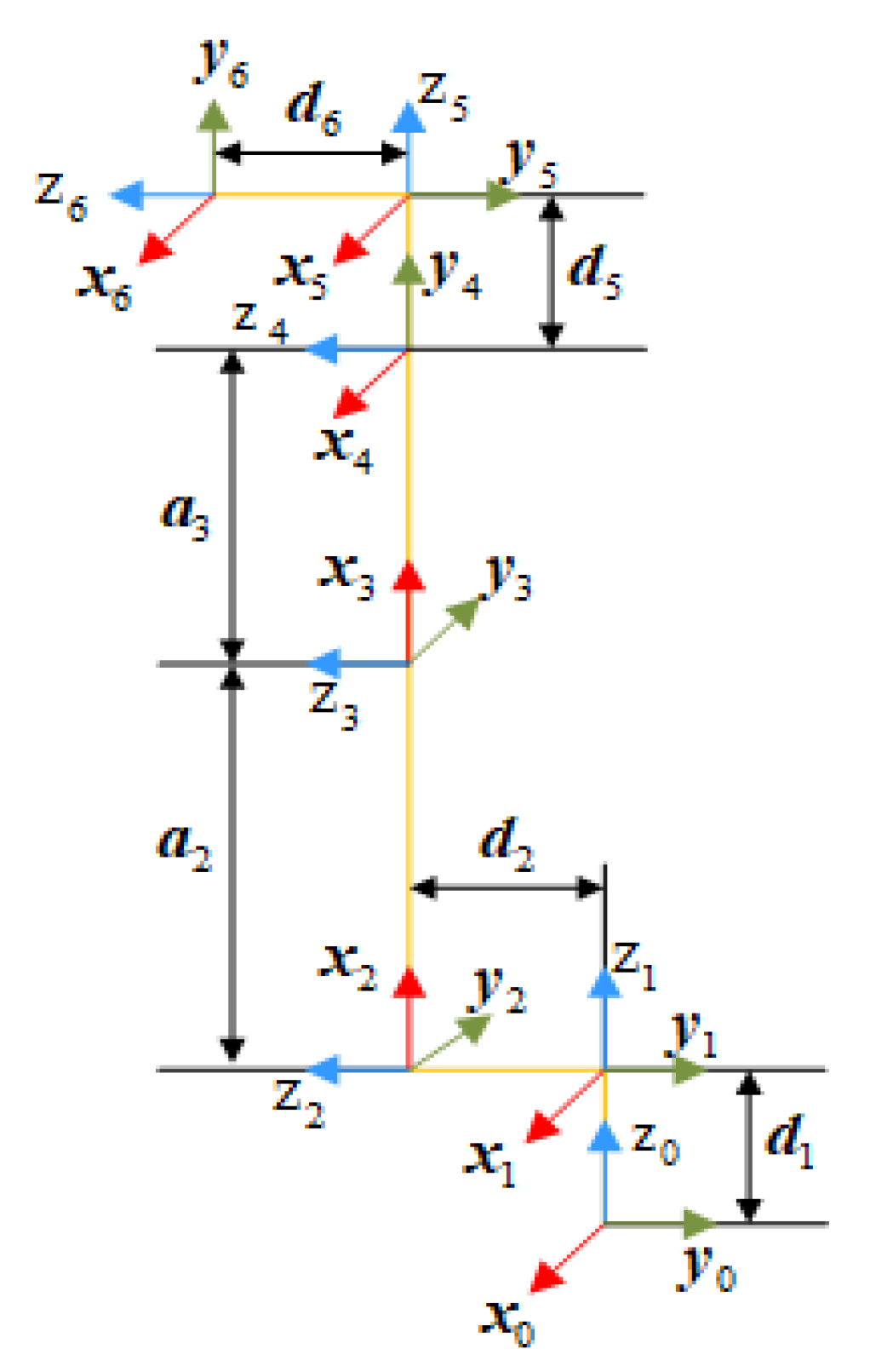
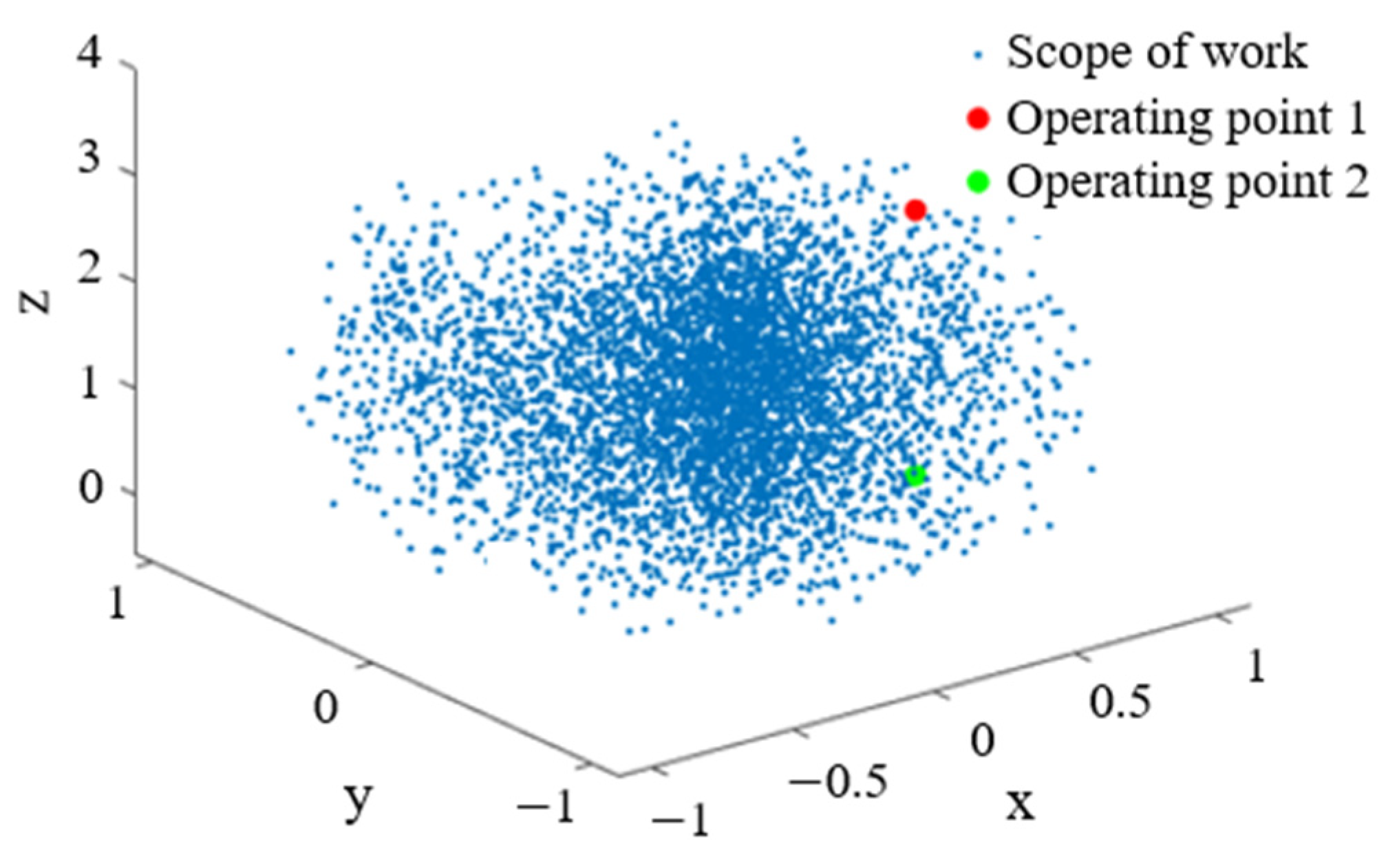









| Joint i | /mm | (rad) | /mm | (rad) | Joint Range (°) |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 121.5 | (0) | |
| 2 | 0 | pi/2 | 121.5 | (pi/2) | |
| 3 | 408 | 0 | 0 | (0) | |
| 4 | 376 | 0 | 0 | (pi/2) | |
| 5 | 0 | pi/2 | 102.5 | (0) | |
| 6 | 0 | pi/2 | 94 | (0) |
| Reference | Path Planning Time of This Algorithm (ms) | Path Planning Time of the Reference Algorithm (ms) |
|---|---|---|
| [13] | 735.4 | 387.8 |
| [14] | 16,366 | 1720.4 |
| [15] | 6160 | 288.4 |
| Branch | Starting Point (m) | Endpoint (m) | Radius (mm) |
|---|---|---|---|
| 1 | (0.00, 0.540, 0.610) | (0.00, −0.210, 0.610) | 29.5 |
| 2 | (0.00, 0.180, 0.610) | (0.00, −0.167, 0.490) | 12.0 |
| 3 | (−0.026, 0.107, 0.661) | (−0.183, −0.101, 0.818) | 13.5 |
| 4 | (0.027, 0.159, 0.625) | (0.230, −0.037, 0.778) | 15.0 |
| Parameter | Traditional ACO | Improve ACO |
|---|---|---|
| Algorithm | Path Length (eil51) | Convergent Algebra | Computing Time (s) | Path Length (att48) | Convergent Algebra |
|---|---|---|---|---|---|
| Traditional ACO | |||||
| Only dynamic | |||||
| Only dynamic | |||||
| Only dynamic | |||||
| Improve ACO |
| Algorithm | Path Length/mm | Number of Iterations/Times | Convergence Time/s |
|---|---|---|---|
| Traditional ACO | 1314.82 | 48 | 0.98 |
| Improved ACO | 1279.95 | 30 | 0.54 |
| Number of Clustered Crabapples | Picking Point | D415 Measurements (X, Y, Z)/m | Actual Measurements (X, Y, Z)/m | Absolute Positioning Error (X, Y, Z)/m |
|---|---|---|---|---|
| 5 | A | (0.203, 0.105, 0.595) | (0.206, 0.110, 0.600) | (0.003, 0.005, 0.005) |
| B | (0.132, −0.064, 0.512) | (0.137, −0.068, 0.514) | (0.005, 0.004, 0.002) | |
| C | (−0.019, −0.072, 0.472) | (−0.023, −0.075, 0.475) | (0.004, 0.003, 0.003) | |
| D | (−0.137, 0.044, 0.651) | (−0.140, 0.040, 0.653) | (0.003, 0.004, 0.002) | |
| E | (−0.189, −0.034, 0.487) | (−0.192, −0.038, 0.490) | (0.003, 0.004, 0.003) | |
| 3 | A | (0.176, −0.043, 0.548) | (0.180, −0.045, 0.550) | (0.004, 0.002, 0.002) |
| B | (−0.023, −0.068, 0.538) | (−0.020, −0.070, 0.542) | (0.003, 0.002, 0.004) | |
| C | (−0.146, 0.029, 0.550) | (−0.145, 0.032, 0.552) | (0.001, 0.003, 0.002) |
| Group | Number of Picking /Clusters | Number of Successful Recognizing/Clusters | Number of Successful Positioning /Clusters | Number of Successful Picking /Clusters | Recognizing Success Rate/% | Positioning Success Rate/% | Picking Success Rate/% | Number of Collisions/Times |
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 3 | 3 | 3 | 100 | 100 | 100 | 0 |
| 2 | 4 | 4 | 4 | 4 | 100 | 100 | 100 | 0 |
| 3 | 5 | 5 | 5 | 5 | 100 | 100 | 100 | 0 |
| 4 | 6 | 6 | 6 | 5 | 100 | 100 | 83.33 | 0 |
| 5 | 7 | 6 | 6 | 6 | 85.71 | 85.71 | 85.71 | 0 |
| 6 | 7 | 7 | 7 | 6 | 100 | 100 | 85.71 | 0 |
| 7 | 8 | 7 | 7 | 7 | 87.50 | 87.50 | 87.50 | 0 |
| 8 | 8 | 8 | 7 | 7 | 100 | 87.50 | 87.50 | 0 |
| sum | 48 | 46 | 45 | 43 | 95.83 | 93.75 | 89.58 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Yuan, L.; Meng, X.; Li, S.; Wang, Q.; Chen, X. Research on Continuous Obstacle Avoidance Picking Planning Based on Multi-Objective Clustered Crabapples. Appl. Sci. 2025, 15, 5724. https://doi.org/10.3390/app15105724
Wu L, Yuan L, Meng X, Li S, Wang Q, Chen X. Research on Continuous Obstacle Avoidance Picking Planning Based on Multi-Objective Clustered Crabapples. Applied Sciences. 2025; 15(10):5724. https://doi.org/10.3390/app15105724
Chicago/Turabian StyleWu, Liguo, Longqiang Yuan, Xiangquan Meng, Sanping Li, Qiyu Wang, and Xingyu Chen. 2025. "Research on Continuous Obstacle Avoidance Picking Planning Based on Multi-Objective Clustered Crabapples" Applied Sciences 15, no. 10: 5724. https://doi.org/10.3390/app15105724
APA StyleWu, L., Yuan, L., Meng, X., Li, S., Wang, Q., & Chen, X. (2025). Research on Continuous Obstacle Avoidance Picking Planning Based on Multi-Objective Clustered Crabapples. Applied Sciences, 15(10), 5724. https://doi.org/10.3390/app15105724






