Abstract
The exchange of gradients is a widely used method in modelling systems for machine learning (e.g., distributed training, federated learning) in privacy-sensitive domains. Unfortunately, there are still privacy risks in federated learning, as servers can reconstruct clients‘ training data through gradient inversion attacks. To protect against such attacks, we need to know when and how privacy is being undermined, largely due to the black box nature of deep neural networks. Although gradient inversion has been used to classify images and text data, its use in time-series is still largely unexplored. In this paper, we empirically evaluate the practicality of recovering lithium-ion battery time-series data from the gradients of a transformer-based model, both without and with differential privacy, in a time-series federated learning framework. It is especially significant in the case of electric vehicles (EVs). As shown in this paper, additional protection by differential privacy leads to the saturation of gradient inversion attacks, i.e., the reconstructed signal maintains a certain error level, depending on the applied privacy budget level. With this empirical evaluation, we provide insights into effective gradient perturbation directions, unfairness with respect to privacy, and privacy-preferred model initialisation.
1. Introduction
Federated learning (FL) [1,2,3] enables collaborative model training while preserving data privacy [4] by keeping the raw data decentralised. In each collaborative round, clients update the global model locally using private training data and then transmit gradients to the central parameter server [5] for aggregation (typically by averaging) and global update, thereby addressing privacy concerns by exposing the raw data [6]. After the aggregation of these updates by the central server, the new model parameters are sent back to the clients and the global training round is completed [7]. This method is particularly relevant for deep neural networks (DNNs), which are increasingly used in various applications due to their ability to model complex patterns [8]. However, training DNNs in an FL environment poses some challenges, particularly with respect to gradient sharing for model updates [9,10,11], which highlights the possibility of reconstructing the original input from the shared gradients (especially in the absence of protection methods) resulting from the transfer of model gradients and parameters.
However, recent studies [12,13] have shown that shared gradients in FL can be exploited by gradient inversion attacks (GIAs), which could allow attackers to reconstruct private training data. While much of the research has focused on the reconstruction of image and text data, in this paper, we explore the application of GIAs using a schematic approach of privacy auditing to time-series data [14,15] in the context of with and without differential privacy (DP).
The project involves data from lithium-ion batteries used in electric vehicles (EVs), where protecting user-sensitive information—such as mileage, usage patterns, and battery health—is a key concern. At the same time, it is essential to collaboratively train a common Artificial Intelligence (AI) model for battery behaviour prediction using federated learning (FL). Analysing time-series data, such as the ageing of lithium-ion batteries, plays a crucial role in understanding patterns in data over time. It enables the prediction and analysis of performance degradation, the optimisation of maintenance schedules, the improvement in reliability and useful life extension, not only in battery ageing but also in similar critical systems through data-driven decisions. Accurate predictions of battery ageing (e.g., capacity degradation or remaining useful life) can improve the safe and reliable operation of battery electric vehicles, facilitate eco-transportation systems in smart cities and recommend appropriate points of interest [16]. There is, therefore, great interest in extending or at least predicting the remaining lifetime of batteries [17]. Recent studies on the ageing of lithium-ion batteries (LIBs) (e.g., persistent degradation during their lifetime) include data-based modelling techniques such as empirical models, equivalent circuit models, machine learning-based and deep learning modelling approaches [18]. Machine learning models provide predictive capabilities for the ageing of LIBs, while deep learning models use algorithms such as deep neural networks.
To adapt GIAs for time-series data in FL, sequence modelling approaches such as transformer-based models or recurrent neural networks are used to capture temporal dependencies in the reconstructed data. Transformers in particular have a great capability in learning time-series and can be scaled for distributed, collaborative or FL scenarios [19].
We address the case where an adversary—such as a compromised or untrusted server—has access to the model updates (i.e., gradient updates, ΔW) from a single client prior to aggregation. In this setting, the adversary may attempt to exploit the exposed updates to reconstruct the client’s original input signal. Importantly, the number of federated learning (FL) clients is not a limiting factor in this attack model, as the adversary operates before any averaging or aggregation occurs.
Motivation for the research. The aim of this work is to find out whether the time series data of the LIB ageing model can be recovered by gradient inversion in a transformer-based architecture in an FL environment and how differential privacy can prevent privacy leakage. The following aspects are considered:
- It is important to model the ageing of LIBs using degradation prediction through machine learning to enable better monitoring and predictive maintenance, which is critical for optimising electric vehicle performance and extending battery useful life.
- The security of existing transformer-based models is critical in the context of the FL framework. By identifying and quantifying privacy leaks using GIAs in the training scenarios, sensitive battery time-series data can be protected.
- Many FL systems incorporate differential privacy. Investigating whether these protections are effective for transformer-based models using privacy auditing is essential for improving the security of FL.
Contributions. The main innovation of this work can be summarised as follows:
- The transformer-based time-series model for LIB ageing is trained, indicating its applicability in the energy sector to evaluate battery longevity, safety and remaining useful life.
- Differential privacy with Gaussian mechanism and with different multiplicative noise factors is incorporated into the battery ageing model to evaluate the privacy-preserving behaviour of the model against privacy leakage.
- The privacy auditing is elaborated using a model inversion approach. The reconstruction of LIB data from transformer-based model gradients is considered applicable in the case of FL. The model to be trained is inverted to extract information.
The rest of this article is organised as follows: The following section introduces the relevant background of the theoretical foundations of time-series federated learning, gradient inversion and differential privacy, including their mathematical definitions and basic properties. Section 3 describes the methodology used to reconstruct battery time series data from transformer-based model gradient updates. Section 4 presents the experimental results obtained under the considered conditions. Section 5 discusses the experimental results and identifies future research.
2. Background
This section presents the brief theoretical foundations for federated time-series learning, gradient inversion attacks and differential privacy.
2.1. Time-Series Federated Learning
Federated learning (FL) [1,2,3,6] is a collaborative learning paradigm that allows multiple clients (data owners) to train machine learning models without sharing the raw data. Instead of centralising the training dataset , the data remains distributed among the clients, which train local models and exchange intermediate parameters with a central server. The global model is maintained on the central server, which coordinates the training process. At each iteration, the central server transmits the model parameters to a selected group of clients, which locally compute the gradients for their respective data samples. The server and the clients then perform a federated aggregation protocol [20] to compute the average gradients, which are used to update the global model using gradient descent.
A widely used optimisation algorithm in FL is federated averaging (FedAvg) [1,21,22], which extends the basic framework of FL by allowing clients to perform multiple local updates before communicating with the central server. The typical case where each client trains its model uniformly is that it trains the model for local steps over batches and updates its model parameters times before sending the update weights back to the central server. Since the reduction in communication overhead is crucial in FL, this approach can reduce communication rounds by a factor of 10 to 100 compared to traditional centralised training. This approach can lead to a reduction in the frequency of data transmission. Some studies report a 12.2-fold reduction in data transmission with comparable model performance [23]. In practical FL scenarios, FedAvg is preferred because clients can process multiple batches within a global round, which reconciles a trade-off between communication efficiency and convergence rate [24]. We define the model update difference as , which represents the change of model parameters during one round. The FL process consists of multiple global rounds. At the beginning of a global round, the server sends the latest global model to the clients. The clients then train the latest model with their own data and send their training results, i.e., gradients or model updates, back to the server. A global federated round with model updates is shown in Figure 1.
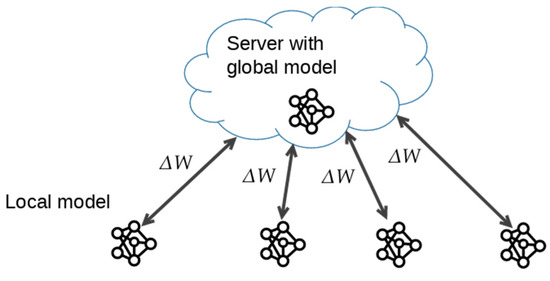
Figure 1.
A global federated learning round with model update.
The local training process usually follows the stochastic gradient descent algorithm, which iterates through the data in batches. A batch may contain the entire local dataset, but in the more general case, a batch is a subset of the local dataset and is also referred to as a mini-batch [25]. During an epoch, clients iterate over their entire training data once. A client can use its entire dataset in a single batch during one round, which then counts as one epoch. We focus on the more general mini-batch case, where the full dataset is split into several mini-batches and the client iterates over these mini-batches in multiple global rounds during an epoch.
Time-series federated learning: This approach combines the power of federated learning with specialised techniques for time-series analysis. Recent advances in the field of federated learning of time-series have focused on innovative data transformation techniques and modelling architectures to improve prediction accuracy while preserving data privacy. One way is to transform data by using language models for time-series analysis. Liu et al. [26] propose Time-FFM, which transforms time-series into text tokens, enabling the use of pre-trained language models for forecasting tasks. This approach enables the creation of a federated foundation model for time-series forecasting while addressing the problems of data scarcity and privacy. Abdel-Sater and Hamza [27] proposed FedTime, a federated large-scale language model tailored for long-range time series prediction that incorporates channel independence and patching to preserve the semantic information locally. Chen et al. [28] proposed Time-FFM, a federated foundation model that uses a prompt adaptation module to dynamically adapt the domain. In addition, hybrid models have been developed [29] that attempt to combine the strengths of neural networks with time-series and image data analysis.
2.2. Gradient Inversion Attacks
Despite the promise of privacy in FL, recent work has shown that the heuristic of sending gradient updates instead of training samples actually provides a false sense of security. In their seminal work, Zhu et al. [30] proposed the Deep Leakage from Gradients method and showed that it is possible for the server to recover the entire batch of training samples when the aggregated gradients are transmitted. Their attack matched the gradients of the reconstructed data and the original gradients leaked from federated learning.
Even if the clients and the server only exchange intermediate learning results, such as models or gradient updates, it has been shown that sensitive information can be derived from local training datasets in FL systems [31,32]. Furthermore, it has been shown that an attacker who gains possession of gradient updates can launch a gradient inversion attack to recover the training patterns used by the clients to generate the gradients [30]. In gradient inversion attacks, it is generally assumed that the attacker is an honest but curious server.
There are studies demonstrating gradient-based inversion attacks using vision transformers (ViTs) [18]. The authors found that vision transformers are significantly more vulnerable than previously studied CNNs due to the presence of the attention mechanism. Gradient inversion attacks in the time-series domain have also gained attention recently, as they are an important privacy concern in FL systems. These attacks aim to reconstruct sensitive data from shared gradient updates, which could compromise the privacy guarantees for federated learning [33]. Li et al. [34] proposed Temporal Gradient Attacks with Robust Optimisation—an optimisation-based reconstruction. This method leverages multiple temporal gradients to enhance reconstruction performance, even for large batch sizes and complex models.
Gradient inversion attacks (GradInvs) are the reconstruction process for solving an optimisation problem that aims to make dummy gradients similar to real gradients. In a GradInv, the attacker observes the gradients that the model has shared during training and attempts to recover the original data or labels. This is usually performed by minimising the distance between the ground truth gradients and the gradients generated by the guessed inputs [25,35,36]. The attacker primarily tries to minimise the distance between a randomly initialised sample gradient and the true gradient shared in FL [37]. This method is known as an iterative reconstruction process and basically solves a dual-optimisation objective [30,38]:
where is the true gradient and is the dummy gradient computed from randomly instantiated data . Attacks are typically considered successful if the correct values are found, i.e., meaning the attacker can recover at least one signal from the batch.
By combining iteration and optimisation approaches, GradInvs, based on iterative optimisation, attempt to reconstruct the private data during the training of a neural network [35]. This process consists of the following: in the forward pass, represents an input (possibly modified or the attacker’s input); denote the weights (W) and biases (b) of the layers of the neural network, from the first layer 1 to layer . are activation functions applied at each layer; are the activation outputs of each layer. The input is passed through the network layer by layer, undergoing a transformation of weights, biases and activation functions. The final layer produces an output , which is the target output or label.
The backward pass and gradient calculation: represents the gradient of the loss with respect to the activation at each layer. The direction of backpropagation is indicated by the flow of these gradients, which are computed and propagated backwards from the output layer to the input layer to update the parameters of the model during the optimisation process. For example, represents the gradient of with respect to a1. are the gradients of the loss with respect to the weights and biases of each layer. These gradients indicate how much each weight and biases contribute to the overall loss. represents the gradients of the loss with respect to the input . The gradients calculated in the backward pass (∇W′ and ) are used to update the weights and biases. This is represented by the “matching” process.
2.3. Protecting Time-Series Data with Differential Privacy
The astonishing success of gradient leakage research has triggered the start of an intense race between attackers [38,39,40,41,42] and defenders of privacy [43,44,45,46]. In response to the increase in privacy violating attacks in FL, many privacy preserving strategies have been proposed to mitigate the risk of information leakage from gradient perturbation, which has been proposed using differential privacy [47,48,49] by adding Gaussian noise to gradients [36] and gradient clipping, which limits the magnitude of gradients to reduce the risk of an inversion attack that exploits extreme gradient values [37] before they are shared to obfuscate sensitive information, they all offer little or no theoretical privacy guarantees. This is partly due to the fact that there is no mathematically rigorous attacker model, and the defences are empirically evaluated against known attacks [4]. This also leads to a variety of proposed defence techniques, such as gradient pruning, i.e., gradient compression by reducing gradient precession, which can make inversion harder while maintaining accuracy techniques [36].
Differential privacy: According to the definition, differential privacy (DP) is a formal mathematical framework designed to protect the privacy of individuals in a dataset while still allowing useful statistical analysis and machine learning.
—the randomisation algorithm (mechanism).
—two datasets that differ by one individual’s data.
—all possible sets of outputs.
—denotes the probability of the algorithm producing a specific result.
—the privacy budget. A smaller value means stronger privacy.
the failure probability error.
Differential privacy ensures that adding or removing a single individual’s data does not significantly change the outcome of a computation. This means an attacker cannot determine whether any specific individual’s data is present in the dataset. Another important issue is the trade-off between data utility and privacy guarantee in DP, which is represented by the privacy guarantee, denoted by the privacy budget and the failure probability error for -DP, also known as approximate DP. The privacy budget is obtained by adding noise to the data sampled from the Gaussian distribution or the Laplace distribution [50]. The description of the distribution being used is called the mechanism [51]. The Gaussian mechanism is central to DP, mainly due to its tighter composition when compared to the Laplace mechanism.
A Gaussian noise with mean and variance is added to the query results, where depends on the sensitivity and privacy parameters and . The sensitivity is the maximum change in query output when data is added/removed. This is a significant benefit, since the sensitivity can be much smaller than the sensitivity. The Gaussian mechanism has relatively thin tails, which results in a significantly improved composition. This is the greatest advantage of the Gaussian mechanism: when answering a large number of queries, it tends to require much less noise for the same level of privacy [50].
The noise added to achieve DP is calibrated based on the privacy budget when querying or releasing information from the dataset. Allocation strategies in DP aim to optimise the balance between data utility and privacy protection. For time-series data, we want to ensure that the release of the model outputs does not reveal sensitive information about individual time steps. Using the Gaussian mechanism for the allocation strategies requires specific approaches to handle temporal correlation and evolving sensitivity. The key strategies for allocation of privacy budgets in the context of time-series data are temporal sensitivity-driven allocation [52], uniform privacy budget allocation [53], non-uniform budgeting [54] and dynamic sensitivity [54]. In this paper, we use DP with the Gaussian mechanism to extend the testing against gradient inversion attacks.
3. Methodology
This section presents the methodology for reconstructing time-series data from FL model gradient updates.
3.1. Problem Definition and Our Approach
In our study, we extracted a separate matching dataset from a battery that was excluded from the training and validation sets. This subset was then used to calculate the FL gradients by combining discrete signal components. Other techniques could also be explored, such as training a separate DL model to reconstruct the input signal from the FL model updates or using an analytical approach. This could be further explored in future work. Figure 2 below shows the process of signal recovery from the DL model.
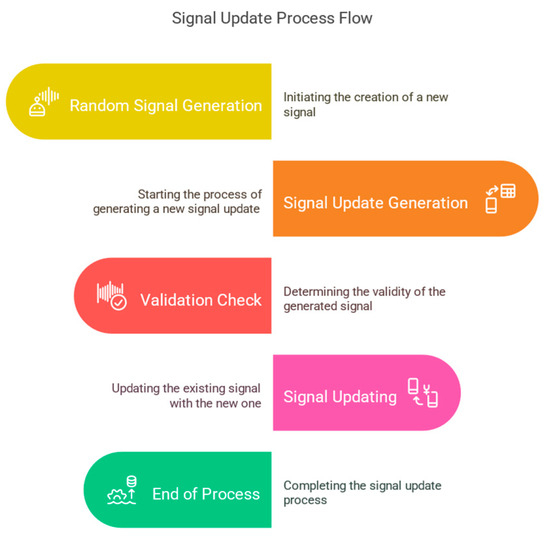
Figure 2.
Process of signal recovery from DL model updates.
We integrate the process described above into a federated learning (FL) framework, both with and without differential privacy (DP). To assess the privacy risks, we perform a model inversion auditing scheme [4], which evaluates how much information about individual data records can be inferred from the model’s outputs—e.g., confidence scores or gradients. In this way, the extent of privacy leakage in the system can be quantified. For privacy auditing, we employ a signal reconstruction algorithm. The corresponding pseudo-algorithm is listed in Algorithm 1.
| Algorithm 1. Signal reconstruction pseudo-algorithm explained |
|
The algorithm encapsulates the process and begins with the generation of a random signal, step 1. Then a loop begins, which is continued until the gradients are close enough to each other. This involves generating a signal update step 2 and checking whether the update is valid for step 3. If it is not valid, a new update is generated until a valid one is found. The signal is then updated with the valid update (4). A check is made to see whether the gradients are close enough to each other; if not, the process is repeated. As soon as the gradients are close enough to each other, the loop is exited and the reconstructed signal is returned. It is an iterative process consisting of different stages that lead back to previous stages depending on the conditions met. This solves the gradient matching problem and restores the unknown signal. In the signal update stage, the various techniques can be used to generate updates, including training a deep learning (DL) model that leads to reinforcement learning.
In our experiments, we used the following: (1) a simple technique of signal recovery with the generation of random signal updates to show that gradient inversion can also be solved, and (2) a discrete set of probing signals with parameter change. The second approach could solve gradient inversion in specific cases, where the probe set consisting of dedicated signals for gradient matching is representative.
3.2. Experimental Details
In our experiments, we investigated signal recovery from FL model updates with and without differential privacy. For our attacks, we used a deep neural network transformer model. This setup simulates a GIA threat, where a server-side adversary can observe raw model updates and attempt to reconstruct private input data. A recent study [55] has shown that transformers can be successfully used to process time-series signals. For example, for classifying time-series using positional encoding and attention over time [56] or combining trend/seasonality decomposition with attention using auto-correlation attention mechanism [57], or using patch-based encoding, inspired by the Vision Transformer on multivariate time-series forecasting benchmarks. Transformer-based methods are increasingly applied to time-series data due to their ability to capture long-range dependencies and interactions, which is particularly beneficial for tasks such as prediction, anomaly detection and classification.
As a data set, we used the data set on the ageing of lithium-ion batteries [58], which is described in more detail in the next subsection. All tasks are implemented using the Python 3.10.16 programming language and the PyTorch 2.5.1 machine learning library. Differential privacy is implemented using the OPACUS Privacy Engine Toolbox.
In our experiments, we first trained transformer-based battery RUL estimation models (with 6 transformer-encoder blocks) under different DP levels. The experiments were performed with a learning rate of 0.0001 and the Adam optimiser. This process generated gradients/model updates and simulated an FL use case. We then applied GradInv methods to recover the input signals responsible for the model updates. The results are presented in more detail in the next section.
The input signal is composed of the current I[n] and the voltage U[n], which are concatenated to form a tensor of the shape (B, 30, 128), where B represents the batch size. The output consists of the time-series of the discharge capacitance with a shape of (B, 1920). In addition, the outputs of the transformer layer can be connected to layers that are responsible for estimating the battery’s remaining useful life (RUL), such as linear classification layers (LC). The structure of the model used is shown in Figure 3.
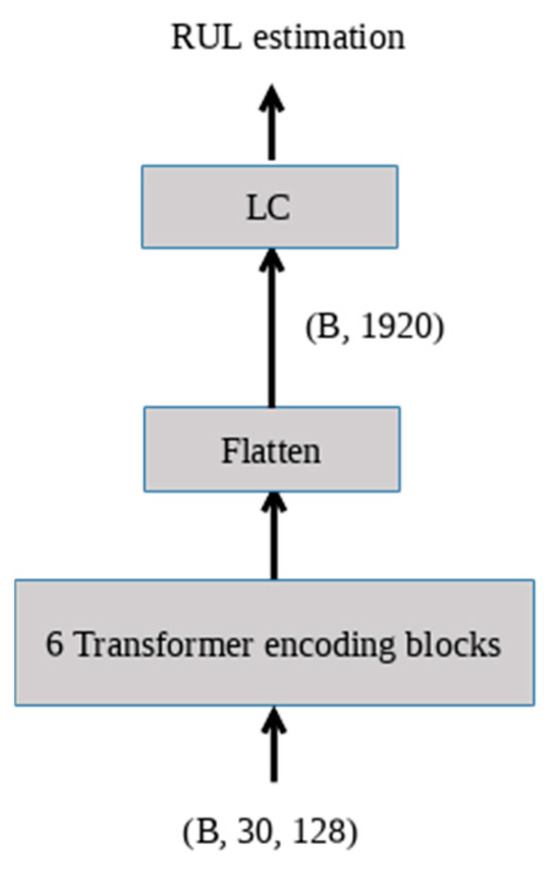
Figure 3.
Local FL transformer model for estimating battery discharge capacity and RUL.
When considering time series data, special aspects must be taken into account, such as temporal dependencies, possible periodicity and sensitivity to timing. In FL, for example, each client could have time series data from different time periods or from different sensors. The model updates would encapsulate patterns in these sequences.
3.3. Dataset
In our experiments, we evaluated the performance of attack and defence strategies on a time-series standard benchmark dataset for testing lithium-ion battery ageing based on electrical vehicle real-driving profiles [58]. Battery data is time-series, which has temporal dependencies and patterns. These batteries, the predominant energy storage system in electric vehicles, are subject to inevitable degradation during storage and use [59]. Diagnosis of battery ageing and remaining useful life (RUL), which enables robust development and fine-tuning of battery ageing models, is critical for ensuring operational safety, maintenance planning and modelling of diagnostic methods [60].
Key aspects of EV battery ageing dataset include real-world driving and diagnostic test data from 10 INR21700-M50T commercial lithium-ion battery cells (manufactured by Samsung SDI, Seoul, Republic of Korea) tested over a 23-month period using various constant current (CC) and constant voltage (CV) charging protocols at charge rates of C/4, C/2, 1C and 3C. The discharge ageing profiles mimic a typical electric vehicle driving pattern in the form of an Urban Dynamometer Schedule (UDDS), which brings the battery‘s state of charge (SOC) from 80% to 20%.
The ageing data set contains the following values of the INR21700 M50T batteries: charge and discharge curves; capacity retention over multiple cycles; voltage profiles during cycling; current rates used for charging and discharging; temperature data during cycling, etc. More information can be found in the paper Pozatto et al. [58].
We focus on the transformer DL architecture for time series tasks and give as input current I(t) and voltage U(t) and as output discharge capacitance ∆C for a defined time window W (discrete samples of all these parameters). The output of the DNN correlates with the state of depreciation of the battery and the remaining utilisation time, RUL. We want to protect this actual information.
In our experiments, the dataset is split into a training set and a validation set in a ratio of 70:30, which is a common practice for a balanced trade-off between learning and evaluation practice in transformer architectures with time-series data. In the case of signal recovery with discrete waveforms, a separate, independent matching/probing set is created from this dataset.
4. Experimental Results and Analysis
In this section, we present a description of the results obtained. We experimentally investigate the gradient inversion attack method without and with differential privacy to recover time-series data. In our experiments, the range of time-series data is the recovered domain. We evaluate gradient reconstruction on time-series data for battery ageing tasks, and we used two specific gradient inversion techniques: (1) signal recovery with randomised signal updates and (2) signal recovery with a discrete matching set.
4.1. Differential Privacy Impact on Deep Learning Training Process
We analysed the effects of the battery ageing model without and with different levels of data protection using differential privacy. The battery ageing model was trained to predict the gradients (i.e., the rate of change) of battery capacity based on the training data. Figure 4 shows the loss of mean squared error (MSE) over 20 epochs for three different training scenarios in a transformer-based model.
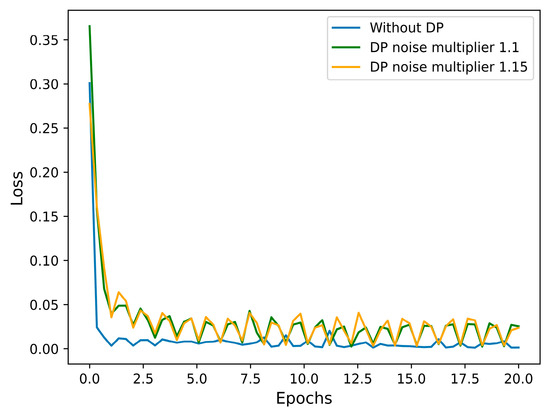
Figure 4.
MSE loses with respect to the epoch of the training without and with differential privacy.
In the first scenario (a), shown by the blue line, the model is evaluated without using the DP mechanism. The MSE loss decreases smoothly and reaches almost zero at the end of training, indicating a good performance of the model without privacy constraints. In the second scenario (b), we investigate the behaviour of the model using DP with the noise multiplier 1.1, represented by the green line. We chose the noise multiplier 1.1 that is noise with standard deviation 1.1 times the gradient clipping norm because it represents a moderate level of noise added to the gradients: high enough to provide privacy, but not so high that it destroys the learning signal. With the noise multiplier 1.1, we still protect individual training sequences (battery degradation profile) and allow our model to learn meaningful ageing dynamics. The loss rises from 0.01 to 0.05 MSE in the worst case, compared to the non-DP model, and the curve shows a more oscillating pattern and slower convergence. This is to be expected due to the noise that makes the gradients stochastic and unstable. In the third scenario (c), we increase the noise level in the model with a noise multiplier of 1.15, which is represented by the orange line. This leads to a higher variance of the noise added to the gradients and more gradient perturbations during training.
4.2. Signal Reconstruction with Gradient Inversion Attack Versus Deep Learning Level
The recovery of private data can be viewed as an iterative optimisation process utilising gradient descent.
Figure 5 shows an iterative optimisation, where each iteration k refines the estimate of the signal as a function of the error magnitude of the recovery iterations k, in a process called iterative randomised signal updating. (a) The blue curve shows the error magnitude when no noise is added to the signal and serves as a baseline. (b, c) The green and orange curves represent scenarios where noise is added at two different levels. In the first method, the MSE error reaches saturation at 0.05 × 10−5 without DP and saturation at 0.15 × 10−5 MSE with DP. In the second method, the saturation is 1 × 10−10 without DP and 0.1 × 10−8 with DP. In all cases, the error magnitude decreases rapidly during the first few recovery iterations. However, the final error magnitude is higher for the curves with DP noise (b, c) and increases with increasing noise level. The moderate noise level of 1.1 that we chose (b) leads to a slightly higher error after convergence. In contrast, the higher noise level 1.15 (c) leads to more distortion and thus a larger final error magnitude. In the absence of any noise (a), the recovery process perfectly matches the true values. It is summarised in Table 1.
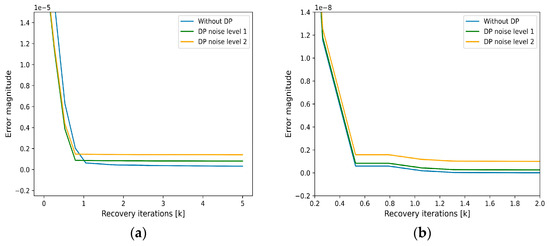
Figure 5.
Iterative randomised signal update. (a) Signal recovery with random signal updates, (b) signal recovery with a discrete probe set.

Table 1.
GIA saturation MSE values.
As can be seen in Figure 6, the original signal (a, blue line) and the recovered signal (b, green line) represent the output after some processing. Initially, the blue line matches the original signal, but there is a sudden deviation around time step 60, followed by a gradual recovery. As time progresses, however, the green line deviates from the original signal. The recovery signal follows the recovery signal very closely at the beginning, which shows that the recovery technique works well for early time steps. Beyond time step 60, the recovered signal continues to grow but does not exactly match the original signal. The recovery process is partially successful, but cannot maintain accuracy across all time steps, especially after a sudden drop (e.g., time step = 60). The significant deviations around time step 60 indicate either noise, a loss of information or an error in the recovery at this point.
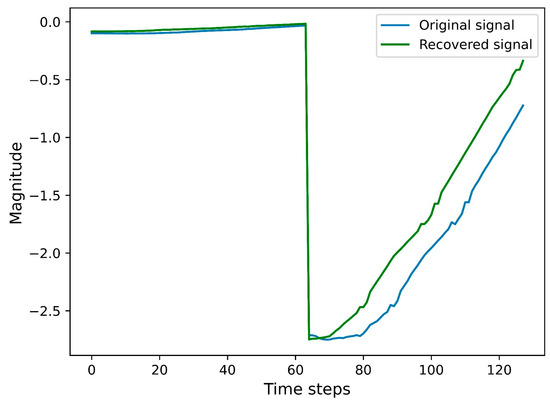
Figure 6.
Comparison between the original signal and the recovered signal over a sequence of time steps without DP. Input volts/t IU.
5. Discussion and Future Research
This paper presents a field data-based framework for battery health management in FL scenarios, which not only provides an important basis for on-board battery health monitoring and prediction, but also paves the way for second-life assessment of batteries. It explores the privacy concerns of battery health management based on AI modelling.
The FL approach enables the development of a common AI model while preserving the privacy of user data. However, gradient inversion attacks can potentially reconstruct user data from deep learning model updates, which raises privacy concerns. As shown in this paper, additional protection by differential privacy DP leads to saturation in gradient inversion attacks, i.e., the reconstructed signal maintains a certain error level depending on the applied DP protection levels.
Future research could investigate more advanced GIA methods, such as training attack networks with reinforcement learning or using the foundation models for gradient inversion attacks. Furthermore, the attention mechanisms in transformers could be investigated as they are self-explanatory.
Author Contributions
Conceptualization, K.S.; methodology, K.S. and I.N.; formal analysis, K.S.; investigation, K.S. and I.N.; resources, I.N.; writing—original draft preparation, I.N.; writing—review and editing, K.S., A.N. and K.O.; project administration, K.O.; funding acquisition, K.O. All authors have read and agreed to the published version of the manuscript.
Funding
This work is the result of activities within the “Digitalization of Power Electronic Applications within Key Technology Value Chains” (PowerizeD) project, which has received funding from the Chips Joint Undertaking under grant agreement No. 101096387. The Chips-JU is supported by the European Union’s Horizon Europe Research and Innovation Programme, as well as by Austria, Belgium, the Czech Republic, Finland, Germany, Greece, Hungary, Italy, Latvia, the Netherlands, Spain, Sweden, and Romania.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- McMahan, H.B.; Moore, E.; Ramage, D.; Agüera y Arcas, B.A. Communication-Efficient Learning of Deep Networks from Decentralized Data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics (AISTATS), Ft. Lauderdale, FL, USA, 20–22 April 2017; Volume 54, pp. 1273–1282. [Google Scholar]
- Cheng, X.; Li, C.; Liu, X. A Review of Federated Learning in Energy Systems. In Proceedings of the 2022 IEEE/AIS Industrial and Commercial Power System Asia (ICPS Asia), Shanghai, China, 8–11 July 2022; IEEE/IAS: Shanghai, China, 2022; pp. 2089–2095. [Google Scholar]
- Grataloup, A.; Jonas, S.; Meyer, A. A Review of Federated Learning in Renewable Energy Applications: Potential, challenges, and Future Directions. Energy AI 2024, 17, 100375. [Google Scholar] [CrossRef]
- Namatevs, I.; Sudars, K.; Nikulins, A.; Ozols, K. Privacy Auditing in Differential Private Machine Learning: The Current Trends. Appl. Sci. 2025, 15, 647. [Google Scholar] [CrossRef]
- Li, M.; Andersen, D.G.; Park, J.W.; Smola, A.J.; Ahmed, A.; Josifovski, V.; Long, J.; Shekita, E.J.; Su, B.-Y. Scaling Distributed Machine Learning with the Parameter Server. In Proceedings of the 11th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 14), Broomfield, CO, USA, 6–8 October 2014; pp. 583–598. [Google Scholar]
- Alsharif, M.H.; Kannadasan, R.; Wei, W.; Nisar, K.S.; Abdel-Aty, A.-H. A Contemporary Survey of Recent in Federated Leaning: Taxonomies, Applications, and Challenges. Internet Things 2024, 27, 101251. [Google Scholar] [CrossRef]
- Bonawitz, K.; Ivanov, V.; Kreuter, B.; Marcedone, A.; McMahan, H.B.; Patel, S.; Ramage, D.; Segal, A.; Seth, K. Practical Secure Aggregation for Federated Learning on User-Held Data. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communication Security (CCS’17), Dallas, TX, USA, 30 October–3 November 2017; pp. 1175–1191. [Google Scholar] [CrossRef]
- Qi, P.; Chiaro, D.; Guzzo, A.; Ianni, M.; Fortino, G.; Piccalli, F. Model Aggregation Techniques in Federated Learning: A Comprehensive Survey. Future Gener. Comput. Syst. 2024, 150, 272–293. [Google Scholar] [CrossRef]
- Shaffe, A.; Awaad, T.A. Privacy Attacks Against Deep Learning Models and Their Countermeasures. J. Syst. Archit. 2021, 114, 101940. [Google Scholar] [CrossRef]
- Tao, Z. Hierarchical Federated Learning with Gaussian Differential Privacy. In AISS’22: Proceedings of the 4th International Conference on Advanced Information Science and System; ACM International Conference Proceeding Series; ACM: New York, NY, USA, 2022; p. 186695. [Google Scholar]
- Rigaki, M.; Garcia, S. Stealing and Evading Malware Classifiers and Antivirus at Low False Positive Conditions. Comput. Secur. 2023, 129, 103192. [Google Scholar] [CrossRef]
- Sotthiwat, E.; Zhen, L.; Zhang, C.; Li, Z.; Goh, R.S.M. Generative Image Reconstruction Gradients. IEEE Trans. Neural Netw. Learn. Syst. 2025, 1, 21–31. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Ma, Z.; Wang, Z.; Chegne, E.J.; Ma, M.; Abuadbba, A.; Bai, G. Uncovering Gradient Inversion Risks in Practical Language Model Training. In Proceedings of the CCS’24—2024 ACM SIGSAC Conference on Computers and Communication Security, Salt Lake City, UT, USA, 14–18 October 2024; ACM: New York, NY, USA, 2024; pp. 3525–3539. [Google Scholar]
- Chen, S.; Yuan, J.; Wang, Z.; Sun, Y. Local Perturbation-based Black-box Federated Learning Attack for Time Series Classification. Future Gener. Comput. Syst. 2024, 158, 488–500. [Google Scholar] [CrossRef]
- Wu, T.; Wang, X.; Qiao, S.; Xian, X.; Liu, Y.; Zhang, L. Small Perturbations are Enough: Adversarial attacks on Time Series Prediction. Inf. Sci. 2022, 587, 794–812. [Google Scholar] [CrossRef]
- Dinev, A. Evaluation of Advances in Battery Health Prediction for Electric Vehicles from Traditional Linear Filters to Least Machine Learning Approaches. Batteries 2024, 10, 356. [Google Scholar] [CrossRef]
- Kröger, T.; Belnarsch, A.; Bilfinger, P.; Ratzke, W. Collaborative Training of Deep Neural Networks for the Lithium-ion Battery Aging Prediction with Federated Learning. eTransportation 2023, 18, 100294. [Google Scholar] [CrossRef]
- Ali, M.A.; Da Silva, C.M.; Amon, C.H. Multiscale Modelling Methodologies of Lithium-Ion Battery Aging: A Review of Most Recent Developments. Batteries 2023, 9, 434. [Google Scholar] [CrossRef]
- Hatamizadeh, A.; Yin, H.; Roth, H.; Li, W.; Kautz, J.; Xu, D.; Molchanov, P. GradViT: Gradient Inversion of Vision Transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Oreleans, LA, USA, 19–24 June 2022; pp. 10021–10030. [Google Scholar] [CrossRef]
- Moshawrab, M.; Adda, M.; Bouzouane, A.; Ibrahim, H.; Raad, A. Reviewing Federated Learning Aggregation Algorithms; Strategies, Contributions, Limitations and Future Perspectives. Electronics 2023, 12, 2287. [Google Scholar] [CrossRef]
- Overman, T.; Klabjan, D. Continuous-Time Analysis in Federated Averaging. arXiv 2025, arXiv:2501.18870. [Google Scholar]
- Liu, W.; Zhang, X.; Duan, J.; Joe-Wong, C.; Zhou, Z.; Chen, X. Federated Learning at the Edge: An Interplay of Mini-Batch Size and Aggregation Frequency. In Proceedings of the IEEE INFOCOM–2023 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Hoboken, NJ, USA, 17–20 May 2023. [Google Scholar] [CrossRef]
- Khalilian Gourtani, S.; Tsouvalas, V.; Ozcelebi, T.; Meratania, N. FedCode: Communication-Efficient Federated Learning via Transferring Codebook. In Proceedings of the 2024 IEEE International Conference on Edge Computing and Communication (IEEE EDGE 2024), San Francisco, CA, USA, 7–13 July 2024; pp. 99–109. [Google Scholar] [CrossRef]
- Li, X.; Huang, K.; Yang, W.; Wang, S.; Zhang, Z. On the Convergence of FedAvg on Non-IID Data. In Proceedings of the 8th International Conference on Learning Representations (ICLR 2020), OpenReview.net, Virtual Event, 26–30 April 2020. [Google Scholar]
- Xu, J.; Hong, C.; Huang, J.; Chen, L.Y.; Decouchant, J. AGIC: Approximate Gradient Inversion Attack on Federated Learning. In Proceedings of the 41st International Symposium on Reliable Distributed Systems (SRDS 2022), Vienna, Austria, 19–22 September 2022; Ceballos, C., Torres, H., Eds.; IEEE: Vienna, Austria, 2022; pp. 12–22. [Google Scholar]
- Liu, Q.; Liu, X.; Liu, C.; Wen, Q.; Liang, Y. TIME-FFM: Towards LM-Empowered Federated Foundation Model for Time Series Forecasting. In Advances in Neural Information Processing Systems 37 (NeurIPS 2024); Curran Associates, Inc.: Red Hook, NY, USA, 2024. [Google Scholar]
- Abdel-Sater, R.; Hamza, A.B. A Federated Large Language Model for Long-Term Time Series Forecasting. In Proceedings of the 27th European Conference on Artificial Intelligence (ECAI 2024), Santiago de Compostela, Spain, 19–24 October 2024; IOS Press: Amsterdam, The Neatherlands, 2024; Volume 392, pp. 2452–2459. [Google Scholar]
- Chen, S.; Long, G.; Jiang, J.; Zhang, C. Federated Foundation Models on Heterogeneous Time Series. arXiv 2024, arXiv:2412.08906. [Google Scholar] [CrossRef]
- Yu, C.; Shen, S.; Wang, S.; Zhang, K.; Zhao, H. Communication-Efficient Hybrid Federated Learning for E-health with Horizontal and Vertical Data Partitioning. arXiv 2024, arXiv:2404.10110. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Liu, Z.; Han, S. Deep Leakage from Gradients. In Advances in Neural Information Processing Systems, 32 (NeurIPS 2019); Curran Associates, Inc.: Sydney, NSW, Australia, 2019; pp. 14774–14784. [Google Scholar]
- Melis, L.; Song, C.; De Cristofaro, E.; Shmatikov, V. Exploiting Unintended Feature Leakage in Collaborative Learning. In Proceedings of the 2019 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 19–23 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 691–706. [Google Scholar]
- Wang, Z.; Song, M.; Zhang, Z.; Song, Y.; Wang, Q.; Qi, H. Beyond Inferring Class Representatives: User-level Privacy Leakage from Federated Learning. In Proceedings of the IEEE INFOCOM 2019-IEEE Conference on Computer Communications, Paris, France, 29 April–2 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2512–2520. [Google Scholar]
- Zheng, L.; Cao, Y.; Jiang, R.; Taura, K.; Shen, Y.; Li, S.; Yoshikawa, M. Enhancing Privacy of Spatiotemporal Federated Learning against Gradient Inversion Attacks. In Proceedings of the 2023 ACM Web Conference (WWW 2023), Austin, TX, USA, 30 April–4 May 2023; Associtaion for Computing Machinery: New York, NY, USA, 2023; pp. 3804–3814. [Google Scholar]
- Li, B.; Gu, H.; Chen, R.; Li, J.; Wu, C.; Ruan, N.; Si, X.; Fan, L. Temporal Gradient Inversion Attacks with Robust Optimization. arXiv 2023, arXiv:2306.07883. [Google Scholar] [CrossRef]
- Zhang, R.; Gou, S.; Wang, J.; Xie, X.; Tao, D. A Survey on Gradient Inversion Attacks, Defense and Future Directions. In Proceedings of the 31st Joint Conference on Artificial Intelligence (IJCAI-22), Messe Wien, Vienna, 23–29 July 2022; Available online: https://www.ijcai.org/proceedings/2022/0791.pdf (accessed on 7 February 2025).
- Wu, R.; Chen, X.; Guo, C.; Weinberger, K.Q. Learning to Invert: Simple Adaptive Attacks for Gradient Inversion in Federated Learning. In Proceedings of the 39th Conference on Uncertainty in Artificial Intelligence (UAI 2023), PMLR, Pittsburgh, PA, USA, 31 July–4 August 2023; Volume 216, pp. 2293–2303. [Google Scholar]
- Huang, Y.; Gupta, S.; Song, Z.; Li, K.; Arora, S. Evaluating Gradient Inversion Attacks and Defenses in Federated Learning. In Advances in Neural Information Processing Systems 34 (NeurIPS 2021); Ranzato, M.A., Beygelzimer, A., Dauphin, Y., Liang, P.S., Wortman Vaughan, J., Eds.; Currant Associates, Inc.: Red Hook, NY, USA, 2021; pp. 7232–7241. [Google Scholar]
- Zhao, B.; Mopuri, K.R.; Bilen, H. idlg: Improved Deep Leakage from Gradients. arXiv 2020, arXiv:2001.02610. [Google Scholar]
- Geiping, J.; Bauermeister, H.; Dröge, H.; Moeller, M. Inverting Gradients–How easy is it to break privacy in federated learning? In Proceedings of the Advances in Neural Information Processing Systems; Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS), Virtual, 6–12 December 2020; Currant Associates, Inc.: Red Hook, NY, USA, 2020; Volume 33, pp. 16937–16947. [Google Scholar]
- Jeon, J.; Kim, J.; Lee, K.; Oh, S.; Ok, J. Gradient Inversion with Generative Image Prior. In Advances in Neural Information Processing Systems 34 (NeurIPS 2021); Ranzato, M.A., Beygelzimer, A., Dauphin, Y., Liang, P.S., Wortman Vaughan, J., Eds.; Currant Associates, Inc.: Red Hook, NY, USA, 2021; pp. 29898–29908. [Google Scholar]
- Fowl, L.; Geiping, J.; Czaja, W.; Goldblum, M.; Goldstein, T. Robbing the End: Directly Obtaining Private Data in Federated Learning with Modified Models. In Proceedings of the 10th International Conference on Learning Representations (ICLR 2022), OpenReview.net, Virtual Event, 25–29 April 2022. [Google Scholar]
- Zhang, X.; Li, M.; Chang, X.; Chen, J.; Roy-Chowdhury, A.K.; Suresh, A.T.; Oymak, S. FedYolo: Augmenting Federated Learning with Pretrained Transformers. arXiv 2023, arXiv:2307.04905. [Google Scholar]
- Sun, G.; Mendieta, M.; Dutta, A.; Li, X.; Chen, C. Towards Multi-modal Transformers in Federated Learning. arXiv 2024, arXiv:2404.12467. [Google Scholar]
- Wei, W.; Liu, L. Gradient Leakage Attack Resilient Deep Learning. IEEE Trans. Inf. Forensic Secur. 2022, 17, 303–316. [Google Scholar] [CrossRef]
- Gao, Y.; Xie, Y.; Deng, H.; Zhu, Z. Gradient Inversion Attack in Federated Learning: Exposing Text Data through Discrete Optimization. In Proceedings of the 31st International Conference on Computation Linguistics (COLING 2025), Abu Dhabi, UAE, 19–24 January 2025; pp. 2582–2591. [Google Scholar]
- Scheliga, D.; Mäder, P.; Seeland, M. PRECODE–A Generic Model Extension to Prevent Deep Gradient Leakage. In Proceedings of the 2022 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2022; pp. 3887–3896. [Google Scholar] [CrossRef]
- Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H.B.; Mironov, I.; Talwar, K.; Zhang, L. Deep Learning with Differential Privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security (CCS), Vienna, Austria, 24–28 October 2016; pp. 308–318. [Google Scholar] [CrossRef]
- Dwork, C.; McSherry, F.; Nissim, K.; Smith, A. Calibrating Noise to Sensitivity in Private Data Analysis. In Theory of Cryptography; Halevi, S., Rabin, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 265–284. [Google Scholar]
- Dwork, C.; Roth, A. The Algorithmic Foundations Of Differential Privacy. In Found. Trends Theor. Comput. Sci. 2014, 9, 211–407. Available online: https://www.nowpublishers.com/article/Details/TCS-042 (accessed on 8 March 2025). [CrossRef]
- Cowan, E.; Shoemate, M.; Pereira, M. Hands-On Differential Privacy; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2024; ISBN 9781492097747. [Google Scholar]
- Balle, B.; Wang, Y.-X. Improving the Gaussian Mechanism for Differential Privacy: Analytical Calibration and Optimal Denoising. In Proceedings of the 35th International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018; pp. 394–403. Available online: https://proceedings.mlr.press/v80/balle18a/balle18a.pdf (accessed on 14 May 2025).
- Li, X.; Qin, B.; Luo, Y.; Zheng, D. Differential Privacy Budget Allocation Algorithm Base on Out-of-Bag Estimation in Random Forest. Mathematics 2022, 10, 4338. [Google Scholar] [CrossRef]
- He, G.; Plagemann, T.; Benndorf, M.; Goebel, V.; Koldehofe, B. Differential Privacy for Protecting Private Patterens in Data Streams. In Proceedings of the 2023 39th International Conference on Data Engineering Workshop (ICDEW), Anaheim, CA, USA, 3–7 April 2023. [Google Scholar] [CrossRef]
- Bai, Y.; Yang, G.; Xiang, Y.; Wang, X. Generalized and Multiple-Queries-Oriented Privacy Budget Strategies in Differential Privacy via Convergent Series. In Security and Communication Networks; Wiley: Hoboken, NJ, USA, 2021; p. 5564176. [Google Scholar] [CrossRef]
- Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; Sun, L. Transformers in Time Series: A Survey. In Proceedings of the 32nd International Conference on Artificial Intelligence (IJCAI-23), Macao, China, 19–25 August 2023. [Google Scholar]
- Zerveas, G.; Jayaraman, S.; Patel, D.; Bhamidipaty, A.; Eickhoff, C. A Transformer-based Framework for Multivariate Time Series Representation Learning. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD 2021), Virtual Event, 14–18 August 2021; Association for Computing Machinery: New York, NY, USA, 2021; pp. 2114–2124. [Google Scholar]
- Wang, Y.; Zhu, J.; Kang, R. DESTformer: A Transformer Based on Explicit Seasonal-Trends Decomposition for Long-Term Series Forecasting. Appl. Sci. 2023, 13, 10505. [Google Scholar] [CrossRef]
- Pozatto, G.; Allam, A.; Onori, S. Lithium-ion Battery Aging Dataset Based on Electric Vehicle Real Driving Profiles. Data Brief. 2022, 41, 107995. [Google Scholar] [CrossRef]
- Liu, D.; Shadike, Z.; Lin, R.; Qian, K.; Li, H.; Li, K.; Wang, S.; Yu, Q.; Liu, M.; Ganapathy, S.; et al. Review of Recent Development of in Situ/Operando Characterization Techniques for Lithium Battery Research. Adv. Mater. 2019, 31, 1806620. [Google Scholar] [CrossRef]
- Harris, S.J.; Noack, M.M. Statistical and Machine Learning-based Durability-Testing Strategies for Energy Storage. Joule 2023, 7, 920–934. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).