Abstract
Football is a complex game that requires combined technical, tactical, and psychological skills. The effect of training methods on players is crucial to improve their performance significantly. Different training methods can improve certain performance; however, the effect of combined training methodologies has not been sufficiently investigated. This study aimed to investigate the differential effects of small-sided games (SSGs), strength training (ST), and a combined training model (CTM) on the physical performance of soccer players. In this study, we analyzed 60 players in three groups. Two groups were trained independently with two single-training methods, small-sided games and a strength training model, and one group was trained independently with a double-training method, a combination of single-training methods. Before each training session, each group was given theoretical education specific to the training program they would perform. Eighteen physical measurements of the players were obtained using sensitive devices before and after they were completed. Four tree-based machine learning models, decision tree, random forest, gradient boosting, and extreme gradient boosting, were applied to solve the complex pattern of training strategies using the measurements. Extensive and comparative experiments were conducted to distinguish the groups of players. The distinction between the initial and final measurements was analyzed separately, and the extreme gradient boosting model achieved 0.73–0.80 and 1.00 accuracy for initial and final tests by outperforming other models. A superior model, XGBoost, was used to analyze the effective decisive factors that improved after the training sessions. The results showed that players in the double-training group demonstrated significantly greater improvements in skill performance compared to both single-training groups. In contrast, the skill gains observed in the single-training groups were modest and partially overlapping, indicating limited differentiation between them. These results suggest that integrated training programs may offer more comprehensive benefits and can inform evidence-based decision-making for coaches seeking to optimize physical development in soccer players.
1. Introduction
Football is a sport with a complex structure, where technical, tactical, psychological, physiological, and physical attributes are integrated [1]. Although aerobic endurance mainly comes to the fore among the physiological requirements of football, many high-intensity movements that require anaerobic endurance are also performed during the game [2,3]. To determine the severity and intensity of football training effectively, it is essential to understand the physical and physiological limits of football players [4]. There are various training methods to convey the complex nature of football to athletes through structured training programs [5,6]. Small-sided game (SSG) training, among these methods, has been widely utilized as an alternative to traditional interval, aerobic, and anaerobic training due to its ability to meet physiological and motoric requirements. However, much of the existing research on SSGs does not clearly link their benefits to specific performance metrics such as speed, agility, and power, which are essential for football performance. Mancini et al. [7] emphasized the importance of perception–action coupling and rapid decision-making under pressure in team sports. The integration of SSGs and strength training aligns with this cognitive–motor framework, as SSGs promote contextualized movement and decision-making while strength training improves neuromuscular readiness.
While SSG training provides a close simulation of the movement patterns and physiological demands unique to football, it also enables athletes to perform their skills under pressure and fatigue [8,9]. In addition to aerobic and anaerobic endurance, its specific effects on key physical attributes like speed, agility, and power are not well understood. Additionally, strength plays a crucial role in football performance [10]. Football players’ ability to perform various dynamic movements during matches is directly related to their strength levels [11]. Improving the physical parameters inherent in football (such as conditioning, strength, and speed) allows players to sustain repetitive short-term high-intensity movements, accelerate recovery, and maintain optimal physical performance throughout a game. Research has indicated that performance in short-term high-intensity movements (such as jumping, 10 m sprint, and 30 m sprint) in football players is associated with maximum muscle strength and explosive power [12].
Recent studies have explored the impact of combined training methods, particularly integrating strength training with small-sided games. Such approaches involve monitoring load intensity with a specific number of players in controlled field dimensions to enhance technical, tactical, and physical development [13]. Studies comparing complex training methods to other training models have demonstrated that motor performance significantly improves when weight training and plyometric exercises are incorporated [14,15,16].
However, analyzing sports performance is inherently complex, requiring advanced tools for a rapid and robust understanding of players’ performance and the factors influencing them. Artificial intelligence (AI) tools, particularly machine learning (ML), have gained significant attention in sports science due to their ability to establish nonlinear relationships between multiple performance variables. Consequently, ML techniques have been frequently employed in various domains, including player injury prevention [17] and performance prediction [18].
Recent research has leveraged machine learning algorithms to analyze football players’ performance, optimize training strategies, and enhance tactical planning. Unlike traditional statistical approaches limited to mean group comparisons, machine learning models offer individual-level predictions and reveal complex, nonlinear relationships among performance variables. This provides a more comprehensive understanding of the effects of training. Morciano et al. [19] utilized football players’ movement and physiological data to predict their performance during training. The data, extracted through wearable sensors, were analyzed using multivariate regression models, achieving over 90% prediction accuracy. Similarly, Manish et al. [18] conducted a comparative study to forecast player performance across different positions using multiple regression, neural networks, extreme gradient boosting (XGBoost), and support vector machines. Their results demonstrated that multiple regression achieved the highest accuracy, with R2 scores ranging between 0.86 and 0.93. Additionally, Wisdom and Javed [20] examined the application of ML models in football performance quantification and strategic planning. By analyzing data from Europe’s top five leagues in the 2018 season, they implemented logistic regression, random forest, and XGBoost algorithms. Their study found that the XGBoost model outperformed other methods with an AUC score of 0.8, significantly enhancing the understanding of performance metrics, real-time strategies, and player contributions to team success.
Although these studies have contributed significantly to football analytics, the effectiveness of different training methodologies remains an understudied area that requires further investigation [13]. In addition, the inclusion of theoretical training before the application, which is absent in other football applied studies, was considered crucial to increase the efficiency of the studies. We also ensured compatibility with the ecological environment, a key aspect in football education, by mirroring the real-world scenario where coaches explain objectives before matches and training practices. In this paper, we analyzed the effects of three distinct training types on football players using machine learning algorithms. Our goal was to determine the distinguishing effects of these training methods and identify key performance indicators influenced by training variations. To achieve this, we collected pre- and post-training measurements from players and employed four machine-learning algorithms to evaluate the impact of each training method. Additionally, this study aimed to investigate how machine learning could be used to analyze and predict the physical parameters of football players, thereby providing deeper insights into training efficiency and player development, which would be one of the first studies investigating the distinction between single- and combined training procedures using machine learning. Furthermore, we analyzed the distinguishing factors between the training methods upon completion. Finally, we supported our findings with statistical analyses to validate the results.
In summary, our study aimed to
(1) Compare the effectiveness of single- and double-training procedures on the physical performance of football players;
(2) Evaluate the predictive value of machine learning models in distinguishing training procedures; and
(3) Investigate the factors that influence the players before and after training procedures.
2. Materials and Methods
2.1. Participants and Study Design
A total of three groups of football players were included in the study. Group 1 (STM 1) consisted of 19 football players with an average age of 27.84 ± 5.65, and only small-sided games were added to their existing training programs. Group 2 (DTM) included 20 football players with an average age of 25.80 ± 4.10, who participated in a combined training model consisting of small-sided games and strength training, in addition to their existing training programs. Group 3 (STM 2) comprised 21 football players with an average age of 20.90 ± 1.58, and only strength training was applied in addition to their regular training programs.
The study was conducted with 60 participants from three teams out of 16 teams in the TRNC Super League. The training models were applied twice a week for eight weeks. All training sessions were conducted on the football field. Prior to each session, participants were given theoretical training, which included lessons on how the practice would physically affect them.
Pre-test assessments were performed one week before the training period, and post-test assessments were conducted one week after the completion of the training. The assessments included standard field and laboratory tests to evaluate strength, body composition, and performance parameters.
This study was conducted in compliance with the principles of the Declaration of Helsinki, and approval was granted by the Ethics Committee of Near East University (Date: 25 November 2021/No: YDU/2021/97-1381).
2.2. Training Programs
2.2.1. Small-Sided Games (SSGs)
A training field based on a small area was implemented with a field size of 30 × 40 m, with two groups and a total of 5 football players (5 vs. 5) in each group. In order to limit the determined field dimensions, training covers were determined within the field, and standard miniature goals specific to football were placed within the field. Extra balls were added to the sides of the field and behind the goals as part of the measures taken to prevent loss of time and not to interrupt the training. Small field training was conducted using the intensive interval method, and the loading intensity was between 80% and 90%. The intensities were determined by taking the maximum heart rate using a Polar-brand heart rate meter watch to determine the load intensity of the participants. After a 20 min warm-up period, the athletes performed three sets of 5 × 5 small field competitions on a 30 × 40 m field. A 2–3 min rest break was given between each set. At the end of the training, the training ended after a 10 min cool-down period. The total training duration lasted 60 min.
2.2.2. Strength Training
The strength training program was conducted twice per week over an 8-week period, totaling 16 sessions. Each session lasted 60 min, beginning with a 10 min warm-up, followed by 40 min of high-intensity interval training (HIIT).
During the main phase, football players completed 8 exercise series per session, with each series lasting 4 min. Each series included eight repetitions of 20 s of exercise followed by 10 s of rest, performed at high intensity. A 1 min passive rest was provided between each series.
The exercises were structured to target different muscle groups in the following sequence:
- Series 1—lower extremities (jump squats),
- Series 2—back muscles (back extensions),
- Series 3—rectus abdominis (crunches),
- Series 4—chest muscles (push-ups),
- Series 5—arm muscles (triceps dips),
- Series 6—oblique abdominal muscles (side crunches),
- Series 7—shoulder girdle muscles (medicine ball military press),
- Series 8—trapezius muscles (chin-ups).
Each session concluded with a 10 min cool-down phase.
2.2.3. Combined Training
In the combined training model, the football players applied HIIT strength training after a 10 min warm-up in each unit of training. After the 20 min strength training, three sets of 5 × 5 small-sided games were played on a 30 × 40 area, and the training was concluded with 10 min cool-down exercises.
Figure 1 summarizes the groups that participated and the experiments in detail, while Table 1 presents the details of group composition, key training elements, and weekly training volume of each training model.
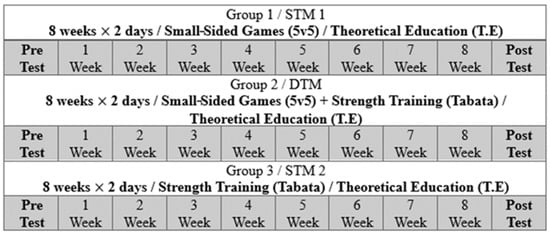
Figure 1.
The details of participants and study design.

Table 1.
Summary of group composition, key training elements, and weekly training volume for each training model.
2.3. Measures and Theoretical Education
2.3.1. Body Mass Index (BMI) Measurement Procedure
In this study, the Body Mass Index (BMI) was calculated to assess the body composition of football players. BMI was determined by dividing the body weight (kg) by the square of height (m2) (BMI = kg/m2).
Measurements were conducted following standard procedures. Height was measured using a high-precision stadiometer (Seca 769, Hamburg, Germany) with an accuracy of 0.1 cm. Body weight and body composition measurements were taken using the Tanita body composition analyzer (Tanita TBF 300 M, Tokyo, Japan) with an accuracy of 0.1 kg. All measurements were performed under controlled conditions: in the morning, on an empty stomach, and while wearing minimal clothing. Data were collected at two different time points: one week prior to the training program (pre-test) and one week after the completion of the eight-week training period (post-test), to evaluate the effectiveness of the training programs.
2.3.2. Sit-And-Reach Test
The sit-and-reach test was applied to determine flexibility. The test bench was 35 cm long, 45 cm wide, and 32 cm high. The sit-and-reach test was used to measure the flexibility of the hamstring and back muscles. The subjects held their feet on the sit-and-reach bench as far as they could without bending their knees, and the distance they could reach was recorded in centimeters. The test was repeated twice, and the best result was accepted as the flexibility value [20].
2.3.3. Takei Vertical Jump Meter (TVJM)
The TVJM (T.K.K. 5406 Jump MD, Takei Scientific Instruments Co., Ltd., Niigata, Japan) is a linear position transducer with a wire-type linear encoder. Chow et al. [21] first used this device for CMJ assessment and reported high reliability (r = 0.90). In this study, participants stood on a Takei rubber mat (approximately 380 mm in diameter and 3 mm thick, weighing 0.4 kg) with a belt around their waist. Two different vertical jump methods were used: hands on waist and hands free. The belt weighed only 0.2 kg and was connected to the mat by a measuring cable that represented the initial distance between the waist and the floor. The cable was extended during a jump. The height of each jump was displayed on the LCD screen on the belt. The smallest unit of measurement was 1 cm, and the error was up to ±2 cm.
2.3.4. Flamingo Balance Test
Testing Procedure
This test required a beam (5 cm in height, 4 cm in width, and 50 cm in length), two supports (2 cm wide and 15 cm long), and a stopwatch. Participants were first given a demonstration of the test procedure. They were then instructed to balance on their preferred foot along the longitudinal axis of the beam for as long as possible. While doing so, they had to bend the opposite leg and hold the back of the foot with the hand on the same side, mimicking a “flamingo” stance. The free foot could be positioned for balance support if necessary. If the participant lost balance, they could briefly receive assistance from the tester to regain their position. The test began once the participant maintained the correct position independently, at which point the tester started the stopwatch. Each time balance was lost, the stopwatch was paused and only resumed once the correct position was regained. This process continued until the participant accumulated a total of 60 s in a balanced position. If the participant experienced 15 interruptions within the first 30 s, the test was terminated, indicating an inability to complete it.
Scoring Procedure
The score corresponded to the number of attempts required to maintain the correct balance position for a total of one minute. As in timed performance tests, a lower score indicated better balance ability.
2.3.5. Ten-Meter, Twenty-Meter, and Thirty-Meter Sprint Tests
In determining the speed, 10 m, 20 m, and 30 m speed tests were applied with and without the ball. The test was performed with athletes starting low from the starting line by determining a distance of 10 m, 20 m, and 30 m, and measurements were made by placing a Newtech brand photocell at the starting and finishing points. Two measurements were made for each athlete, and the best result was recorded on the information form.
2.3.6. Thirty-Second Sit-Up Test
The 30 s sit-up test was conducted using a handheld stopwatch with 1/1000 s precision. Participants lay in a supine position with knees bent at a 90-degree angle, hands placed behind the neck, and feet flat on the ground. Upon the “start” command, they were instructed to perform as many sit-ups as possible within 30 s. To ensure consistency, participants were allowed one practice trial before the actual test. Throughout the test, care was taken to maintain foot contact with the ground. A repetition was considered valid if the participant’s shoulders touched the floor while lying down and their elbows made contact with their knees when sitting up. The number of correctly performed sit-ups within 30 s was recorded on the data form [22].
2.3.7. Thirty-Second Push-Up Test
A handheld stopwatch with 1/1000 precision was used for the 30 s push-up test of the participants. The participant took the starting position on the gymnastics mat on the floor, with arms shoulder-width apart, elbows tense, knees not touching the ground, and waist not hanging down. With the start command, the athlete brought his/her body 90 degrees closer to the ground and returned to the starting position. The test continued in this manner for 30 s, and the value obtained by the participant at the end of the test period was recorded on the information form as the test score [23].
2.3.8. Wingate Anaerobic Test
Anaerobic power and capacity were assessed using the Wingate Test on a computer-connected cycle ergometer (Monark 894E, Peak Bike, Sweden). Following a briefing about the test procedures, participants completed a standardized 5 min warm-up at a workload of 60–70 W and a pedaling cadence of 60–70 rpm. This was followed by a 5 min passive rest period. Subsequently, the saddle and handlebars were adjusted individually for each participant, and the feet were secured to the pedals using clips. The external resistance for the test was set at 7.5% of the participant’s body weight and loaded onto the ergometer before the test began. Participants were instructed to accelerate to their maximum pedaling speed without resistance. Once a cadence of 150 rpm was reached, the resistance was automatically applied, initiating the 30 s test phase. During this period, participants pedaled at maximal effort while receiving verbal encouragement.
Power data were transferred to the software via RS-232 connection, and the accompanying program calculated all performance parameters.
2.3.9. Twenty-Meter Shuttle Run Test
Maximal oxygen uptake (VO2max) was determined using the 20 m shuttle run test. The test involves continuous running between two lines placed 20 m apart, synchronized with auditory signals. The interval between beeps shortens every minute, progressively increasing the running pace. The protocol includes 23 levels, each lasting one minute. The test begins at a speed of 8.5 km/h, with an increment of 0.5 km/h at each subsequent level.
A single beep signals the end of a shuttle, while three beeps indicate the start of a new level. Participants completed a 10 min warm-up prior to the test. During the test, if the participant reached the 20 m line on time, they waited for the next beep before resuming. The test was terminated if the participant failed to reach the line twice consecutively. However, if a participant missed the line once but reached it on the next attempt, the test continued. The test was performed once, and the final level achieved was recorded as the result [24].
2.3.10. Theoretical Education (T.E)
In this study, structured theoretical information was provided to the participants on the fundamentals of football dynamics, small-sided games, strength training, and combined strength training before starting the training process. The players were informed about the training procedures, advantages, and expected outcomes as listed below:
A small-sided game is a training model applied to develop players’ technical skills, improve their game vision, and increase their ability to make quick decisions. These games, played in small areas, focus on high-tempo passing, making correct decisions under pressure, and increasing mobility. Within the scope of this training, the integration of small-sided games into football training and the advantages it provides were emphasized.
Combined strength training is a training model developed to increase both the maximal strength and functional endurance of football players. Different components of strength (maximal strength, power, endurance, and reactive strength) were addressed during the training process, and how these concepts would be included in training programs was explained. In addition, information was provided on resistance exercises, plyometric studies, and core region training aimed at increasing the performance of athletes.
Strength training includes training protocols applied to strengthen the musculoskeletal system, increase physical capacity, and reduce the risk of injury. In training, strength training methods specific to the football branch (free weight use, body weight exercises, isometric and isokinetic studies) were discussed, and the physiological effects of these methods were examined in detail. In addition, how strength training should be planned throughout the season and periodization strategies were emphasized.
Within the scope of this theoretical training, the scientific foundations of all training procedures were presented. The objective was to promote informed athlete participation, ensuring players understood the mechanisms of adaptation, expected training outcomes, and performance benefits. Each theoretical training lasted 15 min.
The SPSS (version 15) package program was used to determine the mean and standard deviation of the pre- and post-test results. Table 2 presents the attributes of the dataset and their basic statistical characteristics.

Table 2.
Dataset attributes and details.
2.4. Machine Learning Models
Tree-based models are highly interpretable models and have the ability to provide a transparent decision-making process. These characteristics allow researchers to analyze the influence of input features on classification outcomes. Since our study aimed to analyze the factors influencing player performances, we decided to implement the interpretable tree-based models. Four tree-based machine learning methods, namely decision tree, random forest, gradient boosting, and extreme gradient boosting, were used in this study to analyze the factors affecting the player’s performance and the effect of training [25].
2.4.1. Decision Tree
Decision trees construct a tree-structured decision-making path starting with an initial root node, followed by leaf and decision nodes. The primary strategy of the decision trees is the divide-and-conquer strategy, which distinguishes features based on their similarity and differences [25].
2.4.2. Random Forests
Random forests use ensemble learning by constructing several trees. The classification ability of the individual trees is optimized during the training and generally achieves higher performance than a single decision tree. However, determining the number of trees is challenging and increases the experimental cost [26].
2.4.3. Gradient Boosting Algorithm
Gradient boosting also constructs several individual trees; however, it focuses on the weak learners to optimize the loss during the training. It uses a gradient descent algorithm to construct new individual trees or to modify existing trees [27].
2.4.4. Extreme Gradient Boosting
Extreme gradient boosting is another ensemble tree method. Similar to the gradient boosting algorithm, it boosts weak learners. However, enhancements and improvements, such as regularization models and built-in cross-validation, are applied to avoid overfitting and improve the results [28].
2.5. Experimental Design and Evaluation Metrics
The dataset was analyzed with several experiments. Binary classification was performed to demonstrate and analyze the effectiveness of the double-training method over single-training methods. First, single-training methods were trained with ML models to observe how the training strategies affected the players. Then, each single-training method was replaced with a double-training method to show the efficiency of the double-training method due to the progress of the player’s abilities. This provided an analysis of how the players’ performance improved after training sessions and how effectively single- and double-training methods were distinguished. Table 3 presents the number of training samples, test type, and details of the experiments performed in this study.

Table 3.
Details of Experiments.
All features were included in the training since removing any feature could cause the misinterpretation of the effects of training strategies on players. However, data normalization (Min-Max normalization) was applied to the whole dataset to scale the data between 0 and 1.
The experiments were performed using 5-fold cross-validation to train and test all the samples and obtain more reliable results. The samples for each fold were selected randomly with a fixed random seed, and the final results were obtained using the mean scores of all folds. The sum of the confusion matrices of all folds was used to present the overall ability of the models.
A grid search was performed independently within each cross-validation fold to determine optimal hyperparameters for each model. For every fold, optimal hyperparameters were determined and used for each model. This approach allowed the model to adapt to variations in the training data across folds and avoided data leakage. Therefore, a robust comparison of the models, independent of the data variety, was conducted.
The experiments were evaluated using accuracy, sensitivity, specificity, and F1-score, which are the primary evaluation metrics for classification tasks.
We used the sensitivity and specificity metrics to measure the sensing ability of the models for different classes, which were the training types of players. Equations (1) and (2) show the formulae of sensitivity and specificity, respectively:
where TP, FN, TN, and FP represent the number of True Positive, False Positive, True Negative, and False Negative samples, respectively.
Sensitivity = TP/(TP + FN)
Specificity = TN/(TN + FP)
We considered accuracy to determine the general classification ability of the models. However, since the data were slightly imbalanced, we used the F1-score to measure the more accurate ability of the models. The formulae of accuracy and F1-score are given in Equations (3) and (4):
Accuracy = (TN + TP)/(TP + TN + FP + FN)
F1-Score = TP/(TP + 1/2(FP + FN))
Additionally, we computed the 95% confidence intervals of accuracy, sensitivity, and specificity metrics for all experiments.
3. Results
This section presents the classification results of each experiment separately. Then, the analysis of player performance and training strategies using the superior model is performed.
3.1. Classification Results
ML models could not achieve reasonable results in classifying the initial tests of different training methods since there was no training to change players’ tests. In differentiating STM1 and DTM, DT produced the lowest results, followed by RF and GradBoost models. Even though the RF and GradBoost models obtained higher results than DT, they could not outperform XGBoost. The superior results for each metric were achieved by the XGBoost model with 0.8 accuracy.
Similar results were obtained for classifying STM2 and DTM; however, RF and GradBoost produced the same classification results by outperforming DT. The XGBoost model achieved superior results.
In differentiating STM1 and STM2, even though GradBoost achieved higher specificity results, RF obtained higher sensitivity, making it achieve higher general recognition ability than GradBoost. DT obtained the lowest results, and XGBoost obtained the highest recognition rates, similar to the previous experiments. Table 4 presents the obtained results in detail for all experiments of the initial tests.

Table 4.
Classification results for initial test data.
When the final tests of the players were used to classify the training methods, it was observed that the distinction between DTM and STM1 and STM2 had significantly improved; however, the classification between STM1 and STM2 did not improve significantly. This shows that DTM substantially influenced the players’ performance.
All of the models’ performance increased when the results were compared to the initial test experiments. DT produced the lowest classification results for the STM1 vs. DTM and STM1 vs. STM2 experiments. However, it achieved the same results with RF in classifying STM2 and DTM. Even though RF and GradBoost obtained higher scores than DT, they could not outperform the XGBoost model. The XGBoost model achieved the highest results with 100%, 100%, and 89.70% accuracy for STM1 vs. DTM, STM2 vs. DTM, and STM1 vs. STM2 experiments, respectively. Table 5 presents the results obtained in detail for all experiments in the final tests.

Table 5.
Classification results for final test data.
Figure 2 presents the confusion matrices for the initial and final test experiments of each training method. Figure 2 clearly indicates that the training of ML models using initial tests could not achieve reasonable results by misclassifying 8, 11, and 11 samples of STM1 vs. DTM, STM2 vs. DTM, and STM1 vs. STM2. After the training procedures were completed, the XGBoost model could determine the player groups of DTM and STM1/STM2 without any misclassification.
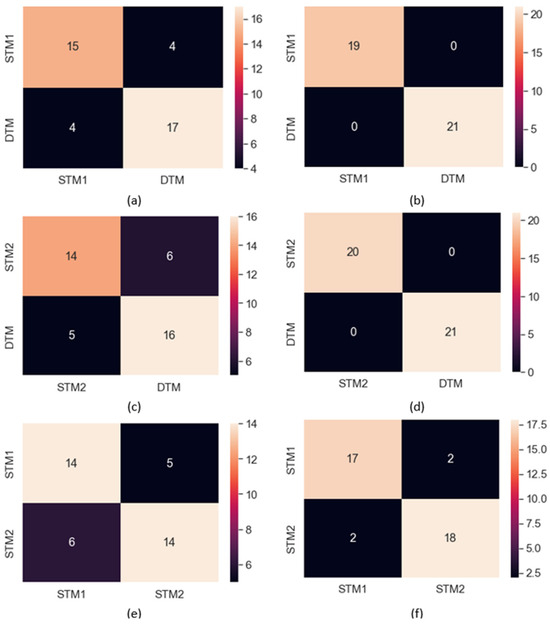
Figure 2.
Confusion matrices of the XGBoost model for classifying STM1, STM2, and DTM. (a,c,e) represent the results from the initial tests, (b,d,f) show the corresponding results from the final tests. Each matrix illustrates the classification performance for different comparisons: (a,b) STM1 vs. DTM, (c,d) STM2 vs. DTM, and (e,f) STM1 vs. STM2.
In order to provide a clearer context for interpreting model performance, we included two baseline classifiers, a random classifier, and a majority class classifier, for each experiment. A random classifier predicts each class with equal probability (50%), and a majority class classifier always predicts the class with the higher sample count.
These baselines allowed us to determine whether the models were truly learning meaningful patterns or simply benefiting from class imbalance. Table 6 shows that both baselines performed substantially worse than the proposed models, especially in terms of F1-score and sensitivity. In particular, the majority classifier achieved moderate accuracy (51–53%) due to class imbalance but completely failed to identify the minority class (0% sensitivity and F1-score), highlighting the limitations of naïve strategies.

Table 6.
Baseline performance metrics for all experiments. The random classifier predicts classes uniformly, while the majority classifier always predicts the more frequent class. Metrics confirm that tree-based models offer substantial improvements over naïve baselines.
In contrast, all tree-based models significantly outperformed the baselines across all metrics, demonstrating reliable and generalizable classification capabilities.
3.2. Factor Analysis
The superior model of the previous experiments, the XGBoost model, was used to analyze the factors that affected the classification ability of the model and demonstrate which characteristics were improved after the training session. The factors that had the most significant influence on classifying each training method were analyzed separately. Even though the classification accuracy of the initial tests for all training methods was low, we compared the initial and final test factors to determine the change in the players’ skills.
For STM1, it was observed that the importance of the sit-and-reach test, 10 m sprint (without a ball), and Wingate anaerobic test average increased after training, indicating their growing role in distinguishing player performance post-intervention. In contrast, the importance of the 20 m sprint (with a ball) decreased after training. Figure 3 illustrates the shift in factor contributions between the initial and final test phases for STM1.
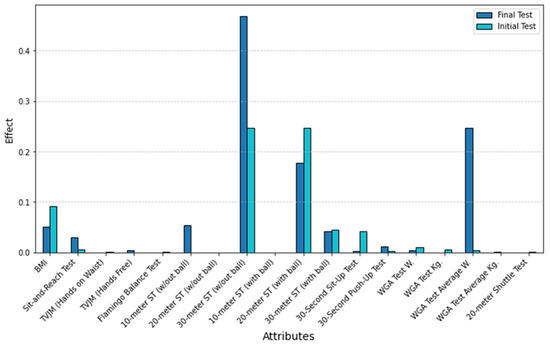
Figure 3.
Feature importance scores of the initial and final test variables in the classification of STM1 using the XGBoost model. The bars represent the relative contribution of each attribute to the model’s decision-making process, highlighting which factors were more influential before (initial test) and after (final test) the intervention.
For STM2, substantial changes were also noted. The sit-and-reach test, 10 m sprint (without a ball), and 30 m sprint (with a ball) gained importance after training. Meanwhile, the importance of the 10 m sprint (with a ball) and 20 m sprint (with a ball) declined, reflecting reduced relevance of ball-control sprints in the STM2 group post-intervention. These patterns are visualized in Figure 4.
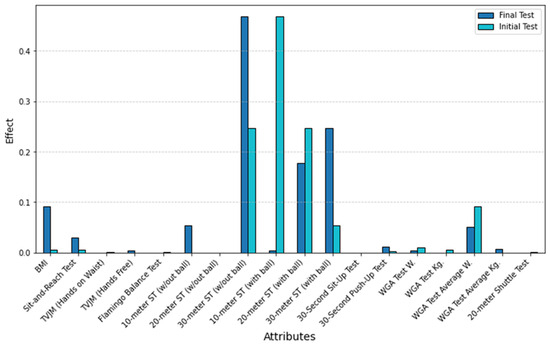
Figure 4.
Feature importance scores of the initial and final test variables in the classification of STM2 using the XGBoost model. The bars represent the relative contribution of each attribute to the model’s decision-making process, highlighting which factors were more influential before (initial test) and after (final test) the intervention.
When the DTM factors were analyzed, it was observed that more consistent changes occurred. The influence of the 20 m sprint (with ball) and 30 s sit-up test decreased, and the 10 m sprint (without a ball) and 30-m sprint (without a ball) performance of the players gained significant importance after DTM. Figure 5 presents the change in the average significance of the factors that affected the initial and final tests of DTM.
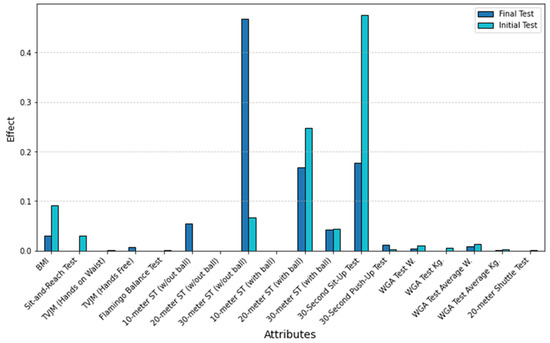
Figure 5.
Feature importance scores of the initial and final test variables in the classification of DTM using the XGBoost model. The bars represent the relative contribution of each attribute to the model’s decision-making process, highlighting which factors were more influential before (initial test) and after (final test) the intervention.
3.3. Statistical Analysis
Statistical analyses showed that all groups experienced significant reductions in BMI following training (STM1: p = 0.000; STM2: p = 0.018; DTM: p = 0.032), with a significant group difference observed in BMI change (p = 0.010). Sprint performance improved notably in the DTM group, with significant pre-to-post gains in 10 m (p = 0.000), 20 m (p = 0.045), and 30 m sprints (p = 0.021), both with and without the ball. The STM1 group also improved in 10 m (p = 0.001) and 30 m sprints (p = 0.000). Group comparisons confirmed these improvements were significantly greater in DTM and STM2 than in STM1 for most sprint variables (p < 0.01).
Sit-and-reach test significantly improved only in STM2 (p = 0.007), and group-level differences were also significant (p = 0.004). In terms of anaerobic power (Wingate test), STM1 and STM2 showed significant gains in peak and average power (STM1: p = 0.007–0.018; STM2: p = 0.003), while DTM improvements were more balanced. Group differences in mean power changes were statistically significant (p = 0.023). STM1 exhibited significant increases in both sit-up and push-up tests (p = 0.000), whereas DTM improved in sit-ups only (p = 0.012). STM2 did not show significant gains in these tests. Group differences in sit-up (p = 0.001) and push-up (p = 0.009) changes were also significant.
Lastly, VO2 max significantly increased only in the DTM group (p = 0.002), though the difference between groups was not statistically significant (p = 0.098). Table 7 presents the statistical results using ANOVA.

Table 7.
Statistical results of pre- and post-test physical and physiological attributes of the groups.
The machine learning results largely supported the outcomes of the statistical analysis. The combined training model (DTM) produced the most substantial improvements across sprint, strength, and anaerobic parameters, and these were reflected in perfect classification performance using the XGBoost model. STM1 and STM2 showed specific gains. STM1 improved in flexibility and core strength, while STM2 improved in anaerobic power. However, their training effects overlapped, resulting in lower classification accuracy and similar statistical results. The ML-based feature importance analysis corroborated these trends, indicating reduced relevance of ball-control sprints in STM2 and increased influence of speed and anaerobic factors in DTM. These aligned findings affirm the robustness of both analytical approaches and demonstrate the practical advantage of combining traditional statistical testing with machine learning interpretability.
4. Discussion
The objective of this study was to analyze the effects of small-sided games (STM1), strength training (STM2), and combined training (DTM) on various performance parameters in soccer players. To this end, machine learning models were employed to evaluate classification accuracy pre- and post-training. The results demonstrated that while all training interventions led to performance improvements, the most distinctive changes were observed in the DTM group. These findings suggest a significant influence of combined training on athletic performance.
Small-sided match (STM1) training includes frequent acceleration, deceleration, and direction changes in accordance with the characteristics of football; therefore, it stimulates both aerobic and anaerobic energy systems and provides very sensitive physical development in players [29]. Although STM1 mainly aims to improve in-game changes and decision-making skills, it can have positive effects on muscle strength and neuromuscular coordination thanks to the high intensity of growth. Strength training (STM2) aims to develop maximal strength, power production, and muscle structure. This type of training can increase sprint performance and lower-extremity epic power [30]. However, since the effects of STM2 on the neuromuscular system can lead to similar significant adaptations to those of STM1, it is expected that similar results will be shown in some measurements in both groups [31]. In contrast, the combined training program (DTM) aims to combine the advantages of both methods and improve both statistical data and muscle strength and power simultaneously. In the literature, it has been stated that the harmonious integration of different training types can provide more comprehensive performance transfers compared to single-training methods [32,33].
Machine learning models emerged as a potent instrument for analyzing the impact of training techniques on players. Physical measurements obtained before and after applying three disparate training techniques revealed substantial changes in performance parameters. Among the four machine learning algorithms utilized in this study, the XGBoost model achieved the highest accuracy, demonstrating its efficacy in classifying player performance. Traditional statistical tests are effective for group-level comparisons and are typically limited to identifying significant differences in mean values or distributions. On the contrary, machine learning (ML) provides individual-level predictive capability and identifies nonlinear, multivariate patterns across features that are not easily captured by univariate tests. Therefore, in our study, they allowed the prediction of class membership (e.g., STM1 vs. DTM) at the individual subject level, which is directly useful for screening applications. Additionally, feature importance analysis using the considered tree-based models revealed which input features most strongly influenced predictions and guided targeted interventions. These advantages go beyond traditional group comparisons and support the development of generalizable and interpretable decision models that could aid trainers.
The classification analysis demonstrated that distinguishing DTM from STM1 and STM2 improved considerably, indicating that combined training induced a unique adaptation profile. Conversely, the differentiation between STM1 and STM2 remained relatively unchanged, suggesting a degree of overlap in their training effects. These findings are consistent with previous studies emphasizing the benefits of multimodal training approaches over isolated methodologies in soccer players [34].
Concerning STM1, significant enhancements were observed in flexibility (sit-and-reach test), short-distance sprinting (10 m sprint without a ball, 20 m sprint with a ball), and anaerobic power (Wingate anaerobic test). These findings align with prior research suggesting that small-sided games enhance agility, anaerobic capacity, and specific movement patterns relevant to soccer [35]. Furthermore, a recent systematic review and meta-analysis highlighted that small-sided games significantly improved overall physical fitness and cardiometabolic health markers, particularly among youth athletes [33]. Additionally, after sensitivity analyses, SSGs were found to significantly improve waist circumference and muscle strength. These findings suggest that SSGs are a viable and engaging intervention for promoting health in youth [36]. Recent research has investigated whether small-sided games adequately prepared elite young soccer players for worst-case match scenarios. That research revealed that while SSGs replicated numerous match demands, they may not fully prepare players for the most extreme match situations [37]. However, it has also been reported that small-sided games alone may not be sufficient for maximizing high-intensity running performance, requiring additional sprint-specific training components [34,35].
The present findings offer preliminary insight into the relationship between small-sided games (SSGs) and specific performance components such as speed, agility, and power, which are underexplored in the existing literature. While not all improvements in these variables were statistically significant, observable trends suggest potential benefits, particularly in agility and lower-body power. These outcomes are consistent with previous research indicating that SSGs can stimulate neuromuscular and physiological responses relevant to explosive performance, especially when structured with appropriate intensity and constraints [38,39]. Variability in the results may be influenced by modifiable training parameters such as pitch size, player count, and work-to-rest ratios [40]. Overall, SSGs appear to contribute to general physical development, though more targeted training strategies may be necessary to achieve consistent improvements in isolated metrics like sprint speed or maximal power output.
In the STM2 group, flexibility (sit-and-reach test), acceleration (10 m and 30 m sprint without a ball), and lower-body power became more critical performance markers post-training, while the significance of 10 m and 20 m sprint with a ball decreased. This finding is consistent with the conclusions of studies indicating that strength training enhances sprinting ability and neuromuscular efficiency. However, these studies suggest that strength training may not necessarily improve dribbling-related speed unless it is combined with sport-specific drills [41].
Conversely, DTM resulted in more balanced and consistent performance enhancements, with the importance of the 20 m sprint with a ball and 30 s sit-up test decreasing and the contributions of the 10 m sprint without a ball and 30 m sprint without a ball significantly increasing. Performance changes exceeding 0.1 s in sprint tests and 5 cm in flexibility are generally considered clinically meaningful in elite football. Several variables in our study, particularly in the DTM group, met or exceeded these thresholds. These results suggest that combined training optimally integrates strength, speed, and endurance components, leading to well-rounded athletic development. This observation is consistent with the findings of studies that emphasize the superiority of hybrid training methods in soccer, particularly for maintaining high-intensity performance across various match scenarios [42].
While STM1 and STM2 each contributed to specific performance gains, their isolated use showed some overlap in outcomes and comparatively limited effects in certain performance measures. Therefore, practitioners are advised to consider multi-component training strategies that address the diverse physical demands of football. Additionally, it is recommended that coaches incorporate combined training (DTM) into their programs to enhance short-distance sprint performance, anaerobic power, and overall fitness, particularly over an 8-week period with two sessions per week.
Furthermore, the structured monitoring and evaluation of training outcomes allowed for the detailed analysis of progress within and between groups.
The key performance variables identified in this study were agility, sprinting ability, flexibility, and anaerobic power, which are essential for football performance. The prominence of these variables highlights their collective influence on a player’s ability to maintain performance, recover quickly, and make rapid decisions. Understanding their importance can help guide training programs aimed at improving various aspects of a player’s physical and technical development.
The findings of the study indicated that XGBoost outperformed all other models, achieving the highest classification accuracies for STM1 vs. DTM (100%), STM2 vs. DTM (100%), and STM1 vs. STM2 (89.70%). The boosting process of XGBoost, which includes regularization, shrinkage, and column subsampling, improves generalization and prevents overfitting. Additionally, while minimizing the loss, it efficiently modelled nonlinear relationships between features and achieved superior results. These results underscore the potential of advanced predictive analytics in monitoring and optimizing training programs. The findings are consistent with previous research that supports the application of machine learning for individualized training prescriptions in team sports [43].
In the final analysis, the present study demonstrated that DTM induced the most distinct performance adaptations, whereas STM1 and STM2 elicited more specific, albeit somewhat overlapping, benefits. The results emphasize the importance of integrated training methodologies in soccer and suggest that machine learning can be a valuable tool for evaluating training efficacy. Future research should explore the long-term impact of these interventions on match performance and injury prevention.
5. Limitations
This study has several limitations. No correction for multiple comparisons (e.g., Bonferroni adjustment) was applied in this study. While this allowed for a broader exploratory analysis, it increased the chance of Type I error, which should be addressed in future research with stricter statistical controls. Even though the group-level classification was performed with high accuracy, the use of ML models created in this study cannot be implemented for personalized prescriptions due to the limited number of players. Another key limitation of this study is the use of BMI to assess body composition, which may not accurately reflect muscle mass and body fat distribution in athletic populations. Future research should consider more precise methods, such as DXA or BIA, for a more detailed analysis. Additionally, this study is limited by the age differences among groups and the absence of randomized group assignment. While all players had completed their biological development, these factors may have introduced bias and should be controlled in future research.
6. Conclusions
Analyzing the impact of training techniques on players is challenging and requires a sensitive approach. Artificial intelligence and machine learning techniques have recently been used to overcome this challenge. Their ability to establish linear or nonlinear relationships between data enables machine learning models to produce more accurate results. In this study, physical measurements of the athletes were obtained before and after applying three different training techniques. In addition, the extent to which training techniques could be separated from each other and the factors affecting this process were analyzed using four tree-based machine-learning models. Even though the considered machine learning models obtained reasonable results, the XGBoost model achieved superior results compared to the other models in distinguishing the single- and double-training groups.
The results suggested that combined training (DTM) leads to more comprehensive improvements in physical performance parameters—including aerobic capacity, anaerobic power, and sprint ability—compared to small-sided games (STM1) or resistance training (STM2) alone. These findings suggest that integrating different training modalities into a single program may be more effective for optimizing the physiological development of football players. Additionally, the results demonstrate that using machine learning to analyze training efficacy and performance evaluation is a valuable tool for evaluating training efficacy. This study is among the first to integrate theoretical education, multimodal football training, and machine learning-based performance analysis. This novel approach offers both conceptual and methodological contributions to sports science.
Future studies should focus on longitudinal monitoring to assess the long-term effects of these training methods on performance and injury prevention. The integration of GPS tracking data could also provide valuable insights into players’ movement patterns and load management. Additionally, expanding research to include female athletes would further enhance the generalizability of the findings across different populations.
Author Contributions
Conceptualization, H.G. and C.T.; methodology, H.G. and B.S. ; software, H.G. and B.S.; validation, H.G., H.U.Y. and C.T.; formal analysis, H.G., M.O. and C.T.; data curation, H.G.; writing—original draft preparation, H.G., H.U.Y., B.S., M.O. and C.T.; writing—review and editing, H.G., H.U.Y., B.S., M.O. and C.T.; visualization, B.S.; supervision, C.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study was performed in line with the principles of the Declaration of Helsinki. Approval was granted by the Ethics Committee of Near East University (Date: 25 November 2021/No: YDU/2021/97-1381).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author, H.G.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Akyildiz, Z.; Nobari, H.; González-Fernández, F.T.; Praça, G.M.; Sarmento, H.; Guler, A.H.; Saka, E.K.; Clemente, F.M.; Figueiredo, A.J. Variations in the physical demands and technical performance of professional soccer teams over three consecutive seasons. Sci. Rep. 2022, 12, 2412. [Google Scholar] [CrossRef] [PubMed]
- Bangsbo, J.; Mohr, M.; Krustrup, P. Physical and metabolic demands of training and match-play in the elite football player. J. Sports Sci. 2006, 24, 665–674. [Google Scholar] [CrossRef]
- Bebek, A. Futbol ve Futsal Oyuncularının Quadriceps Ve Hamstring Kas Kuvvetlerinin İzokinetik Yöntemle Karşılaştırılması, Sakatlık Eğilimlerinin İncelenmesi. Master of Science’s Thesis, Mersin Üniversitesi Eğitim Bilimleri Enstitüsü Beden Eğitimi Ve Spor Anabilim Dalı, Mersin, Turkey, 2020. [Google Scholar]
- Erkmen, N.; Kaplan, T.; Taşkın, H. Profesyonel Futbolcuların Hazırlık Seonu Fiziksel ve Fizyolojik Parametrelerinin Tespiti ve Karşılaştırılması. Spormetre Beden Eğitimi Ve Spor Bilimleri Dergisi 2005, 3, 137–144. [Google Scholar] [CrossRef]
- Dellal, A.; Owen, A.; Wong, D.; Krustrup, P.; van Exsel, M.; Mallo, J. Technical and physical demands of small vs. large sided games in relation to playing position in elite soccer. Hum. Mov. Sci. 2012, 31, 957–969. [Google Scholar] [CrossRef] [PubMed]
- Clemente, F.M.; Martins, F.M.L.; Mendes, R.S. Developing Aerobic and Anaerobic Fitness Using Small-Sided Soccer Games. Strength Cond. J. 2014, 36, 76–87. [Google Scholar] [CrossRef] [PubMed]
- Mancini, N.; Di Padova, M.; Polito, R.; Mancini, S.; Dipace, A.; Basta, A.; Colella, D.; Limone, P.; Messina, G.; Monda, M.; et al. The Impact of Perception–Action Training Devices on Quickness and Reaction Time in Female Volleyball Players. J. Funct. Morphol. Kinesiol. 2024, 9, 147. [Google Scholar] [CrossRef]
- Gabbett, T.J.; Kelly, J.N.; Sheppard, J.M. Speed, Change of Direction Speed, and Reactive Agility of Rugby League Players. J. Strength Cond. Res. 2008, 22, 174–181. [Google Scholar] [CrossRef]
- Halouani, J.; Chtourou, H.; Gabbett, T.; Chaouachi, A.; Chamari, K. Small-sided games in team sports training: A brief review. J. Strength Cond. Res. 2014, 28, 3594–3618. [Google Scholar] [CrossRef] [PubMed]
- Canüzmez, A.E.; Acar, M.F.; Özçaldıran, B. İç Üst Vuruşta Kullanılan Kas Grupları Zirve Tork Güçlerinin Topa Vuruş Mesafesiyle Arasındaki İlişki. In Proceedings of the Muğla Üniversitesi 9. Uluslararası Spor Bilimleri Kongresi, Menteşe, Turkey, 3–5 November 2006; pp. 246–249. [Google Scholar]
- Wisløff, U.; Castagna, C.; Helgerud, J.; Jones, R.; Hoff, J. Strong correlation of maximal squat strength with sprint performance and vertical jump height in elite soccer players. Br. J. Sports Med. 2004, 38, 285–288. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Di Salvo, V.; Baron, R.; González-Haro, C.; Gormasz, C.; Pigozzi, F.; Bachl, N. Sprinting analysis of elite soccer players during European Champions League and UEFA Cup matches. J. Sports Sci. 2010, 28, 1489–1494. [Google Scholar] [CrossRef] [PubMed]
- Kharatzadeh, M.; Minasian, V.; Thapa, R.; Clemente, F.; Faramarzi, M. Effects of small-sided games combined with high-intensity interval training versus high-intensity interval training alone on physical fitness of youth soccer players. Trends Sport Sci. 2025, 32, 31. [Google Scholar]
- Potteiger, J.A.; Lockwood, R.H.; Haub, M.D.; Dolezal, B.A.; Almuzaini, K.S.; Schroeder, J.M.; Zebas, C.J. Muscle Power and Fiber Characteristics Following 8 Weeks of Plyometric Training. J. Strength Cond. Res. 1999, 13, 275–279. [Google Scholar]
- Delecluse, C.; Van Coppenolle, H.; Willems, E.; Van Leemputte, M.; Diels, R.; Goris, M. Influence of high-resistance and high-velocity training on sprint performance. Med. Sci. Sports Exerc. 1995, 27, 1203–1209. [Google Scholar] [CrossRef] [PubMed]
- Adams, D.A.; Nelson, R.R.; Todd, P.A. Perceived Usefulness, Ease of Use, and Usage of Information Technology: A Replication. MIS Q. 1992, 16, 227–247. [Google Scholar] [CrossRef]
- Oliver, J.L.; Ayala, F.; Croix, M.B.D.S.; Lloyd, R.S.; Myer, G.D.; Read, P.J. Using machine learning to improve our understanding of injury risk and prediction in elite male youth football players. J. Sci. Med. Sport 2020, 23, 1044–1048. [Google Scholar] [CrossRef] [PubMed]
- Manish, S.; Bhagat, V.; Pramila, R. Prediction of Football Players Performance using Machine Learning and Deep Learning Algorithms. In Proceedings of the 2021 2nd International Conference for Emerging Technology (INCET), Belagavi, India, 21–23 May 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Morciano, G.; Zingoni, A.; Morachioli, A.; Calabrò, G. Machine Learning prediction of the expected performance of football player during training. In Proceedings of the 2022 IEEE International Conference on Metrology for Extended Reality, Artificial Intelligence and Neural Engineering (MetroXRAINE), Rome, Italy, 26–28 October 2022; pp. 574–578. [Google Scholar] [CrossRef]
- Wisdom, C.; Javed, A. Machine Learning for Data Analytics in Football: Quantifying Performance and Enhancing Strategic Decision-Making. 2023. Available online: https://ssrn.com/abstract=4558733 (accessed on 15 September 2024).
- Chow, G.C.-C.; Kong, Y.-H.; Pun, W.-Y. The Concurrent Validity and Test-Retest Reliability of Possible Remote Assessments for Measuring Countermovement Jump: My Jump 2, HomeCourt & Takei Vertical Jump Meter. Appl. Sci. 2023, 13, 2142. [Google Scholar] [CrossRef]
- Pekel, H.A.; Balcı, Ş.S.; Arslan, Ö.; Bağcı, E. Atletizm Yapan Çocukların Performansla İlgili Fiziksel Uygunluk Test Sonuçlarının ve Bazı Antrepometrik Özelliklerinin Değerlendirilmesi. Kastamonu Educ. J. 2007, 15, 427–438. [Google Scholar]
- Mackenzie, B. 101 Performance Evaluation Tests; Jonathan Pye: London, UK, 2005. [Google Scholar]
- Lemmink, K.A.; Visscher, C.; Lambert, M.I.; Lamberts, R.P. The interval shuttle run test for intermittent sport players: Evaluation of reliability. J. Strength Cond. Res. 2004, 18, 821–827. [Google Scholar] [CrossRef] [PubMed]
- Sekeroglu, B.; Ever, Y.K.; Dimililer, K.; Al-Turjman, F. Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression Problems. Data Intell. 2022, 4, 620–652. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Dellal, A.; Chamari, K.; Pintus, A.; Girard, O.; Cotte, T.; Keller, D. Physiological responses and time–motion characteristics of various small-sided soccer games in youth players. J. Sports Sci. 2012, 26, 477–485. [Google Scholar]
- Suchomel, T.J.; Nimphius, S.; Stone, M.H. The importance of muscular strength in athletic performance. Sports Med. 2016, 46, 1419–1449. [Google Scholar] [CrossRef] [PubMed]
- Kunz, P.; Engel, F.A.; Holmberg, H.C.; Sperlich, B. A meta-comparison of the effects of Sprint vs. jump training on sport-specific performance in young athletes. Front. Physiol. 2019, 10, 1344. [Google Scholar]
- Jones, T.W.; Howatson, G.; Russell, M.; French, D.N. Performance and endocrine responses to differing ratios of concurrent strength and endurance training. J. Strength Cond. Res. 2017, 31, 405–412. [Google Scholar] [CrossRef]
- Fyfe, J.J.; Bishop, D.J.; Stepto, N.K. Interference between concurrent resistance and endurance exercise: Molecular bases and the role of individual training variables. Sports Med. 2014, 44, 743–762. [Google Scholar] [CrossRef]
- Gómez-Álvarez, N.; Boppre, G.; Hermosilla-Palma, F.; Reyes-Amigo, T.; Oliveira, J.; Fonseca, H. Effects of Small-Sided Soccer Games on Physical Fitness and Cardiometabolic Health Biomarkers in Untrained Children and Adolescents: A Systematic Review and Meta-Analysis. J. Clin. Med. 2024, 13, 5221. [Google Scholar] [CrossRef]
- Clemente, F.M.; Ramirez-Campillo, R.; Afonso, J.; Sarmento, H. Effects of Small-Sided Games vs. Running-Based High-Intensity Interval Training on Physical Performance in Soccer Players: A Meta-Analytical Comparison. Front. Physiol. 2021, 12, 642703. [Google Scholar] [CrossRef]
- Moran, J.; Blagrove, R.C.; Drury, B.; Fernandes, J.F.T.; Paxton, K.; Chaabene, H.; Ramirez-Campillo, R. Effects of Small-Sided Games vs. Conventional Endurance Training on Endurance Performance in Male Youth Soccer Players: A Meta-Analytical Comparison. Sports Med. 2019, 49, 731–742. [Google Scholar] [CrossRef] [PubMed]
- Hammami, A.; Chamari, K.; Slimani, M.; Shephard, R.; Yousfi, N.; Tabka, Z.; Bouhlel, E. Effects of recreational soccer on physical fitness and health indices in sedentary healthy and unhealthy subjects. Biol. Sport 2016, 33, 127–137. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Kunz, P.; Engel, F.A.; Holmberg, H.-C.; Sperlich, B. A Meta-Comparison of the Effects of High-Intensity Interval Training to Those of Small-Sided Games and Other Training Protocols on Parameters Related to the Physiology and Performance of Youth Soccer Players. Sports Med. Open 2019, 5, 7. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Hill-Haas, S.V.; Dawson, B.; Impellizzeri, F.M.; Coutts, A.J. Physiology of small-sided games training in football. Sports Med. 2011, 41, 199–220. [Google Scholar] [CrossRef] [PubMed]
- Buchheit, M.; Laursen, P.B. High-intensity interval training, solutions to the programming puzzle. Sports Med. 2013, 43, 313–338. [Google Scholar] [CrossRef] [PubMed]
- Clemente, F.M.; Afonso, J.; Sarmento, H. Small-sided games: An umbrella review of systematic reviews and meta-analyses. PLoS ONE 2021, 16, e0247067. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Bujalance-Moreno, P.; Latorre-Román, P.Á.; García-Pinillos, F. A systematic review on small-sided games in football players: Acute and chronic adaptations. J. Sports Sci. 2019, 37, 921–949. [Google Scholar] [CrossRef] [PubMed]
- Davids, K.; Araújo, D.; Correia, V.; Vilar, L. How Small-Sided and Conditioned Games Enhance Acquisition of Movement and Decision-Making Skills. Exerc. Sport Sci. Rev. 2013, 41, 154–161. [Google Scholar] [CrossRef] [PubMed]
- Clemente, F.M.; Afonso, J.; Castillo, D.; Arcos, A.L.; Silva, A.F.; Sarmento, H. The effects of small-sided soccer games on tactical behavior and collective dynamics: A systematic review. Chaos Solitons Fractals 2020, 134, 109710. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).