An Effective Off-Grid DOA Estimation Algorithm Using Difference Coarrays with Limited Snapshots
Abstract
1. Introduction
2. Signal Model
3. The Proposed Method
3.1. Initial DOA Estimation
3.2. Fine Estimation
4. Performance Analysis
4.1. The CRB Derivation
4.2. Computational Complexity Analysis
5. Simulation Results
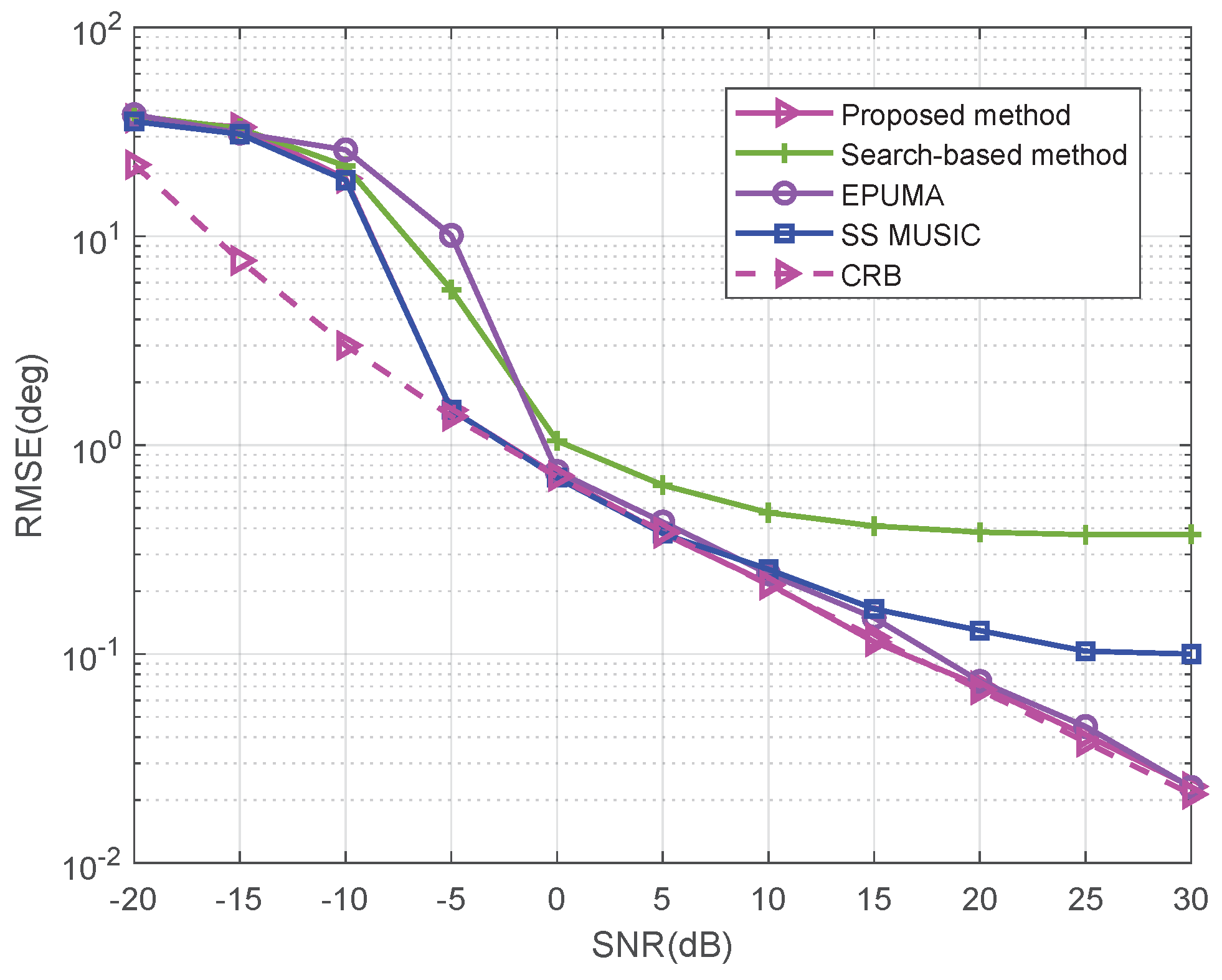
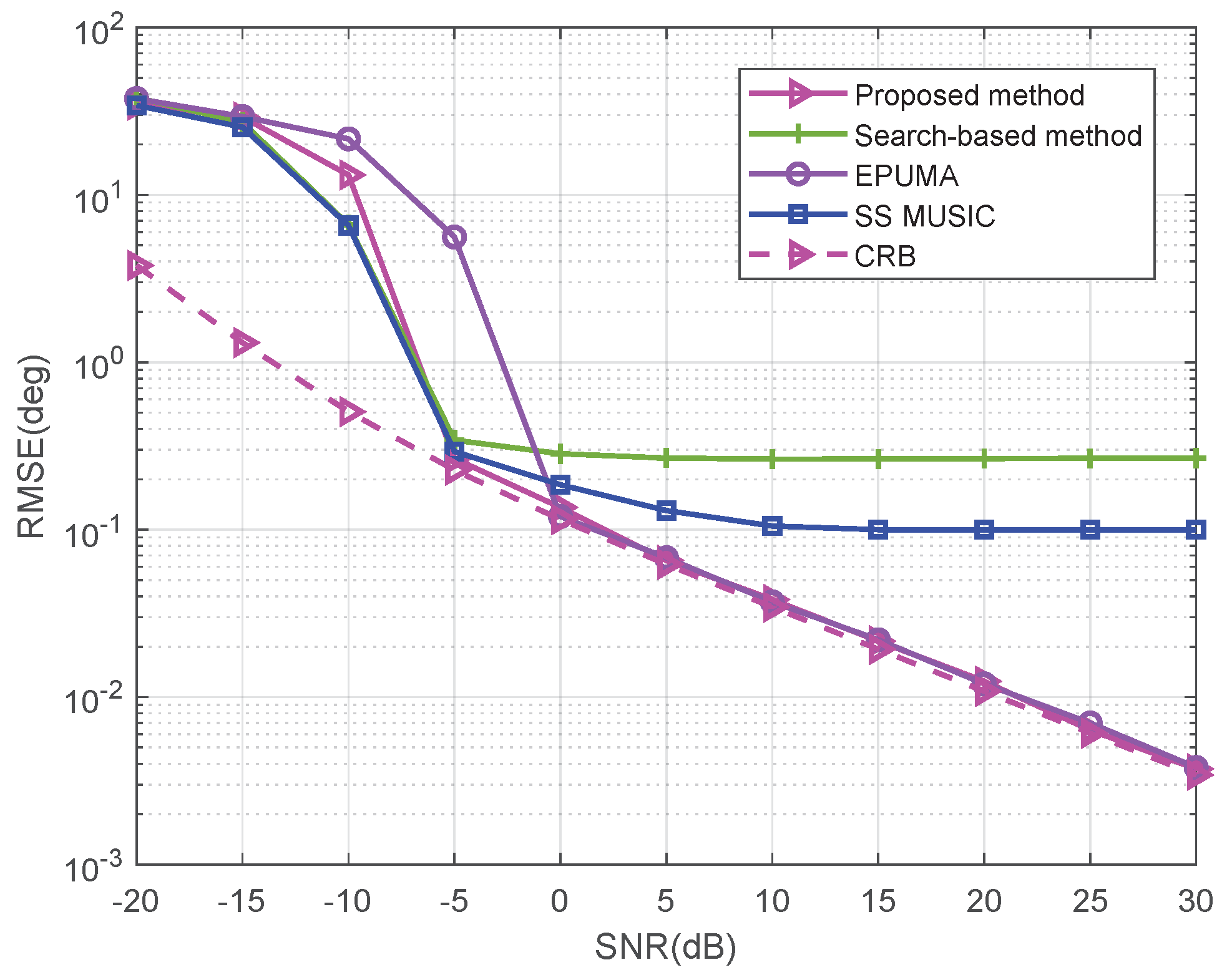
5.1. Fewer Sources than Sensors Case for ULA
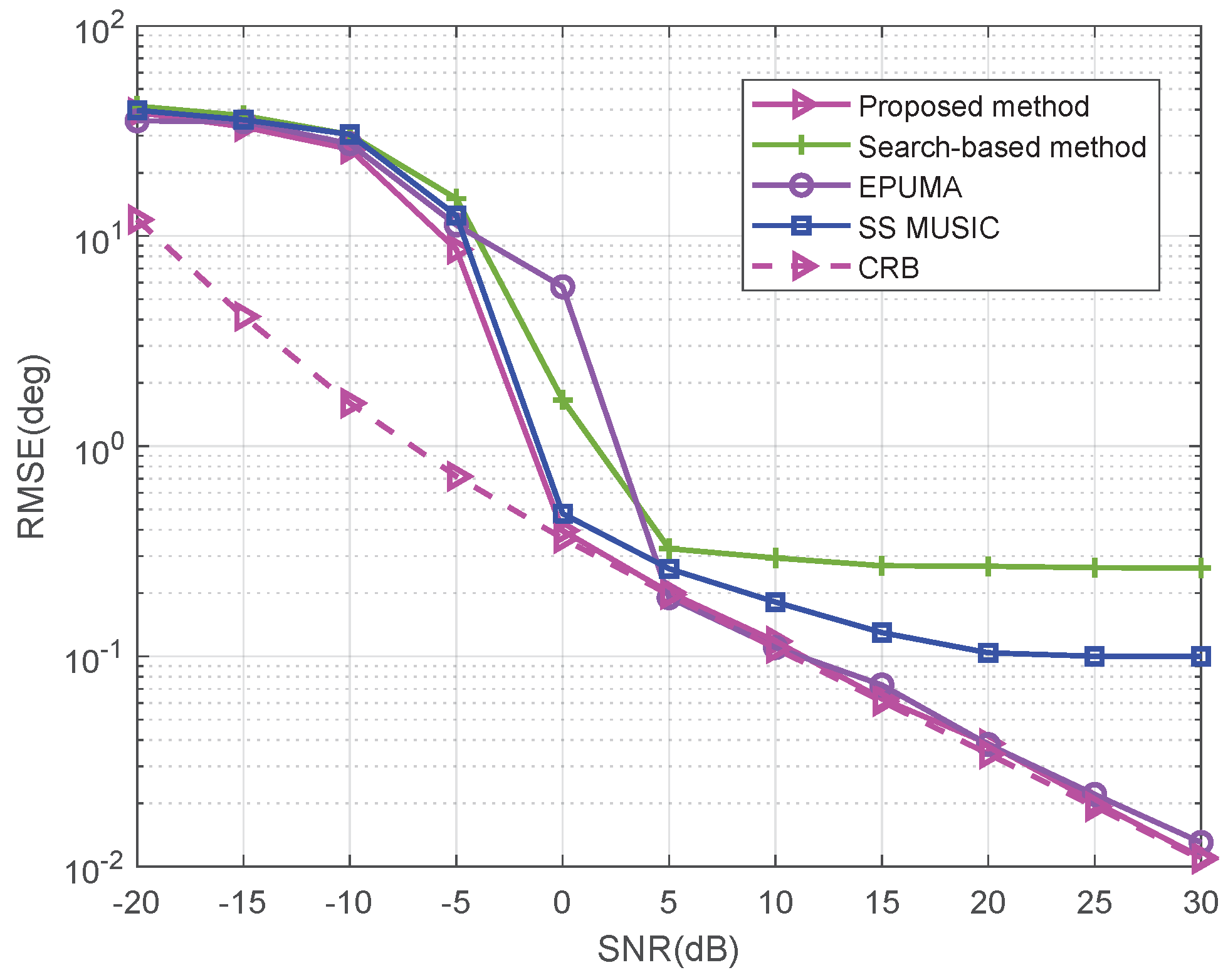
5.2. Fewer Sources than Sensors Case for NLA
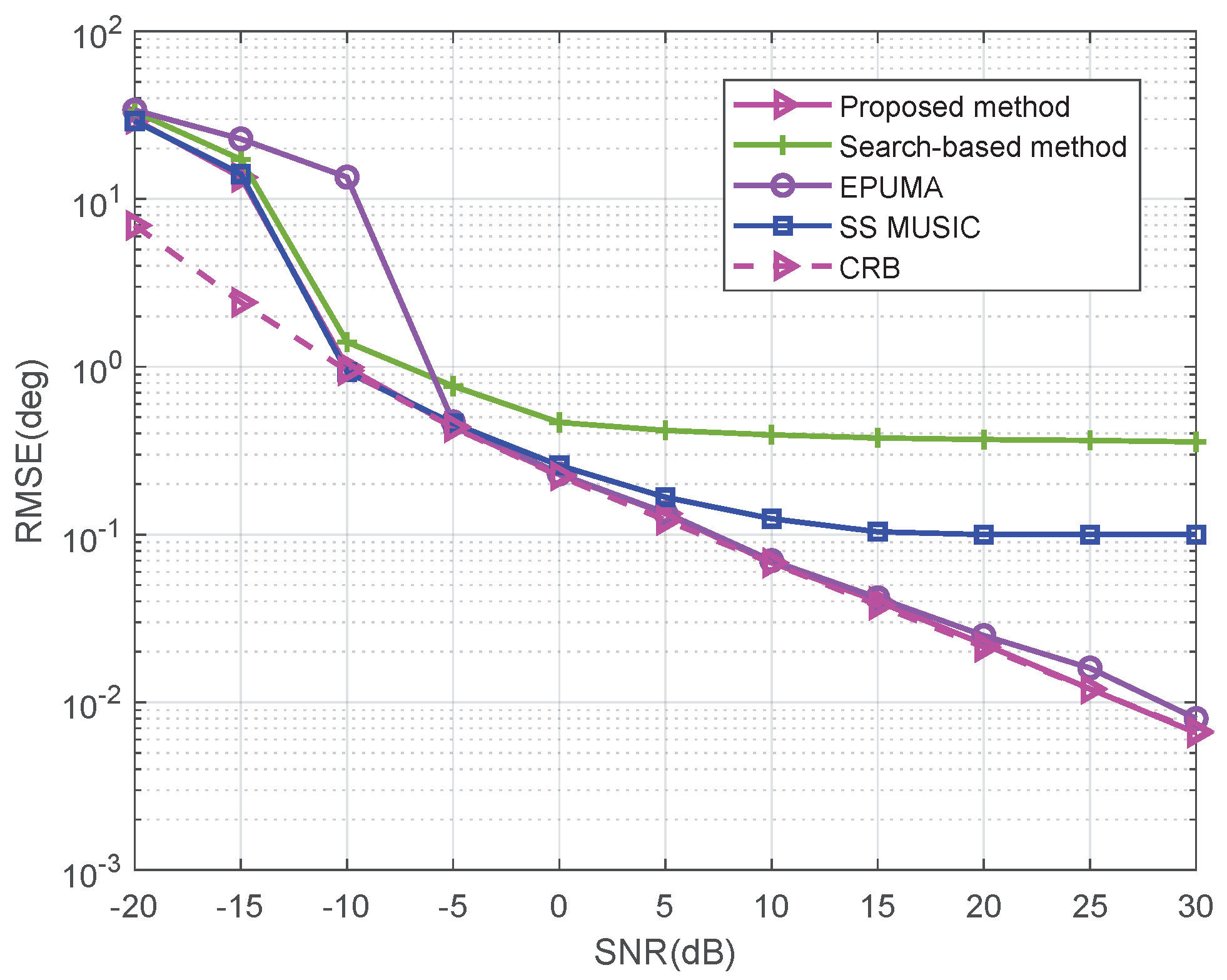
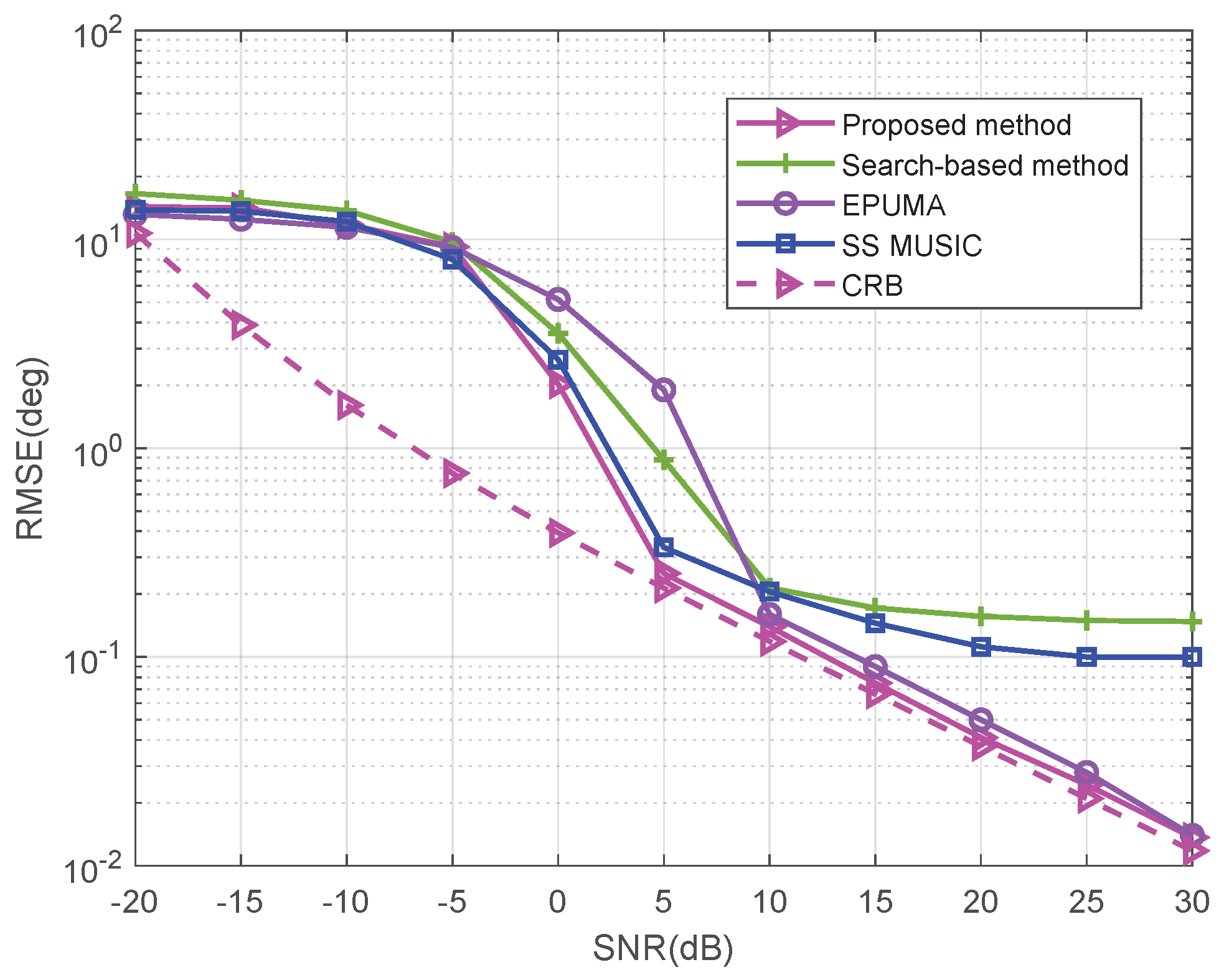
5.3. More Sources than Sensors Case for NLA
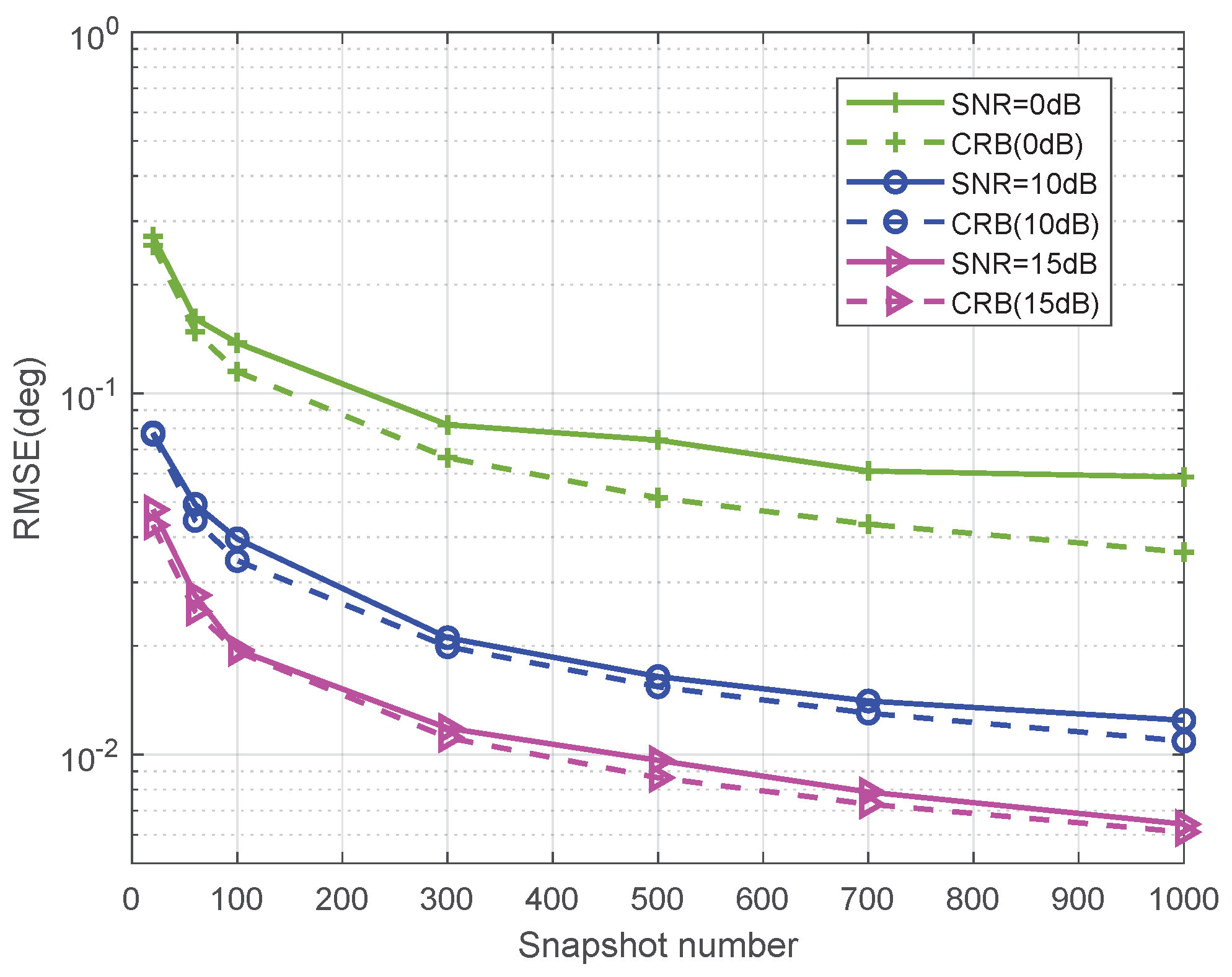
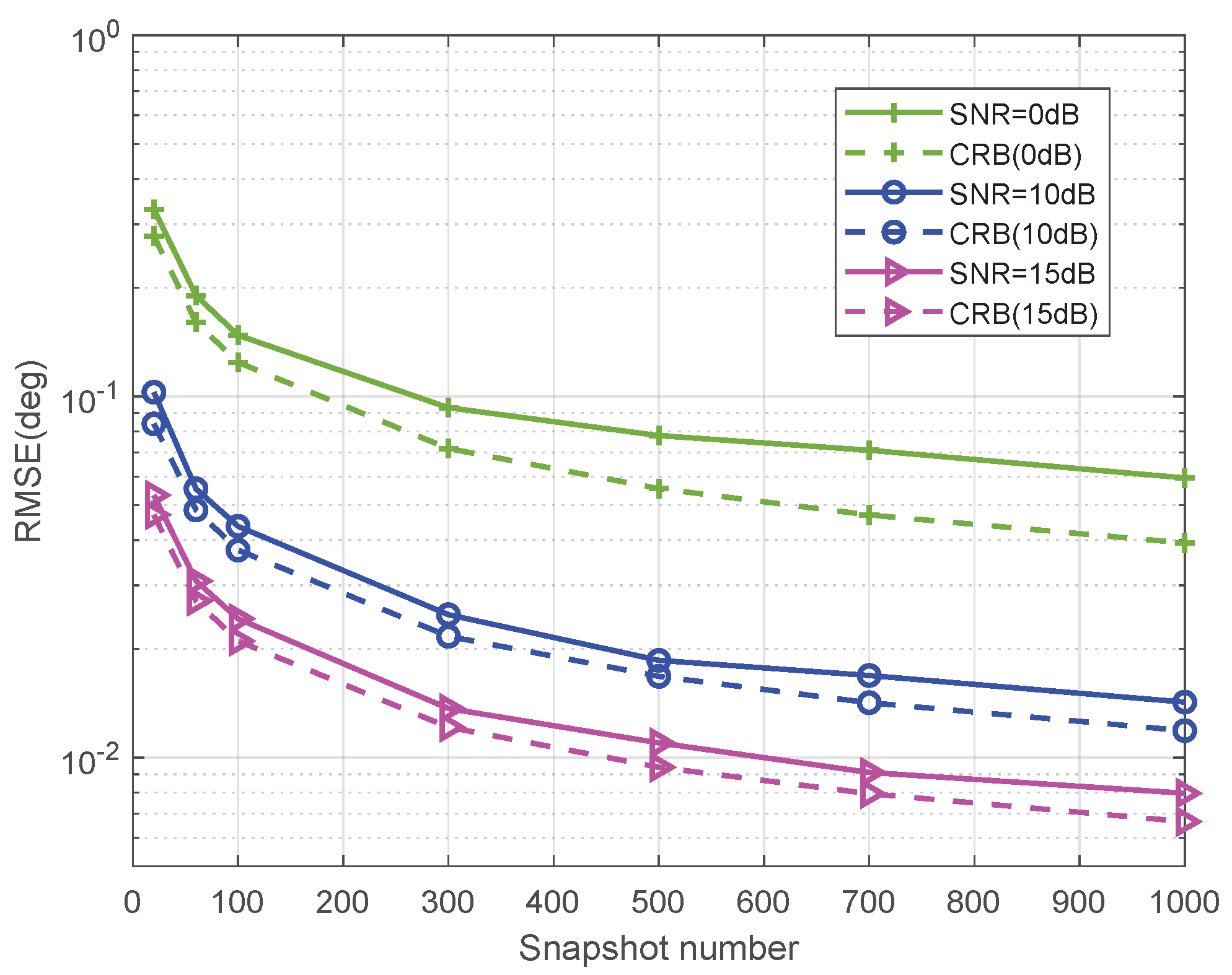
5.4. Estimation Performance Versus Snapshot Number for NLA
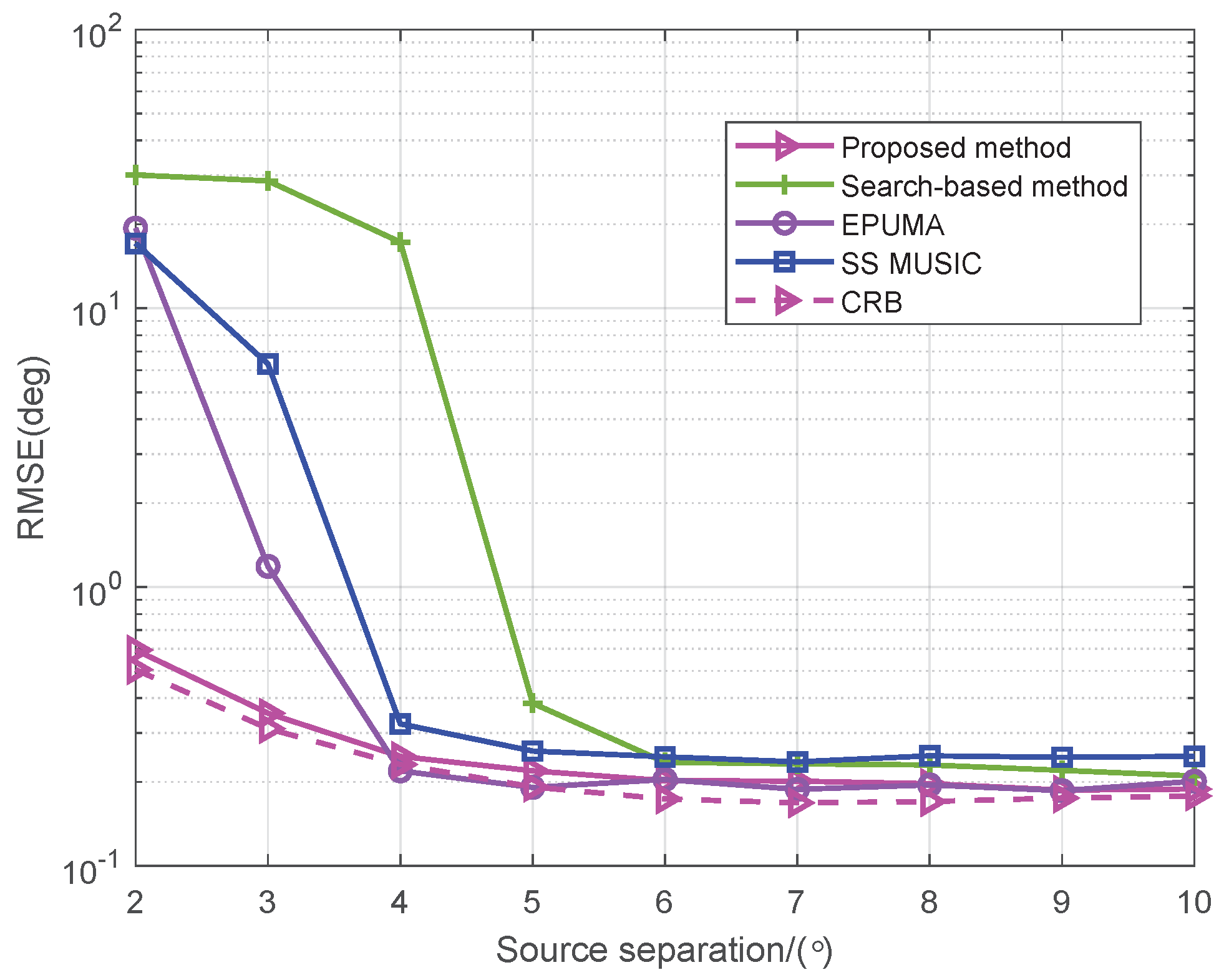
5.5. Resolution Performance for NLA
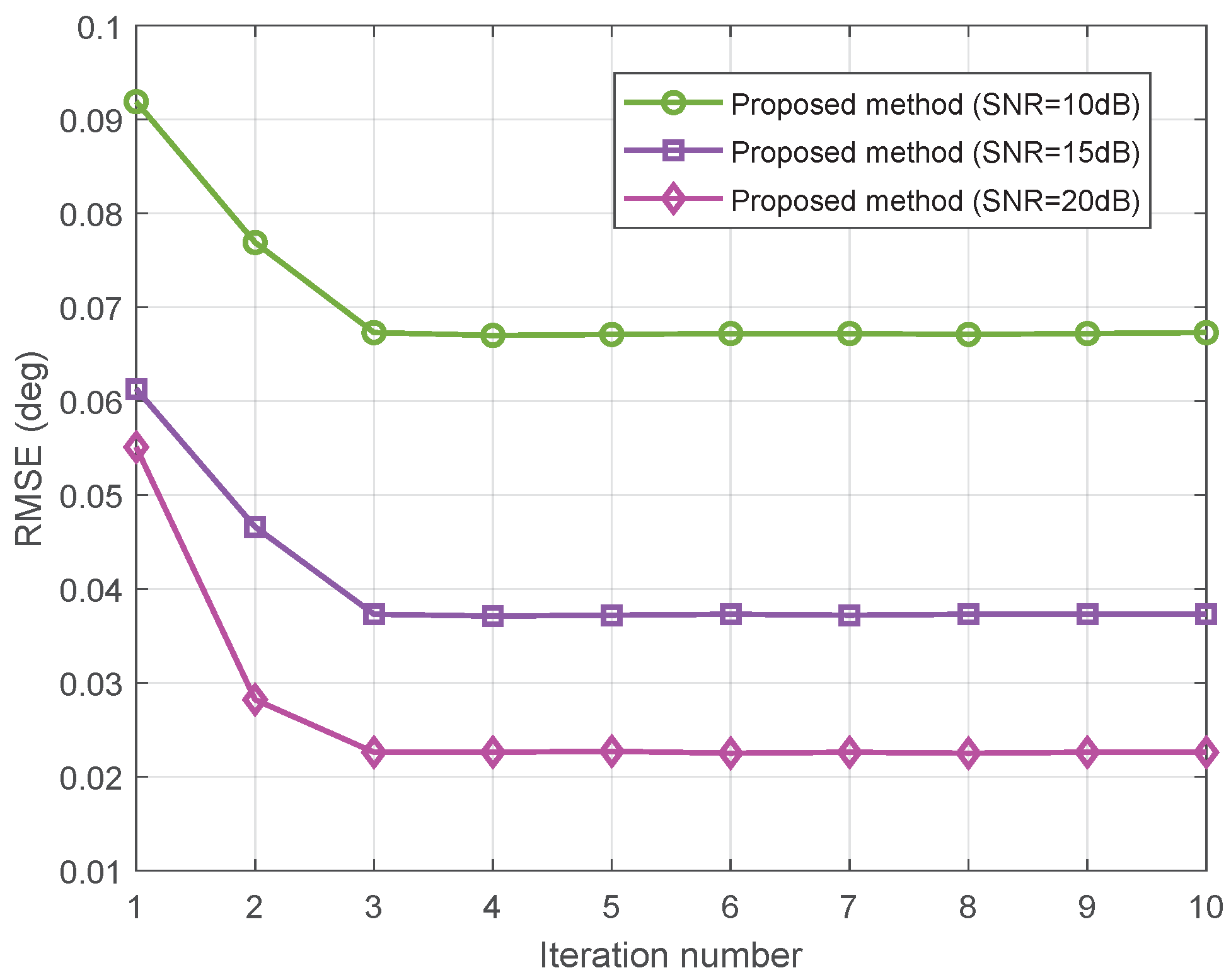
5.6. Convergence Performance for NLA
5.7. Performance Comparison
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, W.; Haardt, M.; Greco, S.M.; Mecklenbrauker, F.C.; Willett, P. Twenty-Five Years of Sensor Array and Multichannel Signal Processing: A review of progress to date and potential research directions. IEEE Signal Process. Mag. 2023, 40, 80–91. [Google Scholar] [CrossRef]
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 2007, 13, 67–94. [Google Scholar] [CrossRef]
- Trees, H.L.V. Detection, Estimation, and Modulation Theory: Optimum Array Processing; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Zhai, W.T.; Wang, X.R.; Cao, X.B.; Greco, M.S.; Gini, F. Reinforcement learning based dual-functional massive MIMO systems for multi-target detection and communications. IEEE Trans. Signal Process. 2023, 71, 741–755. [Google Scholar] [CrossRef]
- Ma, Y.; Cao, X.; Wang, X. Multi-source off-grid DOA estimation with single snapshot using non-uniform linear arrays. Signal Process. 2021, 189, 108–238. [Google Scholar] [CrossRef]
- Wang, X.; Amin, M.; Ahmad, F. Interference DOA estimation and suppression for GNSS receivers using fully augmentable arrays. IET Radar Sonar Navig. 2017, 11, 474–480. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Florio, A.; Avitabile, G.; Talarico, C.; Coviello, G. A reconfigurable full-digital architecture for angle of arrival estimation. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 1443–1455. [Google Scholar] [CrossRef]
- Florio, A.; Coviello, G.; Talarico, C.; Avitabile, G. Adaptive DDS-PLL beamsteering architecture based on real-time angle-of-arrival estimation. In Proceedings of the 2024 IEEE 67th International Midwest Symposium on Circuits and Systems (MWSCAS), Springfield, MA, USA, 11–14 August 2024; pp. 628–631. [Google Scholar]
- Pal, P.; Vaidyanathan, P.P. Nested Arrays: A Novel Approach to Array Processing With Enhanced Degrees of Freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Lai, X.; Zhang, X.F.; Han, S.X.L.; Ahmad, M. Multi-Layer Filled Coprime Arrays for DOA Estimation With Extended Hole-Free Coarray. IEEE Trans. Veh. Technol. 2024, 73, 2621–2632. [Google Scholar] [CrossRef]
- Ma, Y.N.; Wang, X.R.; Cao, X.B. Coarray beamspace transformation based DOA estimation for uniform circular arrays. In Proceedings of the 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018; pp. 0792–0797. [Google Scholar]
- Pal, P.; Vaidyanathan, P.P. Coprime sampling and the music algorithm. In Proceedings of the 2011 Digital Signal Processing and Signal Processing Education Meeting (DSP/SPE), Sedona, AZ, USA, 4–7 January 2011; pp. 289–294. [Google Scholar]
- Liu, C.L.; Vaidyanathan, P.P. Remarks on the Spatial Smoothing Step in Coarray MUSIC. IEEE Signal Process. Lett. 2015, 22, 1438–1442. [Google Scholar] [CrossRef]
- Xie, Q.P.; Pan, X.Y.; Xiao, S.P. Enhance Degrees of Freedom for Coprime Array Using OptSpace Algorithm. IEEE Access 2019, 7, 32672–32680. [Google Scholar] [CrossRef]
- Yadav, S.K.; George, N.V. xMISC: Coarray MUSIC-Group Delay: High-Resolution Source Localization Using Non-Uniform Arrays. IEEE Trans. Veh. Technol. 2021, 70, 9597–9601. [Google Scholar] [CrossRef]
- Joel, S.; Yadav, S.K.; George, N.V. Coarray LMS: Adaptive Underdetermined DOA Estimation With Increased Degrees of Freedom. IEEE Signal Process. Lett. 2024, 31, 591–595. [Google Scholar]
- Cao, R.Z.; Liu, B.Y.; Gao, F.F.; Zhang, X.F. A low-complex one-snapshot DOA estimation algorithm with massive ULA. IEEE Commun. Lett. 2017, 21, 1071–1074. [Google Scholar] [CrossRef]
- Qian, C.; Huang, L.; Sidiropoulos, D.N.; So, C.H. Enhanced PUMA for direction-of-arrival estimation and its performance analysis. IEEE Trans. Signal Process. 2016, 64, 4127–4137. [Google Scholar] [CrossRef]
- Khanna, S.; Murthy, C.R. On the Support Recovery of Jointly Sparse Gaussian Sources via Sparse Bayesian Learning. IEEE Trans. Inf. Theory 2022, 68, 7361–7378. [Google Scholar] [CrossRef]
- Qiao, H.; Pal, P. On Maximum-Likelihood Methods for Localizing More Sources than Sensors. IEEE Signal Process. Lett. 2017, 24, 703–706. [Google Scholar] [CrossRef]
- Pote, R.R.; Rao, B.D. Maximum Likelihood-Based Gridless DoA Estimation Using Structured Covariance Matrix Recovery and SBL with Grid Refinement. IEEE Trans. Signal Process. 2023, 71, 802–815. [Google Scholar] [CrossRef]
- Ma, Y.N.; Cao, X.B.; Wang, X.R. xMISC: Enhanced off-grid DOA estimation by corrected power Bayesian inference using difference coarray. Eng. Technol. 2019, 21, 7989–7993. [Google Scholar]
- Fu, M.C.; Zheng, Z.; Wang, W.Q.; So, H.C. Coarray Interpolation for DOA Estimation Using Coprime EMVS Array. IEEE Signal Process. Lett. 2021, 28, 548–552. [Google Scholar] [CrossRef]
- Fu, M.C.; Zheng, Z.; Wang, W.Q.; So, H.C. Virtual Array Interpolation for 2-D DOA and Polarization Estimation Using Coprime EMVS Array via Tensor Nuclear Norm Minimization. IEEE Trans. Signal Process. 2023, 71, 3637–3650. [Google Scholar] [CrossRef]
- Fu, M.C.; Zheng, Z.; Wang, W.Q.; So, H.C. DOA Estimation of Mixed Circular and Noncircular Sources Using Nonuniform Linear Array. IEEE Trans. Aerosp. Electron. 2022, 58, 5703–5710. [Google Scholar]
- Shi, J.P.; Wen, F.Q.; Liu, T.P. Nested MIMO Radar: Coarrays, Tensor Modeling, and Angle Estimation. IEEE Trans. Aerosp. Electron. 2021, 57, 573–585. [Google Scholar] [CrossRef]
- Alawsh, S.A.; Muqaibel, A.H. Sparse DOA Estimation Based on Multi-Level Prime Array with Compression. IEEE Access 2019, 7, 70828–70841. [Google Scholar] [CrossRef]
- Tan, Z.; Nehorai, A. Sparse direction-of-arrival estimation using co-prime arrays with off-grid targets. IEEE Signal Process. Lett. 2014, 21, 26–29. [Google Scholar] [CrossRef]
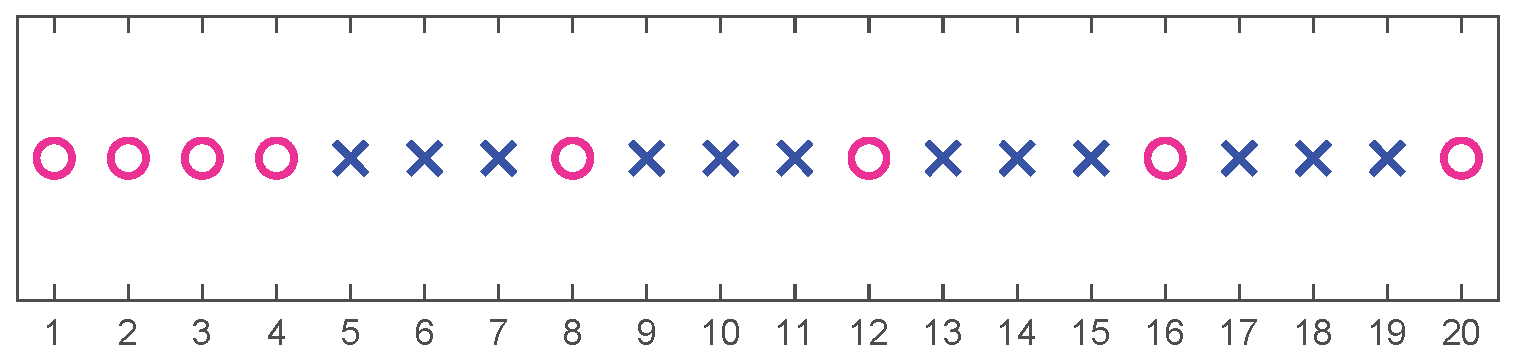


| Algorithm | Computational Complexity |
|---|---|
| Search-based [19] | |
| EPUMA [20] | |
| SS-MUSIC [15] | |
| Proposed method |
| Algorithm | Search-Based | EPUMA | SS-MUSIC | Proposed |
|---|---|---|---|---|
| Conditions | ||||
| ULA (fewer sources) (10 snapshots) | 0.475 | 0.242 | 0.255 | 0.214 |
| ULA (fewer sources) (100 snapshots) | 0.393 | 0.070 | 0.124 | 0.068 |
| NLA (fewer sources) (10 snapshots) | 0.294 | 0.118 | 0.181 | 0.110 |
| NLA (fewer sources) (100 snapshots) | 0.264 | 0.037 | 0.105 | 0.036 |
| NLA (more sources) (10 snapshots) | 0.214 | 0.160 | 0.205 | 0.140 |
| NLA (more sources) (100 snapshots) | 0.154 | 0.046 | 0.122 | 0.043 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Wang, J.; Cao, L.; Guo, P.; Fan, G. An Effective Off-Grid DOA Estimation Algorithm Using Difference Coarrays with Limited Snapshots. Appl. Sci. 2025, 15, 5668. https://doi.org/10.3390/app15105668
Ma Y, Wang J, Cao L, Guo P, Fan G. An Effective Off-Grid DOA Estimation Algorithm Using Difference Coarrays with Limited Snapshots. Applied Sciences. 2025; 15(10):5668. https://doi.org/10.3390/app15105668
Chicago/Turabian StyleMa, Yanan, Jian Wang, Lu Cao, Pengyu Guo, and Guangteng Fan. 2025. "An Effective Off-Grid DOA Estimation Algorithm Using Difference Coarrays with Limited Snapshots" Applied Sciences 15, no. 10: 5668. https://doi.org/10.3390/app15105668
APA StyleMa, Y., Wang, J., Cao, L., Guo, P., & Fan, G. (2025). An Effective Off-Grid DOA Estimation Algorithm Using Difference Coarrays with Limited Snapshots. Applied Sciences, 15(10), 5668. https://doi.org/10.3390/app15105668







