Abstract
Torsional vibration dampers effectively mitigate torsional oscillations and additional stresses in diesel engine crankshaft systems, ensuring operational safety and reliability. Traditional damper selection principles, grounded in dual-pendulum dynamic models, focus on minimizing maximum torsional angles but fail to accurately characterize vibration behaviors in multi-cylinder engines. This study addresses this limitation by investigating dynamic modeling and numerical methods for an eight-cylinder diesel crankshaft system. A torsional vibration model was developed using Cholesky decomposition and the Jacobi sweep method for free vibration analysis, followed by dynamic response calculations through model decoupling and modal superposition. Parameter optimization of the damper was achieved via the NSGA-II multi-objective algorithm combined with a Bayesian-hyperparameter-optimized BP neural network. The results show that high-inertia-ratio dampers effectively suppress vibration and stress, while low-inertia-ratio configurations require approximately 20% elevated tuning ratios beyond theoretical parameters to achieve an additional 5% stress reduction, albeit with amplified torsional oscillations. Additionally, the study critically evaluates the numerical reliability of conventional dual-pendulum-based tuning ratio selection methods. This integrated approach enhances the precision of damper parameter matching for multi-cylinder engine applications.
1. Introduction
The crankshaft system, a core component of diesel engines, operates under complex conditions and directly impacts engine power output, making the study of its vibrations—particularly torsional oscillation suppression—a long-standing research priority. Conventional mitigation methods involve installing torsional vibration dampers at the crankshaft free end, where optimal damper parameter selection critically determines vibration control efficacy [1,2,3,4]. Although traditional damper selection relies on dual-pendulum models, the inherent simplicity of this low-degree-of-freedom framework inevitably introduces inaccuracies and uncertainties when characterizing torsional dynamics in multi-cylinder engine systems. Furthermore, evolving demands for diesel engine reliability necessitate more comprehensive and precise damper-engine matching strategies. This study addresses these challenges through advanced dynamic modeling and systematic parameter optimization, establishing methodologies to enhance vibration suppression accuracy while balancing operational stresses—an approach particularly relevant for modern high-performance multi-cylinder configurations.
The early torsional vibration analysis of crankshaft systems primarily employed the Holzer method combined with dual-pendulum models for damper parameter matching. Subsequent studies have expanded optimization approaches. Zhang et al. [5] enhanced energy harvesting in regenerative arm-teeth shock absorbers via Taguchi-based tuning for ISO road profiles, and Liu et al. [6] achieved a 72.6% weight reduction in TI-6AL-4V brackets through topology optimization. Syrakos et al. [7] developed mathematical models linking piston displacement to viscosity-temperature interactions in silicone oil dampers, whereas Sezgen et al. [8] achieved a 50.17% vibration reduction in DMRV-TVD systems through genetic algorithm-driven viscous material optimization. While these efforts have significantly advanced parameter-specific tuning, limitations persist in holistically addressing multi-cylinder system complexities and balancing conflicting objectives like stress mitigation versus vibration suppression.
Recent progress has shifted toward multi-objective optimization frameworks. Liu et al. [9] pioneered adaptive MR-TVAs with axial/circumferential coil configurations that simultaneously achieve load-specific damping and lightweight design. However, Jee et al. [10] critically noted that conventional damper designs relying solely on theoretical optimal parameters risk over-idealization, warning that neglecting crankshaft stress variations under changing conditions may lead to fatigue fractures. This critical understanding has propelled the integration of sophisticated monitoring technologies into optimization processes [11,12,13]. Shatskyi et al. [14] devised shell dampers incorporating quasi-static hysteresis modeling for the control of industrial vibrations. Dai et al. [15] formulated a hybrid framework combining variational mode decomposition and least mean squares (VMD-LMS) and a long short-term memory (LSTM) network optimized by the northern goshawk algorithm, thereby achieving remarkable accuracy in spindle vibration prediction. Oh et al. [16] deployed low-power smart sensors integrated with near real-time deep neural networks, which enabled micron-level precision in spindle condition monitoring.
Despite significant progress in the optimization of dampers for vibration control, there are still aspects that require further improvement. The existing methods have the following issues: Firstly, the traditional dual-pendulum model is overly simplistic and fails to accurately represent the complex dynamics of multi-cylinder diesel engines. This limitation hinders the selection of dampers with optimal performance. Secondly, the current proprietary software has deficiencies in achieving the maximum efficiency and precision in the selection of dampers. Finally, the single-objective optimization framework has proven inadequate for reconciling the competing performance requirements inherent in modern crankshaft systems. To address these limitations, this study proposes an innovative multi-objective optimization approach. This new paradigm incorporates two key advancements: (1) A high-fidelity lumped-parameter model combined with the Cholesky–Jacobi hybrid algorithm for the calculation of torsional vibrations; (2) an enhanced Non-dominated Sorting Genetic Algorithm II (NSGA-II) framework, which is augmented by a Bayesian-optimized neural network. These innovations collectively enable the simultaneous minimization of the torsional angle and the stress peak. This method effectively overcomes the oversimplification of previous models and computational bottlenecks, providing a systematic solution for multi-criteria crankshaft optimization. It significantly differs from traditional single-objective methods and software-dependent methodologies, offering a more comprehensive and efficient optimization strategy.
2. Research Methodology
2.1. Torsional Vibration Calculation Model
The lumped-parameter model remains a highly efficient approach for torsional vibration analysis due to its simplified structure and strong correlation with experimental data [17,18]. Figure 1 illustrates this methodology applied to an eight-cylinder diesel engine crankshaft, where the system is discretized into 20 rotational degrees of freedom with concentrated masses: J1 represents the combined moment of inertia of the front shaft and main journal, J20 corresponds to the rear shaft and flywheel assembly, and J19 characterizes the rear shaft with crank throws. Intermediate masses J2–J18 model individual crank throws and pins, incorporating reciprocating masses at the crankpins. System dynamics are further defined by Cri (internal crankshaft damping), Coi (cylinder-piston assembly damping), and Ki (the torsional stiffness of the shaft segments, i = 1–19). This configuration balances computational efficiency with mechanical fidelity. This is particularly advantageous for iterative optimization processes that require fast parameter scanning. The internal crankshaft damping is viscous damping, while the cylinder-piston damping constitutes hybrid damping. The computational model in this study is based on an idealized formulation that disregards temperature variations and clearance effects.
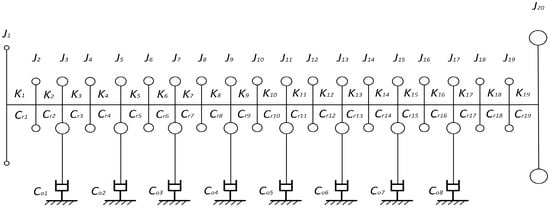
Figure 1.
Aggregate parameter model diagram.
The torsional vibration dynamic model of the eight cylinder diesel engine is
where is the rotational moment of inertia matrix, is the damping matrix, is the stiffness matrix, and is the torque excitation. The torsion angle of the corresponding unit for the shaft system is . And the above matrix of the simplified crankshaft model can be expressed as:
In the simplified crankshaft model employing the lumped parameter method for dynamic characteristic analysis, a typical crankshaft system primarily consists of stepped shaft segments and periodically distributed crank throws [19]. For a typical hollow cylinder, its torsional stiffness can be expressed as
where is the shear elastic modulus, is the length of shaft end, is the outer diameter of the shaft end, and is the inner diameter of the shaft end.
Due to diameter transitions in stepped shafts, the thicker segments exhibit negligible deformation, and their torsional stiffness can be expressed as
where is the length of the thin segments, is the length of the thick segments, is the diameter of the thin segments, is the diameter of the thick segments, and is the length of the coarse axis that does not participate in deformation.
The crankshaft is subjected to torsional stress during engine operation, assuming that the main journal and connecting rod journal only undergo pure torsional deformation, and the crank arm only undergoes pure bending deformation; its torsional stiffness can be expressed as
where is the main spindle neck outer diameter, is the inner diameter of the spindle neck, is the outer diameter of the crankshaft pin, is the inner diameter of the crankshaft pin, is the crank pin length, is the length of the main spindle neck, is the thickness of the curved arm, is the turning radius, and is the width of the crank arm.
2.2. Free Vibration Calculation
The current free vibration analysis of crankshaft systems predominantly employs the Holzer method, which involves laborious tabular computations. To enhance computational efficiency and adaptability, this study adopts numerical approaches for solving free vibration equations. Firstly, the differential equation of free vibration [20] is
Let its general solution be
where is the n-order mode array vector, which is called the main array of the system; is the circular frequency; and is the initial phase. Substituting the solution of the equation into Equation (5) yields
The symmetric positive definite mass matrix can be decomposed into
due to being a lower triangular matrix. The generalized eigenvalue eigenvector problem (4) can be transformed into a standard eigenvalue eigenvector problem
where the eigenvalue of the matrix is the square of the natural circular frequency of the system, and its corresponding eigenvector is . The matrix is represented as
The symmetric positive-definite property of the matrix facilitates efficient eigenvalue and eigenvector computation. However, the multi-degree-of-freedom crankshaft model adopted in this study, while improving analytical accuracy, introduces numerical challenges due to significant disparities between rotational inertia and torsional stiffness across shaft segments. Such mechanical heterogeneity results in ill-conditioned matrices, where high condition numbers degrade computational precision, causing eigenvalue distortion or even divergence in eigenvector solutions. This inherent instability underscores the necessity of robust numerical algorithms tailored for systems with extreme parameter variations, particularly when balancing computational efficiency against fidelity in torsional vibration analysis.
For systems with limited degrees of freedom and potential zero-frequency modes, the Jacobi iterative method remains practical due to its simplicity. While the Lanczos method offers superior precision and flexibility for large-scale structural vibration analyses, its higher computational overhead renders it less suitable for crankshaft-specific applications. To address systems with limited torsional degrees of freedom and poor numerical conditioning, this study enhances the Jacobi Screening method by incorporating dynamic threshold mechanisms. The specific iterative process is shown in Figure 2.
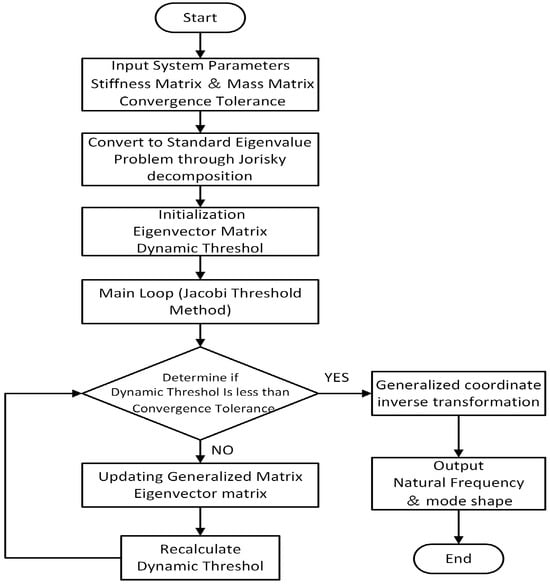
Figure 2.
Schematic diagram of free vibration calculation.
These adaptations systematically reduce computational redundancy and oscillation artifacts—common pitfalls in ill-conditioned crankshaft models—thereby improving both convergence rates and solution accuracy. The refinements strike an optimal balance between algorithmic robustness and computational economy, particularly critical when resolving closely spaced eigenvalues or mitigating round-off errors in systems exhibiting extreme stiffness-to-inertia ratios. This tailored approach circumvents the excessive resource demands of Lanczos methods while surpassing conventional Jacobi iterations in precision, making it uniquely suited for torsional vibration analyses where model fidelity and numerical stability outweigh sheer computational scale. The formula is
where is the constant term of the -th equation, represents the element in the -th row and -th column of the coefficient matrix, indicates the value of the -th element after the iteration, is the old value from the -th iteration of the element, and represents the diagonal elements of the coefficient matrix.
The case study employs an eight-cylinder diesel engine with a cylinder bore of 170 mm, crank radius of 100 mm, and connecting rod length of 360 mm. Free vibration characteristics were computed using three methodologies: the conventional Jacobi iterative method, the modified Jacobi screening method proposed in this study, and the Lanczos method via ANSYS commercial software. The stability and fatigue life of the crankshaft system are primarily influenced by the natural frequencies of its lower-order modes, whereas higher-order modes predominantly induce localized vibrations with a negligible impact on the global dynamic behavior [21]. Consequently, this study validates the accuracy of the numerical model by comparing the first five natural frequencies of the crankshaft system against simulation data.
As summarized in Table 1, the modified Jacobi sweep demonstrates exceptional agreement with Lanczos-derived results, exhibiting frequency deviations below 1% across all calculated modes. This precision validates the numerical stability of the threshold-enhanced Jacobi algorithm despite the system’s inherent stiffness-inertia disparities. These findings confirm the method’s robustness in handling ill-conditioned matrices typical of multi-cylinder crankshaft models, effectively bridging the gap between simplified numerical method and high-fidelity finite element analyses.

Table 1.
Crankshaft natural frequency table.
2.3. Forced Vibration Calculation
In the dynamic analysis of mechanical systems, solving forced vibration responses necessitates incorporating the coupling effects of periodic external excitation loads and damping dissipation mechanisms. This process requires the application of the Fast Fourier Transform (FFT) to decompose the time-varying cylinder excitation torque into discrete harmonic components. Subsequently, based on the crankshaft’s structural modal parameters, the coupled multi-degree-of-freedom differential equations are decoupled into independent single-degree-of-freedom equations through modal coordinate transformation. The harmonic responses from each order are then superimposed to obtain the torque and additional stresses on the crankshaft system components, enabling subsequent investigations into parameter matching optimization for crankshaft vibration dampers.
The differential equation for forced torsional vibration of the crankshaft system is:
Per classification society standards [19], the first 12 harmonics of each cylinder’s output torque must be considered. Through engine excitation analysis, it is observed that the excitation torque diminishes with increasing harmonic order. Consequently, forced vibration analysis typically focuses on the vibrational responses of low-order dominant harmonics. For the eight-cylinder diesel engine case study, the single-cylinder excitation torque is expanded into a Fourier series:
where is the harmonic order, is the circular frequency corresponding to the fundamental frequency, is the phase angle of the -th harmonic, and is the amplitude of the -th harmonic.
The comprehensive response of nodes is the superposition of various harmonic responses. It can be expressed as:
where is the amplitude of the -th mode, is the circular frequency of the -th mode, and is the phase angle of the -th mode.
By calculating the comprehensive response of nodes and combining them with the corresponding torsional stiffness, the torque of each unit in the crankshaft system can be obtained. The magnitude of the torque of each unit in the crankshaft system is related to the displacement difference of its corresponding node. Therefore, the expressions for torque and additional stress can be expressed as:
In the above equation, is the torsional stiffness of the unit, is the maximum value of the time-domain response of the node, is the minimum value of the time-domain response of the node, and is the diameter of the circular cross-section where the unit is located.
To validate the accuracy of the proposed model and algorithm, comparative analyses were conducted using AVL Excite commercial software for torsional vibration calculations in the crankshaft system. As shown in Figure 3a,b, the results for dominant harmonic responses and torque amplitudes exhibit deviations of 4.04% and 1.78%, respectively, between the proposed method and Excite simulations. These minor discrepancies demonstrate high computational reliability, confirming the methodology’s suitability for optimizing torsional damper configurations in multi-cylinder engine systems. The close alignment with industry-standard software underscores the robustness of the numerical framework in balancing computational efficiency with predictive accuracy—a critical requirement for iterative design optimization under complex dynamic loading conditions.
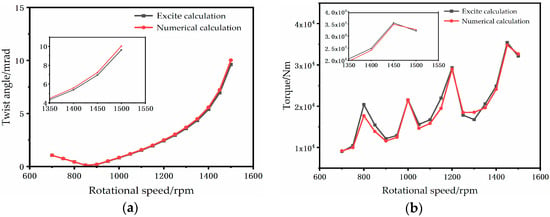
Figure 3.
Comparison of calculation results for eight cylinder shaft system: (a) diagram of primary harmonic response of shaft system; (b) diagram of maximum torque of shaft system.
2.4. Selection of Optimization Parameters for Shock Absorbers
Traditional torsional damper configuration, rooted in the dual-pendulum model, faces limitations in accurately characterizing multi-cylinder engine dynamics [22,23]. Nevertheless, empirical guidelines derived from decades of practice—such as maintaining a damper-to-crankshaft inertia ratio between 0.1 and 0.3—provide critical baseline parameters for initial optimization scoping. Given that excitation torque at the first-order natural frequency predominantly induces resonant stresses, damper tuning prioritizes the suppression of this dominant mode. In the dual-pendulum framework, the crankshaft system is simplified as a lumped inertial-elastic unit, where equivalent rotational inertia and torsional stiffness can expressed as:
Among them, is the moment of inertia of the -th node of the crankshaft system without torsional vibration dampers, is the torsional vibration amplitude of the -th node of the crankshaft system without torsional vibration dampers, and is the first-order natural frequency of the original crankshaft system.
According to Equations (17) and (18), the equivalent moment of inertia and equivalent torsional stiffness of the crankshaft system of an eight cylinder diesel engine without torsional vibration dampers are 22.20 and 10.34 , respectively.
According to the calculation of the double torsion pendulum model, when the inertia ratio is constant, the optimal tuning ratio is the damper-to-system frequency ratio. It can be expressed as
In the above equation, is the damper to crankshaft inertia ratio. When the optimal tuning ratio is chosen for the double pendulum model, the vibration amplitude of the crankshaft system is minimized, and the corresponding optimal damping ratio can be expressed as
Given the correlation between tuning ratio selection and critical rotational speeds, conventional optimal tuning ratios may not universally apply across a diesel engine’s full operating range. To address this, parameter optimization was conducted at both upper and lower bounds of the recommended inertia ratio (2.22–6.66 ). The search domain was expanded by ±5% around baseline tuning ratios and corresponding damping coefficients, yielding stiffness and damping optimization ranges of 0.771–2.025 and 483–2160 , respectively. A dataset of 10,000 randomly generated parameter combinations was systematically evaluated using the developed algorithm to quantify torsional responses and stress concentrations. This multi-variable screening approach enables the identification of Pareto-optimal damper configurations that simultaneously minimize vibrational amplitudes and fatigue-inducing stresses, particularly critical for resonant frequency mitigation under transient operating conditions.
2.5. Neural Network Training of Torsional Vibration Damper Parameters
The nonlinear relationships between torsional damper parameters (the moment of inertia, stiffness, and damping) and system responses (the maximum torsional angle and stress amplitudes) necessitate advanced modeling techniques. Neural networks excel at mapping these input–output correlations, yet their predictive accuracy critically depends on hyperparameter tuning. Bayesian optimization algorithms outperform conventional genetic algorithms in both precision and computational efficiency for hyperparameter selection [24,25,26], making them ideal for this high-dimensional problem.
Figure 4 presents the Bayesian optimization framework proposed in this study, which automates the adjustment of a fully connected neural network’s hidden layer architecture (depth/width) and learning rate. The framework integrates damper input features to constrain the hyperparameter search space. A Gaussian process surrogate model efficiently evaluates hyperparameter candidates, combined with cosine annealing learning rate scheduling and early stopping to prevent overfitting. This method significantly reduces prediction errors for vibration and stress metrics, resulting in a compact, high-fidelity surrogate model that supports multi-objective damper optimization under tight tolerance constraints.
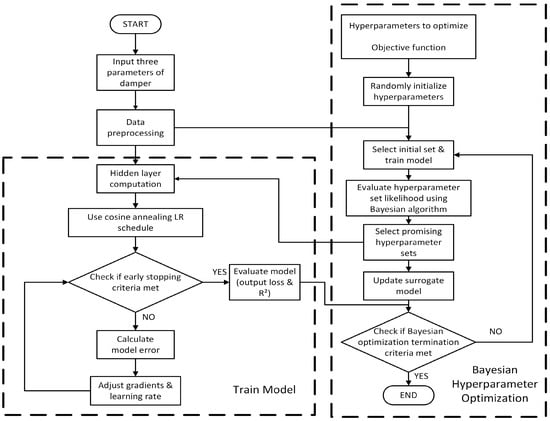
Figure 4.
Bayesian hyperparameter optimization neural network framework.
The relationship between torsional damper parameters and crankshaft responses is represented through a hyperparameter-optimized neural network. This optimized network enables the more accurate prediction of the crankshaft system’s dynamic responses and maximum component stress compared to conventional approaches.
The Bayesian optimization algorithm, functioning as a global optimization framework, relies on probabilistic surrogate models to approximate the probability distribution of the objective function. Through iterative cycles, the algorithm refines its search for optimal solutions. Central to this process is the construction of Gaussian process-based surrogate models, where parameter combinations are systematically evaluated to balance the exploration of underexamined regions and the exploitation of known high-performance domains—a mechanism critical for avoiding local optima traps in high-dimensional design spaces [27,28].
In the equation, is the mean function and is a covariance function.
The probabilistic surrogate model iteratively approximates the objective function by initializing prior information and progressively refining estimates through Bayesian updates. At each iteration, an acquisition function (Equation (22)) strategically selects high-potential evaluation points to balance the exploration of uncertain regions and the exploitation of known optima [29].
Figure 5 demonstrates the predictive performance of the Bayesian-hyperparameter-optimized neural network, achieving a coefficient of determination (R2) of 0.9683 on the training set and 0.9495 on the testing set. Corresponding mean squared error (MSE) values reached 0.0643 (training) and 0.076 (testing), confirming the model’s robust predictive capabilities. These metrics validate the network’s effectiveness in capturing nonlinear relationships between damper parameters and system responses.
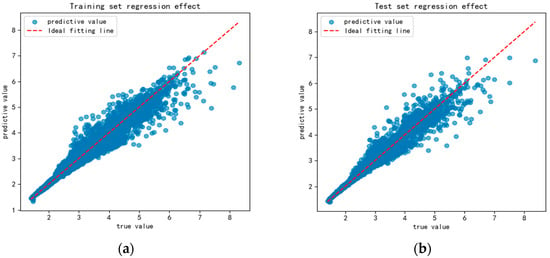
Figure 5.
Neural network regression effect diagram. (a) Training set testing regression effect diagram; (b) test set regression effect diagram.
The SHAP analysis quantifies the contributions of the torsional stiffness, moment of inertia, and damping coefficients to twist angle and stress, uncovering inherent contradictions in multi-objective optimization and parameter control. As shown in Figure 6, high torsional stiffness reduces twist deformation but amplifies stress concentration, demonstrating a vibration stress trade off. The bidirectional fluctuations of the moment of inertia confirm its nonlinear effects. The consistent positive impact of damping coefficients aligns with the engineering practices of adhering to upper-bound values. SHAP exposes the limitations of traditional methods and offers a quantitative foundation for strategies such as tuning ratio adjustments and stiffness compensation, bridging model insights to engineering implementation.
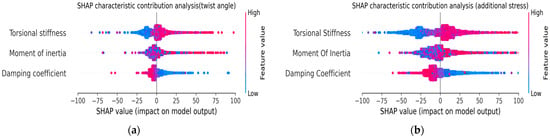
Figure 6.
SHAP analysis of crankshaft system response to torsional damper parameters. (a) SHAP contribution analysis of twist angle; (b) SHAP contribution analysis of additional stress.
2.6. Dual Objective Optimization of Torsional Vibration Dampers
The conventional dual-pendulum model, while historically valuable for torsional damper design, suffers from the oversimplification of multi-cylinder diesel engine dynamics, leading to inaccurate predictions of crankshaft vibration responses. Moreover, single-objective optimization approaches focusing solely on nodal angular displacements overlook the cumulative stress effects under variable operating conditions—a critical oversight that risks fatigue-induced crankshaft failures. To address these limitations, this study proposes a multi-objective optimization framework targeting the simultaneous minimization of both torsional angles and component stress amplitudes.
Leveraging the pre-trained Bayesian hyperparameter-optimized neural network model, this study implements the NSGA-II algorithm to conduct multi-objective optimization of torsional vibration responses in a crankshaft system equipped with torsional vibration dampers. The optimization framework explicitly targets two critical performance metrics: the minimization of nodal angular displacements and the reduction in component stress concentrations . By systematically varying three key damper parameters—the moment of inertia , torsional stiffness , and damping coefficient —within the theoretically constrained ranges prescribed by dual-pendulum modeling, the algorithm generates Pareto-optimal solution sets that quantify inherent tradeoffs between vibration attenuation and structural integrity preservation. This methodology advances conventional practices by resolving the oversimplification inherent in single-objective optimization approaches while maintaining compatibility with established engineering design boundaries.
The objective function is
The constraint range is
In the NSGA-II dual objective optimization algorithm model, the initial population size is set to 30, the crossover probability is 0.9, and the mutation probability is 0.3. After 1000 iterations of optimization, a Pareto front solution set was obtained, and the parameters of the torsional vibration damper with the best suppression effect were predicted.
3. Results
Figure 7 demonstrates the Pareto frontier solutions obtained through iterative optimization, revealing a positive correlation between the torsional damper’s rotational inertia and the maximum additional stress in shaft systems. Post-crowding distance calculation identifies damper parameters with damping coefficients approaching the upper bounds of specified ranges. Two optimal parameter sets emerge:
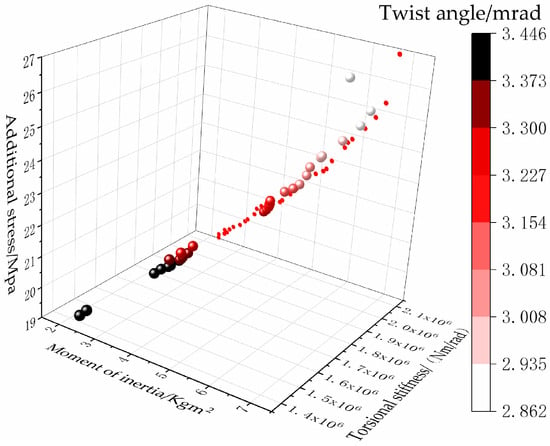
Figure 7.
Pareto optimization torsional damper parameter diagram.
For stress suppression: rotational inertia of 2.2–3.3 kg·m2 (inertia ratio of 0.1–0.15) with torsional stiffness of 1.3–1.7 (MN·m/rad).
For nodal response control: rotational inertia of 5.5–6.6 kg·m2 (inertia ratio of 0.25–0.3) with torsional stiffness of 1.5–1.9 (MN·m/rad).
To validate the accuracy of the Pareto predictions, this study compares Pareto-optimized parameters with computational results. As shown in Table 2, the parameters derived from Pareto optimization demonstrate less than 1% deviation from computational results in vibration suppression effectiveness, confirming the validity of Pareto-optimized torsional damper parameters.

Table 2.
Pareto optimization parameters.
Table 3 compares parameters between Pareto-optimized solutions and dual-pendulum model dampers with equivalent inertia ratios. The data demonstrate close alignment between high-inertia-ratio Pareto solutions and theoretical dual-pendulum model parameters. However, low-inertia-ratio solutions show significant discrepancies in torsional stiffness—the optimized configuration increases the stiffness adjustment ratio by approximately 20% while achieving a 5% reduction in additional stress.

Table 3.
Comparison parameters between Pareto optimization and theoretical shock absorbers.
4. Discussion
The findings of this study highlight critical advancements in torsional damper optimization for multi-cylinder diesel engines while revealing nuanced trade-offs between vibration suppression and stress mitigation. The following points synthesize the implications of these results within the broader context of torsional vibration control.
The modified Jacobi sweep algorithm, enhanced with dynamic thresholds, resolves ill-conditioned matrices in multi-degree-of-freedom crankshaft models, achieving <1% frequency deviations from ANSYS 19.2 benchmarks. Coupled with a Bayesian-optimized neural network and NSGA-II derived Pareto frontiers, this framework provides actionable engineering guidelines. High-inertia dampers are optimal for vibration-sensitive applications, while low-inertia solutions demand stiffness compensation to reconcile lightweight design with fatigue risks.
The current study presents several inherent limitations stemming from its idealized framework, which assumes constant stiffness and damping characteristics while neglecting critical physical factors such as friction and thermal effects. The linearized model formulation may restrict the analysis to steady-state conditions and potentially obscures transient operational dynamics that could influence system stability.
Future work should integrate multi-physics models (thermal-structural coupling) and validate Pareto-optimized parameters experimentally. This integrated methodology bridges theoretical simplifications and industrial demands, offering a systematic pathway for precision damper design in modern multi-cylinder diesel engines. By quantifying parameter interactions and exposing hidden trade-offs, it advances torsional vibration control toward adaptive, reliability-driven solutions.
5. Conclusions
To address the limitations of dual-pendulum-based damper configuration methods, this study proposes an integrated framework combining three critical advancements. First, a multi-degree-of-freedom dynamic model accurately characterizes crankshaft system dynamics, enabling high-precision free vibration analysis via the modified Jacobi sweep method—demonstrating superior numerical stability and computational accuracy compared to conventional Jacobi iterations. Harmonic responses are subsequently derived through decoupling transformations and modal superposition. Second, a Bayesian-hyperparameter-optimized neural network establishes nonlinear mapping relationships between damper parameters and system responses, achieving 96.8% prediction accuracy on validation datasets. SHAP interpretability analysis further quantifies inherent trade-offs: torsional stiffness suppresses the twist angle but amplifies stress concentration, while damping coefficients exhibit unidirectional benefits for vibration control, aligning with their upper-bound optimization. Finally, NSGA-II multi-objective optimization generates Pareto-optimal solutions that simultaneously minimize torsional amplitudes and component stresses. Key findings include:
- Multi-cylinder diesel crankshaft models frequently exhibit poor numerical conditioning. The modified Jacobi sweep method resolves this through threshold-controlled iterations, reducing eigenfrequency errors to <1% relative to ANSYS benchmarks.
- Traditional inertia ratio recommendations (0.1–0.3) fail to concurrently optimize vibration suppression and stress mitigation. SHAP analysis confirms bidirectional effects of inertia ratios: high inertia ratios (>0.25) effectively reduce torsional amplitudes but marginally impact stress concentrations, while low ratios (<0.15) decrease peak alternating stresses despite slightly increased vibrations.
- Tuning ratio optimization reveals distinct regimes: high-inertia dampers (0.25–0.3) achieve near-theoretical tuning ratios for balanced performance, whereas low-inertia configurations require 15–20% upward tuning ratio adjustments to maximize stress reduction. SHAP-based sensitivity maps validate this compensation mechanism, linking stiffness-tuning trade-offs to nonlinear inertia-stress coupling.
- Damping coefficients consistently converge to the upper bounds of dual-pendulum recommendations, enhancing both vibration attenuation and fatigue resistance. SHAP values reinforce this practice, showing damping’s unidirectional positive contributions.
Author Contributions
Conceptualization, Z.T. and Z.G.; methodology, Z.T.; software, Z.T.; validation, Z.T. and Z.G.; formal analysis, Z.G.; investigation, Z.T.; resources, Z.T.; data curation, Z.G.; writing—original draft preparation, Z.G.; writing—review and editing, Z.T.; visualization, Z.G.; supervision, Z.T.; project administration, Z.T.; funding acquisition, Z.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key R&D Program of China (14th Five-Year Plan), grant number 2023YFD2400800.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ali, A.; Ahmed, A.; Ali, M.; Azam, A.; Wu, X.; Zhang, Z.; Yuan, Y. A review of energy harvesting from regenerative shock absorber from 2000 to 2021: Advancements, emerging applications, and technical challenges. Environ. Sci. Pollut. Res. 2023, 30, 5371–5406. [Google Scholar] [CrossRef]
- Singh, W.; Srilatha, N. Design and analysis of shock absorber: A review. Mater. Today Proc. 2018, 5, 4832–4837. [Google Scholar] [CrossRef]
- Zheng, P.; Wang, R.; Gao, J. A comprehensive review on regenerative shock absorber systems. J. Vib. Eng. Technol. 2020, 8, 225–246. [Google Scholar] [CrossRef]
- Martande, S.; Jangale, Y.N.; Motgi, N.S. Design and analysis of shock absorber. Int. J. Appl. Inov. Eng. Manag. 2013, 2, 195–199. [Google Scholar]
- Zhang, R.; Wang, X. Parameter study and optimization of a half-vehicle suspension system model integrated with an arm-teeth regenerative shock absorber using Taguchi method. Mech. Syst. Signal Process. 2019, 126, 65–81. [Google Scholar] [CrossRef]
- Liu, Y.; Pan, L.; Cui, Q.; Meng, D. A Case Study on Structural Optimization Design of Shock Absorber Brackets in Automobile Suspension. IEEE Access 2023, 11, 131064–131072. [Google Scholar] [CrossRef]
- Syrakos, A.; Dimakopoulos, Y.; Tsamopoulos, J. Theoretical study of the flow in a fluid damper containing high viscosity silicone oil: Effects of shear-thinning and viscoelasticity. Phys. Fluids 2018, 30, 030708. [Google Scholar] [CrossRef]
- Sezgen, H.Ç.; Tinkir, M. Optimization of torsional vibration damper of cranktrain system using a hybrid damping approach. Eng. Sci. Technol. Int. J. 2021, 24, 959–973. [Google Scholar] [CrossRef]
- Liu, G.; Hu, H.; Ouyang, Q.; Zhang, F. Multi-objective optimization design and performance comparison of magnetorheological torsional vibration absorbers of different configurations. Materials 2023, 16, 3170. [Google Scholar] [CrossRef]
- Jee, J.; Kim, C.; Kim, Y. Design improvement of a viscous-spring damper for controlling torsional vibration in a propulsion shafting system with an engine acceleration problem. J. Mar. Sci. Eng. 2020, 8, 428. [Google Scholar] [CrossRef]
- Sun, Y.; Feng, T.; Jin, Z. Review on vibration signal analysis of rotating machinery based on deep learning. J. Phys. Conf. Ser. 2021, 1820, 012034. [Google Scholar] [CrossRef]
- Bagri, I.; Tahiry, K.; Hraiba, A.; Touil, A.; Mousrij, A. Vibration Signal Analysis for Intelligent Rotating Machinery Diagnosis and Prognosis: A Comprehensive Systematic Literature Review. Vibration 2024, 7, 1013–1062. [Google Scholar] [CrossRef]
- Guo, Q.; Yang, X.; Li, K.; Li, D. Parameters identification of magnetorheological damper based on particle swarm optimization algorithm. Eng. Appl. Artif. Intell. 2025, 143, 110016. [Google Scholar] [CrossRef]
- Shatskyi, I.; Velychkovych, A. Analytical model of structural damping in friction module of shell shock absorber connected to spring. Shock Vib. 2023, 2023, 4140583. [Google Scholar] [CrossRef]
- Dai, Y.; Liu, X.; Pang, J.; Li, Y.; Lv, Y.; Niu, Y. Vibration trend forecasting of motorized spindle on the basis of signal processing and deep learning. Nonlinear Dyn. 2025, 113, 17477–17490. [Google Scholar] [CrossRef]
- Oh, L.; Pitz, E.; Pochiraju, K. Spindle condition monitoring with a smart vibration sensor and an optimized deep neural network. J. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2023, 6, 021003. [Google Scholar] [CrossRef]
- Mangalasseri, A.S.; Mukunda, S.; Mahesh, V.; Ponnusami, S.A.; Harursampath, D. Vibration-based energy harvesting characteristics of functionally graded magneto-electro-elastic beam structures using lumped parameter model. J. Vib. Eng. Technol. 2022, 10, 1705–1720. [Google Scholar] [CrossRef]
- Safian, A.; Zhang, H.; Liang, X.; Wu, N. Dynamic simulation of a cylindrical roller bearing with a local defect by combining finite element and lumped parameter models. Meas. Sci. Technol. 2021, 32, 125111. [Google Scholar] [CrossRef]
- GD15-2021; Guidelines for Vibration Control on Ships. China Classification Society (CCS): Beijing, China, 2021.
- Yalcin, H.S.; Arikoglu, A.; Ozkol, I. Free vibration analysis of circular plates by differential transformation method. Appl. Math. Comput. 2009, 212, 377–386. [Google Scholar] [CrossRef]
- Mayes, R.L.; Pacini, B.R.; Roettgen, D.R. A modal model to simulate typical structural dynamic nonlinearity. In Dynamics of Coupled Structures, Volume 4: Proceedings of the 34th IMAC, A Conference and Exposition on Structural Dynamics 2016; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Repin, S.; Litvin, R.; Kuzmichev, V.; Vorontsov, I. Automotive shock absorbers’ applicability for damping resonant oscillations in construction machines. Archit. Eng. 2021, 6, 81–87. [Google Scholar] [CrossRef]
- Maureira-Carsalade, N.; Villagrán-Valenzuela, M.; Sanzana-Jara, D.; Roco-Videla, A. Proof of concept of a novel frictional shock absorber; analytical model and experimental analysis. Eng. Struct. 2021, 230, 111657. [Google Scholar] [CrossRef]
- Wang, X.; Jin, Y.; Schmitt, S.; Olhofer, M. Recent advances in Bayesian optimization. ACM Comput. Surv. 2023, 55, 1–36. [Google Scholar] [CrossRef]
- Alibrahim, H.; Ludwig, S.A. Hyperparameter optimization: Comparing genetic algorithm against grid search and bayesian optimization. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021. [Google Scholar]
- Turner, R.; Eriksson, D.; McCourt, M.; Kiili, J.; Laaksonen, E.; Xu, Z.; Guyon, I. Bayesian optimization is superior to random search for machine learning hyperparameter tuning: Analysis of the black-box optimization challenge 2020. In Proceedings of the NeurIPS 2020 Competition and Demonstration Track. PMLR, Virtual, 6–12 December 2020. [Google Scholar]
- Wu, K.; Kim, K.; Garnett, R.; Gardner, J.R. The behavior and convergence of local bayesian optimization. Adv. Neural Inf. Process. Syst. 2023, 36, 73497–73523. [Google Scholar]
- Victoria, A.H.; Maragatham, G. Automatic tuning of hyperparameters using Bayesian optimization. Evol. Syst. 2021, 12, 217–223. [Google Scholar] [CrossRef]
- Nguyen, X.D.J.; Liu, Y. Methodology for hyperparameter tuning of deep neural networks for efficient and accurate molecular property prediction. Comput. Chem. Eng. 2025, 193, 108928. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).