Abstract
Middle rock pillars (MRPs) play a crucial role in the stability of bifurcated small clear-distance tunnels. Assessing the stability of the MRP is a key challenge in design and construction. This study focuses on the bifurcated small clear-distance section of the Xiamen Haicang Shugang evacuation channel underground interchange tunnels. The stability criteria for the MRP during both the early design and later construction stages were analyzed by using the strength reduction method (SRM) via numerical simulations. In the design stage, the SRM was applied to determine the stability limit state of the MRP. Relationships between rock mass density, cohesion, and elastic modulus were identified, and these parameters were combined with basic cohesion values for an initial stability assessment. During the construction stage, the full excavation process was analyzed by examining the distribution and changes in the plastic zone of the rock mass. Two key construction stages, a 10 m excavation on the main line upper step and a 10 m excavation on the ramp upper step, were identified as points where the plastic zone of the MRP began to form on the sidewall and the center, respectively. Multiple linear regression was used to determine the displacement, stress, and plasticity criteria for MRP stability. A comprehensive criteria formula incorporating the width–span ratio, tunnel vault settlement, and horizontal clearance convergence was developed, providing technical guidance and a scientific basis for similar projects.
1. Introduction
Rapid urbanization has led to a significant increase in the urban population, causing a growing demand for urban transportation that cannot be met by the limited ground area available. This has resulted in a worsening problem of ground traffic bottlenecks. As a solution, underground urban transportation has emerged as an excellent alternative because it is not restricted by ground conditions. Today, it has become one of the main approaches for developing and utilizing underground spaces in cities [1,2,3,4,5,6]. The critical nodes that connect the underground transportation network are underground interchange tunnels. These tunnels can be classified into two types: planar and three-dimensional intersections. The planar intersection type, known as bifurcated tunnels, typically consists of a separated portion, a small clearance section, a continuous arch section, and a large span section [7]. A specific type of tunnel layout is the small clear-distance tunnel, where the double tunnel clear distance is less than the recommended value [8]. Small clear-distance tunnels are widely used because they offer advantages such as easier line extension, reduced land occupation, lower costs, simpler construction techniques, and fewer terrain constraints [9,10,11,12,13,14]. However, the middle rock pillar (MRP) between small-clearance tunnels is relatively thin, which means that it is subjected to multiple disturbances during construction, leading to more complex stresses on the surrounding rock [15,16,17,18]. The MRP plays a crucial role in supporting small clear-distance tunnels, and excavating tunnels inevitably damages and affects their mechanical behavior. Therefore, the key technology in constructing small clear-distance tunnels lies in strictly controlling the damage caused during tunnel construction. Ensuring that the MRP has sufficient strength and stability is vital [19,20]. Consequently, it is necessary to determine the bearing state of the MRP to ensure the safety of small-clearance tunnel construction [21,22].
During the construction process of small-clearance tunnels, the excavation of the advance tunnel alters the initial stress state of the surrounding rock. This, in turn, affects the excavation of the backward tunnel and can potentially lead to the deformation of the MRP. Failure to implement appropriate protective measures promptly can further escalate the occurrence of engineering accidents [23,24]. Numerous scholars have employed various methods, such as the complex function method [25], the bipolar coordinate method [26,27], the Schwarz alternation method [28,29], and other approaches [30], to derive the stress distribution in the surrounding rock of small-clearance tunnels. In addition, Li et al. [31], Zhang et al. [27], Xia [13], and Luo et al. [32] established different types of models to investigate the stress characteristics of MRPs and proposed judgment criteria for the stability of continuous arches and small-clearance tunnels. Moreover, the instability and failure characteristics of mid-adjacent rock under various construction conditions have been analyzed [13]. The stress distribution rule of the MRP in small interval tunnels can be approximated by calculating the interface normal stress and shear stress analysis via the concept of the reserved support hypothesis, along with considering the average stress and an additional bending moment of the MRP, ultimately leading to the final stress distribution of the rock wall [33].
In recent years, numerous experimental analyses, in situ monitoring studies, and numerical simulations have been conducted to evaluate pressures and deformations around small clear-distance tunnels. Lee et al. investigated the stability of small-clearance tunnels and the soil arching effect through centrifugal model tests and numerical simulations and revealed that the failure mode of the interbeds in small-clearance tunnels is similar to that of slopes, mostly involving shear failure [34]. Lei et al. proposed an experimental program to analyze the change in and distribution of tunnel pressures [35]. Based on a 3D large-scale geomechanical model test of excavation and support in a large cross-section tunnel, the progressive failure of the surrounding rock mass, as well as the evolution of deformation and stress in the rock mass, was studied [36,37].
Compared with theoretical analysis and model tests, numerical simulation offers several advantages, including shorter timeframes, lower costs, and higher calculation accuracy. As a result, it has become widely utilized in the calculation of small clear-distance tunnels [20,38,39]. Yao et al. employed a 2D elastoplastic numerical calculation method to investigate the stress and deformation characteristics of the MRP in parallel twin tunnels with surrounding rocks graded III, IV, and V. Their findings indicated that the stress and deformation of the MRP were adversely affected by the presence of a parallel tunnel with a smaller interval [39]. Liu and Zhou proposed the concept of rock–column zone division and calculated the yield proximity of surrounding rocks on the basis of numerical simulation results. This enabled them to assess the stability of the MRP via yield proximity criteria [40]. A novel nonlinear reinforcement analysis method was proposed for analyzing the stability of a large-span tail water branch tunnel with complex three-dimensional geometry [41]. Zhang et al. developed the yield approach index (YAI) function, which is based on the Mohr–Coulomb shear yield criteria and tensile yield criteria, to analyze the mechanical characteristics of rock that is shared between two styles of neighboring tunnels [42]. These studies were conducted via numerical analysis and centrifugal tests.
Considering the instability mode of the MRP, Mortazavi et al. conducted a numerical simulation to analyze the process of loading until destabilization occurred [43]. When examining the stability of the surrounding rock, the strength reduction method (SRM) is commonly employed [44,45,46]. The SRM, as a limit analysis method, offers the advantage of not requiring prior knowledge of the failure surface of the project. Consequently, it is effective in assessing overall failure in geotechnical engineering [47]. By utilizing the SRM, it is possible to determine the stability safety factor of the overall failure of a rock tunnel as a basis for tunnel design. The finite element SRM has gained wide popularity for analyzing the stability of rock surrounding tunnels [48,49,50]. Both the finite element limit analysis method and the SRM are employed to derive the stability factor formula of the tunnel face, which includes the penetration force, and apply it to actual tunnel engineering [51,52]. Xia et al. investigated the stability of tunnel-surrounding rock via the DDA method, the SRM, and catastrophe theory [53]. The stability coefficient of shallow tunnels was studied under the upper and lower bound theories of limit analysis by Yang and Huang, employing the strength reduction theory [54]. Zhou et al. used finite element SRM, physical model tests, and numerical simulations to study the influence of the principal stress direction on the stability of sandstone tunnels [55]. Zhou et al. proposed a quantitative calculation method for the stability coefficient of shallow tunnel faces and developed a support optimization system, clarifying the effectiveness of various reinforcement measures on face stability [56]. Recently, Yang et al. [57] systematically investigated the evolution of surrounding rock stability in multi-line parallel tunnels using the upper bound method with rigid translational elements, revealing that the middle rock pillar plays a dominant role in failure under small spacing conditions. Xu et al. [58] established three-dimensional collapse mechanisms for tunnel roofs based on a modified Mohr–Coulomb criterion and analyzed how tensile strength reduction and geometric characteristics influence stability numbers and required supporting pressures. Man et al. [59] developed a combined rigid-block failure model for evaluating face stability in large cross-section tunnels excavated by the bench method, considering weak interlayers, excavation footage, and bench geometry to enhance stability assessment accuracy. These studies have focused primarily on the distribution of surrounding rock pressure, analysis of stability-influencing factors, and damage modes of small-clearance tunnels. However, scholars have not yet reached a consensus on the stability criteria of the MRP for small-clearance tunnels. Therefore, there is a strong motivation to develop a simple yet rigorous approach to determine the stability of the MRP for small-clearance tunnels.
This study investigated the Xiamen Haicang Shugang evacuation channel underground interchange tunnels, focusing on ultrasmall clear-distance sections, with distances ranging from 1.03 to 5.0 m. To evaluate rock stability during the design phase, the SRM was used to determine the mechanical parameters for the limit state in small-spacing tunnels. Additionally, the SRM was combined with a detailed construction mechanics analysis, in which the arch bottom settlement and clearance convergence were used as independent variables to establish stability criteria. This method enables the assessment of various factors influencing the stability of the MRP. Extensive data analysis was conducted to explore the relationship between cross-sectional deformation in small clear-distance tunnels and the deformation and stress characteristics in different areas of the rock mass. On the basis of this analysis, stability criteria for the MRP were established, with a focus on displacement, stress, and plastic zone limits. These criteria provide a foundation for ensuring safe construction and guiding the implementation of reinforcement measures in tunnels.
2. Project Overview
The Xiamen Haicang Shugang evacuation channel underground interchange tunnel, known as the Lushu underground interchange, is located in Haicang District, Xiamen city, China (Figure 1). Luao Road runs along a north–south axis and intersects with the Haicang evacuation channel, forming an underground interchange with ramp tunnels A, B, C, and D. The A and D ramp tunnels are formed through the gradual bifurcation of Tunnel 2# of the Haicang evacuation channel. During this bifurcation process, a section of ultrasmall clear-distance tunnel, with a minimum clearance of 1.60 m, transitions into small clear-distance tunneling and then separated tunneling. Our research focused on the small clear-distance segment between the left line of Tunnel 2# and Ramp A. The small clear-distance segment of the main line of Tunnel 2# spans from ZK2+665 to ZK2+775 with section type number SX3 III, whereas the segment for Ramp A extends from AK1+600 to AK1+490 with section type number ZX III. The total length of this small-clearance study section is 110 m.
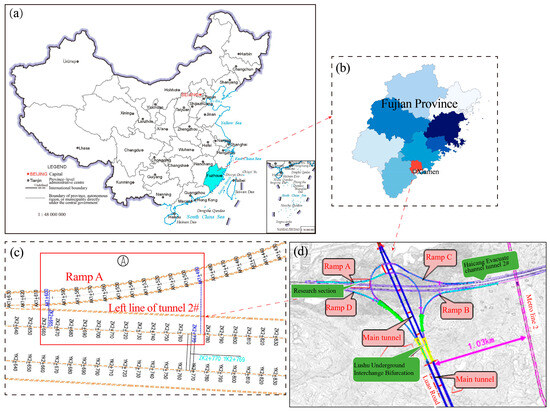
Figure 1.
The layout of the Xiamen Haicang Shugang evacuation channel underground interchange tunnel. (a) Map of China; (b) Fujian Province, China; (c) Research section; (d) Layout plan of Lushu underground interchange project. “#” denotes tunnel number.
In the SX3 III section, the maximum excavation span was 16.17 m, with a height of 11.32 m and a clearance span of 14.45 m. In the ZX III section, the maximum excavation span was 12.62 m, with a height of 10.40 m and a clearance span of 11.10 m. This SX3 III–ZX III section transitioned from a large cross-section segment.
According to the geological survey report, the surrounding rock in this section was primarily classified as grade III, based on the Chinese Standard for Engineering Classification of Rock Masses (GB 50218-2014). Classification is determined by factors such as weathering degree, rock mass structure, joint development, and groundwater influence. The small clear-distance section of the tunnel bifurcation passes through the second intrusion of granite stratum in the late Yanshan period, which is of medium-coarse grained structure, blocky structure, and dominated by medium weathering. It is characterized by joints and fissures, with the main joints oriented N10~39° E/65~85° S. Some fissures are filled with quartz veins, and the rock mass is relatively intact. The groundwater consisted of fissure water in bedrock, which is mainly stored in the joints and fractures of the granite.
3. Numerical Model and Material Parameters
3.1. Numerical Model
Tunnel sections were selected primarily for their pronounced clear-distance variation and their representation of typical ultrasmall clear-distance bifurcated tunnel configurations. The tunnel section selected in this study was the segment between Tunnel #2 and Ramp A from the Xiamen Haicang Shugang evacuation channel underground interchange project. This section featured typical small clear distances ranging from 1.6 m to 18.0 m, which resulted in varying mechanical behaviors of the MRP.
The numerical model was established by using ABAQUS (version 6.14) software. To minimize the boundary effect on the calculation results, the left and right boundaries, as well as the lower boundary of the model, were set four times the excavation span away from the tunnel. Thus, the model domain measured 200 m × 110 m × 160 m (Figure 2). The two tunnels intersected at an angle, with the main tunnel section aligned with the z-axis and the ramp section deviating from the z-axis by 8.28°, as shown in Figure 2a. The tunnels gradually transitioned from a small clear-distance configuration to separate tunnels. The numerical model was meshed using hexahedral elements, with local mesh refinement applied to key areas such as the tunnel excavation face and surrounding rock. To ensure the accuracy of the numerical results, a mesh sensitivity analysis was conducted. The mesh was refined iteratively in critical areas such as the excavation face and surrounding rock until the variation in displacement and stress results between successive mesh refinements was less than 5%. The C3D8R elements in ABAQUS were used to simulate the surrounding rock, tunnels, primary lining, secondary lining, and temporary support. The model comprises a total of 117,355 units, with the element grids of the excavated rock, primary lining, secondary lining, and temporary support shown in Figure 2. In terms of boundary conditions, the lateral boundaries were constrained to prevent horizontal displacements, the bottom boundary was fixed to prevent vertical displacements, and the top boundary was left free to simulate ground deformation.
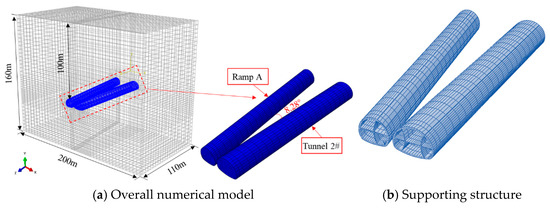
Figure 2.
Numerical model. The “#” denotes tunnel number.
3.2. Constitutive Models and Material Parameters
The study section involved surrounding rock grades III to V, although predominantly grade III. In the numerical simulation, the physical and mechanical parameters of the surrounding rock and the lining were adjusted based on the investigation report. The surrounding rock was treated as elastic–plastic material, adhering to the Mohr–Coulomb failure criteria to describe the behavior of rocks and soils under applied stress, with cohesion and the internal friction angle as parameters of the failure criteria. The lining structure was considered an elastic body, with the elastic modulus and Poisson’s ratio as parameters of the failure criteria. The Mohr–Coulomb constitutive model was used for calculation. This model is consistent with previous research and has been validated for its reliability [19]. The material parameters of the model are provided in Table 1.

Table 1.
Material parameters used in the numerical analysis (Mohr–Coulomb model).
4. Stability Criteria of the MRP Before Construction
Assessing and evaluating the stress and deformation of rock during the design process was crucial for ensuring the safe control of early small clear-distance tunnels. This evaluation ensured that the deformation and stress of the rock remained within acceptable limits, allowing safe excavation. By adhering to these criteria, the construction process can be dynamically managed to maintain safety.
To study the stability changes in small clear-distance tunnels under various parameters, the grade of the surrounding rock was focused on and quantified the mechanical properties of the MRP. The mechanical properties of the surrounding rock were influenced mainly by cohesion [13]. When the stability criteria of the rock surrounding a tunnel were calculated, it was crucial to determine the failure limit state of the MRP first. The cohesion in the failure limit state of the MRP was determined via the SRM. In the SRM, cohesion was obtained by gradually increasing the weakening coefficient of the original rock and the cohesive properties of the soil. This value was then substituted into finite element numerical software for iterative trial calculations until the program stopped solving due to calculation convergence. At this point, the rock mass was considered to be in the ultimate state of instability, and the cohesion obtained was the cohesion in the ultimate state of tunnel stability. For the purposes of simulation, a standard construction condition known as the bench method was selected. The main line tunnel was excavated first at a staggered distance of 15 m, serving as the simulation model. The strength reduction method was used to vary the cohesion from 0.2 MPa to 2.0 MPa to explore the failure process of tunnel stability.
Figure 3 illustrates the variation process with different cohesion values. The clear-distance value, d, at the non-convergence position, steady state, and clear distance d were represented on the right axis of the histogram. The length of the main line tunnel excavation, L, was represented on the main axis of the folded line graph. A non-convergence state was indicated by a numerical value of 1, whereas a convergence state was represented by 2. In the steady state, the cohesion ranged from 1.4 MPa to 2.0 MPa, and the length of the mainline tunnel excavation reached a maximum value of 110 m, indicating the completion of the excavation of the two tunnels. On the other hand, a cohesion range of 0.2 MPa to 1.3 MPa indicated a non-convergence state, with the excavation of the two tunnels not yet completed. Consequently, under specified conditions of density and elastic modulus, a stable critical state existed within the cohesion range of 1.3 MPa to 1.4 MPa. When the cohesion was less than 1.32 MPa, the calculation did not converge, but when the cohesion ranged from 1.32 MPa to 2.0 MPa, the calculation converged. Thus, a cohesion value of 1.32 MPa represented the failure limit of the MRP.
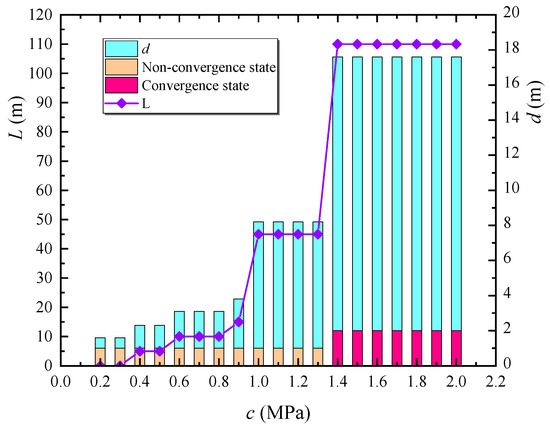
Figure 3.
Variation process of overall stability and cohesion of tunnel.
Therefore, in the design stage, the stability state of the tunnel can be determined in the early stage by comparing the cohesion value of the rock mass with the change process of the cohesion in Figure 3. However, the density and elastic modulus of the rock are also key factors influencing rock deformation and construction conditions. To eliminate the interference of multiple variables and isolate the influence of each parameter, a single-factor analysis approach was adopted. Specifically, a series of numerical simulations was conducted by varying the density and elastic modulus separately in predefined gradients while keeping other parameters constant. For each gradient level, the cohesion value gradually increased in 0.1 MPa increments to identify the minimum cohesion required for numerical convergence of the model. The corresponding minimum cohesion values that made the model converge were obtained through simulations under different densities and moduli, which are shown in Table 2 and Table 3, respectively.

Table 2.
Density and the corresponding convergence value of cohesion.

Table 3.
Elastic modulus and the corresponding convergence value of cohesion.
Based on the data in Table 2 and Table 3, a relationship curve between the density, elastic modulus, and cohesion value was derived and illustrated in Figure 4. As the density and elastic modulus increased, the minimum cohesion required for model convergence also increased. The influence of different densities and elastic moduli on the cohesion value ranged between 0.1 MPa and 0.3 MPa. Therefore, during the design stage, the cohesion values of the surrounding rock, as depicted in Figure 4, can be combined with the corresponding density and modulus of elasticity to preliminarily assess the stability of the small-clearance tunnels.
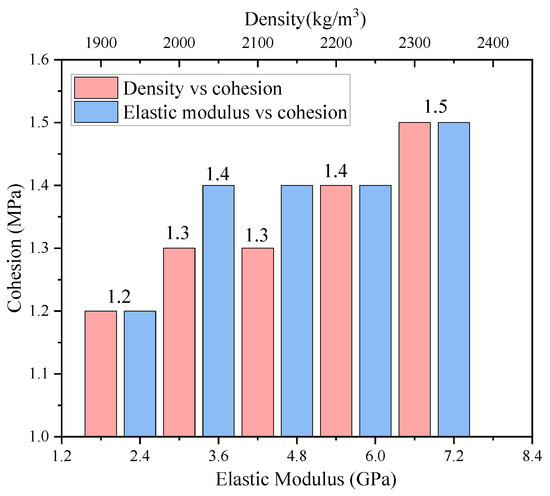
Figure 4.
Relationship between density, elastic modulus, and cohesion.
5. Stability Criteria of the MRP During Construction
5.1. Numerical Cases Design
To assess the stability of intercalated rock based on criteria, it is necessary to determine the lower limit of the stability value for intercalated rock. If it exceeds this value, it can be considered stable, and the parameters of the surrounding rock at each level fall within a certain range. To characterize the variation characteristics of the plastic zone in the MRP, adjustments were made to the parameters of grades III–IV based on the previous section. Using the previous criteria, a cohesion value adjustment unit of 0.01 MPa was selected, and the idea and method of strength reduction for the cohesion value were employed to find the limit state close to the failure of the MRP, thereby establishing the parameters. At this juncture, the cohesion value was determined to be 1.32 MPa, as indicated in Table 4. The initial state values of the surrounding rock in Table 4 represent the parameters of the surrounding rock before excavation after achieving in situ stress balance. During the excavation of the face, it is necessary to reduce the modulus of the excavated rock area to achieve the joint action of support and surrounding rock. Additionally, to account for the influence of factors such as large-scale mechanical work, blasting, and groundwater on the mechanical state of the intercalated rock, the plastic index of the MRP mass gradually decreased after each rock mass was excavated during the construction stage. The reduction range is displayed in Figure 5. Because cohesion was the main factor, it was reduced by 70%, so the cohesion of the MRP was reduced to 0.93 MPa.

Table 4.
Parameters of surrounding rock simulation.
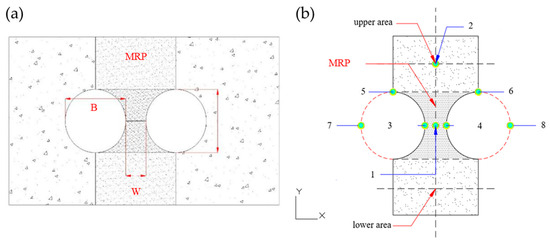
Figure 5.
Monitoring points of the MRP: (a) range of the MRP; (b) the layout of monitoring points for the MRP. W is the clearance between the two tunnels. B is the width of the tunnel.
To ensure safety control during the construction period of the small clear-distance tunnel, a total of 14 numerical simulation working conditions were designed, as shown in Table 5. These conditions consisted of the basic working conditions and various comparative working conditions. In particular, case 14 focused on the impact of the built-up tunnel crossing above. By analyzing the stress, displacement, and plastic zone under different working conditions, combined with the width–span ratio (W/B) in the rock classification, comprehensive stability criteria for the rock were developed under different criteria and influence factors.

Table 5.
Numerical modeling scheme design.
In terms of the areas divided by the MRP, the upper area experienced significant vertical displacement, whereas the middle area experienced unfavorable horizontal displacement and concentrated stress. To establish a reliable dataset for the various criteria of the MRP and apply them effectively to actual construction monitoring, it was necessary to correlate the characteristic data of the MRP with the characteristic data on the cross-sectional profile of the two tunnels. Monitoring points were set up accordingly, with points 1–2 representing internal points of rock intercalation and points 3–6 representing common points of rock intercalation, the tunnel arch waist, and the vault. Additionally, points 7–8 were arranged at the arch waist on the other side of the two tunnels, as shown in Figure 5.
5.2. Displacement Criteria
5.2.1. Horizontal Displacement Criterion
The displacement values of the monitoring points were extracted under various working conditions after tunnel penetration. Monitoring point 1 was an internal horizontal displacement monitoring point located in the central region of the MRP. Monitoring points 3 and 7 were the horizontal displacement monitoring points for the right and left arch waists of the ramp tunnel, whereas monitoring points 4 and 8 were the horizontal displacement monitoring points for the left and right arch waists of the mainline tunnel. The convergence of the horizontal headroom of the two tunnels applied in the field can be determined by comparing the horizontal displacement of the two tunnel arches. The distribution of horizontal displacement data points under different working conditions was obtained statistically, as shown in Figure 6.
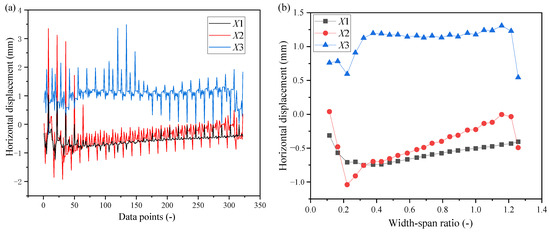
Figure 6.
Distribution of horizontal displacement data points: (a) distribution of horizontal displacement data points; (b) trend of horizontal displacement with width–span ratio under working condition 1. X1 is the horizontal displacement of point 1. X2 is the horizontal clearance convergence of the ramp tunnel. X3 is the horizontal clearance convergence of the main tunnel.
The distribution of horizontal displacement data under various conditions is illustrated in Figure 6. As shown in Figure 6a, convergence data points for the mainline tunnel were predominantly positive, indicating a bulging tendency at both arch waists. This bulging at the left arch waist caused compression in the MRP, influencing its boundary shape. In contrast, the ramp tunnel’s horizontal convergence data were mostly negative, suggesting an inward bulging of both arch waists, which increased surrounding rock pressure on the ramp’s lining support system. The horizontal displacement at monitoring point 1 was also negative, indicating an overall horizontal shift towards the ramp side in the MRP’s central region. Notably, some anomalous data points of −2 mm and +3 mm were observed under case 8, which indicated an unstable state and failure points in the surrounding rock. These points corresponded to an unstable state and represented failure points under the surrounding rock level. Assessing the stability of the intermediate rock involved selecting deformation values close to the unstable state.
As seen in Figure 6b, the displacement trend displayed by the three curves shows a gradual decrease in stability as the width–span ratio increased, with a sharp change observed in the 0.2 to 0.3 range. However, the transition for the intermediate rock was relatively smooth, suggesting that horizontal displacement within the complete clear-distance range can be effectively predicted by the convergence value between the two tunnels.
The abovementioned horizontal displacement data points were analyzed via the multiple linear regression method. The horizontal displacement X1 at monitoring point 1 was considered the dependent variable, whereas the horizontal clearance convergence of ramp X2 and the horizontal clearance convergence of mainline tunnel X3 were treated as the independent variables. The multiple regression equation derived from the multiple linear regression equation is shown in Figure 7a. The data of X1 closely align with the regression plane, indicating a good fit of the multiple regression model. The analysis of residuals shows that the mean value of the residuals is close to zero, suggesting an unbiased model, as shown in Figure 7b. Overall, the multiple linear regression model provides a reasonable fit for the data, and the regression plane effectively demonstrates the relationships between X2, X3, and X1.
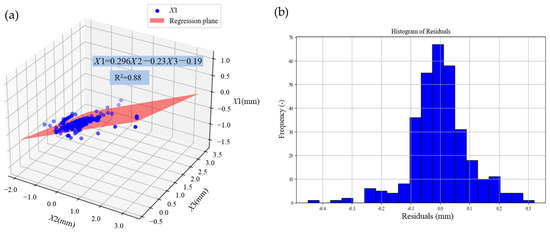
Figure 7.
Multiple regression model analysis: (a) regression plane; (b) histogram of residuals.
After eliminating the unstable data points in condition 8, a comparison diagram between the actual horizontal displacement and the predicted value of monitoring point 1 is presented in Figure 8. The predicted value closely matches the actual value, with most data points located below the actual point. This finding indicates that the predicted value is conservative and plays a protective role. The distributions of the real horizontal displacement at the center of the intermediate rock under various working conditions are shown in Figure 9. The horizontal displacement ranging from −0.8 mm to −0.4 mm constituted 90.3% of the total data points, with −0.6 mm to −0.4 mm accounting for 54.52% of the total data points. The maximum horizontal displacement recorded is −1.21 mm, which serves as the control limit. Therefore, the criterion for horizontal displacement can be determined via the following formula:
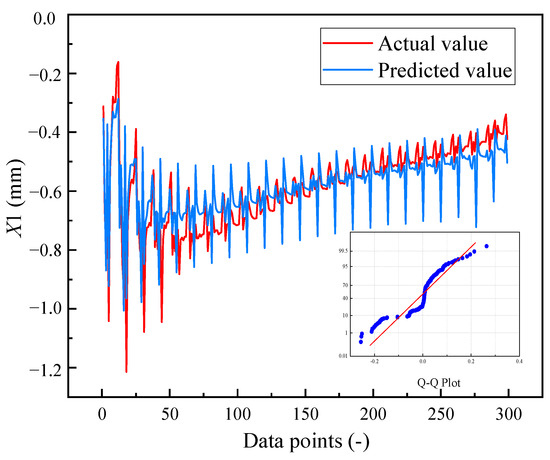
Figure 8.
Comparison of actual horizontal displacement and predicted value of X1. The inset shows a Q-Q plot of residuals, where the dots represent sample quantiles and the solid line represents theoretical quantiles under a normal distribution.
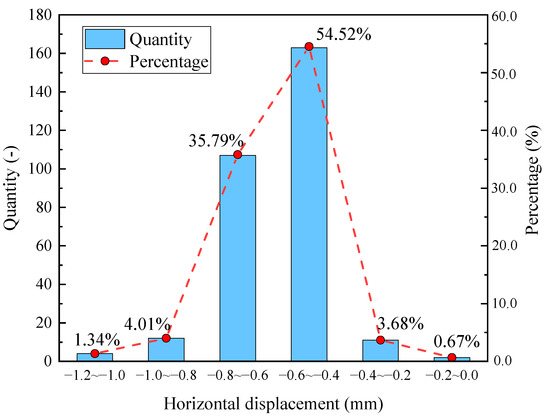
Figure 9.
Numerical distribution of the actual horizontal displacement at the center of the MRP.
5.2.2. Vertical Displacement Criterion
The distribution of each vertical displacement data point is depicted in Figure 10. Figure 10a shows that the vertical displacement data points in the upper area of the MRP are above the ramp and the vault data points of the main line tunnel, and the distribution is relatively stable. In Figure 10b, for example, in case 1, the curve change process is stable without any mutation points, indicating that the vertical displacement of the MRP can be uniformly analyzed within the full clear distance of the tunnel.
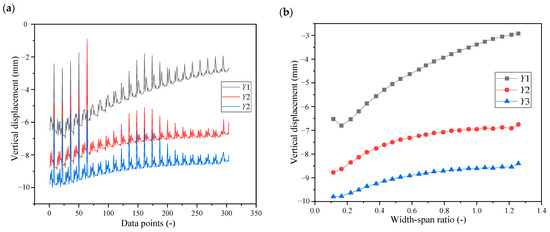
Figure 10.
Distribution of vertical displacement data points: (a) Distribution of vertical displacement data points; (b) Trend of vertical displacement with width–span ratio under case 1. Y1 is the vertical displacement of point 2. Y2 is the crown settlement of the ramp tunnel. Y3 is the crown settlement of the main tunnel.
The vertical displacement of the MRP through the vault settlement of two tunnels was predicted and analyzed via the multiple linear regression method with the same horizontal displacement. The dependent variable was the vertical displacement (Y1) at monitoring point 2, whereas the independent variables were the crown settlement of the ramp (Y2) and the crown settlement of the main tunnel (Y3). The relationship among these variables is shown in Figure 11a. The Y1 data closely matched the regression plane, indicating a good fit for the multiple regression model. The residual analysis revealed that the mean of the residuals was close to zero, indicating an unbiased model. Overall, the multiple linear regression model provided a reasonable fit for the data, and the regression plane effectively illustrated the relationships between Y2, Y3, and Y1.
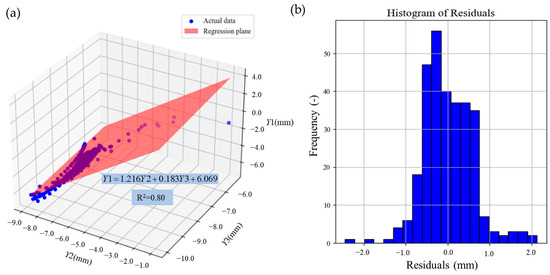
Figure 11.
Multiple regression model of the vertical displacement: (a) Regression plane; (b) Histogram of residuals.
The predicted vertical displacement was compared with the monitored vertical displacement, as shown in Figure 12. The predicted values fluctuated on both sides of the real values, showing a certain linear change. To further validate the accuracy of the model fitting, Figure 12 presents the Q-Q plot of the actual vertical displacement versus the predicted values. From the Q-Q plot, it can be seen that the residual points of the actual vertical displacement generally follow a 45-degree diagonal line, indicating that the residuals approximately follow a normal distribution. This suggests that the residuals of the regression model do not significantly deviate from normality, and the model’s fit is reasonable. The distributions of the real vertical displacement in the middle rock under various working conditions are shown in Figure 13. The vertical displacement was evenly distributed in the range of −7.0 mm~4.5 mm, with −4.0 mm−2.5 mm accounting for 92.39% of the total displacement. The maximum vertical displacement was −7.0 mm, which served as the control limit. Therefore, the criterion for vertical displacement was obtained via the following formula:
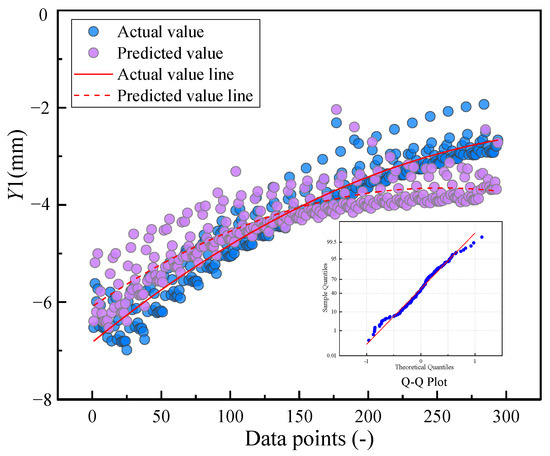
Figure 12.
Comparison of actual vertical displacement and predicted value of the vertical displacement of point 2. The inset Q-Q plot shows the residual quantiles (dots) versus the theoretical quantiles under a normal distribution (line), indicating the degree of normality in residual distribution.
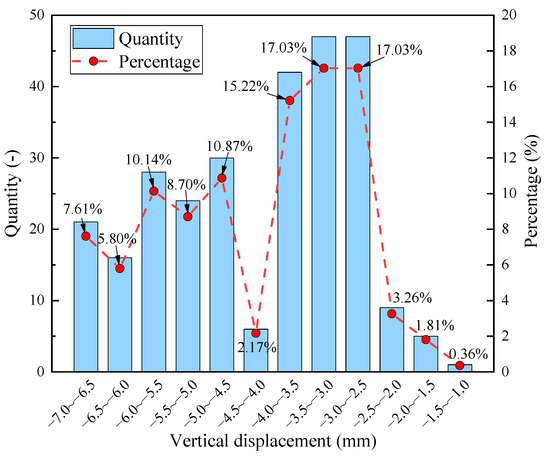
Figure 13.
Numerical distribution of true vertical displacement inside the upper area of the MRP.
In summary, on the basis of the displacement data and the layout of the joint monitoring points, a stable judgment of the MRP displacement was achieved through monitoring the settlement and clearance convergence of the small clear-distance tunnel during construction. This was performed by combining Formulas (1) and (2).
5.3. Stress Criteria of the MRP
To prevent rock mass fracture caused by excessive stress in the MRP when the displacement does not reach the limit value, it is necessary to establish stress-related criteria and improve the overall criteria system. Considering that the site conditions usually required measurement of vault settlement and clearance convergence, monitoring stress was challenging because of large data fluctuations and monitoring difficulties. Therefore, the area of maximum stress concentration in the MRP, specifically internal measurement point 1 in the central region, was selected as the stress monitoring point. The displacement was measured by the vault settlement value (measuring points 5 and 6) and clearance convergence value (measuring points 3, 7, 4, and 8) of the two tunnels, and relevant data were extracted.
Figure 14a shows the overall distribution of the data points of the stress at the center point of the MRP, the vault settlement of the two tunnels, and the convergence value of the horizontal clearance. The stress concentration was distributed mainly between 2 MPa and 4 MPa. Case 1 in Figure 14b demonstrates that as the clear distance increased, the stress value consistently decreased, whereas the displacement change trend was not significant. To quantify and describe the relationship between stress value and displacement monitoring variables, the multiple linear regression method was employed for data analysis. Considering the stress value at monitoring point 1 as the output (S1), the settlement of the ramp vault as Y2, the settlement of the mainline tunnel vault as Y3, the convergence of the ramp horizontal clearance as X2, and the convergence of the mainline tunnel horizontal clearance as inputs, the regression formula was , R2 = 0.618.
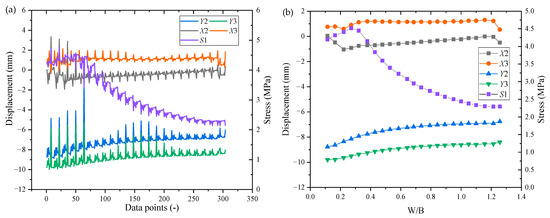
Figure 14.
Stress distribution of the central points of the MRP: (a) the distribution of the central stress; (b) the changing trend of the central stress with the width–span ratio in case 1.
Figure 15 compares the predicted and actual stress values, with the x-axis representing data points corresponding to different clear-distance ranges. The results indicate that the fitting effect was satisfactory within the range of 100~200 data points, where the corresponding clear-distance range was 6.7 m~11.8 m, and the range of W/B was 0.48~0.84. However, the predicted stress was lower than the monitored value for clear distances between 1.6 m and 6.7 m (data points 1–99), reducing prediction accuracy. Conversely, the predicted stress exceeded the monitored value for clear distances of 11.8 m to 17.6 m (data points 201–322), indicating a conservative bias in the prediction results. Therefore, the auxiliary coefficient should be adjusted for these two ranges. Considering the relatively stable distribution of values within these ranges, a correction coefficient of 1.184 was applied to data points 1~99, whereas a correction coefficient of 0.810 was used for data points 201~322. The distributions of the predicted revised value and Q-Q plots are shown in Figure 15. The predicted values are closely aligned with the monitoring stress. The Q-Q plot provides a visual representation of the normality of the residuals, which is crucial for assessing the validity of the regression model. Compared with the Q-Q plots of the unrevised predicted and actual values, the revised Q-Q plots show a more desirable alignment, and the residual distribution is closer to the normal distribution, indicating that the corrected model exhibits higher accuracy and reliability in fitting the actual data. By recalculating the regression, the relationship between the actual stress and the predicted revised value resulted in an improved R2 of 0.818, indicating a better alignment with the actual stress value.
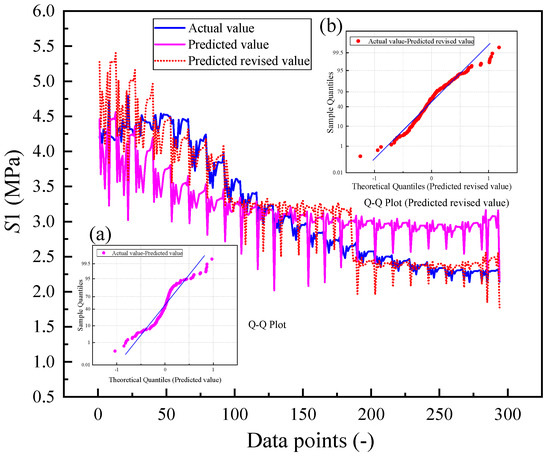
Figure 15.
Comparison of the actual stress and the predicted value of S1. (a) Residuals between actual values and predicted values; (b) Residuals between actual values and revised predicted values. In both Q-Q plots, the dots represent the sample quantiles of residuals, and the blue line represents the theoretical quantiles under a normal distribution.
Figure 16 displays the distribution of actual stress values at the center under various working conditions. The three highest stress ranges were 2.2~2.4 MPa, 2.4~2.6 MPa, and 4.2~4.6 MPa, accounting for 20.98%, 13.77%, and 9.84%, respectively. The maximum stress observed was 4.80 MPa. As the stress criteria limit value, the stress criteria were determined by the following formula:
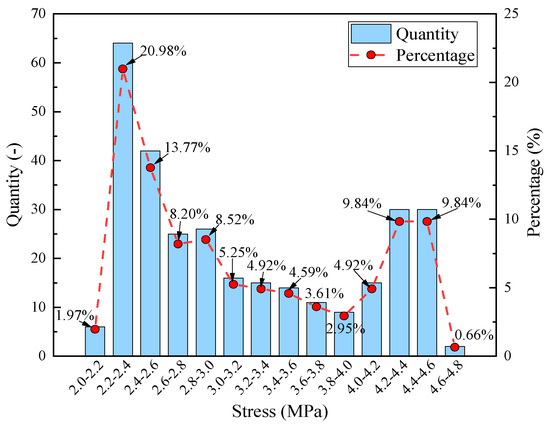
Figure 16.
Distribution of actual stress value in the center of the MRP.
In conclusion, based on the stress data, there was an association between the values of vault settlement, clearance convergence of the two tunnels, and the stress limit value. The tunnel deformation index in Formula (3) was converted to the stress value of the MRP, allowing for stable operation of the MRP.
5.4. Plasticity Criteria of the MRP
5.4.1. Distribution of the Plastic Zone
The change process of the plastic zone during construction at case 1 is depicted in Figure 17, providing the basis for optimizing the key excavation nodes.
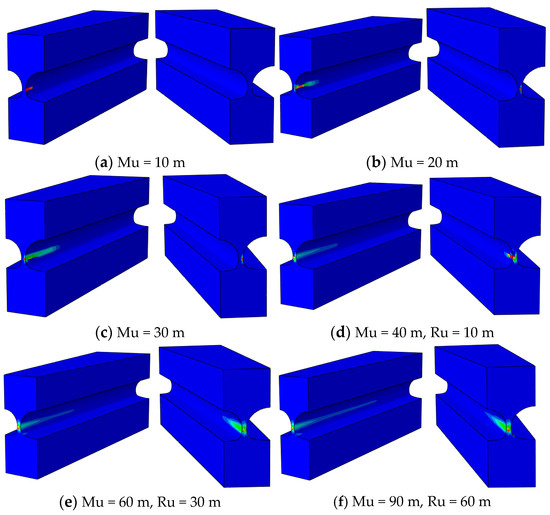
Figure 17.
The change in the plastic zone of the MRP during the construction process. Mu is the length of the upper step excavation distance from the entrance of the main tunnel. Ru is the length of the upper step excavation distance from the entrance of the ramp tunnel.
Upon entering the tunnel, the plastic zone initially appeared in the middle part of the left wall, 10 m from the upper bench excavation. No plastic zone was observed in the middle area of the middle rock or the ramp side. As shown in Figure 6a, as the upper step face of the main line tunnel progressed, the plastic zone extended along the left wall and increased in size toward the lower right of the intercalated rock area, whereas the ramp tunnel had not yet entered the tunnel.
Figure 17b, c illustrate that once the ramp tunnel entered the tunnel and the upper step face was excavated for 10 m, the plastic zone of the MRP was primarily distributed in the center, with both tunnels exhibiting a plastic distribution near the sidewall of the MRP. As shown in Figure 17d, as both tunnel faces continued to advance, the plastic zone in the central area increased. Additionally, the plastic zone in the sidewall of the ramp was found to be larger than that in the sidewall of the main tunnel, mainly because of the ramp’s late entrance and the close distance between the tunnel face and the opening.
In Figure 17e,f, the plastic zone in the sidewall of the main line tunnel extended from the entrance to the exit, corresponding to the upper steps of the main line tunnel. Therefore, after the main tunnel and ramp were excavated, the plastic zone of the MRP was mainly distributed in the inner wall and center of the tunnel during the construction process. It is crucial to carefully consider the construction speed and implement appropriate support measures to ensure construction safety and the stability of the rock mass.
The previous sections analyzed the stability of the MRP via displacement and stress. While these were key factors, the size and extent of the plastic zone in the rock also played important roles in determining rock stability. In practical engineering, the plastic zone cannot be measured with standard methods, but it reflects the yield state and range of the rock mass. Therefore, it is essential to establish criteria for the plastic zone and enhance the overall stability criteria.
5.4.2. Plasticity Criteria Analysis of the MRP
To evaluate the size and influence of the plastic zone across different clear distances and working conditions, the plastic zone index C was used. This index combined the horizontal length of the plastic zone (L), the clear distance (W), and the maximum equivalent plastic strain (PEEQmax) on the section, as shown in Figure 18. The value of index C was calculated via Formula (4). A larger equivalent plastic strain corresponded to a larger plastic zone and a smaller clear distance, making the MRP less stable. This index measures the size of the plastic zone and its effect.
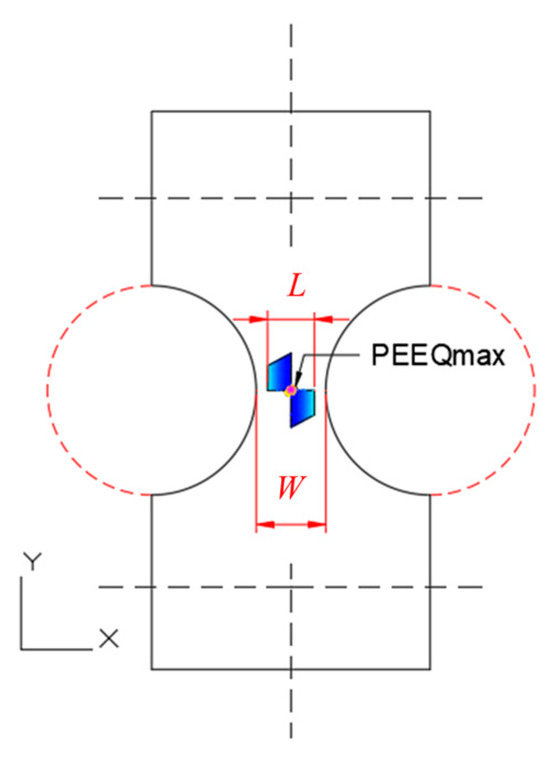
Figure 18.
Schematic diagram of the composition of index C in the plastic zone of the MRP.
By considering the relationship between the displacement index and the plastic zone, the plastic zone index can be calculated via Formula (4). The displacement index was determined on the basis of the vault settlement values (measuring points 5 and 6) and clearance convergence values (measuring points 3, 7, 4, and 8) of the two tunnels. The plastic zone index distributions under various working conditions and different clear distances can be extracted from these data. In Figure 19a, the overall distributions of the plastic zone index, vault settlement values, and horizontal clearance convergence values of the MRP are shown, corresponding to the variation curve of condition 1 with the width–span ratio in Figure 19b. The overall variation in the displacement curve was not significant, but the plastic zone index C curve experienced a sudden change at a width–span ratio of 0.30, after which it became flat and stable. Therefore, analyzing the data of all clear-distance ranges together was not accurate.
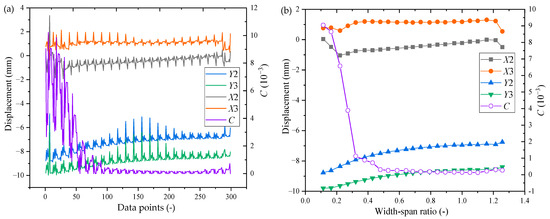
Figure 19.
Distribution of the index of the plastic zone in the MRP: (a) the distribution of the index data points of the plastic zone; (b) the trend of the index of the plastic zone changing with the width–span ratio (W/B) in case 1.
To conduct multiple regression analysis, the width–span ratio of 0.11~1.26 was split into two sections: 0.11~0.30 and 0.30~1.26. The output variable was the plastic zone index C, which was calculated via Formula (4). The input variables included the settlement of the ramp vault (Y2), the settlement of the mainline tunnel vault (Y3), the convergence of the ramp horizontal clearance (X2), and the convergence of the mainline tunnel horizontal clearance (X3). By multiple regression analysis, the fitting parameters in Table 6 were obtained, with an R2 value of 0.776 in the width–span ratio range of 0.11–0.30, closely matching the measured residual value. In the width–span ratio range of 0.30–1.26, the R2 value was 0.637, with some deviation from the actual value.

Table 6.
Multiple regression formulas of the plastic zone index C.
Figure 20 shows the comparison between the actual values and the predicted values of the plastic zone index C calculated via the fitting formula. In Figure 20a, the predicted values were generally higher than the actual values, indicating a high degree of fit but a conservative estimation. In Figure 20b, the predicted values and the actual values varied among the different data points. The latter segment shows a greater degree of fit, whereas the former segment needed adjustments based on the numerical characteristics.
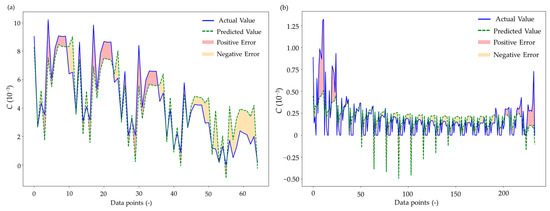
Figure 20.
Comparison between the actual value and the predicted value of the index of the plastic zone in the MRP: (a) Comparison between the predicted value and actual value width–span ratio of 0.11~0.30; (b) Comparison between predicted value and actual value width–span ratio of 0.30~1.26.
The distribution of the predicted values in Figure 20b reveals that there was a significant numerical fluctuation before the 30th data point. After that, the numerical curve remained stable within the range of 0.2~0.5 for data points 1~30. This corresponded to a clear-distance length of 6.7 m and a width–span ratio of 0.48. Therefore, the width–span ratio of 0.30~1.26 was divided into two sections: 0.30–0.48 and 0.48~1.26. The predicted values of these two sections were then corrected by multiplying them by auxiliary coefficients of 1.326 and 1.000. Figure 21 shows the comparison between the corrected predicted values and the actual values. After the correction, the values were closer to the actual values, and the abnormal points were eliminated. The correction curve now covered the original actual values.
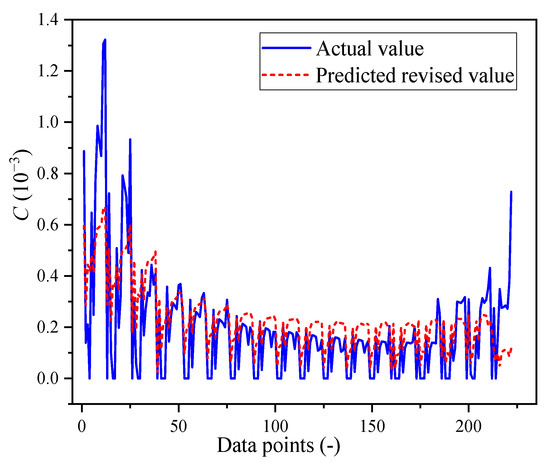
Figure 21.
Comparison of the revised value of the index C of the plastic zone in the MRP with the actual value (width–span ratio: 0.30~1.26).
Figure 22 shows the distribution of the plastic zone index C in the intercalated rock under various working conditions. The highest index C values were observed in the range of 0~0.5, accounting for 73.75%. Specifically, the range of 0.1~0.5 had the highest proportion, accounting for 46.18%. However, within this range, the index values were relatively small, and the area of the plastic zone distributed in the MRP was limited. Therefore, the maximum index value was considered the criteria for the plastic zone limit.
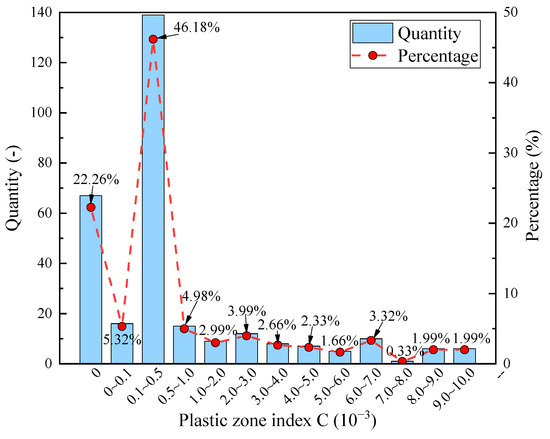
Figure 22.
Numerical distribution of index C in the plastic zone of the MRP.
In conclusion, the limit value of the plastic zone index C was established based on the above equivalent plastic strain data and its association with the vault settlement and clearance convergence of the two tunnels. By transforming the tunnel deformation index in Formula (5) into the distribution characteristics of the plastic zone of the MRP, a stability assessment from the perspective of the plastic zone of the medium rock inclusion was successfully achieved.
6. Discussion
Following the aforementioned research, separate evaluations were performed on the stability of the medium rock inclusions on the basis of displacement, stress, and the plastic zone. To assess the state of the MRP inclusions during the construction process, three evaluation criteria must be considered. Consequently, the comprehensive criteria, represented by Formula (6) and derived from the unified Formulas (1)–(5), were developed. When these criteria were used, it was necessary to define the clear-distance width between the middle and intercalated rock, determine the width–span ratio, identify the stress criteria formula and the plastic zone criteria formula corresponding to the width–span ratio range, and finally obtain the values of X1, Y1, S1, and C on the basis of the deformation data acquired from the vault settlement and horizontal clearance convergence of the two tunnels.
If any of the four values exceeded the corresponding limit value when the rock mass parameters of the section for stability analysis were close to the initial parameters of the surrounding rock, as shown in Table 4, the MRP was deemed to have lost its stability. Furthermore, if the section grade of the MRP was higher than that of the rock mass corresponding to the initial parameters of the surrounding rock, according to Figure 4, the cohesion corresponding to the limit state also increased, resulting in an increase in the stress value at the center of the intermediate rock mass. Therefore, when evaluating the stability of this type of rock mass, the primary factors were the X1, Y1, and C values obtained from the displacement and plastic zone criteria, whereas the stress criteria served as a supplementary factor. When the stress value exceeded the limit value alone, the instability of the rock mass cannot be determined. On the other hand, if any of the X1, Y1, and C values exceeded the corresponding limit values, the MRP was considered unstable.
Additionally, if the section grade of the MRP was lower than that of the rock mass corresponding to the initial parameters of the surrounding rock, according to Figure 4, the cohesion and elastic moduli corresponding to the limit state also decreased. Consequently, this led to increased vertical displacement in the upper region and horizontal displacement in the middle region of the intermediate rock mass, as well as decreased stress in the center of the MRP. In this scenario, when assessing the stability of this type of MRP, the S1 and C values obtained from the stress criteria and plastic zone criteria were the primary factors, with the displacement criteria X1 and Y1 serving as supplementary factors. Notably, when only the displacement values X1 and Y1 exceeded the limit value, the instability of the MRP could not be determined. However, if any of the S1 and C values exceeded the corresponding limit values, the MRP was considered unstable.
The main advantage of using these criteria was the ability to dynamically adjust the target of evaluation, connecting it to the deformation and stress of the MRP with respect to the construction process. This enabled the control of MRP stability. Furthermore, by reflecting the fundamental principles of deformation and stress between the tunnel and the MRP, the criteria avoided the influence of construction methods, excavation progress, and other factors, making it more aligned with actual requirements.
This study focused on examining the displacement, stress, and plastic zone criteria to determine the stability of intermediate rocks. In the construction process, it was essential to assess intermediate rock inclusions. This can be achieved by synthesizing three evaluation angles, as depicted in Figure 23, to establish comprehensive criteria. To apply these criteria effectively, it is necessary to determine the net distance between the rock and clarify the width–span ratio. Furthermore, H, V, S, and C values must be obtained based on the stress criteria formula and plastic zone criteria formula, taking into account the width–span ratio. Additionally, deformation data were determined by analyzing the settlement of the arch roof and the convergence of the horizontal clearance of the two tunnels.
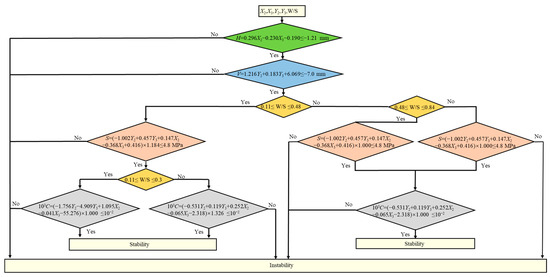
Figure 23.
Comprehensive criteria for stability of the MRP.
If the fracture rock mass parameters required for stability analysis were proximate to the initial parameters of the surrounding rock (as illustrated in Table 4 and if one of the indicators, such as displacement, stress, or the plastic zone, exceeded the corresponding limit value, the MRP was considered unstable. In cases where the grade of the MRP exceeded grade III, the cohesion force corresponding to the limit state increased, as did the stress value at the central position of the MRP. Consequently, when assessing the stability of the MRP, the dominant parameters to consider were H, V, and C derived from the displacement criteria and the plastic zone criteria, whereas the stress criterion S serves as a secondary parameter. If the H, V, and C values exceed their respective limit values, this indicates instability in the MRP.
Alternatively, if the grade of the MRP was lower than grade III, the cohesive force and elastic modulus corresponding to the limit state decreased. This results in increased vertical displacement in the upper region of the MRP and increased horizontal displacement in the middle region. Furthermore, the stress at the central position of the MRP decreased. In such cases, when assessing the stability of this type of MRP, the main parameters to consider were S and C derived from the stress criteria and the plastic zone criteria, whereas the displacement criteria H and V serve as secondary parameters. Judging the instability of the MRP solely on the basis of H and V values exceeding the limit value was not possible. However, if either the S or C value exceeds the corresponding limit value, it indicates instability in the MRP.
On the whole, the use of these criteria was subject to dynamic change and can be attributed to the deformation and stress of the MRP as a result of the construction process. It was used to ensure the stability of the MRP by monitoring the deformations of the two tunnels. Additionally, by reflecting the fundamental laws of deformation and stress between the tunnel and the MRP, it can also account for factors such as construction schemes and excavation methods. Therefore, the criteria were better suited to practical requirements.
The proposed criteria were derived from a concrete engineering case study, with the methodology applicable to future tunnel projects. When extending this approach, tunnel sections should be selected based on lithological variations, structural layout, and construction methods, while ensuring consideration of clear-distance range, geological complexity, and data availability. The framework of the criteria can be the same, and the threshold and variable value may be determined according to the current work.
7. Conclusions
This study focused on the bifurcation small clear-distance tunnel of the Xiamen Haicang Shugang evacuation channel under the underground interchange tunnel. The stability criteria of the MRP during the design and construction phases were analyzed through numerical simulation. The main conclusions are as follows:
- (1)
- By varying the cohesion of the surrounding rock while keeping the other parameters constant, the stability state of a small clear-distance tunnel was investigated. It was observed that increasing the cohesion of the surrounding rock resulted in a longer distance of stable tunnel excavation. When the cohesion exceeded 1.4 MPa, the small clear-distance tunnel remained stable even with increasing clear distance. The minimum cohesion at convergence of the small-clearance tunnel excavation model increased as the density and modulus of elasticity of the surrounding rock increased. Therefore, this study proposes an initial determination of small-clearance tunnel stability on the basis of the parameters of the surrounding rock density, modulus of elasticity, and cohesion during the design stage.
- (2)
- By analyzing displacement data from monitoring points obtained through simulation, the relationships between horizontal clearance convergence and vertical displacement of the main line tunnel and ramp tunnel and between horizontal displacement and vertical displacement of the MRP were examined. This analysis led to the establishment of horizontal and vertical displacement criteria for the MRP.
- (3)
- This study analyzes the relationship between the convergence of horizontal clearance and the vertical displacement of the main line tunnel and ramp tunnel, as well as the stress of the MRP. The stress criteria for ensuring the stability of the MRP were determined via the linear regression method.
- (4)
- By analyzing the distribution and changes in the plastic zone of the MRP during excavation, it was determined that the plastic zone was initially distributed in the inner wall and center of the tunnel after the main tunnel and ramp were excavated. It was important to carefully consider construction speed and support measures to ensure construction safety and rock mass quality.
- (5)
- To assess the stability of the MRP, a plasticity zone index called C was introduced. By examining the correlation between C and the convergence of the horizontal headroom and the vertical displacement of the vault in small-clearance tunnels, the plasticity criteria for the stability of the MRP were proposed.
- (6)
- In the construction of a bifurcated small-clearance tunnel, the stability of the MRP can be dynamically determined and controlled by considering the displacement, stress, and plasticity zone.
- (7)
- The proposed criteria, derived from a concrete engineering case study, can be extended to other similar projects with comparable frameworks. The threshold values and variables should be determined based on project-specific characteristics, such as clear-distance range, geological complexity, and data availability.
Author Contributions
Conceptualization, J.W., T.C., Y.G. and X.L.; methodology, J.W., Y.L. and T.C.; software, Y.L. and T.C.; validation, J.W., Y.L., T.C., A.C., H.L. and X.L.; formal analysis, J.W., Y.L., T.C. and A.C.; investigation, J.W., T.C. and X.L.; resources, J.W. and X.L.; data curation, Y.L., T.C., A.C. and H.L.; writing—original draft preparation, J.W., Y.L. and A.C.; writing—review and editing, J.W., Y.L., X.L. and Y.G.; visualization, J.W. and Y.L.; supervision, J.W.; project administration, J.W., T.C., L.L. and X.L.; funding acquisition, J.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Sinohydro Bureau No. 11 Co., Ltd. (kh0023020232375; kh0023020232660); Xiamen Road and Bridge Co., Ltd. [Xialu Investment (Third East Passage-2024-137)]; Shanghai Tunnel Engineering Co., Ltd. (2022-SK-02); Shanghai Shallow Geothermal Energy Engineering Technology Research Center (DRZX-202302); Guangzhou Metro Design and Research Institute Co., Ltd. (kh0023020240166); the Research Project of Shanghai Housing and Urban Rural Development Management Committee (2024-Z02-007); China Railway 15 Bureau Group Co., Ltd. (CR15CG-XLDYH7-2019-GC01).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We want to express our thanks to the authors whose publications we cited and the efficient editor.
Conflicts of Interest
Author Luyu Lin was employed by the company Sinohydro Bureau No. 11 Co., Ltd and author Yuanbo Gao was employed by the company Xiamen Road and Bridge Engineering Investment Development Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Lyu, H.M.; Sun, W.J.; Shen, S.L.; Arulrajah, A. Flood risk assessment in metro systems of mega-cities using a GIS-based modeling approach. Sci. Total Environ. 2018, 626, 1012–1025. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.M.; Jiang, C.W.; Yu, M.F.; Zhou, L.Y.; Mo, S.Y. Layout and Exploitation of Underground Traffic Space with City Growth. Chin. J. Undergr. Space Eng. 2019, 15, 980–989. [Google Scholar]
- Ren, D.J.; Shen, S.L.; Arulrajah, A.; Wu, H.N. Evaluation of ground loss ratio with moving trajectories induced in double-O-tube (DOT) tunnelling. Can. Geotech. J. 2018, 55, 894–902. [Google Scholar] [CrossRef]
- Tan, Y.; Jiang, W.Z.; Luo, W.J.; Lu, Y.; Xu, C.J. Longitudinal Sliding Event during Excavation of Feng-Qi Station of Hangzhou Metro Line 1: Postfailure Investigation. J. Perform. Constr. Facil. 2018, 32, 04018039. [Google Scholar] [CrossRef]
- Tan, Y.; Wei, B.; Lu, Y.; Yang, B. Is Basal Reinforcement Essential for Long and Narrow Subway Excavation Bottoming Out in Shanghai Soft Clay? J. Geotech. Geoenviron. Eng. 2019, 145, 05019002. [Google Scholar] [CrossRef]
- Ye, G.L.; Hashimoto, T.; Shen, S.L.; Zhu, H.H.; Bai, T.H. Lessons learnt from unusual ground settlement during Double-O-Tube tunnelling in soft ground. Tunn. Undergr. Space Technol. 2015, 49, 79–91. [Google Scholar] [CrossRef]
- Gong, Y.F.; Wang, Z.Y.; Zhang, J.R.; Li, S.P.; Zhang, H. Study on Supporting Effect of Middle Rock Pillars in Small Clear Distance Section of Long-span Forked Tunnel with Five lanes. J. Highw. Transp. Res. Dev. 2021, 38, 123–133. (In Chinese) [Google Scholar] [CrossRef]
- Song, S.G.; Li, S.C.; Li, L.P.; Shi, S.S.; Zhou, Z.Q.; Liu, Z.H.; Shang, C.S.; Sun, H.Z. Model test study on vibration blasting of large cross-section tunnel with small clearance in horizontal stratified surrounding rock. Tunn. Undergr. Space Technol. 2019, 92, 103013. [Google Scholar] [CrossRef]
- Gong, J.W.; Xia, C.C.; Lei, X.W. Analysis of field measurement and theoretical calculation on rock pressure in shallow-buried twin tunnels with small spacing. Chin. J. Rock Mech. Eng. 2010, 29, 4139–4145. [Google Scholar]
- Hou, F.J.; Liu, C.; Wang, K.; Yuan, Z.; Li, T.; Zhou, S. Net distance optimization of super-large section tunnel using new elastoplastic-damage model combining tensile and shear yield modes. Arab. J. Geosci. 2021, 14, 2657. [Google Scholar] [CrossRef]
- Jiang, Q.; Song, S.G.; Li, T.; Wang, K.; Gu, R.H. Study on Surrounding Rock Stability of Small Clear-Distance Twin Highway Tunnel with Eight Lanes. Geotech. Geol. Eng. 2019, 37, 593–598. [Google Scholar] [CrossRef]
- Shi, C.H.; Cao, C.Y.; Lei, M.F. Construction technology for a shallow-buried underwater interchange tunnel with a large span. Tunn. Undergr. Space Technol. 2017, 70, 317–329. [Google Scholar] [CrossRef]
- Xia, M.R. Influence factors of surrounding rock stability of neighborhood tunnel. J. Civ. Environ. Eng. 2021, 43, 73–80. [Google Scholar] [CrossRef]
- Yang, X.L.; Sui, Z.Y. Numerical simulation of construction sequence for shallow embedded bias tunnels with small clear distance. J. Cent. South Univ. Sci. Technol. 2007, 38, 764–770. [Google Scholar]
- Chen, J.X.; Xu, Z.L.; Luo, Y.B.; Song, J.K.; Liu, W.W.; Dong, F.F. Application of the Upper-Bench CD Method in Super Large-Span and Shallow Tunnel: A Case Study of Letuan Tunnel. Adv. Civ. Eng. 2020, 2020, 8826232. [Google Scholar] [CrossRef]
- Sahoo, J.P.; Kumar, J. Stability of long unsupported twin circular tunnels in soils. Tunn. Undergr. Space Technol. 2013, 38, 326–335. [Google Scholar] [CrossRef]
- Yamaguchi, I.; Yamazaki, I.; Kiritani, Y. Study of Ground-Tunnel Interactions of Four Shield Tunnels Driven in Close Proximity, in Relation to Design and Construction of Parallel Shield Tunnels. Tunn. Undergr. Space Technol. 1998, 13, 289–304. [Google Scholar] [CrossRef]
- Yamamoto, K.; Lyamin, A.V.; Wilson, D.W.; Sloan, S.W.; Abbo, A.J. Stability of a circular tunnel in cohesive-frictional soil subjected to surcharge loading. Comput. Geotech. 2011, 38, 504–514. [Google Scholar] [CrossRef]
- Wang, J.X.; Cao, A.S.; Li, Z.H.; Wu, Z.; Lin, L.H.; Liu, X.T.; Li, H.B.Q.; Sun, Y.W. Mechanical Behavior and Excavation Optimization of a Small Clear-Distance Tunnel in an Urban Super Large and Complex Underground Interchange Hub. Appl. Sci. 2023, 13, 254. [Google Scholar] [CrossRef]
- Zhang, W.G.; Goh, A.T.C. Numerical study of pillar stresses and interaction effects for twin rock caverns. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 193–206. [Google Scholar] [CrossRef]
- Tan, Z.; Zhou, Z.; Kong, H.; Zhao, B.; Zhao, J. Single excavation face method for super-large-span bifurcated tunnels. Proc. Inst. Civ. Eng. Geotech. Eng. 2021, 174, 406–418. [Google Scholar] [CrossRef]
- Zhou, S.; Li, L.P.; An, Z.M.; Liu, H.L.; Yang, G.Y.; Zhou, P.F. Stress-Release Law and Deformation Characteristics of Large-Span Tunnel Excavated with Semi Central Diaphragm Method. KSCE J. Civ. Eng. 2021, 25, 2275–2284. [Google Scholar] [CrossRef]
- Fang, Q.; Zhang, D.L.; Wong, L.N.Y. Shallow tunnelling method (STM) for subway station construction in soft ground. Tunn. Undergr. Space Technol. 2012, 29, 10–30. [Google Scholar] [CrossRef]
- Li, L.P.; Shang, C.S.; Chu, K.W.; Zhou, Z.Q.; Song, S.G.; Liu, Z.H.; Chen, Y.H. Large-scale geo-mechanical model tests for stability assessment of super-large cross-section tunnel. Tunn. Undergr. Space Technol. 2021, 109, 103756. [Google Scholar] [CrossRef]
- Fu, J.Y.; Yang, J.S.; Yan, L.; Abbas, S.M. An analytical solution for deforming twin-parallel tunnels in an elastic half plane. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 524–538. [Google Scholar] [CrossRef]
- Radi, E. Path-independent integrals around two circular holes in an infinite plate under biaxial loading conditions. Int. J. Eng. Sci. 2011, 49, 893–914. [Google Scholar] [CrossRef]
- Zhang, D.L.; Chen, L.P.; Fang, Q.; Song, R.G. Research and application on central rock wall dike stability of small interval tunnel. J. Beijing Jiaotong Univ. 2016, 40, 1–11. (In Chinese) [Google Scholar] [CrossRef]
- Su, F.; Chen, F.Q.; Shi, Y.Z. Analytic continuation solution of deep twin-tunnels. Chin. J. Rock Mech. 2012, 31, 365–374. (In Chinese) [Google Scholar]
- Kooi, C.B.; Verruijt, A. Interaction of circular holes in an infinite elastic medium. Tunn. Undergr. Space Technol. 2001, 16, 59–62. [Google Scholar] [CrossRef]
- Lyu, H.M.; Shen, S.L.; Zhou, A.N.; Chen, K.L. Calculation of pressure on the shallow-buried twin-tunnel in layered strata. Tunn. Undergr. Space Technol. 2020, 103, 103465. [Google Scholar] [CrossRef]
- Li, S.C.; Wang, H.P.; Zheng, X.F. Forked tunnel stability analysis and its construction optimization research. Chin. J. Rock Mech. Eng. 2008, 27, 447–457. (In Chinese) [Google Scholar]
- Luo, Y.B.; Wang, S.H.; Chen, J.X.; Wang, C.W. Calculation method of surrounding rock pressure in deep buried neighborhood tunnels considering safety reserve of middle rock pillar. J. Shandong Univ. Eng. Sci. 2023, 54, 81–93. Available online: https://link.cnki.net/urlid/37.1391.T.20230719.1526.002 (accessed on 5 June 2024). (In Chinese).
- Ying, G.G.; Zhang, S.L.; Zhou, M.; Chen, L.P. A Simplified Method for Calculating Stresses in Middle Rock Wall of Small Interval Tunnels Based on Reserved Supporting Hypothesis. J. Highw. Transp. Res. Dev. 2018, 35, 95–103. (In Chinese) [Google Scholar] [CrossRef]
- Lee, C.J.; Wu, B.R.; Chen, H.T.; Chiang, K.H. Tunnel stability and arching effects during tunneling in soft clayey soil. Tunn. Undergr. Space Technol. 2006, 21, 119–132. [Google Scholar] [CrossRef]
- Lei, M.F.; Peng, L.M.; Shi, C.H. Model test to investigate the failure mechanisms and lining stress characteristics of shallow buried tunnels under unsymmetrical loading. Tunn. Undergr. Space Technol. 2015, 46, 64–75. [Google Scholar] [CrossRef]
- Li, L.P.; Fan, H.Y.; Liu, H.L.; Li, S.G.; Cheng, S.; Zhang, Q.H.; Tu, W.F.; Zhou, S. Model test and numerical simulation research on the mechanical response law of lager span and small interval tunnels constructed by CD method. Tunn. Undergr. Space Technol. 2023, 132, 104947. [Google Scholar] [CrossRef]
- Zhu, H.H.; Huang, F.; Xu, Q.W. Model test and numerical simulation for progressive failure of weak and fractured tunnel surrounding rock under different overburden depths. Chin. J. Rock Mech. Eng. 2010, 29, 1113–1122. [Google Scholar]
- Tyagi, A.; Lee, F.H. Influence of tunnel failure on the existing large-diameter tunnel in improved soil surround. Tunn. Undergr. Space Technol. 2022, 120, 104276. [Google Scholar] [CrossRef]
- Yao, Y.; He, C.; Xie, Z.X. Study of mechanical behavior and reinforcing measures of middle rock wall of parallel tunnel with small interval. Rock Soil Mech. 2007, 28, 1883–1888. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, Y.B. Study on Partition and Reinforcement Method of Middle Rock Pillar in Soft Rock Tunnel with Small Clear Distance. Chin. J. Undergr. Space Eng. 2013, 9, 373–379. [Google Scholar]
- Lin, P.; Zhou, Y.N.; Liu, H.Y.; Wang, C. Reinforcement design and stability analysis for large-span tailrace bifurcated tunnels with irregular geometry. Tunn. Undergr. Space Technol. 2013, 38, 189–204. [Google Scholar] [CrossRef]
- Zhang, H.J.; Qiu, W.G.; Feng, J.M. Mechanical performance of shared rock of neighborhood tunnels. Chin. J. Geotech. Eng. 2010, 32, 434–439. [Google Scholar]
- Mortazavi, A.; Hassani, F.P.; Shabani, M. A numerical investigation of rock pillar failure mechanism in underground openings. Comput. Geotech. 2009, 36, 691–697. [Google Scholar] [CrossRef]
- Schneider-Muntau, B.; Medicus, G.; Fellin, W. Strength reduction method in Barodesy. Comput. Geotech. 2018, 95, 57–67. [Google Scholar] [CrossRef]
- Chen, X.; Ren, J.L.; Wang, D.Y.; Lyu, Y.N.; Zhang, H. A Generalized Strength Reduction Concept and Its Applications to Geotechnical Stability Analysis. Geotech. Geol. Eng. 2019, 37, 2409–2424. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, J.Q.; Li, A. The Application of the Strength Reduction Shortest Path Method to the Stability Analysis of Shallow Buried Tunnel. Geotech. Geol. Eng. 2022, 40, 1091–1101. [Google Scholar] [CrossRef]
- Dawson, E.M.; Roth, W.H.; Drescher, A. Slope stability analysis by strength reduction. Géotechnique 1999, 49, 835–840. [Google Scholar] [CrossRef]
- Zienkiewicz, C.; Humpheson, C.; Lewis, R.W. Associated and non-associated visco-plasticity and plasticity in soil mechanics. Géotechnique 1975, 25, 671–689. [Google Scholar] [CrossRef]
- Peng, C.; Ji, D.; Zhao, L.; Qian, Z.Y.; Ren, F.H. Stability Analysis of Dump Slope Based on FEM Strength Reduction Method. Appl. Mech. Mater. 2014, 501–504, 51–55. [Google Scholar] [CrossRef]
- Tang, X.S.; Zheng, Y.R.; Wang, Y.F. Application of FEM Strength Reduction Method in Stability Analysis and Control of Tunnel Construction. Mod. Tunn. Technol. 2020, 57, 45–55+64. [Google Scholar] [CrossRef]
- An, Y.L.; Li, J.H.; Yue, J.; Zhou, J. Effect of Seepage Force on Tunnel Face Stability Using Limit Analysis with SRM. Geotech. Geotech. Geol. Eng. 2021, 39, 1743–1751. [Google Scholar] [CrossRef]
- Su, Y.; Su, Y.; Zhao, M.; Vlachopoulos, N. Tunnel Stability Analysis in Weak Rocks Using the Convergence Confinement Method. Rock Mech. Rock Eng. 2021, 54, 559–582. [Google Scholar] [CrossRef]
- Xia, C.C.; Xu, C.B.; Zhao, X. Study of the strength reduction dda method and its application to mountain tunnel. Int. J. Comput. Methods 2012, 9, 1250041. [Google Scholar] [CrossRef]
- Yang, X.L.; Huang, F. Stability analysis of shallow tunnels subjected to seepage with strength reduction theory. J. Cent. South Univ. Technol. 2009, 16, 1001–1005. [Google Scholar] [CrossRef]
- Zhou, L.; Zhu, Z.M.; Li, Y.X. Influence of Principal Stress Orientation on Tunnel Stability Based on the Finite-Element Strength Reduction Method. Mod. Tunn. Technol. 2017, 54, 61–67. [Google Scholar] [CrossRef]
- Zhou, G.N.; Yang, T.T.; Sun, Z.; Li, H.; Cheng, Y.; Song, Z.P.; Han, J.J. Investigation of Quantitative Evaluation Method and Engineering Application of Shallow Buried Tunnel Face Stability. Appl. Sci. 2022, 12, 6656. [Google Scholar] [CrossRef]
- Yang, F.; Gao, L.Z.; Gao, Y.K.; Yang, J.S. Stability of surrounding rock and failure mode of parallel multi-line tunnels. Chin. J. Geotech. Eng. 2023, 45, 976–985. (In Chinese) [Google Scholar] [CrossRef]
- Xu, J.S.; Liu, W.C.; Wang, X.R.; Du, X.L. Stability analysis of three-dimensional tunnel roofs in soil based on a modified MC criterion. Acta Geotech. 2024, 19, 5989–6004. [Google Scholar] [CrossRef]
- Man, J.H.; Huang, H.W.; Dias, D.; Wang, F.Y.; Chen, J.Y. Stability evaluation model for the tunnel face of large cross-section tunnel excavated by the bench method. Comput. Geotech. 2024, 170, 106311. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).