Fracture Behavior and Cracking Mechanism of Rock Materials Containing Fissure-Holes Under Brazilian Splitting Tests

Abstract

Fractures and voids are widely distributed in slope rock masses. These defects promote crack initiation and propagation, ultimately leading to rock mass failure. Investigating their damage evolution mechanisms and strength characteristics is of significant importance for slope hazard prevention. A numerical simulation study of Brazilian splitting tests on disk samples containing prefabricated holes and fractures was conducted using the Finite Element Method with Cohesive Zone Modeling (FEM-CZM) in ABAQUS by embedding zero-thickness cohesive elements within the finite element model. This 2021 study analyzed the effects of fracture angle and length on tensile strength and crack propagation characteristics. The results revealed that when the fracture angle is small, cracks initiate near the fracture and propagate and intersect radially as the load increases, ultimately leading to specimen failure, with the crack coalescence pattern exhibiting local closure. As the fracture angle increases, the initiation location of the crack shifts. With an increase in fracture length, the crack initiation position may transfer to other parts of the fracture or near the hole, and longer fractures may result in more complex coalescence patterns and local closure phenomena. During the tensile and stable failure stages, the load–displacement curves of samples with different fracture angles and lengths exhibit similar trends. However, the fracture angle has a notable impact on the curve during the shear failure stage, while the fracture length significantly affects the peak value of the curve. Furthermore, as displacement increases, the proportion of tensile failure undergoes a process of rapid decline, slow rise, and then rapid decline again before stabilizing, with the fracture angle having a significant influence on the proportion of tensile failure. Lastly, as the fracture angle and length increase, the number of damaged cohesive elements shows an upward trend. This study provides novel perspectives on the tensile behavior of fractured rock masses through the FEM-CZM approach, contributing to a fundamental understanding of the strength characteristics and crack initiation mechanism of rocks under tensile loading conditions.

1. Introduction

Many rocks exhibit brittle characteristics, characterized by their markedly superior compressive strength compared to tensile strength, with the tensile strength typically being only approximately one-tenth of the compressive strength [1,2,3]. As shown in Figure 1, fractures and voids are widely distributed in slope rock masses. These defects not only serve as potential nucleation sites for cracks but also facilitate crack propagation and interconnection with other defects, ultimately leading to the overall failure of the rock mass. Consequently, these natural defects are pivotal in controlling the mechanical behavior and tensile properties of rock masses [4,5,6]. Given this, an in-depth investigation into the damage evolution mechanisms and strength characteristics of defective rock masses holds significant scientific importance for preventing and mitigating slope engineering disasters.

The Brazilian splitting test is one of the main methods to study the tensile strength and failure mode of rocks [7,8,9]. Currently, scholars have conducted research on the tensile properties of rock masses containing voids and fractures. Yang et al. [10] studied the influence of tensile strength and crack propagation characteristics of rock under three cracks. Cracks of natural rock mass in regular engineering rock mass usually exist in the form of crosses, and some researchers have paid attention to the mechanical characteristics of rock mass failure under the condition of cross fracture. Zhang et al. [11] found that cracks can weaken the tensile strength of rocks, and the number of cracks, the inclination angle of cracks, and the geometric arrangement of cracks affect the fracture morphology and tensile strength of samples. Wang et al. [12] pointed out that the change in bedding and fracture inclination will affect the fracture characteristics and failure mode of the rock, and the strength of the rock is variable. Janeiro et al. [13] conducted uniaxial compression tests on prismatic gypsum specimens containing single or double fractures and analyzed their mechanical properties and failure modes. Kamgue Tiam et al. [14] investigated the growth of cracks between two adjacent holes when gneiss was internally pressurized with a mixed-water NEEM and evaluated the effect of hole spacing on crack generation and growth. QIN et al. [15] utilized the Peridynamics (PD) method to model and analyze the splitting failure of Brazilian disks. It achieves a numerical simulation of the entire process of compressive splitting failure in Brazilian disks containing central cracks with different inclination angles using the PD method. It is noteworthy that, despite the extensive literature available on the mechanical properties of rock masses containing fractures, there remains a significant research gap in the study of tensile properties of rock masses with combined defects of voids and fractures. This lack of research in this area may limit our ability to fully understand the mechanical behavior of rock masses with complex defects. Therefore, it is particularly important to further strengthen the research on the tensile properties of rock masses with combined void-fracture defects.

The preparation of specimens containing combined defects of voids and fractures is extremely challenging. However, compared to laboratory experiments, numerical simulations offer advantages such as computational accuracy, intuitive representation, economy, and convenience, which can compensate for the deficiencies of laboratory experiments in this regard [16,17,18]. The finite element-cohesive force model (FEM-CZM) method can describe the continuity and discontinuity of rock material and can simulate the mechanics and failure behavior of rock mass [19,20,21]. By using the FEM-CZM method, HAN et al. [22,23] conducted a shear numerical simulation of rock mass with fractures and analyzed the mechanical properties and failure modes of rock mass. WANG et al. [24] simulated the shear process of jointed rock mass under constant normal load by using the method of global embedding zero-thickness cohesive force element.

With the in-depth study on the mechanical properties and failure modes of fractured rock mass, scholars have achieved a large number of fruitful results, but these studies mostly focus on the compression and shear of rock mass with single and double fractures and a lack of in-depth research on the tensile characteristics of rock mass with combined defects of caverns and fissures. In addition, the finite-cohesive force model (FEM-CZM), considering the composition and distribution of rock mass, can better describe the continuity and discontinuity of rock materials. In summary, based on the FEM-CZM method, this study establishes a numerical model of rock masses containing intermittent double fractures and conducts Brazilian splitting tests to analyze the influence of fracture geometric parameters on tensile performance and failure modes. The research findings can provide a scientific basis for disaster prevention and mitigation in slope engineering.

2. FEM-CZM Method

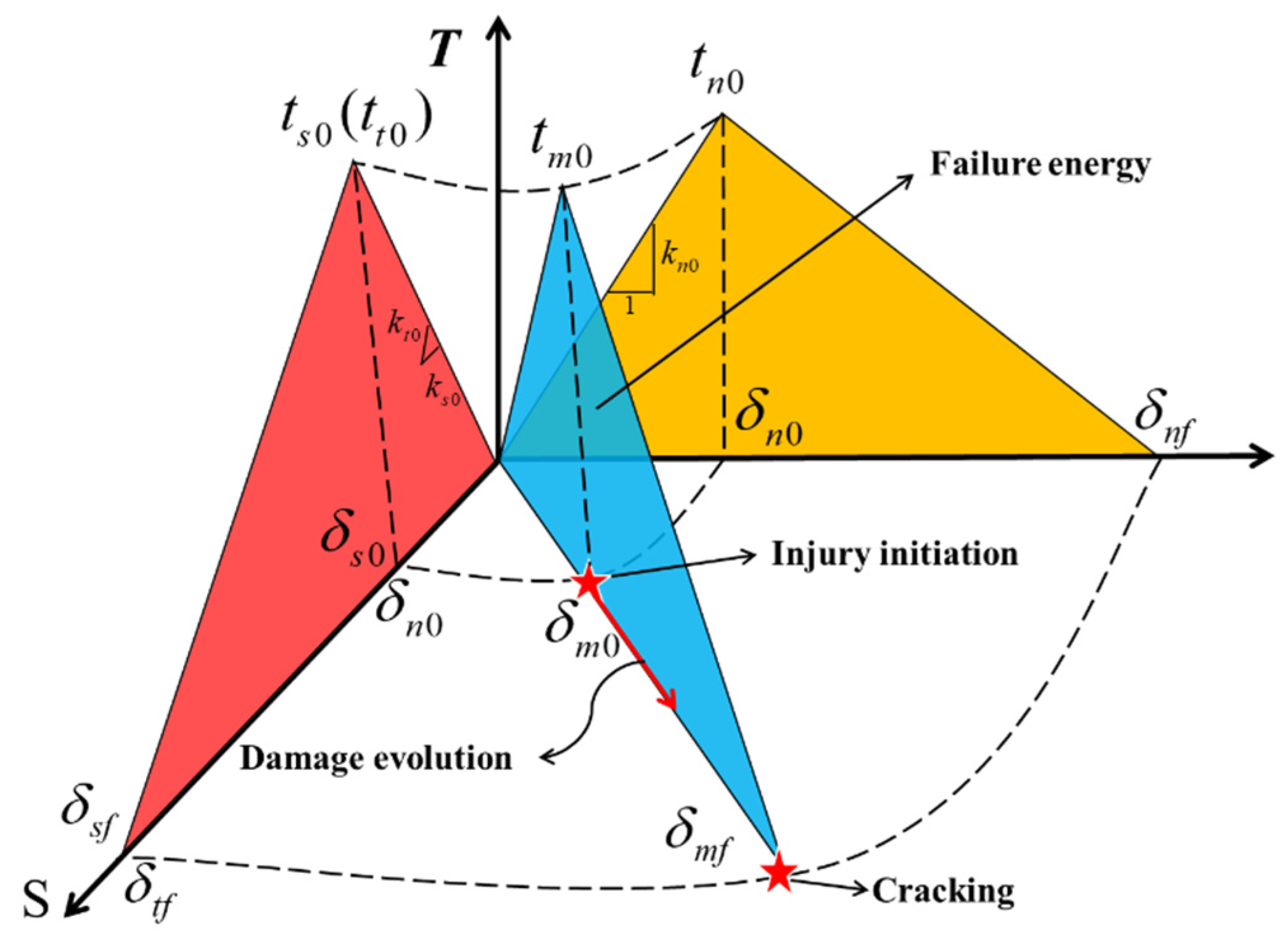
2.1. Separation-Traction Criteria

In the ABAQUS 2021 software, the cohesive zone model (CZM) adheres to the traction-separation law, with its constitutive model illustrated in Figure 2 Specifically, the model exhibits linear elastic hardening prior to the onset of damage evolution and transitions to linear softening after damage evolution initiates. By introducing a modified parameter to characterize the functional relationship between the external force acting on the cohesive element and the initial damage stress, the model becomes more suitable for analyzing elastoplastic problems [25,26]. Prior to reaching the damage evolution stage, the external force applied to the cohesive element has not yet reached the initial damage stress, and the relationship between stress and strain follows Hooke’s Law. To facilitate parameter calibration, the constitutive thickness of cohesive elements was set to 1 while maintaining the default geometric thickness of 0, thereby ensuring that the nodal separation displacement equals the nominal strain. The linear elastic properties of the cohesive element can be described by the following matrix:

$$t=\left\{\begin{array}{c}{t}_n\\ t_s\\ t_t\end{array}\right\}={\displaystyle \frac{I}{L}}\left[\begin{array}{ccc}{E}_{nn}& E_{ns}& E_{nt}\\ E_{ns}& E_{ss}& E_{st}\\ E_{nt}& E_{st}& E_{tt}\end{array}\right]\left\{\begin{array}{c}{\delta }_n\\ {\delta }_s\\ {\delta }_t\end{array}\right\}=\left[\begin{array}{ccc}{K}_{nn}& K_{ns}& K_{nt}\\ K_{sn}& K_{ss}& K_{st}\\ K_{nt}& K_{st}& K_{tt}\end{array}\right]\left\{\begin{array}{c}{\delta }_n\\ {\delta }_s\\ {\delta }_t\end{array}\right\}.$$

(1)

In the equation, $t$ represents the traction stress vector; $t_n$ is the normal traction force; $t_s$ and $t_t$ are the two tangential traction forces; ${\delta }_n$, ${\delta }_s$, ${\delta }_t$ are the three components of strain; $L$ is the initial thickness of the cohesive element; and $K$ is the stiffness matrix of the cohesive element.

After reaching the stage of damage evolution, the stiffness of the cohesive elements will linearly decrease. In ABAQUS, a scalar $D$ is used to represent the degree of damage, with an initial value of 0 and gradually increasing to 1. To accurately describe the damage evolution within the cohesive elements, a function related to the effective displacement ${\delta }_m$ is introduced as follows:

$${\delta }_m=\sqrt{{\delta }_n^2+{\delta }_s^2+{\delta }_t^2}.$$

(2)

Here, $\langle \rangle$ denotes the Macaulay brackets, which ensure that damage in the cohesive elements only occurs under tensile forces. When $〈{\delta }_n\ge 0〉$, it indicates tension, and $〈{\sigma }_n〉$ is equal to ${\sigma }_n$ itself. When $〈{\delta }_n\le 0〉$, it indicates compression, and $〈{\delta }_n〉$ is equal to zero. The damage variable $D$ evolves according to the following expression:

$$D={\displaystyle \frac{{\delta }_{mf}({\delta }_{mm}-{\delta }_{mo})}{{\delta }_{mm}({\delta }_{mf}-{\delta }_{mo})}}.$$

(3)

In the context of loading history, let ${\delta }_{mm}$ represent the maximum effective displacement, ${\delta }_{mo}$ denote the effective displacement at the onset of cracking, and ${\delta }_{mf}$ represent the effective displacement at failure. The normal stress during the softening phase can be expressed as follows:

$$\begin{array}{c}{t}_n=\left\{\begin{array}{cc}(1-D)t_{no},& t_{no}\ge 0\\ t_{no},& t_{no}<0\end{array}\right.\\ t_s=(1-D)t_{so}\\ t_t=(1-D)t_{to}\end{array}.$$

(4)

The stiffness of the cohesive element can be expressed using the following formula:

$$\begin{array}{l}{K}_n=(1-D)K_{no}\\ K_s=(1-D)K_{so} \\ K_t=(1-D)K_{to}\end{array}.$$

(5)

The change in separation displacement is represented as follows:

$$\begin{array}{l}{\delta }_n={\displaystyle \frac{t_n}{(1-D)}}{K}_n\\ {\delta }_s={\displaystyle \frac{t_s}{(1-D)}}{K}_s\\ {\delta }_t={\displaystyle \frac{t_t}{(1-D)}}{K}_t\end{array}$$

(6)

2.2. The Formation Process of Zero Thickness Cohesive Force Unit

To more accurately simulate the discontinuities between real rock particles and capture the macroscopic fracture initiation and failure patterns of rock masses, this study employs zero-thickness cohesive elements embedded within predefined cracks in the initial finite element mesh. The embedding process of cohesive elements is illustrated in Figure 3, among them, the numbers 1 to 12 are the nodes of the model. As shown in Figure 3a, the solid elements are first discretized, and node information is read. In Figure 3b, the finite element mesh and element nodes on the coinciding surfaces are separated, and the nodes are rearranged. In Figure 3c, zero-thickness cohesive elements are embedded between the originally coinciding element faces. These cohesive elements have a thickness of zero, ensuring that embedding them does not alter the model dimensions; they share nodes with their adjacent mesh elements. Finally, a model containing zero-thickness cohesive elements is formed, as shown in Figure 3d.

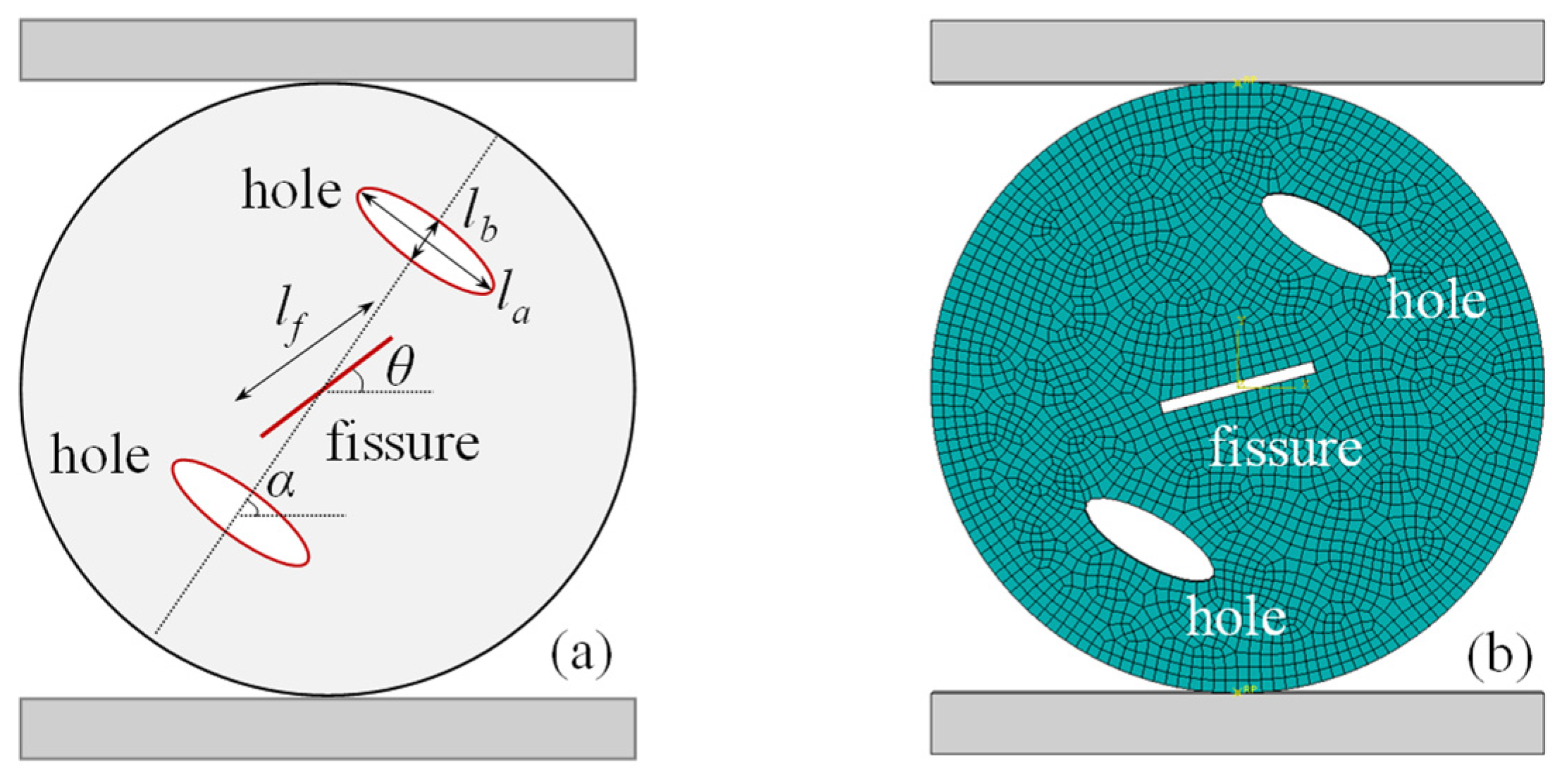
3. Model Establishment

To investigate the fracture behavior and cracking mechanism of rocks with intermittent double fractures, this paper conducts Brazilian test simulations on specimens containing two intermittent pre-existing fractures; the specimen model and the embedded zero-thickness cohesive elements are shown in Figure 4 and Figure 5, respectively. For the relevant simulation, the modeling parameters of DU et al. [27] were selected to ensure consistency with the conditions, as shown in

Table 1. Parameters applied in the model.

Materials	Parameters	Value
Solid elements	Density/kg·m−3	2500
	Young’s modulus/GPa	15
	Poisson’s ratio	0.3
Cohesive elements	$K_{n0}$/GPa·mm−1	15
	$K_{s0}$/GPa·mm−1	5.28
	$K_{t0}$/GPa·mm−1	5.28
	$t_n$/MPa	5.5
	$t_n$/MPa	20
	$t_t$/MPa	20
	Model-I fracture energy/N/mm	0.055
	Model-II fracture energy N/mm	0.16

. The fracture inclination angle of the specimen is denoted as θ, the fracture length as lf, the elliptical hole inclination angle as α, the length of the long axis of the elliptical hole as la, and the length of the short axis of the elliptical hole as lb. Herein, the fracture inclination angle refers to the angle between the fracture and the horizontal direction, while the elliptical hole inclination angle represents the angle between the elliptical hole and the horizontal direction. To study the influence of the geometric distribution of double fractures on the fracture behavior and cracking mechanism, the following two simulation schemes are designed:

(1)

Changing the crack Angle θ (0°, 15°, 60°, 90°, 150°), lf = 13 mm, α = 60°, la = 12 mm, lb = 4 mm;

(2)

Changing the fracture length lf (20 mm, 28 mm, 40 mm), θ = 15°, α = 60°, la = 12 mm, lb = 4 mm.

4. Test Result

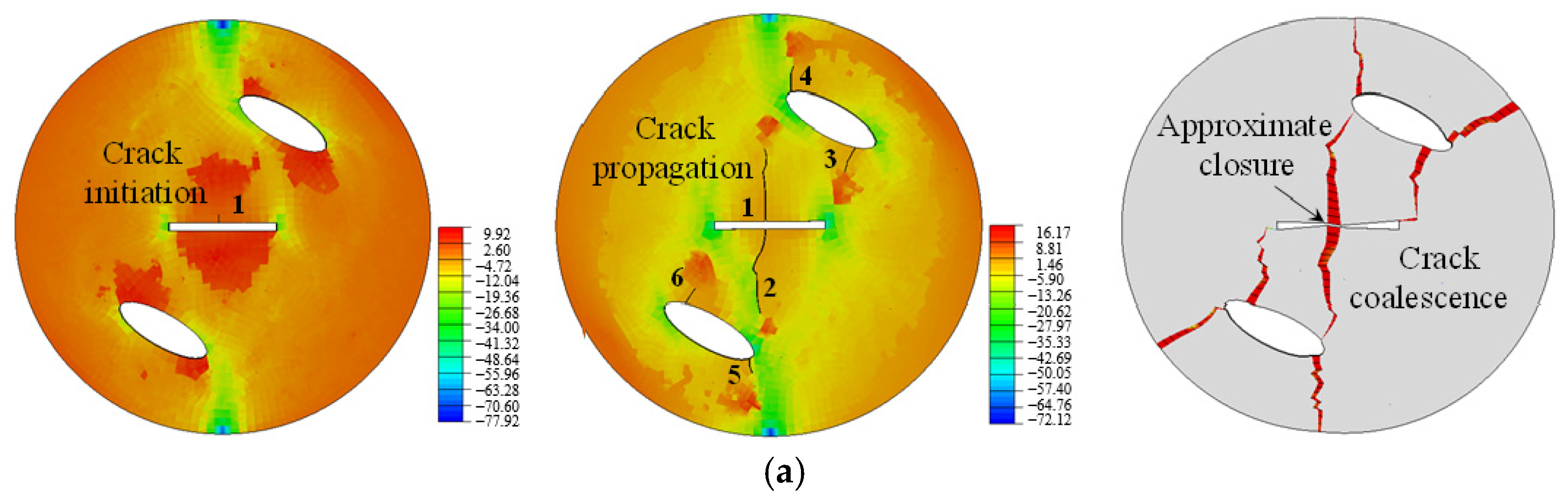
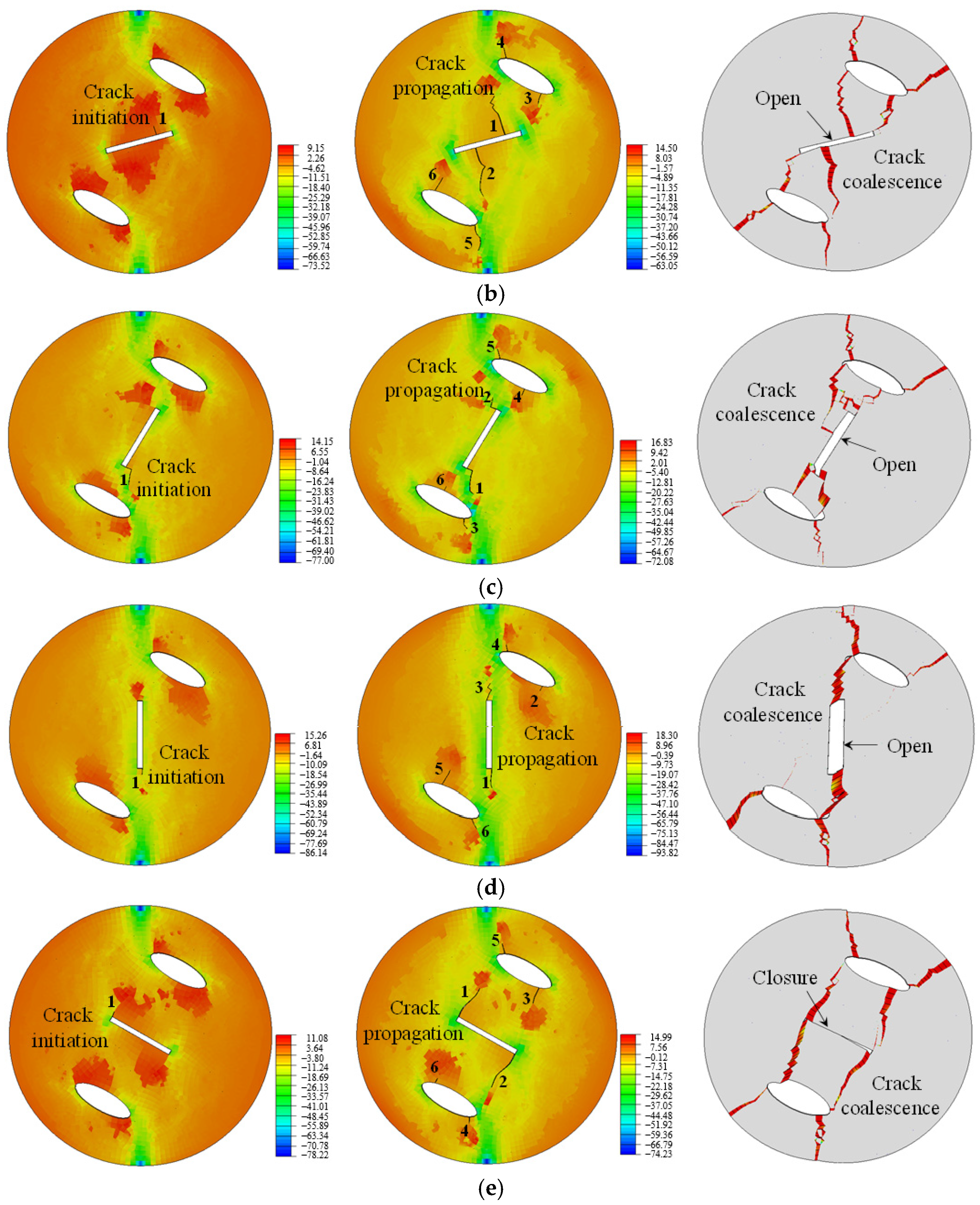
4.1. Principle of Crack Generation

This section examines the impact of variations in different parameters on the fracture behavior and cracking mechanism of specimens containing intermittent double fractures. Figure 6 illustrates the cracking principle of the modeled specimen. Crack initiation occurs due to the failure of cohesive elements. At the initial stage of the test, the specimen experiences relatively low forces, and the cohesive elements remain intact, preventing crack formation. As the load increases, the cohesive elements at the upper end of the secondary fracture first enter a state of failure, undergoing irreversible damage. This leads to a reduction in tensile strength at the rear, causing local cracks to form and stiffness to decrease. The transfer of primary tensile stress to other locations due to these local cracks and stiffness reduction results in a more uniform stress distribution. Consequently, the tensile strength of the specimen can further increase, accompanied by the formation of cracks.

4.2. Mechanical Characteristic Analysis

4.2.1. Influence of Crack Angle on Cracking Characteristics

Figure 7 depicts the influence of variations in fracture inclination angle on the crack initiation sequence and propagation pattern in the specimen. As shown in Figure 7a, when the fracture inclination angle is 0°, the first crack (Crack 1) initiates at a certain distance to the left of the upper part of the fracture. While Crack 1 propagates along the loading direction, Crack 2 initiates at the same distance below the fracture, Crack 3 initiates at a certain distance below the lower right end of elliptical hole ②, Crack 4 initiates at a certain distance above the upper left end of elliptical hole ②, Crack 5 initiates at a certain distance below the lower right end of elliptical hole ①, and Crack 6 initiates at a certain distance above the upper left end of elliptical hole ①. As the external load increases, Cracks 1, 2, 3, 4, 5, and 6 all propagate radially. The cracks continue to expand and intersect, and the specimen enters a stage of crack coalescence. Ultimately, the fracture becomes fully connected, and local closure occurs between Crack 1 and Crack 2, leading to failure of the specimen.

As shown in Figure 7b, when the fracture inclination angle is 15°, the initiation points of Cracks 1 and 2 shift to the right and left, respectively. Ultimately, no closure of the fracture is observed.

Figure 7c illustrates that when the fracture inclination angle is 60°, the initiation points of Cracks 1 and 2 shift to the left and right ends of the fracture, and the initiation points of Cracks 3, 4, and 5 also change. For example, Crack 3 initiates at a certain distance below the lower right end of elliptical hole ①. Again, no closure of the fracture is observed.

Figure 7d demonstrates that when the fracture inclination angle is 90°, the initiation points of Cracks 1, 2, 3, 5, and 6 all change. For instance, Crack 6 initiates at a certain distance below the lower right end of elliptical hole ①, and Crack 2 initiates at a certain distance below the lower right end of elliptical hole ②. As the external load increases, Crack 5 barely propagates. Ultimately, no closure of the fracture is observed in this case as well.

As observed in Figure 7e, when the fracture inclination angle reaches 150°, the initiation points of Cracks 1, 2, 4, and 5 undergo changes. Specifically, Crack 4 initiates at a certain distance below the lower right end of elliptical cavity ①, while Crack 5 initiates at a certain distance above the upper left end of elliptical cavity ②. Ultimately, the fracture exhibits an overall closure phenomenon.

4.2.2. Influence of Crack Length on Cracking Characteristics

Figure 8 shows the influence of the crack length change on crack cracking sequence and penetration mode of the sample. As can be seen from Figure 8a, when the crack length is 20 mm, the specimen first initiates the crack at a certain distance from the lower part of the crack to the left. As Crack 1 propagates along the loading direction, Crack 2 is generated at a certain distance from the upper part of the crack to the right, Crack 3 is generated at a certain distance from the lower part of the lower right end of the elliptical hole (1), Crack 4 is generated at a certain distance from the upper left upper end of the elliptical hole (2), and Crack 5 is generated at a certain distance from the upper left upper end of the elliptical hole (1). With the increase in external load, Cracks 1, 2, 3, 4 and 5 spread radially. Cracks continued to expand, intersecting, and the specimen entered the stage of crack consolidation. Finally, the fracture appeared through the phenomenon; the fracture did not appear closed, and the specimen is damaged.

As can be seen from Figure 8b, when the crack length is 28 mm, the initiation locations of Cracks 3, 4, and 5 change, and an additional Crack 6 is generated at a certain distance from the upper left end of the elliptical hole (2). There is a partial closure between Crack 1 and Crack 2.

As can be seen from Figure 8c, when the crack length is 40 mm, the initial crack location of Cracks 1 and 2 changes, and the crack initiation occurs at a certain distance from the upper part of the crack to the right and at a certain distance from the lower part to the left. As the external load increases, Cracks 3 and 5 barely expand. Partial closure appeared on the left side of Crack 2.

4.3. Crack Cracking Mechanism

To investigate the mechanisms underlying crack formation, this paper employs cohesive elements to identify the types of cracks that arise based on the damage they exhibit. The Mixed-Mode Index for Damage Evolution Measurement (MMIXDME) is utilized to determine the damage type within the cohesive elements by characterizing the proportion of fracture modes during the damage evolution process. Specifically, when the MMIXDME value falls within the range of 0 to 0.5, the cohesive elements are primarily subject to tensile damage, leading to the formation of tensile cracks. Within the range of 0.5 to 1, the cohesive elements are dominated by splitting damage (splitting cracks). When this value reaches 1, the cohesive elements undergo shear forces but do not result in damage to the cohesive elements themselves.

Figure 9 provides a detailed illustration of the influence of fracture inclination angle on the crack initiation mechanism. Upon overall observation, when the specimen undergoes failure, the primary cracks interconnect through the prefabricated holes and fractures, forming a crack network that spans the entire specimen. During this process, the specimen primarily undergoes tensile failure, manifested by the gradual propagation of cracks under tensile stress, ultimately leading to the fracture of the specimen. Additionally, small-scale shear failure occurs at both ends of the prefabricated fracture due to stress concentration and the action of shear stress.

Further analysis reveals that the angle of the prefabricated fracture has a significant impact on the crack initiation and propagation patterns. As the angle of the prefabricated fracture increases, the shear stress at the fracture ends also rises, resulting in an increase in the number of shear cracks generated at these ends. This phenomenon is particularly evident when the fracture inclination angle is 90°, at which point the fracture is nearly perpendicular to the tensile direction, causing the shear stress at the fracture ends to reach its maximum value, thereby promoting the generation and propagation of shear cracks.

Figure 10 presents a detailed examination of the influence of fracture length on the crack initiation mechanism. When the fracture length is 20 mm, the specimen primarily undergoes tensile failure during loading, manifested by the gradual propagation of cracks under tensile stress. In the vicinity of the hole, due to the stress concentration effect, small-scale shear failure zones emerge. Simultaneously, around the prefabricated fracture, the presence of the fracture leads to significant stress concentration, which further exacerbates the generation and propagation of cracks.

As the fracture length increases to 28 mm and 40 mm, tensile cracks dominate the failure mode of the specimen. This is because, with the increase in fracture length, the specimen is more prone to forming continuous tensile stress zones during loading, thereby facilitating the initiation and propagation of tensile cracks. In contrast, the occurrence of shear cracks becomes relatively infrequent, possibly because, as the fracture length increases, the specimen tends to form a global tensile fracture mode upon failure rather than localized shear failure.

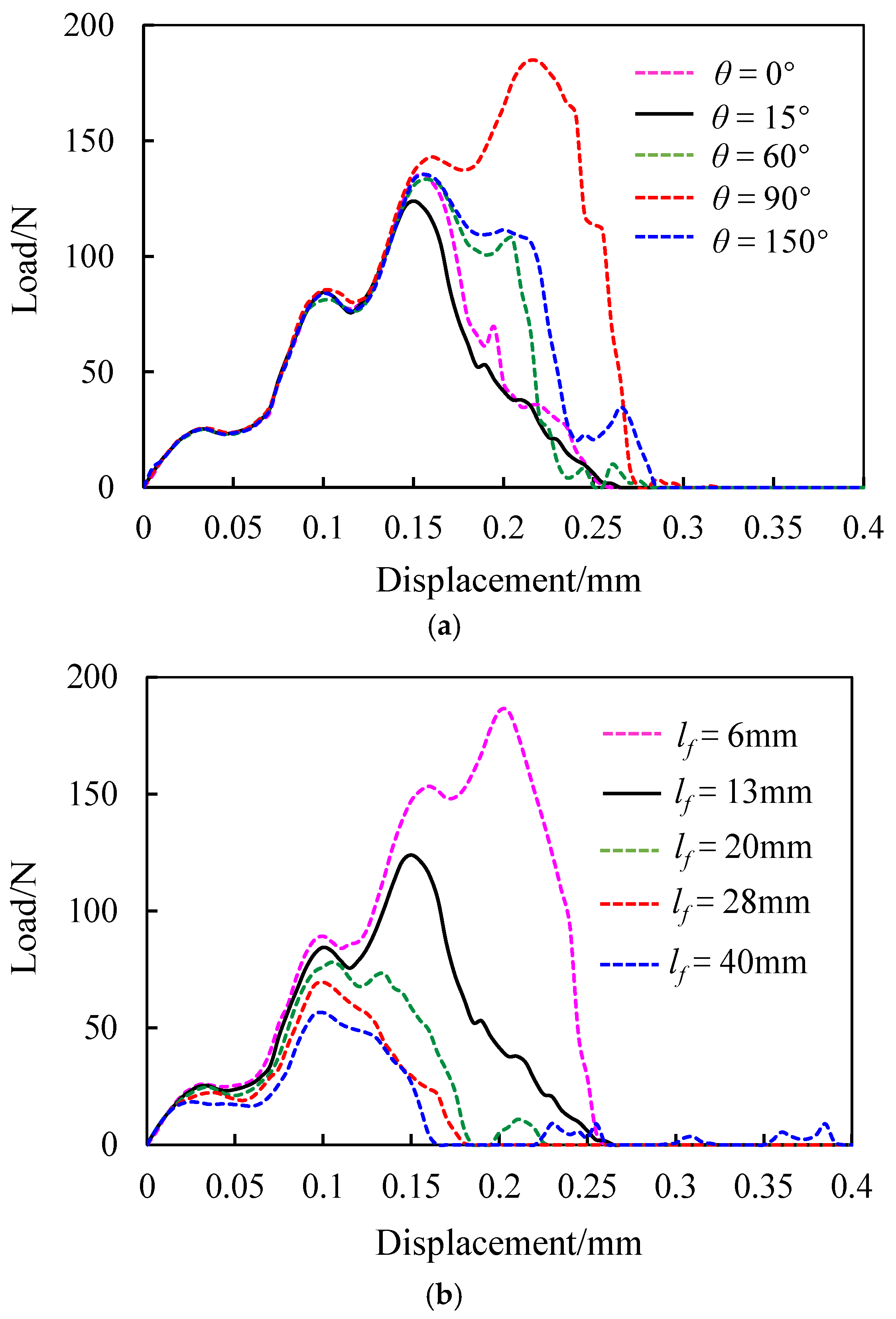
4.4. Load Displacement Curve Change Trend

As shown in Figure 11a, before a displacement of 0.05 mm, the load–displacement curve increases linearly. As the displacement increases, the curve undergoes three gradual decreases followed by a rapid increase to reach a peak, then experiences one rapid decrease before finally stabilizing. Notably, the specimen with a fracture inclination angle of 90° exhibits the highest peak load, while the specimen with a fracture inclination angle of 15° has the lowest. It is worth noting that all four curves stabilize at the same point in time, with the curves largely coinciding during the tensile failure and stable failure stages, differing only during the shear failure stage. This indicates that variations in fracture inclination angle do not significantly impact the load–displacement curve.

Observing Figure 11b, it can be seen that the trend of the load–displacement curve for different fracture lengths is similar to that of different fracture inclination angles. Before a displacement of 0.05 mm, the load–displacement curve rises linearly. As the displacement increases, the curve undergoes three gradual decreases followed by a rapid increase to reach a peak, then experiences one rapid decrease before finally stabilizing. The specimen with a fracture length of 6 mm exhibits the highest peak load, while the specimen with a fracture length of 40 mm has the lowest.

4.5. Sample Failure Mode

As illustrated in Figure 12a, before a displacement of 0.15 mm, tensile failure is the primary mode of cracking in the specimens. As the load increases, the proportion of tensile failure initially drops rapidly, then rises slowly, followed by a rapid decrease, and finally stabilizes. Notably, the peak values of the four curves are identical. When stabilizing, the specimens with fracture inclination angles of 0° and 15° exhibit the highest proportions of tensile failure, while the specimen with a fracture inclination angle of 90° has the lowest. This indicates that variations in fracture inclination angle have a significant impact on the proportion of tensile failure.

Observing Figure 12b, it can be seen that the trend of tensile failure ratio for different fracture lengths is similar to that observed with different fracture inclination angles. Before a displacement of 0.15 mm, tensile failure is the primary mode of cracking in the specimens. As the displacement increases, the proportion of tensile failure initially drops rapidly, then experiences a small rebound and fluctuations, followed by a rapid decrease, and finally stabilizes. Analysis of the curve variations reveals that in the initial stage of cracking, the cracks are relatively fine and primarily caused by tensile failure. As the displacement continues to increase, the cracks expand, resulting in more pronounced cracks, and the proportion of tensile failure decreases. When the load continues to increase, the lining failure stabilizes, and the tensile failure ratio also stabilizes.

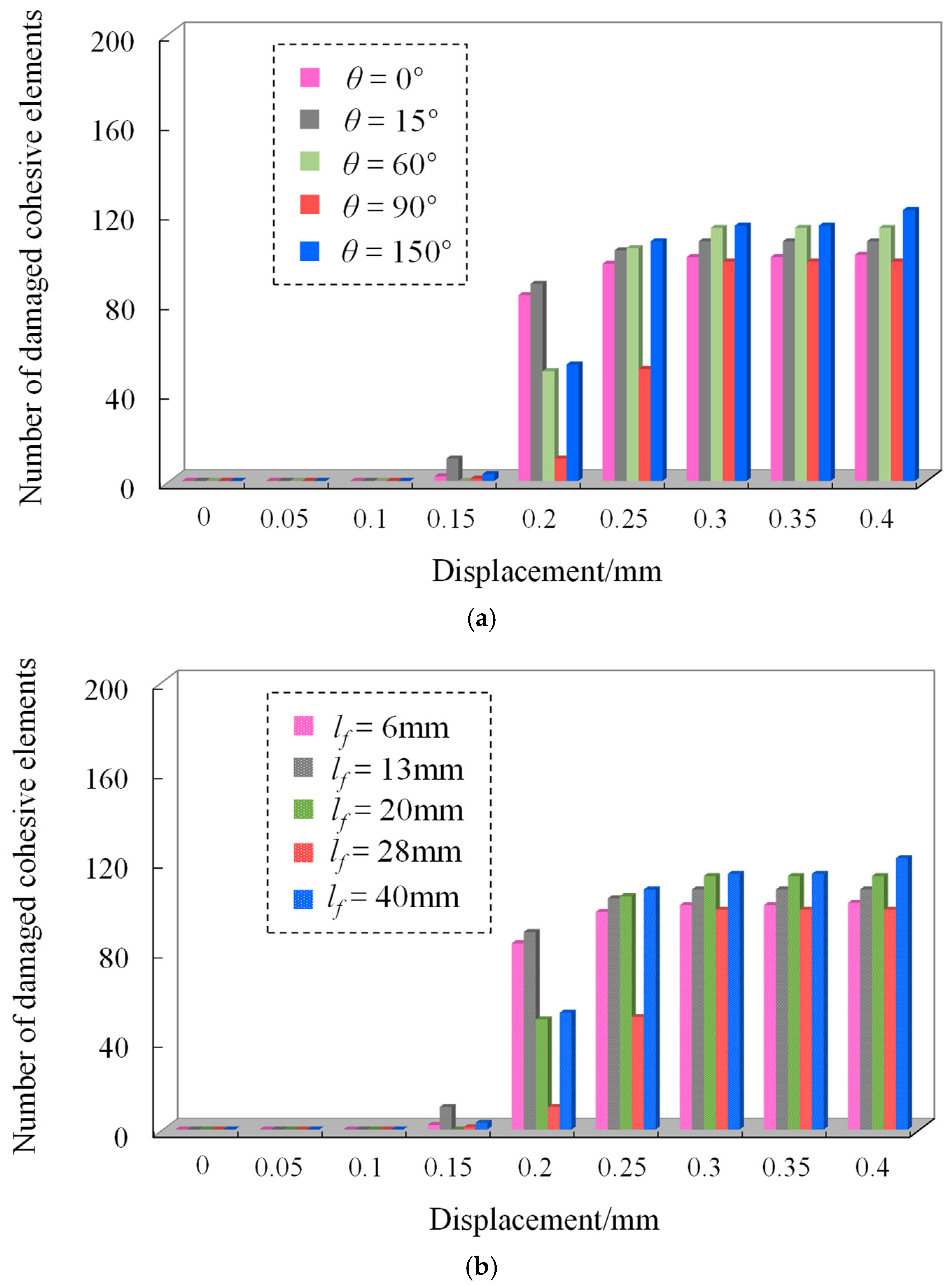
4.6. The Number of Cohesiveness Unit Damage

Observing Figure 13a, it can be seen that in the initial stages of displacement, the number of damaged cohesive elements is relatively low. As the displacement continues to increase, so does the number of damaged cohesive elements. When the displacement reaches its maximum value of 0.4 mm, the specimen with a fracture inclination angle of 150° has the highest number of damaged cohesive elements, while the specimen with a fracture inclination angle of 90° has the lowest. Notably, on the whole, as the fracture inclination angle increases, the number of damaged cohesive elements tends to rise at the same displacement. However, between displacements of 0.15 and 0.2 mm, the number of damaged cohesive elements caused by a fracture inclination angle of 15° exceeds that caused by a fracture inclination angle of 60°. This indicates that the fracture inclination angle has a significant impact on fracture behavior.

Observing Figure 13b, the overall trend is approximately equal to the trend of cohesive element damage in Figure 13a. In the initial stages of displacement, the number of damaged cohesive elements is low. As the displacement continues to increase, so does the number of damaged cohesive elements. When the displacement reaches its maximum value of 0.4 mm, the specimen with a fracture length of 40 mm has the highest number of damaged cohesive elements, while the specimen with a fracture length of 28 mm has the lowest. Similarly, it is worth noting that at the same displacement, as the fracture length increases, the number of damaged cohesive elements generally rises. However, between displacements of 0.15 and 0.2 mm, the number of damaged cohesive elements caused by a fracture length of 13 mm exceeds that caused by a fracture length of 20 mm. Combining the above, there is a close relationship between fracture length and fracture behavior.

5. Conclusions

A comprehensive study on the tensile properties of rock materials containing fractures and voids has been conducted using the finite element method (FEM) combined with the cohesive zone model (CZM). In the numerical simulations, all initial finite mesh discretizations utilized zero-thickness cohesive elements globally, which facilitated the description of combined continuous and discontinuous properties. Based on this method, the following main conclusions can be drawn:

(1)

When the crack angle is small, the crack typically initiates at a specific distance from the initial crack. As the external load increases, the crack propagates and intersects along the radial direction, potentially leading to specimen failure. The crack propagation mode exhibits local closure. With an increase in the crack inclination angle, the initiation location shifts, becoming more pronounced as the angle further increases. As crack length increases, the initiation location may shift to other parts of the crack or near the hole. Shorter cracks tend to penetrate more easily but do not necessarily exhibit closure, whereas longer cracks may show local closure with a more complex penetration pattern.

(2)

The load–displacement curves for samples with different fracture angles coincide during the tensile and stability failure stages but diverge in the shear failure stage due to varying fracture angles. The fracture angle has a negligible effect on the overall trend of the load–displacement curve. Similarly, the load–displacement curves for samples with different crack lengths exhibit characteristics of an initial straight rise, followed by three gradual declines, a rapid rise to the peak, a rapid decline, and eventual stabilization. While the fracture length significantly influences the peak value of the load–displacement curve, it has minimal impact on the overall trend.

(3)

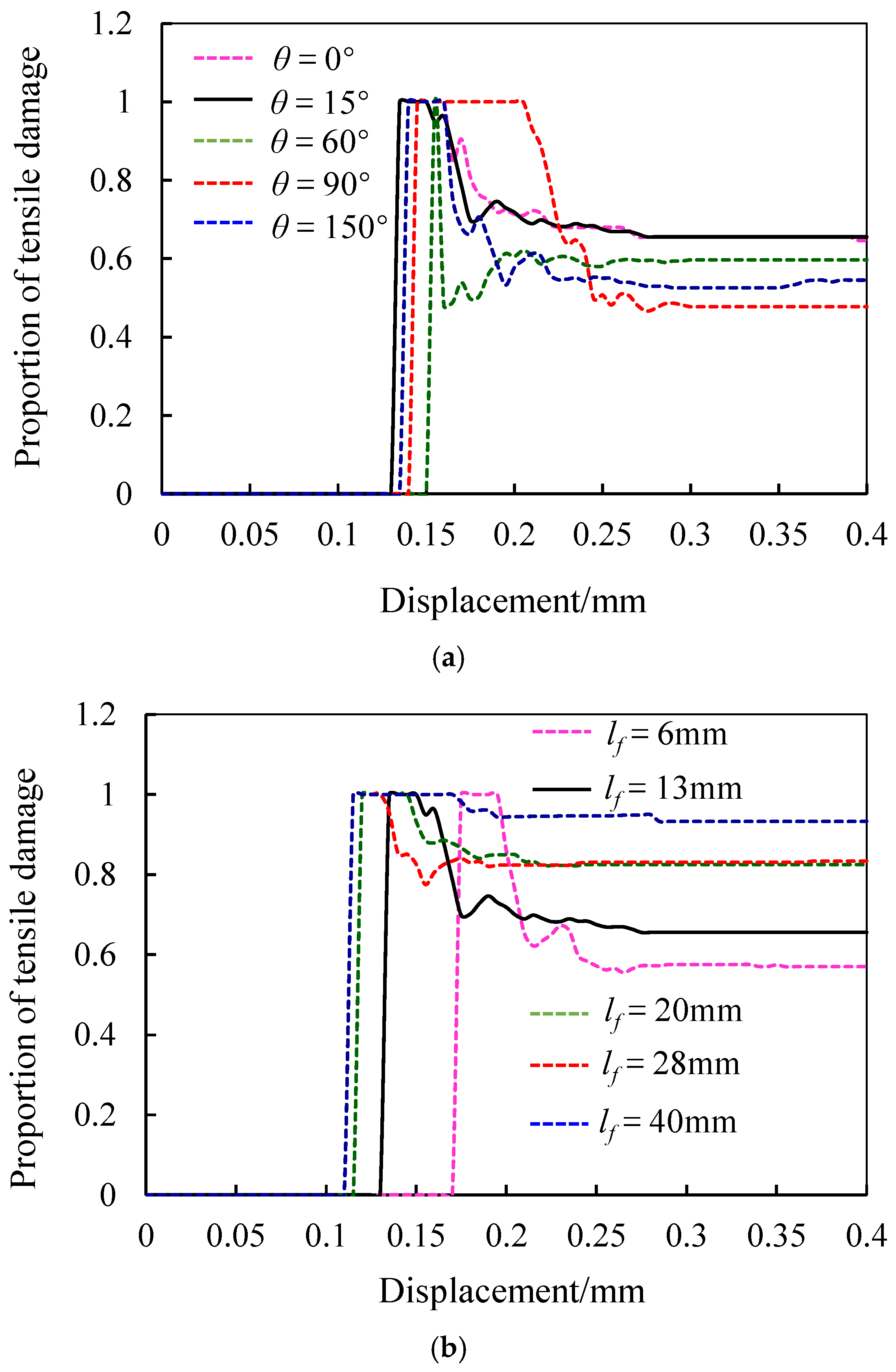
As displacement increases, the proportion of tensile failure undergoes a process of rapid decline, slow rise, another rapid decline, and finally stabilizes. Specimens with crack inclinations of 0° and 15° have the highest tensile failure ratio at stability, while those with a 90° inclination have the lowest. Crack inclination significantly affects the tensile failure ratio. Although fracture length influences the specific value of the tensile failure ratio, it does not affect the overall change trend.

(4)

As the crack angle and crack length increase, the damage quantity of cohesive force units also increases.