Dynamic Response Analysis of Parallel Twin Tunnels Under Different Train Loads

Featured Application

The static and dynamic response analysis of parallel twin tunnels under different train loads is helpful to the ensure the safety of tunnels during operation.

Abstract

Due to the spatial constraints of underground environments, the spacing between dual-line tunnels in urban metro systems is often limited, leading to potential mutual interference during the operation of trains in closely spaced parallel tunnels. In this study, a twin-tunnel model was developed using PFC2D to simulate the variations in displacement, velocity, porosity, and strain of the T2 structure and its surroundings under eight conditions (F_i = 62.4–131.5 kN, i = 1, 2, 3…, 8), elucidating the static and dynamic responses of the adjacent tunnel structure and its surroundings. The results indicate that the vertical response of T2 sleepers is significantly larger than the horizontal response under the same load. Increasing train loads induce non-uniform deformation in T2 liners, and excessive overloading may result in microcracks or structural failure. The velocity and displacement at the ground surface are substantially more significant than those in the surrounding areas closer to the vibration source, primarily due to the surface amplification effect. The surroundings of the adjacent tunnel experience uneven compressive forces, potentially causing liner separation. Under the A₇ condition, the static and dynamic responses of the tunnel structure and its surroundings sharply decreased due to the combined effects of pressure and train load dynamics. This phenomenon is attributed to the interplay between the pressure effect and the dynamic amplification effect of the train load. It is recommended that the operational train load in practical engineering should not exceed the A₄ condition (92.0 kN). This study can provide a reference for analyzing the static and dynamic responses of twin-tunnel structures under metro overloading conditions.

1. Introduction

Metro train overloading poses a significant threat to the structural integrity of tunnels. As the underground space becomes increasingly scarce and transportation demand continues to rise, the construction of closely spaced twin tunnels has become more prevalent. Train overlapping not only compromises the structural stability of the tunnels in which they operate but also poses significant safety risks to adjacent tunnels. Consequently, the impact of underground train overloading on the structure and surroundings of adjacent tunnels has attracted increasing attention.

The effects of overloaded train loads on tunnels predominantly concern single tunnels. Li et al. [1] investigated the dynamic responses of heavy-haul railway tunnels under varying loads using empirical data and theoretical analysis, emphasizing that axle load is a critical factor in track bed fatigue damage, particularly at the track location. Holmes et al. [2] discovered that train vibrations cause elastic resonance in heterogeneous rock, significantly disturbing the surroundings and structures. Liu et al. [3] utilized ABAQUS to analyze the dynamic response characteristics of heavy-haul railway tunnel surroundings, quantifying the impact of axle loads and identifying vulnerable areas under the tracks. Sekiya et al. [4] used accelerometers to monitor tunnel displacements and segment deformations, visualizing damage caused by metro train vibrations for targeted maintenance. Faizan et al. [5] found that peak acceleration values of ground increased significantly in soft, medium, and dense soils compared to rock sites. Based on existing studies, heavy-haul train loads exert a more substantial influence on the structural dynamic responses of tunnels compared to conventional train loads.

Research on twin-tunnel dynamics has mainly focused on conventional train loads. Yuan et al. [6] developed an analytical solution for twin-tunnel vibrations, demonstrating that the presence of a second tunnel substantially influences soil responses at varying distances and angles. Zhou et al. [7] found that the presence of an adjacent tunnel markedly amplifies soil vibrations through a three-dimensional analytical model. Deng et al. [8] used LS-DYNA to analyze stress distribution in twin tunnels, identifying that floors, roofs, corners, and sidewalls are particularly susceptible to cracking under combined static and dynamic loads. Li et al. [9] used FLAC3D to investigate tunnel depth, lining thickness, and diameter effects, observing more pronounced impacts in shallower tunnels. Zhao et al. [10] found that high-speed train vibrations significantly affect adjacent damaged tunnels, necessitating reconstruction and anchoring for safety. Zhou et al. [11] conducted 50 g centrifuge tests, revealing that twin-tunnel interactions amplify dynamic responses. Hu et al. [12] investigated the ground settlement and tunnel deformation induced by stacked shield tunnel construction and nearby train loads, concluding that train load exacerbates deformations in such tunnels. Lei et al. [13] conducted model tests and numerical simulations to study the ground deformation caused by the construction of overlapping tunnels at different spacings (d/D = 0.50, 0.75, and 1.00) under metro train vibration loads, revealing that the patterns of ground displacement are significantly influenced by tunnel spacing. These studies primarily focused on findings obtained under standard train loading conditions.

The research on the dynamic responses of twin tunnels under varying train load conditions remains limited. Heidary et al. [14] developed a three-dimensional finite element model (3D FEM) to investigate the influence of train axle loads on ground vibration responses in twin-tunnel configurations. Their findings indicated that ground vibrations increase with higher axle loads of both trains, especially when there are differences between the two trains. He et al. [15] analyzed the mutual influence between adjacent tunnels in saturated soil using 3D FEM, observing strong dynamic interactions between adjacent tunnels influenced by tunnel diameter. They further emphasized that these interactions are localized and highly frequency dependent. Zhang et al. [16] conducted a 1:40 scale model test to examine the deformation characteristics, crack behavior, ultimate bearing capacity, and internal forces of large-section tunnels under different train loads. They observed that cracks primarily developed at the invert and spring of twin tunnels with increasing load. These studies highlight the need for further investigation into the impacts of overloaded trains in twin-tunnel systems on adjacent tunnels.

In summary, current research primarily focuses on the static and dynamic responses of single-tunnel structures under varying load conditions and the static and dynamic responses of twin-tunnel structures under conventional train loads. However, limited investigation has been conducted on the responses of closely spaced parallel twin tunnels under different train load conditions. This study employs Particle Flow Code (PFC2D) to establish a twin-tunnel model. Eight distinct load conditions (F_i = 62.4–131.5 kN, i = 1, 2, 3…, 8) are simulated to explore the effects of train overload on adjacent tunnel structures. This study comprises two primary sections. The first section analyzes the static and dynamic responses of the twin-tunnel structure under different train loads, focusing on the displacement and velocity of tunnel sleepers and liners. The second section examines the effects of different train loads on the surrounding environment, emphasizing displacement, velocity, porosity, and strain in the surface above and around the tunnel. The innovation of this paper is the exploration of the static and dynamic response characteristics of super-close twin tunnels under different train loads by DEM.

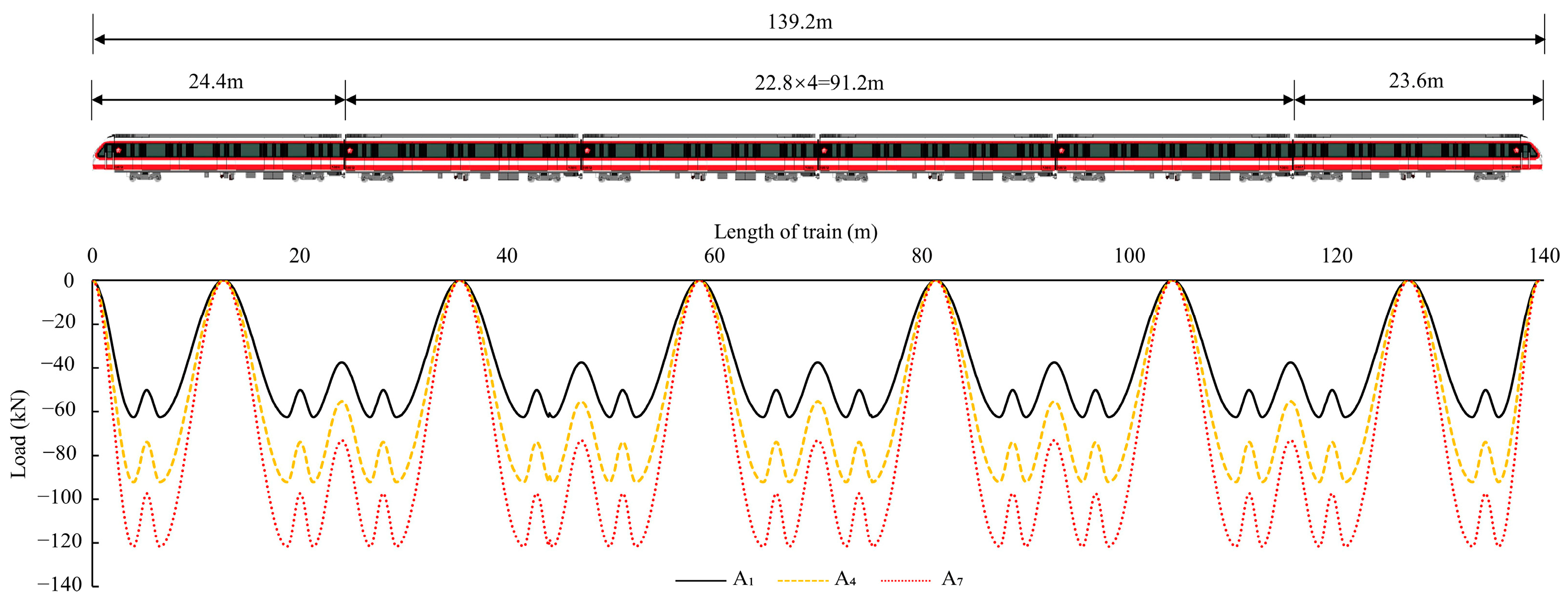
2. Background Project and Vibration of Train Type A

The engineering background is a super-close twin tunnel in Wuhan designed for high-capacity type A trains [17] that is suitable for an exploration of overload issues. The tunnel segment is precast by C60 concrete, with an outer diameter of D = 6.2 m and a segment thickness of 0.35 m. The net distance between the two tunnels is 0.25 D, with a buried depth of 1.5 D. The soil layer crossed is mainly silty sand, characterized by a bulk density of 20 kN/m³, compressive modulus of 21.9 MPa, friction of 31.9°, cohesion of 7.0 kPa, and Poisson’s ratio of 0.49. The dynamic responses of the structure and the surroundings of the right tunnel (T2) are investigated when type A trains with different loads pass through the left tunnel (T1). The weight of the carriage is 38 tons. Based on crowd weights of 0 t, 6 t, 12 t, 18 t, 24 t, 30 t, 36 t, and 42 t, eight conditions (A₁–A₈) are defined. Crowd weights of 0–6 tons are classified as normal load conditions, while all other conditions are considered overload conditions. The load vibration curve of the type A train can be expressed by a sinusoidal function with time [18], as shown in Figure 1.

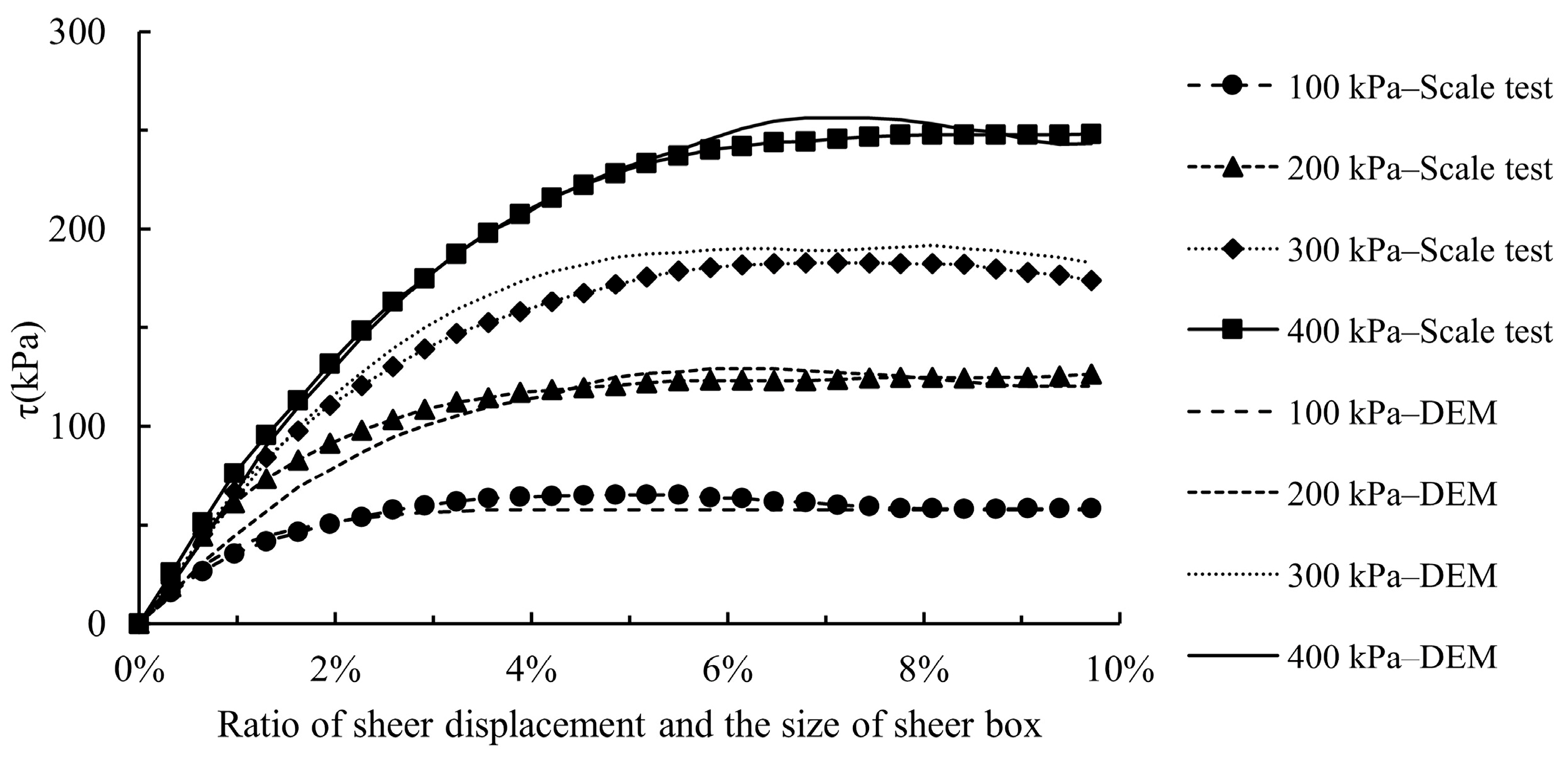
3. DEM Model

Particle flow method (PFC5.0) is a mesoscopic analysis software based on the general discrete element model (DEM) framework, applicable for both the three-dimensional model (PFC3D) and two-dimensional model (PFC2D). PFC has been successfully applied in a series of cutting-edge scientific research applications in mining, civil engineering, machinery, materials science, and other fields [19,20,21,22]. There are many studies on the establishment of large-scale models using DEM. In this study, PFC2D is used because it is recommended in the user manual for its convenience.

Before establishing the super-close twin-tunnel model with D = 6.2 m using DEM, it was necessary to determine the meso-parameters of silty sand and C60 concrete, which can be influenced by particle size in DEM. This parameter determination followed the methodology established in our previous research [23,24]. To enhance the accuracy and reduce calculation time, the model used tiny particles (silty sand ①) near the tunnel and larger particles (silty sand ②) at greater distances from the tunnel.

The calibration process for silty sand ① is described as follows. First, the shear stress–strain curve of silty sand was obtained through direct shear tests in the laboratory. Second, a numerical direct shear test model was established in DEM. The normal stiffness, tangential stiffness, and friction coefficient of particles in the model were adjusted to obtain the shear force–displacement curve. Under varying loading pressures (100, 200, 300, and 400 kPa), when the curve aligned with that obtained from the direct shear tests, the resulting meso-parameters of the silty sand were essential for the model, as shown in Figure 2. The meso-parameters for silty sand and C60 concrete are presented in

Table 1. Micro-parameters of silty sand in the DEM model.

Parameters	Silty Sand ①	Silty Sand ②	C60 Concrete
Radius of particles (m)	r1 = 0.06–0.1	r2 = 0.03–0.05	r3 = 0.009–0.012
Density (kg/m3)	2000	2000	2500
Contact Young’s modulus (Pa)	2.19 × 107	2.27 × 107	3.65 × 1010
The ratio of contact normal to shear stiffness	1.0	1.0	1.0
Coefficient of friction	0.63	0.63	0.84
The normal strength of the parallel bond (Pa)	−	−	1.0 × 10100
Tangential strength of parallel bond (Pa)	−	−	1.0 × 10100
Contact Young’s modulus of parallel bond (Pa)	−	−	3.65 × 1010
The ratio of parallel bond contact normal to shear stiffness	−	−	1.0
Parallel bonding radius	−	−	1.0

.

The specific modeling steps of the super-close twin-tunnel model under different loading conditions are as follows:

(1)

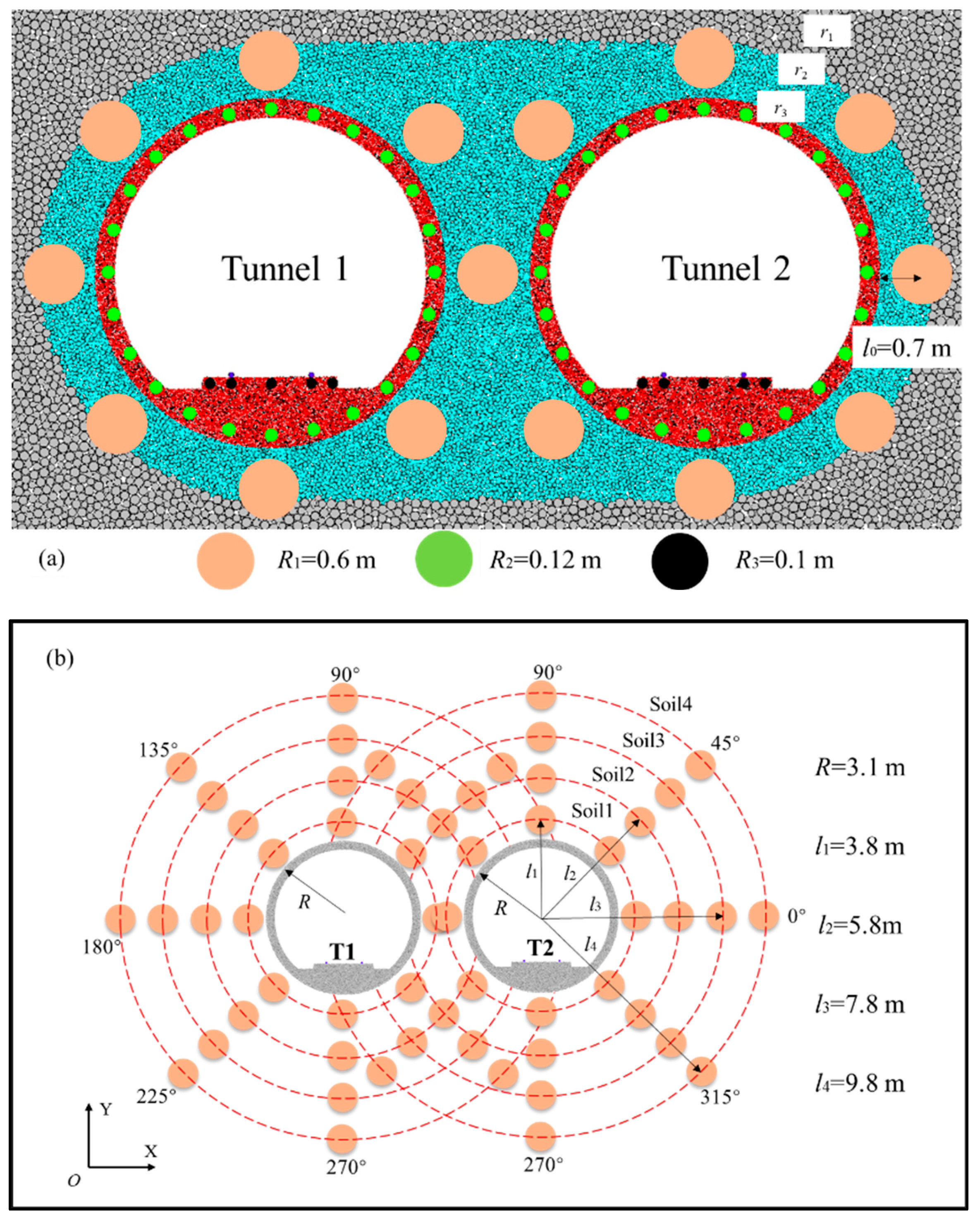
Generate walls and particles. Specifically, particles with r₁ = 0.06–0.1 m are placed far from the tunnel area, particles with r₂ = 0.03–0.05 m are positioned closer to the tunnel area, and particles with r₃ = 0.009–0.012 m are set near the tunnel area. The overall model is shown in Figure 3.

(2)

The gravity is set to g = 9.81 m/s², and the damping is set to 0.7 during the model equilibrium phase and 0.1 during the subway train operation phase.

(3)

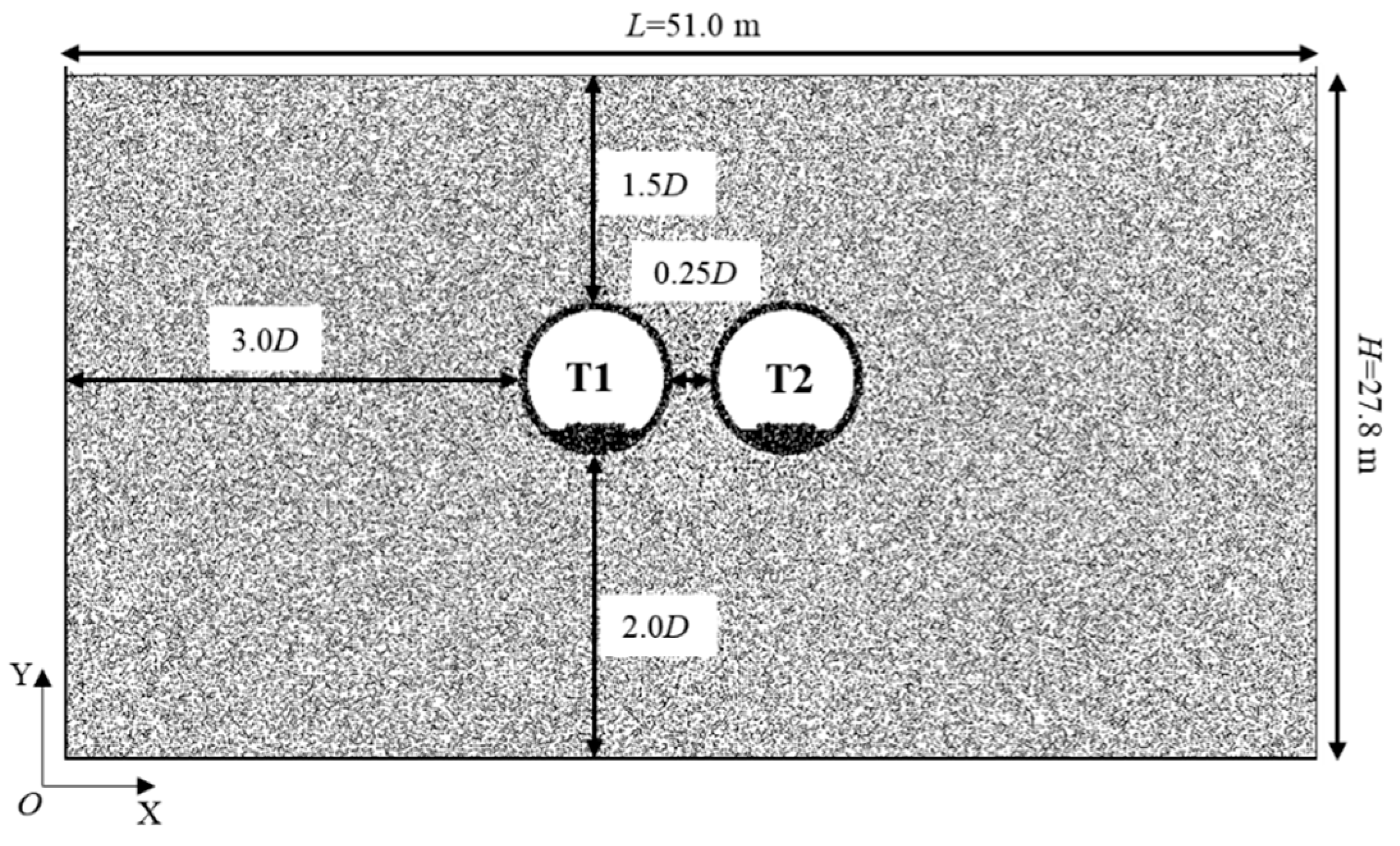
Set up monitoring points. The monitoring points are arranged in the twin-tunnel structure and its surroundings, with surface monitoring points established at intervals of 0.5 m. The detailed layout of the monitoring points within the tunnel structure and its surroundings is illustrated in Figure 4. Due to the proximity of T1 and T2, a single monitoring point is placed at 0° of T1 and 180° of T2.

(4)

Apply train loads. The train load is applied to the steel rails of Tunnel 1 under eight different conditions at a running speed of 120 km/h. The time required for a train to pass through the tunnel’s cross-section is calculated to be 4.18 s. The static and dynamic characteristics of the tunnel structure and its surroundings during train operation are monitored through the established observation points.

4. Results and Discussion

This chapter is divided into two sections. The first analyzes the impact of train overload on the twin-tunnel structure, focusing on sleeper and liner displacement (D_H and D_V) and velocity (V_H and V_V). The second examines the effect on surroundings, including the static and dynamic responses of the surroundings and surface above the tunnel. F_a represents the amplitude load under each condition (a = 1, 2, 3…).

4.1. Twin-Tunnel Structure Response

The dynamic and static responses of tunnel sleepers and liners are crucial for studying tunnel structural response. The effects of train overload on adjacent tunnel structures are examined by analyzing the dynamic responses of T1 and T2 under various load conditions.

4.1.1. Sleepers

Figure 5 illustrates the time–history curves of vertical displacement (D_V) at the midpoint (S₃) of T2 sleepers under three conditions: A₁ (F₁ = 62.4 kN), A₄ (F₄ = 92.0 kN), and A₇ (F₇ = 121.6 kN). The label A₁–S₃ represents the D_V of the midpoint (S₃) of the sleeper under the A₁ condition. The D_V values are observed to fluctuate in response to varying train loads. During 0–2.7 s, the D_V amplitude first decreases and then increases, stabilizing after 2.7 s, indicating model equilibrium. As the load increases, the positive D_V value first rises and subsequently decreases, while the absolute magnitude of the negative D_V value increases until stabilization, suggesting that overloading causes settlement in adjacent tunnel sleepers. Notably, the D_V of A₁–S₃ is the smallest, while those of A₄–S₃ and A₇–S₃ are nearly identical. The maximum D_V values recorded under each condition are −2.64, −3.80, and −4.07 mm, with those of A₄–S₃ and A₇–S₃ increasing by 43.94% and 54.17% compared to that of A₁–S₃. This suggests that the D_V increases as the load rises under the A₁ to A₄ conditions, but the pattern under the A₄ to A₇ conditions remains unclear and requires further investigation.

To further investigate the displacement pattern of the sleepers in T2, the D_H and D_V of T2 sleepers are compared under different loads (A₁–A₈), as shown in Figure 6. The displacements are peak-to-peak values, representing the difference between the maximum and minimum displacements at the monitoring point. Five monitoring points on T2 sleepers are monitored: left endpoint (S₁), left quarter point (S₂), midpoint (S₃), right quarter point (S₄), and right endpoint (S₅). S₂ and S₄ serve as the train action points during T2 operation.

The D_H of each monitoring point of T2 sleepers is shown in Figure 6a. Under the A₇ condition, the D_H values closely resemble those observed under the A₄ condition, but they exhibit a significant increase as the load transitions under the A₄ to A₇ conditions. For a more comprehensive comparison, the D_H values of T2 sleepers under different loads are compiled in Figure 6b. The D_H curves of each monitoring point completely overlap, indicating that the influence of train load on the D_H of T2 sleepers is consistent, which can be attributed to the high stiffness of concrete sleepers. The average D_H values under the A₁ to A8 conditions are 1.07, 1.23, 1.38, 1.54, 1.69, 1.85, 1.55, and 2.15 mm, with differences of 0.16, 0.15, 0.16, 0.15, 0.16, −0.3, and 0.60 mm between adjacent loads, respectively. These results indicate that the D_H increases linearly under the A₁ to A₆ conditions but decreases to the level under the A₄ condition under the A₇ condition, then sharply rises under the A₈ condition, reaching 1.38 times the value observed under the A₇ condition. This special displacement phenomenon has not been previously reported.

The D_V curves of T2 sleeper monitoring points under varying loads are presented in Figure 6c. The maximum and minimum D_V are 3.54 mm and 3.34 mm under the A₁ conditions, increasing to 7.21 mm and 6.80 mm under the A₈ condition. The D_V under the A₇ condition closely matches that under the A₄ condition. A visual comparison of D_V across monitoring points is graphically represented in Figure 6d. Under the A₁ to A₈ conditions, the D_V differences between monitoring points S₅ and S₁ are 0.20, 0.23, 0.26, 0.29, 0.32, 0.35, 0.28, and 0.41 mm, respectively. Analysis revealed that D_V increases with distance from the vibration source, a trend more pronounced at higher loads. This phenomenon can be attributed to the stabilizing effect of the twin tunnel reinforcement on the central area, which results in points closer to the source exhibiting smaller vertical dynamic responses than those farther away.

Figure 6 analysis shows that both the D_H and D_V of T2 sleepers exhibit similar trends across different conditions, with a significant drop under the A₇ condition followed by a sharp rise, a phenomenon that requires further investigation. Under equivalent loading conditions, the D_V of T2 sleepers surpasses their D_H by approximately threefold, indicating that D_V analysis should be given greater attention due to its heightened criticality in structural assessment.

Figure 7 presents the V_H and V_V of T2 sleepers under eight conditions, with velocity defined as the peak-to-peak differences between maximum and minimum values at monitoring points. Figure 7a, b show that the V_H values across monitoring points exhibit high consistency under identical loading conditions, matching the observed D_H patterns, which could be attributed to the structure’s high stiffness. The minimum V_H values under the A₁ to A₈ conditions are 13.54, 15.30, 17.09, 18.86, 20.69, 22.66, 19.10, and 26.21 mm/s, respectively. Notably, the velocity under the A₈ condition nearly doubles that under the A₁ condition, indicating a significant amplification in the dynamic response of the adjacent tunnel structure by the overload.

The V_V of T2 sleepers under different conditions is illustrated in Figure 7c, d. Under the A₁ condition, the minimum and maximum V_V values are 35.01 mm/s and 36.67 mm/s, increasing to 70.86 mm/s and 73.61 mm/s under the A₈ condition, respectively. Notably, all monitoring points consistently exceed 35 mm/s under all conditions. Under the A₁ to A₈ conditions, the differences in V_V between S₅ and S₁ of T2 sleepers are 1.66, 1.82, 2.00, 2.17, 2.32, 2.44, 2.20, and 2.75 mm/s, respectively, demonstrating a positive correlation between the V_V and the distance from the vibration source under identical loading conditions. Figure 7 shows that the V_V values at all monitoring points surpass their horizontal counterparts by approximately threefold under identical conditions. Consequently, subsequent research should prioritize the analysis of V_V due to its critical implications for structural assessment.

Combined with Figure 6 and Figure 7, the horizontal and vertical displacements and velocities of T2 sleepers exhibit a linear increase with the vibration load under the A₁ to A₆ conditions. However, under the A₇ condition, all parameters abruptly decrease before sharply rising again under the A₈ condition. This transition requires an in-depth investigation into the static and dynamic responses of T2 when the load exceeds that under the A₄ condition (92.0 kN), especially the mechanisms behind this shift. Furthermore, the D_V is approximately three times the D_H, and the V_V is twice the V_H. Differential displacements and velocities at the sleeper end increase with higher loads, suggesting excessive overloading may cause vertical misalignment and cracking in adjacent tunnel sleepers. Such significant differentials pose potential derailment risks for high-speed metro trains, threatening passenger safety and operational integrity.

Figure 6 and Figure 7 analyze the effects of train vibration loads on adjacent tunnel sleepers, and Figure 8 shows the differential between the maximum and minimum D_V of primary tunnel (T1) sleepers under different conditions. Negative D_V values represent the overall downward displacement of T1 sleepers, with zero being the maximum D_V. As demonstrated in Figure 8a, the D_V of T1 sleepers generally increases with higher loads, except under the A₇ condition, where displacement decreases compared to under the A₆ and A₈ conditions. Under identical loading conditions, T1 sleepers show slightly higher D_V values at the right-side monitoring point (S₅) than at the left side (S₁), while T2 sleepers exhibit the opposite trend, where the left-side (S₁) displacements exceed those at the right side (S₅). This phenomenon is possibly due to the stabilizing effect of the tunnel linings in the central region between the twin tunnels, reducing displacements on the right side (S₅) of T1 and left side (S₁) of T2 under train loading.

Figure 8b illustrates the D_V of T1 sleepers under varying loads, which generally increases with higher loads but decreases unexpectedly under the A₇ condition compared to that under the A₆ and A₈ conditions. Comparing Figure 6d and Figure 8b, both tunnels exhibit similar D_V patterns under identical conditions. 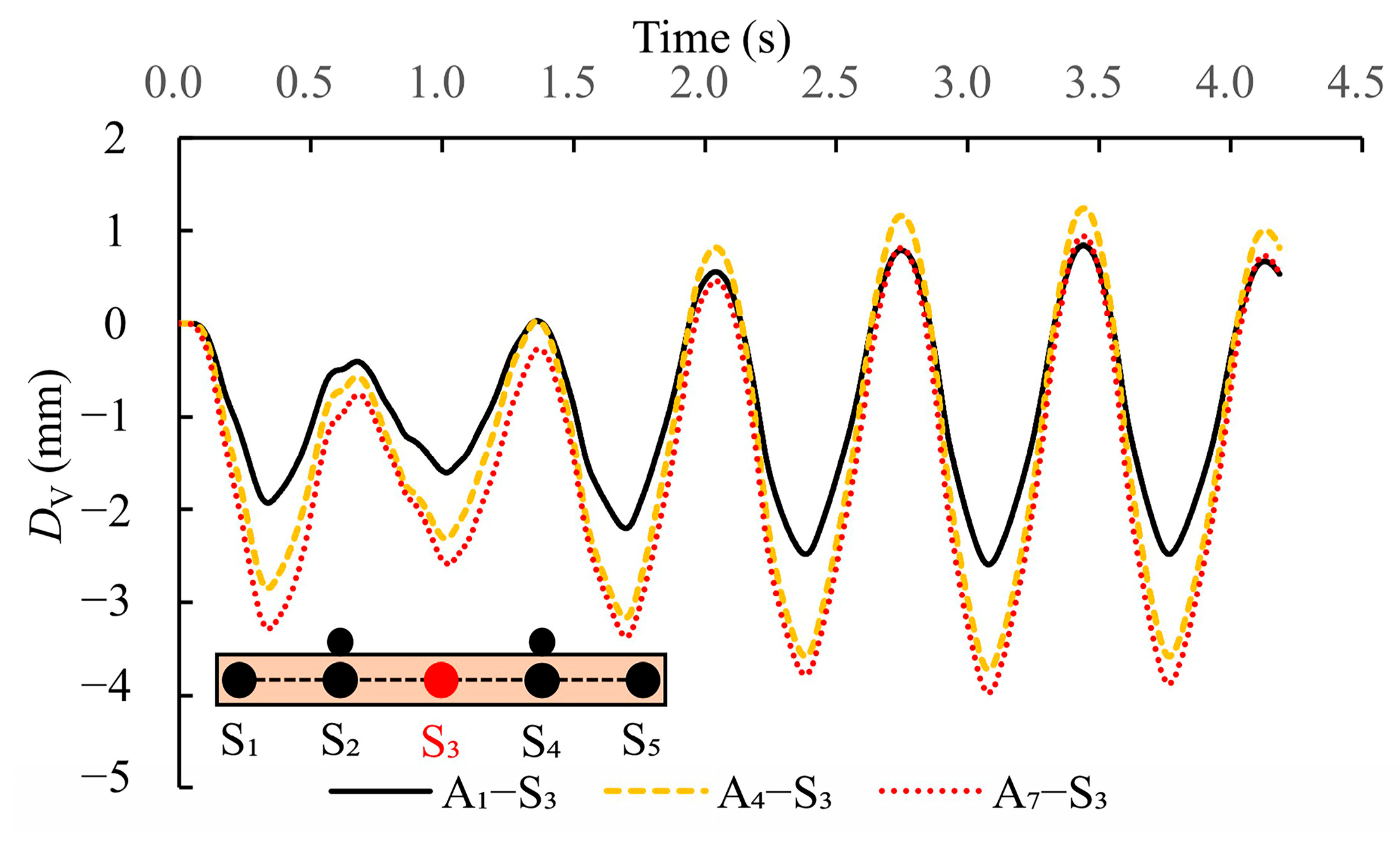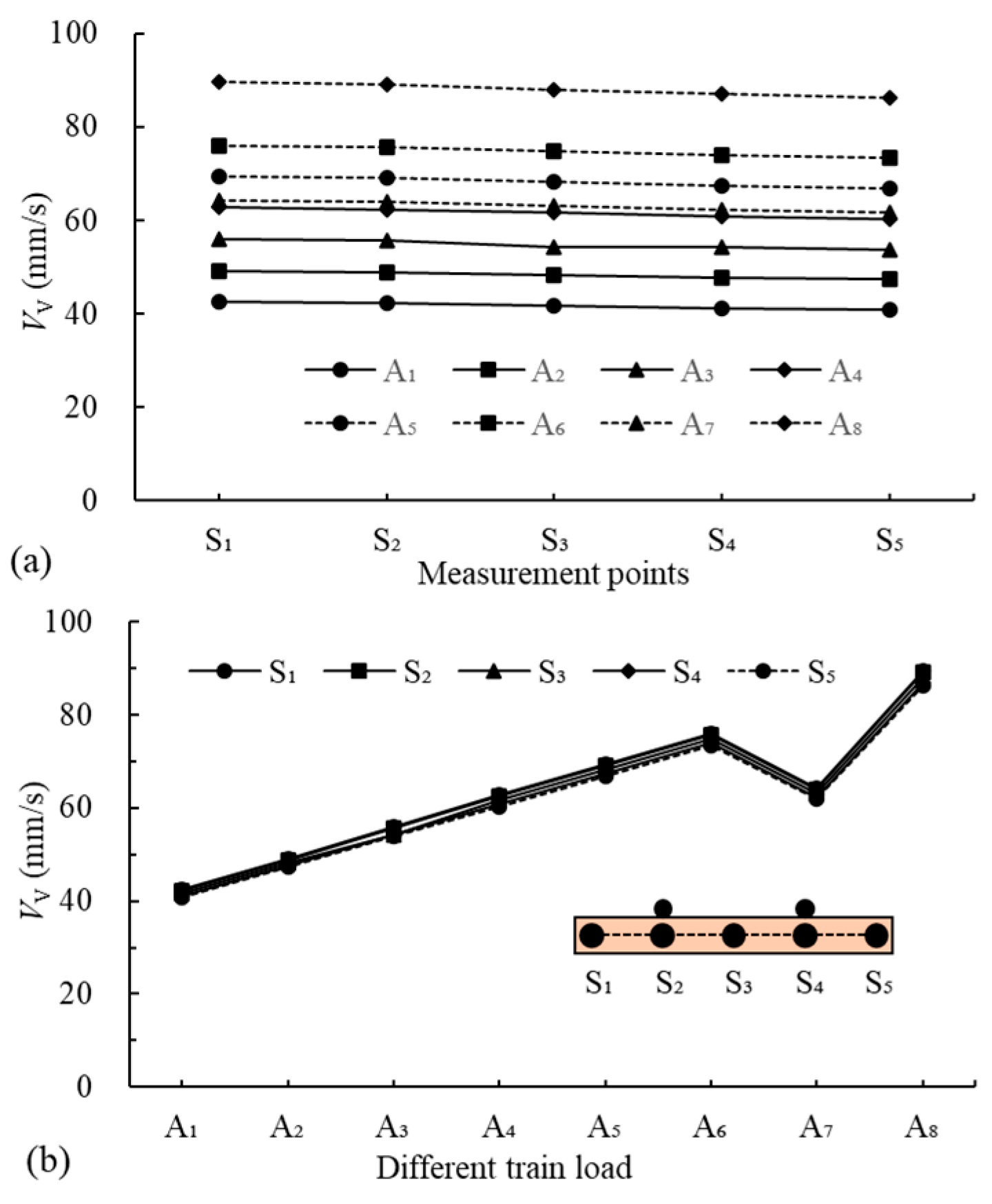Under the A₇ condition, the D_V of T1 sleepers (−5.88 mm) approximates that under the A₅ condition (−5.98 mm), while the D_V of T2 sleepers (4.92 mm) closely corresponds to that under the A₄ condition (4.97 mm). Under the same load, the D_V of T1 sleepers at each monitoring point is slightly higher than that of T2.

The V_V of T2 sleepers is more critical than its V_H (Figure 7). Figure 9 shows the difference between the maximum and minimum V_V of T1 sleepers under various loading conditions, providing further insight into their dynamic responses. The V_V anomalously decreases under the A₇ condition compared to that under the A₆ and A₈ conditions. Under identical loading conditions, the right-side monitoring points consistently demonstrate higher V_V values than the left-side points, with more pronounced variation rates than in the D_V. The comparison between Figure 7d and Figure 9b reveals that both tunnels exhibit similar V_V patterns, with T1 sleepers consistently maintaining higher V_V values than T2 under various loading conditions.

Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 show that both T1 and T2 sleepers have similar patterns in vertical and horizontal displacement and velocity responses under all conditions, with T1 showing slightly more significant responses than T2. The difference in velocity responses between tunnels is greater than that in the displacement responses. Under the A₁ to A₆ conditions, all monitoring points display linear increases in vertical and horizontal displacements and velocities as loading increases. However, under the A₇ condition, parameters exhibit an abrupt reduction to levels intermediate between those observed under the A₄ and A₅ conditions, followed by a rapid resurgence under the A₈ condition.

The dynamic responses in the vertical direction are significantly more pronounced compared to those in the horizontal direction, warranting particular attention to D_V and V_V in sleeper assessment. Furthermore, the reinforcement effect inherent in the twin-tunnel structure enhances the stability of static and dynamic responses on the side adjacent to the inter-tunnel region. Therefore, it is crucial to conduct meticulous monitoring of vertical displacements in the sleepers of adjacent tunnels to prevent the potential initiation of microcracks, thereby ensuring structural integrity.

4.1.2. Liners

Figure 10 presents the maximum resultant displacements (D_R) and velocities (V_R) at T2 liner monitoring points under various conditions. The calculation formulas for D_R and V_R are as follows:

$$D_{\mathrm{R}}=\sqrt{D_{\mathrm{H}}^2+D_{\mathrm{V}}^2},{ V}_{\mathrm{R}}=\sqrt{V_{\mathrm{H}}^2+V_{\mathrm{V}}^2}$$

(1)

Figure 10a reveals that the maximum D_R occurs at the 180° position adjacent to T1 and gradually decreases toward the 0° position opposite T1. This pattern indicates that D_R negatively correlates with distance from the vibration source, with closer points showing stronger responses. The D_R values at 180°are 2.82, 3.24, 3.65, 4.06, 4.48, 4.89, 4.39, and 5.71 mm under the eight conditions, generally increasing with higher loads. However, an anomalous reduction occurs under the A₇ condition, where the D_R decreases to levels similar to under the A₅ condition.

Figure 10b illustrates the D_R at four key positions (0°, 90°, 180°, and 270°) of T2 liners. Under identical conditions, the D_R follows a consistent descending order: 180° > 90° > 270° > 0°. This pattern indicates the influence of proximity to the vibration source and varying tunnel burial depth, which enhances stability and reduces the load impact at greater depths. Under the A₁ to A₈ conditions, the D_R increases with higher train load (excluding the drop under the A₇ condition). Higher loads also exacerbate non-uniform displacement in T2 liners, potentially leading to microcracks and structural deterioration.

Figure 10c presents the maximum V_R at various angular positions of T2 liners under different conditions. The maximum V_R consistently occurs at 210° (lower-left liner), while the minimum is at 15° (upper-right liner). Notably, these positions do not align with those of D_R, indicating that velocity measurements are more sensitive to burial depth variations and spatial deviations from displacement patterns. The comparison between Figure 10a, c reveals that the V_R distribution across angular positions is more uniform than that of D_R. Despite similar maximum V_R values across different angular positions, higher vibration load increases the difference between values. Figure 10d illustrates the V_R variation at four critical positions (0°, 90°, 180°, and 270°). Although V_R follows the same order as D_R (180° > 90° > 270° > 0°), the differences are smaller, as indicated by the nearly overlapping trend lines.

Figure 6, Figure 7 and Figure 10 show similar patterns in displacement and velocity responses between T2 sleepers and liners under all conditions. Both structural components demonstrate consistent increases in displacement and velocity as the vibration load increases under the A₁ to A₆ conditions, followed by an abrupt reduction under A₇ and a rapid increase under the A₈ condition.

Figure 11 shows the D_R and V_R of T1 liners under various conditions to investigate the impact of train vibration load on twin-tunnel liners. As illustrated in Figure 11a, the D_R values at different angular positions of T1 liners are highly consistent under the same conditions, indicating that the vibration source dominates displacement patterns. Figure 11b reveals the variation patterns of D_R at four critical positions (0°, 90°, 180°, and 270°) under different conditions, following the order: 180° > 270° > 90° > 0°. The higher D_R value at 180° compared to that at 270° (the position closest to the vibration source) can be explained by: (1) the downward loading direction at 270° potentially constrains the liner’s D_R; and (2) greater geostatic pressure at 270° due to increased burial depth.

As evidenced by Figure 11c,d, the V_R values at various angular positions of T1 liners remain relatively consistent under identical conditions, with the maximum V_R following the order: 270° > 180° > 0° > 90°. This pattern differs from the V_R characteristics, suggesting that velocity measurements are more sensitive to train vibrations and positively correlate with proximity to the vibration source. Furthermore, the twin-tunnel structure influences the V_R distribution, resulting in a higher V_R value at 180° compared to that at 0°.

Figure 10 and Figure 11 reveal that the maximum D_R at the 180° position of T2 liners is 72% to 76% of that in T1, while the maximum V_R varies from 88% to 93%, highlighting significant static and dynamic responses in adjacent tunnel liners induced by train operations. These results demonstrate that metro train vibrations significantly affect closely spaced adjacent tunnels. Increasing load exacerbates displacement differentials more in adjacent tunnels than in the operating tunnel. Therefore, both the operating tunnel and the static and dynamic responses of adjacent tunnel structures need to be monitored, with particular emphasis on liner displacements to prevent cracks caused by overloading.

Under the A₇ condition, T1 and T2 show significant decreases in displacement and velocity responses. Since T1 exhibits stronger static and dynamic responses than T2 under all conditions, the similar patterns observed under the A₇ condition likely stem from a shared underlying cause. Additionally, T2’s transitional behavior is probably influenced by T1’s structural responses.

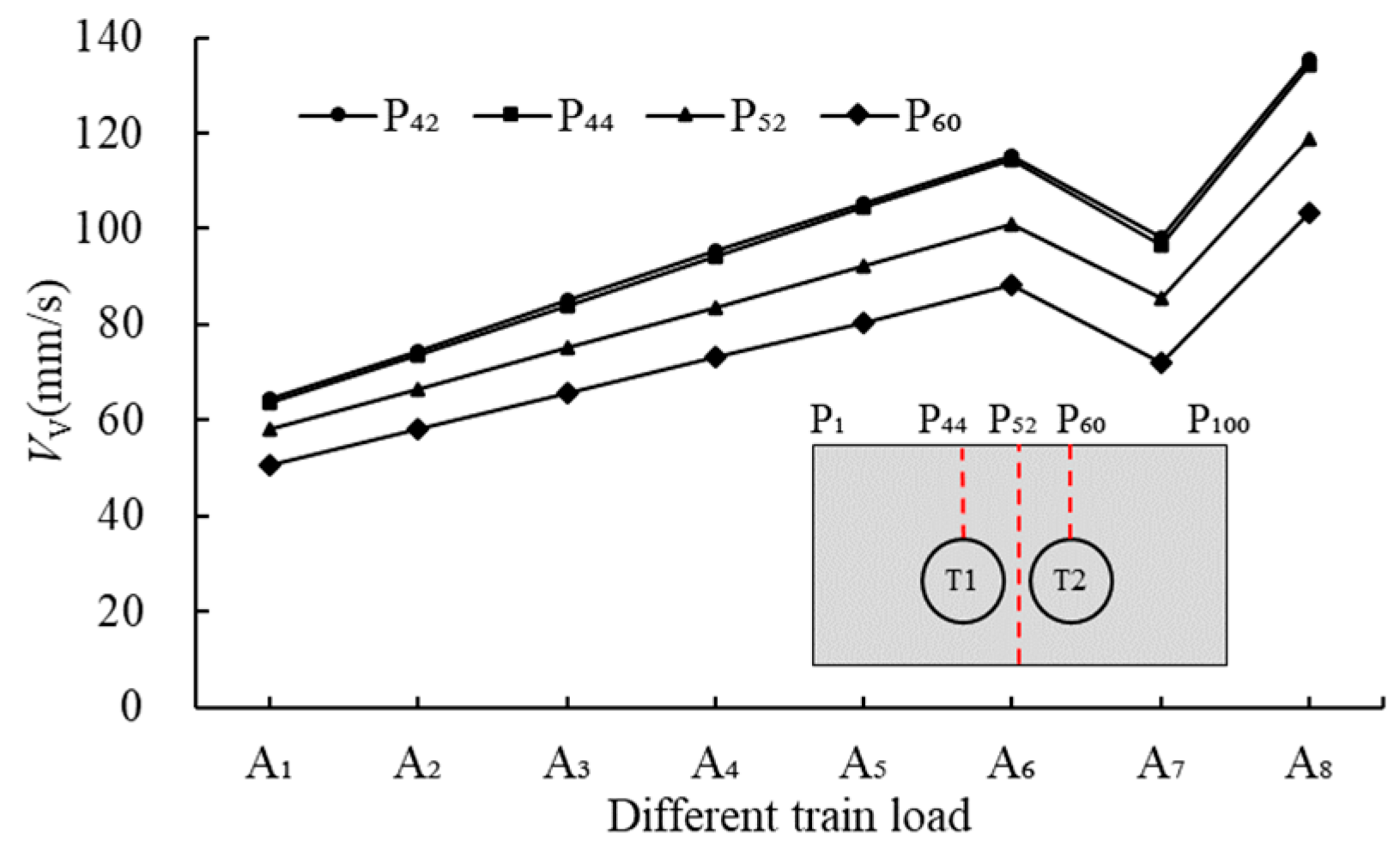
This mutation phenomenon is a unique finding of this study and is rarely reported in the existing literature. It is found that the overload value set in the existing literature is mainly divided into the following three cases:

(1)

It does not reach the value under the A₇ condition (121.6 kN).

(2)

It exceeds the value under the A₇ condition (121.6 kN), for example, Li et al. [1] studied the railway tunnel under 300 kN load and Liu et al. [3] studied the train axle load between 27 and 30 t.

(3)

The load setting spacing between conditions is too large, for example, Heidary et al. [14] studied the load response to the surface when the axle loads were 10 t, 14 t, and 18 t.

The structure’s static and dynamic responses to train loading may stem from two factors: (1) the increase in subway train load significantly enhances the vibration effect, which amplifies the dynamic response of the structure; and (2) the downward force of subway train loading on T1 sleepers exerts a pressure effect, partially suppressing vibrations in both the T1 sleeper and liner, thereby reducing the vibration of the T2 structure.

Under the A₁–A₆ conditions, the dynamic amplification effect outweighs the pressure effect, leading to a progressive increase in T2’s dynamic response with increased loading. However, under the A₇ condition, the pressure effect surpasses dynamic amplification, causing a substantial increase in T2’s dynamic characteristics to levels seen under the A₄–A₅ conditions. Under the A₈ condition, dynamic amplification significantly exceeds pressure, causing a dramatic rise in T2’s dynamic response. Further increases in loading will continue to escalate T2’s dynamic response, potentially leading to plastic failure.

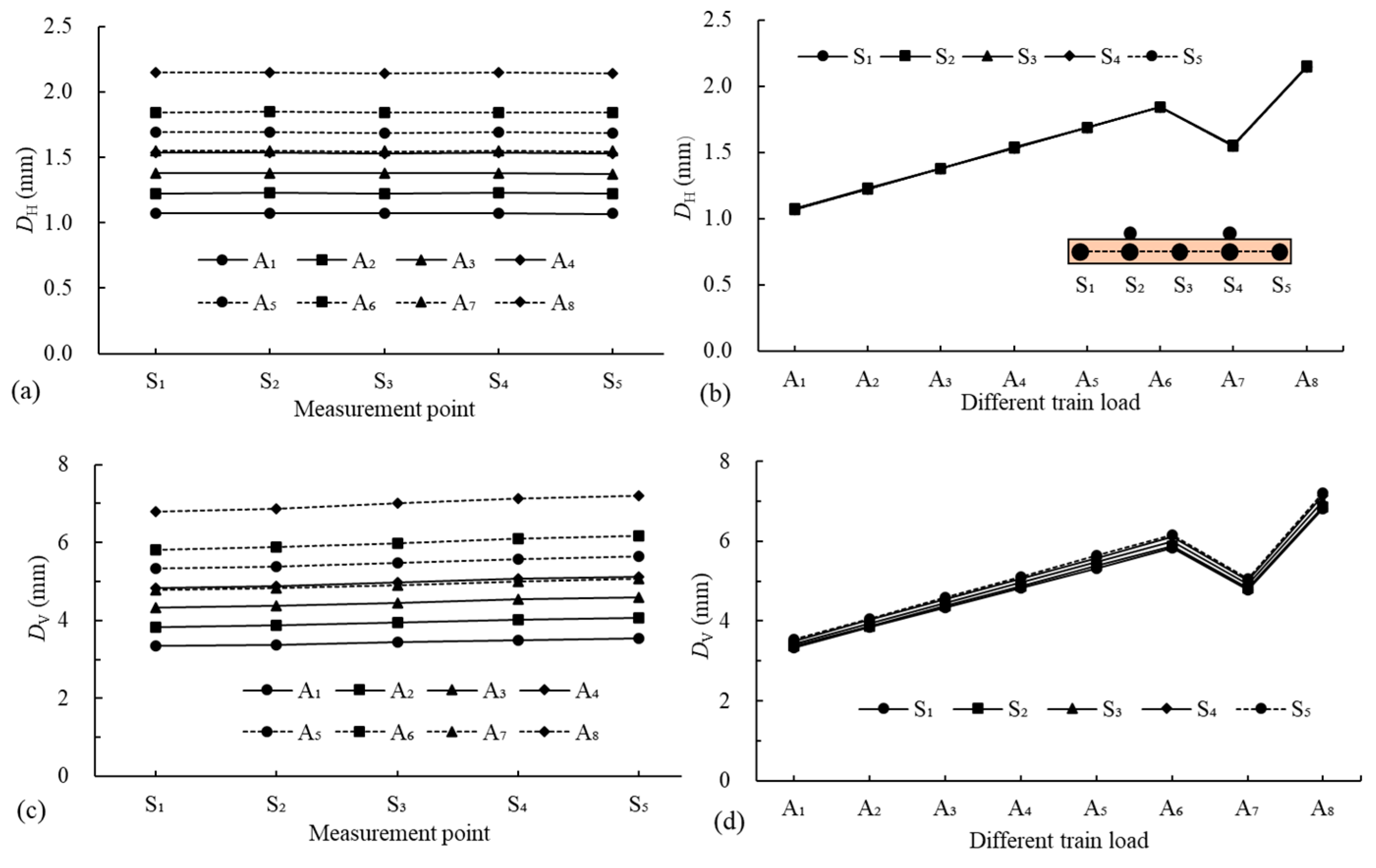
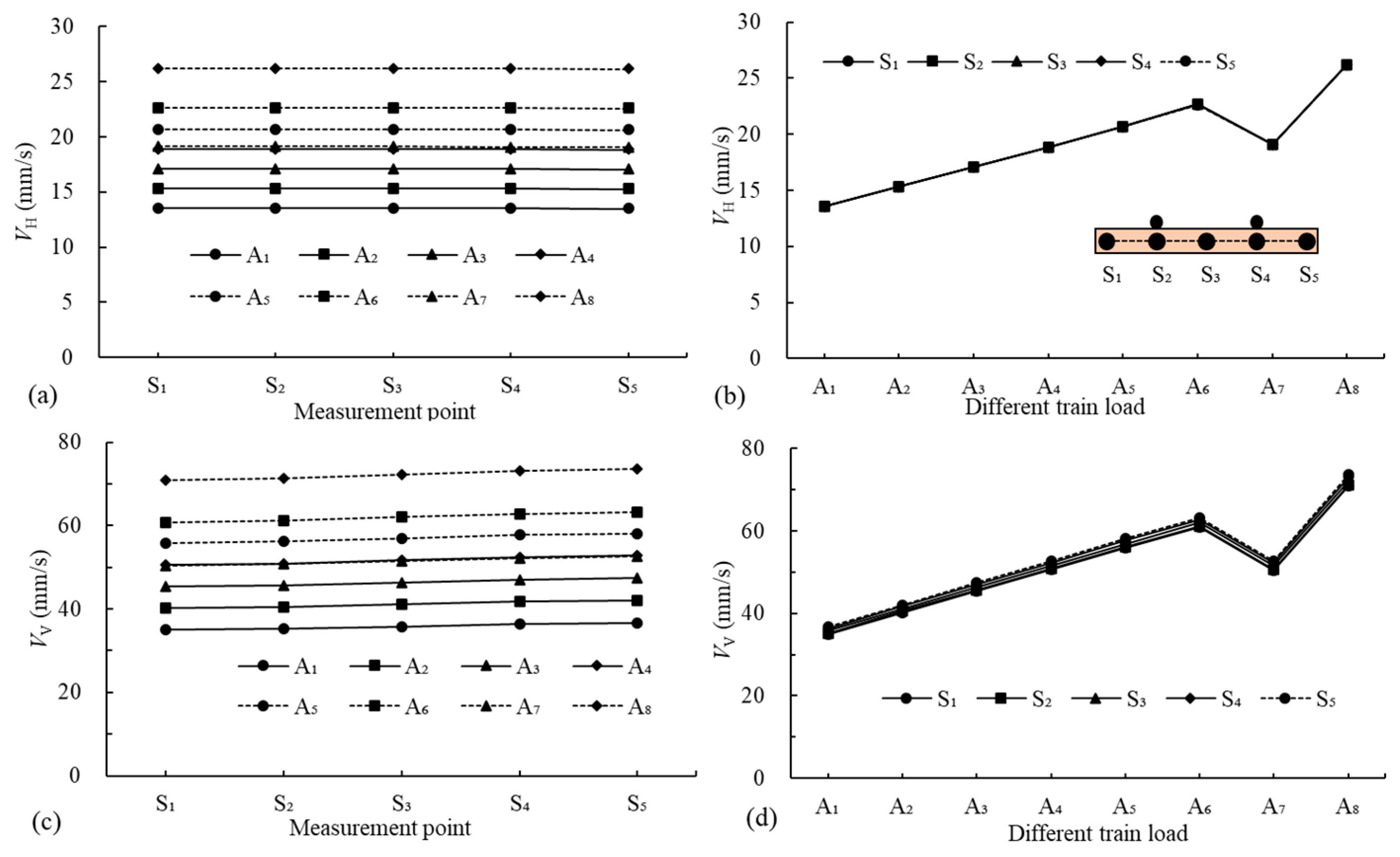
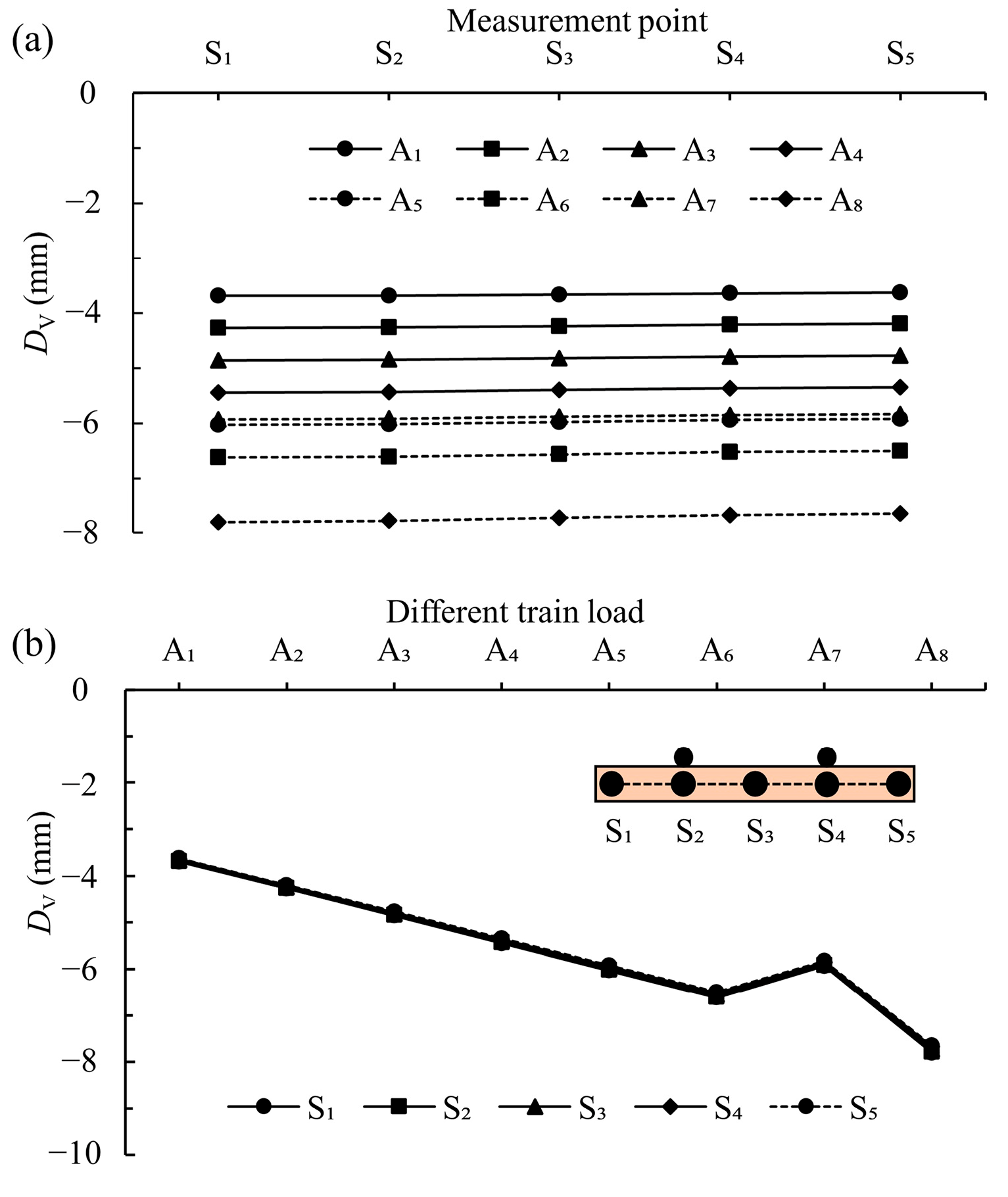
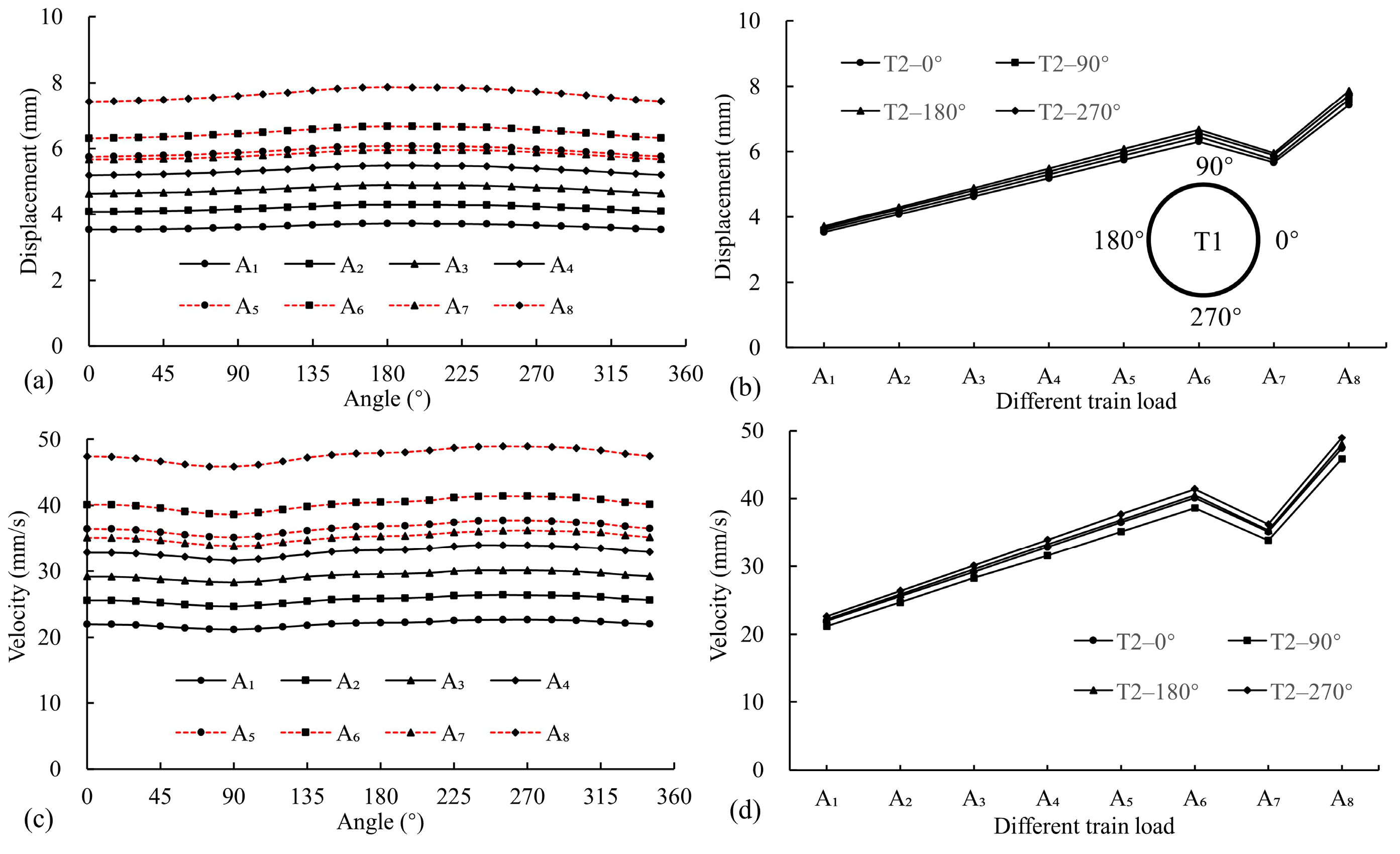
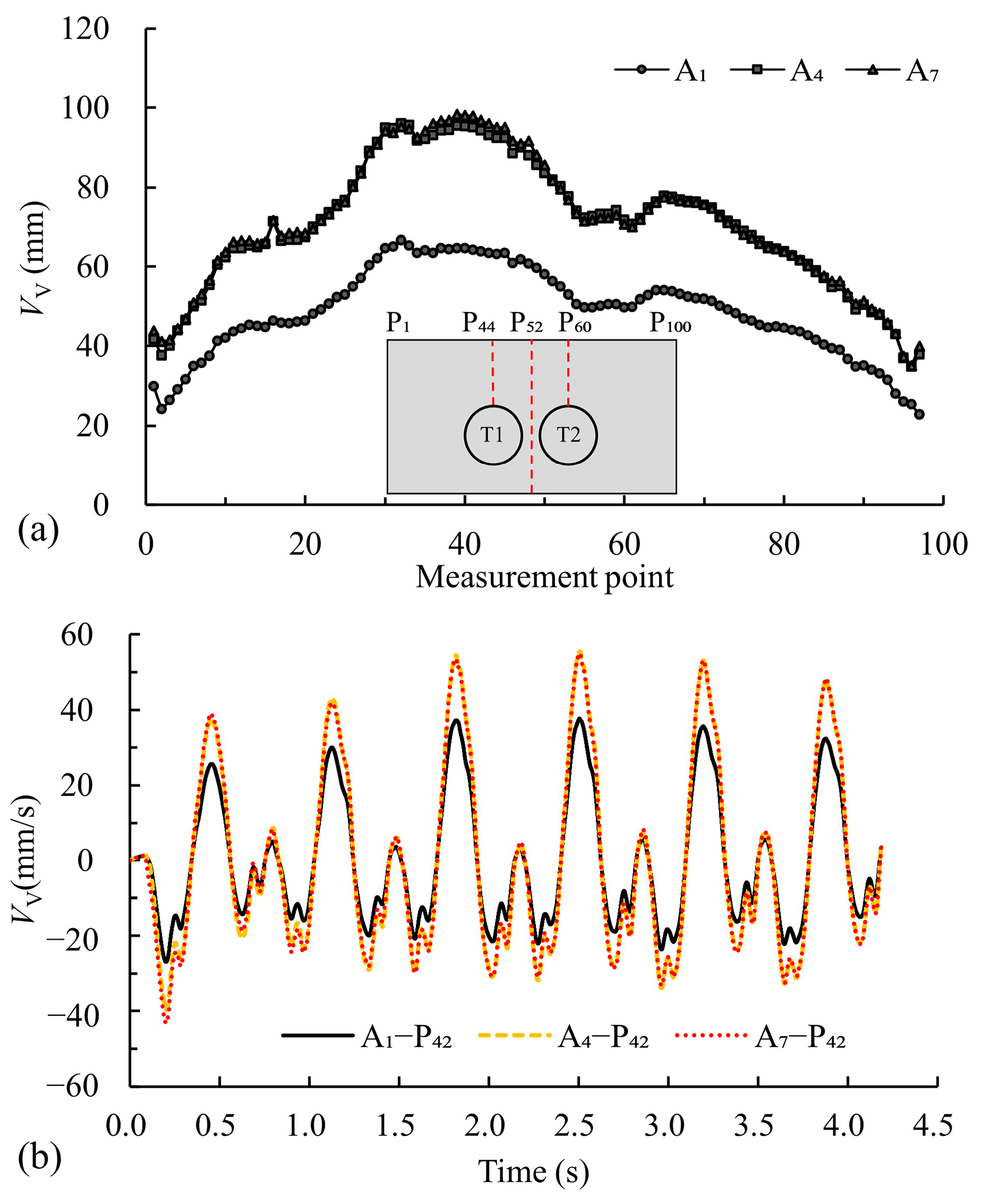
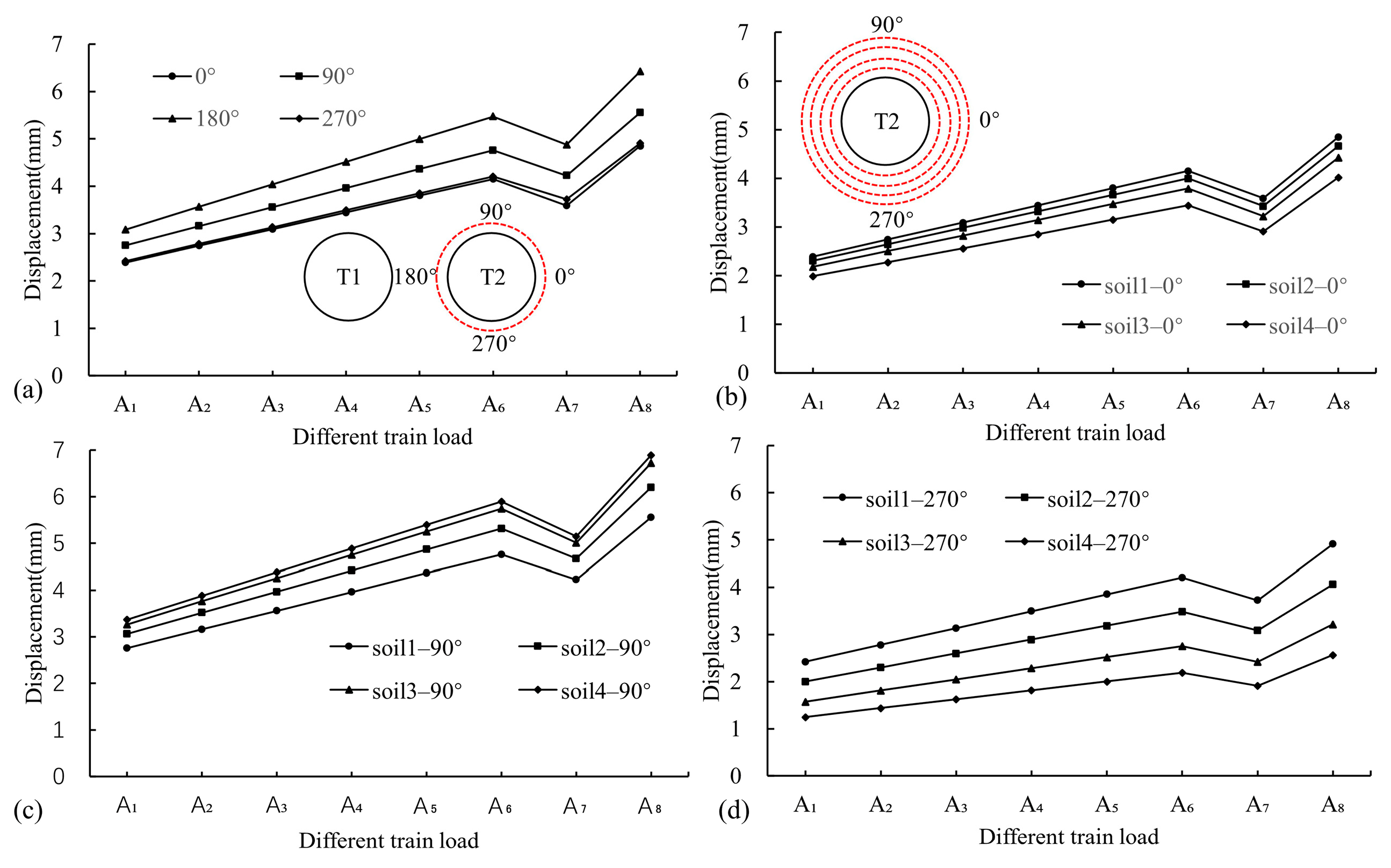
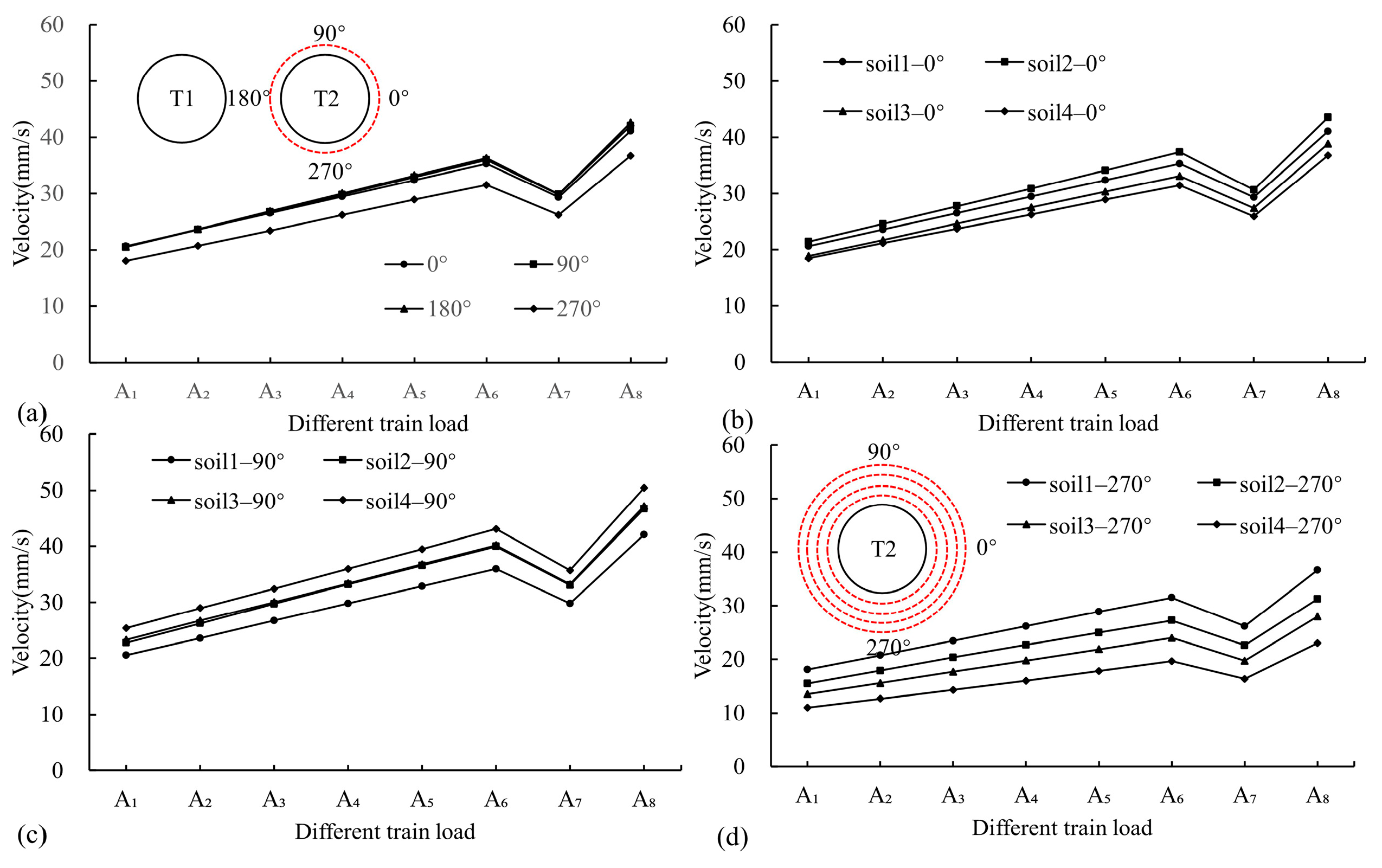
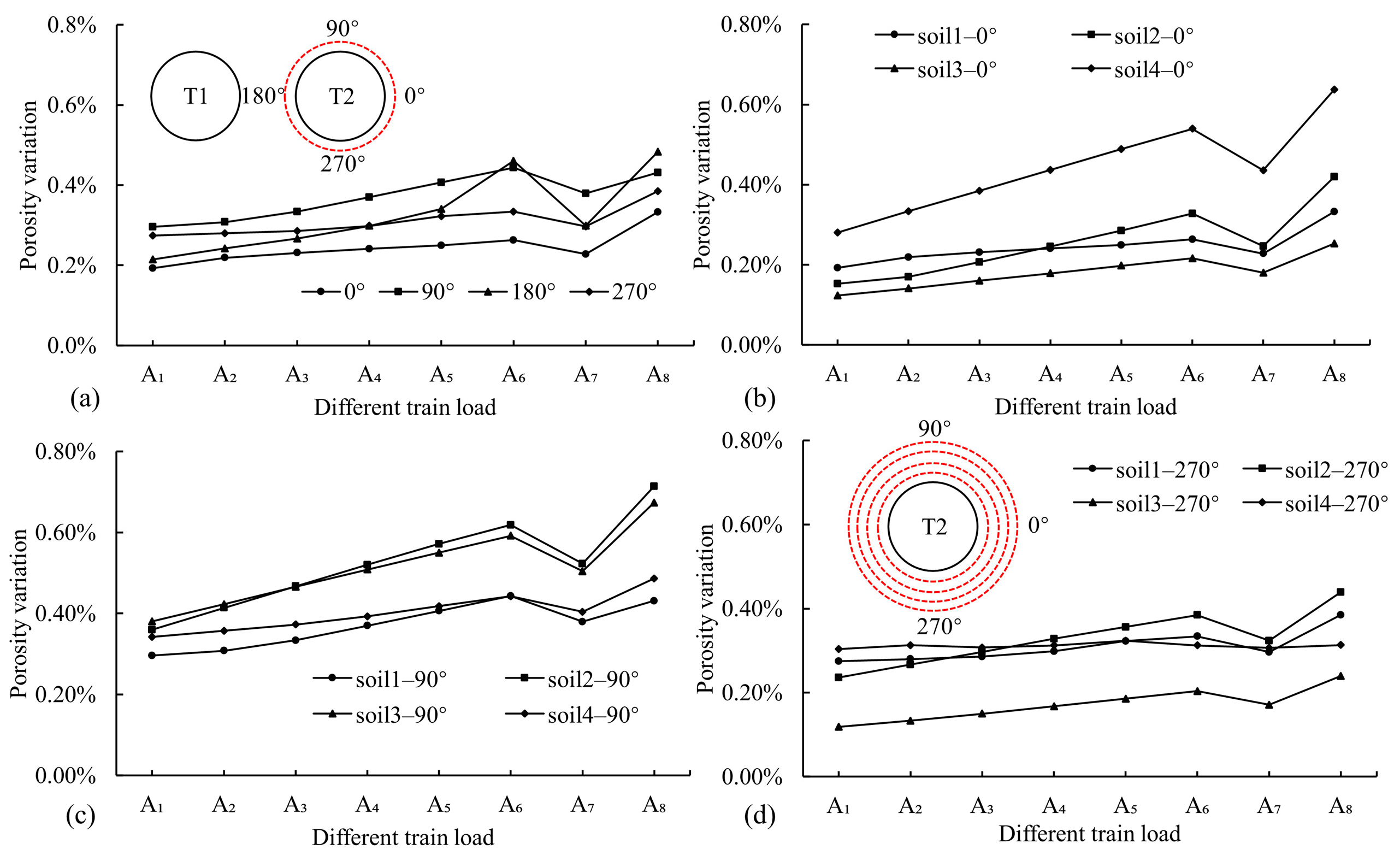
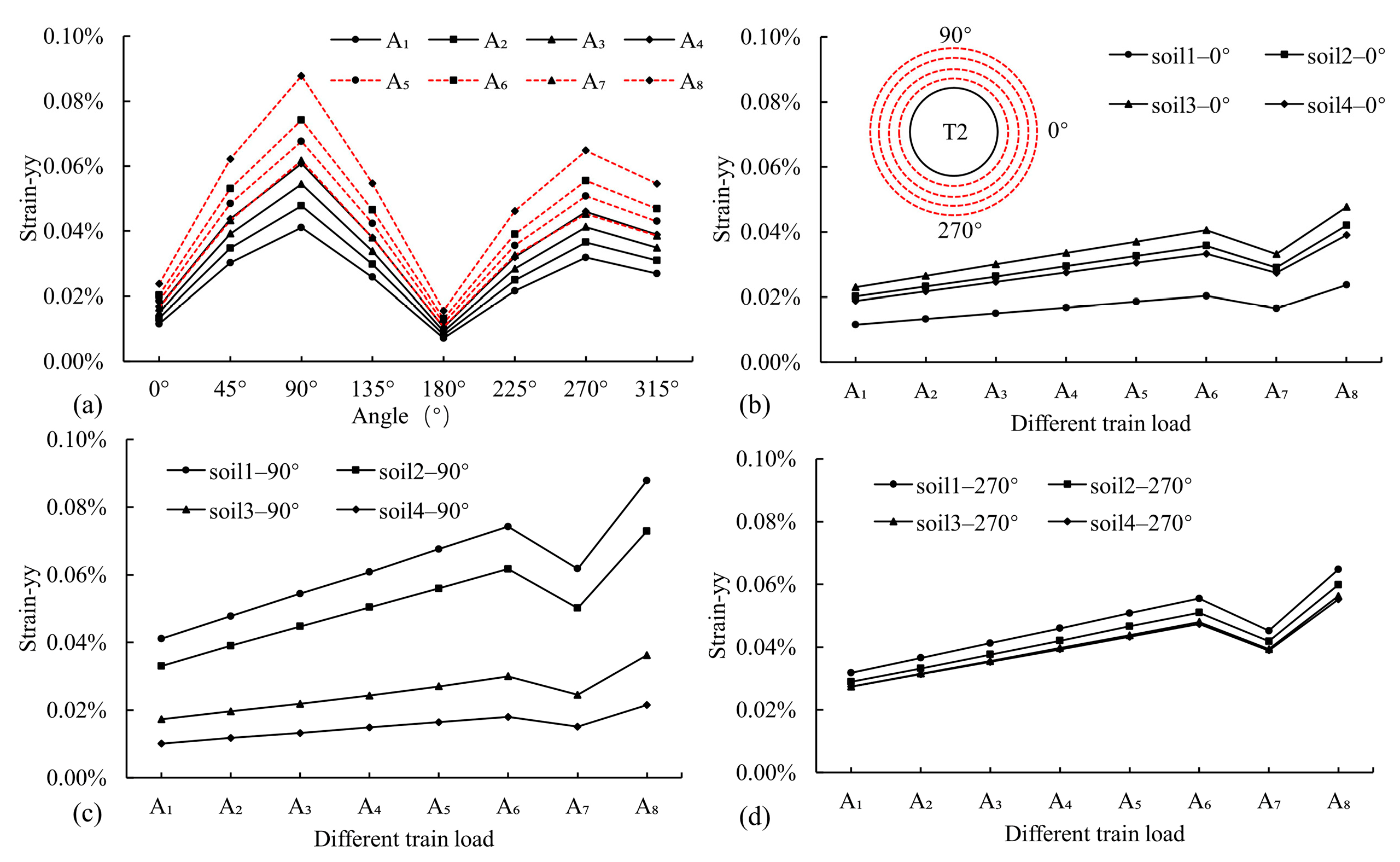
4.2. Surrounding Soil Response

The response of the surrounding soil to tunnel conditions is an essential aspect of train overloading studies. In this section, the hydrostatic response of different train vibration loads to the tunnel environment and ground is analyzed.

4.2.1. Surface

Train operations can cause ground vibrations, leading to surface subsidence that worsens with increasing train loads. Figure 12 shows the surface settlement curves under various conditions. P₄₄ is above T1’s center, P₅₂ is between the twin tunnels, and P₆₀ is above T2’s center.

Figure 12a shows that the surface settlement is most pronounced above T1, gradually diminishing toward both sides, with a more rapid decrease on the left side. The maximum surface D_V occurs at P₄₂, slightly to the left of T1’s center, attributed to the loading effect of T1 and the reinforcing influence of the twin tunnels. Under the A₁ to A₈ conditions, the maximum D_V values at monitoring point P₄₂ are −4.31, −4.97, −5.63, −6.28, −6.94, −7.59, −6.62, and −8.90 mm, respectively. Although surface settlement generally increases at higher train loads, a significant drop occurs under the A₇ condition, followed by a rapid increase under the A₈ condition.

Figure 12b illustrates the maximum D_V at four characteristic points (P₄₂, P₄₄, P₅₂, and P₆₀) under all conditions. The variation patterns at each point are mainly consistent, with the D_V curves for P₄₂ and P₄₄ being nearly identical and exhibiting the highest values. P₅₂ shows intermediate displacement, and P₆₀ demonstrates the least displacement. This trend suggests that the surface D_V decreases with increasing distance from the vibration source.

Figure 11b and Figure 12b show that the D_R of T1 liners is less than the absolute D_V at the surface above T1 (P₄₄). Under the A₁ condition, the maximum D_R of T1 liners is 3.72 mm, and the absolute D_V at P₄₄ is 4.27 mm. Under the A₈ condition, the maximum D_R of T1 liners increases to 7.87 mm, and the absolute D_V at P₄₄ increases to 8.91 mm. This difference highlights the amplified surface response to train vibrations, emphasizing the need to monitor the impact of subway trains on surface displacement.

Figure 12c shows the surface settlement curves under the A₁, A₄, and A₇ conditions. The maximum surface D_V under the A₇ condition is slightly higher than that under the A₄ condition, with nearly no difference at point P₆₀ on the right. This suggests that at the A₇ level, the twin-tunnel structure may reach a new “equilibrium” to accommodate overloading.

Figure 12d presents the time–history curves of surface D_V at point P₄₂ under these conditions. The label A₁–P₄₂ represents the vertical displacement of the point P₄₂ of the surface under the A₁ condition. Equilibrium is achieved at approximately 1.3 s, with the D_V variation patterns remaining consistent under all conditions and oscillating in response to changes in trainload. Comparing the maximum positive D_V at point P₄₂, the order is A₄ > A₁ > A₇, while for the maximum absolute negative D_V, it is A₇ > A₄ > A₁. These observations demonstrate that as train vibration load increases, the surface initially experiences stronger D_V fluctuations, followed by an overall downward trend.

Figure 12 shows that both proximity to the vibration source and the magnitude of the vibrational load influence surface D_V. The surface D_V increases with higher train vibration loads, and excessive overloading can exacerbate surface settlement, which should be avoided.

Under the A₇ condition, a comparable change in surface settlement was observed, aligning with the dynamic response of the T2 structure. This phenomenon suggests that under these conditions, the static pressure effect of the train load predominates over its dynamic effect, resulting in simultaneous reductions in both the static and dynamic responses of the tunnel structure and the surface.

Figure 13 compares the peak-to-peak V_V at four characteristic points (P₄₂, P₄₄, P₅₂, and P₆₀). The data indicate that train load significantly influences the surface V_V, with the maximum V_V exceeding 40 mm/s under different conditions, surpassing even the V_V of T1 sleepers. This further confirms the surface amplification effect [25,26]. Figure 12b and Figure 13 illustrate the variation patterns of D_V and V_V at each point, which are consistent with increasing load. However, the differences in the maximum V_V among points P₄₄, P₅₂, and P₆₀ are more uniform than those in the D_V, probability due to a more sensitive and faster propagation of velocity changes.

The comparison of surface V_V under three conditions is depicted in Figure 14. The V_V values under the A₄ and A₇ conditions significantly exceed that under the A₁ condition, as illustrated in Figure 14a. At point P₃₄, the differences between the maximum and minimum V_V are 66.57, 96.04, and 95.22 mm/s under the A₁, A₄, and A₇ conditions, respectively; at point P₄₂, these differences are 64.64, 95.35, and 98.08 mm/s, respectively. This indicates that the maximum V_V shifts from point P₃₄ to P₄₂ as the train vibration load increases. Under the A₁ to A₆ conditions, the maximum V_V occurs at P₃₄, but under the A₇ condition, the maximum shifts to P₄₂, suggesting structural reorganization under higher loads, reducing tunnel displacements and velocities. Notably, the maximum V_V remains at P₄₂ under the A₈ condition.

Figure 14b shows the time–history curves of V_V at point P₄₂ under three conditions for comparison with surface D_V. Equilibrium is achieved approximately at 1.5 s. Before 2.8 s, the V_V under the A₄ conditions exceeds that under the A₇ condition; after 2.8 s, the V_V under the A₄ condition drops below that under the A₇ condition. This shift suggests that the T1 structure may have reorganized or been damaged under the A₇ condition. Figure 12d and Figure 14b reveal that the variation patterns of D_V and V_V at point P₄₂ are similar under the three conditions, oscillating with train vibration load change. When D_V is negative, V_V also exhibits a negative value. In contrast to the relatively smooth D_V time–history curves, the V_V curves show more peaks and sensitive variations, indicating a more intense response.

Figure 12, Figure 13 and Figure 14 show that the dynamic response of surface soil under various conditions is consistent with that of the tunnel structure. Under train vibration loads, the surface D_V and V_V align in the same direction. As the load increases, the overall dynamic response shifts downward. Under the A₇ condition (121.6 kN), the reductions in V_V and D_V at surface points may be attributed to tunnel structural reorganization, establishing a new “equilibrium” to handle overloading or indicating potential damage. To ensure tunnel safety and longevity, loads exceeding class A₄ (92.0 kN) should be avoided in actual metro operations.

4.2.2. Surroundings

Analyzing the response of the surroundings to train loads is crucial for understanding their support role for tunnel liners, making such disturbances a key observational parameter. Figure 15 illustrates the maximum D_R of the T2 surroundings under different conditions. Specifically, Figure 15a shows that the variation pattern of soil1 D_R in T2 is similar to that of the surface. Figure 10b and Figure 15a reveal that under the same conditions, the D_R values at four points in the T2 surroundings correspond to those in tunnel liners, ranked from highest to lowest: 180°, 90°, 270°, and 0°. The D_R is highest at 180° and lowest at 0°, indicating that propagation distance is a decisive factor. Additionally, the D_R at 90° slightly exceeds that at 270°, suggesting that depth affects the displacement response; deeper rock layers, characterized by higher initial stress, exhibit greater stability and smaller displacements under equivalent loads. The soil1 D_R values at 90° and 180° slightly exceed those in tunnel liners, while at 0° and 270°, they are marginally lower. This discrepancy indicates uneven compressive forces in T2’s lower-right and upper-left regions under train loads, potentially leading to rock fracturing and void formation.

Figure 15b–d compare the maximum D_R across four layers of surroundings on the T2 right side (0°, 90°, and 270°). The data indicate that as the distance from the vibration source increases, the D_R gradually decreases. Specifically, the D_R reduction rate increases with distance at 0° and 90°, while it exhibits a slight decrease at 270°. The D_R reaches its peak at 90°, followed by 0°, and is lowest at 270°. This pattern highlights the tunnel crown as the most vulnerable area under vibration loads, a conclusion substantiated by extensive studies [27,28,29]. By contrast, the D_R at the tunnel invert (270°) is relatively small and rapidly attenuates with depth, indicating that it is the safest region.

The comparison between Figure 10 and Figure 15 shows that the surroundings and tunnel structure exhibit similar displacement patterns, with a significant abrupt change observed under the A₇ condition. However, the maximum D_R of T2 liners occurs at 180° (closest to T1), while the surroundings’ maximum D_R is at the crown of T2. This difference can be attributed to the granular nature of the surrounding soil, where particle displacement under train vibrations reduces porosity at the crown, causing larger displacements. By contrast, T2 liners, being a tightly bonded monolithic structure, experience minimal changes in porosity, resulting in greater displacement responses closer to the vibration source.

Figure 16 compares the maximum V_R of the T2 surroundings under different conditions. As depicted in Figure 16a, the V_R variation patterns under all conditions resemble those of D_R. Notably, the soil1 V_R values at 0°, 90°, and 180° in the T2 surroundings are similar. Under the same condition, the V_R values at the four monitoring points in the T2 surroundings follow the order of 180°, 90°, 0°, and 270°. This indicates that while the V_R magnitude in the T2 surroundings is mainly influenced by distance from the vibration source, the liner depth has a more pronounced impact on V_R compared to D_R. Figure 10d and Figure 16a show that the V_R of T2 liners remains relatively stable when propagating to the surroundings, except at 270°, where the V_R slightly attenuates due to burial depth effects.

The maximum V_R of the surrounding layers on the T2 right side (0°, 90°, and 270°) under different conditions is illustrated in Figure 16b–d. As depicted in Figure 16b, under the same condition, the maximum V_R values across the four layers at 0° follow the order: soil2 > soil1 > soil3 > soil4. This observation, along with the uneven displacement between T2 liners and the surroundings in Figure 15, explains why the D_R of the T2 right-side surroundings initially increases and then decreases with distance from the tunnel.

Figure 16c,d show that the V_R values in the surroundings above T2 (90°) follow the order: soil4 > soil3 > soil2 > soil1. Conversely, the pattern below T2 (270°) is inverted, with the soil1 V_R being lower beneath T2 compared to above it. This suggests that greater burial depth increases the earth pressure on the T2 surroundings, leading to reduced V_R.

Figure 17 shows the rate of porosity variations (R_P) in the T2 surroundings under eight conditions. As the train load increases, the adjacent tunnel surroundings reorganize to accommodate the additional stress, leading to significant changes in soil porosity, with the R_P in the T2 surroundings increasing accordingly. Notably, the R_P decreases under the A₇ condition before rapidly increasing again. As shown in Figure 17a, the R_P values in T2 soil1 follow the order: 90° > 270° > 180° > 0°. The maximum R_P occurs at the T2 crown (90°), validating the conclusion from Figure 15 that train vibrations displace the surrounding particles downward, causing significant porosity changes above the tunnel. Meanwhile, the R_P value on the T2 left side (180°) is higher than that on the right (0°) due to its greater distance from the vibration source. After the A₄ condition, the R_P curve for the T2 left side (180°) diverges, reaching 0.46% under the A₆ condition, surpassing the crown R_P. This indicates destabilization of the soil between the twin tunnels as the load increases, especially after the A₅ condition.

Figure 17b–d illustrate the R_P in the T2 surrounding layers (0°, 90°, and 270°). Under all conditions, the R_P on the right side of T2 is highest in soil4 and lowest in soil3. Following the A₄ condition, the R_P in soil2 exceeds that in soil1, supporting the conclusion from Figure 15a that the T2 lower-right corner experiences uneven compressive stress under train loads. Furthermore, the R_P above T2 is significantly higher than that below, with soil4 below T2 exhibiting nearly constant R_P values under all conditions. This suggests that the influence of train load on soil structure diminishes with increasing depth.

Figure 17 shows that the R_P of the tunnel surroundings is influenced by train load, tunnel structural configuration, and burial depth. Notably, the region between dual tunnels experiences the most significant combined effects, leading to the highest value of R_P.

Figure 18 compares the maximum strain-yy values in the T2 surroundings under various conditions. Strain, which reflects soil deformation under external forces, is a key indicator for assessing soil deformation and surrounding structure stability. Figure 18a illustrates that the maximum strain-yy values at different angles in T2 soil1 under the A₄ and A₇ conditions are nearly identical. Strain-yy peaks at the top (90°) and bottom (270°) of T2, with lower values at the right (0°) and left (180°) sides. This suggests that under train loading, the T2 surroundings tend to form a vertically oriented elliptical deformation, which intensifies with higher train loads.

Figure 18b–d compare the maximum strain-yy values at 0°, 90°, and 270° for each layer of the T2 surroundings under various conditions. At the right side of T2 (0°), strain-yy values for the four layers follow the order: soil3 > soil2 > soil4 > soil1, indicating that strain-yy initially increases and then decreases with distance from T2. Additionally, when comparing strains at the top and bottom of T2 across different conditions, the vertical strain decreases as the distance from the tunnel increases, with slower reduction rates observed at greater burial depths.

Figure 15, Figure 16, Figure 17 and Figure 18 reveal that the dynamic response of the T2 surroundings mirrors the tunnel structure’s behavior: it increases with train load under the A₁ to A₆ conditions, decreases to levels similar to under the A₄ condition under the A₇ condition, and then sharply rises under the A₈ condition. In T1, train-induced vibrations, burial depth, and the twin-tunnel structure create uneven compressive forces in the T2 surroundings, especially in the lower-right and upper-left regions. Overloading exacerbates this issue, potentially leading to the detachment of tunnel liners from the surrounding soil. Thus, in practical applications, the impact of overloading on adjacent tunnel surroundings, especially in the upper regions of T2, demands significant attention.

In this paper, the static and dynamic response characteristics of adjacent tunnels of parallel double tunnels under eight different loads (F_i = 62.4–131.5 kN, i = 1, 2, 3…, 8) are studied by PFC. Compared with the field monitoring adopted by Li et al. [1], this paper analyzes the influence of different loads on the dynamic responses of the whole tunnel structure and its surroundings. Compared with the finite element method used by Liu et al. [3,30,31], this paper not only find the influence of axle load on the bottom of the tunnel but also analyzes the dynamic response to the surface and finds the amplification effect of the surface. Compared with the scale test adopted by Heidary et al. [14,32,33], this paper not only finds that the increase in train load will increase the dynamic response of the tunnel structure and surface but also finds that it will decrease under the A₇ condition.

5. Conclusions

This study investigates the influence of train operations in Tunnel 1 on the structure of Tunnel 2 and the surrounding environment. Conditions A₁ to A₈ (from 62.4 to 131.5 kN) were established by PFC to quantitatively analyze the static and dynamic responses of the T2 structure and its surroundings under varying loadings. The main findings are summarized as follows:

• The D_V of T2 sleepers is approximately three times the D_H, while the V_V is roughly twice the V_H, highlighting the predominance of vertical responses over horizontal ones as a critical focus. The reinforcement characteristics inherent in the twin-tunnel structure enhance the stability of the intermediate region between the tunnels, resulting in relatively small responses in the T2 sleeper region closer to the vibration source. Overloading of trains may cause uneven displacements in T2 liners, potentially leading to microcracks or even structural failure.
• The maximum D_V and V_V points on the surface are located slightly to the left above T1, surpassing those of the tunnel sleepers under the same conditions. The dynamic response of the surroundings under train loads is significantly influenced by the burial depth and tunnel structure, causing uneven compressive forces in the lower-right and upper-left regions of the T2 surroundings. Consequently, it causes elliptical deformation and potential liner–rock separation. When the train vibration load exceeds 92.0 kN (A₄), the R_P above the tunnel becomes significantly pronounced, emphasizing the significant impact of overload on the tunnel’s surroundings, particularly near the surface.
• The train vibration load in T1 significantly amplifies both the static and dynamic responses of T2 and its surroundings. However, a sudden decrease is observed under the A₇ condition. This reduction can be attributed to the dynamic amplification effect dominating the pressure effect under A₁ to A₆ conditions, leading to a progressive increase in the dynamic response of T2. Under the A₇ condition, the pressure effect surpasses dynamic amplification, leading to a sharp decline in T2’s dynamic characteristics. When the load reaches the A₈ condition, the dynamic amplification effect far exceeds the pressure effect, resulting in a dramatic increase in T2’s dynamic response.
• In practical engineering applications, it is crucial to monitor the static and dynamic responses of overloaded trains on adjacent tunnel structures, with particular emphasis on the static and dynamic responses of the liners and surrounding areas on the T2 side proximate to T1. During construction, critical zones within the T2 structure must be closely monitored when T1 experiences train overloading to ensure the safety and integrity of the tunnel throughout its operational life. It is recommended that the operational load of the tunnel be maintained within the threshold of the A₄ condition (92.0 kN) to mitigate potential risks.

This study examines the static and dynamic responses of adjacent tunnels under single train operation. However, since train loading represents a long-term condition, its adverse effects on adjacent tunnels are expected to be more pronounced. Future research will explore the impact of prolonged train loading on these responses.