Research on Numerical Calculation Methods for Modelling the Dynamics of Diesel Engine Crankshaft System Substructures
Abstract
1. Introduction
2. Crankshaft System Substructure Modelling
3. Calculation of Free Vibration of Crankshaft System Substructures
4. Methods for Calculating the Dynamic Response of Crankshaft System Substructures
4.1. Crankshaft Substructure Forced Vibration Calculation Method
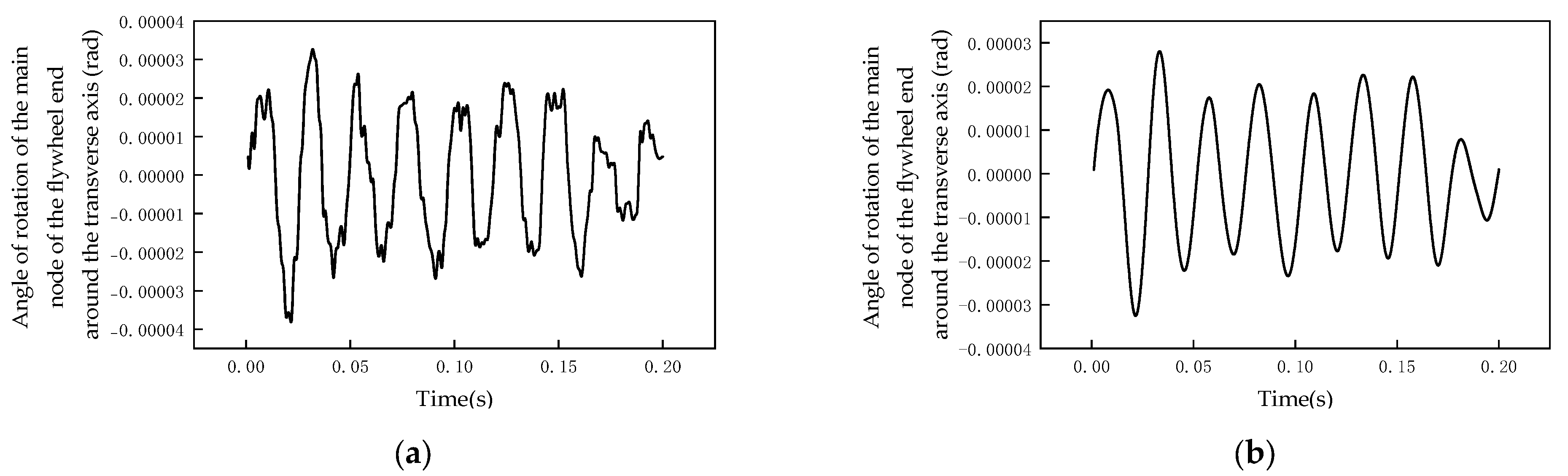
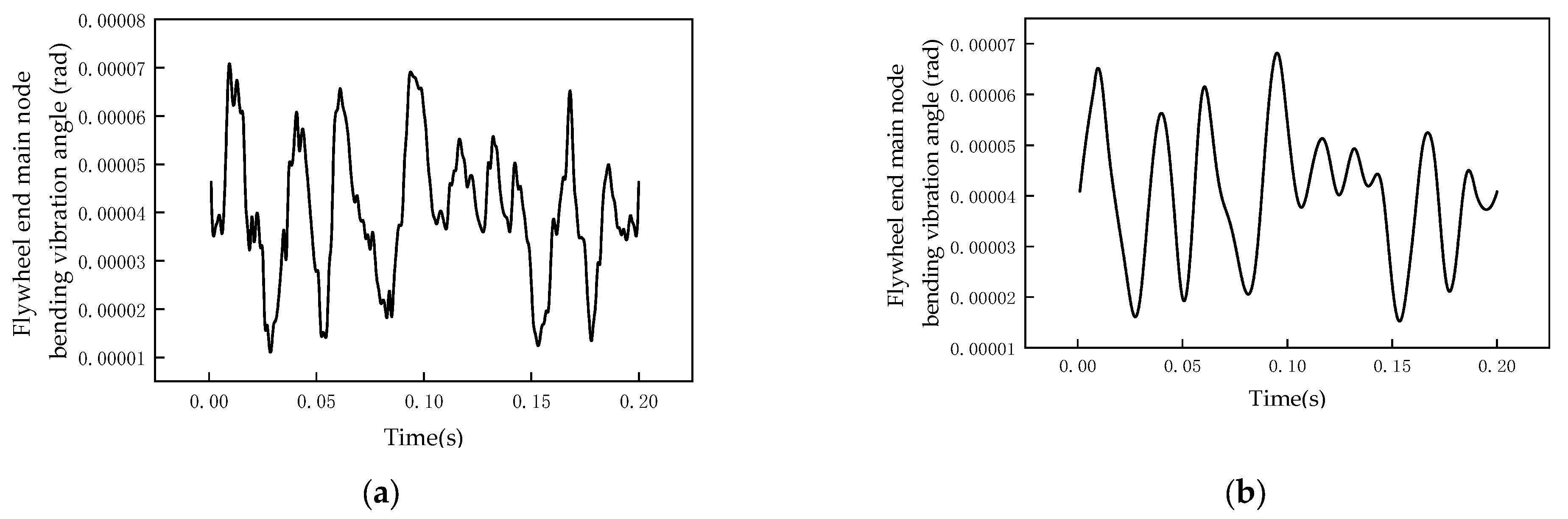
4.2. Verification of Dynamic Response Calculation Results
- (1)
- The results from both methods align well regarding the main frequencies and amplitudes, indicating that the programme is relatively reliable.
- (2)
- The substructure dynamic calculation programme provides richer frequency components with a more detailed description of high-frequency harmonics.
- (3)
- The programme’s results show noticeable interference in the torsional response for certain time periods, smoothing one peak. This phenomenon arises because the substructure model includes components beyond the observed direction, resulting from torsional, bending, and longitudinal vibration coupling.
- (4)
- Due to the proximity of the bearing installation positions to the flywheel end, the bending vibration amplitudes in all directions at the flywheel end are relatively small compared to the torsional vibration amplitude. This is because the nearby bearing support provides greater structural constraint, effectively limiting bending deformation in that region. As a result, the dynamic response at the flywheel end is dominated by torsional behaviour, while bending contributions remain minimal under the same loading conditions.
5. Study of Factors Influencing Dynamic Response of Crankshaft System
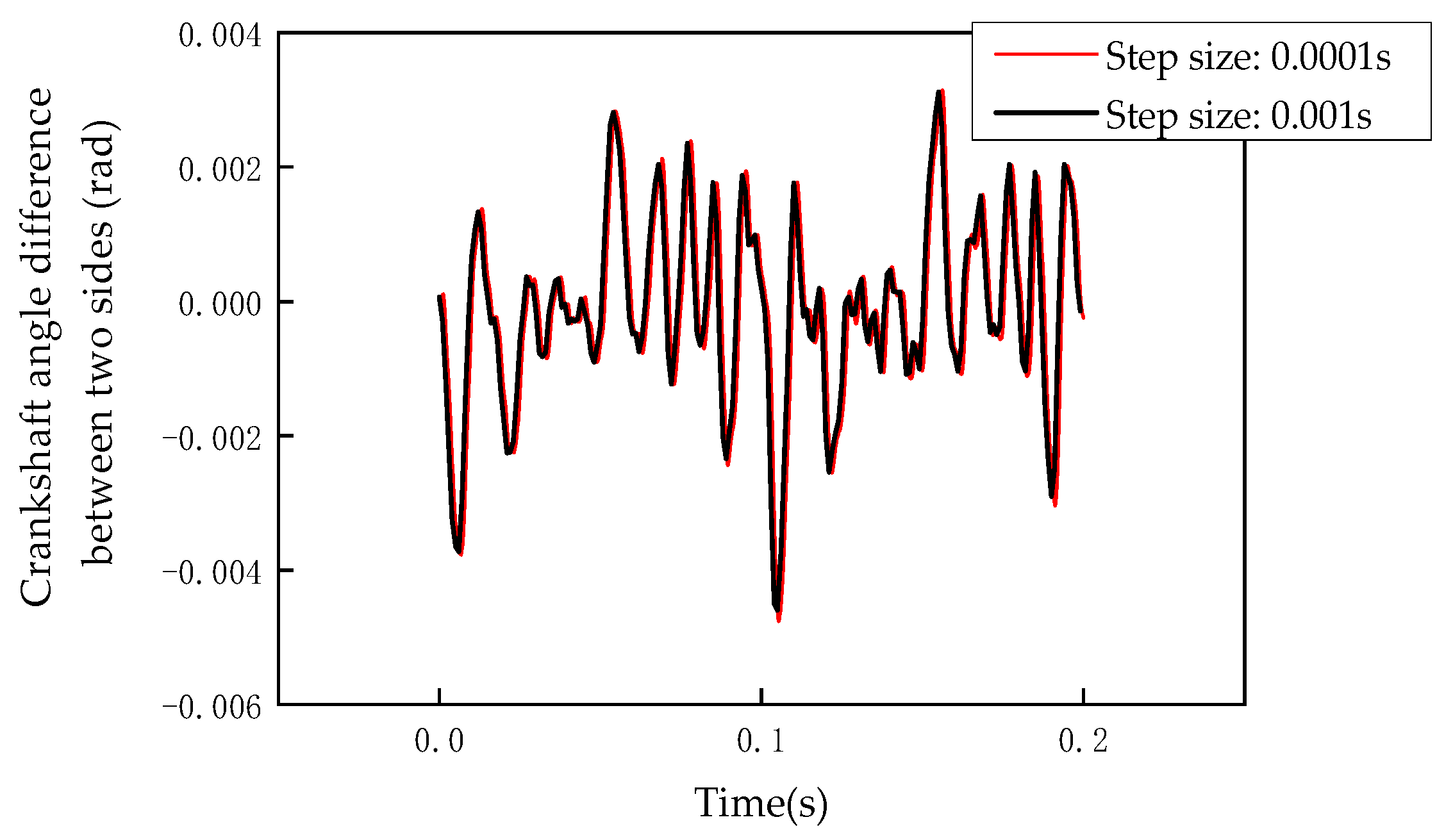
5.1. Integration Step Size
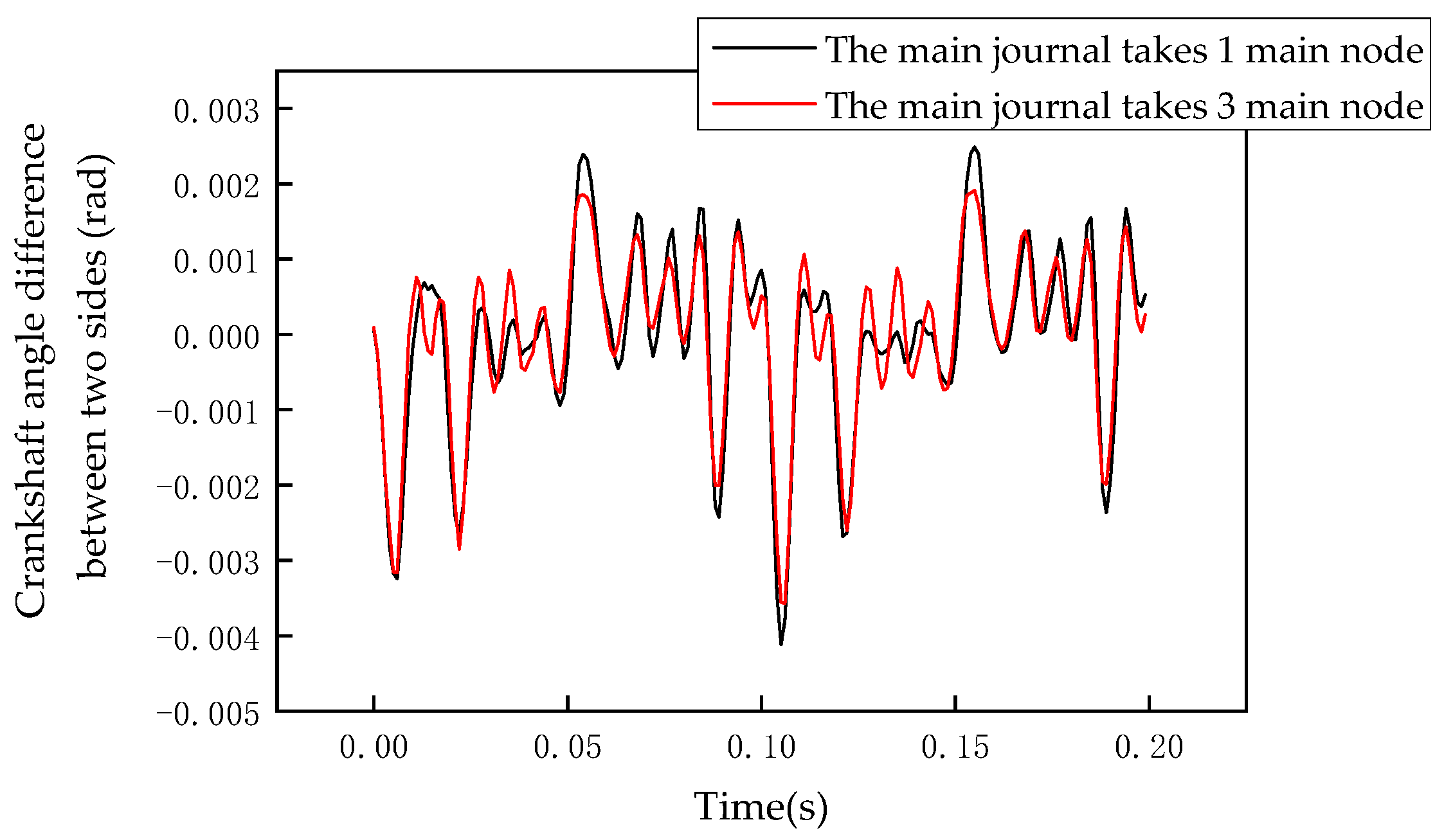
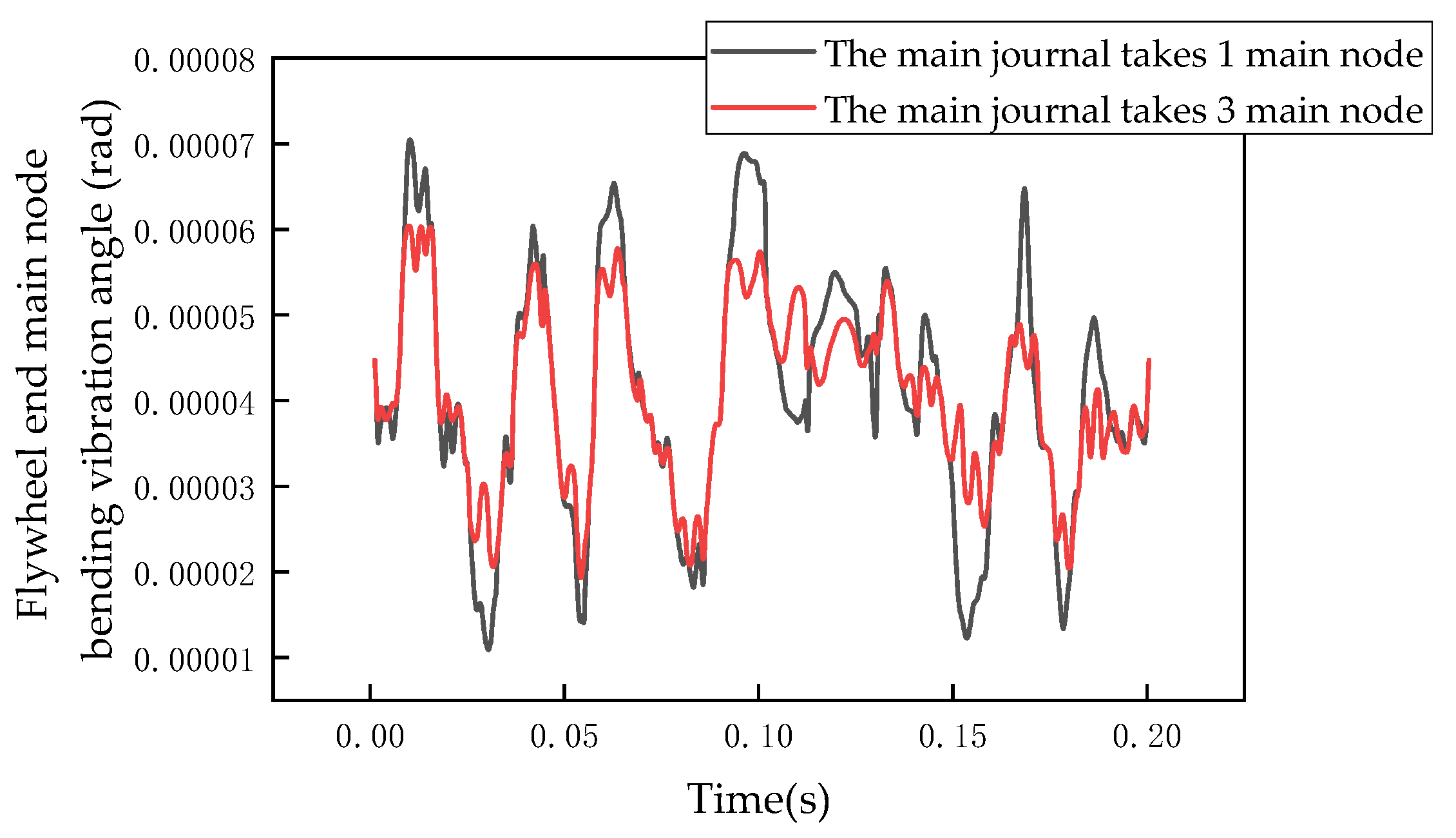
5.2. Selection of the Number of Main Nodes
5.3. Degree of Freedom Coupling Region
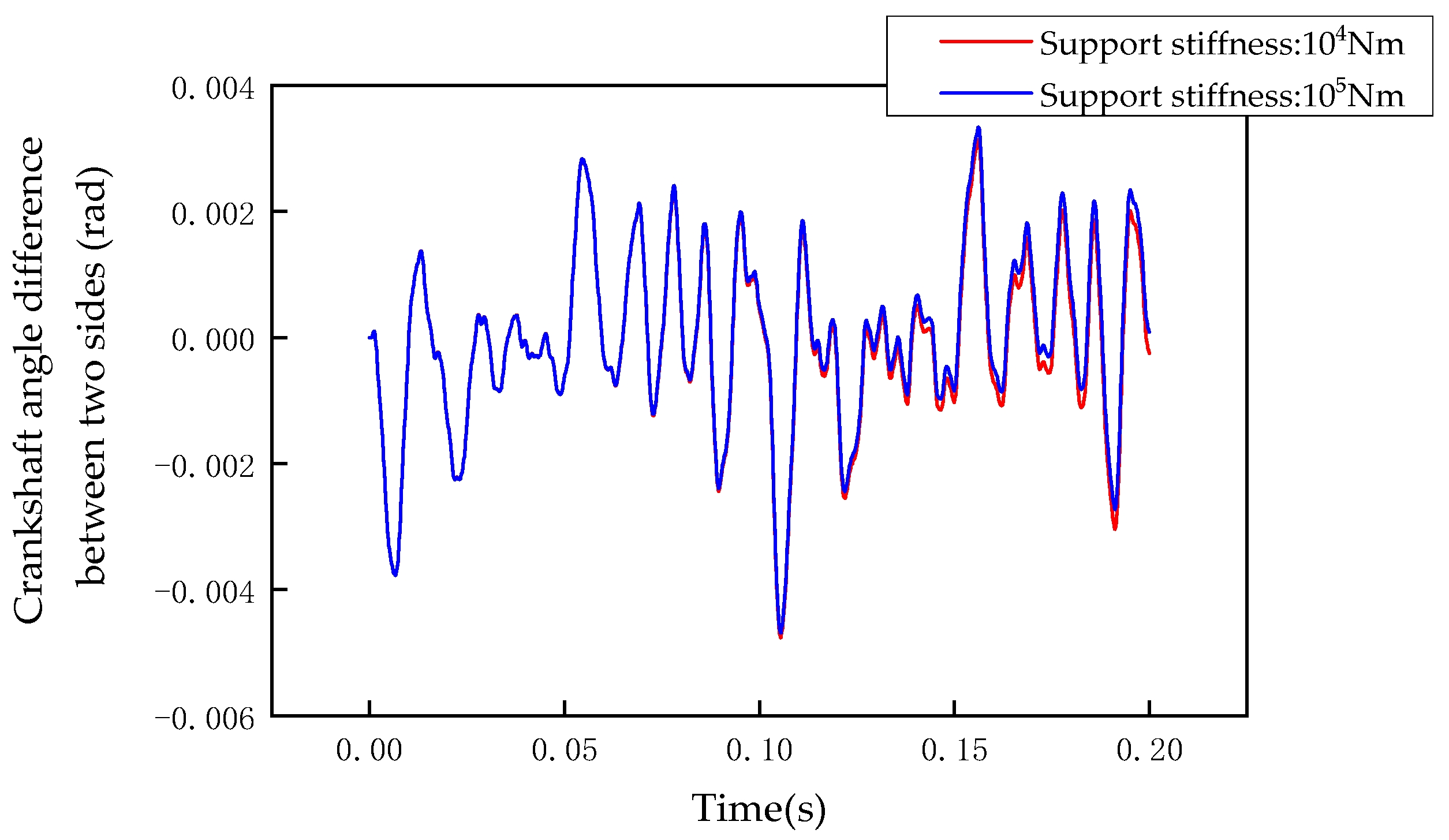
5.4. Bearing Support Stiffness
6. Conclusions
- (1)
- The crankshaft substructure model was effectively established by setting predefined thresholds to construct coupling constraints between the main and auxiliary nodes and performing degree-of-freedom reduction. This method significantly reduces the computational degrees of freedom while retaining the primary dynamic characteristics of the system.
- (2)
- The Cholesky decomposition and Jacobi iterative methods were found to accurately and efficiently solve the free vibration of the crankshaft system, demonstrating that the substructure model can effectively replace the finite element model. Additionally, increasing the number of main nodes helps improve model accuracy.
- (3)
- Under the framework of the implicit Newmark-β method, the combination of a prediction-correction mechanism and dynamic relaxation factors to adjust the iterative convergence path, along with an adaptive time step strategy driven by energy gradients, can effectively balance numerical stability and the capture of high-frequency response details.
- (4)
- In dynamic response calculations, appropriately increasing the number of main nodes, reducing the time step size, and narrowing the coupling region enhance the description of high-frequency local vibration details. Increasing the coupling region can more accurately reflect the dynamic properties of the structure.
- (5)
- Using a smaller initial step size combined with the energy gradient criterion for adaptive step size can optimize computational accuracy and efficiency. An increase in support stiffness will cause an upward shift in the local response results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gomes, J.; Gaivota, N.; Martins, R.F.; Silva, P.P. Failure analysis of crankshafts used in maritime V12 diesel engines. Eng. Fail. Anal. 2018, 92, 466–479. [Google Scholar] [CrossRef]
- Deng, X.; Zhang, B. Summary on Torsional Vibration of Crankshaft System in Internal Combustion Engines. Automob. Parts 2012, 1, 76–78. [Google Scholar]
- Kimura, J.; Kobayashi, S.; Hoshina, K.; Kawase, K.; Matsui, K.; Yamamoto, A. Crankshaft Impact Noise and Three-Dimensional Vibration; 0148-7191; SAE Technical Paper; SAE International: Warrendale, PA, USA, 2014. [Google Scholar]
- Tsitsilonis, K.M. A Systematic Methodology Enabling Marine Engine Health Assessment by Employing First-Principles Digital Twins. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2023. [Google Scholar]
- Carrera, E.; Pagani, A.; Petrolo, M.; Zappino, E. Recent developments on refined theories for beams with applications. Mech. Eng. Rev. 2015, 2, 14–00298-00214-00298. [Google Scholar] [CrossRef]
- Hurty, W.C. Dynamic analysis of structural systems using component modes. AIAA J. 1965, 3, 678–685. [Google Scholar] [CrossRef]
- Craig Jr, R.R.; Bampton, M.C. Coupling of substructures for dynamic analyses. AIAA J. 1968, 6, 1313–1319. [Google Scholar] [CrossRef]
- Wang, F.; Luo, G.-H.; Yan, S.; Cui, H.-T. A Comparison Study on Co-and Counterrotating Dual-Rotor System with Squeeze Film Dampers and Intermediate Bearing. Shock. Vib. 2017, 2017, 5493763. [Google Scholar] [CrossRef]
- Wang, F.; Luo, G.-H.; Yang, X.-G.; Cui, H.-T. Research on modeling and dynamic characteristics of complex coaxial rotor system. J. Vibroengineering 2017, 19, 1524–1545. [Google Scholar] [CrossRef][Green Version]
- Zhai, Y.-J.; Ma, Z.-S.; Chang, H.-Z.; Ding, Q. Model order reduction and dynamic characteristic analysis of the bolted flange structure with free-free boundaries. Structures 2021, 34, 149–157. [Google Scholar] [CrossRef]
- Gao, F.; Sun, W. Reduced-order modeling for and vibration characteristics analysis of a hard-coated mistuned blisk. Coatings 2017, 7, 103. [Google Scholar] [CrossRef]
- Zheng, Z.; Xie, Y.; Zhang, D. Reduced-order modeling for stability and steady-state response analysis of asymmetric rotor using three-dimensional finite element model. J. Eng. Gas Turbines Power 2019, 141, 101001. [Google Scholar] [CrossRef]
- Hou, S. Review of modal synthesis techniques and a new approach. Shock. Vib. Bull. 1969, 40, 25–39. [Google Scholar]
- Wang, T.; Cheng, C.; Guo, X. Model-based predicting and correcting algorithms for substructure online hybrid tests. Earthq. Eng. Struct. Dyn. 2012, 41, 2331–2349. [Google Scholar] [CrossRef]
- Huang, D.; Liu, Y.; Liu, H.; Yi, J. Resonances of elastic rotor induced by roller bearing with consideration of cage vibration. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2018, 232, 446–456. [Google Scholar] [CrossRef]
- Yu, Y.; Jin, X.; Fu, Y.; Zhao, T. Study on the coupled vibration characteristics of a two-stage bladed disk rotor system. Appl. Sci. 2021, 11, 8600. [Google Scholar] [CrossRef]
- Ying, L.; Hongguang, L.; Yue, L. Accelerated parametric model order reduction method. J. Aerosp. Power 2019, 34, 2264–2270. [Google Scholar]
- Ying, L.; Hongguang, L.; Yun, L. A component-based parametric model order reduction method. J. Vib. Shock 2020, 39, 148–154. [Google Scholar]
- Bai, B.; Bai, G.-c. Dynamic probabilistic analysis of stress and deformation for bladed disk assemblies of aeroengine. J. Cent. South Univ. 2014, 21, 3722–3735. [Google Scholar] [CrossRef]
- Bai, B.; Bai, G.C.; Li, C. Application of multi-stage multi-objective multi-disciplinary agent model based on dynamic substructural method in Mistuned Blisk. Aerosp. Sci. Technol. 2015, 46, 104–115. [Google Scholar] [CrossRef]
- Bai, B.; Li, H.; Zhang, W.; Cui, Y. Application of extremum response surface method-based improved substructure component modal synthesis in mistuned turbine bladed disk. J. Sound Vib. 2020, 472, 115210. [Google Scholar] [CrossRef]
- Géradin, M.; Rixen, D.J. A ‘nodeless’ dual superelement formulation for structural and multibody dynamics application to reduction of contact problems. Int. J. Numer. Methods Eng. 2016, 106, 773–798. [Google Scholar] [CrossRef]
- Wu, Z.; Xia, L.; Wang, S.; Shi, T. Topology optimization of hierarchical lattice structures with substructuring. Comput. Methods Appl. Mech. Eng. 2019, 345, 602–617. [Google Scholar] [CrossRef]
- Weng, S.; Zhu, H.; Xia, Y.; Li, J.; Tian, W. A review on dynamic substructuring methods for model updating and damage detection of large-scale structures. Adv. Struct. Eng. 2020, 23, 584–600. [Google Scholar] [CrossRef]
- Mourelatos, Z.P. A crankshaft system model for structural dynamic analysis of internal combustion engines. Comput. Struct. 2001, 79, 2009–2027. [Google Scholar] [CrossRef]
- Besset, S.; Jezequel, L. Dynamic substructuring based on a double modal analysis. J. Vib. Acoust. 2008, 130, 011008. [Google Scholar] [CrossRef]
- Tian, Z.; Li, J.; Lin, X.; Hu, P. Research on generating technology of diesel engine crankshaft substructure dynamic model. Manuf. Autom. 2022, 44, 21–24+60. [Google Scholar]

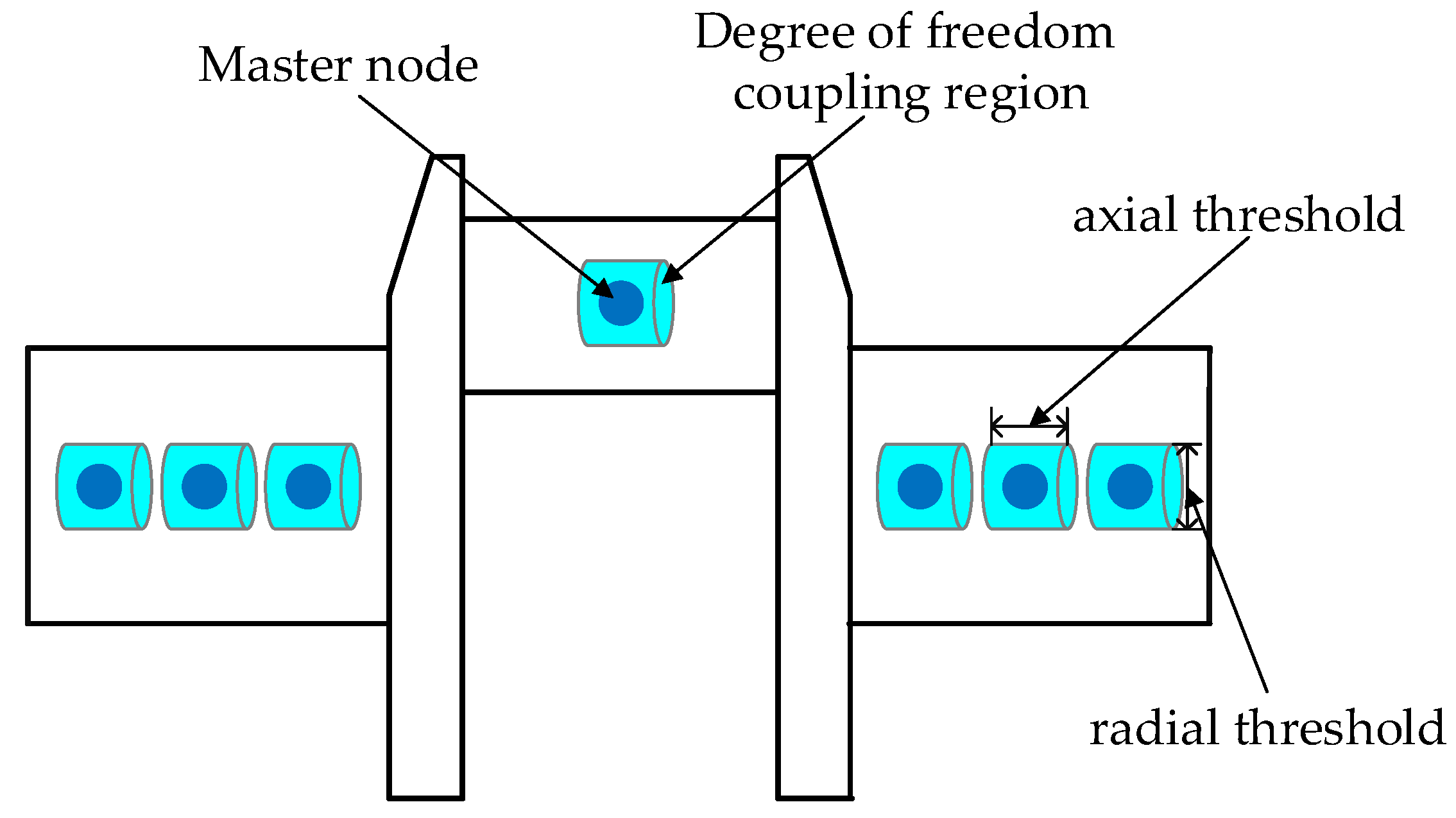
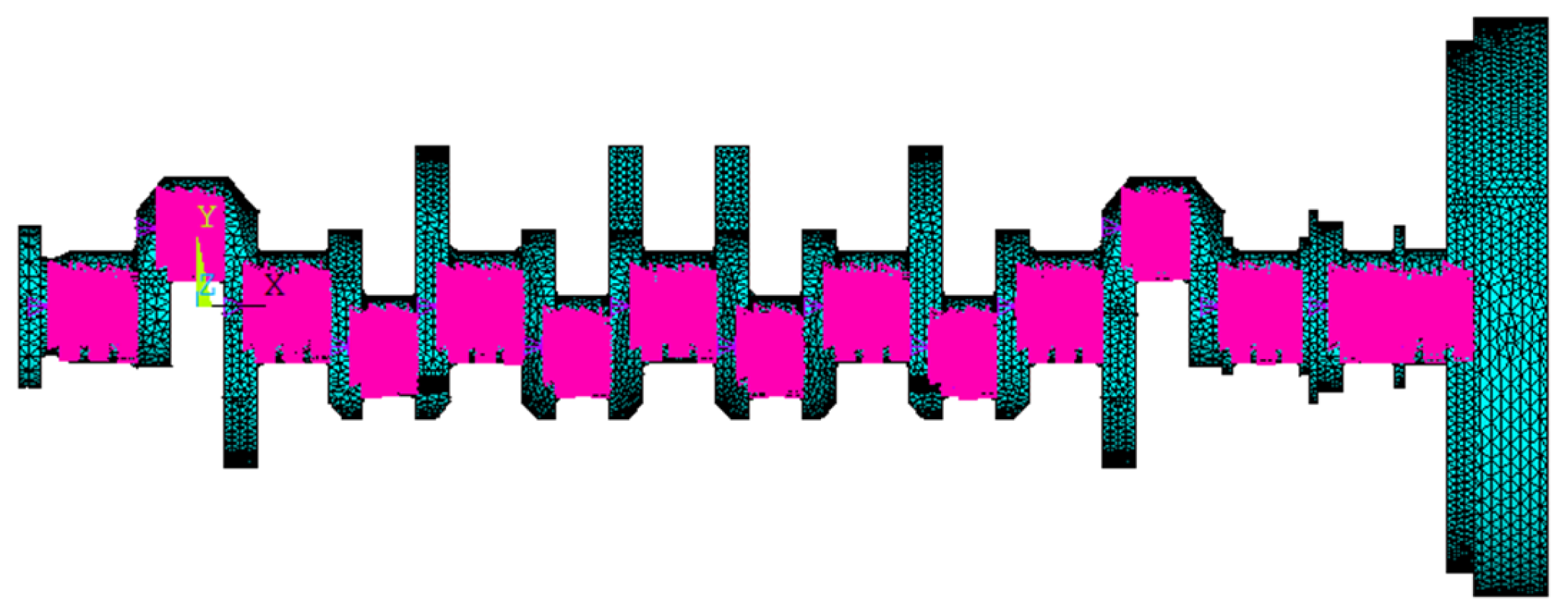
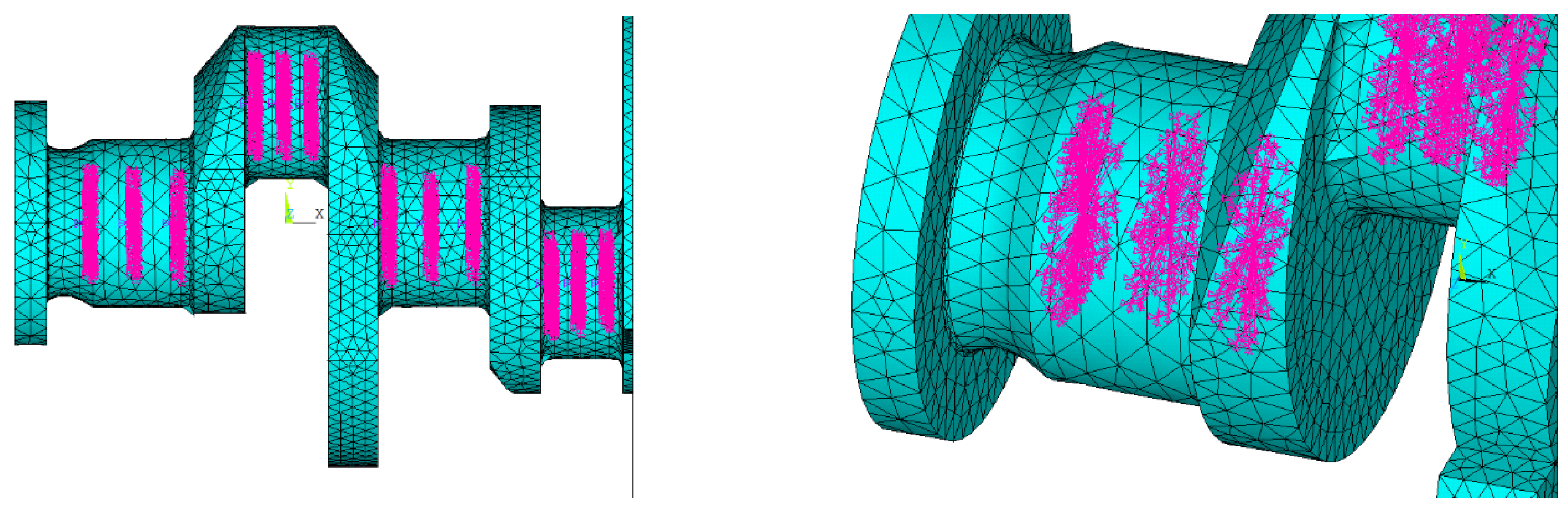



| Coupling Region Size | Radial Threshold | Axial Threshold |
|---|---|---|
| Moderate coupling region | d/3 | d/20 |
| Small coupling region | d/5 | d/50 |
| Frequency Order | Take 1 Master Node and a Moderate Coupling Region (Hz) | Take 3 Master Nodes and a Moderate Coupling Region (Hz) | Take 3 Master Nodes and a Small Coupling Region (Hz) | ANSYS 19.2 Calculations (Hz) |
|---|---|---|---|---|
| 1 | 28.946 | 29.874 | 29.209 | 30.85 |
| 2 | 30.186 | 31.238 | 30.461 | 32.38 |
| 3 | 77.591 | 80.103 | 79.259 | 80.307 |
| 4 | 83.034 | 86.236 | 84.135 | 86.754 |
| 5 | 91.382 | 93.684 | 91.407 | 95.053 |
| 6 | 140.508 | 145.361 | 141.203 | 143.42 |
| 7 | 151.237 | 156.025 | 154.349 | 152.89 |
| 8 | 168.614 | 175.562 | 171.268 | 160.93 |
| 9 | 224.381 | 233.316 | 226.185 | 229.62 |
| 10 | 258.979 | 268.536 | 261.762 | 266.52 |
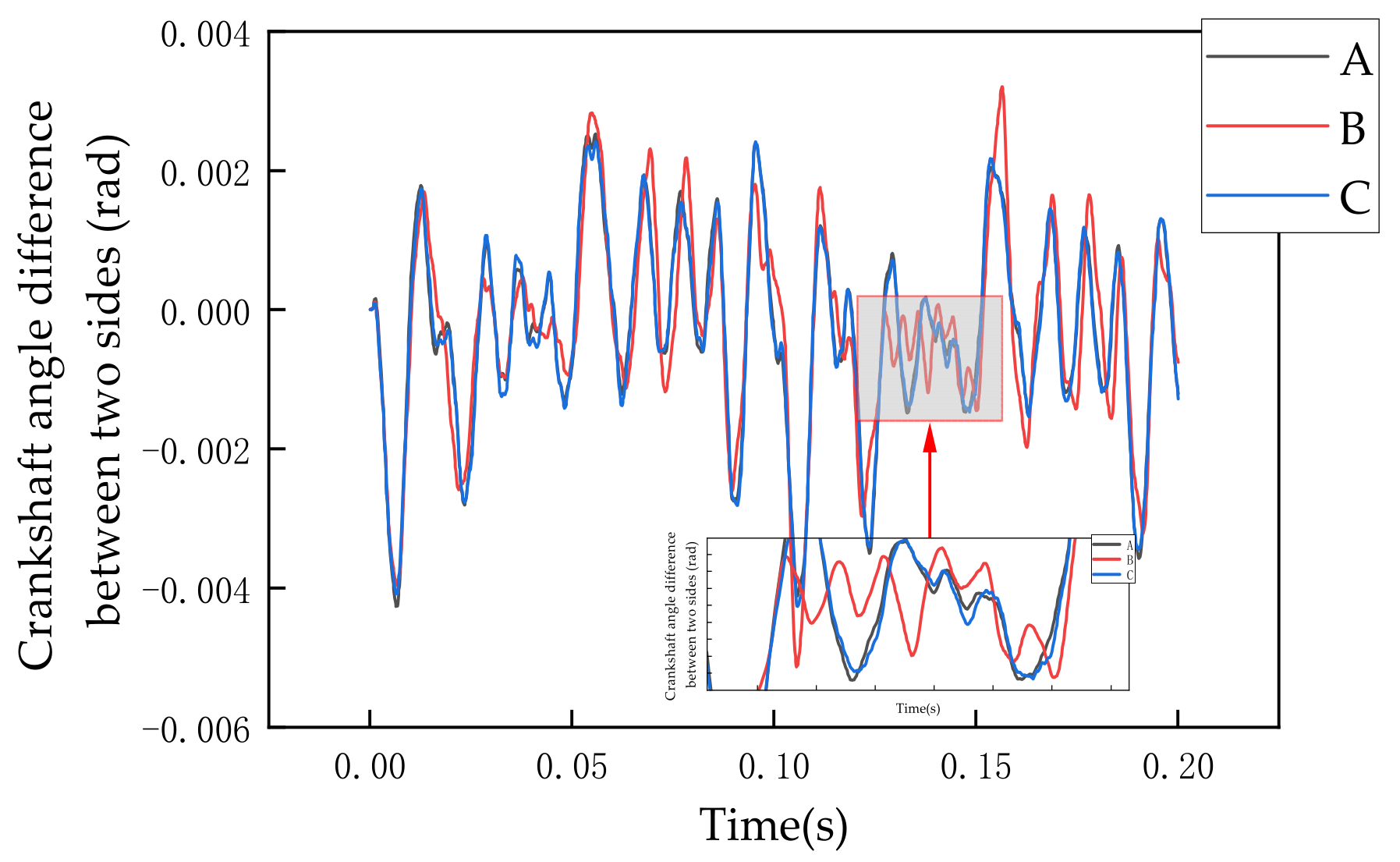
| Curved Line | Radial Threshold | Axial Threshold |
|---|---|---|
| A | d/3 | d/20 |
| B | d/5 | d/50 |
| C | 2d/3 | d/10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Z.; Sun, Z.; Zhou, Y.; Zhou, Y. Research on Numerical Calculation Methods for Modelling the Dynamics of Diesel Engine Crankshaft System Substructures. Appl. Sci. 2025, 15, 5551. https://doi.org/10.3390/app15105551
Tian Z, Sun Z, Zhou Y, Zhou Y. Research on Numerical Calculation Methods for Modelling the Dynamics of Diesel Engine Crankshaft System Substructures. Applied Sciences. 2025; 15(10):5551. https://doi.org/10.3390/app15105551
Chicago/Turabian StyleTian, Zhongxu, Zengbin Sun, Yun Zhou, and You Zhou. 2025. "Research on Numerical Calculation Methods for Modelling the Dynamics of Diesel Engine Crankshaft System Substructures" Applied Sciences 15, no. 10: 5551. https://doi.org/10.3390/app15105551
APA StyleTian, Z., Sun, Z., Zhou, Y., & Zhou, Y. (2025). Research on Numerical Calculation Methods for Modelling the Dynamics of Diesel Engine Crankshaft System Substructures. Applied Sciences, 15(10), 5551. https://doi.org/10.3390/app15105551





