Featured Application
The design of a robust tracking controller for a four-link manipulator arm is an important subject for many industrial applications such as COVID-19 prevention robotics, agricultural mobile robotics, mining mobile robotics, space exploration mobile robotics, lower limb rehabilitation robotics, biped walking robotics and underwater robotics.
Abstract
The globally robust control of a four-link manipulator arm (FLMA) is an important subject for a wide range of industrial applications such as COVID-19 prevention robotics, lower limb rehabilitation robotics and underwater robotics. This article uses the feedback linearized approach to stabilize the complex nonlinear FLMA without applying a nonlinear approximator that includes the fuzzy approach and neural network optimal approach. This article proposes a new approach based on the “first” derived nonlinear convergence rate formula of the FLMA to control highly nonlinear dynamics. The linear quadratic regulator (LQR) method is often applied in the balance controlling space of the underactuated manipulator. This proposed approach takes the place of the LQR approach without the necessary trial and error operations. The implications of the proposed approach are “globally” effective, whereas the Jacobian linearized approach is “locally” valid. In addition, the main innovation of the proposed approach is to perform “simultaneously” additional performances including almost disturbance decoupling performance, which takes the place of the traditional posture–energy approach and avoids some torque chattering behaviour in the swing-up space, and globally exponential stable performance, without the need to solve the Hamilton–Jacobin equation. Simulations of comparative examples show that the proposed controller is superior to the singular perturbation and fuzzy approaches.
1. Introduction
The automation of manipulator arms has gained tremendous attention in recent decades due to their wide range of engineering applications, such as agricultural mobile robotics [1], mining mobile robotics [1], space exploration mobile robotics [2], lower limb rehabilitation robotics [3], biped walking robotics [4], unmanned ground vehicle [5] and underwater robotics [6]. There are two types of manipulator arms: the underactuated one [7,8,9], which is a kind of a nonlinear system with fewer control inputs than degrees of freedom, and the fully actuated one [5,6,10,11], which is not. In general, underactuated manipulator arms are grouped into vertical types, which are controlled by gravity, and planar types, which are not.
For the vertical underactuated manipulator, the linear Jacobian approximated model of the inverted equilibrium position is completely controllable because the controllability matrix of the linear Jacobian approximated model is full rank. For most traditional approaches to solving the complexity of a vertical underactuated manipulator, the operation space is mainly separated into a swing-up space and a balance space. In the swing-up space, the control methods include the posture–energy approach [9], the energy-based approach [12], the direct fuzzy control approach [11], the fuzzy model reference learning control approach [11], and the adaptive fuzzy control approach [11], and the linear quadratic regulator (LQR) optimal method [13] is applied in the balance space. However, to be quickly captured in the swing-up space for the manipulator arm, the control needs an exact combination of energy and posture to be built, and this property is difficult to be accomplished due to the complexity of the system’s dynamics [9]. Moreover, some torque chattering changes occur in the swing-up space and then the energy is quickly pumped into the system [9]. In general, in order to control the nonlinear dynamics well, disturbance decoupling and global stability should be simultaneously met [14]. To achieve these requirements, some significant approaches, such as model predictive control [15], deep learning [16], multi-objective control [17], backstepping control [18] and preview control [19], have been adopted for complex nonlinear systems. However, in the aforementioned approaches, a serious common drawback is that the considered nonlinear systems should be approximated via linear dynamics by the Taylor expansion for small-effect operating ranges. This serious drawback may be impractical for the FLMA. To solve the nonlinear serious drawback of the FLMA, nonlinear function approximators, such as the neural network optimal approach [20] and famous fuzzy method [21], have been adopted to reduce the caused errors [22]. The main drawback of the famous fuzzy method is that constructing the fuzzy rule base relies on a lot of past accumulated knowledge, and the system’s performance is almost determined by the constructed experience rule base [23]. The neural network optimal approach is an intelligent supervised learning approach that requires the operating network to offer many sample points [24]. The performance of controller design for the neural network method is completely limited by only applying the current state value. Moreover, complicated interconnecting structures and digital computing loads mean that the physical realization of nonlinear function approximators is impractical. LQR is a common method that calculates the weighting matrices Q and R for a Jacobian linearized system via a trial and error operation. Some improved approaches of calculating the weighting matrices, such as the genetic algorithm approach and Kalman’s pole-assignment approach, have been proposed in recent decades. However, their main serious drawbacks including their high computing effort and slow convergent rate of the globally optimal solution limit their performances [25].
On the other hand, the planar underactuated manipulator is not constrained by gravity, so any position of the manipulator arm is the equilibrium point and the linear Jacobian approximated model at any equilibrium point is uncontrollable [7]. The control approaches for the vertical underactuated manipulator cannot be applied for the planar underactuated manipulator. Studies on the controlling planar underactuated manipulator are extensive and some important methods, such as the nilpotent approximated method [26], the converting-chained form method [27] and the order reduction method [28], have been proposed to perform position control for the planar underactuated manipulator. However, the aforementioned approaches of controlling the planar underactuated manipulator are only valid for the nominal plant model. In real systems, nonlinear acting factors need to be considered [29] and the aforementioned approaches cannot be applied for the practical planar underactuated manipulator.
So far, it is obvious to see that the robust tracking controller design for manipulator arms is still a challenging subject due to the strict global stability requirement and disturbance reduction involving nonlinear system dynamics. Stimulated by these points, we apply the feedback linearized approach to construct the robust tracking controller of a manipulator arm with the almost disturbance decoupling, adjustable convergence rate and “globally” exponentially stable performances, taking the place of the “locally” Jacobian linearized method. The feedback linearized approach has contributed to many significant studies [30,31,32,33,34] in industrial applications, such as the dual parallel-PMSM system [30], grid-tied packed e-cell inverter [31], PHEV charging station [32], artificial pancreas [33] and weak AC grid integration [34].
References [35,36] have exploited the fact that the stricter tracking error condition of almost disturbance decoupling performance including the absolute error, integral error and input-to-state-stable error is involved to reduce the disturbance effect. However, the almost disturbance decoupling performance of a nonlinear system can only be achieved without the disturbance being multiplied by nonlinearity and in the presence of non-Lipschitz nonlinearity. Therefore, the almost disturbance decoupling performance cannot be achieved for the following nonlinear system:
where and are the output and control input, respectively. On the contrary, almost disturbance decoupling performance is more likely to be achieved by the proposed method. The main novelty of this study is in its design of a robust tracking controller for a nonlinear complex FLMA. The major contributions of this study are summarized as follows:
(i) This study is the “first” to present the convergence rate formula of a nonlinear FLMA.
(ii) The FLMA is the first to be designed by applying the feedback linearized approach with almost disturbance decoupling performance, which takes the place of the traditional posture–energy approach and avoids some torque chattering change behaviour in the swing-up space. Moreover, the proposed approach takes the place of the LQR approach without the necessary trial and error operations.
(iii) A robust tracking controller is presented to obtain global exponential stability without solving the Hamilton–Jacobi equation that must to be solved for the famous H-infinity approach.
(iv) This study proposes a new approach to improve the shortcomings of traditional fuzzy function approximators without requiring a lot of design experience and knowledge.
(v) The implications of this proposed method are “globally” valid, whereas the Jacobian linearized approach is “locally” valid.
2. Complete Mathematical Model for Four-Link Manipulator Arm
The FLMA is a great platform for industrial mechanics as it is a highly nonlinear control system with disturbances. In this section, we apply Euler–Lagrange equation to derive the dynamic equations of the FLMA, as shown in Figure 1.
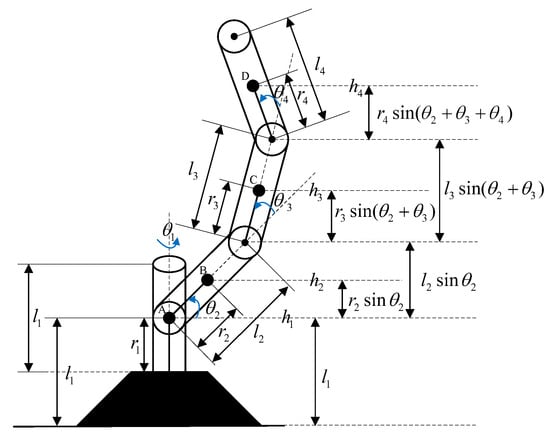
Figure 1.
The four-link manipulator robot arm.
The four-link manipulator arm is made up of aluminium. The dynamic model parameters are selected as follows: the length of the link , the distance of the centre of mass , the mass of the link and the inertia moment of the link . In this section, we give complete derivations of the dynamic mathematical equation for the nonlinear FLMA system. We define the state, input and noise variables of the FLMA as the following physical quantities: , , , , , , , , , , , , and .
From Appendix A, the state-space dynamic model of the FLMA with real physical values can be represented as
Then, the nominal system is
and it is assumed to have the vector relative frequency [37].
(i) The following condition holds:
for all , , where the symbol L is the Lie operator.
(ii) The square matrix
has a nonsingular property. The norms of pre-specified tracking signals and its first derivatives are bounded by positive constants as
and the spanning distribution
is involutive.
3. Robust Tracking Controller Design of FLMA System
Since the FLMA system has a well-defined relative degree property and involutive distribution performance, then the mapping
defined as
and
is a one-to-one infinitely continuous and differentiable function according to reference [37,38], i.e.,
We assume that the nonlinear FLMA system possesses a well-defined involutive property. The mapping defined by (30)~(33) has a one-to-one infinitely continuous and differentiable function and it can transform the original nonlinear system into a partially linear subsystem and partially nonlinear subsystem as follows [37,38]:
Since
the transformed dynamics of the nonlinear FLMA system (45)~(51) can be rewritten as
Hence,
To build the robust feedback linearization controller
we use the vector
and the virtual input [37]
Then, we can transform (58) into the following model:
From (64), we obtain
Next, we demonstrate in detail how to design the globally robust tracking controller with the pre-specified tracking signals . The initial values of the states are set as
The desired robust tracking controller is built by
where is the desired tracking signal and represents elements of the Hurwitz matrix shown by
Based on the feedback linearization approach, we then propose that the robust controller possesses the pre-specified tracking signals as follows:
For the convenience of the following discussions, let us define some related parameters as
where the Lyapunov system matrix is a Hurwitz matrix whose eigenvalues lie in the left half coordinate plane, and one can use Matlab 5.3 to obtain the adjoining Lyapunov system matrix from the following Lyapunov equation:
and
To further demonstrate the complete feedback linearization control design of the nonlinear FLMA system, let us define one assumption and two definitions as follows.
Assumption 1.
The following inequality holds:
where and .
Definition 1.
We consider nonlinear system with Lipschitz input , where is the Lipschitz state variable and is differentiable and infinitely continuous. This system is defined to be input-to-state stable if
where
is a
class function and
denotes a
class function.
Definition 2.
and
where belongs to the class function, and are positive constants, and , belong to class functions. From (65), we obtain
A nonlinear system with noise input is determined to possess almost disturbance decoupling performance if the following properties hold:
(i) The nonlinear system has an input-to-state stable property for noise input .
(ii) Output tracking errors meet the following two inequalities for initial time and initial state :
From (77), (79) and (94), we obtain
Substituting (67) and (68) into (95) yields
Then, from (51), (59), (68), (80) and (96), we obtain
where
It is worth noting that the one-to-one infinitely continuous and differentiable function converts the original nonlinear FLMA into a partially nonlinear subsystem and partially linear subsystem whose state variables are denoted by and , respectively. In order to meet the requirements (90) and
we construct and as the Lyapunov functions of the nonlinear subsystem
(98)
and linear subsystem
(97), respectively, and then combine these Lyapunov functions to form a composite Lyapunov function as follows:
where function satisfies and
Then, the differentiation of the composite Lyapunov function is described as
where matrix is positive definite, and
i.e.,
where denotes the minimum eigenvalue of matrix .
We define
Applying (123) to (122) yields
We define
and obtain
Next, we prove the fact that the proposed feedback linearization control achieves the almost disturbance decoupling performance and globally exponential stability of the FLMA system, as seen in Appendix B. Therefore, the proposed robust tracking control (69) can indeed cause the tracking errors of the FLMA system to converge to the global ultimate attractor.
It is worth noting that we can extend the above complete design process to obtain one more general significant theorem for general uncertain nonlinear control systems with disturbances as follows:
i.e.,
where and denote the input and output, respectively, is the state variable, is the noise vector, and denotes the noise adjoint vector. We assume , and to be continuous functions and to be the matched uncertainty vector term , where is defined as the uncertainty vector.
Assumption 2.
The following inequality holds:
where and .
Then, the nominal system is
and it is assumed to have the vector relative frequency [37].
(i) The following condition holds:
for all
,
, where the symbol L is the Lie operator.
(ii) The square matrix
has a nonsingular property. The norms of pre-specified tracking signals and its first
derivatives are bounded by positive constants
as follows:
and the spanning distribution
is involutive. Then, the mapping defined as
and
is a one-to-one infinitely continuous and differentiable function according to reference [37].
We let and be the Lyapunov functions of the nonlinear subsystem and linear subsystem, respectively, and then combine these Lyapunov functions to form composite Lyapunov function
as follows:
Theorem 1.
For a differentiable and infinitely continuous function, , of the transformed nonlinear subsystem, the following three inequalities hold:
We design the robust tracking controller according to the following:
The nonlinear system possesses almost disturbance decoupling performance with globally exponential stability:
where matrix
is positive definite, and continuous function
satisfies
and
Moreover, the desired tracking errors can be exponentially reduced by adjusting parameter
with the convergence rate formula
and the desired tracking errors of the control system exponentially converge to global final attractorwith the convergence radius formula
To effectively build a robust tracking controller, a significant algorithm and a block diagram, shown in Figure 2, of the FLMA are designed and summarized, and a powerful Python 3.7 software system of the controller design can be constructed according to this proposed algorithm.
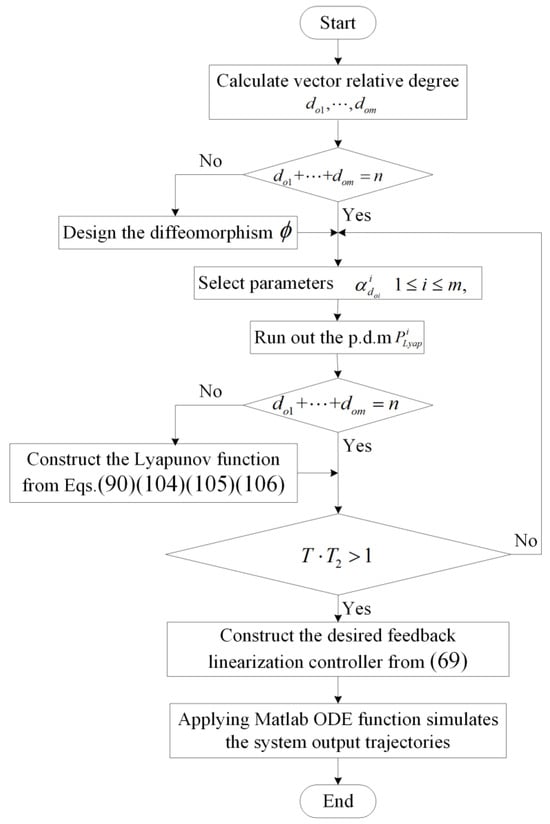
Figure 2.
Block diagram of proposed algorithm.
(Step 1) Obtain vector relative frequency according to given outputs .
(Step 2) Appropriately construct one-to-one infinitely continuous and differentiable function based on (29)~(33).
(Step 3) From (68) and (84), appropriately choose parameters such that represents Hurwitz matrices with stable eigenvalues and obtain the positive definite of the Lyapunov equation with the aid of the Matlab toolbox.
(Step 4) Choose Lyapunov function to meet the requirements (90) and (102)~(104). If the vector relative frequency is equal to the system dimension, i.e., , then omit this step and directly go to (Step 5).
(Step 5) From (118)~(121), (123)~(126), appropriately design parameters to meet . It is worth noting that if the value of is larger, the convergence rate is faster.
(Step 6) Finally, the robust tracking controller can be built by (69).
4. Simulations of the FLMA System
It can be verified that the related requirements of Theorem 1 hold if we choose , , , , , , , , and . Hence, the robust tracking controller can make the tracking errors converge to the global final attractor by Theorem 1. The real tracking errors of the FLMA system (epsion = 0.01) are plotted in Figure 3. Therefore, the designed controller can indeed make the outputs track pre-specified signals . From (166)~(167) and Figure 3 and Figure 4, it is obvious to see that the convergent rate of the tracking error with a smaller epsion is better than with a larger epsion. Moreover, the dynamic trajectories show the overall tracking errors “before”, “on” and “after” entering the global final attractor in the positive z direction for Figure 5, Figure 6 and Figure 7, respectively, where the length of the arrow denotes the convergence radius of the global final attractor. Other individual tracking errors of output 1~output 4 are shown in the positive x direction, negative x direction, positive y direction and negative y direction for Figure 5, Figure 6 and Figure 7, respectively.
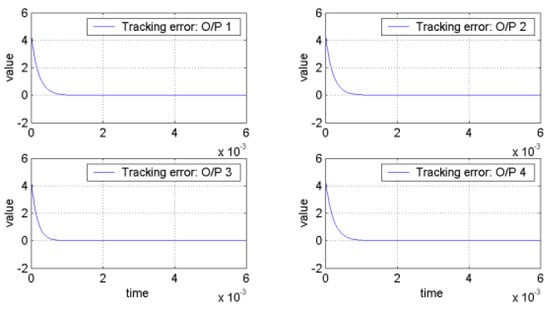
Figure 3.
The tracking errors of outputs for .
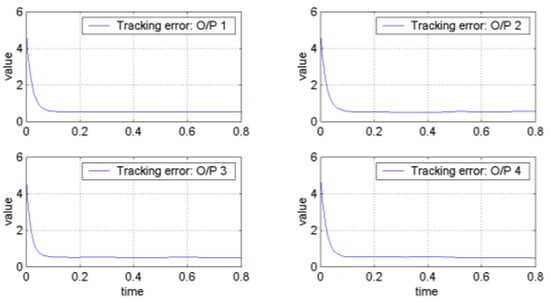
Figure 4.
The tracking errors of outputs for .
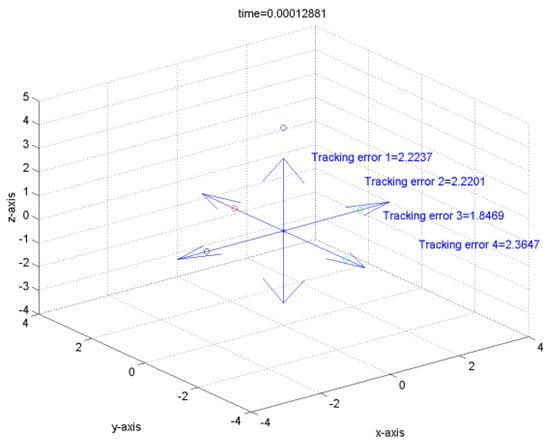
Figure 5.
The tracking error before entering the global final attractor.
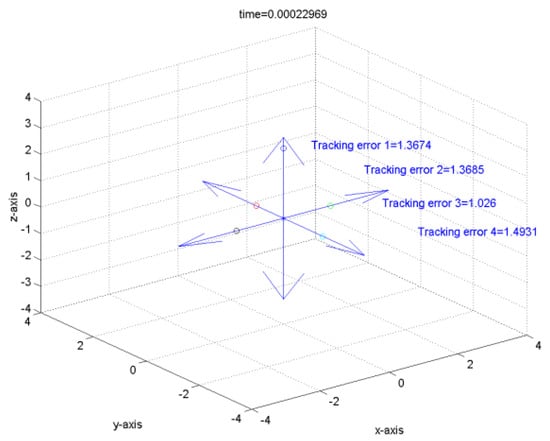
Figure 6.
The tracking error upon entering the global final attractor.
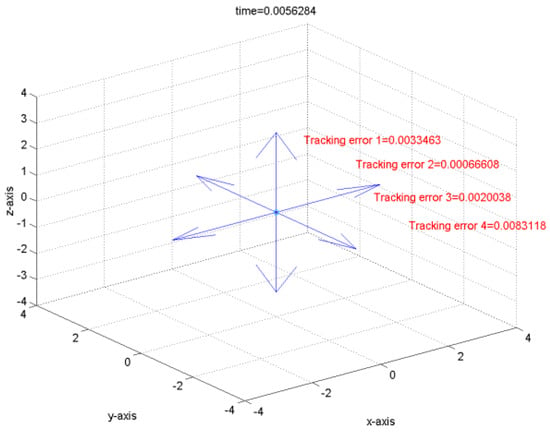
Figure 7.
The tracking error after entering the global final attractor.
5. Comparisons to Traditional Approaches
In this section, we compare the performance of the proposed approach with the traditional fuzzy approach [39] and the singular perturbation method with high-gain feedback [36].
Figure 8 shows the general structure of the traditional fuzzy approach whose input variables of the IF-THEN rules are assigned as tracking error and its time derivative . The output variable is fuzzy control . To make the calculation easier, the desired membership functions of , and are assigned as the triangular-shaped functions, as shown in Figure 9, Figure 10 and Figure 11. The desired fuzzy control rule base for is constructed in Table 1. The rule base, fuzzy inference engine and defuzzifier adopt the standard Macvicar-Whelan rule base, the Mamdani method and the centroid method, respectively.
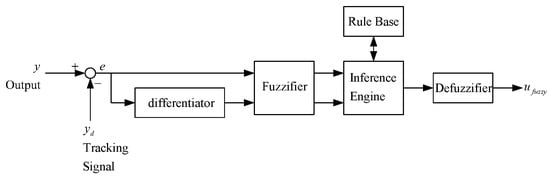
Figure 8.
General structure of traditional fuzzy approach.
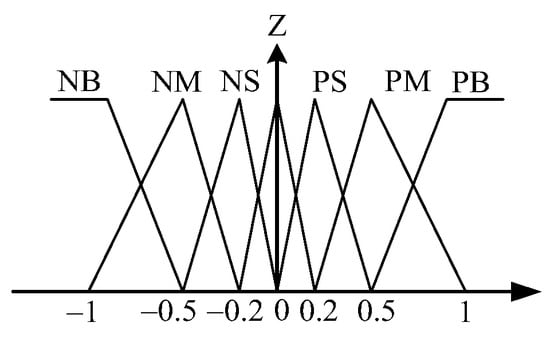
Figure 9.
Triangular-shaped membership functions for .
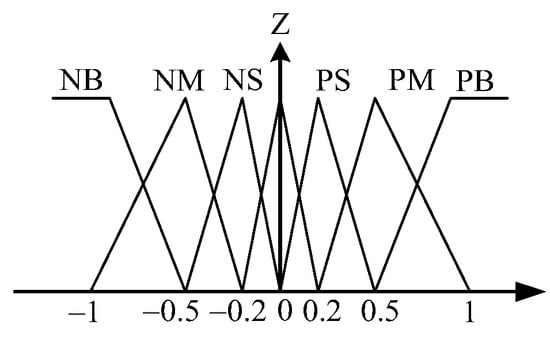
Figure 10.
Triangular-shaped membership functions for .
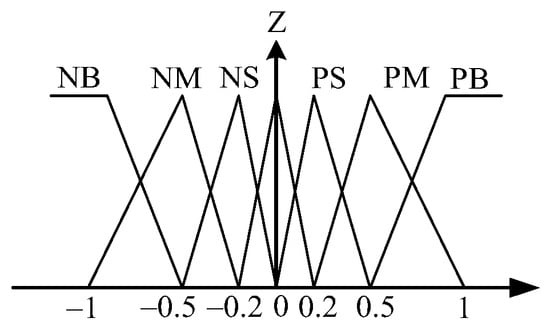
Figure 11.
Triangular-shaped membership functions for .

Table 1.
Macvicar-Whelan fuzzy control rule base.
With the aid of the Matlab fuzzy toolbox, comparative tracking error responses of the proposed approach and traditional fuzzy controller design for the FLMA are shown in Figure 12, Figure 13, Figure 14 and Figure 15. From Figure 12, Figure 13, Figure 14 and Figure 15, it is obvious to see that the convergence rate of the proposed approach is faster than that of the traditional fuzzy approach.
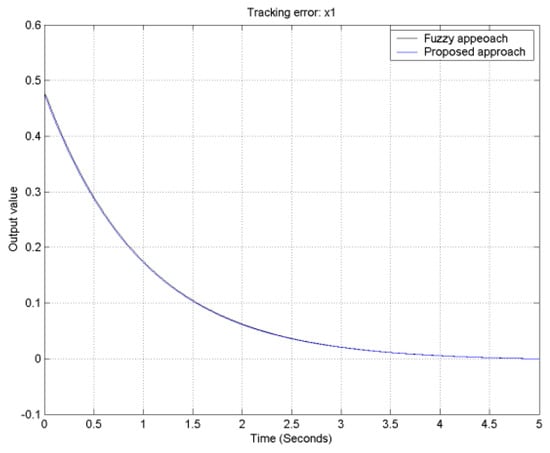
Figure 12.
The output tracking error for output 1.
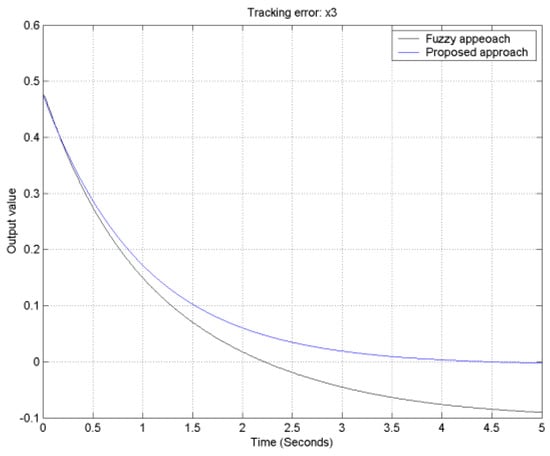
Figure 13.
The output tracking error for output 2.
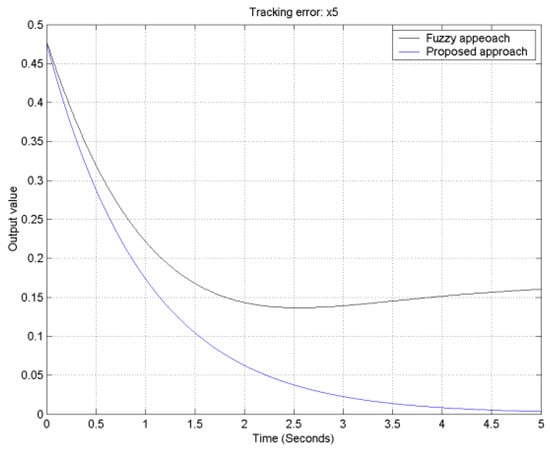
Figure 14.
The output tracking error for output 3.
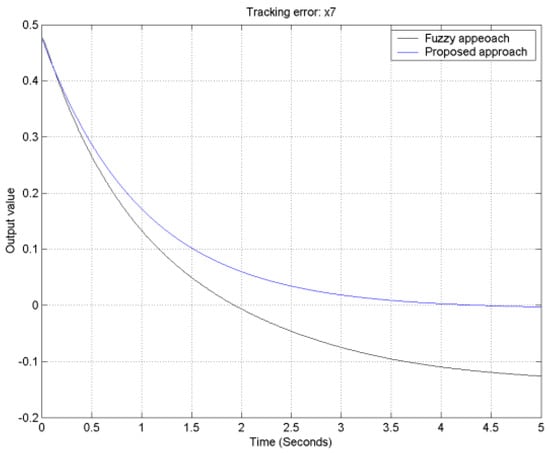
Figure 15.
The output tracking error for output 4.
Following the second comparative example, we make some comparisons between the proposed approach and the famous singular perturbation method [35,36]. The sufficient condition in [35,36] requires that the nonlinearity multiplied by the disturbance meets the structural triangle criterion.
References [35,36] have exploited the fact that the following system cannot achieve almost disturbance decoupling performance:
It is easy to derive the following items: , , , and
Hence, the sufficient condition of [35,36] is not satisfied since is not complete, and the almost disturbance decoupling problem cannot be not solved. On the contrary, this almost disturbance decoupling problem can be solved via the proposed approach by the controller:
The output tracking error trajectory of the nonlinear system for (169) is shown in Figure 16. Therefore, the designed controller can indeed make the output track pre-specified signals and achieve almost disturbance decoupling performance.
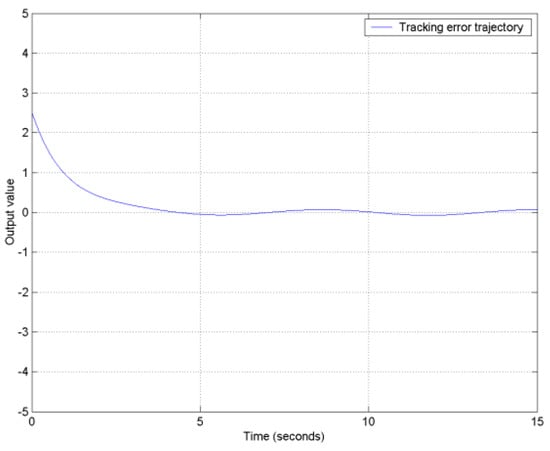
Figure 16.
The tracking error trajectory of the feedback-controlled system for (169).
6. Conclusions
The continuous spreading of the COVID-19 virus stimulates us to design a robust controller of a highly nonlinear FLMA by the feedback linearized approach, which possesses almost disturbance decoupling performance and takes the place of the traditional posture–energy approach, avoiding torque chattering change behaviour in the swing-up space, and other globally exponential stability performances, without the need to solve the famous Hamilton–Jacobin equation. The disturbance has a sensitive effect on the FLMA, and this article addresses stricter disturbance requirements including the absolute value error, integration error and input-to-state stable condition.
This study successfully derives the nonlinear convergence rate formula of the FLMA and the related convergence radius of the global final attractor. Moreover, in order to clearly show that dynamic trajectories of the output tracking errors for the nonlinear FLMA system converge to the global final attractor, Matlab 5.3 software is completely designed to demonstrate the tracking error trajectories before, on and after entering the globally final attractor.
The simulation results of two demonstrative examples show that the convergence rate using the proposed controller is faster than using a traditional fuzzy controller, and it is superior to the traditional singular perturbation approach.
In future works, we hope that a real FLMA system with the proposed main algorithm can be implemented via hardware devices. Implementing the algorithm into a real physical system would provide stronger evidence of its practical applicability and robustness under real-world conditions, especially given the system’s sensitivity to disturbances. Based on the important contribution that this article has in being the first to propose the convergence rate formula of the general nonlinear system, we may use the particle swarm optimization and linear quadratic regulator algorithms to achieve more optimal performances for nonlinear FLMA systems with the guarantee of attaining globally exponential stability. In order to show the superiority of this article and allow one to easily build nonlinear controllers, we will apply the famous artificial intelligence language Python to carefully design a powerful software system according to the proposed theorem and algorithm in the near future. Moreover, so far, it is obvious to see that the robust tracking controller design for both “underactuated” and “fully actuated” manipulator arms is still a challenging subject due to the strict global stability requirement and disturbance reduction involving nonlinear system dynamics. In this article, we discussed a robust tracking controller design for a “fully actuated” manipulator arm in depth. In the near future, we will extend all the results of this article to provide a robust tracking controller design for “underactuated” manipulator arms.
Author Contributions
Conceptualization, K.-H.C.; methodology, C.-C.C.; software, Y.-F.H.; validation, Y.-F.H.; formal analysis, Y.-F.H.; investigation, Y.-F.H.; resources, K.-H.C.; data curation, K.-H.C.; writing—original draft preparation, C.-C.C.; writing—review and editing, K.-H.C. and Y.-F.H.; visualization, K.-H.C.; supervision, C.-C.C.; project administration, K.-H.C. and C.-C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
In Appendix A, we give complete derivations of the dynamic mathematical equation for the nonlinear FLMA system. Defining potential energy , kinetic energy , joint torque , and Lagrangian term as the difference between the kinetic energy and potential energy and applying the Euler–Lagrange equation yield the dynamic equation of the FLMA as follows:
Let the centroid translational position vector and velocity vector of link be and and the centroid rotational position vector and velocity vector of link be and . From the fundamental definitions of the position vector and velocity vector, we obtain
and
Then, kinetic energy of the manipulator arm is given by
We define
Substituting (A10)~(A12) to (A9) yields
From (A1), (A2) and (A13), we obtain
Then,
Since matrix possesses a positive definite property and , we obtain
i.e.,
We define
and
From (A17)~(A19), it is more practical to rewrite the Euler–Lagrange equation of the manipulator arm in a more compact form for control purposes as follows:
where is the vector of gravity force and denotes the Coriolis matrix of the manipulator arm. Observing the structure of (A19) yields
where
We define
and
Then, (A12) can be rewritten as
Observing Figure 1 yields the centroid translational position vectors , , and
where and ., , , and . Applying (A6) to the centroid translational position vector yields
Observing Figure 1 yields the centroid rotational position vectors , , and . Applying (A8) to the centroid rotational position vector yields
Substituting (A24)~(A25) and (A27)~(A34) to (A25) yields matrix as follows:
where
Let us combine (A21) and (A22) and obtain matrix as follows:
where
From Figure 1, we obtain the potential energy of the manipulator arm as follows:
where . Applying (A19) yields
Using (A35) yields the inverse of the matrix as follows:
From (A43) and (A63), we obtain
where
Multiplying (A63) with (A19) yields
where
From (A20), we obtain
Substituting (A63), (A71) and (A86) to (A91) yields
Appendix B
In Appendix B, we prove that the nonlinear FLMA system with the proposed control can achieve three almost all disturbance decoupling performances, the convergent radius formula and globally exponential stability. First, applying (130) easily helps us achieve this.
i.e.,
We integrate both sides of the inequality (A97) to obtain
i.e.,
Therefore,
Similarly, we can extend above result as follows:
and then we can conclude that the third almost disturbance decoupling requirement is achieved. Next, we achieve the first almost disturbance decoupling performance. Equation (128) can be rewritten as
Let
Combining (A102) and (A103) yields
Then,
Therefore, the state trajectory lying in the outside of the global ultimate attractor is described by
Then,
From (87), (104), (107) and (110), we obtain
We define and can obtain
Similarly, we can achieve
We define and can obtain
Combining (A109) and (A111) results in
From (A106), (A107) and (A112) and the input-to-state stable theorem [38], we can conclude that the first almost disturbance decoupling requirement is achieved. Next, we achieve the first almost disturbance decoupling performance. Combining (A102), (A103), (A112) and (125) results in
Applying the comparison theorem to (A113) yields
Then, we can obtain
and
Observing (A116) verifies the second almost disturbance decoupling requirement and the convergence rate of tracking errors is . It is obvious to see that we can change the value of to adjust the convergence rate. Moreover, from (A102), (A103) and (125), we obtain
Considering the output trajectory for yields , and then any sphere
will be a global final attractor of the nonlinear FLMA system with the convergent radius .
Next, we verify the globally exponential stability of the nonlinear FLMA system. Combining (A112) and (A114) yields
and
Then,
Hence, we can achieve the globally exponential stability of the global final attractor.
References
- Marinovic, S.A.; Torriti, M.T.; Cheein, F.A. General dynamic model for skid-steer mobile manipulators with wheel-ground interactions. IEEE/ASME Trans. Mechatron. 2017, 22, 433–444. [Google Scholar] [CrossRef]
- Li, Z.; Ge, S.S. Fundamentals in Modeling and Control of Mobile Manipulators; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Wu, J.; Gao, J.; Song, R.; Li, R.; Li, Y.; Jiang, L. The design and control of a 3 DOF lower limb rehabilitation robot. Mechatronics 2016, 33, 13–22. [Google Scholar] [CrossRef]
- Wang, X.; Zeng, H.; Zhou, H. A spatial four-link 4R biped walking mechanism. In Proceedings of the 2019 IEEE 9th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems, Suzhou, China, 29 July–2 August 2019; pp. 203–208. [Google Scholar]
- Masood, M.U.; Mujtaba, M.; Sami, M.A.; Rashid, N.; Iqbal, J. Design and experimental testing of an in-parallel actuated 3 DOF serial robotic manipulator for unmanned ground vehicle. In Proceedings of the 2018 3rd Asia-Pacific Conference on Intelligent Robot Systems (ACIRS), Singapore, 21–23 July 2018; pp. 45–49. [Google Scholar]
- Leborne, F.; Creuze, V.; Chemori, A.; Brignone, L. Dynamic modeling and identification of an heterogeneously actuated underwater manipulator arm. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 4955–4960.
- Reyhanoglu, M.; van der Schaft, A.; Mcclamroch, N.H.; Kolmanovsky, I. Dynamics and control of a class of underactuated mechanical systems. IEEE Trans. Autom. Control 1999, 44, 1663–1671. [Google Scholar] [CrossRef]
- Lai, X.; Wangm; Wu, M.; Cao, W. Stable Control Strategy for Planar Three-Link Underactuated Mechanical System. IEEE/ASME Trans. Mechatron. 2016, 21, 1345–1356. [Google Scholar] [CrossRef]
- Lai, X.Z.; Zhang, A.C.; She, J.H.; Wu, M. Motion control of underactuated three-link gymnast robot based on combination of energy and posture. IET Control Theory Appl. 2011, 5, 1484–1492. [Google Scholar] [CrossRef]
- Thompson, M.R.; Torriti, M.T.; Auat Cheeina, F.A.; Troni, G. H∞-Based Terrain Disturbance Rejection for Hydraulically Actuated Mobile Manipulators With a Nonrigid Link. IEEE/ASME Trans. Mechatron. 2020, 25, 2523–2533. [Google Scholar] [CrossRef]
- Brown, S.C.; Passino, K.M. Intelligent control for an acrobat. J. Intell. Robot. Syst. 1997, 18, 209–248. [Google Scholar] [CrossRef]
- Fantoni, I.; Lozano, R.; Spong, M.W. Energy-based control of the pendubot. IEEE Trans. Autom. Control 2002, 45, 725–729. [Google Scholar] [CrossRef]
- Anditio, B.; Andrini, A.D.; Nazaruddin, Y.Y. Integrating PSO Optimized LQR Controller with Virtual Sensor for Quadrotor Position Control. In Proceedings of the 2018 IEEE Conference on Control Technology and Applications, Copenhagen, Denmark, 21–24 August 2018; pp. 1603–1607. [Google Scholar]
- Yang, J.; Ding, Z. Global output regulation for a class of lower triangular nonlinear systems: A feedback domination approach. Automatica 2017, 76, 65–69. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, H.; Liu, Z.; Gu, M. Ride comfort optimization via speed planning and preview semi-active suspension control for autonomous vehicles on uneven roads. IEEE Trans. Veh. Technol. 2020, 69, 8343–8355. [Google Scholar] [CrossRef]
- Liu, M.; Li, Y.; Rong, X.; Zhang, S.; Yin, Y. Semi-Active Suspension Control Based on Deep Reinforcement Learning. IEEE Access 2020, 8, 9978–9986. [Google Scholar]
- Chen, H.; Sun, P.Y.; Guo, K.-H. A multi-objective control design for active suspensions with hard constraints. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4371–4376. [Google Scholar]
- Lin, J.S.; Huang, C.J. Nonlinear backstepping active suspension design applied to a half-car model. Veh. Syst. Dyn. 2004, 42, 373–393. [Google Scholar] [CrossRef]
- Gohrle, C.; Schindler, A.; Wagner, A.; Sawodny, O. Design and vehicle implementation of preview active suspension controllers. IEEE Trans. Control Syst. Technol. 2014, 22, 1135–1142. [Google Scholar] [CrossRef]
- Tang, L.; Ma, D.; Zhao, J. Adaptive neural control for switched non-linear systems with multiple tracking error constraints. IET Signal Process. 2019, 13, 330–337. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Y.L.; Li, D.; Tong, S.; Wang, Z. Barrier Lyapunov function-based adaptive fuzzy FTC for switched systems and its applications to resistance–inductance–capacitance circuit system. IEEE Trans. Cybern. 2020, 50, 3491–3502. [Google Scholar] [CrossRef]
- Cui, R.; Yang, C.; Li, Y.; Sharma, S. Adaptive neural network control of AUVs with control input nonlinearities using reinforcement learning. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1019–1029. [Google Scholar] [CrossRef]
- Wang, D.Y.; Wang, H. Control method of vehicle semi active suspen-sions based on variable universe fuzzy control. China Mech. Eng. 2017, 28, 366–372. [Google Scholar]
- Li, H.; Feng, Y.H.; Su, L. Vehicle active suspension vibration control based on robust neural network. Chin. J. Construct. Mach. 2017, 15, 324–337. [Google Scholar]
- Nazaruddin, Y.Y.; Astuti, P. Development of intelligent controller with virtual sensing. ITB J. Eng. Sci. 2009, 41, 17–36. [Google Scholar] [CrossRef]
- Luca, A.D.; Mattone, R.; Oriolo, G. Stabilization of an underactuated planar 2R manipulator. Int. J. Robust Nonlinear Control 2000, 10, 181–1812. [Google Scholar] [CrossRef]
- Yoshikawa, T.; Kobayashi, K.; Watanabe, T. Design of a desirable trajectory and convergent control for 3-DOF manipulator with a nonholonomic constraint. In Proceedings of the IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000; Volume 2, pp. 1805–18052. [Google Scholar]
- Xiong, P.Y.; Lai, X.Z.; Wu, M. A stable control for second-order nonholonomic planar underactuated mechanical system: Energy attenuation approach. Int. J. Control 2018, 91, 1630–16302. [Google Scholar] [CrossRef]
- Zapolsky, S.; Drumwright, E. Inverse dynamics with rigid contact and friction. Auton. Robot. 2017, 41, 831–8312. [Google Scholar] [CrossRef]
- Liu, T.; Ma, X.; Zhu, F.; Fadel, M. Reduced-Order Feedback Linearization for Independent Torque Control of a Dual Parallel-PMSM system. IEEE Access 2021, 9, 27405–27415. [Google Scholar] [CrossRef]
- Mehrasa, M.; Babaie, M.; Sharifzadeh, M.; Haddad, K.A. An Input-Output Feedback Linearization Control Method Synthesized by Artificial Neural Network (ANN) for Grid-Tied Packed E-Cell Inverter. IEEE Trans. Ind. Appl. 2021, 57, 3131–3142. [Google Scholar] [CrossRef]
- Awais, M.; Khan, L.; Badar, R.; Mumtaz, S.; Ahmad, S.; Ullah, S. Wavelet-Hybridized NeuroFuzzy Feedback Linearization based Control Strategy for PHEVs Charging Station in a Smart Microgrid. In Proceedings of the 2020 International Symposium on Recent Advances in Electrical Engineering & Computer Sciences (RAEE & CS), Pakistan, Islamabad, 20–22 October 2020; pp. 1–6. [Google Scholar]
- Babar, S.A.; Ahmad, I.; Mughal, I.S.; Khan, S.A. Terminal Synergetic and State Feedback Linearization based Controllers for Artificial Pancreas in Type 1 Diabetic Patients. IEEE Access 2021, 9, 28012–28019. [Google Scholar] [CrossRef]
- Khazaei, J.; Tu, Z.; Asrari, A.; Liu, W. Feedback Linearization Control of Converters with LCL Filter For Weak AC Grid Integration. IEEE Trans. Power Syst. 2021, 36, 3740–3750. [Google Scholar] [CrossRef]
- Marino, R.; Respondek, W.; Van Der Schaft, A.J. Almost disturbance decoupling for single-input single-output nonlinear systems. IEEE Trans. Automat. Contr. 1989, 34, 1013–1017. [Google Scholar] [CrossRef]
- Marino, R.; Tomei, P. Nonlinear output feedback tracking with almost disturbance decoupling. IEEE Trans. Automat. Contr. 1999, 44, 18–28. [Google Scholar] [CrossRef]
- Isidori, A. Nonlinear Control System; Springer: New York, NY, USA, 1989. [Google Scholar]
- Khalil, H.K. Nonlinear Systems; Prentice-Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Dhiman, H.S.; Deb, D. Fuzzy TOPSIS and fuzzy COPRAS based multi-criteria decision making for hybrid wind farms. Energy 2020, 202, 117755. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).