A Lightweight Neural Network for Denoising Wrapped-Phase Images Generated with Full-Field Optical Interferometry
Abstract
1. Introduction
- A synthetic dataset is generated by combining a ramp function and multiple Gaussian functions, incorporating various degrees of randomness and noise levels to enhance the model’s capability to handle diverse noise conditions.
- We propose WPD-Net, specifically designed to extract phase information distorted by noise while preserving fine structural details. The architecture includes RDABs that enhance phase reconstruction.
- Instead of using only the mean squared error (MSE) loss, we employ a dynamic hybrid loss function that adaptively balances Structural Similarity Index (SSIM) and MSE during training for optimal intensity and structural preservation.
2. Method
2.1. Residual Dense Attention Block (RDAB)
2.2. Dense Feature Fusion (DFF)
2.3. Advantages of WPD-Net
2.4. Loss Function
3. Training
3.1. Dataset Preparation
3.2. Training Parameters and Evaluation Metrics
- Gaussian noise dataset—Phase images were corrupted by Gaussian noise with a normal distribution, defined by SNR ranging from 10 dB to 0 dB.
- Speckle noise dataset—Images were degraded by speckle noise, with variance ranging between 0.05 and 0.1.
- Mixed Noise Dataset—Phase images were affected by a combination of Gaussian noise (SNR ranging from 5 dB to 0 dB) and speckle noise (variance between 0.08 and 0.1), simulating more challenging and realistic noise conditions.
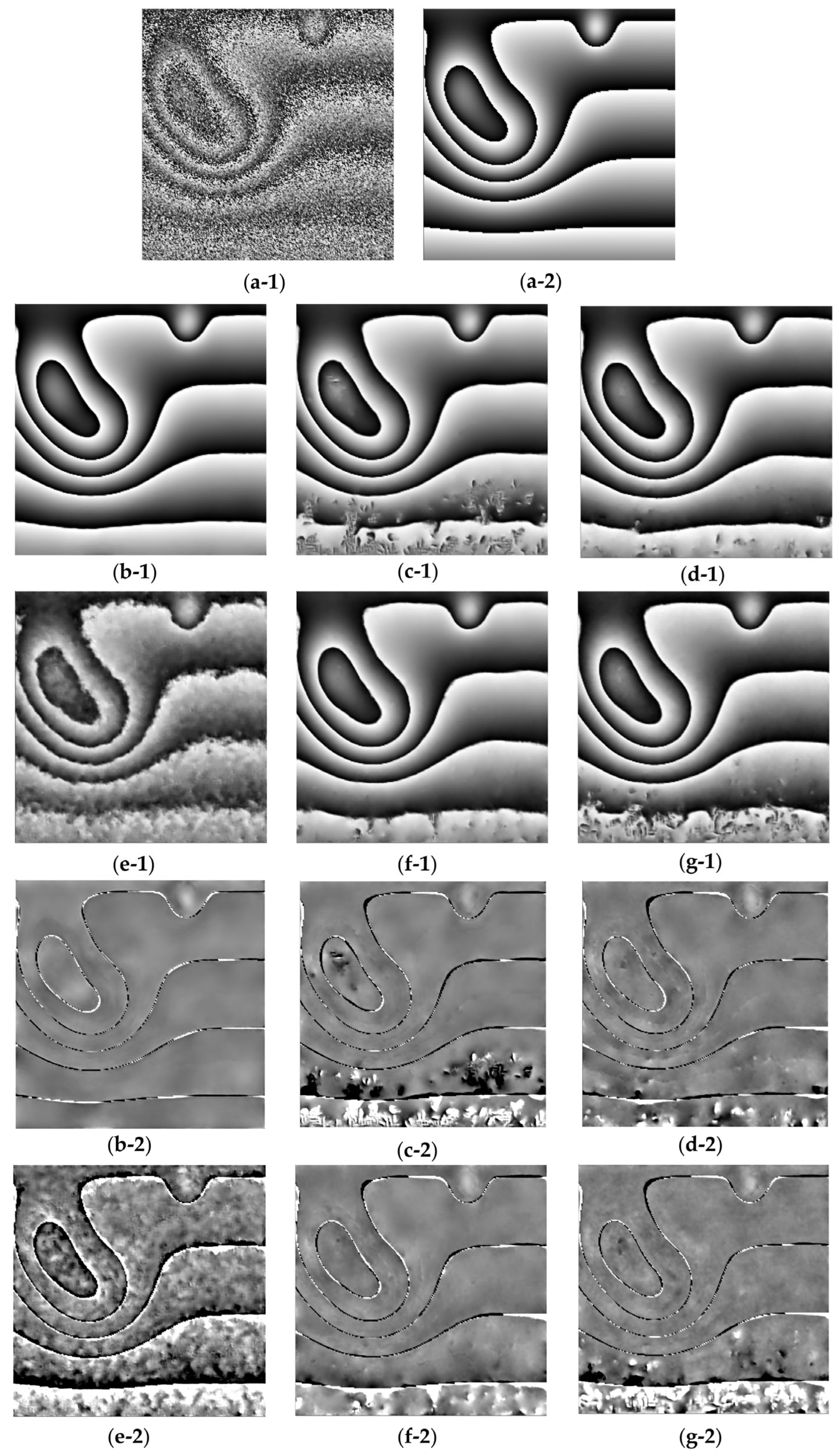
4. Results
4.1. Experiments with Synthetic and Real Data
4.2. Ablation Study
4.3. Model Complexity
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wyant, J.C. Dynamic Interferometry. Opt. Photonics News 2003, 14, 36–41. [Google Scholar] [CrossRef]
- Ghiglia, D.C. Two-Dimensional Phase Unwrapping: Theory, Algorithms and Software; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Huntley, J.M. Random Phase Measurement Errors in Digital Speckle Pattern Interferometry. Opt. Lasers Eng. 1997, 26, 131–150. [Google Scholar] [CrossRef]
- Aebischer, A.H.; Waldner, S. A Simple and Effective Method for Filtering Speckle-Interferometric Phase Fringe Patterns. Opt. Commun. 1999, 162, 205–210. [Google Scholar] [CrossRef]
- Goodman, J.W. Speckle Phenomena in Optics: Theory and Applications; Roberts and Company Publishers: Greenwood Village, CO, USA, 2007. [Google Scholar]
- Montresor, S.; Picart, P. Quantitative Appraisal for Noise Reduction in Digital Holographic Phase Imaging. Opt. Express 2016, 24, 14322–14343. [Google Scholar] [CrossRef]
- Piniard, M.; Sorrente, B.; Hug, G.; Picart, P. Theoretical Analysis of Surface-Shape-Induced Decorrelation Noise in Multi-Wavelength Digital Holography. Opt. Express 2021, 29, 14720–14735. [Google Scholar] [CrossRef]
- Montresor, S.; Picart, P. On the Assessment of De-Noising Algorithms in Digital Holographic Interferometry and Related Approaches. Appl. Phys. B 2022, 128, 59. [Google Scholar] [CrossRef]
- Kemao, Q. Windowed Fourier Transform for Fringe Pattern Analysis. Appl. Opt. 2004, 43, 2695–2702. [Google Scholar] [CrossRef]
- Kemao, Q. Two-Dimensional Windowed Fourier Transform for Fringe Pattern Analysis: Principles, Applications and Implementations. Opt. Lasers Eng. 2007, 45, 304–317. [Google Scholar] [CrossRef]
- O’Shea, K.; Nash, R. An Introduction to Convolutional Neural Networks. arXiv 2015, arXiv:1511.08458. [Google Scholar]
- Wang, P.; Zhang, H.; Patel, V.M. SAR Image Despeckling Using a Convolutional Neural Network. IEEE Signal Process. Lett. 2017, 24, 1763–1767. [Google Scholar] [CrossRef]
- Jeon, W.; Jeong, W.; Son, K.; Yang, H. Speckle Noise Reduction for Digital Holographic Images Using Multi-Scale Convolutional Neural Networks. Opt. Lett. 2018, 43, 4240–4243. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Li, J.; Yang, Z.; Ma, X. Learning a Dilated Residual Network for SAR Image Despeckling. Remote Sens. 2018, 10, 196. [Google Scholar] [CrossRef]
- Choi, G.; Ryu, D.; Jo, Y.; Kim, Y.; Park, W.; Min, H.S.; Park, Y. Cycle-Consistent Deep Learning Approach to Coherent Noise Reduction in Optical Diffraction Tomography. Opt. Express 2019, 27, 4927–4943. [Google Scholar] [CrossRef]
- Wang, M.; Zhu, W.; Yu, K.; Chen, Z.; Shi, F.; Zhou, Y.; Ma, Y.; Peng, Y.; Bao, D.; Feng, S.; et al. Semi-Supervised Capsule cGAN for Speckle Noise Reduction in Retinal OCT Images. IEEE Trans. Med. Imaging 2021, 40, 1168–1183. [Google Scholar] [CrossRef] [PubMed]
- Yan, K.; Yu, Y.; Sun, T.; Asundi, A.; Kemao, Q. Wrapped Phase Denoising Using Convolutional Neural Networks. Opt. Lasers Eng. 2020, 128, 105999. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef]
- Lin, B.; Fu, S.; Zhang, C.; Wang, F.; Li, Y. Optical Fringe Patterns Filtering Based on Multi-Stage Convolution Neural Network. Opt. Lasers Eng. 2020, 126, 105853. [Google Scholar] [CrossRef]
- Figueroa, A.R.; Flores, V.H.; Rivera, M. Deep Neural Network for Fringe Pattern Filtering and Normalization. Appl. Opt. 2021, 60, 2022–2036. [Google Scholar] [CrossRef]
- Montresor, S.; Tahon, M.; Laurent, A.; Picart, P. Computational De-Noising Based on Deep Learning for Phase Data in Digital Holographic Interferometry. APL Photonics 2020, 5, 030801. [Google Scholar] [CrossRef]
- Fang, Q.; Xia, H.; Song, Q.; Zhang, M.; Guo, R.; Montresor, S.; Picart, P. Speckle Denoising Based on Deep Learning via a Conditional Generative Adversarial Network in Digital Holographic Interferometry. Opt. Express 2022, 30, 20666–20683. [Google Scholar] [CrossRef]
- Yan, K.; Chang, L.; Andrianakis, M.; Tornari, V.; Yu, Y. Deep Learning-Based Wrapped Phase Denoising Method for Application in Digital Holographic Speckle Pattern Interferometry. Appl. Sci. 2020, 10, 4044. [Google Scholar] [CrossRef]
- Fang, Q.; Li, Q.; Song, Q.; Montresor, S.; Picart, P.; Xia, H. Convolutional and Fourier Neural Networks for Speckle Denoising of Wrapped Phase in Digital Holographic Interferometry. Opt. Commun. 2024, 550, 129955. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, D.; Wang, K. Denoising of Wrapped Phase in Digital Speckle Shearography Based on Convolutional Neural Network. Appl. Sci. 2024, 14, 4135. [Google Scholar] [CrossRef]
- Li, J.; Tang, C.; Xu, M.; Fan, Z.; Lei, Z. DBDNet for Denoising in ESPI Wrapped Phase Patterns with High Density and High Speckle Noise. Appl. Opt. 2021, 60, 10070–10079. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Tang, C.; Xu, M.; Lei, Z. Uneven Wrapped Phase Pattern Denoising Using a Deep Neural Network. Appl. Opt. 2022, 61, 7150–7157. [Google Scholar] [CrossRef]
- Wang, L.; Li, R.; Tian, F.; Fang, X. Application of Attention-DnCNN for ESPI Fringe Patterns Denoising. J. Opt. Soc. Am. A 2022, 39, 2110–2123. [Google Scholar] [CrossRef]
- He, H.; Tang, C.; Liu, L.; Zhang, L.; Lei, Z. Generalized Denoising Network LGCT-Net for Various Types of ESPI Wrapped Phase Patterns. J. Opt. Soc. Am. A 2024, 41, 1664–1674. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Yu, H.; Yang, T.; Zhou, L.; Wang, Y. PDNet: A Lightweight Deep Convolutional Neural Network for InSAR Phase Denoising. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5239309. [Google Scholar] [CrossRef]
- Hao, F.; Tang, C.; Xu, M.; Lei, Z. Batch Denoising of ESPI Fringe Patterns Based on Convolutional Neural Network. Appl. Opt. 2019, 58, 3338–3346. [Google Scholar] [CrossRef]
- Xu, M.; Tang, C.; Hong, N.; Lei, Z. MDD-Net: A Generalized Network for Speckle Removal with Structure Protection and Shape Preservation for Various Kinds of ESPI Fringe Patterns. Opt. Lasers Eng. 2022, 154, 107017. [Google Scholar] [CrossRef]
- Gurrola-Ramos, J.; Dalmau, O.; Alarcón, T. U-Net Based Neural Network for Fringe Pattern Denoising. Opt. Lasers Eng. 2022, 149, 106829. [Google Scholar] [CrossRef]
- Yan, K.; Yu, Y.; Huang, C.; Sui, L.; Qian, K.; Asundi, A. Fringe Pattern Denoising Based on Deep Learning. Opt. Commun. 2019, 437, 148–152. [Google Scholar] [CrossRef]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep Sparse Rectifier Neural Networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics (AISTATS), Fort Lauderdale, FL, USA, 11–13 April 2011; JMLR W&CP. pp. 315–323. [Google Scholar]
- Park, J.; Woo, S.; Lee, J.Y.; Kweon, I.S. BAM: A Simple and Lightweight Attention Module for Convolutional Neural Networks. Int. J. Comput. Vis. 2020, 128, 783–798. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the International Conference on Machine Learning (ICML), Lille, France, 7–9 July 2015; PMLR: London, UK, 2015; pp. 448–456. [Google Scholar]
- Awais, M.; Yoon, T.; Hwang, C.O.; Lee, B. DenSFA-PU: Learning to Unwrap Phase in Severe Noisy Conditions. Opt. Laser Technol. 2025, 187, 112757. [Google Scholar] [CrossRef]
- Wang, K.; Li, Y.; Kemao, Q.; Di, J.; Zhao, J. One-Step Robust Deep Learning Phase Unwrapping. Opt. Express 2019, 27, 15100–15115. [Google Scholar] [CrossRef]
- Qin, Y.; Wan, S.; Wan, Y.; Weng, J.; Liu, W.; Gong, Q. Direct and Accurate Phase Unwrapping with Deep Neural Network. Appl. Opt. 2020, 59, 7258–7267. [Google Scholar] [CrossRef]
- Chen, J.; Kong, Y.; Zhang, D.; Fu, Y.; Zhuang, S. Two-Dimensional Phase Unwrapping Based on U2-Net in Complex Noise Environment. Opt. Express 2023, 31, 29792–29812. [Google Scholar] [CrossRef]
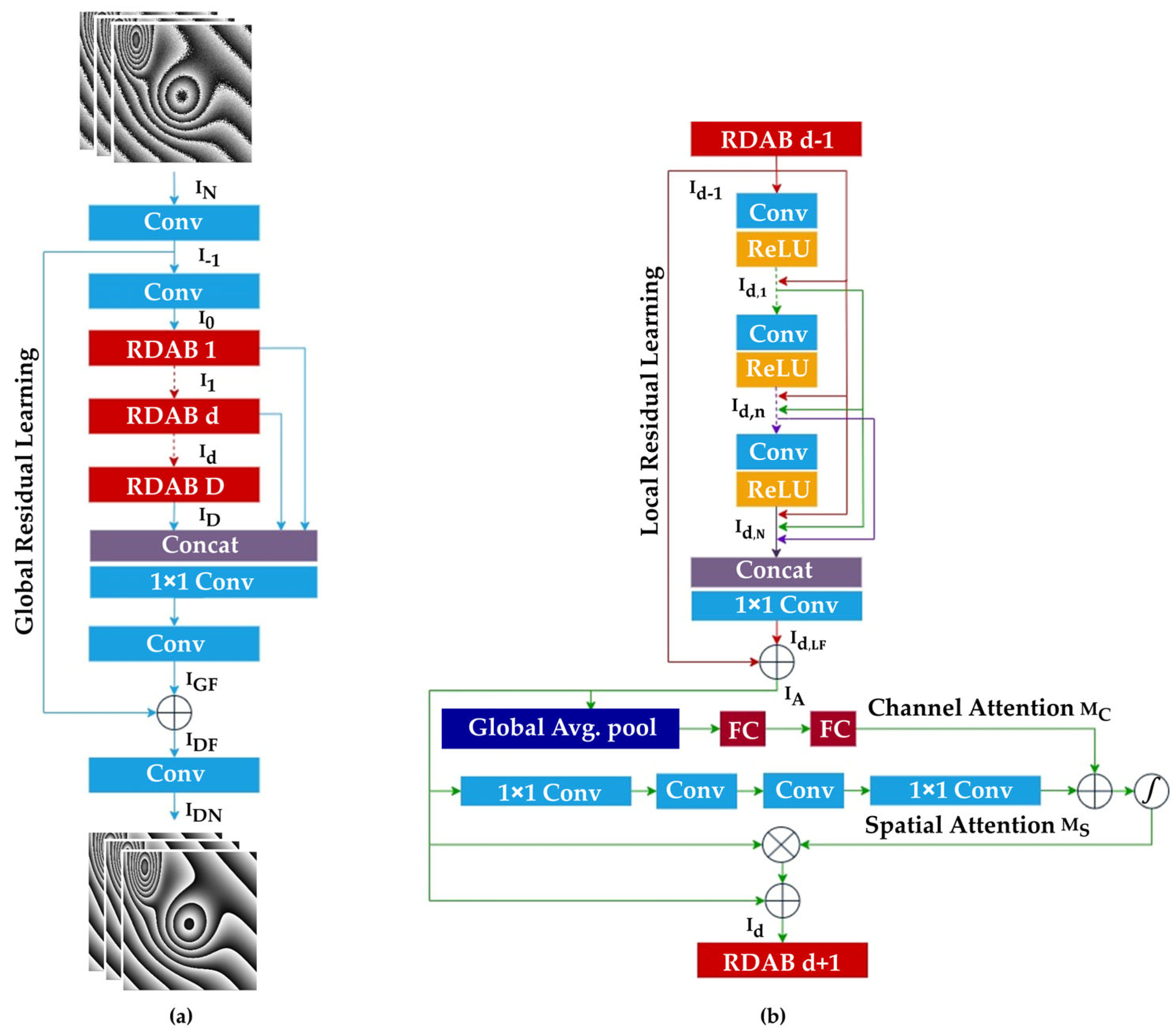










| Layer | Feature Map (H × W × C) | Padding | Dilation |
|---|---|---|---|
| Input | 256 × 256 × 1 | - | - |
| Shallow Feature Extraction (Conv C ReLU) | 256 × 256 × 48 | 1 | 1 |
| Residual Dense Attention Block 1 (RDAB1) | 256 × 256 × 24 | 1 | 1 |
| Residual Dense Attention Block 2 (RDAB2) | 256 × 256 × 24 | 1 | 1 |
| Residual Dense Attention Block 3 (RDAB3) | 256 × 256 × 24 | 1 | 1 |
| Residual Dense Attention Block 4 (RDAB4) | 256 × 256 × 24 | 1 | 1 |
| Global Feature Fusion (1 × 1 Conv) | 256 × 256 × 48 | 1 | 1 |
| Global Feature Fusion (3 × 3 Conv) | 256 × 256 × 48 | 1 | 1 |
| Global Residual Learning (Residual Connection) | 256 × 256 × 48 | 1 | 1 |
| Final Convolution (Output Layer) | 256 × 256 × 1 | 1 | 1 |
| Samples | MSE | PSNR | SSIM |
|---|---|---|---|
| Image with Speckle noise of Variance 0.05 | 0.0056 | 27.68 | 0.989 |
| Image with Speckle noise of Variance 0.08 | 0.0069 | 26.93 | 0.979 |
| Image with Gaussian noise of SNR 10 | 0.0062 | 27.57 | 0.981 |
| Image with Gaussian noise of SNR 5 | 0.0073 | 25.72 | 0.975 |
| Methods | Speckle Noise | Gaussian Noise | Combined Noise | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MSE | PSNR | SSIM | MSE | PSNR | SSIM | MSE | PSNR | SSIM | |
| DBDNet [26] | 0.0351 | 18.674 | 0.884 | 0.0412 | 17.935 | 0.827 | 0.2163 | 8.536 | 0.621 |
| DBDNet2 [27] | 0.0103 | 22.455 | 0.963 | 0.0185 | 22.476 | 0.958 | 0.0852 | 19.745 | 0.863 |
| AD-CNN [28] | 0.0098 | 25.036 | 0.974 | 0.0106 | 24.962 | 0.971 | 0.0983 | 17.627 | 0.826 |
| LGCT-Net [29] | 0.0146 | 21.945 | 0.953 | 0.0284 | 20.854 | 0.933 | 0.0617 | 20.529 | 0.857 |
| LRDUNet [34] | 0.0082 | 24.015 | 0.975 | 0.0153 | 23.711 | 0.964 | 0.0994 | 18.262 | 0.878 |
| WPD-Net | 0.0068 | 26.586 | 0.987 | 0.0085 | 25.981 | 0.973 | 0.0135 | 23.871 | 0.959 |
| MSE | PSNR | SSIM | |
|---|---|---|---|
| WPD-Net with MSE loss | 0.0298 | 16.335 | 0.816 |
| With RDAB and no DFF module | 0.0173 | 20.108 | 0.884 |
| With RDB and no attention | 0.0149 | 21.834 | 0.913 |
| Our proposed | 0.0076 | 26.164 | 0.982 |
| Models | Parameters (Millions) | FLOPs (Millions) | Run Time (ms) |
|---|---|---|---|
| DBDNet [26] | 0.988 | 298.9 | 26.30 |
| DBDNet2 [27] | 0.951 | 341.3 | 27.61 |
| AD-CNN [28] | 1.637 | 421.2 | 29.58 |
| LGCT-Net [29] | 8.796 | 859.7 | 51.39 |
| LRDUNet [34] | 4.213 | 276.8 | 32.74 |
| WPD-Net | 0.859 | 225.1 | 21.19 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awais, M.; Kim, Y.; Yoon, T.; Choi, W.; Lee, B. A Lightweight Neural Network for Denoising Wrapped-Phase Images Generated with Full-Field Optical Interferometry. Appl. Sci. 2025, 15, 5514. https://doi.org/10.3390/app15105514
Awais M, Kim Y, Yoon T, Choi W, Lee B. A Lightweight Neural Network for Denoising Wrapped-Phase Images Generated with Full-Field Optical Interferometry. Applied Sciences. 2025; 15(10):5514. https://doi.org/10.3390/app15105514
Chicago/Turabian StyleAwais, Muhammad, Younggue Kim, Taeil Yoon, Wonshik Choi, and Byeongha Lee. 2025. "A Lightweight Neural Network for Denoising Wrapped-Phase Images Generated with Full-Field Optical Interferometry" Applied Sciences 15, no. 10: 5514. https://doi.org/10.3390/app15105514
APA StyleAwais, M., Kim, Y., Yoon, T., Choi, W., & Lee, B. (2025). A Lightweight Neural Network for Denoising Wrapped-Phase Images Generated with Full-Field Optical Interferometry. Applied Sciences, 15(10), 5514. https://doi.org/10.3390/app15105514








