Hydrogen Purification Performance of Pressure Swing Adsorption in Coal-Derived Activated Carbon/Zeolite 13X Layered Bed
Abstract
1. Introduction
2. Mathematical Modeling
- (1)
- The ideal gas law is applicable.
- (2)
- An axially dispersed plug flow model is used to describe the flow pattern.
- (3)
- Radial variations in temperature, pressure, concentration, and velocity are negligible.
- (4)
- The inter-phase mass transfer coefficient is expressed using the linear driving force (LDF) model.
- (5)
- The aging of adsorbents is not considered.
2.1. Mass Conservation Equation
2.2. Energy Conservation Equation
2.3. Momentum Conservation Equation
2.4. Adsorption Isotherms and Kinetics
2.5. Ideal Gas Equation of State
3. Validation
3.1. Validation of Adsorption Isotherms
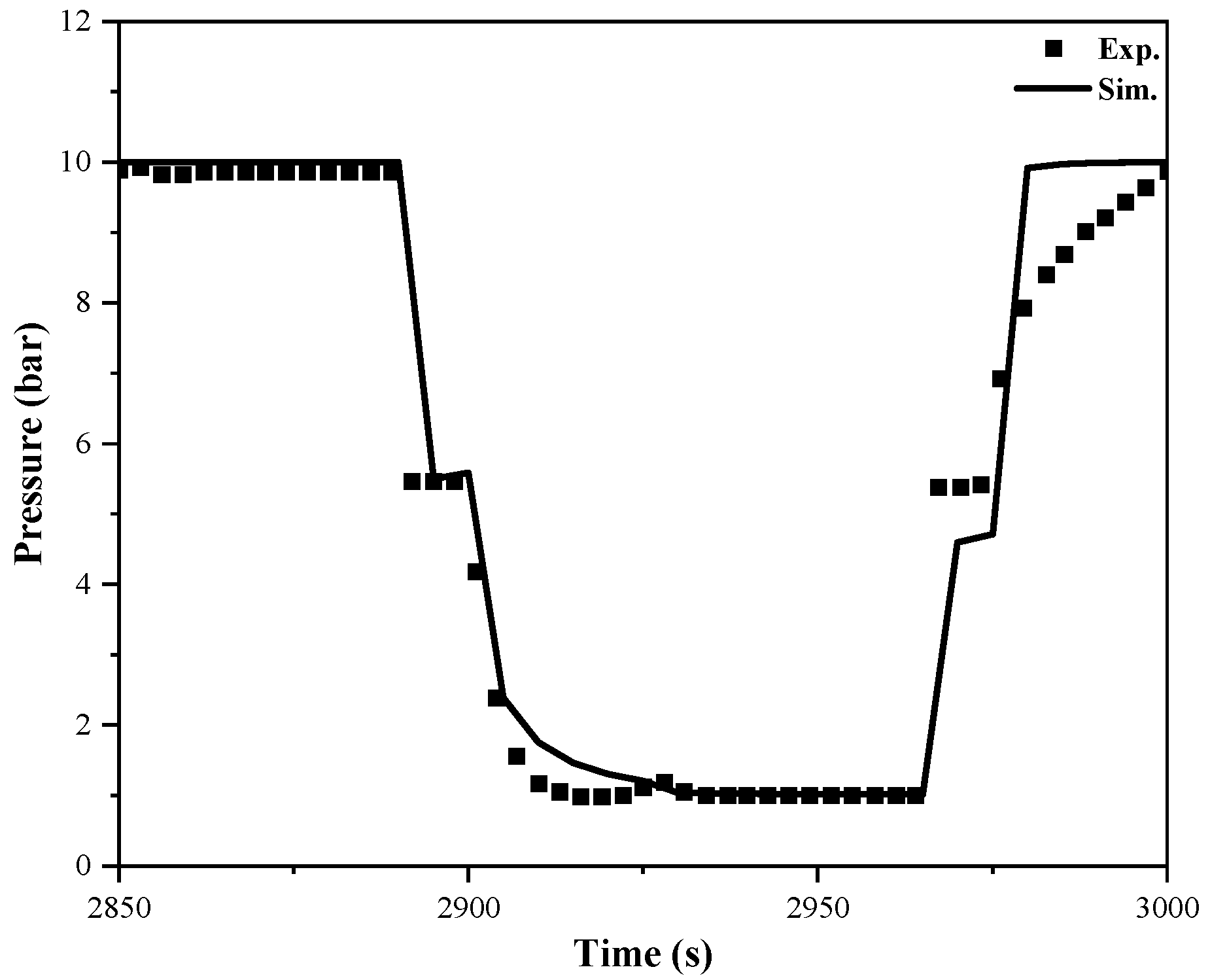
3.2. Validation of Breakthrough Curves on Adsorption Beds
4. Results and Discussion
4.1. Parametric Study on Breakthrough Curves of AC/Zeolite 13X Layered Bed
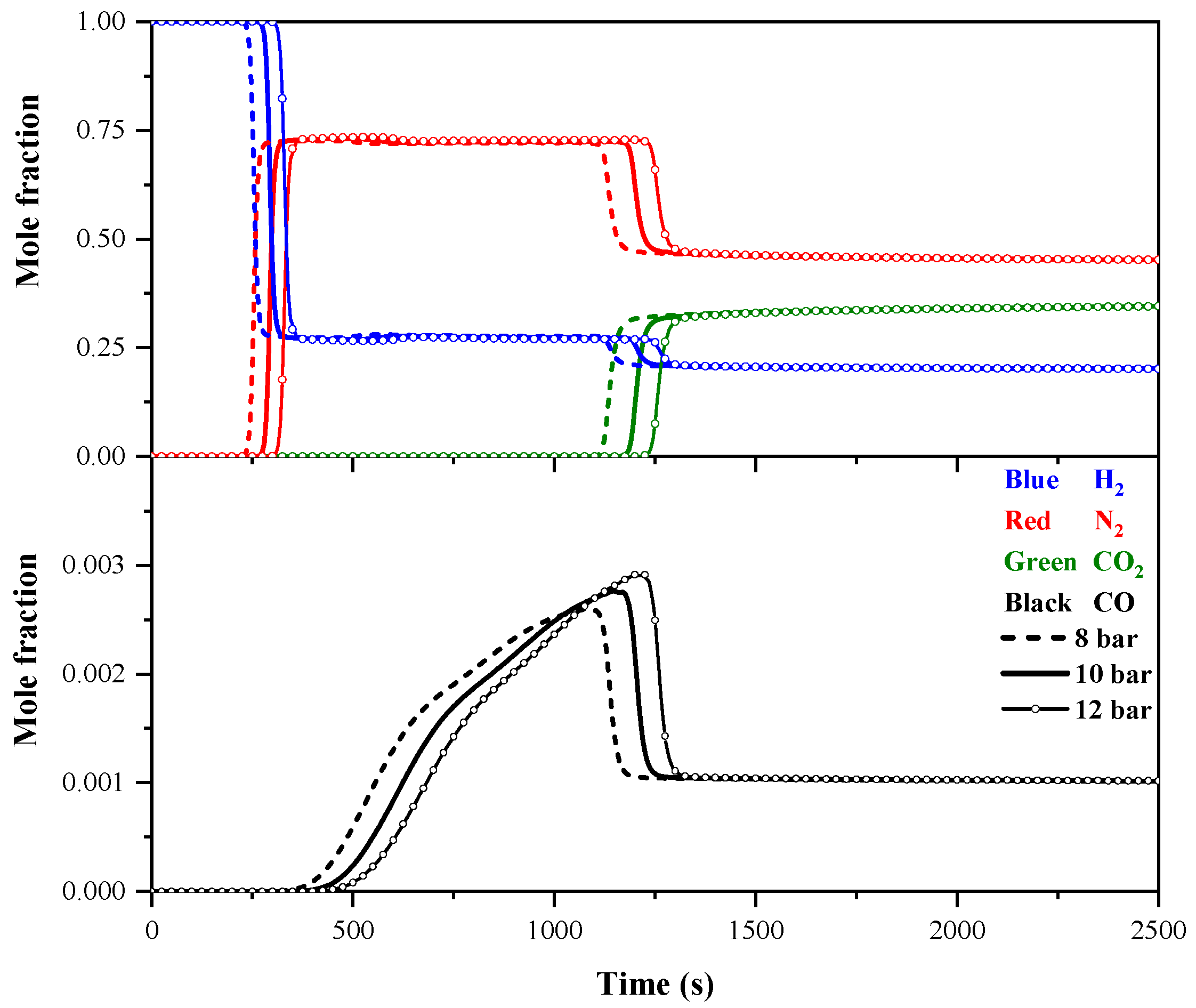
4.1.1. Effect of Feed Pressure on Breakthrough Curves
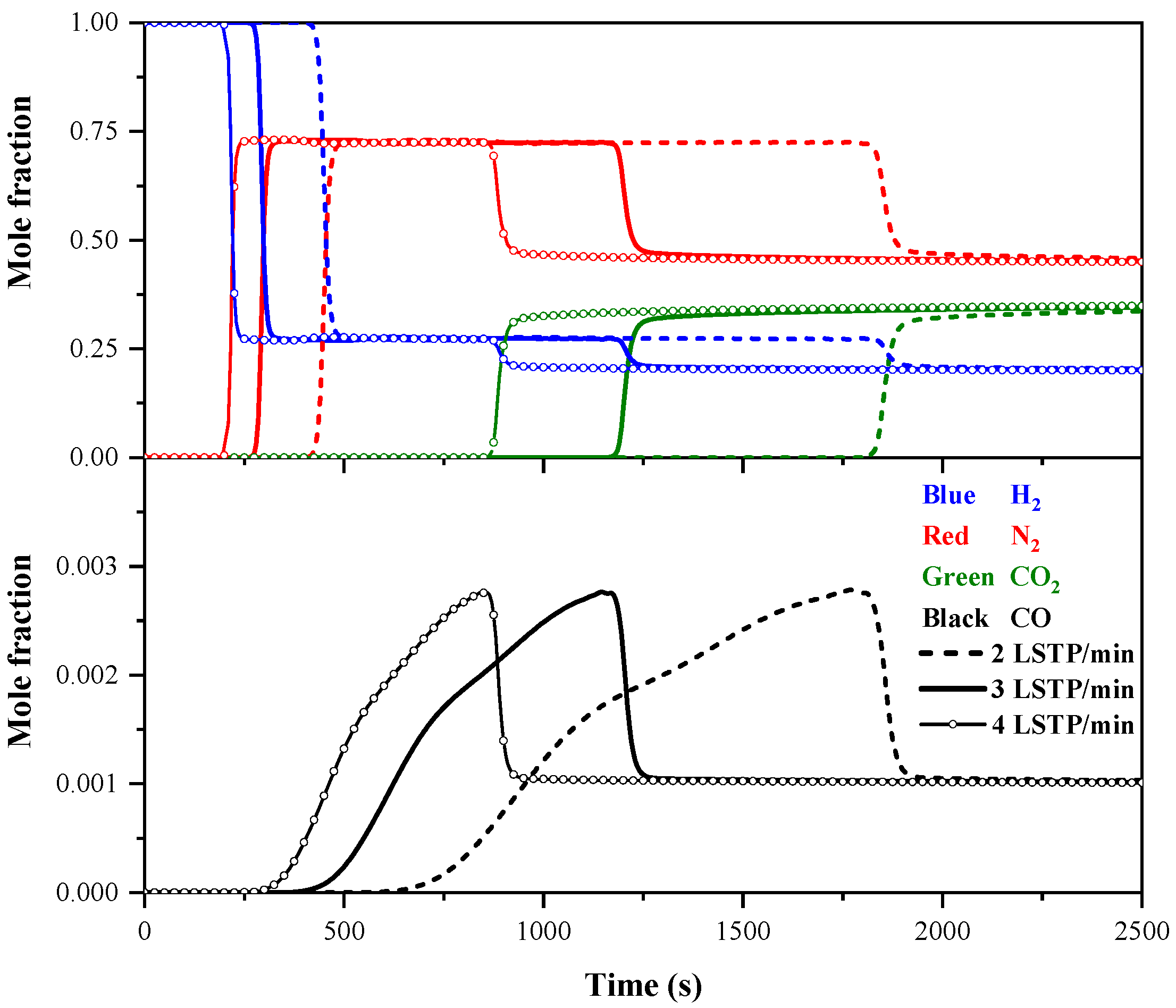
4.1.2. Effect of Feed Flow Rate on Breakthrough Curves
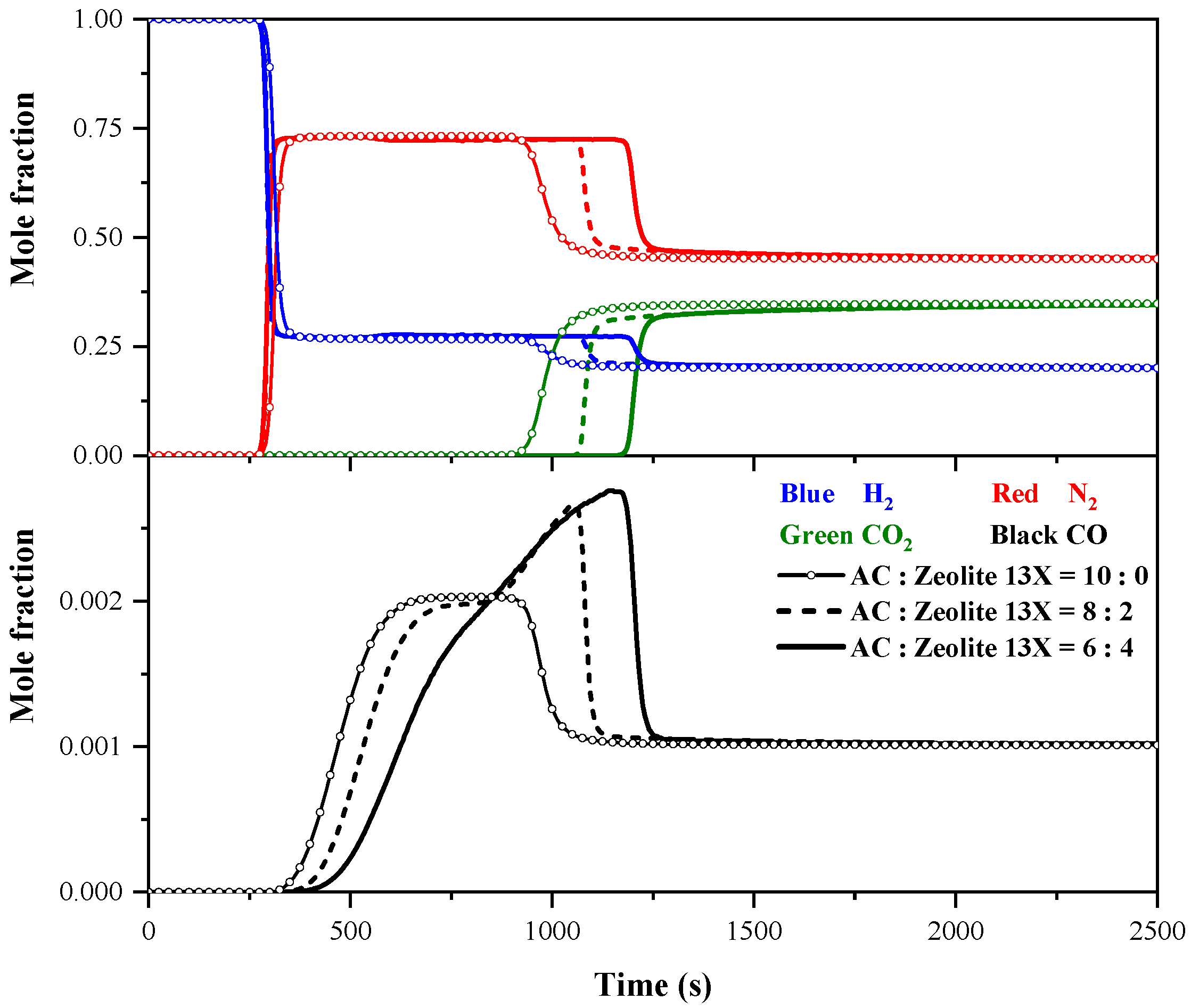
4.1.3. Effect of AC/Zeolite 13X Ratio on Breakthrough Curves
4.2. Modeling and Validation of PSA Cycle
4.3. Parametric Study on Hydrogen Purification Performance
4.3.1. Effect of Feed Pressure
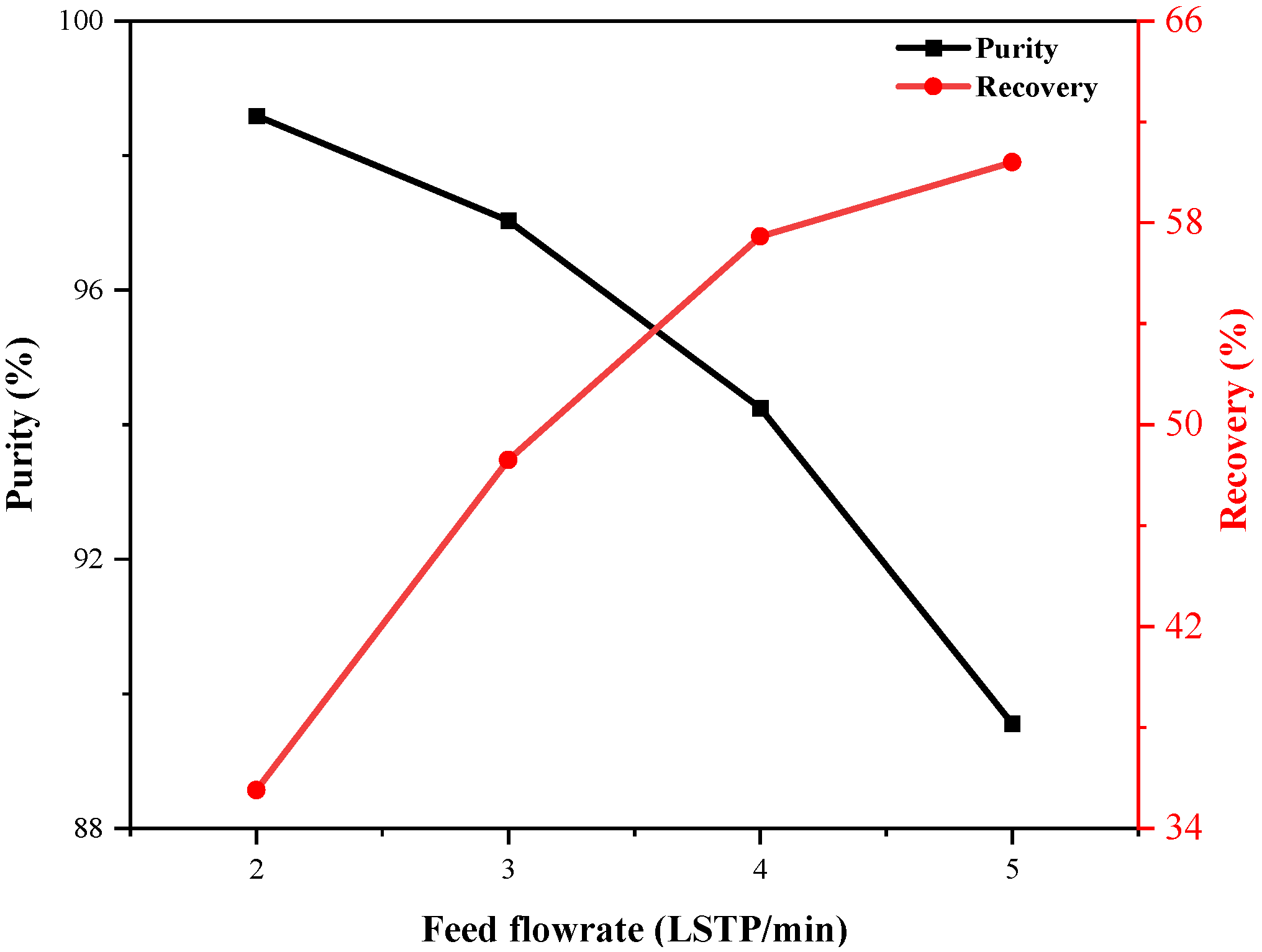
4.3.2. Effect of Feed Flow Rate
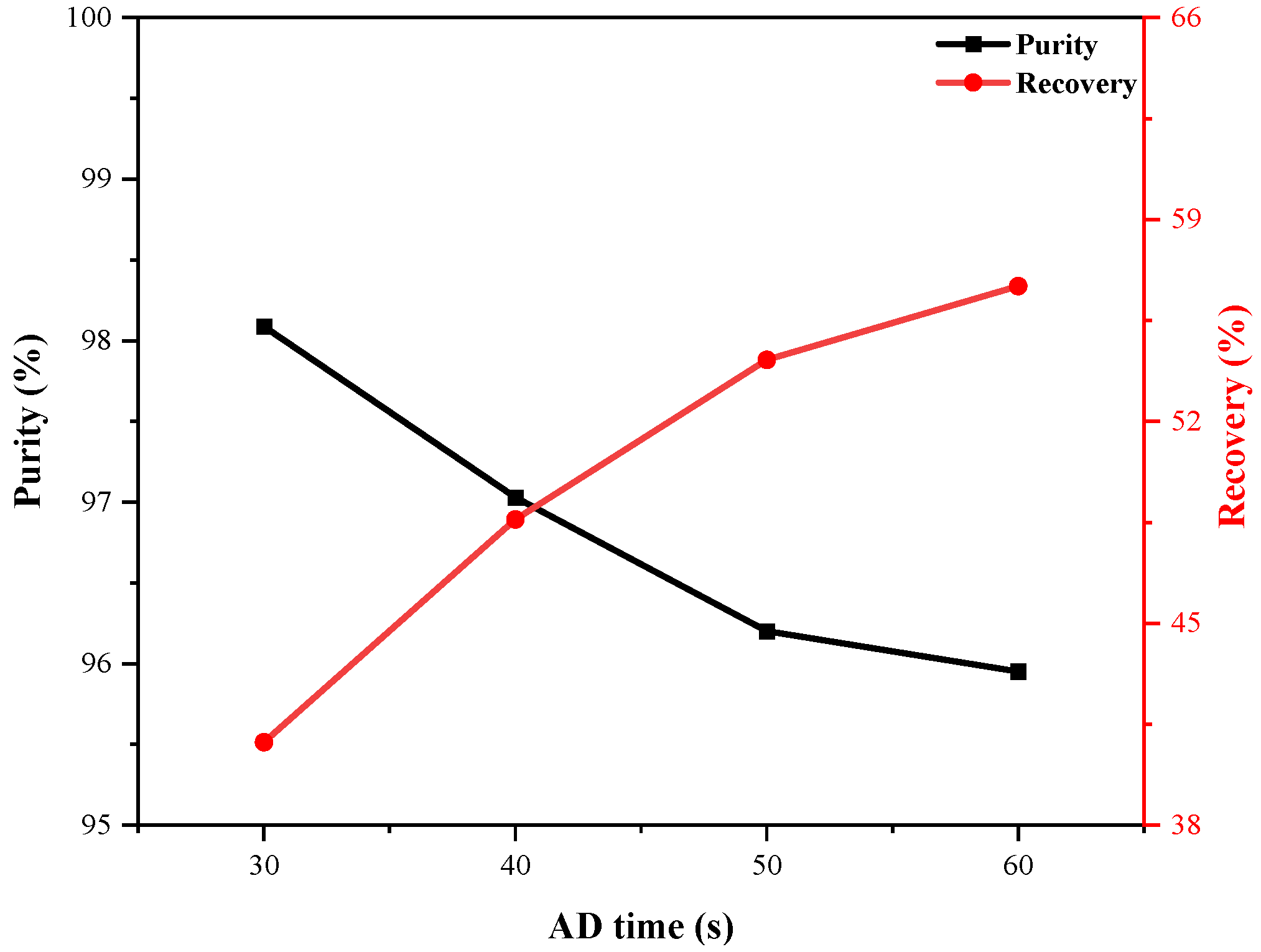
4.3.3. Effect of AD Time
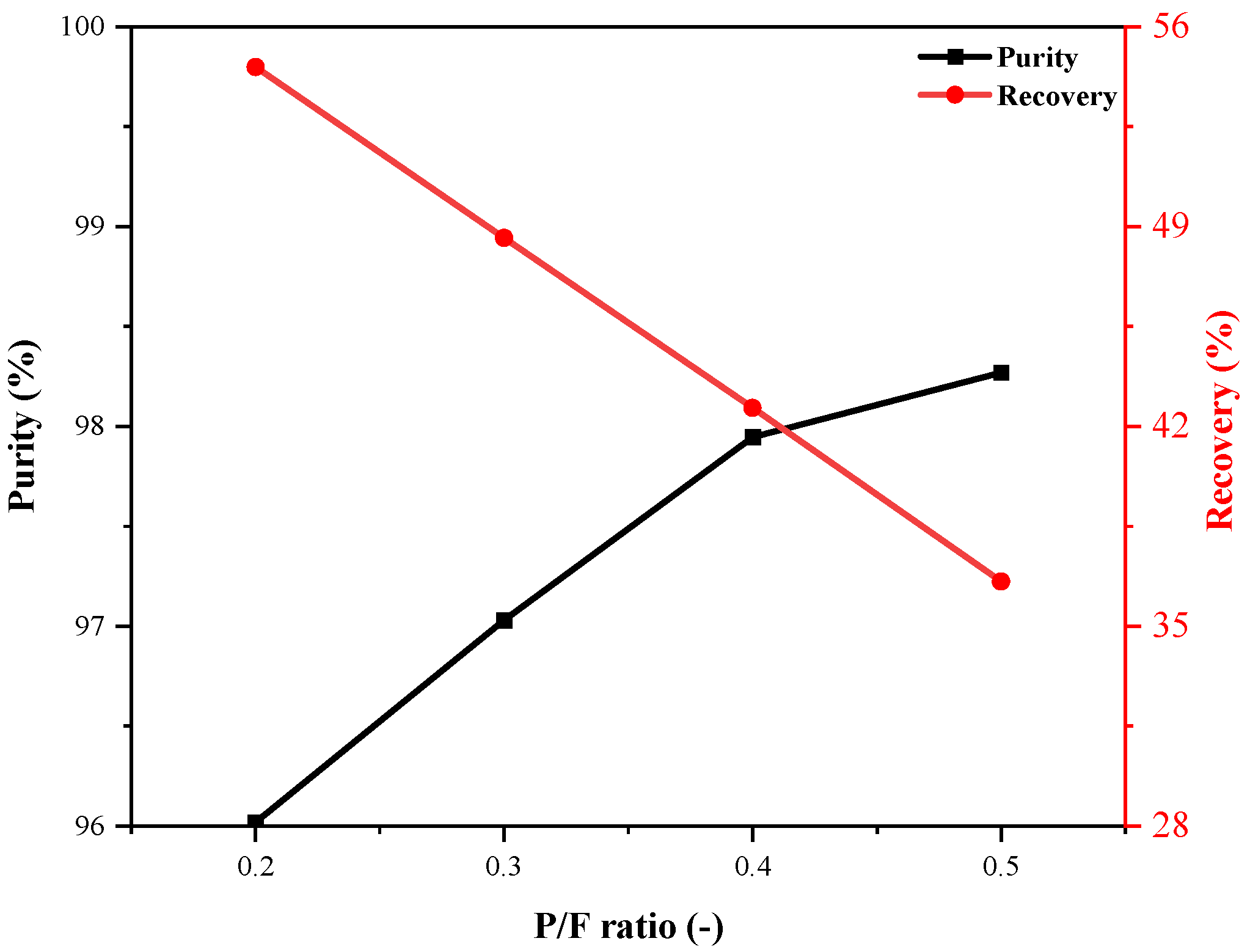
4.3.4. Effect of P/F Ratio
4.3.5. Effect of AC/Zeolite 13X Ratio
5. Conclusions
- (1)
- Increasing the feed pressure and decreasing the feed flow rate delay the breakthrough of impurity gases in the adsorption bed. A higher pressure enhances impurity gas adsorption and improves purity but reduces recovery due to greater feed gas consumption. A higher feed flow rate boosts recovery by processing more gas but reduces purity due to insufficient gas–adsorbent contact.
- (2)
- Extending the AD time improves recovery but may lead to early adsorbent saturation and reduced purity. A higher P/F ratio increases hydrogen usage during the purge step, enhancing purity but lowering recovery.
- (3)
- The performance of a layered bed is superior compared with that of an AC or zeolite 13X single-layer bed. Within a certain range, increasing the proportion of zeolite 13X on the layered bed can enhance the dynamic separation of impurity gases across the entire adsorption bed, further improving the overall purification performance. The highest purity of 97.38% and highest recovery of 49.13% occur at AC/zeolite 13X ratios of 5:5 and 3:7, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Coal-derived activated carbon |
| AD | Adsorption |
| BD | Blowdown |
| CNG | Compressed natural gas |
| DPE | Depressurizing pressure equalization |
| DSL | Dual-site Langmuir |
| FP | Feed pressurization |
| LDF | Linear driving force |
| LSTP/min | Liter per minute at standard state (273.15 K and 101.3 kPa) |
| P/F | Purge/feed |
| PG | Purge |
| PPE | Pressurizing pressure equalization |
| PSA | Pressure swing adsorption |
| TD DSL | Temperature-dependent dual-site Langmuir |
| VPSA | Vacuum pressure swing adsorption |
References
- Fan, Z.; Weng, W.; Zhou, J.; Gu, D.; Xiao, W. Catalytic decomposition of methane to produce hydrogen: A review. J. Energy Chem. 2021, 58, 415–430. [Google Scholar] [CrossRef]
- Guo, R.; Li, L.; Chang, C.; Di, Z. Steel slag-enhanced reforming process for blue hydrogen production from coke oven gas: Techno-economic evaluation. J. Clean. Prod. 2022, 379, 134778. [Google Scholar] [CrossRef]
- Okere, C.J.; Sheng, J.J. Review on clean hydrogen generation from petroleum reservoirs: Fundamentals, mechanisms, and field applications. Int. J. Hydrogen Energy 2023, 48, 38188–38222. [Google Scholar] [CrossRef]
- Zhang, X.; Bao, C.; Zhou, F.; Lai, N.-C. Modeling study on a two-stage hydrogen purification process of pressure swing adsorption and carbon monoxide selective methanation for proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2023, 48, 25171–25184. [Google Scholar] [CrossRef]
- Shi, X.; Song, W.; Wei, T.; Zhang, K.; Shao, Z. Improved CO tolerance of Pt nanoparticles on polyaniline-modified carbon for PEMFC anode. Fuel 2025, 382, 133239. [Google Scholar] [CrossRef]
- Wang, J.; Chen, X.; Du, T.; Liu, L.; Webley, P.A.; Kevin Li, G. Hydrogen production from low pressure coke oven gas by vacuum pressure swing adsorption. Chem. Eng. J. 2023, 472, 144920. [Google Scholar] [CrossRef]
- Xiao, J.; Mei, A.; Tao, W.; Ma, S.; Bénard, P.; Chahine, R. Hydrogen purification performance optimization of vacuum pressure swing adsorption on different activated carbons. Energies 2021, 14, 2450. [Google Scholar] [CrossRef]
- Zhu, X.; Shi, Y.; Li, S.; Cai, N. Two-train elevated-temperature pressure swing adsorption for high-purity hydrogen production. Appl. Energy 2018, 229, 1061–1071. [Google Scholar] [CrossRef]
- Zhu, X.; Shi, Y.; Li, S.; Cai, N. Elevated temperature pressure swing adsorption process for reactive separation of CO/CO2 in H2-rich gas. Int. J. Hydrogen Energy 2018, 43, 13305–13317. [Google Scholar] [CrossRef]
- Zafanelli, L.F.A.S.; Aly, E.; Henrique, A.; Rodrigues, A.E.; Mouchaham, G.; Silva, J.A.C. Green hydrogen recovery from natural gas grids by vacuum pressure swing adsorption. Ind. Eng. Chem. Res. 2024, 63, 6333–6346. [Google Scholar] [CrossRef]
- Vo, N.D.; Oh, D.H.; Kang, J.-H.; Oh, M.; Lee, C.-H. Dynamic-model-based artificial neural network for H2 recovery and CO2 capture from hydrogen tail gas. Appl. Energy 2020, 273, 115263. [Google Scholar] [CrossRef]
- Mihaylov, M.; Ivanova, E.; Zdravkova, V.; Andonova, S.; Drenchev, N.; Chakarova, K.; Kefirov, R.; Kukeva, R.; Stoyanova, R.; Hadjiivanov, K. Purification of hydrogen from CO with Cu/ZSM-5 adsorbents. Molecules 2021, 27, 96. [Google Scholar] [CrossRef] [PubMed]
- Baamran, K.; Al-Naddaf, Q.; Lawson, S.; Ali Rownaghi, A.; Rezaei, F. Kinetic process assessment of H2 purification over highly porous carbon sorbents under multicomponent feed conditions. Sep. Purif. Technol. 2023, 306, 122695. [Google Scholar] [CrossRef]
- Yang, T.; Zhan, C.; Fang, L.; Bénard, P.; Chahine, R.; Xiao, J. Improvement of temperature profiles using variable heat of adsorption in modeling H2/CO2 breakthrough experiments. Int. J. Energy Res. 2022, 46, 15099–15115. [Google Scholar] [CrossRef]
- Xiao, J.; Fang, L.; Bénard, P.; Chahine, R. Parametric study of pressure swing adsorption cycle for hydrogen purification using Cu-BTC. Int. J. Hydrogen Energy 2018, 43, 13962–13974. [Google Scholar] [CrossRef]
- Dehdari, L.; Xiao, P.; Gang Li, K.; Singh, R.; Webley, P.A. Separation of hydrogen from methane by vacuum swing adsorption. Chem. Eng. J. 2022, 450, 137911. [Google Scholar] [CrossRef]
- Brea, P.; Delgado, J.A.; Águeda, V.I.; Gutiérrez, P.; Uguina, M.A. Multicomponent adsorption of H2, CH4, CO and CO2 in zeolites NaX, CaX and MgX. Evaluation of performance in PSA cycles for hydrogen purification. Microporous Mesoporous Mater. 2019, 286, 187–198. [Google Scholar] [CrossRef]
- Silva, B.; Solomon, I.; Ribeiro, A.M.; Lee, U.H.; Hwang, Y.K.; Chang, J.-S.; Loureiro, J.M.; Rodrigues, A.E. H2 purification by pressure swing adsorption using CuBTC. Sep. Purif. Technol. 2013, 118, 744–756. [Google Scholar] [CrossRef]
- Delgado, J.A.; Agueda, V.I.; Uguina, M.A.; Sotelo, J.L.; Brea, P. Hydrogen recovery from off-gases with nitrogen-rich impurity by pressure swing adsorption using CaX and 5A zeolites. Adsorption 2015, 21, 107–123. [Google Scholar] [CrossRef]
- Divekar, S.; Arya, A.; Hanif, A.; Chauhan, R.; Gupta, P.; Nanoti, A.; Dasgupta, S. Recovery of hydrogen and carbon dioxide from hydrogen PSA tail gas by vacuum swing adsorption. Sep. Purif. Technol. 2021, 254, 117113. [Google Scholar] [CrossRef]
- Hong, S.-H.; Jung, M.Y.; Lee, C.-H. Performance and dynamic behavior of H2 layered-bed PSA processes using various activated carbons and zeolite LiX for steam methane reforming gas. Chem. Eng. J. 2023, 473, 144942. [Google Scholar] [CrossRef]
- Zhang, N.; Bénard, P.; Chahine, R.; Yang, T.; Xiao, J. Optimization of pressure swing adsorption for hydrogen purification based on Box-Behnken design method. Int. J. Hydrogen Energy 2021, 46, 5403–5417. [Google Scholar] [CrossRef]
- Moon, D.-K.; Park, Y.; Oh, H.-T.; Kim, S.-H.; Oh, M.; Lee, C.-H. Performance analysis of an eight-layered bed PSA process for H2 recovery from IGCC with pre-combustion carbon capture. Energy Convers. Manag. 2018, 156, 202–214. [Google Scholar] [CrossRef]
- Li, C.; Yuan, C.; Yang, T.; Luo, H.; Chahine, R.; Tong, L.; Yuan, Y.; Xiao, J. Breakthrough curves of H2/CO2 adsorptions on CuBTC and MIL-125(Ti)_NH2 predicted by empirical correlations and deep neural networks. Sep. Purif. Technol. 2025, 354, 129450. [Google Scholar] [CrossRef]
- Jamali, S.; Mofarahi, M.; Rahideh, H.; Lee, C.-H. Cu-BTC adsorbent for H2 purification: A study on adsorption kinetics and PSA performance. Sep. Purif. Technol. 2025, 360, 131095. [Google Scholar] [CrossRef]
- Park, Y.; Ju, Y.; Park, D.; Lee, C.-H. Adsorption equilibria and kinetics of six pure gases on pelletized zeolite 13X up to 1.0 MPa: CO2, CO, N2, CH4, Ar and H2. Chem. Eng. J. 2016, 292, 348–365. [Google Scholar] [CrossRef]
- Park, Y.; Moon, D.-K.; Kim, Y.-H.; Ahn, H.; Lee, C.-H. Adsorption isotherms of CO2, CO, N2, CH4, Ar and H2 on activated carbon and zeolite LiX up to 1.0 MPa. Adsorption 2014, 20, 631–647. [Google Scholar] [CrossRef]
- Park, Y.; Kang, J.-H.; Moon, D.-K.; Jo, Y.S.; Lee, C.-H. Parallel and series multi-bed pressure swing adsorption processes for H2 recovery from a lean hydrogen mixture. Chem. Eng. J. 2021, 408, 127299. [Google Scholar] [CrossRef]
- Zafanelli, L.F.; Aly, E.; Henrique, A.; Rodrigues, A.E.; Silva, J.A. Dual-stage vacuum pressure swing adsorption for green hydrogen recovery from natural gas grids. Sep. Purif. Technol. 2025, 360, 130869. [Google Scholar] [CrossRef]






| Adsorbate | CO2 | N2 | H2 | CO |
|---|---|---|---|---|
| AC | ||||
| [s−1] | 0.050 | 0.220 | 0.900 | 0.350 |
| [mol/kg] | 6.611 | 8.755 | 248.5 | 4.65 |
| [kPa−1] | 1.04 × 10−7 | 8.75 × 10−7 | 1.38 × 10−7 | 3.27 × 10−6 |
| [K] | 3306 | 1777 | 765 | 1720 |
| [mol/kg] | 0.011 | 0.121 | 0.017 | 0.099 |
| [kPa−1] | 7.76 × 10−7 | 2.74 × 10−6 | 1.06 × 10−11 | 2.24 × 10−7 |
| [K] | 3300 | 2805 | 7010 | 3390 |
| [kJ/mol] | −22.5 | −14.0 | −12.0 | −15.0 |
| Zeolite 13X | ||||
| [s−1] | 0.120 | 0.650 | 0.900 | 0.750 |
| [mol/kg] | 3.395 | 2.761 | 3.101 | 2.708 |
| [kPa−1] | 1.80 × 10−5 | 1.18 × 10−6 | 6.64 × 10−7 | 2.66 × 10−7 |
| [K] | 2964 | 1955 | 1294 | 2502 |
| [mol/kg] | 2.305 | 0.547 | 1.118 | 1.165 |
| [kPa−1] | 6.30 × 10−9 | 7.33 × 10−8 | 3.82 × 10−5 | 3.92 × 10−7 |
| [K] | 4291 | 3064 | 52.41 | 3006 |
| [kJ/mol] | −32.2 | −18.0 | −8.00 | −21.0 |
| Adsorbent | AC | Zeolite 13X |
|---|---|---|
| [m] | 0.00085–0.0012 | 0.0010–0.0011 |
| [kg/m3] | 750 | 1050 |
| [kg/m3] | 558 | 751 |
| 0.256 | 0.284 | |
| 0.698 | 0.673 | |
| [J/kg/K] | 1570 | 1100 |
| Pore volume [cm3/g] | 0.46 | 0.39 |
| Total surface area [m2/g] | 1306.4 | 742.9 |
| Adsorption bed | ||
| [m] | 1.0 | |
| [m] | 0.021 | |
| [m] | 0.0022 | |
| [J/kg/K] | 502.8 | |
| [kg/m3] | 7830 | |
| [W/m/K] | 16 | |
| Step | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Bed1 | AD | DPE | BD | PG | PPE | FP |
| Bed2 | PG | PPE | FP | AD | DPE | BD |
| Time [s] | 40 | 10 | 25 | 40 | 10 | 25 |
| Run | Operating Condition | Bed Configuration | Performance | ||||
|---|---|---|---|---|---|---|---|
| Feed Pressure [Bar] | Feed Flow Rate [LSTP/min] | AD Time [s] | P/F Ratio | AC/Zeolite 13X | Purity [%] | Recovery [%] | |
| 1 | 10 | 3 | 40 | 0.3 | 6:4 | 97.03 | 48.60 |
| 2 | 8 | 3 | 40 | 0.3 | 6:4 | 96.93 | 50.72 |
| 3 | 12 | 3 | 40 | 0.3 | 6:4 | 97.36 | 46.29 |
| 4 | 14 | 3 | 40 | 0.3 | 6:4 | 97.98 | 43.79 |
| 5 | 10 | 2 | 40 | 0.3 | 6:4 | 98.59 | 35.52 |
| 6 | 10 | 4 | 40 | 0.3 | 6:4 | 94.25 | 57.46 |
| 7 | 10 | 5 | 40 | 0.3 | 6:4 | 89.56 | 60.40 |
| 8 | 10 | 3 | 30 | 0.3 | 6:4 | 98.09 | 40.87 |
| 9 | 10 | 3 | 50 | 0.3 | 6:4 | 96.20 | 54.14 |
| 10 | 10 | 3 | 60 | 0.3 | 6:4 | 95.95 | 56.69 |
| 11 | 10 | 3 | 40 | 0.2 | 6:4 | 96.02 | 54.58 |
| 12 | 10 | 3 | 40 | 0.4 | 6:4 | 97.95 | 42.64 |
| 13 | 10 | 3 | 40 | 0.5 | 6:4 | 98.27 | 36.57 |
| 14 | 10 | 3 | 40 | 0.3 | 10:0 | 86.28 | 47.38 |
| 15 | 10 | 3 | 40 | 0.3 | 0:10 | 95.07 | 48.30 |
| 16 | 10 | 3 | 40 | 0.3 | 5:5 | 97.38 | 48.79 |
| 17 | 10 | 3 | 40 | 0.3 | 3:7 | 97.19 | 49.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, T.; Yang, Z.; Li, C.; Tong, L.; Chen, B.; Li, X.; Yuan, Y.; Yuan, C.; Xiao, J. Hydrogen Purification Performance of Pressure Swing Adsorption in Coal-Derived Activated Carbon/Zeolite 13X Layered Bed. Appl. Sci. 2025, 15, 5505. https://doi.org/10.3390/app15105505
Yang T, Yang Z, Li C, Tong L, Chen B, Li X, Yuan Y, Yuan C, Xiao J. Hydrogen Purification Performance of Pressure Swing Adsorption in Coal-Derived Activated Carbon/Zeolite 13X Layered Bed. Applied Sciences. 2025; 15(10):5505. https://doi.org/10.3390/app15105505
Chicago/Turabian StyleYang, Tianqi, Ziyu Yang, Chenglong Li, Liang Tong, Ben Chen, Xuefang Li, Yupeng Yuan, Chengqing Yuan, and Jinsheng Xiao. 2025. "Hydrogen Purification Performance of Pressure Swing Adsorption in Coal-Derived Activated Carbon/Zeolite 13X Layered Bed" Applied Sciences 15, no. 10: 5505. https://doi.org/10.3390/app15105505
APA StyleYang, T., Yang, Z., Li, C., Tong, L., Chen, B., Li, X., Yuan, Y., Yuan, C., & Xiao, J. (2025). Hydrogen Purification Performance of Pressure Swing Adsorption in Coal-Derived Activated Carbon/Zeolite 13X Layered Bed. Applied Sciences, 15(10), 5505. https://doi.org/10.3390/app15105505









