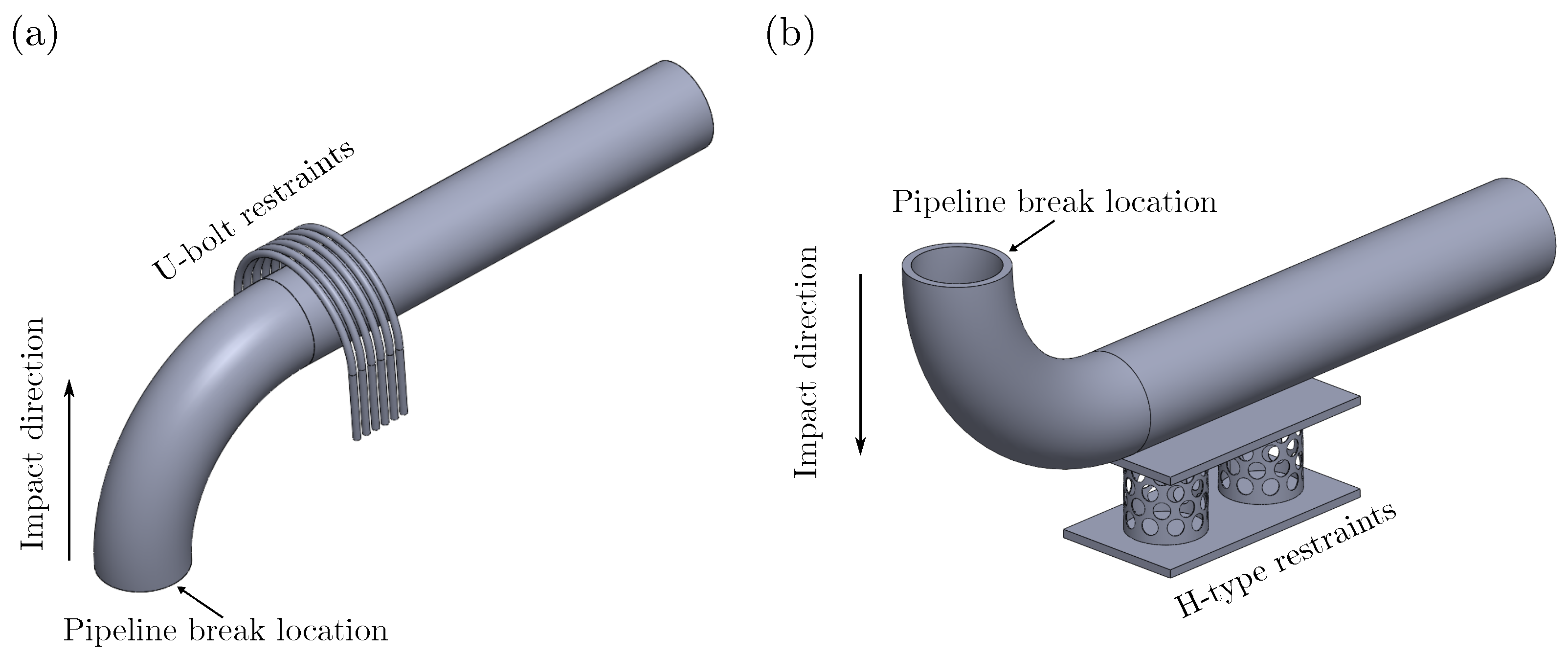
On the Design of Bionic Hierarchical H-Type Whip Restraints for Nuclear Power Plants
Abstract
1. Introduction
2. Materials and Method
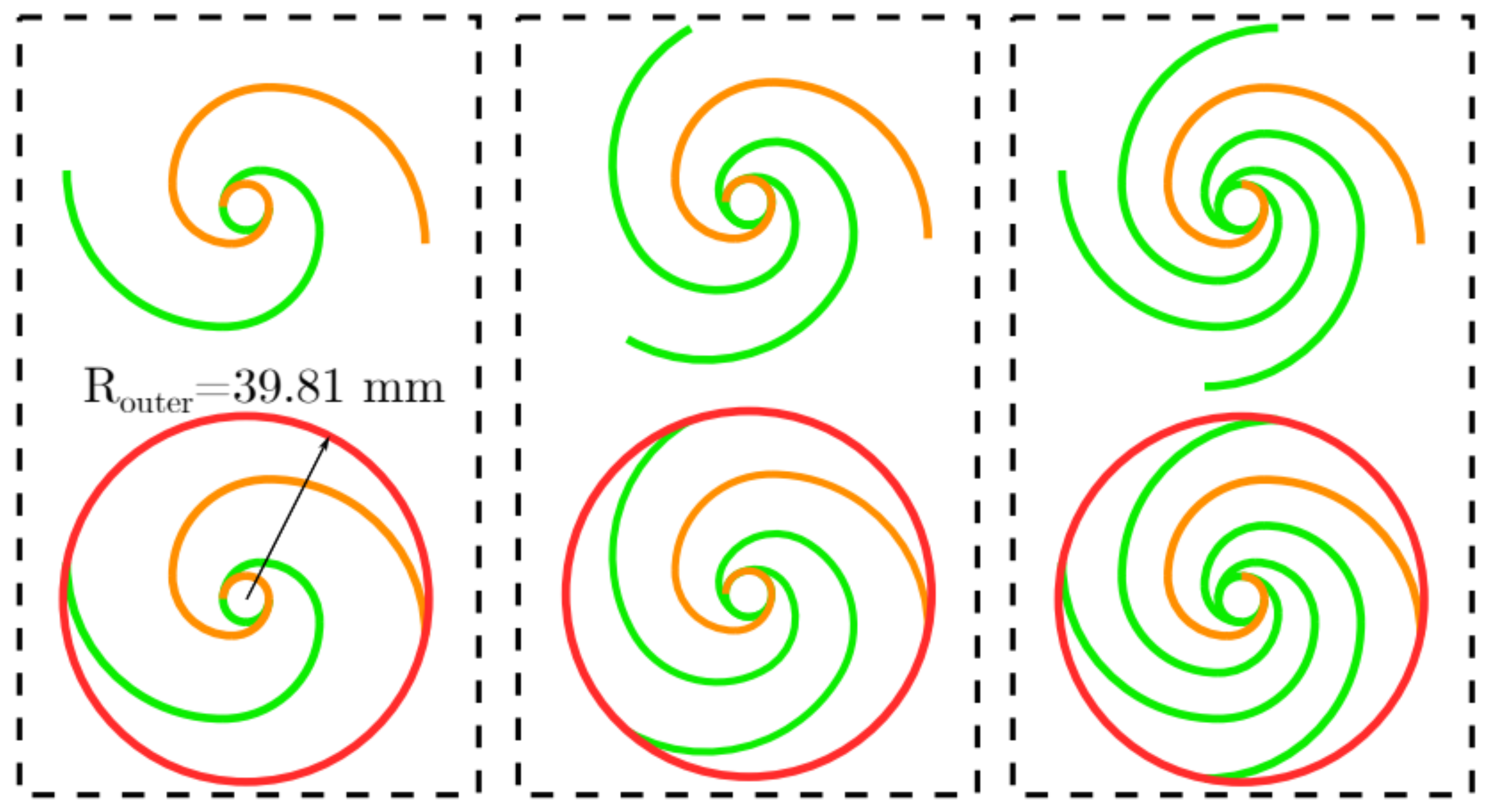
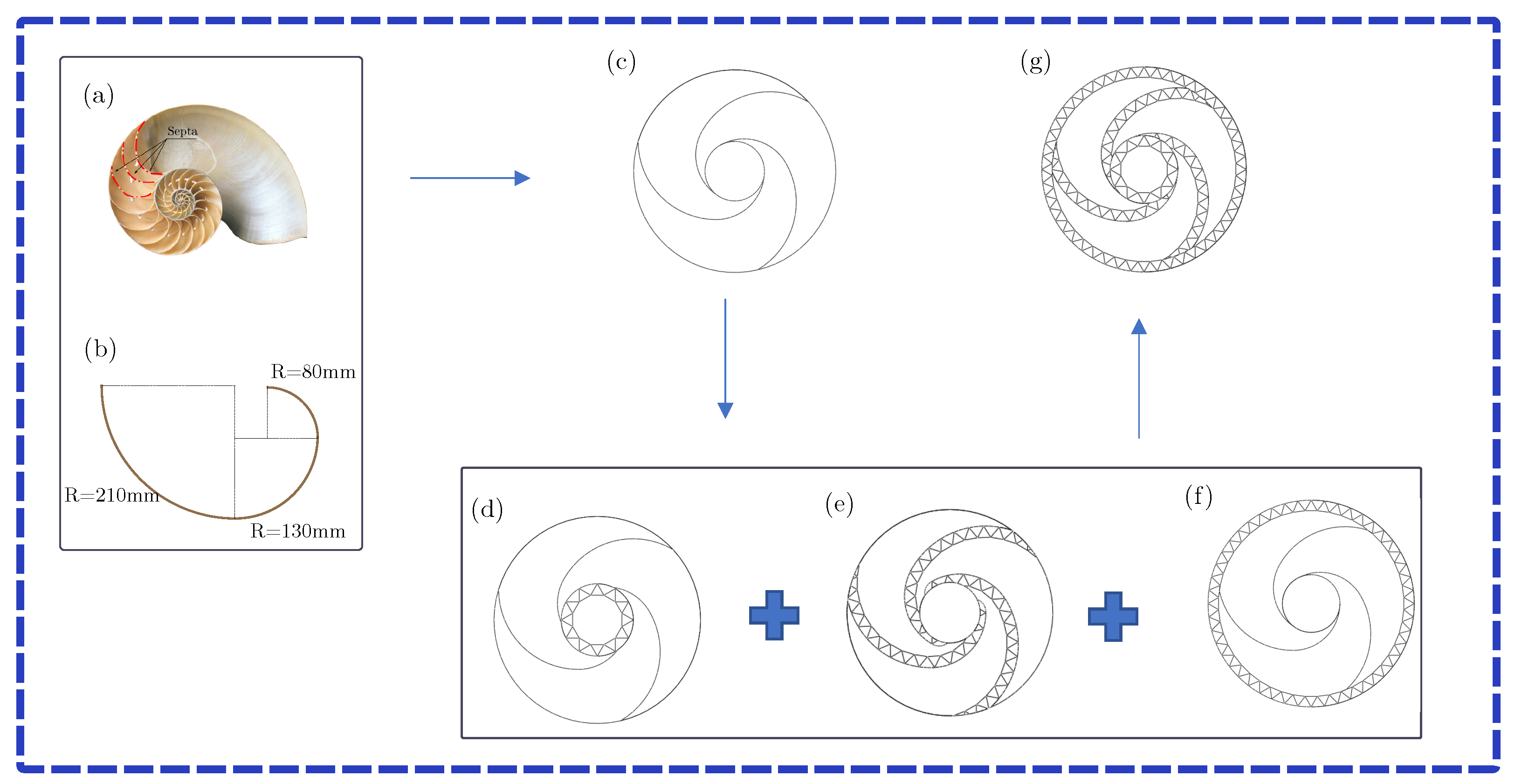
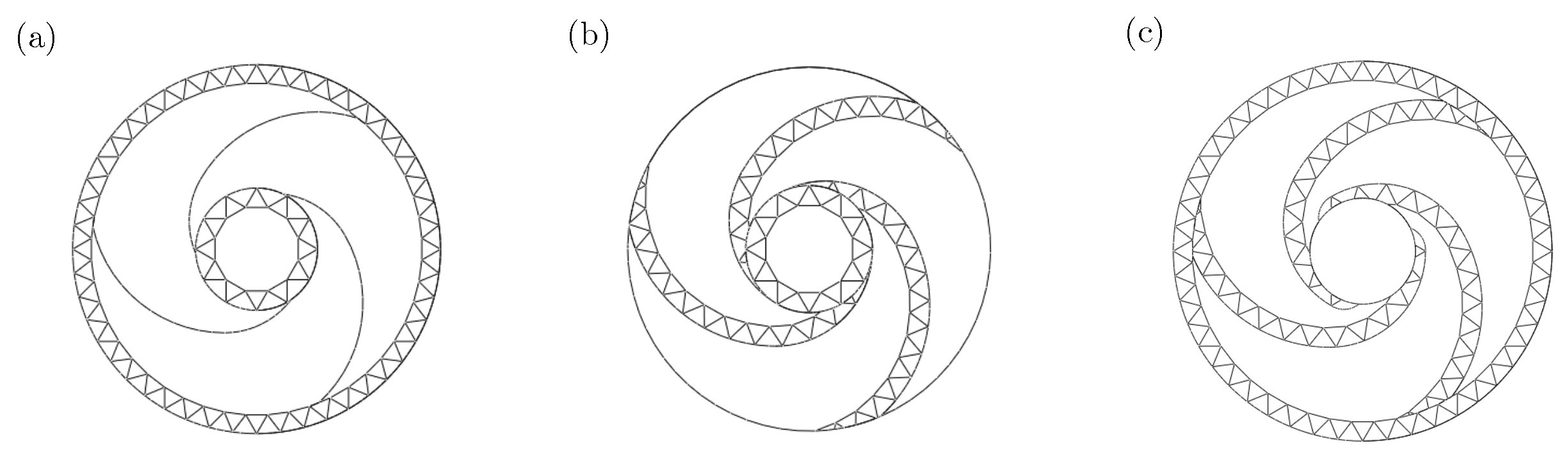
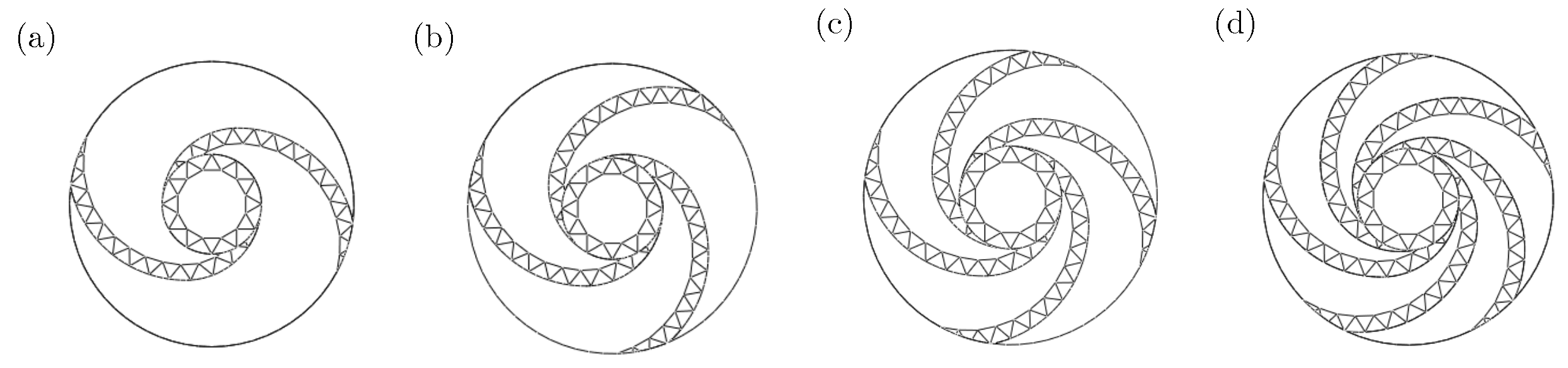
2.1. Bio-Inspired Nautilus Structure Design
2.2. Crashworthiness Evaluation Indicators
2.3. Finite Element Model Construction
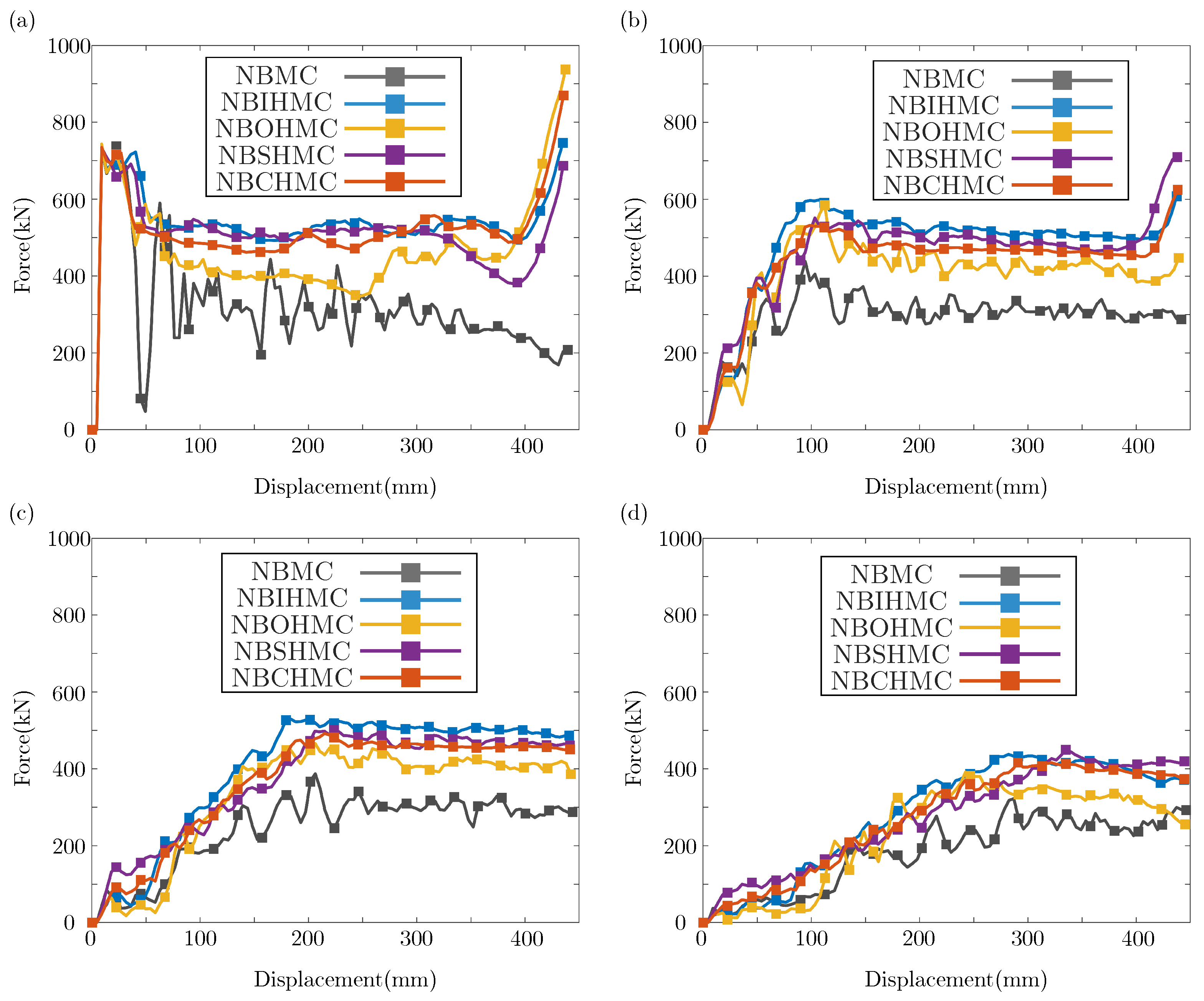
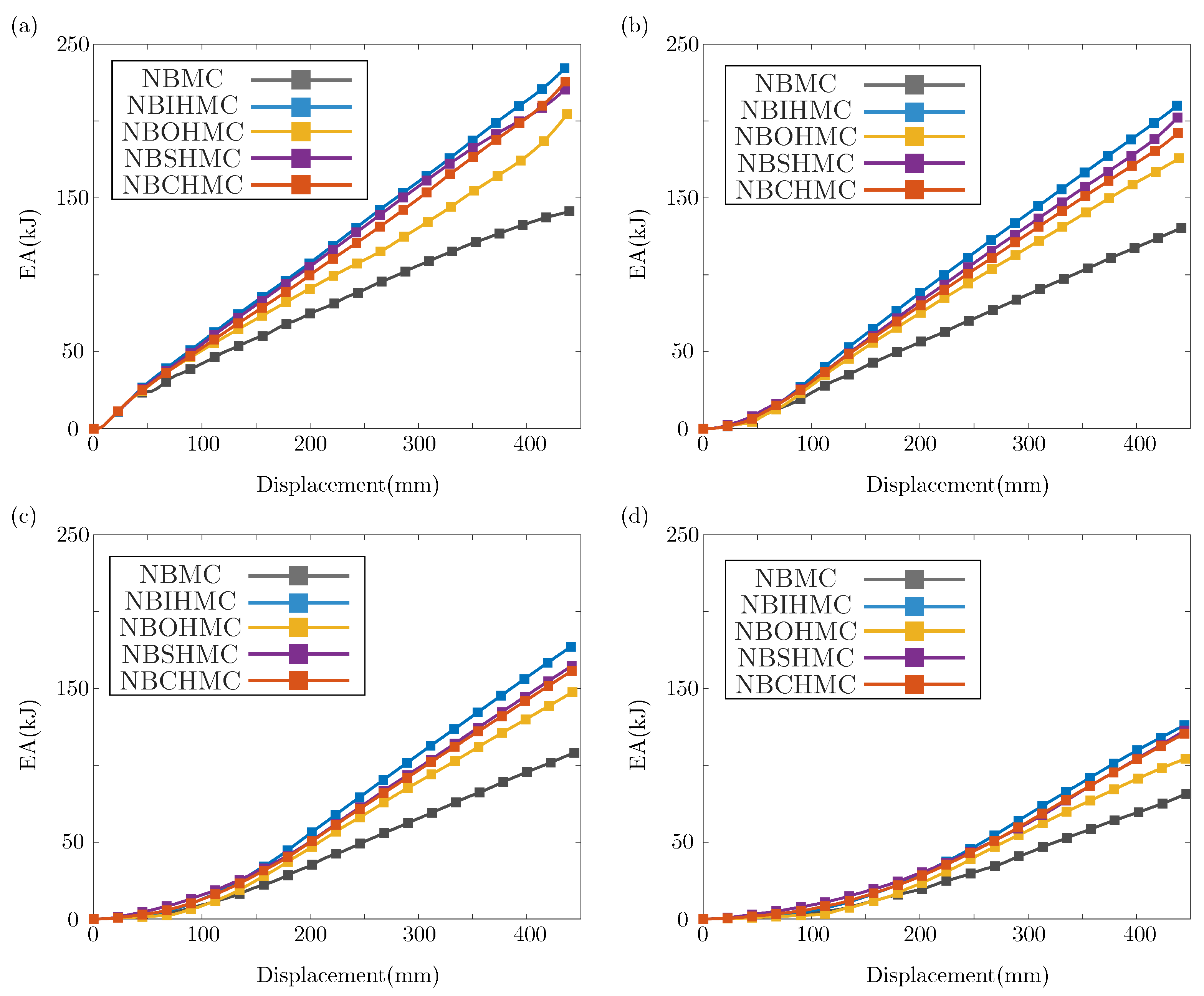
3. Crashworthiness Analysis
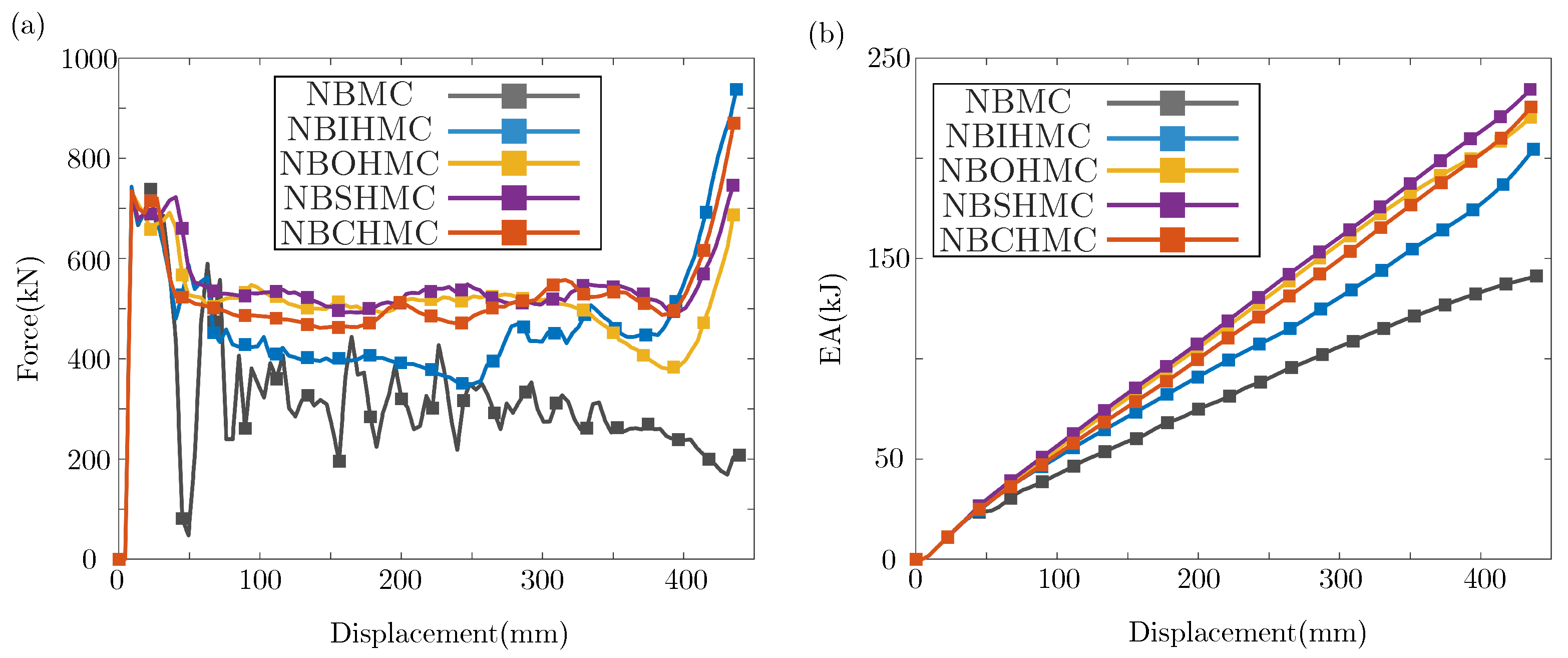
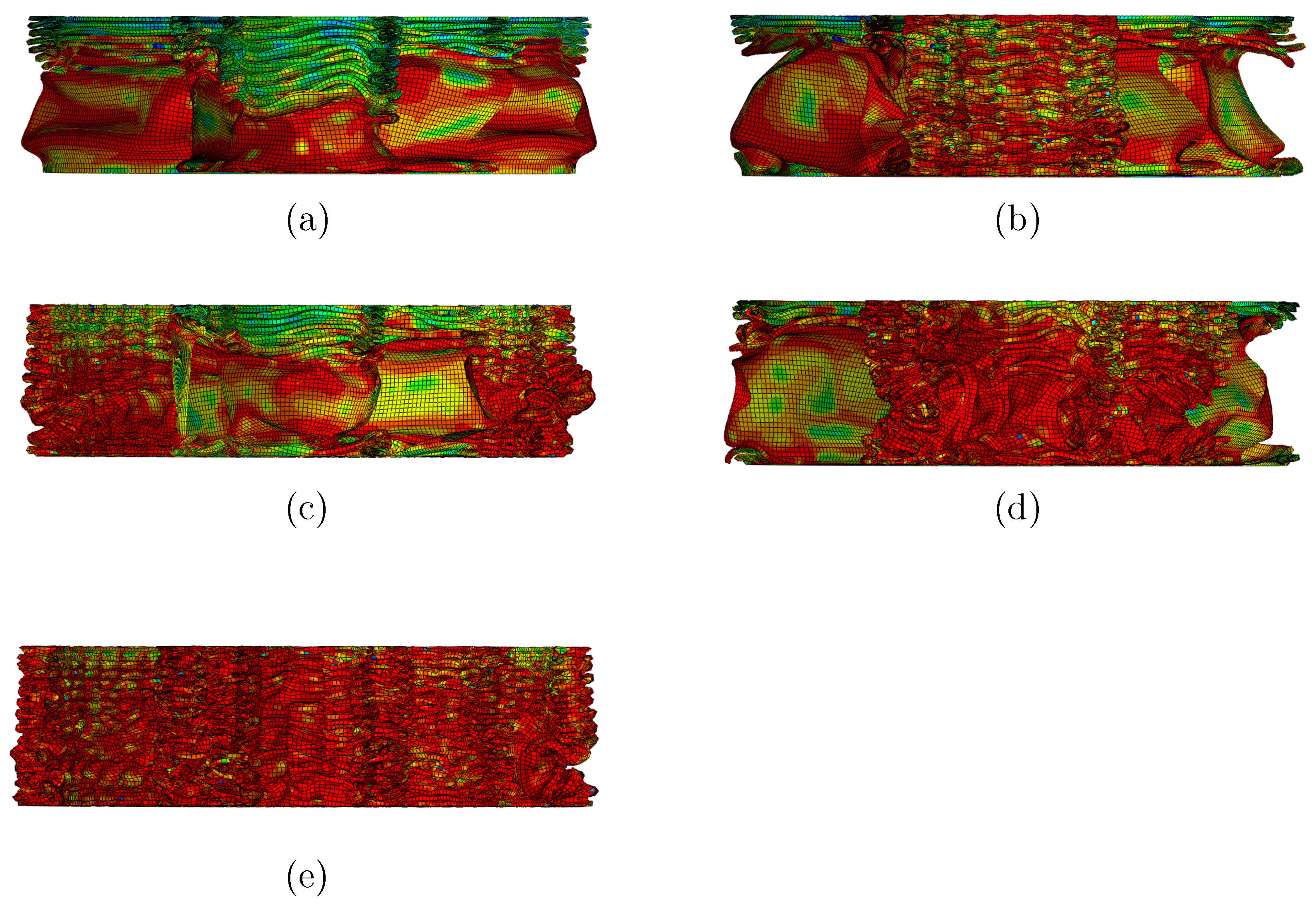
3.1. Crashworthiness Analysis Under Axial Impact
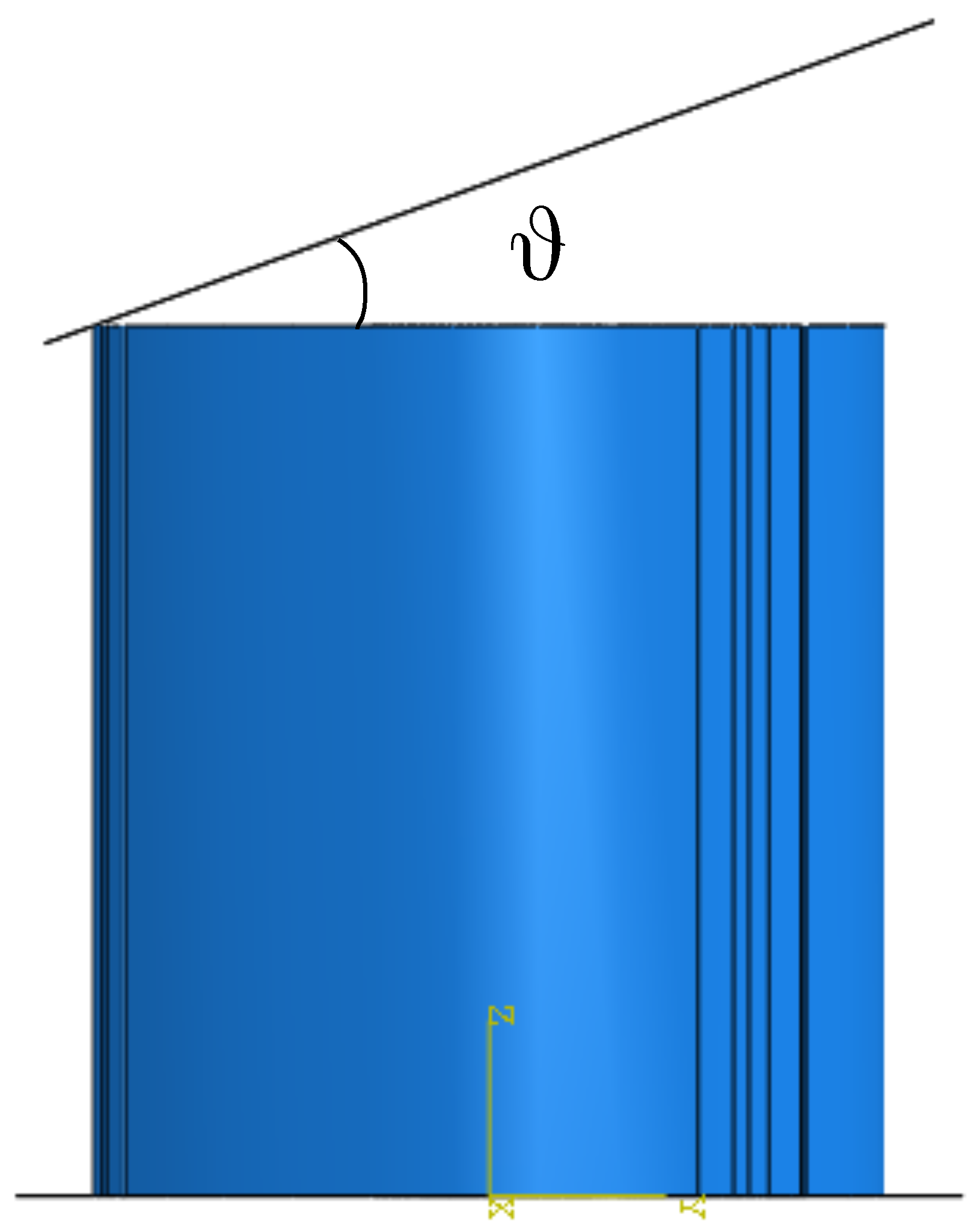
3.2. Crashworthiness Analysis Under Oblique Impact
4. Parametric Analysis
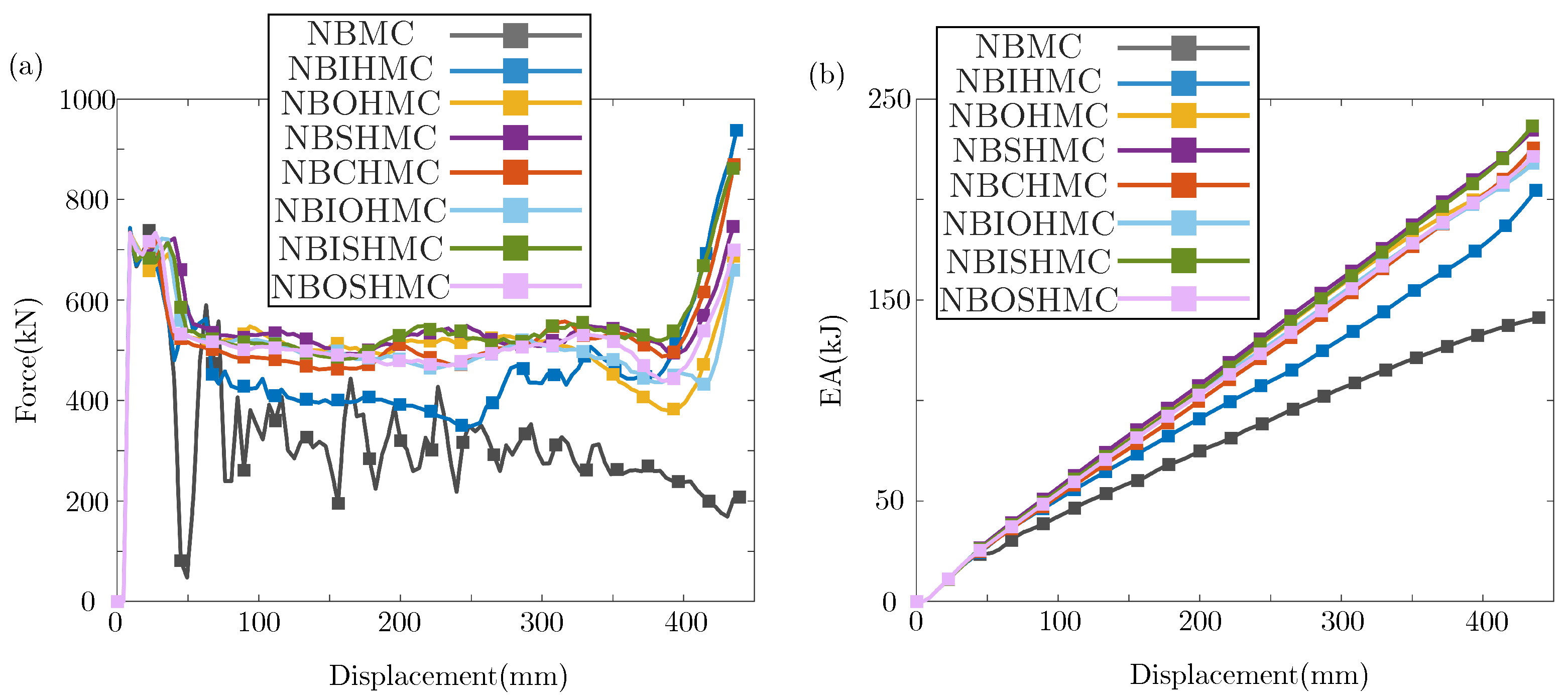
4.1. Effect of Hierarchical Portion Combination Mode
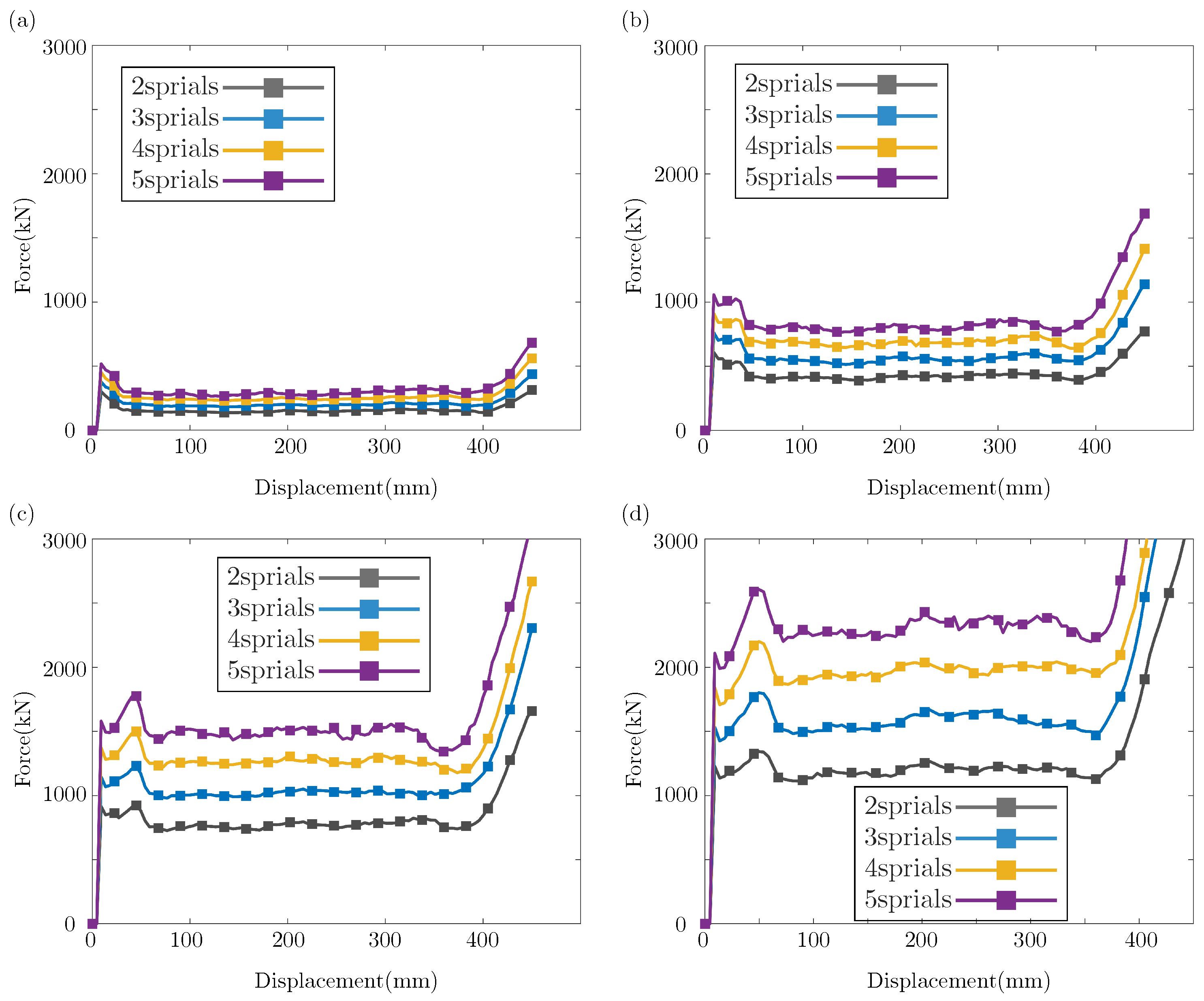
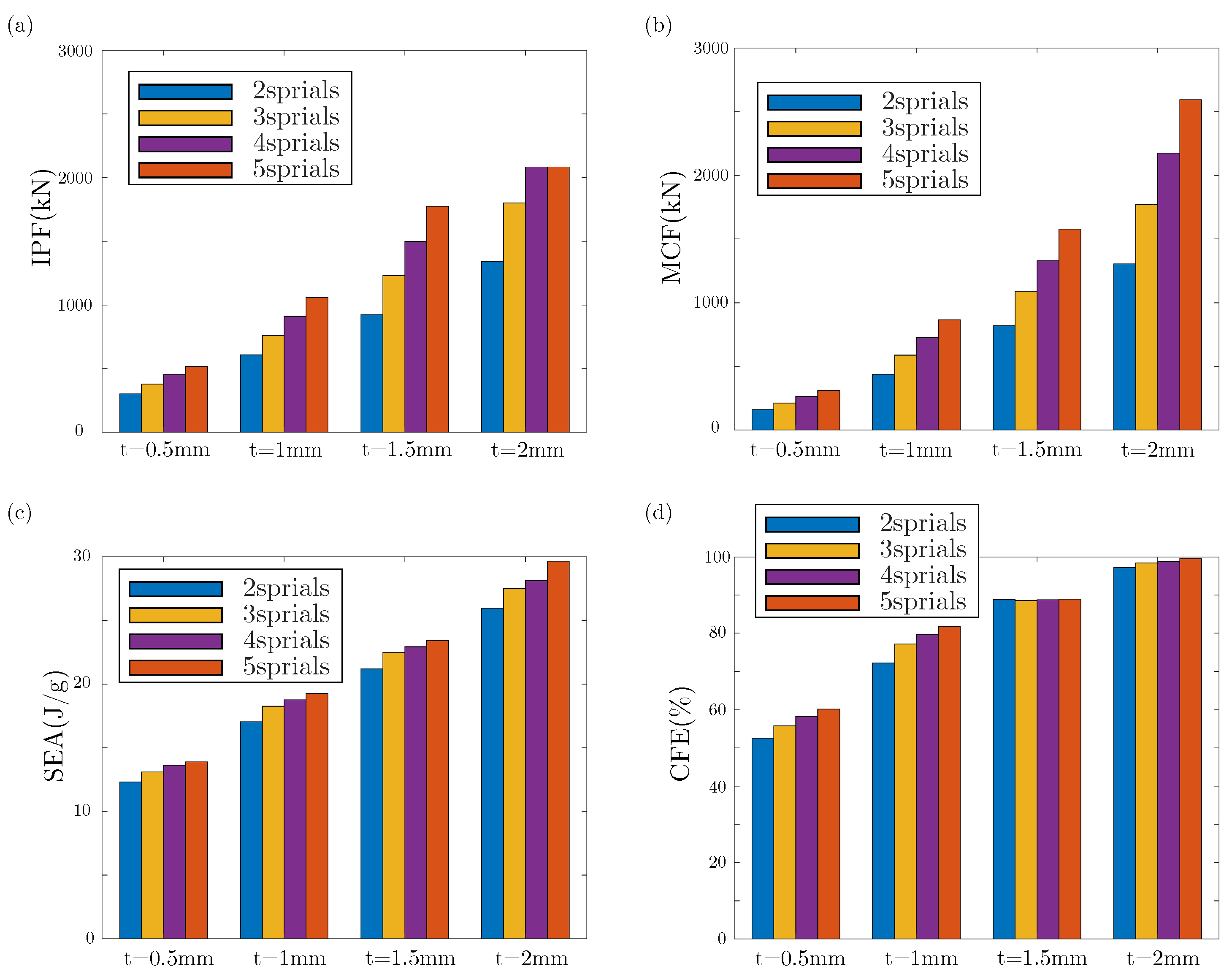
4.2. Effect of Hierarchical Level
4.3. Effect of Bionic Hierarchical Cross-Section Characteristics
5. Conclusions
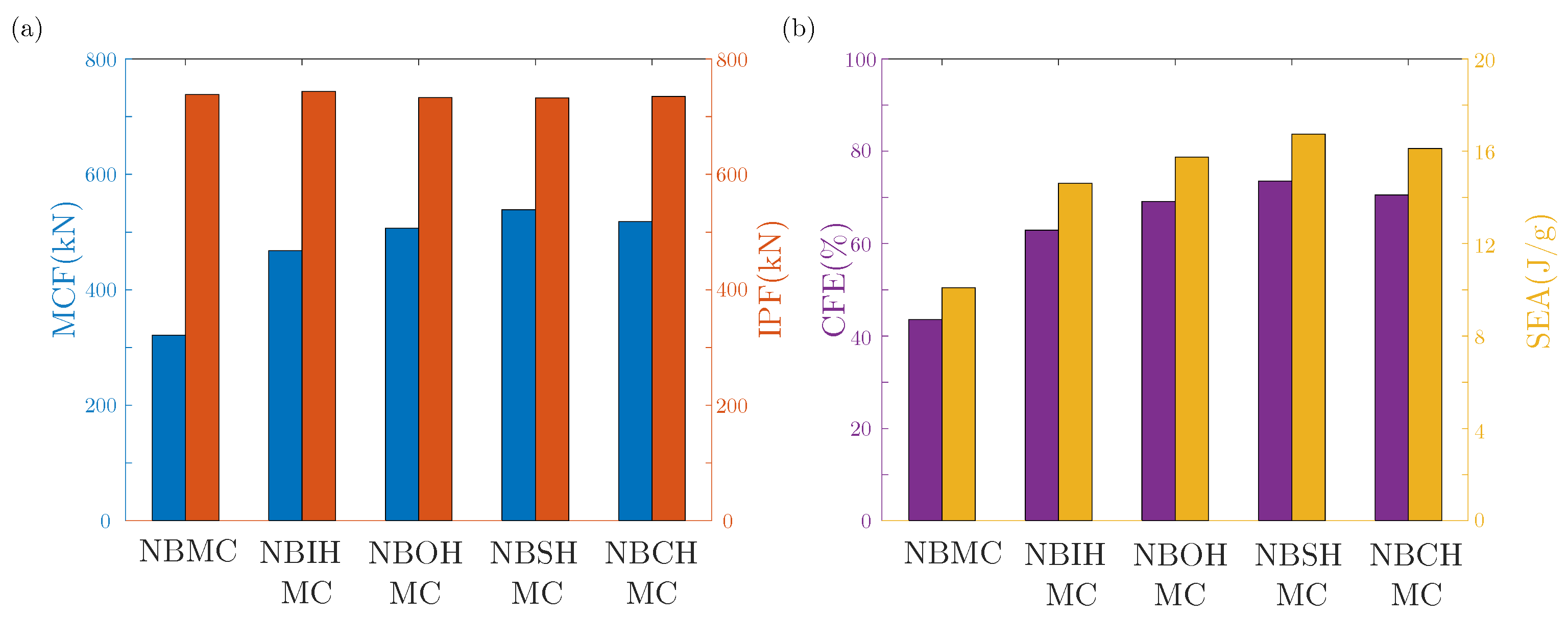
- Compared with hollow tubes and NBDHMCs, several NBDHMCs have shorter wavelengths and more folds under pressure, and exhibit better energy absorption capacity. Among them, NBSHMC exhibits the highest CFE of . Under the action of an oblique impact, the deformation mode of the structure changes and the energy absorption capacity decreases;
- Considering the hierarchical portion combination mode, three structural forms were added for comparison, and the optimal structure was finally confirmed as NBISHMC;
- Parametric investigation results indicate that with increase in S and t, the crashworthiness parameters of the thin-walled structures, such as SEA, MCF, CFE, and IPF, increased significantly. Therefore, in order to maintain high SEA and low IPF, it is necessary to choose a reasonable t and S;
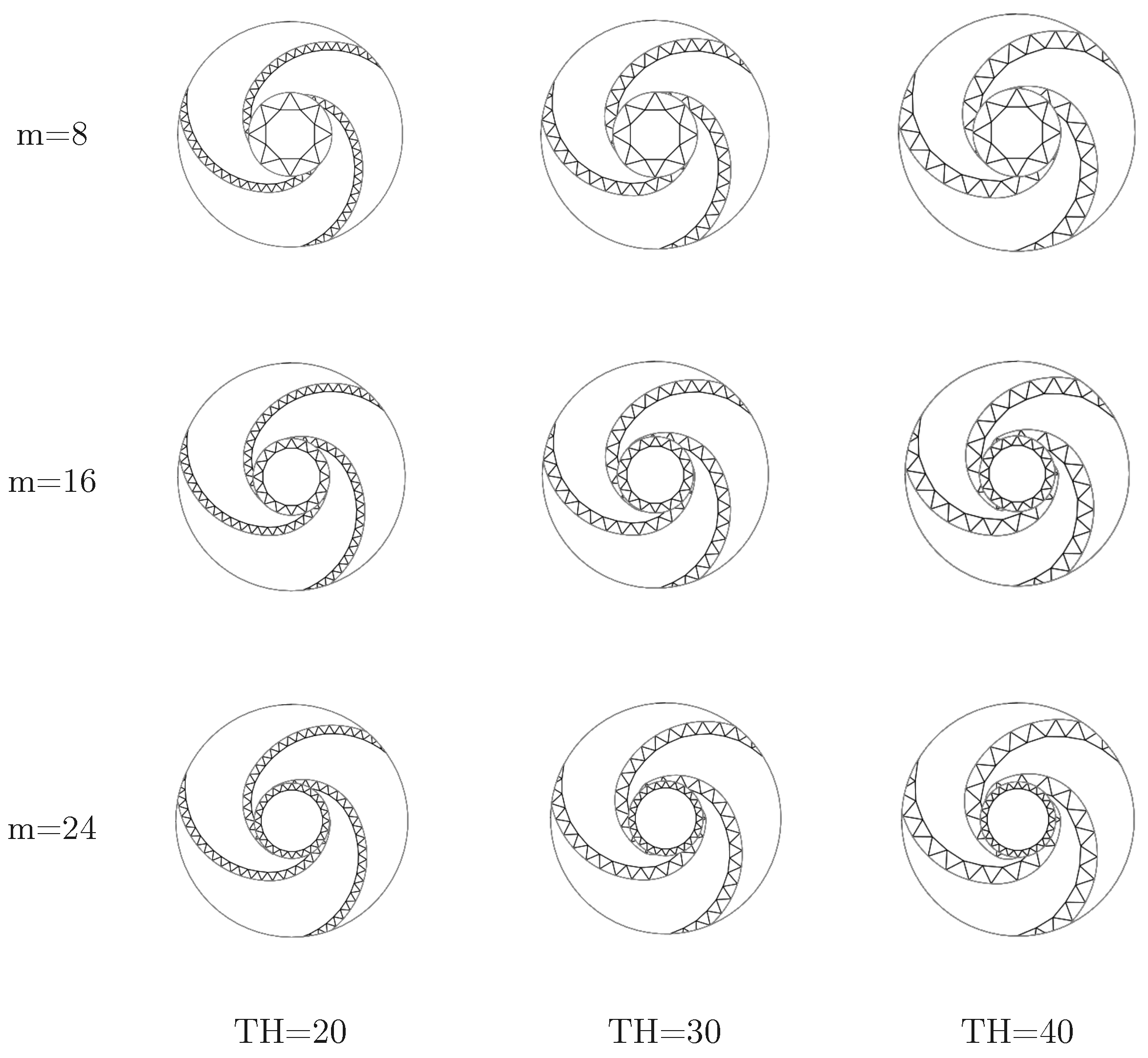
- By changing m and TH under the condition of equal wall thickness, it was found that when m increases and TH decreases, the four crashworthiness parameters are improved. However, an increase in TH leads to an increase in CFE when the m value reaches 24.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dundulis, G.; Uspuras, E.; Kulak, R.F.; Marchertas, A. Evaluation of pipe whip impacts on neighboring piping and walls of the Ignalina Nuclear Power Plant. Nucl. Eng. Des. 2007, 237, 848–857. [Google Scholar] [CrossRef]
- Pate, S.B.; Solomon, I.S.M.; Dundulis, G.; Griskevicius, P. Applications of the FEM to pipe whip analysis using coupled modelling technique. Nucl. Eng. Des. 2024, 418, 112941. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, J.; Wang, X.; Wu, S. Dynamic analysis of whipping behavior induced by the circumferential fracture of high energy pipes considering fluid-structure interaction effect. Int. J. Press. Vessels Pip. 2024, 212, 105336. [Google Scholar] [CrossRef]
- Hu, J.; Wang, X.; Li, Y.; Wen, X.; Wu, Y.; Huang, Y. Investigation of whipping effect on high energy pipe based on fluid-structure interaction method. Int. J. Impact Eng. 2023, 173, 104463. [Google Scholar] [CrossRef]
- Shi, L.; Lu, Y.; Peng, L.; Qiao, J.; Zhang, R.; Sun, T. Antiwhip Measures for High-Energy Piping in Nuclear Power Plants Using Lead Extrusion Impact Damping Devices: Tests and Simulations. Struct. Control Health Monit. 2025, 2025, 8829452. [Google Scholar] [CrossRef]
- Luo, X.; Wang, S.; Wang, J.; Wang, P.; Wang, Y.; Zhao, W. Analysis of whipping effect on high energy pipe in a nuclear power plant. Fusion Eng. Des. 2020, 150, 111359. [Google Scholar] [CrossRef]
- Zhang, X.; Cao, F.; Ding, Y.; Wang, J.; Fang, J. Load analysis of hypothetical ruptures and optimum design of H-type anti-whip restraint devices for high energy pipes based on bilinearity method. Nucl. Power Eng. 2011, 32, 64–68. [Google Scholar]
- Olabi, A.G.; Morris, E.; Hashmi, M. Metallic tube type energy absorbers: A synopsis. Thin-Walled Struct. 2007, 45, 706–726. [Google Scholar] [CrossRef]
- Xing, J.; Xu, P.; Yao, S.; Zhao, H.; Zhao, Z.; Wang, Z. Study on the layout strategy of diaphragms to enhance the energy absorption of thin-walled square tubes. Structures 2021, 29, 294–304. [Google Scholar] [CrossRef]
- Xie, S.; Chen, P.; Wang, N.; Wang, J.; Du, X. Crashworthiness study of circular tubes subjected to radial extrusion under quasi-static loading. Int. J. Mech. Sci. 2021, 192, 106128. [Google Scholar] [CrossRef]
- Liu, J.; Chen, W.; Hao, H.; Wang, Z. In-plane crushing behaviors of hexagonal honeycombs with different Poisson’s ratio induced by topological diversity. Thin-Walled Struct. 2021, 159, 107223. [Google Scholar] [CrossRef]
- Sun, D.; Zhang, W. Energy absorption performance of staggered triangular honeycombs under in-plane crushing loadings. J. Eng. Mech. 2013, 139, 153–166. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X. Crashworthiness performance of conical tubes with nonlinear thickness distribution. Thin-Walled Struct. 2016, 99, 35–44. [Google Scholar] [CrossRef]
- Li, X.; Yin, Y.; Zhu, X.; Wang, R.; Li, T.; Zhang, Q.; Li, W. Performance of hollow and aluminum foam-filled multi-cell thin-walled aluminum alloy tubes (6063-T5) under axial impact. Structures 2023, 47, 1803–1821. [Google Scholar] [CrossRef]
- Mozafari, H.; Khatami, S.; Molatefi, H.; Crupi, V.; Epasto, G.; Guglielmino, E. Finite element analysis of foam-filled honeycomb structures under impact loading and crashworthiness design. Int. J. Crashworthiness 2016, 21, 148–160. [Google Scholar] [CrossRef]
- Li, Q.; Jia, X.; Ye, X.; Tan, H.; Wang, F.; Hu, L. Axial compression property of a novel dendritic lattice structure. Mater. Today Commun. 2025, 46, 112668. [Google Scholar] [CrossRef]
- Zhang, Y.; Ge, P.; Lu, M.; Lai, X. Crashworthiness study for multi-cell composite filling structures. Int. J. Crashworthiness 2018, 23, 32–46. [Google Scholar] [CrossRef]
- Latifzadeh, F.; Keshavarzi, A.; Saeidi Googarchin, H. Crashworthiness of adhesively bonded bio-inspired AL/CFRP hybrid tubes under lateral loading. In Mechanics of Advanced Materials and Structures; Taylor: Abingdon, UK, 2025; pp. 1–18. [Google Scholar]
- Wei, Y.; Yang, Z.; Yan, H.; Guo, Y.; Wu, X.; Huang, C. Proactive regulation of axial crushing behavior of thin-walled circular tube by gradient grooves. Int. J. Mech. Sci. 2016, 108, 49–60. [Google Scholar] [CrossRef]
- Wang, H.; Fu, Y.; Su, M.; Hao, H. Effect of structure design on compressive properties and energy absorption behavior of ordered porous aluminum prepared by rapid casting. Mater. Des. 2019, 167, 107631. [Google Scholar] [CrossRef]
- Deng, X.; Qin, S.; Huang, J. Multiobjective optimization of axially varying thickness lateral corrugated tubes for energy absorption. Mech. Adv. Mater. Struct. 2022, 29, 4259–4272. [Google Scholar] [CrossRef]
- Gong, C.; Bai, Z.; Wang, Y.; Zhang, L. On the crashworthiness performance of novel hierarchical multi-cell tubes under axial loading. Int. J. Mech. Sci. 2021, 206, 106599. [Google Scholar] [CrossRef]
- San Ha, N.; Pham, T.M.; Hao, H.; Lu, G. Energy absorption characteristics of bio-inspired hierarchical multi-cell square tubes under axial crushing. Int. J. Mech. Sci. 2021, 201, 106464. [Google Scholar]
- Li, Z.; Ma, W.; Yao, S.; Xu, P. Crashworthiness performance of corrugation-reinforced multicell tubular structures. Int. J. Mech. Sci. 2021, 190, 106038. [Google Scholar] [CrossRef]
- Teng, L.; Deng, Q.; Li, X. Energy absorption and deformation modes of several thin-walled tubes under dynamic compression. Structures 2023, 54, 890–897. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H. Some problems on the axial crushing of multi-cells. Int. J. Mech. Sci. 2015, 103, 30–39. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, Y.; Chen, X.; Liu, Z.; Xu, Y.; Gao, Y. Crushing behaviors of hierarchical sandwich-walled columns. Int. J. Mech. Sci. 2019, 161, 105021. [Google Scholar] [CrossRef]
- Qin, R.; Wang, X.; Gao, F.; Chen, B. Energy absorption performance of hexagonal multi-cell tube with hierarchy under axial loading. Thin-Walled Struct. 2021, 169, 108392. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Shi, C.; Zhou, W. Mechanical performance of vertex-based hierarchical vs square thin-walled multi-cell structure. Thin-Walled Struct. 2019, 134, 102–110. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, T.; Xu, X.; Hu, Z. Out-of-plane mechanical behaviors of a side hierarchical honeycomb. Mech. Mater. 2020, 140, 103227. [Google Scholar] [CrossRef]
- Tsang, H.; Raza, S. Impact energy absorption of bio-inspired tubular sections with structural hierarchy. Compos. Struct. 2018, 195, 199–210. [Google Scholar] [CrossRef]
- San Ha, N.; Lu, G.; Xiang, X. High energy absorption efficiency of thin-walled conical corrugation tubes mimicking coconut tree configuration. Int. J. Mech. Sci. 2018, 148, 409–421. [Google Scholar]
- Ufodike, C.O.; Wang, H.; Ahmed, M.F.; Dolzyk, G.; Jung, S. Design and modeling of bamboo biomorphic structure for in-plane energy absorption improvement. Mater. Des. 2021, 205, 109736. [Google Scholar] [CrossRef]
- Sun, G.; Liu, T.; Fang, J.; Steven, G.P.; Li, Q. Configurational optimization of multi-cell topologies for multiple oblique loads. Struct. Multidiscip. Optim. 2018, 57, 469–488. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, E.T.; Wang, G.; Ng, B.F. In-plane crushing behavior and energy absorption of a novel graded honeycomb from hierarchical architecture. Int. J. Mech. Sci. 2022, 221, 107202. [Google Scholar] [CrossRef]
- Liang, H.; Wang, Q.; Pu, Y.; Zhao, Y.; Ma, F. In-plane compressive behavior of a novel self-similar hierarchical honeycomb with design-oriented crashworthiness. Int. J. Mech. Sci. 2021, 209, 106723. [Google Scholar] [CrossRef]
- Wu, F.; Chen, Y.; Zhao, S.; Hong, Y.; Zhang, Z.; Zheng, S. Mechanical properties and energy absorption of composite bio-inspired multi-cell tubes. Thin-Walled Struct. 2023, 184, 110451. [Google Scholar] [CrossRef]
- Wei, Z.; Wang, H.; Bi, Y.; Li, Y.; Li, B.; Wang, B. Crashworthiness and gradient optimization of multi-cell thin-walled structures inspired by leaf venation in royal water lily. In Mechanics of Advanced Materials and Structures; Taylor & Francis: Abingdon, UK, 2024; pp. 1–17. [Google Scholar]
- Li, Y.; Hu, D.; Yang, Z. Crashworthiness design of a sponge-inspired multicell tube under axial crushing. Int. J. Mech. Sci. 2023, 244, 108070. [Google Scholar] [CrossRef]
- Song, J.; Xu, S.; Liu, S.; Zou, M. Study on the crashworthiness of bio-inspired multi-cell tube under axial impact. Int. J. Crashworthiness 2022, 27, 390–399. [Google Scholar] [CrossRef]
- Hu, L.; Cong, Y.; Gu, S.; Zhang, G.; He, Z.; Feng, Z. Energy absorption characteristics of novel bionic H-type whip restraints for nuclear power plants. Nucl. Eng. Des. 2024, 424, 113243. [Google Scholar] [CrossRef]
- Zhu, G.; Sun, G.; Yu, H.; Li, S.; Li, Q. Energy absorption of metal, composite and metal/composite hybrid structures under oblique crushing loading. Int. J. Mech. Sci. 2018, 135, 458–483. [Google Scholar] [CrossRef]
- Qin, S.; Deng, X.; Liu, X. Crashworthiness analysis of bioinspired hierarchical gradient multicell tubes under axial impact. Thin-Walled Struct. 2022, 179, 109591. [Google Scholar] [CrossRef]


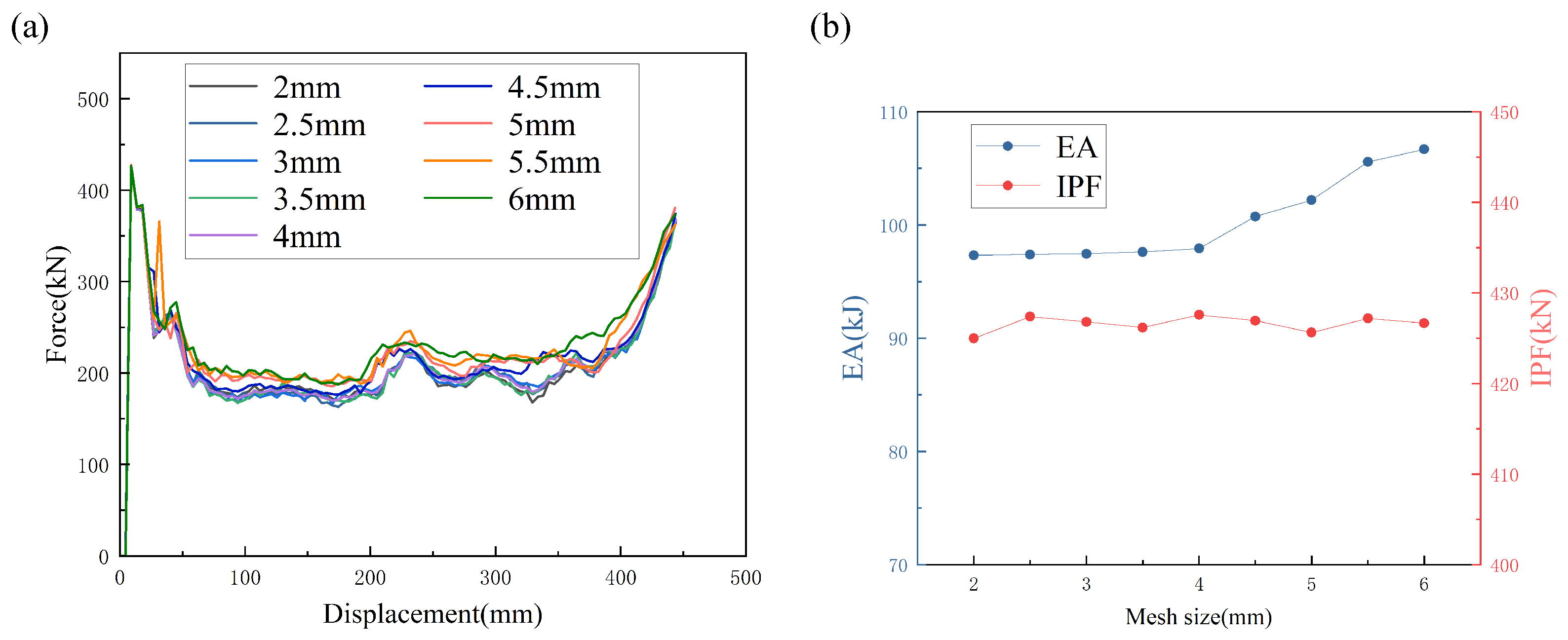



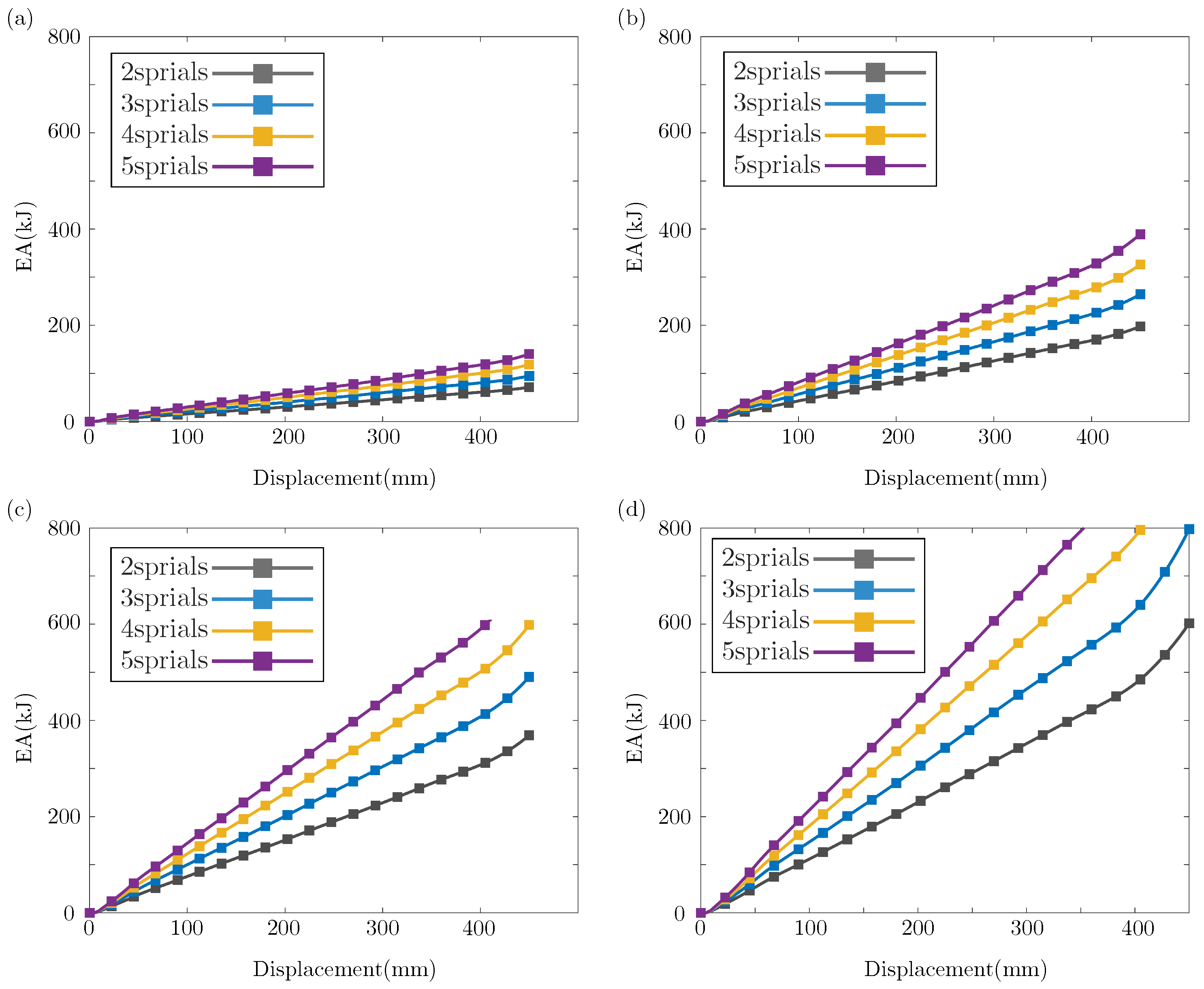


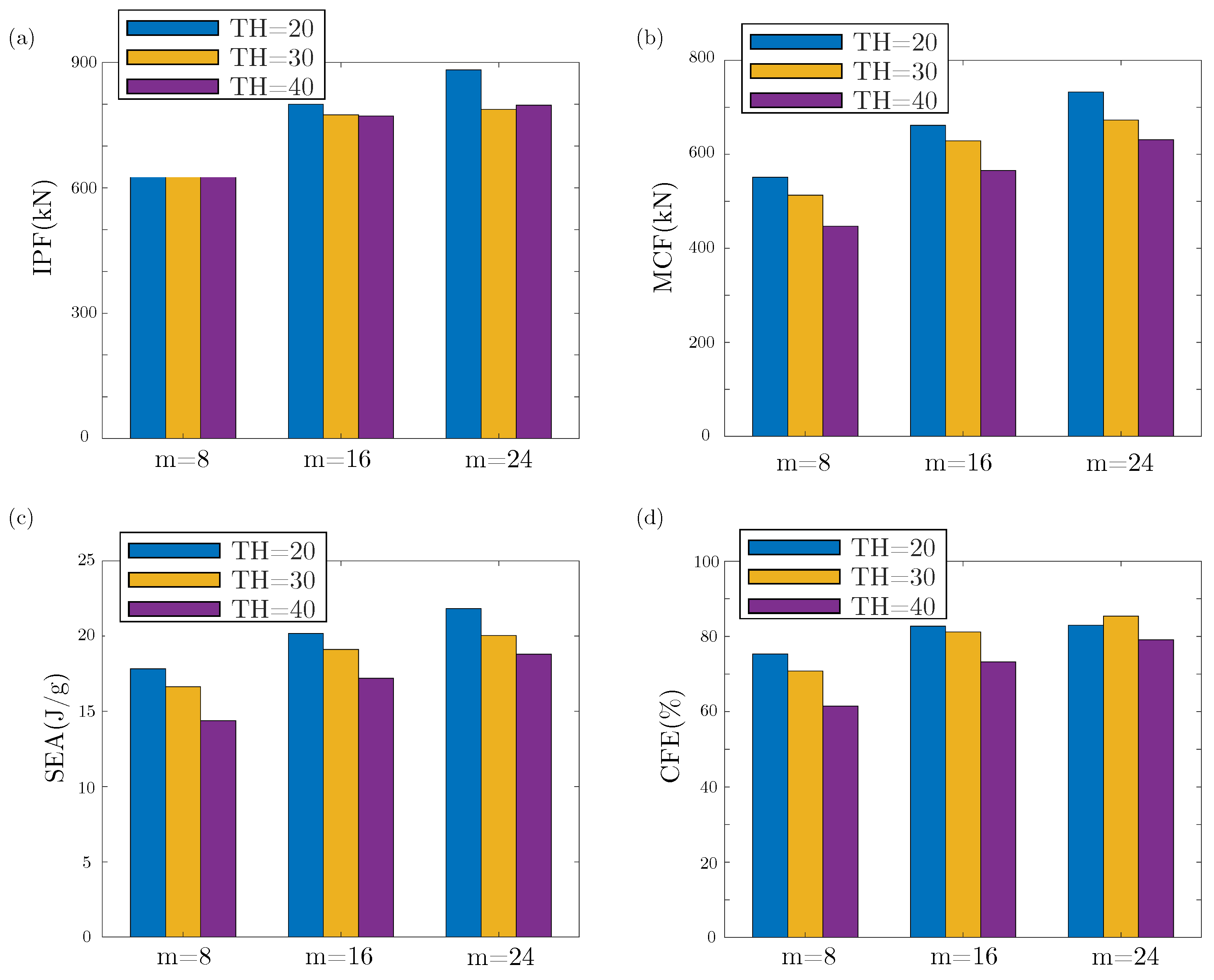
| Mesh Size (mm) | EA (kJ) | EA Difference (%) | IPF (kN) | IPF Difference (%) |
|---|---|---|---|---|
| 2 | 97.32 | 0 | 424.98 | 0 |
| 2.5 | 97.38 | 0.06 | 427.38 | 0.56 |
| 3 | 97.46 | 0.14 | 426.80 | 0.42 |
| 3.5 | 97.61 | 0.30 | 426.18 | 0.28 |
| 4 | 97.92 | 0.62 | 427.58 | 0.61 |
| 4.5 | 100.74 | 3.51 | 426.94 | 0.46 |
| 5 | 102.20 | 5.01 | 425.63 | 0.15 |
| 5.5 | 105.57 | 8.47 | 427.18 | 0.52 |
| 6 | 106.67 | 9.61 | 426.66 | 0.73 |
| Structure | t (mm) | m (kg) | EA (kJ) | IPF (kN) | SEA (kJ/kg) | MCF (kN) | CFE (%) |
|---|---|---|---|---|---|---|---|
| NBHMC | 2.265 | 14 | 141.279 | 737.934 | 10.091 | 321.461 | 43.562 |
| NBIHMC | 1.76 | 14 | 204.519 | 743.311 | 14.609 | 467.679 | 62.918 |
| NBOHMC | 1 | 14 | 220.503 | 732.929 | 15.750 | 506.620 | 69.123 |
| NBSHMC | 1.052 | 14 | 234.386 | 732.417 | 16.742 | 538.735 | 73.556 |
| NBCHMC | 0.624 | 14 | 225.644 | 734.639 | 16.117 | 518.018 | 70.513 |
| Structure | t (mm) | m (kg) | EA (kJ) | IPF (kN) | SEA (kJ/kg) | MCF (kN) | CFE (%) |
|---|---|---|---|---|---|---|---|
| NBIOHMC | 0.886 | 14 | 217.992 | 731.272 | 15.571 | 500.674 | 68.466 |
| NBISHMC | 0.965 | 14 | 236.574 | 731.407 | 16.989 | 543.851 | 74.357 |
| NBOSHMC | 0.685 | 14 | 221.410 | 734.032 | 15.815 | 508.430 | 69.265 |
| Structure | t (mm) | m (kg) | EA (kJ) | IPF (kN) | SEA (kJ/kg) | MCF (kN) | CFE (%) |
|---|---|---|---|---|---|---|---|
| 2 spirals | 0.5 | 5.8 | 71.447 | 301.920 | 12.318 | 158.780 | 52.590 |
| 1 | 11.6 | 197.527 | 607.717 | 17.028 | 438.950 | 72.241 | |
| 1.5 | 17.4 | 368.876 | 922.221 | 21.200 | 819.770 | 88.891 | |
| 2 | 23.2 | 602.028 | 1343.330 | 25.950 | 1337.844 | 99.592 | |
| 3 spirals | 0.5 | 7.25 | 94.9 | 378.006 | 13.09 | 210.847 | 55.779 |
| 1 | 14.5 | 264.6 | 761.48 | 18.248 | 587.972 | 77.216 | |
| 1.5 | 21.8 | 490.33 | 1230.28 | 22.492 | 1089.774 | 88.579 | |
| 2 | 29 | 797.626 | 1801.18 | 27.504 | 1772.55 | 98.411 | |
| 4 spirals | 0.5 | 8.7 | 118.652 | 452.825 | 13.622 | 263.664 | 58.226 |
| 1 | 17.4 | 326.364 | 910.792 | 18.757 | 725.248 | 79.633 | |
| 1.5 | 26.1 | 598.321 | 1498.25 | 22.924 | 1329.588 | 88.743 | |
| 2 | 34.8 | 978.366 | 2200.59 | 28.114 | 2174.162 | 98.799 | |
| 5 spirals | 0.5 | 10.1 | 140.37 | 518.512 | 13.898 | 311.899 | 60.153 |
| 1 | 20.2 | 389.242 | 1060.26 | 19.269 | 865.076 | 81.834 | |
| 1.5 | 30.3 | 709.627 | 1774.77 | 23.42 | 1578.144 | 88.921 | |
| 2 | 40.5 | 1200.732 | 2606.7 | 29.648 | 2594.02 | 99.514 |
| m | TH (mm) | m (kg) | EA (kJ) | IPF (kN) | SEA (kJ/kg) | MCF (kN) | CFE (%) |
|---|---|---|---|---|---|---|---|
| 8 | 20 | 13.9 | 247.836 | 731.471 | 17.83 | 551.095 | 75.34 |
| 30 | 13.9 | 231.226 | 724.804 | 16.635 | 513.033 | 70.78 | |
| 40 | 14 | 201.287 | 726.296 | 14.378 | 446.824 | 61.52 | |
| 16 | 20 | 14.7 | 296.629 | 799.496 | 20.179 | 661.467 | 82.736 |
| 30 | 14.8 | 282.866 | 774.318 | 19.113 | 628.522 | 81.171 | |
| 40 | 14.8 | 254.463 | 771.876 | 17.193 | 565.422 | 73.253 | |
| 24 | 20 | 15.1 | 329.508 | 882.063 | 21.822 | 731.958 | 82.982 |
| 30 | 15.1 | 302.604 | 787.428 | 20.04 | 672.467 | 85.4 | |
| 40 | 15.1 | 283.889 | 797.428 | 18.801 | 630.914 | 79.119 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Z.; Yang, Y.; Hu, L.; Gu, S. On the Design of Bionic Hierarchical H-Type Whip Restraints for Nuclear Power Plants. Appl. Sci. 2025, 15, 5507. https://doi.org/10.3390/app15105507
He Z, Yang Y, Hu L, Gu S. On the Design of Bionic Hierarchical H-Type Whip Restraints for Nuclear Power Plants. Applied Sciences. 2025; 15(10):5507. https://doi.org/10.3390/app15105507
Chicago/Turabian StyleHe, Zheng, Yuhang Yang, Libang Hu, and Shuitao Gu. 2025. "On the Design of Bionic Hierarchical H-Type Whip Restraints for Nuclear Power Plants" Applied Sciences 15, no. 10: 5507. https://doi.org/10.3390/app15105507
APA StyleHe, Z., Yang, Y., Hu, L., & Gu, S. (2025). On the Design of Bionic Hierarchical H-Type Whip Restraints for Nuclear Power Plants. Applied Sciences, 15(10), 5507. https://doi.org/10.3390/app15105507







