A 13.44-Bit Low-Power SAR ADC for Brain–Computer Interface Applications
Abstract
1. Introduction
- Compared to conventional architectures, the segmented monotonic switching scheme significantly reduces the capacitor array’s footprint and power dissipation while introducing redundancy to enhance tolerance to parasitic capacitance and relax performance requirements for backend comparators.
- The circuit design primarily employs fully dynamic comparators and a dynamic logic array with enhanced latching speed to minimize total power consumption.
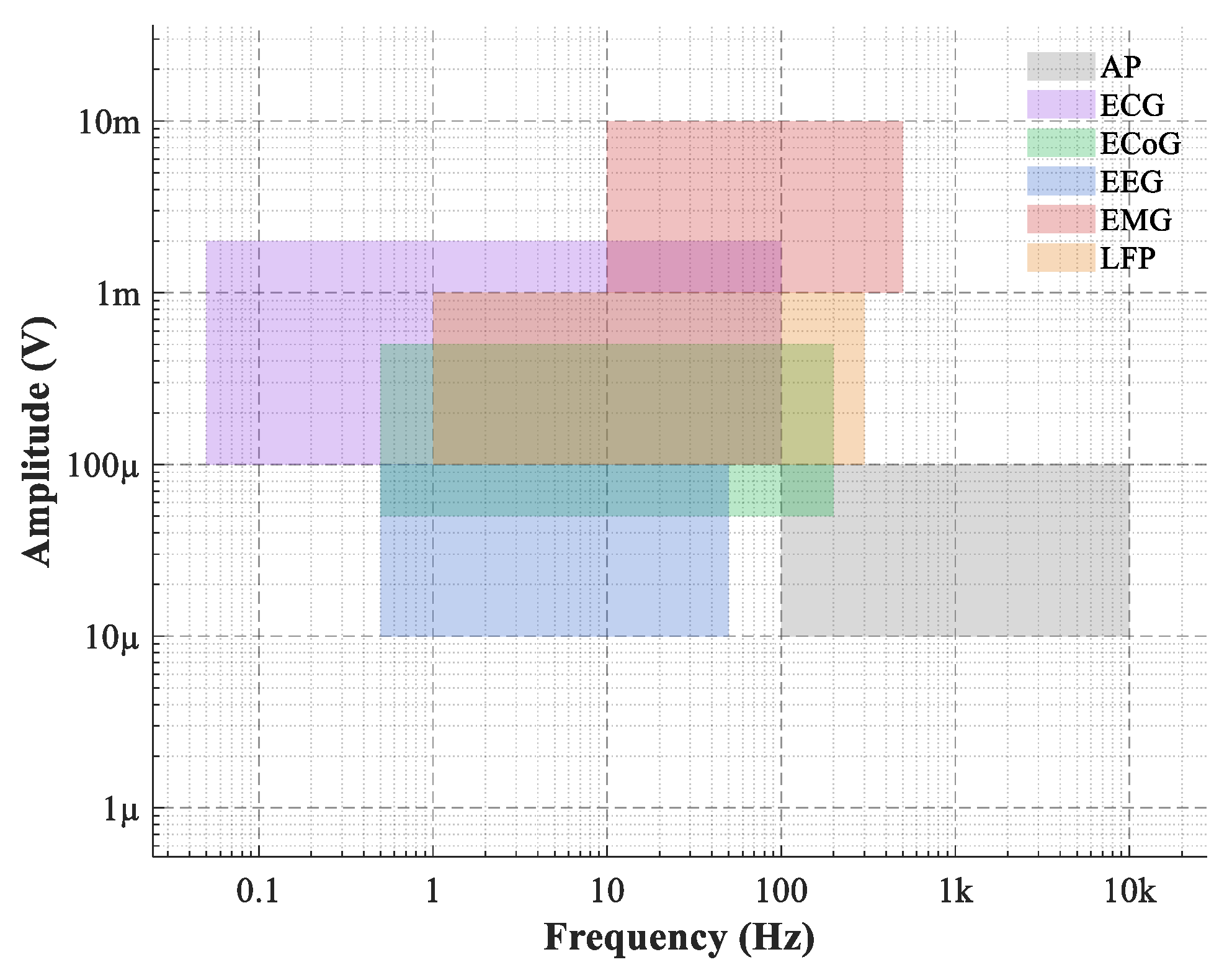
- A relatively high ±500mV input range and a bandwidth extending up to 10 kHz enable the front-end AFE (Analog Front-End) to achieve higher amplification gain, thereby effectively reducing the system’s input-referred noise.
2. Circuit Topology
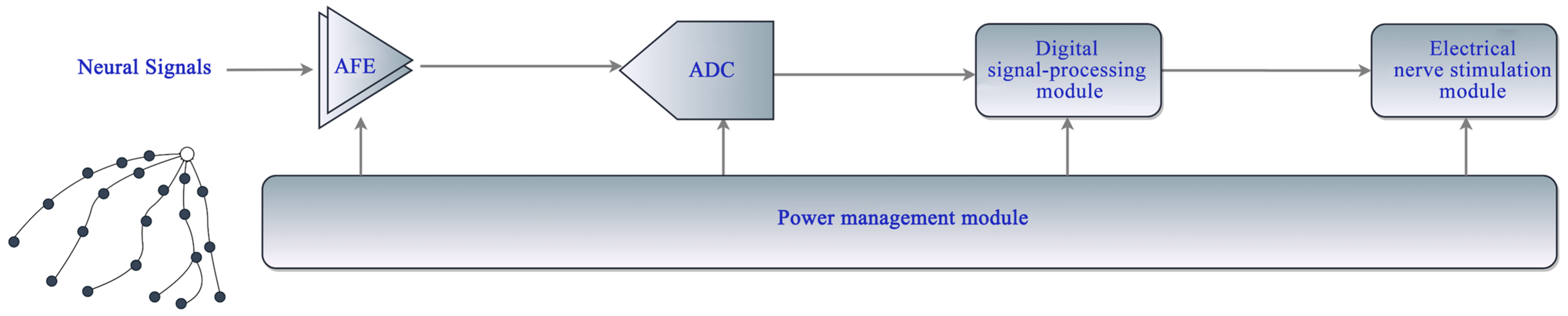
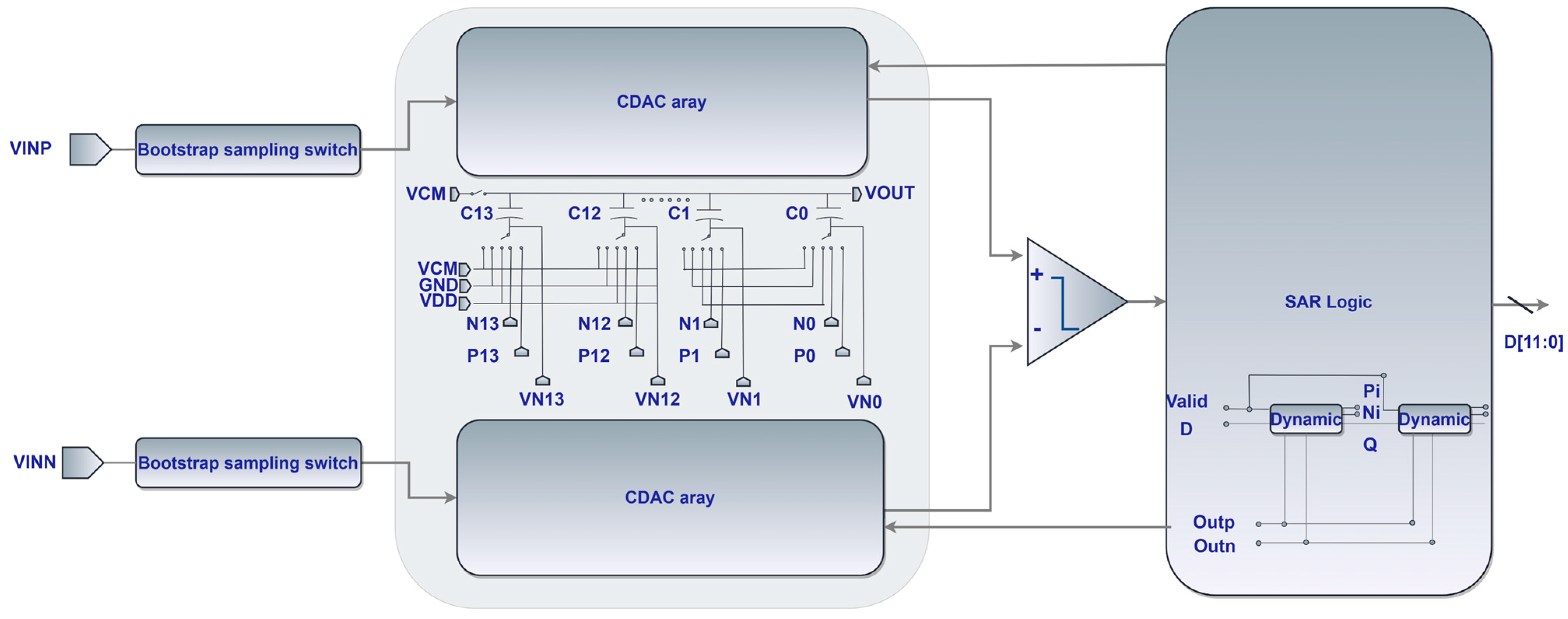
2.1. Architectural Overview
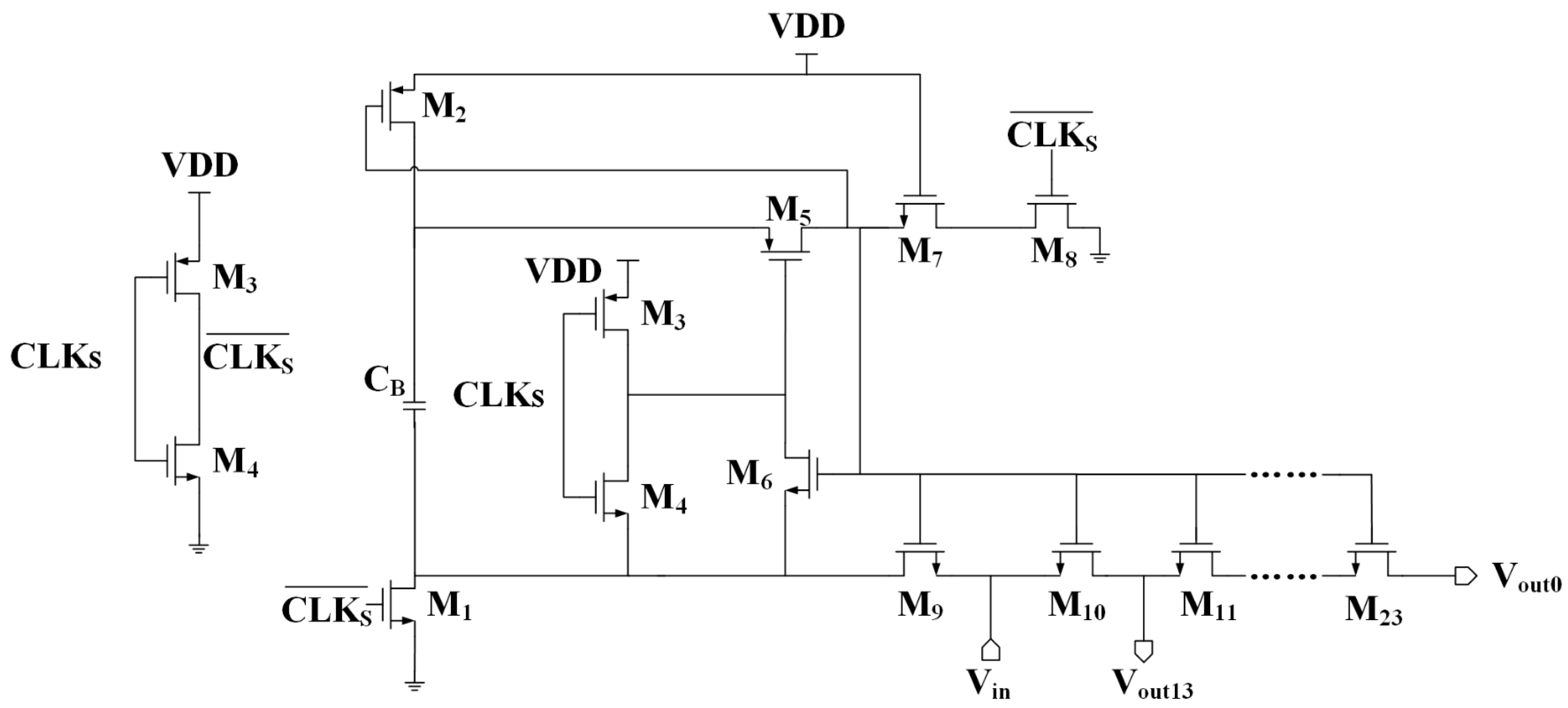
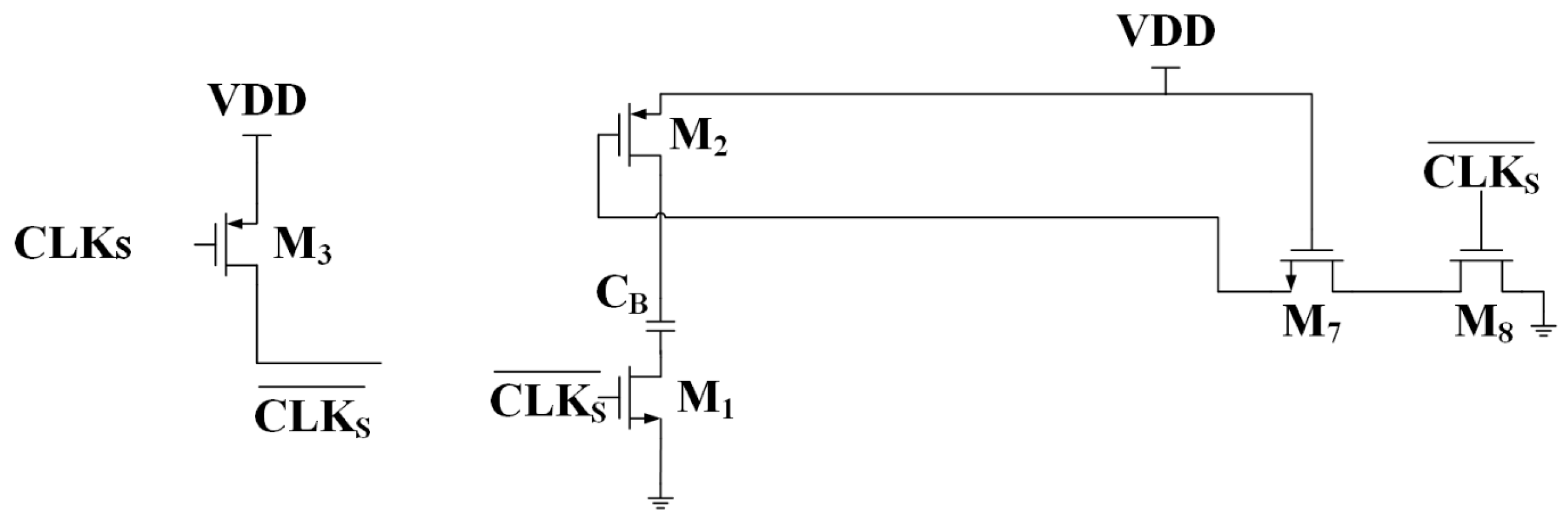
2.2. Bootstrapped Sampling Switch Design
- Φ1 (Reset Phase):
- 2.
- Φ2 (Sampling Phase):
- The charge injection effect in switch transistors manifests when the device turns off, as the inversion layer channel charge redistributes through the source/drain terminals, inducing an error voltage ΔV on the sampled-and-held signal.
- Clock Feedthrough Effect: when the clock signal transitions, it couples onto the sampling capacitor through the gate-drain overlap capacitance (Cgd) or gate-source overlap capacitance (Cgs) of the switch transistor, introducing nonlinear perturbations at the sampled output.
- Body Effect (Substrate Bias Effect): in n-well processes, the body effect in NMOS switch transistors must be rigorously considered, as the threshold voltage (VTH) exhibits a nonlinear dependence on the input signal (Vin), directly contributing to sampling nonlinearity.
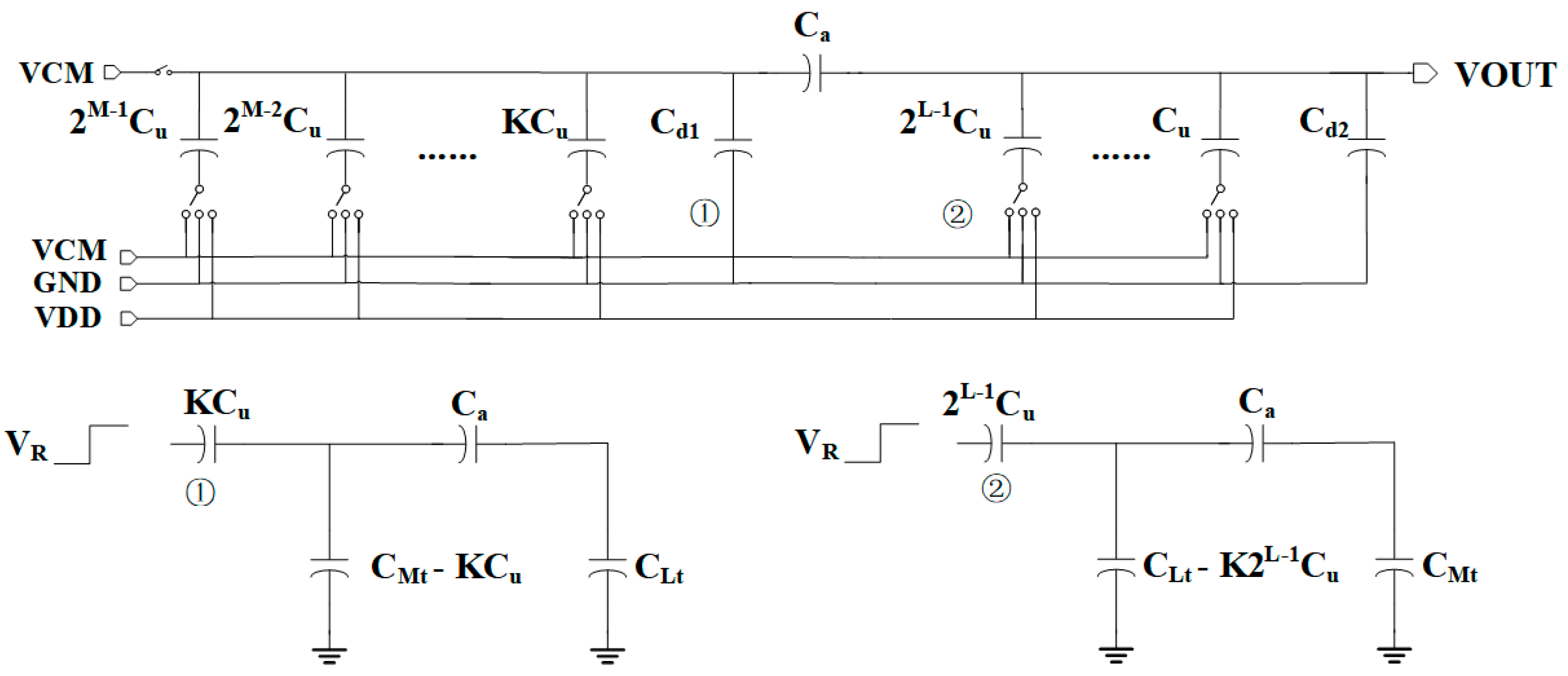
2.3. Capacitive DAC Array Design
- kT/C noise constraint
- 2.
- Capacitor mismatch
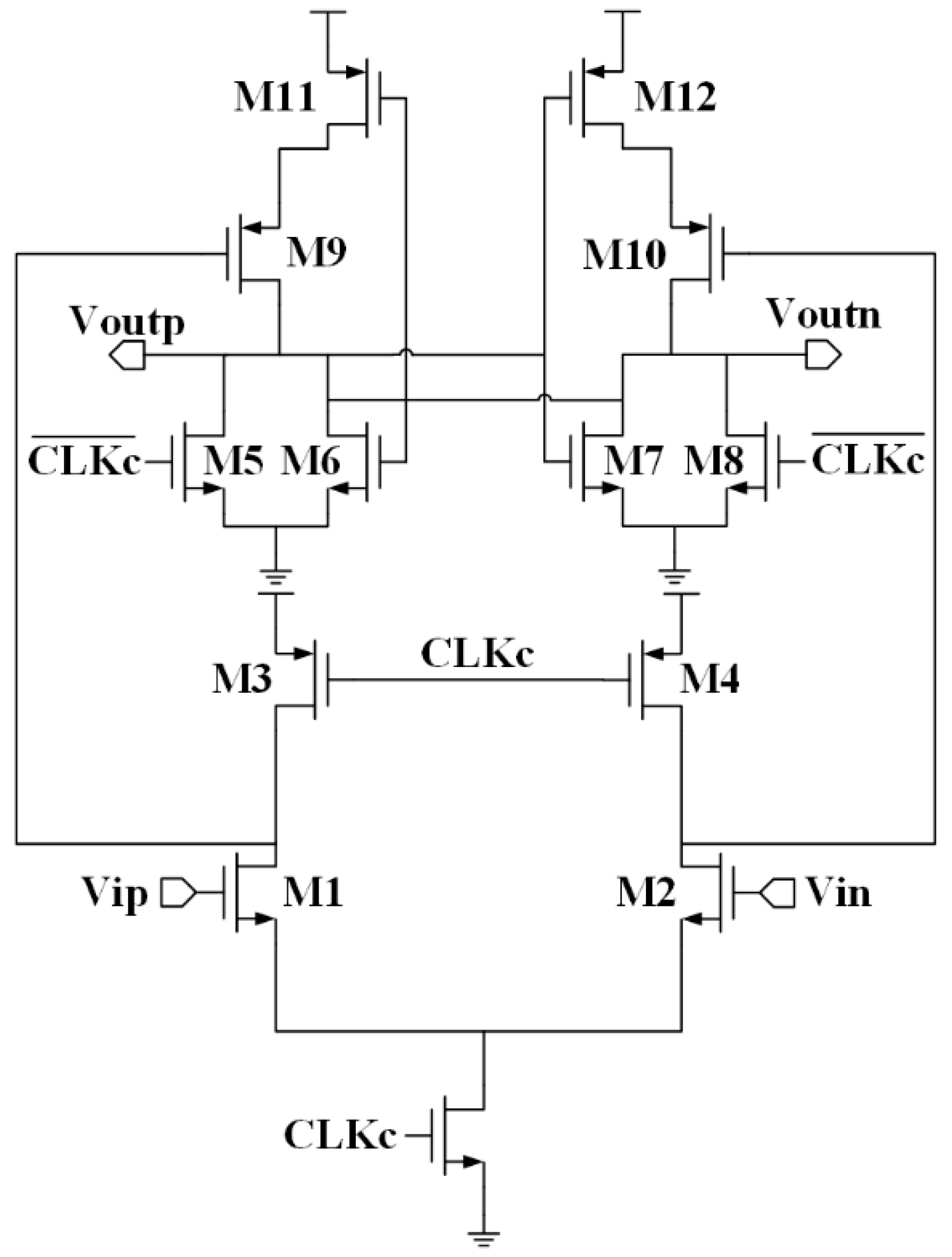
2.4. Dynamic Comparator Design
- Static Current Elimination
- 2.
- Controlled Regeneration
- Noise Compliance
- 2.
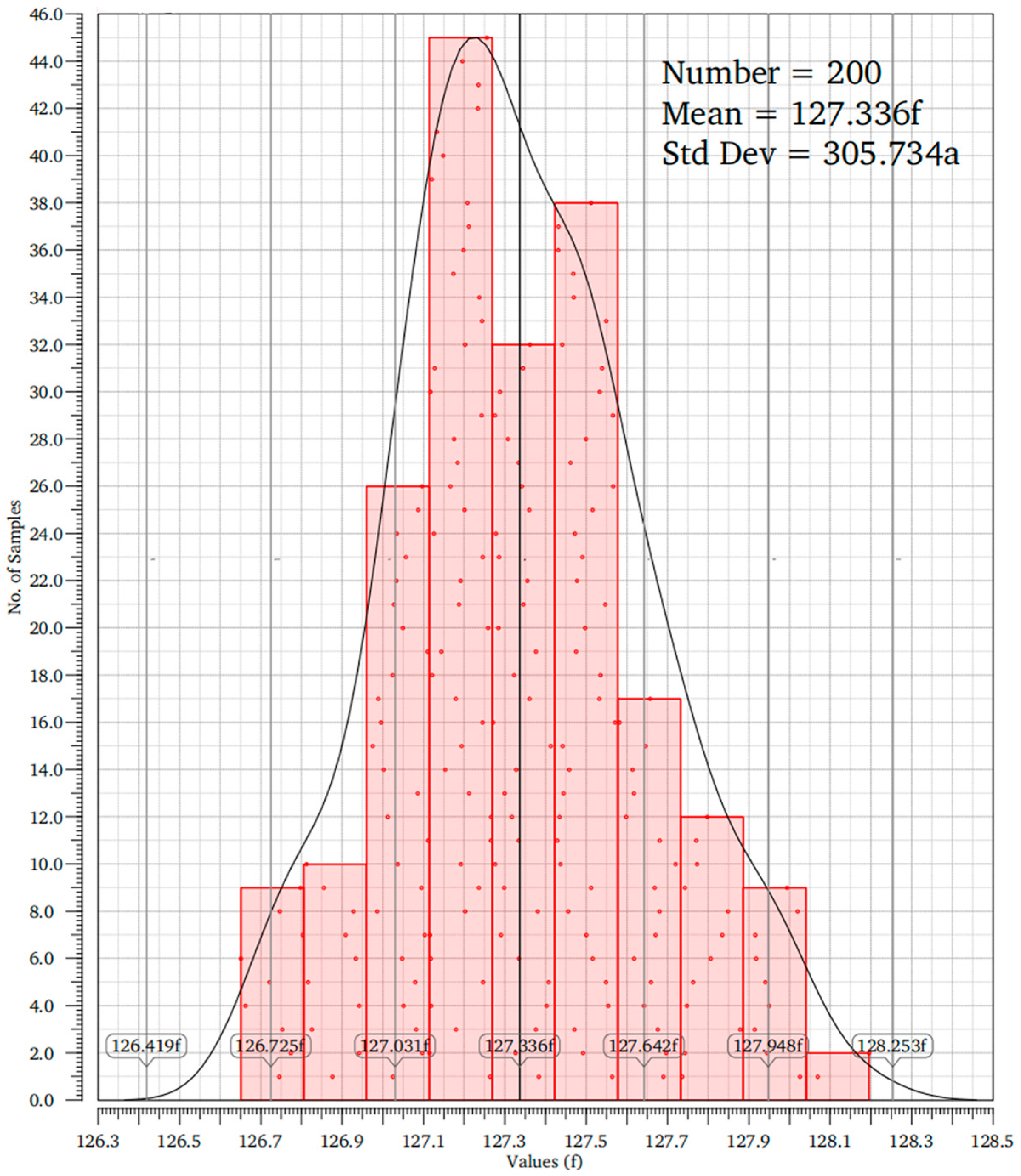
- Monte Carlo Offset Analysis
- 3.
- Speed–Noise–Power Tradeoff
2.5. SAR Logic Array Design
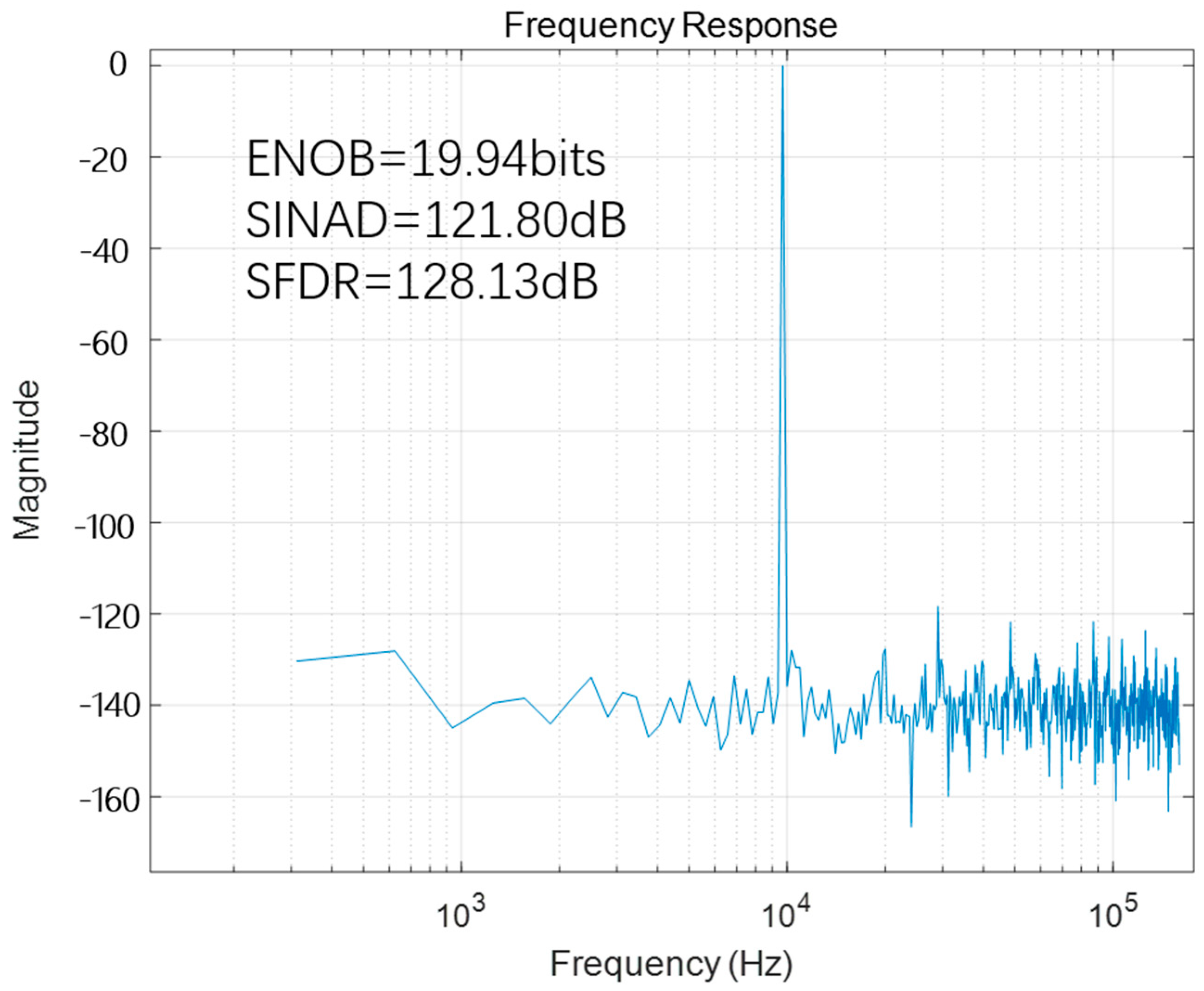
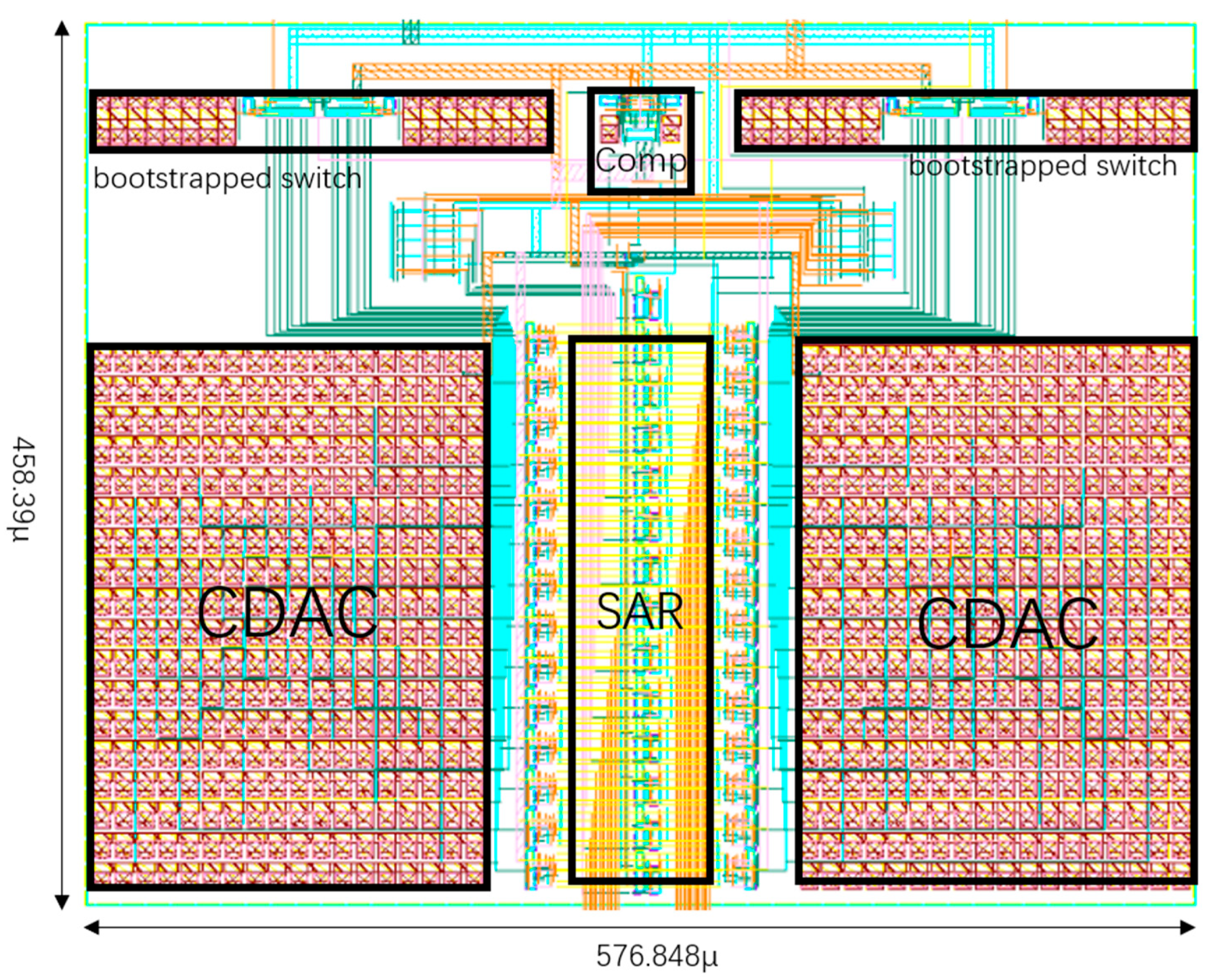
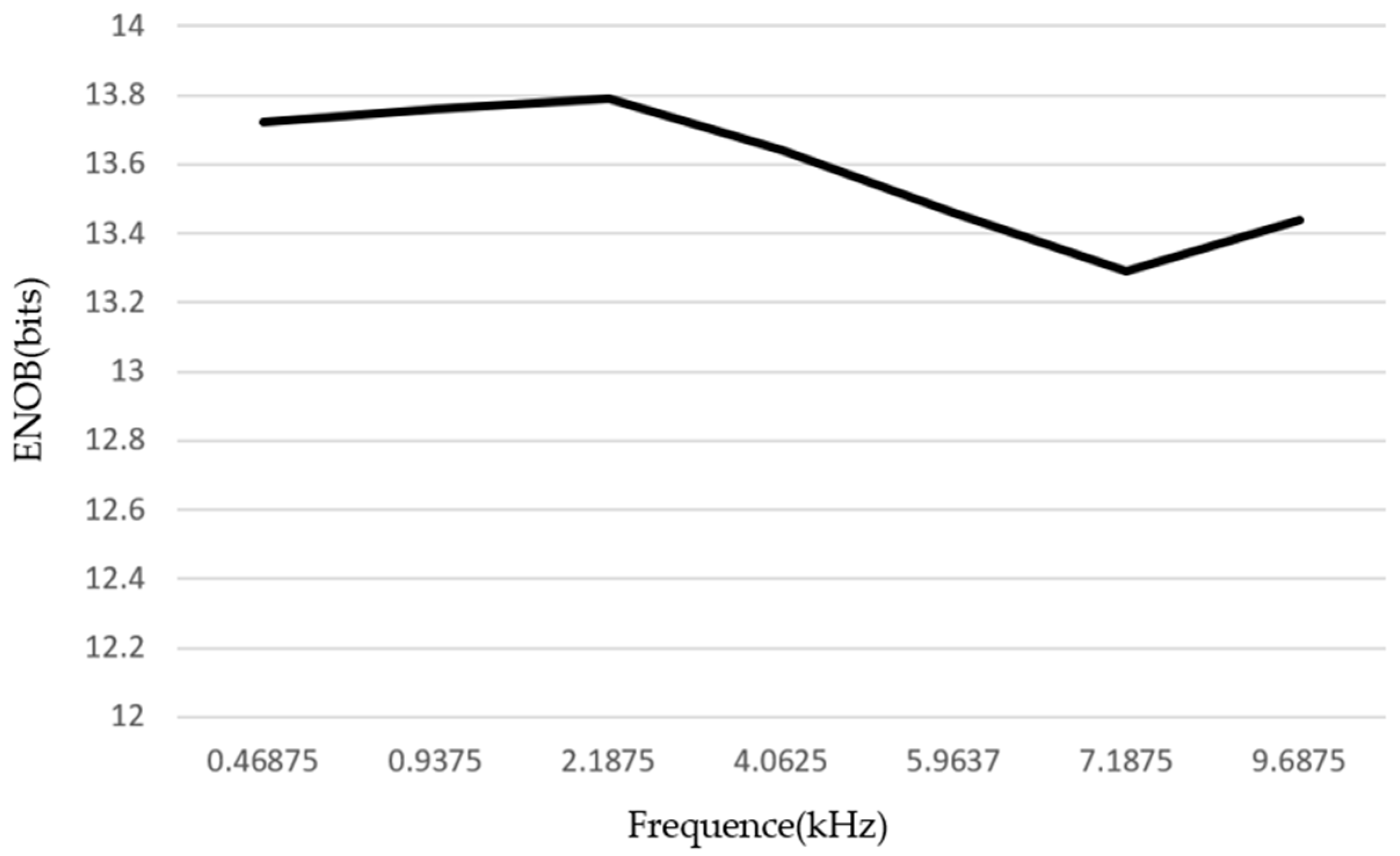
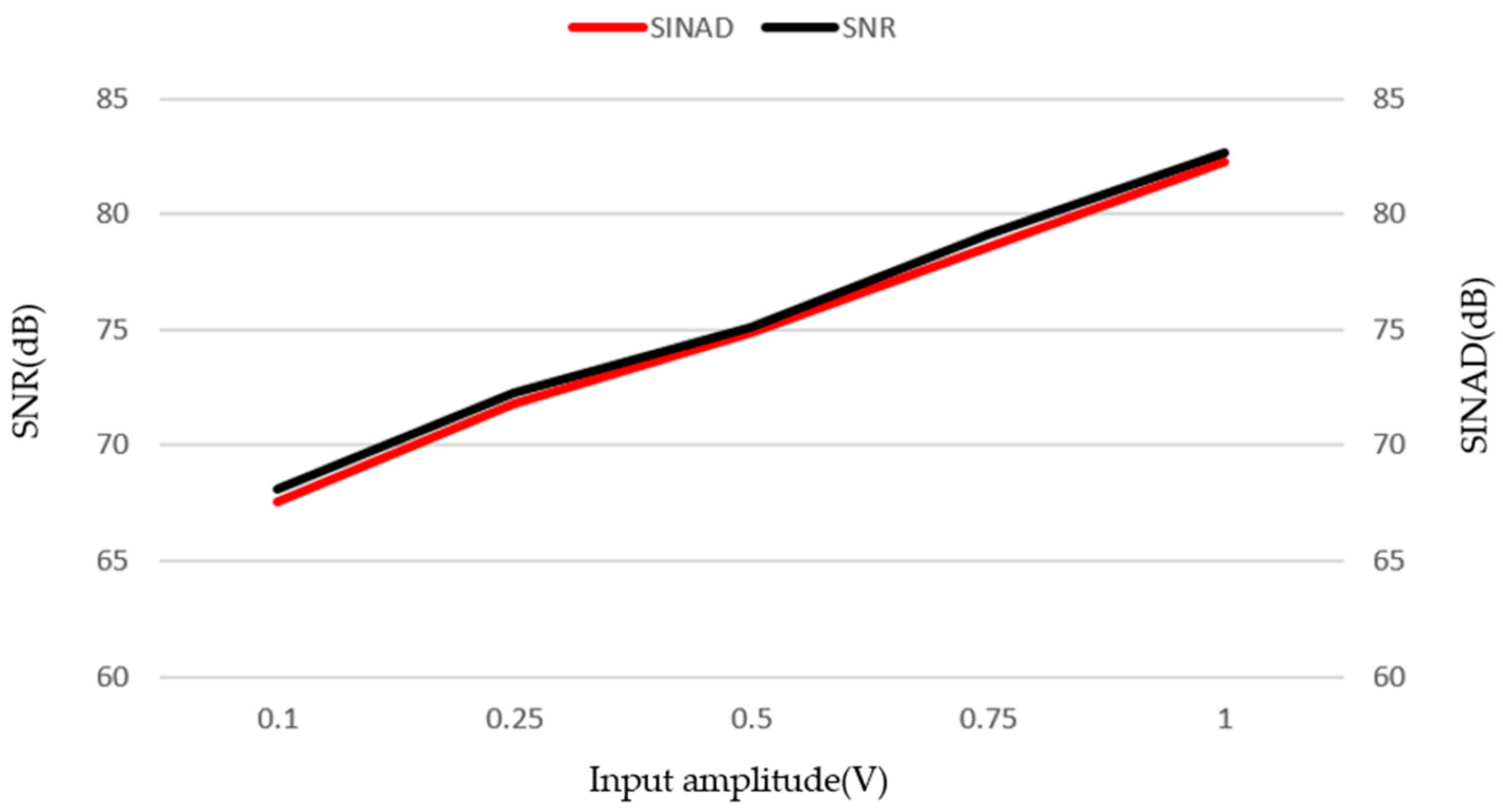
3. Layout Implementation and Post-Layout Simulation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jeong, K.; Ha, S.; Je, M. A 15.4-ENOB, Fourth-Order Truncation-Error-Shaping NS-SAR-Nested ΔΣ Modulator With Boosted Input Impedance and Range for Biosignal Acquisition. IEEE J. Solid-State Circuits 2023, 59, 528–539. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Zhang, L.; Bais, A. Dynamical system based compact deep hybrid network for classification of Parkinson disease related EEG signals. Neural Netw. 2020, 130, 75–84. [Google Scholar] [CrossRef] [PubMed]
- Koller-Schlaud, K.; Ströhle, A.; Bärwolf, E.; Behr, J.; Rentzsch, J. EEG Frontal Asymmetry and Theta Power in Unipolar and Bipolar Depression. J. Affect. Disord. 2020, 276, 501–510. [Google Scholar] [CrossRef] [PubMed]
- Eldele, E.; Chen, Z.; Liu, C.; Wu, M.; Kwoh, C.-K.; Li, X.; Guan, C. An attention-based deep learning approach for sleep stage classification with single-channel EEG. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 809–818. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Zhang, J.; He, C.; Wu, H.; Cheng, L. A Novel Emotion Recognition Method Based on the Feature Fusion of Single-Lead EEG and ECG Signals. IEEE Internet Things J. 2023, 11, 8746–8756. [Google Scholar] [CrossRef]
- Chen, M.; Chun, H.S.; Castro, I.D.; Torfs, T.; Lin, Q.; van Hoof, C.; Wang, G.; Lian, Y.; van Helleputte, N. A 400 GΩ Input-Impedance Active Electrode for Non-Contact Capacitively Coupled ECG Acquisition With Large Linear-Input-Range and High CM-Interference-Tolerance. IEEE Trans. Biomed. Circuits Syst. 2019, 13, 376–386. [Google Scholar] [CrossRef] [PubMed]
- Casson, A.J.; Saunders, R.; Batchelor, J.C. Five day attachment ECG electrodes for longitudinal bio-sensing using conformal tattoo substrates. IEEE Sens. J. 2017, 17, 2205–2214. [Google Scholar] [CrossRef]
- Cogan, S.F. Neural stimulation and recording electrodes. Annu. Rev. Biomed. Eng. 2008, 10, 275–309. [Google Scholar] [CrossRef] [PubMed]
- Jie, L.; Tang, X.; Liu, J.; Shen, L.; Li, S.; Sun, N.; Flynn, M.P. An Overview of Noise-Shaping SAR ADC: From Fundamentals to the Frontier. IEEE Open J. Solid-State Circuits 2021, 1, 149–161. [Google Scholar] [CrossRef]
- Boni, A.; Giuffredi, L.; Pietrini, G.; Ronchi, M.; Caselli, M. A low-power Sigma-Delta modulator for healthcare andmedical diagnostic applications. IEEE Trans. Circuits Syst. I Regul. 2021, 69, 207–219. [Google Scholar] [CrossRef]
- Zheng, Z.; Wei, L.; Lagos, J.; Martens, E.; Zhu, Y.; Chan, C.H.; Craninckx, J.; Martins, R.P. 163 A single-channel 5.5 mW 3.3 GS/s 6b fully dynamic pipelined ADC with post-amplification residue generation. In Proceedings of the 2020 IEEE Intemational SolidState Circuits Conference-(ISSCC), San Francisco, CA, USA, 16–20 February 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 254–256. [Google Scholar]
- Yu, W.; Sen, S.; Leung, B. Distortion analysis of MOS track-and-hold sampling mixers using time-varying Volterra series. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1999, 46, 101–113. [Google Scholar] [CrossRef]
- Razavi, B. Principles of Data Conversion System Design; Wiley: New York, NY, USA, 1995; pp. 7–28. [Google Scholar]
- Zhu, Y.; Chan, C.H.; Chio, U.F.; Sin, S.W.; Martins, R.P.; Maloberti, F. A 10-Bit 100-MS/s Reference-Free SAR ADCin 90 nm CMoS. IEEE J. Solid-State Circuits 2010, 45, 1111–1121. [Google Scholar] [CrossRef]
- Kobayashi, T.; Nogami, K.; Shirotori, T.; Fujimoto, Y.; Watanabe, O. A current-mode latch sense amplifier and a staticpower saving input buffer for low-power architecture. In 1992 Symposium on VLSI Circuits Digest of Technical Papers; IEEE: Piscataway, NJ, USA, 1992; pp. 28–29. [Google Scholar]
- Razavi, B. The strongarm latch [a circuit for all seasons]. IEEE Solid-State Circuits Mag. 2015, 7, 12–17. [Google Scholar] [CrossRef]
- Schinkel, D.; Mensink, E.; Klumperink, E.; Van Tuijl, E.; Nauta, B. A doubletail latchtype voltage sense amplifier with 18ps setuphold time. In Proceedings of the 2007 IEEE International SolidState Circuits Conference Digest of Technical Papers (ISSCC), San Francisco, CA, USA, 11–15 February 2007; p. 314605. [Google Scholar]
- Chung, Y.-H.; Kuo, J.-H. A 12b Dual-Mode SAR ADC for Bio-Medical Applications. In Proceedings of the 2024 IEEE Biomedical Circuits and Systems Conference (BioCAS), Xi’an, China, 28–30 April 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Kumaradasan, D.; Kar, S.K.; Sarkar, S. An 8-bit 1 MS/s Low-Power SAR ADC with an Enhanced EPC for Implantable Medical Devices. In Proceedings of the 2024 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Knoxville, TN, USA, 1–3 July 2024; pp. 9–14. [Google Scholar] [CrossRef]
- Tiwari, V.; Batra, C.; Nagaria, R. KLow power SAR ADC for bio-medical application. In Proceedings of the 2024 International Conference on Integrated Circuits, Communication, and Computing Systems (ICIC3S), Una, India, 8–9 June 2024; pp. 1–3. [Google Scholar] [CrossRef]
- Gao, Z.; Wang, S.; Chen, M. A 32-bit Two-step Incremental-ADC with 125.6 dB Dynamic-range for Non-invasive BCI Applications. In Proceedings of the 2024 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Taipei, Taiwan, 7–9 November 2024; pp. 566–570. [Google Scholar] [CrossRef]





| K | |||
|---|---|---|---|
| 1 | 1 | 2L − 1 | The parasitic capacitance at the LSB node, . |
| 1 | 2 | 2 × (2L − 1) | The parasitic capacitance at the LSB node, 2L − 1. |
| 1 | 4 | 4 × (2L − 1) | The parasitic capacitance at the LSB node, 3 × (2L − 1). |
| 2 | 4 | 2 × (2L − 2) | The parasitic capacitance at the LSB node, 2L – 3. |
| C13 | C12 | C11 | C10 | C9 | C8 | C7 | C6 | C5 | C4 | C3 | C2 | C1 | C0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Weight accumulation result | 2048 | 1024 | 512 | 256 | 256 | 128 | 64 | 32 | 16 | 8 | 8 | 4 | 2 | 1 |
| Weight accumulation result of LSB | 2311 | 1287 | 775 | 519 | 263 | 135 | 71 | 39 | 23 | 15 | 7 | 3 | 1 | 0 |
| Redundancy (LSB) | 264 | 264 | 264 | 264 | 8 | 8 | 8 | 8 | 8 | 8 | 0 | 0 | 0 | 0 |
| [18] | [19] | [20] | [21] | This Work | |
|---|---|---|---|---|---|
| Topology | IADC2-1 | SAR | SAR | SAR | SAR |
| Process (nm) | 180 | 90 | 180 | 180 | 180 |
| Sampling frequency (Hz) | 768 k | 20 M | 1 k | 1 M | 320 k |
| Supply (V) | 5 | 1.8 | 0.5/1 | 1.8 | 1.8 |
| Power (W) | 2.95 m | 31.6 μ | 35.9 μ | 40.5 μ | 27.9 μ |
| Peak input (V) | - | 500 m | 1 | - | 1 |
| Bandwidth (Hz) | 0.5 k | 1.25 M | 5 k | 50 k | 10 k |
| Resolution (bits) | 32 | 5 | 12 | 8 | 14 |
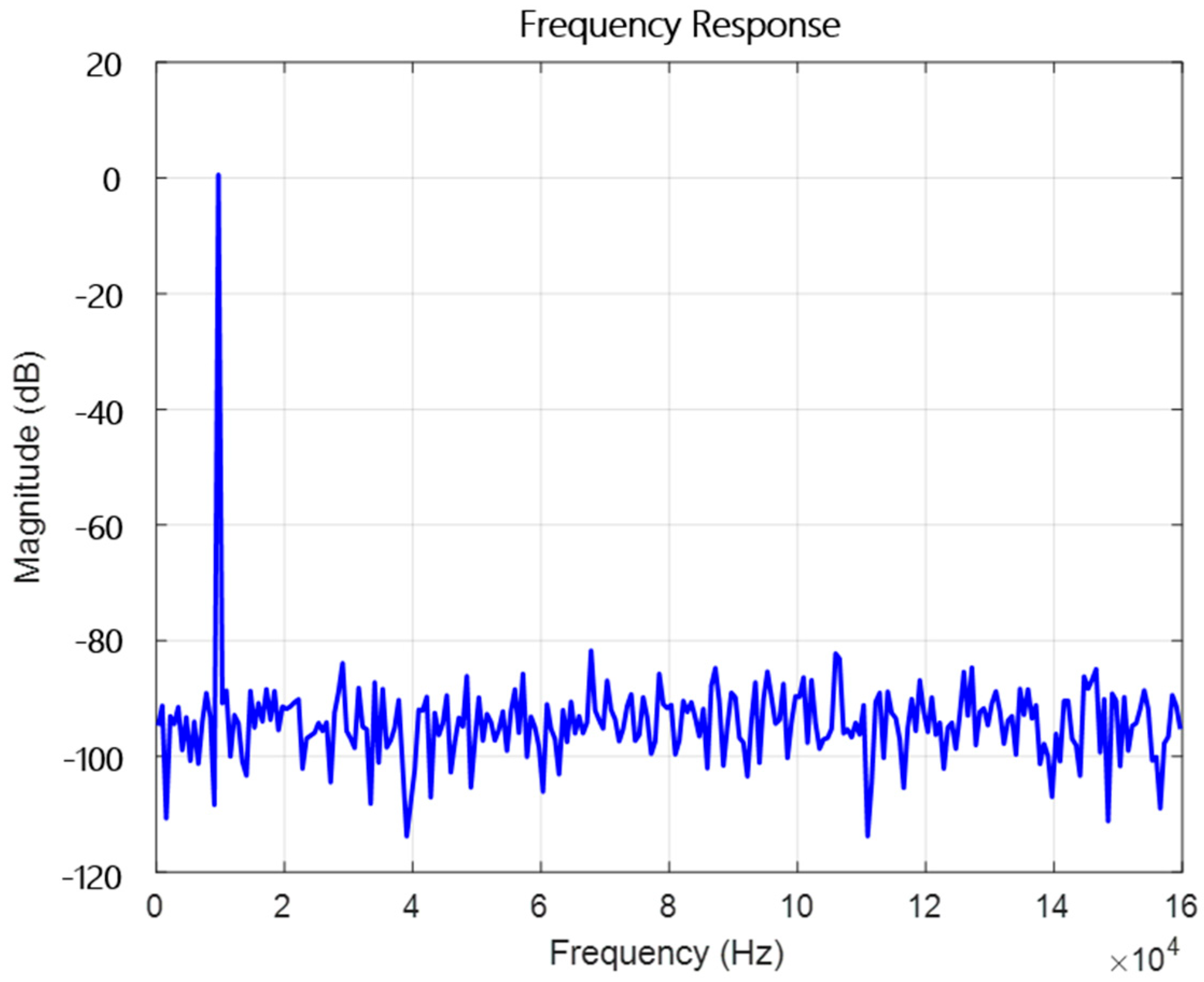
| ENOB (bits) | 18.16 | 4.53 | 11.12 | 7.7 | 13.44 |
| SINAD (dB) | 111.1 | 29 | 68.7 | 48.15 | 82.67 |
| SFDR (dBc) | - | - | 83 | 55.52 | 89.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Cheong, J.; Liu, C. A 13.44-Bit Low-Power SAR ADC for Brain–Computer Interface Applications. Appl. Sci. 2025, 15, 5494. https://doi.org/10.3390/app15105494
Yang H, Cheong J, Liu C. A 13.44-Bit Low-Power SAR ADC for Brain–Computer Interface Applications. Applied Sciences. 2025; 15(10):5494. https://doi.org/10.3390/app15105494
Chicago/Turabian StyleYang, Hongyuan, Jiahao Cheong, and Cheng Liu. 2025. "A 13.44-Bit Low-Power SAR ADC for Brain–Computer Interface Applications" Applied Sciences 15, no. 10: 5494. https://doi.org/10.3390/app15105494
APA StyleYang, H., Cheong, J., & Liu, C. (2025). A 13.44-Bit Low-Power SAR ADC for Brain–Computer Interface Applications. Applied Sciences, 15(10), 5494. https://doi.org/10.3390/app15105494





