Shear Resistance Evolution of Geogrid Reinforced Expansive Soil Under Freeze–Thaw Cycles
Abstract
1. Introduction
2. Test Materials and Procedures
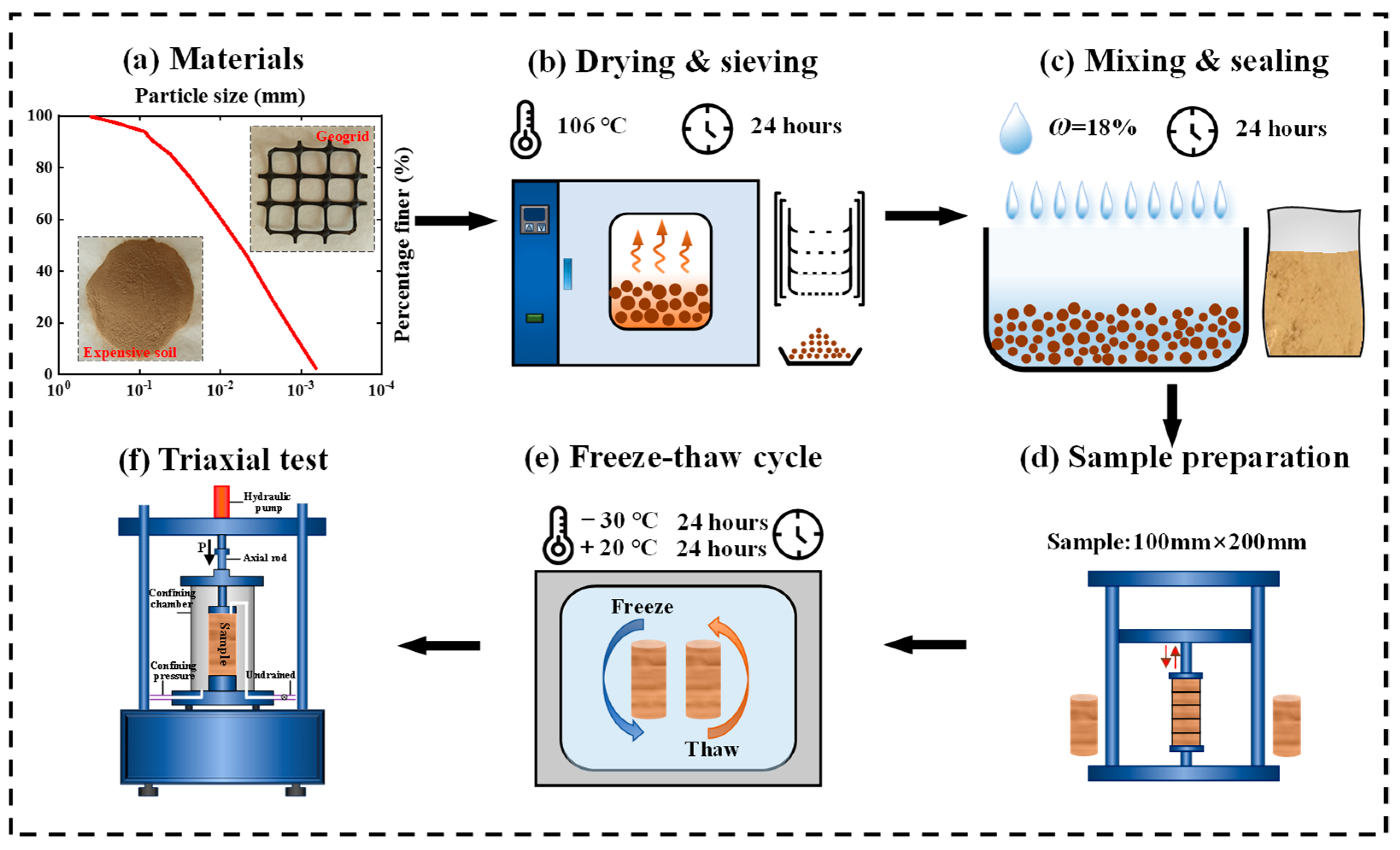
2.1. Materials
2.2. Test Procedure
2.2.1. Specimen Preparation
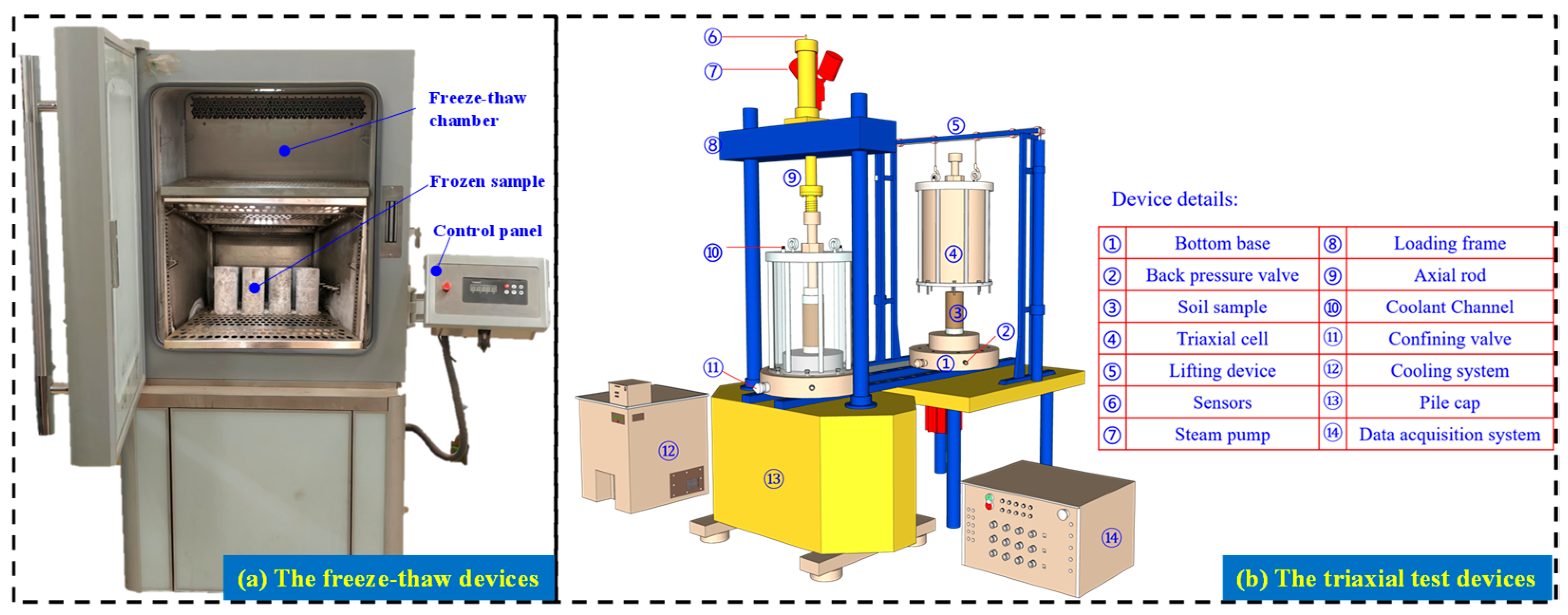
2.2.2. F-T Cycle
2.2.3. Triaxial Test
3. Results and Discussion
3.1. Specimen Damage Pattern
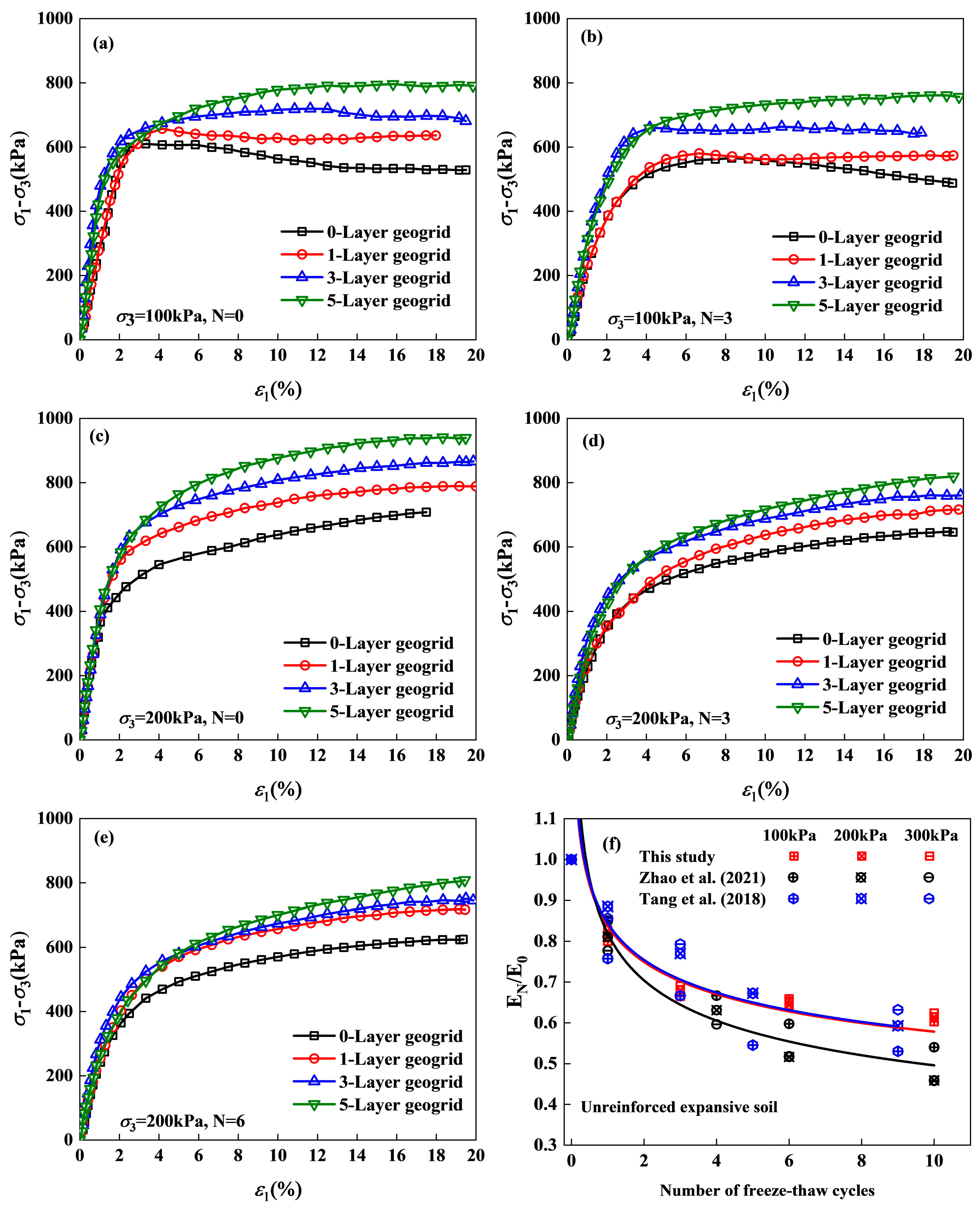
3.2. Stress–Strain Behavior
- (1)
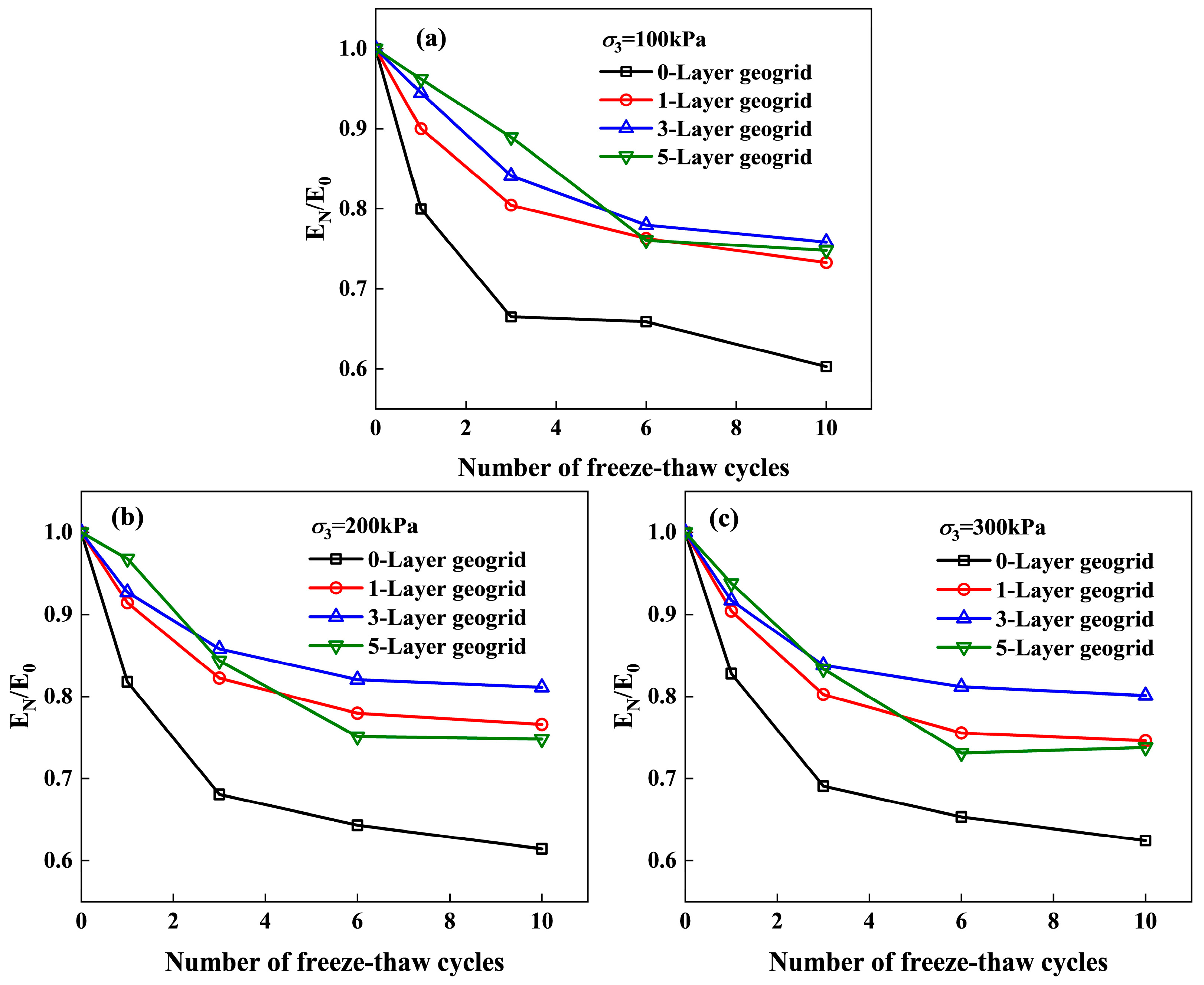
- The effect of F-T cycles: F-T cycles destroyed the chain between soil particles, changed the internal structure of the soil, caused an increase in the number and size of pores, small pores linked to form large pores, and reduced the strength of the soil body [40,41]. The strength of the specimens decreased with the increase in the number of freeze–thaw cycles, which was more obvious in unreinforced specimens than in reinforced specimens. Friction between the expansive soil and the geogrid and the geogrid’s embedded locking effect indirectly provided additional pressure, limiting the increase and enlargement of pores. However, the decrease was not obvious after six F-T cycles, and the internal structure of the soil tended to stabilize and reach dynamic equilibrium. Previous studies have shown that the physical and mechanical properties tend to be stabilized after 5–7 F-T cycles [35,36], which is basically consistent with the present study.
- (2)
- The effect of geogrid layers: With the increase in geogrid layers, the stress–strain curve changed from strain-softening to strain-hardening type. Geogrids create a restraining effect through a three-dimensional reinforcing network. Interfacial friction and mechanical occlusion between geogrid and soils redistribute the stress field, inhibit the localized development of the shear zone, and promote the transformation of the soil body from brittle damage to progressive plastic deformation. Through the synergistic reinforcing effect of multi-layer geogrids, the overall stiffness and ductility of the soil body can be significantly improved, and the freezing–expansion–contraction cyclic damage of expansive soils can be suppressed. Additionally, it was more obvious at low confining pressure, which indicates that the reinforcing effect was better at low confining pressure. The reason for this trend is that the lateral deformation of the specimen is greater at low perimeter pressures than at high perimeter pressures, the relative displacement between the tendons and soils is significant, and the geogrid restrains the soil particles more obviously.
- (3)
- The effect of confining pressure: When the confining pressure is 100 kPa, the stress–strain curve of the expansive soil specimens exhibited strain-softening. When the confining pressure is 200 kPa, the stress–strain curve of the expansive soil specimens exhibits strain hardening. At high confining pressures, soil particles reorganize, cracks close, and soil strength is increased [42].
- (4)
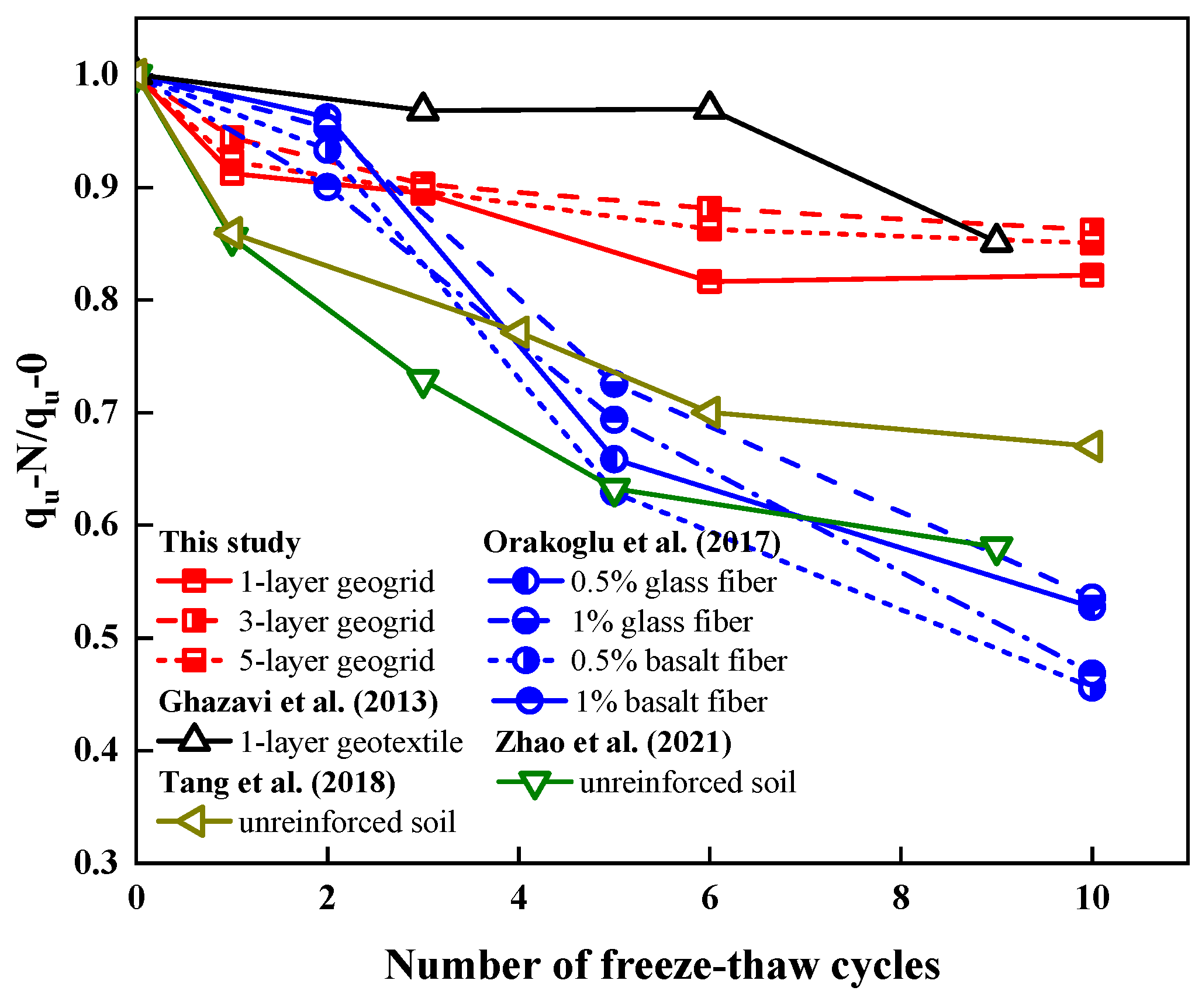
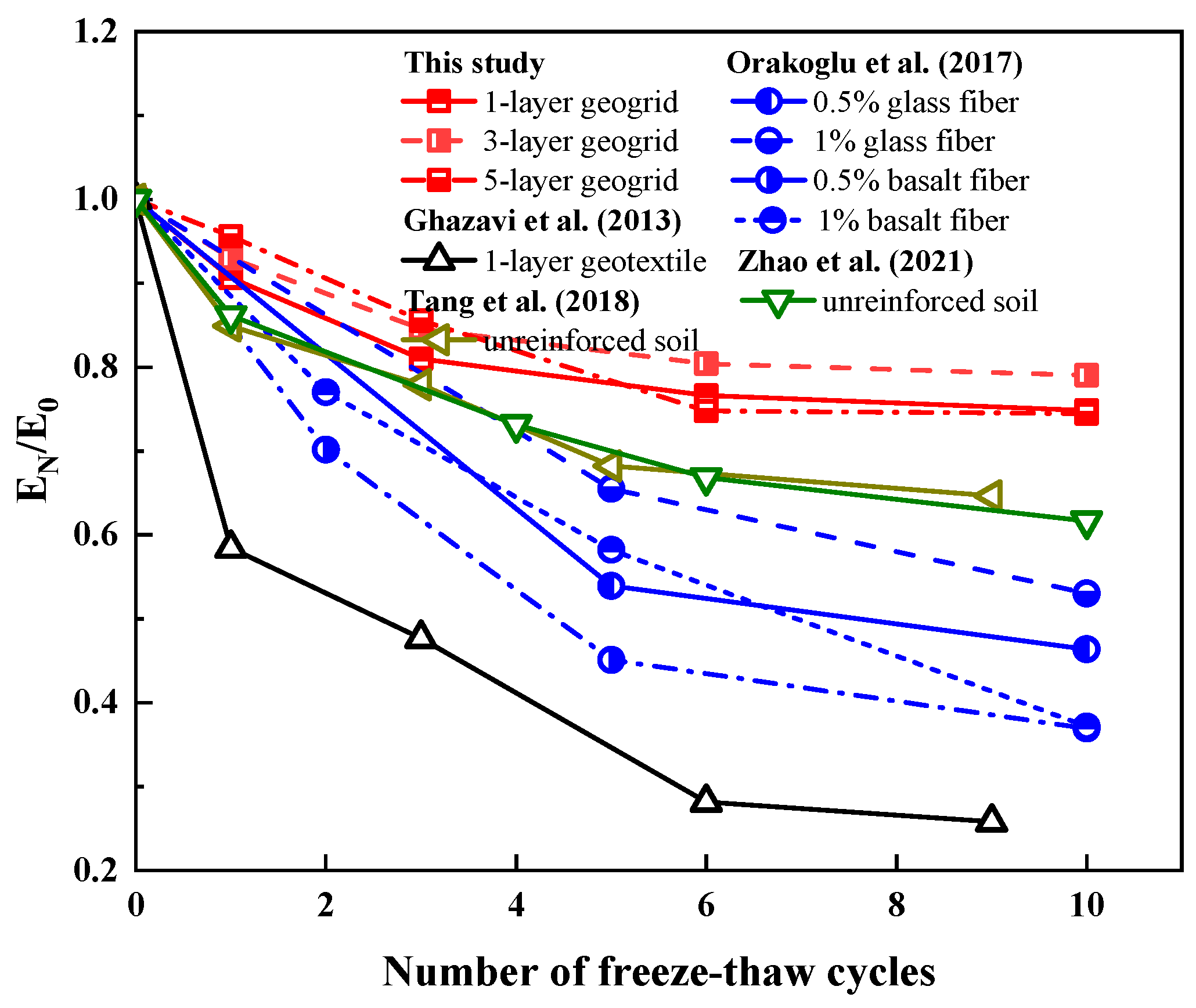
- Compared to previous studies: The correlation between elastic modulus and freeze–thaw cycle frequency in untreated expansive soil is quantitatively characterized in Figure 5f, compared to Tang et al. [9] and Zhao et al. [39]. The elastic modulus is normalized for easy comparison. Figure 5f demonstrates strong congruence between the current experimental data and established findings from prior investigations, thereby validating the methodological reliability of this study.
3.3. Shear Strength
3.4. Elastic Modulus
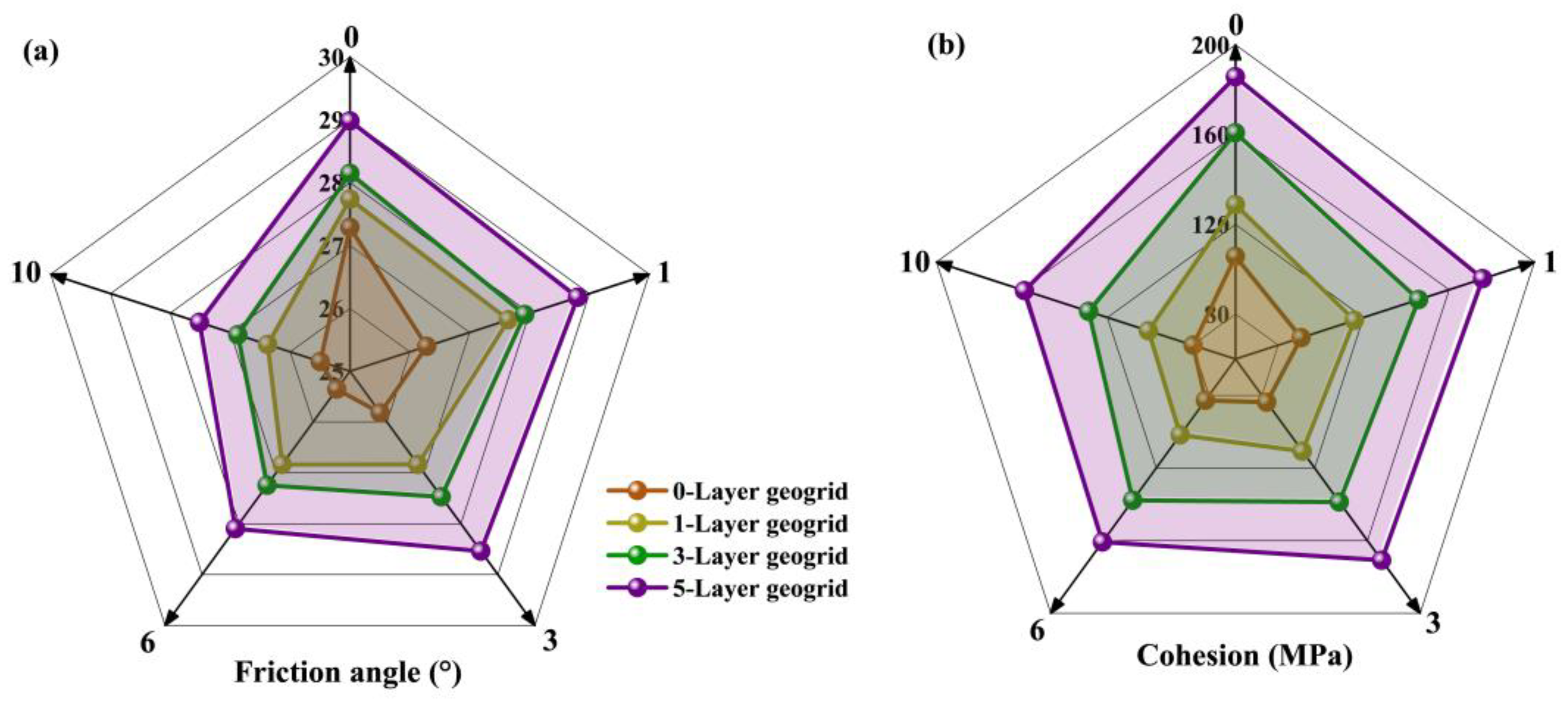
3.5. Friction Angle and Cohesion
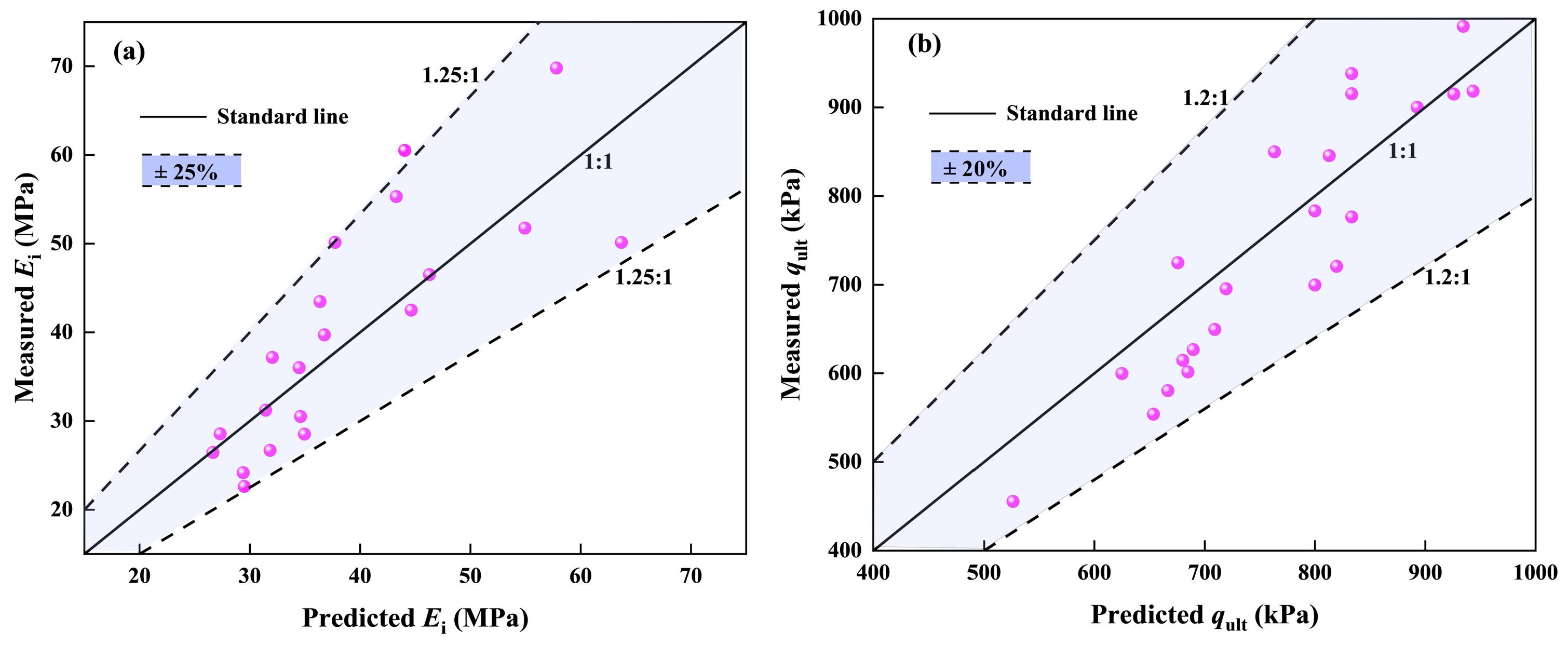
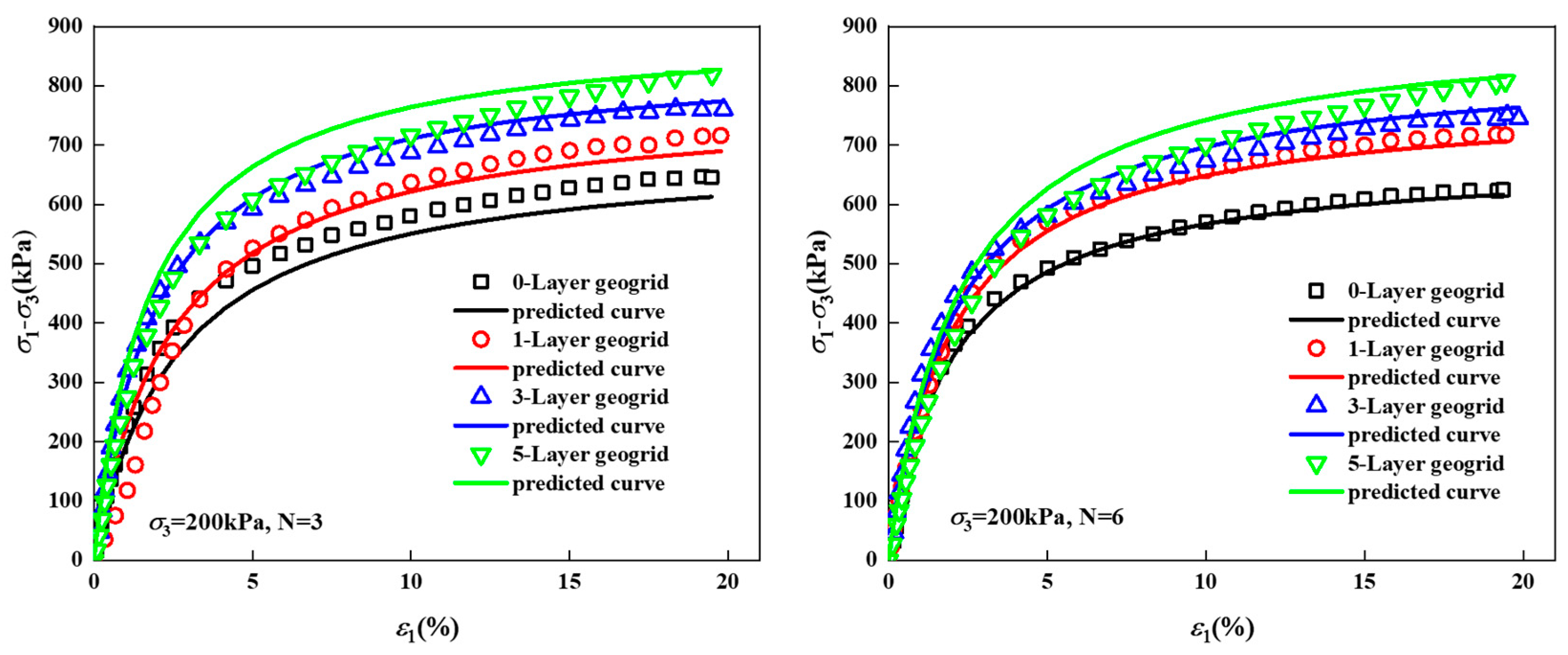
3.6. Establishment and Validation of the Empirical Formula
4. Conclusions
- (1)
- The dilatancy deformation of the expanded soils was effectively limited by geogrids, which was significantly smaller compared to the plain expanded soil. The geogrid reinforced impact zone appeared to overlap with the increase in geogrid layers when the geogrid layers exceeded three layers.
- (2)
- Friction between the expansive soil and the geogrid and the geogrid-embedded locking effect indirectly provided additional pressure, limited shear deformation. With the increase in reinforced layers, the stress–strain curve changed from strain-softening to strain-hardening type.
- (3)
- The elastic modulus first decreased and then tended to stabilize with the increase in F-T cycles; the decrease was obvious after 1–3 F-T cycles and tended to stabilize to reach dynamic equilibrium after 6 F-T cycles. After the six F-T cycles, the elastic modulus decreased by about 35.7%, 23.3%, 18.3%, and 23.5% for 0-, 1-, 3-, and 5-layer GRES.
- (4)
- The friction angle and cohesion decreased with the increment of F-T cycles and increased with the increment of geogrid layers. After the six F-T cycles, the cohesion decreased by about 24.5%, 21%, 14.3%, 14.5% for 0-, 1-, 3-, and 5-layer GRES, and 7.6%, 5.9%, 4.5%, and 5.1% of the friction angle.
- (5)
- A modified Duncan–Zhang model with the confining pressure, the F-T cycles, and the geogrid layers was proposed; the predicted values agreed with the measured values by more than 90%, which can be used as a prediction formula for the stress–strain characteristics of GRES under freeze–thaw cycling conditions. The research results can provide important theoretical support for the practical engineering design of GRES in cold regions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gavrilova, M. Climate and permafrost. Permafr. Periglac. Process. 1993, 4, 99–111. [Google Scholar] [CrossRef]
- Genc, D.; Ashlock, J.C.; Cetin, B.; Ceylan, H.; Cetin, K.; Horton, R. Comprehensive in-situ freeze-thaw monitoring under a granular-surfaced road system. Transp. Geotech. 2022, 34, 100758. [Google Scholar] [CrossRef]
- Koerner, R.M.; Koerner, G.R. A data base, statistics and recommendations regarding 171 failed geosynthetic reinforced mechanically stabilized earth (MSE) walls. Geotext. Geomembr. 2013, 40, 20–27. [Google Scholar] [CrossRef]
- Yang, B.C.; Qin, Z.P.; Zhou, Q.P.; Li, H.W.; Li, L.; Yang, X.S. Pavement damage behaviour of urban roads in seasonally frozen saline ground regions. Cold Reg. Sci. Technol. 2020, 174, 103035. [Google Scholar] [CrossRef]
- Jia, J.; Wei, H.Y.; Yang, D.H.; Wu, Y.C. The Impact of Freeze-Thaw Cycles on the Shear and Microstructural Characteristics of Compacted Silty Clay. Buildings 2023, 13, 2308. [Google Scholar] [CrossRef]
- Liu, J.K.; Chang, D.; Yu, Q.M. Influence of freeze-thaw cycles on mechanical properties of a silty sand. Eng. Geol. 2016, 210, 23–32. [Google Scholar] [CrossRef]
- Qi, J.; Vermeer, P.A.; Cheng, G. A review of the influence of freeze-thaw cycles on soil geotechnical properties. Permafr. Periglac. Process. 2006, 17, 245–252. [Google Scholar] [CrossRef]
- Qi, J.L.; Ma, W.; Song, C.X. Influence of freeze-thaw on engineering properties of a silty soil. Cold Reg. Sci. Technol. 2008, 53, 397–404. [Google Scholar] [CrossRef]
- Tang, L.; Cong, S.Y.; Geng, L.; Ling, X.Z.; Gan, F.D. The effect of freeze-thaw cycling on the mechanical properties of expansive soils. Cold Reg. Sci. Technol. 2018, 145, 197–207. [Google Scholar] [CrossRef]
- Zhang, Y.G.; Liu, S.H.; Deng, G.; Fang, B.X.; Zhang, Y.Y.; Lu, Y. Effect of freeze-thaw cycles on mechanical behavior of clay-gravel mixtures. J. Mt. Sci. 2022, 19, 3615–3626. [Google Scholar] [CrossRef]
- Zhou, Z.W.; Ma, W.; Zhang, S.J.; Mu, Y.H.; Li, G.Y. Effect of freeze-thaw cycles in mechanical behaviors of frozen loess. Cold Reg. Sci. Technol. 2018, 146, 9–18. [Google Scholar] [CrossRef]
- Estabragh, A.R.; Moghadas, M.; Javadi, A.A. Effect of different types of wetting fluids on the behaviour of expansive soil during wetting and drying. Soils Found. 2013, 53, 617–627. [Google Scholar] [CrossRef]
- Khemissa, M.; Mahamedi, A. Cement and lime mixture stabilization of an expansive overconsolidated clay. Appl. Clay Sci. 2014, 95, 104–110. [Google Scholar] [CrossRef]
- Seco, A.; Ramírez, F.; Miqueleiz, L.; García, B. Stabilization of expansive soils for use in construction. Appl. Clay Sci. 2011, 51, 348–352. [Google Scholar] [CrossRef]
- Li, G.X. From “Xi-rang” to geosynthetics. Chin. J. Geotech. Eng. 2013, 35, 144–149. [Google Scholar]
- Fan, K.; Pei, Q.; Liu, L.; Han, Z.; Zou, W. Strength and microstructure of a lignin fiber-reinforced expansive soil in cold regions. Geosynth. Int. 2022, 29, 622–629. [Google Scholar] [CrossRef]
- Liu, C.; Lv, Y.R.; Yu, X.J.; Wu, X. Effects of freeze-thaw cycles on the unconfined compressive strength of straw fiber-reinforced soil. Geotext. Geomembr. 2020, 48, 581–590. [Google Scholar] [CrossRef]
- Sun, Z.X.; Wang, R.C.; Yang, Z.N.; Lv, J.H.; Shi, W.; Ling, X.Z. Dynamic Behavior of Rubber Fiber-Reinforced Expansive Soil under Repeated Freeze-Thaw Cycles. Polymers 2024, 16, 2817. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.N.; Sun, Z.X.; Ling, X.Z.; Cai, G.J.; Wang, R.C.; Meng, X. Influence of Mixing Rubber Fibers on the Mechanical Properties of Expansive Clay under Freeze-Thaw Cycles. Appl. Sci. 2024, 14, 5437. [Google Scholar] [CrossRef]
- Yarbasi, N. Effect of Freeze-Thaw on Compressive Strength of Clayey Soils Reinforced with Wool. J. Nat. Fibers 2022, 19, 382–393. [Google Scholar] [CrossRef]
- Zhang, L.F.; Hu, Z.Q.; Li, H.R.; She, H.C.; Wang, X.L.; Han, X.N.; Yang, X. Mechanical Properties and Mesostructure Evolution of Fibre-Reinforced Loess under Freeze-Thaw Cycles. Adv. Civ. Eng. 2023, 2023, 3847003. [Google Scholar] [CrossRef]
- Lai, Y.M.; Zhang, S.M.; Yu, W.B. A new structure to control frost boiling and frost heave of embankments in cold regions. Cold Reg. Sci. Technol. 2012, 79–80, 53–66. [Google Scholar] [CrossRef]
- Li, C.; Vennapusa, P.K.R.; Ashlock, J.; White, D.J. Mechanistic-based comparisons for freeze-thaw performance of stabilized unpaved roads. Cold Reg. Sci. Technol. 2017, 141, 97–108. [Google Scholar] [CrossRef]
- Wang, D.R.; Wang, S.L.; Tighe, S.; Bhat, S.; Yin, S.D. Construction of Geosynthetic-Reinforced Pavements and Evaluation of Their Impacts. Appl. Sci. 2023, 13, 10327. [Google Scholar] [CrossRef]
- Tiwari, N.; Satyam, N. An experimental study on strength improvement of expansive subgrades by polypropylene fibers and geogrid reinforcement. Sci. Rep. 2022, 12, 6685. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.T.; Liu, F.C.; Yang, J. Stress-strain-strength behavior of geosynthetic reinforced rubber-sand mixtures. Acta Geotech. 2023, 18, 4835–4846. [Google Scholar] [CrossRef]
- Bai, Q.Y.; Liu, J.; Wang, Y.; Du, H.Y.; Wang, B. Experimental Investigation of Interface Characteristics between Geogrid and Coarse-Grained Soil in a Seasonally Frozen Area. Appl. Sci. 2022, 12, 10187. [Google Scholar] [CrossRef]
- Meng, Y.; Xu, C.; Yang, Y.; Du, C.X.; Jia, B.; Zhao, C.X. Study on the mechanism of freeze-thaw cycles on the shear strength of geogrid-sand interface. Cold Reg. Sci. Technol. 2024, 225, 104275. [Google Scholar] [CrossRef]
- Wang, Z.J.; Jacobs, F.; Ziegler, M. Visualization of load transfer behaviour between geogrid and sand using PFC2D. Geotext. Geomembr. 2014, 42, 83–90. [Google Scholar] [CrossRef]
- Cui, F.; Xiao, C.; Han, J.; Gao, S.; Tian, W. Performance of laboratory geogrid-reinforced retaining walls under freeze-thaw cycles. Geosynth. Int. 2022, 29, 81–98. [Google Scholar] [CrossRef]
- Xiao, C.Z.; Cui, F.L.; Ding, L.Q.; Wang, F.; Tian, W.L. Temperature Distributions in Geogrid-Reinforced Soil Retaining Walls Subjected to Seasonal Freeze-Thaw Cycles. Int. J. Geomech. 2022, 22, 04022234. [Google Scholar] [CrossRef]
- GB/T 50123-2019; Standard for geotechnical testing method. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2019.
- Kravchenko, E.; Liu, J.K.; Niu, W.W.; Zhang, S.J. Performance of clay soil reinforced with fibers subjected to freeze-thaw cycles. Cold Reg. Sci. Technol. 2018, 153, 18–24. [Google Scholar] [CrossRef]
- Orakoglu, M.E.; Liu, J. Effect of freeze-thaw cycles on triaxial strength properties of fiber-reinforced clayey soil. KSCE J. Civ. Eng. 2017, 21, 2128–2140. [Google Scholar] [CrossRef]
- Ghazavi, M.; Roustaie, M. The influence of freeze–thaw cycles on the unconfined compressive strength of fiber-reinforced clay. Cold Reg. Sci. Technol. 2010, 61, 125–131. [Google Scholar] [CrossRef]
- Roustaei, M.; Eslami, A.; Ghazavi, M. Effects of freeze–thaw cycles on a fiber reinforced fine grained soil in relation to geotechnical parameters. Cold Reg. Sci. Technol. 2015, 120, 127–137. [Google Scholar] [CrossRef]
- Wang, X.; Guo, M.; Hu, B. Triaxial testing study of expansive soil reinforced with geogrid. Rock Soil Mech. 2011, 32, 1649–1653. [Google Scholar] [CrossRef]
- Cui, K.; Zhang, D.J.; Li, Q.L.; Yang, S.C.; Zhang, H.D. Experimental investigation on the accumulated strain of coarse-grained soil reinforced by geogrid under high-cycle cyclic loading. Geotext. Geomembr. 2023, 51, 233–244. [Google Scholar] [CrossRef]
- Zhao, G.T.; Han, Z.; Zou, W.L.; Wang, X.Q. Evolution of mechanical behaviours of an expansive soil during drying-wetting, freeze–thaw, and drying-wetting-freeze–thaw cycles. Bull. Eng. Geol. Environ. 2021, 80, 8109–8121. [Google Scholar] [CrossRef]
- Han, X.N.; Hu, Z.Q.; Li, H.R.; Yin, Y.; Zhang, B.B.; Zhang, L.F. Study on the mechanical properties and microstructural evolution of loess under different wet-dry and freeze-thaw coupled cycling paths. Case Stud. Constr. Mater. 2024, 21, e03924. [Google Scholar] [CrossRef]
- Zou, W.L.; Han, Z.; Zhao, G.T.; Fan, K.W.; Vanapalli, S.K.; Wang, X.Q. Effects of cyclic freezing and thawing on the shear behaviors of an expansive soil under a wide range of stress levels. Environ. Earth Sci. 2022, 81, 77. [Google Scholar] [CrossRef]
- Wang, D.Y.; Ma, W.; Niu, Y.H.; Chang, X.X.; Wen, Z. Effects of cyclic freezing and thawing on mechanical properties of Qinghai–Tibet clay. Cold Reg. Sci. Technol. 2007, 48, 34–43. [Google Scholar] [CrossRef]
- Ghazavi, M.; Roustaei, M. Freeze–thaw performance of clayey soil reinforced with geotextile layer. Cold Reg. Sci. Technol. 2013, 89, 22–29. [Google Scholar] [CrossRef]
- Wei, L.; Chai, S.X.; Xue, M.L.; Wang, P.; Li, F. Structural damage and shear performance degradation of fiber-lime-soil under freeze-thaw cycling. Geotext. Geomembr. 2022, 50, 845–857. [Google Scholar] [CrossRef]
- Li, L.; Shao, W.; Li, Y.; Cetin, B. Effects of climatic factors on mechanical properties of cement and fiber reinforced clays. Geotech. Geol. Eng. 2015, 33, 537–548. [Google Scholar] [CrossRef]
- Duncan, J.M.; Chang, C.-Y. Nonlinear analysis of stress and strain in soils. J. Soil Mech. Found. Div. 1970, 96, 1629–1653. [Google Scholar] [CrossRef]



| Natural Moisture Content/% | Optimal Moisture Content/% | Saturated Moisture Content/% | Dry Density /(g/cm³) | Free Swelling Rate/% | Cohesion /MPa | Friction Angle/° |
|---|---|---|---|---|---|---|
| 5.67 | 18 | 34.8 | 1.6 | 90 | 11.5 | 27.3 |
| Material | Elongation/% | Grid Size / mm | Elastic Modulus/GPa | Tensile Strength/(KN/m) | |
|---|---|---|---|---|---|
| Longitudinal | Transversal | ||||
| polypropylene | ≤10 | 20 × 20 | 65 | 25 | 25 |
| Test Condition | F-T (N) | Geogrid Layers | Confining Pressure/kPa | Loading Rate/mm∙min−1 |
|---|---|---|---|---|
| CU | 0/1/3/6/10 | 0/1/3/5 | 100/200/300 | 0.2 |
| Sample Number | F-T | Geogrid Layers | Confining Pressure/kPa | /MPa | /kPa | |
|---|---|---|---|---|---|---|
| GRES-1 | 0 | 3 | 200 | 63.69 | 925.9 | 0.999 |
| GRES-2 | 1 | 37.74 | 892.9 | 0.999 | ||
| GRES-3 | 3 | 36.36 | 833.3 | 0.999 | ||
| GRES-4 | 6 | 36.76 | 813 | 0.999 | ||
| GRES-5 | 10 | 32.05 | 800 | 0.999 | ||
| GRES-6 | 3 | 0 | 200 | 26.45 | 719.4 | 0.999 |
| GRES-7 | 1 | 31.21 | 773.3 | 0.999 | ||
| GRES-8 | 3 | 36.36 | 833.3 | 0.999 | ||
| GRES-9 | 5 | 44.05 | 917.4 | 0.999 | ||
| GRES-10 | 10 | 3 | 100 | 27.32 | 601.59 | 0.994 |
| GRES-11 | 200 | 32.05 | 801.25 | 0.999 | ||
| GRES-12 | 300 | 43.36 | 961.58 | 0.999 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Liu, J.; Zhang, R.; Shi, W.; Yuan, S. Shear Resistance Evolution of Geogrid Reinforced Expansive Soil Under Freeze–Thaw Cycles. Appl. Sci. 2025, 15, 5492. https://doi.org/10.3390/app15105492
Yang Z, Liu J, Zhang R, Shi W, Yuan S. Shear Resistance Evolution of Geogrid Reinforced Expansive Soil Under Freeze–Thaw Cycles. Applied Sciences. 2025; 15(10):5492. https://doi.org/10.3390/app15105492
Chicago/Turabian StyleYang, Zhongnian, Jia Liu, Runbo Zhang, Wei Shi, and Shaopeng Yuan. 2025. "Shear Resistance Evolution of Geogrid Reinforced Expansive Soil Under Freeze–Thaw Cycles" Applied Sciences 15, no. 10: 5492. https://doi.org/10.3390/app15105492
APA StyleYang, Z., Liu, J., Zhang, R., Shi, W., & Yuan, S. (2025). Shear Resistance Evolution of Geogrid Reinforced Expansive Soil Under Freeze–Thaw Cycles. Applied Sciences, 15(10), 5492. https://doi.org/10.3390/app15105492