Robot Joint Vibration Suppression Method Based on Improved ADRC
Abstract
1. Introduction
- (1)
- The parameters of dampers or structural optimization are fixed, making it difficult to cope with dynamic load variations or complex environments (such as changes in temperature and humidity).
- (2)
- Although mechanical vibration absorbers can achieve broadband vibration suppression, their adjustment range is limited by the physical properties of the materials and cannot adapt to high-frequency abrupt vibrations.
- (3)
- Model-based active control, such as input shaping algorithms, requires an accurate robot dynamics model. However, the nonlinear and time-varying characteristics of robot systems can easily lead to changes in the model.
- (4)
- There is a discrepancy between laboratory environments and real-world scenarios. Most studies validate their methods in ideal conditions, such as constant-temperature and electromagnetic interference-free environments, without considering the multi-variable and multi-disturbance characteristics of industrial sites.
2. Mathematical Model of Robot Joint Module
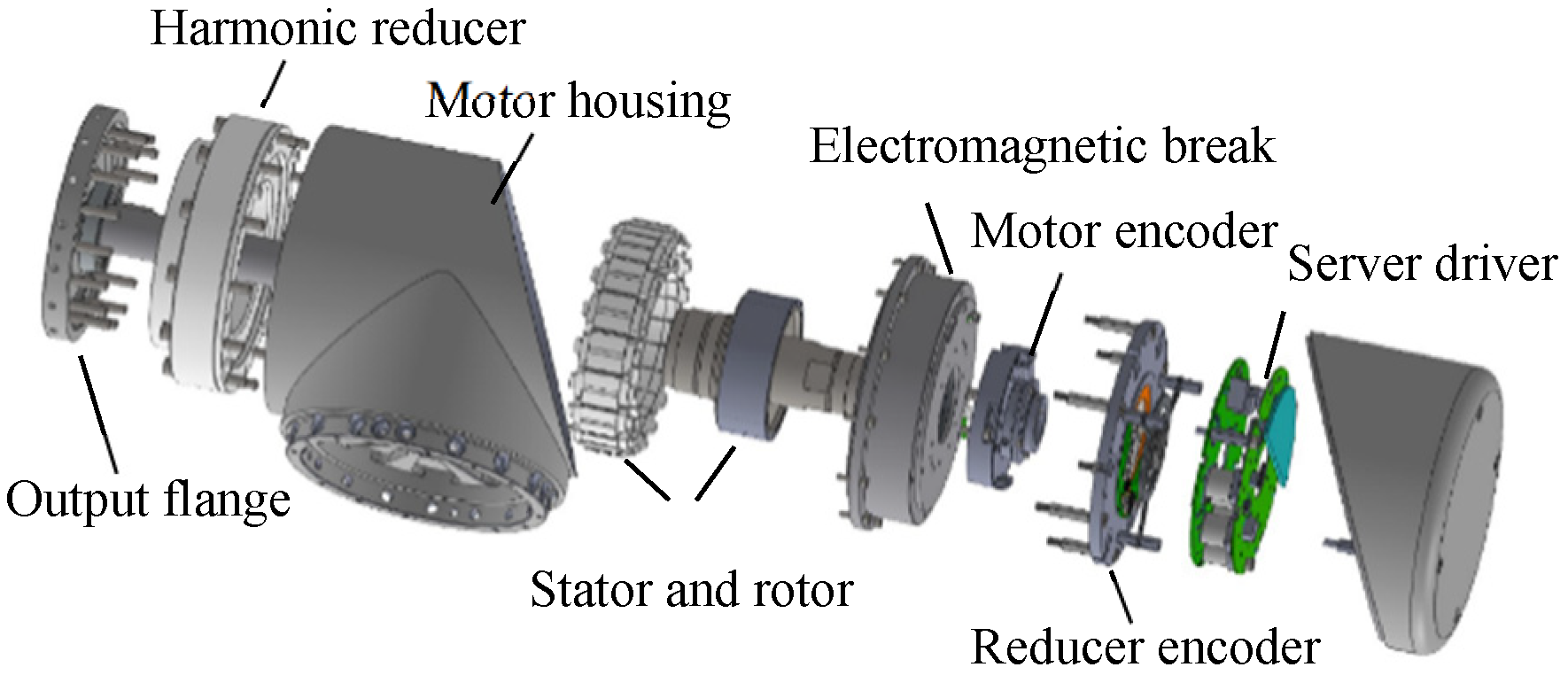
2.1. Structure of Harmonic Reducer
2.2. Dynamic Response Analysis of Robot Joint Module
3. ADRC Control of Robot Joint Module
3.1. Vibration Disturbance Model of Joint Module
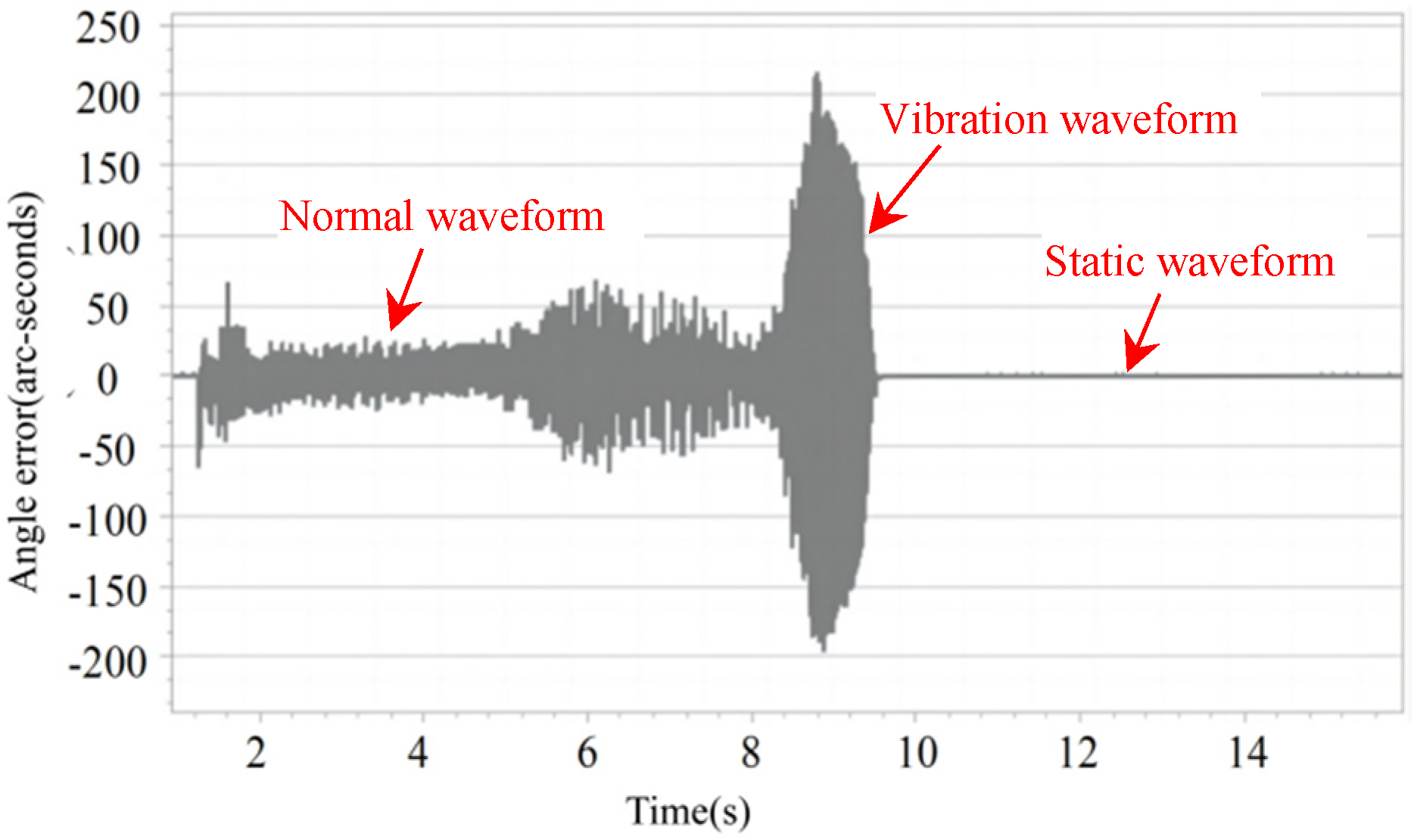
3.1.1. Extraction of Vibration Signals
3.1.2. Vibration Model Analysis of Robot Joint Module
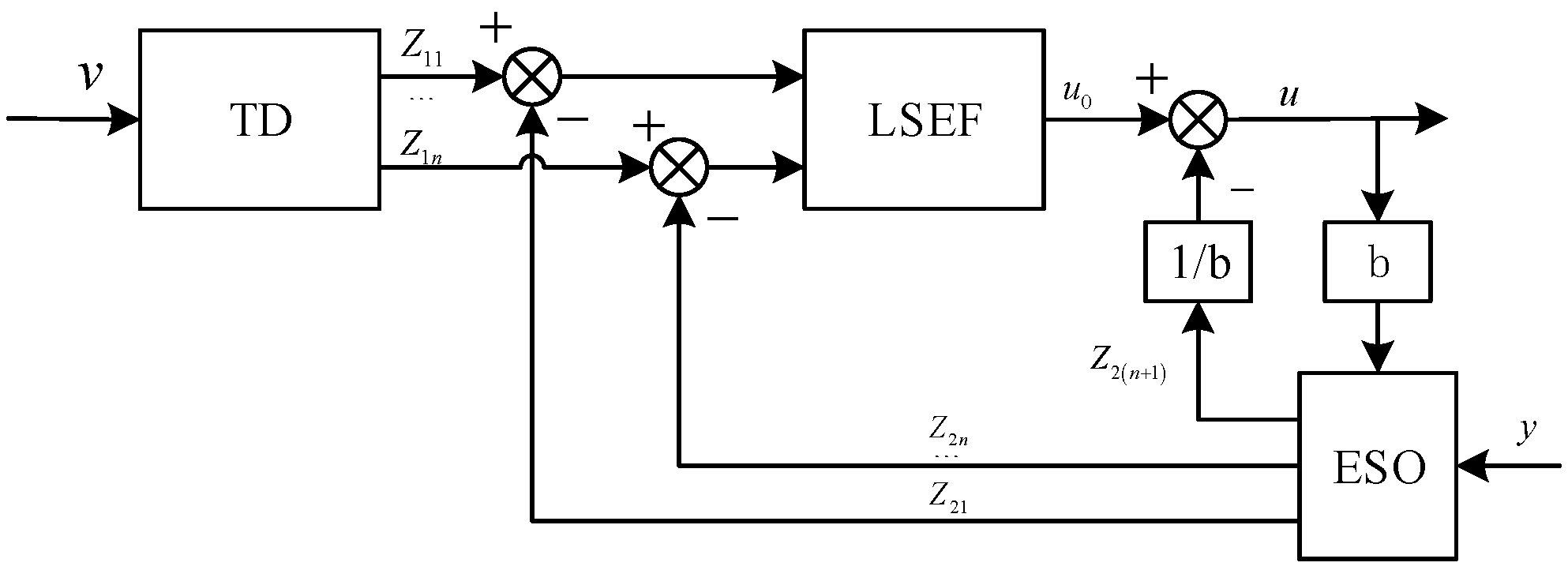
3.2. ESO Design
3.2.1. Mathematical Model of PMSM
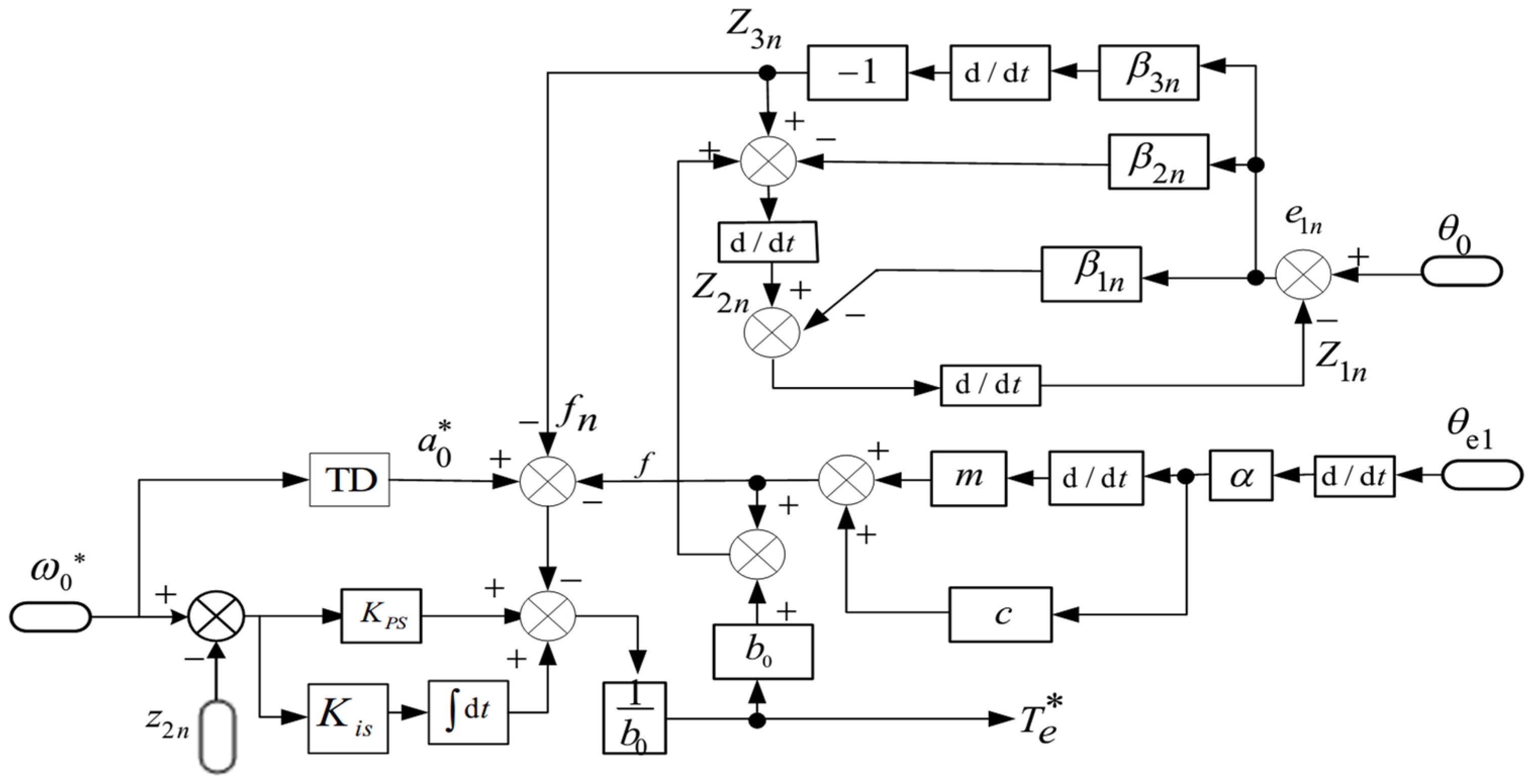
3.2.2. Speed Loop ESO Design
3.2.3. Mathematical Stability Analysis of ADRC
3.2.4. LSEF Design
3.3. ADRC Control Strategy
4. Comparison and Analysis of Experimental Results
4.1. Experimental Setup and Methods
4.1.1. Robot Integrated Joint Module and Collaborative Robot
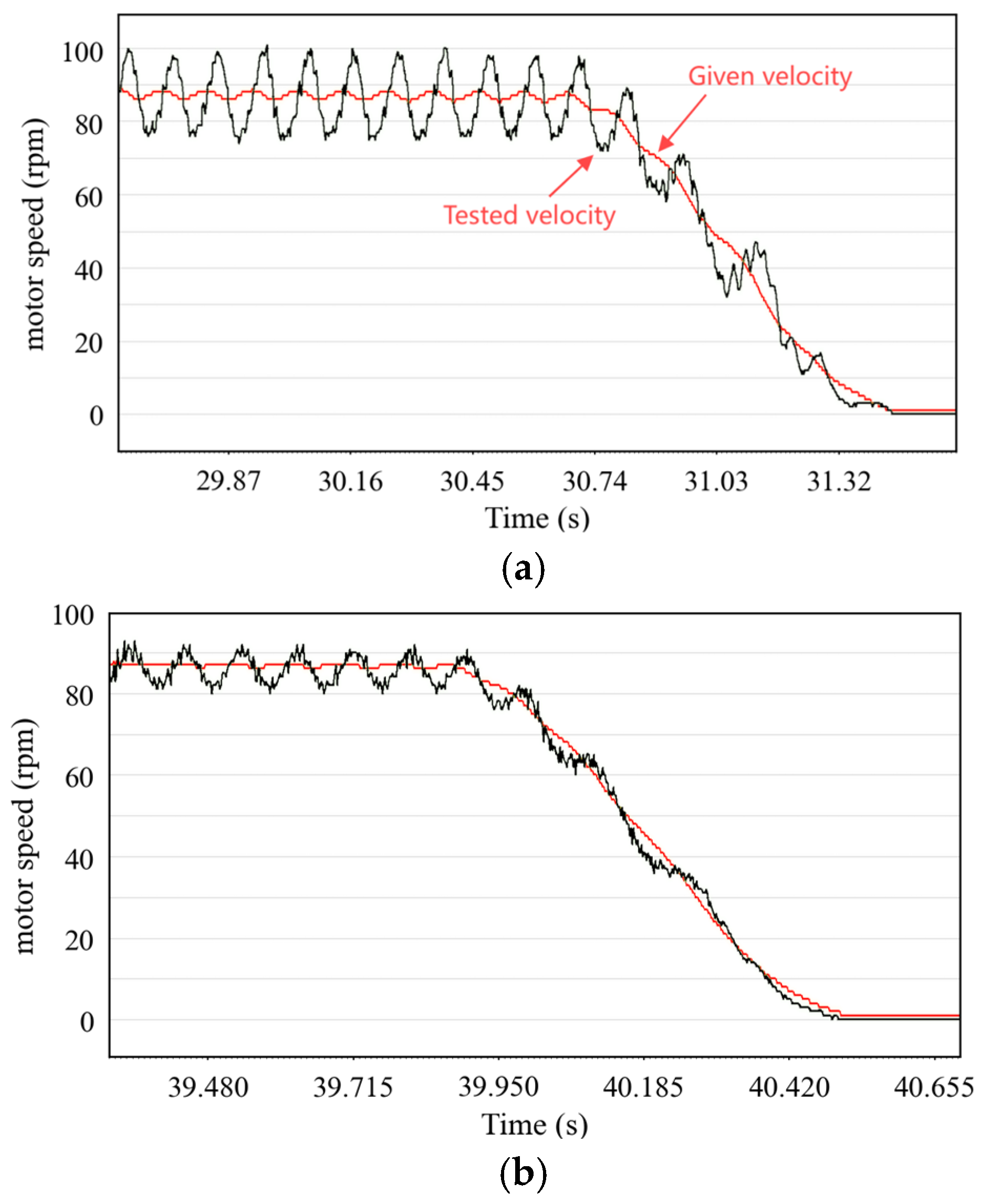
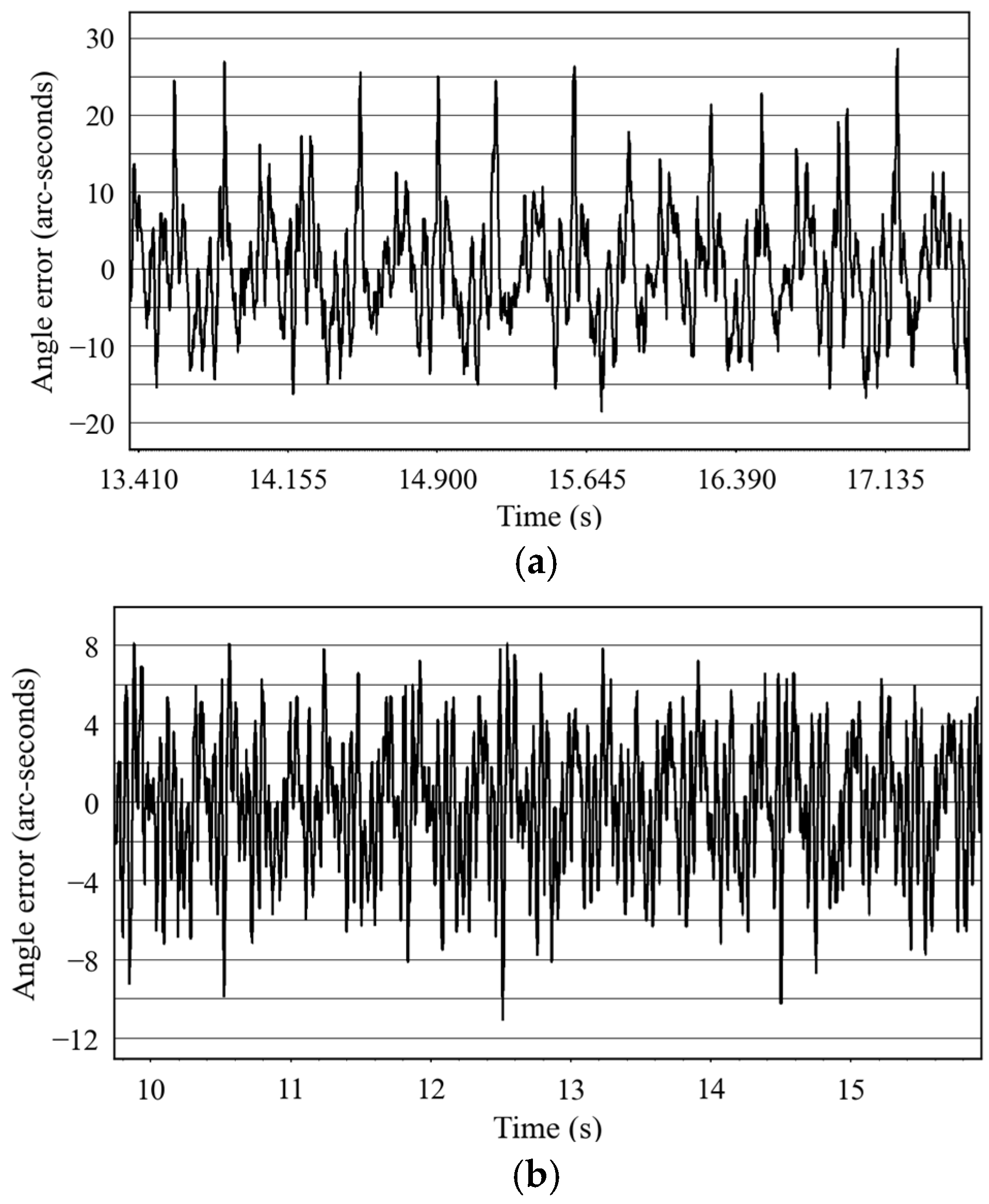
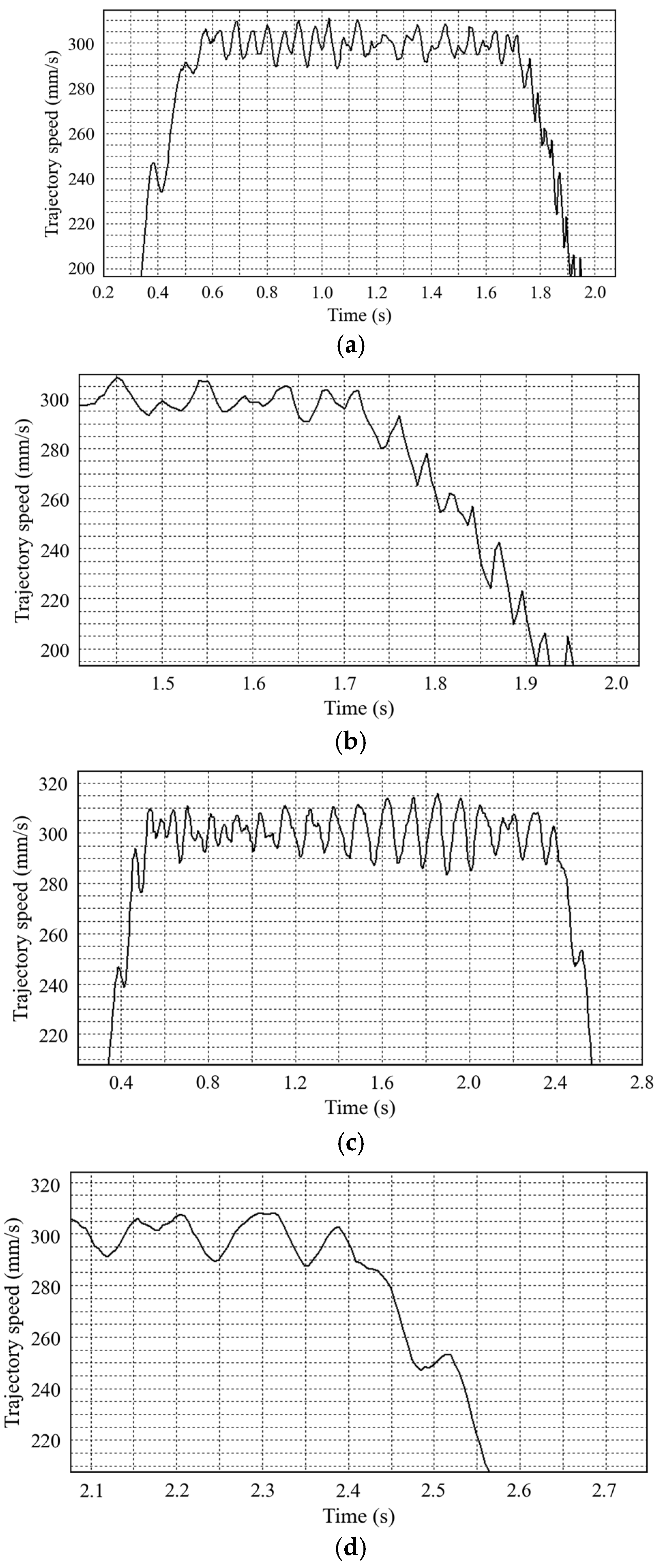
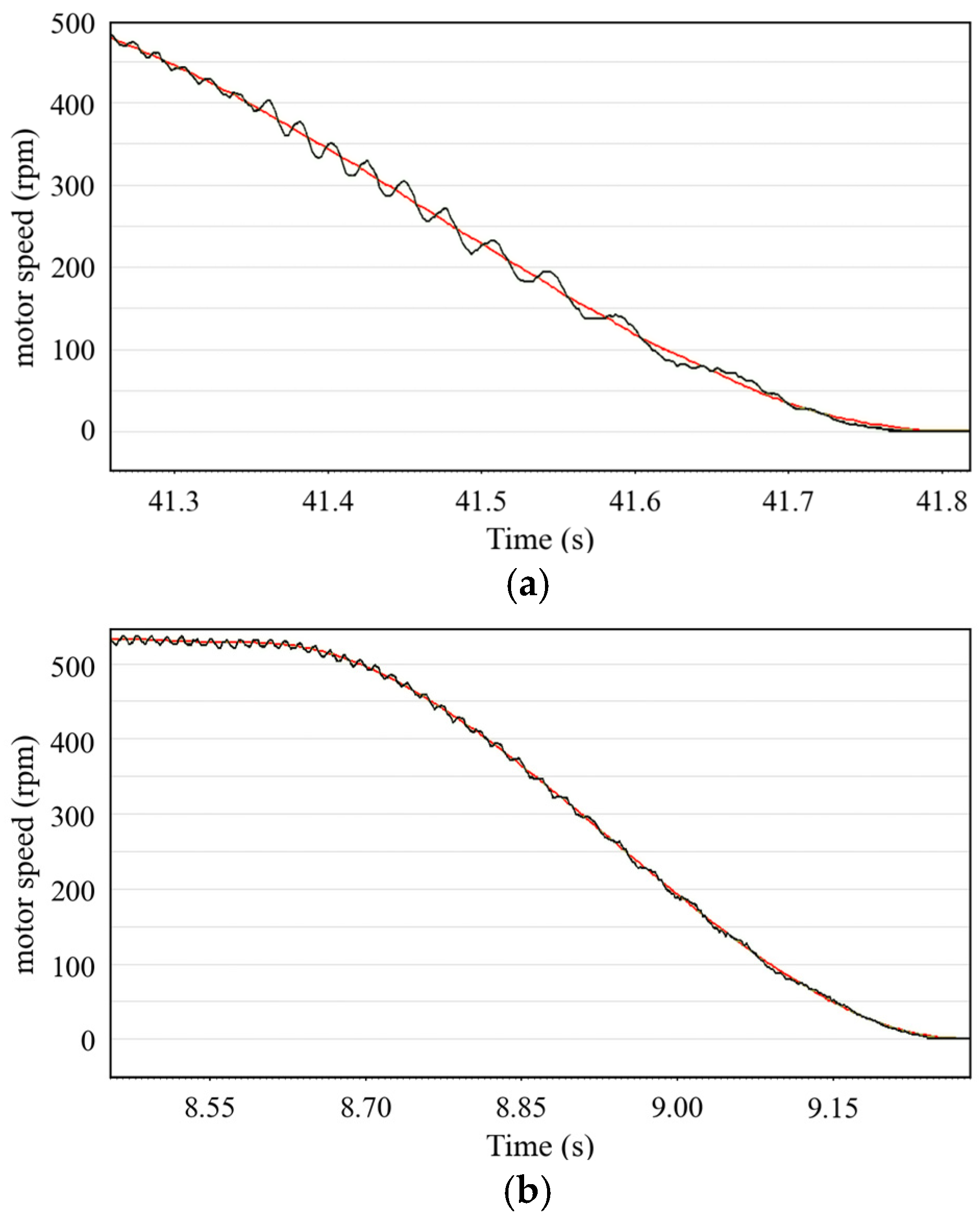
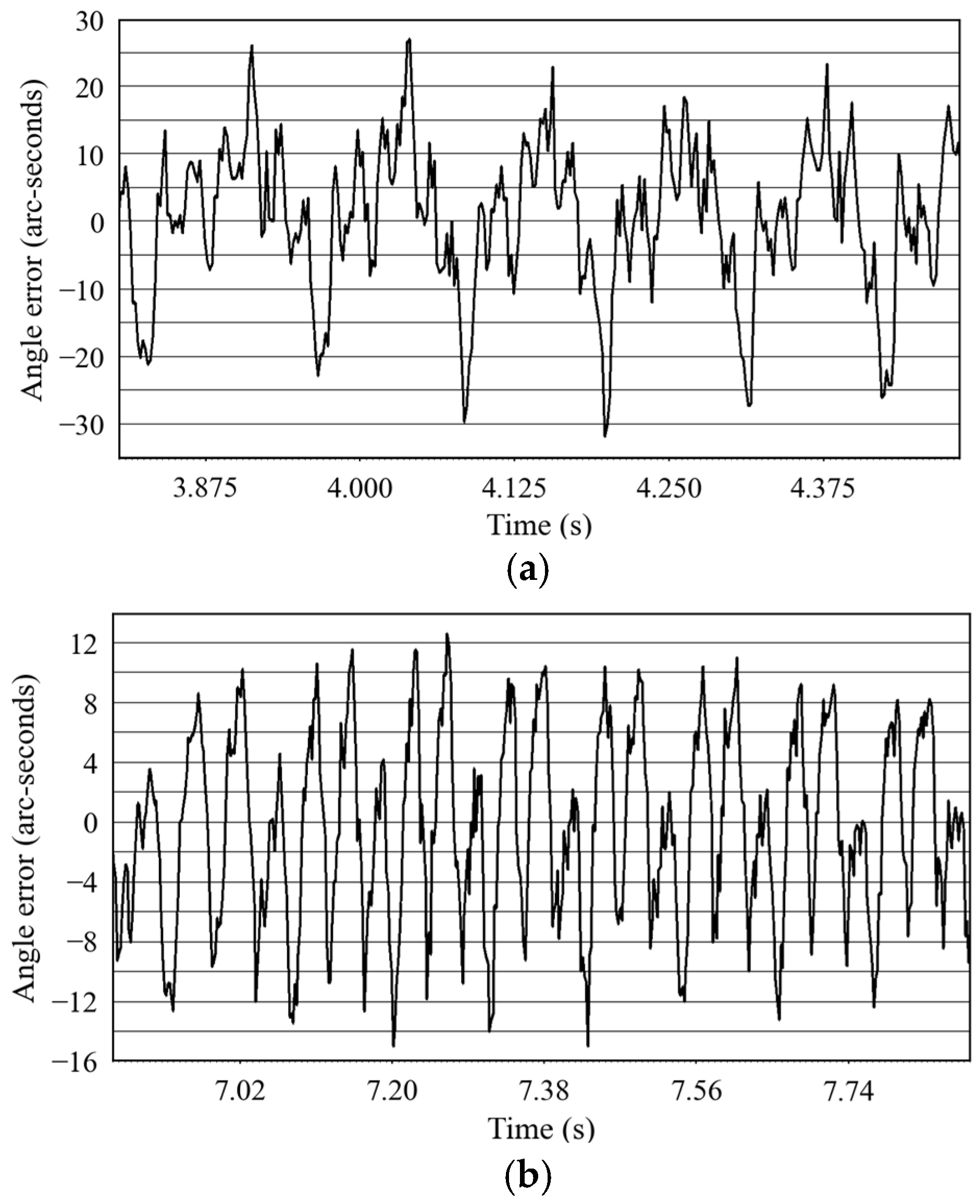
4.1.2. Experimental Results and Analysis
- (1)
- Robot trajectory jitter waveform.
- (2)
- Velocity waveform of robot joint module PMSM.
- (3)
- data waveform.
- (4)
- The vibration peak data read by the vibrometer.
- A.
- Experimental results of 50 mm/s
- B.
- Experimental results of 300 mm/s
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation Expression | Complete Expression |
| PMSM | permanent magnet synchronous motor |
| ADRC | disturbance rejection control |
| FEM | finite element method |
| SBE | spatial beam element |
| TD | tracking differentiator |
| LSEF | linear state error feedback |
| ESO | extended state observer |
| FOC | field-oriented control |
References
- Javaid, M.; Haleem, A.; Singh, R.P.; Suman, R. Substantial capabilities of robotics in enhancing industry 4.0 implementation. Cogn. Robot. 2021, 1, 58–75. [Google Scholar] [CrossRef]
- Islam, R.U.; Iqbal, J.; Manzoor, S.; Khalid, A.; Khan, S. An autonomous image-guided robotic system simulating industrial applications. In Proceedings of the 2012 7th International Conference on System of Systems Engineering (SoSE), Genova, Italy, 16–19 July 2012; pp. 344–349. [Google Scholar] [CrossRef]
- Erden, M.S.; Billard, A. Hand impedance measurements during interactive manual welding with a robot. IEEE Trans. Robot. 2015, 31, 168–179. [Google Scholar] [CrossRef]
- Ma, X.; He, X.; Wang, Y.; Jin, L.; Xu, Y.; Yao, J.; Zhao, Y. Error identification and accuracy compensation algorithm for improved 2RPU/UPR+R+P hybrid robot. IEEE Robot. Autom. Lett. 2024, 9, 8547–8554. [Google Scholar] [CrossRef]
- Gong, J.; Cai, G.; Wei, W.; Zhang, K.; Peng, S. Research on the Residual Vibration Suppression of a Controllable Mechanism Robot. IEEE Access 2022, 10, 39436–39455. [Google Scholar] [CrossRef]
- Sancak, C.; Itik, M. Out-of-Plane Vibration Suppression and Position Control of a Planar Cable-Driven Robot. IEEE/ASME Trans. Mechatron. 2022, 27, 1311–1320. [Google Scholar] [CrossRef]
- Maki, T.; Zhao, M.; Okada, K.; Inaba, M. Elastic vibration suppression control for multilinked aerial robot using redundant degrees-of-freedom of thrust force. IEEE Robot. Autom. Lett. 2022, 7, 2859–2866. [Google Scholar] [CrossRef]
- Yang, Z.; Xu, X.; Kuang, M.; Zhu, D.; Yan, S.; Ge, S.S.; Ding, H. Dynamic compliant force control strategy for suppressing vibrations and over-grinding of robotic belt grinding system. IEEE Trans. Autom. Sci. Eng. 2024, 21, 4536–4547. [Google Scholar] [CrossRef]
- Sun, L.; Yin, W.; Wang, M.; Liu, J. Position control for flexible joint robot based on online gravity compensation with vibration suppression. IEEE Trans. Ind. Electron. 2018, 65, 4840–4848. [Google Scholar] [CrossRef]
- Park, J.; Chang, P.-H.; Park, H.-S.; Lee, E. Design of learning input shaping technique for residual vibration suppression in an industrial robot. IEEE/ASME Trans. Mechatron. 2006, 11, 55–65. [Google Scholar] [CrossRef]
- Zhang, G.; Furusho, J.; Sakaguchi, M. Vibration suppression control of robot arms using a homogeneous-type electrorheological fluid. IEEE/ASME Trans. Mechatron. 2000, 5, 302–309. [Google Scholar] [CrossRef]
- Ramirez-Neria, M.; Sira-Ramirez, H.; Garrido-Moctezuma, R.; Luviano-Juarez, A.; Gao, Z. Active disturbance rejection control for reference trajectory tracking tasks in the pendubot system. IEEE Access 2021, 9, 102663–102670. [Google Scholar] [CrossRef]
- Shen, W.; Lou, Z.; Du, Z.; Gao, H.; Wang, X. Torque sensor developed with a strain rosette ring for in situ integration in harmonic reducer. IEEE Sens. J. 2024, 24, 25802–25813. [Google Scholar] [CrossRef]
- Song, Y.; Huang, H.; Liu, F.; Xi, F.; Zhou, D.; Li, B. Torque estimation for robotic joint with harmonic reducer based on deformation calibration. IEEE Sens. J. 2020, 20, 991–1002. [Google Scholar] [CrossRef]
- Garcia, O.; Avial, M.; Cobos, J.; Uceda, J.; Gonzalez, J.; Navas, J. Harmonic reducer converter. IEEE Trans. Ind. Electron. 2003, 50, 322–327. [Google Scholar] [CrossRef]
- Miyazaki, T.; Ohishi, K. Robust speed control system considering vibration suppression caused by angular transmission error of planetary gear. IEEE/ASME Trans. Mechatron. 2002, 7, 235–244. [Google Scholar] [CrossRef]
- Sira-Ramirez, H.; Linares-Flores, J.; Garcia-Rodriguez, C.; Contreras-Ordaz, M.A. On the control of the permanent magnet synchronous motor: An active disturbance rejection control approach. IEEE Trans. Control Syst. Technol. 2014, 22, 2056–2063. [Google Scholar] [CrossRef]
- Zhao, J.; Yan, S. Coupling vibration analysis for harmonic drive in joint and flexible arm undergoing large range motion. In Proceedings of the 2016 International Symposium on Flexible Automation (ISFA), Cleveland, OH, USA, 1–3 August 2016; pp. 442–449. [Google Scholar] [CrossRef]
- Xu, M. Research on composite vibration damping system based on adaptive gasket. In Proceedings of the 2022 International Conference on Manufacturing, Industrial Automation and Electronics (ICMIAE), Rimini, Italy, 26–28 August 2022; pp. 11–15. [Google Scholar] [CrossRef]
- Ahn, J.-H.; Choi, J.-Y.; Park, C.H.; Han, C.; Kim, C.-W.; Yoon, T.-G. Correlation between rotor vibration and mechanical stress in ultra-high-speed permanent magnet synchronous motors. IEEE Trans. Magn. 2017, 53, 8209906. [Google Scholar] [CrossRef]
- Liu, P.; Wu, Z. Resonance analysis and suppression of harmonic reducer in low speed servo system. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 2873–2878. [Google Scholar] [CrossRef]
- Wang, F.; Zuo, K.; Tao, P.; Rodríguez, J. High performance model predictive control for PMSM by using stator current mathematical model self-regulation technique. IEEE Trans. Power Electron. 2020, 35, 13652–13662. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Z.; Zhang, P.; Zhang, Y. Model predictive current control for PMSM drives based on nonparametric prediction model. IEEE Trans. Transp. Electrif. 2024, 10, 711–719. [Google Scholar] [CrossRef]
- El-Sousy, F.F.M.; Amin, M.M.; Soliman, A.S.; Mohammed, O.A. Optimal adaptive ultra-local model-free control based-extended state observer for PMSM driven single-axis servo mechanism system. IEEE Trans. Ind. Appl. 2024, 60, 7728–7745. [Google Scholar] [CrossRef]
- Xue, W.; Bai, W.; Yang, S.; Song, K.; Huang, Y.; Xie, H. ADRC with adaptive extended state observer and its application to air–fuel ratio control in gasoline engines. IEEE Trans. Ind. Electron. 2015, 62, 5847–5857. [Google Scholar] [CrossRef]
- Zhao, Z.-L.; Guo, B.-Z. On convergence of nonlinear extended stated observers with switching functions. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 664–669. [Google Scholar]
- Guo, B.-Z.; Zhao, Z.-L. On convergence of tracking differentiator and application to frequency estimation of sinusoidal signals. In Proceedings of the 2011 8th Asian Control Conference (ASCC), Kaohsiung, Taiwan, 15–18 May 2011; pp. 1470–1475. [Google Scholar]
- Garran, P.T.; Garcia, G. Design of an optimal PID controller for a coupled tanks system employing ADRC. IEEE Lat. Am. Trans. 2017, 15, 189–196. [Google Scholar] [CrossRef]
- Muñoz-Hernandez, G.A.; Díaz-Téllez, J.; Estevez-Carreon, J.; García-Ramírez, R.S. ADRC attitude controller based on ROS for a two-wheeled self-balancing mobile robot. IEEE Access 2023, 11, 94636–94646. [Google Scholar] [CrossRef]





| Item | Parameters | Unit |
|---|---|---|
| Rated speed | 1500 | rpm |
| Rated current | 19.4 | A |
| Rated torque | 3.32 | N∙m |
| Phase resistance | 0.25 | ohms |
| Phase inductance | 4.9 | mH |
| Back electromotive force | 13.6 | Vrms/krpm |
| Encoder resolution | 20 | bit |
| Harmonic reducer transmission ratio | 1:81 | |
| Rated torque of harmonic reducer | 107 | N∙m |
| Peak torque of harmonic reducer | 169 | N∙m |
| Positioning accuracy | 25 | arcseconds |
| Algorithm | Vector Control | ADRC |
|---|---|---|
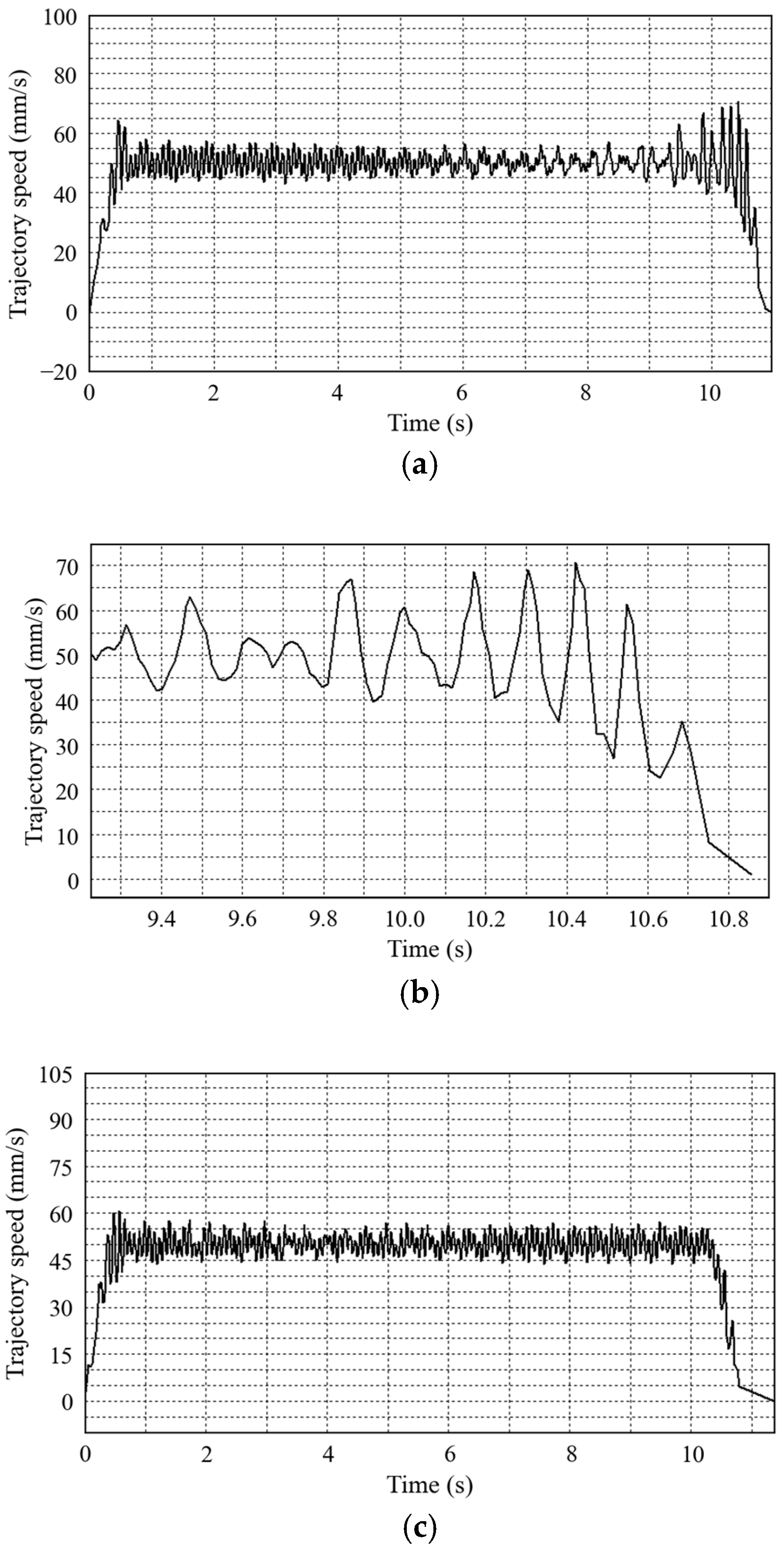
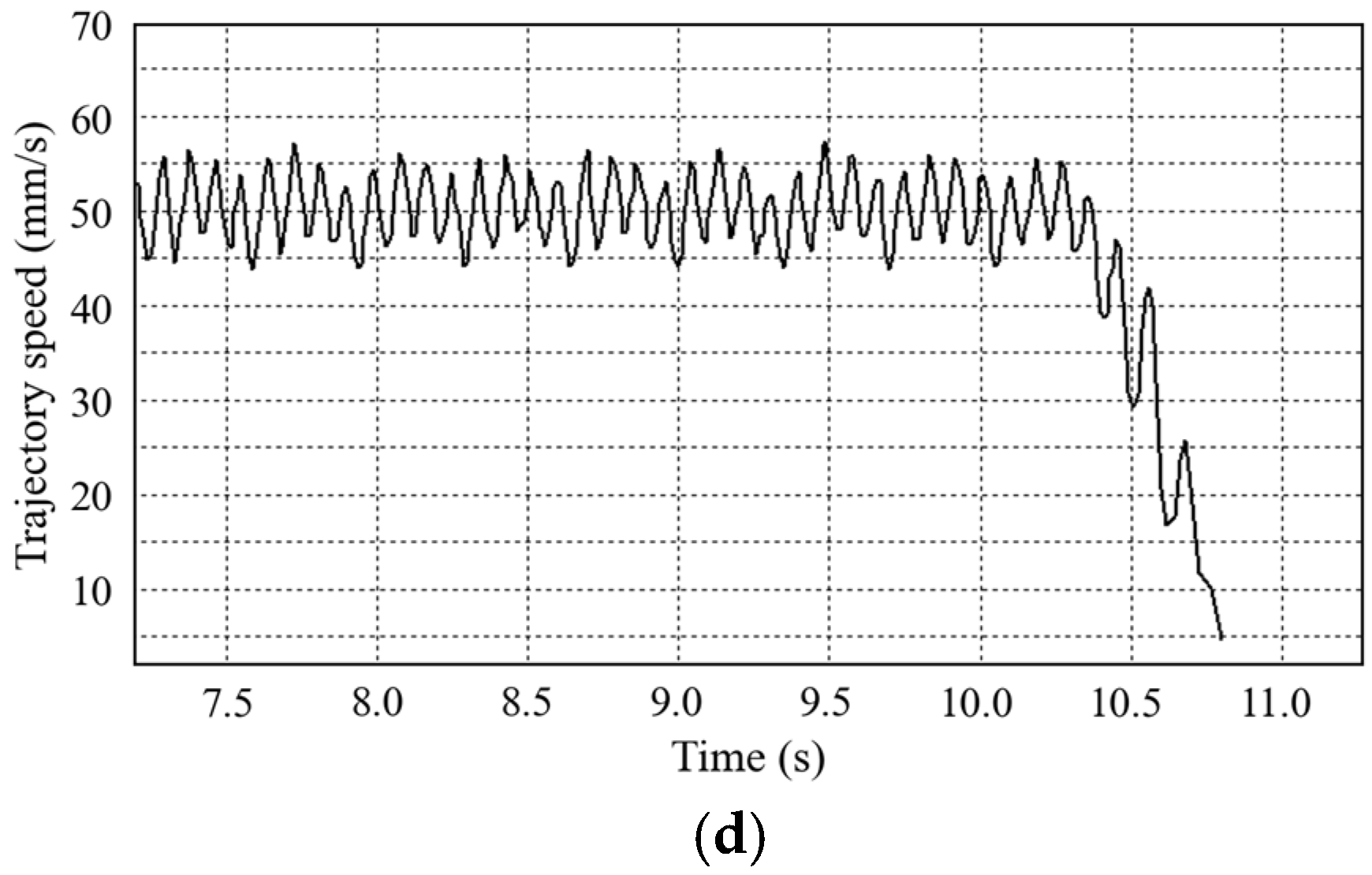
| Robot trajectory speed | 50 mm/s | 50 mm/s |
| Trajectory speed fluctuation | ±20 mm/s | ±5 mm/s |
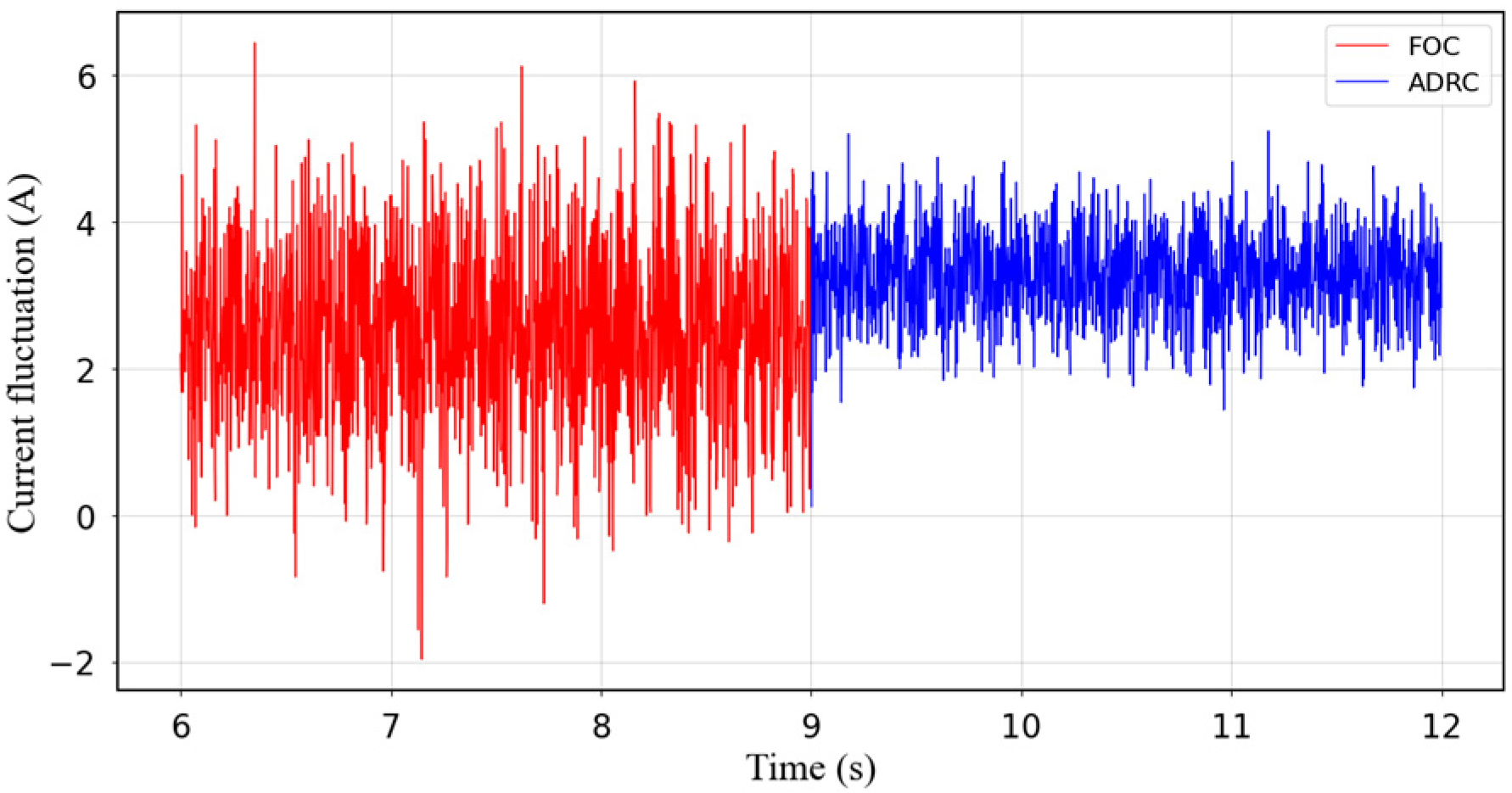
| Joint PMSM speed fluctuation | ±11 rpm | ±5 rpm |
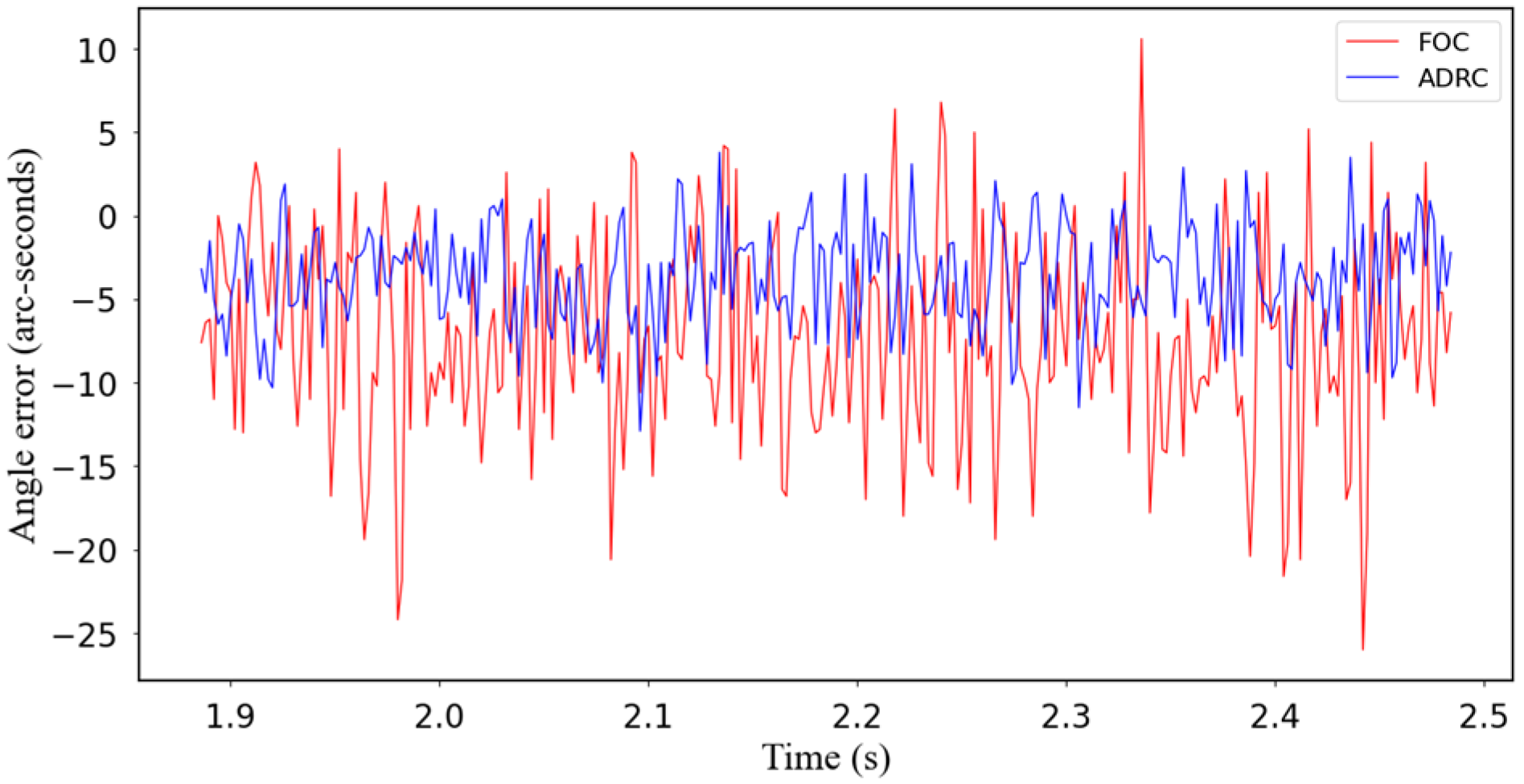
| Joint angle error | ±25 arcseconds | ±9 arcseconds |
| Amplitude | 0.599 mm | 0.231 mm |
| Vibration velocity | 9.65 mm/s | 4.77 mm/s |
| Vibration acceleration | 0.47 m/s2 | 0.33 m/s2 |
| Algorithm | Vector Control | ADRC |
|---|---|---|
| Robot trajectory speed | 300 mm/s | 400 mm/s |
| Fluctuations during trajectory deceleration | ±11 mm/s | ±4 mm/s |
| Joint PMSM speed fluctuation | ±12 rpm | ±5 rpm |
| Joint angle error | ±28 arcseconds | ±13 arcseconds |
| Amplitude | 0.322 mm | 0.311 mm |
| Vibration velocity | 8.32 mm/s | 6.86 mm/s |
| Vibration acceleration | 1.19 m/s2 | 0.52 m/s2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Fang, S.; Xu, Q. Robot Joint Vibration Suppression Method Based on Improved ADRC. Appl. Sci. 2025, 15, 5476. https://doi.org/10.3390/app15105476
Wang G, Fang S, Xu Q. Robot Joint Vibration Suppression Method Based on Improved ADRC. Applied Sciences. 2025; 15(10):5476. https://doi.org/10.3390/app15105476
Chicago/Turabian StyleWang, Gang, Shuhua Fang, and Qiangren Xu. 2025. "Robot Joint Vibration Suppression Method Based on Improved ADRC" Applied Sciences 15, no. 10: 5476. https://doi.org/10.3390/app15105476
APA StyleWang, G., Fang, S., & Xu, Q. (2025). Robot Joint Vibration Suppression Method Based on Improved ADRC. Applied Sciences, 15(10), 5476. https://doi.org/10.3390/app15105476






