Path Tracking Control Strategy Based on Adaptive MPC for Intelligent Vehicles
Abstract
1. Introduction
2. MPC Path Tracking Controller
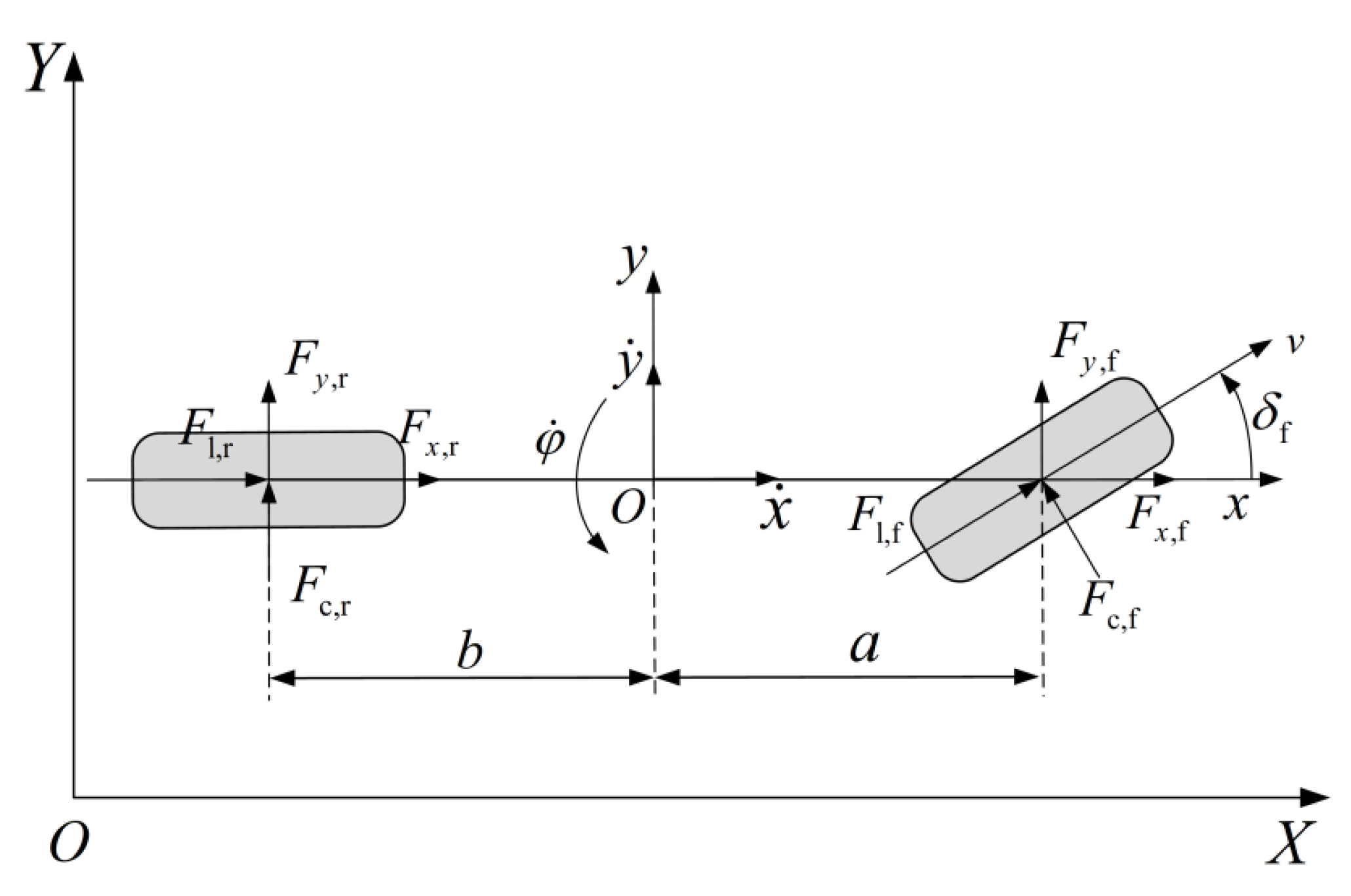
2.1. Vehicle Dynamics Modeling
2.2. Model Linearization and Prediction Equation
3. MPC Controller Design Based on Stability Boundary
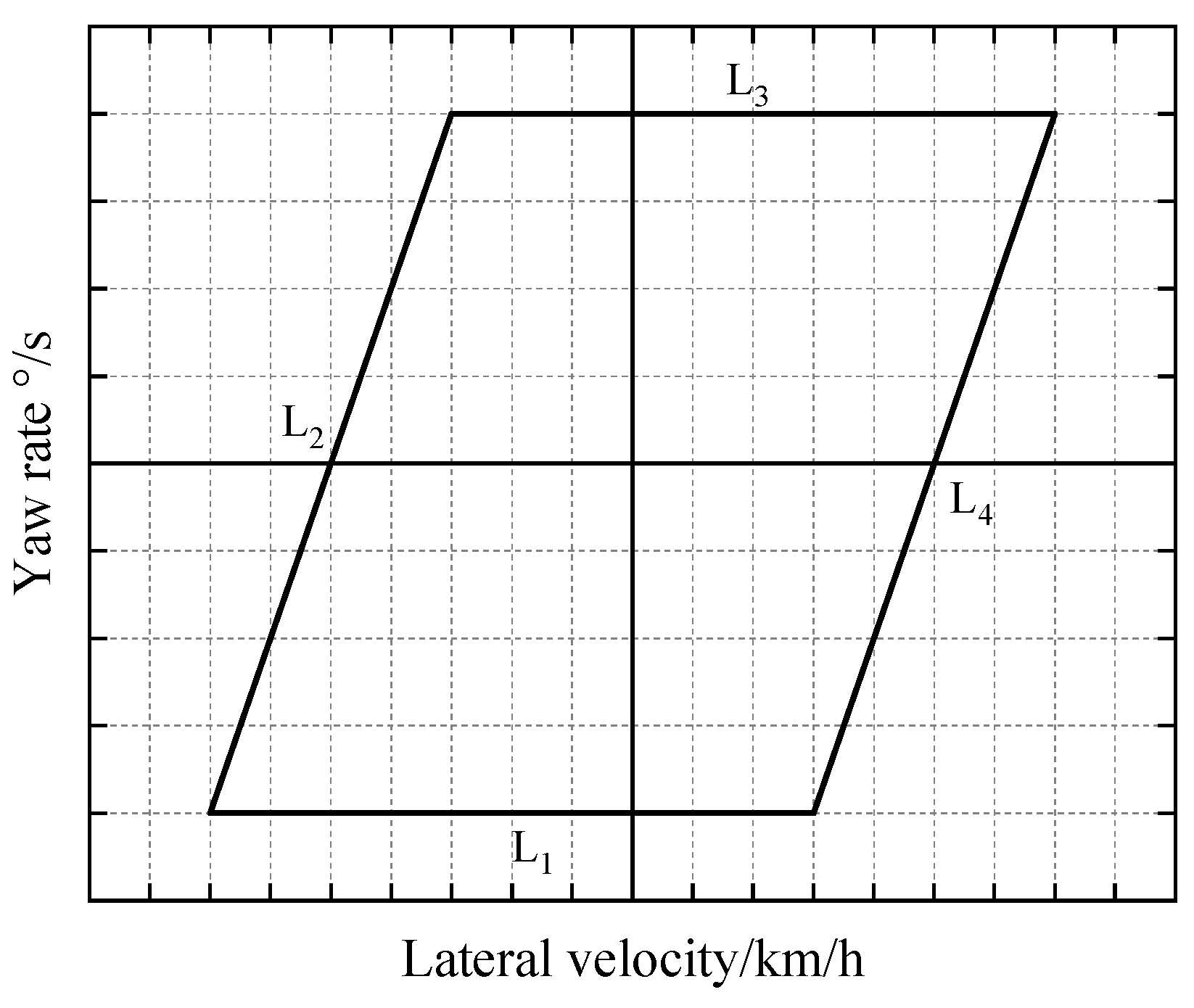
3.1. Vehicle Stability Boundary
3.2. Solve MPC Controller
- (1)
- Determination of Weighting Matrices Q and R:
- (2)
- Relaxation Factor Weight (ρ):
- (3)
- Sampling Period (T):
4. Condition-Adaptive MPC Controller
4.1. Factors Affecting MPC Path Tracking
4.2. Division of Steady-State Steering Conditions
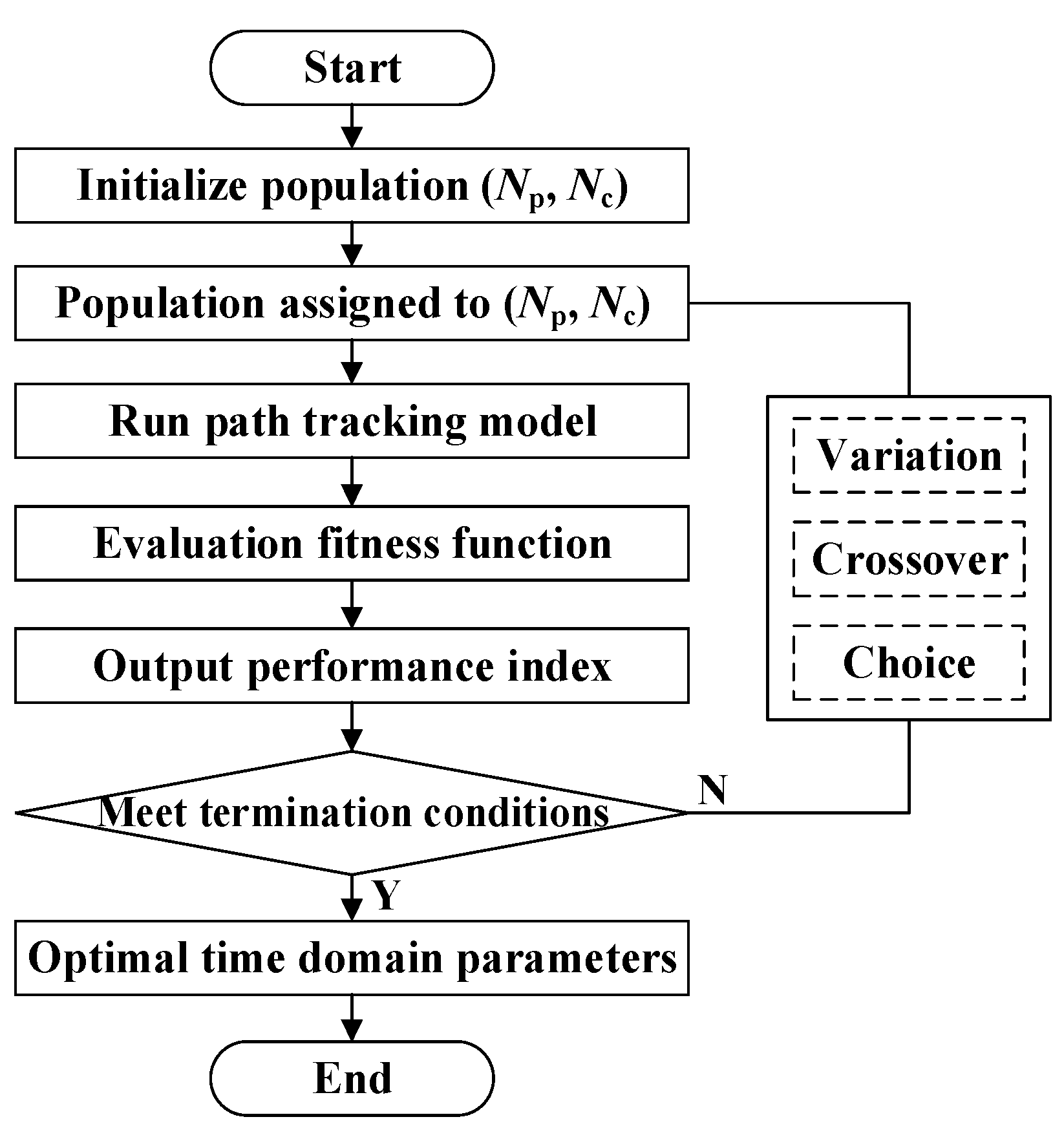
4.3. Solving Optimal Time Domain Parameter Combination Based on GA
- (1)
- Optimization Problem Definition:
- (2)
- GA Configuration and Performance:
- (3)
- Integer Constraints Enforcement:
4.4. Implementation of Condition-Adaptive MPC Controller
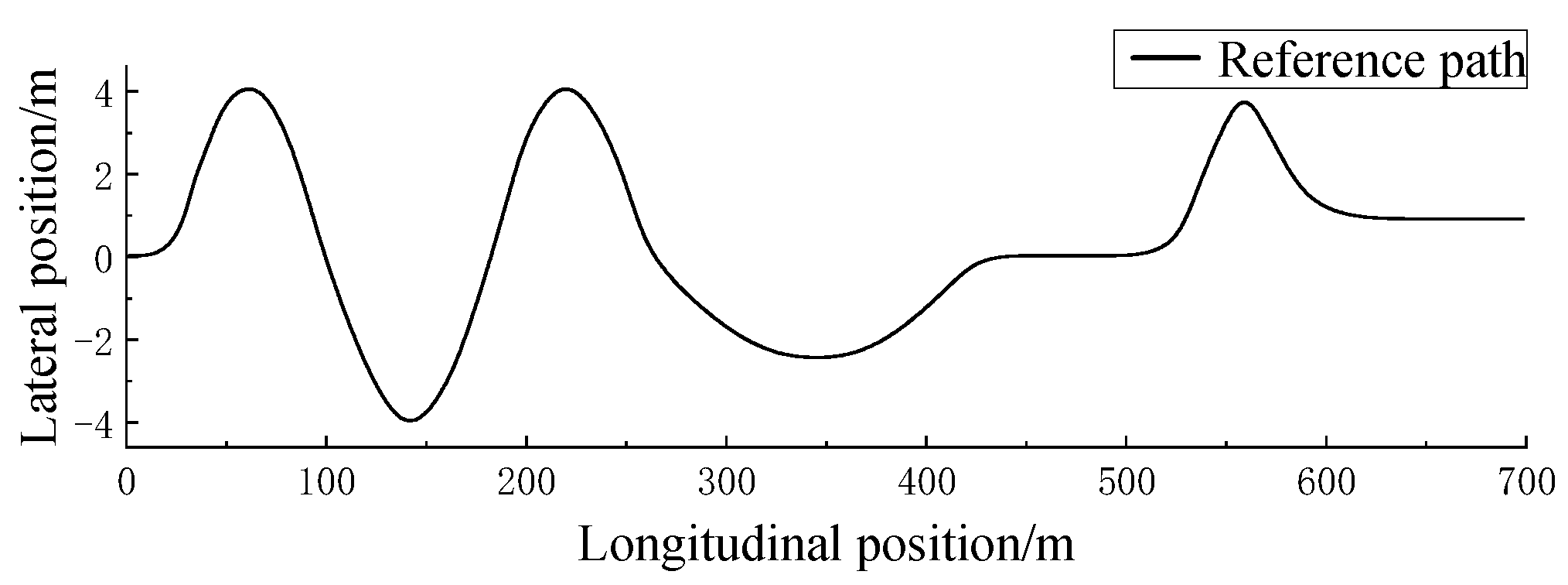
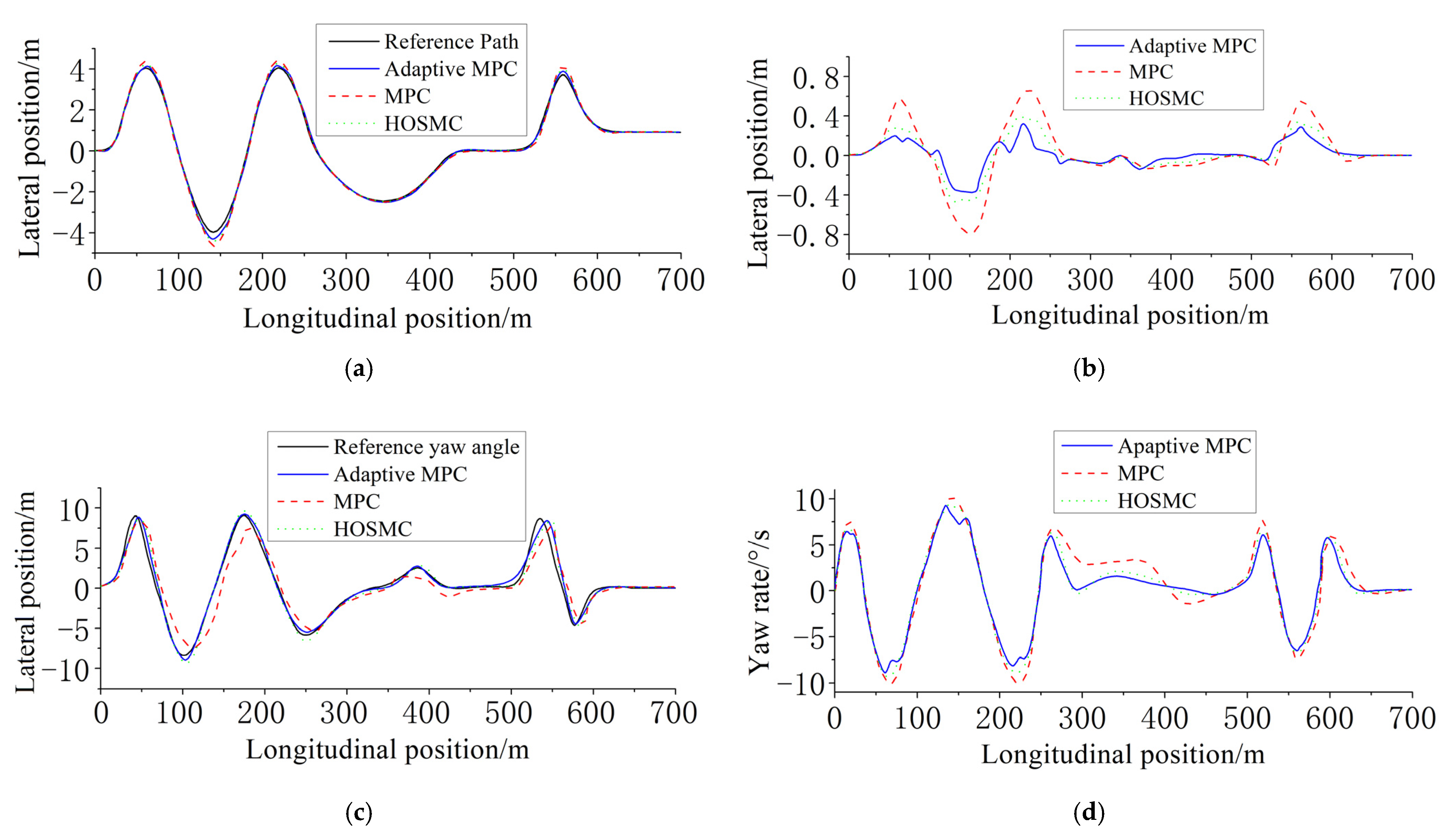
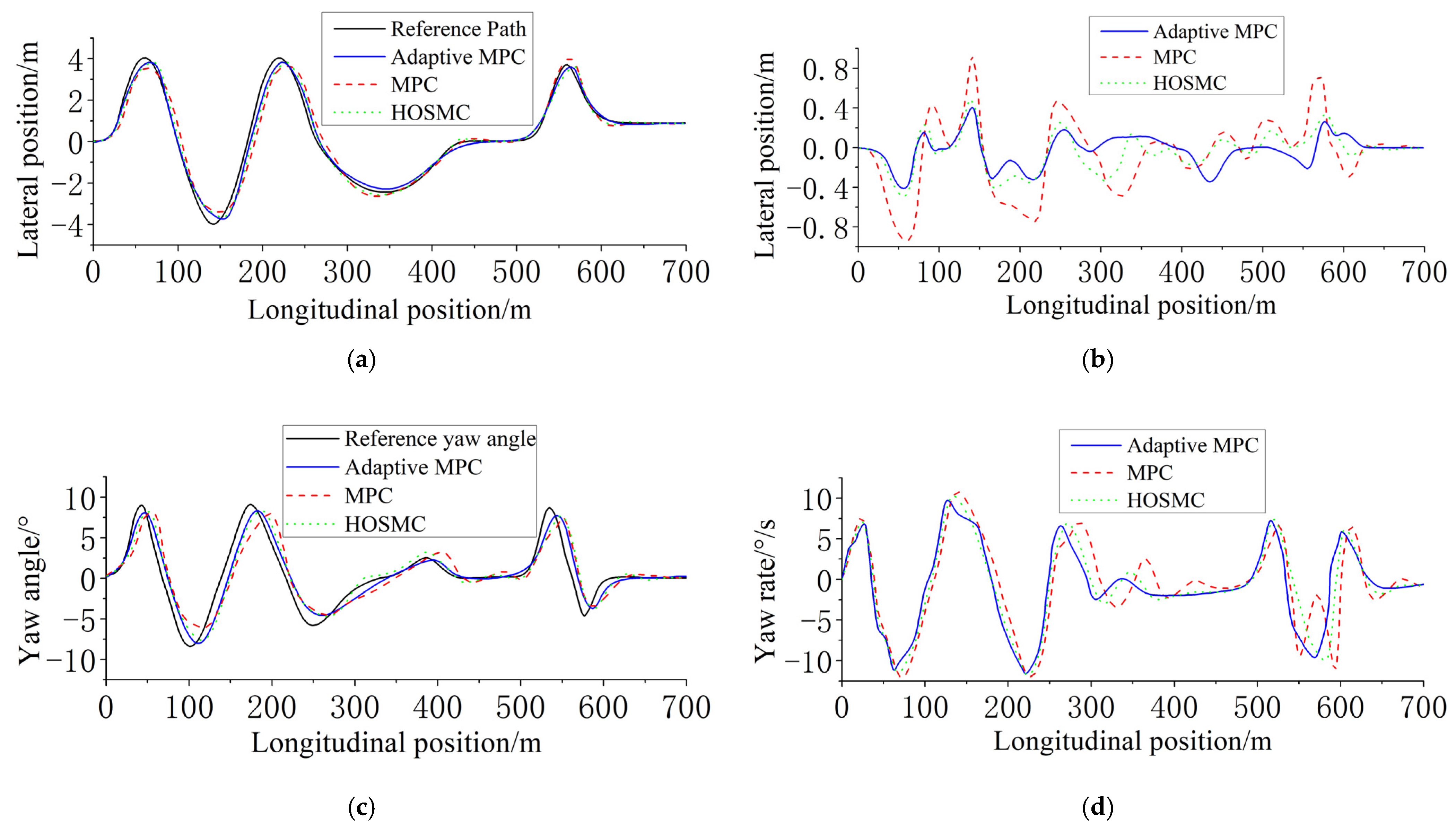
5. Simulation Verification
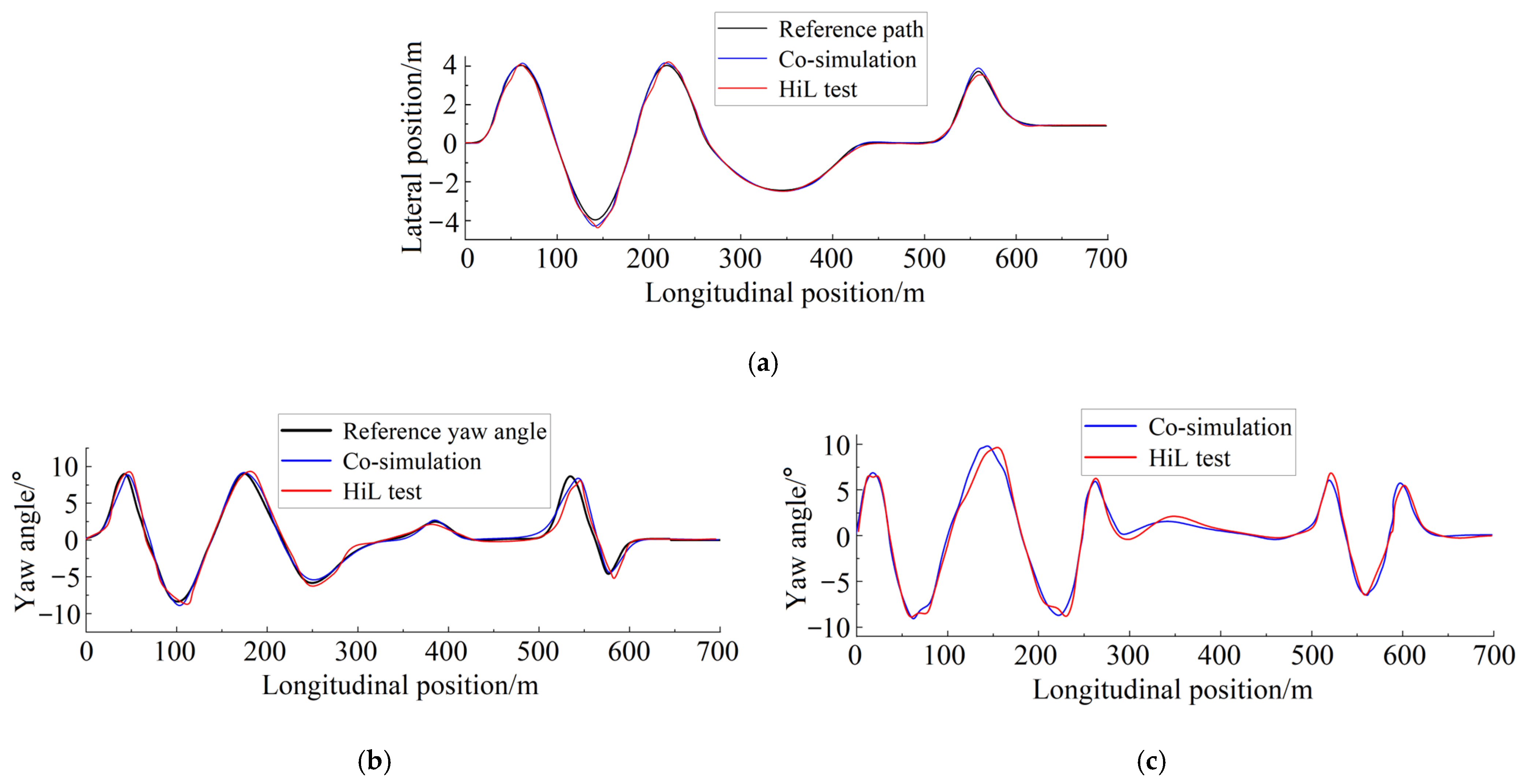
6. Hardware-in-the-Loop Test
7. Conclusions
8. Future Work and Limitations
8.1. Limitations
- (1)
- Computational Complexity: The real-time implementation of the adaptive MPC controller, especially under complex dynamic environments, requires substantial computational resources. Although the current system meets real-time requirements (average latency of 5.2 ms per control cycle), further optimization is needed for scenarios with higher-frequency state updates or more stringent real-time constraints.
- (2)
- Curvature Estimation Dependency: The controller’s performance heavily relies on accurate real-time curvature estimation. In scenarios where curvature data are noisy or delayed (e.g., due to sensor limitations or communication latency), the tracking performance may degrade. Future work could explore robust curvature prediction methods to mitigate this issue.
- (3)
- Validation Scope: The current study validates the controller under predefined variable curvature conditions and low/high-adhesion road surfaces. However, real-world driving scenarios may involve more complex dynamics, such as sudden obstacles, dynamic traffic participants or extreme weather conditions. Extending the validation to these scenarios would further demonstrate the controller’s robustness.
8.2. Future Work
- (1)
- Integration with V2X Technologies: Future research will focus on leveraging vehicle-to-everything (V2X) communication to enable dynamic curvature forecasting. By incorporating real-time data from connected vehicles and infrastructure, the controller can proactively adjust parameters, enhancing tracking accuracy and stability in anticipation of upcoming road conditions.
- (2)
- Enhanced Real-Time Adaptability: Exploring machine-learning techniques, such as online learning or neural networks, could further optimize the controller’s adaptability. These methods could enable the system to learn from real-time driving data and continuously refine its control strategies.
- (3)
- Expanded Hardware-in-the-Loop (HIL) Testing: Future work will include more extensive HIL testing under a wider range of scenarios, such as mixed urban and highway environments, to validate the controller’s performance in diverse operational conditions.
- (4)
- Multi-Objective Optimization: The current controller prioritizes path tracking accuracy and stability. Future iterations could incorporate additional objectives, such as energy efficiency or passenger comfort, into the optimization framework to achieve a more holistic control strategy.
- (5)
- Generalization to Other Vehicle Types: While the current study focuses on intelligent passenger vehicles, the proposed methodology could be extended to other vehicle types, such as commercial trucks or agricultural machinery, by adapting the dynamic model and constraints accordingly.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bai, G.; Meng, Y.; Liu, L.; Luo, W.; Gu, Q.; Liu, L. Review and Comparison of Path Tracking Based on Model Predictive Control. Electronics 2019, 8, 1077. [Google Scholar] [CrossRef]
- Su, J.; Lou, J.; Jiang, X. Overview of intelligent vehicle core technology and development. IOP Conf. Ser. Earth Environ. Sci. 2021, 769, 042054. [Google Scholar] [CrossRef]
- Li, J.; Wu, Z.; Li, M.; Shang, Z. Dynamic Measurement Method for Steering Wheel Angle of Autonomous Agricultural Vehicles. Agriculture 2024, 14, 1602. [Google Scholar] [CrossRef]
- Mao, Z.; Cai, Y.; Guo, M.; Ma, Z.; Xu, L.; Li, J.; Li, X.; Hu, B. Seed Trajectory Control and Experimental Validation of the Limited Gear-Shaped Side Space of a High-Speed Cotton Precision Dibbler. Agriculture 2024, 14, 717. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, K.; Ding, R.; Jiang, Y.; Jiang, Y. A Novel Hydraulic Interconnection Design and Sliding Mode Synchronization Control of Leveling System for Crawler Work Machine. Agriculture 2025, 15, 137. [Google Scholar] [CrossRef]
- Zhang, F.; Teng, S.; Wang, Y.; Guo, Z.; Wang, J.; Xu, R. Design of bionic goat quadruped robot mechanism and walking gait planning. Int. J. Agric. Biol. Eng. 2020, 13, 32–39. [Google Scholar] [CrossRef]
- Lu, E.; Ma, Z.; Li, Y.; Xu, L.; Tang, Z. Adaptive backstepping control of tracked robot running trajectory based on real-time slip parameter estimation. Int. J. Agric. Biol. Eng. 2020, 13, 178–187. [Google Scholar] [CrossRef]
- Song, X.; Li, H.; Chen, C.; Xia, H.; Zhang, Z.; Tang, P. Design and Experimental Testing of a Control System for a Solid-Fertilizer-Dissolving Device Based on Fuzzy PID. Agriculture 2022, 12, 1382. [Google Scholar] [CrossRef]
- Ji, X.; Wang, A.; Wei, X. Precision Control of Spraying Quantity Based on Linear Active Disturbance Rejection Control Method. Agriculture 2021, 11, 761. [Google Scholar] [CrossRef]
- Liu, Q.J.; Chen, S.Z. The control method about four wheels steering car based on LQR theory. Trans. Beijing Inst. Technol. 2014, 34, 1135. [Google Scholar]
- Li, J.; Shang, Z.; Li, R.; Cui, B. Adaptive Sliding Mode Path Tracking Control of Unmanned Rice Transplanter. Agriculture 2022, 12, 1225. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Z.; Ding, S.; Xia, J.; Xing, G. Adaptive disturbance observer-based fixed time nonsingular terminal sliding mode control for path-tracking of unmanned agricultural tractors. Biosyst. Eng. 2024, 246, 96–109. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y. Distributed coordination control of traffic network flow using adaptive genetic algorithm based on cloud computing. J. Netw. Comput. Appl. 2018, 119, 110–120. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, B.; Pan, S.; Ye, Y.; Wang, E.; Mao, H. Task Allocation of Multi-Machine Collaborative Operation for Agricultural Machinery Based on the Improved Fireworks Algorithm. Agronomy 2024, 14, 710. [Google Scholar] [CrossRef]
- Zhu, Z.; Zeng, L.; Chen, L.; Zou, R.; Cai, Y. Fuzzy Adaptive Energy Management Strategy for a Hybrid Agricultural Tractor Equipped with HMCVT. Agriculture 2022, 12, 1986. [Google Scholar] [CrossRef]
- Chen, J.; Ning, X.; Li, Y.; Yang, G.; Wu, P.; Chen, S. A Fuzzy Control Strategy for the Forward Speed of a Combine Harvester Based on KDD. Appl. Eng. Agric. 2017, 33, 15–22. [Google Scholar]
- Liu, R.; Wei, M.; Sang, N.; Wei, J. Research on Curved Path Tracking Control for Four-Wheel Steering Vehicle considering Road Adhesion Coefficient. Math. Probl. Eng. 2020, 2020, 3108589. [Google Scholar] [CrossRef]
- Xin, Z.; Chen, H.; Lin, Z.; Sun, E.; Sun, Q.; Li, S. Lateral Trajectory Following for Automated Vehicles at Handling Limits. J. Mech. Eng. 2020, 56, 138–145. [Google Scholar]
- Liu, H.; Yan, S.; Shen, Y.; Li, C.; Zhang, Y.; Hussain, F. Model predictive control system based on direct yaw moment control for 4WID self-steering agriculture vehicle. Int. J. Agric. Biol. Eng. 2021, 14, 175–181. [Google Scholar] [CrossRef]
- Lu, E.; Xue, J.; Chen, T.; Jiang, S. Robust Trajectory Tracking Control of an Autonomous Tractor-Trailer Considering Model Parameter Uncertainties and Disturbances. Agriculture 2023, 13, 869. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.; Lv, L.; Shi, Y.; Yu, X. Study on Modeling Method of a Multi-Parameter Control System for Threshing and Cleaning Devices in the Grain Combine Harvester. Agriculture 2022, 12, 1483. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, R.; Ye, Q.; Wei, Z.; Yan, B. Investigation of Intelligent Vehicle Path Tracking Based on Longitudinal and Lateral Coordinated Control. IEEE Access 2020, 8, 105031–105046. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, H.; JIANG, Z. Simulation analysis of obstacle avoidance path planning and tracking control for intelligent vehicles. China Meas. Test 2021, 47, 71. [Google Scholar]
- Zhang, Y.; Huang, M. Path-following Control of Autopilot Vehicles Based on Model Prediction. Digit. Manuf. Sci. 2019, 17, 21. [Google Scholar]
- Swain, S.K.; Rath, J.J.; Veluvolu, K.C. Neural Network Based Robust Lateral Control for an Autonomous Vehicle. Electronics 2021, 10, 510. [Google Scholar] [CrossRef]
- Nugroho, S.A.; Chellapandi, V.P.; Borhan, H. Vehicle Speed Profile Optimization for Fuel Efficient Eco-Driving via Koopman Linear Predictor and Model Predictive Control. In Proceedings of the 2024 American Control Conference (ACC), Toronto, ON, Canada, 10–12 July 2024; IEEE: Piscataway, NJ, USA, 2024. [Google Scholar]
- Jianmin, D.; Xiaosheng, T.; Tian, X.; Zhixue, S. Research on Target Path Tracking Method of Intelligent Vehicle Based on Model Predictive Control. Automob. Technol. 2017, 8, 6–11. [Google Scholar]
- Wang, X.; Yuan, L.; Huang, J.; Gao, Y.; Li, H. Research on continuous obstacle avoidance trajectory planning and tracking control strategies for low speed intelligent vehicles with different road curvature changes. Mech. Sci. Technol. Aerosp. Eng. 2024, 1–12. [Google Scholar]
- Zhang, Z.; Li, Y.; Yu, Y.; Zhang, Z.; Zheng, L. Study on Local Path Planning and Tracking Algorithm of Intelligent Vehicle in Complex Dynamic Environment. China J. Highw. Transp. 2022, 35, 372. [Google Scholar]
- Zhang, L.; Tian, S.; Pan, F.; Yan, T.; Li, B. Intelligent Vehicle Path Planning and Tracking Control based on MPC. J. Henan Univ. Sci. Technol. (Nat. Sci.) 2024, 45, 1. [Google Scholar]
- Guo, M.; Ji, P.; Huan, H. Unmanned Vehicle Path Planning and Tracking Control Based on Improved Artificial Potential Field Method. J. Syst. Simul. 2024, 36, 2423. [Google Scholar]
- Yang, D.; Liu, D.; Han, B.; Lu, G.; Kong, L.; Huang, C.; Li, J. Trajectory planning and tracking control for vehicles with tire blowout in complex traffic flows. Sci. China Inf. Sci. 2025, 68, 132202. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Guo, H.-Q.; Chen, Z.-G.; Song, P. Longitudinal Collision Avoidance and Lateral Stability Adaptive Control System Based on MPC of Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 21, 2376–2385. [Google Scholar] [CrossRef]
- Hun, J.; Xiao, F.; Lin, Z.; Huang, J.; Deng, C. Vehicle Yaw Stability Control Based on Fuzzy Sliding Mode Direct Yaw Moment. J. Tongji Univ. (Nat. Sci.) 2023, 51, 954. [Google Scholar]
- Jun, L.; Tang, S.; Huang, Z.; Zhou, W. Longitudinal and lateral coordination control method of high-speed unmanned vehicles with integrated stability. J. Traffic Transp. Eng. 2020, 20, 205. [Google Scholar]
- Xia, Q.; Chen, P.; Xu, G.; Sun, H.; Li, L.; Yu, G. Adaptive Path-Tracking Controller Embedded With Reinforcement Learning and Preview Model for Autonomous Driving. IEEE Trans. Veh. Technol. 2025, 74, 3736–3750. [Google Scholar] [CrossRef]
- Chen, C.; Guo, J.; Guo, C.; Chen, C.; Zhang, Y.; Wang, J. Adaptive Cruise Control for Cut-In Scenarios Based on Model Predictive Control Algorithm. Appl. Sci. 2021, 11, 5293. [Google Scholar] [CrossRef]
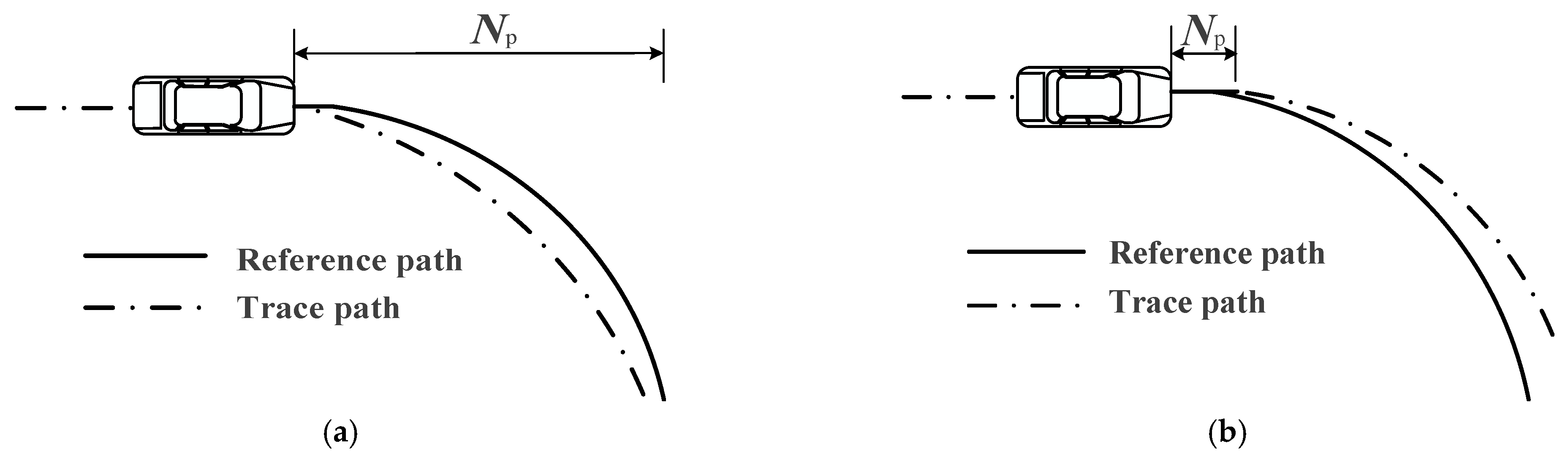






| Parameter/Unit | Value |
|---|---|
| Full mass of vehicle/m (kg) | 1723 |
| Distance from centroid to front axle/a (m) | 1.232 |
| Distance from centroid to rear axle/b (m) | 1.468 |
| Moment of inertia about Z-axis/Iz (kg·m2) | 4175 |
| Front wheel lateral stiffness/Cc,f (N·rad−1) | 66,900 |
| Rear wheel lateral stiffness/Cc,r (N·rad−1) | 62,700 |
| Parameter/Unit | Value |
|---|---|
| Sampling period T | 0.05 |
| Weighting matrix Q | Diag [200, 100, 100] |
| Weighting matrix R | [5 × 104] |
| Weight coefficient ρ | 1000 |
| Speed/km/h | 20 | 30 | 40 | 60 | 80 | 100 | 120 |
| Minimum radius of curvature (general value)/m | 30 | 65 | 100 | 200 | 400 | 700 | 1000 |
| Minimum radius of curvature (limit value)/m | 15 | 30 | 60 | 125 | 250 | 400 | 650 |
| Speed/km/h | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Radius of road curvature /m | 6 | 15 | 30 | 60 | 90 | 125 | 185 | 250 | 320 | 400 |
| 8 | 20 | 35 | 65 | 100 | 135 | 200 | 270 | 350 | 440 | |
| 10 | 25 | 40 | 70 | 110 | 145 | 215 | 290 | 380 | 480 | |
| 12 | 30 | 45 | 75 | 120 | 155 | 230 | 310 | 410 | 520 | |
| 14 | 35 | 50 | 80 | 130 | 165 | 245 | 330 | 440 | 560 | |
| 16 | 40 | 55 | 85 | 140 | 175 | 260 | 350 | 470 | 600 | |
| 18 | 45 | 60 | 90 | 150 | 185 | 275 | 370 | 500 | 640 | |
| 20 | 50 | 65 | 95 | 160 | 195 | 290 | 390 | 530 | 680 | |
| 22 | 55 | 70 | 100 | 170 | 205 | 305 | 410 | 560 | 720 | |
| 24 | 60 | 75 | 105 | 180 | 215 | 320 | 430 | 590 | 760 |
| Speed/km/h | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Group 1 | 5.1 | 7.1 | 8.2 | 10.2 | 12.3 | 15.4 | 17.4 | 17.5 | 18.6 | 20.6 |
| Group 2 | 5.1 | 7.1 | 8.2 | 10.2 | 12.3 | 16.4 | 17.4 | 18.5 | 19.6 | 20.7 |
| Group 3 | 5.1 | 7.1 | 9.2 | 10.2 | 13.3 | 16.4 | 17.5 | 18.6 | 20.7 | 21.7 |
| Group 4 | 5.1 | 7.1 | 9.2 | 10.2 | 14.3 | 17.4 | 17.6 | 19.6 | 20.7 | 22.7 |
| Group 5 | 5.1 | 7.1 | 9.2 | 11.2 | 15.3 | 17.5 | 18.6 | 19.6 | 22.7 | 23.8 |
| Group 6 | 5.1 | 7.1 | 10.2 | 11.2 | 15.3 | 17.5 | 18.6 | 20.6 | 22.8 | 24.9 |
| Group 7 | 5.1 | 8.1 | 10.2 | 11.2 | 15.3 | 17.5 | 19.6 | 20.7 | 23.9 | 25.9 |
| Group 8 | 5.1 | 8.1 | 10.2 | 12.2 | 15.3 | 18.5 | 19.6 | 20.7 | 24.9 | 27.10 |
| Group 9 | 5.1 | 8.1 | 10.2 | 12.2 | 16.4 | 18.5 | 19.6 | 20.7 | 24.10 | 28.10 |
| Group 10 | 6.1 | 8.1 | 10.2 | 12.2 | 16.4 | 18.5 | 20.7 | 20.8 | 25.10 | 30.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Jiang, H.; Yang, X.; Wei, Q. Path Tracking Control Strategy Based on Adaptive MPC for Intelligent Vehicles. Appl. Sci. 2025, 15, 5464. https://doi.org/10.3390/app15105464
Li C, Jiang H, Yang X, Wei Q. Path Tracking Control Strategy Based on Adaptive MPC for Intelligent Vehicles. Applied Sciences. 2025; 15(10):5464. https://doi.org/10.3390/app15105464
Chicago/Turabian StyleLi, Chenxu, Haobin Jiang, Xiaofeng Yang, and Qizhi Wei. 2025. "Path Tracking Control Strategy Based on Adaptive MPC for Intelligent Vehicles" Applied Sciences 15, no. 10: 5464. https://doi.org/10.3390/app15105464
APA StyleLi, C., Jiang, H., Yang, X., & Wei, Q. (2025). Path Tracking Control Strategy Based on Adaptive MPC for Intelligent Vehicles. Applied Sciences, 15(10), 5464. https://doi.org/10.3390/app15105464







