The Development of an Optimized Impact Pad for a Six-Strand Tundish Using CFD Simulations

Abstract

The behavior of molten steel within a tundish plays a crucial role in achieving uniform temperature and chemical composition, enhancing the removal efficiency of non-metallic inclusions, and reducing the wear of refractory linings. These aspects are key for ensuring the production of steel with superior quality. In multi-strand delta-type tundishes, such as the six-strand configuration, flow dynamics become particularly challenging. Key considerations include strand-specific residence times, the uniform distribution of steel flow, and the mitigation of refractory degradation. This paper presents a detailed numerical analysis aimed at designing an optimally shaped impact pad. The effectiveness of each proposed design was assessed through a tracer-based visualization of flow behavior and the evaluation of residence time distribution (RTD) curves. RTD curves were created in isothermal conditions, while the calculations of the temperature fields of steel in the tundish were made in non-isothermal conditions. The results of the simulations were verified by a real plant trial test and indicate that the use of the “SPHERIC-K4” impact pad can greatly enhance the flow characteristics of liquid steel during the continuous casting process. These improvements include preventing the erosion of the tundish refractory lining, improving the distribution of residence times between individual casting strands, and adjusting the proportions of the mixing zones.

1. Introduction

A tundish is an essential component of a continuous casting machine. It acts as a metal reservoir when the main ladle is replaced. It is also the last refractory-lined section that can influence the quality of the casted steel. The tundish is now used not only to transport liquid steel to individual outlets but also to deoxidize micro-alloy, homogenize the temperature and chemicals of the steel, and refine the steel via interphase reactions at the steel–slag interface [1,2,3,4]. It is also a continuous metallurgical reactor with optimal residence times for the separation of non-metallic inclusions and coagulated slag through the flotation and optimization of the flow zones with different flow characteristics. Three zones are monitored: the dead zone, the mixed zone, and the plug flow zone [4,5,6]. The optimization of tundish furniture is affected by multiple factors, such as the number and spacing of outlets, the position of the ladle, casting velocity, the profile of the casted product, ladle turnover time, casting start-up, slag removal, the steel flow pattern, and impact pads.

In the past, extensive research was aimed at studying tundish impact pads used in steel flow control during casting [7].

The main reasons for the modifications were to improve steel flow characteristics throughout the tundish volume, increase the residence time for enhanced refining potential, and prevent refractory lining erosion primarily in the slag line area [8].

The development of turbulence inhibitors began with simple impact pads, which later evolved into structured and modern impact pads. Nowadays, hybrid impact pads are commonly used. A hybrid impact pad is designed to decrease mass, increase safety during casting, improve tundish refractory lining lifetime, and adapt the steel flow pattern to individual tundishes [9,10].

In their study [11], the authors investigated the removal of non-metallic inclusions in a five-strand asymmetric tundish using a newly developed impact pad. The authors of the study [12] investigated the dissipation of micro-bubbles, the collision between bubbles, and the function of a turbulence inhibitor. The extended principles of the mathematical simulations and the results of the industrial trials of the newly developed impact pad for the casting of ultra-clean steel were presented in the study [13]. The important tasks of impact pads in preventing steel reoxidation and steel splashing during casting are shown in the study [14].

Refractory material producers are working to optimize their products to provide customers with a comprehensive package that includes simulation results for their specific tundish. The primary goal of these companies is to improve the flow of steel under the slag layer and increase the minimum residence time of steel in the tundish [9,15].

In all the studies mentioned above, the flow of steel with various types of impact pads was observed, but in different types of tundishes. It is observed that various shaped impact pads were used to control the flow of steel in the tundish. Therefore, it is not possible to establish a universal type of impact pad. Instead, it is necessary to search for the optimal shape of the impact pad for a specific type of tundish to ensure the desired parameters.

Mathematical simulations are used to optimize the flow characteristics in created models. The results are then verified in real operating conditions. Evaluation methods such as residence time, RTD curves, and mixing area ratios are highly suitable because these results can be compared with data from real plants.

2. Materials and Methods

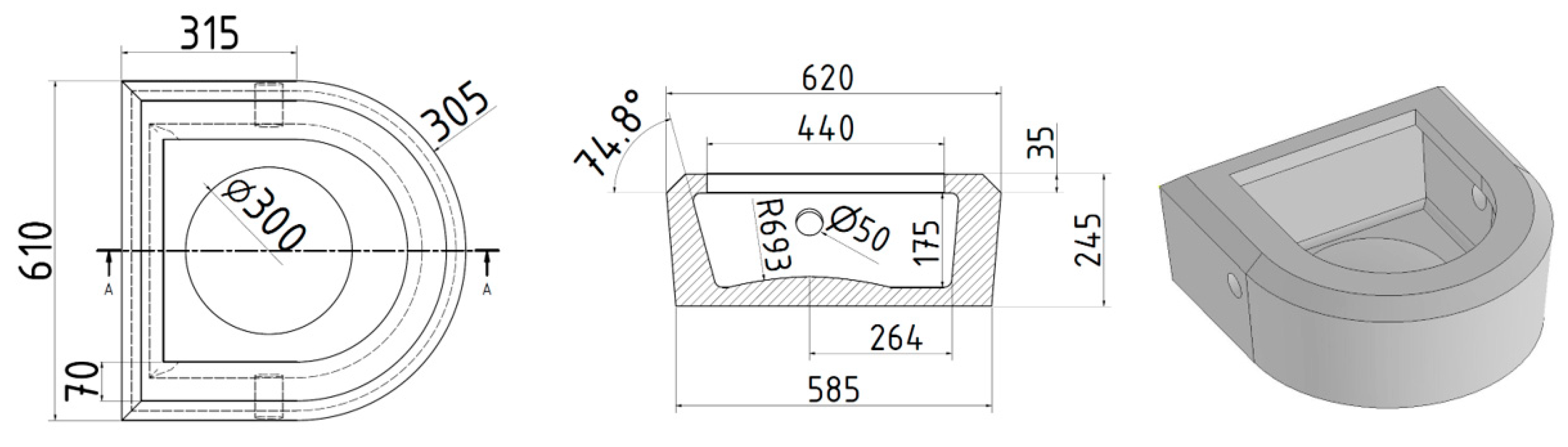
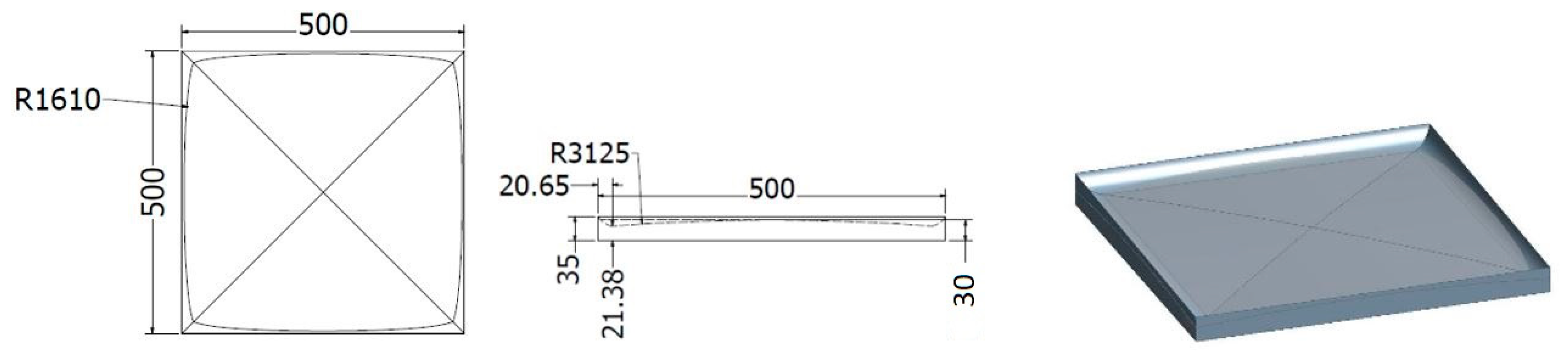
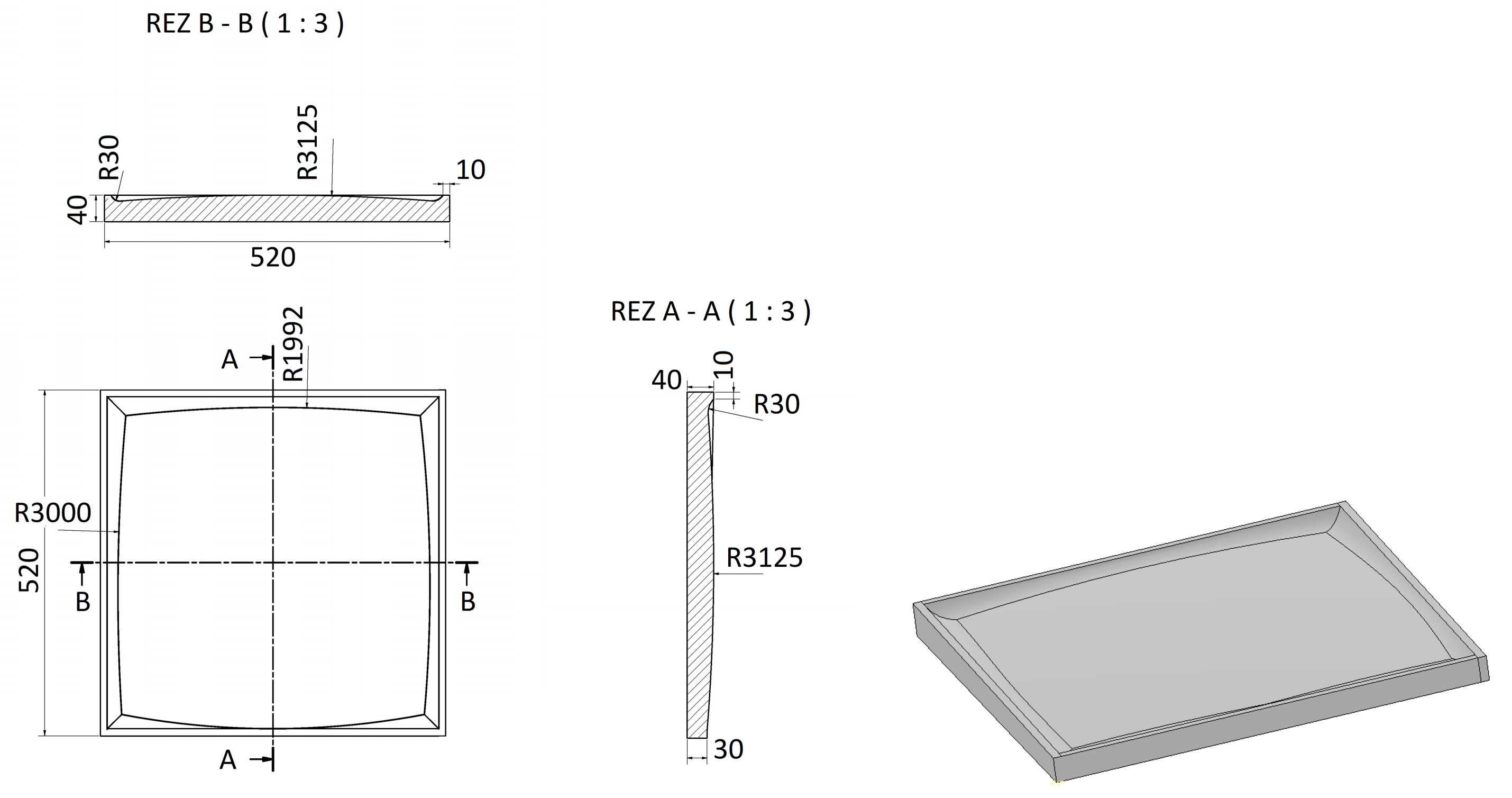
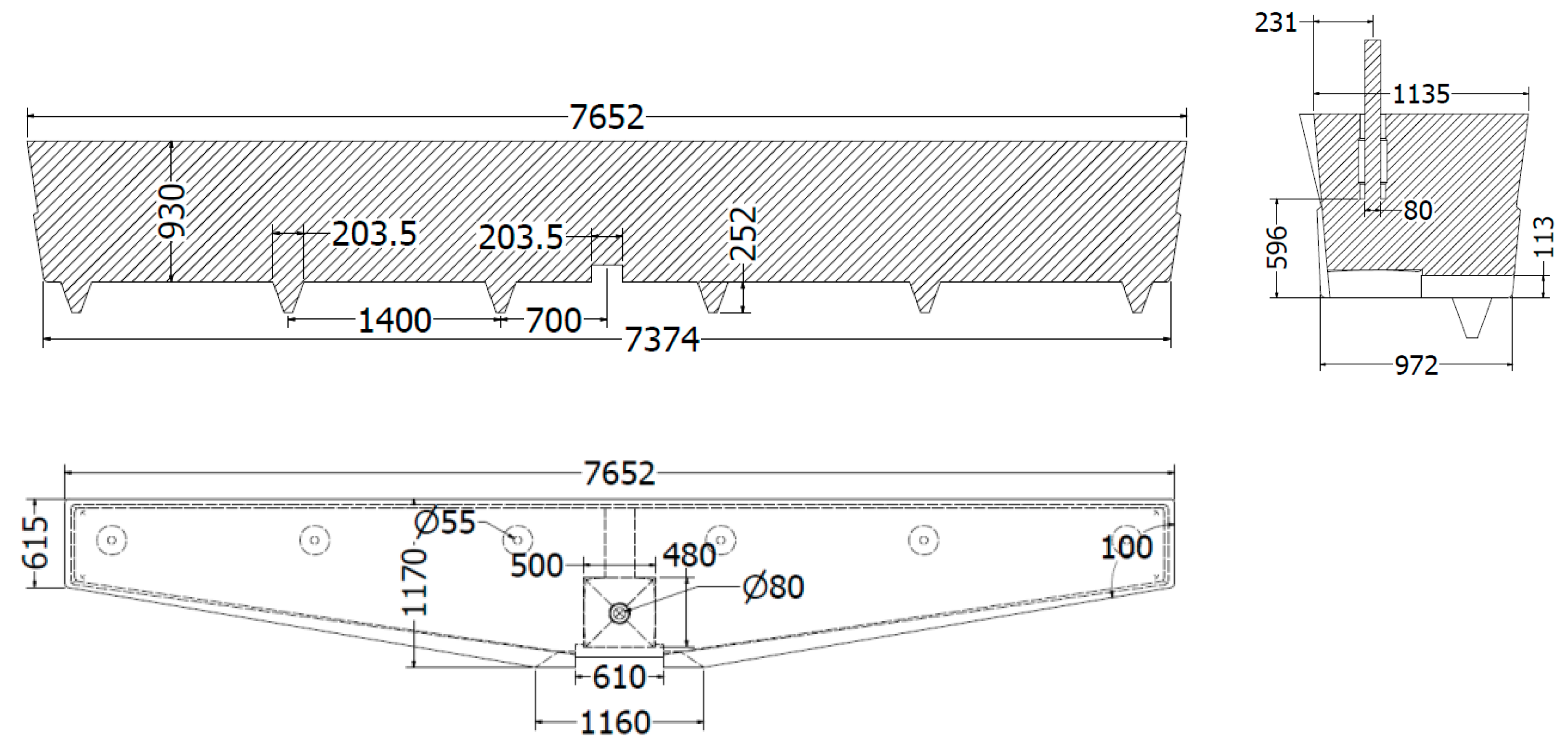
Description of Impact Pads

The objective of this study was to enhance the flow behavior and temperature uniformity of molten steel within the tundish, with a specific focus on minimizing refractory wear in the upper inflow region. To fulfill this goal, various impact pad geometries were tested through numerical simulations to assess their influence on tundish hydrodynamics. Flow characteristics were analyzed using a combination of vector fields, contour plots, streamlines, residence time distribution (RTD) curves, and calculated minimum and maximum residence times. These methods enabled the evaluation of temperature profiles; the assessment of the tundish’s refining potential, particularly for non-metallic inclusion removal; and the prediction of lining degradation patterns [16]. The main reason for the implementation of modifications to the SPHERIC impact pad, which is patented by one of the authors of the article, was to exploit the potential of the spherical surface to reduce the hydrodynamic drag of the incident stream and consequently to ensure targeted direction of the steel stream to prevent wear of the refractory lining of the tundish in the area of the slag line. The initial stage of the research was grounded in the concept of the “SPHERIC” impact pad, as referenced in international patent documentation [7,16,17], with a core hypothesis that optimized pad geometry could reduce the hydrodynamic resistance of the molten steel direct stream. This hypothesis was examined through an analysis involving the drag coefficient (C), which is a key parameter in determining the resistive force (F) based on fluid dynamics principles.

$$\mathrm{F}={\displaystyle \frac{1}{2}}\mathrm{C}·\mathrm{\rho }·\mathrm{S}·\mathrm{v}$$

(1)

where C represents the drag coefficient [-]; $\rho$ represents the fluid density [kg·m⁻³]; S represents the reference area (the planform area of the impact pad) [m²]; and $v$ represents the relative velocity of the impinging molten steel stream [m·s⁻¹] [16].

The coefficient C (

Table 1. Values of drag coefficients for different geometries and surface profiles [16,20].

Shapes and Surface Profiles of Solid Bodies	C—Coefficient of Drag
Circular plate	1.11
Square plate	1.05 to 1.27
Hollow hemisphere	1.35 to 1.40
Convex hemisphere	0.30 to 0.40
Round cylinder	1.20

) is a dimensionless parameter which may be regarded as a constant with only small changes in velocity. Experimental values of the drag coefficient for objects in a free-flowing stream were 1.17 for a square plate and 0.40 for a convex hemisphere [16,18,19,20]. The proposed spherical pad had a square planform and a hemispherical upper surface with a large diameter [16,20].

Each tundish is uniquely engineered, and as such, a universal impact pad design cannot be effectively applied across all tundish configurations. The internal flow behavior is heavily influenced by the specific geometry, structural layout, and overall design of the tundish. Consequently, impact pads must be customized to suit the distinct operational and design parameters of each individual tundish.

The primary objective behind modifying the original “SPHERIC” impact pad was to ensure a more uniform distribution of molten steel throughout the tundish volume. This optimization promotes balanced residence times across all outlets, thereby supporting better thermal and chemical homogeneity. Moreover, this design aims to limit refractory wear in the upper inflow region and protect the permanent lining from thermal stress and excessive heat transfer.

Advanced tundish operation increasingly relies on advanced digital tools. Among these, computational simulations play a vital role in refining internal flow patterns and enhancing the tundish’s refining performance. These numerical methods allow for the accurate representation of complex real-world processes without disrupting plant operations.

By employing simulation techniques, engineers can evaluate varying boundary conditions, detect inefficiencies, and propose design improvements. One significant benefit of these models is their applicability in scenarios where experimental validation on real systems is impractical or impossible [11,21,22].

Preliminary analyses were performed using ANSYS Discovery 2022 (developed by ANSYS, Canonsburg, PA, USA), leading to the development of a modified version of the “SPHERIC” design, referred to as the SPHERIC prototype, which featured raised lateral barriers. This redesign was tailored to meet the specific operational demands of the targeted tundish configuration.

ANSYS Discovery is an integrated simulation platform that combines modeling, numerical analysis, and optimization in a single environment. It provides a powerful solution for engineers and designers seeking to evaluate and enhance the performance of their concepts quickly and effectively [23].

The reference tundish setup used the “KTHE/C” impact pad manufactured by Zakłady Magnezytowe “ROPCZYCE” S.A. (Postępu 15c Street, 02-676 Warsaw, Poland). The dimensional specifications of the evaluated impact pad variants are illustrated in Figure 1 for “KTHE/C”, Figure 2 for “SPHERIC”, Figure 3 for “SPHERIC-K2”, and Figure 4 for “SPHERIC-K4”, with all dimensions expressed in millimeters.

In this investigation, three different impact pads were compared, in particular “KTHE/C”, “SPHERIC-K2”, and “SPHERIC-K4”, when used in a six-strand trough-type tundish; the comparison was carried out using CFD simulations.

The SP-K2 modification design is an initial modification to the impact pad to reduce the impact of piston flow and the formation of surface exposure in the steel inflow area and to prevent wear on the refractory lining in the slag line area. The design of modification SP-K4 follows SP-K2, which is one of many modifications tested that resulted in a significant reduction in the intensity of wear on the lining in the slag line area and the avoidance of the effect of level opening in the steel inflow area for the type of tundish.

The spherical impact pad SP-K2 has a universal shape, which serves as a starting point for the design of specific shapes of spherical impact pads for various types and shapes of tundishes. The spherical impact pad SPHERIC-K4 represents a unique shape based on the SP-K2 pad and is adapted to the conditions of a specific six-stream delta-shaped tundish. The primary problem of the mentioned tundish was significant wear on the working lining of the tundish in the area of the slag line on the wall adjacent to the impact pad. The primary goal of the development of the K4 impact pad was to eliminate significant wear on the working lining of the tundish while maintaining or improving other operating characteristics of the mentioned tundish.

3. Numerical Modeling

3.1. Description of the CFD Model

The study was performed using computational fluid dynamics (CFD) simulations within Ansys Fluent (ANSYS Inc., Canonsburg, PA, USA). The simulation process was based on three-dimensional models.

To analyze turbulent flow behavior, the most widely applied approach in engineering practice is the Reynolds-Averaged Navier–Stokes (RANS) method. This approach involves time-averaging the flow variables to represent the effects of turbulence, which significantly reduces computational demands while still maintaining reliable accuracy. Within this framework, the RANS equations incorporate the impact of velocity fluctuations through turbulence models. Depending on the selected RANS formulation, additional transport equations are introduced to approximate turbulent characteristics. Models such as k-ε and k-ω incorporate the Boussinesq approximation, which allows for the calculation of turbulent viscosity based on the mean flow field [24,25,26,27].

The k-ω (k-ω) turbulence model is a widely used model to capture the effect of turbulent flow conditions. The k-ω SST model provides a better prediction of steel flow than most RANS models and accounts for its good behavior under adverse pressure gradients. It can account for the transfer of principal shear stress in adverse pressure gradient boundary layers. The k-ω SST model is the most commonly used model in the industry due to its high accuracy and cost ratio.

The k-ω SST model combines the robustness and accuracy of the k-ω model near walls with the suitability of the k-ε model in regions further from the walls. This makes it more advantageous for various types of flow [24,25,26,27,28,29].

Turbulent viscosity was calculated using Equation (2):

$${\mu }_t={\displaystyle \frac{\rho k}{\omega }}{\displaystyle \frac{1}{max\left[\frac{1}{{\alpha }^{\mathrm{*}}},\frac{S{F}_2}{{\alpha }_1\omega }\right]}}$$

(2)

where $\rho$ represents the fluid’s density [kg·m⁻³]; k denotes the turbulent kinetic energy; ω is the specific rate of turbulence dissipation (approximately ε/k); S refers to user-defined source terms; α* is a damping coefficient affecting turbulent viscosity; a stands for the inverse of the effective turbulent Prandtl number; F indicates the internal body force per unit volume [N·m⁻³]; and α₁ is a constant specific to the SST k-ω turbulence model.

For the simulations, the k-ω SST model was utilized based on these facts (

Table 2. Constants of the SST k-ω model [27].

${\mathit{\alpha }}_{\mathbf{\infty }}^{\mathbf{*}}$	${\mathit{\alpha }}_{\mathbf{\infty }}$	${\mathit{\alpha }}_0$	${\mathit{\beta }}_{\mathbf{\infty }}^{\mathbf{*}}$	Rβ	Rk	Rω	ζ*	Mt0	σk,1	σω,1	σk,2	σω,2	α1	βi,1	βi,2
1	0.52	1/9	0.09	8	6	2.95	1.5	0.25	1.176	2.0	1.0	1.168	0.31	0.075	0.0828

).

Thermal conditions for walls refer to the boundary conditions related to heat transfer at the surfaces (walls) of a physical system. These conditions define how heat interacts with the walls, influencing the overall temperature distribution and heat flow within the system. In computational simulations and thermal analysis, specifying accurate thermal conditions for walls is crucial for achieving realistic and reliable results.

Heat flux is a measure of the rate of heat energy transfer through a given surface per unit area. It is a vector quantity, indicating not only the magnitude of heat transfer but also its direction. In practical applications, heat flux is crucial for understanding how materials behave under thermal loads, for designing thermal management systems, and for evaluating the efficiency of heat exchangers, among other things.

The heat transfer equation used in Ansys Fluent is based on the general form of the heat conduction equation. Equation (3) is represented as follows:

$$\rho c_p{\displaystyle \frac{\partial \mathrm{T}}{\partial \mathrm{t}}}+\nabla ·\left(\rho v{c}_{p}T\right)=\nabla ·\left(\mathrm{k}\nabla \mathrm{T}\right)+ST$$

(3)

where ρ is the material’s density [kg/m³]; $c_p$ is the specific heat capacity at constant pressure [J/kg·K]; T is the temperature [K]; t is the time [s]; v is the velocity vector of the flow [m/s]; k is the thermal conductivity [W/(m\K)]; and $ST$ is the heat source term [W/m³]

Wall shear stress is computed using the following Equation (4) [30]:

$$\begin{array}{c}{\displaystyle \frac{\mathrm{\rho }{v}_p{c}_3^{\frac{1}{4}}{k}_p^{\frac{1}{2}}}{{\tau }_w}}={\displaystyle \frac{1}{k}}ln\left(E{\displaystyle \frac{\mathrm{\rho }{y}_p{c}_3^{\frac{1}{4}}{k}_p^{\frac{1}{2}}}{\mu }}\right)\\ C_3—0.09, \mathrm{E} = 9.793\end{array}$$

(4)

where $\mathrm{\rho }$ is the fluid’s density [kg/m³]; $v_p$ is the characteristic velocity near the wall [m/s]; $C_3 \mathrm{a}\mathrm{n}\mathrm{d} k_p$ are flow-dependent constants; ${\tau }_w$ is the wall shear stress [Pa]; k is the von Karman constant; E is an empirical constant; $y_p$ is the distance from the wall [m]; and $\mu$ is the dynamic viscosity of the fluid [Pa·s].

For the prediction of the refining potential of the tundish, it is essential to determine the ratios of the different flow zones, namely the mixed zone, the dead zone, and the plug flow zone. To calculate the volumes of these zones, Equations (5)–(9) are utilized. The volume of the plug flow zone can be calculated using Equation (5):

$${\displaystyle \frac{V_p}{V}}={\displaystyle \frac{{\tau }_{min}}{\overline{\tau }}}$$

(5)

where

• $V_p$ is the plug volume, measured in [m³];
• ${\tau }_{min}$ is the minimum residence time, measured in [s];
• $\overline{\tau }$ is the theoretical mean residence time, measured in [s].

$$\overline{\tau }={\displaystyle \frac{V}{Q}}$$

(6)

where

• V is the tundish volume, measured in [m³];
• Q is the volumetric flow rate [m³·s⁻¹].

The volume in the dead zone was calculated using Equation (7):

$${\displaystyle \frac{V_d}{V}}=1-{\displaystyle \frac{{\overline{\tau }}_{real}}{\overline{\tau }}}$$

(7)

where

• $V_d$ is the dead zone volume, measured in [m³];
• ${\overline{\tau }}_{real}$ is the real mean residence time flow in the equipment [s] (8).

$${\overline{\tau }}_{real}={\displaystyle \frac{\int c·\tau ·d\tau }{\int c·d\tau }}$$

(8)

The mixed volume was calculated using Equation (9):

$${\displaystyle \frac{V_m}{V}}=1-{\displaystyle \frac{V_p}{V}}-{\displaystyle \frac{V_d}{V}}$$

(9)

where

• $V_m$ is the mixed volume, measured in [m³].

3.2. Particle Transport Model

To determine the time and duration of liquid steel presence inside the tundish, the residence time is a crucial factor. To identify this time, the particle transport model was used. The method involves injecting a tracer that has the same physical properties as the main flowing medium. After 10 s, the tracer inflow into the tundish is stopped, allowing for the monitoring of tracer concentrations at the outlets throughout the entire flow duration.

The mathematical model expressed the injection of the tracer into the tundish by using a simple deterministic function. The function characterized a time-dependent dynamic of tracer concentrations at the inlet into the calculation model by using the unit impulse, also known as the Dirac Delta function.

The unit impulse or Dirac Delta function δ(t) can be modeled by considering the Fourier series of a rectangular pulse train.

Equation (10) uses a convection–diffusion equation to predict tracer quantities in the volume. It has the following general form:

$${\displaystyle \frac{\partial }{\partial t}}\left(\rho Y_i\right)+\nabla .\left(\rho \overrightarrow{v}{Y}_i\right)=-\nabla ·\overrightarrow{J_i}+R_i+S_i$$

(10)

where $Y_i$ is the local quantity of each particle; $R_i$ is the ratio of particles i formed by chemical reactions; and $S_i$ is the rate of particle formation by the addition from a dispersed phase and any defined source [31,32].

Tracer served as a supplementary tool for RTD analysis and a comparison of outputs from the tundish.

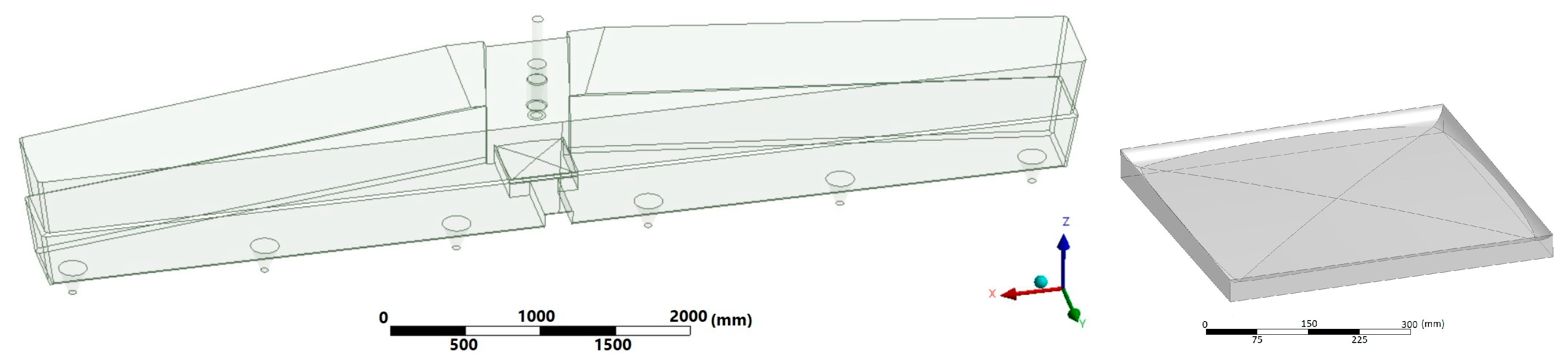
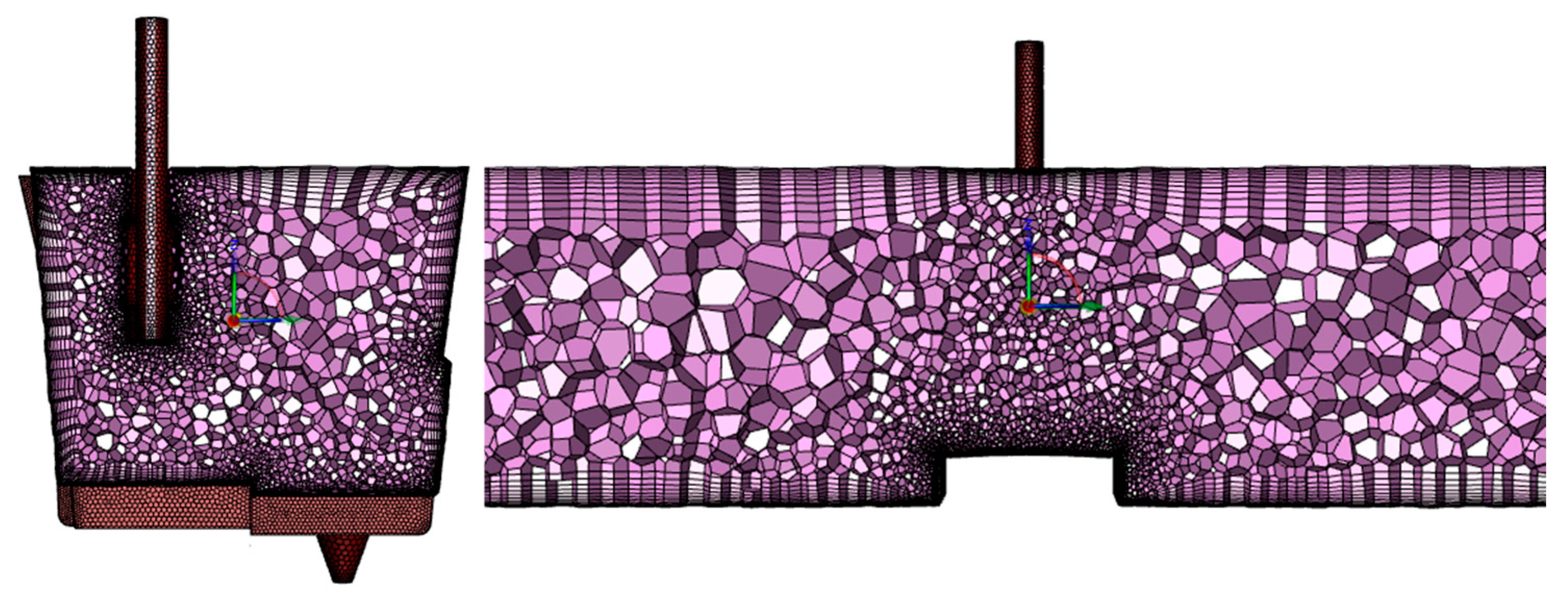
3.3. Geometry, Computational Mesh, and Boundary Conditions

For the purpose of flow modeling, a model representing the internal volume of the tundish (5.7 m³) was created to simulate the fluid flow inside the tundish. The simulations were carried out for a casting speed of 1.3 m.min⁻¹ for a casting block of 280 × 280 mm on a real continuous casting machine. The basic dimensions of the tundish with the “KTHE/C” impact pad are shown in Figure 5. Three different configurations were analyzed, namely configuration K for the “KTHE/C” impact pad (Figure 6), the SP-K2 configuration for the “SPHERIC-K2” impact pad (Figure 7), and the SP-K4 configuration for the “SPHERIC-K4” impact pad. The geometries were drawn using the DesignModeler environment of the Ansys 2023 R1 software package.

A polyhedral computational mesh was generated for the simulation domain, as illustrated in Figure 8, comprising over 1.4 million mesh elements. The structured nature of the mesh was intended to enable the accurate resolution of velocity gradients, particularly within the boundary layer regions. Mesh quality was assessed using skewness and orthogonality metrics, yielding values of 0.32 and 0.99, respectively, which indicate a high-quality grid. Given the turbulent characteristics of the flow under investigation, boundary layer refinement was applied during mesh generation. In addition, specific regions corresponding to the inlet, outlet, and tundish walls were clearly defined to ensure the accurate implementation of the initial and boundary conditions in the simulation setup.

To verify the reliability of the computational mesh quality, a mesh independence analysis was performed. Three levels of mesh refinement—coarse (912,874 elements), medium (1,404,422 elements), and fine (1,895,970 elements)—were compared by evaluating output variables such as tracer concentration and temperature field distribution. The results of the analysis showed that while the coarse mesh exhibited noticeable deviations, the differences between the medium and fine meshes were less than 2%, indicating that the model results are mesh-independent, and that the medium mesh provides a good balance between accuracy and computational efficiency.

The analysis was performed in transient modes, with a total of 8000 time steps and a maximum time step of 0.1 s. The calculation took into account the effect of gravity.

The computational model used in the simulation was defined with a ladle shroud diameter of 80 mm, a molten steel depth of 930 mm, and a ladle shroud immersion depth of 334 mm. The total internal volume of the tundish was 5.7 m³. The ladle shroud had an outside diameter of 80 mm.

The material properties of the molten steel included an inlet temperature of 1813 K, a density of 7030 kg·m⁻³, a viscosity of 0.0067 kg·m⁻¹·s⁻¹, a specific heat capacity of 751 J·kg⁻¹·K⁻¹, and a thermal conductivity of 41.5 W·m⁻¹·K⁻¹. The heat flux applied was 15 kW·m⁻².

At the inlet, the mass flow rate of the molten steel was set to 11.36 kg·s⁻¹, with a turbulent intensity of 3.48% and a hydraulic diameter of 0.08 m. Outlet conditions were defined with a pressure outlet set to 0, a turbulent intensity of 3.64%, and a hydraulic diameter of 0.055 m.

Thermal boundary conditions at the tundish walls included a constant temperature of 1777 K. Heat losses were specified as 2.5 kW·m⁻² through the wall and 15 kW·m⁻² through the surface.

For tracer-based flow analysis, the tracer was injected for a duration of 10 s.

4. Evaluation and Discussion

The evaluation of the CFD simulation results was carried out through an analysis of flow structures visualized using the contour maps, vector fields, streamlines, and temperature distributions of the molten steel across specific cross-sectional planes for both configurations. In addition, steel flow behavior over time was assessed by comparing residence time distribution (RTD) curves and associated residence time values. For the tundish under investigation, the theoretical mean residence time of molten steel was calculated to be 502.8 s. Furthermore, the analysis included the identification and characterization of distinct flow regions within the tundish, namely the plug flow zone, the mixed flow region, and the dead zone, which reflect real reactor behavior in interconnected flow environments [33,34,35].

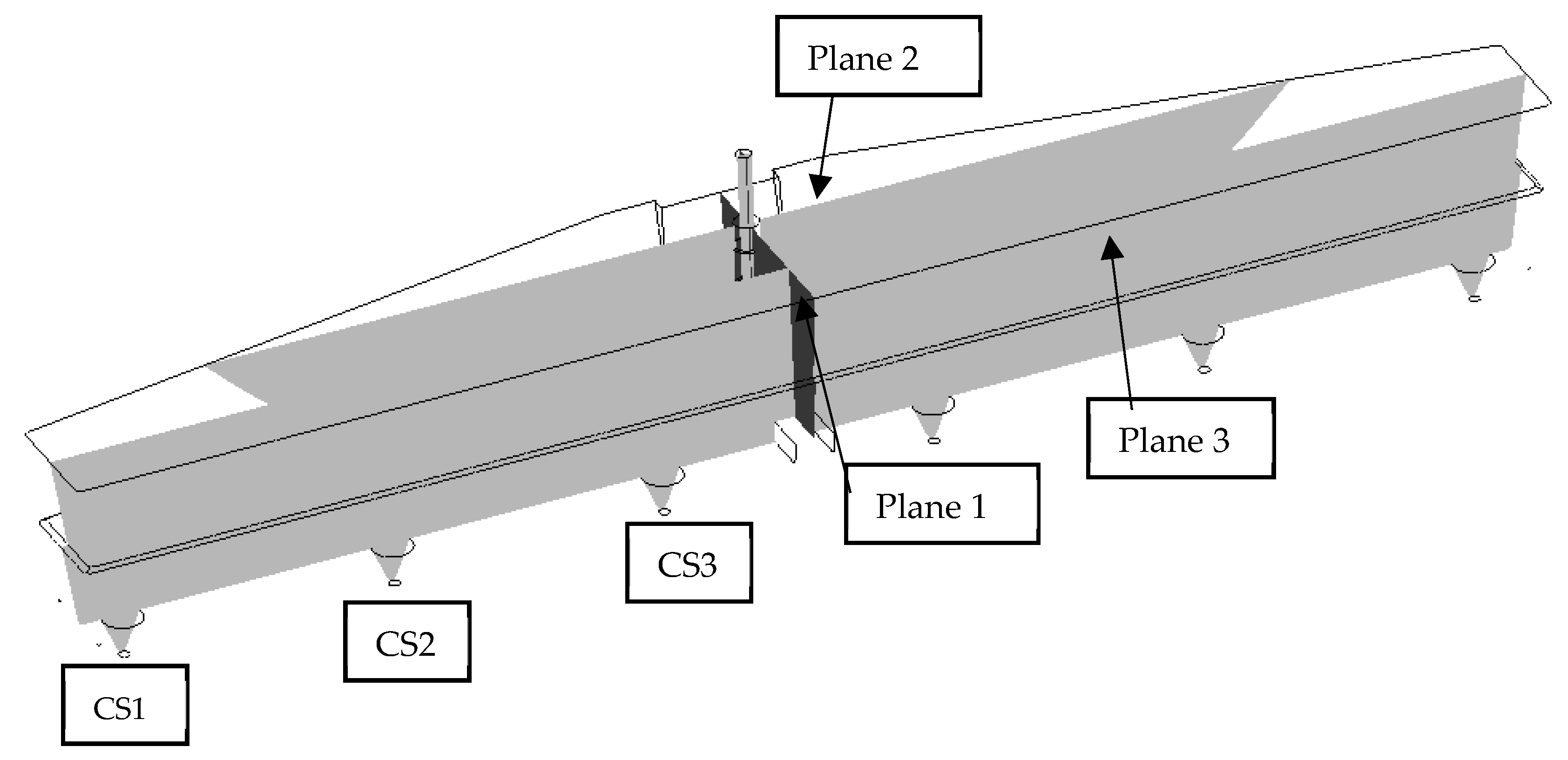
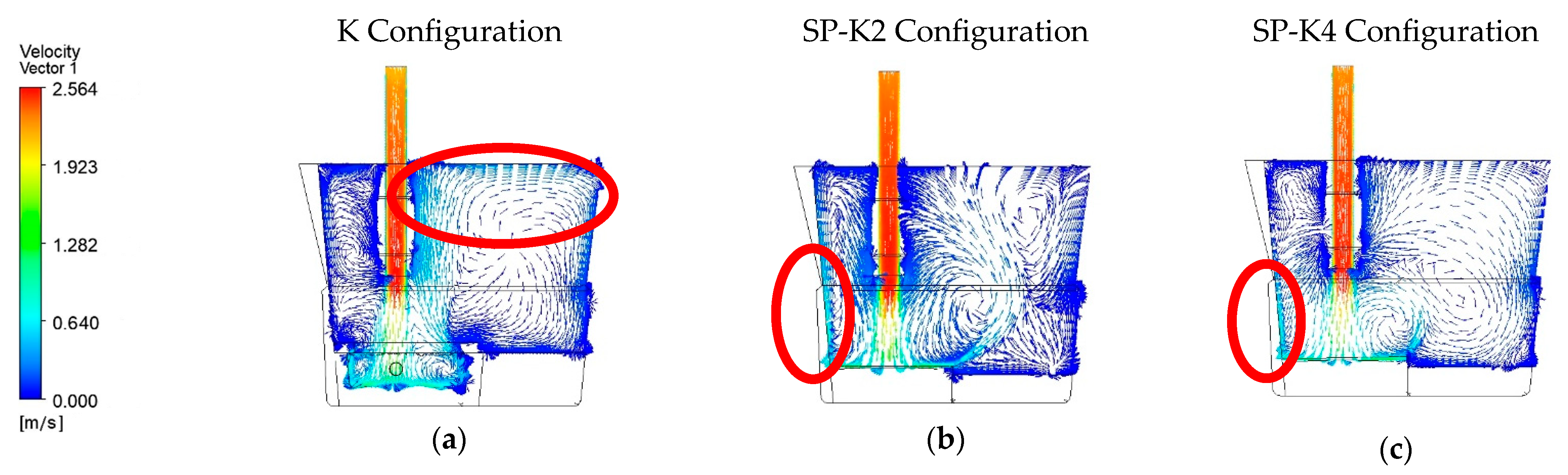
4.1. Flow Characteristic Evaluation

The visual evaluation of the flow characteristics based on vectors, contours, and streamlines was carried out in three planes: the YZ plane (a cross-section)—Plane 1, the XZ plane—Plane 2, and the XZ plane—Plane 3 (coming through the outlets) (Figure 9).

The tracer flow pattern observed at 20 s, based on contour visualization in the ZY plane (Plane 1), is presented in Figure 10. The comparison between configurations allowed for clear differentiation in flow behavior as a result of the applied impact pad design. In the K configuration, the flow pattern resembled a typical plug flow, which may lead to the exposure of the molten steel surface and contribute to the formation of the so-called slag “red eye” phenomenon. In contrast, the SP-K2 configuration exhibited a notable redirection of flow toward the upper frontal region of the tundish. This redistribution supports a more uniform dispersion of molten steel throughout the tundish volume, enhancing the overall efficiency of space utilization. The SP-K4 configuration further modified the flow by promoting partial dispersion throughout the tundish while simultaneously directing part of the flow along the axis of the ladle shroud.

The observation of the tracer flowing through the XZ plane (Plane 2) revealed that it was necessary to prevent a short-circuit flow primarily at the CS3 outlet. It was achieved with both analyzed configurations—SP-K2 and SP-K4 (Figure 11).

The visualization of the tracer flow patterns at 80 s shows certain differences between the SP-K2 and SP-K4 configurations as well as a more even distribution across the whole tundish volume (Figure 12).

The observation of the flow patterns in Plane 3 revealed that the tracer only flew in the upper section of the inflow area with the K configuration. This phenomenon might cause increased erosion of the lining in the slag line area (Figure 13).

Flow behavior near the tundish walls can be effectively analyzed using vector fields, which reveal both the direction and magnitude of molten steel movement. This approach provides insights into potential erosion intensity caused by flow acting on the working lining. From the vector analysis corresponding to the K configuration, it was determined that the upper central region of the tundish particularly close to the ladle shroud is subjected to the highest stress and is therefore most susceptible to wear. In contrast, under the SP-K2 and SP-K4 configurations, the region exhibiting the greatest stress concentration was located in the rear section of the tundish, specifically behind the ladle shroud, as illustrated in Figure 14.

The cross-section of Plane 2 shows the flow vectors in the analyzed configurations (Figure 15), with visible differences in the flow across the entire tundish volume.

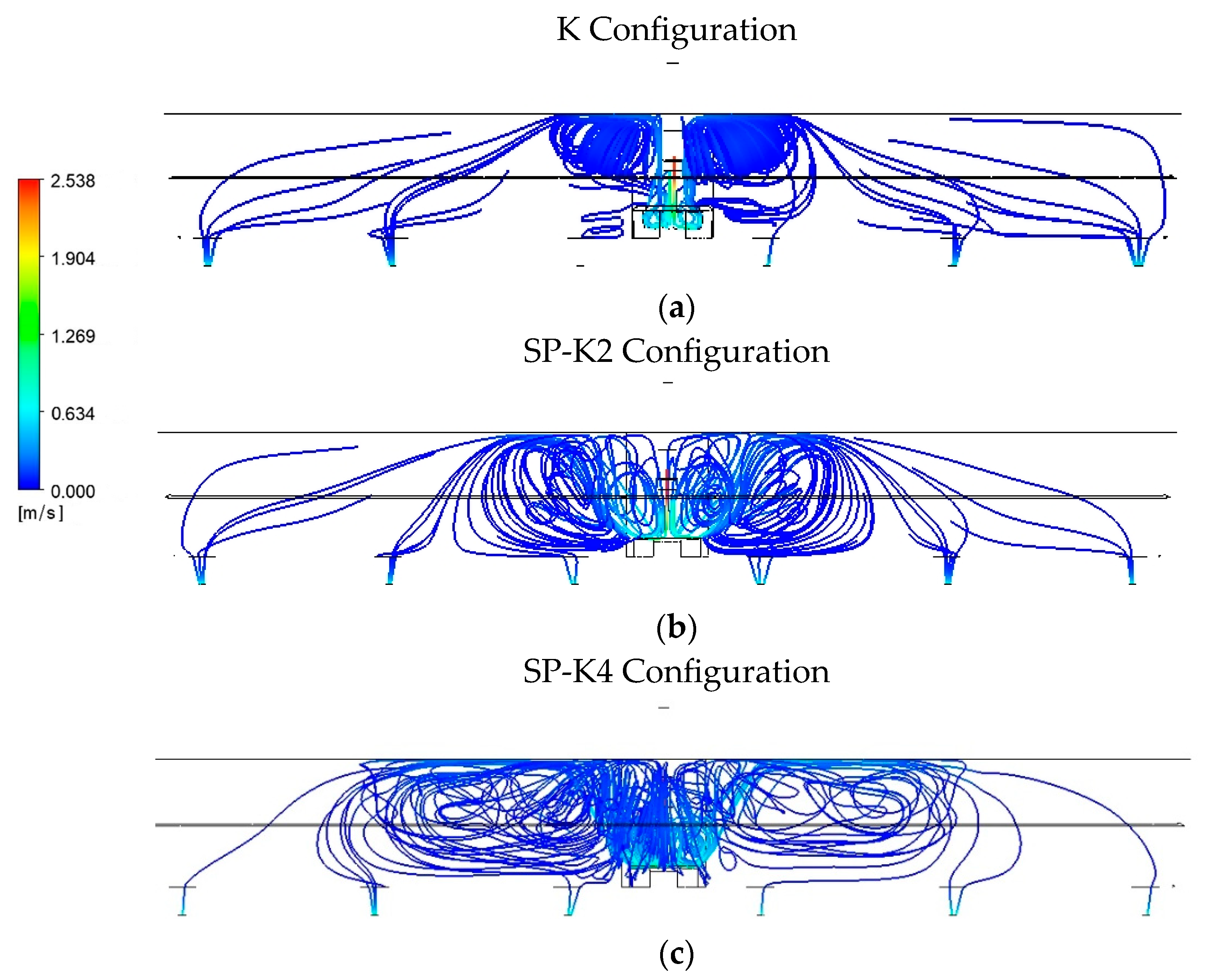
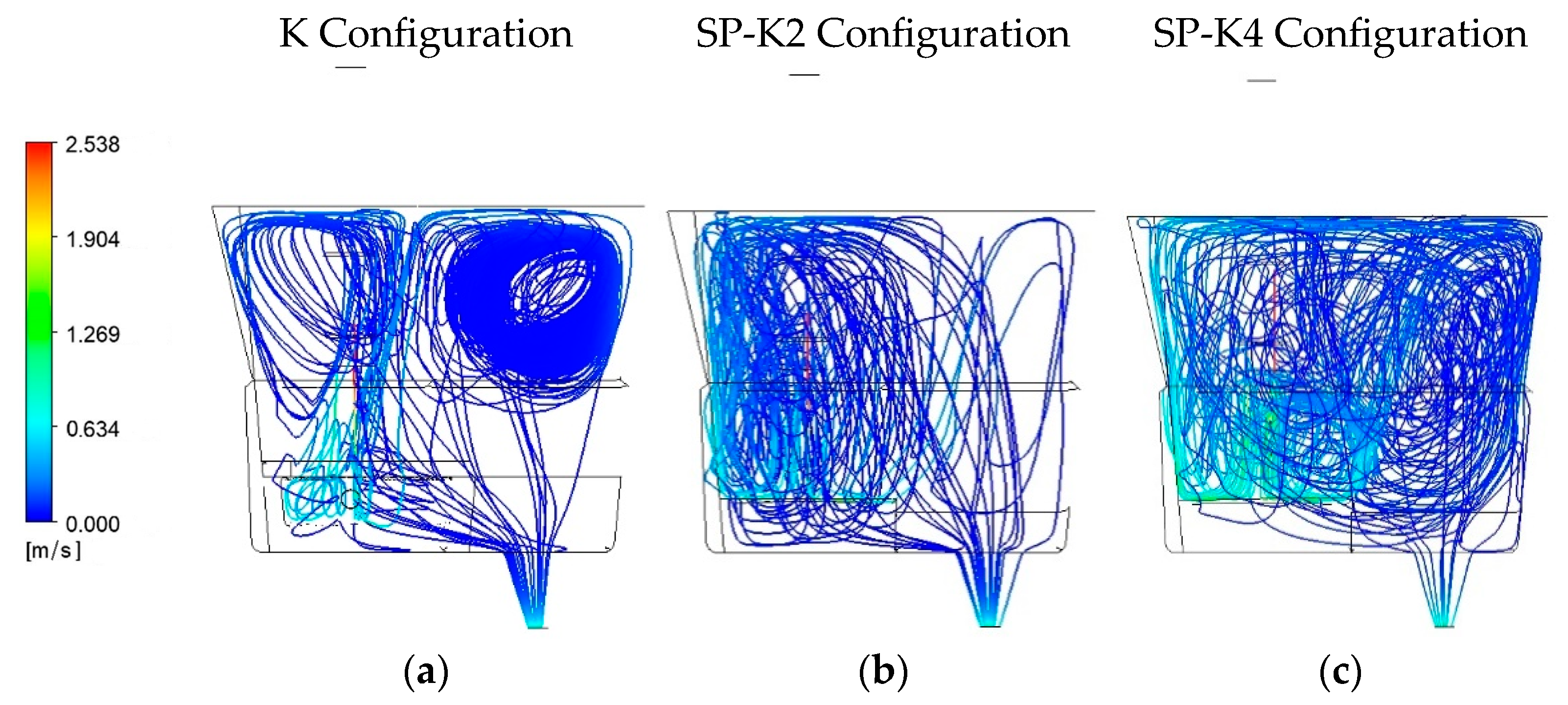
4.2. Streamlines

The visualization of streamlines from a top-down perspective of the tundish enabled the tracking of the flow path of a monitored fluid particle from its entry point to the outlet. In the SP-K2 configuration, the streamlines were initially directed toward the rear section of the inlet zone before progressing to the outlets. In contrast, the reference (K) configuration showed streamlines oriented mainly toward the central outlets, resulting in extended residence times for strand CS3, as illustrated in Figure 16. In the case of the SP-K4 configuration, the flow distribution in the inlet zone appeared more balanced, with streamlines spreading uniformly in all directions, contributing to improved flow symmetry and potentially enhanced mixing.

The tundish in the K configuration had a denser initial flow in the upper front inflow area near the central outlet CS3. This caused erosion and wear of the lining in that specific section of the tundish. Afterwards, the streamlines were directed towards individual outlets. On the other hand, the SP-K2 configuration facilitated the dispersion of the flow to a wider rear section of the tundish with lower flow intensity, resulting in higher values of minimum residence time at CS3, as shown in Figure 17. Similarly, with the SP-K4 configuration, the flow pattern observed was similar to that of SP-K2, but with an even wider dispersion across the entire tundish volume.

A closer look at the flow of the steel in the tundish shows that in the K configuration, the steel flow was concentrated near the center of the tundish, causing erosion and wear of the lining in the upper front section of the tundish. In contrast, with the SP-K2 configuration, the flow was directed towards the rear part of the tundish along its entire height, resulting in lower flow velocity and less wear on the lining in the tundish outlet area. The streamlines were evenly distributed across the entire cross-section of the tundish with the SP-K4 configuration (Figure 18).

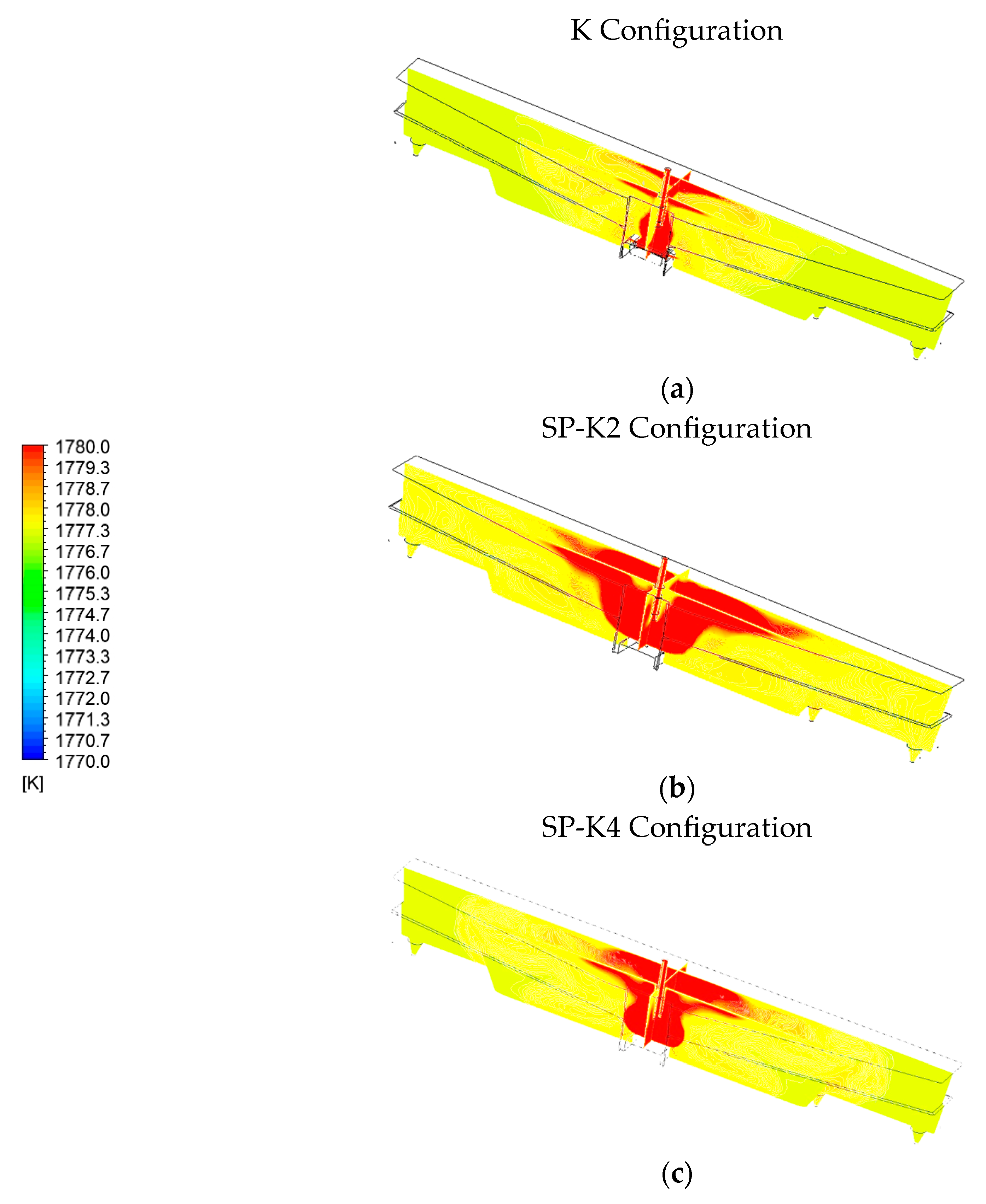
4.3. Heat Transfer

Section 3.3 summarizes the input parameters of the incoming molten steel used in the heat transfer analysis. Figure 19 illustrates the temperature distribution within selected cross-sectional planes for the various configurations evaluated. When comparing the SP-K2 configuration with the reference K configuration, it was noted that the highest temperature zones were located within the inlet zone of the tundish. This observation suggests enhanced thermal homogenization as a result of the modified flow patterns induced by the SPHERIC-K2 and SPHERIC-K4 impact pad designs.

Additionally, the SP-K configurations demonstrated more uniform temperature distribution in areas located further away from the impact pad, indicating improved dispersion of thermal energy throughout the tundish volume. In contrast, the reference KTHE/C impact pad configuration exhibited localized high temperatures in the upper rear and frontal regions near the ladle shroud, which correlates with a plug flow regime. This flow behavior suggests less effective mixing between the incoming molten steel and the bulk steel within the tundish.

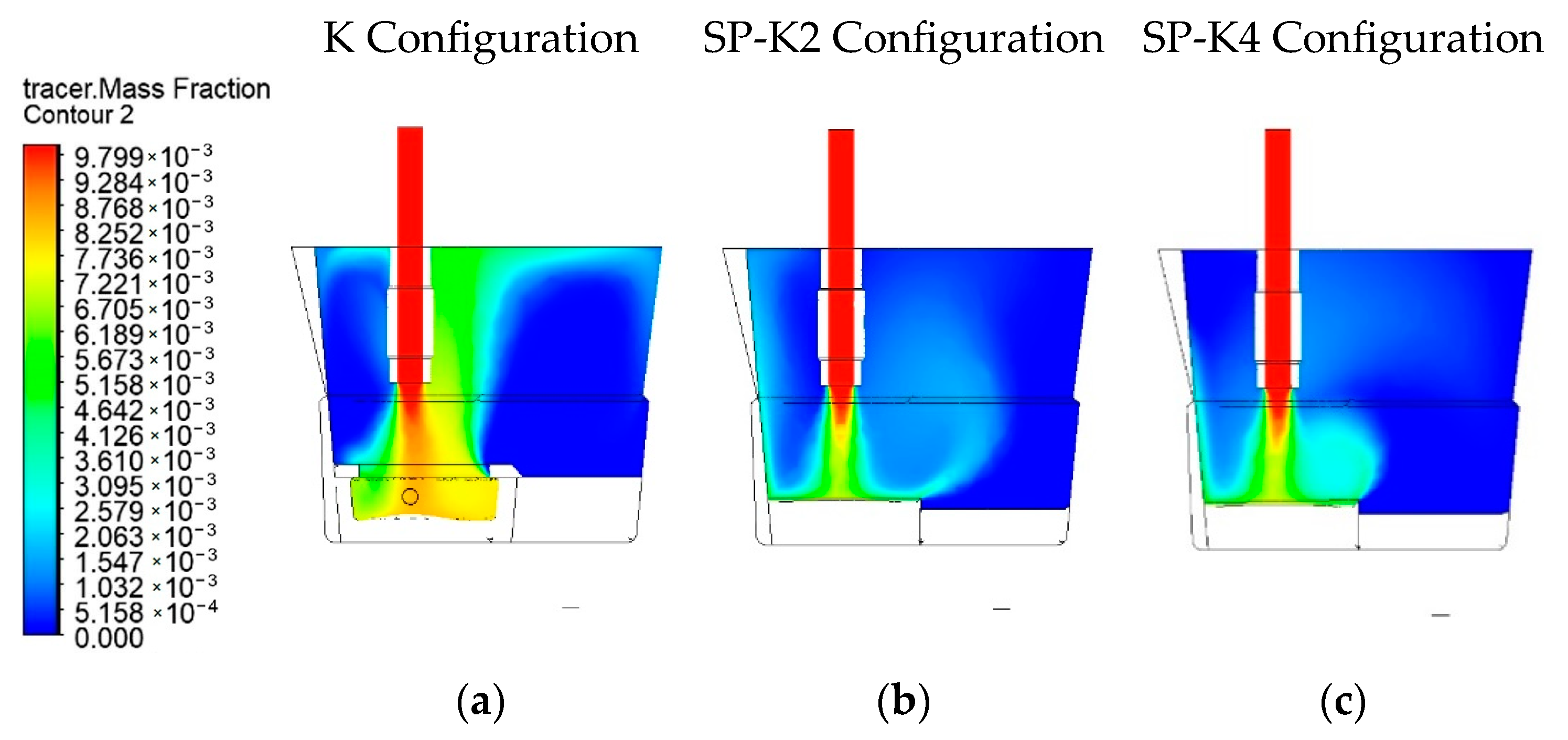
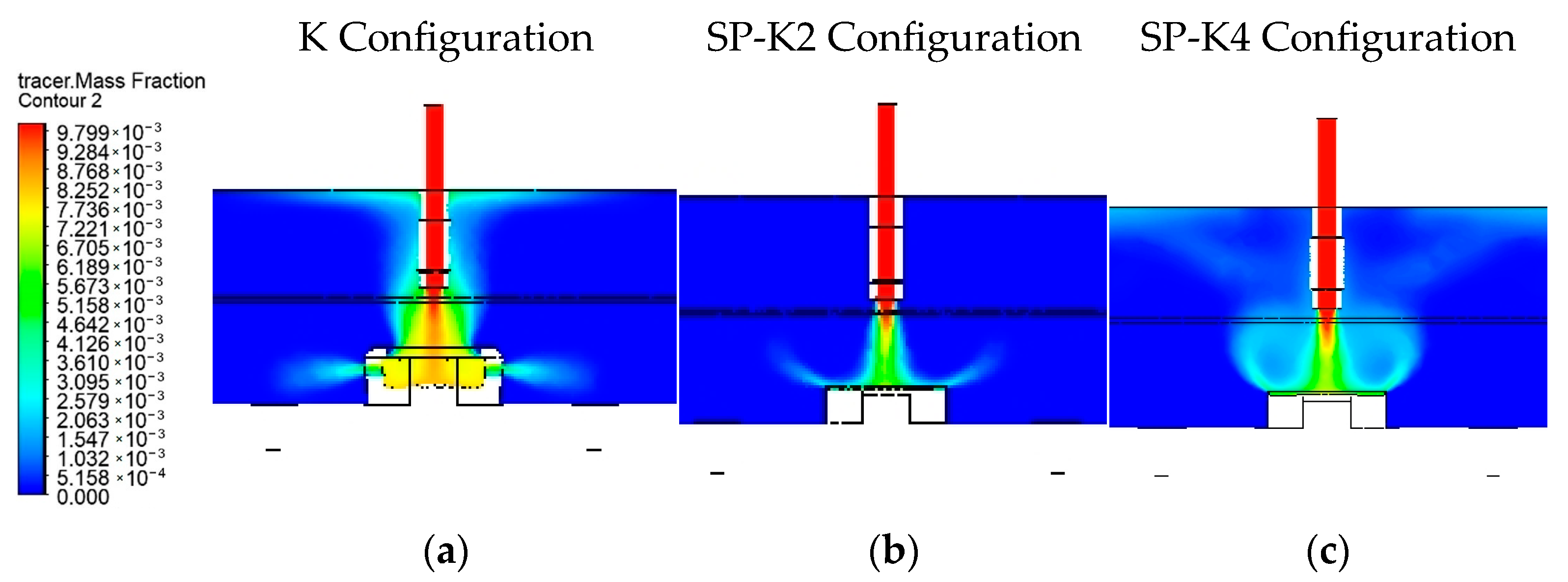
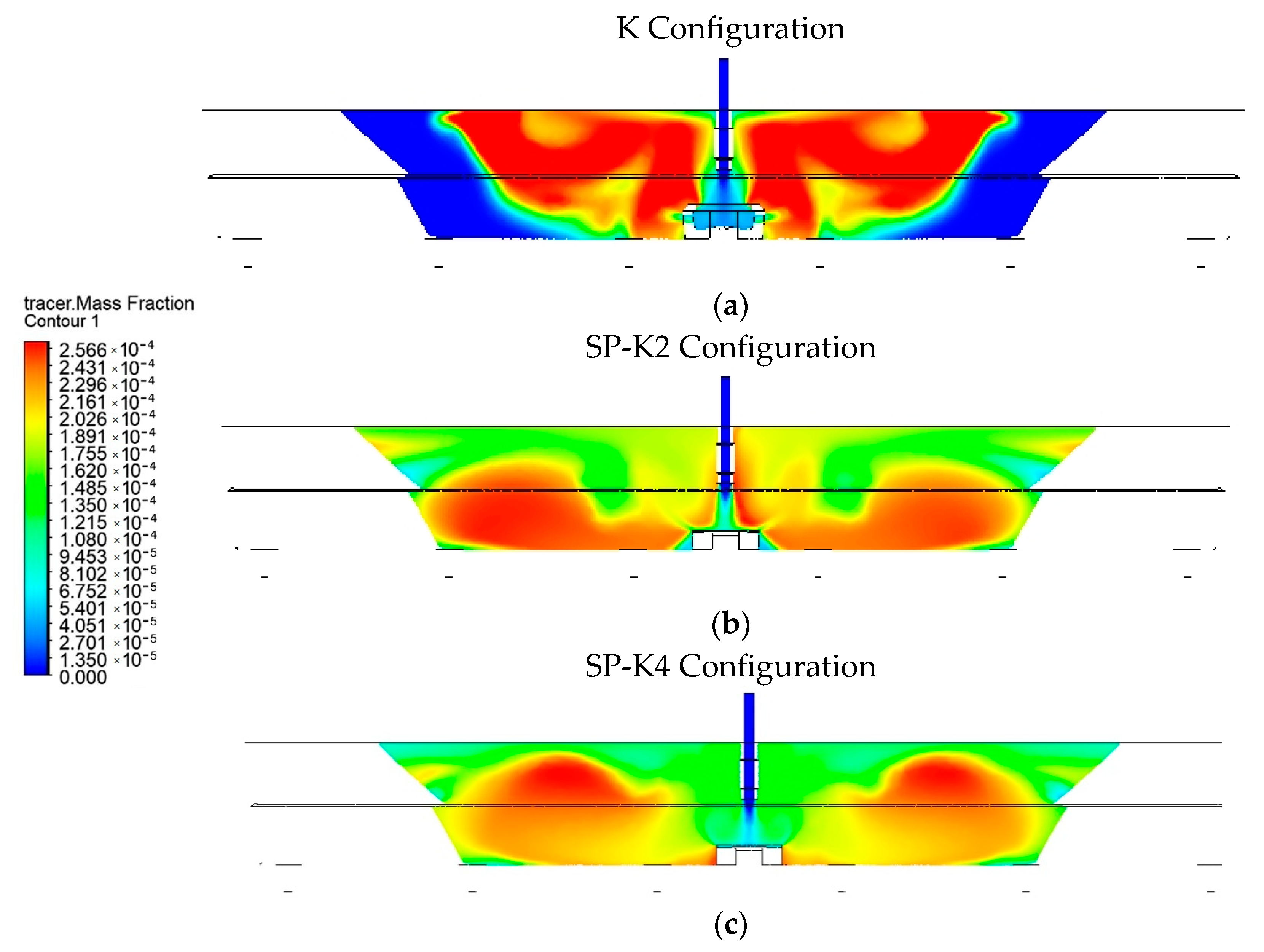
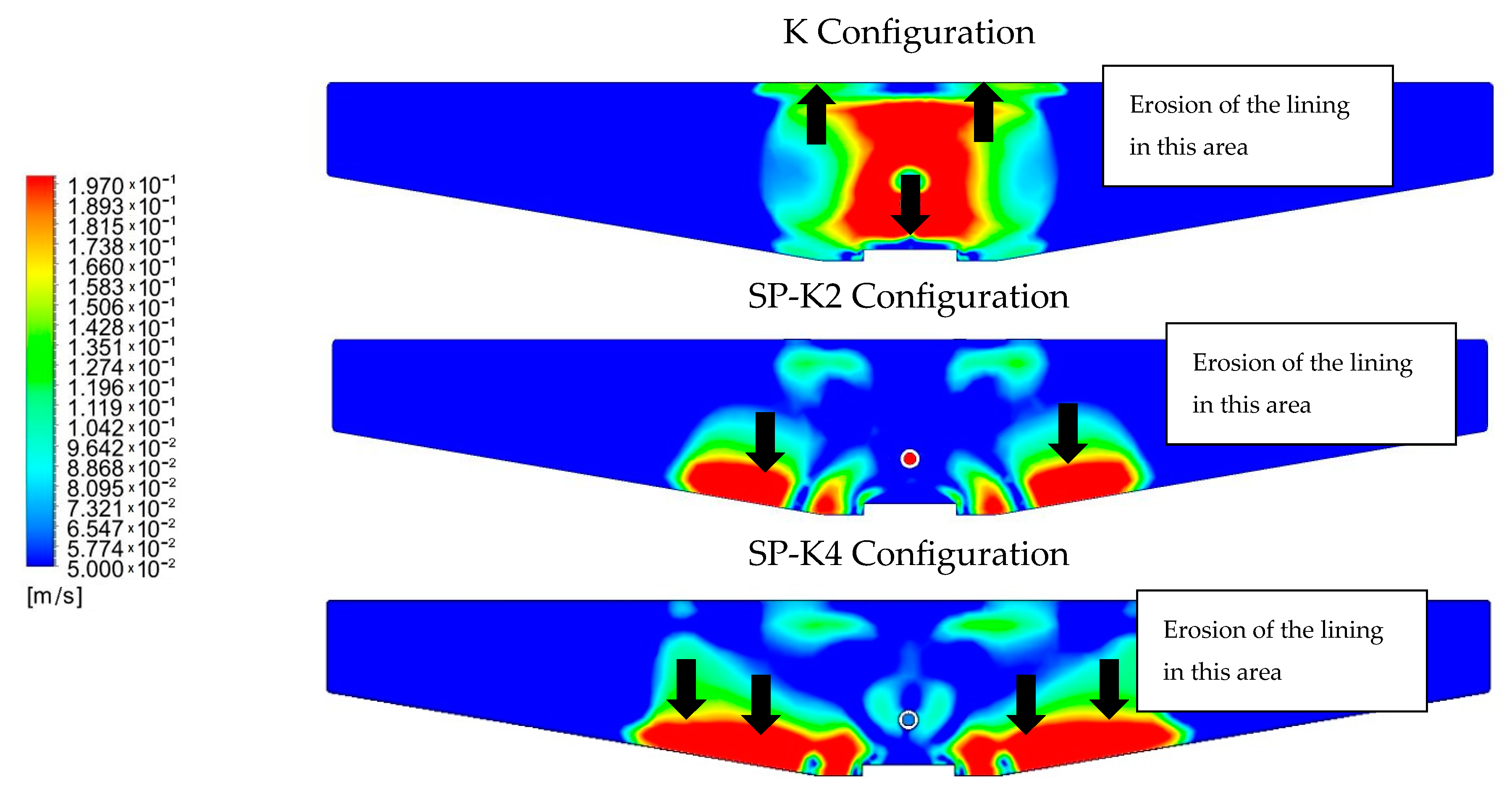
4.4. A Comparison of Contours Based on Flow Velocity

A plane section was created 10 mm below the slag level to observe the contours near the slag line. A velocity color spectrum ranging from 0.05 to 0.2 m/s was used. Based on the observations, it is possible to conclude that the velocity field has changed. With the SP-K2 and SP-K4 configurations, lower flow velocities were observed near the ladle shroud. This could have a positive impact on reducing the wear of the refractory lining in the central part of the tundish. This trend has also been confirmed by the results of the tracer distribution and the specified vectors shown in Figure 20.

Based on the turbulent kinetic energy [36,37] analysis in the KTHE/C impact pad area, a high value (~1.4 × 10⁻¹ m²/s²) was recorded at the impact point, indicating significant turbulent activity. There is almost no flow near the walls of the tundish, which may lead to the formation of dead zones. At the melt surface, the activity is moderate, but with a risk of lining erosion and slag shearing, which may adversely affect the metallurgical quality of the steel.

Compared to the SP-K4 impact pad configuration, the turbulent kinetic energy in the impact zone was significantly lower (~1.7 × 10⁻³ m²/s²), indicating effective damping of the influent flow. The flow near the walls is uniformly distributed with finely flowing regions, while the melt level remains stable and virtually free of turbulent activity, contributing to protection from slag contamination.

In terms of the rate of dissipation [37] of the turbulent energy, the impact zone in the case of the KTHE/C impact pad is characterized by a broad, intensely dissipating flow that also reaches the surface, thereby disturbing it. This poses a risk of slag entrainment and uncontrolled mixing, which can impair melt purity.

In contrast, with the SP-K4 impact pad, there is targeted dissipation in the impact area and a steady flow at the walls, leaving the surface almost untouched. This configuration allows for higher metallurgical quality, and although the mixing efficiency is lower, it is more controllable and uniform.

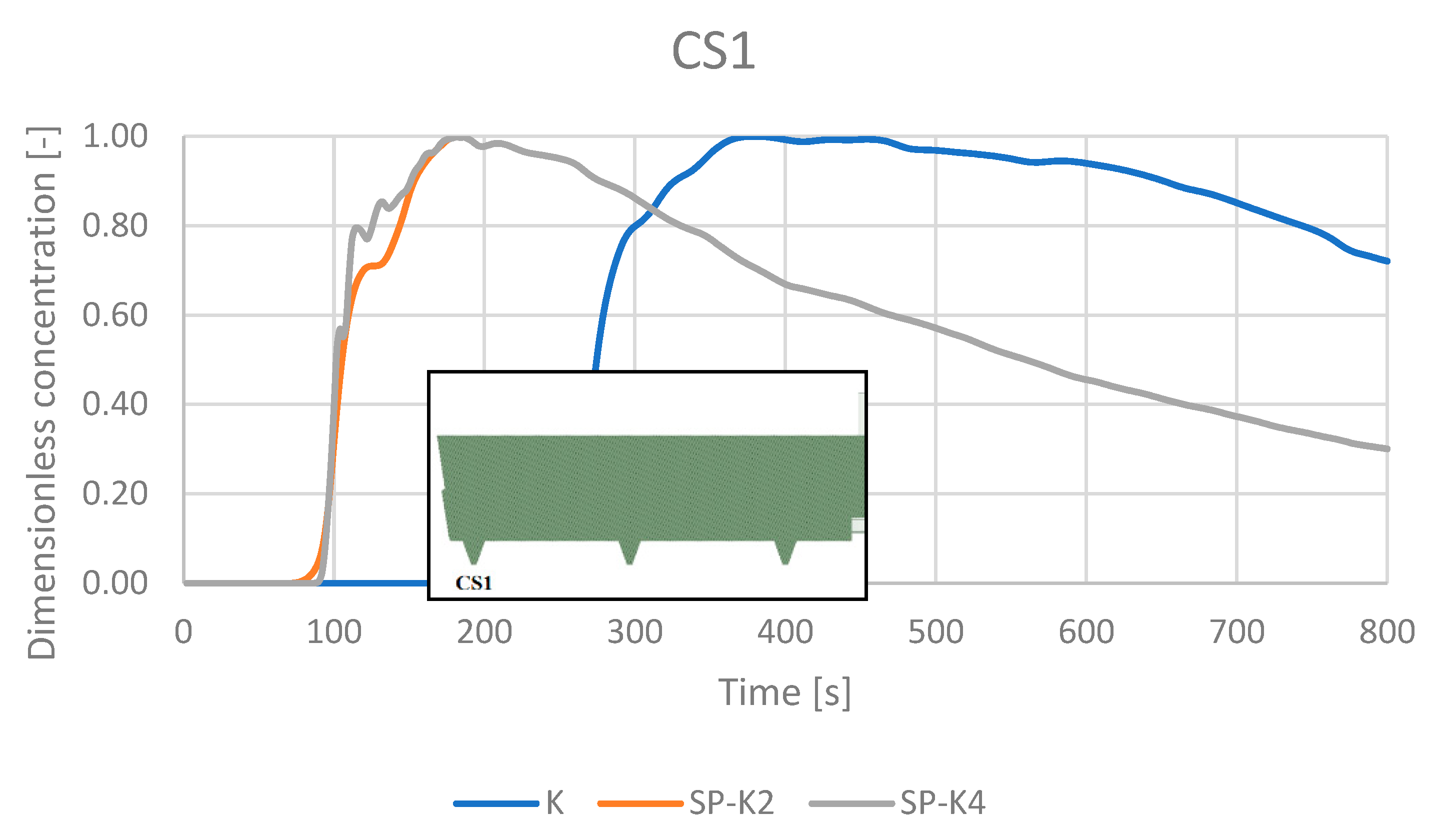
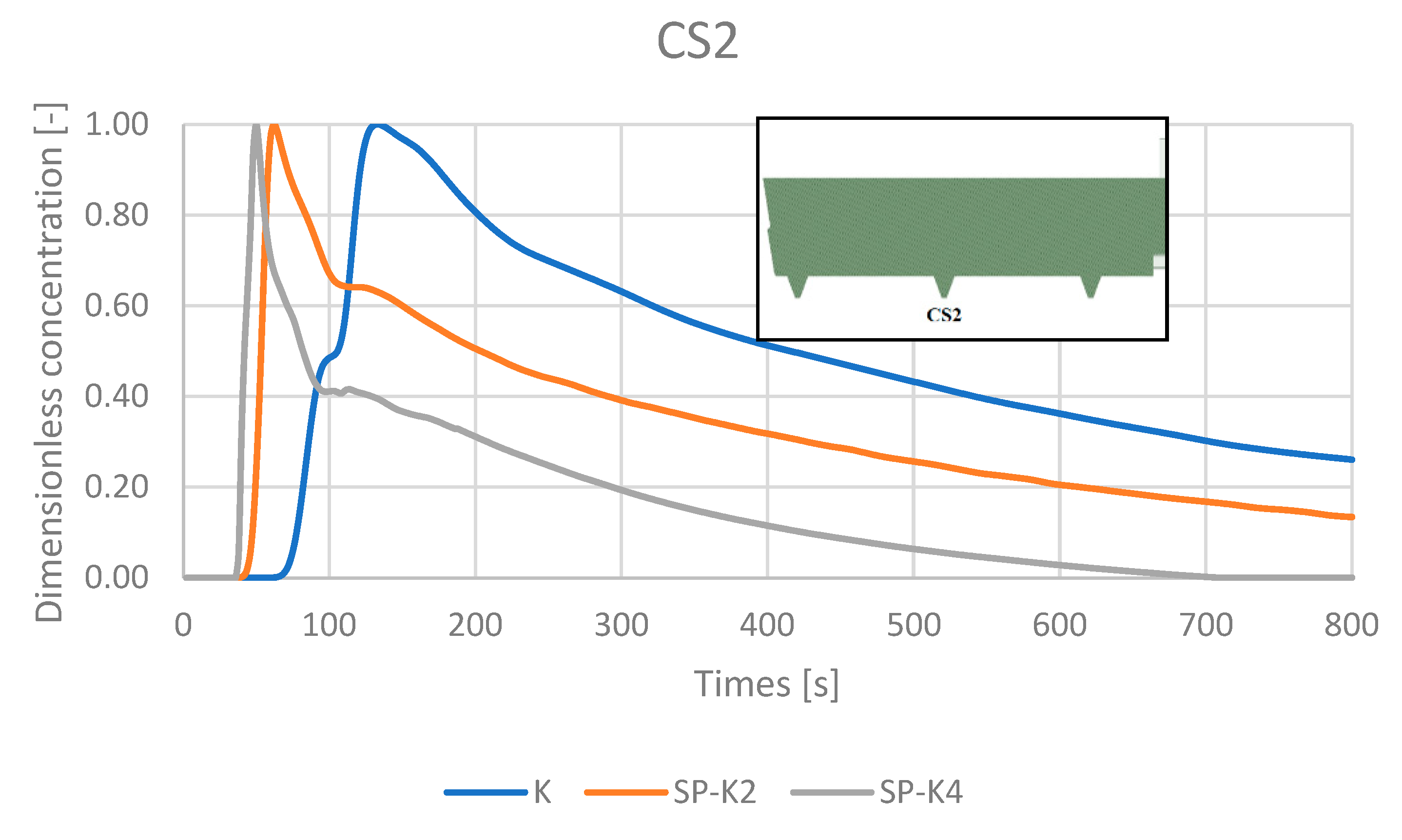
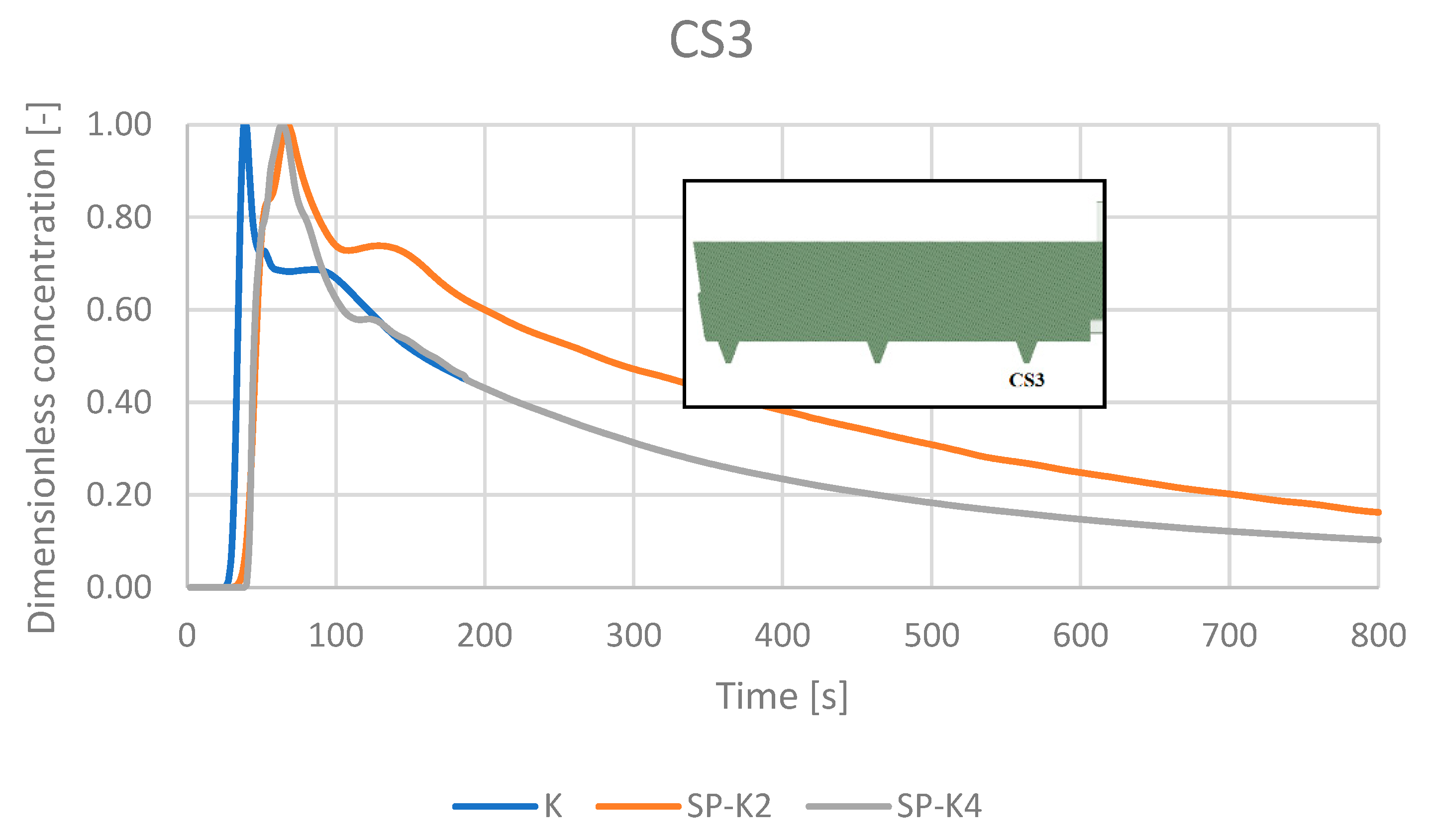
4.5. RTD Curves

From the first results of the simulations, the effect of the symmetry of the tundish was confirmed. Therefore, only three outlets on one side of the tundish were evaluated for further comparison of the residence time results. The flow characteristics of the CS1, CS2, and CS3 outlets were evaluated using RTD curves to determine the minimum and maximum residence times (Figure 21, Figure 22 and Figure 23).

The values of the minimum and maximum residence times, identified based on the C-curves at individual outlets for the analyzed configurations, and the percentage differences from the reference K configuration are listed in

Table 3. Calculation parameters for RTD and flow rate volume proportions for the K, SP-K2, and SP-K4 configurations.

Resulting Min. and Max. Residence Times							$\frac{{\mathit{V}}_{\mathit{d}}}{\mathit{V}}$	$\frac{{\mathit{V}}_{\mathit{p}}}{\mathit{V}}$	$\frac{{\mathit{V}}_{\mathit{m}}}{\mathit{V}}$
	Tmin [s]			Tmax [s]			[%]
	CS1	CS2	CS3	CS1	CS2	CS3
K configuration	168	56	28	387	103	37	19.9	25.8	54.3
SP-K2 configuration	80	41	33	180	60	65	31.7	15.2	53.1
Percentage difference [%]	−52.4	−26.8	17.9	−53.5	−41.7	75.7	-	-	-
SP-K4 configuration	65.2	39.5	43.3	180	50	73.9	19.9	9.8	70.3
Percentage difference [%]	−61.2	−29.5	54.6	−53.5	−51.5	99.7	-	-	-

.

One of the main goals of developing the new impact pad (SP-K4 configuration) was to ensure that the residence times between each casting strand are as consistent as possible. This was a challenging task as there are significant variations in the distances between the impact pad and the individual casting strands.

In configuration SP-K4, we have made significant improvements in the liquid steel flow pattern in the tundish volume. We have successfully reduced the residence time of the farthest casting strand, CS1, by 61.2%, which will greatly decrease the dead zone volumes. Moreover, we have extended the residence time of the nearest casting strand, CS3, by 54.6%. This modification will significantly enhance the refining capacity of the tundish.

When comparing the calculation of the dead volume based on the residence times on the individual casting strands in the K and SP-K4 configurations, the values were the same, and in the case of the SP-K4 configuration, there was a reduction in the plug flow and an increase in the mixing zone.

Furthermore, based on the comparison of the analyzed configurations, a ratio of mixed volume to the dead volume was calculated ${\displaystyle \raisebox{1ex}{${\mathrm{V}}_{\mathrm{m}}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{V}}_{\mathrm{d}}$}\right.}$; it expresses the quality of thermal and chemical homogenisation in the tundish and is a ratio of plug flow to dead flow ${\displaystyle \raisebox{1ex}{${\mathrm{V}}_{\mathrm{p}}$}\!\left/ \!\raisebox{-1ex}{${\mathrm{V}}_{\mathrm{d}}$}\right.}$; it expresses the conditions for the favorable flotation of non-metallic inclusions [2], as shown in

Table 4. Comparison of ratios of different tundish volumes.

Configuration	Vm/Vd	Vp/Vd
K	2.7	1.3
SP-K2	1.7	0.5
SP-K4	3.5	0.5

.

It can be assumed that the initial experimental SP-K2 configuration will lower thermal and chemical homogeneity, leading to the favorable flotation of non-metallic inclusions, based on calculated values for the mixed zone and dead zone volumes. On the other hand, the second experimental SP-K4 configuration has better V_m/V_d and V_p/V_d ratios, leading to a significant improvement in steel cleanliness, as well as thermal and chemical homogeneity.

5. Industrial Plant Trials

Verification tests were performed for the SP-K4 configuration with the “SPHERIC—K4”-shaped impact pad developed based on the results of numerical simulations. The casting speed in the verification tests was 1.3 m/min for a casting block of 280 × 280 mm. During the tests, structural steel designated as S355, which is used for more demanding construction, was casted. A magnesite gunning mix with a composition of 80% MgO, 6.5% CaO, 2.5% SiO₂, and 7% FeO was used for the working lining. The primary objective was to observe and compare the erosion areas of the working refractory lining caused by incoming molten steel in the upper part of the tundish slag line area. The first verification test was realised over 8–10 h on 12 heats and the second verification test was realised over 18 h on 18 heats. For comparison during the verification tests, the reference configuration K for the shaped impact pad “KTHE/C” was used, which is shown in Figure 24. The test configuration “SP-K4” with the shaped impact pad “SPHERIC—K4” is shown in Figure 25.

Plant trials were realized with the same count of heat settings, steel grade, and casting speed. During plant trials, the compactness of the slag layer around the ladle shroud was monitored, and the creation of the red-eye phenomenon was observed in reference configuration K (Figure 26), which can lead to a significant decrease in steel cleanliness.

Figure 27 shows significant wearing on the working lining and permanent lining after 18 heat cycles in the slag line area using reference configuration K.

Figure 28 indicates no visible wear on the working lining after 18 heat cycles in the slag line area using experimental configuration SP-K4 (impact pad SPHERIC K4).

6. Discussion

Developing new flow modifiers using mathematical simulations before deployment can improve the efficiency of steel casting.

The flow of liquid steel in a six-strand tundish was studied using mathematical simulations with different impact pad shapes while keeping the casting velocity constant. Three types of impact pads were evaluated and compared based on the results of the simulations. The analysis involved using contours, velocity vectors, and a tracer to determine the flow characteristics and steel temperature distribution throughout the tundish. The minimum and maximum residence times were identified using C-curves, and the volumes of interconnected flow zones such as the dead volume, mixed volume, and plug volume were calculated for each configuration.

The results of the simulations showed that by directing the steel flow to the rear of the section in the whole volume of the tundish and gradually directing the flow to the slag area at the steel surface, the erosion of this area was eliminated. By observing the flow characteristics based on vectors, it was possible to identify the optimal flow direction.

The characteristics of the flow in the tundish space have changed, resulting in more consistent residence times at each tundish outlet according to the RTD curves. When evaluating the arrangement of flow zones as a criterion for assessing thermal and chemical homogeneity and conditions for the flotation of non-metallic inclusions, the K configuration resulted in better outcomes compared to the SP-K2 configuration. However, with the SP-K4 configuration, the values for the criterion of thermal and chemical homogeneity were higher than those observed with the reference K configuration. For the evaluation of a more even distribution of temperatures of molten steel based on visual observation across the entire tundish space, it was found that the temperature field in the inflow area was more extended in the configuration with the “SPHERIC-K2” and “SPHERIC-K4” impact pads.

7. Conclusions

The results of this study clearly demonstrate that the shape and design of the impact pad play a decisive role in controlling the flow dynamics, temperature distribution, and wear resistance within the tundish during continuous casting. While the SPHERIC-K2 and SPHERIC-K4 impact pads significantly improved flow symmetry and reduced refractory erosion compared to the conventional KTHE/C pad, the findings also underscore a fundamental principle: there is no universal impact pad suitable for all tundish configurations.

Each tundish has unique geometric, operational, and process-specific parameters, including the number and arrangement of outlets, casting speeds, ladle shroud positions, and refractory materials. Therefore, it is critical that impact pads be custom-designed for individual tundish geometries and operational needs. SPHERIC-K4, as an optimized solution for the tested six-strand tundish, proved effective in balancing residence times, minimizing surface turbulence, and improving steel cleanliness. However, its performance cannot be generalized without considering context-specific constraints.

Based on the results of both CFD simulations and plant trials, the following recommendations are proposed for the future development of impact pads:

• Prioritize the customization of pad shape according to tundish geometry and strand arrangement.
• Use numerical simulations as a standard tool in the design phase to evaluate flow uniformity, thermal homogenization, and inclusion flotation zones.
• Implement wear resistance studies for refractory materials in high-turbulence regions.

Finally, despite the progress achieved, further research is needed in two key areas:

(1)

The effect of chemical erosion mechanisms caused by steel–refractory interaction;

(2)

The impact of transient flow instabilities, particularly those associated with ladle shroud exchanges and level fluctuations in the tundish. These phenomena can significantly influence the inclusion content, slag entrapment, and lining lifetime and thus require advanced modeling and experimental validation.