Smart Nutrient Solution Temperature Control System for Oversummering Lettuce Cultivation Based on Adaptive Dung Beetle Optimizer-Fuzzy PID
Abstract
1. Introduction
2. Materials and Methods
2.1. Test Area
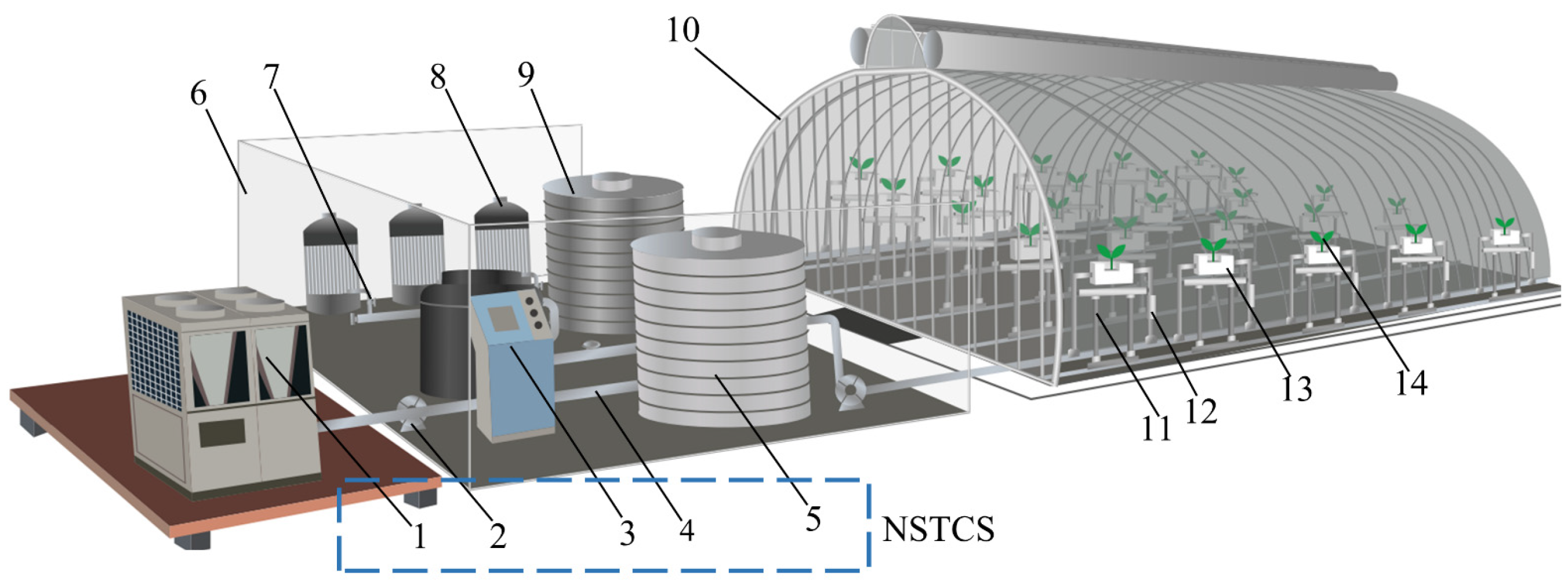
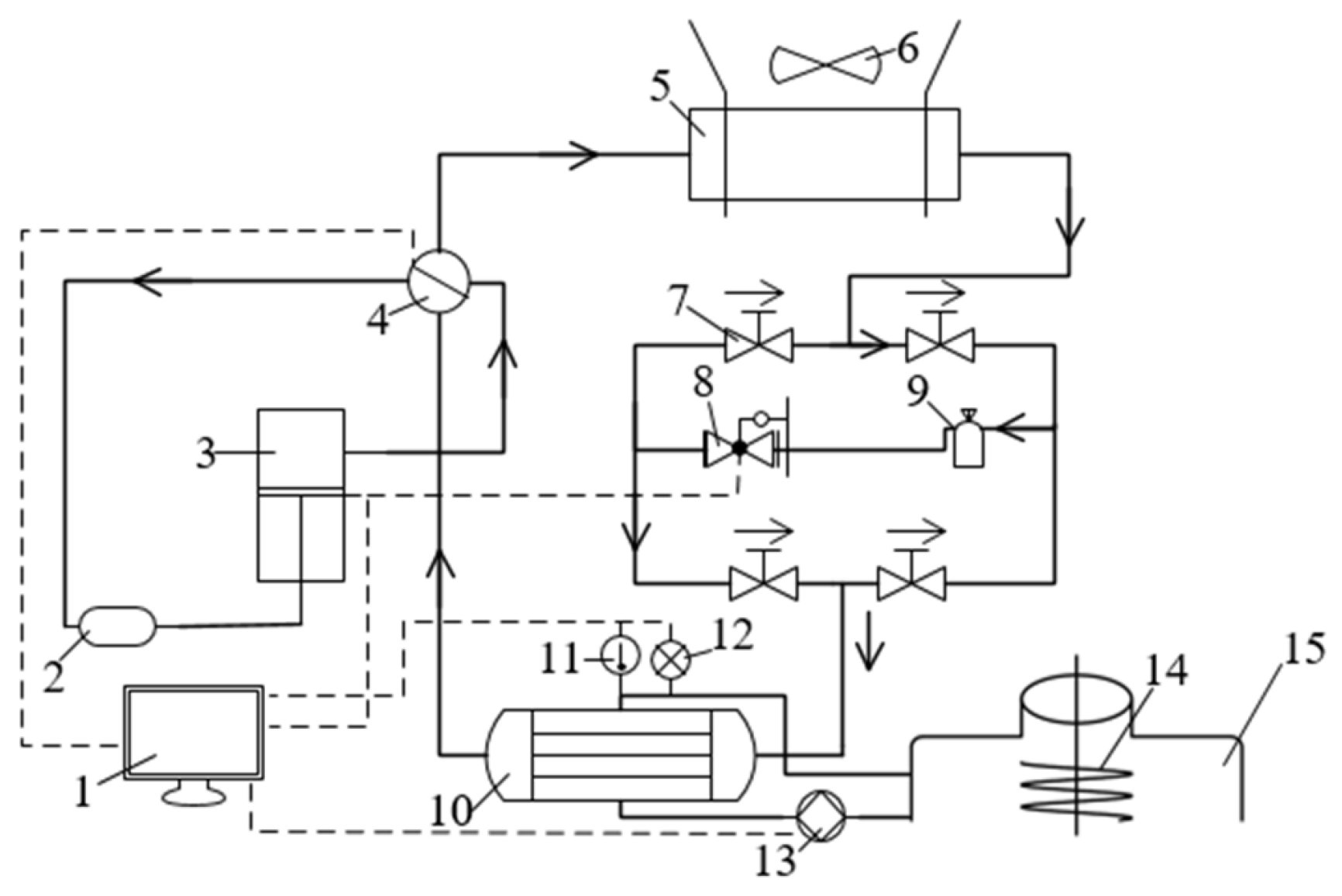
2.2. Overall Design and Working Method of the System
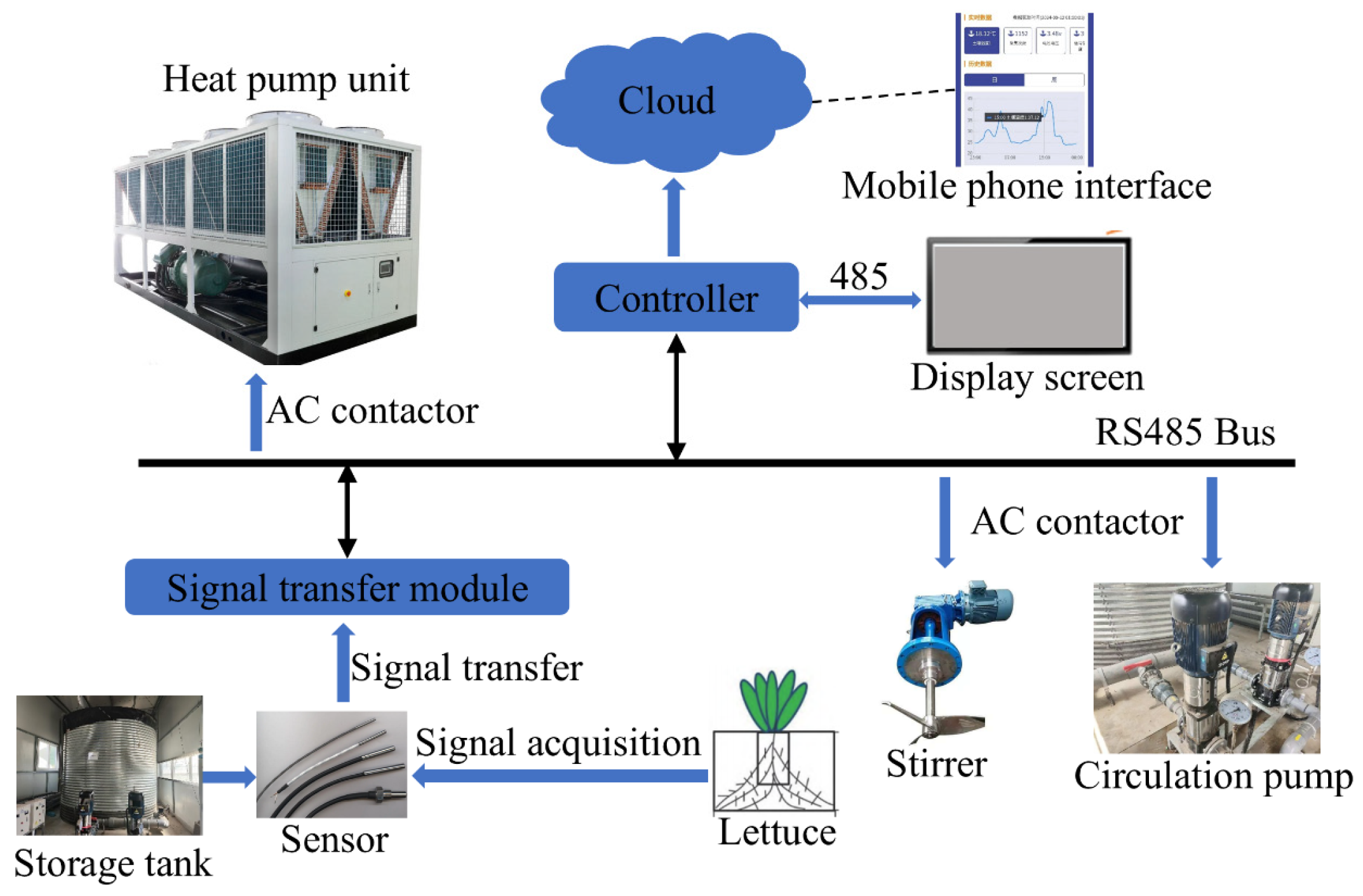
2.3. Hardware Design of Temperature Control System
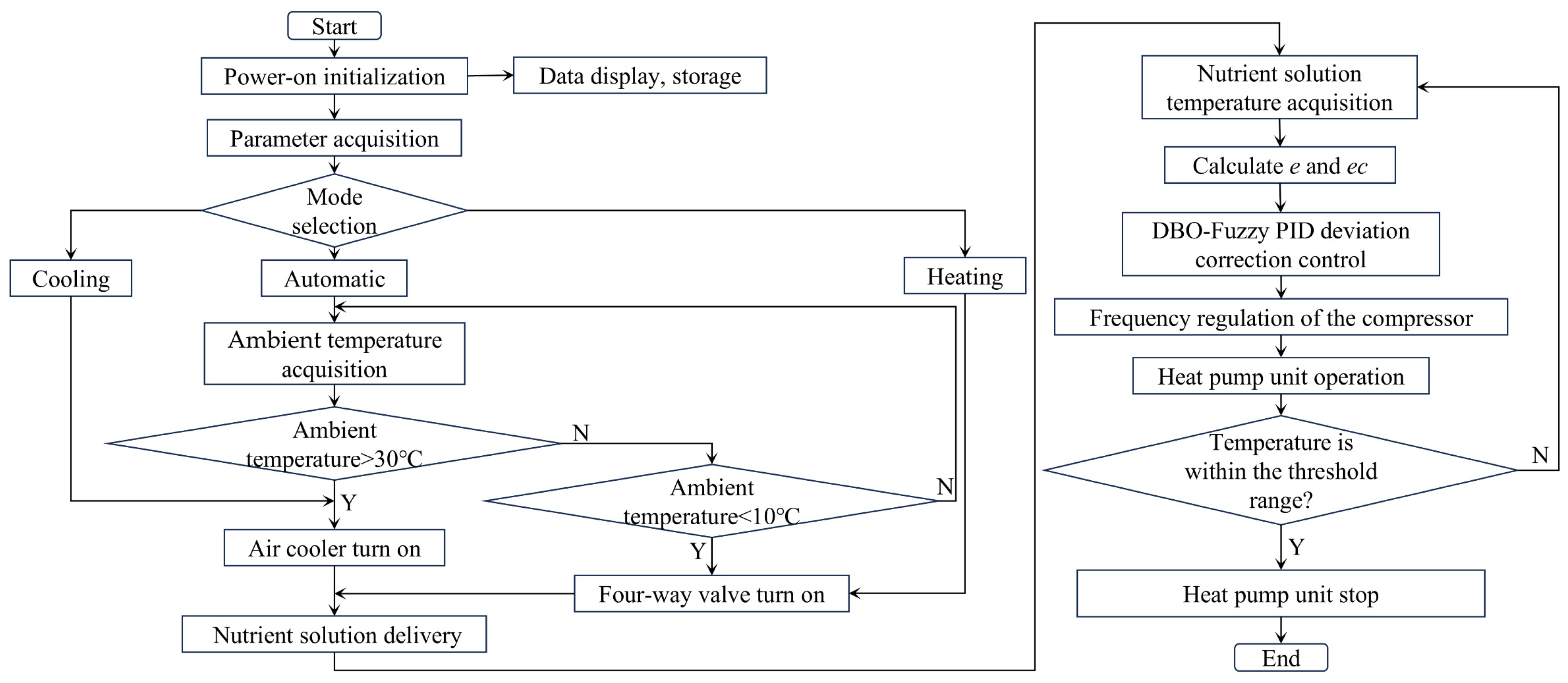
2.4. Control System Main Program
2.5. Fuzzy PID Controller Design Based on Adaptive Dung Beetle Algorithm Optimization
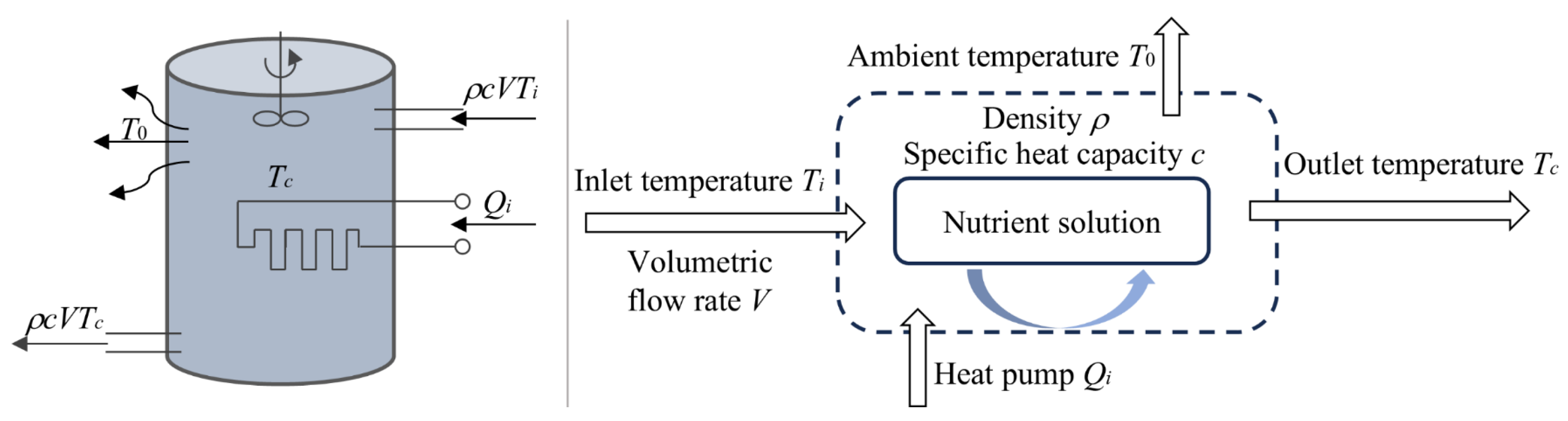
2.5.1. Mathematical Model
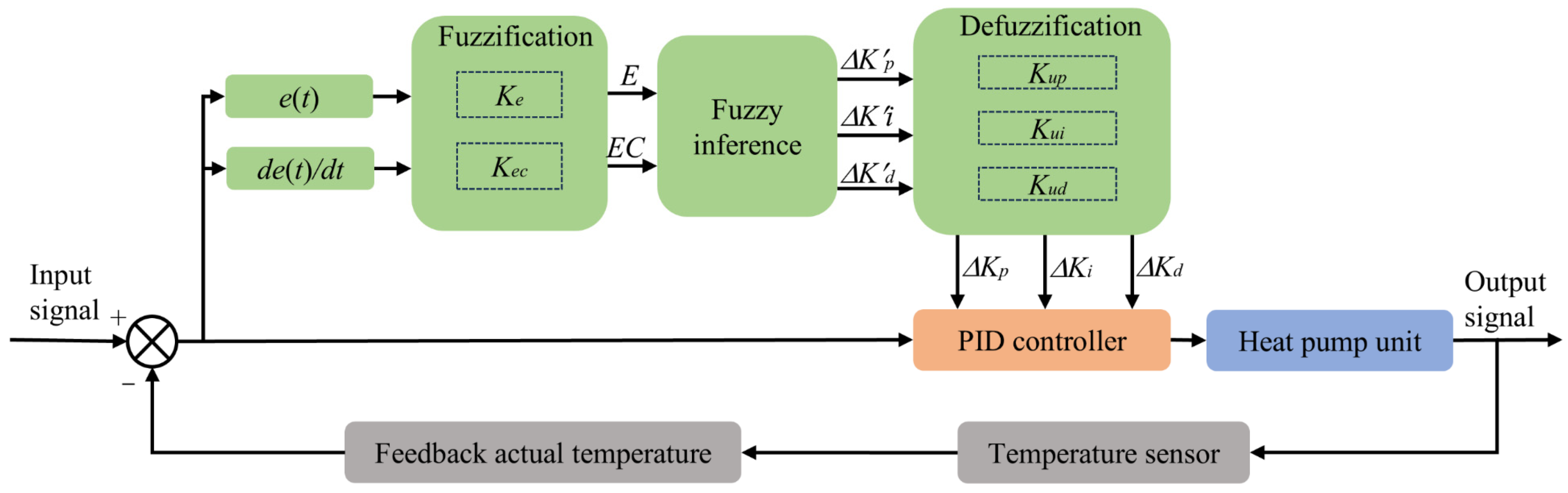
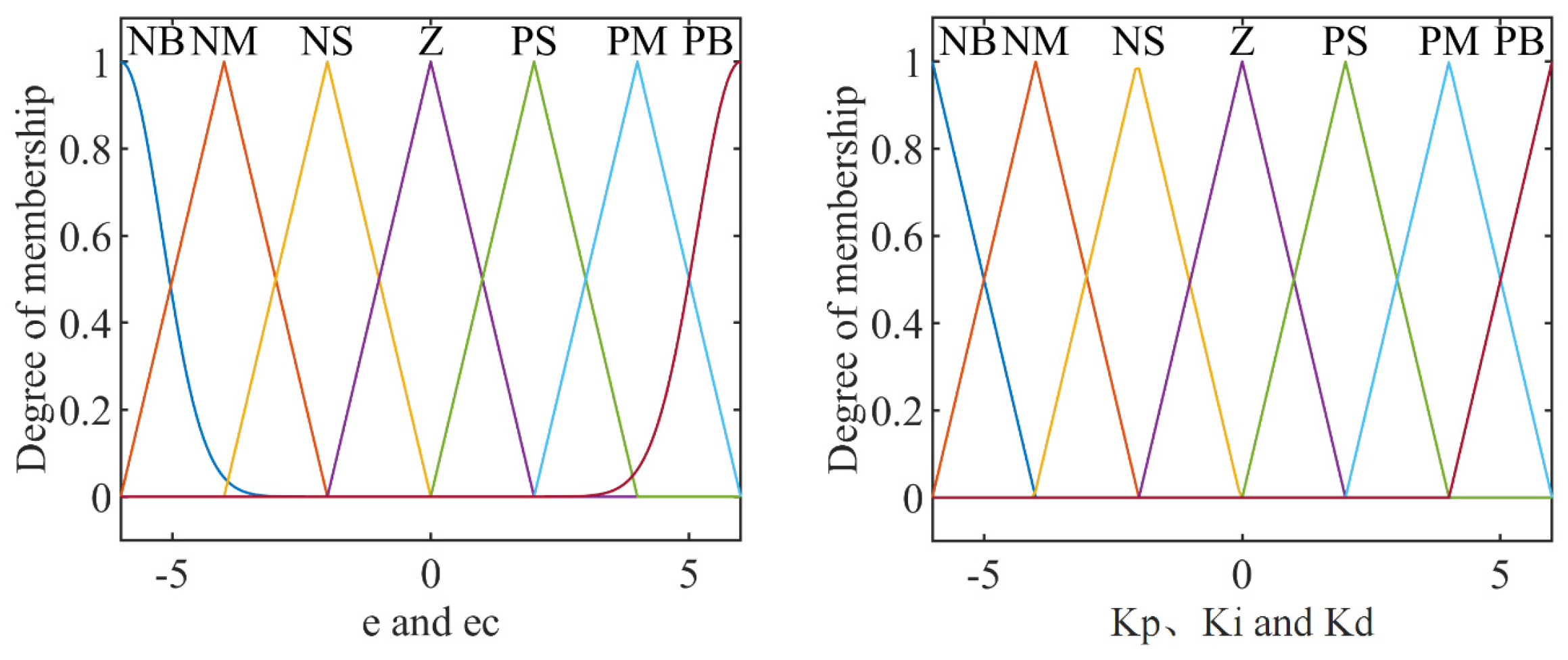
2.5.2. Fuzzy PID Controller
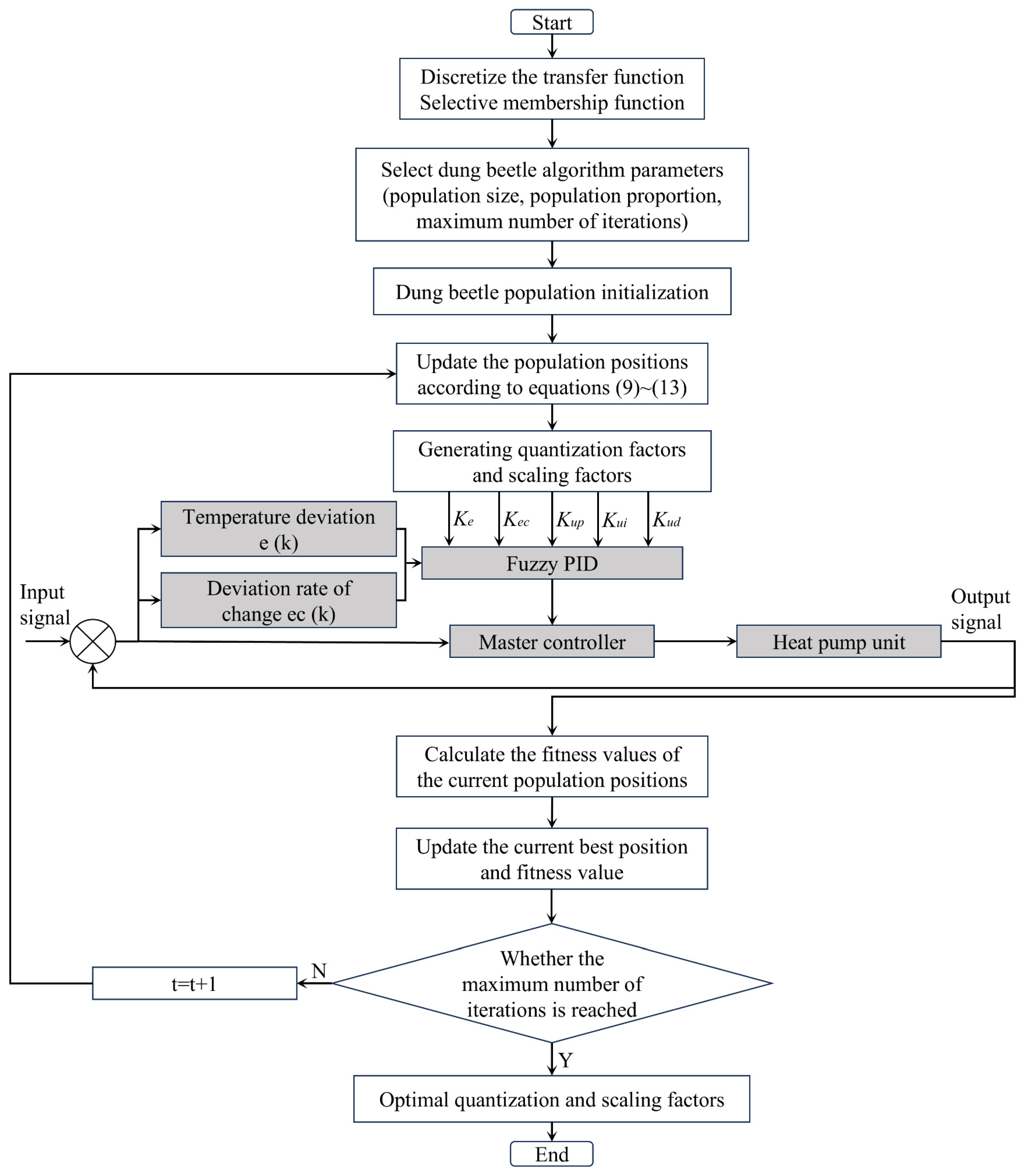
2.5.3. Optimization of Fuzzy PID Based on Adaptive Dung Beetle Algorithm
3. Experiments and Results
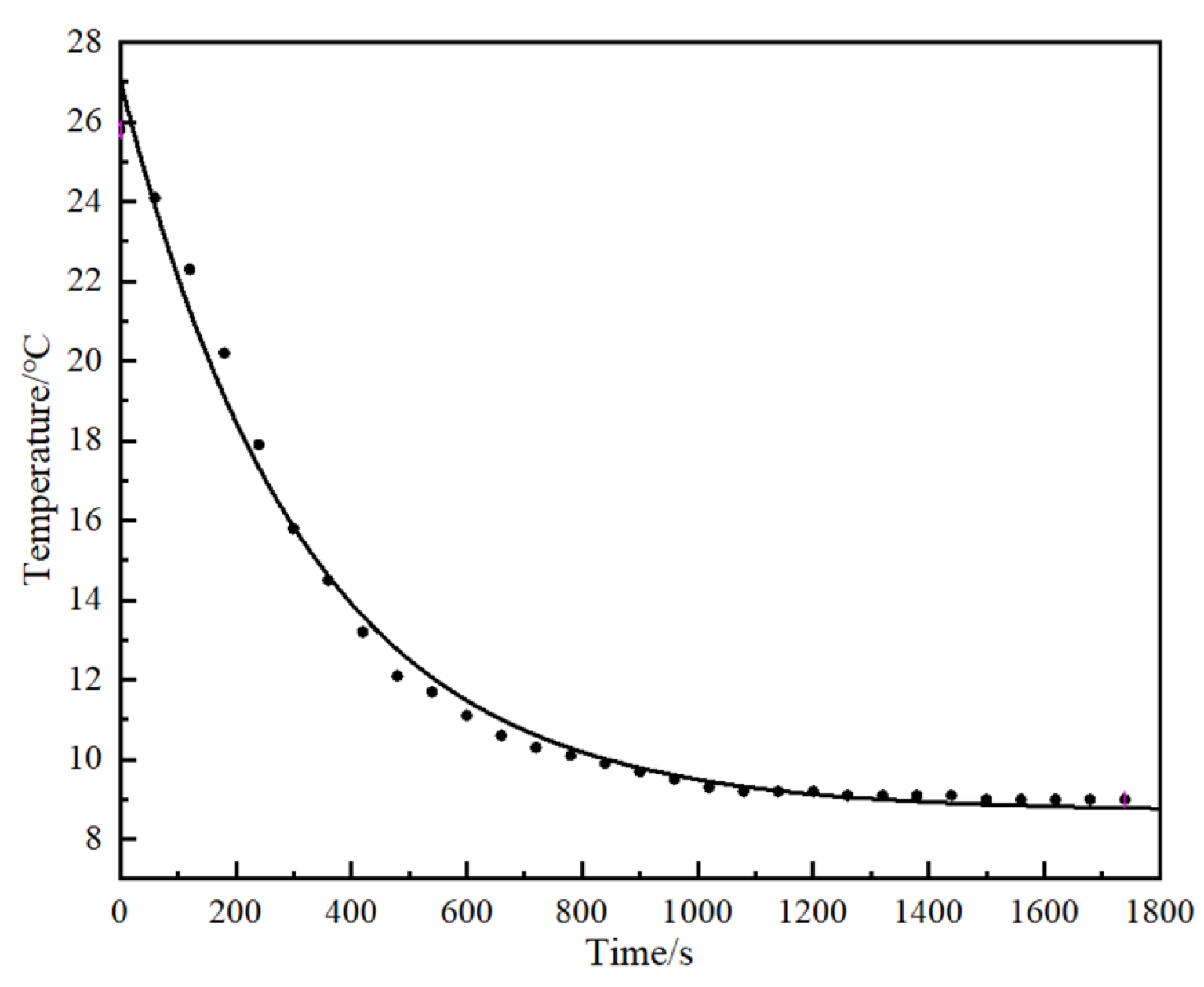
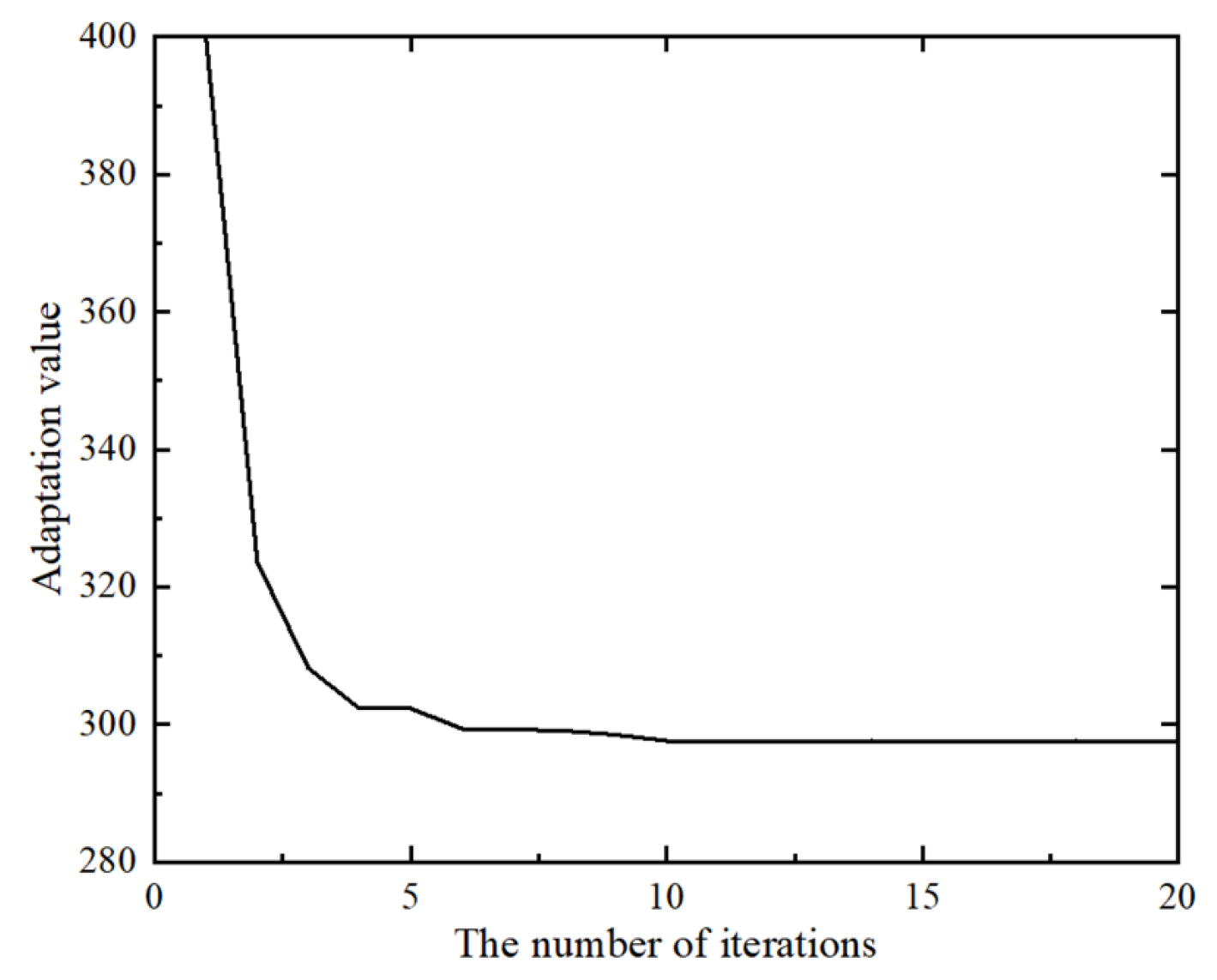
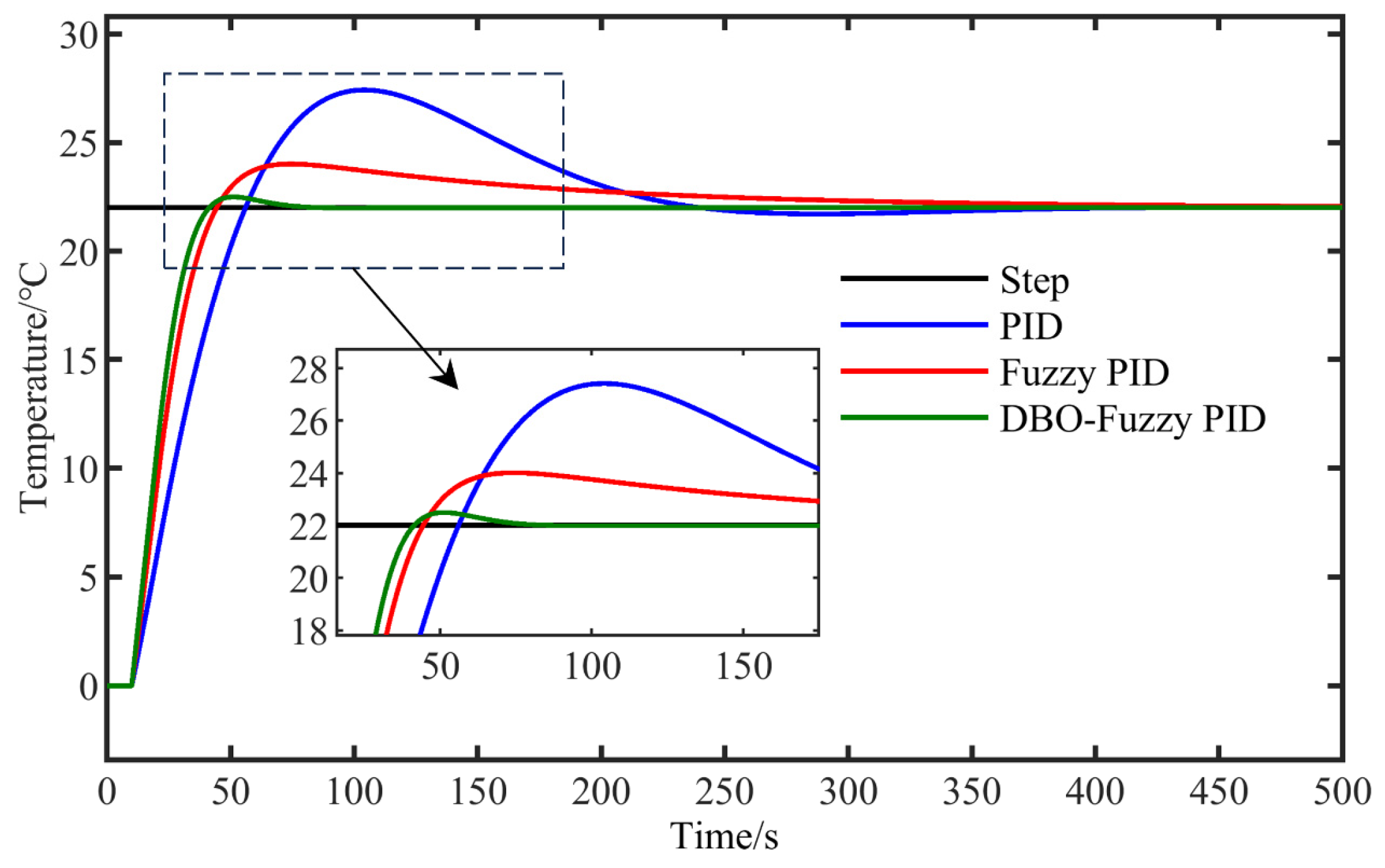
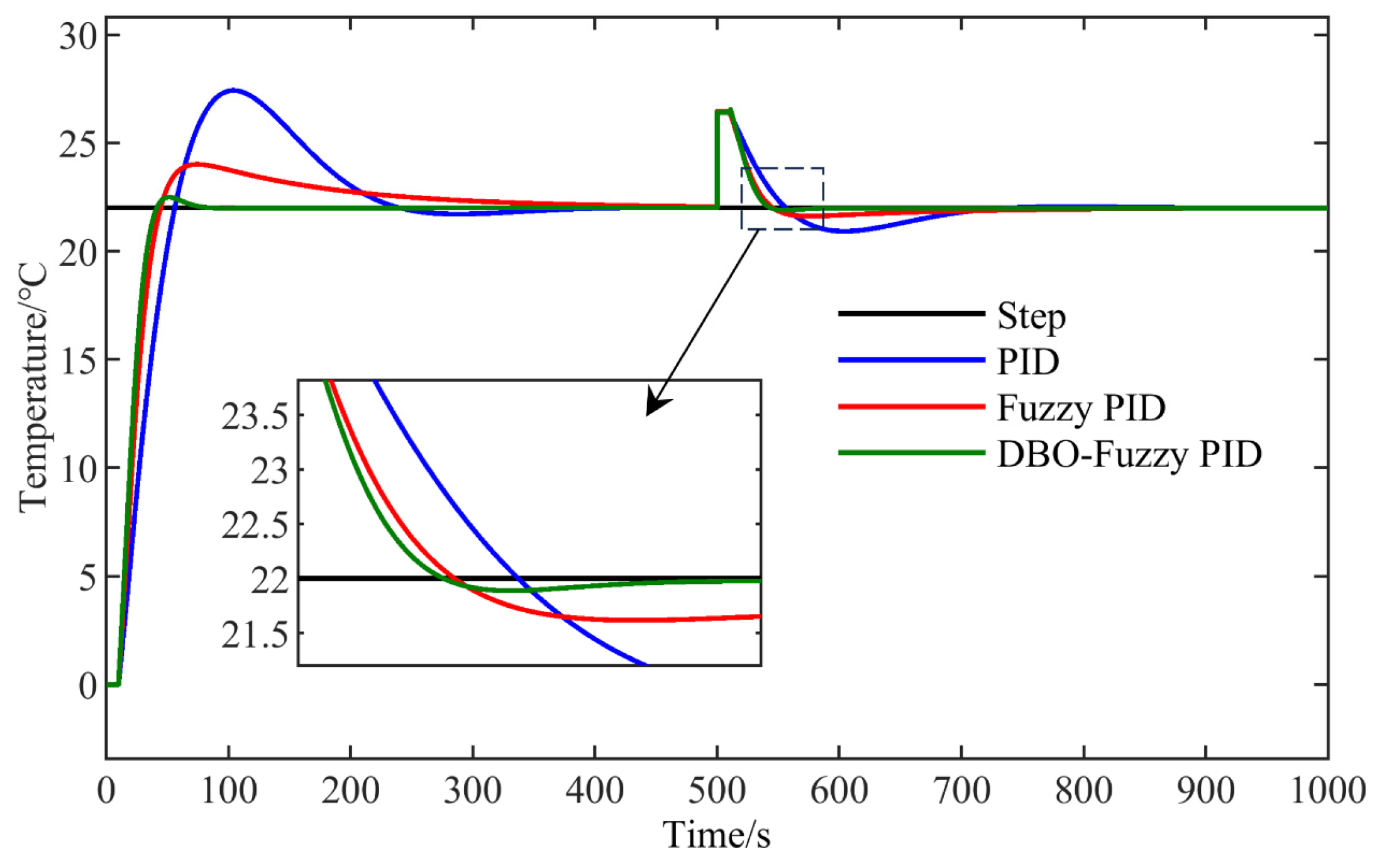
3.1. Simulation Experiment
3.2. Field Experients
3.2.1. Verification Test of Performance
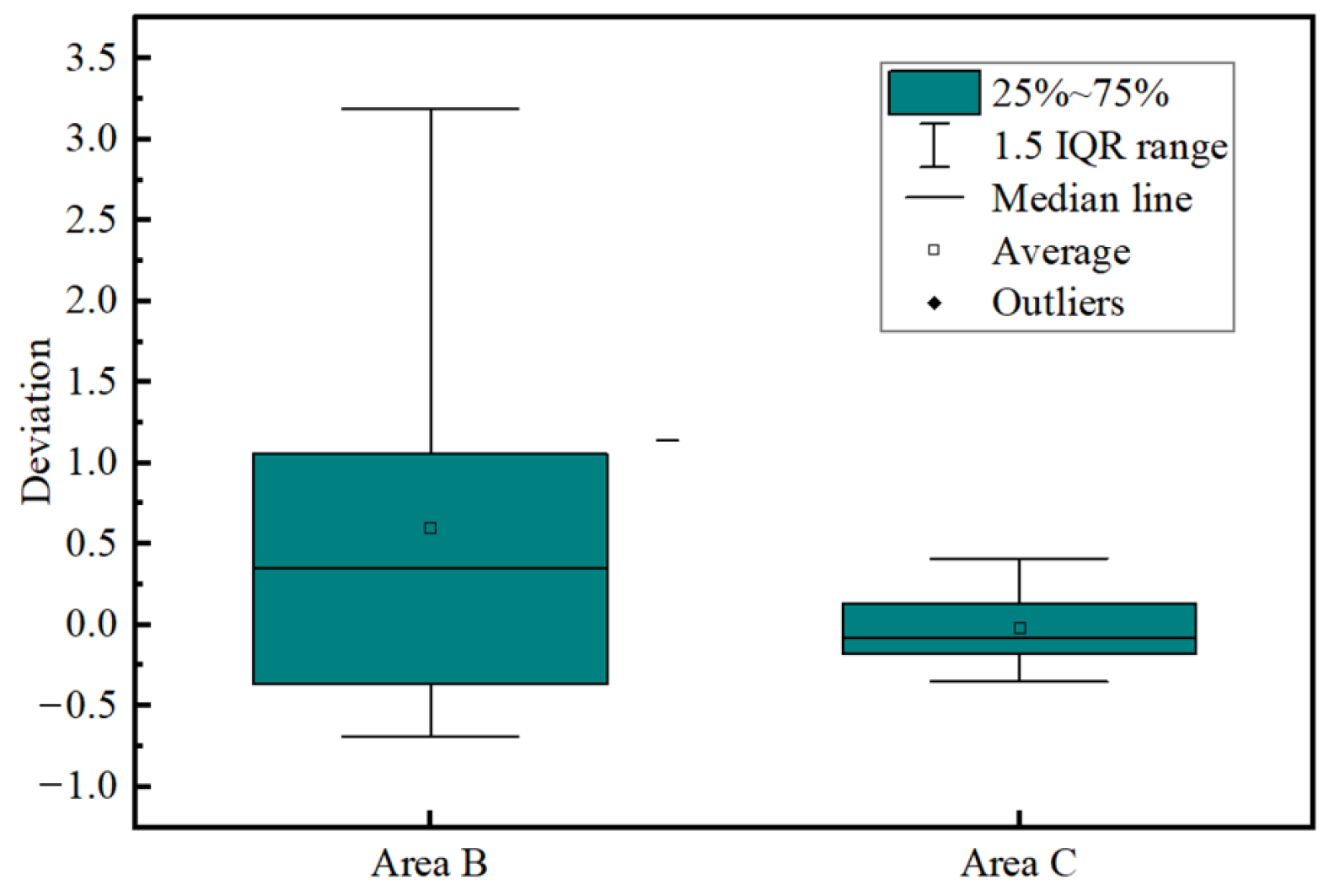
3.2.2. Verification Test of Cultivation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PID | Proportional–Integral–Derivative |
| DBO | Dung Beetle Optimizer |
| NSTCS | nutrient solution temperature control system |
| NFT | Nutrient Film Technique |
References
- Park, M.; Kang, T.; Yun, S.; Lim, R.; Son, J.; Kang, D. Analysis and monitoring of environmental parameters in a single-span greenhouse during strawberry cultivation. J. Environ. Sci. Int. 2021, 30, 907–914. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Y.; Fu, Y.; Zeng, L.; Wang, X.; Zhu, G. Influence of Cutting Regeneration Technique at High Density on Physiological Growth of Oversummering Hydroponics Lettuce in Hainan. China Cucurbits Veg. 2018, 31, 12–16, (In Chinese with English Abstract). [Google Scholar]
- Rahman, M.A.; Chakraborty, N.R.; Sufiun, A.; Banshal, S.K.; Tajnin, F.R. An AIoT-based Hydroponic System for Crop Recommendation and Nutrient Parameter Monitorization. Smart Agric. Technol. 2024, 8, 100472. [Google Scholar] [CrossRef]
- Song, M.; Wen, X.; Li, Y. Effects of High Rhizosphere Temperature on Plant Growth and Metabolism: A review. Chin. J. Ecol. 2010, 29, 2258–2264, (In Chinese with English Abstract). [Google Scholar]
- Kun, L.I.; Hui, F.; Zou, Z.R.; Cheng, R. Optimization of Rhizosphere Cooling Airflow for Microclimate Regulation and Its Effects on Lettuce Growth in Plant Factory. J. Integr. Agric. 2021, 20, 2680–2695. [Google Scholar]
- Cortella, G.; Saro, O.; De Angelis, A. Temperature Control of Nutrient Solution in Floating System Cultivation. Appl. Therm. Eng. 2014, 73, 1055–1065. [Google Scholar] [CrossRef]
- Hooks, T.; Sun, L.; Kong, Y.; Masabni, J.; Niu, G. Effect of Nutrient Solution Cooling in Summer and Heating in Winter on the Performance of Baby Leafy Vegetables in Deep-water Hydroponic Systems. Horticulturae 2022, 8, 749. [Google Scholar] [CrossRef]
- Hu, J.; Yang, Y.; Li, Y.; Hou, J.; Sun, Z.; Wang, H.; He, D. Analysis and Prospect of the Environment Control Systems for Greenhouse. Trans. CSAE 2024, 40, 112–128, (In Chinese with English Abstract). [Google Scholar]
- Silva, S.; Nascimento, R.; Oliveira, H.; Cardoso, J.A.F.; Xavier, D.A.; Silva, S.S. Levels of Nitrate, Pigments and Thermographic Analysis of Lettuce under Different Temperatures of Nutrient Solution. Afr. J. Agric. Res. 2016, 11, 1668–1673. [Google Scholar]
- Levine, C.P.; Hayashi, S.; Ohmori, Y.; Kusano, M.; Kobayashi, M.; Nishizawa, T. Controlling Root Zone Temperature Improves Plant Growth and Pigments in Hydroponic Lettuce. Ann. Bot. 2023, 132, 455–470. [Google Scholar] [CrossRef]
- Thanulla, D.; Dunn, B.; Hu, B.; Goad, C.; Maness, N. Nutrient Solution Temperature Affects Growth and Brix Parameters of Seventeen Lettuce Cultivars Grown in an NFT Hydroponic System. Horticulturae 2021, 7, 321. [Google Scholar] [CrossRef]
- Fussy, A.; Papenbrock, J. An Overview of Soil and Soilless Cultivation Techniques—Chances, Challenges and the Neglected Question of Sustainability. Plants 2022, 11, 1153. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.S.; Chandra, D.; Son, J. Growth, Physicochemical, Nutritional, and Postharvest Qualities of Leaf Lettuce (Lactuca sativa L.) as Affected by Cultivar and Amount of Applied Nutrient Solution. Horticulturae 2022, 8, 436. [Google Scholar] [CrossRef]
- Majid, M.; Khan, J.N.; Shah, Q.M.A.; Masoodi, K.Z.; Afroza, B.; Parvaze, S. Evaluation of Hydroponic Systems for the Cultivation of Lettuce (Lactuca sativa L., var. Longifolia) and Comparison with Protected Soil-based Cultivation. Agric. Water Manag. 2021, 245, 106572. [Google Scholar] [CrossRef]
- Li, F.; Chen, X. Response of Over-summer Hydroponic Lettuce to Nutrient Solution Temperature Control. Agric. Sci. Technol. 2017, 18, 1072. [Google Scholar]
- Falah, M.A.F.; Wajima, T.; Yasutake, D. Responses of Root Uptake to High Temperature of Tomato Plants (Lycopersicon esculentum Mill.) in Soil-less culture. J. Agric. Technol. 2010, 6, 543–558. [Google Scholar]
- Al-Rawahy, M.S.; Al-Rawahy, S.A.; Al-Mulla, Y.A.; Nadaf, S.K. Influence of nutrient solution temperature on its oxygen level and growth, yield and quality of hydroponic cucumber. J. Agric. Sci. 2019, 11, 75–92. [Google Scholar] [CrossRef]
- Myung, J.; Cui, M.; Lee, B.; Lee, H.; Shin, J.; Chun, C. Development of A Root-zone Temperature Control System using Air-source Heat Pump and its Impact on the Growth and Yield of Paprika. AoB Plants 2024, 16, plae047. [Google Scholar] [CrossRef]
- Zhou, J.; Bu, C.; Huang, D.; Niu, Q. Application and Analysis of Soilless Culture System with Adjustable Rhizosphere Temperature in Winter Tomato Production. China Veg. 2020, 8, 41–47, (In Chinese with English Abstract). [Google Scholar]
- Walker, J.M. One-degree increments in soil temperatures affect maize seedling behavior. Soil Sci. Soc. Am. J. 1969, 33, 729–736. [Google Scholar] [CrossRef]
- Wang, J.F.; Xu, H.; Wang, K.; Xie, J.; Yu, K.S.; Ye, G.S.; Jiang, J.L.; Han, X.R. Performance Analysis and PID Control Strategy Optimization of the Electronic Expansion Valve on the Single-tube Heat Exchange Experimental Platform. Appl. Therm. Eng. 2024, 250, 123532. [Google Scholar] [CrossRef]
- Taler, D.; Sobota, T.; Jaremkiewicz, M.; Taler, J. Control of the temperature in the hot liquid tank by using a digital PID controller considering the random errors of the thermometer indications. Energy 2022, 239, 122771. [Google Scholar] [CrossRef]
- He, G.; Cai, X.; Bai, Y.; Zhu, L.; Wang, D.; Hou, Y. Design and Test of Temperature Control System of Calf Milk Replacer Solution based on Fuzzy PID. Trans. Chin. Soc. Agric. Mach. 2022, 53, 266–276, (In Chinese with English Abstract). [Google Scholar]
- Sheng, T.; Luo, H.; Wu, M. Design and Simulation of a Multi-channel Biomass Hot Air Furnace with an Intelligent Temperature Control System. Agriculture 2024, 14, 419. [Google Scholar] [CrossRef]
- Tang, H.; Ma, R.; Chen, Y.; Huang, L.; Jiao, R. Temperature Regulation of Hot Vapor Preservation Treatment of Litchi Based on PSO-Fuzzy PID. Appl. Sci. 2023, 13, 6888. [Google Scholar] [CrossRef]
- Meng, J.; Gao, H.; Ruan, M.; Guo, H.; Zhou, X.; Zhang, D. Design of vacuum annealing furnace temperature control system based on GA-Fuzzy-PID algorithm. PLoS ONE 2023, 18, e0293823. [Google Scholar] [CrossRef] [PubMed]
- Qin, Z.; Wang, X.; Zhang, H.; Liu, F.; Yin, C.; Han, Z.; Weng, W. Research on heat pump air conditioner compressor speed control strategy based on whale algorithm. Case Stud. Therm. Eng. 2024, 53, 103939. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung Beetle Optimizer: A New Meta-heuristic Algorithm for Global Optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Zhou, Y.; He, Y.; Xing, Z.; Shao, K.; Li, Z.; Lei, L. Power Transformer Vibration Signal Prediction based on IDBO-ARIMA. J. Electron. Meas. Instrum. 2023, 37, 11–20, (In Chinese with English Abstract). [Google Scholar]
- Rehman, S.; Menesy, A.S.; Zayed, M.E.; Zaery, M.; Al-Shaikhi, A. Synergistic sizing and energy management strategy of combined offshore wind with solar floating PV system for green hydrogen and electricity co-production using multi-objective dung beetle optimization. Results Eng. 2025, 25, 104399. [Google Scholar] [CrossRef]
- Long, Z.; Li, J.; Yang, H.; Chen, W.; Zhang, G.; Wang, B.; Wang, W. Methods and experiments for automatic control of surface back pressure based on dung beetle optimizer-PID controller. Process Saf. Environ. Prot. 2024, 191, 360–374. [Google Scholar] [CrossRef]
- Zhong, K.; Li, Y.; Huan, W.; Weng, X.; Wu, B.; Chen, Z.; Liang, H.; Feng, H. A novel near infrared spectroscopy analytical strategy for soil nutrients detection based on the DBO-SVR method. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2024, 315, 124259. [Google Scholar] [CrossRef]
- Wu, Z.; Sha, L.; Zhao, M.; Wang, X.; Ma, H.; Zhang, Y. Performance Analyses and Optimization of a Reverse Carnot Cycle-organic Rankine Cycle Dual-function System. Energy Convers. Manag. 2020, 212, 112787. [Google Scholar] [CrossRef]
- Lakshmanan, V.; Sæle, H.; Degefa, M.Z. Electric water heater flexibility potential and activation impact in system operator perspective–Norwegian scenario case study. Energy 2021, 236, 121490. [Google Scholar] [CrossRef]
- Yang, Y.; Pan, Y.; Zhao, Y. Process Control and Automatic Instruments, 3rd ed.; China Machine Press: Beijing, China, 2017; pp. 125–132. [Google Scholar]
- Xie, J.; Chen, Y.; Gao, P.; Sun, D.; Xue, X.; Yin, D.; Han, Y.; Wang, W. Smart Fuzzy Irrigation System for Litchi Orchards. Comput. Electron. Agric. 2022, 201, 107287. [Google Scholar] [CrossRef]
- Cao, W.; Liu, Z.; Song, H.; Li, G.; Quan, B. Dung Beetle Optimized Fuzzy PID Algorithm Applied in Four-Bar Target Temperature Control System. Appl. Sci. 2024, 14, 4168. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, X.; Wang, H.; Li, K.; Zhang, G.; Yi, Y.; Pan, S. Prediction Model for Winter and Summer Lettuce Root Zone Temperature based on Dung Beetle Algorithm to Optimize BP. Trans. Chin. Soc. Agric. Eng. 2024, 40, 231–238, (In Chinese with English Abstract). [Google Scholar]
- Cui, J. Plant Growth, Quality and Elemental Absorption of Lettuce as Affected by Nutrient Solution Heating in Intermittent Fluid Supply Nutrient Film Technique System. Mol. Plant Breed. 2024, 10, 1–10, (In Chinese with English Abstract). [Google Scholar]
- Li, H.; Lu, M.; Yuan, K.; Zhang, M.; Wang, D.; Hu, J. Acquisition and analysis of the optimal nutrient solution temperature range for lettuce using U-chord curvature. Int. J. Agric. Biol. Eng. 2024, 17, 93–100. [Google Scholar] [CrossRef]
- Nisar, M.M.; Mahmood, R.; Tayyab, S.; Anees, M.; Nadeem, F. Comparative efficacy of non-electric cooling techniques to reduce nutrient solution temperature for the sustainable cultivation of summer vegetables in open-air hydroponics. Front. Plant Sci. 2024, 15, 1340641. [Google Scholar]
- Zhang, Y.; Ni, X.; Zhang, K.; Xu, Y. Cooling performance for temato root zone with intelligence ecological planting matrix temperature control system driven by photovoltaic in greenhouse. Trans. Chin. Soc. Agric. Eng. 2020, 36, 212–219, (In Chinese with English Abstract). [Google Scholar]
- Zhang, K.; As’arry, A.; Zhu, L.; Hairuddin, A.A.; Hassan, M.K.; Zain, M.Z.M. Enhancing ride comfort of semi-active suspension through collaboration control using dung beetle optimizer optimized Fuzzy PID controller. Adv. Mech. Eng. 2025, 17, 16878132251314332. [Google Scholar] [CrossRef]
- Hu, C.; Wu, F.; Zou, H. New PID parameter tuning based on improved dung beetle optimization algorithm. Can. J. Chem. Eng. 2024, 102, 4297–4316. [Google Scholar] [CrossRef]






| Product Name | Specification or Model | Product Description |
|---|---|---|
| Single Chip Microcomputer | STM32F103RCT6 | Based on the ARM 32-bit Cortex-M architecture. |
| Resistive Temperature Sensor | PT100 | Measurement range: −50~150 °C. Accuracy: ± 0.1 °C. |
| Signal Transfer Module | MAX6675 | Convert analog signals into digital signals. |
| 4G Module | Air724UG | Provide fast and reliable wireless connectivity. |
| AC Contactor | LC1N50 | High-voltage power controller. |
| Thermal Relay | LRN357N | Overload protection. |
| Heat Pump Unit | BLD-60AH | Input power: 49.8 kW. Refrigerant: R410 A. |
| Solution Agitator | BLD10-1.5 | Impeller diameter: 400 mm. |
| Circulation Pump | 25CDL2-200 | Input power: 2.2 kW. Lift: 150 m. |
| Input/Output Variables | e | ec | ΔKp | ΔKi | ΔKd |
|---|---|---|---|---|---|
| Fuzzy language | E | EC | ΔKP | ΔKI | ΔKD |
| Basic domain | [−12, 12] | [−3, 3] | [−0.3, 0.3] | [−0.06, 0.06] | [−0.03, 0.03] |
| Fuzzy domain | [−6, 6] | [−6, 6] | [−6, 6] | [−6, 6] | [−6, 6] |
| Fuzzy subset | {Positive Big (PB), Positive Middle (PM), Positive Small (PS), Zero (Z), Negative Small (NS), Negative Middle (NM), Negative Big (NB)} | ||||
| E | EC | ||||||
|---|---|---|---|---|---|---|---|
| NB | NM | NS | Z | PS | PM | PB | |
| NB | Z/NB/NS | Z/NB/NS | Z/NM/NS | Z/NS/NS | PS/PS/NS | PS/NM/PS | PS/Z/PS |
| NM | Z/NB/NS | Z/NB/NS | Z/NM/NS | Z/NS/NS | PS/NS/NS | PS/Z/PS | PS/Z/PM |
| NS | PS/NB/NS | PS/NM/NS | PS/Z/NS | PS/Z/Z | PS/Z/Z | PM/PS/PS | PM/Z/PM |
| Z | PS/NM/NS | PS/NM/NS | PS/NS/NS | PS/Z/Z | PS/PS/Z | PM/PM/PS | PM/PM/PM |
| PS | PM/Z/NS | PM/NS/NS | PM/Z/Z | PM/PS/Z | PM/PS/Z | PB/PM/PS | PB/PB/PM |
| PM | PM/Z/NS | PM/Z/NS | PM/PS/Z | PM/PM/PS | PM/PM/PS | PB/PB/PS | PB/PB/PB |
| PB | PM/Z/NS | PM/Z/NS | PM/PS/Z | PM/PM/PS | PM/PM/PS | PB/PB/PS | PB/PB/PM |
| Control Method | Settling Time/s | Overshoot/% | Steady-State Error/°C |
|---|---|---|---|
| PID | 200.36 | 24.50 | 0.035 |
| Fuzzy PID | 158.42 | 9.10 | 0.016 |
| DBO-Fuzzy PID | 35.23 | 2.18 | 0.009 |
| Group | Root Fresh Weight/g | Root Dry Weight/g | Leaf Fresh Weight/g | Leaf Dry Weight/g |
|---|---|---|---|---|
| Area A | 6.48 ± 1.31c | 0.27 ± 0.02c | 47.26 ± 5.07b | 2.11 ± 0.12c |
| Area B | 8.61 ± 1.19b | 0.32 ± 0.02b | 70.87 ± 2.84a | 3.05 ± 0.08b |
| Area C | 9.48 ± 1.21a | 0.36 ± 0.01a | 74.01 ± 2.23a | 3.23 ± 0.07a |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Y.; Zhao, Z.; Guo, W.; Xu, H.; Teng, Y.; Han, X.; Zhao, Q.; Wang, L. Smart Nutrient Solution Temperature Control System for Oversummering Lettuce Cultivation Based on Adaptive Dung Beetle Optimizer-Fuzzy PID. Appl. Sci. 2025, 15, 5381. https://doi.org/10.3390/app15105381
Cai Y, Zhao Z, Guo W, Xu H, Teng Y, Han X, Zhao Q, Wang L. Smart Nutrient Solution Temperature Control System for Oversummering Lettuce Cultivation Based on Adaptive Dung Beetle Optimizer-Fuzzy PID. Applied Sciences. 2025; 15(10):5381. https://doi.org/10.3390/app15105381
Chicago/Turabian StyleCai, Yuliang, Zelan Zhao, Wenzhong Guo, Hailing Xu, Yunfei Teng, Xiaobei Han, Qian Zhao, and Lichun Wang. 2025. "Smart Nutrient Solution Temperature Control System for Oversummering Lettuce Cultivation Based on Adaptive Dung Beetle Optimizer-Fuzzy PID" Applied Sciences 15, no. 10: 5381. https://doi.org/10.3390/app15105381
APA StyleCai, Y., Zhao, Z., Guo, W., Xu, H., Teng, Y., Han, X., Zhao, Q., & Wang, L. (2025). Smart Nutrient Solution Temperature Control System for Oversummering Lettuce Cultivation Based on Adaptive Dung Beetle Optimizer-Fuzzy PID. Applied Sciences, 15(10), 5381. https://doi.org/10.3390/app15105381





