Abstract
This study focuses on the development of a decision support system for complex production systems. As a promising approach to resource allocation challenges, the application of AI tools, particularly the multi-agent approach, is proposed. It is hypothesized that a decision support system based on multi-agent systems (MASs), grounded in an invariant ontology and utilizing game-theoretic tools, will enhance the effectiveness of managerial decisions by accounting for the inherent multi-agent nature of complex production systems, manifested in diverse objective functions and intricate interaction structures. The work identifies key features of intelligent agent interactions in multi-agent systems. Drawing on interaction types relevant to complex production systems and the selected MAS implementation architecture, an ontological model of multi-agent interactions and an ontological model for managing complex production systems are designed. The proposed models are tested using data from an oil and gas enterprise, and a formalization of utility functions for its agents is provided using game-theoretic tools. The resulting ontological model of multi-agent interactions in complex production systems is practical and easy to implement. It enables the design of MASs for diverse complex production systems, as demonstrated through a resource management case study in the oil and gas industry. Future study will refine the ontological model via industry-specific validation and expand the mathematical and computational tools for model implementation.
1. Introduction
Real-world production systems are characterized by the presence of multiple stakeholders, each pursuing their own objectives, particularly the fulfillment of specific performance metrics [1,2,3,4]. Strategic management in such distributed systems aims to achieve global goals but often neglects the interests of individual agents. Consequently, managerial decisions will, first, face resistance from individual agents within the system and, second, lead to a deterioration in these agents’ performance metrics. For example, profit maximization may be achieved by reducing the quality of materials or increasing production volumes, which ultimately leads to an increase in the proportion of defects and a corresponding decrease in demand for products, which sooner or later will lead to a drop in profits. However, in the short term, such solutions may dominate over more pragmatic options involving the allocation of resources in terms of work in all areas of the production chain. The above necessitates the development of tools for identifying sustainable solutions that enable both the system and its agents to achieve their target objectives [1,2,3,4].
However, the design of decision support systems for complex production systems introduces a mathematical challenge rooted in the inherent complexity of solving such problems. Certain tasks in this domain are classified as NP-complete problems, i.e., problems with nondeterministic polynomial-time complexity [5]. These problems may lack stable solutions or require significant time and computational resources to resolve. This requires the use of complex algorithms to obtain satisfactory solutions [6,7].
To address these challenges, the use of a multi-agent approach is proposed. A distinctive feature of the multi-agent approach lies in transitioning from passive agents, modeled as object classes in object-oriented paradigms, to active intelligent agents capable of perceiving their environment and responding to its changes. Each agent in such a system possesses unique characteristics, goals, and thus, behavioral strategies. Software-implemented models based on the multi-agent approach represent specialized AI tools that can be integrated into decision support systems across various domains of economic activity [8,9]. The application of the multi-agent approach in the context of the problem under study is driven by the necessity to account for the inherent multi-agent nature of production systems, at least in terms of reconciling the diverse objective functions of individual agents and the system as a whole. Therefore, the analysis of multi-agent interactions, the development of adequate models for such interactions, and the design of practice-oriented decision support methods and informational frameworks for managing multi-agent systems require thorough investigation, as their outcomes may directly enhance economic activities, particularly through the rational allocation of resources to achieve the required economic indicators or, in the form of an inverse problem, to calculate the need for resources and their redistribution. [4,9,10,11,12]. Existing multi-agent systems that represent organizational systems do not offer a universal model of organizational production structure. They provide ontologies to address the resource allocation problem, considering entities of the production process, but neglect the specifics of organizational structure [8,10]. Other solutions, such as ADEPT [9], allow for the management of business processes but propose systems with a limited set of role types. The list of roles they offer enables a comprehensive description of stakeholders in a real organization only at the level of a single enterprise, without covering other levels of system consideration (such as enterprise networks or employees of a single enterprise), and does not take into account the diversity of external stakeholders not part of the organization. Some studies provide a detailed model of the agent environment [11] or the objects they operate on [12], but do not detail the roles of agents within the enterprise. Defining a standard set of agent roles for a multi-agent system that represents an organizational structure, when implementing the tool, will simplify the development of computational models for specific enterprises.
Consequently, the objective of this work is to develop an ontological model of multi-agent interactions in a complex production system as the foundation for a corresponding decision support system, along with its validation using data from an oil and gas industry company. So, in the proposed model of a multi-agent system, the set of agent roles is described using an invariant ontology of production system management. The roles of agents within the structure of the multi-agent system are introduced in accordance with the set of typical stakeholder groups in the organizational system, including the types of departments considered in the works of predecessors, as well as employees with various decision-making powers within the company and agents from the external environment.
Thus, the study highlights the distinctive features of intelligent agent interactions in multi-agent systems. Drawing on interaction types relevant to complex production systems and the selected MAS implementation architecture, an ontological model of multi-agent interactions and an ontological model for managing complex production systems are designed. The proposed models are tested using data from an oil and gas enterprise, and a formalization of utility functions for its agents is provided using game-theoretic tools.
2. Materials and Methods
2.1. Interactions of Intelligent Agents in MASs
Multi-agent systems (MASs) consist of intelligent agents that interact with both the external environment and each other. In the context of multi-agent system research, a multitude of properties of intelligent agents are outlined, depending on the application domain of such systems (e.g., robotics, social process modeling [11,12], production scheduling [8], resource management [8,10]) and the focus of individual research schools (direction, thematic scope).
Initially, MASs were developed as tools for controlling physical objects, such as robotic systems. However, as the field evolved, MASs also emerged as a modeling methodology for domains where system components can themselves be represented as intelligent agents [4,8,10].
A key feature of MASs is the agents’ ability to dynamically reorganize in response to environmental changes. Researchers thus emphasize the multi-agent approach as a framework for designing and describing self-organizing systems [13]. In MASs, interactions serve as the primary mechanism for computation and coordinating the behavior of multiple autonomous software or physical agents. According to existing standards, agents communicate via high-level languages using predefined protocols. These protocols govern asynchronous or synchronous “dialogues” between agents, including notifications of changes, proposal exchanges, responses to proposals, and other interactions. Messages from one agent to another must be transmitted at any time, regardless of the recipient’s state [4].
Agent interactions—and their resulting collective behavior—may serve diverse purposes. MAS agents can cooperate to solve complex or large-scale tasks [4,13]. In such cases, a task is decomposed (e.g., by a user) into simpler subtasks assigned to different agents. Here, interactions aim to coordinate local solutions to achieve a globally optimal outcome, either through fully distributed coordination or varying degrees of centralized control. Alternatively, agents may interact when pursuing individual goals but lacking the capacity to achieve them independently, necessitating assistance from others. While this scenario also involves cooperation, agents may refuse requests based on mutual agreements termed commitments. Under certain conditions, agents may transition between competition and cooperation, a relationship termed coopetition (from cooperation + competition) [4,13].
Thus, the following typical agent interaction paradigms can be identified [4,13,14]:
- Cooperation: Agents collaborate toward a shared goal, often exchanging information to improve collective decisions.
- Negotiation/Debate: Agents engage in adversarial interactions, advocating for their own solutions while critiquing others’.
- Competition: Agents pursue conflicting objectives, prioritizing individual goals over collective outcomes.
2.2. Description of Intelligent Agent Interactions Based on BDI
Numerous tools have been developed for implementing MASs, with the internal architecture of agents in the predominant majority of them being based on the BDI concept [15,16,17,18]. In general, a BDI (Belief–Desire–Intention) agent is defined in terms of beliefs, desires, and intentions. Here, beliefs represent the agent’s knowledge of the world, desires correspond to its objectives, and intentions denote the actions the agent deems necessary to execute. When implementing BDI, the agent’s knowledge system is augmented with behavioral model components that refine its decision-making. Within the agent’s architecture, concepts such as rational behavior, reasoning, goals, plans, and others may be formalized.
BDI-based agents can reason and represent their thought process in a human-readable format, are capable of communicating with each other, and can plan their actions. However, such agents are not well-suited for tasks that require modeling emotions and making changes to communication norms. Additionally, learning is a challenging task for BDI agents. To overcome learning difficulties, agents can be implemented using a hybrid approach that combines BDI with other artificial intelligence methods, such as machine learning. While BDI agents have less capability to model emotions compared to other cognitive architectures, such as Kismet, they are sufficient to predict the impact of emotions on an agent’s behavior. Making changes to communication norms in BDI agents is difficult, but these challenges can be addressed when developing the architecture of a multi-agent system. The BDI model does not reflect the biological and neurological foundations of thinking, which limits its application in modeling biological systems. However, this simplification makes it easier to use in modeling production systems—its abstraction allows not only describing the behavior of employees but also the behavior of departments and enterprises, which is necessary in the type of systems under consideration. Despite all its shortcomings, the BDI model is the most suitable for developing models of both social systems in general and production systems in particular.
The agent’s belief system can be predefined and updated during simulation. Desires may either be prescribed or emerge through interactions with the environment. Intentions are determined during modeling based on desires and beliefs [15,16,17,18]. Designing a multi-agent system (MAS) for complex technical and socio-economic systems does not require the development of agent-specific belief systems, as established approaches can be employed. Similarly, there are no constraints on how desires are formed or how agents select actions to execute.
The standard BDI model, in order to simplify the application of the model by standardizing agent capabilities, is proposed to be supplemented with a plan library. Plans here are sequences of actions to achieve specific goals in prescribed situations. This addition is not new—although plans are not defined in the standard BDI model, they are introduced in most architectures based on this concept. For example, plans are specified when implementing agents according to the PRS, JAM, dMARS, and InteRRaP architectures, and others, as well as when creating agents using standard frameworks and platforms for developing MASs, such as JaCaMo, Jadex, and others [19]. Adding plans to the BDI concept when creating a model for a production system simulation tool simplifies the development of models for specific enterprises and does not reduce the flexibility in choosing implementation tools for solutions. To define behavior, a set of plans must be generated to achieve desired outcomes, evaluated, and optimized while accounting for other agents’ actions. The list of plans corresponding to a desire may be fixed or dynamically updated. This depends on the planning methodology, which can range from predefined strategies to plans generated autonomously by intelligent agents, e.g., using STRIPS or other artificial intelligence planning languages.
We describe the basic interaction of agents in a multi-agent system using the BDI framework [15,16,17,18].
To simplify event processing in the model, planning mechanisms are introduced. A plan library forms part of the agent’s beliefs. Thus, the agent’s architecture comprises beliefs (including plans and actions for perceiving the environment), desires, and intentions. The agent influences other system entities through its actions and registers external influences (Figure 1). The reasoning process of the agent in the proposed model follows the standard BDI model, enhanced with plans [9,19]. The agent perceives the actions of other agents and changes in the environment (perception), updates its beliefs (beliefs) based on the perceived information, checks whether it has achieved the desired goal (desires), determines the appropriate strategy for achieving the desired goal given the current beliefs (plans), defines the intention to carry out a certain action according to the plan, and then executes it [20].
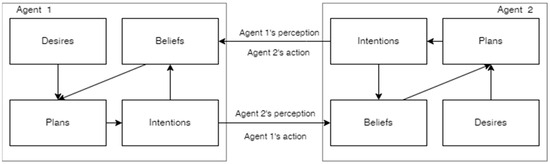
Figure 1.
Interaction of agents in a multi-agent system.
Desires determine which set of plans should be considered to achieve goals. Desires also assign costs to strategies corresponding to the plans. Optimal plans form the agent’s intentions. An agent may revise its beliefs through intentions if a relevant desire exists.
3. Results
3.1. Development of an Ontological Model of Multi-Agent Interactions in Complex Production Systems
The properties of complex production systems stem from the distinctive features of complex organizational systems. Their key characteristics include structural diversity of agents, multiplicity of heterogeneous connections, variability of tasks, adaptability of structure and operational rules, and openness [1,2,3,4]. To accurately define system adaptation and self-regulation in a model, it is essential to reflect the strong interdependence of its components. The dynamic nature of complex organizational systems necessitates models that are both adaptive and capable of evolution. Interaction with the external environment must also be incorporated into the model.
Let us describe the parameters of the system architecture, including the base set of agents and types of relationships between them.
As the MAS architecture, we propose a resource management ontology. Building upon a foundational planning ontology [21], we construct an invariant ontology for complex technical and socio-economic systems. The result is illustrated in Figure 2.
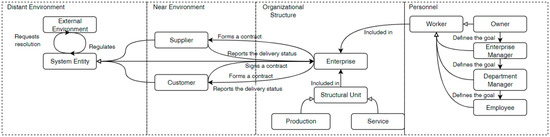
Figure 2.
Invariant ontology for managing a complex production system.
The ontology, which is a model of a production system, describes the set of roles of MAS agents. The roles of the agents are one of the components of the organizational structure of the multi-agent system. Another component of the organizational structure of the MAS is the protocols [9]. The communication method of the agents is determined by the protocols, which should be selected when transitioning to the software implementation.
These entity types can be modeled as BDI agents. Desires determine which set of plans should be considered to achieve goals. Desires also assign costs to strategies corresponding to the plans. Optimal plans form the agent’s intentions. An agent may revise its beliefs through intentions if a relevant desire exists. Near Environment refers to entities external to the production process but influencing specific stages of the order lifecycle. This category includes Supplier and Customer. A Supplier is an entity responsible for timely resource provision to the Enterprise. A Customer is an entity requesting product manufacturing or service execution.
The Enterprise is considered the core agent of the system, governing the production process. Within the Enterprise, Structural Units perform distinct task types. These are classified as Production Units (creating products) and Support Units (maintaining Enterprise operations). All entities in this category belong to the Personnel group.
The primary operational resource in system management is the Worker. Workers execute tasks at the Enterprise. The Worker category includes: the Owner (owning the organization), the Enterprise Manager (defining goals at the Enterprise level), the Department Manager (organizing the unit’s operations), and the Employee (executing tasks within the Structural Unit).
These entity types can be modeled as BDI agents. Their beliefs depend on their agent group. The Near Environment knows the order readiness status (including delivery stages) and contractual terms with the Enterprise. The Personnel group is hierarchically organized, so agent beliefs are similar and inherited from the Worker agent. Agents know goals set by superiors and goals assigned to subordinates. The Enterprise knows its Structural Units, their current task stages, external tasks assigned by the environment, resource requests from Units, and contractual terms with Suppliers and Customers. The Enterprise, Supplier, and Customer are classified as System Subjects. They can autonomously interact with the External Environment, which tracks regulatory requests from System Subjects and the state of the regulated system. Thus, the core agents are Worker, Enterprise, Structural Unit, Supplier, Customer, and External Environment. Their possible desires and beliefs are defined in Table 1.

Table 1.
Basic desires and beliefs of agents.
Having defined the framework of basic interactions and the architecture of the multi-agent system (MAS) for complex technical and socio-economic systems, we can proceed to describe multi-agent interactions considering the selected system type.
Figure 3 shows which agents in the proposed system can interact and how. The model represents a system with an organizational structure that has hierarchical features. This is done to ensure the realism of the model— in real-world organizational systems, the enterprise is the highest entity in the hierarchy, followed by the structural unit, and then the subdivisions of the structural unit and their employees. Agent 0, the enterprise agent, can directly communicate only with agents at the division level and manage them. Agent 1, the production division, and Agent 2, the service division, can communicate with Agent 0, with the agents under their control at the production site level, and with each other. Agent 1 manages the agents at the production site level, Agent 1.i, where i is the number of an agent at the production site level subordinate to Agent 1. The same applies to Agent 2 and its subordinates. Agents at the production site level, who are subordinate to the same unit-level agent, can communicate with each other.
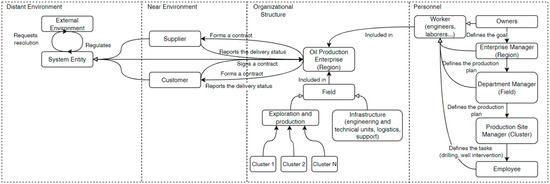
Figure 3.
Invariant ontological model of multi-agent interactions for complex production systems.
The development of a MAS for complex production systems does not require task-specific internal agent architectures. However, game-theoretic methods are convenient for modeling social interactions among agents.
In the simplest case, an agent’s plan selection task is represented as a normal-form game, where players are agents, pure strategies are agents’ plans, and the game is resolved in pure strategies.
The game-theoretic model is defined by three sets: , where , , and correspond to the problem statement. In game-theoretic terms, is the set of strategic agents influencing production; is the set of strategy profiles for each agent; is the set of utility functions for each agent; is the number of agents involved in the process.
In this case, enterprise, production unit, support unit, production site-1, …, production site-m, , where is the number of production sites (executors).
For each agent, a set of pure strategies is defined, forming the strategy profile set .
is an enterprise, {execute the production plan}.
is a production unit, is a support unit, since agents and have a “cooperation” interaction type, their strategies are identical: {allocate task execution plans and resources; allocate additional resources; refuse additional resource allocation}. In this case, and must jointly select a unified strategy.
are production sites. Production sites can produce output volumes according to allocated resources. Accordingly, production sites may request additional resources or collaborate with other sites to fulfill the plan. Thus: {produce autonomously; collaborate with another production site; exchange resources with another production site; redistribute resources via competitive actions}, where .
Each agent is assigned a utility function , which collectively forms the set of objective functions .
In these formulas, for each -th agent: is produced output quantity; are available resources; is a unit product cost (expressed in resource units).
are resources invested in cooperation; is the set of participants selecting the “cooperation” strategy; is the output quantity obtained from cooperation; is the planned output quantity; is the agent’s share of participation in cooperation (calculated based on total and individual contributed resources). Production sites may form selective coalitions depending on the required output quantity and available resources, uniting into separate groups. Thus, the set may include any number of participants.
are resources invested in exchange; is the quantity of resources received from the -th agent via exchange; is the quantity of resources redistributed from the -th agent to the -th agent through competitive actions; is a redistribution coefficient (probability), is the probability of -th agent making a decision to reallocate resources, is the probability of -th agent making a decision to reallocate resources.
Based on the results obtained in previous sections, we can proceed to construct industry-specific models of multi-agent interactions.
3.2. Modeling Multi-Agent Interactions in an Oil and Gas Industry Enterprise
Let us consider the adaptation of the obtained invariant ontological model of multi-agent interactions for the oil and gas industry.
First, it is necessary to define the elements of the organizational structure of the oil production enterprise system (Figure 4).
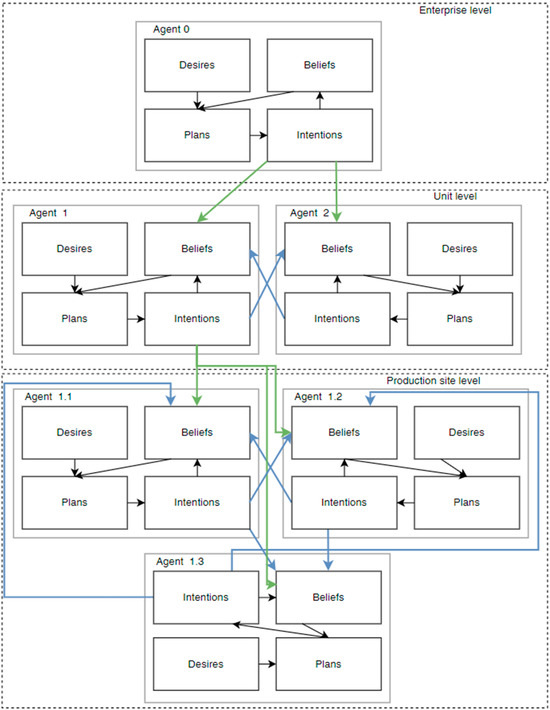
Figure 4.
Management ontology of the oil production enterprise system.
Thus, in accordance with the basic model of the oil production enterprise [22], the main agents of the system are: agent—Region (Enterprise); agent—Field, Extraction, and Exploration (Production Unit); agent—Field, Infrastructure (Support Unit); agent—Cluster (Production Site).
Based on the invariant ontological model of multi-agent interactions for complex technical and socio-economic systems, developed in the previous section, it is necessary to define sets of beliefs, desires, plans, and intentions for each agent type (Table 2).

Table 2.
Sets of beliefs, desires, plans, and intentions for agents of the oil production enterprise.
Let us provide the mathematical formalization of the utility functions for the agents. For the considered example of the ontological model of multi-agent interactions in the oil production enterprise system, the utility function for cluster takes the following form:
where are actual oil flow rate values; are allocated crews for well intervention and drilling; is the cost per ton of oil, expressed in crew units; are resources invested in cooperation; is the set of participants selecting the “cooperation” strategy; is the oil flow rate value obtained through cooperation; is the planned oil flow rate target; agent’s participation share in cooperation (calculated based on total and individual contributed resources); are resources invested in exchange; is the quantity of resources received from agent via exchange; is the quantity of resources redistributed from agent to agent through competitive resource redistribution actions; is the redistribution coefficient (probability).
The multiplicity of levels of decision-making complicates the process itself, because the target functions will vary for each level. So, an example of a task for which this model may be used is a flexible allocation of resources based on the actual needs of production sites, considering the requirements for the implementation of the plan. In the context of the oil and gas industry production systems this means that the communication of agents at the cluster level to redistribute resources will maximize the utility function, because the number of resources received of each type (drilling crews, GTM crews) will tend to the actual need, and not to the calculated values from the regional level, which were obtained through modeling with high degree of abstraction. The oil and gas industry is just one example of a production system to which this model may be applied. In the next stages of the project, a set of industry models will be developed to identify specific features and develop industry libraries for modeling multi-agent interactions, as an addition to the ontological model of multi-agent interactions.
4. Discussion
Existing solutions for modeling organizational systems using MASs [8,9,10,11,12] offer a limited set of agent roles reflecting the types of production departments, but not the types of their employees and environmental agents. Overcoming this limitation by introducing an invariant ontology for managing complex production systems simplifies the development of models for specific enterprises.
The developed foundational ontological model of multi-agent interactions in complex production systems is practical and easy to implement. It enables the design of multi-agent systems (MASs) for diverse complex production systems, as demonstrated using the example of resource management in the oil and gas industry. Refining the ontology in accordance with modern approaches to managing complex production systems and advancing the mathematical framework for defining rational agent behavior could enhance the performance of the decision support system based on the proposed model.
Within this project, game-theoretic tools were selected for implementation. Complex production systems require tools capable of simulating not only agent actions but also their influence and interactions with the environment. Thus, game theory is widely applied in MAS development, as it provides a mathematical framework for analyzing interaction strategies among agents with divergent interests and objectives [23,24,25,26,27]. Furthermore, game theory is increasingly combined with machine learning methods, facilitating further model refinement due to its flexibility and integrability [23,24,25,26,27].
Another key feature of the proposed model is the use of the BDI (Belief–Desire–Intention) concept for designing the internal architecture of intelligent agents. Literature describes various intelligent agent models such as Soar, ACT-R, ICARUS, BDI, subsumption architecture, CLARION [20], among which BDI and Soar are the most prominent. BDI [28] is straightforward to implement compared to Soar, a low-level architecture rooted in fundamental aspects of intelligence and was among the first models successfully commercialized in frameworks [29]. The BDI model has limitations, such as low capabilities for agent learning, modeling emotions, and making changes to communication norms [30]. These shortcomings can be compensated for by implementing the architecture of a cognitive agent, environment, and system organizational structure, including the selection of a cognitive architecture, framework, or platform for development. Despite the limited descriptive capabilities of the BDI model, it remains the most suitable choice for modeling production systems.
The choice of BDI was also driven by the requirements for the software implementation of the multi-agent interaction model [30]. This work prioritizes flexible and scalable solutions that can be developed either from scratch using specialized libraries (MASON, Pade, NL4Py, Repast4Py) or frameworks (JADE, RePast, INGENIAS) or built upon dedicated platforms (JADE, Jadex, INGENIAS, JACK, MadKit, JaCaMo), most of which adopt the BDI architecture.
Selecting optimal tools for the software implementation of the multi-agent interaction model in complex production systems is a focus of the project’s next stages.
5. Conclusions
The paper proposes an invariant ontological model of multi-agent interactions in complex production systems based on resource management ontology, and their validation using data from an oil and gas enterprise. Mathematical formalization of agents’ utility functions is provided using game theory tools. A mathematical formalization of the agents’ utility functions is provided using game-theoretic tools.
Future research will refine the ontological model through industry-specific validation projects. Additionally, the expansion of mathematical and computational tools for implementing the proposed production system models is planned.
Author Contributions
Conceptualization, A.M.G.; methodology, P.A.S. and D.A.Z.; validation, K.N.P.; formal analysis, Z.V.B. All authors have read and agreed to the published version of the manuscript.
Funding
The research is funded by the Ministry of Science and Higher Education of the Russian Federation (contract No. 075-03-2025-256 dated 16 January 2025).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hofman, J.M.; Watts, D.J.; Athey, S. Integrating explanation and prediction in computational social science. Nature 2021, 595, 181–188. [Google Scholar] [CrossRef] [PubMed]
- Lakemond, N.; Holmberg, G.; Pettersson, A. Digital transformation in complex systems. IEEE Trans. Eng. Manag. 2021, 71, 192–204. [Google Scholar] [CrossRef]
- Schilling, M. Technology Shocks, Technological Collaboration, and Innovation Outcomes. Organ. Sci. 2015, 26, 668–686. [Google Scholar] [CrossRef]
- White, B. Managing Complexity by George Rzevski and Petr Skobelev Southhampton; WIT Press: Boston, MA, USA, 2014; pp. 49–50. ISBN 978-1-84564-936-4. [Google Scholar] [CrossRef]
- Agerbeck, C.; Hansen, M.O. A Multi-Agent Approach to Solving NP-Complete Problems. Master’s Thesis, Technical University of Denmark, DTU, Lyngby, Denmark, 2008. [Google Scholar]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness, 1st ed.; Klee, V., Ed.; Series of Books in the Mathematical Sciences; W. H. Freeman and Company: New York, NY, USA, 1979; p. 347. [Google Scholar]
- Moukrim, A.; Quilliot, A.; Toussaint, H. An effective branch-and-price algorithm for the Preemptive Resource Constrained Project Scheduling Problem based on minimal Interval Order Enumeration. Eur. J. Oper. Res. 2015, 224, 360–368. [Google Scholar] [CrossRef]
- Gorodetsky, V.I.; Kozhevnikov, S.S.; Novichkov, D.; Skobelev, P.O. The Framework for Designing Autonomous Cyber-Physical Multi-agent Systems for Adaptive Resource Management. In Industrial Applications of Holonic and Multi-Agent Systems; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11710, pp. 52–64. [Google Scholar] [CrossRef]
- Wooldridge, M.J. An Introduction to Multiagent Systems; John Wiley & Sons Publ.: Chichester, UK, 2009; p. 461. [Google Scholar]
- Skobelev, P. Multi-agent systems for real time resource allocation, scheduling, optimization and controlling: Industrial applications. In Proceedings of the International Conference on Industrial Applications of Holonic and Multi-Agent Systems, Toulouse, France, 29–31 August 2011; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2011; Volume 6867, pp. 1–14. [Google Scholar] [CrossRef]
- Magomedov, O.R.; Chernyshev, S.A. Multi-agent decision support system for minimizing the cost of grouped goods. Vestn. Rosnou Complex Syst. Models Anal. Manag. 2022, 4, 97–107. [Google Scholar] [CrossRef]
- Shvetcov, A.N.; Dianov, S.V.; Dianov, D.S. Designing a multi-agent system for resolving interfunctional conflicts in an enterprise. Cherepovets State Univ. Bull. 2022, 1, 74–89. (In Russian) [Google Scholar] [CrossRef]
- Abbas, H.; Shaheen, S.; Amin, M. Organization of Multi-Agent Systems: An Overview. Int. J. Intell. Inf. Syst. 2015, 4, 46. [Google Scholar] [CrossRef]
- Guo, T.; Chen, X.; Wang, Y.; Chang, R.; Pei, S.; Chawla, N.; Wiest, O.; Zhang, X. Large Language Model based Multi-Agents: A Survey of Progress and Challenges. arXiv 2024, arXiv:2402.01680. [Google Scholar] [CrossRef]
- Ambroszkiewicz, S.; Komar, J. A model of BDI-agent in game-theoretic framework. In Formal Models of Agents: ESPRIT Project ModelAge Final Workshop Selected Papers; Springer: Berlin/Heidelberg, Germany, 1999; pp. 8–19. [Google Scholar]
- Caillou, P.; Gaudou, B.; Grignard, A.; Truong, C.Q.; Taillandier, P. A simple-to-use BDI architecture for agent-based modeling and simulation. In Advances in Social Simulatio; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Rao, A.S. AgentSpeak(L): BDI agents speak out in a logical computable language. In European Workshop on Modelling Autonomous Agents in a Multi-Agent World; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1996; Volume 1038, pp. 42–55. [Google Scholar] [CrossRef]
- Bordini, R.; Hübner, J. BDI Agent Programming in AgentSpeak Using Jason; Springer: Berlin/Heidelberg, Germany, 2006; pp. 143–164. [Google Scholar]
- Research on Approaches to Creating Intelligent Multi-Agent Systems for Predictive and Prescriptive Analytics in Industry” for 2024, Reg. No. R&D 124062900023-5. (In Russian)
- Chong, H.-Q.; Tan, A.-H.; Ng, G.-W. Integrated cognitive architectures: A survey. Artif. Intell. Rev. 2007, 28, 103–130. [Google Scholar] [CrossRef]
- Zhilyaev, A.A. Ontology as a tool for creating open multi-agent resource management systems. Ontol. Des. 2019, 9, 261–281. [Google Scholar] [CrossRef]
- Fedyaevskaya, D.E.; Burlutskaya, Z.V.; Gintciak, A.M.; Dixit, S. Hierarchical Cybernetic Model of Oil Production Enterprise with Distributed Decision-Making Centers. In Digital Transformation: What Is the Company of Today? Springer Nature: Cham, Switzerland, 2023; pp. 21–34. [Google Scholar]
- Wang, L.; Fu, F.; Chen, X. Mathematics of multi-agent learning systems at the interface of game theory and artificial intelligence. Sci. China Inf. Sci. 2024, 67, 1–3. [Google Scholar] [CrossRef]
- Oroojlooy, A.; Hajinezhad, D. A review of cooperative multi-agent deep reinforcement learning. arXiv 2019, arXiv:1908.03963. [Google Scholar] [CrossRef]
- Jain, G.; Kumar, A.; Bhat, S.A. Recent developments of game theory and reinforcement learning approaches: A systematic review. IEEE Access 2024, 12, 9999–10011. [Google Scholar] [CrossRef]
- Galin, R.; Meshcheryakov, R.; Kamesheva, S. Distributing tasks in multi-agent robotic system for human-robot interaction applications. In Proceedings of the International Conference on Interactive Collaborative Robotics, St. Petersburg, Russia, 7–9 October 2020; Springer: Cham, Switzerland, 2020; pp. 99–106. [Google Scholar] [CrossRef]
- Munavalli, J.R.; Rao, S.V.; Srinivasan, A.; van Merode, G. An intelligent real-time scheduler for out-patient clinics: A multi-agent system model. Health Inform. J. 2020, 26, 2383–2406. [Google Scholar] [CrossRef] [PubMed]
- Bratman, M.E. Intentions, Plans, and Practical Reason; Harvard University Press: Cambridge, MA, USA, 1987. [Google Scholar] [CrossRef]
- Jarvis, D.; Jarvis, J.; Rönnquist, R.; Jain, L. Multiagent Systems and Applications: Volume 2: Development Using the GORITE BDI Framework; Springer: Berlin/Heidelberg, Germany, 2013; Volume 46, p. 148. [Google Scholar] [CrossRef]
- Adam, C.; Gaudou, B. BDI agents in social simulations: A survey. Knowl. Eng. Rev. 2016, 31, 207–238. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).