Abstract
In sonar collaborative search tasks, effectively evaluating the collaborative search efficiency is an important way to measure whether a task can be successful, which can also provide strong support for optimizing search schemes. In complex marine environments, sonar collaboration search faces challenges such as uncertain task scenes and real-time changing situations. Traditional evaluation methods cannot meet the evaluation requirements in these tasks since they do not analyze the involved dynamic modeling process. To bridge this gap, in this paper, we propose a novel evaluation method for sonar collaborative search efficiency based on adaptive information fusion and dynamic deduction. Specifically, we develop an information fusion method for multi-sensor detection based on adaptive weight calculation first, weights are assigned to each sensor based on the real-time changing detection probability to obtain more accurate detection probability fusion results. Then, we introduce the Monte Carlo sampling concept to establish an efficiency evaluation model based on the information fusion results. It discretizes the sonar search path and target motion trajectory in the time and space, and calculates the sonar detection efficiency point by point, which can overcome the challenge of uncertain situation conditions due to the uncertainty of target motion by dynamic spatial-temporal deduction. Compared with the average weighted fusion method, the variance of the proposed adaptive fusion method decreases from 0.01 to 0.0071, which proves its better stability. The results of the one-sample t-test indicate that at the level of , there is a significant difference between the average detection probability and the random probability of 0.5, indicating statistical significance. Moreover, we verify the effectiveness of the proposed method in fully-passive and multi-base working modes, and compare the impact of each sonar on the overall detection capability of the multi-sonar system, which also demonstrates the advantages and reliability of the new model.
1. Introduction
With the continuous growth of ocean resource exploitation and maritime security needs, the sonar for target search tasks has emerged as a pivotal technological way in fields of ocean exploration [1,2]. With the increasing complexity of maritime tasks, single sonar platform has exposed its limitation in detection capability and efficiency. By multi-sonar collaboration, detection efficiency can be significantly improved, which plays an increasingly important role in maritime tasks such as reconnaissance, surveillance and target searching [3,4,5,6].
The collaborative search efficiency of a multi-sonar system refers to the actual performance of the search capability in specific search tasks. Therefore, evaluating the collaborative search efficiency is an effective way to measure whether a task can be successful, which can provide support for making the collaborative search strategies. It is also of great significance in the optimization of resource allocation and can enhance the situational awareness and response capabilities in the dynamic scenes [7].
The evaluation of the collaborative search efficiency of multi-sonar systems belongs to the research field of efficiency evaluation. Some researchers have made great efforts in solving this problem. Jiang et al. analyzed the main indicators and factors that affect the UAV cluster combat efficiency through the OODA (Observe, Orient, Decide, Act) loop, and proposed a comprehensive evaluation method based on AHP–FCE (Analytic Hierarchy Process–Fuzzy Comprehensive Evaluation) to obtain numerical efficiency values [8]. Jia et al. proposed an efficiency evaluation method for UAV cluster combat systems based on system dynamic modeling and conducted model simulation research [9]. Sun et al. proposed a conditional entropy-based weight combination method to evaluate the UAV collaborative combat efficiency, which addresses the problem of excessive index weight coefficients and considers the interrelationships between indicators in traditional entropy-based methods [10]. Liang et al. conducted research on the efficiency evaluation of multiple wake-guided torpedoes carried by UUV based on the ADC model [11]. Cheng et al. proposed an improved multi-expert combined weight (MMCW)–fuzzy comprehensive evaluation (FCE) method to address the subjectivity of expert opinions in performance evaluation, and applied it to evaluate the AUV intelligence [12]. Liu et al. proposed a distributed combat efficiency evaluation method for UAV cluster based on DoDAF (Department of Defense Architecture Framework) to address the issues of insufficient completeness and systematicity, as well as strong subjectivity in traditional distributed combat efficiency evaluation of UAV clusters [13]. He et al. used the System Effectiveness Analysis (SEA) method to evaluate the reconnaissance effectiveness of UUV systems, and constructed mathematical models for effectiveness evaluation indicators, system mapping, and mission mapping [14]. Wang et al. established a multiple unmanned surface vehicles collaborative efficiency evaluation model based on GA-BP neural network, which improved the efficiency of efficiency evaluation [15]. Yuanming et al. proposed a collaborative efficiency evaluation method for UUVs based on GAPSO-BP neural network and verified it through simulation analysis [16].
There is relatively little research on the evaluation of sonar search path detection efficiency, and how to evaluate sonar search efficiency in dynamic scenarios is still an open issue. We analyzed the entire process of the multi-sonar collaborative search task, and found there are two issues that urgently need to be studied and resolved.
- A. Research Question 1: Evaluation of Collaborative Detection Efficiency of Multi-Sonar Systems in Real-Time Situation-Changing Environments
The collaborative search based on multi-sonar system is a dynamic process with real-time changes in relative position due to the mobility of the sonar and the target, and the efficiency evaluation model needs to adapt to the complex dynamic changes of the scene. Traditional efficiency evaluation methods are not suitable for this problem, because most traditional methods are limited to static modeling, which lacks dynamic analysis and adaptive adjustment capability, and cannot cope with the dynamic situations with real-time changes. In the process of multi-sonar collaborative search, due to the uncertainty of target motion, the relative position and situation between the sonar and the target are changing in real time, resulting in a real-time change of the sonar detection probability. This is an efficiency evaluation problem under uncertain target situation conditions, and it is difficult for us to establish a mathematical model that can accurately characterize the law of detection probability change. Therefore, traditional static modeling and evaluation methods have difficulty meeting the dynamic change requirements of the search process. To address this question, we discretize the sonar search path and target motion trajectory in time and space, and perform point-by-point deduction calculations. Through spatiotemporal discretization modeling and point-by-point dynamic deduction, the spatiotemporal interaction process between sonars and targets is accurately characterized, enhancing dynamic adaptability. To solve the problem of uncertain situations, we generate many target motion trajectories via the Monte Carlo method, and then transform uncertain situations into multiple relatively certain situations.
- B. Research Question 2: Adaptive Fusion Method of Multi-Sonar Detection Information
In the search process, the detection capability of multi-sonar system is strongly correlated with the detection capability of each sonar platform. It is necessary to integrate the detection capability of each sonar platform to derive the overall detection capability. However, due to the real-time changes in the relative situation of the scene, the effective detection ability of each sonar platform also changes. We consider that sonar detection probability has a certain level of confidence, so multi-sonar detection information fusion is also in a “dynamic” state of change, that is, a high detection probability should be given high confidence and high weight. The traditional methods do not consider the ‘dynamic’ characteristics in the information fusion process. To address this issue, in this paper, we propose a multi-sensor detection information fusion method based on adaptive weight calculations. Among them, we use a linear function to calculate the confidence of the detection probability value, and normalize the confidence of multiple sonars before weighting them to obtain the overall detection probability. The accuracy of the fusion result is improved through adaptive weight allocation.
In summary, we introduce the Monte Carlo sampling concept to establish a collaborative search efficiency evaluation model of multi-sonar system based on information fusion and dynamic deduction under uncertain target situations. We overcome the challenges posed by dynamicity in two ways. First, the dynamic change in the scenario can be accurately characterized by simulating the task process. Second, by a novel Monte Carlo-based searching strategy, the uncertainty of the target situations can be transformed into multiple relatively deterministic situations. Our proposed model is more in line with an actual scenario, and the efficiency evaluation results are more accurate and reliable. Our main innovations and contributions are summarized as follows.
(1) We establish a collaborative search efficiency evaluation model for the multi-sonar system based on information fusion and dynamic deduction under uncertain situations. This model can dynamically analyze and adapt to the changes in situations, which can achieve more accurate evaluation of collaborative search efficiency.
(2) We propose a multi-sensor detection information fusion method based on adaptive weight calculations. By assigning greater weights to sensors with better detection performance, the proposed model can take full advantage of each sensor at different times, which improves the accuracy of fusion results and enhances the adaptability and robustness of the system.
(3) We conduct a set of numerical simulations to evaluate the target collaborative search efficiency of multi-sonar system in fully-passive and multi-base working modes. Especially, the influence of different combinations of sonar systems under multi-base working mode on evaluation indicators, the influence of different sonar parameters and target parameters on evaluation indicators, and the contribution of each sonar on the overall detection capability were fully studied, which verified the effectiveness of the proposed method.
The rest of this paper is organized as follows. In Section 2, we analyze the collaborative search efficiency evaluation model of multi-sonar system, and then establishes corresponding mathematical models and efficiency evaluation index systems; Section 3 constructs simulation scene and conducts relevant numerical simulation calculations and analysis; Section 4 discusses relevant issues in efficiency evaluation and case simulation research; Finally, Section 5 provides a summary of the entire text.
2. Research on the Collaborative Search Efficiency Evaluation Model of Multi-Sonar System
When establishing the collaborative search efficiency evaluation model of multi-sonar system, the following information needs to be known: (1) Task requirements; (2) Collaborative search scheme; (3) Target motion model; (4) Sonar detection model; (5) Multi-sensor information fusion model; (6) Efficiency evaluation indicators. The following text mainly studies the target motion model, Sonar detection model, Multi-sensor information fusion model, and efficiency evaluation indicators. Firstly, the following assumptions are made: (1) Regardless of the size of the sonar and the target, consider both of them as particles. (2) The working depth between the multi-sonar system and the target remains unchanged, and there will be no collision during the task process. (3) The hydrological conditions in the task area are good, and threats on the route are not considered [17].
2.1. Target Motion Model
Under the assumption that, in the collaborative search task, the target disappears and escapes from a certain point, its motion model is as follows: after disappearance, the first step of motion direction is randomly selected within the range of 0∼. Starting from the second step of the motion direction, due to the limitation of the target maneuverability, the next step of the motion direction can only be randomly selected within a range of 90 degrees on both sides based on the previous step of the motion direction to continue moving forward. A schematic diagram of the target motion model is shown in Figure 1.
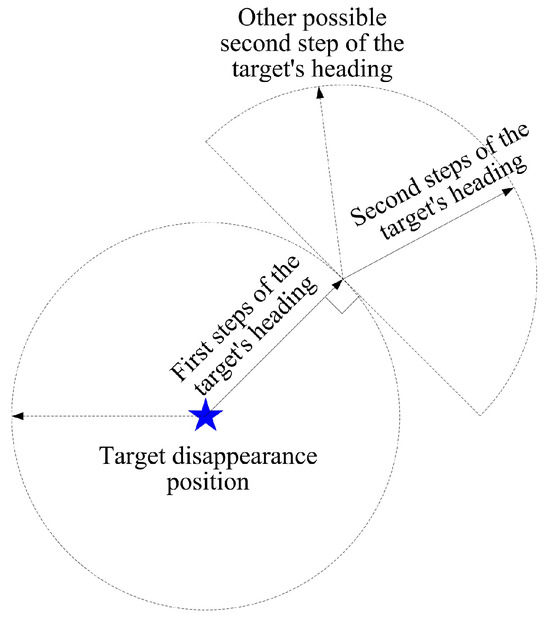
Figure 1.
Schematic diagram of the target motion model.
Assuming that the target motion speed v remains constant and moves forward d meters within the time interval , the expression for the target motion trajectory is as follows:
2.2. Sonar Detection Model
We assume that the sonar has detection blind spots within a certain opening angle at both the head and tail during the working process, as shown in Figure 2 [18,19].
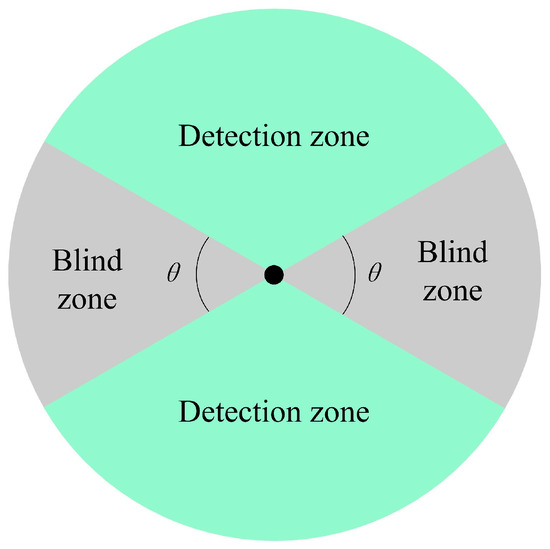
Figure 2.
Schematic diagram of the sonar detection range.
The sonar detection probability is closely related to various factors such as target radiation noise, self-noise, marine environmental noise, relative situation, blind zone location, etc. Based on the sonar equation, the signal excess is calculated to solve the detection probability. The relationship between the signal excess and detection probability can be expressed as [20]:
where represents the false alarm probability, usually taken as , and is the signal-to-noise ratio obtained when equals 0.5. represents the signal excess, which can be calculated using sonar equation.
In the passive working mode of sonar, when noise is the main interference type, the signal excess is expressed as [21]: . Where represents the target radiation sound source level, represents the transmission loss between the target and the receiver, represents the marine environmental noise level, represents the sonar detection threshold, and represents the receiving directionality index. Among them, is calculated according to the empirical formula: , where r represents the distance between the target and the receiver, represents the attenuation coefficient, and its relationship with frequency is expressed as follows [22]:
In the active working mode of sonar [23], when noise is the main type of interference, the signal excess is expressed as: . Among them, represents the emission sound source level, represents the target strength, which is strongly correlated with the real-time situation and is constantly changing. The meanings of the other parameters are the same as those in the previous text.
In the sonar dual-base working mode [24,25,26,27,28], when noise is the main type of interference, the signal excess is represented as: . Among them, represents the transmission loss between the transmitting node and the target, and represents the transmission loss between the target and the receiving node. The meanings of the other parameters are the same as those in the previous text.
In the sonar dual-base working mode, in addition to the detection blind zone at the head and tail positions, there is also a pulse width blind zone, as shown in the gray area in Figure 3 [29]. Assuming that the pulse width of the actively emitted sound wave is , the time required for the sound wave to transmit from the emitting node to the target is , the time required for the sound wave to transmit from the target to the receiving node is , and the time required for the sound wave to directly reach the receiving node from the emitting node is , the condition of the pulse width blind zone is: .
Figure 3.
Schematic diagram of the pulse width blind zone.
2.3. Multi-Sensor Detection Information Fusion Model
Information fusion refers to the comprehensive processing of information from multiple sensors or data sources to obtain more comprehensive and accurate results. It is of great significance in improving the detection accuracy of sensor systems, enhancing system robustness, and improving decision reliability [30,31,32,33,34,35]. The multi-sensor fusion center fuses the detection results reported by each sensor to obtain the overall detection probability for the target. The detection probability values of each sensor can be fused into the overall detection probability value via the following methods:
(1) Product method: This method is suitable for scenarios where each sensor detection process is an independent event [36].
(2) Weighted average method: Assign a certain weight to each detection probability, and then calculate the weighted average probability.
(3) Maximum value method: Take the maximum detection probability of each sensor as the overall detection probability.
The collaborative search process of multi-sonar system has the following characteristics: (1) The scene situation changes in real time, that is, at any time, the signal excess received by each sonar changes in real time; (2) At each moment, each sonar has a detection probability for the target, and each detection probability corresponds to a certain confidence level. Generally, the larger the signal excess, the higher the confidence level of the detection result. At each moment, there is a certain correlation between the detection results of each sonar on the target.
On the basis of the above characteristics, we propose a multi-sensor detection probability fusion method based on dynamic adaptive weight calculation. The flowchart of this fusion method is shown in Figure 4.
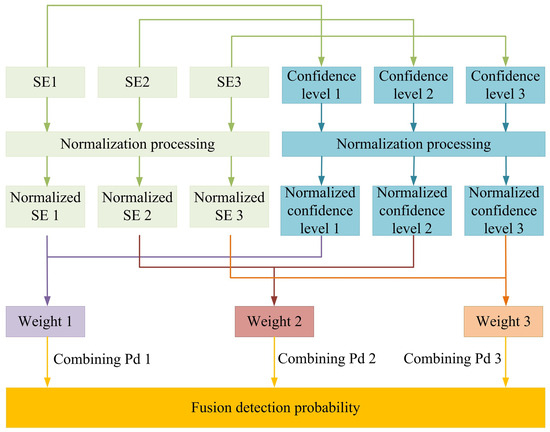
Figure 4.
Flow chart of the multi-sensor detection probability fusion method based on dynamic adaptive weight calculation.
The specific calculation steps are as follows:
(1) Dynamic calculation of the confidence level under uncertain situation conditions
In real-time situations, the signal excess is first obtained based on the sonar equation. Then, we define a relationship between signal excess and confidence level, which can be empirical, linear, or nonlinear. We assume a simple linear relationship between the signal excess and confidence level: , where represents the detection confidence level of the i-th sensor, represents the signal excess of the i-th sensor, a or b represents the coefficient. The detection confidence level should meet the requirement that , if is less than 0, it should be uniformly calculated as 0, if is greater than 1, it should be uniformly calculated as 1. Therefore, to be precise, the confidence level is a ‘piecewise function’, expressed as follows:
(2) Normalization of the signal excess and detection confidence level
When normalizing a set of signal excesses, it is inevitable that some signal excesses may be less than 0. To solve this problem, the first step is to perform ‘exponential power’ processing.
(3) Comprehensive weight calculation of each sensor
The weighted sum method is used to obtain the weights of each sensor, namely , where represents a fixed weight coefficient, .
(4) Calculation of the overall detection probability
By combining the detection probabilities of each sensor with the comprehensive weights, the overall detection probability can be determined. Assuming that the detection probability of the i-th sensor is , the overall detection probability is .
2.4. Efficiency Evaluation Indicators
We select two indicators, the detection probability and cumulative detection probability, to evaluate the collaborative search efficiency of the multi-sonar system.
- (1)
- Detection probability
The detection probability represents the instantaneous detection capability of sonar for surrounding targets at a certain moment and in a certain determined situation, which can be calculated via Formula (2). It is closely related to factors such as sonar performance parameters, target radiation noise, marine environmental noise, self-noise, and the relative situation.
- (2)
- Cumulative detection probability
The detection probability represents only the sonar detection result at a certain moment. In practical tasks, we should consider the entire task process in conjunction, that is, the cumulative detection probability. It is defined as the probability that the search platform can effectively detect the target after a period of searching during the search process. The cumulative detection probability is based on the instantaneous detection probability, and is accumulated during the deduction process to evaluate the possibility of the target being detected throughout the entire process, which more comprehensively reflects the performance of the detection system. Owing to the certain correlation between the two detection results with a small time interval, the process model considering temporal correlation is used to construct the formula for calculating the cumulative detection probability. The calculation process is as follows [37]:
where, represents the instantaneous detection probability corresponding to N time points, represents the maximum value of , , represents the sonar detection time interval, and represents the signal jump rate.
On the basis of the target motion model, the sonar detection model, and the multi-sensor information fusion model, with detection probability and cumulative detection probability as evaluation indicators, combined with task requirements and a target collaborative search scheme, a collaborative search efficiency evaluation model of multi-sonar system based on information fusion and dynamic deduction under uncertain situation conditions was established based on the Monte Carlo method. The model schematic diagram is shown in Figure 5.
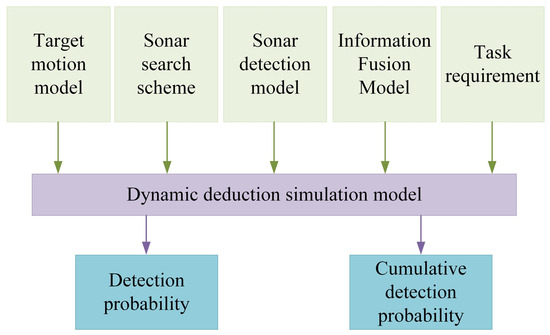
Figure 5.
Schematic diagram of the collaborative search efficiency evaluation model of multi-sonar system.
3. Case Simulation and Result Analysis
3.1. Task Scene Construction
We assume that a multi-sonar system consists of three sonars, and each sonar is a transceiver sonar. The multi-sonar system receives the task of searching for the target; within a certain area, the disappearance point of the target is known, the speed is known, and the heading information is unknown. The search route for each sonar is designated, and three sonars search back and forth along the designated search routes until the end of the task. A schematic diagram of the scene is shown in Figure 6.
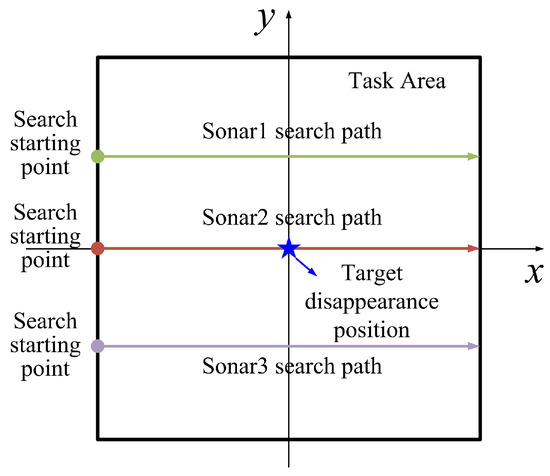
Figure 6.
Schematic diagram of the task scene.
3.2. Simulation and Results Analysis
3.2.1. Simulation and Analysis of Collaborative Search Efficiency Evaluation of Multi-Sonar System Under Two Working Modes
This section distinguishes between the fully-passive working mode and multi-base working mode of sonar, and evaluates the collaborative search efficiency. Among them, in the multi-base working mode, the second sonar works actively, and the first and third sonars work passively.
From the analysis of Figure 7, it can be observed that the instantaneous detection probability curve shows a cyclic trend of increasing first and then decreasing, which is consistent with the scene of three sonars executing search tasks back and forth along designated search routes. The instantaneous detection probability of 2nd sonar in the initial stage is almost zero, because the target is always within the blind zone range of 2nd sonar at the beginning stage.
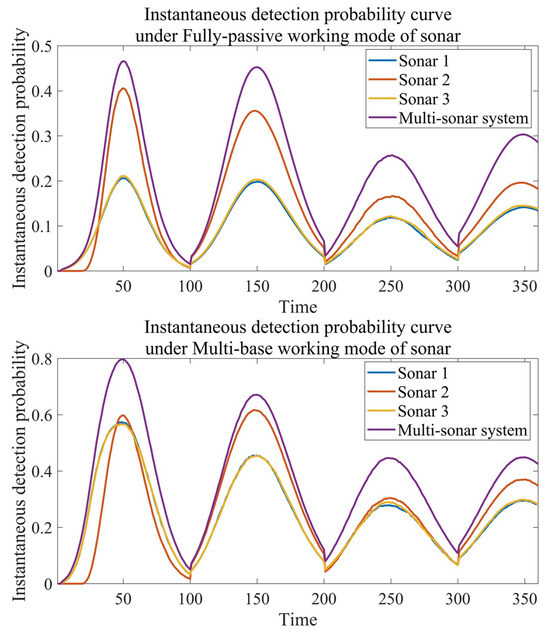
Figure 7.
Instantaneous detection probability curves under two working modes.
According to the analysis of Figure 8, in the fully passive working mode of the sonar, when the target passes through the detection blind zone of 2nd sonar, the cumulative detection probability growth rate of 2nd sonar for the target is relatively high. This is because at this stage, the target is closer to 2nd sonar, and it has a slight “search advantage”. The cumulative detection probability of 2nd sonar in the initial stage is almost zero, which is consistent with the analysis above, because the target is always within the blind zone range of 2nd sonar at the beginning stage.
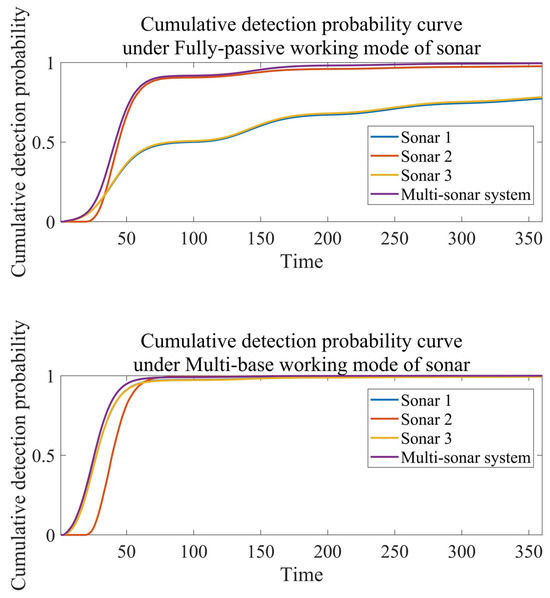
Figure 8.
Cumulative detection probability curves under two working modes.
The measurement standard is the time required for the cumulative detection probability to reach 0.9. Table 1 lists the time required for the cumulative detection probability to reach 0.9 under different conditions.

Table 1.
Time required for cumulative detection probability to reach 0.9 under different conditions.
By analyzing the data in Table 1, the following conclusions can be drawn:
(1) The detection efficiency of the Multi-sonar system is greater than that of each sonar, which intuitively reflects the advantages of collaboration.
(2) The detection efficiency of the Multi-sonar system in multi-base working mode is superior to that in fully-passive working mode.
3.2.2. The Influence of Different Sonar Transceiver Combinations on Evaluation Indicators Under the Multi-Base Working Mode
On the basis of the collaborative search efficiency evaluation model established in this paper, this section studies the influence of different sonar transceiver combinations on the instantaneous detection probability and cumulative detection probability of the Multi-sonar system under the multi-base working mode through simulation calculations. The simulation results are shown in Figure 9 and Figure 10.
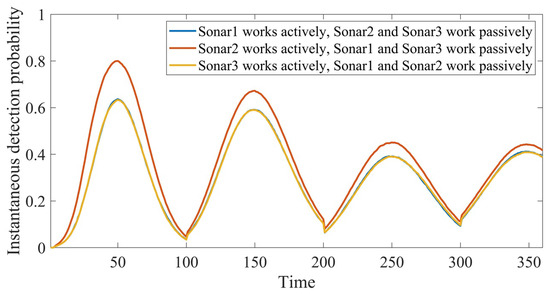
Figure 9.
The influence Schematic diagram of different sonar transceiver combinations on the instantaneous detection probability of the Multi-sonar system under the multi-base working mode.
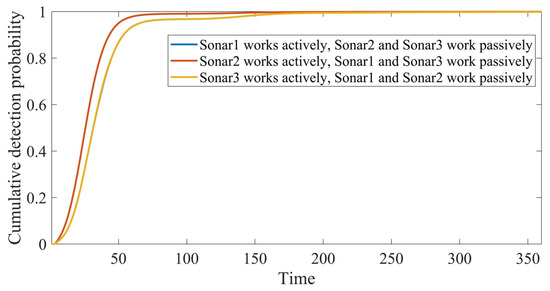
Figure 10.
The influence Schematic diagram of different sonar transceiver combinations on the cumulative detection probability of the Multi-sonar system under the multi-base working mode.
According to the simulation results, when the sonar transceiver combination is active working of second sonar and passive working of first and third sonars, the instantaneous detection probability and cumulative detection probability of the multi-sonar system are both the highest. The instantaneous detection probability and cumulative detection probability of the multi-sonar system under the other two forms of sonar transceiver combinations are almost the same. This is because the search routes of the first and third sonars are symmetrically distributed relative to the centerline of the task area and the disappearance position of the target. Therefore, regardless of who actively works, the final effect is the same for the first and third sonars.
3.2.3. The Influence of Different Sonar Parameters and Target Parameters on Evaluation Indicators
On the basis of the collaborative search efficiency evaluation model established in this paper, this section studies the influence of different sonar parameters and target parameters on the instantaneous detection probability and cumulative detection probability of the multi-sonar system under the fully-passive working mode and multi-base working mode through simulation calculations.
- (1)
- The influence of sonar search speed on evaluation indicators
Assuming that the search speeds of the three sonars are always the same and remain constant, the search speeds are set to , , , and the other parameters are the same as those in the previous text. The simulation results are shown in Figure 11.
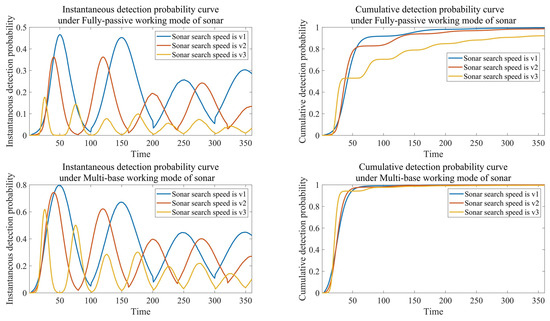
Figure 11.
The influence of different sonar search speeds on evaluation indicators.
According to the simulation results, as the sonar search speed increases, its detection capability gradually weakens. This is because the increase in speed leads to an increase in the background noise level of the sonar, such as propeller noise and flow noise, which affects its detection capability. Owing to the increase in search speed, the round-trip search period of the sonar decreases, which is reflected in the instantaneous detection probability. The reduction in detection capability is reflected in the decrease in instantaneous detection probability, resulting in a decrease in the maximum cumulative detection probability. However, the increase in search speed allows the multi-sonar system to approach the target at a faster speed, so the growth rate of the cumulative detection probability in the beginning stage increases.
- (2)
- The influence of the target escape speed on evaluation indicators
We set the target escape velocities to , , , and , all other parameters are the same as those in the previous text. The simulation results are shown in Figure 12.
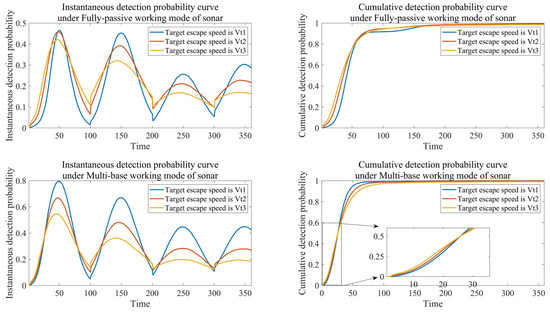
Figure 12.
The influence of target escape speed on evaluation indicators.
According to the simulation results, it can be concluded that: (1) As the target escape speed increases, its radiated noise level increases, resulting in an increased probability of being detected. But at the same time, it also brings another problem: the increase in target escape speed leads to an increase in escape distance at the same time, resulting in an increase in the distance between the multi-sonar system and the target at certain moments, thus reducing the probability target detection. (2) During each round-trip search cycle, as time passes, a larger target escape speed will cause the multi-sonar system to approach the target at a relatively fast speed. Therefore, in the initial short period of time, a larger target escape speed corresponds to a relatively higher instantaneous detection probability, resulting in a relatively higher cumulative detection probability.
- (3)
- The influence of the target disappearance position on evaluation indicators
We set the target disappearance positions as , , , , and , where a is a positive number greater than 0 and ensures that all 5 points are within the task area. The other parameters are the same as those in the previous text. The simulation results are shown in Figure 13.
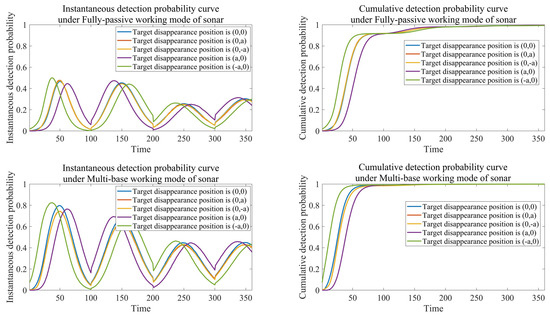
Figure 13.
The influence of the target disappearance position on evaluation indicators.
According to the simulation results, it can be concluded that changing the target disappearance position point can achieve a ’translation’ of the instantaneous detection probability and cumulative detection probability on the time axis, because different target disappearance positions result in different times for the Multi-sonar system to approach the target. When the target disappears at position (-, the Multi-sonar system takes the shortest time to approach the target, the instantaneous detection probability peak appears first, and the cumulative detection probability begins to increase first; When the target disappears at positions , , and -, the time it takes for the multi-sonar system to approach the target is centered, the time when the instantaneous detection probability peak occurs is centered, and the time when the cumulative detection probability begins to increase is centered. When the target disappears at position , the multi-sonar system takes the longest time to approach the target, the instantaneous detection probability peak appears last, and the cumulative detection probability finally begins to increase.
3.2.4. Analysis and Simulation Study on the Influence of Each Sonar on the Overall Detection Capability
The correlation coefficient (CC) can be used to measure the degree of association between two random variables, while mutual information (MI) can reflect the degree of dependence and information transmission between two random variables. The instantaneous detection probability vector only reflects the detection capability of sensors at different times, and is more suitable for analyzing the real-time dynamic characteristics of multi-sensor collaboration. The cumulative detection probability vector integrates the detection results of all members throughout the entire mission process, making it more suitable for evaluating the overall detection efficiency under long-term missions. In order to analyze the influence of each sonar on the overall detection capability during the entire target search task, this section calculates the correlation coefficient and mutual information between the cumulative detection probability vector of each sonar and the overall cumulative detection probability vector, and analyzes and simulates the influence of each sonar on the overall detection capability. The calculation formula for the correlation coefficient and mutual information is [38,39,40,41,42,43,44,45,46]:
where, X and Y represent two random variables, with values of and , respectively. Their corresponding entropies are and , and their joint entropy is . and correspond to the mean values of random variables X and Y, respectively, and represents the correlation coefficient. and correspond to the probability density functions of random variables X and Y, respectively. is the joint probability density function of random variables X and Y, and represents the mutual information value. The higher the correlation coefficient, the greater the mutual information value, indicating that the sonar has a more significant influence on the overall detection capability.
On the basis of the collaborative search efficiency evaluation model established in this paper, we calculate the cumulative detection probability vectors under two working modes, and the relevant parameter settings are the same as those in the previous text. Based on two key indicators of correlation coefficient and mutual information, we simulate and study the influence of each sonar on the overall detection results. The simulation results are shown in Figure 14 and Figure 15.
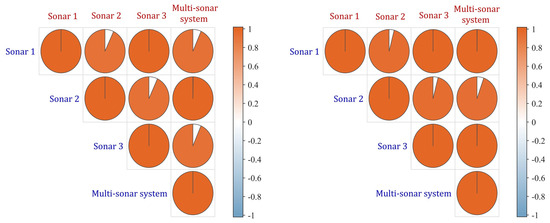
Figure 14.
Cumulative detection probability correlation coefficient between each sonar and the whole under two working modes.
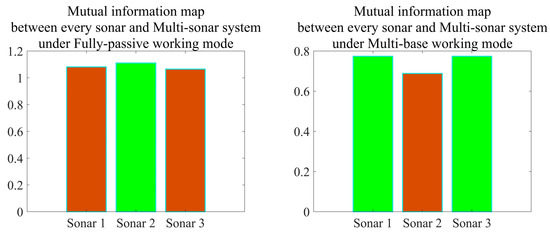
Figure 15.
Cumulative detection probability mutual information diagram between each sonar and the whole under two working modes.
According to the simulation results, it can be concluded that: (1) Under the two working modes, the influences of the first and third sonars on the overall detection results are almost the same. (2) In the fully−passive working mode, the second sonar has a relatively significant influence on the overall detection results. In the multi−base working mode, the influence of second sonar on the overall detection results is relatively small.
4. Discussion
In this section, we further discuss the multi-sonar detection information fusion, case simulation, research limitations, and other related issues in the research process.
4.1. Multi-Sensor Detection Information Fusion Method
In this paper, we adopt a detection information fusion method based on adaptive weight allocation for multi-sonar detection probability fusion processing. We consider that high detection probability corresponds to high confidence and should be given higher weights. Therefore, the proposed method allocates weights based on real-time detection probability values from multiple sonars. The detection probability is calculated through the signal excess, and there is a one-to-one correspondence between the two. The relationship between the signal excess and detection probability is illustrated in Figure 16.
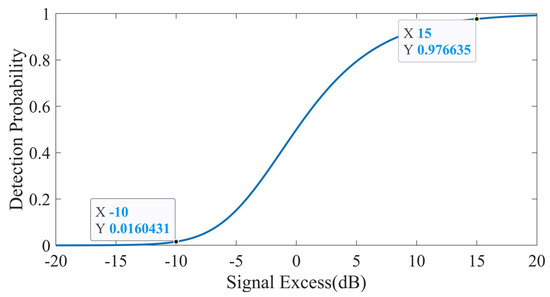
Figure 16.
Relationship curve between the signal excess and detection probability.
According to Figure 16, when the signal excess is −10 dB, the detection probability is almost 0; when the signal excess is 15 dB, the detection probability is almost 1. The detection probability is directly proportional to the signal excess. As the signal excess increases, the detection probability also increases, and the corresponding confidence level also increases. In this work, we assume a linear relationship between the signal excess and confidence level, that is, when the signal excess is less than or equal to −10 dB, the confidence level is 0; when the signal excess is greater than or equal to 15 dB, the confidence level is 1. The relationship between the signal excess and confidence level is illustrated in Figure 17.
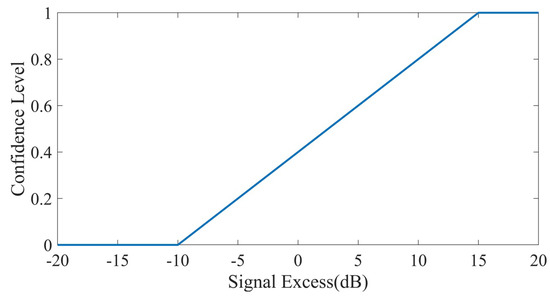
Figure 17.
Relationship curve between the signal excess and confidence level.
When the signal excess and detection confidence corresponding to each sonar are known, we normalize them according to the calculation method of Formula (8) and comprehensively consider the influence of signal excess and detection confidence on the weights. We use the weighted sum method to obtain the formation detection probability value.
To quantify the advantages of adaptive weight allocation, we compare it with the average weighting fusion method. We take a discrete time point on a certain target trajectory as an example and explain it via variance as the evaluation index.
At a discrete time point on the trajectory of a certain target, the relative situation between the sonar and the target is known. At this point, the signal excesses of the three sonars for the target are −5 dB, 0 dB, and 5 dB, respectively. The detection probabilities for the target are 0.1518, 0.5, and 0.7937, respectively. The detection probability variances for the three sonars are , , and , respectively.
(1) If the average weighting method is used for multi-sonar detection information fusion processing, the weight assigned to each sensor is: . The variance of the fusion result is: , and the calculated value is 0.01.
(2) If the method proposed in this paper is used for multi-sonar detection information fusion processing, according to the information fusion process in Section 2.3, the weight assigned to each sensor is: . The variance of the fusion result is: , and the calculated value is 0.0071.
Based on the simulation results, we can conclude that the detection information fusion method based on adaptive weight allocation has lower variance and better stability. However, in this method, we assume a simple linear relationship between signal excess and confidence level, which has certain limitations and requires further research on the mathematical model between them.
4.2. Explanation of the Simulation Results
In the case simulation analysis of this paper, we conduct a comprehensive simulation study. For different variable conditions such as different sensor speeds, target speeds and target initial positions, the corresponding detection probability change curves under the two working modes of fully-passive and multi-base are calculated and given in detail. However, there are two issues that need further clarification.
(1) The calculation of the detection probability is based on ideal conditions. Specifically, the calculation of the detection probability is closely related to various parameters of the sonar equation. However, we assume that the relevant sonar equation parameters are constant or model calculated values, which exposes certain limitations. In a real marine environment, the background noise NL of the marine environment varies due to changes in hydrological conditions. In addition, in this paper, the transmission loss (TL) is obtained through empirical formulas, which also results in certain errors. In the next step of our research, we plan to add a certain disturbance to the NL value to reflect the changing characteristics of the marine environment, and use models such as the Bellhop sound field to calculate the TL value to more accurately reflect the influence of hydrological conditions, sea surface and seabed characteristics, and other factors on the propagation of underwater acoustic signals.
(2) The simulation results under different experimental conditions are the means of multiple Monte Carlo results, which indicates that the simulation results have certain statistical significance. To further determine whether the mean of the detection probability has statistical significance and improve the reliability of the simulation results, we take the instantaneous detection probability results in Figure 11 as an example (in this example, the sonar is working in multi-base mode, the sonar search speed is , and the time point T is 50 min), and the one-sample t-test method is used in significance testing to test whether the mean of sonar detection probability significantly differs from the assumed random horizontal probability value. We design a significance test method according to the following steps:
- (A)
- Clarifying the basic setting of hypothesis testing
a. Null hypothesis (): The mean probability of sonar detection is equal to the random horizontal probability value, i.e., .
b. Alternative hypothesis (): It is bilateral test, the mean of sonar detection probability significantly differs from the random horizontal probability value, i.e., .
- (B)
- Data preparation
We use the Monte Carlo method to generate multiple sonar detection probabilities that meet the conditions, . These detection probability data are independent and the sample mean is approximately normally distributed.
- (C)
- Calculation of the test statistic (t-value) and p-value
a. Calculate the sample mean: . According to the simulation results in Figure 11, the mean of instantaneous detection probability is 0.5870.
b. Calculate the standard deviation of the sample: . The standard deviation of instantaneous detection probability is 0.3040.
c. Calculate the t-statistic: . By calculation, the t-statistic is 28.6285.
d. Calculate the p-value. By calculation, the p-value is , which is almost zero.
- (D)
- Determining statistical significance
The calculated p-value is compared with the significance level (usually taken as 0.05): (1) If , the null hypothesis is rejected, indicating that the mean of detection probability is significantly different from 0.5 (statistically significant). (2) If , the null hypothesis is not rejected, indicating that the mean of detection probability does not have statistical significance.
The calculated p-value is , which is much smaller than 0.05, indicating that the null hypothesis is rejected at the level, and the mean of detection probability is significantly different from the random probability of 0.5, indicating the statistical significance of the mean of detection probability.
4.3. Other Research Outlooks
The process of target collaborative search is a complex and dynamic process, in which our sensors and the target engage in a real-time adversarial game, where the target makes real-time decisions based on its detection information to avoid detection by our sensors. In this paper, we did not consider the avoidance behavior of the target. In the next step of our research, we consider abstracting the collaborative search scene as a dynamic game model of multi-party strategy confrontation, where each participant (including the sonar platform and the target) is regarded as an intelligent participant in the game model. By constructing a multi-stage game model, the dynamic interaction between sonars and targets is regarded as an adversarial process to simulate target avoidance behavior, thus, a sonar detection efficiency evaluation model is constructed on the basis of a dynamic evolutionary game framework.
5. Conclusions
We consider that collaborative search based on multi-sonar system is a dynamic process with real-time changes in relative position. Traditional efficiency evaluation methods are limited to static modeling, which lacks dynamic analysis and adaptive adjustment capability, and cannot cope with the dynamic situations with real-time changes. In addition, due to the confidence level of sonar detection probability, we consider that multi-sensor detection information fusion is also in a “dynamic” state of change, that is, a high detection probability should be given high confidence and high weight. To solve this problem, in this paper, we introduce the Monte Carlo sampling concept to establish a collaborative search efficiency evaluation model of multi-sonar system based on information fusion and dynamic deduction under uncertain target situations. To quantify the advantages of adaptive weight allocation, we compare it with the average weighting fusion method. According to the simulation results, the variance decreases from 0.01 to 0.0071, which proves that the proposed information fusion method has better stability. To further determine whether the mean of the detection probability has statistical significance, we design the one-sample t-test method. The simulation results show that at the a = 0.05 level, the null hypothesis is rejected, and the mean of the detection probability is significantly different from the random probability of 0.5, indicating its statistical significance. Moreover, through simulation case analysis, we evaluate the collaborative search efficiency of multi-sonar system in fully-passive and multi-base working modes, and compare the impact of each sonar on the overall detection capability, which verifies the effectiveness of the proposed method. This work can provide strong support for the development of collaborative search schemes for multi-sonar system and a theoretical basis for their practical application.
Author Contributions
Conceptualization, S.W., W.C., Z.L. and X.C.; methodology, S.W., W.C., Z.L. and X.C.; software, S.W.; data curation, S.W., W.C., Z.L. and X.C.; writing—original draft preparation, S.W., W.C., Z.L. and X.C.; writing—review and editing, S.W., W.C., Z.L. and X.C.; visualization, S.W., W.C., Z.L. and X.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 62201605).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to confidentiality agreement.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, J.; Zhang, G.; Jiang, C.; Zhang, W. A survey of maritime unmanned search system: Theory, applications and future directions. Ocean Eng. 2023, 285, 115359. [Google Scholar] [CrossRef]
- Peng, Y.; Yang, Y.; Cui, J.; Li, X.; Pu, H.; Gu, J.; Xie, S.; Luo, J. Development of the USV ‘JingHai-I’and sea trials in the Southern Yellow Sea. Ocean Eng. 2017, 131, 186–196. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, M.; Hao, Y. A Novel Region-Construction Method for Multi-USV Cooperative Target Allocation in Air–Ocean Integrated Environments. J. Mar. Sci. Eng. 2023, 11, 1369. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, Z.; Xu, J.; Wang, X.; Lu, Y.; Yu, J. A cooperative hunting method for multi-usv based on the a* algorithm in an environment with obstacles. Sensors 2023, 23, 7058. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Guo, H.; Liu, X.; Pan, S. USV Cluster Cooperative Navigation Algorithm based on factor graph. In Proceedings of the 2022 IEEE 6th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Beijing, China, 3–5 October 2022; pp. 955–959. [Google Scholar]
- Yao, P.; Lou, Y.; Zhang, K. Multi-USV cooperative path planning by window update based self-organizing map and spectral clustering. Ocean Eng. 2023, 275, 114140. [Google Scholar] [CrossRef]
- Liu, S.G.; Shao, M.J. A review on UAV autonomous combat effectiveness evaluation techniques. Electron. Opt. Control 2024, 31, 55–64. [Google Scholar]
- Jiang, W.; Chen, Z.; Wu, Y.; Hua, B.; Zhao, X. Research on Combat Effectiveness Evaluation of UAV Swarm Based on AHP-FCE. In Proceedings of the International Conference on Autonomous Unmanned Systems, Xi’an, China, 23–25 September 2022; Springer: Singapore, 2022; pp. 1648–1660. [Google Scholar]
- Jia, N.; Yang, Z.; Yang, K. Operational effectiveness evaluation of the swarming UAVs combat system based on a system dynamics model. IEEE Access 2019, 7, 25209–25224. [Google Scholar] [CrossRef]
- Sun, L.; Chang, J.; Zhang, J.; Fu, Z.; Zou, J. Evaluation of Unmanned Aerial Vehicles Cooperative Combat Effectiveness Based on Conditional Entropy Combination Weight Method. J. Aerosp. Technol. Manag. 2021, 13, e3621. [Google Scholar] [CrossRef]
- Liang, Q.; Luo, M.; Wang, Y.; Hao, X. Multi-attacks effectiveness evaluation of UUV based on wake guidance. Ocean Eng. 2022, 266, 112654. [Google Scholar] [CrossRef]
- Cheng, J.; Zhao, Y.; Cai, J. An MMCW-FCE method for evaluating AUV intelligence on the algorithm level. IEEE Access 2022, 10, 132071–132082. [Google Scholar] [CrossRef]
- Liu, J.y.; Sun, L.n.; Zhao, Z.m. Unmanned Aerial Vehicle Cluster Distributed Combat Effectiveness Evaluation Based on DoDAF. In Proceedings of the International Conference on Autonomous Unmanned Systems, Xi’an, China, 23–25 September 2022; Springer: Singapore, 2022; pp. 2264–2272. [Google Scholar]
- He, X.; Huang, F.; Zhu, J.; Lin, W. Reconnaissance Efficiency of Unmanned Underwater Vehicle Based on SEA. Ship Electron. Eng. 2016, 36, 161–164. [Google Scholar]
- Wang, C.; Ni, H.; Wang, Y.; Huang, B. Effectiveness evaluation for multiple unmanned surface vehicles cooperative combat based on GA-BP neural network. Ship Sci. Technol. 2024, 46, 109–114. [Google Scholar]
- Yuanming, D.; Chengyang, L.; Qian, L.; Min, Z. Effectiveness evaluation of UUV cooperative combat based on GAPSO-BP neural network. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 4620–4625. [Google Scholar]
- Feng, W.; Ma, Y.; Li, H.; Liu, H.; Meng, X.; Zhou, M. Optimal search path planning of UUV in battlefeld ambush scene. Def. Technol. 2024, 32, 541–552. [Google Scholar] [CrossRef]
- Wei, K.; Fang, S.; Tao, J. Enhanced Near-Field Interference Suppression Scheme for the Non-Cooperative Underwater Acoustic Pulse Detection of the Towed Linear Array. J. Mar. Sci. Eng. 2022, 10, 250. [Google Scholar] [CrossRef]
- Yang, M.; Han, D.; Li, N. Noise Suppression of Towed Line Array Sonar Platform Based on Spatial Filtering Technique. In Proceedings of the Journal of Physics: Conference Series, IOP Publishing, Online, 9–13 May 2022; Volume 2363, p. 012005. [Google Scholar]
- Ji, H.; Hu, H.; Peng, X. Multi-underwater gliders coverage path planning based on ant colony optimization. Electronics 2022, 11, 3021. [Google Scholar] [CrossRef]
- Lan, C.; Yu, Z.; Chen, H.; Zhang, L.; Zhang, M. Research on Underwater Collaborative Detection Method Based on Complex Marine Environment. IEEE Access 2024, 12, 3464–3475. [Google Scholar] [CrossRef]
- Guo, L.; Liu, T.; Zou, J.; Zhou, Q.; Sheng, X. Research on performance analysis and optimization methods of bistatic collaborative detection. In Proceedings of the 13th International Conference on Underwater Networks & Systems, Shenzhen, China, 3–5 December 2018; pp. 1–6. [Google Scholar]
- Li, M.; Liu, K.; Li, H.; Sun, Y.; Chen, X.; Mao, K. Quantitative analysis on the influence of the oceanic front on underwater acoustic detection with investigated marine data. J. Mar. Sci. Eng. 2023, 11, 1574. [Google Scholar] [CrossRef]
- Sheng, X.; Lu, J.; Dong, W.; YIn, J.; Guo, L.; Wu, X. The research on the coverage area of multistatic sonar in various working modes. In Proceedings of the Meetings on Acoustics, AIP Publishing, Shymkent, Kazakhstan, 11–13 September 2014; Volume 21. [Google Scholar]
- Bi, W.; Zhou, J.; Wu, Y.; Zhang, A. Array Optimization of Multistatic Sonar Buoy Sensors and Its Application in Submarine Search. IEEE Sens. J. 2024, 25, 3584–3596. [Google Scholar] [CrossRef]
- Fu, L.; Zhou, M.; Xu, L.; Dong, X.; Kou, Z.; Kang, C. Effective deployment strategies for optimizing area coverage in multistatic sonar detection based on Cassini oval approximation and a virtual force algorithm. Ain Shams Eng. J. 2024, 15, 103147. [Google Scholar] [CrossRef]
- Zhao, Y.; Qin, R.; Liu, S.; Zhang, W. Impact of Typhoon Noise on the Detection Performance of Multi-Static Sonobuoy Array. In Proceedings of the 2024 7th International Conference on Information Communication and Signal Processing (ICICSP), Zhoushan, China, 21–23 September 2024; pp. 745–750. [Google Scholar]
- Zhang, Y.; Zhang, X. A Study on Multistatic Sonar Localization Method with Consideration of AUV Mobility. In Proceedings of the 2024 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Bali, Indonesia, 19–22 August 2024; pp. 1–4. [Google Scholar]
- Jingfeng, X.; Shuping, H.; Xianglan, S.; Xin, M.; Yongfeng, D. A High Resolution Algorithm of Direct Path Interference Suppression for Bistatic Sonar. J. Electron. Inf. Technol. 2015, 37, 2929–2934. [Google Scholar]
- Thurman, E.; Riordan, J.; Toal, D. Multi-sonar integration and the advent of senor intelligence. In Advances in Sonar Technology; I-Tech Education and Publishing: Vienna, Austria, 2009; pp. 151–164. [Google Scholar]
- Zhang, Y.; Tu, C.; Gao, K.; Wang, L. Multisensor information fusion: Future of environmental perception in intelligent vehicles. J. Intell. Connect. Veh. 2024, 7, 163–176. [Google Scholar] [CrossRef]
- Tao, J.; Liu, Y.; Yang, D. Bearing fault diagnosis based on deep belief network and multisensor information fusion. Shock Vib. 2016, 2016, 9306205. [Google Scholar] [CrossRef]
- Wang, C.; Xin, C.; Xu, Z.; Qin, M.; He, M. Mix-VAEs: A novel multisensor information fusion model for intelligent fault diagnosis. Neurocomputing 2022, 492, 234–244. [Google Scholar] [CrossRef]
- Tian, T.; Sun, S.; Li, N. Multi-sensor information fusion estimators for stochastic uncertain systems with correlated noises. Inf. Fusion 2016, 27, 126–137. [Google Scholar] [CrossRef]
- Qiu, S.; Zhao, H.; Jiang, N.; Wang, Z.; Liu, L.; An, Y.; Zhao, H.; Miao, X.; Liu, R.; Fortino, G. Multi-sensor information fusion based on machine learning for real applications in human activity recognition: State-of-the-art and research challenges. Inf. Fusion 2022, 80, 241–265. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, G.; He, X.; Tang, J. Information fusion in networked underwater target detection. In Proceedings of the OCEANS 2015, Genova, Italy, 18–21 May 2015; pp. 1–4. [Google Scholar]
- Wei, X.; Liu, X.; Fu, D.; Yang, T.; Yang, J. Platform Path Optimization Method Based on Cumulative Detection Probability of Sonar Search. J. Syst. Simul. 2024, 36, 2674–2683. [Google Scholar]
- Karlović, I.; Pavlić, K.; Posavec, K. Analysis of the hydraulic connection of the Plitvica stream and the groundwater of the Varaždin alluvial aquifer. Geofizika 2021, 38, 15–35. [Google Scholar] [CrossRef]
- Da, C.; Hu, L.; Shen, B.; Yang, Y.; Wan, S.; Song, J. Theoretical Study and Numerical Experiment on the Influence of Trend Changes on Correlation Coefficient. Atmosphere 2022, 13, 66. [Google Scholar] [CrossRef]
- Ruiz-Abellon, M.d.C.; Gabaldón, A.; Guillamón, A. Dependency-aware clustering of time series and its application on energy markets. Energies 2016, 9, 809. [Google Scholar] [CrossRef]
- Osmane, A.; Savola, M.; Kilpua, E.; Koskinen, H.; Borovsky, J.E.; Kalliokoski, M. Quantifying the non-linear dependence of energetic electron fluxes in the Earth’s radiation belts with radial diffusion drivers. In Proceedings of the Annales Geophysicae; Copernicus Publications: Göttingen, Germany, 2022; Volume 40, pp. 37–53. [Google Scholar]
- Whitnall, C.; Oswald, E. A comprehensive evaluation of mutual information analysis using a fair evaluation framework. In Proceedings of the Annual Cryptology Conference, Santa Barbara, CA, USA, 14–18 August 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 316–334. [Google Scholar]
- Bao-Gang, H.; Yong, W. Evaluation criteria based on mutual information for classifications including rejected class. Acta Autom. Sin. 2008, 34, 1396–1403. [Google Scholar]
- Sakar, C.O.; Kursun, O. A method for combining mutual information and canonical correlation analysis: Predictive mutual information and its use in feature selection. Expert Syst. Appl. 2012, 39, 3333–3344. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, X.; Zhu, R. Feature selection based on mutual information with correlation coefficient. Appl. Intell. 2022, 52, 5457–5474. [Google Scholar] [CrossRef]
- Amiri, F.; Yousefi, M.R.; Lucas, C.; Shakery, A.; Yazdani, N. Mutual information-based feature selection for intrusion detection systems. J. Netw. Comput. Appl. 2011, 34, 1184–1199. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).