Abstract
Due to the intersection of three mining rights in a mining area, the stability of the rock mass is mutually affected after mining operations. To study the optimal backfill ratio and the surface stability after backfilling in the adjacent goaf areas of the three mines in this mining area, a mineral deposit model is established using Rhino software. The model spans 2500 m in the east–west direction, 3000 m in the north–south direction, and ranges from an underground elevation of −610 m below. FLAC3D software was then used to analyze the surface stability under two different backfill ratios after the complete excavation of the ore body. Additionally, 52 monitoring points were set up at critical buildings and structures. The results revealed that after the complete excavation of the ore body, large-scale surface subsidence occurred in the mining area, with the main subsidence center located in the Yinzhushan mining area. Under backfill condition 1, six monitoring points experienced settlements exceeding 30.00 mm, with a maximum settlement of 53.98 mm. Under backfill condition 2, three monitoring points exceeded 30.00 mm, with a maximum settlement of 51.93 mm. The level displacement deformation at the monitoring points under both conditions met the stability requirements specified by national standards. By comparing the settlements at the monitoring points, it was determined that backfill condition 2 represents the optimal backfill ratio. This study provides a theoretical basis for practical backfilling operations in the mine.
1. Introduction
As the demand for resources continues to grow, the urgency for mining has increased. However, mining activities can affect surface stability, leading to surface subsidence, geological hazards, and damage to surface structures, thereby endangering the safety of people and property [1,2]. Currently, the filling mining method is widely adopted for ore extraction. It has become one of the key technical approaches to addressing subsidence issues related to buildings, rivers, roads, and other structures [3,4,5].
Currently, many scholars have conducted research and analysis on surface subsidence following mining activities [6,7]. Liu et al. [8] predicted the extension of surface subsidence in the Xiaowanggou iron mine and compared the prediction results with satellite image observations. They found that although the model could not provide a clear boundary after extension, the predicted extension of directional surface subsidence helped mitigate the impact of geological hazards. Xu [9] used InSAR and GNSS technologies to analyze ground deformation in the goaf of the gypsum mine in the Diaoyu District of Jingmen City. They discovered that surface deformation was primarily characterized by horizontal displacement and used FLAC3D simulations to analyze the stability of the goaf, determining the area of surface subsidence. Li et al. [10] studied the filling mining of steeply inclined ore bodies and concluded that the main factors influencing surface subsidence were the convergence deformation of surrounding rock and the damage to the central pillar from the formation of mining channels to the filling stage. Li et al. [11] used FLAC3D software to simulate underground mining with three different mining methods in a phosphate mine. They found that using the filling mining method to backfill the mined-out areas effectively reduced surface subsidence. Researchers such as Shi et al., Li et al., Jia et al., and Dai et al. [12,13,14,15] have studied surface stability by focusing on the deformation of goafs after ore extraction. This research approach for single mining rights has matured, and the simulation results are practical and feasible. However, studies involving multiple mines, overlapping mining rights, and simultaneous extraction are rare. In actual mining operations, it is common to encounter situations where two or more mining rights intersect or overlap. When one mine is being exploited, buildings within the mining rights area of another mine may also be affected. Therefore, the mining methods and backfill schemes used by both mines must consider the overall surface stability of the mining area. This paper primarily focuses on the overlapping mining areas of the Baojia, Yinzhushan, and Yinhai mining zones as research subjects to study the impact of backfilling on surface stability.
Backfill mining, as a green and efficient mining method, is highly effective in improving ore recovery rates and controlling surface deformation [16,17]. However, the cost investment and economic benefits of different backfill schemes vary significantly, which increases the complexity of selecting backfill mining plans [18,19,20]. Liang et al. [21] studied the impact of different backfill schemes on roof stability through laboratory experiments, theoretical analysis, and numerical simulations. They found that the stability of the backfill roof was optimal when the upper and lower layered mining methods were arranged vertically or nearly vertically. Li et al. [22] optimized the backfill scheme for the Renjiazhuang mining area using numerical simulation software and discovered that the backfill ratio is a critical factor influencing backfill effectiveness. An appropriate backfill ratio can significantly reduce surface subsidence in goaf areas. Liu et al. [23] investigated the influence of different backfill strengths on surface subsidence patterns using the Donggou Coal Mine as a case study. They found that surface subsidence decreased as the depth of the ore body increased. Yang et al. [24] used numerical simulation software to study the impact of backfilling on surface subsidence in the Xincheng Gold Mine. They concluded that backfilling effectively reduces surface subsidence and the range of ground pressure activities. They also emphasized the need for dynamic monitoring of surface subsidence through the establishment of monitoring points under complex geological conditions.
In summary, this paper focuses on a silver–lead–zinc mine in Jiangxi as the research subject under complex engineering geological conditions. Based on laboratory rock mechanics parameter testing, the study uses FLAC3D finite difference numerical simulation software to simulate surface subsidence and horizontal displacement during the mining and backfilling processes, providing practical recommendations for mine backfilling. The goal of this study is to optimize the filling rate of mines in multi-mineral rights intersection areas by using numerical simulation methods and evaluate its impact on surface stability.
2. Overview
2.1. General Situation of Mining Area
The mining area is located in Guixi City, Jiangxi Province. Through on-site investigation and a review of the feasibility study report, it is evident that the main geological units of the mining area include the quaternary loose layer, silver–lead–zinc ore body, crystal tuff, and granite porphyry. The geological conditions of the area are generally of medium type; Figure 1 is the geological profile of the mining area. Surrounding the Yinzhushan mining area are key buildings and structures such as Xiabao Village, Fengshuzui Village, Xiaoyuan Village, the Lengshui River, highways, the main shaft, and the return air shaft. In the Baojia mining area, the primary structures include the inclined shaft, high-level pool, Yinluling subsidence area, and filling station. The main structures in the Yinhai mining area consist of industrial sites, concentrators, and tailings ponds.
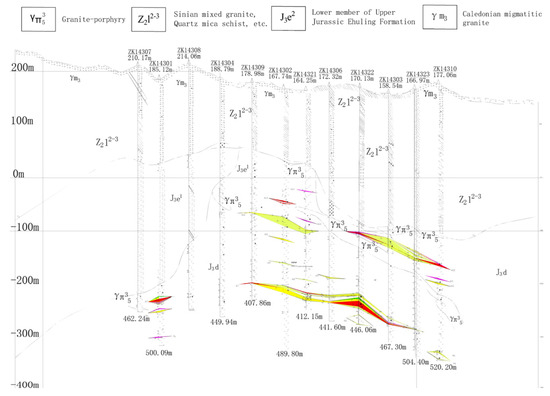
Figure 1.
Geological profile of mining area.
Since the mine obtained the mining license for the Yinzhushan mining area from the Jiangxi Provincial Department of Land and Resources in 1999, it has undergone more than 20 years of mining activities, including acquisitions and changes in mining rights. This has resulted in differing mining rights along the height direction of the mining area, meaning that the upper and lower parts of the mine are owned by different mining enterprises, as shown in Figure 2a,b represent two views in different directions. This situation has created significant challenges in determining whether the mine should be filled and what the appropriate filling rate should be during the mining process. Therefore, it is essential to simulate the mining, filling, and surface stability processes in this area.
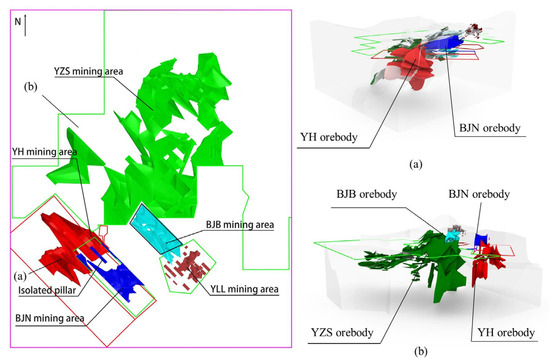
Figure 2.
Mining rights distribution diagram.
2.2. Layout of Monitoring Points
The arrangement of monitoring points is to monitor some important buildings and structures within the mining area, such as main shafts, highways, etc.; these places have strict deformation and settlement restrictions. Due to the presence of roads, rivers, villages, factories, and other facilities above the ore body, as well as important mine infrastructures such as the main shaft, high pool, and filling station, some collapses have occurred during the excavation of the Yinluling mining area around the mine. In order to ensure the safety of the buildings and structures within the mining area during mining, it is necessary to monitor the surface subsidence, terrain curvature deformation, ground inclined deformation, and lateral deformation in these places. A total of 52 monitoring points have been established. In the Baojia mining area, 12 monitoring points have been set up due to the location of some buildings within the surface movement zone. Additionally, 3 monitoring points are located in the village, 4 in the river, 5 along the highway, 9 in the factory area, and 19 in the Yinhai mining area. Because there are villages, factories, and other places with frequent human activities around the mine, 30 important monitoring points are set up in 52 monitoring points. These points are designated as BJ1-BJ12, CZ1-CZ3, GC1, GC2, GC4, GC6-GC9, YH9-YH15, and YH17, with BJ representing the Baojia mining area, YH representing the Yinhai mining area, and the remaining points representing the Yinzhushan mining area (the following text uniformly uses YZS to represent this). The specific layout is shown in Figure 3.
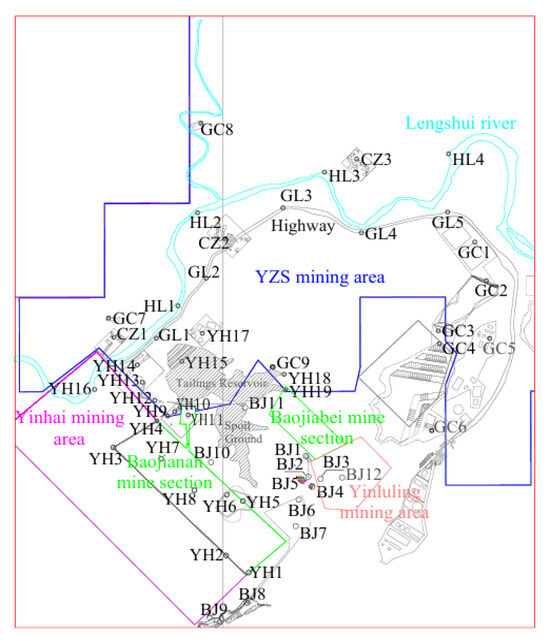
Figure 3.
Layout of monitoring points.
2.3. Stability Criterion
In this study, the surface stability criterion index is based on several standards, including the ‘Non-Ferrous Metal Mining Design Specification’ (GB50771-2012), the ‘Coal Mine Goaf Geotechnical Engineering Survey Specification’ (GB51044-2014), the ‘Goaf Collapse Prevention Engineering Design Specification (Trial)’ (TCAGHP 012-2018), the ‘Geological Disaster Ground Tilt Monitoring Technical Specification (Trial)’ (T-CAGHP 051-2018), the ‘Coal Mine Survey Specification’ (2013 Edition), and the ‘Building, Water, Railway and Main Roadway Coal Pillar Retaining and Coal Mining Specification.’ These standards help determine the degree of damage to surface buildings and the allowable values for surface settlement, based on topographic curvature deformation, surface tilt deformation, and lateral deformation. The safe use of surface buildings is allowed within the surface deformation values as shown in Table 1.

Table 1.
Allowable surface deformation value of buildings.
3. Model Establishment and Parameter Determination
3.1. Model Establishment
To reasonably simulate the surface deformation characteristics during mining and their impact on surface stability, the study thoroughly analyzed geological data and the range of the surface displacement belt. The spatial distribution of each stratum and its positional relationship with the ore body were comprehensively considered. The model assumes that the rock and ore bodies are quasi-homogeneous blocks/sections, thus conveying that they occupy approximately the same area and can be defined with the same parameters. The surrounding rock is simplified into granite porphyry (hanging wall) and crystal tuff (footwall), while the ore body consists of silver–lead–zinc ore. Using Rhino software, a mine model was established, covering three mining areas with an east–west length of 2500 m, a north–south width of 3000 m, and a vertical height ranging from −610 m elevation to the surface. To simulate a more realistic mining scheme, the model includes the adjacent BJ and YH mining areas. To reduce the number of grids, the ore body grid size was set to 5 m, and the surrounding rock grid size was set to 25 m. Figure 4 shows the ore body model, with a total of 9,105,363 nodes and 55,090,665 elements.

Figure 4.
Ore body model.
3.2. Parameter Selection
Based on the geological data provided by the mine, the hanging wall surrounding rock of the ore body is granite porphyry, and the footwall is crystal tuff. The mechanical parameters of the rock in the numerical simulation come from the measurement of the mine drilling core. The core obtained is shown in Figure 5. All types of rock exhibit high strength. Therefore, the mechanical parameters of three types of rock were determined through laboratory tests: granite porphyry, crystal tuff, and porphyry ore body. For each type of rock, uniaxial compression, shear, and tensile tests were conducted. To avoid randomness, each test was repeated four times. The mine uses cemented backfill, and the backfill parameters were provided by the mine. The measured parameters were then reduced using the GSI method to better align with actual mining conditions. The reduced physical and mechanical parameters of the rock and backfill are listed in Table 2.

Figure 5.
Indoor experiment diagram.

Table 2.
Summary of physical and mechanical parameters.
4. Analysis of Numerical Simulation Results
Before conducting excavation simulations and monitoring using FLAC3D, the displacement of the model’s four boundaries was set to 0, and the displacement of the bottom boundary was also set to 0. The top of the model was set as a free surface, and constitutive models, material parameters, and initial conditions were assigned. Prior to designing the backfill schemes, the ore body within the model was excavated using FLAC3D software. The results revealed large-scale subsidence within the mining area, with the maximum surface subsidence reaching 17.63 cm. The subsidence was primarily concentrated in the YZS mining area, and the extent of the collapse is illustrated in the right diagonal cross-section shown in Figure 6. Since the YH and BJ mining areas have already been backfilled, with backfill ratios set at 94% and 90%, respectively, and considering the preliminary geological exploration of the mine and the experience of similar local mines in terms of backfill materials and ratios, two backfill schemes were designed. Figure 6a: YZS backfilled at 90%, YH at 94%, and BJ at 90%. Figure 6b: YZS backfilled at 100%, YH at 94%, and BJ at 90%.
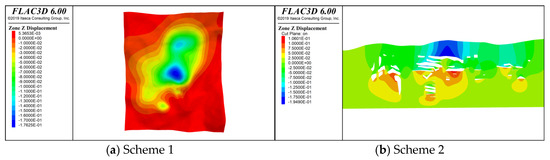
Figure 6.
Surface subsidence map and diagonal section diagram of the whole mining.
4.1. Calculation Formulas for Surface Subsidence and Horizontal Displacement Deformation
In 1969, Peck analyzed a large number of surface subsidence data and found that the surface subsidence trough conforms to the concept of a Gaussian distribution. He hypothesized that the surface subsidence trough equals the volume of ground loss, and he believed that ground deformation is caused by ground loss. He also noted that surface subsidence due to construction occurs under undrained conditions [25]. Since no drainage measures are typically applied to mine surfaces, the calculation of surface subsidence in mining can follow Peck’s formula. Equations (1) and (2) are the formulas for calculating surface subsidence:
In the formula, S is the settlement value of any point on the ground, mm; Smax is the maximum ground settlement value, mm; x is the distance between the center of the maximum settlement point and the settlement point, m; i is the distance between the symmetrical center of the settlement curve and the inflection point, m; and V is the formation loss per unit length, m3/m.
Surface Tilt: This refers to the ratio of the vertical subsidence difference between two adjacent points to their horizontal distance (essentially the average slope between the two points). It reflects the slope of the surface movement basin along a certain direction, with a positive sign indicating the uphill direction and a negative sign indicating the downhill direction. Equation (3) is the formula for calculating surface tilt:
In the formula, is the surface tilt value between adjacent points m and n, mm/m; and are the heights of the points, m; and is the horizontal distance between adjacent points m and n, m.
Surface Curvature: This refers to the ratio of the tilt difference between two adjacent segments to the horizontal distance between the midpoints of the segments. It reflects the degree of bending on the observation line cross-section. Curvature can be positive or negative, with convex upward curves being positive and concave downward curves being negative. Equation (4) is the formula for calculating surface curvature:
In the formula, is the surface curvature between points m,n, and p, mm/m2.
Lateral deformation: This refers to the ratio of the horizontal displacement difference between two adjacent points to their horizontal distance. It reflects the degree of stretching or compression of the segment, with positive values indicating tensile deformation and negative values indicating compressive deformation. Equation (5) is the formula for calculating lateral deformation [26]:
In the formula, is the lateral deformation value between adjacent points m and n, mm/m; is the displacement between points m and n, m.
4.2. Results and Analysis
- (1)
- Surface subsidence
A total of 52 monitoring points were set up in this simulation, including villages, rivers, highways, and mine industrial sites. Table 3 shows the settlement heights of the monitoring points under the two schemes. Comparing the two schemes, it was found that increasing the backfill ratio in the YZS mining area could reduce subsidence at most monitoring points. Under Scheme 1 in Table 3, 7 out of the 52 monitoring points experienced surface subsidence exceeding 30.00 mm, with the maximum subsidence of 53.98 mm occurring at YH6. Among the key monitoring points, BJ12, GC9, and YH17 exceeded the standard value of 30.00 mm, with subsidence values of 46.50 mm, 41.43 mm, and 33.72 mm, respectively. Under Scheme 2 in Table 3, 3 out of the 52 monitoring points experienced surface subsidence exceeding 30.00 mm, with the maximum subsidence of 51.93 mm occurring at YH6. Among the key monitoring points, BJ12 exceeded the standard value of 30.00 mm, with a maximum subsidence of 45.54 mm. Comparing the two filling schemes and improving the filling rate of YZS, the settlement of BJ12 is reduced by 0.96 mm, the settlement of GC9 is reduced by 39.58 mm, the settlement of YH5 is reduced by 2.5 mm, the settlement of YH6 is reduced by 2.05 mm, the settlement of YH8 is reduced by 1.68 mm, the settlement of YH17 is reduced by 32.94 mm, and the settlement of YH18 is reduced by 22.86 mm. Figure 7 shows the right diagonal cross-section of the model under the two scenarios. It can be observed that when the backfill ratio in the YZS mining area is 90%, a significant subsidence zone appears in the upper part of the mining area. However, after increasing the backfill ratio in the YZS mining area, the subsidence values in this zone significantly decreased. Nevertheless, small-scale roof collapses may occur within the BJ mining area, so additional measures are needed to mitigate potential roof collapses in this area. Figure 8 shows the surface subsidence contour maps under the two scenarios. By comparing Figure 8, it is evident that after increasing the backfill ratio in the YZS mining area, the subsidence center shifted, and the subsidence range was significantly reduced.

Table 3.
Settlement height of each monitoring point.
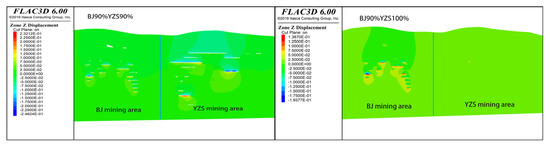
Figure 7.
Z-displacement diagram of the right diagonal section.
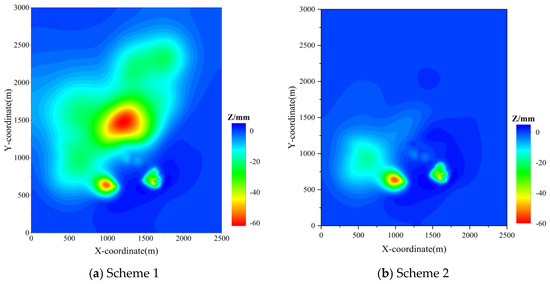
Figure 8.
Surface subsidence cloud map.
- (2)
- Surface tilt rate
Figure 9 shows the surface tilt contour maps under the two scenarios. Under Figure 9a, Scheme 1, the surface tilt values are very small, with the maximum tilt value of 0.223 mm/m occurring at monitoring point YH8. Under Figure 9b, Scheme 2, the surface tilt values are also very small, with the maximum tilt value of 0.174 mm/m occurring at monitoring point BJ6, which is far below the standard requirement. An analysis of Figure 9 reveals that the surface tilt rates at all points under both scenarios are very small. Increasing the backfill ratio in the YZS mining area slightly affects the surface tilt rate, but the impact is not significant.
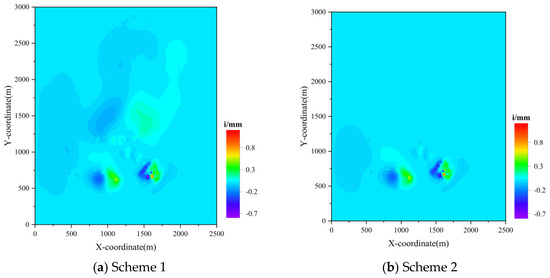
Figure 9.
Surface tilt cloud map.
- (3)
- Terrain curvature
Figure 10 shows the surface curvature contour maps under the two scenarios. Under Figure 10a, Scheme 1, the surface curvature values are very small, with the maximum curvature of 0.012 mm/m2 occurring at monitoring point CZ2. Under Figure 10b, Scheme 2, the maximum curvature of 0.006 mm/m2 occurs at monitoring point YH19. An analysis of Figure 10 reveals that increasing the backfill ratio in the YZS mining area has almost no effect on surface curvature. According to the stability criteria, the curvature values under both scenarios are far below the critical deformation limit of 3 mm/m2, indicating that surface curvature has almost no impact on the ground under either scheme.
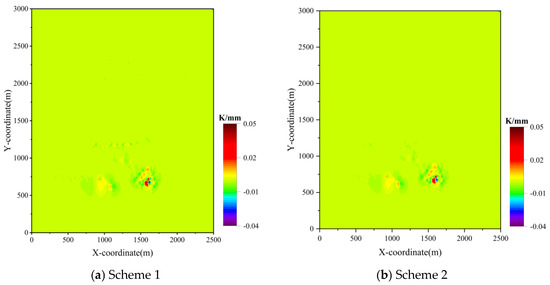
Figure 10.
Surface curvature cloud map.
- (4)
- Lateral deformation
Figure 11 shows the lateral deformation contour maps under the two scenarios. Under both Figure 11a,b, Scheme 1 and Scheme 2, the lateral deformation values on the surface are very small. Under Figure 11a, Scheme 1, the maximum deformation value of 0.37 mm/m occurs at monitoring point CZ2 among the 52 monitoring points. Under Figure 11b, Scheme 2, the maximum deformation value of 0.35 mm/m occurs at monitoring point BJ12 among the 52 monitoring points. However, the lateral deformation values are far below the standard requirements. As shown in Figure 11, distinct deformation centers are observed under both scenarios. Increasing the backfill ratio in the YZS mining area slightly reduces the lateral deformation within the mining area, indicating that raising the backfill ratio in the YZS mining area decreases lateral deformation, but the effect is not significant.
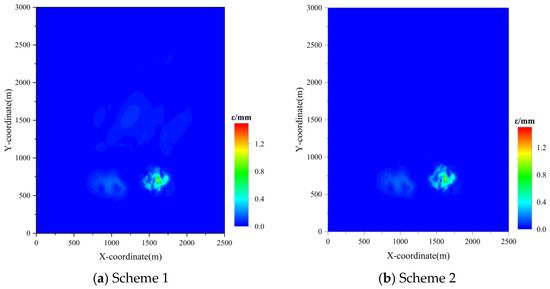
Figure 11.
Lateral deformation cloud map.
5. Conclusions and Recommendations
Based on the mining technical conditions, the impact of mining and backfilling processes on surface structures was analyzed using numerical simulation. The results are as follows:
- To ensure that the main building clusters remain within safe limits during the mining and backfilling process, and to guarantee the safety and stability of key structures within the surface movement zone, the backfill ratio for the YZS mining area is carefully considered. Surface subsidence, terrain curvature deformation, ground inclined deformation, and lateral deformation within the simulation range were calculated for two different backfill ratios. By combining these results with stability criteria, an appropriate backfill ratio was selected, providing a reference for practical mine backfilling.
- Considering the actual situation of the mine, a total of 52 surface monitoring points were set up. Under the condition of working condition 1, the settlement value of 7 monitoring points exceeded 30.00 mm, and a large area of subsidence occurred in the YZS mining area. Under the condition of working condition 2, the surface subsidence of 3 monitoring points exceeded 30.00 mm, and the subsidence range of the YZS mining area was also significantly reduced. In addition, after improving the filling rate of the YZS mining area, the terrain curvature deformation, ground inclined deformation, and lateral deformation also decreased to varying degrees, indicating that improving the filling rate of the YZS mining area has a significant effect on the safety and stability of the mine surface. Therefore, it is suggested that the filling rate in the mine using plan 2 (100% of YZS filling, 94% of YH filling, and 90% of BJ filling) should be taken as the actual filling rate.
- It is recommended that the mine establish a comprehensive surface displacement monitoring system to verify the accuracy of the numerical simulations.
Author Contributions
Conceptualization: Z.Y.; methodology: Y.R.; formal analysis and investigation: Z.Y. and X.Z.; writing—original draft preparation: Y.G. and Z.X.; writing—review and editing: Z.Y. and Q.Z.; funding acquisition: Y.R.; resources: Y.R. and X.Z.; and supervision: Z.X. and Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
Research grants from funding agencies: 2023 Jiangxi Province ‘Science and Technology + Emergency’ Joint Plan Project (No.2023KYG01002); Jiangxi Provincial Key Laboratory of Environmental Pollution Prevention and Control in Mining and Metallurgy (No.2023SSY01071).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
All the authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Tzampoglou, P.; Loupasakis, C. Mining geohazards susceptibility and risk mapping: The case of the Amyntaio open-pit coal mine, West Macedonia, Greece. Environ. Earth Sci. 2017, 76, 1–16. [Google Scholar] [CrossRef]
- Zhou, D.W.; Wu, K.; Bai, Z.H.; Hu, Z.Q.; Li, L.; Xu, Y.K.; Diao, X.P. Formation and development mechanism of ground crack caused by coal mining: Effects of overlying key strata. Bull. Eng. Geol. Environ. 2019, 78, 1025–1044. [Google Scholar]
- Qiu, X.Y.; He, X.R.; Cao, R.H.; Qiu, H.J.; Shi, X.Z.; Gou, Y.G.; Li, X.Y.; Zhi, W. Study on the Surface Subsidence Trend of Fill Mining in Underground Mines with Different Mining Depths. Adv. Civ. Eng. 2024, 2024, 4407757. [Google Scholar] [CrossRef]
- Song, G.Y.; Du, K.; Zhang, Y.D.; Li, Z.X.; Hu, L. Study of the Overlying Strata Movement Law for Paste-Filling Longwall Fully Mechanized in Gaohe Coal Mine. Appl. Sci. 2023, 13, 8017. [Google Scholar] [CrossRef]
- Gu, W.; Chen, L.; Xu, D.L. Research on the Overburden Movement Law of Thick Coal Seam Without-Support Gangue-Filling Mining. Minerals 2022, 13, 53. [Google Scholar] [CrossRef]
- Yuan, L.W.; Li, C.Y.; Li, S.M.; Ma, X.S.; Zhang, W.; Liu, D.R.; Wang, G.; Chen, F.; Hou, X. Mine Slope Stability Based on Fusion Technology of InSAR Monitoring and Numerical Simulation. Sci. Program. 2022, 2022, 8643586. [Google Scholar] [CrossRef]
- Liu, X.; Wang, J.; Du, S.; Deng, K.; Chen, G.; Qin, X. Monitoring and Law Analysis of Secondary Deformation on the Surface of Multi-Coal Seam Mining in Closed Mines. Remote Sens. 2024, 16, 3223. [Google Scholar] [CrossRef]
- Liu, Y.; Ge, Y.; Zhang, C.; Ren, F.; Ma, J.; Ren, G. Cylindrical Caved Space Stability Analysis for Extension Prediction of Mining-Induced Surface Subsidence. Geofluids 2021, 2021, 1–13. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, W.; Zhu, Z.; Zhao, J. Research on Monitoring and Stability Evaluation of Ground Subsidence in Gypsum Mine Goaf. Front. Environ. Sci. 2023, 10, 1097874. [Google Scholar] [CrossRef]
- Li, G.; Liu, S.; Ma, F.; Guo, J.; Hui, X. Ground Subsidence Mechanism of a Filling Mine with a Steeply Inclined Ore Body. J. Mt. Sci. 2023, 20, 2358–2369. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Hu, Y.; Zhou, C.; Zhang, H. Numerical Investigation on Stratum and Surface Deformation in Underground Phosphorite Mining Under Different Mining Methods. Front. Earth Sci. 2022, 10, 831856. [Google Scholar] [CrossRef]
- Shi, K.; Wang, S.; Liu, X.; Ma, W.; Chang, Y. Surface Movement and Stability Analysis of Buildings Above Mined-Out Areas. J. Eng. Sci. Technol. Rev. 2024, 17, 228–234. [Google Scholar] [CrossRef]
- Li, H.; Jin, L.; Liu, P. Analysis of Soil Slope Stability Under Underground Coal Seam Mining Using Improved Radial Movement Optimization with Lévy Flight. Mathematics 2024, 12, 1566. [Google Scholar] [CrossRef]
- Jia, H.; Yan, B.; Guan, K.; Liu, H.; Wu, Q.; Yin, Y.; Liu, H. Stability Analysis of Shallow Goaf Based on Field Monitoring and Numerical Simulation: A Case Study at an Open-Pit Iron Mine, China. Front. Earth Sci. 2022, 10, 897779. [Google Scholar] [CrossRef]
- Dai, G.; Li, H.; Liu, C.; Li, H.; Chang, Y.; Chen, Y.; Gao, Y.; Yuan, Y.; Huo, W. Goaf Site Stability Detection in the Overlap Area of Coal Mining Subsidence and Urban Construction. Adv. Civ. Eng. 2024, 2024, 5375733. [Google Scholar] [CrossRef]
- Chen, S.J.; Yin, D.W.; Cao, F.W.; Liu, Y.; Ren, K.Q. An Overview of Integrated Surface Subsidence-Reducing Technology in Mining Areas of China. Nat. Hazards 2016, 81, 1129–1145. [Google Scholar] [CrossRef]
- Liu, H.; Deng, X.; Shi, X.; Wang, Z.; Jia, N.; Yilmaz, E.; Bian, L. A New Index and Control Method of Filling Effect for Cemented Paste Backfill in Coal Mines. Int. J. Min. Reclam. Environ. 2023, 37, 805–825. [Google Scholar] [CrossRef]
- Bai, E.; Guo, W.; Tan, Y.; Li, X.; Shen, C.; Ma, Z. Green Coal Mining Under Buildings by Overburden Grout Injection for Coalmine Sustainable Development of Central China. Heliyon 2023, 9, e18965. [Google Scholar] [CrossRef]
- Gong, Y.; Zha, J.; Guo, Q.; Guo, G. A New Indicator for Estimating the Degree of Mining-Induced Land Subsidence: The Overburden’s Average GSI Value. Sci. Rep. 2024, 14, 332. [Google Scholar] [CrossRef]
- Ma, J.; Ma, C.; Liu, T.; Zhu, X.; Li, S.; Jin, L. Preferential Evaluation of Coal Filling Mining Scheme Under Building Pressure Based on Improved Grey Target Decision-Making Model of Game Theory. Sci. Rep. 2024, 14, 15686. [Google Scholar] [CrossRef]
- Zhao, K.; Liang, N.; Zeng, P.; Wang, W.; Gong, C.; Xiong, L.; Liu, H. Research on Optimization and Numerical Simulation of Layout Scheme of Mining Approach in Downward Slicing and Filling Method. Appl. Sci. 2023, 13, 8688. [Google Scholar] [CrossRef]
- Li, C.; Chen, D.; Yang, K. Filling Parameters and Process Optimization of Mining–Filling Synergistic Coal-Based Solid Waste Paste in Renjiazhuang Mine. Front. Mater. 2023, 10, 1234145. [Google Scholar] [CrossRef]
- Liu, Y.-F.; Wu, X.-H.; Zhu, T.; Wang, X.-J.; Zhang, G.-Y.; Wang, Z.-G. Influence of Mechanical Properties of Filling Paste on Overlying Strata Movement and Surface Settlement. Shock Vib. 2022, 2022, 4687200. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, M.; Hu, G.; Guan, K. Simulations of Goaf Surface Subsidence via Filling Control. PLoS ONE 2022, 17, e0261740. [Google Scholar] [CrossRef]
- Peck, R.B. Deep excavation and tunneling in soft ground. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico, 1969; pp. 225–281. [Google Scholar]
- Fan, H.; Deng, K. DInSAR Information Extraction Method for Surface Subsidence Monitoring in Mining Area; China University of Mining and Technology Press: Xuzhou, China, 2018; pp. 16–17. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).