Research on Mechanical Properties of Core-Filled Desulfurized Gypsum Masonry
Abstract
1. Introduction
2. Test Overview
2.1. Specimen Design
2.2. Test Procedure
2.3. Failure Mode
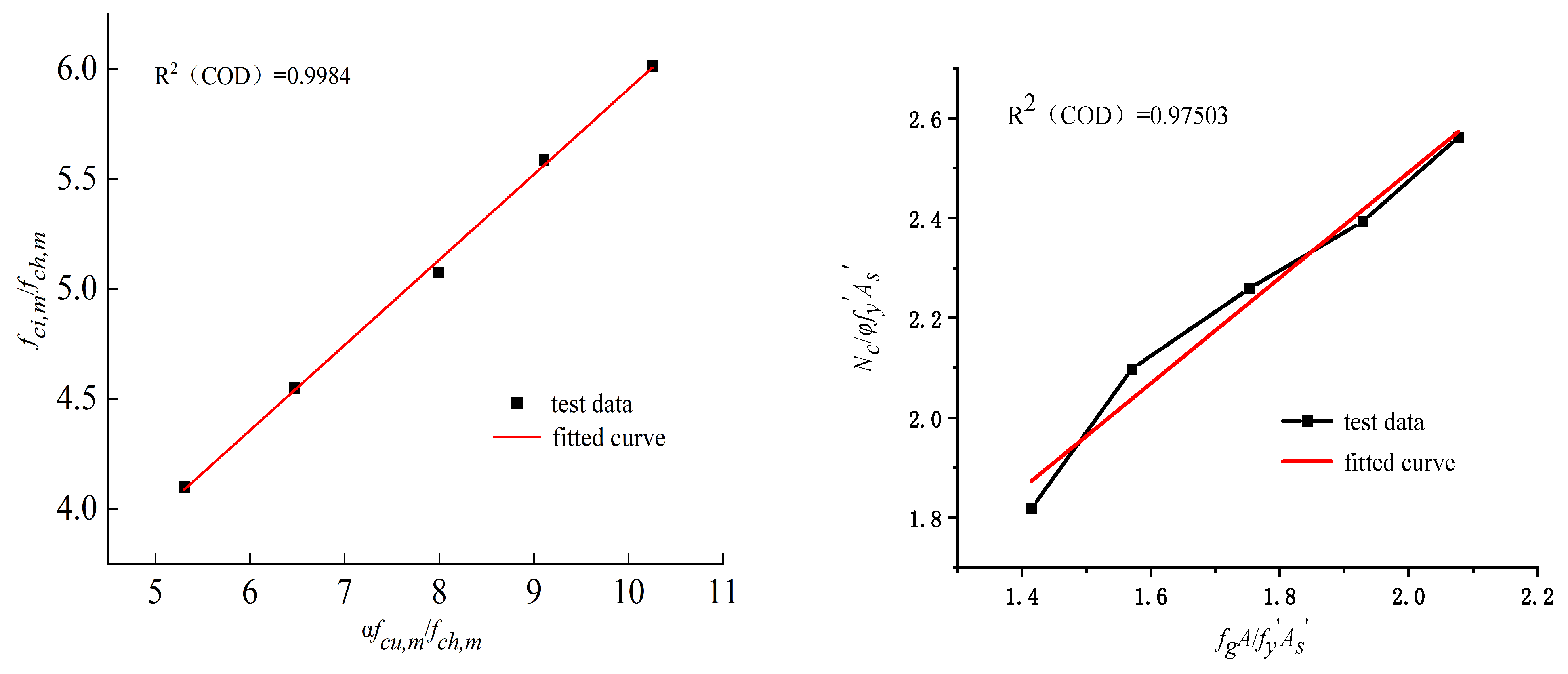
3. Compressive Strength Calculation Formula
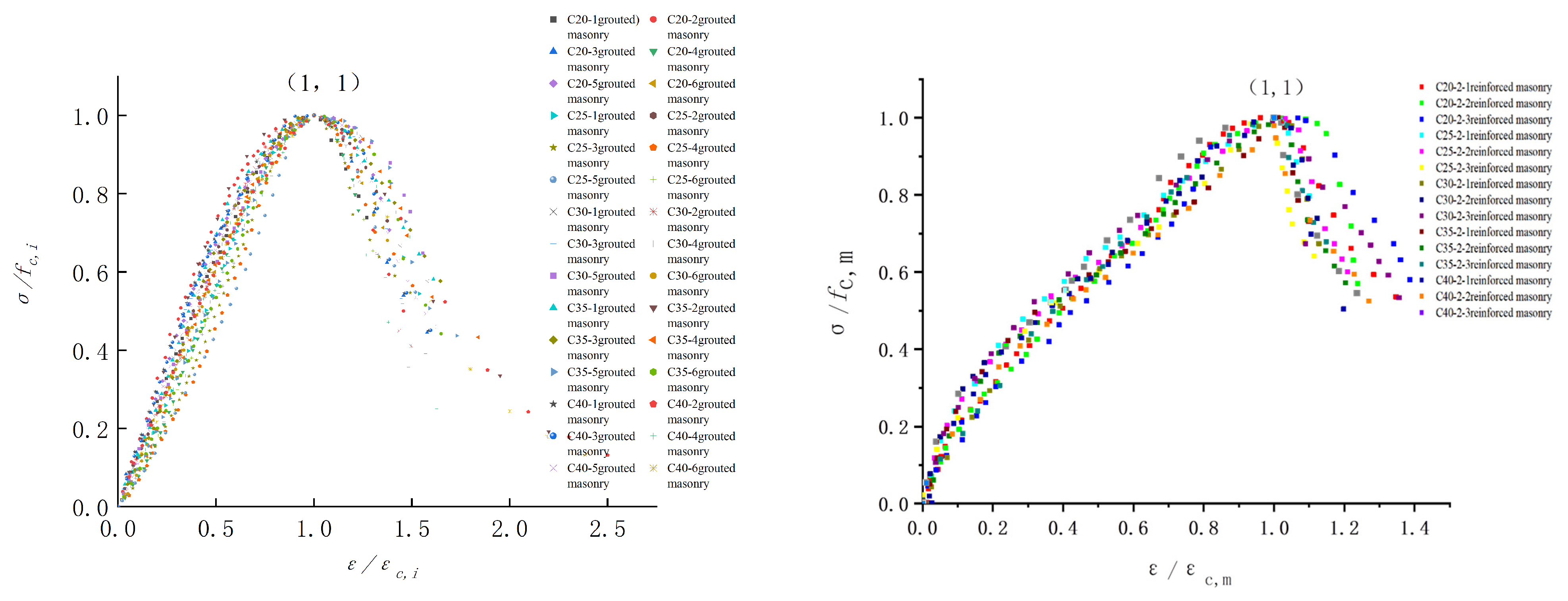
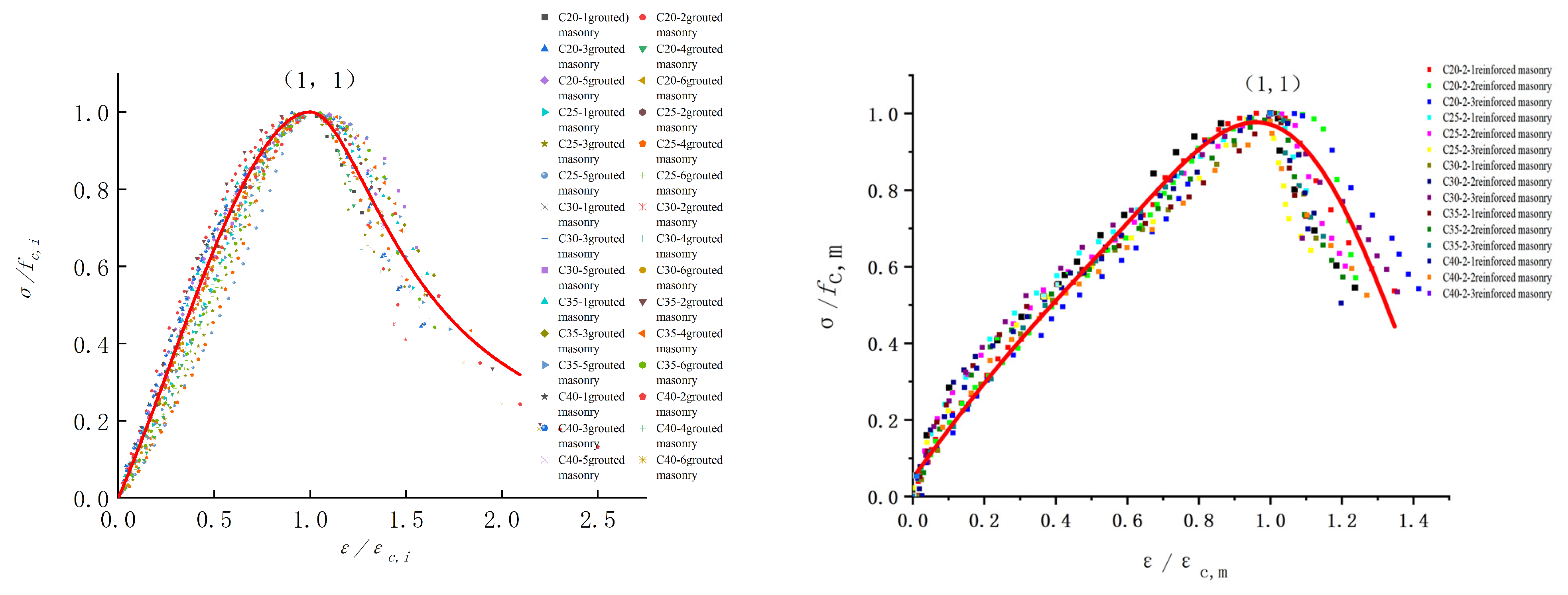
4. Elastic Modulus Calculation Formula
5. Conclusions
- (1)
- The calculation of the compressive strength of new high-precision gypsum core-filled masonry blocks and reinforced masonry blocks using the standard formula shows significant errors and tends to be unsafe.
- (2)
- Based on the test observations, the grouted masonry and reinforced masonry specimens undergo three main stages during the entire compression process: the elastic stage, the elastoplastic stage, and the softening stage. The failure process of grouted masonry and reinforced masonry exhibits distinct phases, with crack development and outer wall spalling being the key factors leading to the reduction in load-bearing capacity. The performance of the core column and steel reinforcement plays a decisive role in the final failure mode.
- (3)
- Based on the test results, this paper proposes the compressive strength calculation Formula (10) for core-filled masonry and the compressive strength calculation Formula (11) for reinforced masonry. The calculated values from Formulas (10) and (11) are in good agreement with the experimental values, providing a new basis and reference for calculating the compressive strength of such masonry. This solves the problem of compressive strength design for new high-precision desulfurized gypsum masonry blocks combined with core-filled concrete when used in load-bearing walls.
- (4)
- Since there is no unified constitutive model for the compressive stress–strain relationship of masonry structures and research on the constitutive relationship of gypsum masonry is relatively limited, a regression analysis of the test data was conducted, resulting in the elastic modulus calculation Formula (18) for grouted masonry and the compressive strength calculation Formula (19) for reinforced masonry. The calculated values from Formulas (18) and (19) align well with the test values. This provides a new basis and reference for calculating the elastic modulus of such masonry. This provides a theoretical foundation for the better application of masonry blocks in practical engineering.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Maiti, S.; Jain, N.; Malik, J. A comprehensive review of flue gas desulphurized gypsum: Production, properties, and applications. Constr. Build. Mater. 2023, 393, 131918. [Google Scholar]
- Guadagnuolo, M.; Aurilio, M.; Basile, A.; Faella, G. Modulus of elasticity and compressive strength of tuff masonry: Results of a wide set of flat-jack tests. Buildings 2020, 10, 84. [Google Scholar] [CrossRef]
- Cascardi, A.; Micelli, F.; Aiello, M.A. Unified model for hollow columns externally confined by FRP. Eng. Struct. 2016, 111, 119–130. [Google Scholar] [CrossRef]
- Mohamad, G.; Lourenço, P.B.; Roman, H.R. Mechanics of hollow concrete block masonry prisms under compression: Review and prospects. Cem. Concr. Compos. 2007, 29, 181–192. [Google Scholar] [CrossRef]
- Köksal, H.O.; Karakoç, C.; Yildirim, H. Compression behavior and failure mechanisms of concrete masonry prisms. J. Mater. Civ. Eng. 2005, 17, 107–115. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, F.; Zhu, F.; Yang, X. Stress–strain model for hollow concrete block masonry under uniaxial compression. Mater. Struct. 2017, 50, 106. [Google Scholar] [CrossRef]
- Priestley, M.J.N.; Elder, D.M. Stress-strain curves for unconfined and confined concrete masonry. J. Proc. 1983, 80, 192–201. [Google Scholar]
- Fei, Z. Research on the Mechanical Properties of Grouted Block Masonry and Reinforced Block Masonry. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2017. (In Chinese). [Google Scholar]
- Liu, X.; Wu, F.; Li, J.; Xu, J. Study on Compressive Performance of New Concrete Horizontal Hole Hollow Block Sandwich Walls. J. Anhui Inst. Archit. Ind. (Nat. Sci. Ed.) 2013, 21, 40–44. (In Chinese) [Google Scholar]
- Zahra, T.; Thamboo, J.; Asad, M. Compressive strength and deformation characteristics of concrete block masonry made with different mortars, blocks and mortar beddings types. J. Build. Eng. 2021, 38, 102213. [Google Scholar] [CrossRef]
- Lv, W.; Lv, W. Calculation of Compressive Strength of Grouted Concrete Block Masonry. Ind. Constr. 2009, 39, 106–109. [Google Scholar]
- Cheng, C.; Wu, M.; Sun, H. Test Study on Compressive Strength and Elastic Modulus of Grouted Concrete Small Block Masonry. Sichuan Build. Sci. 2003, 29, 56–59. [Google Scholar]
- Sun, H. Test Study on Basic Mechanical Properties and Shear Resistance of Reinforced Masonry Wall Panels. Struct. Eng. 2003, 5, 25–28. (In Chinese) [Google Scholar]
- Mahrous, A.; AbdelRahman, B.; Galal, K. Experimental investigation of the effects of different reinforcement configurations on the shear strength of reinforced concrete block masonry. Eng. Struct. 2025, 322, 118925. [Google Scholar] [CrossRef]
- Xu, T.; Tang, D. Experimental study on the mechanical behavior of eccentrically compressed reinforced block masonry columns. Build. Blocks Block Build. 2004, 9–12. (In Chinese) [Google Scholar]
- Hu, J. Test Research on Out-of-Plane Eccentrically Compressed Reinforced Masonry Wall Panels. Master’s Thesis, Tongji University, Shanghai, China, 2006. (In Chinese). [Google Scholar]
- Wang, J.; Wang, X.; Duan, Y.; Su, Y.; Yi, X. The investigation on mechanical performances of high-strength steel reinforced concrete composite short columns under axial load. Materials 2022, 15, 329. [Google Scholar] [CrossRef]
- Dhanasekar, M.; Shrive, N.G. Strength and Deformation of Confined and Unconfined Grouted Concrete Masonry. ACI Struct. J. 2002, 99, 819–826. [Google Scholar]
- Qian, J.R.; Chen, L.R.; Zhou, D.L. Central compression behavior of concrete columns confined by ordinary stirrups. Tsinghua Sci. Technol 2002, 42, 1369–1373. [Google Scholar]
- Marvel, L.; Doty, N.; Lindquist, W.; Hindi, R. Axial behavior of high-strength concrete confined with multiple spirals. Eng. Struct. 2014, 60, 68–80. [Google Scholar] [CrossRef]
- Zheng, X. Test Study on Axial Compressive Performance of Block Masonry with Confined Core Columns and Spiral Hoops. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2018. (In Chinese). [Google Scholar]
- Eltaly, B.A.; Shaheen, Y.B.; EL-boridy, A.T.; Fayed, S. Ferrocement composite columns incorporating hollow core filled with lightweight concrete. Eng. Struct. 2023, 280, 115672. [Google Scholar] [CrossRef]
- Wei, X.; Li, Y. Analysis of the Advantages of Prefabricated Walls Using Quick-Assembly High-Precision Desulfurized Gypsum Lightweight Blocks. Constr. Technol. 2020, 49, 1055–1057. (In Chinese) [Google Scholar]
- GB/T 50129-2011; Standard for Test Methods of Basic Mechanical Properties of Masonry. GB Standards: Beijing, China, 2011. (In Chinese)
- JGJ 55-2011; Specification for Mix Proportion Design of Ordinary Concrete. Chinese Standard: Beijing, China, 2011. (In Chinese)
- Hognestad, E. Confirmation of inelastic stress distribution in concrete. J. Struct. Div. 1957, 83, 1189. [Google Scholar] [CrossRef]
- Guo, Z. Strength and Constitutive Relationship of Concrete—Principles and Applications; China Architecture Building Press: Beijing, China, 2004; pp. 35–38. (In Chinese) [Google Scholar]






| Specimen Number | Age (In Days) | Cement (kg/m3) | Water (kg/m3) | Gravel (kg/m3) | Sand (kg/m3) | Average Compressive Strength (MPa) |
|---|---|---|---|---|---|---|
| C20 | 28 | 15.34 | 18.57 | 21.04 | 21.04 | 14.95 |
| C25 | 28 | 12.63 | 12.63 | 12.63 | 12.63 | 18.24 |
| C30 | 28 | 46.94 | 45.30 | 44.03 | 44.03 | 22.52 |
| C35 | 28 | 45.10 | 43.52 | 42.31 | 42.31 | 25.66 |
| C40 | 28 | 15.34 | 252.5 | 832.4 | 799.8 | 28.89 |
| Masonry Group | Average Compressive Strength Test Value (MPa) | Code-Specified Value (MPa) | Ratio of the Average Compressive Strength Test Value to the Code-Specified Value |
|---|---|---|---|
| C20 grouted masonry | 5.45 | 5.78 | 0.94 |
| C25 grouted masonry | 6.05 | 6.75 | 0.90 |
| C30 grouted masonry | 6.75 | 8.03 | 0.84 |
| C35 grouted masonry | 7.43 | 8.96 | 0.83 |
| C40 grouted masonry | 8.00 | 9.92 | 0.80 |
| Masonry Group | Average Compressive Strength Test Value (MPa) | Code-Specified Value (MPa) | Ratio of the Average Compressive Strength Test Value to the Code-Specified Value |
|---|---|---|---|
| C20 Reinforced Masonry | 6.90 | 8.40 | 0.82 |
| C25 Reinforced Masonry | 7.96 | 9.00 | 0.89 |
| C30 Reinforced Masonry | 8.57 | 9.68 | 0.88 |
| C35 Reinforced Masonry | 9.08 | 10.35 | 0.88 |
| C40 Reinforced Masonry | 9.72 | 10.92 | 0.89 |
| Specimen Group | ||
|---|---|---|
| C20 Grouted Masonry | 4.10 | 5.31 |
| C25 Grouted Masonry | 4.55 | 6.47 |
| C30 Grouted Masonry | 5.08 | 7.99 |
| C35 Grouted Masonry | 5.59 | 9.11 |
| C40 Grouted Masonry | 6.02 | 10.25 |
| Specimen Group | ||
|---|---|---|
| C20 Reinforced Masonry | 1.42 | 1.82 |
| C25 Reinforced Masonry | 1.57 | 2.10 |
| C30 Reinforced Masonry | 1.75 | 2.26 |
| C35 Reinforced Masonry | 1.93 | 2.39 |
| C40 Reinforced Masonry | 2.08 | 2.56 |
| Specimen Group | Specimen Number | Grouting Ratio α | Compressive Strength of Hollow Masonry (MPa) | Compressive Strength of Core Columns (MPa) | Test Value of Compressive Strength of Grouted Masonry (MPa) | Calculated Value of Compressive Strength of Grouted Masonry (MPa) | |
|---|---|---|---|---|---|---|---|
| C20 | 20-1 | 0.472 | 1.33 | 14.95 | 5.77 | 5.45 | 1.06 |
| 20-2 | 5.23 | 0.96 | |||||
| 20-3 | 5.5 | 1.01 | |||||
| 20-4 | 4.94 | 0.91 | |||||
| 20-5 | 5.26 | 0.96 | |||||
| 20-6 | 5.82 | 1.07 | |||||
| C25 | 25-1 | 0.472 | 1.33 | 18.24 | 6.00 | 6.06 | 0.99 |
| 25-2 | 6.42 | 1.06 | |||||
| 25-3 | 6.11 | 1.01 | |||||
| 25-4 | 6.07 | 1.00 | |||||
| 25-5 | 5.69 | 0.94 | |||||
| 25-6 | 6.03 | 1.00 | |||||
| C30 | 30-1 | 0.472 | 1.33 | 22.52 | 6.41 | 6.85 | 0.94 |
| 30-2 | 6.68 | 0.98 | |||||
| C30 | 30-3 | 0.472 | 1.33 | 22.52 | 6.90 | 6.85 | 1.01 |
| 30-4 | 7.20 | 1.05 | |||||
| 30-5 | 6.87 | 1.00 | |||||
| 30-6 | 6.41 | 0.94 | |||||
| C35 | 35-1 | 0.472 | 1.33 | 25.66 | 7.40 | 7.42 | 1.00 |
| 35-2 | 7.98 | 1.07 | |||||
| 35-3 | 7.45 | 1.00 | |||||
| C35 | 35-4 | 0.472 | 1.33 | 25.66 | 7.51 | 7.42 | 1.01 |
| 35-5 | 7.39 | 1.00 | |||||
| 35-6 | 6.83 | 0.92 | |||||
| C40 | 40-1 | 0.472 | 1.33 | 28.89 | 7.98 | 8.02 | 1.00 |
| 40-2 | 8.08 | 1.01 | |||||
| 40-3 | 8.12 | 1.01 | |||||
| 40-4 | 8.05 | 1.00 | |||||
| 40-5 | 8.19 | 1.02 | |||||
| 40-6 | 8.27 | 1.03 | |||||
| Specimen Group | Specimen Number | Height-to Thickness Ratio | Stability Factor of Reinforced Masonry | Vertical Reinforcement Cross-Sectional Area (mm2) | Cross-Sectional Area of Vertical Reinforcement (mm2) | Test Value of Compressive Strength of Reinforced Masonry (MPa) | Calculated Value of Compressive Strength (MPa) | |
|---|---|---|---|---|---|---|---|---|
| C20 | C20-2-1 | 3.85 | 0.985 | 120,000 | 1231.5 | 6.90 | 7.13 | 0.97 |
| C20-2-2 | 6.94 | 0.97 | ||||||
| C20-2-3 | 6.87 | 0.96 | ||||||
| C25 | C25-2-1 | 3.85 | 0.985 | 120,000 | 1231.5 | 8.02 | 7.13 | 1.03 |
| C25-2-2 | 7.98 | 1.03 | ||||||
| C25 | C25-2-3 | 3.85 | 0.985 | 120,000 | 1231.5 | 7.87 | 7.13 | 1.01 |
| C30 | C30-2-1 | 3.85 | 0.985 | 120,000 | 1231.5 | 8.67 | 7.13 | 1.02 |
| C30-2-2 | 8.55 | 1.01 | ||||||
| C30-2-3 | 8.49 | 1.00 | ||||||
| C35 | C35-2-1 | 3.85 | 0.985 | 120,000 | 1231.5 | 9.12 | 7.13 | 0.99 |
| C35-2-2 | 9.18 | 1.00 | ||||||
| C35-2-3 | 8.95 | 0.97 | ||||||
| C40 | C40-2-1 | 3.85 | 0.985 | 120,000 | 1231.5 | 9.77 | 7.13 | 1.00 |
| C40-2-2 | 9.73 | 0.99 | ||||||
| C40-2-3 | 9.67 | 0.99 |
| Specimen Group | Specimen Number | Strain (%) | Axial Strain of 0.4 (%) | Test Value of Elastic Modulus (MPa) | Average Test Value of Elastic Modulus (MPa) | Compressive Strength (MPa) | Calculated Value of Elastic Modulus (MPa) | |
|---|---|---|---|---|---|---|---|---|
| C20 | C20-1 | 0.215 | 0.065 | 3675.34 | 3985.44 | 5.77 | 3597.46 | 1.02 |
| C20 | C20-2 | 0.174 | 0.044 | 4754.55 | 3985.44 | 5.23 | 4034.93 | 1.18 |
| C20-3 | 0.166 | 0.044 | 4966.14 | 5.50 | 4450.29 | 1.12 | ||
| C20-4 | 0.177 | 0.067 | 2946.43 | 4.94 | 3665.29 | 0.80 | ||
| C20-5 | 0.182 | 0.050 | 4208.00 | 5.26 | 3881.93 | 1.08 | ||
| C20-6 | 0.215 | 0.069 | 3362.19 | 5.82 | 3617.89 | 0.93 | ||
| C25 | C25-1 | 0.136 | 0.049 | 4887.98 | 4764.21 | 6.00 | 5835.19 | 0.84 |
| C25-2 | 0.147 | 0.047 | 5598.29 | 6.42 | 5841.31 | 0.96 | ||
| C25-3 | 0.126 | 0.053 | 4620.04 | 6.11 | 6241.38 | 0.74 | ||
| C25-4 | 0.125 | 0.057 | 4274.65 | 6.07 | 6109.10 | 0.70 | ||
| C25-5 | 0.112 | 0.052 | 4321.71 | 5.69 | 6361.09 | 0.68 | ||
| C25-6 | 0.126 | 0.049 | 4882.59 | 6.03 | 6250.44 | 0.78 | ||
| C30 | C30-1 | 0.130 | 0.044 | 6090.09 | 6410.23 | 6.41 | 6562.08 | 0.93 |
| C30-2 | 0.145 | 0.048 | 5778.78 | 6.68 | 6144.84 | 0.94 | ||
| C30-3 | 0.138 | 0.037 | 7439.35 | 6.9 | 6716.03 | 1.11 | ||
| C30-4 | 0.142 | 0.046 | 6315.79 | 7.20 | 6778.21 | 0.93 | ||
| C30-5 | 0.127 | 0.040 | 6870.00 | 6.87 | 7239.39 | 0.95 | ||
| C30-6 | 0.127 | 0.043 | 5967.36 | 6.41 | 6722.29 | 0.89 | ||
| C35 | C35-1 | 0.136 | 0.040 | 7344.91 | 7200.77 | 7.40 | 7299.71 | 1.01 |
| C35-2 | 0.140 | 0.038 | 8461.54 | 7.98 | 7656.30 | 1.11 | ||
| C35-3 | 0.124 | 0.040 | 7450.00 | 7.45 | 8029.41 | 0.93 | ||
| C35-4 | 0.125 | 0.043 | 6986.05 | 7.51 | 7988.69 | 0.87 | ||
| C35-5 | 0.122 | 0.045 | 6642.70 | 7.39 | 8001.25 | 0.83 | ||
| C35-6 | 0.115 | 0.043 | 6319.44 | 6.83 | 7812.55 | 0.81 | ||
| C40 | C40-1 | 0.121 | 0.031 | 10,165.61 | 9697.42 | 7.98 | 8856.45 | 1.15 |
| C40-2 | 0.107 | 0.034 | 9478.01 | 8.08 | 10,099.39 | 0.94 | ||
| C40 | C40-3 | 0.114 | 0.065 | 10,684.21 | 9697.42 | 8.12 | 9567.16 | 1.12 |
| C40-4 | 0.097 | 0.044 | 8923.08 | 8.05 | 11,060.72 | 0.81 | ||
| C40-5 | 0.120 | 0.044 | 9829.55 | 8.19 | 9158.68 | 1.07 | ||
| C40-6 | 0.105 | 0.067 | 9104.05 | 8.27 | 10,510.78 | 0.87 |
| Specimen Group | Specimen Number | Strain (%) | Compressive Strength (MPa) | Axial Strain of 0.4 (%) | Test Value of Elastic Modulus (MPa) | Calculated Value of Elastic Modulus (MPa) | |
|---|---|---|---|---|---|---|---|
| C20 | C20-2-1 | 0.16 | 6.90 | 0.047 | 5843.47 | 5889.17 | 0.99 |
| C20-2-2 | 0.15 | 6.94 | 0.045 | 6130.13 | 6564.56 | 0.93 | |
| C20-2-3 | 0.10 | 6.87 | 0.047 | 5833.10 | 8032.26 | 0.73 | |
| C25 | C25-2-1 | 0.15 | 8.02 | 0.039 | 8231.79 | 7519.19 | 1.09 |
| C25-2-2 | 0.17 | 7.98 | 0.038 | 8480.44 | 6908.01 | 1.23 | |
| C25-2-3 | 0.15 | 7.87 | 0.038 | 8205.24 | 7320.58 | 1.12 | |
| C30 | C30-2-1 | 0.16 | 8.67 | 0.038 | 9147.92 | 7669.78 | 1.19 |
| C30-2-2 | 0.15 | 8.55 | 0.038 | 9108.05 | 8044.58 | 1.13 | |
| C30-2-3 | 0.19 | 8.49 | 0.039 | 8818.03 | 6584.28 | 1.34 | |
| C35 | C35-2-1 | 0.18 | 9.12 | 0.035 | 10,298.04 | 7584.92 | 1.36 |
| C35-2-2 | 0.19 | 9.18 | 0.041 | 8932.55 | 6951.85 | 1.28 | |
| C35-2-3 | 0.15 | 8.95 | 0.042 | 8549.05 | 8161.21 | 1.05 | |
| C40 | C40-2-1 | 0.16 | 9.77 | 0.033 | 11,804.76 | 9018.46 | 1.31 |
| C40-2-2 | 0.17 | 9.73 | 0.042 | 9246.68 | 7986.89 | 1.16 | |
| C40-2-3 | 0.14 | 9.67 | 0.045 | 8598.36 | 9298.32 | 0.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Liu, S.; Zhang, C.; Li, J.; Tian, Z. Research on Mechanical Properties of Core-Filled Desulfurized Gypsum Masonry. Appl. Sci. 2025, 15, 5315. https://doi.org/10.3390/app15105315
Zhang T, Liu S, Zhang C, Li J, Tian Z. Research on Mechanical Properties of Core-Filled Desulfurized Gypsum Masonry. Applied Sciences. 2025; 15(10):5315. https://doi.org/10.3390/app15105315
Chicago/Turabian StyleZhang, Tongzhen, Shujie Liu, Chuanshuai Zhang, Jilong Li, and Zhongxi Tian. 2025. "Research on Mechanical Properties of Core-Filled Desulfurized Gypsum Masonry" Applied Sciences 15, no. 10: 5315. https://doi.org/10.3390/app15105315
APA StyleZhang, T., Liu, S., Zhang, C., Li, J., & Tian, Z. (2025). Research on Mechanical Properties of Core-Filled Desulfurized Gypsum Masonry. Applied Sciences, 15(10), 5315. https://doi.org/10.3390/app15105315






